1 Introduction

Scientists have been aware of the existence of mem-elements for two centuries [19], but they were not discussed until Chua postulated the existence of the first mem-element which represents the missing link between the charge q(t) and the flux φ(t) which is called the memristor (from memory+resistor) [8]. Recently, the theory of mem-elements was generalized [9, 23] to include higher-order elements such as the memcapacitor which offers a link between time integral of charge σ(t) and flux φ(t), and the meminductor which links charge q(t) and time integral of the flux ρ(t). The SPICE model of the mem-elements is introduced in [1, 18].

Nowadays, the mem-elements are very useful in different applications such as chaotic oscillators [5, 6], synapse modeling [14, 17], memories [16, 21], biomedical applications [7, 16], phase locked loops [24], and relaxation oscillators [11–13].

The first general meminductor model was introduced in [9] which described the nth-order current-controlled meminductive system

$$\begin{aligned} \varphi(t)&=L_m(x,i,t)i(t), \end{aligned}$$
(1a)
$$\begin{aligned} \dot{x}&=f(x,i,t), \end{aligned}$$
(1b)

where L m is the meminductance.

However, there has not been any solid-state meminductor fabricated until now. Biolek et al. introduced a meminductor model based on the idea of a simple electro-mechanical system (any other meminductor model can be analyzed by following the same procedure used in this paper) [4]. The meminductance introduced by Biolek’s L m is enclosed between the minimum meminductance L min and the maximum meminductance L max which is given as follows:

$$ L_m(t)\approx\bigl(\sqrt{L_{\min}}+x(t) ( \sqrt{L_{\max}}-\sqrt{L_{\min}}) \bigr)^2, $$
(2)

where the rate of change in the state variable x(t) is given by

$$ \frac{dx}{dt}=K_Li(t). $$
(3)

The rate of change of the state variable is directly proportional to the mobility factor K L .

Mathematical modeling of mem-elements is essential for the study of their behavior in order to easily implement them in circuits where different current and voltage signals will be applied. New definitions were defined for mem-elements like saturation time and mem-element range. These definitions are defined for the memristor in [20].

This paper is arranged as follows: Sect. 2 will discuss the mathematical meminductor model under general current excitations. Then, this model is used to develop a meminductor emulator in Sect. 3. Moreover, Sect. 4 discusses the response under DC current excitation and the saturation time of the meminductor. Then, the meminductor is subjected to a sinusoidal current source in Sect. 5 where closed form expressions for instantaneous meminductance are derived. Finally, the meminductor is subjected to non-periodic signal excitations, and the instantaneous meminductance is derived.

2 Mathematical Model of a Meminductor

In the linear circuit theory, the voltage across the conventional inductor is proportional to the rate of change of the current passing through the inductor, and the proportionality constant is the known inductance. However, the inductance of the meminductor was given by (2), and it is a function of the state variable x. Therefore, the implicit relation of the meminductance can be obtained by differentiating (2) with respect to time and substituting into (3)

$$ \frac{1}{2\sqrt{L_m(t)}}\frac{dL_m(t)}{dt}=K_L(\sqrt{L_{\max}}- \sqrt{L_{\min}})i(t). $$
(4)

By integrating both sides with respect to time, the meminductance is given by

$$ L_m(t)={\bigl(\sqrt{L_o}+K'_L q(t)\bigr)}^2 , $$
(5)

where \(K'_{L}=K_{L}(\sqrt{L_{\max}}-\sqrt{L_{\min}})\), \(q(t)=\int^{t}_{-\infty}{i(\tau)\,d\tau}\), and L o represents the initial meminductance. The instantaneous meminductance is a quadratic equation of the charge q(t). It is important to note that the effect of any initial current in the meminductor will affect the initial meminductance L o . Therefore, there is no need to study the effect of the initial current since it is inherently inside the initial meminductance.

3 Proposed Meminductor Emulator

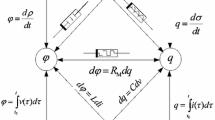
A meminductor emulator is built using a memristor and mutator to transform the memristor into a meminductor as shown in Fig. 1 [2, 22]. The relations of MR and ML are accomplished by a linear transformation which is given by the following matrix:

$$ \begin{bmatrix} v_{1}\\ i_{1} \end{bmatrix} = \begin{bmatrix} sk_x & 0 \\ 0 & k_y \end{bmatrix} \begin{bmatrix} v_{2}\\ -i_{2} \end{bmatrix}, $$
(6)

where k x and k y are real constants and their values depend on the mutator implementation. This linear transformation transforms (φ,q) to (ρ,q), which represents the constitutive relation of the meminductor, so that the meminductance is given by

$$ L_m=\frac{k_x}{k_y}R_m. $$
(7)
Fig. 1
figure 1

Proposed meminductor emulator block diagram

Full size image

According to the previous equation, to build a meminductor having the same proposed meminductance, we need to build a memristor of memristance \(R_{m}=\frac{k_{y}}{k_{x}}L_{m}\) and use (4). The memristance should be

$$ R_m=\frac{k_y}{k_x} \bigl(L_o+2K'_L \sqrt{L_o} q(t)+K^{\prime2}_L q^2(t) \bigr). $$
(8)

However, memristor samples are not commercially available, yet; thus we will use a memristor emulator instead of a solid-state memristor. Also the proposed model is different from the previous emulator models so the emulator should be modified to fit the proposed model.

Recently, different memristor emulators were introduced, showing good behavior [3, 15]; however, the most practical one was introduced in [10] where the authors implemented and tested the emulator experimentally. Despite the fact that this emulator is designed to model the memresistance R m =R s +kq(t), it should be modified to fit the proposed model. Figure 2 shows the modified memristor’s emulator where the input current of the memristor i mr is given by

$$ i_{\mathrm{mr}}=\frac{V_{\mathrm{mr}}-V_{\mathrm{fb}}}{R_s}. $$
(9)

The feedback voltage V fb is given by

$$ V_{\mathrm{fb}}= \biggl(\frac{R^2}{20R_1C_1}q_{\mathrm{mr}}(t)+ \frac{R^3}{200R^2_1C^2_1}q_{\mathrm{mr}}^2(t) \biggr)i_{\mathrm{mr}}. $$
(10)

By substituting into (9), the input voltage of the memristor V mr is given by

$$ V_{\mathrm{mr}}= \biggl(R_s+\frac{R^2}{20R_1C_1}q_{\mathrm{mr}}(t)+ \frac{R^3}{200R^2_1C^2_1}q_{\mathrm{mr}}^2(t) \biggr)i_{\mathrm{mr}}, $$
(11)

so the input memresistance is

$$ R_m= \biggl(R_s+\frac{R^2}{20R_1C_1}q_{\mathrm{mr}}(t)+ \frac{R^3}{200R^2_1C^2_1}q_{\mathrm{mr}}^2(t) \biggr). $$
(12)
Fig. 2
figure 2

Modified memristor’s emulator

Full size image

By comparing the coefficients in (12) and (8), the emulator parameters can be obtained as \(R_{s}=\frac {k_{y}}{k_{x}}L_{o}\), \(R=8\frac{k_{y}}{k_{x}}L_{o}\) and \(R_{1}C_{1}=\frac{1.6L^{3/2}_{o}}{K'_{L}}\). Figure 3 shows the transient input current and input voltage, and the I–V hysteresis of the proposed memristor emulator under current excitation with i(t)=0.5sin(200πt) mA where the circuit parameters are R s =1 kΩ,R=2 kΩ,R 1=0.5 kΩ,C 1=1 μF and R 2=1 kΩ.

Fig. 3
figure 3

Circuit model simulation of modified memristor’s emulator: (a) transient input current and voltage and (b) current–voltage hysteresis

Full size image

The designed memristor emulator is connected to the mutator to obtain the complete realization of meminductor emulator where k x and k y are equal to 0.001 and 1, respectively. Figures 4(a)–4(b) shows a transient simulation of the meminductor current I ml, voltage V ml and flux φ ml; moreover, Figs. 4(c)–4(d) show the I–V and I–φ hysteresis, respectively.

Fig. 4
figure 4

Transient simulation results of meminductor emulator

Full size image

4 Step Response

A DC current is mathematically defined by the step current i(t)=i DC u(t), where u(t) is the unit step function and the amplitude i DC may be positive or negative. By substituting into (5), the meminductance is given by

$$ L_m(t)={\bigl(\sqrt{L_o}+K'_Li_{\mathrm{DC}}t \bigr)}^2. $$
(13)

When the step input current increases, the meminductance increases in the case i DC is positive and with a rate that depends on the amplitude of the applied current until the meminductance reaches its maximum L max. Moreover, in the case of a negative applied current, the meminductance decreases, as the absolute value of the applied voltage increases until it reaches its minimum L min as shown in Figs. 5(a)–5(b) for L min, L max, L o and K L are equal to 0.1 mH, 10 mH, 1 mH and 10 A−1 s−1, respectively (these values are used throughout the paper).

Fig. 5
figure 5

Step response of meminductor due to DC current excitation for (a) positive current and (b) negative current

Full size image

From the previous discussion, there is a certain time duration in which the meminductance reaches its boundary value, either maximum or minimum, depending on the sign of the input voltage so the saturation time should be calculated. The saturation time is given by

$$ t_{\mathrm{sat}}=\frac{\sqrt{L_{\mathrm{bd}}}-\sqrt{L_o}}{K'_Li_{\mathrm{DC}}}, $$
(14)

where L bd represents the boundary meminductance at either L max or L min depending on the polarity of the applied current. The maximum saturation time is reached when the meminductor changes its state from the minimum to maximum value, or vice versa. Therefore, the maximum saturation time is

$$ t_{\mathrm{sat}_{\max}}=\frac{\sqrt{L_{\max}}-\sqrt{L_{\min}}}{K'_L |i_{\mathrm{DC}}|}=\frac{1}{K_L|i_{\mathrm{DC}}|}, $$
(15)

where the maximum saturation time is inversely proportional to the amplitude and mobility factor of the meminductor.

5 Sinusoidal Response

The inductor has a linear relation between flux φ(t) and current i(t) and a circular relation between voltage V(t) and current i(t). But the meminductor has a pinched hysteresis between flux φ(t) and current i(t) as shown in Fig. 6(a) and an nonlinear persimmon-shaped relation between voltage V(t) and current i(t) as shown in Fig. 6(b). The pinched hysteresis shrinks until it becomes linear by increasing the applied frequency, and the elliptic relation expands till it becomes circular as shown in Figs. 6(a) and 6(b), respectively. As obvious from Fig. 6(b), the I–V hysteresis has an even symmetry around the voltage axis.

Fig. 6
figure 6

Sinusoidal response of meminductor for different frequencies: (a) flux–current hysteresis and (b) current–voltage hysteresis

Full size image

Assuming a single tone current is applied on the meminductor given by i(t)=i o sin(ω o t), and then by substituting into (5), the meminductance is given by

$$ L_m(t)= \biggl(\sqrt{L_o}+2K'_L \frac{i_0}{{\omega}_o}\sin^2 \biggl(\frac{{\omega}_ot}{2} \biggr) \biggr)^{2}. $$
(16)

The meminductance range decreases until it reaches a value of zero where the meminductance will not change its initial value L o by increasing the applied frequency as shown in Fig. 7 at L o =1 mH for positive or negative applied current.

Fig. 7
figure 7

Meminductance range versus applied frequency

Full size image

6 Periodic Signals Response

Any periodic signal can be expanded using Fourier series expansion as a sum of a DC signal and sinusoidal signals (sines and cosines)

$$ i(t)=a_o+\sum^{\infty}_{n=1}{a_n{ \cos(n{\omega}_ot)}+b_n \sin(n{\omega }_ot)}, $$
(17)

where a o represents the average of the applied signal (DC component) and a n and b n represent the amplitude of the sinusoidal signals with different frequencies. By substituting (17) into (5), the instantaneous meminductance is given by

$$ L_m(t)= \Biggl(\sqrt{L_o}+k'_L \Biggl(a_ot+\sum^{\infty}_{n=1} \frac{1}{n{\omega}_o} \biggl(a_n{\sin(n{\omega}_ot)} +2b_n \sin\biggl(\frac{n{\omega}_ot}{2} \biggr) \biggr) \Biggr) \Biggr)^2. $$
(18)

The DC component is represented by a o which causes the meminductor to saturate, reaching one of its boundaries, so the average number of periods where the meminductor saturates is given by:

$$ N_{\mathrm{sat}}=\frac{\sqrt{L_{\mathrm{bd}}}-\sqrt{L_o}}{K'_La_oT}. $$
(19)

For example, we will apply this concept to the square wave signal in the following subsection.

6.1 Square Wave Signal Response

The meminductor is biased by a square wave signal which is defined by

$$ i(t)= \begin{cases} i_{o1}&0<\tau<\alpha T, \\ i_{o2}&\alpha T<\tau<T, \end{cases} \quad0<\alpha<1, $$
(20)

where τ=tmod(T). The applied signal alternates between positive and negative voltages with sharp transitions. By applying Fourier series expansion to the input signal, the coefficients are given by

$$\begin{aligned} &a_o=\alpha i_{o1}+(1-\alpha)i_{o2}, \end{aligned}$$
(21a)
$$\begin{aligned} &a_n=\frac{(i_{o1}-i_{o2})}{n\pi}{\sin(2\alpha n\pi),} \end{aligned}$$
(21b)
$$\begin{aligned} &b_n=\ \frac{(i_{o1}-i_{o2})}{n\pi}\bigl(1-{\cos(2\alpha n\pi)}\bigr). \end{aligned}$$
(21c)

As obvious from (18), the DC term, a o , leads to the saturation, so the square wave signal shows two cases:

  1. 1.

    Zero DC component means that the accumulated charge after each period is zero, so \(\frac{i_{o1}}{i_{o2}} =\frac{\alpha-1}{\alpha }\) should be satisfied. Figure 8(a) shows the instantaneous meminductance under a square wave input with i o1, i o2 and α equal to 10 mA, −10 mA, and 0.5, respectively, where the meminductance increases and decreases depending on the sign of the applied current with nonlinear curves. Also its hysteresis curve is shown in Fig. 8(b). The instantaneous meminductance expression can be written by using the behavior of the square signal where the discussed step response can be used periodically, by using the last-obtained value as the initial value of the next step. So the meminductance changes up and down as the current changes periodically, which is given during any period by

    $$ L_m(t)= \begin{cases} (\sqrt{L_o}+K'_Li_{o1}\tau )^2,&0<\tau<\alpha T, \\ (\sqrt{L_o}+K'_L (i_{o1}\alpha T+i_{o2}(\tau-\alpha T) ) )^2,&\alpha T<\tau<T. \end{cases} $$
    (22)
    Fig. 8
    figure 8

    Square wave response for different frequencies: (a) instantaneous meminductance and (b) flux–current hysteresis

    Full size image
  2. 2.

    Nonzero DC component means that the accumulated charge, due to DC components, leads the meminductor become saturated. Figure 9 shows that the instantaneous meminductance increases with time until it reaches the maximum meminductance L max where i o1,i o2 and α are equal to 10 mA, −10 mA, and 0.6, respectively. The meminductance reaches saturation after an average number of periods which is given by

    $$ N_{\mathrm{sat}}=\frac{\sqrt{L_{\mathrm{bd}}}-\sqrt{L_o}}{K'_LT(\alpha i_{o1}+(1-\alpha)i_{o2})}. $$
    (23)
    Fig. 9
    figure 9

    Instantaneous meminductance for different frequencies under square wave signal with DC component

    Full size image

7 Conclusion

A new emulator was introduced to emulate the behavior of the meminductor depending on the proposed mathematical model. The response of the meminductor was discussed under periodic current excitations. Moreover, expressions for instantaneous meminductance were provided for a step current signal, where the saturation time formula was derived. Also a closed form expression for any periodic signal was derived using Fourier series expansion. An example was also introduced and analyzed when a square wave signal was used with and without a DC component.