1 Introduction

Recently, increasing efforts have been made to construct new chaotic dynamics from simple models playing on the equilibrium types [1, 2] that can be without equilibrium points [3, 4], with equilibrium surfaces [5], equilibrium curves [6] with only stable equilibrium Points [7], or even non-hyperbolic curves. Many of these examples belong to a new category of dynamic systems known as hidden attractors [3, 8, 9]. This type of dynamics is very recent and the causes are not yet well defined in the literature. However, all of the work above has focused mainly on the structure and characteristics of equilibrium points, while there are other important features in chaotic systems and one of them is innovation as ruled by Sprott [10]. So, new chaotic systems are created without reference to the equilibrium points and with particularly rich dynamics: with multi-scroll attractors for example [11,12,13,14,15] or even with the simplest equations possible and imaginable [16,17,18,19,20]. Other new systems are obtained by modifying a famous oscillator and underlining the richness of its dynamics such as Chua circuit [21, 22], Colpitts oscillators [23], Lorenz system [24], Rössler system [25], and Van der Pol-Duffing circuit [26]. The oscillator known as Colpitts was reported in 1918 by Edwin H [27]. Colpitts. This oscillator has been widely used in electronics and its related fields due to its characteristics of frequency stability, wide frequency range, simple circuit and even in generating undistorted sine wave signals. It was in 1994 that Kennedy reported that the Colpitts oscillator can generate chaotic behavior [28]. Chaos then became a reference in nonlinear research and widely exploited in various fields of engineering. An ontological review of possible topologies over the 100 years of the Colpitts oscillator is recently reviewed by Azadmehr and colleagues [29]. In this work, 30 different types of circuits related to the Colpitts oscillator are listed. The authors showed the different variations and improvements undergone by Colpitts oscillators ranging from vacuum tube bipolar to modern CMOS. Thus, Colpitts oscillators can be made using different types of gain stages including common source, common gate, common drain, and common emitter as well as their equivalents in bipolar technology and many other techniques. Similarly, the main characteristics of Colpitts oscillators are analyzed by Hemmati and Dehghani [30]. These authors investigated the different CMOS Colpitts oscillator topologies, including single-ended and differential configurations. Thus, different coupling methods, used for the coupling of VCOs and classification of Colpitts QVCOs have been introduced.

There is little knowledge about the specific characteristics of memory element-based chaotic oscillators; so, a rarer but very interesting perspective of innovation is to study the impact of the addition of nonlinear memory elements on the dynamics of some existing system.

Chua and colleagues have proposed the concept of meminductor and memcapacitor generalized from the memristor in 2009 [31], whose properties depend on the history of the device; this property makes them be very special components. Although actual memcapacitors have not been manufactured so far, potential importance has attracted more and more attention. Unlike the hysteresis loop of the memristor which is done according to the charge and voltage, a memcapacitor appears as a hysteretic loop between current and voltage.

Nowadays, potential research based on memory components is growing. These components should be memory storage devices useful in the design of computers. This implies low energy consumption and less thermal design to manage. Memory elements like the memristor, meminductor, and memcapacitor are typically nonlinear and easy to use as generators of chaotic vibration signals [32, 33]. Several challenge situations arise in particular, investigating chaotic systems/circuits in order to better master them, to develop nonlinear science. Prevent damage from chaotic phenomena in various applications. Produce chaotic signals using memory components like memcapacitor which are useful and potential in many applications such as aerospace industry, secure communications, and many others [34, 35]. Memory elements (commonly referred to as mem-elements) including the memristor, memcapacitor, and meminductor are considered as key to the development of new generation of intelligent and neuromorphic devices [36,37,38]. These mem-elements can also be used to mimic biological neural synapses, describe electromagnetic induction effects, and simulate neuronal magnetic coupling. Dynamic circuits based on Memcapacitors also find their applications in an adaptive learning circuit because these circuits perform satisfactorily for a wide frequency range and pass the non-volatility test [39]. Memcapacitive systems can be used in information security because they can resist various attacks including brute force attacks due to the high number of state variables of nonlinear systems corresponding to the large space of the secret key [40, 41]. Memory elements also find their applications in biology in neural synapses. In this application, these elements can be used to reinforce the memory of synapses thus increasing the autonomous capacity of artificial intelligence [42,43,44].

The Colpitts oscillator is widely investigated in the literature starting from the standard transistor oscillator circuit, with operational amplifier but very little work on the Colpitts oscillator with memcapacitor [9, 23, 45,46,47,48,49]. In this paper, the appealing aspect of memcapacitor due to its functional and dynamic similarities to the memristor but with much lower power requirements is used to give new life to the classic and well-known Colpitts oscillator. From this alliance was born a new chaotic circuit based on memcapacitors. The memcapacitor-based oscillator presented in [50] has only two components compared to the one proposed in this work which has rather three components; but it is good to note that in the present work, the novelty is not mainly to propose a circuit with the smallest possible number of components as in [50]. The objective of this work is to modify Colpitts’ LC tank circuit by replacing its two normal linear capacitors with two nonlinear memcapacitors blocks, in order to obtain a new simple architecture of the Colpitts oscillator based on memcapacitors and thus to enrich the literature with a new type of Colpitts circuit with very interesting properties.

Another contribution of this work is the choice of memcapacitors with respect to the nature of memcapacitance (its nonlinearity). The memcapacitance used in [50] has a nonlinear function of degree 4 whereas that used in the present work is quadratic and therefore simpler. A quadratic nonlinearity is recommended compared to others (hyperbolic, trigonometric, exponential, and other functions) that take enough execution time in encryption processes [51,52,53]. As a result, the chaotic system-based encryption techniques with the proposed circuit will have a reasonable runtime and be sufficiently robust against brute-force, known-plaintext, and chosen-plaintext attacks.

Compared to the standard chaotic Colpitts circuit, which usually consists of an active component (bipolar junction transistor, field effect transistor, operational amplifier, etc.) connected to an LC tank oscillator circuit, the Colpitts oscillator based on memcapacitors proposed in this work is much simpler, since it does not need either the capacitors or any active component based on a bipolar junction transistor, field-effect transistor, or operational amplifier to operate. This simplicity comes to the fact that the two introduced memcapacitors blocks perform three functions simultaneously, namely amplification, nonlinearity, and capacitance. To the best of our knowledge, the structure of the electrical circuit proposed in this work is different from all the circuits with two memcapacitors proposed in the literature. The particularities of the proposed circuit are summarized as follows:

  • The simple circuit proposed is designed from the LC-tank circuit of Colpitts. It consists only of three dynamic elements, including two memcapacitors blocks and an inductor;

  • The proposed circuit although simple presents chaos and very complex dynamic behaviors including, offset-boosting, multistability, and many others;

  • The mathematical model resulting from the proposed circuit is a simple third-order equation system that is easy to manipulate both analytically and numerically;

  • Multistability in this circuit gives rise to the coexistence of two, three, and four, attractors, which is usually difficult to find in such circuits.

  • It is suitable for engineering applications such as securing communications

  • The memcapacitors-based Colpitts oscillator introduced in this work has not yet been presented and explored in the literature.

The rest of the paper is structured as follows: In Sect. 2, circuit design and mathematical model of the modified memcapacitor-based Colpitts oscillator are proposed. Based on the mathematical model of the proposed circuit, its dynamics analysis is performed. Basic properties of the system are also explored analytically. In Sect. 3, the effect and influence of parameters through bifurcation diagrams, Lyapunov exponents, stability, and system influence diagrams are explored. Phenomena like multistability and offset-boosting are also observed. In addition, a PSpice study based on the corresponding analog computer of the dynamic system is made for electronic validation. The last section concludes the paper.

2 Circuit and mathematical model

2.1 Circuit description

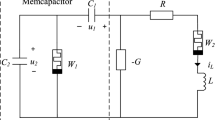
The idea of designing the memcapacitors-based chaotic circuit is inspired by the standard chaotic Colpitts circuit which consists of an active component (bipolar junction transistor, field-effect transistor, operational amplifier, etc.) acting as an amplifier and also as a non-linear element responsible for the chaotic behavior due to their intrinsic non-linearity; its output is linked to an oscillatory circuit, also called LC circuit (two capacitors and an inductor). As shown in Fig. 1, the objective of this work is to propose a simple oscillator designed from the Colpitts’ LC tank circuit by replacing the two normal capacitors \(C_{1}\) and \(C_{2}\) by two nonlinear memcapacitors \(C_{m1}\) and \(C_{m2}\), in parallel with conductances \(G_{1}\) and \(- G_{2}\) respectively. Compared to the standard Colpitts oscillator, the proposed circuit does not need either the two capacitors (\(C_{1}\) and \(C_{2}\)) or any active component based on a bipolar junction transistor, field-effect transistor, or operational amplifier to work properly. The simplicity of the proposed circuit comes from the fact that the two memcapacitors simultaneously perform three functions in particular: amplification, nonlinearity, and state variables (\(x_{1}\) and \(x_{2}\)). Therefore, the circuit in Fig. 1 can be seen as a simple oscillator composed of three dynamic elements, including an inductor and two memcapacitors blocks. The first block which is a passive capacitive circuit, includes a memcapacitor in parallel with a positive conductance, while the second block which is an active capacitive circuit [54], instead includes a memcapacitor in parallel with a negative conductance that provides energy to the whole circuit in order to maintain a continuous oscillation. The complex dynamics of the circuit result from the nonlinearities of the two memcapacitors which play a central role in the generation of chaotic behavior. To the best of our knowledge, the structure of the electrical circuit proposed in Fig. 1 is different from all the circuits with two memcapacitors proposed in the literature.

Fig. 1
figure 1

Simple memcapacitor-based oscillator, designed from the Colpitts’ LC tank circuit. It is composed of three dynamic elements, including two memcapacitors blocks and an inductor.

Full size image

2.2 Memcapacitors and oscillator’s mathematical model

The charge-controlled memcapacitor equation considered in this work is defined by referring to the work carried out in [31]. The generalized form for a system made up of several memcapacitors is defined by Eq. (1).

$$\left\{ {\begin{array}{*{20}l} {u_{c} (t) = C^{ - 1} \left( {\sigma (t)} \right)q(t),} \hfill \\ {\dot{\sigma }(t) = q(t),} \hfill \\ \end{array} } \right.$$
(1)

where \(u_{c} (t)\) and \(q(t)\) are the voltage and charge across the memcapacitor at time \(t\), \(C^{ - 1}\) the inverse memcapacitance and \(\sigma (t)\) the integral of \(q(t)\). The inverse memcapacitance of the two memcapacitors in the proposed circuit in Fig. 1 is defined as follows [55, 56]:

$$C_{i}^{ - 1} = m_{i} + n_{i} \sigma_{i}^{2} ,\;i = 1,2$$
(2)

From Eq. (2) and Eq. (1), the model of the two memcapacitors is described as (for simplicity, we have omitted time dependence):

$$\left\{ {\begin{array}{*{20}l} {u_{ci} = \left( {m_{i} + n_{i} \sigma_{i}^{2} } \right)q_{i} ,} \hfill \\ {\dot{\sigma }_{i} = q_{i} ,} \hfill \\ \end{array} } \right.,\;i = 1,2$$
(3)

where \(m_{i}\) and \(n_{i}\) are real constants. Due to the existence of only three dynamical energy storage elements, and considered the same approach of made in Refs. [55, 56], the proposed circuit can be simply modeled by a third-order system. Thus, by the volt-ampere characteristics of each element and the Kirchhoff's current law, we obtain the differential equation:

$$\left\{ {\begin{array}{*{20}l} {L\frac{{di_{L} }}{dt} = u_{c1} - u_{c2} } \hfill \\ {\frac{{dq_{1} }}{dt} = i_{L} - G_{1} u_{c1} } \hfill \\ {\frac{{dq_{2} }}{dt} = i_{L} + G_{2} u_{c2} } \hfill \\ \end{array} } \right.$$
(4)

By applying integral operation to Eqs. (3) and (4) directly with respect to time \(t\), the following equations with variables \(q_{L}\), \(\sigma_{1}\) and \(\sigma_{2}\) can be obtained by Eq. (5).

$$\left\{ {\begin{array}{*{20}l} {L\frac{{dq_{L} }}{dt} = \varphi_{c1} - \varphi_{c2} ,} \hfill \\ {\frac{{d\sigma_{1} }}{dt} = - q_{L} - G_{1} \varphi_{c1} ,} \hfill \\ {\frac{{d\sigma_{2} }}{dt} = q_{L} + G_{2} \varphi_{c2} ,} \hfill \\ \end{array} } \right.$$
(5)

where \(\varphi_{c1}\) and \(\varphi_{c2}\) are the time integrals of voltage \(u_{c1}\) and \(u_{c2}\) respectively. \(\sigma_{1}\) and \(\sigma_{2}\) are the integrals of charge \(q_{1}\) and \(q_{2}\) respectively. \(q_{L}\) is the time integral of current \(I_{L}\). Based on Eq. (5), \(\varphi_{ci}\) can be provided by Eq. (6).

$$\varphi_{ci} = m_{i} \sigma_{i} + \left( {n_{i} \sigma_{i}^{3} /3} \right) = a_{i} \sigma_{i} + b_{i} \sigma_{i}^{3} \;i = 1,2$$
(6)

By exploiting the following changes \(q_{L} = x_{1}\), \(\sigma_{1} = x_{2}\), \(\sigma_{2} = x_{3}\), \(c = 1/L\), \(d = G_{1}\), \(e = G_{2}\) and substituting Eq. (6) into (5), the dynamics of the model of Fig. 1 is expressed by Eq. (7).

$$\left\{ {\begin{array}{*{20}l} {\dot{x}_{1} = c\left( {a_{1} x_{2} + b_{1} x_{2}^{3} - a_{2} x_{3} - b_{2} x_{3}^{3} } \right),} \hfill \\ {\dot{x}_{2} = - x_{1} - d\left( {a_{1} x_{2} + b_{1} x_{2}^{3} } \right),} \hfill \\ {\dot{x}_{3} = x_{1} + e\left( {a_{2} x_{3} + b_{2} x_{3}^{3} } \right),} \hfill \\ \end{array} } \right.$$
(7)

where \(a_{1}\), \(b_{1}\), \(a_{2}\) and \(b_{2}\) are considered as the intrinsic parameters of the two memcapacitors. Obviously, the designed new nonlinear circuit is a three-dimensional system whose cubic nonlinearities are \(x_{2}^{3}\) and \(x_{3}^{3}\).

2.3 Symmetry and fixed points

The transformation \(\left( {x_{1} ,x_{2} ,x_{3} } \right) \Leftrightarrow \left( { - x_{1} , - x_{2} , - x_{3} } \right)\) leaves invariant system (7). It means that all of the assymetrical attractors appear in pair (with their symmetrical twins) in the system. Hence, each asymmetric attractor in this oscillator coexists with its asymmetric twin which will be obtained by algebrical inversion of the initial conditions. The fixed points are obtained solving Eq. (8).

$$\left\{ {\begin{array}{*{20}l} {a_{1} x_{2} + b_{1} x_{2}^{3} - a_{2} x_{3} - b_{2} x_{3}^{3} = 0} \hfill \\ { - x_{1} - d\left( {a_{1} x_{2} + b_{1} x_{2}^{3} } \right) = 0} \hfill \\ {x_{1} + e\left( {a_{2} x_{3} + b_{2} x_{3}^{3} } \right) = 0} \hfill \\ \end{array} } \right.$$
(8)

This resolution allows us to assert that the system has nine equilibrium points namely: \(E_{0} = \left( {0,\,0,\,0} \right)\), \(E_{1,2} = \left( {0,\,0,\, \pm \sqrt { - \frac{{a_{2} }}{{b_{2} }}} } \right)\), \(E_{3,4} = \left( {0,\, \pm i\sqrt {\frac{{a_{1} }}{{b_{1} }}} ,\,0} \right)\), \(E_{5,6} = \left( {0,\, \pm i\sqrt {\frac{{a_{1} }}{{b_{1} }}} ,\,\sqrt { - \frac{{a_{2} }}{{b_{2} }}} } \right)\), and \(E_{7,8} = \left( {0,\, \pm i\sqrt {\frac{{a_{1} }}{{b_{1} }}} ,\, - \sqrt { - \frac{{a_{2} }}{{b_{2} }}} } \right)\). The analysis of the dynamics cannot be done without a prior analysis of the stability of these nine fixed points of the system. Thus, at any fixed point \(E = \left( {\overline{x}_{1} ,\,\overline{x}_{2} ,\,\overline{x}_{3} } \right)\) the Jacobian matrix of system (7) is follows:

$$J_{E} = \left[ {\begin{array}{*{20}c} 0 & {c\left( {a_{1} + 3b_{1} \overline{x}_{2}^{2} } \right)} & {c\left( { - a_{2} - 3b_{2} \overline{x}_{3}^{2} } \right)} \\ { - 1} & { - d\left( {a_{1} + 3b_{1} \overline{x}_{2}^{2} } \right)} & 0 \\ 1 & 0 & {e\left( {a_{2} + 3b_{2} \overline{x}_{3}^{2} } \right)} \\ \end{array} } \right]$$
(9)

The eigenvalues of fixed points are solution of the characteristic equation \(\det \left( {J_{E} - \lambda I_{4} } \right)\) where \(I_{4}\) is the \(4 \times 4\) identity matrix. These eigenvalues for the set of system parameters \(a_{1} = 0.38\), \(b_{1} = 1\), \(a_{2} = - 1\), \(b_{2} = 1\), \(c = 2\), \(d = 1\), and \(e = 0.45\) are listed in Table 1. It should be noted that all fixed points are unstable. Therefore, system (7) may exhibit self-excited attractors [8, 20, 57].

Table 1 Fixed points and eigenvalues of system (5) for \(a_{1} = 0.38\), \(b_{1} = 1\), \(a_{2} = - 1\), \(b_{2} = 1\), \(c = 2\), \(d = 1\), and \(e = 0.45\)
Full size table

3 Numerical results

This section is devoted to investigatigations on the dynamic phenomena in the new memcapacitors-based Colpitts circuit using quantitative and qualitative nonlinear tools such as Lyapunov exponents computation, bifurcation plots, cross-section of basin of attraction, phase portrait, two-parameter diagram, and frequency spectra in specific range of system parameters.

3.1 Influence of system parameters on the dynamic

When we consider the parameter \(e\) as bifurcation control parameter and for some discrete values of the parameter \(c\), the dynamics of the system change considerably. Thus, Fig. 2 presents some bifurcation diagrams as well as their corresponding graphs of maximum Lyapunov exponents.

Fig. 2
figure 2

Effect of parameter \(c\) on the dynamics following the control parameter \(e\). Other parameters and initial conditions with values are \(a_{1} = 0.38\), \(b_{1} = 1\), \(a_{2} = - 1\), \(b_{2} = 1\), \(d = 1\), \(x_{1} \left( 0 \right) = 0.1\), \(x_{2} \left( 0 \right) = 0.0\), and \(x_{3} \left( 0 \right) = 0.0\)

Full size image

These bifurcation diagrams are obtained by plotting the maxima of the variable \(x_{3}\) as a function of the parameter \(e\) in the \(0.25 \le e \le 0.55\) interval. For each discrete value of the parameter \(c\), there is a period-doubling road to chaos. In light of Fig. 2, the data in green are obtained by continuously increasing the values of the bifurcation parameter and those in red by similarly decreasing the values of the same bifurcation parameter. The color difference highlights the phenomenon of hysteresis for a coexistence of two types of behavior for a given set of initial conditions.

Another route to chaos is observed when varying the control parameter \(d\) as shown in Fig. 3. The bifurcation method of Fig. 2 is exploited to obtain the two diagrams (green and red) of Fig. 3. Through careful observation, a window of hysteresis phenomenon is also observed in \(1.173\le d\le 1.189\) and \(1.383\le d\le 1.385\) intervals. This bifurcation change can be observed or some discrete value for parameter d. As a result, we can have a pair of Period-1, Period-2, and Period-4 limit cycles for \(d = 0.8\), \(d = 1\), and \(d = 1.09\) respectively; a pair of single band chaotic attractors for \(d = 1.14\), a symmetric Period-5 limit cycle for \(d = 1.3\), a double band chaotic stange attractor for \(d = 1.45\); and a symmetric Period-3 limit cycle for \(d = 1.7\). A sample of phase portraits of this road to chaos is presented in the next section for comparative purposes.

Fig. 3
figure 3

Bifurcation diagrams highlighting the route to double-band chaos by variation of the control parameter d in the \(0.8 \le d \le 1.7\) range for \(a_{1} = 0.3\), \(b_{1} = 1\), \(a_{2} = - 1\), \(b_{2} = 1\), \(c = 2\), \(e = 0.45\), and \(x_{1} \left( 0 \right) = 0.1\), \(x_{2} \left( 0 \right) = 0.0\), and \(x_{3} \left( 0 \right) = 0.0\)

Full size image

Noted that if the intrinsic parameter \(a > 0\) we have a positive memcapacitor, while for \(a < 0\) we have a negative memcapacitor. When we consider a change of the intrinsic parameters of the memcapacitors of Fig. 1.i.e. the parameters \(a_{1}\), \(b_{1}\), \(a_{2}\), and \(b_{2}\), the dynamics of system (7) change considerably. A sample of this change in dynamics is shown in Fig. 4 by the bifurcation diagram (Fig. 4(a)) and Lyapunov maximal exponent graph (Fig. 4(b)).

Fig. 4
figure 4

Bifurcation diagram (a) and graph of maximum Lyapunov exponents (b) when changing the intrinsic parameters

Full size image

With regard to these figures, the dynamics do not follow any classic bifurcation, hence the importance of choosing the parameters and initial conditions. The importance of this choice of parameters is especially crucial in the encryption process because the dynamics are almost chaotic.

As a result, the complex shape of the chaotic behavior for the set of parameters \(a_{1} = - 0.4\), \(b_{1} = 0.6\), \(a_{2} = - 1.2\), \(b_{2} = 0.6\), \(c = 10\), \(d = 1\), and \(e = 0.46\), is presented in Fig. 5 on all coordinate planes of the system and their corresponding frequency spectrum and time series. Initial conditions are \(x_{1} \left( 0 \right) = 0.1\), \(x_{2} \left( 0 \right) = 0.0\), and \(x_{3} \left( 0 \right) = 0.0\). For a global view of the influence of system parameters, standard Lyapunov stability diagrams are drawn showing this mutual influence between parameters. Thus, the mutual influence of the parameters (\(e,c\)) and (\(c,d\)) and the intrinsic parameters of the memcapacitors (\({a}_{1},{a}_{2}\)), (\({b}_{1},{b}_{2}\)), (\({b}_{1},{a}_{1}\)), and (\({b}_{2},{a}_{2}\)) on the system dynamics are plotted and presented in Fig. 6. We can observe this influence by the color differences. The diagrams of Fig. 6(a and b) are obtained for the set of fixed parameters \(a_{1} = - 0.4\), \(b_{1} = 0.6\), \(a_{2} = - 1.2\), \(b_{2} = 0.6\), \(d = 1\), and \(e = 0.45\) respectively. Similarly, the intrinsic parameter diagrams of Fig. 6(c–f) are obtained for the fixed parameters \(c = 10\), \(e = 0.46\), \(d = 1\) but mutually varying \(a_{1}\), \(b_{1}\), \(a_{2}\), and \(b_{2}\) as shown in the stability diagrams.

Fig. 5
figure 5

Projection on the different coordinate planes of the phase portrait as well as the corresponding frequency spectrum and time series of the chaotic attractor when changing the intrinsic parameters

Full size image
Fig. 6
figure 6

Standard Lyapunov Stability diagram highlighting the complexity of the system. Note that the black shading reflects areas of no oscillation. Lyapunov's exponent bands justify the color difference and corresponding behavior

Full size image

The overall observation on these influences is the impact that each parameter brings to the dynamic behavior of the system. The parameters \(e,c, {a}_{1},{b}_{1},\) and \(d\) cause varied dynamics while the other parameters \({a}_{2}\) and \({b}_{2}\) have a weak influence on the dynamics of the system. This influence is strongly observed through the band of Lyapunov exponents which shows some correspondence between the types of behavior represented with the colors of each diagram. It is important to mention that the black shading observed on the influence of the intrinsic parameters to the memcapacitors (\(a_{1}\), \(b_{1}\), \(a_{2}\), and \(b_{2}\)) reflects the zones without oscillation. From a design point of view, it is preferable to make a choice for positive set of parameter \(b_{1}\) and \(b_{2}\) because the dynamics are greater (chaotic tendency) when these intrinsic parameters are positive, whereas the suitable choice of the intrinsic parameters \(a_{1}\) and \(a_{2}\) can be positive or negative.

3.2 Coexisting bifurcations and multistability

Coexistence is the presence of totally different dynamics for the same rank parameters, depending on the initial state of the system [58,59,60,61]. In this section, we highlight some ranges of parameters for which several different dynamics coexist. For this purpose, a bifurcation diagram and its enlargement are computed. By considering the parameter \(c\) as a bifurcation control parameter, the bifurcation diagrams in the \(1\le c\le 2.5\) range of Fig. 7 are observed. From the first diagram, a parallel branch of bifurcation is observed in black. To better observe the phenomenon produced, a widening of the diagram in the \(1.8\le c\le 2\) range is also drawn (as indicated by the second diagram in Fig. 7). In the first diagram, the green and magenta curves are plotted backward starting from \(c = 2.5\) with initial conditions \(\left( {x_{1} \left( 0 \right),x_{2} \left( 0 \right),x_{3} \left( 0 \right)} \right) = \left( { \pm 0.1,0,0} \right)\) respectively. The black 4-branch bifurcation is obtained plotting upward starting from \(c = 1.847\) with initial conditions \(\left( {x_{1} \left( 0 \right),x_{2} \left( 0 \right),x_{3} \left( 0 \right)} \right) = \left( { - 0.35,0,0} \right)\). The rest of the setting parameters are \(a_{1} = 0.3\), \(b_{1} = 1\),\(a_{2} = - 1\), \(b_{2} = 1\),\(d = 1\) and \(e = 0.45\). In these diagrams of Fig. 7, the memcapacitor-based Colpitts system admits a coexistence of a pair of asymmetric attractors in the \(1.847 \le c \le 1.87\) range showing coexistence of four attractors.

Fig. 7
figure 7

Bifurcation diagram following the control parameter \(c\) showing the coexistence of two different types of dynamics. This graph is obtained by keeping the other parameters at constant values: \(a_{1} = 0.3\), \(b_{1} = 1\), \(a_{2} = - 1\), \(b_{2} = 1\), \(d = 1\), and \(e = 0.45\)

Full size image

These four coexisting attractors are highlighted by the phase portraits in Fig. 8 where a pair of chaotic attractors (Fig. 8(a)) coexists with a pair of Period-4 limit cycles (Fig. 8(b)). These attractors are obtained for \(c=1.848\) with the initial conditions \((\pm 0.44, 0, 0)\) for chaotic attractors and \((\pm 0.2, 0, 0)\) for periodic attractors.

Fig. 8
figure 8

Coexistence of four different attractors (a pair of period-4 and a pair chaotic attractors and their cross-sections of basin of attraction (for \(x_{2} (0) = 0\) and \(x_{1} (0) = 0\) respectively). See the text for more details

Full size image

The corresponding cross-sections of basin of attraction in the initial condition \(\left( {x_{1} \left( 0 \right),\,x_{3} \left( 0 \right)} \right)\) and \(\left( {x_{2} \left( 0 \right),\,x_{3} \left( 0 \right)} \right)\) planes leading to each of the four coexisting attractors are also depicted in Fig. 8, where magenta colors of initial conditions are associated to the asymmetric pair of chaotic attractors while the yellow regions lead to trajectories associated with the pair of periodic attractors. Divergence is associated with red data. Note that several other multistability windows are also observed for other sets of system parameters. Thus, the zones of color differences in the bifurcation diagrams of Figs. 2 and 3 highlights this phenomenon of multistability where a coexistence of two and three other attractors which coexist can be observed.

From bifurcations of Fig. 2 for \(c=1.25\) in the \(0.37\le e\le 0.41\) interval, a coexistence of three attractors is observed including a limit cycle of period 5 which coexists with two asymmetric chaotic attractors. This coexistence is presented in detail in Fig. 9 where the periodic attractor obtained by initial conditions \((0.28, 0, 0.68)\) is observed in Fig. 9(a), chaotic attractors by initial conditions \((\pm 0.7, 0, \pm 0.7)\) in Fig. 9(b), and their basin of attraction are also presented in Fig. 9(c, d) for the set of parameters. Concerning the basins of attractions, the data in blue correspond to all the initial conditions giving rise to chaotic attractors, those in cyan to the periodic attractor, and the data in red correspond to the zones of divergence.

Fig. 9
figure 9

The coexisting phase portraits (a) and (b) as well as the set of initial conditions giving rise to these attractors (c) and (d) for the parameters \(a_{1} = 0.38\), \(b_{1} = 1\), \(a_{2} = - 1\), \(b_{2} = 1\), \(c = 1.25\),\(d = 1\), and \(e = 0.39\)

Full size image

Another type of coexistence is observed by the color difference of the bifurcations of Fig. 2 for c = 1.2 in the \(0.44\le e\le 0.47\) interval. Thus, coexistence of two different symmetric attractors is presented in Fig. 10 where the periodic attractor obtained by the initial conditions \((0.9, 0, 0)\) is observed in Fig. 10(a), the chaotic attractors by the initial conditions \((0.4, 0, 0.95)\) in Fig. 10(b) and their basin of attraction are also presented in Fig. 9(c, d) for the parameters \(a_{1} = 0.38\), \(b_{1} = 1\), \(a_{2} = - 1\), \(b_{2} = 1\), \(c = 1.2\),\(d = 1\), and \(e = 0.45\). In light of the basins of attractions, the data in blue correspond to the chaotic attractors, those in cyan to the periodic attractor, and the data in red one to the zones of divergence.

Fig. 10
figure 10

The coexisting phase portraits (a) and (b) as well as the set of initial conditions giving rise to these attractors (c) and (d) for the parameters \(a_{1} = 0.38\), \(b_{1} = 1\), \(a_{2} = - 1\), \(b_{2} = 1\), \(c = 1.2\),\(d = 1\), and \(e = 0.45\). See in text for more detail

Full size image

3.3 Offset bossting behavior

In system (7), since the variable \(x_{1}\) appears with the lowest occurrence, it would be convenient to choose it as the optimal variable for offset. Thus, the state variable will be replaced by its equivalent added to a constant \(k\): \(x_{1} \to x_{1} + k\). This variable change has the effect of translating the control phase state variable from a bipolar to a unipolar signal. Henceforth, the attractors in phase space become either unipolar negative or positive, according to the algebraic values of the offset boosting constant. Indeed, this particular property of translation becomes very important for applications that require unipolar signals [57, 62,63,64,65,66].

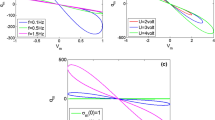
Figure 11(d) illustrates the qualitative invariability of the attractor across the Lyapunov exponent spectrum plot following \(k\). The bifurcation diagram shows the translation of all the attractors of the phase space according to the state variable \(x_{1}\). when the control constant k takes some discrete values -1, 0, and + 1. This shift is illustrated in Fig. 11(a–c) where we drew three chaotic attractors each in two different planes and corresponding to three different values ​​of the offest boosting parameter. In summary for k = 0, the attractor is unipolar and symmetrical. it is polarized when the constant varies (unipolar positively for k = 1 and unipolar negatively for k = − 1). these results are obtained when the other parameters have the value: \(a_{1} = 0.3\), \(b_{1} = 1\),\(a_{2} = - 1\), \(b_{2} = 1\),\(c = 2\),\(d = 1.55\) and \(e = 0.45\).

Fig. 11
figure 11

Translational effects of the offset-boosting phenomenon on the bifurcation diagram and the double-scroll strange attractor and qualitative invariability demonstrated by the exponent spectrum. Parameters values are: \(a_{1} = 0.3\), \(b_{1} = 1\), \(a_{2} = - 1\), \(b_{2} = 1\), \(c = 2\), \(d = 1.55\), and \(e = 0.45\)

Full size image

3.4 PSpice simulations

Previous numerical studies have allowed us to realize that the memcapacitors-based Colpitts oscillator is able to show complex and varied dynamic behavior. The purpose of this paragraph is to confirm the numerical and theoretical results obtained by doing a study under Pspice by analog simulations. Since the memcapacitors are components that do not yet physically exist, we implement here an analog circuit to illustrate the accuracy and feasibility of the theoretical circuit of the Fig. 1. As shown in Fig. 12, the proposed analog circuit is made up of nine operational amplifiers (TL084), four multipliers (MULT), three capacitors, and several resistors. The analog circuit described in Fig. 12 is simulated in the Orcad PSpice environment with the same component values as listed in the legend of the figure. The following equations describes the dynamics of the circuit in Fig. 12.

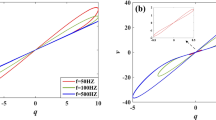
$$\left\{ {\begin{array}{*{20}l} {\dot{V}_{C1} = \frac{R}{{R_{c} }}\left( {\frac{R}{{R_{a1} }}V_{C2} + \frac{R}{{R_{b1} }}V_{C2}^{3} - \frac{R}{{R_{a2} }}V_{C3} - \frac{R}{{R_{b2} }}V_{C3}^{3} } \right),} \hfill \\ {\dot{V}_{C2} = - V_{C1} - \frac{R}{{R_{d} }}\left( {\frac{R}{{R_{a1} }}V_{C2} + \frac{R}{{R_{b1} }}V_{C2}^{3} } \right),} \hfill \\ {\dot{V}_{C3} = V_{C1} + \frac{R}{{R_{e} }}\left( {\frac{R}{{R_{a2} }}V_{C3} + \frac{R}{{R_{b2} }}V_{C3}^{3} } \right),} \hfill \\ \end{array} } \right.$$
(10)

where \(V_{C1} = x_{1}\), \(V_{C2} = x_{2}\), \(V_{C3} = x_{3}\), \(a_{1} = \frac{R}{{R_{a1} }}\), \(b_{1} = \frac{R}{{R_{b1} }}\), \(a_{2} = \frac{R}{{R_{a2} }}\), \(b_{2} = \frac{R}{{R_{b2} }}\), \(c = \frac{R}{{R_{c} }}\), \(d = \frac{R}{{R_{d} }}\) and \(e = \frac{R}{{R_{e} }}\). The correspondence of the Matlab time unit according to that of PSpice (time scaling) is \(T_{Pspice} = RCT_{Matlab} = 10^{ - 4} T_{Matlab}\), with \(R = 10k\Omega\) and \(C = 10nF\). According to the system parameters using in Fig. 3, the values of the components of Fig. 12 are chosen as \(R_{a1} = 33.333k\Omega\), \(R_{b1} = 10k\Omega\), \(R_{a2} = 10k\Omega\), \(R_{b2} = 10k\Omega\), \(R_{c} = 5k\Omega\), \(R_{e} = 22.222k\Omega\). It is important to mention that, the power supply voltage is \(\pm 15Vdc\). By varying \(R_{d}\), i.e. the parameter \(d\), the scenario leading to chaos by period-doubling was found during analog simulations as shown by phase portraits in Fig. 13, which presents a good agreement between the results obtained through Matlab (right) and PSpice (left) simulations. Figures 14, 15 and 16 which correspond to Figs. 8, 9 and 10, show the coexistence of four, three and two different attractors respectively. Herein, a good agreement between numerical and analog simulation is also observed.

Fig. 12
figure 12

PSpice representation of the corresponding analog circuit of the proposed memcapacitors-based Colpitts oscillator

Full size image
Fig. 13
figure 13figure 13

Phase portraits showing the road to chaos via Matlab (right) and PSpice (left) simulations for discrete values of the parameter \(d\): a–c a pair of Period-1, Period-2, and Period-4 limit cycles for \(d = 0.8\) \((R_{d} = 12.5\,{\text{k}}\Omega )\), \(d = 1\) \((R_{d} = 10\,{\text{k}}\Omega )\), and \(d = 1.09\) \((R_{d} = 9.174\,{\text{k}}\Omega )\) respectively; d a pair of single band chaotic attractors for \(d = 1.14\) \((R_{d} = 8.772\,{\text{k}}\Omega )\), e a symmetric Period-5 limit cycle for \(d = 1.3\) \((R_{d} = 7.692\,{\text{k}}\Omega )\), f a double band chaotic stange attractor for \(d = 1.45\)\((R_{d} = 6.896\,{\text{k}}\Omega )\); and g a symmetric Period-3 limit cycle for \(d = 1.7\) \((R_{d} = 5.882\,{\text{k}}\Omega )\)

Full size image
Fig. 14
figure 14

Coexistence of four different attractors via PSpice simulations for \(R_{a1} = 33.333k\Omega\), \(R_{e} = 22.222k\Omega\), \(R_{c} = 5.411k\Omega\); the values of the other components remain unchanged

Full size image
Fig. 15
figure 15

Coexistence of three different attractors via PSpice simulations for \(R_{a1} = 26.316k\Omega\), \(R_{e} = 25.641k\Omega\), \(R_{c} = 8k\Omega\); the values of the other components remain unchanged

Full size image
Fig. 16
figure 16

Coexistence of two different attractors via PSpice simulations for \(R_{a1} = 26.316k\Omega\), \(R_{e} = 22.222k\Omega\), \(R_{c} = 8.333k\Omega\); the values of the other components remain unchanged

Full size image

4 Conclusion

This paper presented the results obtained from the investigations on the new memcapacitor-based Colpitts oscillator and related discussions. One of the key contributions in this area was the introduction of a simple memcapacitors-based oscillator, set up from the Colpitts' LC tank circuit. The proposed circuit is distinguished from the others found in the literature primarily by its unique structure based on memcapacitors and by the new and innovative results in the Colpitts-type oscillators. Numerical, analytical, and analogical analyses have been carried out. These investigations allowed us to highlight some very interesting phenomena such as offset-boosting, single and double-band chaos, and the coexistence of four different solutions. The practice feasibility of this circuit is confirmed by the PSpice simulations.