1 Introduction

Stiffened plates have been extensively used in engineering practices to provide enhanced stiffness and stability to structural systems with the extra advantage of light weight. The vibration of stiffened plates has been investigated through various analytical and numerical techniques. Two types of models were adopted for stiffened plates in the early literature as Mukherjee and Mukhopadhyay summarized in their review papers: One is the orthotropic model with which the plate is treated as an equivalent orthotropic plate considering the contribution of the stiffener [1], and the other is the grillage approximation with which the stiffener is considered as a grid attached to the plate [2]. There are numerous researches that focus on bending, buckling and vibration of flat plate [3,4,5,6,7,8]. Furthermore, different approaches have been proposed to model the behavior of plates and, among others, the Ritz method has been successfully used, showing adequate accuracy and computational efficiency [9]. Recently, a mixed modeling was proposed to create separately the models of the plate and its stiffening beam. Afterward, a complete model is formed to incorporate the displacements of the plate and the stiffener through the condition for compatibility of displacement. With this approach, the vibration of stiffened plates can be analyzed numerically through the Ritz method [10, 11], the finite difference method [12], the finite element method [13,14,15,16], the differential quadrature method [17] and the meshless method [18, 19], among others.

A stiffened structure may be ceaselessly subjected to large irregular load or cyclic load and finally lead to fatigue damage. Cracks are one of the most common types of damage in these structures. The existence of a crack in a stiffened plate can introduce a local flexibility and reduces the structural stiffness that may affect the structural vibrational characteristics, such as natural frequencies, mode shapes and modal strain energy [20, 21], and can eventually lead to an unexpected failure of the structure. To understand the mechanism of how the structural stiffness is weakened, the presence of crack in an intact stiffened plate must be taken into consideration. Previous efforts have been made concerning how the damage caused by cracks affects the vibration of panels. Qian et al. [22] devised a finite element model for vibration of cracked plates. M. Bachene et al. [23] adopted the extended finite element method (X-FEM) to analyze vibrations of cracked plates. Chen et al. [24] studied the nonlinear vibration of thin plate with an all-over breathing crack based on a piecewise model.

Yuan and Dickinson [25] used the domain decomposition method to study the vibration of a thin, simply supported rectangular plate with a side crack. The same method was adopted by Yuan and Young [26] in their investigation of vibration of a completely free annular plate with side and internal cracks. A similar method was used by Liew et al. for vibration of cracked rectangular plates [27]. The cracked domain in the plate was divided into smaller subdomains to establish a discrete model with the appropriate shape functions of displacement that satisfied the boundary conditions of displacement. The eigenvalues of vibration were obtained considering free and simply supported boundary conditions for all edges. In the majority of these approaches, the Ritz method was applied with admissible functions to express properly the displacement field and the boundary conditions of the stiffened plate and the structural defection due to the cracks. Leissa and Huang [28] proposed a set of modal functions of algebraic polynomial and corner functions as the admissible functions for free vibration of a rectangular plate with a side crack. Huang [29, 30] extended the method to investigate the vibration of rectangular Mindlin plates and Reddy plates with functionally graded material.

For the problem of stability of cracked stiffened plates Dang and Kapania [31] analyzed buckling of a cracked, stiffened panel via the Ritz method adopting locally distributed trigonometric series as the admissible function of displacement. Milazzo and Oliveri [32] presented a PB-2 Rayleigh–Ritz variational approach to determine the post-buckling behavior of cracked composite plates. Cracks were modeled using the subdomain decomposition of the plate displacement coupled with penalty techniques to augment the variational statement with the needed continuity conditions along the connected subdomains edges. Their study was extended to the buckling and post-buckling analyses of stiffened composite panels [33].

The objective of this paper is to investigate the free vibration of a reinforced plate considering the effect of stiffener location and key parameters of a side crack. Based on the classical theories of plate and beam, the strain energy and kinetic energy for a flat plate and a stiffener are expressed separately and are combined through implementing the compatibility conditions for displacements of the plate and the stiffener. The modal displacement is approximated with two sets of functions: one is the orthogonal polynomials for the intact stiffened plate, and the other is the corner function to describe the singularity in stress at the crack tip as well as the discontinuity in displacement and slope across the crack. Natural frequencies and modes are obtained from the eigenvalue problem derived through the Ritz method considering two typical boundary conditions. The first condition is simply supported on all edges (SSSS), and the second condition is two simply supported edges and two free edges (FSFS). The accuracy and performance in convergence of the present approach are tested with example. The results are compared with finite element solutions.

2 Problem formulation

2.1 The cracked stiffened plate

Consider a flat, square plate with the geometry and dimension shown in Fig. 1. The plate is reinforced by a horizontally or a vertically placed stiffener. A side crack is considered to start from an arbitrary position on the edge \(x=a.\) It is assumed that the plate and the stiffeners are both damaged by the same through-the-thickness crack of Mode I that may penetrate the stiffener as it propagates along the dashed line.

Fig. 1
figure 1

Geometry and dimensions of a cracked, stiffened flat plate

Full size image

Based on the classical theory of plate, the strain energy and kinetic energy in the modal space for the plate are

$$\begin{aligned} U_p= & {} \frac{D}{2}\mathop \int \int \nolimits _\varOmega \left( {\frac{\partial ^{2}W}{\partial x^{2}}+\frac{\partial ^{2}W}{\partial y^{2}}} \right) ^{2}-2\left( {1-\upsilon } \right) \left( {\frac{\partial ^{2}W}{\partial x^{2}}\frac{\partial ^{2}W}{\partial y^{2}}-\left( {\frac{\partial ^{2}W}{\partial x\partial y}} \right) ^{2}} \right) \hbox {d}x\hbox {d}y,\nonumber \\ T_p= & {} -\frac{\omega ^{2}\rho h}{2}\mathop \int \int \nolimits _\varOmega W^{2}\hbox {d}x\hbox {d}y, \end{aligned}$$
(1)

respectively, where \(W=W({x,y})\) is the transverse modal displacement in the mid-plane of the plate. \(D=Eh^{3}/12\left( {1-\upsilon } \right) ^{2}\) is the flexural rigidity; E is Young’s modulus; \(\upsilon \) is Poisson ratio; \(\omega \) is the natural frequency; h is the thickness of the plate, \(\rho \) is the mass density of material. The stiffener is modeled as a beam for its cross-sectional dimensions are usually small compared to its length. It is also assumed that the stiffener is firmly attached to the middle surface of the plate, and the elastic strain in the z-direction is negligible following the classic theory of beam.

The compatibility condition for the displacements is used to integrate the plate and the stiffener into a single structural system. For instance, the displacement of the vertical stiffener is expressed as a function of the plate displacement \(W\left( {x=x_s ,y} \right) \), where \(x_s\) denotes the location of stiffener in the x direction. In this case, the strain and kinetic energy of the stiffener are dependent only on the y coordinate. The potential energy and kinetic energy of the vertical stiffener in the modal space can be obtained

$$\begin{aligned} U_{sy}= & {} \frac{1}{2}EI\mathop \int \nolimits _0^l \left[ {\frac{\partial ^{2}}{\partial y^{2}}W\left( {x_s ,y} \right) } \right] ^{2}\hbox {d}y,\nonumber \\ T_{sy}= & {} -\frac{1}{2}\omega ^{2}\rho b_s h_s \mathop \int \nolimits _0^l W^2 \left( {x_s ,y} \right) \hbox {d}y, \end{aligned}$$
(2)

where \(EI=Eb_s h_s ^{3}/12\) is the bending stiffness; \(b_s \) and \(h_s \) are the width and thickness of the stiffener, respectively. In a similar fashion, the strain energy and the kinetic energy of all of the horizontal stiffeners are expressed as

$$\begin{aligned} U_{sx}= & {} \frac{1}{2}EI\mathop \int \nolimits _0^l \left[ {\frac{\partial ^{2}}{\partial x^{2}}W({x,y_s })} \right] ^{2}\hbox {d}y,\nonumber \\ T_{sx}= & {} -\frac{1}{2}\omega ^{2}\rho b_s h_s \mathop \int \nolimits _0^l W^2 \left( {x,y_s } \right) \hbox {d}y. \end{aligned}$$
(3)

The total energy of the stiffened plate in free vibration is

$$\begin{aligned} \Pi =U_p +U_{sy} +U_{sx} +T_p + T_{sy} +T_{sx} . \end{aligned}$$
(4)

Substitution of Eqs. (1) through (3) into Eq. (4) leads to

$$\begin{aligned} \Pi= & {} \frac{D}{2}\mathop \int \int \nolimits _\varOmega \left( {W_{,xx} +W_{,yy} } \right) ^{2}-2\left( {1-\upsilon } \right) \left( {W_{,xx} W_{,yy} -\left( {W_{,xy} } \right) ^{2}} \right) \hbox {d}x\hbox {d}y\nonumber \\&+\frac{EI}{2}\left[ {\mathop \int \nolimits _0^l W_{,yy}^2 \left( {x_s ,y} \right) \hbox {d}y+\mathop \int \nolimits _0^l W_{,xx}^2 \left( {x,y_s } \right) \hbox {d}x} \right] \nonumber \\&-\frac{\omega ^{2}\rho }{2}\left[ {\mathop \int \int \nolimits _\varOmega W^{2}h\hbox {d}x\hbox {d}y+\mathop \int \nolimits _0^l W^2 \left( {x_s ,y} \right) b_s h_s \hbox {d}y\left. {+\mathop \int \nolimits _0^l W^2 \left( {x,y_s } \right) b_s h_s \hbox {d}x} \right] } \right. . \end{aligned}$$
(5)

Two typical boundary conditions are considered in the present study: SSSS with which all of the four edges are simply supported and FSFS with which two opposite edges are simply supported and the rest two are free.

2.2 Modal problem of the cracked stiffened plate

The Ritz method is applied to obtain the vibration characteristics of the cracked stiffened plate. The key step is to create a field of displacement considering the existence of crack in the stiffened plate and the prescribed boundary conditions. For the free vibration of the stiffened plate, the modal displacement function is approximated through

$$\begin{aligned} W( {x,y} )=W_p ( {x,y} )+W_c ( {x,y} ), \end{aligned}$$
(6)

where \(W_p ( {x,y} )\) stands for a series of complete, orthogonal polynomials with an infinite number of terms included. In this study, \(W_p ( {x,y} )\) is selected as

$$\begin{aligned} W_p ( {x,y} )=\mathop \sum \limits _{i=1}^I \mathop \sum \limits _{j=1}^J A_{ij} X_i ( x ) Y_j ( y ), \end{aligned}$$
(7)

where \(X_i (x )\) and \(Y_j ( y )\) are orthogonal polynomials that satisfy boundary conditions, both generated through the Gram–Schmidt orthogonalization [34].

For intact plates the smooth function of \(W_p \left( {x,y} \right) \) is able to converge to the true displacement field when both I and J approach infinity. For a cracked stiffened plate the singularity in stress at the tip of the crack as well as the discontinuity in displacement and rotation across the crack should be taken into account. In the present study, a supplemental polynomial \(W_c \left( {x,y} \right) \) is adopted to describe the effect of the crack, which reads

$$\begin{aligned} W_c ( {x,y} )=g( {x,y} )W_c ( {r,\theta } ), \end{aligned}$$
(8)

where g(x, y) is attached to ensure that the base functions satisfy the essential boundary conditions of the plate. To satisfy the SSSS boundary condition \(g( {x,y} )=x( {x-a} )y( {y-b} )\) is used for the out-of-plane displacement in Eq. (8). For the FSFS condition one may choose \(g( {x,y} )=y( {y-b} ). \quad W_c ( {r,\theta } )\) is called corner function which was developed from the asymptotic solutions by Huang and Chang [18] for describing the aforementioned singularity and discontinuity due to the crack, and can be expressed as

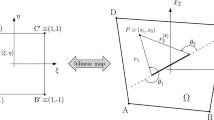
$$\begin{aligned} W_c ( {r,\theta } )=\left( \mathop \sum \limits _{n=1}^{N_1 } \mathop \sum \limits _{l=0}^n B_{nl} r^{( {2n-1} )/2}\hbox {cos}\frac{2l+1}{2}\theta +\mathop \sum \limits _{n=1}^{N_2 } \mathop \sum \limits _{l=0}^n C_{nl} r^{( {2n-1} )/2}\hbox {sin}\frac{2l+1}{2}\theta \right) , \end{aligned}$$
(9)

where \(B_{nl} \) and \(C_{nl} \) are undetermined coefficients. In the polar coordinate system, \(( {r,\theta })\) originates at the tip of the crack (see Fig. 2) with the assumption of \(-{\uppi }\le \theta \le \pi \). The stiffened plate can be partitioned into four subzones and the stiffener is considered broken into two parts once the crack grows long enough to reach it, as shown in Fig. 2. The plate is divided by the extension of the crack and the dashed lines parallel to the y axis. Let the length of the crack be d, the originating position of the crack be c. Assume (\(x_0,y_0 )\) is the Cartesian coordinates of P, \(\alpha \) is the orientation angle of the crack. One has

$$\begin{aligned} r= & {} \sqrt{({x-x_0})^{2}+({y-y_0 })^{2}}, \end{aligned}$$
(10)
$$\begin{aligned} \theta= & {} \arctan \frac{y-y_0 }{x-x_0 }-\alpha \hbox { for subzones I and II,}\nonumber \\ \theta= & {} \arctan \frac{y-y_0 }{x-x_0 }+\pi -\alpha \hbox { for subzone III, (11)}\nonumber \\ \theta= & {} \arctan \frac{y-y_0 }{x-x_0 }-\pi -\alpha \hbox { for subzone IV,} \end{aligned}$$
(11)

where \(x_0 =a-d\cos \alpha ,y_0 =c-d\cos \alpha \).

Fig. 2
figure 2

Partition of the side-cracked stiffened plate

Full size image

In the Cartesian coordinate system, the crack and its extension can be expressed through the function

$$\begin{aligned} y=c-a \hbox { tan}\alpha +x \hbox { tan}\alpha . \end{aligned}$$
(12)

The intersection of the vertical stiffener and the crack extension line is (\(x_s , y_c =c-a \hbox { tan}\alpha +x_s \hbox { tan}\alpha )\). In the case of \(x_0 \ge x_s \), the crack does not reach the vertical stiffener, i.e., the stiffener is located at subzones I and II. The expression of \(\theta \) in the displacement function of the stiffener can be written as

$$\begin{aligned} \theta =\arctan \frac{y-y_0 }{x_s -x_0 }-\alpha \quad 0\le y\le b. \end{aligned}$$
(13)

Then, the crack function of displacement function for the vertical stiffener can be expressed as

$$\begin{aligned}&W_c \left( {r,\theta } \right) \mid _{x=x_s } \nonumber \\&\quad = \left\{ {\mathop \sum \limits _{n=1}^{N_1 } \mathop \sum \limits _{l=0}^n B_{nl} \left[ {\sqrt{\left( {x_s -x_0 } \right) ^{2}+\left( {y-y_0 } \right) ^{2}}} \right] ^{\frac{2n-1}{2}}\hbox {cos}\left[ {\frac{2l+1}{2}\left( {\arctan \frac{y-y_0 }{x_s -x_0 }-\alpha } \right) } \right] } \right. \nonumber \\&\qquad \left. {+\mathop \sum \limits _{n=1}^{N_2 } \mathop \sum \limits _{l=0}^n C_{nl} \left[ {\sqrt{\left( {x_s -x_0 } \right) ^{2}+\left( {y-y_0 } \right) ^{2}}} \right] ^{\frac{2n-1}{2}}\hbox {sin}\left[ {\frac{2l+1}{2}\left( {\arctan \frac{y-y_0 }{x_s -x_0 }-\alpha } \right) } \right] } \right\} \end{aligned}$$
(14)

As \(x_0 \ge x_s \), the vertical stiffener is penetrated by the crack, which means the stiffener is located at subzones III and IV. The expression of \(\theta \) in the displacement function of the stiffener is a piecewise function in the y direction

$$\begin{aligned} \theta =\left\{ {{\begin{array}{l} {\arctan \frac{y-y_0 }{x-x_0 }-\pi -\alpha ,0\le y\le y_c \mid _{x=x_s } } \\ \\ {\arctan \frac{y-y_0 }{x-x_0 }+\pi -\alpha ,y_c \mid _{x=x_s } \le y\le b} \\ \end{array} }} \right. \end{aligned}$$
(15)

Thus, the crack function of displacement function for the vertical stiffener in the range of \(0\le y\le y_c \mid _{x=x_s } \) is in the form of

$$\begin{aligned}&W_c \left( {r,\theta } \right) \mid _{x=x_s } \nonumber \\&\quad = \left\{ {\mathop \sum \limits _{n=1}^{N_1 } \mathop \sum \limits _{l=0}^n B_{nl} \left[ {\sqrt{\left( {x_s -x_0 } \right) ^{2}+\left( {y-y_0 } \right) ^{2}}} \right] ^{\frac{2n-1}{2}}\hbox {cos}\left[ {\frac{2l+1}{2}\left( {\arctan \frac{y-y_0 }{x-x_0 }-\pi -\alpha } \right) } \right] } \right. \nonumber \\&\qquad +\left. {\mathop \sum \limits _{n=1}^{N_2 } \mathop \sum \limits _{l=0}^n C_{nl} \left[ {\sqrt{\left( {x_s -x_0 } \right) ^{2}+\left( {y-y_0 } \right) ^{2}}} \right] ^{\frac{2n-1}{2}}\hbox {sin}\left[ {\frac{2l+1}{2}\left( {\arctan \frac{y-y_0 }{x-x_0 }-\pi -\alpha } \right) } \right] } \right\} \end{aligned}$$
(16)

As \(y_c \mid _{x=x_s } \le y\le b\), the crack function of the vertical stiffener can be expressed as

$$\begin{aligned}&W_c \left( {r,\theta } \right) \mid _{x=x_s } \nonumber \\&\quad =\left\{ {\mathop \sum \limits _{n=1}^{N_1 } \mathop \sum \limits _{l=0}^n B_{nl} \left[ {\sqrt{\left( {x_s -x_0 } \right) ^{2}+\left( {y-y_0 } \right) ^{2}}} \right] ^{\frac{2n-1}{2}}\hbox {cos}\left[ {\frac{2l+1}{2}\left( {\arctan \frac{y-y_0 }{x-x_0 }+\pi -\alpha } \right) } \right] } \right. \nonumber \\&\qquad \left. {+\mathop \sum \limits _{n=1}^{N_2 } \mathop \sum \limits _{l=0}^n C_{nl} \left[ {\sqrt{\left( {x_s -x_0 } \right) ^{2}+\left( {y-y_0 } \right) ^{2}}} \right] ^{\frac{2n-1}{2}}\hbox {sin}\left[ {\frac{2l+1}{2}\left( {\arctan \frac{y-y_0 }{x-x_0 }+\pi -\alpha } \right) } \right] } \right\} \end{aligned}$$
(17)

The undetermined coefficients \(A_{ij} ,B_{nl}\) and \(C_{nl} \) in Eqs. (7) and (9) are assembled into vector \(\mathbf{q}=\left( {q_1 ,q_2 ,\ldots ,q_{\bar{N}} } \right) ^{T}\) for convenience of presentation, where \(\bar{N} =IJ+N\left( {N+3} \right) \). The displacement function \(W\left( {x,y} \right) \) can be expressed as

$$\begin{aligned}&W\left( {x,y} \right) = \mathop \sum \limits _{{L = 1}}^{{\bar{N}}} q_{L} \bar{W} _{L} \left( {x,y} \right) = \mathop \sum \limits _{{i = 1}}^{I} \mathop \sum \limits _{{j = 1}}^{J} q_{{I\left( {i - 1} \right) + j}} ~X_{i} \left( x \right) ~Y_{j} \left( y \right) \nonumber \\&\quad +\, g\left( {x,y} \right) \left( \mathop \sum \limits _{{n = 1}}^{{N_{1} }} \mathop \sum \limits _{{l = 0}}^{n} q_{{IJ + \frac{{3 + \left( {n - 1} \right) }}{2}\left( {n - 1} \right) + \left( {l + 1} \right) }} r^{{\left( {2n - 1} \right) /2}} {\text {cos}}\frac{{2l + 1}}{2}\theta ~ \nonumber \right. \\&\quad \left. +\, \mathop \sum \limits _{{n = 1}}^{{N_{2} }} \mathop \sum \limits _{{l = 0}}^{n} q_{{IJ + \frac{{3 + N_{1} }}{2}N_{1} + \frac{{3 + \left( {n - 1} \right) }}{2} \left( {n - 1} \right) }+(l+1)} r^{{\left( {2n - 1} \right) /2}} {\text {sin}}\frac{{2l + 1}}{2}\theta ~\right) \end{aligned}$$
(18)

For simplicity of notation, \(N_1 \) and \(N_2 \) in Eq. (18) are set equal to N. Following the Ritz method, functional \(\Pi \) is minimized with respect to each \(q_L \), yielding

$$\begin{aligned} \frac{\partial \Pi }{\partial q_L }=0. \end{aligned}$$
(19)

which leads to the eigenvalue problem

$$\begin{aligned} \mathbf{Kq}={\upomega }^{2}{} \mathbf{Mq}. \end{aligned}$$
(20)

where the stiffness and mass matrices can be assembled using

$$\begin{aligned} K_{{mn}}= & {} D\left[ {\mathop {\iint }\limits _{\varOmega } \left( {\bar{W} _{{m,xx}} + \bar{W} _{{m,yy}} } \right) \left( {\bar{W} _{{n,xx}} + \bar{W} _{{n,yy}} } \right) } \right. \nonumber \\&\left. { - \left( {1 - \upsilon } \right) \left( {\bar{W} _{{m,xx}} \bar{W} _{{n,yy}} + \bar{W} _{{m,yy}} \bar{W} _{{n,xx}} - 2\bar{W} _{{m,xy}} \bar{W} _{{n,xy}} } \right) ~\hbox {d}x\hbox {d}y} \right] \nonumber \\&+ EI\mathop \int \nolimits _{0}^{b} \bar{W} _{{m,yy}} \left( {x_{s} ,y} \right) \bar{W} _{{n,yy}} \left( {x_{s} ,y} \right) \hbox {d}y + EI\mathop \int \nolimits _{0}^{a} \bar{W} _{{m,xx}} \left( {x,y_{s} } \right) \bar{W} _{{n,xx}} \left( {x,y_{s} } \right) \hbox {d}x \end{aligned}$$
(21)
$$\begin{aligned} M_{{mn}}= & {} \rho h\mathop {\iint }\limits _{\varOmega } \bar{W} _{m} \bar{W} _{n} \hbox {d}x\hbox {d}y + \rho b_{s} h_{s} \mathop \int \nolimits _{0}^{b} \bar{W} _{m} \left( {x_{s} ,y} \right) \bar{W} _{n} \left( {x_{s} ,y} \right) \hbox {d}y \nonumber \\&+ \rho b_{s} h_{s} \mathop \int \nolimits _{0}^{a} \bar{W} _{m} \left( {x,y_{s} } \right) \bar{W} _{n} \left( {x,y_{s} } \right) \hbox {d}x \end{aligned}$$
(22)

3 Convergence study

The natural vibration of a square plate reinforced by a horizontal stiffener is analyzed to verify the accuracy of the present approach. The boundary condition of the plate is simply-supported for all four edges. The location of the stiffener relative to the plate is \(y_s =0.5b\). The ratios of the stiffener dimensions to the plate thickness are \(h_s /h=5\) and \(b_s /h=1\), respectively . There is a side crack that is originated at \(c=0.4b\) with the length \(d=0.4a\). The angle between the crack and the horizontal edges of the plate is \(\alpha =15^{\circ }\). The dimensions of the plate \(a\times b\times h=0.5\times 0.5\times 0.005\) m, and the cross section of the stiffener is \(h_s \times b_s =0.025\times 0.005\) m. The material properties are \(\hbox {E}=210\hbox { GPa}\), \(\rho =7.83\times 10^{3} \hbox { kg}/\hbox {m}^{3}\) and \(\upsilon =0.3\).

The natural frequencies are determined using Eq. (20) and are transferred to non-dimensional quantities through being multiplied with \(a^{2}\sqrt{\rho h/D}\). In Table 1, these frequencies were obtained using 8, 9 and 10 orthogonal polynomials in both x and y-directions in Eq. (7). For the corner function in Eq. (9), four choices of N are presented in the summation of \(W_c \left( {r,\theta } \right) \), where \(N=0\) represents the case of an intact plate free of crack. From Table 1, it can be observed that the frequencies of all orders obtained with only \(W_p \) in Eq. (6) converged to the corresponding solution of the intact plate, while those obtained with the full set of \(W_p \) and \(W_c \) tended to converge to the exact solutions with increasing number of terms of polynomials. The results are also compared with the shell finite element model using commercial software ABAQUS, where 42,000 shell elements of type S4R were used to discretize the stiffener and the plate. It can be seen that the finite element results are in good agreement with the solutions from the present approach. The maximum relative difference of frequencies in all cases is 3.2%. The vibration modes of intact plate and cracked plate are also presented and consistent with the results obtained by ABAQUS, as shown in Fig. 3.

Table 1 Convergence of non-dimensional frequency \(\omega a^{2}\sqrt{\rho h/D}\) for a simply supported square stiffened plate
Full size table
Fig. 3
figure 3

Modes of intact and cracked stiffened plate under SSSS boundary condition

Full size image

4 Modal analyses for the cracked stiffened plate

In this section, the natural frequencies and modes of the previously presented plate are analyzed with various settings of stiffener and side crack. Aside from the SSSS boundary, one more condition is added, i.e., two simply supported opposite edges and two free edges (FSFS). Table 2 gives the first five non-dimensional natural frequencies of the intact SSSS plate reinforced with a vertical stiffener placed at various locations. It can be observed that the first three frequencies increase as the stiffener is placed closer and closer to the center line \(x_s =0.5a\). The change in frequencies of orders 4 and 5 is different. Table 3 presents the first five frequencies of the plate reinforced by one stiffener with a side crack of various lengths, orientations and originations to examine how these key parameters affect the vibration of the plate. Only one stiffener, either horizontal or vertical, is considered hereafter.

Table 2 Non-dimensional frequency \(\omega a^{2}\sqrt{\rho h/D}\) for a SSSS stiffened plate with a vertical stiffener
Full size table
Table 3 Non-dimensional frequency \(\omega a^{2}\sqrt{\rho h/D}\) of a SSSS stiffened plate with a side crack
Full size table

As expected, an increasing length of crack reduces the natural frequency of each order due to the decreasing flexural stiffness of the plate. For the stiffened plate (reinforced by a horizontal or vertical stiffener) with a short crack of \(d=0.1a\) and various orientations, the first five frequencies are slightly reduced by less than 1% compared with those of the intact plate. By contrast, a larger horizontal crack with \(\hbox {d}=0.5\hbox {a}\) will lead to reductions in the first- and second-order frequencies by more than 3.6% and 14%, respectively, for the plate reinforced by a vertical stiffener.

The fundamental frequency increases with an increasing orientation angle of the crack. The variations in higher-order frequencies caused by the crack are more complicated.

For a center placed vertical stiffener, i.e., \(x_s =0.5a\), a crack with a length ratio \(d/a=0.5\) will just penetrate the stiffener in the plate. The first and the third frequencies are drastically reduced by 22.8% and 26.8%, respectively, as shown in Table 4. With the increasing crack length, the second frequency of the plate changes little. It should be noted that the stiffener and the plate are cracked together when the crack reaches the stiffener.

The first five frequencies for a FSFS stiffened plate reinforced by a vertical stiffener at \(x_s =0.5a\) are presented in Table 4 considering a crack with various lengths and orientations. Among them the fourth frequency is reduced up to 55% in the case of \(d/a=0.4\) and \(\alpha =0^{{\circ }},15^{{\circ }}\) compared with that of the intact plate. The fifth frequency appears to be the least sensitive to the crack length with less than 0.5% reduction when the crack length is raised to \(d/b=0.5\). It can be drawn from the above analysis that the frequencies of the stiffened plate are affected both by the length and orientation of the crack. It is also observed that the natural frequencies of a FSFS stiffened plate are more likely affected by the crack length than those of a SSSS stiffened plate (Table 3), except for the third frequency.

Table 4 Non-dimensional frequency \(\omega a^{2}\sqrt{\rho h/D}\) of a FSFS stiffened plate with side cracks
Full size table

The effects of crack configuration and stiffener distributions on the first-order frequency of SSSS stiffened plate are investigated as well. With a fixed length of the crack \(d=0.4a\), the fundamental frequency of the plate reinforced by a vertical stiffener is presented in Fig. 4 with different settings of crack origination and orientation. Based on the results, the fundamental frequency is closely related to the crack orientation angle \(\alpha \). It is also observed that the closer the crack tip is to the center line \(y=b/2\), the smaller the fundamental frequency will be. For the horizontal crack with the orientation of \(\alpha =0^{\circ }\), the curve of the fundamental frequency with various c / b is symmetrical to the center line \(y=b/2\), due to the symmetry in both structural geometry and boundary conditions. The flexural rigidity of the plate will be reduced to the maximum extent as the structure is torn by the crack along \(y=b/2\). In Fig. 4, the variations of the fundamental frequency for two symmetrical orientations \(\alpha =15^{\circ }\) and \(-15^{\circ }\) show a mirror-like symmetry with respect to \(c/b=0.5\). It is also worth pointing out that the minimum values of the fundamental frequency with \(\alpha =15^{\circ }\) and \(-15^{\circ }\) are both smaller compared with that value with \(\alpha =0^{\circ }\) given the same length of crack.

Fig. 4
figure 4

Non-dimensional fundamental frequency \(\omega a^{2}\sqrt{\rho h/D}\) of the stiffened plate (vertical stiffener at \(x_s =0.5a)\) with various locations and orientations of crack \(d=0.4\)

Full size image

Next, the fundamental frequency of the plate reinforced by a vertical stiffener is presented in Fig. 5 with various lengths of a horizontal crack that starts at \(c=0.5b\). For such a damaged plate, the fundamental frequency decreases mildly with the growing crack and then drops drastically as soon as the crack breaks the stiffener. In all situations the biggest reduction in frequency happens when the stiffener is placed the closest to the origin of the crack, i.e., \(x_s =0.675a\). With \(x_s =0.675a\), the stiffener breaks once the crack grows up to the threshold value, which is 0.325a. For a very long, penetrating crack \((d=0.5a)\), the fundamental frequencies with different locations of stiffener are very close, the influence of the location of the stiffener on the frequency of the cracked stiffened plate will be almost negligible as the crack breaks the stiffener in the middle, as shown in Fig. 5.

Fig. 5
figure 5

Non-dimensional first-order natural frequencies \(\omega a^{2}\sqrt{\rho h/D}\) of stiffened plates with various lengths of crack and stiffener locations

Full size image

Figure 6 presents the influences of the crack location c on the fundamental frequency with different locations of the stiffener. The length and orientation angle of the crack are \(d=0.5a\) and \(\upalpha =0^{{\circ }}\), respectively. The fundamental frequency decreases as the starting position of the crack is moved further from the upper and lower edges of the plate. The greatest reduction in the fundamental frequency occurs when the crack grows from the center line of the plate, i.e., \(y=b/2\). Again, the location of the stiffener plays a role as the lowest frequency always comes along with \(x_s =0.675a\) for each single choice of \(d=0.5a.\)

Fig. 6
figure 6

Non-dimensional first-order natural frequencies \(\omega a^{2}\sqrt{\rho h/D}\) of stiffened plates with various locations of crack origination and stiffener

Full size image

In the above analysis, the changes in frequencies of stiffened plate are not sensitive to small crack, as the crack length \(d/a\le 0.4\). However, the effect of crack length, location and orientation can be specifically reflected on the vibration modes of the stiffened plate. In Fig. 7, the three-dimensional views of the first four modes of the cracked stiffened plate are shown. The discontinuities in the displacement and its slope across the crack can be seen in each mode of the cracked plate under the boundary conditions of SSSS and FSFS. Figure 8 depicts the first five modes of the intact stiffened plate along with the cracked stiffened plate with side cracks at two different locations (\(c=0.25b\) and 0.5b) and orientations (\(\upalpha =0^{{\circ }}\hbox { and }15^{{\circ }})\). Compared with the modes of the intact stiffened plate, the contour lines in the modes of the cracked stiffened plates are discontinuous or redistributed due to the existence of the cracks, especially for the high-order modes. In the previous frequency analysis, the third-order natural frequency of cracked SSSS stiffened plate with vertical stiffener have a significant reduction when the crack length d reaches 0.4a and the crack location c is 0.5b,  as shown in Table 3. Corresponding to the decrease in natural frequency, the third-order mode changed greatly by the crack is completely different from the mode of intact plate, which can be seen in Fig. 8. Figure 9 presents the modes of FSFS stiffened plate with a side crack of various lengths and orientation. Compare to the intact plate, the fourth modes are changed dramatically by the crack with length \(d\ge 0.2a\), which corresponds to the greatly reduced of fourth frequency as shown in Table 4.

Fig. 7
figure 7

Three-dimensional views for first four modes of cracked stiffened plate with crack parameters (\(d/a =0.5,\upalpha =15^{{\circ }}\), \(c=0.5b\), \(x_s =0.5a)\)

Full size image
Fig. 8
figure 8

Modes of intact stiffened plates and cracked stiffened plates with crack length \(d/a=0.4\) under SSSS boundary condition

Full size image
Fig. 9
figure 9

Modes of intact stiffened plates and cracked stiffened plates with crack location \(c/b=0.5\) under FSFS boundary condition

Full size image

5 Conclusions

In this paper, the free vibration of a cracked stiffened cracked plate is investigated through the Ritz method considering a displacement field expressed by a set of orthogonal polynomials and crack functions. The plate and its stiffener are modeled separately and jointed by implementing the condition for compatibility of displacement. With the present method, one can establish the model with a stiffened plate reinforced by a stiffener at an arbitrary location and can appropriately describe the behavior of stress singularity at the tip of the crack as well as the discontinuity in both displacement and slope across the crack. With the advantages of the method, the coupling effect of the crack parameters (i.e., the length, location and orientation of the crack) and stiffening locations on the natural frequency can be investigated. Furthermore, the situation of a fractured stiffener by the crack can be analyzed. The changes in natural frequencies with the crack’s length and locations before and after the stiffener breaks can be obtained, which has not been published for stiffened plates with a side crack. The solutions of natural frequencies and modes agree well with those obtained with the finite element software ABAQUS. Two typical boundary conditions, namely SSSS and FSFS, are considered. The results from this paper are summarized as follows:

  1. 1.

    As the crack length increases, the stiffness of the plate decreases, and all the frequencies of the stiffened plate decrease. The effects of crack location and orientation depend on the modes of stiffened plate under the constraints of boundary conditions.

  2. 2.

    The fundamental frequency decreases mildly with the increase in crack length and then drops drastically as soon as the crack breaks the stiffener. The effect of the location of the stiffener on the frequency of the cracked stiffened plate will be almost negligible as the crack breaks the stiffener in the middle.

  3. 3.

    Compared to the influence of crack on natural frequency, the modes of crack stiffened plate can better reflect the specific location and orientation of crack. The boundary condition of the stiffened plate determines the configuration of the mode, and the mode determines the influence of the crack location and orientation on the vibration characteristics of the plate.