1 Introduction

Buckling and vibration of plates are two popular research fields that have been studied by many researchers. Some of these studies have focused on the buckling or vibration of plates considering the in-plane load effects. The in-plane loads affect the plate stiffness and change its vibrational behavior and in a limiting case, cause the plate to buckle. Bassily and Dickinson [1] investigated the buckling and vibration of rectangular plates subjected to arbitrary in-plane stresses using the Ritz method based on the classical plate theory (CPT). Dawe and Roufaeil [2] studied the flexural vibration of square plates based on Mindlin plate theory. Lam et al. [3] used a numerical method based on the polynomial functions for vibration analysis of isotropic and orthotropic plates with cutout. Vibration and buckling of elastically supported rectangular plates under uniform in-plane load were studied by Gorman [4]. He used the superposition of three forced vibration problems to calculate the frequencies and buckling loads. Karami and Malekzadeh [5] studied the stability of skewed and trapezoidal plates with different boundary conditions. They mapped the irregular physical domain into a square domain and solved the transformed governing equations by using the differential quadrature (DQ) method. Srivastava et al. [6] used the finite element (FE) method to study the buckling and vibration of stiffened plates subjected to partial in-plane edge loads. Leissa and Kang [7, 8] studied the vibration and buckling of rectangular plates loaded by linearly varying in-plane stresses on two opposite simply supported edges. The formulation was based on CPT, and the solution was performed by the method of Frobenius series. Zhou et al. [9] used the Ritz method for vibrational analysis of homogeneous circular, annular and rectangular plates. Devarakonda and Bert [10, 11] adopted the Airy’s stress function method to study the flexural vibration and buckling of plates under sinusoidal distributed in-plane loads. Nayak [12] and Nayak et al. [13] used the FE method based on a refined higher-order shear deformation theory to investigate the buckling and vibration of initially stressed composite sandwich plates. Civalek [14] studied the buckling, bending and vibration of columns and plates with different shapes. He presented some numerical results based on DQ and harmonic differential quadrature (HDQ) methods. The method of discrete singular convolution (DSC) based on regularized Shannon’s delta (RSD) kernel was used by Civalek [15] to investigate the vibration of isotropic and orthotropic plates with varying thickness. He also used this method to study the vibration and buckling of thick rectangular plates [16]. Civalek et al. [17] considered buckling of Kirchhoff plates under linearly varying in-plane loads with different boundary conditions by DSC method. Wang et al. [18] used DQ method to study the buckling and vibration of rectangular plates and compared the accuracy and convergence of their solution with Leissa and Kang [7]. Buckling of plates subjected to cosine-distributed in-plane loads was investigated with DQ method by Wang et al. [19]. Dong [20] used the Ritz method for three-dimensional vibration analysis of functionally graded (FG) annular plates in which the displacement field was estimated by a set of Chebyshev polynomial series multiplied by the functions that satisfy the boundary conditions. Jana and Bhaskar [21, 22] presented a solution based on the superposition of Airy’s stress functions for stress distribution of an isotropic plate with non-uniform in-plane loading. They calculated the buckling load of the plate by Galerkin’s method. Akhavan et al. [23] studied the buckling and vibration of moderately thick rectangular plates subjected to uniformly and linearly distributed in-plane loads and resting on the Winkler–Pasternak elastic foundation. They presented a closed-form solution based on the Mindlin plate theory. Malekzadeh et al. [24] used a formulation based on three-dimensional (3D) theory of elasticity and DQ method to study the vibration of FG plates subjected to initial thermal stresses. Panda and Ramachandra [25] studied the buckling of rectangular composite plates with non-uniform loading based on the higher-order shear deformation theory. They obtained the prebuckling stress distribution by minimizing the membrane strain energy and used the Galerkin’s approximation method to calculate the buckling loads. Hashemi et al. [26] used the third-order shear deformation theory to study the in-plane and out-of-plane free vibration of thick laminated plates. They derived four uncoupled equations and presented Levy-type solutions to obtain the natural frequencies of the plate. Katsikadelis and Babouskos [27] worked on thickness optimization of thin plates with different geometries to maximize the stiffness or buckling load of the plate. They used the boundary element method to obtain the eigenvalue problem for optimization. Tang and Wang [28] used stress functions based on Chebyshev polynomials to study the buckling of laminates under parabolic edge compression. Ramachandra and Panda [29] investigated the dynamic instability of composite plates subjected to linear and parabolic in-plane loads based on the energy method. Hasheminejad et al. [30] studied the in-plane vibration of elliptical plates with an arbitrarily located elliptical cutout by using Navier’s displacement equation of motion for the state of plane stress. They used the Helmholtz’s decomposition method to obtain an analytical solution. Bambill and Rossit [31] used the Ritz method to investigate the vibration of a plate subjected to linearly varying loads. Thai and Choi [32] investigated the bending, buckling and vibration of rectangular plates under uniform uniaxial and biaxial in-plane loads by a two-variable refined plate theory that accounts for parabolic variation of transverse shear stress through the plate thickness without using shear correction factor.

In this study, the effect of different profiles of non-uniformly distributed in-plane loads is investigated on the vibration behavior of rectangular plates with constraint on in-plane displacements. To calculate the vibration frequencies and buckling loads, the equations of plane elasticity are solved. The solution can be obtained based on the stress or displacement formulation. Many researchers use the stress formulation with considering the Airy’s stress function, but applying the in-plane displacement constraint is difficult in this approach. As a result, the equations of plane elasticity are written in terms of displacement components. For these equations, which are a system of coupled partial differential equations, an analytical solution is developed and the resultant forces are calculated. Then, the Ritz method is employed to extract an eigenvalue problem based on the first-order shear deformation theory (FSDT). Finally, by solving the obtained eigenvalue problem, the buckling loads and vibration frequencies of the plate are calculated. Also, a sensitivity analysis is performed on the problem.

2 Problem formulation

Consider an isotropic and homogeneous plate with length a, width b and thickness h. A coordinate system with its origin located at the plate center and the x, y and z axes along the plate length, width and thickness, respectively, is used to describe the displacements. The displacement field of a deformed plate according to FSDT is expressed as [33]:

$$\begin{aligned} u=u_0 \left( {x,y,t} \right) +zu_1 \left( {x,y,t} \right) , v=v_0 \left( {x,y,t} \right) +zv_1 \left( {x,y,t} \right) , w=w\left( {x,y,t} \right) \end{aligned}$$
(1)

where \(u_0, v_0, w\) represent the displacement components of a point on the mid-plane at \(z=0\), and \(u_1, v_1\) represent the rotation of a line initially perpendicular to the mid-plane relative to y and x axes, respectively. The governing equations of the plate using the principle of virtual work are expressed as [33]:

$$\begin{aligned} \frac{\partial N_{xx}}{\partial x} + \frac{\partial N_{xy} }{\partial y}=\rho h\frac{\partial ^{2}u_0 }{\partial t^{2}}, \frac{\partial N_{yy} }{\partial y}+\frac{\partial N_{xy} }{\partial x}=\rho h\frac{\partial ^{2}v_0 }{\partial t^{2}} \end{aligned}$$
(2)

where \(\rho \) is plate density. The in-plane force resultants are defined as:

$$\begin{aligned} \left\{ {N_{xx}, N_{yy}, N_{xy} } \right\} =\int _{-h/2}^{h/2} {\left\{ {\sigma _{xx}, \sigma _{yy}, \tau _{xy} } \right\} } \hbox {d}z. \end{aligned}$$
(3)

When the strains and rotations are small, the in-plane displacements \(u_{0},v_{0}\) are uncoupled from out-of-plane displacements, i.e., \(u_{1},v_{1}\) and w [33]. This means that the in-plane displacement field does not change during lateral deflection and the values of \(\partial ^{2}u_0 /\partial t^{2}\) and \( \partial ^{2}v_0 /\partial t^{2}\) are zero. As a result, Eq. (2) reduce to

$$\begin{aligned} \frac{\partial N_{xx} }{\partial x}+\frac{\partial N_{xy} }{\partial y}=0, \frac{\partial N_{yy} }{\partial y}+\frac{\partial N_{xy}}{\partial x}=0. \end{aligned}$$
(4)

Equation (4) can be solved easily for some simple cases, such as a plate with free boundary conditions and subjected to uniform or linearly varying in-plane loads at the edges. In these cases, the in-plane loading function satisfies Eq. (4) directly. But for a plate with in-plane constraints or a plate which is subjected to nonlinear in-plane loading profiles, Eq. (4) cannot be solved directly and the stress-strain relations and material constitutive equations must be invoked to rewrite Eq. (4) in terms of displacement components. The strain components are expressed as:

$$\begin{aligned} \varepsilon _x =\frac{\partial u_0 }{\partial x}+z\frac{\partial u_1 }{\partial x}, \varepsilon _y =\frac{\partial v_0 }{\partial y}+z\frac{\partial v_1 }{\partial y}, \gamma _{xy} =\frac{\partial u_0 }{\partial y}+\frac{\partial v_0 }{\partial x}+z\left( {\frac{\partial u_1 }{\partial y}+\frac{\partial v_1 }{\partial x}} \right) . \end{aligned}$$
(5)

According to the Hooke’s law for an elastic material, the constitutive equations are [34]:

$$\begin{aligned} \sigma _{ij} =\lambda \varepsilon _{kk} \delta _{ij} +2G\varepsilon _{ij}, i,j=1,2,3. \end{aligned}$$
(6)

where \(\delta _{ij}\) is the Kronecker delta and \(G,\lambda \) are Lamé’s constants which are expressed as:

$$\begin{aligned} \lambda =\frac{E\nu }{\left( {1+\nu } \right) \left( {1-2\nu } \right) }, G=\frac{E}{2\left( {1+\nu } \right) }. \end{aligned}$$
(7)

where E and \(\nu \) are elastic modulus and Poisson’s ratio, respectively. Using Eqs. (5) and (6), the in-plane force resultants are expressed as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ \end{array} }} \right\} =\int \limits _{-h/2}^{h/2} \left\{ {{\begin{array}{l} {\sigma _{xx} } \\ {\sigma _{yy} } \\ {\tau _{xy} } \\ \end{array} }} \right\} \hbox {d}z=h\left[ {{ \begin{array}{l@{\quad }l@{\quad }l} A&{} \lambda &{} 0 \\ \lambda &{} \mathrm{A}&{} 0 \\ 0&{} 0&{} G \\ \end{array} }} \right] \left\{ {{ \begin{array}{c} {\frac{\partial u_0 (x,y)}{\partial x}} \\ {\frac{\partial v_0 (x,y)}{\partial y}} \\ {\frac{\partial u_0 (x,y)}{\partial y}+\frac{\partial v_0 (x,y)}{\partial x}} \\ \end{array} }} \right\} ; A=\lambda +2G \end{aligned}$$
(8)

By substituting the force resultants from Eqs. (8) into (4), we have:

$$\begin{aligned} A\frac{\partial ^{2}u_0 }{\partial x^{2}}+\left( {G+\lambda } \right) \frac{\partial ^{2}v_0 }{\partial x\partial y}+G\frac{\partial ^{2}u_0 }{\partial y^{2}}=0, A\frac{\partial ^{2}v_0 }{\partial y^{2}}+\left( {G+\lambda } \right) \frac{\partial ^{2}u_0 }{\partial x\partial y}+G\frac{\partial ^{2}v_0 }{\partial x^{2}}=0. \end{aligned}$$
(9)

The equations represented in (9) are a system of coupled partial differential equations and they are solved analytically here. The solution of Eq. (9) is considered as the following:

$$\begin{aligned} u_0 (x,y)=(A_0 +A_1 x+A_2 y)e^{\alpha x+\beta y}, v_0 (x,y)=(B_0 +B_1 x+B_2 y)e^{\alpha x+\beta y} \end{aligned}$$
(10)

where the constants \(A_{i}, B_{i}, i=0,1,2\) are determined later. By substituting Eqs. (10) into (9), two algebraic equations are derived as follows:

$$\begin{aligned}&\left( {A_1 \left( {\left( {2\nu -2} \right) \alpha ^{2}+\left( {2\nu -1} \right) \beta ^{2}} \right) -B_1 \alpha \beta } \right) x+\left( {A_2 \left( {\left( {2\nu -2} \right) \alpha ^{2}+\left( {2\nu -1} \right) \beta ^{2}} \right) -B_2 \alpha \beta } \right) y \nonumber \\&\qquad +\left( {A_0 \left( {\left( {2\nu -2} \right) \alpha ^{2}+\left( {2\nu -1} \right) \beta ^{2}} \right) -B_0 \alpha \beta +A_1 \left( {4\nu -4} \right) \alpha -B_1 \beta +A_2 \left( {4\nu -2} \right) \beta -B_2 \alpha } \right) =0. \end{aligned}$$
(11)
$$\begin{aligned}&\left( {B_1 \left( {\left( {2\nu -2} \right) \beta ^{2}+\left( {2\nu -1} \right) \alpha ^{2}} \right) -A_1 \alpha \beta } \right) x+\left( {B_2 \left( {\left( {2\nu -2} \right) \beta ^{2}+\left( {2\nu -1} \right) \alpha ^{2}} \right) -A_2 \alpha \beta } \right) y \nonumber \\&\qquad + \left( {B_0 \left( {\left( {2\nu -2} \right) \beta ^{2}+\left( {2\nu -1} \right) \alpha ^{2}-A_0 \alpha \beta } \right) +B_2 \left( {4\nu -4} \right) \beta -A_1 \beta +B_1 \left( {4\nu -2} \right) \alpha -A_2 \alpha } \right) =0. \end{aligned}$$
(12)

To satisfy these two algebraic equations, the coefficients of x, y and also the remaining terms in Eqs. (11) and (12) must vanish. This leads to a system of algebraic equations in the form \([H]\{V\}=\{0\}\) where [H] is the matrix of coefficients and \(\{V\}\) is the following vector:

$$\begin{aligned} \mathbf{V}=\{ A_{0}, A_{1}, A_{2}, B_{0}, B_{1}, B_{2}\}^{T}. \end{aligned}$$
(13)

The obtained homogeneous system of equations has a nontrivial solution only if the determinant of [H] equates to zero. By solving this equation, we have:

$$\begin{aligned} \left| {\varvec{H}} \right| =0\rightarrow \alpha =\pm i\beta . \end{aligned}$$
(14)

To calculate the vector of constants \(\mathbf{V}\), the value of \(\alpha =i\beta \) is substituted into \({\varvec{H}}\) and the obtained system of equations is solved. The solution gives three linearly independent vectors as follows:

$$\begin{aligned} {\varvec{V}}_{1} =\left\{ {i, 0, 0, 1, 0, 0} \right\} ^{T}, {\varvec{V}}_{2} =\left\{ {\frac{4\nu -3}{\beta }, i, 0, 0, 1, 0} \right\} ^{T}, {\varvec{V}}_{3} =\left\{ {-\frac{4\nu -3}{\beta }i, 0, i, 0, 0, 1} \right\} ^{T}. \end{aligned}$$
(15)

The vectors corresponding to \(\alpha =-i\beta \) are complex conjugate of the vectors in Eq. (15). Now the solution of Eq. (9) can be written as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {u_0 (x,y)} \\ {v_0 (x,y)} \\ \end{array} }} \right\} =\sum _{j=1}^3 {\left( {C_{1j} {\varvec{B}} {\varvec{V}}_{\varvec{j}} e^{i\beta x+\beta y}+C_{2j} {\varvec{B}}\bar{{\varvec{V}}}_{{\varvec{j}}} e^{-i\beta x+\beta y}} \right) } \end{aligned}$$
(16)

where \(C_{1j}\) and \(C_{2j}\) are constants, \(\bar{{\varvec{V}}}_{{\varvec{j}}} \) is complex conjugate of \({\varvec{V}}_{{\varvec{j}}} \), and the matrix \({\varvec{B}}\) is defined as follows:

$$\begin{aligned} {\varvec{B}}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1&{} x&{} y&{} 0&{} 0&{} 0 \\ 0&{} 0&{} 0&{} 1&{} x&{} y \\ \end{array} }} \right] . \end{aligned}$$
(17)

By substituting \({\varvec{V}}_{{\varvec{j}}}, \hbox {j}=1,2,3\) from Eqs. (15) into (16), the solution of Eq. (9) is expressed as:

$$\begin{aligned} u_0 (x,y)= & {} \left( {C_1 +C_4 x+C_6 y} \right) \left( {\cosh (\beta y)\cos (\beta x)+\sinh (\beta y)\cos (\beta x)} \right) \nonumber \\&+\left( {C_2 -C_3 x-C_5 y} \right) \left( {\cosh (\beta y)\sin (\beta x)+\sinh (\beta y)\sin (\beta x)} \right) , \end{aligned}$$
(18)
$$\begin{aligned} v_0 (x,y)= & {} \left( {-C_2 +C_3 x+\frac{4\nu -3}{\beta }C_4 +C_5 \left( {\frac{4\nu -3}{\beta }+y} \right) } \right) \left( {\cosh (\beta y)\cos (\beta x)+\sinh (\beta y)\cos (\beta x)} \right) \nonumber \\&+\left( {C_1 +\frac{4\nu -3}{\beta }C_3 +C_4 x+C_6 \left( {\frac{4\nu -3}{\beta }+y} \right) } \right) \left( {\cosh (\beta y)\sin (\beta x)+\sinh (\beta y)\sin (\beta x)} \right) . \end{aligned}$$
(19)

In Eqs. (18) and (19), the constants are calculated by applying the boundary conditions.

2.1 Boundary conditions

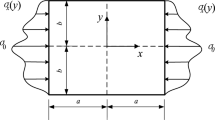
Consider a rectangular plate with symmetric in-plane loading applied along x direction. The plate is constrained against in-plane deformation along y direction (Fig. 1). Due to symmetry, some terms in Eqs. (18) and (19) are removed and the final solution for this case is expressed as:

$$\begin{aligned} u_0 (x,y)= & {} C_4 x\cosh (\beta y)\cos (\beta x) +C_2 \cosh (\beta y)\sin (\beta x)-C_5 y\sinh (\beta y)\sin (\beta x), \end{aligned}$$
(20)
$$\begin{aligned} v_0 (x,y)= & {} C_5 y\cosh (\beta y)\cos (\beta x)+\left( {-C_2 +\frac{4\nu -3}{\beta }C_4 +\frac{4\nu -3}{\beta }C_5 } \right) \sinh (\beta y)\cos (\beta x) \nonumber \\&+\,C_4 x\sinh (\beta y)\sin (\beta x). \end{aligned}$$
(21)
Fig. 1
figure 1

Boundary conditions of a rectangular plate subjected to symmetric non-uniform loading

Full size image

In Eqs. (20) and (21), the constants \(C_{2}, C_{4}, C_{5}\) and the value of \(\beta \) are determined from the boundary conditions. According to Fig.1, the in-plane boundary conditions can be written as:

$$\begin{aligned} v_0 \left( {x,y=\pm \frac{b}{2}} \right) =0; \quad N_{xy} \left( {x,y=\pm \frac{b}{2}} \right) =0; \quad N_{xy} \left( {x=\pm \frac{a}{2},y} \right) =0; \quad N_{xx} \left( {x=\pm \frac{a}{2},y} \right) =-F(y). \end{aligned}$$
(22)

The first three boundary conditions in Eq. (22) are satisfied in the following two cases:

$$\begin{aligned} 1.\qquad C_2= & {} 0, \,\,C_5 =-\frac{4\nu -3}{2(2\nu -1)}C_4, \quad \beta =0. \end{aligned}$$
(23)
$$\begin{aligned} 2.\qquad C_5= & {} 0,\,\, C_2 =\frac{\sin (\beta a/2)(4\nu -4)-a\beta \cos (\beta a/2)}{2\beta \sin (\beta a/2)}C_4, \quad \beta =\frac{2n\pi i}{b} (n=1,2,3,\ldots ). \end{aligned}$$
(24)

Two sets of solutions corresponding to the above states are expressed as

$$\begin{aligned}&1.\qquad u_0 (x,y)=C_{40} x ; v_0 (x,y)=0 \end{aligned}$$
(25)
$$\begin{aligned}&2. \qquad \left\{ {\begin{array}{l} u_0 (x,y)=\sum \limits _{n=1}^\infty {C_{4n} \left( {A_n \cosh (\beta _n y)\sin (\beta _n x)+x\cosh (\beta _n y)\cos (\beta _n x)} \right) } \\ v_0 (x,y)=\sum \limits _{n=1}^\infty {C_{4n} \left( {-A_n \cosh (\beta _n y)\sin (\beta _n x)+\frac{4\nu -3}{\beta _n }\sinh (\beta _n y)\cos (\beta _n x)+x\sinh (\beta _n y)\sin (\beta _n x)} \right) } \\ \end{array}} \right. \nonumber \\&\hbox {where}\,A_n =\frac{\sin (\beta _n a/2)(4\nu -4)-a\beta _n \cos (\beta _n a/2)}{2\beta _n \sin (\beta _n a/2)}. \end{aligned}$$
(26)

Here the values of \(C_{4n}, n=0,1,2,\ldots \) must be calculated such that the final solution satisfies the in-plane loading at the plate edges [the fourth boundary condition of Eq. (22)]. To do this, the value of \(N_{xx}\) is calculated at the plate edges \((x=\pm a/2)\) from the obtained solution in Eqs. (20) and (21) and it is equated to the cosine expansion of the loading function F(y), as follows:

$$\begin{aligned} N_{xx} (x=\pm a/2,y)= & {} F(y)\rightarrow b_0 +\sum _{n=1}^\infty {b_n \cos \left( {\frac{n\pi }{b}y} \right) } =C_0 \frac{Eh\left( {\nu -1} \right) }{\left( {1+\nu } \right) \left( {2\nu -1} \right) } \nonumber \\&+ \sum _{n=1}^\infty {C_n \frac{Eh\left( {2\cos \left( {\frac{\beta _n a}{2}} \right) \sin \left( {\frac{\beta _n a}{2}} \right) +\beta _n a} \right) \cosh \left( {\beta _n y} \right) }{2\left( {1+\nu } \right) \sin \left( {\frac{\beta _n a}{2}} \right) }}. \end{aligned}$$
(27)

Now the values of \(C_n, n=0,1,2,\ldots \) are calculated by multiplying the two sides of Eq. (27) by \(\cos (m\pi y/b)\) and integrating with respect to y from \(-b/2\) to b / 2 for \(m=0,1,2,\ldots \). As a result, a system of algebraic equations is obtained and by solving this system, the values of constants \(C_n\) are determined. Finally, the in-plane force resultants are calculated based on Eq. (8). After obtaining the in-plane displacement field and force resultants, the Ritz method in conjunction with Hamilton’s principle is used to calculate the buckling load and natural frequencies of the plate.

3 Energy of plate based on FSDT

The total potential energy of the plate during lateral deflection is \(\Pi =U_1 +U_2 \), where \(U_1 \) is the strain energy of bending deformations, and \(U_2 \) is the potential energy due to in-plane forces during lateral deflection [35, 36]:

$$\begin{aligned} U_1= & {} \frac{1}{2}\iint \limits _S {\left( {\left\{ {M_{xx}, M_{yy} ,M_{xy} } \right\} \left\{ {\frac{\partial u_1 }{\partial x}, \frac{\partial v_1 }{\partial y}, \frac{\partial u_1 }{\partial y}+\frac{\partial v_1 }{\partial x} } \right\} ^{T}+\left\{ {Q_x, Q_y } \right\} \left\{ {u_1 +\frac{\partial w}{\partial x}, v_1 +\frac{\partial w}{\partial y}} \right\} ^{T}} \right) } \hbox {d}x\hbox {d}y, \nonumber \\ U_2= & {} \frac{1}{2}\iint \limits _S {\left( {N_{xx} \left( \frac{\partial w}{\partial x}\right) ^{2}+N_{yy} \left( \frac{\partial w}{\partial y}\right) ^{2}+2N_{xy} \frac{\partial w}{\partial x}\frac{\partial w}{\partial y}} \right) \hbox {d}x\hbox {d}y} \end{aligned}$$
(28)

where S is the mid-plane area, and the moment resultants and transverse shear forces are defined as:

$$\begin{aligned} \left\{ {M_{xx}, M_{yy}, M_{xy} } \right\} =\int \limits _{-h/2}^{h/2} \left\{ {\sigma _{xx} ,\sigma _{yy}, \tau _{xy} } \right\} z\hbox {d}z, \left\{ {Q_x,Q_y } \right\} =k_s \int \limits _{-h/2}^{h/2} \left\{ {\tau _{xz} ,\tau _{yz} } \right\} \hbox {d}z. \end{aligned}$$
(29)

Here \(k_{s}\) is the shear correction factor, and its value is equal to 5/6 for isotropic plate [35]. By substituting Eqs. (5) and (6) into (29), the moment resultants and transverse shear forces are related to displacements as:

$$\begin{aligned} \left\{ {{\begin{array}{l} {M_{xx} } \\ {M_{yy} } \\ {M_{xy} } \\ \end{array} }} \right\} =\frac{h^{3}}{12}\left[ {{ \begin{array}{c@{\quad }c@{\quad }c} A&{} \lambda &{} 0 \\ \lambda &{} A&{} 0 \\ 0&{} 0&{} G \\ \end{array} }} \right] \left\{ {{ \begin{array}{c} {\frac{\partial u_1 }{\partial x}} \\ {\frac{\partial v_1 }{\partial y}} \\ {\frac{\partial u_1 }{\partial y}+\frac{\partial v_1 }{\partial x}}\\ \end{array} }} \right\} , \left\{ {{ \begin{array}{l} {Q_x } \\ {Q_y } \\ \end{array} }} \right\} =k_s Gh\left[ {{ \begin{array}{c@{\quad }c} 1&{} 0 \\ 0&{} 1 \\ \end{array} }} \right] \left\{ {{ \begin{array}{c} {u_1 +\frac{\partial w}{\partial x}} \\ {v_1 +\frac{\partial w}{\partial y}} \\ \end{array} }} \right\} . \end{aligned}$$
(30)

The kinetic energy of the plate is expressed as

$$\begin{aligned} T=\frac{1}{2}\rho {\int \!\!\int \!\!\int }_V {\left( {\left( {\frac{\partial u}{\partial t}} \right) ^{2}+\left( {\frac{\partial v}{\partial t}} \right) ^{2}+\left( {\frac{\partial w}{\partial t}} \right) ^{2}} \right) \hbox {d}x \hbox {d}y \hbox {d}z}. \end{aligned}$$
(31)

By substituting the displacement field from Eqs. (1) into (31) and equating the values of \(\partial ^{2}u_0 /\partial t^{2}\) and \(\partial ^{2} v_0 /\partial t^{2}\) to zero, as was explained in the previous section, Eq. (31) is simplified as:

$$\begin{aligned} T=\frac{\rho h^{3}}{24}\iint _S {\left( {\left( {\frac{\partial u_1}{\partial t}} \right) ^{2}+\left( {\frac{\partial v_1}{\partial t}} \right) ^{2}} \right) } dS+\frac{\rho h}{2}\iint _S {\left( {\left( {\frac{\partial w}{\partial t}} \right) ^{2}} \right) } \hbox {d}x\hbox {d}y. \end{aligned}$$
(32)

For a vibrating plate, the solution can be expressed as a function of time and spatial variables as follows:

$$\begin{aligned} u_1 (x,y,t)=X(x,y) e^{i\omega t},\,\, v_1 (x,y,t)=Y(x,y) e^{i\omega t},\,\, w(x,y,t)=W(x,y) e^{i\omega t} \end{aligned}$$
(33)

where \(\omega \) is the natural frequency of the plate. For a plate with simply supported boundary conditions, the spatial part of displacements is expressed as:

$$\begin{aligned} X(x,y)= & {} \sum \limits _{m=1}^\infty \sum \limits _{n=1}^\infty X_{mn} \cos \left( {\frac{m\pi \left( {x-a/2} \right) }{a}} \right) \sin \left( {\frac{n\pi \left( {y-b/2} \right) }{b}} \right) , \nonumber \\ Y(x,y)= & {} \sum \limits _{m=1}^\infty \sum \limits _{n=1}^\infty Y_{mn} \sin \left( {\frac{m\pi \left( {x-a/2} \right) }{a}} \right) \cos \left( {\frac{n\pi \left( {y-b/2} \right) }{b}} \right) , \nonumber \\ W(x,y)= & {} \sum \limits _{m=1}^\infty \sum \limits _{n=1}^\infty W_{mn} \sin \left( {\frac{m\pi \left( {x-a/2} \right) }{a}} \right) \sin \left( {\frac{n\pi \left( {y-b/2} \right) }{b}} \right) \end{aligned}$$
(34)

where \(X_{mn}, Y_{mn}, W_{mn}\) are constants that will be determined. Hamilton’s principle is expressed as [35]:

$$\begin{aligned} \delta \int \limits _{t_1 }^{t_2 } {(\Pi -T)\hbox {d}t=0}. \end{aligned}$$
(35)

By substituting the displacement field from Eqs. (33) and (34) into (28) and (32), the integrand of Eq. (35) is obtained as a function of constants \(X_{mn}, Y_{mn}, W_{mn}\). By applying the Ritz minimization method, we have:

$$\begin{aligned} \frac{\partial (\Pi -T)}{\partial X_{mn} }=0, \frac{\partial (\Pi -T)}{\partial Y_{mn} }=0, \frac{\partial (\Pi -T)}{\partial W_{mn} }=0. \end{aligned}$$
(36)

Equation (36) is written in the matrix form as follows:

$$\begin{aligned} ({\varvec{K}}_{{\varvec{b}}} -\eta {\varvec{K}}_{{\varvec{G}}} -\omega ^{2} {\varvec{M}}) {\varvec{d}}=0 \end{aligned}$$
(37)

where \({\varvec{M}}\) is the mass matrix, \({\varvec{K}}_{{\varvec{b}}}\) and \({\varvec{K}}_{{\varvec{G}}}\) are the bending and geometric stiffness matrices, which are related to the bending strain energy \((U_1)\) and potential energy \((U_2)\), respectively, \({\varvec{d}}\) is the vector of constants, and \(\eta \) is the loading factor. Equation (37) has a nontrivial solution only if the following determinant is zero:

$$\begin{aligned} \left| {{\varvec{K}}_{{\varvec{b}}} -\eta {\varvec{K}}_{{\varvec{G}}} -\omega ^{2} {\varvec{M}}} \right| =0. \end{aligned}$$
(38)

According to Eq. (38), three problems can be considered:

  1. a.

    Free vibration in the absence of in-plane loads: In this case, \(\eta =0\) and Eq. (38) reduces to \(\left| {{\varvec{K}}_{{\varvec{b}}} -{\varvec{M}}\omega ^{2}} \right| =0\). By solving this equation, the natural frequencies of the plate are calculated.

  2. b.

    Vibration of a plate subjected to in-plane loading: In this case, the value of \(\eta \) is known and by solving Eq. (38), the natural frequencies of the plate are calculated.

  3. c.

    Buckling of the plate: In this case, \(\omega =0\), and Eq. (38) reduces to\(\left| {{\varvec{K}}_{{\varvec{b}}} -\eta {\varvec{K}}_{{\varvec{G}}} } \right| =0\). The solution of this equation results the buckling load.

4 FE analysis

Besides the analytical solution, a numerical solution based on FE analysis has been performed by using the ABAQUS commercial package. S4R element has been used for meshing. This element is a four-node, quadrilateral, stress/displacement shell element with reduced integration and a large-strain formulation, which is suitable for analyzing thick or thin plates and shells [37]. The size of each element is approximately \(2\times 2\,\hbox {mm}\), which is selected by a mesh sensitivity analysis. The in-plane load is applied at \(x=\pm a/2\). Also the in-plane and out-of-plane boundary conditions are applied at the corresponding plate edges.

5 Results and discussion

In this paper, the effect of four types of in-plane loading profiles, i.e., constant, parabolic, cosine and triangular loading (Fig. 2) on the buckling and vibration of an isotropic plate, is studied. The calculations are performed in Maple mathematical environment. The characteristics of the plate are listed in Table 1. In order for the results to be comparable, the equivalent static load, which is the value of \({\int }_{-b/2}^{b/2} {F(y)\hbox {d}y}\), is constant and equal to \(N_{0}b\) for all load profiles. The governing equations of in-plane displacement field for a plate subjected to non-uniform loading (Eq. 9) have been solved analytically for each loading profile. After that, the resultant forces \(N_{xx}, N_{yy}\) and \(N_{xy}\) are calculated. In Fig. 3, the contour plots of the resultant forces are shown for different loading profiles. The resultant forces are normalized by the loading amplitude \(N_0\).

Fig. 2
figure 2

Different types of in-plane loading. a Constant, b Parabolic, c Cosine, d Triangular

Full size image
Table 1 Plate characteristics
Full size table

At first, the buckling load of a square plate with \(h=2.5\,\hbox {mm}\) has been evaluated for different values of “n” in Eq. (27). The results of this study are shown in Table 2, and the calculations are compared with FE results. In the last column, the difference between analytical and FE values is reported as: \(\hbox {diff}(\%)={\vert }(\hbox {analytical value}-\hbox {FE value})/ \hbox {FE value} {\vert }*100\). The results show good convergence of the obtained solution. According to Table 2, the value of \(n=5\) is selected for calculations.

Fig. 3
figure 3

Contour of normalized resultant forces, a–c cosine loading, d–f parabolic loading, g–i triangular loading

Full size image
Table 2 Solution convergence for buckling load (N/mm) of a square plate in terms of different values of “n”
Full size table

In Table 3, the non-dimensional buckling load \(\bar{N}_\mathrm{cr} =N_\mathrm{cr} b^{2}/\pi ^{2}D\) of an unrestrained plate is calculated by the present method and is compared with the existing results from different methods, such as DQ, DSC and Airy’s stress function method. Here \(D=Eh^{3}/12(1-\nu ^{2})\) is the flexural rigidity of the plate, and \(N_\mathrm{cr}\) is the critical load at which the plate buckles.

Table 3 Comparison of buckling load \(\bar{N}_\mathrm{cr}\) with existing results for different loading profiles
Full size table

In Table 4, the natural frequencies of a square plate with different in-plane loading profiles are presented and compared with the FE results. In this table, the effect of \(N_{0}/N_\mathrm{cr}\) on the plate frequencies has been investigated. It is seen that by increasing this ratio, the frequency decreases in all modes, and for \(N_{0}/N_\mathrm{cr}=1\), the frequency of the first mode becomes zero, which is an indication of the buckling instability. Also it is interesting to note that the vibrational frequency of the first mode is the same for all loading profiles and only depends on \(N_{0}/N_\mathrm{cr}\). Comparison of the results with FE solution shows a good agreement, which indicates that the obtained analytical solution can predict the frequencies and buckling loads with appropriate accuracy.

Table 4 Natural frequencies (Hz) of a square plate subjected to in-plane loading with different intensities
Full size table

Table 5 represents the non-dimensional buckling load \(\bar{N}_\mathrm{cr}\) of rectangular plates with different aspect ratios (a / b) and thickness ratios (b / h) for four types of loading profiles.

Table 5 Buckling load \(\bar{N}_\mathrm{cr}\) of a plate under different loading profiles
Full size table

The effect of in-plane compressive loading on vibration behavior of plates with different aspect ratios and thickness ratios is shown in Figs. 4, 5, 6. In these figures, variation of the fundamental frequency of a rectangular plate subjected to different in-plane loading profiles is plotted. The horizontal axis is non-dimensional loading amplitude expressed as \(\overline{N_0} =N_0 b^{2}/\pi ^{2}D\), and the vertical axis is non-dimensional natural frequency expressed as \(\bar{\omega }=\omega b^{2}\sqrt{\rho h/D}\).

Fig. 4
figure 4

Fundamental frequency of plates with different aspect ratios and subjected to in-plane loading for \(b/h=40\)

Full size image
Fig. 5
figure 5

Fundamental frequency of plates with different aspect ratios and subjected to in-plane loading for \(b/h=20\)

Full size image
Fig. 6
figure 6

Fundamental frequency of plates with different aspect ratios and subjected to in-plane loading for \(b/h=10\)

Full size image

When a plate is subjected to in-plane compressive loading, its stiffness decreases and as a result, the natural frequencies of the lateral vibration decrease too. As the value of in-plane load approaches the buckling load, the fundamental frequency approaches to zero and finally the plate buckles. This behavior has been shown in Figs. 4, 5, 6. These figures show that the buckling load and vibrational frequency of a plate with parabolic loading are always higher than other loading profiles. Also plates with constant loading have higher buckling loads and frequencies in comparison with the triangular and cosine loading profiles. The plates with triangular and cosine loading have similar behavior. By increasing the aspect ratio, the effect of loading profile on vibrational frequency reduces and the graphs become similar for higher aspect ratios. Also, by increasing the plate aspect ratio, the vibrational frequency decreases.

In Fig. 7, the effect of plate thickness on fundamental frequency of a square plate subjected to in-plane parabolic loading has been shown. A similar trend happens for other loading profiles. According to Fig. 7, the fundamental frequency of a plate without in-plane loads \((N_{0}=0)\) has linear variation with thickness in the studied range. The vibrational frequency of a plate under compressive loading is always lower than a plate without in-plane or under tensile loads. For plates under compressive loading, as the plate thickness decreases, the vibrational frequency decreases rapidly and finally becomes zero at buckling instability. For a plate subjected to tensile in-plane loads, the graph has a minimum value. In this case, when the plate thickness increases, the frequency decreases up to a minimum point and then, the frequency increases. In fact, increasing the thickness increases the mass which can reduce the frequency. Also the tensile load increases the stiffness and as a result, increases the frequency, and the effect of tensile load is dominant beyond this point. It is also seen that when the plate thickness increases, the vibrational behavior of the plate for these three cases (compressive, tensile and no load) becomes similar and the effect of in-plane load value on frequency vanishes.

Fig. 7
figure 7

Effect of plate thickness on vibrational frequency of a square plate

Full size image

6 Conclusions

In this paper, the buckling and vibration of rectangular plates subjected to different non-uniform in-plane loading profiles were studied. An analytical solution was presented for calculating the prebuckling distribution of in-plane resultant forces by solving the equations of in-plane displacement field. The Ritz method was used for calculating the buckling load and vibrational frequencies of the plate.

In numerical methods such as DSC and DQ, the domain of solution must be discretized and an appropriate grid system must be used. Also in FE method, the domain must be meshed, while in the presented solution, no meshing or grid points are required. The numerical methods suffer from instabilities, such as shear locking in FE or divergency due to grid size. In DSC and DQ, there are different methods and kernels for calculating the weighting coefficients, and selecting the best method for each problem is not an easy procedure. Also, applying the boundary conditions is not straightforward in DSC and DQ methods. The presented analytical procedure is free from mentioned difficulties, and it seems that, the introduced analytical method is more appropriate with respect to the numerical methods. Also by preparing a simple code on a mathematical environment (e.g., Maple), it is possible to perform sensitivity analysis easily and it is not necessary to discretize or mesh the problem domain for each case.

Using the presented method, the effect of four types of in-plane loading profiles, intensity of the in-plane loading, aspect ratio and thickness ratio of the plate on the vibrational frequencies and buckling load was investigated. A good agreement with FE and some existing results proves the correctness and accuracy of the proposed procedure. The results are summarized as the following:

  • For the same equivalent static loading, the plates which are subjected to parabolic loading have higher buckling loads and frequencies with respect to the other considered load distributions.

  • The buckling load and frequencies of plates with uniform loading are higher than the plates subjected to triangular and cosine loading profiles, while there is no significant difference between behavior of plates with cosine and triangular loading.

  • When the plate thickness increases, the non-dimensional buckling load and frequencies decrease.

  • The frequency of the plate decreases as its aspect ratio increases. Also by increasing the aspect ratio, the effect of loading profile on vibrational frequency decreases.

  • The effect of the plate thickness on frequency depends strongly on the mode of in-plane loading (i.e., tensile, compressive or free load). In a plate without in-plane loading, the vibrational frequency varies linearly with thickness in the studied range, while for the compressive loading, the frequency decreases rapidly near the buckling load and finally the plate buckles. Also in the case of tensile loading, for small thicknesses, by increasing the plate thickness, the vibrational frequency decreases and for a certain thickness, the frequency has its lowest value. After this point, the frequency increases by increasing the plate thickness.