Keywords

1 Introduction

Composite materials have long been widely used in aerospace, mechanical and civil engineering due to its features of high strength-to-weight and stiffness-to-weight ratios [2]. Such materials can be generally modeled as orthotropic plates by utilizing anisotropic materials and altering the isotropic properties along perpendicular directions in manufacturing processes [21]. In thermal environment, the presence of cracks can accelerate the change of material properties, inducing the loss of stability and reliability. Hence, the understanding of dynamic response of orthotropic plates subject to both cracking and thermal effects is crucial for engineers and researchers.

In the past, various plate theories have been well established for structural analysis [9, 10, 13]. To study the influence of cracks on the dynamic responses of plates, Rice and Levy [14] proposed a ling-spring model (LSM) based on the classical Kirchhoff plate theory, where the part-through crack located at the center of rectangular plates can be represented by a line-spring. Recently, Israr et al. [3] and Joshi et al. [5] extended their works and developed analytical models for vibration analysis of cracked isotropic and orthotropic plates, respectively. However, only a few number of articles have been published on the dynamic analysis of cracked plates subject to thermal conditions. Natarajan et al. [11] analyzed the cracked functionally graded plates under various parameters, such as crack length and temperature variation. In addition, Joshi et al. [6] proposed an analytical model to study the vibration characteristics of heated and cracked thin orthotropic plates.

The prime objective of this work is to present accurate solutions for the prediction of structural responses of cracked plates in thermal environment by using the discrete singular convolution (DSC) method. The DSC method emerges as an efficient numerical method that was firstly proposed by Wei [17]. It is regarded as a local method with good flexibility for dealing complex geometries and boundary conditions, but also it holds a high level of accuracy [12, 19, 20]. To go beyond the restriction of the original DSC technique, the incorporation of the Taylor series expansion method was proposed for the treatment of structural elements with free edges [15, 16]. Although the DSC method has been further explored for solving a variety of plate problems [1, 7], it is still a lack of applications on the analysis of cracked plates. This study firstly attempts to apply this method to fill this knowledge gap. The obtained solutions herein are compared with those from the open literature to validate the accuracy and reliability. Some accurate benchmark solutions are also presented. In addition, this paper aims to share and introduce this work to other participants of the 25th Australasian Conference on Mechanics of Structures and Materials with common research interests. A comprehensive investigation for this research, including thermal buckling analysis, vibration mode shapes and special restrained manner of simply-supported conditions, can be referred to the authors’ recent work [8].

2 Theoretical Formulation

2.1 Governing Equation

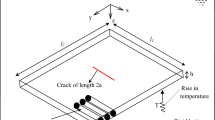
The governing equation of rectangular orthotropic plates subject to both crack and thermal effects has been rigorously treated by Joshi et al. [6]. Figure 1 shows the geometry and coordinate system of an orthotropic plate, wherein two linear surface cracks with lengths 2a and 2b are parallel to the x-axis and y-axis, respectively. The plate has a uniform thickness h that is sufficiently thin when comparing to its in-plane dimensions (i.e., length L1 and width L2).

Fig. 1
figure 1

Geometry and coordinate system of an orthotropic plate with surface part-through cracks subject to thermal loads

Full size image

According to the classical plate theory, the governing equation of orthotropic rectangular plates with a surface crack (along the x-axis) in thermal environment is expressed as [6]

$$\begin{aligned} & D_{x} \frac{{\partial^{4} w}}{{\partial x^{4} }} + 2B_{o} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + D_{y} \frac{{\partial^{4} w}}{{\partial y^{4} }} \\ & \quad = - \rho h\frac{{\partial^{2} w}}{{\partial t^{2} }} - N_{x}^{T} \frac{{\partial^{2} w}}{{\partial x^{2} }} - N_{y}^{T} \frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{{\partial^{2} M_{x}^{T} }}{{\partial x^{2} }} - \frac{{\partial^{2} M_{y}^{T} }}{{\partial y^{2} }} + \frac{{\partial^{2} \bar{M}_{y} }}{{\partial y^{2} }} \\ & \quad\quad + \bar{N}_{y} \frac{{\partial^{2} w}}{{\partial y^{2} }} + P_{z} \\ \end{aligned}$$
(1)

where Bo = Dxvy + Gxyh3/6, Dx = Exh3/[12(1 − vxvy)] and Dy = Eyh3/[12(1 − vxvy)] are the flexural rigidities with Young’s modulus (Ex, Ey), Poisson’s ratio (vx, vy) and shear modulus (Gxy); \(N_{x}^{T}\) and \(N_{y}^{T}\) are the in-plane forces per unit length due to the thermal effect; \(M_{x}^{T}\) and \(M_{y}^{T}\) are the moments induced by heating loads; \(\bar{N}_{y}\) and \(\bar{M}_{y}\) represent the in-plane force and moment resulted by the presence of cracks, respectively; and \(P_{z}\) denotes the transverse load per unit area acting on the plate surface.

2.2 Formulation of Crack Terms

Using the LSM, we transform the cracked plate into a two-dimensional problem. The uniformly distributed tensile stress and the bending stress at the far edges of the plate are written as [14]

$$\begin{aligned} \sigma_{rs} & = \frac{{N_{rs} }}{h} = \frac{1}{h}\int\limits_{ - h/2}^{h/2} {\tau_{rs} (x,y,z)dz\,} \ \text{and} \\ {m}_{rs} & = \frac{6}{h}M_{rs} = \frac{6}{{h^{2} }}\int\limits_{ - h/2}^{h/2} {z\tau_{rs} (x,y,z)dz} \\ \end{aligned}$$
(2)

where τrs(x, y, z) is the stress state, r and s are intermediate variables, Nrs and Mrs are, respectively, the force and moment per unit length in the direction perpendicular to the crack length at the edges of the plate. The crack is represented as a continuous line-spring with compliance, and these compliance coefficients are used to raise the relationship between the tensile stress and the bending stress at the far sides of the plate and the crack location as follows

$$\begin{aligned} \bar{\sigma }_{rs} & = \left[ {\frac{2a}{{(6\alpha_{tb}^{o} + \alpha_{tt}^{o} )(1 - v^{2} )h + 2a}}} \right]\sigma_{rs} \ \text{and} \\ \bar{m}_{rs} & = \left[ {\frac{2a}{{3(\alpha_{bt}^{o} /6 + \alpha_{bb}^{o} )(3 + v)(1 - v)h + 2a}}} \right]m_{rs} \\ \end{aligned}$$
(3)

where \(\alpha_{bb}^{o} ,\alpha_{tt}^{o} ,\alpha_{bt}^{o} ( = \alpha_{bt}^{o} )\) denote the non-dimensional bending compliance, stretching compliance and stretching-bending compliance, respectively. Their values depend on the ratio ζ = d/h (where d is the crack depth and h is the  plate thickness) in the range of 0.1–0.7 [14]. The tensile force and the moment caused by a crack along the x-axis can be expressed as

$$\bar{N}_{y} \equiv - \bar{N}_{rs} = - \left[ {\frac{2a}{{(6\alpha_{tb}^{o} + \alpha_{tt}^{o} )(1 - v_{x}^{2} )h + 2a}}} \right]N_{rs}$$
(4)
$$\bar{M}_{y} \equiv - \bar{M}_{rs} = - \left[ {\frac{2a}{{3(\alpha_{bt}^{o} /6 + \alpha_{bb}^{o} )(3 + v_{x} )(1 - v_{x} )h + 2a}}} \right]M_{rs}$$
(5)

where the negative signs are due to the reduction of the overall stiffness from damages. The bending stress at the far sides of the plate is given by

$$M_{rs} = - D_{y} \left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + v_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)$$
(6)

2.3 Thermal Effect

In this work, the uniformly distributed heating load is considered. The in-plane shear force is then vanished and only the membrane force is considered. The thermal stress parameters are defined as

$$\sigma_{x}^{T} = \frac{{E_{x} T(z)}}{{1 - v_{x} v_{y} }}(\alpha_{x} + \alpha_{y} v_{y} ),\sigma_{y}^{T} = \frac{{E_{y} T(z)}}{{1 - v_{x} v_{y} }}(\alpha_{y} + \alpha_{x} v_{x} ),\tau_{xy}^{T} = 0$$
(7)

where αx and αy are the coefficients of thermal expansion in the x- and y-directions, respectively. The variation of temperature at the plate is assumed as T(z) = ΔT. The in-plane forces and the moments caused by the thermal effect can be written as

$$N_{x}^{T} = \frac{{E_{x} h\Delta T(\alpha_{x} + \alpha_{y} v_{y} )}}{{1 - v_{x} v_{y} }},N_{y}^{T} = \frac{{E_{y} h\Delta T(\alpha_{y} + \alpha_{x} v_{x} )}}{{1 - v_{x} v_{y} }},M_{x}^{T} = M_{y}^{T} = 0$$
(8)

Making use of the LSM, only the membrane force due to the change of temperature is considered (i.e., \(N^{T} = N_{rs}\)). For generality and simplicity, the dimensionless parameters are defined as

$$X = \frac{x}{{L_{1} }},Y = \frac{y}{{L_{2} }},W = \frac{w}{{L_{1} }},\lambda = \frac{{L_{1} }}{{L_{2} }},\Omega = \omega L_{1}^{2} \sqrt {\frac{\rho h}{{D_{x} }}}$$
(9)

where ω is a circular frequency. Using Eq. (9) and substituting the crack terms and thermal terms stated above into the governing Eq. (1), we have

$$\begin{aligned} & \frac{{\partial^{4} W}}{{\partial X^{4} }} + 2\frac{{B_{o} \lambda^{2} }}{{D_{x} }}\frac{{\partial^{4} W}}{{\partial X^{2} Y^{2} }} + \lambda^{4} \frac{{D_{y} }}{{D_{x} }}\frac{{\partial^{4} W}}{{\partial Y^{4} }} \\ & \quad =\Omega ^{2} W - \frac{{L_{1}^{2} }}{{D_{x} }}\left[ {\frac{{E_{x} h\Delta T(\alpha_{x} + \alpha_{y} v_{y} )}}{{1 - v_{x} v_{y} }}\frac{{\partial^{2} W}}{{\partial X^{2} }} + \lambda^{2} \frac{{E_{y} h\Delta T(\alpha_{y} + \alpha_{x} v_{x} )}}{{1 - v_{x} v_{y} }}\frac{{\partial^{2} W}}{{\partial Y^{2} }}} \right] \\ & \quad + A\frac{{D_{y} }}{{D_{x} }}\left( {\lambda^{4} \frac{{\partial^{4} W}}{{\partial Y^{4} }} + v_{x} \lambda^{2} \frac{{\partial^{4} W}}{{\partial X^{2} Y^{2} }}} \right) - B\frac{{L_{1}^{2} }}{{D_{x} }}\frac{{E_{y} h\Delta T(\alpha_{y} + \alpha_{x} v_{x} )}}{{1 - v_{x} v_{y} }}\left( {\lambda^{2} \frac{{\partial^{2} W}}{{\partial Y^{2} }}} \right) \\ & \quad + \frac{{L_{1}^{4} P_{z} }}{{D_{x} }} \\ \end{aligned}$$
(10)

where \(A = \frac{2a}{{3(\alpha_{bt}^{o} /6 + \alpha_{bb}^{o} )(3 + v_{x} )(1 - v_{x} )h + 2a}}\) and \(B = \frac{2a}{{(6\alpha_{tb}^{o} + \alpha_{tt}^{o} )(1 - v_{x}^{2} )h + 2a}}\). For a free vibration analysis, we assume \(P_{z} = 0\) in Eq. (10).

It is known that the fundamental frequency of an intact plate is zero at the critical buckling temperature [6]. This can also be applied to cracked plates. By substituting the general solution w(x, y) = Wmn sin(mπx/L1) sin(nπy/L2) to Eq. (10), the critical buckling temperature becomes

$$T_{cr} = \frac{{h^{2} \pi^{2} }}{{12L_{1}^{2} }}\left[ {\frac{{D_{x} m^{4} + 2B_{o} \lambda^{2} m^{2} n^{2} + D_{y} \lambda^{4} n^{4} - AD_{y} (\lambda^{4} n^{4} + v_{x} \lambda^{2} m^{2} n^{2} )}}{{D_{x} (\alpha_{x} + \alpha_{y} v_{y} )m^{2} + (1 + B)D_{y} (\alpha_{y} + \alpha_{x} v_{x} )\lambda^{2} n^{2} }}} \right]$$
(11)

where m and n are the number of half sine waves in both directions. Equation (11) can be reduced to the model proposed by Jones [4] for plates without cracks. To satisfy the material properties, the minimum critical buckling temperature can be obtained by setting m = n = 1.

3 Solution Procedure

3.1 DSC Algorithm

Following the DSC algorithm, a weighted linear combination of the function values at uniformly distributed points \((2M + 1)\) is employed to approximate the nth derivatives of a function f(x). It can be discretized as

$$f^{(n)} (x_{i} ) = \sum\limits_{k = - M}^{M} {\delta_{\alpha ,\Delta }^{(n)} f(x_{k} )}$$
(12)

where Δ is a grid spacing, δα,Δ is a delta kernel of the Dirichlet type. In this work, the regularized Shannon’s delta kernel (RSK) [17] is employed as

$$\delta_{\alpha ,\Delta }^{{}} (x - x_{k} ) = \frac{{\sin [(\pi /\Delta )(x - x_{k} )]}}{{(\pi /\Delta )(x - x_{k} )}}\exp \left[ { - \frac{{(x - x_{k} )^{2} }}{{2\sigma^{2} }}} \right]$$
(13)

where σ is a controllable parameter to determine the effective computational bandwidth. To formulate the governing equation in terms of the DSC method, a column vector W is introduced

$${\mathbf{W}} = (W_{0,0} , \ldots ,W_{{0,N_{Y} }} ,W_{1,0} , \ldots ,W_{{N_{X} ,N_{Y} }} )^{\text{T}}$$
(14)

where each element denotes the transverse displacement of an arbitrary point in the orthotropic plate. A differential matrix \({\mathbf{D}}_{q}^{n}\)(q = X, Y; n = 1, 2, …) with the elements is given by

$$[{\mathbf{D}}_{q}^{n} ]_{i,j} = \left[ {\left( {\frac{d}{dq}} \right)^{n} \delta_{\alpha ,\Delta }^{(n)} (q - q_{j} )} \right]_{{q = q_{i} }} = C_{m}^{n} ,\quad i,j = 0,1, \ldots ,N_{q}$$
(15)

where m = (qi \(-\) qj)/Δ. The matrix D is distributed to i − j = m = −M, …, 0, …, M. After that, the governing equation for cracked orthotropic plate can be written as

$$\begin{aligned} & \left( {{\mathbf{D}}_{X}^{4} \otimes {\mathbf{I}}_{Y} + 2\frac{{B_{o} \lambda^{2} }}{{D_{x} }}{\mathbf{D}}_{X}^{2} \otimes {\mathbf{D}}_{Y}^{2} + \lambda^{4} \frac{{D_{y} }}{{D_{x} }}{\mathbf{I}}_{X} \otimes {\mathbf{D}}_{Y}^{4} } \right){\mathbf{W}} \\ & \quad =\Omega ^{2} {\mathbf{W}} - \frac{{L_{1}^{2} }}{{D_{x} }}\left[ {\frac{{E_{x} h\Delta T\left( {\alpha_{x} + \alpha_{y} v_{y} } \right)}}{{1 - v_{x} v_{y} }}{\mathbf{D}}_{X}^{2} \otimes {\mathbf{I}}_{Y} } \right. \\ & \quad \quad \left. + { \lambda^{2} \frac{{E_{y} h\Delta T\left( {\alpha_{y} + \alpha_{x} v_{x} } \right)}}{{1 - v_{x} v_{y} }}{\mathbf{I}}_{X} \otimes {\mathbf{D}}_{Y}^{2} } \right]{\mathbf{W}} \\ & \quad \quad + A\frac{{D_{y} }}{{D_{x} }}\left( {\lambda^{4} {\mathbf{I}}_{X} \otimes {\mathbf{D}}_{Y}^{4} + v_{x} \lambda^{2} {\mathbf{D}}_{X}^{2} \otimes {\mathbf{D}}_{Y}^{2} } \right){\mathbf{W}} \\ & \quad \quad - B\frac{{L_{1}^{2} }}{{D_{x} }}\frac{{E_{y} h\Delta T\left( {\alpha_{y} + \alpha_{x} v_{x} } \right)}}{{1 - v_{x} v_{y} }}\left( {\lambda^{2} {\mathbf{I}}_{X} \otimes {\mathbf{D}}_{Y}^{2} } \right){\mathbf{W}} \\ \end{aligned}$$
(16)

where Iq is the (Nq + 1) × (Nq + 1) unit matrix and ⊗ denotes the tensional product.

3.2 Boundary Conditions

For the treatment of rectangular plates with simply supported and clamped boundaries, the anti-symmetric and symmetric extension methods can be applied, respectively [7, 18, 19]. As the primitive version of the DSC method is limited by dealing with the vibration of plates with free edges, a new scheme that incorporates the DSC method with the Taylor series expansion technique was reported to overcome this issue [8, 15, 16]. Hence, the imposition of boundary constraints is different for the following three general supporting conditions:

$${\text{Simply}}\,{\text{supported}}\,{\text{edges}}\, ( {\text{S):}}\,w_{x} = M_{x} = 0\,{\text{and}}\,w_{y} = M_{y} = 0$$
(17)
$${\text{Clamped}}\,{\text{edges}}\, ( {\text{C):}}\,w_{x} = \frac{\partial w}{\partial x} = 0\,{\text{and}}\,w_{y} = \frac{\partial w}{\partial y} = 0$$
(18)
$${\text{Free}}\,{\text{edges}}\, ( {\text{F):}}\,Q_{x} = M_{x} = 0,\,{\text{and}}\,R = 0$$
(19)

where wi (i = x, y) are the transverse displacements, Mi (i = x, y) are the bending moments, Qi (i = x, y) are the shear forces and R is the corner force.

Consider the above boundary conditions, the governing equation of cracked orthotropic plates can be expressed in a compact form as

$$\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{{{\mathbf{II}}}} } & {{\mathbf{K}}_{{{\mathbf{IA}}}} } \\ {{\mathbf{K}}_{{{\mathbf{AI}}}} } & {{\mathbf{K}}_{{{\mathbf{AA}}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{W}}_{{\mathbf{I}}} } \\ {{\mathbf{W}}_{{\mathbf{A}}} } \\ \end{array} } \right\} =\Omega ^{2} \left[ {\begin{array}{*{20}c} {\mathbf{I}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{W}}_{{\mathbf{I}}} } \\ {{\mathbf{W}}_{{\mathbf{A}}} } \\ \end{array} } \right\}$$
(20)

where WI and WA denote the transverse displacements of the inner points and the additional degree-of-freedom (DOF) points, respectively. If the boundary is a simply supported or a clamped edge, the corresponding elements are set to zero in WA. By properly rearranging the displacement vectors, Eq. (20) can be further simplified by vanishing the vector WA as

$${{[{\bar{\mathbf{K}}]}W}}_{{\mathbf{I}}} =\Omega ^{2} {\mathbf{W}}_{{\mathbf{I}}}$$
(21)

which can be solved by a standard eigenvalue solver.

4 Analysis Results and Discussion

In this study, the material properties and fundamental frequencies of orthotropic plates are presented in Tables 1, 2 and 3 [8]. The natural frequencies are expressed in terms of a non-dimensional form as \(\Omega = \omega L_{1}^{2} \sqrt {\rho h/D}\). The uniform rise in temperature is expressed as a non-dimensional variation of temperature T* = ΔT/Tcr, where Tcr is critical buckling temperature. In all cases, the value of ζ = d/h in the LSM is assumed to 0.6. The number of grid points and the half bandwidth used in the DSC algorithm are N = 32 and M = 25, respectively.

Table 1 Properties of an orthotropic rectangular plate [8]
Full size table
Table 2 Fundamental frequencies for cracked SSSS orthotropic plates (h = 0.01 m)
Full size table
Table 3 Fundamental frequencies for cracked SSSS orthotropic plates in thermal environment (L1 = L2 = 1 m, h = 0.01 m)
Full size table

Table 2 presents the fundamental frequency of SSSS orthotropic plates for various crack length ratios under the thermal condition of T* = 0. The results of the DSC method are very close to the existing results from the Galerkin’s method [6]. In Table 3, a higher variation of temperature reduces the natural frequency of the orthotropic plate intensively. It is found that the analysis results obtained by the DSC method show good agreement with those from the publication. In Fig. 2, the variation of natural frequencies of the rectangular orthotropic plates with free edges (i.e., FFFF and CSFF cases) due to the crack effect is first studied. A reduction of the fundamental frequency is observed as the crack length increases for different aspect ratios, λ = 1, 1.5 and 2.

Fig. 2
figure 2

Effect of crack length on fundamental frequencies: a FFFF plate; b CSFF plate

Full size image

5 Conclusions

This work presents the free vibration analysis of orthotropic plates under both crack and thermal effects. The surface cracks on orthotropic plates are simulated using the line-spring model, and the temperature heating load is considered as a uniformly distributed effect. Based on the mathematical model, the DSC method is first applied to address this problem. By incorporating with the Taylor series expansion approach, the limitation of the DSC method for the treatment of plate problems with free edges has been overcome. The effects of boundary condition, aspect ratio, crack length and thermal load on the dynamic responses of orthotropic plates are considered herein. The analysis results indicate that the presented scheme can achieve a high level of reliability and accuracy. As the temperature rises and the crack length increases, the vibration frequency of the plates would decrease. This is mainly due to the change of material properties under these effects.