X-Ritz Solution for Nonlinear Free Vibrations of Plates with Embedded Cracks

Abstract

The analysis of large amplitude vibrations of cracked plates is considered in this study. The problem is addressed via a Ritz approach based on the first-order shear deformation theory and von Kármán’s geometric nonlinearity assumptions. The trial functions are built as series of regular orthogonal polynomial products supplemented with special functions able to represent the crack behaviour (which motivates why the method is dubbed as eXtended Ritz); boundary functions are used to guarantee the fulfillment of the kinematic boundary conditions along the plate edges. Convergence and accuracy are assessed to validate the approach and show its efficiency and potential. Original results are then presented, which illustrate the influence of cracks on the stiffening effect of large amplitude vibrations. These results can also serve as benchmark for future solutions of the problem.

1 Introduction

Plates are frequently used in aerospace, automotive, naval and civil engineering structures. During their service life, plates may sometimes experience damage in the form of cracks, which can reduce their stiffness and produce significant changes in their dynamic behaviour. Such occurrences have to be accounted for the effective and reliable design of plate structures in which the presence of cracks may result in the loss of functionality and/or safety. The availability of tools able to predict the effects of cracks on the plate dynamics may help to prevent undesired effect and improve structural design towards enhanced safety.

The dynamic characteristics of plates are primarily described by their natural vibration modes. Many studies focused on the linear vibration analysis of both isotropic and composite thin and thick plates, providing for a comprehensive knowledge of the plate dynamic behaviour and design guidelines [16]. However, for an accurate appraisal of the plate dynamics, in some applications, it is needed to investigate the nonlinear free vibration problem. A literature survey evidences that the investigation about the large amplitude vibrations of plates received considerable attention and both analytical and numerical solutions have been proposed and used to investigate the effects of the involved parameters [1, 26]. Many of these solutions refer to Kirchhoff or classical laminate plate theory with nonlinear von Kármán’s strains and are suitable for thin-plates analysis. First- and higher-order shear deformation theories have also been proposed especially for composite laminates and an outline of the relevant literature can be found in Refs. [18, 30].

Notwithstanding, there are few works dealing with the vibrations of cracked plates. Different solutions have been proposed, based on integral equations [27, 28], finite elements (e.g., [2, 7, 14]), Fourier series solutions [11], generalized differential quadrature finite element method [31] and Ritz method [9, 10, 12, 17, 32]. The proposed solutions for cracked plates have been generally obtained for the linear case and, to the best of the authors knowledge, only the line spring model approach has been recently proposed for nonlinear forced vibrations of isotropic circular and rectangular Kirchhoff’s plates with cracks [3, 4, 13].

In view of the above observations and literature survey, the large amplitude free vibrations of cracked plates are studied in the present paper. The problem solution is based on an eXtended Ritz approach, dubbed as X-Ritz, recently proposed by the authors for buckling and post-buckling of plates [19, 20], which is here extended to nonlinear free vibrations analysis. The formulation assumes first-order shear deformation theory and von Kármán’s nonlinear strains, and has been used to obtain results for large amplitude vibrations of cracked isotropic and laminated plates whose characteristics are discussed.

2 Formulation

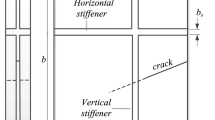
Let us consider a quadrilateral plate containing a straight through-the-thickness crack. The plate is referred to a Cartesian coordinate system $Ox_1x_2x_3$ with the $x_1$ and $x_2$ axes lying on the plate reference plane $\varOmega$ and the $x_3$ axis directed along the thickness h. The natural coordinate system $O\xi \eta$ is also introduced, which maps the square domain $[-1,1]\times [-1,1]$ onto the plate mid-plane coordinates via standard bilinear shape functions [21]. Eventually, for plates with cracks, a polar coordinates system $Or_k\theta _k$ is introduced at each crack tip as shown in Fig. 1, which illustrates the plate geometry and reference systems.

Fig. 1

Plate geometry and reference systems

The present formulation is developed considering the first-order shear deformation theory and von Kármán’s nonlinear strains, whose fundamentals can be found in Refs [21, 24]. Assuming that the strain–displacement relationships, the plate constitutive relationships and the kinematical boundary conditions are fulfilled, the governing equations for the plate vibrations are obtained by the stationarity of the following functional

$$\begin{aligned} \varPi= & {} \frac{1}{2} \int _{\varOmega } \left[ \, {\varvec{\varepsilon }}^T \varvec{A} \varvec{\varepsilon } + {\varvec{\varepsilon }}^T \varvec{B} \varvec{\kappa }+{\varvec{\kappa }}^T \varvec{B} \varvec{\varepsilon }+ {\varvec{\kappa }}^T \varvec{D} \varvec{\kappa }+{\varvec{\gamma }}^T \varvec{G} \varvec{\gamma }\,\right] d\varOmega \nonumber \\&-\frac{1}{2}\, \omega ^2 \int _{\varOmega } \left[ \, \varvec{u}^T \varvec{J}_0 \varvec{u} + \varvec{u}^T \varvec{J}_1 \varvec{\vartheta } + \varvec{\vartheta }^T \varvec{J}_1^T \varvec{u} + \varvec{\vartheta }^T \varvec{J}_2 \varvec{\vartheta } \,\right] d\varOmega \end{aligned}$$

(1)

where

• (i) $\varvec{u}=\{\begin{array}{lll} u_1&u_2&u_3\end{array}\}^T$ and $\varvec{\vartheta }=\{\begin{array}{ll} \vartheta _1&\vartheta _2 \end{array}\}^T$ are the midplane displacement vector and the section rotation vectors, depending on the $x_1$ and $x_2$ coordinates only;

• (ii) $\varvec{\varepsilon }$, $\varvec{\kappa }$ and $\varvec{\gamma }$ are the plate generalized strain vectors, namely the in-plane strain vector, the curvature vector and the out-of-plane shear strain vector $\varvec{\gamma }$, which depend on $\varvec{u}$ and $\varvec{\vartheta }$ via the strain–displacement relationships [21];

• (iii) $\varvec{A}$, $\varvec{B}$, $\varvec{D}$ and $\varvec{G}$ are the extensional, bending–extension coupling, bending and shear stiffness matrices, respectively [24];

• (iv) $\varvec{J}_0$, $\varvec{J}_1$, $\varvec{J}_2$ are the mass moments of inertia matrices, whose expressions are given in Appendix A;

• (v) $\omega$ is the vibrational natural frequency.

The problem solution is, therefore, given in terms of generalized displacements $\varvec{u}$ and $\varvec{\vartheta }$ that make the functional $\varPi$ stationary.

The solution of the nonlinear vibration problem of cracked plates is obtained by a Ritz approach, called X-Ritz, that approximates the generalized displacements via suitable defined enriched trial functions able to describe the crack opening and the crack tip fields[19, 20]. In the case of an embedded crack, the generalized displacement $\chi \in \{u_1,u_2,u_3,\theta _1,\theta _2\}$ is approximated as

$$\begin{aligned} \chi= & {} f_\chi (\xi ,\eta ) \sum _{m=0}^{M_{\chi }} \sum _{n=0}^{N_{\chi }} \mathscr {L}_{m}(\xi ) \mathscr {L}_{n}(\eta ){C_{\chi }}_{mn}^{\langle 0\rangle } \nonumber \\&+g_\chi (\xi ,\eta ) \sum _{m=\overline{m}_\chi }^{{\overline{N}}_{\chi }^{\langle 1\rangle }}\sum _{n=0}^{m} {r_1}^{\frac{2m-1}{2}}\cos \left( \frac{2n+1}{2}\theta _1\right) {C_{\chi }}_{mn}^{\langle 1\rangle }\nonumber \\&+g_\chi (\xi ,\eta ) \sum _{m=\overline{m}_\chi }^{{\overline{N}}_{\chi }^{\langle 2\rangle }}\sum _{n=0}^{m} {r_2}^{\frac{2m-1}{2}}\cos \left( \frac{2n+1}{2} \theta _2\right) {C_{\chi }}_{mn}^{\langle 2\rangle }\nonumber \\&+g_\chi (\xi ,\eta ) \sum _{m=\overline{m}_\chi }^{{\overline{N}}_{\chi }^{\langle 3\rangle }}\sum _{n=0}^{m} \sqrt{{r_2}^{3}}\sin ^2(\theta _2/2) r_1^{\frac{2m-1}{2}}\nonumber \\&\sin \left( \frac{2n+1}{2}\theta _1\right) {C_{\chi }}_{mn}^{\langle 3\rangle }\nonumber \\&+g_\chi (\xi ,\eta ) \sum _{m=\overline{m}_\chi }^{{\overline{N}}_{\chi }^{\langle 4\rangle }}\sum _{n=0}^{m} \sqrt{{r_1}^{3}}\sin ^2(\theta _1/2) r_2^{\frac{2m-1}{2}}\nonumber \\&\sin \left( \frac{2n+1}{2}\theta _2\right) {C_{\chi }}_{mn}^{\langle 4\rangle }, \end{aligned}$$

(2)

where $\mathscr {L}_j(\zeta )$ is the j-th order Legendre polynomial of the coordinate $\zeta$ and the ${C_{\chi }}_{mn}^{\langle k\rangle }$ are the unknown coefficients. The functions $f_\chi (\xi ,\eta )$ and $g_\chi (\xi ,\eta )$ are used to guarantee the fulfillment of the kinematical boundary conditions and read as

$$\begin{aligned} f_\chi (\xi ,\eta )= & {} (1+\xi )^{c_1}(1-\xi )^{c_2}(1+\eta )^{c_3}(1-\eta )^{c_4} \end{aligned}$$

(3)

$$\begin{aligned} g_\chi (\xi ,\eta )= & {} (1-\xi ^2)(1-\eta ^2), \end{aligned}$$

(4)

where $c_i$ equals unity if $\chi$ is constrained along the edge implicitly described by the corresponding power base, whereas it equals zero in case of unknown $\chi$. The geometrical quantities involved in Eq. (2) are defined in Fig. 1. Details on the characteristics of the enriched trial functions defined in Eq. (2) can be found in Refs. [10, 19, 20]. Here, only some remarks are given:

• (i) The first series in Eq. (2) considers regular functions able to describe the global plate behaviour disregarding crack opening and crack tip singularities;

• (ii) The other four series enrich the above-mentioned regular functions and are able to describe the crack opening and singular fields at the crack tips. Their terms guarantee continuity along the segments $\theta _1=0^\circ$ and $\theta _2=0^\circ$ and the correct singular behavior at both crack tips. The starting index $\overline{m}_\chi$ of these series governs the asymptotic behavior at the crack tips. It is chosen assuming that the strain energy density asymptotically behaves as $r^{-1}$ when $r\rightarrow 0$. This is consistent with the available theoretical findings for small displacements in Kirchoff and Mindlin plates and large displacements in Kirchhoff plates [22, 33, 34]. In the case of small displacements linear analysis, this means setting $\overline{m}_\chi =1$ for all of the displacement components, namely $\chi \in \{u_1,\,u_2,\,u_3,\,\vartheta _1,\,\vartheta _2\}$. On the other hand, for von Kármán’s strains, one has to set $\overline{m}_{u_3}=2$ for the approximation of the transverse displacement and $\overline{m}_\chi =1$ for $\chi \in \{u_1,\,u_2,\,\vartheta _1,\,\vartheta _2\}$. It is worth noting that the enrichment functions are forced to zero on the plate edges via the boundary function $g_\chi (\xi ,\eta )$ to localize their effect in the crack zone.

• (iii) The trial function in Eq. (2) can obviously be used for uncracked plates by setting ${\overline{N}}_{\chi }^{\langle 1\rangle }={\overline{N}}_{\chi }^{\langle 2\rangle }={\overline{N}}_{\chi }^{\langle 3\rangle }={\overline{N}}_{\chi }^{\langle 4\rangle }=0$.

By substituting the strain–displacement relationships and in turn the generalized displacements approximations into Eq. (1), the discretized form of the functional $\varPi$ is obtained. Applying the standard calculus of variations, the stationarity condition of the discretized functional $\varPi$ provides the plate governing equations as [19, 20]

$$\begin{aligned} \left[ \varvec{K}+\varvec{K}_{NL}\left( \varvec{X}\right) -\omega ^2 \varvec{M}\right] \varvec{X}= \varvec{0}, \end{aligned}$$

(5)

where $\varvec{X}$ is the vector collecting the Ritz coefficients of the generalized displacements approximations (see Appendix A). The expression of the stiffness matrices $\varvec{K}$ and $\varvec{K}_{NL}$ can be found in Refs. [19, 20], whereas the derivation of the mass matrix $\varvec{M}$ is presented in Appendix A. Eq. (5) identifies a nonlinear eigenvalue problem, whose solution can be achieved iteratively for a fixed amplitude of the eigenvectors.

3 Results

Numerical results are presented for rectangular plates, which are widely investigated in the literature and are of general practical interest. The employed geometrical data refer to the scheme shown in Fig. 2.

Fig. 2

Geometrical scheme of cracked rectangular plates

3.1 Uncracked plates

To verify the proposed approach and assess its accuracy, the formulation was tested comparing the present free vibrations results for uncracked plates with the solution cases available in the literature. First, a square isotropic plate with edge length $\ell$ and thickness h, simply supported on all the edges, was analyzed assuming the Poisson’s coefficient $\nu =0.3$. Convergence characteristics of the method are studied for the linear free vibration problem by varying the number of trial functions used in the generalized displacement approximations. More in detail, the same approximation scheme is used for all of the generalized displacements using the same number of orthogonal polynomials for the two plate reference directions, i.e., $M_\chi =N_\chi$. The results of the convergence analyses for the thin plate having $h/\ell =0.001$ are listed in Table 1; percentage errors have been calculated with respect to the frequencies obtained by the Kirchoff’s theory [16].

Table 1 Convergence of the linear natural frequencies $\bar{\omega }_L=\omega _L\ell ^2\sqrt{\frac{\rho }{E h^2}}$ for an isotropic, square, simply–supported plate with $h/\ell =0.001$

Convergence analyses have been performed also for different plate thickness and for nonlinear vibrations providing the same considerations and guidelines as the results of Table 1; they are not reported here for the sake of conciseness. The results show that an approximation with $M_\chi =N_\chi =8$ can be considered accurate and thus the following results for nonlinear vibrations refer to such an approximation scheme.

Table 2 lists the nonlinear–linear frequency ratio $\omega _{NL}/\omega _L$ for the first vibrational mode of isotropic, simply supported, square plates with two different thickness ratio $h/\ell =0.001$ and $h/\ell =0.1$. Results are reported, as usual, for different vibration amplitudes defined in terms of the ratio $w_{max}/h$ between the plate maximum deflection and thickness. The comparison with analytical [5] and finite elements [6, 23] solutions shows a good accuracy of the proposed method whose results agree with those obtained using different approaches.

Table 2 First mode nonlinear–linear frequency ratio $\omega _{NL}/\omega _L$ of isotropic, simply supported, square plates with different thickness ratio

As validation case for laminated plates, a fully clamped rectangular plate with edges length ratio $a/b=1.5$ and thickness ratio $a/h=480$ has been investigated considering the $\left[ 90/-45/45/0\right] _S$ layup made of plies with $E_{11}=120.5\, \text {GPa}$, $E_{22}=9.63\, \text {GPa}$, $G_{12}=G_{13}=G_{23}=3.58\, \text {GPa}$, $\nu _{12}=0.32$ and $\rho =1540\, \text {kg}/\text {m}^3$. The approximation scheme $M_\chi =N_\chi =8$ has been used in the analyses. Table 3 lists the plate nonlinear–linear frequency ratio $\omega _{NL}/\omega _L$ for the first vibrational mode and its comparison with literature results. It is observed that the present results are in good agreement with those obtained by finite elements [8, 25] and the element-free kp-Ritz formulation [15].

Table 3 First mode nonlinear–linear frequency ratio $\omega _{NL}/\omega _L$ of uncracked $\left[ 90/-45/45/0\right] _S$ laminated fully clamped rectangular plate

The comparison of the present results with other solutions validates the present approach for uncracked plates nonlinear vibration analysis and on this basis, the method is applied to cracked plates in the next section.

3.2 Cracked plates

To ascertain the convergence behavior of the proposed approach for the cracked plate case, analyses were carried out for an isotropic, simply supported square plate containing a center horizontal crack of length a. Convergence has been investigated considering the value of the first five mode nondimensional frequencies in the linear case with respect to the number of regular and enrichment approximation functions. More in detail, the same approximation scheme is used for all of the generalized displacements; it uses the same number of orthogonal polynomials for the two plate reference directions, i.e., $M_\chi =N_\chi$, and the same number of terms to describe the crack behaviour, i.e ${{\overline{N}}_{\chi }^{\langle 1\rangle }}={{\overline{N}}_{\chi }^{\langle 2\rangle }}={{\overline{N}}_{\chi }^{\langle 3\rangle }}={{\overline{N}}_{\chi }^{\langle 4\rangle }}=N_c.$ Tables 4 and 5 list the results of the described convergence analysis along with results from the literature for two different crack length, namely $a/\ell =0.2$ and $a/\ell =0.5.$

Table 4 Convergence of the linear natural frequencies $\omega _L\ell ^2\sqrt{\frac{\rho }{E h^2}}$ of the isotropic, simply supported, square plate with a central horizontal crack ($\beta =0^\circ$) having length $a/\ell =0.2$

Table 5 Convergence of the linear natural frequencies $\omega _L\ell ^2\sqrt{\frac{\rho }{E h^2}}$ of the isotropic, simply-supported, square plate with a central horizontal crack ($\beta =0^\circ$) having length $a/\ell =0.5$

Good convergence characteristics are observed for the linear case; analyses of nonlinear vibrations for fixed amplitude show similar trends. It is observed that the convergence of the first mode, which is a primary concern in nonlinear vibration analysis, is achieved with a relatively low number of crack functions showing the computational efficiency of the approach. In the subsequent analyses, a discretization scheme with $M_\chi =N_\chi =8$ and $N_c=5$ has been used.

Figs. 3 and 4 illustrate some original results for large amplitude vibrations of cracked isotropic square plates. For the plate first vibration mode, they show the backbone curves linking the nonlinear–linear frequency ratio to the vibration amplitude. Fig. 3 reports the results for an horizontal ($\beta =0^\circ$) crack with different lengths ($a/\ell =0.2$ and $a/\ell =0.5$) considering two different plate thickness values ($h/\ell =0.001$ and $h/\ell =0.1$). The stiffening effect of large amplitude on free vibrations is clearly observed; this effect reduces with the crack length and increases with thickness; the influence of thickness on the stiffening effect reduces with increasing crack length.

Fig. 3

Backbone curves for the first mode of the isotropic, simply supported, square plates having different thickness $h/\ell$ and a central horizontal crack ($\beta =0^\circ$) with different lengths $a/\ell$

Fig. 4 reports the results for plates with two different thickness values ($h/\ell =0.001$ and $h/\ell =0.1$) containing a crack of length $a/\ell =0.5$ and different inclination angles $\beta$. The results show that the stiffening effect of the large amplitude is slightly influenced by the crack orientation and that it reduces with increasing $\beta$.

Fig. 4

Backbone curves for the first mode of the isotropic, simply supported, square plates having different thickness $h/\ell$ and a central crack of length $a/\ell =0.5$ with different inclinations $\beta$

Representative results are also presented for composite laminate plates considering the $\left[ 90/-45/45/0\right] _S$ laminated clamped rectangular plate previously analysed in the uncracked case. Figs. 5 and 6 illustrate the effect of the crack parameters on the large amplitude free vibrations. They show the results corresponding to the first vibration mode and similar trends were observed also for the higher modes, not reported here for the sake of brevity. It is observed that the stiffening effect of large amplitude reduces with the crack length; on the other hand, for fixed crack length, it increases with the crack inclination angle.

Fig. 5

Backbone curves for the first mode of the $\left[ 90/-45/45/0\right] _S$ laminated, clamped, rectangular plate ($\ell /b = 1.5$) with a central horizontal crack ($\beta =0^\circ$) having different lengths $a/\ell$

Fig. 6

Backbone curves for the first mode of the $\left[ 90/-45/45/0\right] _S$ laminated, clamped, rectangular plate ($\ell /b = 1.5$) with a central crack having length $a/\ell =0.5$ and different inclinations $\beta$

Eventually, Fig. 7 shows the nonlinear first mode shape with amplitude $w_{max}/h=1.0$ for the considered laminated plate with a central crack having length $a/\ell =0.5$ and different inclination angles $\beta$.

Fig. 7

Illustration of the nonlinear first mode shape with amplitude $w_{max}/h=1.0$ for the $\left[ 90/-45/45/0\right] _S$ laminated clamped rectangular plate ($\ell /b = 1.5$) with central crack having length $a/\ell =0.5$ and different inclination $\beta$

4 Conclusions

A single-domain extended Ritz approach has been used to analyze the large amplitude vibrations of cracked plates. It implements the first-order shear deformation theory coupled with the von Kármán’s assumptions for geometrical nonlinearity. Regular polynomial functions supplemented with special functions able to describe the discontinuity across the crack and the singularity at the crack tips are used as trial functions; the kinematical boundary conditions are fulfilled by suitable boundary functions. Convergence and accuracy investigations have been carried out comparing the present results with those available in the literature, which are limited to uncracked plates. Original results are proposed and discussed for large amplitude vibrations of cracked plates. The presented results may provide a benchmark for future solutions.

A Plate inertia properties and mass matrix

The inertia matrices are defined as

$$\begin{aligned} \varvec{J}_0 = \left[ \begin{array}{lll} J_0 &{} 0 &{} 0 \\ 0 &{} J_0 &{} 0\\ 0 &{} 0 &{} J_0 \end{array}\right] , \quad \varvec{J}_1 = \left[ \begin{array}{ll} J_1 &{} 0 \\ 0 &{} J_1 \\ 0 &{} 0 \end{array}\right] , \quad \varvec{J}_2 = \left[ \begin{array}{lll} J_2 &{} 0 &{} 0 \\ 0 &{} J_2 &{} 0\\ 0 &{} 0 &{} J_2 \end{array}\right] , \end{aligned}$$

(A1)

where denoted by $\rho$ the material density, $J_0$, $J_1$ and $J_2$ are the plate mass moments of inertia given by

$$\begin{aligned} J_k =\int _h \rho \, x_3^k \, dx_3 \end{aligned}$$

(A2)

The mass matrix is deduced applying the variational calculus to the second integral of the functional $\varPi$ after its discretization via Eqs. (2) To this aim, the plate generalized displacements approximation is formally rearranged in compact matricial form as

where the Ritz coefficients ${C_{\chi }}_{mn}^{\langle k\rangle }$ ($\chi \in \{u_1,u_2,u_3,\theta _1,\theta _2\}$ and $k=0,1,2,3,4$) are arranged in the column vectors $\varvec{X}_{\chi }$ with a corresponding arrangement of the approximation functions in the row vectors $\varvec{\varPhi }_{\chi }$. Substituting this expression in the second integral of $\varPi$, one obtains

$$\begin{aligned}&\frac{1}{2}\, \omega ^2\int _{\varOmega } \left[ \, \varvec{u}^T \varvec{J}_0 \varvec{u} + \varvec{u}^T \varvec{J}_1 \varvec{\vartheta } + \varvec{\vartheta }^T \varvec{J}_1^T \varvec{u} + \varvec{\vartheta }^T \varvec{J}_2 \varvec{\vartheta } \,\right] d\varOmega \nonumber \\&\quad =\frac{1}{2}\, \omega ^2 \varvec{X}^T\int _{\varOmega } \left[ \, \varvec{\varPsi }_u^T \varvec{J}_0 \varvec{\varPsi }_u + \varvec{\varPsi }_u^T \varvec{J}_1 \varvec{\varPsi }_\vartheta \right. \nonumber \\&\left. \qquad + \varvec{\varPsi }_\vartheta ^T \varvec{J}_1^T \varvec{\varPsi }_\vartheta + \varvec{\varPsi }_\vartheta ^T \varvec{J}_2 \varvec{\varPsi }_\vartheta \,\right] d\varOmega \varvec{X}= \frac{1}{2}\, \omega ^2 \varvec{X}^T\varvec{M}\varvec{X} \end{aligned}$$

(A4)

which define the mass matrix as

$$\begin{aligned} \varvec{M}= \int _{\varOmega } \left[ \, \varvec{\varPsi }_u^T \varvec{J}_0 \varvec{\varPsi }_u + \varvec{\varPsi }_u^T \varvec{J}_1 \varvec{\varPsi }_\vartheta + \varvec{\varPsi }_\vartheta ^T \varvec{J}_1^T \varvec{\varPsi }_\vartheta + \varvec{\varPsi }_\vartheta ^T \varvec{J}_2 \varvec{\varPsi }_\vartheta \,\right] d\varOmega \end{aligned}$$

(A5)