DNA Mechanics and Topology

Abstract

We review the current understanding of the mechanics of DNA and DNA-protein complexes, from scales of base pairs up to whole chromosomes. Mechanics of the double helix as revealed by single-molecule experiments will be described, with an emphasis on the role of polymer statistical mechanics. We will then discuss how topological constraints— entanglement and supercoiling—impact physical and mechanical responses. Models for protein–DNA interactions, including effects on polymer properties of DNA of DNA-bending proteins will be described, relevant to behavior of protein–DNA complexes in vivo. We also discuss control of DNA entanglement topology by DNA-lengthwise-compaction machinery acting in concert with topoisomerases. Finally, the chapter will conclude with a discussion of relevance of several aspects of physical properties of DNA and chromatin to oncology.

2.1 Overview of DNA Mechanics and Nuclear Function

Over the past several decades our understanding of the cell has become increasingly based on the concept of “molecular machines” that groups of enzymes associate together to accomplish specific tasks. In many cases, these enzyme machines perform “mechanical” functions, for example, transporters that actively push a specific “cargo” across a cell membrane. Many of the most impressive examples of active biomolecular machines are found in the cell nucleus, where very highly processive enzyme motors are involved in transcription, replication, and repair of double helix DNA molecules. Given that the DNAs in human cells are on the order of centimeters in length, the physical properties of DNA are essential to understanding how cell nuclear machinery operates. Proper regulation of DNA transcription, replication, and repair is essential to controlling cell behavior and development, and dysfunction of these processes is the root of many genetic diseases including many cancers.

The mechanics of DNA and DNA–protein complexes (notably chromatin, i.e., strings of nucleosomes formed on DNA as occur in eukaryote chromosomes) affects many different aspects of nuclear function. For example, the flexibility of DNA and its modification by DNA-binding proteins affects how DNA bends and fluctuates, and therefore the probabilities and rates at which DNA sequences along the same molecule can “meet”: this meeting of distant sequences occurs when distant sequences regulate genes. In some cases, it is known that gene activation repositions genes in the nucleus, another process which is affected on DNA mechanics. Homologous-sequence-based DNA repair depends on the transport together of sequence-matching DNA segments from different homologous chromosomes, a process which is still only partially understood, but which undoubtedly depends on DNA mechanics. Perhaps most impressive is the process by which chromosomal DNAs are replicated, and then the duplicated sister chromatids are physically and topologically separated from one another, culminating in mitosis and cell division, perhaps the most mechanically impressive feat carried out by eukaryote cells.

This chapter will focus on the mechanics of DNA and DNA–protein structures, focusing on the behavior of the double helix at scales from base pairs up to whole chromosomes. As might be expected, different force scales and descriptions are relevant at microscopic (few nanometer [nm]/single-molecular) and at mesoscopic (micron[μm]/chromosome-cell nucleus) scales. We will begin by focusing on the microscopic scales, discussing mechanics of the double helix as revealed by single-molecule biophysics experiments; we will then discuss how the topological properties of DNA impact its thermodynamics and mechanics. We will then discuss how proteins which bind to DNA can change its mechanical properties, which is the situation we find in vivo and in particular in chromosomes throughout the cell cycle. Finally we will conclude with a very brief summary of the chapter and a very brief discussion of relevance of DNA and chromatin mechanics to cancer.

Before launching into quantitative aspects of DNA mechanics, we begin with a few words about DNA chemical structure (Fig. 2.1) and basic physical properties. DNA molecules in cells are found in double helix form, consisting of two long polymer chains wrapped around one another, with complementary chemical structures (Fig. 2.1b). The double helix encodes genetic information through the sequence of chemical groups—the bases adenine, thymine, guanine, and cytosine (A, T, G, and C). Corresponding bases on the two chains in a double helix bind one another according to the complementary base-pairing rules A=T and G≡C. These rules follow from the chemical structures of the bases, which permit two hydrogen bonds to form between A and T (indicated by =), versus three that form between G and C (indicated by ≡). Each base pair has a chemical weight of about 600 Daltons (Da). The presence of the two complementary copies along the two polynucleotide chains in the double helix provides redundant storage of genetic information and also facilitates DNA replication, via the use of each chain as a template for assembly of a new complementary polynucleotide chain.

Fig. 2.1

DNA double helix structure. (a) Chemical structure of one DNA chain, showing the deoxyribose sugars (note numbered carbons) and charged phosphates along the backbone, and the attached bases (A, T, G, and C following the 5 to 3 direction from top to bottom). (b) Space-filling diagram of the double helix. Two complementary-sequence strands as in (a) noncovalently bind together via base-pairing and stacking interactions, and coil around one another to form a regular helix. The two strands can be seen to have directed chemical structures, and are oppositely directed. Note the different sizes of the major (M) and minor (m) grooves, and the negatively charged phosphates along the backbones (dark groups). The helix repeat is 3.6 nm, and the DNA cross-sectional diameter is 2 nm. Image reproduced from [1]. (c) Molecular-dynamics snapshot suggestive of a typical double helix DNA conformation for a short 10 bp molecule in solution at room temperature. Reproduced from [2]

Inside the double helix, the two polynucleotide strands wrap around one another, forming a structure which has on average about 0.34 nm of helix length (“rise”) per base pair, and with one helix repeat per 10.5 base pairs (a good scale to keep in mind is that there are approximately three base pairs per nm along the double helix axis). Now, double helix DNAs in vivo are long polymers: the chromosome of the bacteriophage (a virus that infects E. coli bacteria) is 48,502 base pairs (bp) or about 16 μm in length; the E. coli bacterial chromosome is 4.6 × 10⁶ bp (4.6 Mb) or about 1.5 mm long; small E. coli “plasmid” DNA molecules used in genetic engineering are typically 2–10 kb (0.7–3 μm) in length; and the larger chromosomal DNAs in human cell nuclei are roughly 200 Mb or a few cm in length.

A key physical feature of DNA that should be kept in mind is that in physiological aqueous solution (e.g., under conditions similar to those found in the human cell nucleus: 150 mM of univalent cations, predominantly K⁺; 1 mM of Mg²⁺; pH 7.5) the phosphates along the backbones (see Fig. 2.1a; shown as the dark groups in Fig. 2.1b) are ionized, giving the double helix a linear charge density of about 2 e⁻ per base pair or about 6 e⁻ per nm. DNA under cellular conditions is therefore a strongly charged polyelectrolyte and has strong electrostatic interactions with other electrically charged biomolecules at short ranges. At ranges beyond the Debye length (λ _D ≈ 0.3 nm/$\sqrt {\mathrm {M}}$, where M is the concentration of 1:1 salt in mol/litre =  M), univalent ions in the cell screen electrostatic interactions, cutting it off beyond a distance of about 1 nm. Thus electrostatic repulsions between DNA molecules can be thought of as giving rise to an effective hard-core diameter of dsDNA of ≈3.5 nm under physiological salt conditions [3].

In the nm-scale world of the double helix (note that the “information granularity” of cells, the size of nucleotides, amino acids, nucleotides, and other elementary molecules is about 1 nm), thermal fluctuations excite individual mechanical degrees of freedom with energy ≈ k _B T ≈ 4 × 10⁻²¹ J (at room temperature, T ≈ 300 K). This energy scale of thermal motion is well below that associated with covalent bonds (≈ 1 eV ≈ 40 k _B T), which is good—thermal fluctuations by themselves can’t easily break the covalently bonded DNA backbone! A second physical consequence of the thermal energy scale is that combined with the 1 nm length of molecular structure, one obtains a molecular-biological force scale of 1 k _B T∕nm = 4 × 10⁻¹² Newtons (4 piconewtons, or pN). This force scale is what must be used to hold a molecule in one place to nm precision, and is on the order of forces generated by single-enzyme biomolecular motors, which typically release several k _B T during reactions causing them to move by a few nm. In fact, RNA and DNA polymerases fall into this class of enzymes, and actually generate forces in the tens of pN range [4, 5] since their step length is roughly 1 nm, the linear distance separating bases along the sugar-phosphate backbone (Fig. 2.1).

2.2 Mechanical Properties of DNA

The stacked nature of the bases makes the double helix a stiff polymer, allowing only a few degrees of lateral bending per base pair. One degree of lateral bend corresponds to roughly 0.03 nm of separation between adjacent bases. However, one may expect to see occasional large bends arising from correlated distortions over many base pairs. In this section, we develop a quantitative understanding of how the double helix responds to mechanical perturbations in a thermal environment.

2.2.1 DNA as a Stiff Polymer

A starting point for modeling DNA is that of a polymer with a bending stiffness or a semiflexible polymer. Our goal is to describe the double helix at longer length scales (few hundreds of nanometers or more), such that we can ignore any potential anisotropy in the bending of our DNA polymer arising from the double helical structure. Let us consider a double helix of total contour length that follows a space curve r(s), where s denotes the parameterization of the arclength of the space curve. The gradient of the tangent vector to the curve gives the local curvature $\kappa = \left | d\hat {\mathbf {t}}/ds \right |$, where $\hat {\mathbf {t}}(s)=d{\mathbf {r}}/ds$ is the tangent vector. The total bending energy for a DNA conformation:

$$\displaystyle \begin{aligned} \beta E_{\mathrm{bend}} = \frac{A}{2}\int_0^L ds \left( \frac{d{\hat{\mathbf{t}}}}{ds} \right)^2 \end{aligned} $$

(2.1)

where A is the persistence length, that controls the bending degree of freedom of the double helix (β ⁻¹ ≡ k _B T). A longer persistence length indicates a stiffer polymer. For DNA, A ≈ 50 nm or 150 bp [6, 7], hence the flexible polymer limit of DNA is achieved in the hundreds-of-nanometers scale (L ≫ A). In the opposite limit L ≪ A, the polymer will essentially be unbent by thermal fluctuations. Note that Eq. (2.1) is similar to that describing small bending of an elastic rod, however, it is perhaps better served to think about the “bending” energy as the free energy describing bending deformations in a thermally fluctuating statistical polymer.

Before discussing the statistical properties of the double helix, let us think about some static configurations and their corresponding energies to better understand the role of the DNA persistence length. For a circular arc of radius R, the curvature $\kappa =\left |d\hat {\mathbf {t}}/ds\right |=1/R$, and hence, from Eq. (2.1), βE _circ = AL∕(2R ²). So, we find that thermal fluctuations of energy k _B T∕2 can induce a 1 rad bend in a DNA segment of length A. Thus, for a long polymer, each persistence length worth of the double helix gets bent by roughly a radian in a random direction.

Along similar lines, a piece of DNA of length L bent into a circle costs energy: βE _circ = 2π ² A∕L ≈ 19.7A∕L. However, the optimal shape of a looped piece of a DNA where the ends are held together is that of a “teardrop” geometry: βE _teardrop ≈ 14.1A∕L [8], which is about 70% of the energy of a circle. This kind of description works well till ≈ 200 bp lengths, some experiments suggest that the simple elastic description may be applicable to ≈ 75 bp long pieces of DNA [9,10,11].

That being said, it is interesting to note that circularly bent segments of DNA, forming nucleosomes are a common occurrence inside the cell. Nucleosomes are a basic unit of DNA compaction in eukaryotic cells, where ≈ 50 nm of DNA is wrapped around a core of ≈ 10 nm diameter constituted of an octamer of histone proteins [12]. The elastic bending energy stored in the DNA forming the nucleosome: E _bend ≈ 50k _B T, which is roughly 0.3k _B T per base pair of the DNA. Although this is a substantial amount of energy, this corresponds to a mere (0.34 nm)/(5 nm)≈ 0.07 rad or 4^∘ of bend per base pair, which only moderately disrupts the stacked double helix structure.

Note that Eq. (2.1) tells us that the zero curvature state or the straight line configuration has the lowest energy. Such a picture ignores any potential inhomogeneity in the double helix structure arising from structural differences of various DNA sequences. It is possible by stacking certain bases in certain specific orders, to generate a permanently bent double helix structure. Some of these strongly bent DNA sequences have biologically relevant roles in modulating the propensity of a DNA segment to be bent or wrapped by proteins. In this way, DNA sequences can play a role in positioning nucleosomes [13, 14]. However, for most sequences in most conditions the coarse-grained model described above is sufficient and will be used in the rest of this chapter.

2.2.2 Statistical Mechanics of DNA

We discussed how different static conformations of the double helix have different energies. In a statistical sense, all these conformations constitute the configuration phase space of a thermally fluctuating polymer, however, the probability of occupancy of a configuration decreases exponentially with the energy of the configuration (Maxwell–Boltzmann statistics). We can write the partition function of an unconstrained polymer:

$$\displaystyle \begin{aligned} Z = \int \mathcal{D}\hat{\mathbf{t}}(s) \exp\left( -\beta E_{\mathrm{bend}} \right),\end{aligned} $$

(2.2)

where $\mathcal {D}\hat {\mathbf {t}}$ represents a path integral. This “free” polymer model can be solved in a closed form [15]. The two-point correlation of tangent fluctuations decays exponentially: $\left < \hat {\mathbf {t}}(s) \cdot \hat {\mathbf {t}}(s+\varDelta ) \right > \propto e^{-|\varDelta |/A}$.

The end-to-end vector of the polymer R can be obtained from the tangent vectors: $\mathbf {R} = \mathbf {r}(L)-\mathbf {r}(0) = \int _0^L ds \hat {\mathbf {t}}(s)$. Using the tangent correlation we can write the mean-squared distance between the ends of the polymer of length L:

$$\displaystyle \begin{aligned} \langle R^2\rangle&=\langle\left|\mathbf{r}(L)-\mathbf{r}(0)\right|{}^2\rangle \\ &=2AL+2A^2\left(e^{-L/A}-1\right), \end{aligned} $$

(2.3)

which furnishes the Gaussian polymer limit (freely jointed chain) for L ≫ A : 〈R ²〉 = 2AL. The correspondence between A and the statistical segment length b for Gaussian polymers is b = 2A, and number of steps N = L∕(2A) = L∕b. The stiff polymer limit is obtained for L ≪ A: 〈R ²〉≈ L ².

2.2.2.1 Elasticity of the Semiflexible Polymer at Low Forces

For a long polymer (L ≫ A), 〈R ²〉≪ L ² implies that work needs to be done to stretch out the ends of the polymer, which gives rise to polymer elasticity. In the absence of force, since $\left < R^2 \right > = \left <x^2\right >+ \left <y^2\right >+ \left <z^2\right >$ where x, y, and z are the Cartesian components of the end-to-end vector R, we have $\left < R^2 \right > = 3\left < x^2 \right >$. In the linear force response regime, the spring constant can be written as k = k _B T∕〈x ²〉 = 3k _B T∕(2AL). This corresponds to a Gaussian polymer, where the spring constant is inversely proportional to polymer length. The low-force response is $f = kx + \mathcal {O}(x^3)$, with the linear response regime essentially holding for f < k _B T∕A. For double helix DNA, this characteristic force is quite low since A = 50 nm; k _B T∕A ≈ 0.1 pN (recall k _B T∕(1 nm) ≈ 4 pN).

As the length of DNA is increased, the self-avoidance of the polymer plays an important role that makes the force response nonlinear [16]. However, for double helix DNA, the narrow effective thickness (≈ 3.5 nm at 100 mM univalent salt including electrostatic effects [3]) of the double helix compared to its segment length b = 2A ≈ 100 nm) leads to quite weak self-avoidance, and makes dsDNA elasticity quite close to that of an ideal polymer for DNA lengths (< 50 kb ≈ 16 μm) routinely studied experimentally [7].

We note that for single stranded nucleic acid molecules (e.g., one of the polynucleotide chains in the double helix) the far shorter persistence length ≈ 1 nm leads to much stronger self-avoidance effects [17, 18], especially for low-salt conditions.

2.2.2.2 Polymer Elasticity Under Applied External Tension

For any polymer model, to go beyond the linear force response, we need to include force in the energy function:

$$\displaystyle \begin{aligned} E = E_{\mathrm{bend}}- \mathbf{f}\cdot\mathbf{R}{} \end{aligned} $$

(2.4)

Force is added as a field coupled to the end-to-end vector, so that averages of end-to-end extension are generated by derivatives of the partition function Z with respect to force, as expected for identification of $-k_{\mathrm {B}} T \ln Z$ as a free energy in the fluctuating-extension, constant-force ensemble (the ensemble relevant to magnetic tweezers experiments, which apply a constant force to a paramagnetic particle attached to one end of a DNA [19]).

There are a number of general consequences for this form of statistical weight. For nonzero force along the z direction, or $\mathbf {f} = f\hat {\mathbf {z}}$, we have an average end-to-end extension $\left < z \right > = \partial \ln Z / (\partial \beta f)$, and an extension fluctuation of $\left < z^2 \right > - \left < z\right >^2 = \partial ^2 \ln Z / \partial (\beta f)^2$. Components of R transverse to the force have zero average by symmetry ($\left < x \right > = \left < y \right > = 0$), but their fluctuations are nonzero, and are computed as $\left < x^2 \right > = \left . \partial ^2 \ln Z / \partial (\beta f_x)^2 \right |{ }_{\mathbf {f}=f\hat {\mathbf {z}}}$.

An important feature of any model of the form of Eq. (2.4), where there is no preferred orientation other than that of the force f, is that the free energy only depends on the magnitude of force f, $\ln Z = \ln Z(|\mathbf {f}|)$. As a result, the extension and transverse fluctuations are related: $\left <x^2\right >= \left <z\right >/(\beta f)$. Therefore, if we measure thermally averaged transverse fluctuations $\left <x^2\right >$, and average extension $\left <z\right >$, we can infer the applied force f. This exact relationship holds for any polymer model with a rotationally symmetric conformational energy (essentially any model without a preferred direction in space other than the applied force, notably including models with polymer self-interactions) and is a powerful tool used for force calibration in magnetic tweezers experiments. This relation is model-independent and not limited to the case of small fluctuations [20].

2.2.2.3 Highly Stretched Semiflexible Polymer

Continuing our discussion of the double helix DNA under a stretching force, we now examine the limit of strong stretching forces (f ≫ k _B T∕A ≈ 0.1 pN), where the transverse fluctuations are small. Using Eq. (2.4) under an applied force $f\hat {\mathbf {z}}$ and the end-to-end vector $\mathbf {R} = \int _0^L ds \, {\hat {\mathbf {t}}}(s)$ we write the energy functional:

$$\displaystyle \begin{aligned} \beta E =\int_0^L ds \left[ \frac{A}{2} \left( \frac{d{\hat{\mathbf{t}}}}{ds} \right)^2-\beta f\hat{\mathbf{z}}\cdot\hat{\mathbf{t}}\right] \end{aligned} $$

(2.5)

The asymptotic high-force behavior is readily obtained using small-fluctuation analysis. We split the tangent vector into components longitudinal and transverse to applied force: $\hat {\mathbf {t}} = t_z \hat {\mathbf {z}} + \mathbf {u}$, with u in the xy plane. Since $|\hat {\mathbf {t}}| = 1 = \sqrt {t_z^2 + u^2}$, we have $t_z = \hat {\mathbf {z}}\cdot \hat {\mathbf {t}} = 1 - u^2/2 + \cdots$. For large force, $\hat {\mathbf {t}}$ is aligned with $\hat {\mathbf {z}}$, so u is small; to Gaussian order we have

$$\displaystyle \begin{aligned} \beta E &= -\beta f L + \frac{1}{2} \int_0^L ds \left[ A \left( \frac{d{\hat{\mathbf{u}}}}{ds} \right)^2 +\beta f u^2\right.\\ &\quad \left.+\mathcal{O}(u^4) \right] \end{aligned} $$

(2.6)

Now using Fourier mode representation [7], we compute the average extension

$$\displaystyle \begin{aligned} \frac{\left< z \right>}{L} &= \left<\hat{\mathbf{z}}\cdot\hat{\mathbf{t}}\right>= 1 - \frac{1}{2}\left< u^2 \right> + \mathcal{O}(u^4)\\ & = 1 - \sqrt{\frac{k_{\mathrm{B}} T}{4 A f}} + \cdots \end{aligned} $$

(2.7)

This characteristic reciprocal square-root dependence of extension on force for a semiflexible polymer in the regime f ≫ k _B T∕A is observed in single-molecule experiments on double helix DNA for forces from about 0.1 up to 10 pN (Fig. 2.2). In the force range of 10–40 pN, the double helix starts to stretch elastically. The extension in this regime is obtained by adding an elastic term (f∕f ₀, where f ₀ ≈ 1 nN) arising from stretching distortions in helix stacking [7, 22].

Fig. 2.2

Force versus extension data for 97 kb dsDNA (L ≈ 33 μm) of Smith et al. [21] compared to predictions from semiflexible polymer model (solid curve) and freely jointed chain model (dashed curve). Inset is proportional to $1/ \sqrt {f}$ and shows a linear dependence on extension as expected for the semiflexible polymer

2.2.2.4 DNA Denaturation by Stress

From DNA “melting” studies, we know that the energy required to separate the helically stacked single-stranded DNAs (ssDNA) is g ≈ 2.5k _B T per base pair [23]. The secondary structure of DNA, which is held together by weak non-covalent bonds of binding energy ≈ k _B T, is expected to strongly deform under highly stressed conditions. This has been observed in a few different ways.

Unzipping

Pulling the two strands of the DNA in opposite directions leads to unzipping of the double helix DNA strands. The helical arclength associated with each base pair is ℓ ≈ 1 nm, which is the length released upon unzipping. Hence, the force, at which the required work to procure ℓ length of ssDNA from a double helix equals the base-pairing energy, gives a simple estimate of the unzipping force: f _unzip ≈ g∕ℓ = 10 pN. The experimentally observed unzipping force ranges from 8 to 15 pN, depending on DNA sequence [24,25,26,27]. The variations in unzipping force has been proposed to be used to analyze DNA sequence.

Overstretching

Under a large applied force a long dsDNA undergoes a structural transition, where the double helix length per base pair increases from 0.34 to 0.6 nm. Again using DNA strand separation energy as the free energy scale, we estimate the overstretching force: f _overstretch ≈ 2.5k _B T/(0.2 nm) ≈ 50 pN. Experimentally observed overstretching transition occurs at a well-defined force 65 pN [28,29,30].

Unwinding

One might imagine an applied torque with a negative helicity (double helix DNA has positive helicity) will unwrap the two single strands of the DNA. Unwinding the DNA releases ≈ 0.6 rad/bp (2π radians per 10.5 bp), which along with the base-pairing energy of 2.5k _B T/bp gives an estimate of the critical unwinding torque: τ _unwind ≈−2.5k _B T/(0.6 rad)≈−16 pN nm (the sign reflects helicity or handedness). The experimentally observed unwinding torque is ≈−10 pN nm (a slightly lower torque than the above estimate occurs since there is left-handed wrapping resulting after denaturation).

Experimental observations and more detailed theoretical work has resulted in development of a force-torque “phase-diagram” for the double helix, with a variety of structural states [31,32,33].

2.3 Topology of DNA

The two helically wrapped strands of a DNA are linked, i.e., for a circular DNA the two strands cannot be separated or unlinked from one another without breaking one of them. This gives rise to an internal linking number for the double helix, which is closely connected to its twist response. All cells have topoisomerase enzymes that manipulate DNA topology, proper functioning of which is critical for the cell.

Topology of a polymer refers to linking or entanglement of the polymer. Topology is invariant under smooth geometric deformations, and only changes when one polymer passes through another. A simple example is the linking of two rings; they can be linked or unlinked, and one cannot pass from the linked to the unlinked state without breaking one of the rings.

2.3.1 Linking Number

The linking number of two oriented closed curves can be computed by counting their signed crossings, according to the rules shown in Fig. 2.4. Dividing the total crossing number by two gives an integer, the linking number Lk of the two curves (Fig. 2.3). This quantity can only change when one curve is passed through another.¹

Fig. 2.3

Simple links of oriented loops. Lk for each pair is computed by adding up the signs of the crossings and dividing the sum by 2. (a) unlinked rings; the signs of the crossings cancel, so Lk = 0. (b) the Hopf link; the signs of the crossings add, so Lk = +1 (Lk would be − 1 if the orientation of one of the loops were reversed). (c) for this link (sometimes called “Solomon’s knot”) the signs of the crossings again add, making Lk = +2. (d) the Whitehead link has canceling signs of its crossings, and has Lk = 0 despite being a nontrivial link

Fig. 2.4

Sign convention for computation of linking number using crossings. Left: left-handed (− 1) crossing. Right: right-handed (+ 1) crossing

The Gauss invariant computes the same quantity, but determines it from the geometry of the two curves:

$$\displaystyle \begin{aligned} \mathrm{Lk} = \frac{1}{4\pi}\oint_{C_1} \oint_{C_2} \frac{ d{\mathbf{r}}_1 \times d{\mathbf{r}}_2 \cdot ({\mathbf{r}}_1 - {\mathbf{r}}_2 ) } {|{\mathbf{r}}_1 - {\mathbf{r}}_2|{}^3} \end{aligned} $$

(2.8)

For DNA, we can distinguish between external linking of two double helix molecules together, and the internal linking property of the double helix itself.

2.3.1.1 Internal Double Helix Linking Number Lk

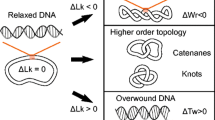
The two strands of a double helix DNA are wrapped around each other in a right-handed manner, with a preferred helix-repeat of one turn every n _h ≈ 10.5 bp, or every h ≈ 3.6 nm. This causes linking of the two strands, resulting in a net linking number associated with the double helix structure: Lk ≈Lk₀ = L∕h = N∕n _h, for a double helix of length L or N base pairs. However, Lk is an integer for a closed double helix, and is not in general equal to Lk₀.

The difference between double helix linking number and the preferred linking number, ΔLk = Lk −Lk₀, is often expressed as a fraction of the preferred linking number (linking number density), σ ≡ ΔLk∕Lk₀ (the excess linking number per DNA length is ΔLk∕L = σ∕h). In E. coli and many other species of bacteria, circular DNA molecules are maintained in a state of appreciably perturbed Lk, with σ ≈−0.05. This is a sufficient perturbation to drive the DNA to supercoil, or wrap around itself in the manner of a twisted extension cord, due to competition between bending and twisting elasticity of the double helix.

2.3.1.2 DNA Twist Stiffness

If Lk is sufficiently different from Lk₀, then there will be a buildup of twist in the DNA, leading to a response in the form of chiral bending. This response is often a wrapping of the double helix around itself, a phenomenon known as supercoiling. One can observe this by taking a stiff cord and twisting it. This behavior arises from a competition between the bending energy [Eq. (2.1)] and the elastic twist energy, the latter being

$$\displaystyle \begin{aligned} \beta E_{\mathrm{twist}} = \frac{C}{2L} \varTheta^2\end{aligned} $$

(2.9)

where Θ is the net twist angle along the double helix. This is just the form of the twisting energy for a uniform elastic rod [35]. Experimentally, this simple linear model has been observed to have a surprisingly wide range of validity for DNA, for C ≈ 100 nm [31].

In the absence of other constraints, thermal fluctuations of twist give rise to a fluctuation

$$\displaystyle \begin{aligned} \left< \varTheta^2 \right> = \frac{L}{C} \end{aligned} $$

(2.10)

suggesting the interpretation of C as a characteristic length for twist fluctuations. For the double helix, this twist persistence length is C ≈ 100 nm. Note that the derivative of E _twist with respect to Θ is the torque or “torsional stress” in the DNA:

$$\displaystyle \begin{aligned} \tau = \frac{\partial E_{\mathrm{twist}}}{\partial\varTheta} = \frac{k_{\mathrm{B}} T C}{L}\varTheta \end{aligned} $$

(2.11)

If there is no bending, then any excess linking number ΔLk goes entirely into twisting the double helix: Θ = 2πΔLk (or σ = Θ∕[2πL∕h]). The mechanical torque in DNA will be τ = 2πk _B TCΔLk∕L = (2πk _B TC∕h)σ. The parameter 2πC∕h ≈ 175 sets the scale for when the linking number density will start to appreciably perturb DNA conformation, i.e., when |τ|≈ k _B T. This level of torque occurs for |σ|≈ 0.005.

2.3.1.3 Decomposition of Double Helix Lk into Twist Tw and Writhe Wr

The previous computation supposed that there was no bending, in which case all of the ΔLk is put into twisting the double helix. This DNA twisting can be quantified through the twist angle Θ, or equivalently through the twisting number.²

If DNA bending occurs, there may be nonlocal crossings of the double helix over itself. These nonlocal crossings contribute to double helix linking number, and the separation of length scales between DNA thickness and the longer scale of DNA self-crossing (controlled by the persistence length A) allows linking number to be decomposed into local (twist) and nonlocal (writhe) crossing contributions:

$$\displaystyle \begin{aligned} \mathrm{Lk} = \mathrm{Tw} + \mathrm{Wr} \end{aligned} $$

(2.12)

or equivalently, ΔLk = ΔTw + Wr. This is known as White’s Theorem.

One can demonstrate this with a thin strip of paper (30 cm by 1 cm works well). Put one twist into the strip, closing it in a ring. The two edges of the strip are linked together once. Now without opening the ring, let it assume a figure-8 shape; you will see that you can make the twist go away: in this state there is only writhe (Fig. 2.5).

Fig. 2.5

Left: a ribbon with Tw ≈−1 and Wr ≈ 0. Right: deforming the ribbon allows the twist to be transferred to writhe, so that Tw ≈ 0 and Wr ≈−1. The linking number is fixed at Lk = −1 as long as the strip is not broken

For elastic ribbon models of DNA, suitable definition of the twist allows Wr to be expressed by the analytical formula [36, 37]:

$$\displaystyle \begin{aligned} \mathrm{Wr} = \frac{1}{4\pi}\oint_{C} \oint_{C} \frac{ d{\mathbf{r}}_1 \times d{\mathbf{r}}_2 \cdot ({\mathbf{r}}_1 - {\mathbf{r}}_2 ) } {|{\mathbf{r}}_1 - {\mathbf{r}}_2|{}^3} \end{aligned} $$

(2.13)

where r ₁ and r ₂ are the two edges of the ribbon. The similarity of this equation to the Gauss invariant, Eq. (2.8), arises from the partitioning of the double integral into contributions from local wrapping of the strands in the double helix (Tw), and from nonlocal contributions (Wr) arising from nonlocal crossings of the centerline of the molecule. Equation (2.13) is the sum of the signed nonlocal crossings for one curve (following the rule of Fig. 2.4), averaged over all orientations [37]. While Lk is a topological property and is quantized for a covalently closed double helix, Wr and Tw are geometrical, and change value smoothly as the molecule is distorted.

2.3.1.4 Supercoiled DNA: Plectonemes

The ability to transfer Tw to Wr suggests that when there is appreciable torsional stress in a flexible filament, it can be relaxed by wrapping the filament around itself. For DNA we should also include the entropic cost of bringing the filament close to itself. A type of model widely used to describe the “plectonemic” wrapping of DNA around itself (Fig. 2.6) is based on treating the wrapping as helical, and by writing down a variational free energy [33, 38,39,40]:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \beta F = \frac{C}{2L}\varTheta^2 + \frac{AL}{2} \kappa^2 + \frac{L}{(Ar^2)^{1/3}} + Lv(r) \\ {} \end{array} \end{aligned} $$

(2.14)

where Θ = 2πΔTw is the DNA twisting (which costs twist elastic energy), κ is the bending curvature, which is κ = r∕[r ² + p ²] for a regular helix of radius r and pitch p (the intercrossing distance is ℓ = πp, Fig. 2.6). The final two terms respectively describe the entropic confinement free energy for a semiflexible polymer in a tube [39, 41, 42] and direct electrostatic and hard-core interactions per molecule length, v(r).³

Fig. 2.6

Geometry of plectonemic supercoil, based on consideration of the shape as two interwound regular helices of radius r and an intercrossing distance ℓ. Note that the helix repeat is 2ℓ and the helix pitch p = ℓ∕π

The confinement entropy is based on estimation of the correlation length ξ for bending fluctuations for a semiflexible chain of persistence length A confined in a cylindrical tube of radius r, where ξ ∼ A ^1∕3 r ^2∕3 [44]. From equipartition theorem, there is ≈ k _B T energy per correlation length. Hence, the entropy cost of radial confinement per unit length is ≈ k _B T∕ξ.

The important final ingredient is Eq. (2.12) which allows the twist to be expressed in terms of linking number and the writhe: Θ = 2πΔTw = 2π(ΔLk −Wr). For a plectoneme based on regular helices, Wr = ∓Lp∕(2π[r ² + p ²]) where the upper/lower signs are for right-/left-handed plectonemic wrapping [39].

Putting this together gives the free energy per length

$$\displaystyle \begin{aligned} \begin{aligned} \frac{\beta F}{L} &= 2\pi^2 C \left( \frac{\varDelta\mathrm{Lk}}{L}-\frac{p}{2\pi(r^2+p^2)}\right)^2 \\ &\quad +\frac{A}{2} \frac{r^2}{(r^2+p^2)^2} + \frac{1}{(Ar^2)^{1/3}} + v(r) \end{aligned}\end{aligned} $$

(2.15)

where the sign of the writhe has been chosen to provide the lower twist energy for positive ΔLk, which is the case of a left-handed superhelix (note that left-handed plectonemes form for ΔLk > 0 while right-handed ones form for ΔLk < 0).

The free energy (2.15) can be optimized numerically to determine r and p [33, 39, 40, 45]. However, an approximate analytical computation for a slender superhelix (r ≪ p) informs of a linking number threshold ΔLk^∗ = kl∕(2π ² C) for the appearance of a valid minimum [$k\sim \mathcal {O}(1)$], introduced by the confinement entropy. Beyond this characteristic value of linking number, the plectoneme becomes stable, and has a free energy below the essentially unwrithed, twisted molecule. This provides a rough idea of the behavior of the full plectoneme model Eq. (2.15) [33, 38, 39, 45]. For sufficient ΔLk, “screening” of the twist energy Eq. (2.9) by the writhe becomes favorable, which has little bending free energy cost if the superhelix radius r is kept relatively small.

Given that the main result for the free energy of the plectoneme is a free energy that rises from zero and eventually becomes superlinear, a useful approximate form to use for the free energy per length of the plectoneme is βF(σ)∕L = (2π ² C _p∕h ²)σ ², where C _p ≈ 25 nm, C _p < C reflecting the twist-energy-screening effect [46].

2.3.1.5 Twisting Stretched DNA

In single-molecule DNA stretching experiments, if a force in the pN range is applied, the double helix will be nearly straight. If it is then slightly twisted while under ≈ pN forces, the molecule will tend to coil chirally, leading to a slight contraction. For larger amounts of twisting, the torque in the DNA will build up to a point where the molecule will buckle, forming plectonemic supercoils.

For small twisting, a small-fluctuation-amplitude computation can be done [47, 48], expanding the tangent vector fluctuations around the force direction (again $\mathbf {t} = t_z \hat {\mathbf {z}} + \mathbf {u}$, where u are the components of t perpendicular to $\hat {\mathbf {z}}$). We begin with the energy for a DNA under tension and twist:

$$\displaystyle \begin{aligned} \beta E &= \frac{2 \pi^2 C}{L}\left( \varDelta\mathrm{Lk} - \mathrm{Wr} \right)^2 - \beta f L\\ &\quad + \frac{1}{2}\int_0^L ds \left[\frac{A}{2}\left(\frac{d\mathbf{u}}{ds}\right)^2 + \frac{\beta f}{2}{\mathbf{u}}^2 \right]\\ &\quad +\mathcal{O}(u^4)\end{aligned} $$

(2.16)

which is just Eq. (2.6) with the addition of the twist energy. For a single-DNA experiment, ΔLk is just the number of full turns made of the end of the molecule (in a magnetic tweezers experiment, the number of times the magnet and therefore the bead at the end of the DNA is rotated [49]).

The challenge is how to include the linking number constraint in Eq. (2.16). The solution is to use an alternative representation of the writhe which takes the form of a single integral over contour length s [50], which can be expanded in u:

$$\displaystyle \begin{aligned} \mathrm{Wr} = \frac{1}{4\pi}\int ds {}\, \hat{\mathbf{z}}\cdot\mathbf{u}\times\frac{d\mathbf{u}}{ds} + \mathcal{O}(u^4) \end{aligned} $$

(2.17)

This quantity is quadratic in u since the writhe of a straight line configuration is zero.

Using this in the twisting energy Eq. (2.16) and expanding to quadratic order in u gives the total elastic Hamiltonian for chiral fluctuations in a twisted stretched DNA. The Hamiltonian shows an elastic instability for a critical DNA torque: $\beta \tau _c = \sqrt {4 \beta A f}$, which is the classical buckling instability of a rod subject to tension and torque [51]. The same instability can be observed in dynamical models of twisted and stretched DNA [52]. This corresponds to a critical linking density σ _c ≈ 0.028 for f = 0.5 pN. The Hamiltonian allows computation of $\left < {\mathbf {u}}^2 \right >$ and the free energy, in a Gaussian approximation. The extension is $\left < \hat {\mathbf {t}}\cdot \mathbf {z} \right > = 1 - \left < {\mathbf {u}}^2 \right >/2 + \mathcal {O}(u^4)$, or

(2.18)

where the neglected terms are of higher order in 1∕f. Changing σ from zero leads to additional shrinkage over the untwisted case, due to chiral bending fluctuations.

Either integration of the extension with force, or direct computation of the partition function gives the free energy per length in a similar 1∕f expansion:

$$\displaystyle \begin{aligned} \frac{\beta F}{L} &= -\frac{\ln Z}{L} = -\beta f + \sqrt{\frac{f}{k_{\mathrm{B}} TA}}\\ &\quad + \frac{2\pi^2 C}{h^2} \left[ 1 - \frac{1}{2}\frac{C}{A}\left(\frac{k_{\mathrm{B}}T}{4Af}\right)^{1/2} \right] \sigma^2\end{aligned} $$

(2.19)

The last term shows that the effect of the chiral fluctuations is to, as for DNA supercoiling, partially screen the twist energy, generating a reduction in the effective twist modulus $C \rightarrow C_f = C\left [ 1 - (C/2A)(k_{\mathrm {B}} T/4Af)^{1/2} \right ]$. This effect was used by Moroz and Nelson [47] to estimate the twist elastic constant C from single-molecule data of Strick et al. [49] and led to a substantial revision in the accepted value of C from 75 nm up to the range 100–125 nm.

2.3.1.6 Coexistence of Supercoiled and Twisted-Stretched DNA

For fixed force and sufficient ΔLk, one has “phase coexistence” of domains of plectonemic supercoiling and extended DNA (sketched in Fig. 2.7) [33, 38, 39, 46]. These “pure” states can be described by free energies per B-DNA length dependent on applied force f and the linking number density σ, say $\mathcal {S}(\sigma )$ for stretched and $\mathcal {P}(\sigma )$ for plectonemic DNA (the free energies per length discussed in the prior two sections, i.e., up to a factor of k _B T, Eqs. (2.19) and (2.15)). For these pure states, the rate at which work is done in injecting linking number is proportional to torque, for example:

$$\displaystyle \begin{aligned} \tau = \frac{1}{\omega_0} \frac{\partial \mathcal{S}(\sigma) }{ \partial \sigma}\end{aligned} $$

(2.20)

The prefactor ω ₀ = 2π∕h = 2π∕(3.6 nm) is the angle of twist per molecule length for relaxed B-DNA, which converts the σ derivatives to ones with respect to angle.

Fig. 2.7

(a) Sketch of a DNA molecule under tension f, and with linking number ΔLk fixed so as to put the double helix under torsional stress. Over a range of applied tension, the molecule breaks up into “domains” of extended and plectonemically supercoiled DNA. Only a single domain of plectonemic DNA is shown for clarity. (b) Free energies of extended (dot-dashed curve, $\mathcal {S}(\sigma )$) and plectonemic supercoil (dashed curve, $\mathcal {P}(\sigma )$) DNA states as a function of linking number σ. For σ < σ _s, the $\mathcal {S}$ state is lower in free energy than either $\mathcal {P}$ or any mixture of the two. Similarly, for σ > σ _p, pure $\mathcal {P}$ is the lowest-free energy configuration. On the other hand, for σ between σ _s and σ _p the tangent construction shown (solid line segment between tangent points indicated by stars), representing coexisting domains of $\mathcal {S}(\sigma _{\mathrm {s}})$ and $\mathcal {P}(\sigma _{\mathrm {p}})$, is the lowest-free energy state. Note that the gap between the two states near σ = 0 is the free energy difference between random coil DNA [$\mathcal {S}(0)$] and stretched unsupercoiled DNA [$\mathcal {P}(0)$]; this difference grows with applied force and is due to the term − βf in the extended state free energy Eq. (2.19)

If the pure state free energy densities, $\mathcal {S}(\sigma )$ and $\mathcal {P}(\sigma )$, plotted as a function of the linking number density σ, never cross or intersect, then one pure state or the other will be the equilibrium state. On the other hand, if the free energy densities cross, there will be a range of σ values over which linking number will be partitioned between the two states exhibiting coexisting domains of the stretched and the plectoneme state. Along a molecule which is a fraction x _s of state $\mathcal {S}$ and fraction x _p = 1 − x _s of state $\mathcal {P}$, the free energy per base pair of the mixed phase is

$$\displaystyle \begin{aligned} \mathcal{F}(\sigma) = x_{\mathrm{s}} \mathcal{S}(\sigma_{\mathrm{s}}) + x_{\mathrm{p}} \mathcal{P}(\sigma_{\mathrm{p}}) \end{aligned} $$

(2.21)

The equilibrium length fraction x _s and the free energy is determined by minimization of this free energy subject to the constraint of fixed linking number: σ = x _s σ _s + x _p σ _p.

Figure 2.7b shows this situation, sketched to correspond to the case of main interest here, where at low values of σ the stretched state is stable (lower in free energy) relative to the plectoneme state, but where at large σ the stability reverses due to “screening” of the twist energy by the plectonemic state’s writhe [7, 33, 38].

Minimization of Eq. (2.21) leads to a double-tangent construction that ensures monotonic increase of torque, which is required for mechanical stability. In the coexistence region, the fractions of the two states in the mixed state depend linearly on σ, as

$$\displaystyle \begin{aligned} x_{\mathrm{s}} = \frac{\sigma_{\mathrm{p}} - \sigma }{ \sigma_{\mathrm{p}}-\sigma_{\mathrm{s}}} \quad \quad \quad x_{\mathrm{p}} = \frac{\sigma - \sigma_{\mathrm{s}} }{ \sigma_{\mathrm{p}}-\sigma_{\mathrm{s}}} \end{aligned} $$

(2.22)

In the coexistence region (σ between the limits σ _s and σ _p) the torques in the two types of domains are equal and σ-independent. Equation (2.22) indicates that the rate of change of the length fractions with σ is constant; ∂x _s∕∂σ = −1∕(σ _p − σ _s). This generates the linear dependence of molecule extension z on linking number in the coexistence state:

$$\displaystyle \begin{aligned} \frac{z }{ L} = -\frac{\partial \mathcal{F} }{ \partial f} = -x_{\mathrm{s}} \frac{ \partial \mathcal{S}(\sigma_{\mathrm{s}}) }{ \partial f} -x_{\mathrm{p}} \frac{\partial \mathcal{P}(\sigma_{\mathrm{p}}) }{ \partial f}\end{aligned} $$

(2.23)

In the coexistence region, the only σ dependence is the linear variation of x _s and x _p, making the dependence of extension on σ linear.

However, the linearity of extension in the coexistence state may not be robust for finite sized molecules. In the finite-size case, contribution from the plectoneme end loops (Fig. 2.7a), loop-shaped chiral structures where the molecule in a plectoneme bends back, is non-negligible. A series of extension versus linking number curves are plotted in Fig. 2.8a showing the initial stretched-unbuckled state and the onset of the plectoneme coexistence state characterized by a steep decrease in the extension. The results shown in Fig. 2.8 are from an improved model (see [40] for details) that considers the coexistence of the stretched state, the plectoneme state, and plectoneme end loops. The end loops associate a nucleation energy cost to a plectoneme domain, which is manifested as a discontinuity in extension and overshoot in the torque at the buckling point (Fig. 2.8). The geometry and the size of the chiral loop are directly related to the first-order-like buckling transition observed in supercoiled DNA [53].

Fig. 2.8

(a) End-to-end extension of the DNA as a function of the linking number ΔLk for various forces f = 0.25 (lowest curve, blue), 0.5 (green), 1 (cyan), 2 (orange), and 4 pN (highest curve, red). The onset of the coexistence state σ _s can be identified from the change in the slope of the extension curves, and σ _p corresponds to zero extension. (b) DNA torque increases linearly and plateaus in the coexistence state. The results are reproduced from a model that considers coexistence of plectoneme end loops, reflected in the discontinuous onset of the buckling transition near σ _s, see [40] for details

DNA torque increases in the stretched state and is nearly constant in the coexistence state (Fig. 2.8b). This is quite useful for experiments on topoisomerases, since measurements carried out in the rather broad plectoneme-extended coexistence regions (along the linear portions of the “hat” curves of Fig. 2.8a) are done at fixed torque, which is controlled by the constant force, e.g., about 7 pN nm at 0.5 pN, approximately the torque in a plasmid with physiological supercoiling σ ≈ 0.06 [46, 54] (note that there is an appreciable torque decrease with increased salt [54], since DNA hard-core diameter drops and therefore plectoneme tightness increases [45] with increased salt concentration).

For 10 pN and positive supercoiling, and for above 0.5 pN for negative supercoiling, one sees the effect of additional “stress-melted” DNA states not included in the model described here; see [33] for details.

An interesting aspect of experiments done on twisted DNA is that now one has an additional control parameter, ΔLk which can be used to construct a thermodynamical “Maxwell relation” involving torque $\left <\tau \right > = \partial F / \partial (2\pi \varDelta \mathrm {Lk})$ and force (and, also, chemical potential of molecules binding to the double helix) [55]. The Maxwell relation involving f and ΔLk has, for example, been used to indirectly measure torque, starting from extension-σ curves at a series of fixed forces [54] in reasonable accord with direct measurements [53].

Branching of the plectoneme is an interesting phenomenon. The energy cost associated with the end loops oppose branching, however, the configuration entropy gain from branched plectoneme structures favors branching. Thus, branching or proliferation of multiple domains of plectoneme is favored when the entropy gain dominates the nucleation energy cost (predominantly bending energy associated with the large curvature of an end loop). However, entropy gain is only logarithmic: $\approx k_{\mathrm {B}}\ln (L/A)$, and is expected to be a small contribution for short molecules (≈ 4 kb); nonetheless, branching can occur in short molecules due to relative instability of the plectoneme superhelical windings caused by a larger excluded diameter of the DNA at low salts.

Structural defects on the double helix, such as a base-mismatched region or a DNA bubble or a single-stranded DNA bulge, introduces kinks along the DNA contour that may spatially pin a plectoneme domain [56,57,58]. This feature also hints at the potential role of supercoiling in cellular base-pair repair mechanism, as the defect placed at the tip of a plectoneme allows easier access to the lesion site [58,59,60,61].

2.3.1.7 Intertwined DNAs

A slightly more complicated structure than a single twisted DNA is that of two nicked ⁴ DNAs wrapped around each other or braided DNAs, such that there is a net inter-DNA linking or catenation number associated with the structure. DNA braids are biologically relevant substrates for type-II topoisomerases, enzymes that manipulate inter-DNA topology to facilitate segregation of catenated sister chromatids. This makes them a suitable substrate for in vitro assays of topoisomerases and recombinases [62,63,64,65,66,67].

The unstressed condition for a DNA braid is that of the unlinked or the zero catenation configuration of the two torsionally unconstrained double helices (Fig. 2.9a). Wrapping the two DNAs around one another introduces catenation, which results in a buildup of torsion. However, the torque in the braid grows nonlinearly [68,69,70], in contrast with a linear torque in twisted DNAs (Fig. 2.8b). The stacked double helical structure of a DNA gives rise to constant twist stiffness (C ≈ 100 nm) which is interpreted as a linear DNA torque; braids, however, are soft structures that exhibit twist stiffening or catenation-dependent twist stiffness.

Fig. 2.9

(a) Sketch of torsionally stressed DNA braid showing buckled plectoneme states (two domains of plectoneme are shown). (b) Braid extension as a function of the catenation number. Note the initial jump in extension which is related to the distance between the tether points on the two DNAs. The change in slope corresponds to the coexistence state, which is characterized by proliferation of multiple domains. See [68] for details

Similar to the twisted double helices, torsionally stressed braids also show coexistence of a stretched-braid state with a braid plectoneme state beyond a critical catenation. This buckled state can be identified in the experiments as the point of change in slope of extension curves.⁵ However, unlike supercoiled single DNAs, the buckled braid-plectoneme state shows proliferation of multiple domains [71], where each domain has an end loop, as is sketched in Fig. 2.9. This contrast in the mechanical response of catenated DNAs with that of single DNAs informs how structural bulkiness plays into mechanical buckling. Another interesting aspect of braids is that the distance between the tether points of the two DNAs or the intertether distance is connected to the torque in the braid, and strongly influences the mechanical response.

We discussed how polymer topology leads to a wide array of mechanical properties of the double helix. Topology manipulation in eukaryote chromatin is a topic of ongoing research. Nucleosomes, the building blocks of chromatin, have a net negative writhe associated with its native structure. As a result, positive supercoiling destabilizes nucleosomes, whereas, negative supercoiling aids assembly; which is interesting given that unzipping of the DNA by polymerases and helicases generates positive (negative) supercoiling downstream (upstream). Single-molecule studies suggest that chromatin fibers are able to absorb substantial amounts of twist, possibly via structural rearrangement in nucleosomes [72, 73]. However, the in vivo role of supercoiling in chromatin fibers is less clear.

2.3.2 Knotting and Catenation of DNA

The DNA molecules inside the nucleus are expected to get knotted, a consequence of their long length. Knotting of DNA poses a topological problem to primary cellular functions such as DNA replication and post-replication segregation of sister chromosomes. Cells possess a special class of enzymes, DNA topoisomerases, which is the topic of our next discussion, that manipulate DNA topology in order to suppress knotting. Now, the enzymes acting locally cannot sense the global topological state of the DNA, nonetheless, they are able to control DNA entanglement. The mechanisms underlying such behavior is a topic on current research [74, 75].

2.3.2.1 DNA Topoisomerases

Single-molecule experiments studying twisted or catenated DNAs change DNA topology (the value of ΔLk or Ca) by directly twisting or intertwining the DNA molecules. In the cell, specialized proteins manipulate DNA topology by introducing transient cuts in the sugar-phosphate backbones of the double helix; depending on whether one or both backbones are cut, topoisomerases are classified as type I or type II [76].

Type-I topoisomerases (topo I) cut one backbone of the double helix, allowing unrestricted rotation of the broken strand about the intact one, thus relaxing DNA linking number. These enzymes do not require ATP for their operation, and they tend to equilibrate DNA linking number to zero, ΔLk → 0. However, the mechanical-chemical equilibrium may be altered by other processes, thus driving topo I activity. At present there are three subclasses of type I topoisomerases, which differ in details of their structures and their mechanisms [76]. The most important distinction is between type IA and IB, the former accomplishing a change in ΔLk = +1 per backbone cut-reseal catalytic cycle, and the latter changing ΔLk by one or more turns per catalytic cycle. Type I topos also can act on separate DNA molecules, facilitating decatenation (disentanglement) of entangled single-stranded DNAs [77].

Type-II topoisomerases (topo II) cut both the strands of a double helix, making a gap through which a second double helix is passed, thus altering the linking or catenation of the two double helices. When a type II topo makes this topology change on two DNA molecules, the result is a change of the sign of a crossing (as in the two crossings shown in Fig. 2.3). Therefore the total number of crossings changes by ± 2, and so the catenation number of the two molecules changes by ± 1. An important example of a type II topoisomerase is Topo IIα, which is the main enzyme acting to remove entanglements between DNAs in eukaryote cells. Type II topoisomerases can also act at two points along a single DNA molecule, leading to a total change in ΔLk of the molecule being operated on by ± 2. Bacteria contain a type II topoisomerase called DNA gyrase which is specially adapted for this function. This is thought to be accomplished via the enzyme binding a + 1-crossing loop, which then is changed in sign to −1. By this mechanism DNA gyrase is able to couple the energy stored in ATP into reduction of ΔLk to negative values (towards unwinding the double helix).

Topo II is thought to perform selective decatenation in order to suppress the equilibrium probabilities of knotted DNA states [78], which is consistent with the fact that topo II mediated decatenation requires ATP hydrolysis (the requirement of ATP seems to ensure that the second molecule is passed through the gap in a specific direction). However, the mechanism underlying active suppression of entanglements via selective decatenation is not fully understood [74, 75, 79].

2.3.2.2 Knotting Probabilities

A single circular molecule is in one of many possible knotted states. We can imagine having an ensemble of circular polymers which are allowed to slowly change their topology, so as to have equilibrated knotting topology (this is possible to achieve using topoisomerases, or using enzymes that alternately linearize and recircularize the molecules). We can ask what the probability P _unknot is that any molecule will be unknotted.

One might ask how P _unknot behaves with the length L of the circles. For small L, (more precisely for L∕b < 1, where b is the segment length; recall A = b∕2 and N = L∕b) there will be a large free energy cost of closing a molecule into a circle making P _knot → 1. One can argue that for large L, $P_{\mathrm {unknot}}\approx \exp [-L/(N_0 b)]$, for some constant N ₀, over some polymer length (say N ₀ segments) the probability of having no knot drops to 1∕e. Applying this probability to each L ₀ along a DNA of length L gives us $P_{\mathrm {unknot}} (L)\approx e^{-L/(N_0 b)}$. This rough argument can be made mathematically rigorous [80].

Remarkably, even for an “ideal” polymer which has no self-avoidance interactions, N ₀ ≈ 300; for a slightly self- avoiding polymer like dsDNA in physiological buffer, N ₀ ≈ 400 [81]. What this means is that to have an appreciable probability (1 − 1∕e) to find even one knot along a double helix DNA, it has to be 400 × 300 = 120, 000 bp long (the long persistence length of DNA - b contains 300 bp, which helps make this number so impressive). The knotting length N ₀ depends very strongly on self-avoidance; for a strongly self-avoiding polymer (meaning an excluded volume per statistical segment approaching b ³), N ₀ ≈ 10⁶. The remarkably low probability of polymer knotting lacks fundamental understanding, being based on numerical simulation results [81].

Experiments on circular DNAs are in good quantitative agreement with statistical mechanical results for the semiflexible polymer model including DNA self-avoidance interactions. For example, it is found that the probability of finding a knot generated by thermal fluctuations for a 10 kb dsDNA is about 0.05 both experimentally and theoretically [3, 82]. This can be interpreted thermodynamically; the free energy of the knotted states relative to the unknotted state in this case is $k_{\mathrm {B}}T\ln (0.95/0.05)\approx 3 k_{\mathrm {B}}T$.

A remarkable experimental observation is that type II topoisomerases are by themselves able to push this probability down, by a factor of between 10 and 100 [78]. Somehow topo II is able to use energy from ATP hydrolysis to actively suppress entanglements.

2.3.2.3 Catenation Probabilities

The Gauss invariant of two closed curves or the catenation number Ca—also computed via summing the signed crossings in a projection plane—is not a unique classifier of the topological states of the two curves, i.e., two non-trivially linked or entangled polymers may have zero catenation number (Fig. 2.3). However, the probability distribution of catenation, more specifically, the broadness of the distribution 〈Ca²〉, is a good identifier of the degree of entanglement in the polymers; larger 〈Ca²〉 indicates higher entanglement.

Consider two circular DNA molecules each containing N segments (L = Nb, $R=b\sqrt {N}$), attached together at one segment (Fig. 2.10), a situation reminiscent of the replicated sister chromatids in the cell. We expect 〈Ca〉 = 0; right- and left-handed crossings occur with equal probabilities.⁶ Now, the width of the distribution 〈Ca²〉 is at least as large as the number of nearby crossings, where the segments involved are a segment length or less in the projection direction. The number of near crossings is ≈ Nϕ, where ϕ ≈ N∕R ³ is the segment density. This implies a scaling relation

$$\displaystyle \begin{aligned} \langle\mathrm{Ca}^2\rangle= a_0N^{1/2}\end{aligned} $$

(2.24)

or, |Ca|≈ N ^1∕4, which has been suggested by Cloizeaux [83] and calculated by Tanaka [84]; numerical simulations suggest a ₀ ≈ 0.25 [85].

Fig. 2.10

Two polymer of N segments each, joined at one point along their contours

In case of self-avoiding polymers the number of nearby crossings drops to O(1) due to segment-position correlations [86], and only the distant nonlocal crossings contribute: $\left <\mathrm {Ca}^2\right >\approx a_1\ln N$ [85].

2.3.2.4 Linking of Confined Polymers

The two examples discussed above—knotting of one polymer and catenation of two polymers tethered together at one point—both indicate that entanglements cost a good deal of free energy, but these were cases of isolated polymers. We now consider entanglements between n polymers each of N segments, in a dense melt or semidilute-solution- like state, confined to a radius-R spherical cavity. The polymers are long enough so that their random-walk size, N ^1∕2 ≫ R, fills the confinement volume. This is a crude model of chromosomes confined to a nucleus, or inside a bacterial cell.⁷

We now ask what the degree of catenation will be if the entanglement topology of these confined chains is equilibrated (for example, by topoisomerases). For a polymer melt, along a chain of N segments, every segment is nearby other segments (not counting the segments to the left and right along the same chain). Most of these near encounters are with segments from other chains, since the number of collisions of a chain with itself is ≈ N ^1∕2 for the random- walk statistics in a melt. This means that each chain has N near collisions with other chains, or N∕n near collisions with any particular chain. But since these near collisions appear in the ensemble of configurations with either crossing sign, we expect 〈Ca²〉≈ N∕n. For this problem, the high segment density and the proximity of the polymers to one another forces them to be much more entangled than isolated chains.

In the semidilute solution case (volume fraction ϕ = nNb ³∕R³ ≪ 1, but with overlapping chains), exactly the same argument can be made, but now for semidilute solution blobs, which each have g ≈ ϕ ^5∕4 segments in them. The result is that 〈Ca²〉 = ϕ ^5∕4 N∕n. Simulations indicate that the two regimes can be described by one scaling formula [90]

$$\displaystyle \begin{aligned} \langle\mathrm{Ca}^2\rangle=\frac{N}{n}c(\phi) {}\end{aligned} $$

(2.25)

where c is a scaling function with limiting behaviors c(ϕ ≪ 1) ∝ ϕ ^5∕4, and c(ϕ → 1) → 1 (Fig. 2.11).

Fig. 2.11

Scaling behavior of catenation fluctuations for circular polymers of N unit-length segments confined to a sphere of R. The segments have a diameter 0.2 times their length (d∕b = 0.2) and interact via excluded-volume interactions. Catenation 〈Ca²〉∕N scales linearly with the segment density ϕ = nN∕R³ for ϕ > 1, and faster than linearly for ϕ < 1. Solid curve is a fit function that interpolates between the asymptotic behaviors ϕ ^5∕4 and ϕ → 1 expected for ϕ < 1 and ϕ > 1, respectively

Closely related to disentanglement of DNA is its lengthwise compaction following replication. Lengthwise compaction modifies the contour length of the DNA to be L ^′ < L, as well as the thickness or the statistical segment length b ^′ > b, thus decreasing the number of segments N ^′ < N. This leads to a decrease in catenation fluctuations in semidilute conditions with constant ϕ [Eq. (2.25)]. Compaction can also drive spatial “condensation” of helical catenations, on which topo II can be expected to act to release catenations. The knotting probabilities also decrease upon lengthwise compaction ($P_{\mathrm {unknot}}\approx e^{-L/[N_0b]})$. We will discuss lengthwise compaction of DNA in more detail in the next section alongside the proteins that facilitate the process.

2.4 Protein–DNA Interactions and Nuclear Mechanics

2.4.1 Overview of DNA–Protein Interactions

In cells, proteins cover the DNA double helix, allowing it to be stored, read, repaired, and replicated. We now briefly review some basic aspects of DNA–protein interactions.

Different proteins have different functions on the double helix. Examples of classes of DNA-acting proteins include:

Architectural

Proteins that help to package DNA, bending and folding it, typically binding to 10–20 bp regions and often without a great deal of sequence dependence; examples include histones (eukaryotes) and HU, H-NS, and Fis (E. coli), which all bind to and bend DNA to help package it.

Regulatory

Proteins that bind to specific DNA sequences from 4 to 20 bp in length, and which act as “landmarks” for starting transcription or other genetic processes; examples include TATA-binding protein (eukaryotes) and Lac repressor (E. coli).

DNA-Sequence-Processing

Proteins which burn NTPs or dNTPs and which move processively along the DNA backbone, reading, replicating, unwinding, or otherwise performing functions while translocating along DNA; examples include RNA polymerases, DNA polymerase, and DNA helicases.

Catalytic. Proteins which cut and paste DNA, accomplishing breaking and resealing of the covalent bonds along the DNA backbone, or inside the bases; examples include topoisomerases, recombinases, and repair enzymes such as DNA oxoguanine glycosylase (Ogg1, an enzyme that recognizes and repairs oxidative chemical damage to the base guanine).

An additional important class of catalytic DNA-interacting proteins are Structural Maintenance of Chromosome (SMC) protein complexes, large protein machines which use energy from ATP hydrolysis to drive looping-organization of DNA, possibly through active “loop-extrusion” processes.

In general all these types of proteins alter DNA structure and therefore DNA mechanics, especially architectural proteins. A few proteins that alter DNA structure either architecturally, or catalytically, are shown in Fig. 2.12.

Fig. 2.12

Structural models of protein–DNA complexes based on X-ray crystallography studies, all shown at approximately the same scale. (a) Fis, a DNA-bending protein and transcription factor from E. coli; the two polypeptide chains are shown in green and blue. Image courtesy of R.C. Johnson. (b) HU, another DNA-bending protein from E. coli. Image reproduced from data of [91]. (c) Four resolvase proteins bound to two DNA segments. The proteins mediate cut-and-paste site-specific recombination between the halves of the DNA segments. Exchange of the cut DNAs is thought to occur by rotation of the flat protein–protein interface in the middle of the structure. Image reproduced from [92]. (d) Topoisomerase V, an archaeal enzyme that cuts one strand of DNA, allowing internal linking number of the double helix to change. Image reproduced from [93]. (e) Eukaryote nucleosome. The roughly 10-nm-diameter particle contains 147 bp of DNA wrapped around eight histone proteins (purple chains). Top view is shown on the left, side view is shown on the right. Image reproduced from data of [12]

2.4.2 Classical Two-State Kinetic/Thermodynamic Model of Protein Binding a DNA Site

The starting point for thinking about protein–DNA interactions is binary chemical reaction kinetics (P + D ↔ C) where P is a particular protein, D is one of its binding sites, and C is the protein–DNA bound “complex.” Consider just one binding site in a sea of proteins at concentration c. Supposing diffusion-limited binding kinetics, we have to wait for a particular protein to “find” the binding site; the on-rate in this case is the result of Smoluchowski, r _on = 4πDac where D is the diffusion constant for the protein, and a is the “reaction radius,” the distance between reactants at which the reaction occurs, a scale comparable in size to the binding site. Since D ≈ k _B T∕(6πηR), where R is the approximate size of the protein, we have r _on = k _on c, where the chemical forward rate constant for the reaction is k _on ≈ (a∕R)k _B T∕η. Since R > a we can take k _B T∕η as a kind of “speed limit” for a binary reaction controlled by three-dimensional diffusion. For T = 300 K and η = 10⁻³ Pa s (appropriate for water at room temperature),

$$\displaystyle \begin{aligned} k_{\mathrm{on}} &< \frac{k_{\mathrm{B}} T}{\eta} = \frac{4 \times 10^{-21}\,\mathrm{J}}{10^{-3}\, \mathrm{Pa}\,\mathrm{s}}\\ {} &= 4 \times 10^{-18}\, \mathrm{m}^3/\mathrm{s} \approx 10^{9}\, \mathrm{M}^{-1}\,\mathrm{s}^{-1} \end{aligned} $$

(2.26)

where the final units indicate a rate per unit concentration (M = mol/l; recall 1 M = 6 × 10²³∕l).

It turns out that this rate can be increased by roughly an order of magnitude if in addition to three-dimensional diffusion, there is also one-dimensional “search” over a restricted region of a long DNA polymer in which a specific binding site is embedded [15, 94]. However, the rate at which initial encounters of protein and DNA occur is still controlled by Eq. (2.26). There remain many interesting problems having to do with (small) proteins binding to a (long) DNA polymer, for example, the dependence of multiple sequential interactions on polymer conformation [95].

Returning to the basic picture of proteins binding to one DNA binding site, once the complex is formed, one usually considers it to have a lifetime, described by a concentration-dependent rate k _off of dissociation of the protein from the DNA (units of k _off measured in s⁻¹).

Once our proteins come to equilibrium with the binding site, the probability that the site will be bound relative to being unbound will be

$$\displaystyle \begin{aligned} \frac{P_{\mathrm{on}}}{P_{\mathrm{off}}} = \frac{k_{\mathrm{on}} c }{k_{\mathrm{off}}} \equiv \frac{c}{K_d}\end{aligned} $$

(2.27)

where the dissociation constant K _d ≡ k _off∕k _on describes the strength of the binding. Since K _d is the concentration at which the site is 50% bound, the smaller K _d is, the tighter the binding.⁸ The site-occupation probability is the familiar Langmuir adsorption isotherm, P _on = c∕(K _d + c).

The Boltzmann distribution gives the equilibrium free energy difference between the bound and unbound states,

$$\displaystyle \begin{aligned} {G_{\mathrm{on}} {-} G_{\mathrm{off}}} = -k_{\mathrm{B}} T \ln \frac{P_{\mathrm{on}}}{P_{\mathrm{off}}} = k_{\mathrm{B}}T \left(\ln K_d - \ln c \right)\end{aligned} $$

(2.28)

The bound state is reduced in free energy (becomes more probable) as solution concentration of protein is increased. Equation (2.28) can be thought of as reflecting the free energy associated with interactions ($G_{\mathrm {int}} = k_{\mathrm {B}} T\ln K_d$; smaller K _d gives a more negative “binding” free energy) in competition with the ideal-gas entropy loss associated with localizing the protein to the DNA binding site ($G_{\mathrm {ent}} = -k_{\mathrm {B}}T\ln c$; an ideal-gas entropy model is appropriate since the volume fraction of any particular DNA-binding protein species is usually very small in vivo or in test-tube experiments).

This basic type of model is widely used to analyze protein–DNA interactions. It should be kept in mind that it has been found for some proteins that the off-rates are strongly dependent on the concentration of other molecules in solution [96,97,98,99,100,101,102,103], an effect which makes definition of binding equilibrium more complex.

2.4.3 Force Effect on Protein–DNA Binding

If tension f is present in a DNA molecule during interaction with proteins (or other molecules that bind DNA, e.g., DNA-intercalating agents like ethidium bromide), that tension can affect the binding. In general there will be some mechanical change in length of a DNA if a protein binds it. This might be only a few nanometers in the case of a single DNA-bending protein (e.g., Fig. 2.12a or b); for a nucleosome it might be the entire 150 bp or ≈ 50 nm of DNA wrapped around the histones (Fig. 2.12e).

Suppose there is a length contraction ℓ > 0 (or a lengthening by ℓ < 0 [104]) of a DNA molecule when binding of a protein occurs. As an example, imagine a protein which bends or loops DNA, cases for which ℓ > 0. Tension plausibly slows down k _on (since now one must get to a transition state by doing work against the applied tension) and plausibly speeds up k _off (the chemical bonds in the complex will be destabilized by any applied tension).

By Eq. (2.27), if binding equilibrium can be achieved, the ratio of these rates and therefore the binding/unbinding probability ratio reflect the presence of the additional mechanical work fℓ [105]:

$$\displaystyle \begin{aligned} \frac{P_{\mathrm{on}}}{P_{\mathrm{off}}} = \frac{c}{K_d} e^{-\beta f \ell}\end{aligned} $$

(2.29)

where β = (k _B T)⁻¹, and where K _d indicates the dissociation constant at zero force. Equation (2.29) suggests that we identify a force-dependent dissociation constant, $K_d(f) = K_d(0) \exp (\beta f \ell )$ and for ℓ > 0 we see that applied force increases the K _d strongly, since tension is destabilizing the bound complex. In the “DNA-lengthening” case ℓ < 0, stretching the double helix stabilizes binding.

This effect becomes dramatic for DNA looping. Note that even in the absence of force, the stiffness of the double helix essentially constrains thermally formed loops to be longer than ≈ 50 nm (somewhat shorter loops can form but at a large free energy cost, i.e., slowly). If tension is present, there is an additional force-retraction free energy cost [105]. For example, even a rather small loop with ℓ ≈ 100 nm under moderate tension of f = 0.5 pN will have fℓ ≈ 12.5k _B T, leading to a large perturbation of the K _d. In such a case, the on-rate will be most strongly affected (suppressed) by applied force, since the “transition state” for the looping reaction requires nearly all of the work fℓ to be done by thermal fluctuation, if the protein-mediated looping interaction is of short range [106, 107].

It is to be emphasized that protein–DNA complexes can easily fall out of binding equilibrium due to the large barriers associated with on- and off-dynamics. An excellent example of this are isolated nucleosomes under tension, the unwinding of which show barrier-crossing nonequilibrium dynamics [108]. However, these barriers, and therefore the kinetics of proteins binding and unbinding to DNA are often profoundly affected by other nearby biomolecules [96, 99, 101]. Notably, in the presence of additional “chaperone” protein molecules associated with nucleosome assembly and disassembly in vivo even large complexes such as nucleosomes can be studied in mechanical-biochemical equilibrium [109].

2.4.4 DNA-Bending Proteins and Effective Persistence Length

DNA in most organisms is covered with “architectural” DNA-bending proteins, to help package it compactly. In eukaryotes the “histone” proteins (two each of histones H2A, H2B, H3, and H4) complex together as octamers to form “nucleosomes,” with each histone acting to bend DNA [110]. In addition a variety of small DNA-bending proteins act to further kink DNA between nucleosomes (including HMG proteins such as HMGB1). In bacteria, “nucleoid” proteins (in E. coli, Fis, HU, H-NS, and StpA) act independently to generate bends along DNA [111].

It follows that one should consider the situation where one has a long dsDNA subject to insertion of kinks when proteins bind to it; this situation has been studied in a variety of single-DNA experiments [112,113,114,115,116], and is a simplified version of the situation occurring with chromosomes in vivo. As long as the proteins do not bind the DNA too densely, the additional bends generated generally act to reduce the persistence length, compacting the DNA contour and increasing the forces needed to stretch out the protein–DNA complex over that of the stiffer naked dsDNA molecule. Indeed this effect has been observed experimentally for a number of DNA-bending proteins, with a shift of the force-extension curve to larger forces as protein concentration is increased [112,113,114,115, 117]; theoretical models for protein-induced bending of DNA show the same effects [55, 118].

It has been observed for at least two DNA-bending proteins that once they reach a high binding density along the double helix, a stiffening effect occurs [113,114,115]. This may be due to the formation of phased bends which act to essentially stretch the DNA double helix contour length.

Finally, the same general comments apply to eukaryote chromatin, which can be considered as a string of nucleosomes, with the added provision that the wrapping of DNA around nucleosomes also compacts the total length of the resulting DNA–protein complex by a factor of very roughly 10.

2.4.5 Chromosome Organization: DNA Loops

At scales larger than individual DNA-bending proteins, which typically bind ≈ 20 bp regions along the double helix, the long DNA molecules of prokaryotes and eukaryotes are generally organized into loops by the binding of two distance segments together by a protein complex. If one imagines constructing a sequential series of loops, this can accomplish a large length compaction, from the original length of the DNA molecule, to approximately the length of the inter-loop DNA along the resulting “loop axis.” Indeed a large number of DNA-binding proteins form loops by binding two sites: a classic example is the lac repressor from the bacterium E. coli. [119]; a key example from human cells is the protein CTCF, which binds together two copies of a specific DNA sequence [120]. In both these examples the interaction between DNA sequences plays a gene-regulatory role.

One mechanism for formation of such loops is simple Brownian polymer dynamics, which can bring distant sites together at a rate roughly proportional to ≈ (R∕L)³ ≈ (A∕L)^3∕2, where L is the inter-site distance and R is the end-to-end distance. While this can be efficient at relatively short (kilobase) scales, is it unclear how loops can be formed efficiently at longer scales by a pure random collision mechanism, or how the tight arrays of loops thought to organize metaphase chromosomes can be efficiently formed. A further point is that folding of chromosomes by dense loop formation, as is thought to occur during cell division in eukaryotes, if done by random collision, can lead to “bad solvent” conditions for chromatin, resulting in a catastrophic sticking of chromosomes together with no hope of sister chromatid resolution or chromosome individualization [85, 90, 121].

2.4.6 Lengthwise Compaction of Chromosomes

Actual chromosomes in cells are substantially lengthwise-compacted by the action of locally acting DNA-binding proteins. In eukaryotes, histone protein octamers wrap 147 bp of dsDNA into nucleosomes about 10 nm in diameter [110]. Chromosomal DNAs typically have short (15–50 bp) “linker” DNA stretches between successive nucleosomes. It is currently thought that a persistence length of this type of “chromatin” fiber contains roughly 10 nucleosomes, or about 2 kb of DNA. This means that even with no self-avoidance, a knot in an isolated chromatin fiber will only become likely for an 800 kb segment (4000 nucleosomes). In a cell, additional proteins that mediate chromatin–chromatin contacts will keep the statistics of the fibers from being those of simple polymers at very large scales, but there should still be a strong knotting suppression by the folding of DNA by architectural proteins.

At larger scales, chromosomes are folded and compacted by other proteins. One of the most important classes of proteins which accomplish this are “Structural Maintenance of Chromosomes” (SMC) complexes (Fig. 2.13) [122,123,124,125]. These protein complexes are based on heterodimers of SMC proteins, which are long (≈ 50 nm), stick-like coiled-coil proteins with a dimerization domain at one end and an ATP-binding/hydrolyzing domain at the other end. These SMC “sticks” dimerize at one end, and are thought to be capable of undergoing conformational changes in response to ATP binding and hydrolysis so as to compact DNA molecules that they are interacting with. Via interactions with a third “kleisin” protein, SMC dimers form a tripartite ring structure that can encircle DNA, indicating a topological element to their DNA-organizing functions [126,127,128]. Furthermore, eukaryote SMCs appear to favor formation of right-handed DNA loops (loops with positive DNA writhe) [129,130,131,132].

Fig. 2.13

Schematic diagrams of cohesin and condensin eukaryote SMC complexes. SMC complexes are built around stick-like heterodimeric SMC proteins, each of which is approximately 50 nm in length. Reproduced from [122]

Single-molecule experiments do indicate that SMC complexes can compact DNA molecules by mediating contacts between distant DNA loci [132,133,134,135]. Cell-biological experiments indicate clearly that the lengthwise compaction that occurs during mitosis in eukaryote cells depends crucially on the presence of “condensin” SMCs [124], and that proper regulation of contacts (“cohesion”) between replicated DNAs depends on “cohesin” SMCs [122, 123]. Cohesins also play a critical role in stabilizing gene-regulating loops along chromosomes in eukaryotes [136, 137]. SMC complexes are found in bacteria and archaea [138], making SMCs the most universal class of DNA-folding proteins, present in all three domains of life.

2.4.7 The Loop Extrusion Hypothesis for SMC Mechanism and Mechanics of Chromosomes

A number of lines of evidence are starting to point to the possibility that SMC complexes are capable of actively organizing looping, by somehow using energy from ATP hydrolysis to “extrude” DNA loops (Fig. 2.14). While this idea began as a hypothesis [139, 140], DNA-sequencing experiments indicate that cohesin is able to organize DNA loops on megabase scales with DNA sequence in a specific orientation [141], an observation which is difficult to explain without invoking an extrusion, or tracking mechanism.

Fig. 2.14

Mechanisms of DNA loop formation. (a) Random collision. Loop-forming sites (black square) meet by random polymer motion to form a loop anchoring complex (left to right shows time sequence). (b) Loop extrusion. A loop-extruding enzyme (bold ⊂) lands on one spot on a DNA molecule, and then actively pulls DNA from the outside to the inside of the loop, gradually increasing the loop in size (left to right shows time sequence). This process may continue increasing the size of the loop until the loop-extruding enzyme dissociates, reaches a loop boundary element, or perhaps collides with an adjacent loop extruding enzyme complex

Secondly, it is hard to explain how the dense arrays of chromatin loops in metaphase chromosomes [142] can be formed by condensin SMCs without crosslinking occurring between different chromatids and chromosomes. Again this is rather naturally accomplished by “loop extrusion” [140, 143, 144], which forces sister chromatids apart by lengthwise-compacting each chromatid into an array of tightly packed loops. The resulting dense structure can then be further compacted by chromatin-crosslinking proteins to form robust metaphase chromosome [145, 146].

Thirdly, recent data from “Hi-C” DNA sequencing experiments in bacteria also suggest that bacterial SMC complexes are able to extrude DNA loops to organize bacterial chromosomes [147]. Finally, very recent results indicate that yeast condensin complexes are able to use ATP to translocate processively along dsDNA [148]. While not definite, all these recent experiments point in the same direction, towards active loop enlargement by SMC complexes. The forced enlargement of DNA loops can help to organize genomes by generating internal osmotic pressure inside individual large DNA molecules, thus providing a driving force for topoisomerases to resolve linkages between distinct DNA molecules and allowing cells to separate replicated chromosomes from one another [121]. It may well be that the basic principle of active extrusion of DNA loops is an essentially universal feature of chromosome organization in all cell types.

The self-crosslinking of DNA molecules resulting from active loop extrusion suggests that in general, genomes should behave as chromatin “gels,” i.e., crosslinked networks of DNA. Indeed, this has been observed for the mechanics of isolated nuclei [149] as well as isolated metaphase chromosomes [145, 146], both of which show DNA-connectivity-dependent mechanics with shear moduli in the few hundred Pa range. While it remains for the precise mechanisms and schemes underlying large-scale genome organization to be fully understood, it does appear at this point that SMCs play a fundamental and central role in chromosome dynamics, folding, and mechanics.

2.5 Conclusion

This chapter has focused on the molecular biomechanics of DNA and DNA–protein interactions, with an emphasis on how global DNA topology, and ultimately chromosome individualization, can be controlled by enzyme-DNA interactions. We close by summarizing main ideas touched on in the chapter, along with indications of their relevance to oncology and to the remaining chapters of this book.

2.5.1 Mechanics of DNA and DNA–Protein Complexes

We have emphasized the importance of DNA-bending properties at the scale smaller than the persistence length (150 bp), as well as the emergence of DNA flexible polymer behavior at larger DNA length scales (Sect. 2.2). It is important to recognize that the fundamental events of gene regulation—the binding of transcription factors to 10–20 bp-long sequences—occur inside the persistence length, while global chromosome dynamics (genome folding, chromosome rearrangement, chromosome segregation) take place at larger than the persistence length.

One must keep in mind that the folding, and all of the mechanics (and polymer statistical mechanics) of DNA vivo is profoundly modulated by the binding of proteins along the double helix, which we have given some rough ideas of how to understand from the point of view of quantitative theory (Sect. 2.4). DNA and chromatin mechanical properties are known to be modulated by epigenetic marks, both on DNA (methylation) [150, 151] and on nucleosomes (notably histone methylation and acetylation) [152].

2.5.2 Control of DNA Topology, Sister Chromatid Segregation, and Chromosome Individualization

As for any long polymer, entanglement topology plays a key role for DNA in vivo, and all cells work hard to avoid having their chromosomes entangled together (especially sister chromatids resulting from DNA replication). Not surprisingly, the enzymes which allow entanglement topology to change, principally type II topoisomerases, are key targets for antibiotics and anti-cancer drugs [153], precisely because cell proliferation requires physical and topological separation of replicated chromatids.

A key recent development in this area is the role that structural maintenance of chromosome (SMC) complexes play in chromosome self-organization, which involves their interplay with the actions of topoisomerases. Increasingly, the condensin SMC complexes are being seen as the key architects defining the folding of chromosomes into their noodle-shaped mitotic form, which we have argued to be central to chromosome individualization and sister chromatid separation. Interestingly, the cohesin SMC complexes, which play a central role in chromosome folding, replicated sister chromatid cohesion, and gene regulation, have been observed to have characteristic mutations associated with specific cancers [154].

2.5.3 Global Nuclear Organization

The G1 eukaryote nucleus as a whole is organized into a highly regulated combination of chromosome “data center” and gene expression factory, with all activities controlled to some degree by the physical properties of DNA and chromatin [155]. Classically, the mechanical stability of the nucleus has been considered in terms of properties of the nuclear envelope, particularly the network of nuclear lamins that give the nucleus its “toughness” to resist large strains [156]. In addition to having a structural role (lamin A), the lamins (lamin B) also play a key gene-regulatory role; interplay between structural and gene-regulation functions is at the base of a variety of “laminopathies” where defects in nuclear shape regulation are correlated with aberrant gene expression, particularly associated with development [157].

Recent work has broadened this view to emphasize the role of chromatin itself in controlling the small-strain mechanics of the nucleus, via mechanisms including organizational changes associated with epigenetic marks. Histone hyperacetylation associated with euchromatin (notably H3K9ac and H3K27ac) has been shown to soften the human cell nucleus, while marks associated with compacted heterochromatin (H3K9me2,3 and H3K27me3) stiffen the nucleus [149]. In addition, adjusting the balance of euchromatin and heterochromatin has been observed to be correlated with instabilities of nuclear shape including the nuclear “blebs” [158], long used as diagnostic marks of many cancers [159]. Indeed, changes in epigenetic histone marks are well known to be associated with many cancers [160], suggesting a chain of links leading from epigenetic marks, chromatin folding and function, nuclear mechanics, nuclear morphology, to genome instability. These effects are amenable to theoretical analysis. Minimal modeling of the behavior of the nucleus in micromechanical studies reveals that the lamina behaves as a bendable meshwork resulting in buckling under strain [161]. This buckling behavior is suppressed by the chromatin, which fills the nucleus, providing further evidence of the importance of chromatin in dictating small-strain mechanics and nuclear shape [158].

In addition to being changed during the development of many cancers and genetic diseases, global nuclear organization is modulated during metazoan development [162]. Nuclei in embryonic cells are known to be quite distinct in chromatin density, euchromatin/heterochromatin balance, and nuclear mechanics. Just as one example, one can imagine rather profound changes in nuclear mechanics via changes in the density of “crosslinking” by SMCs, or by proteins like HP1α [163] which are thought to act to compact heterochromatin. Micromechanical experiments on nuclei from cells at different stages of developmental pathways, as well as experiments on nuclei with different degrees of chromosomal ploidy are also of interest. Understanding the control of nuclear mechanics and organization via redistribution of epigenetic marks and chromatin crosslinkers such as SMC complexes is an objective for the near future.