Abstract
In this contribution, we review mortar finite element methods (FEM), which are nowadays the most well-established computational technique for contact modeling of solids and structures in the context of finite deformations and frictional sliding. Based on some concepts of nonlinear continuum mechanics, the mortar approach is first presented for the more accessible case of mesh tying (also referred to as tied contact). Mortar methods for unilateral contact then follow in a rather straightforward manner, despite the fact that several complexities, such as inequality constraints, are added to the problem formulation. A special focus is set on practical aspects of the implementation of mortar methods within a fully nonlinear, 3D finite element environment. Specifically, the choice of suitable discrete Lagrange multiplier bases, aspects of high performance computing (HPC), numerical integration procedures and new discretization techniques such as isogeometric analysis (IGA) using NURBS are discussed. Eventually, the great potential of mortar methods in the more general field of computational interface mechanics is exemplified through applications such as wear modeling and coupled thermo-mechanical interfaces.
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
1 Introduction and Motivation
Contact phenomena are virtually omnipresent in nature and biological systems. The associated length and time scales cover the entire spectrum from the nanoscale to the macroscopic level and from hypervelocity impact to quasi-static contact interaction, respectively. For example, the plate tectonics process of the continental drift, the simple motion sequence when walking or the flow of red blood cells (erythrocytes) through blood vessels are all representatives of processes largely dominated by contact and associated physical effects. Beyond that, science and engineering have exploited the principles of contact mechanics to develop processes, such as deep-drawing or extrusion-molding, as well as technical systems and machine parts, including car tires, fluid bearings, gears, shafts and splines or elastomeric seals.
Contact mechanics can be looked at from several different perspectives. For some scenarios, e.g. in nanotribology, it is helpful or even mandatory to investigate contact interaction at an atomistic level. For many contact applications, however, a purely macroscopic viewpoint based on classical continuum assumptions is sufficient. Throughout this chapter, a continuum approach will be followed, mainly considering contact mechanics as a particularly challenging subclass of solid and structural mechanics. The geometrical constraint of non-penetration of different solid bodies can then easily be identified as the most important underlying principle of contact interaction. In addition, the overall contact phenomenon is commonly also influenced by one or several closely related interface effects, for example sticking and sliding friction, adhesion, elastohydrodynamic lubrication and wear. Altogether, contact and its associated phenomena introduce strong additional nonlinearities into solid mechanics problems, where contact itself can basically be interpreted as a set of complex boundary conditions, possibly changing over time. Together with the already typical nonlinearities inherent in general solid mechanics, i.e. large deformations and nonlinear constitutive (material) behavior, this evinces the challenges and difficulties of mathematically describing and solving contact interactions, even if the given problem setup is quite simple. Due to this complexity, only very few contact problem settings exist, where analytical solution techniques are actually applicable. The early work conducted by Hertz (1882) on pressure distributions between contacting elastic bodies more than a century ago, is commonly considered to be the origin of modern contact analysis. A comprehensive overview of the basic principles of contact mechanics, together with the most important analytical solution techniques can be found in the textbooks by Johnson (1985) and Timoshenko and Goodier (1970).
With general contact problems being hardly accessible for mathematical analysis, experimental procedures and numerical modeling are naturally becoming the focus of attention. Physical experiments are a convenient way of gaining information about certain aspects of contact mechanics, e.g. for determining coefficients of friction related to different material pairings. However, for the majority of contact scenarios, the applicability of experimental procedures is either limited or practically impossible. As a prominent example, experimental crashworthiness assessment, in accordance with safety regulations and consumer protection tests, causes considerable costs in the automotive industry. Complex contact phenomena in patient-specific surgery planning or during the design of medical devices, e.g. guaranteeing the optimal placement and minimum leakage of arterial stents, do not even allow for meaningful experimental tests at all. Thus, combining the aforementioned exemplary arguments, it becomes obvious that there is a very high and ever-growing demand for powerful numerical modeling and simulation techniques in the field of contact mechanics. What makes improved contact simulation approaches even more promising and likely to generate significant impact is the fact that the resulting numerical algorithms can typically be employed for a very broad range of scientific and technical interests. In fundamental physical, chemical or biological research, as well as in the applied sciences, novel methods and tools of computational contact mechanics allow for a better understanding of complex systems, which are influenced by contact phenomena. On the other hand, many aspects of engineering practice and product development (e.g. minimizing the frictional loss in gear transmissions, optimizing the structural integrity of car bodies in crash situations) also heavily benefit from improvements in contact modeling and simulation.
2 Contact Mechanics and FEM
All ideas and methods of computational contact mechanics will be exclusively discussed in the context of the finite element method (FEM) throughout this chapter. Since the 1960s, the FEM has gradually evolved as the dominating numerical approximation technique for the solution of partial differential equations (PDEs) in various fields, especially solid and structural mechanics including contact mechanics, but also in fluid mechanics, thermodynamics and for the treatment of coupled problems. The general FEM literature is abundant, exemplarily the interested reader is referred to the monographs by Bathe (1996), Hughes (2000), Belytschko et al. (2000), Reddy (2004), Zienkiewicz et al. (2005) and Zienkiewicz and Taylor (2005). Other approaches for the numerical simulation of contact mechanics are only mentioned very briefly here for the sake of completeness. Multibody dynamics are a fitting tool when analyzing contact and impact phenomena of rigid bodies, with possible extensions to elastic multibody dynamics allowing for a certain degree of deformation of the contacting bodies. Moreover, particle methods such as the discrete element method (DEM) are frequently used for investigating granular and particulate materials, whose mechanical behavior is largely dominated by contact interaction. While finite elements would not be the method of choice for such applications, this chapter is mainly related to contact of elastic solid bodies, possibly including very large deformations. In this context, the FEM undoubtedly provides a very convenient framework for numerical modeling and simulation. Furthermore, there is an increasing interest in the interplay of contact mechanics with other physical phenomena, such as thermomechanics, wear and the lubrication behavior of thin fluid films, where finite elements are also an eligible approach, e.g. due to their generality and geometrical flexibility.
First contributions to the treatment of contact mechanics within the FEM can be traced back to the 1970s and 1980s. In Francavilla and Zienkiewicz (1975) and Hughes et al. (1976), contact conditions are formulated based on a very simple, purely node-based approach, which requires node-matching finite element meshes at the contact interface and is restricted to small deformations. Subsequently, a different idea was expedited, typically denoted as node-to-surface or node-to-segment (NTS) approach and characterized by a discrete, point-wise enforcement of the non-penetration condition at the finite element nodes. This NTS approach could readily be applied to the case of finite deformations and large sliding motions, therefore soon becoming the standard procedure in computational contact mechanics. Without claiming that the following listing is exhaustive, the reader is referred to Bathe and Chaudhary (1985), Hallquist et al. (1985), Benson and Hallquist (1990), Simo and Laursen (1992), Laursen (1992), Laursen and Simo (1993) and Wriggers et al. (1990) for a comprehensive overview. An important basis for the methods to be proposed in this chapter is formed by the first investigations on the so-called segment-to-segment (STS) approach in Papadopoulos and Taylor (1992) and Simo et al. (1985). In contrast to the purely point-wise procedure typical of NTS methods, the STS approach is based on a thorough sub-division of the contact surface into individual segments for numerical integration together with an independent approximation of the contact pressure. Thereby, the STS approach can be interpreted as precursor of mortar finite element methods for computational contact mechanics, which will be the main topic here.
Before reviewing the literature on mortar methods, however, an overview of other important aspects of computational contact mechanics aside from the discretization approach (NTS, STS, mortar) is given. One main focus of attention has been set on different procedures for the enforcement of contact constraints, with the most prominent representatives being penalty methods, Lagrange multiplier methods and Augmented Lagrange methods, see Alart and Curnier (1991) for an excellent overview and discussion. Further questions related to contact modeling within a finite element framework comprise efficient search algorithms (Williams and O’Connor 1999), mesh adaptivity (Wriggers and Scherf 1995; Carstensen et al. 1999; Hüeber and Wohlmuth 2012), covariant surface description (Laursen and Simo 1993; Schweizerhof and Konyukhov 2005), surface smoothing (Wriggers et al. 2001; Puso and Laursen 2002), the treatment of contact on enriched and embedded interfaces (Laursen et al. 2012), modeling of interface effects other than friction (Yang and Laursen 2009; Sauer 2011), beam contact (Wriggers and Zavarise 1997; Zavarise and Wriggers 2000) and energy conservation in the context of contact dynamics (Laursen and Chawla 1997; Laursen and Love 2002; Hager et al. 2008; Hesch and Betsch 2009), among others. Apart from numerous original papers, a comprehensive introduction to most of these topics can be found in the textbooks by Laursen (2002) and Wriggers (2006).
Nevertheless, novel robust discretization techniques for finite deformation contact problems, and especially mortar finite elements adapted for this purpose, have arguably received most attention in the field of computational contact mechanics in recent years. Mortar methods, which were originally introduced as an abstract domain decomposition technique (Bernardi et al. 1994; Ben Belgacem 1999; Seshaiyer and Suri 2000), are characterized by an imposition of the occurring interface constraints in a weak sense and by the possibility to prove their mathematical optimality. In the context of contact analysis, this allows for a variationally consistent treatment of non-penetration and frictional sliding conditions despite the inevitably non-matching interface meshes for finite deformations and large sliding motions. Early applications of mortar finite element methods for contact mechanics can, for example, be found in Ben Belgacem et al. (1998), Hild (2000) and McDevitt and Laursen (2000), though limited to small deformations. Gradually, restrictions of mortar-based contact formulations with respect to nonlinear kinematics have been removed, leading to the implementations given in Puso and Laursen (2004a, b), Fischer and Wriggers (2005), Fischer and Wriggers (2006), Hesch and Betsch (2009), Tur et al. (2009) and Hesch and Betsch (2011).
An alternative choice for the discrete Lagrange multiplier space, so-called dual Lagrange multipliers, was proposed in Wohlmuth (2000, 2001) and, in contrast to the standard mortar approach, generates interface coupling conditions that are much easier to realize without impinging upon the optimality of the method. Applications of this approach to small deformation contact problems can be found in Hüeber and Wohlmuth (2005), Flemisch and Wohlmuth (2007), Brunssen et al. (2007) and Hüeber et al. (2008), and first steps towards finite deformations have been undertaken in Hartmann (2007) and Hartmann et al. (2007). A fully nonlinear extension of the dual mortar approach including consistent linearization of all deformation-dependent quantities has been proposed in Popp et al. (2009, 2010), with extensions to frictional sliding, second-order finite elements and a consistent treatment of dropping-edge problems following shortly afterwards (Cichosz and Bischoff 2011; Popp et al. 2012; Wohlmuth et al. 2012; Popp et al. 2013; Popp and Wall 2014). Another interesting feature of dual Lagrange multiplier interpolation is that it naturally fits together with so-called primal-dual active set strategies for constraint enforcement. It is well-known from the mathematical literature on constrained optimization problems and also from applications in computational contact mechanics, that primal-dual active set strategies can equivalently be interpreted as semi-smooth Newton methods (Alart and Curnier 1991; Qi and Sun 1993; Christensen et al. 1998; Christensen 2002; Hintermüller et al. 2002), thus allowing for the design of very efficient global solution algorithms, especially in the context of nonlinear material behavior and finite deformations.
Recent developments in the meanwhile rather broad field of mortar finite element methods for computational contact mechanics include, without being complete, the following topics: smoothing techniques (Tur et al. 2012), isogeometric analysis using NURBS (Temizer et al. 2011, 2012; De Lorenzis et al. 2014; Brivadis et al. 2015), improved numerical integration schemes (Farah et al. 2015), complex interface models such as wear (Cavalieri and Cardona 2013; Farah et al. 2016, 2017), treatment of embedded interfaces (Laursen et al. 2012) as well as aspects of adaptivity and high performance computing (Popp and Wall 2014; Kindo et al. 2014). While a few different discretization approaches have been suggested, see e.g. the contact domain method proposed in Hartmann et al. (2009) and Oliver et al. (2009), and while NTS methods are still very popular in engineering practice, mortar-based contact formulations have become quite well-established in the meantime and can arguably be seen as state-of-the-art method for computational contact mechanics.
3 Overview of Nonlinear Continuum Mechanics
In this section, the basic concepts of nonlinear continuum mechanics are reviewed with a focus on the governing equations for solid dynamics and contact interaction required later. These remarks are not intended to give an exhaustive overview of the topic, but are rather geared towards outlining the necessary basics for contact mechanics. For more extensive reviews in the field of solid and structural dynamics, the reader is referred to the corresponding literature, e.g., Gurtin (1981), Marsden and Hughes (1994), Ogden (1997), Bonet and Wood (1997), Holzapfel (2000) and Simo and Hughes (1998). Large parts of this section are based on the author’s previously published work (Popp 2012).
3.1 Kinematics
In this section, the fundamental kinematic relationships describing the deformation of a homogeneous body are presented. The classical (Boltzmann) continuum model in a three-dimensional Euclidean space description is assumed. Two distinct observer frames are defined: the reference configuration \(\Omega _0 \subset \mathbb {R}^3\) denotes the domain occupied by all material points \(\varvec{X}\) at time \(t=0\), while the current configuration \(\Omega _t \subset \mathbb {R}^3\) describes the changed positions \(\varvec{x}\) at a certain time t. The motion and deformation from reference to current configuration are tracked with the bijective nonlinear deformation map
which also allows for the notations \(\varvec{x}=\Phi _t(\varvec{X},t)\) and \(\varvec{X}=\Phi _t^{\mathsf {-1}}(\varvec{x},t)\). The absolute displacement of a material point (see again Fig. 1) is then described as
Within the total Lagrangian approach, kinematic relations and all derived quantities are described with respect to the material points in the reference configuration \(\Omega _0\). Thus, the material point position \(\varvec{X}\) plays the role of an independent variable for the problem formulation, while the primary unknown to be solved for is the time-dependent deformation map \(\Phi _t(\varvec{X},t)\), or equivalently the displacement vector \(\varvec{u}(\varvec{X},t)\).
A fundamental measure for deformation and strain in the context of finite deformation solid mechanics is given by the deformation gradient \({\varvec{F}}\), defined as partial derivative of the current configuration with respect to the reference configuration:
where \({\varvec{I}}\) is the second-order identity tensor. Assuming as usual bijectivity and smoothness of the deformation map \(\Phi _t\), the inverse deformation gradient \({\varvec{F}}^{\mathsf {-1}}=\partial \varvec{X} / \partial \varvec{x}\) is also well-defined, therefore guaranteeing a positive determinant \(J = \det {\varvec{F}} > 0\). This quantity, also commonly denoted as Jacobian determinant of the deformation, represents the transformation of an infinitesimal volume element between the two configurations:
The deformation gradient also allows for the mapping of an infinitesimal, oriented area element from reference to current configuration, yielding
which is commonly referred to as Nanson’s formula. Herein, the infinitesimal area elements are interpreted as vectors \(\mathrm {d} \varvec{A}_0 = \mathrm {d} A_0 \, \varvec{N}\) and \(\mathrm {d} \varvec{A} = \mathrm {d} A \, \varvec{n}\), where \(\varvec{N}\) and \(\varvec{n}\) denote unit normal vectors of the area element in the reference and current configuration, respectively.
An apparent choice for a suitable nonlinear strain measure is the so-called Green–Lagrange strain tensor \({\varvec{E}}\) defined in the material configuration as
Although strain measures are never unique, the Green–Lagrange strain tensor is a very common choice in nonlinear solid mechanics, and can be considered particularly convenient if large deformations occur but only a moderate amount of stretch and compression.
The first and second time derivatives of the displacement vector \(\varvec{u}(\varvec{X},t)\) in material description, i.e. velocities \(\dot{\varvec{u}}(\varvec{X},t)\) and accelerations \(\ddot{\varvec{u}}(\varvec{X},t)\), are defined as follows:
Corresponding rate forms (i.e. time derivatives) of the deformation measures, such as the material velocity gradient \({\varvec{L}}=\dot{{\varvec{F}}}\) or the material strain rate tensor \(\dot{{\varvec{E}}} = \frac{1}{2} (\dot{{\varvec{F}}}^{\mathsf {T}} \cdot {\varvec{F}} + {\varvec{F}}^{\mathsf {T}} \cdot \dot{{\varvec{F}}}) = \frac{1}{2} \dot{{\varvec{C}}}\) are readily defined, too.
3.2 Stresses and Constitutive Laws
The motion and deformation of an elastic body effects internal stresses. This is readily described by the traction vector \(\varvec{t}\) in the current configuration:
yielding the limit value of the resulting force \(\varvec{f}\) acting on an arbitrary surface area \(\Delta A\) characterized by its unit surface normal vector \(\varvec{n}\). The Cauchy theorem then correlates tractions and stresses via
Herein, the symmetric Cauchy stress tensor \({\varvec{\sigma }}\) represents the true internal stress state within a body in its a priori unknown current configuration, with diagonal and off-diagonal components components being interpretable as normal stresses and shear stresses, respectively. A multitude of alternative stress definitions is also prevailing in nonlinear continuum mechanics. Exemplarily, the first Piola–Kirchhoff stress tensor \({\varvec{P}}\) maps the material surface element \(\mathrm {d} \varvec{A}_0 = \mathrm {d} A_0 \varvec{N}\) onto the spatial resulting force \(\varvec{f}\). Its definition is obtained from the Cauchy stress tensor \({\varvec{\sigma }}\) by applying Nanson’s formula (5), yielding
Consequently, it is possible to construct a stress tensor purely based on quantities in the reference configuration, too. By also transforming the resulting force vector \(\varvec{f}\) accordingly, the symmetric second Piola–Kirchhoff stress tensor \({\varvec{S}}\) emerges as
With typical measures for both strains and stresses being established, constitutive relations provide the missing link between kinematics and material response. Throughout this chapter, only homogeneous bodies undergoing purely elastic deformation processes without internal dissipation are considered. Moreover, the existence of a so-called strain energy function or elastic potential \(\Psi ({\varvec{F}})\) is assumed, which only depends upon the current state of deformation (hyperelastic material behavior). The requirement of objectivity implies that \(\Psi \) remains unchanged when an arbitrary rigid body rotation is applied to the current configuration. A common formulation of hyperelastic materials in the reference frame then follows as
The relation between \({\varvec{S}}\) and \({\varvec{E}}\) given by (13) will in general be nonlinear. Thus, it is possible (and necessary within typical finite element procedures) to determine the fourth-order material elasticity tensor \(\pmb {\mathscr {C}}_{\mathsf {m}}\) via repeated derivation, yielding
Exemplarily, only one prevailing constitutive model is presented here: the St.-Venant–Kirchhoff material model is an isotropic, hyperelastic model based on a quadratic strain energy function
In this context, \(\lambda \) and \(\mu \) represent the so-called Lamé parameters, which are correlated with the more common Young’s modulus E and Poisson’s ratio \(\nu \) via
Inserting (15) into (13) and (14), it can easily be observed that the St.-Venant–Kirchhoff material model defines a linear relationship between Green–Lagrange strains \({\varvec{E}}\) and second Piola–Kirchhoff stresses \({\varvec{S}}\), and can therefore be interpreted as an objective generalization of Hooke’s law to the geometrically nonlinear realm. Many other constitutive laws exist for miscellaneous applications (e.g. the well-known Neo–Hookean, Mooney–Rivlin or Ogden models for rubber materials). However, with the focus of this chapter being on contact interaction rather than constitutive modeling, the interested reader is referred to the abundant literature on hyperelasticity, viscoelasticity or elastoplasticity for further details, e.g. in Holzapfel (2000), Ogden (1997) and Simo and Hughes (1998).
3.3 Initial Boundary Value Problem
Exemplarily, the IBVP will be presented in the reference configuration here, however the spatial description is derived analogously. For the definition of suitable boundary conditions, \(\partial \Omega _0\) is decomposed into two complementary sets in the absence of contact: \(\Gamma _{\sigma }\) represents the Neumann boundary, where the tractions \(\hat{\varvec{t}}_0\) are given, and \(\Gamma _{{\mathsf {u}}}\) denotes the Dirichlet boundary, where displacements \(\hat{\varvec{u}}\) are prescribed. Neumann and Dirichlet boundaries are disjoint sets, i.e.
The initial boundary value problem in material description can be summarized as follows :
Herein, T denotes the end of the considered time interval. Due to the time dependency within the balance of linear momentum in (18), which contains second derivatives with respect to time t, suitable initial conditions for the displacements \(\hat{\varvec{u}}_0(\varvec{X})\) and velocities \(\hat{\dot{\varvec{u}}}_0(\varvec{X})\) at time \(t=0\) are needed, viz.
The definition of a material model, such as for instance the one given in (15), eventually rounds off the initial boundary value problem of finite deformation solid mechanics. The IBVP is also commonly referred to as strong formulation of nonlinear solid mechanics, as Eqs. (18)–(22) are enforced at each individual point within the domain \(\Omega _0\).
3.4 Contact Kinematics
From the viewpoint of mathematical problem formulation, contact and impact procedures can be classified into several different categories. A problem setup consisting of one single deformable body and a rigid obstacle is commonly referred to as Signorini contact, while the typical general problem formulation rests upon the assumption of two deformable bodies undergoing contact interaction. Moreover, self contact and contact involving multiple bodies represent well-known special cases. While it is usually advantageous or even essential to design specific numerical algorithms for the aforementioned special cases, all mathematical basics concerning contact kinematics and contact constraints can yet be perfectly derived for the case of two deformable bodies.
Hence, deformable-deformable contact of two bodies undergoing finite deformations, as illustrated in Fig. 2, serves as prototype exclusively considered here. Let the open sets \(\Omega _0^{(1)}\), \(\Omega _0^{(2)} \subset \mathbb {R}^3\) and \(\Omega _t^{(1)}\), \(\Omega _t^{(2)} \subset \mathbb {R}^3\) represent two bodies in the reference and current configuration, respectively. As the two bodies approach each other and may potentially come into contact on parts of their boundaries, the surfaces \(\partial \Omega _0^{(i)}\), \(i=1,2\), are now divided into three disjoint subsets, viz.
where \(\Gamma _{{\mathsf {u}}}^{(i)}\) and \(\Gamma _{\sigma }^{(i)}\) are the well-known Dirichlet and Neumann boundaries, and \( \Gamma _{{\mathsf {c}}}^{(i)}\) represents the potential contact surface. The counterparts in the current configuration are denoted as \(\gamma _{{\mathsf {u}}}^{(i)}\), \(\gamma _{\sigma }^{(i)}\) and \(\gamma _{{\mathsf {c}}}^{(i)}\). It is characteristic of contact problems that the actual, so-called active contact surface \(\Gamma _{{\mathsf {a}}}^{(i)} \subseteq \Gamma _{{\mathsf {c}}}^{(i)}\) is unknown, possibly continuously changing over time and thus has to be determined as part of the nonlinear solution process. For the sake of completeness, and to be mathematically precise, the currently inactive contact surface \(\Gamma _{{\mathsf {i}}}^{(i)} = \Gamma _{{\mathsf {c}}}^{(i)} \setminus \Gamma _{{\mathsf {a}}}^{(i)}\) should technically be interpreted as part of the Neumann boundary \(\Gamma _{\sigma }^{(i)}\).
A classical nomenclature in contact mechanics is retained throughout this chapter by referring to \(\Gamma _{{\mathsf {c}}}^{(1)}\) as the slave surface and to \(\Gamma _{{\mathsf {c}}}^{(2)}\) as the master surface, although the master-slave concept actually only makes sense in the context of finite element discretization and although its traditional meaning will not be entirely conveyed to the mortar FE approach presented later on.
Both bodies are required to satisfy the initial boundary value problem previously presented in Sect. 3.3, with the motion and deformation being described by the absolute displacement vectors \(\varvec{u}^{(i)} = \varvec{x}^{(i)} - \varvec{X}^{(i)}\). Moreover, a new fundamental geometric measure for proximity, potential contact and penetration of the two bodies is introduced with the so-called gap function \(\varvec{g}_{\mathsf {n}}(\varvec{X},t)\) in the current configuration. It is evident that the gap function and other contact-related quantities need to be examined in a spatial description, even though the IBVP may still be formulated with respect to the reference configuration. The gap function is defined as
where some alternatives exist for the identification of the contact point \(\hat{\varvec{x}}^{(2)}\) on the master surface associated with each point \(\varvec{x}^{(1)}\) on the slave surface and also for the corresponding contact normal vector \(\varvec{n}_{\mathsf {c}}\). The classical and perhaps most intuitive choice in contact mechanics is based on the so-called closest point projection (CPP), which determines \(\hat{\varvec{x}}^{(2)}\) as
Consequently, \(\varvec{n}_{\mathsf {c}}\) is then chosen to be the outward unit normal to the current master surface \(\gamma _{\mathsf {c}}^{(2)}\) in \(\hat{\varvec{x}}^{(2)}\). A very comprehensive overview of the closest point projection, its mathematical properties and possible pitfalls due to non-uniqueness and certain pathological cases can be found in Konyukhov and Schweizerhof (2008). However, a slightly different approach is followed here, with the outward unit normal to the current slave surface \(\gamma _{\mathsf {c}}^{(1)}\) being considered as contact normal \(\varvec{n}_{\mathsf {c}}\). Hence, the master side contact point \(\hat{\varvec{x}}^{(2)}\) is the result of a smooth interface mapping \(\chi : \gamma _{{\mathsf {c}}}^{(1)} \rightarrow \gamma _{{\mathsf {c}}}^{(2)}\) of \(\varvec{x}^{(1)}\) onto the master surface \(\gamma _{{\mathsf {c}}}^{(2)}\) along \(\varvec{n}_{\mathsf {c}}\), see Fig. 2. Especially in the context of mortar finite element discretization, this choice has some practical advantages over the classical closest point projection common for node-to-segment discretization.
Together with two vectors \(\varvec{\tau }_{\mathsf {c}}^{\xi }\) and \(\varvec{\tau }_{\mathsf {c}}^{\eta }\) taken from the tangential plane, \(\varvec{n}_{\mathsf {c}}\) forms a set of orthonormal basis vectors in the slave surface point \(\varvec{x}^{(1)}\). As these basis vector are attached to \(\varvec{x}^{(1)}\) and also move accordingly, they are commonly referred to as slip advected basis vectors. In this context, it is worth noting that the contact surface \(\gamma _{\mathsf {c}}^{(1)}\) is a two-dimensional manifold, which means that the tangential plane in each point \(\varvec{x}^{(1)}\) locally defines an \(\mathbb {R}^2\) space embedded into the global \(\mathbb {R}^3\). Therefore, any quantity on \(\gamma _{\mathsf {c}}^{(1)}\) is readily parametrized with the two local coordinates \(\xi (\varvec{X}^{(1)},t)\) and \(\eta (\varvec{X}^{(1)},t)\). While the gap function characterizes contact interaction in normal direction, the primary kinematic variable for frictional sliding in tangential direction is given by the relative tangential velocity
Note that this expression for \(\varvec{v}_{\tau ,{\mathsf {rel}}}\) is only exact in the case of perfect sliding and persistent contact, i.e. assuming \(\varvec{g}_{\mathsf {n}} = \dot{\varvec{g}}_{\mathsf {n}}=0\). Nevertheless, it is typically employed for quantifying the relative tangential movement of contacting bodies in all cases, even if the described prerequisites are not met exactly. To clarify the notation in (26), it is pointed out that \(\dot{\hat{\varvec{x}}}^{(2)}\) represents the current velocity of the material point \(\widehat{\varvec{X}}^{(2)}\), viz. the material contact point associated with \(\varvec{X}^{(1)}\) at time t. Therefore, it does not include a change of the material contact point \(\widehat{\varvec{X}}^{(2)}\) itself, or in other words, it does not include a change of the CPP of slave point \(\varvec{x}^{(1)}\). Based on the tangential plane defined above, \(\varvec{v}_{\tau ,{\mathsf {rel}}}\) can be decomposed into
As already mentioned, the definition of the relative tangential velocity given above is only frame-indifferent when perfect sliding occurs (\(\varvec{g}_{\mathsf {n}}=0\)), see e.g. Laursen (2002). However, since an objective measure of the slip rate is essential for formulating frictional contact conditions in finite deformation formulations, an appropriate algorithmic modification of the slip rate is typically carried out later in the course of finite element discretization.
Similar to the kinematic measures \(\varvec{g}_{\mathsf {n}}\) and \(\varvec{v}_{\tau ,{\mathsf {rel}}}\), the contact traction \(\varvec{t}_{\mathsf {c}}^{(1)}\) on the slave surface \(\gamma _{\mathsf {c}}^{(1)}\) can be split into normal and tangential components, yielding
Moreover, due to the balance of linear momentum on the contact interface, the traction vectors on slave side \(\gamma _{\mathsf {c}}^{(1)}\) and master side \(\gamma _{\mathsf {c}}^{(2)}\) are identical except for opposite signs, i.e.
For further details on these topics, the interested reader is referred to classical textbooks on contact mechanics, e.g. Johnson (1985) and Kikuchi and Oden (1988), or to more recent monographs on computational methods for contact mechanics, e.g. Laursen (2002) and Wriggers (2006).
3.5 Tied Contact Constraints
While the main focus of this chapter is on unilateral contact problems, the integration of mesh tying or tied contact problems for connecting dissimilar meshes suggests itself due to the numerous conceptual similarities. Mesh tying applications are also closely connected to the notion of domain decomposition. Thus, in Sect. 5, mesh tying serves as simplified model problem through which many methodological and later also implementational aspects of computational contact mechanics can be clearly illustrated.
As will be seen in the following, mesh tying (or tied contact) perfectly fits into the framework of contact kinematics defined above and can simply be interpreted as a special case from now on. The fundamental kinematic measure for mesh tying is simply the relative displacement between the two bodies, sometimes also referred to as gap vector \(\varvec{g}(\varvec{X},t)\), viz.
Since it is typically assumed that the two bodies to be tied together share a common interface \(\Gamma _{\mathsf {c}}^{(1)} \equiv \Gamma _{\mathsf {c}}^{(2)} \equiv \Gamma _{\mathsf {c}}\) in the reference configuration, the gap vector is equivalently expressed as
thus demonstrating the similarity with the scalar gap function \(\varvec{g}_{\mathsf {n}}(\varvec{X},t)\) for unilateral contact defined in (24) even more clearly. As compared with unilateral contact, mesh tying firstly requires no distinction between normal and tangential directions at the interface, and secondly results in a simple vector-valued equality constraint:
3.6 Normal Contact Constraints
After the short interlude on mesh tying, the focus in now again set on unilateral contact conditions. Examining the gap function defined in (24) in more detail, it becomes obvious that a positive value \(\varvec{g}_{\mathsf {n}}(\varvec{X},t)>0\) characterizes points currently not in contact, while a negative value \(\varvec{g}_{\mathsf {n}}(\varvec{X},t)<0\) denotes the (physically non-admissible) state of penetration. Therefore, the classical set of Karush–Kuhn–Tucker (KKT) conditions, commonly also referred to as Hertz–Signorini–Moreau (HSM) conditions for frictionless contact on the contact boundary can be stated as
As can be seen from Fig. 3, the KKT conditions not only define a non-smooth and nonlinear contact law, but one that is multi-valued at \(\varvec{g}_{\mathsf {n}}(\varvec{X},t)=0\). However, this set of inequality conditions also allows for a very intuitive physical interpretation. Due to the sign convention of the gap function introduced here, the first KKT condition simply represents the geometric constraint of non-penetration, whereas the second KKT condition implies that no adhesive stresses are allowed in the contact zone. Finally, the third KKT condition, well-known as complementarity condition, forces the gap to be closed when non-zero contact pressure occurs (contact) and the contact pressure to be zero when the gap is open (no contact). Note, that the type of KKT conditions defined in (33) also arise in many other problem classes of constrained optimization, and thus standard solution techniques (e.g. based on Lagrange multiplier methods and active set strategies) from optimization theory can readily be adapted for contact mechanics.
For the sake of completeness, the so-called persistency condition is also mentioned here. In the context of contact dynamics, the persistency condition is sometimes considered as an additional contact condition, requiring that
Herein, \(\dot{\varvec{g}}_{\mathsf {n}}(\varvec{X},t)\) represents the material time derivative of the gap function. Therefore, the persistency condition in combination with the KKT conditions in (33) basically demands that the contact pressure is only non-zero when the bodies are in contact and also remain so (persistent contact). On the contrary, the contact pressure is zero in the instant of bodies coming into contact and in the instant of separation. The persistency condition plays an important role in the design of energy conserving numerical algorithms for contact dynamics, see e.g. Laursen and Chawla (1997), Laursen and Love (2002), and bears a certain resemblance to the consistency condition in plasticity, see e.g. Simo and Hughes (1998).
3.7 Frictional Contact Constraints
While frictionless response (i.e. \(\varvec{t}_{\tau }=\varvec{0}\)) is a common modeling assumption, and especially helpful for a thorough development of computational methods for contact mechanics, the real contact behavior of many technical systems is determined by the frictional response to tangential loading. The associated scientific field of tribology is extremely broad, also encompassing physical phenomena such as adhesion, wear or elastohydrodynamic lubrication. The following overview is restricted to a purely macroscopic observation of dry friction, classically described by Coulomb’s law. One possible and widely used notation of Coulomb friction is given by
Herein, \(\Vert \ \cdot \, \Vert \) denotes the \(L^2\)-norm in \(\mathbb {R}^3\), \(\mathfrak {F} \ge 0\) is the friction coefficient and \(\beta \ge 0\) is a scalar parameter. An intuitive physical interpretation of Coulomb’s law as described in (35) is readily available, too. The first (inequality) condition, commonly referred to as slip condition, requires that the magnitude of the tangential stress \(\varvec{t}_{\tau }\) does not exceed a threshold defined by the coefficient of friction \(\mathfrak {F}\) and the normal contact pressure \(p_{\mathsf {n}}\). The frictional response is then characterized by two physically distinct situations. The stick state, defined by \(\beta = 0\), does not allow for any relative tangential movement in the contact zone, i.e. \(\varvec{v}_{\tau ,{\mathsf {rel}}}=\varvec{0}\). In contrast, the slip state, defined by \(\beta > 0\), implicates relative tangential sliding of the two bodies in accordance with the so-called slip rule given as second equation in (35). The last equation in (35) is again a complementarity condition, here separating the two independent solution branches of stick and slip. A commonly cited similarity of Coulomb’s law exists with the most simple formulations of elastoplasticity, see e.g. Simo and Hughes (1998). This similarity is especially interesting in the course of developing numerical algorithms for friction, which usually reuse well-known methodologies from computational inelasticity.
Finally, it is pointed out that frictional response in contact is a path-dependent process, thus introducing mechanical dissipation and making a system representation based on elastic potentials infeasible. Path-dependency can easily be observed in the fact that the tangential contact traction \(\varvec{t}_{\tau }\) depends on the velocity \(\varvec{v}_{\tau ,{\mathsf {rel}}}\) or on the rate of change of the tangential displacement if interpreted incrementally.
4 Overview of Nonlinear FEM
This section provides a brief introduction to the numerical treatment of nonlinear solid mechanics problems with finite element methods. Based on a weak formulation of the previously derived IBVP, the FEM for space discretization as well as typical implicit time stepping schemes for time discretization are presented. Large parts of this section are based on the author’s previously published work (Popp 2012).
4.1 From Strong Formulation to Weak Formulation
Many numerical methods for the solution of partial differential equations, and finite element methods in particular, require a transformation of the IBVP defined in (18)–(22) within a so-called weak or variational formulation. Although other variational principles exist, the well-known principle of virtual work (PVW) is derived exclusively here, with the starting point being a weighted residual notation of the balance equation (18) and the traction boundary condition (20), i.e.
Herein, the weighting or test functions \(\varvec{w}\) are initially arbitrary and can be interpreted as virtual displacements, i.e. \(\varvec{w} = \delta \varvec{u}\). Since the solution for the displacements is known on the Dirichlet boundary \(\Gamma _{\mathsf {u}}\), it is required that
Applying Gauss divergence theorem and inserting (37) and (12) yields
Three distinct contributions to the PVW can be identified. The first term in (38) represents the kinetic virtual work contribution \(\delta \mathcal {W}_{{\mathsf {kin}}}\), the second term denotes the internal virtual work contribution \(\delta \mathcal {W}_{{\mathsf {int}}}\), and the third and fourth term together form the virtual work of external loads \(\delta \mathcal {W}_{{\mathsf {ext}}}\). The PVW emerges as a very general principle of solid mechanics, as it does not require the existence of an associated potential \(\mathcal {W}\). As an example, no constitutive assumptions whatsoever enter the weak formulation in (38), thus making it also valid and applicable for problems such as elastoplasticity, frictional sliding or non-conservative loading.
It can easily be shown that solutions of the IBVP (i.e. of the strong formulation) also satisfy the weak formulation (38). As long as no restrictions are set on the choice of the weighting functions \(\delta \varvec{u}\), the two are formally identical, see e.g. Hughes (2000). However, due to the manipulations introduced above, the weak formulation poses weaker differentiability requirements to the solution functions \(\varvec{u}\), because only first derivatives of \(\varvec{u}\) with respect to \(\varvec{X}\) appear in (38) instead of second derivatives as in (18). Thus, the following solution and weighting spaces can be defined:
Herein, \( H^1 (\Omega )\) denotes the Sobolev space of functions with square integrable values and first derivatives. While the solution space \(\varvec{\mathcal {U}}\) may in general depend on the time t due to a possible time dependency of the Dirichlet boundary conditions, the weighting space \(\varvec{\mathcal {V}}\) does not depend on the time t in any way. In conclusion, the weak formulation of the nonlinear solid mechanics problems at hand can be restated as follows: Find \(\varvec{u} \in \varvec{\mathcal {U}}\) such that
4.2 Space Discretization
Space discretization is exclusively considered in the context of finite element methods here. However, as a detailed introduction to all important aspects of the FEM is beyond the scope of this chapter, only the basic ideas and notation will be highlighted. For a more elaborate survey of finite element methods, the reader is again referred to the corresponding literature, e.g. in Bathe (1996), Hughes (2000), Belytschko et al. (2000), Reddy (2004), Zienkiewicz and Taylor (2005) and Zienkiewicz et al. (2005).
Simply speaking, the concept of finite element discretization in this context is based on finding a numerical solution to (41) at discrete points, commonly referred to as nodes. The nodes are connected to form elements, which allows to formulate the following approximate partitioning of the domain \(\Omega _0\) into \({\mathsf {nele}}\) element subdomains:
The displacement solution \(\varvec{u}^{(e)}\) on element e is then typically approximated by local interpolation functions \(N_k(\varvec{X})\), yielding
where the discrete nodal values of the displacements \({\varvec{\mathsf {d}}}_k(t)\) have been introduced. Furthermore, the subscript \(\cdot _h\) signifies a spatially discretized quantity throughout this chapter and \({\mathsf {nnod}}^{(e)}\) represents the number of nodes associated with the element e. The interpolation functions \(N_k(\varvec{X})\), commonly referred to as shape functions, are typically (but not exclusively) low-order polynomials, e.g. Lagrange polynomials, thus meeting the differentiability requirements of the weak form. Based on the so-called isoparametric concept, the element geometry in the reference configuration \(\varvec{X}^{(e)}\) and current configuration \(\varvec{x}^{(e)}\) is approximated using the same shape functions. Typically, \(\Omega _0^{(e)}\) is mapped to a reference element geometry or parameter space \(\varvec{\xi } = (\xi ,\eta ,\zeta )\), e.g. the cube \([-1,1]\times [-1,1]\times [-1,1]\), which defines an element Jacobian matrix \(\varvec{J}^{(e)} = \partial \varvec{X}^{(e)} / \partial \varvec{\xi }\). Thus, the interpolation of displacements, current geometry and reference geometry at the element level is alternatively expressed as
with nodal positions \({\varvec{\mathsf {X}}}_k\) and \({\varvec{\mathsf {x}}}_k(t)\) in the reference and current configuration, respectively. Finally, time derivatives of the displacements, e.g. the accelerations \(\ddot{\varvec{u}}\), and the weighting functions \(\delta \varvec{u}\) are also interpolated using the same shape functions. The latter convention is commonly referred to as Bubnov–Galerkin approach, as compared with a Petrov–Galerkin approach, where an independent set of shape functions is chosen for interpolating the weighting functions.
Examining (44) more closely, it becomes obvious that the finite element method basically introduces restrictions on the solution and weighting spaces defined in (39) and (40). In the discrete setting, these spaces only contain a finite number of solution and weighting functions, respectively, which is expressed mathematically in terms of finite dimensional subspaces \(\varvec{\mathcal {U}}_h \subset \varvec{\mathcal {U}}\) and \(\varvec{\mathcal {V}}_h \subset \varvec{\mathcal {V}}\). The limited selection of solution and weighting functions then serves as a basis for the numerical solution, i.e. the weak formulation is recast into a discrete form, which is no longer equivalent to strong and weak formulation, but rather represents an approximation.
The individual contributions to the discretized weak form are integrated element-by-element using Gauss quadrature and then sorted into global vectors based on the so-called assembly operator, which governs the arrangement of local vectorial quantities into global vectors. After inserting the interpolations given by (44) into the weak formulation (38), the final spatially discretized formulation emerges as
with the global mass matrix \({\varvec{\mathsf {M}}}\), the global vector of nonlinear internal forces \({\varvec{\mathsf {f}}}_{{\mathsf {int}}}\) and the global vector of external forces \({\varvec{\mathsf {f}}}_{{\mathsf {ext}}}\). Moreover, \(\delta {\varvec{\mathsf {d}}}\), \(\ddot{{\varvec{\mathsf {d}}}}\) and \({\varvec{\mathsf {d}}}\) are global vectors comprising all discrete nodal values of virtual displacements, accelerations and displacements. Due to the interpolation introduced above, all vectors in (47) are of the size \({\mathsf {ndof}} = {\mathsf {ndim}} \cdot {\mathsf {nnod}}\), where \({\mathsf {nnod}}\) is the total number of nodes in the entire domain and \({\mathsf {ndim}}\) is the number of spatial dimensions. The variable name \({\mathsf {ndof}}\) refers to the fact that the discrete values of the nodal displacements \({\varvec{\mathsf {d}}}\) are also denoted as degrees of freedom. Since (47) must hold for arbitrary virtual displacements \(\delta {\varvec{\mathsf {d}}}\), it can equivalently be written as
This defines a system of \({\mathsf {ndof}}\) ordinary differential equations (ODEs), commonly referred to as semi-discrete equations of motion. So far, only space discretization with the finite element method has been established, but the system is still continuous with respect to time.
4.3 Time Discretization
There exists a large variety of finite difference methods suitable for time discretization of the semi-discrete equations of motion (48). In doing so, time derivatives are approximated by their discrete counterparts, the difference quotients. Based on the introduction of a constant time step size \(\Delta t\), the time interval of interest \(t \in [0,T]\) is subdivided into several intervals \([t_n,t_{n+1}]\), where \(n \in \mathbb {N}_0\) is the time step index, and thus the spatially discretized displacement solution \({\varvec{\mathsf {d}}}(t)\) is computed at a series of discrete points in time.
In principle, time integration methods can be divided into implicit and explicit schemes. While implicit methods lead to a fully coupled system of \({\mathsf {ndof}}\) nonlinear discrete algebraic equations for the unknown displacements \({\varvec{\mathsf {d}}}_{n+1} := {\varvec{\mathsf {d}}}(t_{n+1})\), explicit methods allow for a direct extrapolation towards \({\varvec{\mathsf {d}}}_{n+1}\) without requiring a solution step. Here, only implicit schemes will be considered. They represent the method of choice for problems dominated by a low frequency response, while explicit methods are widely used in the context of high frequency responses and wave-like phenomena, e.g. in high velocity impact situations. In general, implicit time integration methods can be shown to be unconditionally stable, thus allowing for relatively large time step sizes as compared with explicit schemes. However, the implementation of implicit methods is more challenging due to the fact that nonlinear solution methods (see Sect. 4.4) including a linearization of the entire finite element formulation are required.
Here, the presentation is restricted to one exemplary and widely used implicit time integration scheme, viz. the generalized-\(\alpha \) method introduced by Chung and Hulbert (1993). This one-step time integration scheme is based on the well-known Newmark method, which allows for expressing the approximate discrete velocities \({\varvec{\mathsf {v}}}_{n+1} \approx \dot{{\varvec{\mathsf {d}}}}(t_{n+1})\) and accelerations \({\varvec{\mathsf {a}}}_{n+1} \approx \ddot{{\varvec{\mathsf {d}}}}(t_{n+1})\) at the end of the considered time interval \([t_n,t_{n+1}]\) solely in terms of already known quantities at time \(t_n\) and the unknown displacements \({\varvec{\mathsf {d}}}_{n+1}\), i.e.
where \(\beta \in [0,1/2]\) and \(\gamma \in [0,1]\) are two parameters characterizing the behavior of the method. The generalized-\(\alpha \) method introduces generalized mid-points \(t_{n+1-\alpha _{\mathsf {m}}}\) and \(t_{n+1-\alpha _{\mathsf {f}}}\) and shifts the evaluation of the individual terms in (48) from \(t_{n+1}\) to these midpoints. The following linear interpolation rules are commonly established for the generalized-\(\alpha \) method:
Eventually, the fully (i.e. space and time) discretized finite element formulation of nonlinear solid mechanics, also referred to as discrete linear momentum balance, is obtained as
One important advantage of the generalized-\(\alpha \) method is that it allows for introducing controllable numerical dissipation into the considered system, while at the same time retaining the important properties of unconditional stability and second-order accuracy. Controllable numerical dissipation in this context means that the parameters \(\beta \), \(\gamma \), \(\alpha _{\mathsf {m}}\) and \(\alpha _{\mathsf {f}}\) can be harmonized such that the desired damping effect is only achieved in the spurious high frequency modes, while damping in the low frequency domain is kept at a minimum. This procedure is usually united in the notion of a spectral radius \(\rho _{\infty }\) as the sole free parameter to choose for a generalized-\(\alpha \) method. The other parameters then follow directly from the requirements of unconditional stability, second-order accuracy and optimized numerical dissipation as
Note that no numerical dissipation is introduced into the system for the choice \(\rho _{\infty }=1\). Moreover, the generalized-\(\alpha \) method also contains the classical Newmark method as a special case by setting \(\alpha _{\mathsf {m}}=\alpha _{\mathsf {f}}=0\).
For the sake of completeness, it is pointed out that quasistatic problems, i.e. neglecting inertia effects, are also considered in the following. In that case, the time parameter t only plays the role of a pseudo-time and no time integration method is needed, but the quasistatic solution is rather computed as a series of static equilibrium states.
4.4 Linearization and Solution Techniques for Nonlinear Equations
Within each time step, the system of \({\mathsf {ndof}}\) nonlinear discrete algebraic Eq. (55) needs to be solved for the unknown displacements \({\varvec{\mathsf {d}}}_{n+1}\). Throughout this contribution, the Newton–Raphson method is employed as an iterative nonlinear solution technique. Within each iteration step i, the residual of the discrete linear momentum balance can be defined as
The Newton–Raphson method is based on repeated linearization of the residual in (57), solution of the resulting linearized system of equations and incremental update of the unknown displacements until a user-defined convergence criterion is met. At first, the linearization is obtained from the truncated Taylor expansion of (57), viz.
where the partial derivative of \({\varvec{\mathsf {r}}}_{{\mathsf {effdyn}}}({\varvec{\mathsf {d}}}_{n+1}^i)\) with respect to the displacements is commonly referred to as dynamic effective tangential stiffness matrix \({\varvec{\mathsf {K}}}_{{\mathsf {effdyn}}}({\varvec{\mathsf {d}}}_{n+1}^i)\) of size \({\mathsf {ndof}} \times {\mathsf {ndof}}\). In the context of the generalized-\(\alpha \) method, the dynamic effective tangential stiffness matrix can be determined based on Newmark’s approximation given in (49) and (50) and the generalized midpoints defined in (51)–(54), yielding
where \({\varvec{\mathsf {K}}}_{\mathsf {T}}({\varvec{\mathsf {d}}}_{n+1-\alpha _{\mathsf {f}}})\) is the tangential stiffness matrix associated with the internal forces as
To sum up, the Newton–Raphson method provides an iterative procedure for finding the unknown solution \({\varvec{\mathsf {d}}}_{n+1}\) for which the residual \({\varvec{\mathsf {r}}}_{{\mathsf {effdyn}}}({\varvec{\mathsf {d}}}_{n+1})\) vanishes. Within each iteration, it is required that
or in other words, the following linear system of equations has to be solved:
Having solved (62), the displacements \({\varvec{\mathsf {d}}}_{n+1}^{i+1}\) at the end of the time step can be updated via
and the iteration counter is increased by one, i.e. \(i \rightarrow i+1\). The procedure in (62) and (63) is repeated until a certain user-defined convergence criterion, usually with regard to the \(L^2\)-norm of the residual \(\Vert {\varvec{\mathsf {r}}}_{{\mathsf {effdyn}}}({\varvec{\mathsf {d}}}_{n+1}^i)\Vert \), is met. The most advantageous property of the Newton–Raphson method is its local quadratic convergence. This means that if the start solution estimate \({\varvec{\mathsf {d}}}_{n+1}^{0}\) is sufficiently close to the actual solution \({\varvec{\mathsf {d}}}_{n+1}\), i.e. within the problem-dependent convergence radius, then the residual norm approaches zero with a quadratic convergence rate.
In this contribution, only exact Newton–Raphson methods are considered as described above or later also their semi-smooth variants for the inclusion of contact constraints. However, the computational cost associated with such an approach can be considerable for nonlinear solid mechanics problems, bearing in mind that it requires a consistent linearization and thus a determination of the tangential stiffness matrix \({\varvec{\mathsf {K}}}_{\mathsf {T}}({\varvec{\mathsf {d}}}_{n+1-\alpha _{\mathsf {f}}})\) within each iteration step. In practice, this often leads to the application of quasi-Newton methods or modified Newton methods, which are based on a computationally cheaper approximation of the stiffness matrix (e.g. via secants), but sacrifice optimal convergence behavior. Apart from that, many extensions of the Newton–Raphson method aim at enlarging its local convergence radius. Popular examples of such globalization strategies are line search methods and the pseudo-transient continuation (PTC) technique, see e.g. Gee et al. (2009) and references therein.
5 Mortar Methods for Tied Contact
Mesh tying (also referred to as tied contact) serves as a model problem for the introduction to mortar finite element methods here. The basic motivation for such mortar mesh tying algorithms is to connect dissimilar meshes in nonlinear solid mechanics in a variationally consistent manner. Reasons for the occurrence of non-matching meshes can be manifold and range from different resolution requirements in the individual subdomains over the use of different types of finite element interpolation to the rather practical experience that the submodels to be connected are commonly meshed independently. Further details and a full derivation of all formulations can be found in the author’s original work (Popp 2012).
5.1 Strong Formulation
Without loss of generality, only the case of a body with one sole tied contact interface is considered. On each subdomain \(\Omega _0^{(i)}\), the initial boundary value problem of finite deformation elastodynamics needs to be satisfied, viz.
The tied contact constraint, also formulated in the reference configuration, is given as
Equations (64)–(69) represent the final strong form of a mesh tying problem in nonlinear solid mechanics. In the course of deriving a weak formulation (see next paragraph), the balance of linear momentum at the mesh tying interface \(\Gamma _{\mathsf {c}}\) is typically exploited and a Lagrange multiplier vector field \(\varvec{\lambda }\) is introduced, thus setting the basis for a mixed variational approach.
5.2 Weak Formulation
To start the derivation of a weak formulation of (64)–(69), appropriate solution spaces \(\varvec{\mathcal {U}}^{(i)}\) and weighting spaces \(\varvec{\mathcal {V}}^{(i)}\) need to be defined as
Moreover, the Lagrange multiplier vector \(\varvec{\lambda }=-\varvec{t}_{\mathsf {c}}^{(1)}\), which represents the negative slave side contact traction \(\varvec{t}_{\mathsf {c}}^{(1)}\) and is supposed to enforce the mesh tying constraint (69), is chosen from a corresponding solution space denoted as \(\varvec{\mathcal {M}}\). In terms of its classification in functional analysis, this space represents the dual space of the trace space \(\varvec{\mathcal {W}}^{(1)}\) of \(\varvec{\mathcal {V}}^{(1)}\). In the given context, this means that \(\mathcal {M} = H^{-1/2}(\Gamma _{\mathsf {c}})\) and \(\mathcal {W}^{(1)} = H^{1/2}(\Gamma _{\mathsf {c}})\), where \(\mathcal {M}\) and \(\mathcal {W}^{(1)}\) denote single scalar components of the corresponding vector-valued spaces \(\varvec{\mathcal {M}}\) and \(\varvec{\mathcal {W}}\).
Based on these considerations, a saddle point type weak formulation is derived next. Basically, this can be done by extending the standard weak formulation of nonlinear solid mechanics as defined in (38) to two subdomains and combining it with Lagrange multiplier coupling terms. Find \(\varvec{u}^{(i)} \in \varvec{\mathcal {U}}^{(i)}\) and \(\varvec{\lambda } \in \varvec{\mathcal {M}}\) such that
Herein, the kinetic contribution \(\delta \mathcal {W}_{{\mathsf {kin}}}\), the internal and external contributions \(\delta \mathcal {W}_{{\mathsf {int,ext}}}\) and the mesh tying interface contribution \(\delta \mathcal {W}_{{\mathsf {mt}}}\) to the overall virtual work on the two subdomains, as well as the weak form of the mesh tying constraint \(\delta \mathcal {W}_{\lambda }\), have been abbreviated as
It is important to point out that, strictly speaking, the coupling bilinear forms \(\delta \mathcal {W}_{{\mathsf {mt}}}\) and \(\delta \mathcal {W}_{\lambda }\) cannot be represented by integrals, because the involved spaces \(H^{1/2}(\Gamma _{\mathsf {c}})\) and \(H^{-1/2}(\Gamma _{\mathsf {c}})\) do not satisfy the requirements for a proper integral definition. Instead, a mathematically correct notation would use so-called duality pairings \(\langle \varvec{\lambda } , (\delta \varvec{u}^{(1)} - \delta \varvec{u}^{(2)}) \rangle _{\Gamma _{\mathsf {c}}}\) and \(\langle \delta \varvec{\lambda } , (\varvec{u}^{(1)} - \varvec{u}^{(2)}) \rangle _{\Gamma _{\mathsf {c}}}\), see e.g. Wohlmuth (2000). However, during finite element discretization the solution spaces are restricted to discrete subsets of \(L^2(\Gamma _{\mathsf {c}})\) functions, and by then at the latest the coupling terms may be formulated as surface integrals. Moreover, even in the mathematical literature the distinction between duality pairing and integral is not treated consistently, and thus the slightly inaccurate formulation in (76) and (77) is preferred here due to readability.
The coupling terms on \(\Gamma _{\mathsf {c}}\) also allow for a direct interpretation in terms of variational formulations and the principle of virtual work. Whereas the contribution in (76) represents the virtual work of the unknown interface tractions \(\varvec{\lambda } = -\varvec{t}_{\mathsf {c}}^{(1)} = \varvec{t}_{\mathsf {c}}^{(2)}\), the contribution in (77) ensures a weak, variationally consistent enforcement of the tied contact constraint (69). Unlike for unilateral contact with inequality constraints, there exist no further restrictions on the Lagrange multiplier space \(\varvec{\mathcal {M}}\) here (such as e.g. positivity). Nevertheless, the concrete choice of the discrete Lagrange multiplier space \(\varvec{\mathcal {M}}_h\) in the context of mortar finite element discretizations is decisive for the stability of the method and for optimal a priori error bounds, cf. Sect. 7.1. Finally, it is pointed out that the weak formulation (72) and (73) possesses all characteristics of saddle point problems and Lagrange multiplier methods.
5.3 Finite Element Discretization
For the spatial discretization of the tied contact problem (72) and (73), standard isoparametric finite elements are employed. This defines the usual finite dimensional subspaces \(\varvec{\mathcal {U}}^{(i)}_h\) and \(\varvec{\mathcal {V}}^{(i)}_h\) being approximations of \(\varvec{\mathcal {U}}^{(i)}\) and \(\varvec{\mathcal {V}}^{(i)}\), respectively. Throughout this chapter, both first-order and second-order interpolation is considered with finite element meshes typically consisting of 3-node triangular (tri3), 4-node quadrilateral (quad4), 6-node triangular (tri6), 8-node quadrilateral (quad8) and 9-node quadrilateral (quad9) elements in 2D, and of 4-node tetrahedral (tet4), 8-node hexahedral (hex8), 10-node tetrahedral (tet10), 20-node hexahedral (hex20) and 27-node hexahedral (hex27) elements in 3D.
With the focus being on the finite element discretization of the coupling terms here, only the geometry, displacement and Lagrange multiplier interpolations on \(\Gamma _{{\mathsf {c}},h}^{(i)}\) will be considered in the following. Discretization of the remaining contributions to (72) is not discussed, but the reader is instead referred to the abundant literature. As explained in Sect. 4.2, the subscript \(\cdot _h\) refers to a spatially discretized quantity. Obviously, there exists a connection between the employed finite elements in the domains \(\Omega _{0,h}^{(i)}\) and the resulting surface facets on the mesh tying interfaces \(\Gamma _{{\mathsf {c}},h}^{(i)}\). For example, a mixed 3D finite element mesh composed of tet4 and hex8 elements yields tri3 and quad4 facets on the surface of tied contact. Consequently, the following general form of geometry and displacement interpolation on the discrete mesh tying surfaces holds:
The total number of slave nodes on \(\Gamma ^{(1)}_{{\mathsf {c}},h}\) is \(n^{(1)}\), and the total number of master nodes on \(\Gamma ^{(2)}_{{\mathsf {c}},h}\) is \(n^{(2)}\). Discrete nodal positions and discrete nodal displacements are given by \({\varvec{\mathsf {x}}}_k^{(1)}\), \({\varvec{\mathsf {x}}}_l^{(2)}\), \({\varvec{\mathsf {d}}}_k^{(1)}\) and \({\varvec{\mathsf {d}}}_l^{(2)}\). The shape functions \(N_k^{(1)}\) and \(N_l^{(2)}\) are defined with respect to the usual finite element parameter space, commonly denoted as \(\xi ^{(i)}\) for two-dimensional problems (i.e. 1D mesh tying interfaces) and as \(\varvec{\xi }^{(i)}=(\xi ^{(i)},\eta ^{(i)})\) for three-dimensional problems (i.e. 2D mesh tying interfaces). As mentioned above, the shape functions are derived from the underlying bulk discretization. Although not studied here, the proposed algorithms can in principle be transferred to higher-order interpolation and alternative shape functions, such as non-uniform rational B-splines (NURBS), see e.g. Cottrell et al. (2009), De Lorenzis et al. (2011) and Temizer et al. (2011, 2012).
In addition, an adequate discretization of the Lagrange multiplier vector \(\varvec{\lambda }\) is needed, too, and will be based on a discrete Lagrange multiplier space \(\varvec{\mathcal {M}}_h\) being an approximation of \(\varvec{\mathcal {M}}\). Some details concerning the choice of \(\varvec{\mathcal {M}}_h\), and especially concerning the two possible families of standard and dual Lagrange multipliers, will follow in Sect. 7.1. Thus, only a very general notation is given at this point:
with the (still to be defined) shape functions \(\Phi _j\) and the discrete nodal Lagrange multipliers \(\varvec{\uplambda }_j\). The total number of slave nodes carrying additional Lagrange multiplier degrees of freedom is \(m^{(1)}\). Typically for mortar methods, every slave node also serves as coupling node, and thus in the majority of cases \(m^{(1)} = n^{(1)}\) will hold. However, in the context of second-order finite elements, it will be favorable to chose \(m^{(1)} < n^{(1)}\) in certain cases. Substituting (78) and (80) into the interface virtual work \(\delta \mathcal {W}_{{\mathsf {mt}}}\) in (72) yields
where \(\chi _h : \Gamma _{{\mathsf {c}},h}^{(1)} \rightarrow \Gamma _{{\mathsf {c}},h}^{(2)}\) defines a suitable discrete mapping from the slave to the master side of the mesh tying interface. Such a mapping (or projection) becomes necessary due to the fact that the discretized coupling surfaces \(\Gamma _{{\mathsf {c}},h}^{(1)}\) and \(\Gamma _{{\mathsf {c}},h}^{(2)}\) are, in general, no longer geometrically coincident. This becomes very clear when thinking of a curved mesh tying interface with non-matching finite element meshes on the two different sides. As illustrated in Fig. 4, tiny gaps and overlaps may be generated in the discretized setting, although the surfaces had still been coincident in the continuum framework. Throughout this contribution, numerical integration of the mortar coupling terms is exclusively performed on the slave side \(\Gamma _{{\mathsf {c}},h}^{(1)}\) of the interface. In (81), nodal blocks of the two mortar integral matrices commonly denoted as \({\varvec{\mathsf {D}}}\) and \({\varvec{\mathsf {M}}}\) can be identified. This leads to the following definitions:
where \(j\,{=}\,1, \ldots ,m^{(1)}, \; k\,{=}\,1, \ldots ,n^{(1)}, \; l=1, \ldots ,n^{(2)}\). Note that \({\varvec{\mathsf {I}}}_{{\mathsf {ndim}}} \in \mathbb {R}^{{\mathsf {ndim}} \times {\mathsf {ndim}}}\) is an identity matrix whose size is determined by the global problem dimension \({\mathsf {ndim}}\), viz. either \({\mathsf {ndim}}=2\) or \({\mathsf {ndim}}=3\). In general, both mortar matrices \({\varvec{\mathsf {D}}}\) and \({\varvec{\mathsf {M}}}\) have a rectangular shape. However, \({\varvec{\mathsf {D}}}\) becomes a square matrix for the common choice \(m^{(1)}=n^{(1)}\). More details concerning the actual numerical integration of the mass matrix type of entries in \({\varvec{\mathsf {D}}}\) and \({\varvec{\mathsf {M}}}\) as well as the implementation of the interface mapping \(\chi _h\) for 3D will be given in Sects. 5.4 and 7.3.
For the ease of notation, all nodes of the two subdomains \(\Omega _0^{(1)}\) and \(\Omega _0^{(2)}\), and correspondingly all degrees of freedom (DOFs) in the global discrete displacement vector \({\varvec{\mathsf {d}}}\), are sorted into three groups: a group \(\mathcal {S}\) containing all slave interface quantities, a group \(\mathcal {M}\) of all master quantities and a group denoted as \(\mathcal {N}\), which comprises all remaining nodes or DOFs. The global discrete displacement vector can be sorted accordingly, yielding \({\varvec{\mathsf {d}}} = ({\varvec{\mathsf {d}}}_{\mathcal {N}},{\varvec{\mathsf {d}}}_{\mathcal {M}},{\varvec{\mathsf {d}}}_{\mathcal {S}})\). Going back to (81), this allows for the following definition:
Herein, the discrete mortar mesh tying operator \({\varvec{\mathsf {B}}}_{{\mathsf {mt}}}\) and the resulting discrete vector of mesh tying forces \({\varvec{\mathsf {f}}}_{{\mathsf {mt}}}(\varvec{\uplambda }) = {\varvec{\mathsf {B}}}_{{\mathsf {mt}}}^{\mathsf {T}} \varvec{\uplambda }\) acting on the slave and the master side of the interface are introduced. To finalize the discretization of the considered mesh tying problem, a closer look needs to be taken at the weak constraint contribution \(\delta \mathcal {W}_{\lambda }\) in (73). Due to the saddle point characteristics and resulting symmetry of the mixed variational formulation in (72) and (73), all discrete components of \(\delta \mathcal {W}_{\lambda }\) have already been introduced and the final formulation is given as
with \({\varvec{\mathsf {g}}}_{{\mathsf {mt}}}({\varvec{\mathsf {d}}})={\varvec{\mathsf {B}}}_{{\mathsf {mt}}} {\varvec{\mathsf {d}}}\) representing the discrete mesh tying constraint at the coupling interface. Taking into account the typical finite element discretization of all remaining contributions to the first part of the weak formulation (72), as previously outlined in Sect. 4.2, the semi-discrete equations of motion including tied contact forces and the constraint equations emerge as
Mass matrix \({\varvec{\mathsf {M}}}\), damping matrix \({\varvec{\mathsf {C}}}\), internal forces \({\varvec{\mathsf {f}}}_{{\mathsf {int}}}({\varvec{\mathsf {d}}})\) and external forces \({\varvec{\mathsf {f}}}_{{\mathsf {ext}}}\) result from standard FE discretization. It is important to point out that the actual mortar-based interface coupling described here is completely independent of the concrete choice of the underlying finite element formulation. The same also holds true for the question which particular material model is applied. As both topics, i.e. nonlinear finite elements for continua and complex material models, are discussed at length in the literature, details will not be repeated here but the focus will remain solely on the mesh tying terms \({\varvec{\mathsf {f}}}_{{\mathsf {mt}}}(\varvec{\uplambda })\) and \({\varvec{\mathsf {g}}}_{{\mathsf {mt}}}({\varvec{\mathsf {d}}})\).
Examining the semi-discrete problem statement in (86) and (87) in more detail, the well-known nonlinearity of the internal forces \({\varvec{\mathsf {f}}}_{{\mathsf {int}}}({\varvec{\mathsf {d}}})\) due to the consideration of finite deformation kinematics and nonlinear material behavior becomes apparent. However, neither the discrete interface forces \({\varvec{\mathsf {f}}}_{{\mathsf {mt}}}(\varvec{\uplambda })\) nor the mesh tying constraints \({\varvec{\mathsf {g}}}_{{\mathsf {mt}}}({\varvec{\mathsf {d}}})\) introduce an additional nonlinearity into the system. This is due to the fact that no relative movement of the subdomains is permitted in mesh tying problems. Therefore, the mortar integral matrices \({\varvec{\mathsf {D}}}\) and \({\varvec{\mathsf {M}}}\) and hence also the discrete mesh tying operator \({\varvec{\mathsf {B}}}_{{\mathsf {mt}}}\) only need to be evaluated once at problem initialization and thus do not depend on the actual displacements, even if finite deformations of the considered body are involved. With respect to numerical efficiency, this means that evaluating the mortar coupling terms for tied contact problems is a one-time cost, which can usually be neglected as compared with the remaining computational costs. Only for the unilateral contact case discussed in Sect. 6, this will no longer be the case. The question how to numerically evaluate the entries of \({\varvec{\mathsf {B}}}_{{\mathsf {mt}}}\) in 3D problems is discussed in the following paragraph.
5.4 Evaluation of Mortar Integrals in 3D
All general concepts of the evaluation of mortar integrals in 3D can also be transferred back to the simple 2D case. The integral entries of both matrices \({\varvec{\mathsf {D}}}\) and \({\varvec{\mathsf {M}}}\) will be computed based on so-called mortar segments in order to achieve the maximum possible accuracy of Gauss quadrature and to guarantee linear momentum conservation in the semi-discrete setting. Projection operations between slave surface \(\Gamma _{{\mathsf {c}},h}^{(1)}\) and master surface \(\Gamma _{{\mathsf {c}},h}^{(2)}\), which consist of two-dimensional facets, are based on nodal averaging and a \(C^0\)-continuous field of normal vectors, cf. Fig. 17. For 3D situations, the averaged nodal normal vector \({\varvec{\mathsf {n}}}_k\) is given as
where the total number of slave facets \(n^{{\mathsf {adj}}}_k\) adjacent to slave node k may vary within a much wider range than in 2D (for instance \(n^{{\mathsf {adj}}}_k=4\) in Fig. 17). In anticipation of unilateral contact formulations, (88) also defines a tangential plane at slave node k, from which the two unit tangent vectors \(\varvec{\uptau }_k^{\xi }\) and \(\varvec{\uptau }_k^{\eta }\) can be chosen to form an orthonormal basis together with \({\varvec{\mathsf {n}}}_k\) as
Mortar segments must be defined such that the shape function integrands in (82) and (83) are \(C^1\)-continuous on these surface subsets. However, it is quite obvious that this task is much more complex in three dimensions than it would be in two dimensions, because mortar segments are arbitrarily shaped polygons as compared with line segments in the 2D case. Beyond that, the choice of an adequate mortar integration surface itself is quite difficult. In the 2D mortar mesh tying formulation that is not discussed here, integration is performed directly on the slave surface \(\Gamma ^{(1)}_{{\mathsf {c}},h}\). Unfortunately, it is not trivial to directly transfer this approach to three dimensions, because of the possible warping of surface facets.
The general topic of numerical integration, and an overview of the available (segment-based and element-based) integration schemes for this purpose is given in Sect. 7.3
5.5 Solution Methods
The attention is now turned back to the actual mortar finite element approach for tied contact derived in Sect. 5.3, and in particular to the final fully discretized version (i.e. after time discretization with the generalized-\(\alpha \) method previously discussed in Sect. 4.3) of (86) and (87). All solution methods for this system of \({\mathsf {ndof}}+{\mathsf {nco}}\) nonlinear discrete algebraic equations, where the global number of constraints is given by \({\mathsf {nco}} = {\mathsf {ndim}} \cdot m^{(1)}\), are based on a standard Newton–Raphson iteration as introduced in Sect. 4.4. With only equality constraints being present, no active set strategies are needed for mesh tying systems, but the iterative solution techniques can be applied directly, thus yielding standard (or smooth) Newton methods. Primal-dual active set strategies and the associated notion of semi-smooth Newton methods only become important in the context of unilateral contact considered in Sect. 6.
As explained in Sect. 4.4, the Newton–Raphson method (or Newton’s method) is based on a subsequent linearization of the residual, here defined by the discrete balance of linear momentum and the discrete mesh tying constraints in the time-discretized versions of (86) and (87). Each nonlinear solution step (iteration index i) then consists of solving the resulting linearized system of equations and an incremental update of the unknown displacements \({\varvec{\mathsf {d}}}_{n+1}\) and Lagrange multipliers \(\varvec{\uplambda }_{n+1-\alpha _{\mathsf {f}}}\) until a user-defined convergence criterion is met. Taking into account that the discrete mesh tying operator \({\varvec{\mathsf {B}}}_{{\mathsf {mt}}}\) defined in (84) does not depend on the displacements, consistent linearization in iteration step i yields:
Herein, the fact that the Lagrange multipliers only enter the discrete mesh tying in a linear fashion has been made use of. Due to this linearity, it is possible to solve directly for the unknown Lagrange multipliers \(\varvec{\uplambda }_{n+1-\alpha _{\mathsf {f}}}^i\) in each iteration step instead of an incremental formulation. Moreover, as mentioned in Sect. 4.4, all discrete force terms (inertia, damping, internal and external forces) except for the additional mesh tying forces \({\varvec{\mathsf {f}}}_{{\mathsf {mt}}}(\varvec{\uplambda }_{n+1-\alpha _{\mathsf {f}}}^i)\) are summarized in the residual \({\varvec{\mathsf {r}}}_{{\mathsf {effdyn}}}({\varvec{\mathsf {d}}}_{n+1}^i)\) and the partial derivative of \({\varvec{\mathsf {r}}}_{{\mathsf {effdyn}}}({\varvec{\mathsf {d}}}_{n+1}^i)\) with respect to the displacements \({\varvec{\mathsf {d}}}\) is commonly referred to as dynamic effective tangential stiffness matrix \({\varvec{\mathsf {K}}}_{{\mathsf {effdyn}}}({\varvec{\mathsf {d}}}_{n+1}^i)\), as introduced in (58). Finally, it is pointed out that the constraints \({\varvec{\mathsf {g}}}_{{\mathsf {mt}}}({\varvec{\mathsf {d}}}_{n+1})={\varvec{\mathsf {0}}}\) are already enforced at time \(t=0\) to assure angular momentum conservation. Thus, the right-hand side of the linearized constraint equation in (91) simply reduces to zero.
The linearized statement in (90) and (91) already gives a hint as to the typical saddle point structure of the resulting Lagrange multiplier system. Analyzing the linearized mesh tying system (90) in more detail and splitting the global displacement vector \({\varvec{\mathsf {d}}} = ({\varvec{\mathsf {d}}}_{\mathcal {N}},{\varvec{\mathsf {d}}}_{\mathcal {M}},{\varvec{\mathsf {d}}}_{\mathcal {S}})\) as well as all other involved quantities into three subsets as defined in Sect. 5.3 leads to the following notation in matrix-vector notation:
Herein, the nonlinear iteration index i and the subscript \(\cdot _{{\mathsf {effdyn}}}\) of the residual vector \({\varvec{\mathsf {r}}}_{{\mathsf {effdyn}}}\) and the tangential stiffness matrix \({\varvec{\mathsf {K}}}_{{\mathsf {effdyn}}}\) have been omitted for the ease of notation. Note that no matrix blocks \({\varvec{\mathsf {K}}}_{\mathcal {M}\mathcal {S}}\) and \({\varvec{\mathsf {K}}}_{\mathcal {S}\mathcal {M}}\) exist, because slave and master side degrees of freedom are only coupled via the mortar approach. Due to the inherent symmetry of \({\varvec{\mathsf {K}}}_{{\mathsf {effdyn}}}\), the global linearized mesh tying system (92) is also symmetric and has the typical saddle point structure with a zero matrix block associated with the Lagrange multipliers \(\varvec{\uplambda }_{n+1-\alpha _{\mathsf {f}}}\) on the main diagonal. Thus, while a conforming discretization would yield a positive definite system, the coupled mesh tying system considered here becomes indefinite with both positive and negative eigenvalues due to the saddle point characteristics of the Lagrange multiplier method.
The linear system (92) needs to be solved within each nonlinear iteration step. Unfortunately, efficient iterative solution techniques and especially the associated preconditioners usually perform very poorly for such indefinite systems or are not applicable at all. The main reason for this lies in the fact that common preconditioning techniques, e.g. the Jacobi and Gauss–Seidel methods, fail for zero diagonal matrix entries as occurring in (92). Nevertheless, there exist some specific solution methods for this type of saddle point matrix block system, which are both well-established and quite efficient. One popular representative, also employed as preconditioner in this contribution whenever large mesh tying and contact systems are considered with a standard Lagrange multiplier approach, is given by the so-called semi-implicit method for pressure-linked equations (SIMPLE) and its many descendants, see e.g. Elman et al. (2008) for a very comprehensive overview in the context of the incompressible Navier–Stokes equations for fluid dynamics.
As will be explained in Sect. 7.1, the dual Lagrange multiplier approach is characterized by its localization of the coupling constraints at the mesh tying interface, and thus algebraically by mortar matrix \({\varvec{\mathsf {D}}}\) reducing to a diagonal matrix. This makes \({\varvec{\mathsf {D}}}\) trivial to invert and allows for efficient condensation operations of the slave side degrees of freedom, i.e. both Lagrange multipliers and the discrete slave side displacements. The basis for this condensation is given by the saddle point system in (92), which is of course equally valid for dual Lagrange multiplier interpolation. In preparation of a first condensation step, the third row of (92) is used to express the unknown Lagrange multipliers \(\varvec{\uplambda }_{n+1-\alpha _{\mathsf {f}}}\) as
Insertion into the second row of (92) yields the following intermediate system:
where the mortar projection operator \({\varvec{\mathsf {P}}} = {\varvec{\mathsf {D}}}^{\mathsf {-1}} {\varvec{\mathsf {M}}}\) that will formally be introduced in (143) is used to abbreviate the notation. As a second step, the constraint equation in the last row of (94) can be expressed as
The final condensed system for the dual Lagrange multiplier approach is then obtained by reinserting this result into the first row and second row of the intermediate system, viz.
This final linearized system unifies several beneficial properties as compared with the equivalent saddle point formulation given in (92). Firstly, the discrete Lagrange multiplier degrees of freedom \(\varvec{\uplambda }_{n+1-\alpha _{\mathsf {f}}}\) have been removed from the global system and thus the commonly cited disadvantage of an increased system size for Lagrange multiplier methods is resolved. In fact, owing to the second condensation step, which removes the slave side displacement degrees of freedom \(\Delta {\varvec{\mathsf {d}}}_{n+1,\,\mathcal {S}}\), the final system size is even reduced as compared with a conforming discretization. Secondly, and more importantly, the typical saddle point structure with a zero diagonal matrix block has been completely removed on the way towards the final system (96), which is instead symmetric and positive definite again.
With regard to linear solvers, the dual Lagrange multiplier approach virtually allows for an “out-of-the-box” application of state-of-the-art iterative solution and preconditioning techniques, such as the CG or GMRES approach in combination with algebraic multigrid (AMG) methods. Simply speaking, all solvers that were optimized for conforming discretizations in nonlinear solid mechanics are equally applicable to the non-conforming mortar formulation with dual Lagrange multipliers in (96) due to similar system properties. The additional computational effort associated with the condensation operations can be considered very low. In a first, naive implementation, setting up the condensed system would simply require some additional matrix-matrix products of interface-sized matrix blocks such as the discrete projection operator \({\varvec{\mathsf {P}}}\). However, a more elaborate implementation could even do without explicit matrix-matrix products, but would rather introduce modified local assembly procedures for the individual finite element contributions to the tangential stiffness matrix blocks \({\varvec{\mathsf {K}}}_{\mathcal {N}\mathcal {S}}\), \({\varvec{\mathsf {K}}}_{\mathcal {S}\mathcal {N}}\) and \({\varvec{\mathsf {K}}}_{\mathcal {S}\mathcal {S}}\), taking into account the associated local entries of the mortar projection operator \({\varvec{\mathsf {P}}}\). In any case, the improved properties and the more efficient solvability of (96) as compared with (92) by far outweigh additional computational costs for the condensation, which makes the dual Lagrange multiplier approach the preferred choice throughout this chapter.
For the sake of completeness, two details should be pointed out. Firstly, the described condensation operations are of course also applicable for standard Lagrange multiplier interpolation with a non-diagonal mortar matrix \({\varvec{\mathsf {D}}}\), at least theoretically. In practice, however, the inverse matrix \({\varvec{\mathsf {D}}}^{\mathsf {-1}}\) would be densely populated in such a case, which forbids the actual computation and storage of \({\varvec{\mathsf {D}}}^{\mathsf {-1}}\) or likewise \({\varvec{\mathsf {P}}}\) for moderate or even large system sizes. For dual Lagrange multiplier interpolation, on the contrary, inversion of \({\varvec{\mathsf {D}}}\) and storage of the sparsely populated matrix \({\varvec{\mathsf {P}}}\) remain easily manageable even for large-scale mortar mesh tying simulations. Secondly, node-matching interface meshes are contained as a special case in the given mortar formulation. This situation basically leads to \({\varvec{\mathsf {P}}}\) becoming an identity operator, establishing a one-to-one mapping between slave side and master side displacements. Expression (96) then reduces to exactly the same linearized system that is obtained for a conforming mesh.
5.6 Numerical Example
Patch tests are arguably one of the most common validation tools in finite element analysis, typically used as a first important step towards an assessment of the consistency of new element formulations, see e.g. Irons (1966) and Taylor et al. (1986). In the present context of mesh tying and contact mechanics, patch tests are investigated in order to analyze the ability of mortar methods to exactly represent the simplest possible (i.e. constant) stress states across arbitrary non-conforming interfaces. However, it is well-known that collocation-based methods such as the classical node-to-segment (NTS) approach for mesh tying and unilateral contact typically fail the patch test. Mortar finite element methods, with their variationally consistent interpolation of the interface traction via discrete Lagrange multipliers \(\varvec{\uplambda }\), guarantee the exact satisfaction of typical patch tests by design.
As a first test setup, two stacked cubes with an inclined but flat mesh tying interface, as illustrated in Fig. 5, are investigated. This geometric model is obtained by first considering two identical cubes of side length 10 and then moving two opposite corners of the interface by a distance of \(\pm 2\) in z-direction. The compressible Neo–Hookean material law introduced in Sect. 3.2 is employed with Young’s modulus \(E=10\) and Poisson’s ratio \(\nu =0.4\). A constant pressure load \(p=-0.2\) is applied to the top surface of the upper block, and the bottom surface of the lower block is supported such that any rigid body movement is precluded, but the bodies are free to expand laterally. The lower block is defined as slave side for mortar coupling and the chosen mesh size ratio of \(h^{(1)}/h^{(2)}=5/6\) generates a non-matching situation at the interface. Figure 5 exemplarily illustrates the displacement solution as well as the Lagrange multiplier (i.e. interface traction) solution in z-direction for a hex8 discretization. As expected, a linear displacement field and constant interface tractions are obtained. The fact that the patch test is actually passed to machine precision for any first-order or second-order finite element type is emphasized in Fig. 6, where the normal stress component in z-direction of the Cauchy stress tensor \({\varvec{\sigma }}\) is visualized. While all presented results have been obtained with dual Lagrange multiplier interpolation according to Sect. 7.1, standard Lagrange multipliers would yield identical results.
The second patch test investigated is a 2D rectangular strip (length \(l=8\), width \(w=3\)) with five subdomains, each discretized with different first-order and second-order finite elements (i.e. tri3, quad4, tri6, quad8 and quad9 elements), see Fig. 7. While this admittedly constitutes a rather academic example, it strikingly demonstrates the mesh generation flexibility offered by mortar methods, and especially also the possibility of a consistent treatment of so-called crosspoints as discussed in Wohlmuth (2001). Again, a compressible Neo–Hookean constitutive model is employed (\(E=10\), \(\nu =0.3\)) and the strip is subject to unilateral loading in y-direction. Both displacement and stress solution confirm that this 2D patch test is passed to machine precision. The treatment of crosspoints is readily extended to three dimensions, see e.g. Wohlmuth (2001).
Finally, the first patch test model is reconsidered, but now with a curved mesh tying interface. The exemplary results for a hex8 mesh in the left part of Fig. 8 illustrate the limits of mortar finite element methods with regard to exact patch test satisfaction. It can be seen quite clearly that the patch test is not satisfied to machine precision in that case, but instead a small error is introduced in the vicinity of the interface. The reason for this result has already been explained in Sect. 5.3 and lies in the fact that the discrete surfaces \(\Gamma _{{\mathsf {c}},h}^{(1)}\) and \(\Gamma _{{\mathsf {c}},h}^{(2)}\) are no longer geometrically coincident for non-matching meshes on curved interfaces, but tiny gaps and overlapping regions appear. Thus, a discrete projection step is needed, which inevitably precludes the constant stress solution to be recovered exactly. This becomes even clearer when analyzing a curved mesh tying interface with node-matching meshes, as visualized in the right part of Fig. 8. In that case, the discrete mesh tying surfaces \(\Gamma _{{\mathsf {c}},h}^{(1)}\) and \(\Gamma _{{\mathsf {c}},h}^{(2)}\) are again coincident, the mortar projection operator \({\varvec{\mathsf {P}}}\) reduces to an identity mapping and the patch test is satisfied exactly. Nevertheless, it should be pointed out that the error of mortar methods in curved patch tests is only marginal and can factually be neglected from an engineering point of view. Besides, the curved patch test behavior of mortar methods is still significantly better than that of classical NTS schemes, see also Hesch and Betsch (2010).
6 Mortar Methods for Unilateral Contact
Contact interaction in nonlinear solid mechanics and the use of mortar finite element methods in this context are the main focus of interest of this chapter. The goal of all developments presented is to be able to analyze and accurately predict the mechanical response in highly nonlinear unilateral contact scenarios, i.e. including very large deformations and sliding, continuous changes of the active contact area and possibly nonlinear material behavior. From a method development point of view, many aspects of mortar methods already introduced for mesh tying in Sect. 5 can either be re-used directly or in a slightly modified way in order to meet contact-specific demands. For further theoretical considerations and an in-depth analysis of the mathematical foundations of contact mechanics, the comprehensive textbook by Kikuchi and Oden (1988) and the recent review article by Wohlmuth (2011) should be consulted. A full derivation of all formulations reviewed here can be found in the author’s original work (Popp 2012).
6.1 Strong Formulation
For the sake of simplicity, only the case of two contacting bodies with one sole contact interface is considered here. However, a generalization to multiple bodies and self contact is rather straightforward and mostly a matter of efficient search algorithms. All necessary notations for the finite deformation unilateral contact problem have already been introduced in Fig. 2, to which the reader is once again referred at this point. The domains \(\Omega _0{(i)} \subset \mathbb {R}^3\) and \(\Omega _t^{(i)} \subset \mathbb {R}^3\), \(i=1,2\), represent two separate bodies in the reference and current configuration, respectively. To allow for the usual Dirichlet and Neumann boundary conditions as well as contact interaction, the surfaces \(\partial \Omega _0^{(i)}\) are divided into three disjoint subsets \(\Gamma _{\mathsf {u}}^{(i)}\), \(\Gamma _{\sigma }^{(i)}\) and \(\Gamma _{\mathsf {c}}^{(i)}\), where \(\Gamma _{\mathsf {c}}^{(i)}\) represents the potential contact surface. Similarly, the spatial surface descriptions \(\partial \Omega _t^{(i)}\) are split into \(\gamma _{\mathsf {u}}^{(i)}\), \(\gamma _{\sigma }^{(i)}\) and \(\gamma _{\mathsf {c}}^{(i)}\). Retaining a customary nomenclature in contact mechanics, \(\Gamma _{\mathsf {c}}^{(1)}\) is again referred to as slave surface and \(\Gamma _{\mathsf {c}}^{(2)}\) as master surface.
On each subdomain \(\Omega _0^{(i)}\) the initial boundary value problem of finite deformation elastodynamics needs to be satisfied, viz.
The contact constraints in normal direction are typically given in form of KKT conditions as defined in (33), while frictional sliding according to Coulomb’s law has been introduced in (35). For the sake of completeness of the strong formulation, both sets of conditions are repeated:
Equations (97)–(103) represent the final strong form of a unilateral contact problem in nonlinear solid mechanics. In the course of deriving a weak formulation (see next paragraph), the balance of linear momentum at the contact interface is typically exploited and a Lagrange multiplier vector \(\varvec{\lambda }\) is introduced, thus setting the basis for a mixed variational approach. In contrast to the mesh tying case in Sect. 5, it is striking that the unilateral contact constraints are typically formulated (and later also numerically evaluated) in the current configuration.
6.2 Weak Formulation
In the first instance, the most general weak formulation including also Coulomb friction is considered. Similar to the pure solid mechanics case in Sect. 4.1 and the mesh tying case in Sect. 5.2, the well-known solution spaces \(\varvec{\mathcal {U}}^{(i)}\) and weighting spaces \(\varvec{\mathcal {V}}^{(i)}\) are defined as
Moreover, the Lagrange multiplier vector \(\varvec{\lambda }=-\varvec{t}_{\mathsf {c}}^{(1)}\), which represents the negative slave side contact traction \(\varvec{t}_{\mathsf {c}}^{(1)}\) and is used to enforce the contact constraints (102) and (103), is chosen from the convex set \(\varvec{\mathcal {M}}(\varvec{\lambda }) \subset \varvec{\mathcal {M}}\) given by
Herein, \(\langle \cdot , \cdot \rangle _{\gamma _{\mathsf {c}}^{(1)}}\) again stands for the scalar or vector-valued duality pairing between \(H^{-1/2}\) and \(H^{1/2}\) on \(\gamma _{\mathsf {c}}^{(1)}\), see also Sect. 5.2. Moreover, \(\varvec{\mathcal {M}}\) is the dual space of the trace space \(\varvec{\mathcal {W}}^{(1)}\) of \(\varvec{\mathcal {V}}^{(1)}\) restricted to \(\gamma _{\mathsf {c}}^{(1)}\), i.e. \(\mathcal {M} = H^{-1/2}(\gamma _{\mathsf {c}}^{(1)})\) and \(\mathcal {W}^{(1)} = H^{1/2}(\gamma _{\mathsf {c}}^{(1)})\), where \(\mathcal {M}\) and \(\mathcal {W}^{(1)}\) denote single scalar components of the corresponding vector-valued spaces \(\varvec{\mathcal {M}}\) and \(\varvec{\mathcal {W}}\). Thus, the definition of the solution cone for the Lagrange multipliers in (106) satisfies the conditions on \(\varvec{\lambda }\) of the Coulomb friction law in a weak sense.
Based on these considerations, the weak saddle point formulation is derived next. Basically, this can be done by extending the standard weak formulation of nonlinear solid mechanics as defined in (38) to two bodies and combining it with contact-specific Lagrange multiplier contributions. Find \(\varvec{u}^{(i)} \in \varvec{\mathcal {U}}^{(i)}\) and \(\varvec{\lambda } \in \varvec{\mathcal {M}}(\lambda )\) such that
Herein, the kinetic contribution \(\delta \mathcal {W}_{{\mathsf {kin}}}\) as well as the internal and external contributions \(\delta \mathcal {W}_{{\mathsf {int,ext}}}\) to the overall virtual work of the two bodies do not change as compared with the mesh tying case in (74) and (75). However, the contact contribution \(\delta \mathcal {W}_{{\mathsf {co}}}\) and the weak constraints \(\delta \mathcal {W}_{\lambda }\), including non-penetration and frictional sliding conditions, are given in full length as
where \(\chi : \gamma _{{\mathsf {c}}}^{(1)} \rightarrow \gamma _{{\mathsf {c}}}^{(2)}\) defines a suitable mapping from slave to master side of the contact surface, see also Sect. 3.4. In contrast to the mesh tying case, where this mapping only came into play in the discrete setting, \(\gamma _{{\mathsf {c}}}^{(1)}\) and \(\gamma _{{\mathsf {c}}}^{(2)}\) cannot even be guaranteed to be identical in the continuum framework for unilateral contact, because they not only comprise the actual contact surfaces but the potential contact surfaces. As explained in detail in Sect. 5.2, the integral expressions in the coupling bilinear forms \(\delta \mathcal {W}_{{\mathsf {co}}}\) and \(\delta \mathcal {W}_{\lambda }\) would need to be replaced by duality pairings \(\langle \cdot , \cdot \rangle _{\gamma _{\mathsf {c}}^{(1)}}\) in order to be mathematically concise. However, the integral diction in (74) and (75) is preferred here due to readability. The coupling terms on \(\gamma _{\mathsf {c}}^{(1)}\) also allow for a direct interpretation in terms of variational formulations and the principle of virtual work. Whereas the contribution in (109) represents the virtual work of the unknown contact tractions \(\varvec{\lambda } = -\varvec{t}_{\mathsf {c}}^{(1)}\), the contribution in (110) ensures a weak, variationally consistent enforcement of the unilateral contact constraints in normal direction as well as the Coulomb friction law. The equivalence of the strong pointwise conditions given in (102) and (103) and the corresponding variational inequalities in (110) can readily be proven, see e.g. Wohlmuth (2011).
The main focus of this chapter is on mortar finite element methods for contact mechanics in general, and on discrete dual Lagrange multiplier spaces in particular, rather than on the physical foundations of frictional sliding or other interface effects. Many scientific questions investigated and answered in the following are completely independent of the precise tangential contact model. Thus, for the sake of simplicity, the weak formulation is restricted to the frictionless case from now on, as well as the upcoming derivations concerning finite element discretization. Nevertheless, Coulomb friction is included in the actual implementation originating from this work, and special remarks on frictional sliding will be given where important, e.g. when considering semi-smooth Newton type active set strategies in Sect. 6.4. Without claiming that this list is exhaustive, details on the mortar finite element discretization of frictional contact can be found in Gitterle et al. (2010), Gitterle (2012), Hüeber et al. (2008), Tur et al. (2009), Wohlmuth (2011), Puso and Laursen (2004b) and Yang et al. (2005).
For frictionless sliding, the tangential part \(\varvec{t}_{\tau }\) of the slave side contact traction \(\varvec{t}_{\mathsf {c}}^{(1)}\) is supposed to vanish, and thus the set of frictional sliding conditions in (103) is simply replaced by
Considering appropriate solution spaces, it becomes obvious that frictionless contact allows for a significant simplification of the convex cone of Lagrange multipliers, which is now given as
Herein, \(\mathcal {W}^{+}\) is a closed non-empty convex cone being defined by \(\mathcal {W}^{+} = \{ w \in \mathcal {W}, \, w \ge 0 \}\). The weak solution of the frictionless contact problem is then obtained from the following saddle point formulation: Find \(\varvec{u}^{(i)} \in \varvec{\mathcal {U}}^{(i)}\) and \(\varvec{\lambda } \in \varvec{\mathcal {M}}^{+}\) such that
The contributions \(\delta \mathcal {W}_{{\mathsf {kin}}}\), \(\delta \mathcal {W}_{{\mathsf {int,ext}}}\) and \(\delta \mathcal {W}_{{\mathsf {co}}}\) remain unchanged as previously defined in (74), (75) and (109). However, the weak contact constraints \(\delta \mathcal {W}_{\lambda }\) now reduce to
Strictly speaking, a scalar Lagrange multiplier \(\lambda _{\mathsf {n}}\) would be completely sufficient to enforce the non-penetration condition here. Yet, in view of the more general case of frictional contact, a vector-valued Lagrange multiplier will also be employed for the frictionless case in this contribution, which allows for the nice interpretation of frictionless sliding as a special case of Coulomb’s law with \(\mathfrak {F} = 0\) and the convex cone of Lagrange multipliers \(\varvec{\mathcal {M}}(\varvec{\lambda })\) reducing to \(\varvec{\mathcal {M}}^{+}\). As compared with the mesh tying case in Sect. 5.2, it is noticeable that the weak formulation contains inequality conditions for unilateral contact. These require a particular numerical treatment based on active set strategies, as will be explained in Sect. 6.4. As mentioned before, all standard terms (representing kinetic, internal and external virtual work) are formulated in the reference configuration, while the contact virtual work term \(\delta \mathcal {W}_{{\mathsf {co}}}\) and the constraints \(\delta \mathcal {W}_{\lambda }\) are typically formulated in the current configuration for the considered finite deformation contact problems. This is convenient due to the fact that the contact mapping \(\chi : \gamma _{{\mathsf {c}}}^{(1)} \rightarrow \gamma _{{\mathsf {c}}}^{(2)}\) needs to be evaluated with respect to the deformed geometry, anyway.
6.3 Finite Element Discretization
Similar to the tied contact case, all common types of first-order and second-order finite element interpolations in 2D and 3D are considered here, which again define finite dimensional subspaces \(\varvec{\mathcal {U}}^{(i)}_h\) and \(\varvec{\mathcal {V}}^{(i)}_h\) being approximations of \(\varvec{\mathcal {U}}^{(i)}\) and \(\varvec{\mathcal {V}}^{(i)}\), respectively. The general notations of slave and master side displacement interpolation given in (78), as well as the Lagrange multiplier interpolation defined in (80) are still valid. Substituting everything into the contact virtual work expression \(\delta \mathcal {W}_{{\mathsf {co}}}\) in (109) yields
Herein, the only two differences to the mesh tying case lie in the integration domain (spatial description \(\gamma _{{\mathsf {c}},h}^{(1)}\) instead of material description \(\Gamma _{{\mathsf {c}},h}^{(1)}\)) and in the fact that the discrete contact mapping \(\chi _h : \gamma _{{\mathsf {c}},h}^{(1)} \rightarrow \gamma _{{\mathsf {c}},h}^{(2)}\) now continuously changes due to a relative movement of slave and master surfaces. Thus, as will be seen later on, it is not sufficient to evaluate the mapping only once as for mesh tying, but the mortar matrices \({\varvec{\mathsf {D}}}\) and \({\varvec{\mathsf {M}}}\) become deformation-dependent instead. Due to the fundamental importance of the discrete mortar matrices, their blockwise definition is repeated here, although only slightly modified as compared with (82) and (83), i.e.
where \(j=1, \ldots ,m^{(1)}, \; k=1, \ldots ,n^{(1)}, \; l=1, \ldots ,n^{(2)}\). In analogy to (84), the discrete contact virtual work contribution can be expressed as
where the discrete mortar contact operator \({\varvec{\mathsf {B}}}_{{\mathsf {co}}}({\varvec{\mathsf {d}}})\) and the resulting discrete vector of contact forces \({\varvec{\mathsf {f}}}_{{\mathsf {co}}}({\varvec{\mathsf {d}}},\varvec{\uplambda }) = {\varvec{\mathsf {B}}}_{{\mathsf {co}}}({\varvec{\mathsf {d}}})^{\mathsf {T}} \varvec{\uplambda }\) acting on slave and master sides of the interface now depend nonlinearly on the current deformation state \({\varvec{\mathsf {d}}}\).
Next, the focus is shifted towards the weak constraint contribution for frictionless contact defined in (115), where more profound differences to the mesh tying case can be expected. As shown in great detail in Hüeber (2008), the discretized version of the weak formulation in (114) and (115) is equivalent to the following set of pointwise conditions:
where the discrete weighted gap \((\tilde{g}_{\mathsf {n}})_j\) at slave node j is given by
Herein, \(\varvec{g}_{{\mathsf {n}},h}\) is the discretized version of the gap function \(\varvec{g}_{\mathsf {n}}\) introduced in (24). Examining the last two equations in more detail, an interesting analogy becomes apparent. Basically, (120) represents nothing less than a discrete formulation of the original KKT conditions in (102) with an additional weighting based on the Lagrange multiplier shape functions \(\Phi _j\). It is worth noting that although a segment-based (mortar) approach has been followed, decoupled constraints at the discrete nodal points are eventually enforced independently, just as it is well-known from traditional NTS schemes. However, the nodal constraints (120) in the mortar formulation convey a substantially increased level of information as compared with the truly nodal constraints in a NTS formulation, owing to the underlying variational approach which is algebraically reflected in the weighted (integral) gap formulation in (121).
For the sake of completeness, it should be pointed out that the nodal decoupling of constraints and thus the final formulation given in (120) is strictly speaking only valid for dual Lagrange multiplier interpolation, see Hüeber (2008) for the corresponding mathematical proof, which relies on biorthogonality as defined in (144). In the case of standard Lagrange multiplier interpolation, the conversion of (114) and (115) into (120) involves an additional, yet only slight, approximation, see Hüeber (2008). Finally, the frictionless sliding constraint contained in the definition of the convex cone \(\varvec{\mathcal {M}}^{+}\) is readily enforced on a discrete nodal basis, i.e. \((\varvec{\uplambda }_{\tau })_j={\varvec{\mathsf {0}}}\). To sum up, the final space discretized but still time continuous problem formulation, consisting of the semi-discrete equations of motion and the frictionless contact constraints for all slave nodes also carrying discrete Lagrange multiplier degrees of freedom, can be expressed as
While this finite element formulation has some strong similarities with the mesh tying case in (86) and (87), it also contains three striking additional complexities. Firstly, unilateral contact involves inequality constraints, which require a suitable active set strategy as part of the global solution algorithm (cf. Sect. 6.4). Secondly, normal and tangential contact directions need to be treated separately in order to enforce the different underlying physical principles (non-penetration, frictionless or frictional sliding). Thirdly, and most importantly from the viewpoint of implementation, the contact forces in (122) as well as the contact constraints in (123) and (124) are deformation-dependent. This introduces an additional nonlinearity into the global system and thus demands for an incessant re-evaluation of mortar coupling terms including a consistent linearization for implicit time integration. Corresponding extensions of the numerical integration scheme for the discrete contact operator \({\varvec{\mathsf {B}}}_{{\mathsf {co}}}({\varvec{\mathsf {d}}})\) and the discrete weighted gaps \((\tilde{g}_{\mathsf {n}})_j\) in both 2D and 3D will be presented in the next three paragraphs.
Finally, a short outlook is also given on the weak constraint contribution for frictional contact according to Coulomb’s law as defined in (110), although the frictional part is not in the focus of interest here. Again, it has been shown in great detail in Hüeber (2008) and can be readily understood that the discretized version of the tangential part of the weak formulation in (108) and (110) is equivalent to the following set of pointwise conditions:
where the discrete relative tangential velocity \((\tilde{{\varvec{\mathsf {v}}}}_{\tau ,{\mathsf {rel}}})_j\) at slave node j is determined such that it satisfies the requirement of frame indifference, see e.g. Yang et al. (2005) and Gitterle et al. (2010) for further explanations. Similar to the non-penetration condition, it can be observed that (125) basically represents a weak formulation of the original Coulomb friction conditions in (103) with an additional weighting based on the Lagrange multiplier shape functions \(\Phi _j\). In the semi-discrete formulation for Coulomb friction, the set of conditions in (125) would simply replace (124), while (122) and (123) would remain unchanged. While by no means exhaustive, the given outlook demonstrates that an extension of the proposed mortar finite element framework towards any tangential constitutive law (e.g. Tresca friction, Coulomb friction) is pretty straightforward. Most importantly, the discrete frictional expressions such as the discrete relative tangential velocity \((\tilde{{\varvec{\mathsf {v}}}}_{\tau ,{\mathsf {rel}}})_j\) do not require any additional numerical integration efforts, but can rather be constructed from the well-known mortar matrices \({\varvec{\mathsf {D}}}\) and \({\varvec{\mathsf {M}}}\) (including history values due to path dependency) and the nodal tangent vectors \(\varvec{\uptau }_j^{\xi }\) and \(\varvec{\uptau }_j^{\eta }\) defined in (89).
The main steps for evaluating the entries of the mortar integral matrices \({\varvec{\mathsf {D}}}\) and \({\varvec{\mathsf {M}}}\) in 3D will be presented in Sect. 7.3 in the context of tied contact and can be directly transferred to unilateral contact. Concretely, this encompasses the definition of averaged nodal normal vectors and the 3D mortar segmentation algorithm (cf. Fig. 18) with its associated projection, clipping and triangulation procedures.
6.4 Active Set Strategy and Semi-smooth Newton Methods
As mentioned before, the semi-discrete problem statement of unilateral contact in (122)–(124), and in particular its final fully discretized version (i.e. after time discretization with the generalized-\(\alpha \) method previously discussed in Sect. 4.3), causes one major additional complexity with regard to global solution schemes as compared with the mesh tying case, namely the contact specific inequality constraints, which divide the set of all discrete constraints (i.e. the equivalent of all slave nodes) into two a priori unknown sets of active and inactive constraints. Mathematically speaking, this introduces an additional source of nonlinearity apart from the well-known geometrical and material nonlinearities of nonlinear solid mechanics. To resolve this contact nonlinearity, so-called primal-dual active set strategies (PDASS) will be employed in the solution algorithms developed here.
The idea of any active set strategy in the context of unilateral contact is to find the correct subset of all slave nodes which are in contact with the master surface at the end of the currently considered time interval \([t_n,t_{n+1}]\). As discussed in Sect. 6.3, the contact constraints can be enforced nodally at each slave node \(j \in \mathcal {S}\), with \(j=1, \ldots ,m^{(1)}\), despite the fact that a segment-based mortar approach is employed here. Consequently, the so-called active set \(\mathcal {A} \subseteq \mathcal {S}\) defines a subset of the set of all slave nodes \(\mathcal {S}\), and the definition of the inactive set \(\mathcal {I} = \mathcal {S} \setminus \mathcal {A}\) is straightforward. Before considering possible formulations of active set strategies, the final KKT conditions defined in (123) are repeated here, with the time index \(n+1\) being omitted in the following for the sake of notational simplicity, i.e.
The aforementioned definitions of the active set and the inactive set in combination with the complementarity condition \((\tilde{g}_{\mathsf {n}})_j (\lambda _{\mathsf {n}})_j = 0\) motivate a first, naive reformulation of the KKT conditions using only equality constraints:
Obviously, the PDASS in (127) suffers from a serious drawback: the contact nonlinearity, i.e. finding the correct active set \(\mathcal {A}\) can not be resolved by a Newton–Raphson type approach. This is due to the fact that no directional derivative of the sets themselves with respect to the nodal displacements \({\varvec{\mathsf {d}}}\) can be extracted from (127). Instead, the given formulation inevitably leads to two nested iterative solution schemes, with the outer (fixed-point type) loop solving for the correct active set and the inner (Newton–Raphson type) loop solving a constrained nonlinear finite element problem while the active set is fixed. Consequently, this approach does not provide the desired efficiency and will not be followed any further in this contribution. Further information on such a fixed-point type treatment of the active set in the context of finite deformation mortar contact can for instance be found in Hartmann et al. (2007) and Hesch and Betsch (2009).
Based on the above considerations, the basic idea of an alternative PDASS formulation is to rearrange the KKT conditions such that a Newton–Raphson type algorithm can be applied not only for geometrical and material nonlinearities, but also for the nonlinearity stemming from contact itself, i.e. the active set search. The resulting primal-dual active set approach is well-known from the general mathematical literature on constrained optimization, see e.g. in Hintermüller et al. (2002) and Qi and Sun (1993), and can equivalently be interpreted as a semi-smooth Newton method. Applications to classical NTS contact formulations can be found in Alart and Curnier (1991), Christensen et al. (1998) and Strömberg et al. (1996), and small deformation mortar contact has been investigated in Hüeber and Wohlmuth (2005). Here, the first successful consistent extension to a finite deformation mortar contact formulation is presented, cf. also Popp et al. (2009, 2010). The main idea is to reformulate the discrete KKT conditions within a so-called nonlinear complementarity (NCP) function, where all details for frictionless and frictional contact are given in the upcoming paragraphs. For the sake of completeness, it should be mentioned that the concept of NCP functions is also applicable to other well-known solid mechanics problems involving inequality constraints such as computational plasticity. For a comprehensive and more general overview, the reader is exemplarily referred to Hager (2010).
The first step for frictionless contact is to reformulate the discrete KKT-conditions in (126) within a complementarity function \(C_j\) for each slave node \(j \in \mathcal {S}\) as
This is a nonlinear function of the discrete displacements as both the nodal normal vector \({\varvec{\mathsf {n}}}_j\) in \((\lambda _{\mathsf {n}})_j = {\varvec{\mathsf {n}}}_j \cdot \varvec{\uplambda }_j\) and the nodal weighted gap \((\tilde{g}_{\mathsf {n}})_j\) defined in (121) depend nonlinearly on \({\varvec{\mathsf {d}}}\). It can be easily shown that the resulting equality constraint \(C_j = 0\) is equivalent to the complete set of KKT inequality conditions in (126), and that this equivalence holds for arbitrary positive values of the so-called complementarity parameter \(c_{\mathsf {n}}\). The concrete role of \(c_{\mathsf {n}}\) will be explained later in this paragraph. Figure 9 exemplarily illustrates the nodal complementarity function and emphasizes the equivalence with the KKT conditions.
It is important to see that a distinction between the active set \(\mathcal {A}\) and the inactive set \(\mathcal {I}\) is implicitly contained in the complementarity function \(C_j\): the \(\max \)-function is non-smooth and thus consists of two different solution branches. In other words, \(C_j\) provides a certain regularization of the non-smooth decision between each slave node being currently active or inactive, yet without introducing any additional approximation. Thus, the resulting PDASS contains derivative information on the sets themselves and allows for the application of a Newton–Raphson type solution scheme also for the nonlinearity stemming from contact. Consequently, all sources of nonlinearities, i.e. finite deformations, nonlinear material behavior and contact itself, can be treated within one single iterative scheme. While \(C_j\) is a continuous function, it is non-smooth and has no uniquely defined derivative at the positions \((\lambda _{\mathsf {n}})_j - c_{\mathsf {n}} (\tilde{g}_{\mathsf {n}})_j = 0\). Yet, it is well-known from mathematical literature on constrained optimization that the max-function can be classified as so-called semi-smooth function, and therefore a semi-smooth (or generalized) Newton method can still be applied. The interested reader is referred to Hintermüller et al. (2002) and Qi and Sun (1993) for more detailed information on semi-smooth Newton methods, for example including a concise proof of their superlinear local convergence behavior. The actual linearization of the NCP function in (128) is based on the concept of generalized derivatives (e.g. the generalized derivative of the \(\max \)-function) and has been presented in the author’s original work in Popp et al. (2009, 2010) along with the remaining parts of the global solution algorithm.

Reprinted with permission from Popp et al. (2009),  2009 John Wiley & Sons, Ltd.
2009 John Wiley & Sons, Ltd.
Exemplary nodal NCP function \(C_j \left( {\varvec{\mathsf {d}}}, \varvec{\uplambda } \right) \) as a function of the nodal weighted gap \((\tilde{g}_{\mathsf {n}})_j\) and the normal part of the nodal Lagrange multiplier \((\lambda _{\mathsf {n}})_j\) for a complementarity parameter \(c_{\mathsf {n}}=1\). The equivalence with the KKT conditions is indicated in red color.
It should be pointed out that the complementarity parameter \(c_{\mathsf {n}}\) represents a purely algorithmic parameter. Although quite some similarities appear at first sight, \(c_{\mathsf {n}}\) is in stark contrast to a penalty parameter, because it does not influence the accuracy of results. Instead, the weak non-penetration condition in (126) will be satisfied exactly, as can be expected from a Lagrange multiplier method. The choice of \(c_{\mathsf {n}}\) only improves or deteriorates convergence of the resulting semi-smooth Newton method. In Hüeber and Wohlmuth (2005), \(c_{\mathsf {n}}\) has been suggested to be chosen at the order of Young’s modulus E of the contacting bodies to obtain optimal convergence. Numerical investigations for 2D and 3D mortar contact in Popp et al. (2009, 2010), though, have shown very little influence on semi-smooth Newton convergence along a very broad spectrum of values for \(c_{\mathsf {n}}\). Even for relatively large step sizes and fine contacting meshes, the correct active set is usually found after only a few Newton steps. Once the sets remain constant, of course, quadratic convergence is obtained due to the underlying consistent linearization.
Examining the NCP function for frictionless contact in (128) in more detail allows for an interesting and important observation: there exists a certain similarity between the proposed PDASS with its algorithmic realization as semi-smooth Newton method and the classical Augmented Lagrange method, see also the seminal paper by Alart and Curnier (1991) in this context. Simply speaking, the Augmented Lagrange approach as discussed in Alart and Curnier (1991) aims at a regularized variational formulation, while the PDASS and NCP function concept applies at a later stage with a regularized constraint enforcement. Again, no detailed derivation of the Coulomb friction case is given here, but the interested reader is instead referred to Hüeber et al. (2008), Gitterle et al. (2010), Gitterle (2012) and Wohlmuth (2011) for all details on the semi-smooth Newton approach for frictional contact problems.
6.5 Solution Methods
Again, the final system consists of \({\mathsf {ndof}}+{\mathsf {nco}}\) nonlinear discrete algebraic equations, where the number of constraints is \({\mathsf {nco}} = {\mathsf {ndim}} \cdot m^{(1)}\). While standard (smooth) Newton–Rapshon methods were the method of choice for mesh tying problems in Sect. 5.5, the active set strategies now require a semi-smooth Newton approach as discussed in the last paragraph. Nevertheless, for frictionless contact this non-smoothness solely affects the contact constraints in normal direction in (123) or to be more precise their reformulation as NCP function in (128). All remaining parts of the nonlinear system, i.e. both the discrete equilibrium of forces in (122) and the frictionless sliding conditions in (124) still show a smooth behavior.
As explained in Sect. 4.4, the Newton–Raphson method is based on a subsequent linearization of the residual, here defined by the discrete balance of linear momentum in (122) and the discrete contact constraints in (124) and (128). Each nonlinear solution step (iteration index i) then consists of solving the resulting linearized system of equations and applying an incremental update of the unknown displacements \({\varvec{\mathsf {d}}}_{n+1}\) and Lagrange multipliers \(\varvec{\uplambda }_{n+1}\) until a user-defined convergence criterion is met. Examining the residual in (122) in more detail, an important difference to the mesh tying case becomes apparent: the contact operator \({\varvec{\mathsf {B}}}_{{\mathsf {co}}}({\varvec{\mathsf {d}}})\) defined in (119), and thus the contact forces \({\varvec{\mathsf {f}}}_{{\mathsf {co}}}({\varvec{\mathsf {d}}},\varvec{\uplambda })\), depend nonlinearly on the displacements and yield additional contact stiffness blocks when being linearized, i.e.
Herein, the contact stiffness \({\varvec{\mathsf {K}}}_{{\mathsf {co}}}\) is defined as
Moreover, it should be pointed out that contact-related quantities from the last converged time step n appear on the right-hand side of (129) due to the employed generalized-\(\alpha \) time integration in combination with a trapezoidal rule interpolation of the contact forces. Similar to the mesh tying case, the interface forces are still linear with respect to the discrete Lagrange multipliers. Consequently, it is possible to solve directly for \(\varvec{\uplambda }_{n+1}^{i+1}\) in each iteration step and no incremental formulation is needed.
Repeatedly performing semi-smooth Newton steps (iteration index i), each to be solved for the primal-dual pair of discrete variables \((\Delta {\varvec{\mathsf {d}}}_{n+1}^{i+1},\varvec{\uplambda }_{n+1}^{i+1})\), yields the following solution algorithm within the time step \([t_n,t_{n+1}]\):
Algorithm 1
-
1.
Set \(i=0\) and initialize the solution \(({\varvec{\mathsf {d}}}_{n+1}^0, \varvec{\uplambda }_{n+1}^0)\)
-
2.
Initialize \(\mathcal {A}_{n+1}^0\) and \(\mathcal {I}_{n+1}^0\) such that \(\mathcal {A}_{n+1}^0 \cup \mathcal {I}_{n+1}^0 = \mathcal {S}\)
-
3.
Find the primal-dual pair \((\Delta {\varvec{\mathsf {d}}}_{n+1}^{i+1}, \varvec{\uplambda }_{n+1}^{i+1})\) by solving
$$\begin{aligned} \tilde{{\varvec{\mathsf {K}}}}_{{\mathsf {effdyn,co}}} \Delta {\varvec{\mathsf {d}}}_{n+1}^{i+1} + (1-\alpha _{\mathsf {f}}) {\varvec{\mathsf {B}}}_{{\mathsf {co}}}({\varvec{\mathsf {d}}}_{n+1}^i) \varvec{\uplambda }_{n+1}^{i+1}&= -\tilde{{\varvec{\mathsf {r}}}}_{{\mathsf {effdyn,co}}} , \end{aligned}$$(131)$$\begin{aligned} (\varvec{\uplambda }_j)_{n+1}^{i+1}&= {\varvec{\mathsf {0}}} \quad \forall \; j \in \mathcal {I}_{n+1}^i , \end{aligned}$$(132)$$\begin{aligned} \Delta ((\tilde{g}_{\mathsf {n}})_j)_{n+1}^i + ((\tilde{g}_{\mathsf {n}})_j)_{n+1}^i&= 0 \quad \forall \; j \in \mathcal {A}_{n+1}^i , \end{aligned}$$(133)$$\begin{aligned} \Delta (\varvec{\uptau }_j^{\xi })_{n+1}^i (\varvec{\uplambda }_j)_{n+1}^i + (\varvec{\uptau }_j^{\xi })_{n+1}^i (\varvec{\uplambda }_j)_{n+1}^{i+1}&= 0 \quad \forall \; j \in \mathcal {S} , \end{aligned}$$(134)$$\begin{aligned} \Delta (\varvec{\uptau }_j^{\eta })_{n+1}^i (\varvec{\uplambda }_j)_{n+1}^i + (\varvec{\uptau }_j^{\eta })_{n+1}^i ({\varvec{\mathsf {\uplambda }}}_j)_{n+1}^{i+1}&= 0 \quad \forall \; j \in \mathcal {S} . \end{aligned}$$(135) -
4.
Update \({\varvec{\mathsf {d}}}_{n+1}^{i+1} = {\varvec{\mathsf {d}}}_{n+1}^{i} + \Delta {\varvec{\mathsf {d}}}_{n+1}^{i+1}\)
-
5.
Set \(\mathcal {A}_{n+1}^{i+1}\) and \(\mathcal {I}_{n+1}^{i+1}\) to
$$\begin{aligned} \mathcal {I}_{n+1}^{i+1}&:= \left\{ j \in \mathcal {S} \, \vert \, ((\lambda _{\mathsf {n}})_j)_{n+1}^{i+1} -c_{\mathsf {n}} ((\tilde{g}_{\mathsf {n}})_j)_{n+1}^{i+1} \ge 0 \right\} , \nonumber \\ \mathcal {A}_{n+1}^{i+1}&:= \left\{ j \in \mathcal {S} \, \vert \, ((\lambda _{\mathsf {n}})_j)_{n+1}^{i+1} -c_{\mathsf {n}} ((\tilde{g}_{\mathsf {n}})_j)_{n+1}^{i+1} < 0 \right\} . \end{aligned}$$(136) -
6.
If \(\mathcal {A}_{n+1}^{i+1} = \mathcal {A}_{n+1}^{i}\), \(\mathcal {I}_{n+1}^{i+1} = \mathcal {I}_{n+1}^{i}\) and \(\Vert {\varvec{\mathsf {r}}}_{{\mathsf {tot}}} \Vert \le \epsilon _{\mathsf {r}}\), then stop, else set \(i:=i+1\) and go to step (3).
Herein, the following abbreviations have been introduced for notational simplicity:
Moreover, the variable \(\epsilon _{\mathsf {r}}\) denotes an absolute Newton convergence tolerance for the \(L^2\)-norm of the total residual vector \({\varvec{\mathsf {r}}}_{{\mathsf {tot}}}\), which comprises the force residual and the residual of the contact constraints (132)–(135). All types of nonlinearities including the search for the correct active set are resolved within one single nonlinear solution scheme, with the sets \(\mathcal {I}_{n+1}^{i}\) and \(\mathcal {A}_{n+1}^{i}\) being updated after each semi-smooth Newton step.
The convergence behavior of the resulting solution scheme is very good. As long as the correct active set is not found, and thus the contact typical non-smoothness is not yet resolved, locally superlinear convergence rates are obtained, see e.g. Hintermüller et al. (2002). Once the sets are fixed, the nonlinear iteration scheme reduces to a standard (smooth) Newton–Raphson method, and thus even locally quadratic convergence rates are achieved in the limit owing to the underlying consistent linearization. While not discussed here, similar observations can also be made for frictional contact according to Coulomb’s law and the associated search for the correct stick and slip sets, see e.g. Gitterle et al. (2010), Gitterle (2012) and Hüeber et al. (2008).
In this section, an algebraic representation of the linearized system to be solved within each semi-smooth Newton step is derived and globally assembled matrix notations for the directional derivatives in (131)–(135) are provided. With the assembly procedure itself being rather straightforward in finite element methods, only the final results are given here. The final system to be solved within each semi-smooth Newton step can be expressed as follows:
Herein, the scalar \(a:=1-\alpha _{\mathsf {f}}\) abbreviates the weighting factor introduced by generalized-\(\alpha \) time integration. Moreover, the nonlinear iteration index i as well as the subscript \(\cdot _{{\mathsf {effdyn,co}}}\) of the residual vector \(\tilde{{\varvec{\mathsf {r}}}}_{{\mathsf {effdyn,co}}}\) given in (137) and the effective stiffness matrix \(\tilde{{\varvec{\mathsf {K}}}}_{{\mathsf {effdyn,co}}}\) defined in (138) have been omitted for the ease of notation.
Again, as has been the case for mesh tying, the dual Lagrange multiplier approach can be beneficially exploited to simplify the final linear system of equations. In a first step, the Lagrange multipliers \(\varvec{\uplambda }_{n+1,\mathcal {I}}\) associated with inactive slave nodes are easily condensed by simply extracting the identity \(\varvec{\uplambda }_{n+1,\mathcal {I}}={\varvec{\mathsf {0}}}\) from the fifth row of (139). This basically removes the fifth row and the fifth column of the original saddle point system. More importantly, based on the fourth row of (139), the Lagrange multipliers \(\varvec{\uplambda }_{n+1,\mathcal {A}}\) associated with active slave nodes can be expressed as
As will be discussed in Sect. 7.3, the active part of the mortar projection operator \({\varvec{\mathsf {P}}} = {\varvec{\mathsf {D}}}^{\mathsf {-1}} {\varvec{\mathsf {M}}}\) can be defined as
Inserting (140) into the second and seventh row of (139) yields
While inevitable for standard Lagrange multiplier interpolation, the undesirable saddle point structure of (139) with its typical zero diagonal block has successfully been removed. Finally, it should be mentioned that the discrete Lagrange multipliers, and thus their physical interpretation as contact tractions, are recovered from the displacement solution in a variationally consistent way. This recovery can be performed as a pure postprocessing step at the end of each time interval based on the relation given in (140).
6.6 Numerical Example
The numerical example presented in this section demonstrates the applicability of the proposed mortar contact formulations, including the parallel search algorithms and dynamic load balancing strategies to be described in Sect. 7.2, for large-scale simulations on parallel high-performance computing (HPC) systems. The investigated setup, illustrated in Fig. 10, consists of two thin-walled tori with a Neo–Hookean material model (\(E=3000\), \(\nu =0.3\), \(\rho _0=0.1\)). The major and minor radius of the two hollow tori is 76 and 24, respectively, and the wall thickness is 4.5. The lower torus lies in the xy-plane and the upper torus is rotated around the y-axis by 45 degrees. Both the chosen geometry and loading conditions are inspired by a very similar analysis presented in Yang and Laursen (2008) to evaluate contact search strategies. Transient structural dynamics using a generalized-\(\alpha \) time integration scheme are considered for the solution within 500 time steps and a constant time step size \(\Delta t =0.02\). As can be seen from the exemplary snapshots of deformation in Fig. 10, the lower torus is first accelerated towards the upper torus by a body force and then a very general oblique impact situation with large structural deformations occurs.
The finite element mesh for this 3D impact model involves 4,255,360 first-order hexahedral (hex8) elements and 13,994,880 degrees of freedom in total, with both slave and master surfaces consisting of 204,800 contact elements each. The numerical solution is performed in parallel on 120 processors within an overall simulation time of approximately 48 h.
Figures 11 and 12 further illustrate the complexity of the considered simulation model with severe changes of the active contact set and an extremely fine mesh resolution. While there always remains room for improvements of the parallel efficiency (e.g. with respect to efficient linear solvers, see Sect. 9), the results nevertheless strikingly emphasize that the implementation devised within this section is already very mature in this regard.
7 Algorithmic Aspects and Extensions
Going beyond the fundamental concepts of mortar finite element methods for mesh tying and unilateral contact (including friction), the following paragraphs shall give an overview of certain important algorithmic aspects that are of utmost importance for the acurate and efficient implementation of such mortar methods within a nonlinear finite element code framework. Specifically, the topics of suitable discrete Lagrange multiplier bases, parallel and high performance computing, numerical integration as well as isogeometric analysis will be highlighted. Further details on each of these topics can be found in the author’s original contributions (Popp et al. 2012; Wohlmuth et al. 2012; Popp et al. 2013; Popp and Wall 2014; Farah et al. 2015; Seitz et al. 2016).
7.1 Discrete Lagrange Multipliers
The discrete Lagrange multiplier space \(\varvec{\mathcal {M}}_h\) and associated shape functions \(\Phi _j\), \(j=1, \ldots ,m^{(1)}\), on the slave side of the mesh tying interface were already introduced in Sect. 5.3, although not specified in detail. Yet, this choice of the discrete Lagrange multiplier space is crucial for both the mathematical properties and the numerical efficiency of the resulting mortar approach. There exists a vast amount of literature discussing all relevant characteristics associated with the choice of \(\varvec{\mathcal {M}}_h\), such as inf-sup stability of the underlying mixed formulation and optimal a priori error bounds, see e.g. Bernardi et al. (1994), Ben Belgacem (1999), Seshaiyer and Suri (2000) and Wohlmuth (2000). With stability investigations and a priori error estimates not being in the focus of interest of this contribution, the following considerations rely on the fact that there exists a well-established framework of proofs and rigorous mathematical analyses, which guarantees the applicability of all discrete Lagrange multiplier spaces discussed here to mortar mesh tying problems. For a comprehensive overview, the reader is referred to Wohlmuth (2001) and the references therein.
Throughout this chapter, two different families of discrete Lagrange multipliers, namely standard and so-called dual Lagrange multipliers, will be distinguished. Standard Lagrange multipliers represent the classical approach for mortar methods (cf. Ben Belgacem 1999; Seshaiyer and Suri 2000) and are usually taken from the finite dimensional subset \(\varvec{\mathcal {W}}^{(1)}_h \subset \varvec{\mathcal {W}}^{(1)}\) on the slave side of the interface, where \(\varvec{\mathcal {W}}^{(1)}\) is the trace space of \(\varvec{\mathcal {V}}^{(1)}\), as explained in Sect. 5.2. Thus, standard mortar methods typically lead to identical shape functions for Lagrange multiplier and slave displacement interpolation, i.e. \(\Phi _j=N_j^{(1)}\).
In contrast, the dual approach is motivated by the observation that the Lagrange multipliers physically represent fluxes (tractions) on the mesh tying interface in the continuous setting. This duality argument is then reflected by constructing dual Lagrange multiplier shape functions based on a so-called biorthogonality condition with the displacements in \(\varvec{\mathcal {W}}^{(1)}_h\), see e.g. Wohlmuth (2000). While they are, in general, not continuous and cannot be interpreted as a trace of conforming finite elements, the biorthogonality condition assures that the Lagrange multiplier shape functions \(\Phi _j\) are again well-defined and satisfy all required approximation properties. One crucial advantage of the dual approach lies in the fact that it heavily facilitates the treatment of typical mortar coupling conditions at the interface, while at the same time preserving the mathematical optimality of the method. Going back to (85), the discrete mesh tying condition can alternatively be expressed as
where \({\varvec{\mathsf {P}}}={\varvec{\mathsf {D}}}^{\mathsf {-1}} {\varvec{\mathsf {M}}}\) represents the discrete interface coupling operator. As will be demonstrated later on for both mesh tying and unilateral contact problems, dual Lagrange multipliers avoid the necessity of solving a mass matrix type of system when evaluating (143), but localize the coupling conditions instead. Algebraically, this advantageous property of dual Lagrange multipliers can be observed by the mortar matrix \({\varvec{\mathsf {D}}}\) in (82) reducing to a diagonal matrix. This allows for very efficient condensation procedures of the discrete Lagrange multiplier degrees of freedom, which completely remove the undesirable saddle point structure of the underlying mesh tying and later unilateral contact systems, see Sects. 5.5 and 6.5.
While the construction of standard Lagrange multiplier bases is absolutely straightforward, the construction of dual Lagrange multiplier bases shall exemplarily be highlighted here for the simple first-order interpolation case in 2D. Details on how to define dual Lagrange multiplier shape functions \(\Phi _j\) using the so-called biorthogonality relationship with the standard displacement shape functions \(N_k^{(1)}\) have first been presented in Scott and Zhang (1990) and Wohlmuth (2000). A common notation of the biorthogonality condition is
Herein, \(\delta _{jk}\) is the Kronecker delta, and the most common choice \(m^{(1)}=n^{(1)}\) is assumed. For practical reasons, the biorthogonality condition is typically applied locally on each slave element e, yielding
where \(m^{(1)}_{e}\) represents the number of Lagrange multiplier nodes of the considered slave element. Taking into account the assumption that all nodes also carry discrete Lagrange multiplier degrees of freedom, \(m^{(1)}_{e}\) is simply the number of nodes of the current slave facet. Comparing (144) and (82) also clearly reveals why dual shape functions reduce the mortar matrix \({\varvec{\mathsf {D}}}\) to a diagonal matrix. The dual shape functions resulting from (144), or rather from the elementwise version in (145), have the same polynomial order as the employed standard shape functions, i.e. \(p_\lambda =p\). Moreover, it can easily be shown that the biorthogonality condition guarantees a partition of unity property, i.e. \(\sum _j \Phi _j = 1\), \(j=1, \ldots ,m^{(1)}_{e}\), see Flemisch and Wohlmuth (2007) for a proof.
As a simple example, the first-order finite element interpolation case in 2D shall be considered in the following. Obviously, this case leads to line2 shaped mortar interface segments. With the Jacobian of line2 segments being constant, the dual Lagrange multiplier shape functions determined by (145) are independent of element distortion, and can be defined a priori instead:
Figure 13 illustrates these dual shape functions along with their standard counterparts, i.e. the first-order slave displacement shape functions \(N_j^{(1)}\). In contrast to the corresponding standard Lagrange multiplier case, dual Lagrange multiplier shape functions can no longer be positive everywhere in order to fulfill the biorthogonality condition. However, integral positivity is still guaranteed. Moreover, the above defined \(\Phi _j\) are indeed locally linear polynomials and satisfy a partition of unity property, but nonetheless they represent discontinuous functions.
In general, dual shape functions depend on the actual distortion of the individual underlying finite element, and cannot be defined a priori for non-constant slave element Jacobian determinants. In that regard, the first-order case in 2D illustrated above was a special case. Instead, a local linear mass matrix system of size \(m^{(1)}_{e} \times m^{(1)}_{e}\) must be solved on each slave element. Details on these quite intricate constructions can for example be found in Wohlmuth (2001), Flemisch and Wohlmuth (2007), Lamichhane et al. (2005), Lamichhane and Wohlmuth (2007), Wohlmuth et al. (2012) and Popp et al. (2012).
7.2 Parallel Computing
The mortar-based mesh tying and contact algorithms developed throughout this contribution are designed for the use on large interconnected computer systems (clusters) with many central processing units (CPUs) and a distributed main memory. Being able to efficiently run large simulations in parallel requires strategies for the partitioning and parallel distribution of the problem data, i.e. finite element meshes (consisting of nodes and elements) as well as global vectors and matrices, into several independent processes, each assigned to a corresponding processor. For the sake of simplicity, the term processor refers to an independent processing unit throughout this chapter without implying any specific hardware configuration (such as a single-core or multi-core architecture). Within the finite element based multiphyiscs research code BACI that has been co-developed by the author at the Institute for Computational Mechanics of TUM, this so-called domain (or data) decomposition functionality is provided by the third-party library ParMETIS, see e.g. Karypis and Kumar (1998).
An example of such decompositions is visualized in Fig. 14 for a simple partitioning including only two processors, see also Gee (2004). It can be seen that each node in the mesh is uniquely assigned to one specific processor, and the same holds true for the elements. In addition, some nodes and elements at the transition between different processors must be stored redundantly within all adjacent processors. Therefore, this type of partitioning is commonly denoted as overlapping decomposition. For the methods developed in this chapter, it is sufficient to consider only the most straightforward case of minimal overlap between the individual partitions, i.e. an overlap of one layer of elements or nodes, respectively. Obviously, this concept of overlapping decomposition fits quite naturally to the typical tasks within a finite element program: first, each processor performs an elementwise integration of its own partition of the computational domain including the (relatively few) elements at the inter-processor boundaries. Then, the resulting quantities (e.g. local element load vectors and stiffness matrices) are assembled into the respective FE nodes of each processor. Thus, overlapping domain decomposition as described above provides a very elegant way of processing finite element integration and assembly, which is completely free of communication due to the distributed storage of the resulting global vector and matrix objects. While this rough introduction is by far not complete or rigorous from the viewpoint of parallel software design, it is sufficient for the following ideas on redistribution and load balancing to be comprehensible. For further details on the C++ based implementation of parallel (i.e. distributed) matrix and vector objects as well as the associated linear algebra, the interested reader is exemplarily referred to the documentation of open-source libraries of the Trilinos Project conducted by Sandia National Laboratories Heroux (2005).
Returning to the efficient parallel treatment of mortar methods and the derived mesh tying and contact algorithms, an exemplary mesh tying problem setup consisting of two cubic bodies as depicted in Fig. 15 is considered now. In total, the FE model contains 681,476 volume elements (with 2,136,177 displacement degrees of freedom) and 15,041 contact interface elements, which are distributed in parallel among several processors. As explained in the last paragraph, this partitioning generated via the ParMETIS library is in a sense optimal for the integration and assembly of the individual volume finite elements of the two bodies, i.e. the corresponding workload is equally distributed among all processors. For both tied and unilateral contact interaction, however, additional (but conceptually similar) tasks have to be performed locally at the interface: as will be explained in detail in Sect. 7.3, computing the interface contributions to the overall discrete problem formulation involves the mortar segmentation process, integration and assembly of the mortar matrices \({\varvec{\mathsf {D}}}\) and \({\varvec{\mathsf {M}}}\), to name only the most important tasks. Especially in three dimensions and for large interfaces, these computations may become quite time-consuming, so that they actually carry considerable weight as compared to the remaining time needed for FE evaluation and linear solvers. In contrast to NTS formulations, the high approximation quality of mortar methods comes at a price here. Unfortunately, the parallel distribution of the mortar interface itself is not optimal at all, which can easily be seen in Fig. 15. In this context, it is important to commemorate the slave-master concept typically used for implementing contact algorithms, where the interface-related workload is completely assigned to the slave side (or non-mortar side) whereas the master side (or mortar side) is passive. Thus, in the given example, the slave side of the interface (and thus the entire workload related to mesh tying) is associated with only 4 out of 16 processors.
The right hand side of Fig. 15 illustrates typical results for the parallel efficiency of the presented mortar algorithms in a so-called strong scaling diagram. Therein, the computation time for numerical integration and assembly of all interface-related quantities T is plotted against the total number of processors \(n_{{\mathsf {proc}}}\) with logarithmic scales applied to both axes. Perfect scalability of the examined numerical algorithm is represented by a straight line with a negative slope of \(-1\), thus representing the evident relation
It can clearly be seen that no perfect scalability is achieved with the presented algorithms without load balancing (blue curve in Fig. 15). This is due to the non-optimal distribution of the slave surface among the participating processors as already described above. The results clearly motivate the development of an efficient parallel redistribution and load balancing strategy for mortar finite element methods. The approach proposed in the following is based on three steps, where the first one is of fundamental importance and is therefore needed for both mesh tying and contact applications. In contrast, the second and third step are purely contact-specific.
The rather simple basic idea of the first step is an independent parallel distribution of the finite elements in the domain and the mortar elements at the mesh tying or contact interface in order to achieve optimal parallel scalability of the computational tasks associated with both, i.e. integration and assembly in \(\Omega ^{(1)}\) and \(\Omega ^{(2)}\) as well as integration and assembly on \(\gamma _{\mathsf {c}}^{(1)}\) and \(\gamma _{\mathsf {c}}^{(2)}\). Again using ParMETIS, this redistribution of the interface elements can readily be performed during problem initialization at \(t=0\). Results for the test model introduced above are also visualized (green curve in Fig. 15), thus demonstrating that this simple modification already allows for excellent parallel scalability within a wide range concerning the number of processors \(n_{{\mathsf {proc}}}\). However, dependent on the considered problem size, parallel redistribution only makes sense up to a certain \(n_{{\mathsf {proc}}}\). It is quite natural that such a limit exists, because there are of course some computational costs associated with the proposed redistribution procedure itself. If too many processors are used in relation to the problem size, these costs (mainly due to communication) become dominant and redistribution is no longer profitable beyond this point.
Motivation for parallel redistribution exemplified with a Hertzian contact example – the active contact region (bottom right) is relatively small as compared with the potential contact surface (i.e. the whole hemisphere). Without redistribution only 6 out of 16 processors would carry the entire workload associated with contact evaluation (bottom left)
As already mentioned, this strategy can be further refined for unilateral contact applications. In contrast to mesh tying, contact interfaces are characterized by two additional complexities: the actual contact zone is not known a priori and it may constantly and significantly vary over time. Thus, in a second and third step, the proposed redistribution strategy is adapted such that it accommodates these additional complexities. Concretely, it can be seen from the Hertzian contact example in Fig. 16 that parallel redistribution must be limited to the actual contact area instead of the potential contact area, because the entire computational effort of numerical integration and assembly is connected with the former. Moreover, whenever finite deformations and large sliding motions occur, the described redistribution needs to be performed dynamically, i.e. over and over again. Such a dynamic load balancing strategy is then typically triggered by a suitable measure for the workload of each individual processor. The parallel balance of the workload among all processors is monitored and a simple criterion whether to apply dynamic load balancing within the current time step or not can be formulated as
Herein, the minimum and maximum computation times of one individual processor in the last time step are denoted as \(T^{{\mathsf {min}}}\) and \(T^{{\mathsf {max}}}\), respectively. The parameter \(r > 1\) represents a user-defined tolerance. For example, choosing \(r = 1.2\) implies that at most 20% unbalance of the parallel workload distribution are tolerated. Of course, the rather simple condition in (148) can easily be extended to incorporate more sophisticated criteria for dynamic load balancing. However, already the short overview given here shows that redistribution and load balancing provide an efficient tool for increased parallel efficiency of mortar algorithms for mesh tying and contact simulations. Corresponding numerical examples (see e.g. Section 6.6) demonstrate that the proposed approach is actually indispensable when considering large-scale applications.
7.3 Numerical Integration
A very efficient, yet at the same time highly accurate coupling algorithm, which performs integration not on the slave surface \(\Gamma ^{(1)}_{{\mathsf {c}},h}\) itself, but on its geometrical approximation with piecewise flat segments, has been proposed in Puso (2004) and will also be employed here. For further details and an in-depth mathematical analysis of this algorithm, the reader is also referred to Puso and Laursen (2004a, b) and Dickopf and Krause (2009). This scheme is referred to as segment-based integration scheme in the following.

Reprinted with permission from Popp et al. (2010),  2010 John Wiley & Sons, Ltd.
2010 John Wiley & Sons, Ltd.
Nodally averaged normal vector \({\varvec{\mathsf {n}}}_k\) at a slave node k with four adjacent slave facets e1 to e4. The element normal vectors \({\varvec{\mathsf {n}}}_k^{(e)}\) are exemplified for elements e2 and e4.
Main steps of 3D mortar coupling of one slave and master element pair. Construct an auxiliary plane (top left), project slave and master nodes into the auxiliary plane (top right), perform polygon clipping (bottom left), divide clip polygon into triangular integration cells and perform Gauss integration (bottom right)
In Fig. 18, the main steps of the 3D numerical integration algorithm for the mortar integrals in \({\varvec{\mathsf {D}}}\) and \({\varvec{\mathsf {M}}}\) are illustrated. In the following, the algorithm is outlined for one pair of slave and master elements \({\mathsf {(s,m)}}\), which are close to each other and thus form an arbitrary overlap.
Algorithm 2
-
1.
Construct an auxiliary plane for numerical integration based on the slave element center \({\varvec{\mathsf {x}}}_0^{(1)}\) and the corresponding unit normal vector \({\varvec{\mathsf {n}}}_0\).
-
2.
Project all \(n_{{\mathsf {s}}}^e\) slave element nodes \({\varvec{\mathsf {x}}}_k^{(1)}, \; k=1, \ldots ,n_{{\mathsf {s}}}^e\) onto the auxiliary plane along \({\varvec{\mathsf {n}}}_0\) to obtain the projected slave nodes \(\tilde{{\varvec{\mathsf {x}}}}_k^{(1)}\). Steps 1 and 2 can also be interpreted as a geometrical approximation of the slave surface removing element warping.
-
3.
Project all \(n_{{\mathsf {m}}}^e\) master element nodes \({\varvec{\mathsf {x}}}_l^{(2)}, \; l=1, \ldots ,n_{{\mathsf {m}}}^e\) onto the auxiliary plane along \({\varvec{\mathsf {n}}}_0\) to obtain the projected master nodes \(\tilde{{\varvec{\mathsf {x}}}}_l^{(2)}\).
-
4.
Find the clip polygon of the projected slave and master elements in the auxiliary plane by applying a clipping algorithm, see e.g. Foley (1997).
-
5.
Establish \(n_{{\mathsf {cell}}}\) triangular integration cells by applying Delaunay triangulation to the clip polygon. Each integration cell consists of three vertices \(\tilde{{\varvec{\mathsf {x}}}}_v^{{\mathsf {cell}}}, \; v=1,2,3\) and is interpolated by standard triangular shape functions on the well-known integration cell parameter space
\(\tilde{\varvec{\eta }} = \left\{ (\tilde{\xi },\tilde{\eta }) | \tilde{\xi } \ge 0, \, \tilde{\eta } \ge 0, \, \tilde{\xi } + \tilde{\eta } \le 1 \right\} \).
-
6.
Define \(n_{{\mathsf {gp}}}\) Gauss integration points with coordinates \(\tilde{\varvec{\eta }}_{g}, \; g=1, \ldots ,n_{{\mathsf {gp}}}\) on each cell and project back along \({\varvec{\mathsf {n}}}_0\) to slave and master elements to obtain \(\varvec{\xi }^{(1)}(\tilde{\varvec{\eta }}_{g})\) and \(\varvec{\xi }^{(2)}(\tilde{\varvec{\eta }}_{g})\).
-
7.
Perform Gauss integration of \(D_{jk{\mathsf {(s,m)}}}\) and \(M_{jl{\mathsf {(s,m)}}}\), \(j,k=1, \ldots ,n_{{\mathsf {s}}}^e\) and \(l=1, \ldots ,n_{{\mathsf {m}}}^e\) on all integration cells
$$\begin{aligned} D_{jk{\mathsf {(s,m)}}}&= \sum _{c=1}^{n_{{\mathsf {cell}}}} \left( \sum _{g=1}^{n_{{\mathsf {gp}}}} w_{g} \, \Phi _j^{(1)} (\varvec{\xi }^{(1)}(\tilde{\varvec{\eta }}_{g})) \, N_k^{(1)} (\varvec{\xi }^{(1)}(\tilde{\varvec{\eta }}_{g})) \, J_{c} \right) , \end{aligned}$$(149)$$\begin{aligned} M_{jl{\mathsf {(s,m)}}}&= \sum _{c=1}^{n_{{\mathsf {cell}}}} \left( \sum _{g=1}^{n_{{\mathsf {gp}}}} w_{g} \, \Phi _j^{(1)} (\varvec{\xi }^{(1)}(\tilde{\varvec{\eta }}_{g})) \, N_l^{(2)} (\varvec{\xi }^{(2)}(\tilde{\varvec{\eta }}_{g})) \, J_{c} \right) . \end{aligned}$$(150)where \(J_{c}\), \(c=1, \ldots ,n_{{\mathsf {cell}}}\) is the integration cell Jacobian determinant.
Expressions (149) and (150) represent contributions to \(D_{jk}\) and \(M_{jl}\) given by one slave and master element pair \({\mathsf {(s,m)}}\). Total quantities are obtained by summing up all slave and master element pair contributions. As pointed out in Puso (2004), the above algorithm relies on the fact that the clip polygons of all slave and master element pairs are convex. For further explanations on prerequisites and properties of this numerical integration procedure, the reader is referred to the original paper by Puso (2004).
In this work, seven point integration is used, which allows to exactly integrate polynomials of up to order five. This order of accuracy is sufficient to exactly integrate (149) and (150) for tri3 surface facets and unwarped quad4 surface facets. Typical constant stress patch tests on flat interfaces could even be satisfied with much fewer quadrature points. However, it should be pointed out that in the case of surface facet warping, the mapping between slave and master sides introduces rational polynomial functions into the integrands in (149) and (150), and thus the numerical quadrature rule can never reproduce the exact integral value in such cases. However, numerical results including mesh refinement studies on curved mesh tying interfaces demonstrate that the suggested choice of seven Gauss points per integration cell provides a sufficiently accurate quadrature rule. Figure 19 illustrates the generation of integration cells for 3D mortar coupling with a more complex example.
While Algorithm 2 undoubtedly provides the highest achievable accuracy for the numerical integration of \(D_{jk}\) and \(M_{jl}\) in 3D, some computationally more efficient alternatives have also been suggested in the literature. One prominent example is the simplified integration algorithm proposed in Fischer and Wriggers (2005, 2006) and later reused in De Lorenzis et al. (2011) and Tur et al. (2009), which will be referred to as element-based integration scheme in the following. Instead of thoroughly sub-dividing the mesh tying or contact interface into mortar segments, the numerical integration is simply performed element-wise in that approach, deliberately ignoring kinks of the functions to be integrated. Consequently, the devised integration schemes may indeed offer an appealing computational efficiency, but inevitably bring about difficulties with respect to accuracy of numerical integration. Even the exact satisfaction of a simple two-dimensional patch test, as investigated in Fischer and Wriggers (2005), is strongly influenced by the total number of Gauss points chosen per slave element. An interesting improvement of this approach is suggested in Unger et al. (2007), where adaptive refinement of the integration cells is performed based on a hierarchical quadtree structure. Simply speaking, refinement is only performed close to the kinks of the integrands in (149) and (150) and thus the associated error of numerical integration can be reduced.
In contrast to the 2D case, an extension of the segmentation and integration algorithm to second-order interpolation needs some additional considerations for three-dimensional mortar mesh tying problems. As explained above, the presented method for first-order interpolation is based on the projection of flattened surface elements. This approach has been directly extended to quadratic finite elements in Puso et al. (2008), and is also employed here. The basic idea in Puso et al. (2008) is to subdivide quadratic surface elements into linearly interpolated segments as exemplarily illustrated in Fig. 20 for quad9 facets. Numerical integration according to Algorithm 2 is then performed on the subsegments. As an example, consider the following mapping between parent element and subsegment space of subsegment sub3 for the quad9 element in Fig. 20, which is given by
Similar mapping rules can also be readily established for tri6 and quad8 surface facets. It is important to point out that the approximation introduced by subdividing mortar elements only affects the integration domain itself, which no longer reflects the quadratic finite element surfaces correctly. Yet, by making use of the aforementioned geometric mappings from parent element space to subsegment space and vice versa, one is still able to properly evaluate the higher-order shape function products in (149) and (150).

Reprinted with permission from Popp et al. (2010),  2010 John Wiley & Sons, Ltd.
2010 John Wiley & Sons, Ltd.
Subdivision of interface elements with second-order interpolation. Exemplarily, a quad9 element is split into four quad4 subsegments sub1–sub4, to which the 3D mortar integration algorithm is then applied nearly unchanged.
Numerical integration using the segment-based scheme and the element-based scheme has been thoroughly compared with regard to accuracy and computational efficiency in Farah et al. (2015). To illustrate the main conclusions that can be drawn from such comparisons, the two tori impact example already introduced in the previous section is revisited here. Therefore, the average required integration times for one Newton step within each time step are plotted in the left subfigure of Fig. 21. In addition, the accuracy of the integration schemes is validated by the right subfigure of Fig. 21, which visualizes the deviations of the relative \(L^2\)-norm of the displacements with respect to a reference solution based on segment-based integration with 12 Gauss points per integration cell. Using 37 or 64 Gauss points per integration cell does not significantly change the displacement norm compared to 12 Gauss points.
For this example, the segment-based integration is tested with 3 and 7 Gauss points per integration cell, and the element-based integration method employs 4 to 64 Gauss points per slave element. For the segment-based integration, 3 Gauss points per integration cell is the smallest sensible number of integration points. Thus, it can be seen that compared to the segment-based integration, the element-based integration method has the ability to significantly reduce the number of integration points. In addition, it is obvious that the required integration time scales linearly with the employed number of integration points, which is why all curves in Fig. 21 have a similar shape. The characteristic shape of the curves depends strongly on the active set. Thus, ups and downs of the curves occur due to time steps with a correspondingly high or low number of nodes being in contact. From time step 190 onwards, the curves are zero-valued due to the fact that the two tori are not in contact any more. Interestingly, the \(L^2\)-displacement errors are only marginal and decrease with more and more integration points. Even 4 Gauss points per element are sufficient for the \(L^2\)-displacement error being negligible. However, with 4 Gauss points per element, only \(7\%\) of integration time of the segment-based integration employing 7 integration points per integration cell are required. All in all, it becomes obvious that the element-based integration scheme allows for dramatic reductions of the computational costs for practical applications, while still maintaining a sufficient level of accuracy. Further details on this topic can be found in the author’s original work in Farah et al. (2015).
7.4 Isogeometric Analysis (IGA)
Robust and accurate contact discretizations for nonlinear finite element analysis have been an active field of research in the past decade and a new class of formulations emerged with the introduction of isogeometric analysis (IGA) (Hughes et al. 2005). IGA is intended to bridge the gap between computer aided design (CAD) and finite element analysis (FEA) by using the smooth non-uniform rational B-splines (NURBS) or T-splines common in CAD also as a basis for the numerical analysis. The use of such smooth basis functions has some advantages over classical Lagrange polynomials for FEA such as a possibly higher accuracy per degree of freedom (Evans et al. 2009; Großmann et al. 2012) and, more importantly, a higher inter-element continuity. While finite elements based on Lagrange polynomials are limited to \(C^0\) inter-element continuity independent of the polynomial order p, NURBS can be constructed with a maximum of \(C^{p-1}\) continuity. This high continuity results, amongst others, in a smooth surface representation which makes the application to computational contact mechanics particularly appealing, which has already been anticipated in the original proposition of IGA in Hughes et al. (2005).
As a consequence, in the past five years various discretization techniques have been developed for IGA or transferred from finite element based contact mechanics to IGA, such as node-to-segment (Matzen et al. 2013), Gauss-point-to-segment (Temizer et al. 2011; De Lorenzis et al. 2011; Dimitri et al. 2014; Dimitri 2015; Lu 2011; Sauer and De Lorenzis 2015) and mortar methods (Temizer et al. 2011; De Lorenzis et al. 2011; Temizer et al. 2012; De Lorenzis et al. 2012; Kim and Youn 2012; Dittmann et al. 2014). We refer to the recent review in De Lorenzis et al. (2014) for a comprehensive discussion of such methods, comparisons to their finite element counterparts and further references. In addition to the mentioned methods based on an isogeometric Galerkin approximation, the higher inter-element continuity of NURBS basis functions allows for the use of collocation methods, see Reali and Hughes (2015) for a general introduction and De Lorenzis et al. (2015), Kruse et al. (2015) for an application to computational contact mechanics. Besides the discretization technique, computational contact algorithms can be distinguished with respect to the underlying solution procedure. While Gauss-point-to-segment approaches are, due to their lack of inf-sup stability (see e.g. Temizer et al. 2011; Dimitri et al. 2014 for numerical investigations), usually combined with a penalty approach, see Dimitri et al. (2014), Dimitri (2015), Lu (2011), Sauer and De Lorenzis (2015), node-to-segment and mortar formulations can be combined with penalty methods (Temizer et al. 2011; De Lorenzis et al. 2011), Uzawa-type algorithms (Temizer et al. 2012), Lagrange multiplier methods (Kim and Youn 2012; Dittmann et al. 2014) or augmented Lagrange methods (De Lorenzis et al. 2012). In contrast to penalty methods, the other mentioned methods fulfill the contact constraints in a discrete sense exactly. In the context of domain decomposition in IGA, optimality and stability of standard mortar methods have only very recently been investigated in Hesch and Betsch (2012), Apostolatos et al. (2014), Dornisch et al. (2015), Brivadis et al. (2015), where also the construction of dual B-spline basis functions has been outlined theoretically.
In this section, the so-called dual mortar method is investigated mainly for contact mechanics using NURBS basis functions. In contrast to standard mortar methods, the use of dual basis functions for the Lagrange multiplier based on the mathematical concept of biorthogonality enables an easy elimination of the additional Lagrange multiplier degrees of freedom from the global system. This condensed system is smaller in size and no longer of saddle point type, but positive definite. A very simple and commonly used element-wise construction of the dual basis functions can directly be transferred to the IGA case. The resulting Lagrange multiplier interpolation satisfies discrete inf-sup stability and biorthogonality, however, the reproduction order is limited to one. In the domain decomposition case, this results in a limitation of the spatial convergence order to \(\mathcal {O}(h^{\nicefrac {3}{2}})\) in the energy norm, whereas for unilateral contact, due to the lower regularity of the solution, optimal convergence rates are still met.
Given some still to be defined basis functions \(\Phi \) as a basis of \(\varvec{\mathcal {M}}_h\) and discrete vector-valued Lagrange multipliers \(\varvec{\lambda }_j\) at each control point on the potential contact surface, the Lagrange multiplier field on the slave side is approximated by
While dual mortar methods are meanwhile well-established in finite elements, the present work, to the author’s knowledge, is the first application of dual basis functions in the context of IGA for both domain decomposition and finite deformation frictional contact. Dual basis functions are characterized by fulfilling a biorthogonality condition (Wohlmuth 2000):
with the Kronecker symbol \(\delta _{ab}\). Different methods to construct such dual bases exist, and we want to follow the most simple one, where the dual basis functions have the same support as their primal counterparts, fulfill a partition of unity and are constructed via element-wise linear combinations of the primal shape functions (Flemisch and Wohlmuth 2007; Wohlmuth 2001; Lamichhane and Wohlmuth 2007; Lamichhane et al. 2005). On each element e one readily obtains
with the coefficient matrix for each element
In the construction of the coefficient matrix, the local integration for every slave element is only performed on that part of the element domain, for which a feasible projection to the master surface is possible. This is crucial for the consistent treatment of partially projecting elements in complex contact scenarios, as has been investigated for Lagrangian finite elements in Cichosz and Bischoff (2011) for two-dimensional mortar formulations and in Popp et al. (2013) for the general three-dimensional case. To properly detect the integration domain and reduce the integration error to a minimum, a segmentation process for isogeometric contact analysis will be described later on. For a well-defined construction of dual shape functions according to (155), the primal shape functions are required to have a non-zero integral value on the integration domain. Higher-order Lagrange polynomials do, in general, not meet this requirement which necessitates the use of a local basis transformation of the primal basis to obtain well defined dual shape functions, see Popp et al. (2012), Wohlmuth et al. (2012). NURBS, on the other hand, are positive on the entire element, such that the construction (154), (155) is well defined without any further modifications and for any approximation order. For a two-dimensional contact problem, i.e. a one dimensional contact boundary, an exemplary set of primal and dual basis functions of second-order is depicted in Fig. 22.

Reprinted with permission from Seitz et al. (2016),  2016 Elsevier B.V.
2016 Elsevier B.V.
Primal (top) and dual (bottom) basis functions for a one dimensional B-spline example. The equations for the shape functions in the central element are given to underline the desired biorthogonality and partition of unity.
It should be pointed out that the dual basis functions generated by (154), (155) only guarantee a partition of unity. Consequently, the global approximation order is limited to one in the \(L^2\)-norm, independent of the local approximation. Since the dual NURBS do not posses the optimal reproduction order, optimal convergence rates as proven in Brivadis et al. (2015) cannot be guaranteed. For dual mortar methods based on Lagrange polynomials optimality can be recovered by a transformation of the primal basis (Lamichhane and Wohlmuth 2007) or by extending the support of the basis functions (Oswald and Wohlmuth 2001). An extension of the latter approach to B-splines is outlined in Brivadis et al. (2015), but in general still unsolved. However, for contact problems the solution is typically in \(H^t( \Omega ^{(i)})^3\) with \(t < \nicefrac {5}{2}\), such that a priori estimates are already limited by the regularity of the solution. Even this simple construction of dual shape functions meets the requirements in Wohlmuth et al. (2012) for optimal a priori estimates for the displacements in the \(H^1\)-norm of order \(\mathcal {O}(h^{\nicefrac {3}{2}})\).
Although the presented element-wise construction of dual shape functions yields sub-optimal convergence in domain decomposition applications, they may still be interesting for unilateral contact applications. In this case, the spatial convergence is usually limited by the reduced regularity of the solution, such that even the simple element-wise construction gives optimal convergence in finite element analysis (Wohlmuth et al. 2012). Hence, in our numerical example below, we want to investigate the spatial convergence properties of the isogeometric dual mortar contact algorithm in detail. We therefore use a two dimensional Hertzian-type contact of a cylindrical body (radius R) with a rigid planar surface under plane strain conditions. The two horizontal upper boundaries undergo a prescribed vertical displacement. To avoid singularities in the isogeometric mapping, we introduce a small inner radius (radius r), see Fig. 23 for the geometric setting, the material parameters and the coarsest mesh. Again meshes using second and third-order NURBS basis functions are used as depicted in Fig. 23 for the coarsest level, where different Bézier elements are marked with different shading. In this setup half of the elements on the potential contact surface are located within one ninth of the circumferential length and \(C^{p-1}\) continuity is ensured over the entire active contact surface. In the convergence study, uniform mesh refinement via knot insertion is performed on each of the patches resulting in a constant local element aspect ratio. Although only relatively small deformations are to be expected, we use a fully nonlinear description of the continuum using nonlinear kinematics and a Saint–Venant–Kirchhoff material under plane strain assumption as well as the nonlinear contact formulation.

Reprinted with permission from Seitz et al. (2016),  2016 Elsevier B.V.
2016 Elsevier B.V.
Hertzian contact - Problem setup and coarsest mesh with Bézier elements in different shading.
In Tables 1 and 2, we compare different refinement levels and study the convergence behavior in terms of the energy norm. Since no analytical solution is available, we use the finest mesh of level 7 with standard third-order NURBS as a numerical reference solution. Tables 1 and 2 give the error decay over six refinement levels for both a standard and dual Lagrange multiplier interpolation of second and third-order together with the numerical convergence order in each step. In the limit, all methods converge with the expected order of \(\mathcal {O}(h^{\nicefrac {3}{2}})\) in the energy norm and also the absolute error values are quantitatively very similar. Only the \(N^3\) standard case gives a slightly higher order in the last step since the next level of this mesh is chosen as the numerical reference solution. In view of these results, the use of dual shape functions for the Lagrange multiplier instead of primal ones does not come at the expense of a reduced accuracy but yields equally accurate results while reducing the total system size to the number of displacement degrees of freedom only. In contrast to the domain decomposition case above, the convergence is now limited by the regularity of the solution, such that both standard and dual interpolations converge with the same order. The use of higher-order NURBS, i.e. third-order in Table 2 or even higher seems questionable from this viewpoint, since no faster convergence is gained from the higher-order interpolation with uniform mesh refinement.
8 Interface Modeling – Wear and Thermomechanics
Since contact can readily be interpreted as a special type of interface problem, it seems advisable not to isolate contact mechanics, but rather to address it in the context of a broader class of problems denoted as computational interface mechanics. Apart from the computational treatment of contact interaction and friction, computational interface mechanics also comprises other related physical phenomena such as wear, thermomechanics and phase boundaries. Put in short terms, computational contact and interface mechanics are concerned with the treatment of complex interface effects at different length scales ranging from atomistic models to micro- and meso-scale models and further to classical continuum models at the macro-scale. The nature of many interface phenomena even requires a multi-scale perspective and associated models to bridge the spectrum of relevant length scales. Exemplarily, the following two sections shall highlight the application of the numerical methods discussed above (i.e. in particular mortar finite element methods) to wear modeling and thermo-mechanical interface problems. All details on the resulting schemes can be found in the author’s original contributions (Farah et al. 2016, 2017; Seitz et al. 2018).
8.1 Wear Modeling
Contact mechanics including wear is one of the main causes for subsequent failure of machines and component damage and thus highly important for industrial applications. It is a process of material removal associated with frictional effects, which might result in finite shape changes due to the accumulation of wear. Wear is a very complex phenomenon, which relates a geometrical setting including external conditions with tribological material behavior in the contact zone, and therefore correct predictions of wear effects are quite difficult to make, see Meng and Ludema (1995). The main wear types from the classifications in Popov (2010) and Rabinowicz (1995) are abrasive, adhesive corrosive and fretting wear. Nevertheless, there are many more wear types for different materials and load cases. The formulation predominantly employed for wear calculations is the phenomenological law by Archard (1953), which was firstly proposed by Holm (1946). It relates the worn volume with the normal contact force, a characteristic sliding length and a problem-specific wear parameter. Archards’s law is also employed in this contribution as general wear description without discussing microscopical effects of special wear types.
In general, there are two different classes of wear treatment in computational contact mechanics: either only the consideration of very small amounts of wear or finite wear resulting in significant shape changes. The first class is usually treated by tailored modifications of the gap function, which results in slightly overlapping bodies (Farah et al. 2016; Rodríguez-Tembleque et al. 2012; Serre et al. 2001; Strömberg 1996). However, this contribution will focus on the second class, which treats finite wear effects. Standard remeshing procedures are employed in various contributions to prevent bulk elements from degeneration (McColl et al. 2004; Molinari et al. 2001; Öqvist 2001; Põdra and Andersson 1999; Paulin et al. 2008; Sfantos and Aliabadi 2006). An alternative approach to guarantee proper mesh quality is the Arbitrary–Lagrangean–Eulerian formulation, where the mesh movement is considered as pseudo-elasticity problem, see Stupkiewicz (2013). Most of the solution procedures for wear evolution are based on an explicit forward-Euler time integration scheme. Concretely, the standard contact problem is evaluated and only afterwards wear is calculated as a post-processing quantity for the last time step or even for a certain number of time steps. This incremental procedure is widely employed for the finite element method (Lengiewicz and Stupkiewicz 2012; McColl et al. 2004; Öqvist 2001; Põdra and Andersson 1999) and for the boundary element method (Rodríguez-Tembleque et al. 2012; Serre et al. 2001; Sfantos and Aliabadi 2006, 2007). Wear algorithms based on implicit time integration schemes are predominantly available for small amounts of wear and usually introduce additional unknowns into the linearized system of equations, see Ben Dhia and Torkhani (2011), Jourdan and Samida (2009), Strömberg (1996). Up to the authors’ knowledge, the algorithm shown in Stupkiewicz (2013) is the only contribution in the context of finite element analysis that treats wear implicitly in a finite deformation and finite wear regime. Yet, it is limited to quasi-steady-state contact scenarios.
Restrictions to periodic cycling and prescribed relative movement of the involved bodies are often made in order to simplify the wear algorithm, see Argatov (2011), Argatov and Tato (2012), Lengiewicz and Stupkiewicz (2013), Páczelt et al. (2012) for reciprocal sliding and Páczelt and Mróz (2005, 2007); Stupkiewicz (2013) for general steady-state simulations. This assumption may be valid for classical tribological test configurations like pin-on-cylinder tests, but it is certainly not applicable to general scenarios.
The underlying contact frameworks for the wear algorithms existing in literature are mostly based on node-to-segment contact formulations, see for example Lengiewicz and Stupkiewicz (2012); Strömberg et al. (1996). Nowadays, the mortar method is undoubtedly the most preferred choice for robust finite element discretizations in computational contact mechanics. Finite deformation mortar algorithms with and without frictional effects can exemplarily be found in Popp et al. (2010), Puso and Laursen (2004b), Puso et al. (2008), Yang et al. (2005). Still, the only wear algorithm based on mortar finite element discretization that can be found in the literature is given in Cavalieri and Cardona (2013), where only small wear effects without shape changes are considered.
The primary aim of this section, which summarizes the author’s recent original work in Farah et al. (2017), is to simulate finite wear effects for arbitrary load paths in a fully implicit manner. To prevent element degeneration due to the loss of material, an Arbitrary–Lagrangean–Eulerian formulation with a nonlinear pseudo-elasticity assumption for the mesh motion is employed. The developed implicit partitioned algorithm is based on the configurationally consistent split between a Lagrangean step, where the finite deformation contact problem is solved and a shape evolution step, which realizes the finite configuration change due to wear. The wear equation based on Archard’s law is enforced in a weak sense to follow the mortar idea and wear is already included in the Lagrangean step as an additional contribution to the gap function, which leads to an artificial penetration of the involved bodies. Within the shape evolution step, this non-physical overlap is then removed. Additional unknowns due to the Lagrange multiplier approach for contact and due to the wear discretization are eliminated by condensation procedures within the Lagrangean step to guarantee a non-increased system size. Within each time step, the Lagrangean step and the shape evolution step are repeated until convergence of the overall nonlinear coupled problem is obtained.
The numerical example shown here is adapted from Stupkiewicz (2013) to compare the presented implicit wear algorithm with a monolithic steady-state wear algorithm. Steady-state assumptions are valid for periodically repeated contact and frictional sliding problems with many cycles, such as pin-on-disc, reciprocating pin-on-flat, and pin-on-cylinder tribological tests. Usually, these problems are based on splitting the time scale into a fast time of the finite deformation problem and a slow time for the shape evolution due to wear, see Lengiewicz and Stupkiewicz (2012), Lengiewicz and Stupkiewicz (2013), Stupkiewicz (2013). However, within our wear framework, we define a state-independent fixed slip increment per integration point to simulate a steady-state sliding process. Concretely, the 2D pin-on-flat example consists of a hyper-elastic pin, which is pressed into an infinitely long rigid plane, see Fig. 24.

Reprinted with permission from Farah et al. (2017),  2017 John Wiley & Sons, Ltd.
2017 John Wiley & Sons, Ltd.
2D pin-on-flat problem: reference configuration with dimensions (left) and material configuration with material displacements after 5 pseudo time steps (right).
The pin is moved laterally with a constant velocity of \(v=1000\frac{{\text {mm}}}{{\text {s}}}\). Consequently, the absolute value of the integration point slip increment is given as \(\vert \vert \varvec{u}_{\tau ,\text {rel}}\vert \vert = v\Delta t\). The simulation is performed within 5 pseudo-time steps with \(\Delta t = 200\,{\text {s}}\). Frictionless sliding is assumed, which leads to a formulation of Archard’s law in terms of the normal contact pressure. The wear coefficient is assumed constant in the material configuration and defined as \(k_\text {w}=10^{-7}\,{\text {MPa}}^{-1}\). The pin is loaded at its top edge with a normal force \(F=20\frac{{\text {N}}}{{\text {mm}}}\) acting in negative y-direction. The strain energy function for the hyper-elastic material model is of neo-Hookean type and given as
Here, \(I_{\varvec{C}}\) and \(I\!I\!I_{\varvec{C}}\) are the invariants of the Cauchy–Green tensor. Furthermore, \(\lambda \) and \(\mu \) represent the so-called Lamé parameters, which are correlated with the Young’s modulus E and the Poisson’s ratio \(\nu \) via
The Young’s modulus is chosen as \(E=20\,{\text {MPa}}\) and the Poisson’s ratio is \(\nu =0.3\). This 2D simulation is based on a plane-strain assumption and volumetric locking effects are avoided by the F-bar formulation for the employed 4-node quadrilateral elements, see de Souza Neto et al. (1996). The resulting material (i.e. worn) configuration is visualized in the Fig. 24. Here, the material displacements, which connect reference and material configuration, are illustrated. It can be clearly seen that not only nodes attached to the contact boundary are relocated but also inner nodes are properly adapted by our ALE approach. This guarantees a very good mesh quality in the worn configuration. In addition, the evolution of the contact boundary is shown in Fig. 25.
Here, we compare our results with the simulation from Stupkiewicz (2013). Our method matches the results from literature very well, which demonstrates that our wear algorithm can also be applied for such steady-state wear simulations. Further numerical examples as well as the entire background for numerical method development can be found in Farah et al. (2016, 2017).
8.2 Thermomechanics Modeling
In many engineering applications, frictional contact, thermomechanics and elasto-plastic material behavior come hand in hand. Just one class of typical well-known examples are metal forming and impact/crash analysis, where, at high strain rates, thermal effects need to be taken into account. The thermo-mechanical coupling appears in several forms: firstly and most obviously, there is heat conduction across the contact interface. Secondly, the dissipation of frictional work leads to an additional heating at the contact interface. Thirdly, also plastic work within the structure is transformed to heat. Vice versa, the current temperature may influence the elastic and especially the plastic material response. All this necessitates robust and efficient solution algorithms for fully coupled thermo-elasto-plastic contact problems, which has been an active research topic over the past 25 years.
Early implementations of thermo-elastic contact based on well-known node-to-segment (NTS) contact formulations in combination with a penalty constraint enforcement can be found in Johansson and Klarbring (1993), Oancea and Laursen (1997), Wriggers and Miehe (1994), Zavarise et al. (1992), Agelet De Saracibar (1998), Pantuso et al. (2000), Xing and Makinouchi (2002). Within the last decade, more sophisticated variationally consistent contact discretizations based on the mortar method have been developed and applied to thermo-mechanical contact in Hansen (2011), Khoei et al. (2015), Temizer (2014), Dittmann et al. (2014), Hüeber and Wohlmuth (2009). In addition, those algorithms satisfy the contact constraints exactly (at least in a weak sense) by using either Lagrange multipliers or an augmented Lagrangian functional instead of a simple penalty approach. Due to an easier implementation and other benefits like symmetric operators, most of the cited works above employ some sort of partitioned solution scheme for solving the structural problem (at constant temperature) and thermal problem (at constant displacement) sequentially. In thermo-plasticity, those partitioned schemes based on an isothermal split are only conditionally stable (Simo et al. 1992). Only a few researchers have employed monolithic solution schemes, which solve for displacements and temperatures simultaneously (Zavarise et al. 1992; Pantuso et al. 2000; Dittmann et al. 2014; Hüeber and Wohlmuth 2009).
Numerical algorithms for finite deformation thermo-plasticity go back to the seminal work by Simo et al. (1992), which is based on the isothermal radial return mapping algorithm presented in Simo (1988). Both partitioned and monolithic solution approaches are discussed in Simo et al. (1992). Several extensions to this algorithm have been presented later, e.g. a monolithic formulation in principle axes (Ibrahimbegovic and Chorfi 2002) and a variant including temperature-dependent elastic material properties (Canajija and Brnić 2004). In a different line of work, a variational formulation of thermo-plasticity has been developed in Yang et al. (2006), where the rate of plastic work converted to heat follows from a variational principle instead of being a (constant) material parameter as in Simo et al. (1992). A comparison to experimental results is presented in Stainier and Ortiz (2010) to support this variational form. We point out that both approaches to determine the plastic dissipation, i.e. Simo et al. (1992) and Yang et al. (2006), are applicable within the algorithm for thermo-plasticity that is illustrated here. Besides the mentioned radial return mapping and variational formulations, a different numerical algorithm to isothermal plasticity at finite strains has been developed in Seitz et al. (2015). Based on fundamental ideas from Hager and Wohlmuth (2009), the plastic deformation at every quadrature point is introduced as an additional primary variable and the plastic inequality constraints are reformulated as nonlinear complementarity functions. This allows for a constraint violation during the nonlinear solution procedure, i.e. in the pre-asymptotic range of Newton’s method, while ensuring their satisfaction at convergence. As usual in computational plasticity, the material constraints are enforced at each material point independently, such that the additional unknowns can be condensed directly at quadrature point level. It could be shown in Seitz et al. (2015) that due to this less restrictive formulation, a higher robustness can be achieved, which allows for larger time or load steps.
The author’s recent original work in Seitz et al. (2018) aims at developing a monolithic solution scheme for the thermo-elasto-plastic frictional contact problem based on a new approach. Mortar finite element methods with dual Lagrange multipliers are applied for the contact treatment using nonlinear complementarity functions to deal with both the inequality constraints arising from frictional contact as well as plasticity in a unified manner. This bears novelty both for the numerical formulation of anisotropic thermo-plasticity within the bulk material as well as for the fully nonlinear thermo-mechanical contact formulation at the interface. Furthermore, full compatibility of the algorithms for thermo-plasticity and thermo-mechanical contact is demonstrated. Concerning plasticity, an extension of Seitz et al. (2015) to coupled thermo-plasticity within a monolithic solution framework is presented. Similar to the isothermal case, the use of Gauss-point-wise decoupled plastic deformation allows for a condensation of the additionally introduced plastic unknowns, where now also thermo-mechanical coupling terms have to be accounted for. The novel thermo-mechanical contact formulation represents a fully nonlinear extension of Hüeber and Wohlmuth (2009) including a consistent linearization with respect to both the displacement and temperature unknowns. Moreover, the use of dual Lagrange multipliers within a mortar contact formulation enables the trivial condensation of the discrete contact Lagrange multipliers such that the final linearized system to be solved consists of displacement and temperature degrees of freedom only. Our new thermo-mechanical contact formulation is applicable for both classical finite elements based on Lagrange polynomial basis functions as well as isogeometric analysis using NURBS basis functions, for which an appropriate dual basis has recently been proposed in Seitz et al. (2016). Owing to the variational basis of the mortar method, the thermo-mechanical contact patch test on non-matching discretizations is satisfied exactly and optimal convergence rates are achieved (Seitz et al. 2016) (Fig. 26).
While the reader is referred to Seitz et al. (2018) for all details of the formulation, we would at least like to present a fully coupled thermo-elasto-plastic contact example to demonstrate the robustness and efficiency of the developed algorithm. Similar to the example in Seitz et al. (2015) and originally inspired by Hager and Wohlmuth (2009), a squeezed metal tube with an inner and outer radius of \(4\,\mathrm {cm}\) and \(5\,\mathrm {cm}\), respectively, and a length of \(40\,\mathrm {cm}\) is analyzed. In the middle of the tube it is squeezed by two rigid cylindrical tools with an inner and outer of radius \(4.5\,\mathrm {cm}\) and \(5\,\mathrm {cm}\), respectively, and a length of \(16\,\mathrm {cm}\). The material properties are the ones given in Seitz et al. (2018), with plastic isotropy, i.e. \(y_{11}=y_0\). Between the tools and the tube, frictional contact with a temperature dependent friction coefficient is assumed with the initial coefficient of friction \(\mu _0=0.25\), the reference temperature \(T_0=293\,\mathrm {K}\) and the damage temperature \(T_d=1793\,\mathrm {K}\). The tools are initially in stress free contact and perform a vertical displacement of \(u(t)=(1-\mathrm {cos}(\frac{t}{1\,\mathrm {s}}\pi ))\cdot 17.5\,\mathrm {cm}\) over time. Figure 27 illustrates the plastic strain and temperature distribution at different times. Due to the symmetry of the problem, only one eighth of the entire model is discretized with about 20.000 elements, and the results are reflected for visualization purposes. First-order hexahedral elements with an F-bar technology are used to avoid volumetric locking, see de Souza Neto et al. (1996) for the original isothermal formulation of this element. In the early deformation stages, plastic deformation and therefore heat generation is mainly located directly beneath the contact zone (see Fig. 27), whereas later the main plastic deformation occurs at the side of the tube, where the highest peak temperatures are reached (see Fig. 27). After contact is released, thermal conduction tends to equilibrate the temperature inhomogeneity, see Fig. 27. To illustrate the efficient nonlinear solution procedure using Newton’s method with a consistent linearization, Fig. 28 displays the convergence behavior of different residual contributions in the time step of maximal tool velocity (\(t=0.5\,\mathrm {s}\)). All residuals clearly exhibit a quadratic rate of convergence asymptotically, until they are at some point limited by machine precision.
9 Summary and Outlook
In this contribution, mortar finite element methods have been reviewed in the context of nonlinear solid mechanics, with a special emphasis on unilateral contact and friction as well as more complex interface problems. As a first step, some well-established basic principles of mortar methods have exemplarily been recapitulated for mesh tying (tied contact). The concepts of both standard and dual Lagrange multiplier interpolation were addressed with a focus on the latter. The most important favorable feature of dual Lagrange multiplier techniques is the resulting localization of the occurring interface constraints based on a biorthogonalization procedure. Algebraically, this is reflected in the possibility to easily condense the discrete Lagrange multiplier degrees of freedom (DOFs) associated with the non-matching mortar interfaces from the final linear systems of equations. Moreover, several important algorithmic aspects for an accurate and efficient implementation of mortar methods within a nonlinear finite element code framework have been discussed, including the construction of suitable discrete Lagrange multiplier bases, efficient parallel algorithms for high performance computing, accurate numerical integration procedures and an extension of the mortar approach to isogeometric analysis using NURBS.
In many engineering applications, however, an accurate treatment of non-penetration and Coulomb friction conditions at the contact interfaces is not sufficient to draw all technically relevant conclusions. Stress analysis and lifetime prediction of blade-to-disc joints in aircraft engines is an illustrative example for this statement. Such analyses require a detailed modeling and simulation of the manifold physical phenomena occurring at the contact interfaces. This possibly includes anisotropic friction, the dependency of friction coefficients on state variables (e.g. temperature), heat transmission, dissipation due to frictional sliding and surface degradation due to wear. As an outlook towards such challenging application scenarios in interface mechanics and real-life engineering, recent extensions of mortar finite element methods for wear modeling and thermomechanical contact modeling have been illustrated. For all mentioned applications, mortar methods provide an important algorithmic building block in order to obtain more accurate numerical solutions than possible to date, or even to gain insight into phenomena that have hardly been accessible for computational analysis until now.
References
C. Agelet De Saracibar. Numerical analysis of coupled thermomechanical frictional contact problems. Computational model and applications. Archives of Computational Methods in Engineering, 5(3):243–301, 1998.
P. Alart and A. Curnier. A mixed formulation for frictional contact problems prone to Newton like solution methods. Computer Methods in Applied Mechanics and Engineering, 92(3):353–375, 1991.
A. Apostolatos, R.t Schmidt, R. Wüchner, and K.-U. Bletzinger. A Nitsche-type formulation and comparison of the most common domain decomposition methods in isogeometric analysis. International Journal for Numerical Methods in Engineering, 97(7):473–504, 2014.
J. F. Archard. Contact and rubbing of flat surfaces. Journal of Applied Physics, 24(8):981–988, 1953.
I. Argatov. Asymptotic modeling of reciprocating sliding wear with application to local interwire contact. Wear, 271(78):1147–1155, 2011.
I. Argatov and W. Tato. Asymptotic modeling of reciprocating sliding wear comparison with finite-element simulations. European Journal of Mechanics - A/Solids, 34:1–11, 2012.
K.-J. Bathe. Finite element procedures. Prentice Hall, 1996.
K.-J. Bathe and A. Chaudhary. A solution method for planar and axisymmetric contact problems. International Journal for Numerical Methods in Engineering, 21(1):65–88, 1985.
T. Belytschko, W. K. Liu, and B. Moran. Nonlinear finite elements for continua and structures. Wiley, 2000.
F. Ben Belgacem. The mortar finite element method with Lagrange multipliers. Numerische Mathematik, 84(2):173–197, 1999.
F. Ben Belgacem, P. Hild, and P. Laborde. The mortar finite element method for contact problems. Mathematical and Computer Modelling, 28(4-8):263–271, 1998.
H. Ben Dhia and M. Torkhani. Modeling and computation of fretting wear of structures under sharp contact. International Journal for Numerical Methods in Engineering, 85(1):61–83, 2011.
D. J. Benson and J. O. Hallquist. A single surface contact algorithm for the post-buckling analysis of shell structures. Computer Methods in Applied Mechanics and Engineering, 78(2):141–163, 1990.
C. Bernardi, Y. Maday, and A. T. Patera. A new nonconforming approach to domain decomposition: the mortar element method. In H. Brezis and J.L. Lions, editors, Nonlinear partial differential equations and their applications, pages 13–51. Pitman/Wiley: London/New York, 1994.
J. Bonet and R. D. Wood. Nonlinear continuum mechanics for finite element analysis. Cambridge University Press, 1997.
E. Brivadis, A. Buffa, B. Wohlmuth, and L. Wunderlich. Isogeometric mortar methods. Computer Methods in Applied Mechanics and Engineering, 284:292–319, 2015.
S. Brunssen, F. Schmid, M. Schäfer, and B. I. Wohlmuth. A fast and robust iterative solver for nonlinear contact problems using a primal-dual active set strategy and algebraic multigrid. International Journal for Numerical Methods in Engineering, 69(3):524–543, 2007.
M. Canajija and J. Brnić. Associative coupled thermoplasticity at finite strain with temperature-dependent material parameters. International Journal of Plasticity, 20(10):1851–1874, 2004.
C. Carstensen, O. Scherf, and P. Wriggers. Adaptive finite elements for elastic bodies in contact. SIAM Journal on Scientific Computing, 20(5):1605–1626, 1999.
F. J. Cavalieri and A. Cardona. Three-dimensional numerical solution for wear prediction using a mortar contact algorithm. International Journal for Numerical Methods in Engineering, 96:467–486, 2013.
P. W. Christensen. A semi-smooth Newton method for elasto-plastic contact problems. International Journal of Solids and Structures, 39(8):2323–2341, 2002.
P. W. Christensen, A. Klarbring, J. S. Pang, and N. Strömberg. Formulation and comparison of algorithms for frictional contact problems. International Journal for Numerical Methods in Engineering, 42(1):145–173, 1998.
J. Chung and G. M. Hulbert. A time integration algorithm for structural dynamics with improved numerical dissipation: The generalized-\(\alpha \) method. Journal of Applied Mechanics, 60:371–375, 1993.
T. Cichosz and M. Bischoff. Consistent treatment of boundaries with mortar contact formulations using dual Lagrange multipliers. Computer Methods in Applied Mechanics and Engineering, 200(9-12):1317–1332, 2011.
J. A. Cottrell, T. J. R. Hughes, and Y. Bazilevs. Isogeometric analysis: toward integration of CAD and FEA. Wiley, 2009.
L. De Lorenzis, I. Temizer, P. Wriggers, and G. Zavarise. A large deformation frictional contact formulation using NURBS-based isogeometric analysis. International Journal for Numerical Methods in Engineering, 87(13):1278–1300, 2011.
L De Lorenzis, P Wriggers, and G Zavarise. A mortar formulation for 3D large deformation contact using NURBS-based isogeometric analysis and the augmented Lagrangian method. Computational Mechanics, 49(1):1–20, 2012.
L. De Lorenzis, P. Wriggers, and T. J. R. Hughes. Isogeometric contact: a review. GAMM-Mitteilungen, 37(1):85–123, 2014.
L. De Lorenzis, J. A. Evans, T. J. R. Hughes, and A. Reali. Isogeometric collocation: Neumann boundary conditions and contact. Computer Methods in Applied Mechanics and Engineering, 284:21–54, 2015.
E. A. de Souza Neto, D. Perić, M. Dutko, and D. R. J. Owen. Design of simple low order finite elements for large strain analysis of nearly incompressible solids. International Journal of Solids and Structures, 33(20-22):3277–3296, 1996.
T. Dickopf and R. Krause. Efficient simulation of multi-body contact problems on complex geometries: A flexible decomposition approach using constrained minimization. International Journal for Numerical Methods in Engineering, 77(13):1834–1862, 2009.
R. Dimitri. Isogeometric treatment of large deformation contact and debonding problems with t-splines: a review. Curved and Layered Structures, 2(1), 2015.
R. Dimitri, L. De Lorenzis, M. A. Scott, P. Wriggers, R. L. Taylor, and G. Zavarise. Isogeometric large deformation frictionless contact using T-splines. Computer Methods in Applied Mechanics and eEgineering, 269:394–414, 2014.
M. Dittmann, M. Franke, I. Temizer, and C. Hesch. Isogeometric analysis and thermomechanical mortar contact problems. Computer Methods in Applied Mechanics and Engineering, 274:192–212, 2014.
W. Dornisch, G. Vitucci, and S. Klinkel. The weak substitution method–an application of the mortar method for patch coupling in NURBS-based isogeometric analysis. International Journal for Numerical Methods in Engineering, 103(3):205–234, 2015.
H. Elman, V. E. Howle, J. Shadid, R. Shuttleworth, and R. Tuminaro. A taxonomy and comparison of parallel block multi-level preconditioners for the incompressible Navier–Stokes equations. Journal of Computational Physics, 227(3):1790–1808, 2008.
J. A. Evans, Y. Bazilevs, I. Babuška, and T. J. R. Hughes. N-widths, sup–infs, and optimality ratios for the k-version of the isogeometric finite element method. Computer Methods in Applied Mechanics and Engineering, 198(21):1726–1741, 2009.
P. Farah, A. Popp, and W. A. Wall. Segment-based vs. element-based integration for mortar methods in computational contact mechanics. Computational Mechanics, 55:209–228, 2015.
P. Farah, M. Gitterle, W. A. Wall, and A. Popp. Computational wear and contact modeling for fretting analysis with isogeometric dual mortar methods. Key Engineering Materials, 681:1–18, 2016.
P. Farah, W. A. Wall, and A. Popp. An implicit finite wear contact formulation based on dual mortar methods. International Journal for Numerical Methods in Engineering, 111:325–353, 2017.
K. A. Fischer and P. Wriggers. Frictionless 2D contact formulations for finite deformations based on the mortar method. Computational Mechanics, 36(3):226–244, 2005.
K. A. Fischer and P. Wriggers. Mortar based frictional contact formulation for higher order interpolations using the moving friction cone. Computer Methods in Applied Mechanics and Engineering, 195(37-40):5020–5036, 2006.
B. Flemisch and B. I. Wohlmuth. Stable Lagrange multipliers for quadrilateral meshes of curved interfaces in 3D. Computer Methods in Applied Mechanics and Engineering, 196(8):1589–1602, 2007.
J. Foley. Computer graphics: Principles and practice. Addison-Wesley, 1997.
A. Francavilla and O. C. Zienkiewicz. A note on numerical computation of elastic contact problems. International Journal for Numerical Methods in Engineering, 9(4):913–924, 1975.
M. W. Gee. Effiziente Lösungsstrategien in der nichtlinearen Schalenmechanik. PhD thesis, Universität Stuttgart, 2004.
M. W. Gee, C. T. Kelley, and R. B. Lehoucq. Pseudo-transient continuation for nonlinear transient elasticity. International Journal for Numerical Methods in Engineering, 78(10):1209–1219, 2009.
M. Gitterle. A dual mortar formulation for finite deformation frictional contact problems including wear and thermal coupling. PhD thesis, Technische Universität München, 2012.
M. Gitterle, A. Popp, M. W. Gee, and W. A. Wall. Finite deformation frictional mortar contact using a semi-smooth Newton method with consistent linearization. International Journal for Numerical Methods in Engineering, 84(5):543–571, 2010.
D. Großmann, B. Jüttler, H. Schlusnus, J. Barner, and A.-V. Vuong. Isogeometric simulation of turbine blades for aircraft engines. Computer Aided Geometric Design, 29(7):519–531, 2012.
M. E. Gurtin. An introduction to continuum mechanics. Academic Press, 1981.
C. Hager. Robust numerical algorithms for dynamic frictional contact problems with different time and space scales. PhD thesis, Universität Stuttgart, 2010.
C. Hager and B. I. Wohlmuth. Nonlinear complementarity functions for plasticity problems with frictional contact. Computer Methods in Applied Mechanics and Engineering, 198(41-44):3411–3427, 2009.
C. Hager, S. Hüeber, and B. I. Wohlmuth. A stable energy-conserving approach for frictional contact problems based on quadrature formulas. International Journal for Numerical Methods in Engineering, 73(2):205–225, 2008.
J. O. Hallquist, G. L. Goudreau, and D. J. Benson. Sliding interfaces with contact-impact in large-scale Lagrangian computations. Computer Methods in Applied Mechanics and Engineering, 51(1-3):107–137, 1985.
G. Hansen. A jacobian-free Newton Krylov method for mortar-discretized thermomechanical contact problems. Journal of Computational Physics, 230(17):6546–6562, 2011.
S. Hartmann. Kontaktanalyse dünnwandiger Strukturen bei großen Deformationen. PhD thesis, Universität Stuttgart, 2007.
S. Hartmann, S. Brunssen, E. Ramm, and B. I. Wohlmuth. Unilateral non-linear dynamic contact of thin-walled structures using a primal-dual active set strategy. International Journal for Numerical Methods in Engineering, 70(8):883–912, 2007.
S. Hartmann, J. Oliver, R. Weyler, J.C. Cante, and J.A. Hernandez. A contact domain method for large deformation frictional contact problems. Part 2: Numerical aspects. Computer Methods in Applied Mechanics and Engineering, 198(33-36):2607–2631, 2009.
M. A. Heroux. An overview of the Trilinos project. ACM Transactions on Mathematical Software, 31(3):397–423, 2005.
H Hertz. Über die Berührung fester elastischer Körper. Journal für die reine und angewandte Mathematik, 92:156–171, 1882.
C. Hesch and P. Betsch. A mortar method for energy-momentum conserving schemes in frictionless dynamic contact problems. International Journal for Numerical Methods in Engineering, 77(10):1468–1500, 2009.
C. Hesch and P. Betsch. Transient three-dimensional domain decomposition problems: Frame-indifferent mortar constraints and conserving integration. International Journal for Numerical Methods in Engineering, 82(3):329–358, 2010.
C. Hesch and P. Betsch. Transient three-dimensional contact problems: mortar method. Mixed methods and conserving integration. Computational Mechanics, 48:461–475, 2011. ISSN 0178-7675.
C. Hesch and P. Betsch. Isogeometric analysis and domain decomposition methods. Computer Methods in Applied Mechanics and Engineering, 213:104–112, 2012.
P. Hild. Numerical implementation of two nonconforming finite element methods for unilateral contact. Computer Methods in Applied Mechanics and Engineering, 184(1):99 – 123, 2000.
M. Hintermüller, K. Ito, and K. Kunisch. The primal-dual active set strategy as a semi-smooth Newton method. SIAM Journal on Optimization, 13(3):865–888, 2002.
R. Holm. Electric contacts. Gebers, 1946.
G. A. Holzapfel. Nonlinear solid mechanics: A continuum approach for engineering. Wiley, 2000.
S. Hüeber. Discretization techniques and efficient algorithms for contact problems. PhD thesis, Universität Stuttgart, 2008.
S. Hüeber and B. I. Wohlmuth. A primal-dual active set strategy for non-linear multibody contact problems. Computer Methods in Applied Mechanics and Engineering, 194(27-29):3147–3166, 2005.
S. Hüeber and B. I. Wohlmuth. Thermo-mechanical contact problems on non-matching meshes. Computer Methods in Applied Mechanics and Engineering, 198(15–16):1338–1350, 2009.
S. Hüeber and B. I. Wohlmuth. Equilibration techniques for solving contact problems with Coulomb friction. Computer Methods in Applied Mechanics and Engineering, 205–208:29–45, 2012.
S. Hüeber, G. Stadler, and B. I. Wohlmuth. A primal-dual active set algorithm for three-dimensional contact problems with Coulomb friction. SIAM Journal on Scientific Computing, 30(2):572–596, 2008.
T. J. R. Hughes. The finite element method: linear static and dynamic finite element analysis. Dover Publications, 2000.
T. J. R. Hughes, R. L. Taylor, J. L. Sackman, A. Curnier, and W. Kanoknukulchai. A finite element method for a class of contact-impact problems. Computer Methods in Applied Mechanics and Engineering, 8(3):249–276, 1976.
T. J. R. Hughes, J. A. Cottrell, and Y. Bazilevs. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 194(39):4135–4195, 2005.
A. Ibrahimbegovic and L. Chorfi. Covariant principal axis formulation of associated coupled thermoplasticity at finite strains and its numerical implementation. International Journal of Solids and Structures, 39(2):499–528, 2002.
B. M. Irons. Numerical integration applied to finite element methods. In Proceedings Conference on the Use of Digital Computers in Structural Engineering. University of Newcastle, 1966.
L. Johansson and A. Klarbring. Thermoelastic frictional contact problems: modelling, finite element approximation and numerical realization. Computer Methods in Applied Mechanics and Engineering, 105(2):181–210, 1993.
K. L. Johnson. Contact mechanics. Cambridge University Press, 1985.
F. Jourdan and A. Samida. An implicit numerical method for wear modeling applied to a hip joint prosthesis problem. Computer Methods in Applied Mechanics and Engineering, 198(27-29):2209 – 2217, 2009.
G. Karypis and V. Kumar. A parallel algorithm for multilevel graph partitioning and sparse matrix ordering. Journal of Parallel and Distributed Computing, 48(1):71–95, 1998.
A. R. Khoei, H. Saffar, and M. Eghbalian. An efficient thermo–mechanical contact algorithm for modeling contact–impact problems. Asian Journal of Civil Engineering, 16(5):681–708, 2015.
N. Kikuchi and J. T. Oden. Contact problems in elasticity: A study of variational inequalities and finite element methods. SIAM, Philadelphia, 1988.
J.-Y. Kim and S.-K. Youn. Isogeometric contact analysis using mortar method. International Journal for Numerical Methods in Engineering, 89(12):1559–1581, 2012.
T. M. Kindo, T. A. Laursen, and J. E. Dolbow. Toward robust and accurate contact solvers for large deformation applications: a remapping/adaptivity framework for mortar-based methods. Computational Mechanics, 54(1):53–70, 2014.
A. Konyukhov and K. Schweizerhof. On the solvability of closest point projection procedures in contact analysis: Analysis and solution strategy for surfaces of arbitrary geometry. Computer Methods in Applied Mechanics and Engineering, 197(33–40):3045–3056, 2008.
R. Kruse, N. Nguyen-Thanh, L. De Lorenzis, and T.J.R. Hughes. Isogeometric collocation for large deformation elasticity and frictional contact problems. Computer Methods in Applied Mechanics and Engineering, 296:73–112, 2015.
B. P. Lamichhane and B. I. Wohlmuth. Biorthogonal bases with local support and approximation properties. Mathematics of Computation, 76:233–249, 2007.
B. P. Lamichhane, R. P. Stevenson, and B. I. Wohlmuth. Higher order mortar finite element methods in 3D with dual Lagrange multiplier bases. Numerische Mathematik, 102(1):93–121, 2005.
T. A. Laursen. Formulation and treatment of frictional contact problems using finite elements. PhD thesis, Stanford University, 1992.
T. A. Laursen. Computational contact and impact mechanics. Springer-Verlag Berlin Heidelberg, 2002.
T. A. Laursen and V. Chawla. Design of energy conserving algorithms for frictionless dynamic contact problems. International Journal for Numerical Methods in Engineering, 40(5):863–886, 1997.
T. A. Laursen and G. R. Love. Improved implicit integrators for transient impact problems - geometric admissibility within the conserving framework. International Journal for Numerical Methods in Engineering, 53(2):245–274, 2002.
T. A. Laursen and J. C. Simo. A continuum-based finite element formulation for the implicit solution of multibody, large deformation-frictional contact problems. International Journal for Numerical Methods in Engineering, 36(20):3451–3485, 1993.
T. A. Laursen, M. A. Puso, and J. Sanders. Mortar contact formulations for deformable-deformable contact: past contributions and new extensions for enriched and embedded interface formulations. Computer Methods in Applied Mechanics and Engineering, 205–208:3–15, 2012.
J. Lengiewicz and S. Stupkiewicz. Continuum framework for finite element modelling of finite wear. Computer Methods in Applied Mechanics and Engineering, 205–208:178–188, 2012.
J. Lengiewicz and S. Stupkiewicz. Efficient model of evolution of wear in quasi-steady-state sliding contacts. Wear, 303(12):611 – 621, 2013.
J. Lu. Isogeometric contact analysis: Geometric basis and formulation for frictionless contact. Computer Methods in Applied Mechanics and Engineering, 200(5):726–741, 2011.
J. E. Marsden and T. J. R. Hughes. Mathematical foundations of elasticity. Dover, 1994.
M. E. Matzen, T. Cichosz, and M. Bischoff. A point to segment contact formulation for isogeometric, NURBS based finite elements. Computer Methods in Applied Mechanics and Engineering, 255:27–39, 2013.
I. R. McColl, J. Ding, and S. B. Leen. Finite element simulation and experimental validation of fretting wear. Wear, 256(11-12):1114 – 1127, 2004.
T. W. McDevitt and T. A. Laursen. A mortar-finite element formulation for frictional contact problems. International Journal for Numerical Methods in Engineering, 48(10):1525–1547, 2000.
H. C. Meng and K. C. Ludema. Wear models and predictive equations: their form and content. Wear, 181–183:443–457, 1995.
J. F. Molinari, M. Ortiz, R. Radovitzky, and E. A. Repetto. Finite element modeling of dry sliding wear in metals. Engineering Computations, 18(3/4):592–610, 2001.
V. G. Oancea and T. A. Laursen. A finite element formulation of thermomechanical rate-dependent frictional sliding. International Journal for Numerical Methods in Engineering, 40(23):4275–4311, 1997.
R. W. Ogden. Non-linear elastic deformations. Dover Publications, 1997.
J. Oliver, S. Hartmann, J. C. Cante, R. Weyler, and J. A. Hernandez. A contact domain method for large deformation frictional contact problems. Part 1: Theoretical basis. Computer Methods in Applied Mechanics and Engineering, 198(33-36):2591–2606, 2009.
M. Öqvist. Numerical simulations of mild wear using updated geometry with different step size approaches. Wear, 249(12):6–11, 2001.
P. Oswald and B. Wohlmuth. On polynomial reproduction of dual FE bases. In Thirteenth International Conference on Domain Decomposition Methods, pages 85–96, 2001.
P. Põdra and S. Andersson. Simulating sliding wear with finite element method. Tribology International, 32(2):71–81, 1999.
I. Páczelt and Z. Mróz. On optimal contact shapes generated by wear. International Journal for Numerical Methods in Engineering, 63(9):1250–1287, 2005.
I. Páczelt and Z. Mróz. Optimal shapes of contact interfaces due to sliding wear in the steady relative motion. International Journal of Solids and Structures, 44(34):895–925, 2007.
I. Páczelt, S. Kucharski, and Z. Mróz. The experimental and numerical analysis of quasi-steady wear processes for a sliding spherical indenter. Wear, 274-275:127–148, 2012.
D. Pantuso, K.-J. Bathe, and P. A. Bouzinov. A finite element procedure for the analysis of thermo-mechanical solids in contact. Computers & Structures, 75(6):551–573, 2000.
P. Papadopoulos and R. L. Taylor. A mixed formulation for the finite element solution of contact problems. Computer Methods in Applied Mechanics and Engineering, 94(3):373–389, 1992.
C. Paulin, S. Fouvry, and C. Meunier. Finite element modelling of fretting wear surface evolution: Application to a Ti-6A1-4V contact. Wear, 264(12):26–36, 2008.
V. Popov. Contact Mechanics and Friction. Springer, 2010.
A. Popp. Mortar methods for computational contact mechanics and general interface problems. PhD thesis, Technische Universität München, 2012.
A. Popp and W. A. Wall. Dual mortar methods for computational contact mechanics – overview and recent developments. GAMM-Mitteilungen, 37(1):66–84, 2014.
A. Popp, M. W. Gee, and W. A. Wall. A finite deformation mortar contact formulation using a primal-dual active set strategy. International Journal for Numerical Methods in Engineering, 79(11):1354–1391, 2009.
A. Popp, M. Gitterle, M. W. Gee, and W. A. Wall. A dual mortar approach for 3D finite deformation contact with consistent linearization. International Journal for Numerical Methods in Engineering, 83(11):1428–1465, 2010.
A. Popp, B. I. Wohlmuth, M. W. Gee, and W. A. Wall. Dual quadratic mortar finite element methods for 3D finite deformation contact. SIAM Journal on Scientific Computing, 34:B421–B446, 2012.
A. Popp, A. Seitz, M. W. Gee, and W. A. Wall. A dual mortar approach for improved robustness and consistency of 3D contact algorithms. Computer Methods in Applied Mechanics and Engineering, 264:67–80, 2013.
M. A. Puso. A 3D mortar method for solid mechanics. International Journal for Numerical Methods in Engineering, 59(3):315–336, 2004.
M. A. Puso and T. A. Laursen. A 3D contact smoothing method using Gregory patches. International Journal for Numerical Methods in Engineering, 54(8):1161–1194, 2002.
M. A. Puso and T. A. Laursen. A mortar segment-to-segment contact method for large deformation solid mechanics. Computer Methods in Applied Mechanics and Engineering, 193(6-8):601–629, 2004a.
M. A. Puso and T. A. Laursen. A mortar segment-to-segment frictional contact method for large deformations. Computer Methods in Applied Mechanics and Engineering, 193(45-47):4891–4913, 2004b.
M. A. Puso, T. A. Laursen, and J. Solberg. A segment-to-segment mortar contact method for quadratic elements and large deformations. Computer Methods in Applied Mechanics and Engineering, 197(6-8):555–566, 2008.
L. Qi and J. Sun. A nonsmooth version of Newton’s method. Mathematical Programming, 58(1):353–367, 1993.
E. Rabinowicz. Friction and wear of materials. Wiley, 1995.
A. Reali and T. J. R. Hughes. An introduction to isogeometric collocation methods. In Isogeometric Methods for Numerical Simulation, pages 173–204. Springer, 2015.
J. N. Reddy. An introduction to nonlinear finite element analysis. Oxford University Press, 2004.
L. Rodríguez-Tembleque, R. Abascal, and M. H. Aliabadi. Anisotropic wear framework for 3d contact and rolling problems. Computer Methods in Applied Mechanics and Engineering, 241-244:1–19, 2012.
R. A. Sauer. Enriched contact finite elements for stable peeling computations. International Journal for Numerical Methods in Engineering, 87(6):593–616, 2011.
R. A Sauer and L. De Lorenzis. An unbiased computational contact formulation for 3D friction. International Journal for Numerical Methods in Engineering, 101(4):251–280, 2015.
K. Schweizerhof and A. Konyukhov. Covariant description for frictional contact problems. Computational Mechanics, 35(3):190–213, 2005.
L. R. Scott and S. Zhang. Finite element interpolation of nonsmooth functions satisfying boundary conditions. Mathematics of Computation, 54:483–492, 1990.
A. Seitz, A. Popp, and W. A Wall. A semi-smooth newton method for orthotropic plasticity and frictional contact at finite strains. Computer Methods in Applied Mechanics and Engineering, 285:228–254, 2015.
A. Seitz, P. Farah, J. Kremheller, B. I Wohlmuth, W. A Wall, and A. Popp. Isogeometric dual mortar methods for computational contact mechanics. Computer Methods in Applied Mechanics and Engineering, 301:259–280, 2016.
A. Seitz, W. A. Wall, and A. Popp. A computational approach for thermo-elasto-plastic frictional contact based on a monolithic formulation using non-smooth nonlinear complementarity functions. Advanced Modeling and Simulation in Engineering Sciences, 5:5, 2018.
I. Serre, M. Bonnet, and R. M. Pradeilles-Duval. Modelling an abrasive wear experiment by the boundary element method. Comptes Rendus de l’Académie des Sciences-Series IIB-Mechanics, 329(11):803–808, 2001.
P. Seshaiyer and M. Suri. hp submeshing via non-conforming finite element methods. Computer Methods in Applied Mechanics and Engineering, 189(3):1011–1030, 2000.
G. K. Sfantos and M. H. Aliabadi. Wear simulation using an incremental sliding boundary element method. Wear, 260(9-10):1119 – 1128, 2006.
G. K. Sfantos and M. H. Aliabadi. A boundary element formulation for three-dimensional sliding wear simulation. Wear, 262(5-6):672 – 683, 2007.
J. C. Simo. A framework for finite strain elastoplasticity based on maximum plastic dissipation and the multiplicative decomposition: Part I. Continuum formulation. Computer Methods in Applied Mechanics and Engineering, 66(2):199–219, 1988.
J. C. Simo and T. J. R. Hughes. Computational inelasticity. Springer, 1998.
J. C. Simo and T. A. Laursen. An augmented Lagrangian treatment of contact problems involving friction. Computers & Structures, 42(1):97–116, 1992.
J. C. Simo, P. Wriggers, and R. L. Taylor. A perturbed Lagrangian formulation for the finite element solution of contact problems. Computer Methods in Applied Mechanics and Engineering, 50(2):163–180, 1985.
J. C. Simo, N. Tarnow, and K. K. Wong. Exact energy-momentum conserving algorithms and symplectic schemes for nonlinear dynamics. Computer Methods in Applied Mechanics and Engineering, 100(1):63–116, 1992.
L. Stainier and M. Ortiz. Study and validation of a variational theory of thermo-mechanical coupling in finite visco-plasticity. International Journal of Solids and Structures, 47(5):705–715, 2010.
N. Strömberg. An augmented lagrangian method for fretting problems. European Journal of Mechanics – A/Solids, 16:573–593, 1996.
N. Strömberg, L. Johansson, and A. Klarbring. Derivation and analysis of a generalized standard model for contact, friction and wear. International Journal of Solids and Structures, 33(13):1817–1836, 1996.
S. Stupkiewicz. An ALE formulation for implicit time integration of quasi-steady-state wear problems. Computer Methods in Applied Mechanics and Engineering, 260:130–142, 2013.
R. L. Taylor, J. C. Simo, O. C. Zienkiewicz, and A. C. H. Chan. The patch test: A condition for assessing FEM convergence. International Journal for Numerical Methods in Engineering, 22(1):39–62, 1986.
I. Temizer. Multiscale thermomechanical contact: computational homogenization with isogeometric analysis. International Journal for Numerical Methods in Engineering, 97(8):582–607, 2014.
I. Temizer, P. Wriggers, and T. J. R. Hughes. Contact treatment in isogeometric analysis with NURBS. Computer Methods in Applied Mechanics and Engineering, 200(9–12):1100–1112, 2011.
I. Temizer, P. Wriggers, and T. J. R. Hughes. Three-dimensional mortar-based frictional contact treatment in isogeometric analysis with NURBS. Computer Methods in Applied Mechanics and Engineering, 209–212:115–128, 2012.
S. P. Timoshenko and J. N. Goodier. Theory of elasticity. McGraw-Hill, 1970.
M. Tur, F. J. Fuenmayor, and P. Wriggers. A mortar-based frictional contact formulation for large deformations using Lagrange multipliers. Computer Methods in Applied Mechanics and Engineering, 198(37-40):2860–2873, 2009.
M. Tur, E. Giner, F.J. Fuenmayor, and P. Wriggers. 2d contact smooth formulation based on the mortar method. Computer Methods in Applied Mechanics and Engineering, 247-248:1–14, 2012.
R. Unger, M. C. Haupt, and P. Horst. Application of Lagrange multipliers for coupled problems in fluid and structural interactions. Computers & Structures, 85(11-14):796–809, 2007.
J. R. Williams and R. O’Connor. Discrete element simulation and the contact problem. Archives of Computational Methods in Engineering, 6(4):279–304, 1999.
B. I. Wohlmuth. A mortar finite element method using dual spaces for the Lagrange multiplier. SIAM Journal on Numerical Analysis, 38(3):989–1012, 2000.
B. I. Wohlmuth. Discretization methods and iterative solvers based on domain decomposition. Springer-Verlag Berlin Heidelberg, 2001.
B. I. Wohlmuth. Variationally consistent discretization schemes and numerical algorithms for contact problems. Acta Numerica, 20:569–734, 2011.
B. I. Wohlmuth, A. Popp, M. W. Gee, and W. A. Wall. An abstract framework for a priori estimates for contact problems in 3D with quadratic finite elements. Computational Mechanics, 49:735–747, 2012.
P. Wriggers. Computational contact mechanics. Springer-Verlag Berlin Heidelberg, 2006.
P. Wriggers and C. Miehe. Contact constraints within coupled thermomechanical analysis - a finite element model. Computer Methods in Applied Mechanics and Engineering, 113(3):301–319, 1994.
P. Wriggers and O. Scherf. An adaptive finite element algorithm for contact problems in plasticity. Computational Mechanics, 17(1):88–97, 1995.
P. Wriggers and G. Zavarise. On contact between three-dimensional beams undergoing large deflections. Communications in Numerical Methods in Engineering, 13(6):429–438, 1997.
P. Wriggers, T. Vu Van, and E. Stein. Finite element formulation of large deformation impact-contact problems with friction. Computers & Structures, 37(3):319–331, 1990.
P. Wriggers, L. Krstulovic-Opara, and J. Korelc. Smooth C1-interpolations for two-dimensional frictional contact problems. International Journal for Numerical Methods in Engineering, 51(12):1469–1495, 2001.
H. L. Xing and A. Makinouchi. Three dimensional finite element modeling of thermomechanical frictional contact between finite deformation bodies using R-minimum strategy. Computer Methods in Applied Mechanics and Engineering, 191(37):4193–4214, 2002.
B. Yang and T. A. Laursen. A contact searching algorithm including bounding volume trees applied to finite sliding mortar formulations. Computational Mechanics, 41(2):189–205, 2008.
B. Yang and T. A. Laursen. A mortar-finite element approach to lubricated contact problems. Computer Methods in Applied Mechanics and Engineering, 198(47-48):3656–3669, 2009.
B. Yang, Tod A. Laursen, and X. Meng. Two dimensional mortar contact methods for large deformation frictional sliding. International Journal for Numerical Methods in Engineering, 62(9):1183–1225, 2005.
Q. Yang, L. Stainier, and M. Ortiz. A variational formulation of the coupled thermo-mechanical boundary-value problem for general dissipative solids. Journal of the Mechanics and Physics of Solids, 54(2):401–424, 2006.
G. Zavarise and P. Wriggers. Contact with friction between beams in 3-D space. International Journal for Numerical Methods in Engineering, 49(8):977–1006, 2000.
G. Zavarise, P. Wriggers, E. Stein, and B. A. Schrefler. Real contact mechanisms and finite element formulation - a coupled thermomechanical approach. International Journal for Numerical Methods in Engineering, 35(4):767–785, 1992.
O. C. Zienkiewicz and R. L. Taylor. The finite element method for solid and structural mechanics. Elsevier Butterworth-Heinemann, 2005.
O. C. Zienkiewicz, R. L. Taylor, and J. Z. Zhu. The finite element method: Its basis & fundamentals. Elsevier Butterworth-Heinemann, 2005.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 CISM International Centre for Mechanical Sciences
About this chapter
Cite this chapter
Popp, A. (2018). State-of-the-Art Computational Methods for Finite Deformation Contact Modeling of Solids and Structures. In: Popp, A., Wriggers, P. (eds) Contact Modeling for Solids and Particles. CISM International Centre for Mechanical Sciences, vol 585. Springer, Cham. https://doi.org/10.1007/978-3-319-90155-8_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-90155-8_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-90154-1
Online ISBN: 978-3-319-90155-8
eBook Packages: EngineeringEngineering (R0)


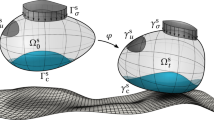




















 2017 John Wiley & Sons, Ltd.
2017 John Wiley & Sons, Ltd.

