Segment-based vs. element-based integration for mortar methods in computational contact mechanics

Abstract

Mortar finite element methods provide a very convenient and powerful discretization framework for geometrically nonlinear applications in computational contact mechanics, because they allow for a variationally consistent treatment of contact conditions (mesh tying, non-penetration, frictionless or frictional sliding) despite the fact that the underlying contact surface meshes are non-matching and possibly also geometrically non-conforming. However, one of the major issues with regard to mortar methods is the design of adequate numerical integration schemes for the resulting interface coupling terms, i.e. curve integrals for 2D contact problems and surface integrals for 3D contact problems. The way how mortar integration is performed crucially influences the accuracy of the overall numerical procedure as well as the computational efficiency of contact evaluation. Basically, two different types of mortar integration schemes, which will be termed as segment-based integration and element-based integration here, can be found predominantly in the literature. While almost the entire existing literature focuses on either of the two mentioned mortar integration schemes without questioning this choice, the intention of this paper is to provide a comprehensive and unbiased comparison. The theoretical aspects covered here include the choice of integration rule, the treatment of boundaries of the contact zone, higher-order interpolation and frictional sliding. Moreover, a new hybrid scheme is proposed, which beneficially combines the advantages of segment-based and element-based mortar integration. Several numerical examples are presented for a detailed and critical evaluation of the overall performance of the different schemes within several well-known benchmark problems of computational contact mechanics.

1 Introduction

Computational contact analysis of strongly nonlinear systems is a fundamental aspect of many problem classes in engineering and applied sciences. Robust discretization schemes for such scenarios have been a field of extensive research over the last years. Today, mortar methods are undoubtedly the most preferred choice for robust finite element discretization in computational contact mechanics. The mortar finite element approach was originally introduced in the context of domain decomposition techniques [3] and its main feature is the imposition of interfacial constraints in a weak (weighted) sense instead of a strong, pointwise enforcement as in collocation methods (e.g. node-to-segment approach). Hence, mortar contact formulations can also be interpreted as a special kind of segment-to-segment approach [41]. The first mortar contact formulations can be found in the regime of small deformations, see [2, 24]. These algorithms have been successfully extended to finite deformations with and without frictional effects, see e.g. [30, 36, 37, 55]. Equally important for the overall performance of the resulting contact formulation is the method of constraint enforcement. Well-known approaches are the penalty, augmented Lagrange and Lagrange multiplier method. In this contribution, we start from a Lagrange multiplier based constraint enforcement, which initially results in an increased number of primary unknowns but guarantees the exact fulfillment of the discrete contact constraints. The disadvantage of an increased system size can be avoided by employing so-called dual Lagrange multiplier shape functions based on a special biorthogonality condition, see [31, 32]. The contact constraints are then equivalently reformulated within so-called nonlinear complementarity functions (NCP), and the entire nonlinear system is solved using a semi-smooth Newton method [4, 16]. Thus, our approach yields a solution algorithm that is closely related, yet not entirely identical, to the one resulting from the classical augmented Lagrange formulation [1, 28] in combination with generalized Newton methods.

The mortar-typical weak definition of the contact constraints requires an integration of quantities of both involved bodies over the discrete contact surface representation of one of them (so-called slave side). Considering the most commonly used first-order elements, it becomes obvious that the locally supported shape functions have kinks at the element nodes and edges. Therefore, the in general non-matching contact interfaces of the bodies inevitably lead to a numerical integration over discontinuities. The evaluation of these integrals is one of the main challenges of mortar methods. The most intuitive way to perform the integration is shown in the left subfigure of Fig. 1 and is based on subdividing each slave side contact element into segments having no discontinuities within their domain, see for example [29, 35]. This procedure will be termed segment-based integration in the following and can be carried out for two-dimensional problems with acceptable computational costs. However, it is both intricate and costly for the three-dimensional case. Due to the high complexity of implementation and the computational cost of evaluation, a second commonly employed integration method was suggested in [10, 11] and is schematically shown in the right subfigure of Fig. 1. Here, the occurring discontinuities are ignored, and one tries to minimize the resulting integration error by employing high-order integration rules. Due to its elementwise procedure without subdividing the element, this method is termed element-based integration.

Fig. 1

The two most commonly used integration schemes for mortar methods: segment-based integration (left) and element-based integration (right)

Over the last years, the research focus shifted from the fundamentals of mortar methods to special applications and improvements of these methods, such as smoothing procedures [48] and isogeometric analysis [6, 7, 45, 46]. However, all of these further investigations postulate just one of the introduced integration methods as algorithmic basis without considering possible drawbacks. To the best of the authors’ knowledge, there exists only one previous contribution, which at least gives a short comparison of the two major integration methods [9]. However, the focus there is mainly on a simple two-dimensional patch test problem, and mortar methods are not discussed. Therefore, the idea and new scientific contribution of this paper is to finally provide a fair and objective comparison of the two most commonly applied integration approaches in the context of mortar contact formulations with respect to the choice of proper integration rules, their extension to quadratically interpolated elements, their applicability for frictional problems as well as their fundamental properties in terms of accuracy and computational efficiency. In addition, a novel combination of the two methods is suggested, which unifies the best features of both while eliminating their shortcomings.

The paper is organized as follows: in Sect. 2, we provide a fundamental description of the two body contact problem in the context of finite deformation kinematics. The evaluation of the mortar integrals is explained and illustrated in detail for both integration methods in Sect. 3. In Sect. 4, a theoretical comparison of the two integration methods is given with respect to some important aspects of contact problems. This theoretical discussion will be evaluated and complemented with quantitative and qualitative numerical results by means of various examples in Sect. 5. Finally, some conclusions are given in Sect. 6.

2 Problem setting

Throughout this paper, finite deformation unilateral contact problems of two elastic bodies in 3D space are considered. Thus, the underlying mechanical foundation consists of the initial-boundary value problem (IBVP) of nonlinear elastodynamics, the classical Karush–Kuhn–Tucker (KKT) conditions of non-penetration and the frictional contact constraints according to Coulomb’s law. The two-dimensional case, frictionless unilateral contact as well as fully tied contact, also commonly referred to as mesh tying, are contained in our general problem statement as special cases, and will be studied in some of the numerical examples in Sect. 5. Moreover, a generalization to multiple bodies and self contact, although not considered here, would be rather straightforward and mostly a matter of efficient search algorithms, see e.g. [53, 54].

2.1 Strong formulation

The domains $\varOmega _0^{(i)} \subset \mathbb {R}^3$ and $\varOmega _t^{(i)} \subset \mathbb {R}^3$, $i=1,2$, represent two separate bodies in the reference and current configuration, respectively. To allow for the usual Dirichlet and Neumann boundary conditions as well as contact interaction, the surfaces $\partial \varOmega _0^{(i)}$ are divided into three disjoint subsets: $\varGamma _{\mathsf {u}}^{(i)}$ is the Dirichlet boundary with prescribed displacements $\hat{\varvec{u}}^{(i)}$, $\varGamma _{\sigma }^{(i)}$ is the Neumann boundary with given surface tractions $\hat{\varvec{t}}_0^{(i)}$ and $\varGamma _{\mathsf {c}}^{(i)}$ is the potential contact surface. Similarly, the spatial surface descriptions $\partial \varOmega _t^{(i)}$ are split into $\gamma _{\mathsf {u}}^{(i)}$, $\gamma _{\sigma }^{(i)}$ and $\gamma _{\mathsf {c}}^{(i)}$. Retaining a customary nomenclature in contact mechanics, $\varGamma _{\mathsf {c}}^{(1)}$ is referred to as slave surface and $\varGamma _{\mathsf {c}}^{(2)}$ as master surface.

Based on the displacement vector $\mathbf {u}^{(i)} = \varvec{x}^{(i)} - \varvec{X}^{(i)}$, where reference and current configuration are denoted as $\varvec{X}^{(i)}$ and $\varvec{x}^{(i)}$, respectively, the material deformation gradient ${\varvec{F}}^{(i)} = \frac{\partial \varvec{x}^{(i)}}{\partial \varvec{X}^{(i)}}$ can be introduced as fundamental nonlinear deformation measure. Material nonlinearities are exemplarily considered by assuming existence of an isotropic hyperelastic strain energy $\varPsi$, with $\mathbf {S}= \frac{\partial \varPsi }{\partial \mathbf {E}}$ and $\mathbb {C} = \frac{\partial ^2 \varPsi }{\partial \mathbf {E}^2}$. Herein, $\mathbb {C}$ is the fourth-order constitutive tensor, introducing a possibly nonlinear relationship between the second Piola–Kirchhoff stress tensor ${\varvec{S}}$ and the Green–Lagrange strain tensor ${\varvec{E}} = \frac{1}{2} \left( {\varvec{F}}^{\mathsf {T}} \, {\varvec{F}} - {\varvec{I}} \right)$. The first Piola–Kirchhoff stress tensor ${\varvec{P}}$ is determined via the relationship ${\varvec{P}} = {\varvec{F}} {\varvec{S}}$.

On each subdomain $\varOmega _0^{(i)}$ the initial boundary value problem of finite deformation elastodynamics needs to be satisfied, viz.

$$\begin{aligned} {\mathrm {Div}} {\varvec{P}}^{(i)} + \hat{\varvec{b}}_0^{(i)} = \rho _0^{(i)} \ddot{\varvec{u}}^{(i)}&\quad \text {in} \; \varOmega _0^{(i)} \times [0,T], \end{aligned}$$

(1)

$$\begin{aligned} \varvec{u}^{(i)} = \hat{\varvec{u}}^{(i)}&\quad \text {on}\; \varGamma _{{\mathsf {u}}}^{(i)} \times [0,T], \end{aligned}$$

(2)

$$\begin{aligned} {\varvec{P}}^{(i)} \varvec{N}^{(i)} = \hat{\varvec{t}}_0^{(i)}&\quad \text {on}\; \varGamma _{\sigma }^{(i)} \times [0,T], \end{aligned}$$

(3)

$$\begin{aligned} \varvec{u}^{(i)}(t=0) = \hat{\varvec{u}}_0^{(i)}&\quad \text {in} \; \varOmega _0^{(i)}, \end{aligned}$$

(4)

$$\begin{aligned} \dot{\varvec{u}}^{(i)}(t=0) = \hat{\dot{\varvec{u}}}_0^{(i)}&\quad \text {in} \; \varOmega _0^{(i)}. \end{aligned}$$

(5)

The contact constraints in normal direction are given in form of the well-known KKT conditions, while frictional sliding is formulated according to Coulomb’s law. Both sets of conditions are stated here as follows:

$$\begin{aligned}&g_n \ge 0, \quad p_n \le 0, \quad p_n \, g_n = 0 \qquad \text {on} \; \gamma _{c}^{(1)} \times [0,T], \end{aligned}$$

(6)

$$\begin{aligned}&\varPhi := \Vert \varvec{t}_{\tau } \Vert - \mathfrak {F} \vert p_n \vert \le 0, \quad \varvec{v}_{\tau ,rel} + \beta \varvec{t}_{\tau } = \varvec{0}, \nonumber \\&\beta \ge 0, \quad \varPhi \beta = 0 \quad \text {on} \; \gamma _{c}^{(1)} \times [0,T]. \end{aligned}$$

(7)

Here, $g_n$ represents the nonlinear gap function, which is a fundamental measure for proximity and penetration of the two contacting bodies. Typically, the gap function is determined by the so-called closest-point projection (CPP) procedure, see e.g. [19] for a comprehensive review. In addition, a local coordinate system consisting of the normal vector $\varvec{n}$ and two tangent vectors $\varvec{\tau }^{\xi }$ and $\varvec{\tau }^{\eta }$ is defined on the slave surface, with the normal and tangential components of the slave side contact traction $\varvec{t}_{c}^{(1)}$ being denoted as $p_n$ and $\varvec{t}_{\tau }$, respectively. In (7), $\Vert \ \cdot \, \Vert$ denotes the $L^2$-norm in $\mathbb {R}^3$, $\mathfrak {F} \ge 0$ is the friction coefficient and $\beta \ge 0$ is a scalar parameter. Finally, $\varvec{v}_{\tau ,rel}$ is the relative tangential velocity of slave and master surfaces and thus the primary kinematic quantity for frictional sliding in tangential direction.

2.2 Weak formulation

For deriving a weak variational formulation, the solution spaces $\varvec{\mathcal {U}}^{(i)}$ and weighting spaces $\varvec{\mathcal {V}}^{(i)}$ are defined as

$$\begin{aligned} \varvec{\mathcal {U}}^{(i)}&= \left\{ \varvec{u}^{(i)} \in H^1 (\varOmega ) \; \vert \; \varvec{u}^{(i)} = \hat{\varvec{u}}^{(i)} \; \text {on} \; \varGamma _{u} \right\} , \end{aligned}$$

(8)

$$\begin{aligned} \varvec{\mathcal {V}}^{(i)}&= \left\{ \delta \varvec{u}^{(i)} \in H^1 (\varOmega ) \; \vert \; \delta \varvec{u}^{(i)} = \varvec{0} \; \text {on} \; \varGamma _{u} \right\} . \end{aligned}$$

(9)

Moreover, the Lagrange multiplier vector $\varvec{\lambda }=-\varvec{t}_{\mathsf {c}}^{(1)}$, which represents the negative slave side contact traction $\varvec{t}_{\mathsf {c}}^{(1)}$ and is supposed to enforce the contact constraints (6) and (7), is chosen from the convex cone $\varvec{\mathcal {M}}(\varvec{\lambda }) \subset \varvec{\mathcal {M}}$ given by

$$\begin{aligned} \varvec{\mathcal {M}}(\varvec{\lambda })&= \left\{ \varvec{\mu } \in \varvec{\mathcal {M}} \; \vert \; \langle \varvec{\mu } , \varvec{v} \rangle _{\gamma _{\mathsf {c}}^{(1)}} \le \langle \mathfrak {F} \lambda _{\mathsf {n}} , \Vert \varvec{v}_{\tau } \Vert \rangle _{\gamma _{\mathsf {c}}^{(1)}} , \right. \nonumber \\&\quad \left. \varvec{v} \in \varvec{\mathcal {W}} \; \text {with} \; v_{\mathsf {n}} \le 0 \right\} . \end{aligned}$$

(10)

Herein, $\langle \cdot , \cdot \rangle _{\gamma _{\mathsf {c}}^{(1)}}$ stands for the scalar or vector-valued duality pairing between $H^{-1/2}$ and $H^{1/2}$ on $\gamma _{\mathsf {c}}^{(1)}$. Moreover, $\varvec{\mathcal {M}}$ is the dual space of the trace space $\varvec{\mathcal {W}}^{(1)}$ of $\varvec{\mathcal {V}}^{(1)}$ restricted to $\gamma _{\mathsf {c}}^{(1)}$, i.e. $\mathcal {M} = H^{-1/2}(\gamma _{\mathsf {c}}^{(1)})$ and $\mathcal {W}^{(1)} = H^{1/2}(\gamma _{\mathsf {c}}^{(1)})$, where $\mathcal {M}$ and $\mathcal {W}^{(1)}$ denote single scalar components of the corresponding vector-valued spaces $\varvec{\mathcal {M}}$ and $\varvec{\mathcal {W}}$. Thus, the definition of the solution cone for the Lagrange multipliers in (10) satisfies the conditions on $\varvec{\lambda }$ of the Coulomb friction law in a weak sense.

Based on these considerations, the weak saddle point type formulation follows as: Find $\varvec{u}^{(i)} \in \varvec{\mathcal {U}}^{(i)}$ and $\varvec{\lambda } \in \varvec{\mathcal {M}}(\lambda )$ such that

$$\begin{aligned}&-\delta \mathcal {W}_{kin,int,ext}(\varvec{u}^{(i)},\delta \varvec{u}^{(i)}) - \delta \mathcal {W}_{co}(\varvec{\lambda },\delta \varvec{u}^{(i)}) = 0\nonumber \\&\quad \forall \; \delta \varvec{u}^{(i)} \in \varvec{\mathcal {V}}^{(i)}, \end{aligned}$$

(11)

$$\begin{aligned}&\delta \mathcal {W}_{\lambda }(\varvec{u}^{(i)},\delta \varvec{\lambda }) \ge 0 \nonumber \\&\quad \forall \; \delta \varvec{\lambda } \in \varvec{\mathcal {M}}(\lambda ). \end{aligned}$$

(12)

Herein, the kinetic contribution $\delta \mathcal {W}_{kin}$ as well as the internal and external contributions $\delta \mathcal {W}_{int}$ and $\delta \mathcal {W}_{ext}$ to the overall virtual work are defined as usual in nonlinear solid mechanics and thus a detailed description is omitted here. Instead, only the contact contribution $\delta \mathcal {W}_{co}$ and the weak constraints $\delta \mathcal {W}_{\lambda }$, including non-penetration and frictional sliding conditions, are given in full length as

$$\begin{aligned}&-\delta \mathcal {W}_{co} = \int _{\gamma _c^{(1)}} \varvec{\lambda } (\delta \varvec{u}^{(1)} - \delta \varvec{u}^{(2)} \circ \chi ) \, \mathrm {d} A, \end{aligned}$$

(13)

$$\begin{aligned}&\delta \mathcal {W}_{\lambda } = \int _{\gamma _c^{(1)}} (\delta \lambda _n - \lambda _n) \, g_n \, \mathrm {d} A \!-\!\int _{\gamma _c^{(1)}} (\delta \varvec{\lambda }_{\tau } - \varvec{\lambda }_{\tau }) \, \varvec{v}_{\tau ,rel} \, \mathrm {d} A, \end{aligned}$$

(14)

where $\chi : \gamma _{c}^{(1)} \rightarrow \gamma _{c}^{(2)}$ defines a suitable mapping from slave to master side of the contact surface. This mapping is necessary since $\gamma _{c}^{(1)}$ and $\gamma _{c}^{(2)}$ cannot be guaranteed to be identical for unilateral contact but may rather be geometrically non-conforming. Note that the integral expressions in the coupling bilinear forms $\delta \mathcal {W}_{co}$ and $\delta \mathcal {W}_{\lambda }$ would need to be replaced by duality pairings $\langle \cdot , \cdot \rangle _{\gamma _c^{(1)}}$ in order to be absolutely mathematically concise. However, the integral diction in (13) and (14) is preferred here due to readability. The equivalence of the strong pointwise conditions given in (6) and (7) and the corresponding variational inequalities in (14) can readily be proven, see e.g. [50].

2.3 Mortar finite element discretization

For the spatial discretization of the unilateral contact problem (11) and (12), standard isoparametric finite elements with first-order and second-order interpolation are employed. This defines the usual finite dimensional subspaces $\varvec{\mathcal {U}}^{(i)}_h$ and $\varvec{\mathcal {V}}^{(i)}_h$ being approximations of $\varvec{\mathcal {U}}^{(i)}$ and $\varvec{\mathcal {V}}^{(i)}$, respectively. With the focus being on the finite element discretization of the contact terms here, only the displacement and Lagrange multiplier interpolations on $\varGamma _{{\mathsf {c}},h}^{(i)}$ will be considered in the following, with the subscript $(\cdot )_h$ referring to a spatially discretized quantity. The displacement interpolation is given as

$$\begin{aligned} \mathbf {u}^{(1)}_h\vert _{\varGamma ^{(1)}_{c,h}} = \sum _{k=1}^{n^{(1)}} N_k^{(1)} \; {\varvec{\mathsf {d}}}_k^{(1)}, \quad \mathbf {u}^{(2)}_h\vert _{\varGamma ^{(2)}_{c,h}} = \sum _{l=1}^{n^{(2)}} N_l^{(2)} \; {\varvec{\mathsf {d}}}_l^{(2)}. \end{aligned}$$

(15)

Herein, the total number of slave nodes on $\varGamma ^{(1)}_{{\mathsf {c}},h}$ is $n^{(1)}$, and the total number of master nodes on $\varGamma ^{(2)}_{{\mathsf {c}},h}$ is $n^{(2)}$. Discrete nodal displacements are given by ${\varvec{\mathsf {d}}}_k^{(1)}$ and ${\varvec{\mathsf {d}}}_l^{(2)}$. The shape functions $N_k^{(1)}$ and $N_l^{(2)}$ are defined with respect to the usual finite element parameter space, commonly denoted as $\varvec{\xi }^{(i)}=(\xi ^{(i)},\eta ^{(i)})$ for three-dimensional problems (i.e. 2D contact interfaces).

Discretization of the Lagrange multiplier vector $\varvec{\lambda }$ is based on a discrete Lagrange multiplier space $\varvec{\mathcal {M}}_h(\varvec{\lambda }_h)$ being an approximation of $\varvec{\mathcal {M}}(\varvec{\lambda })$. All details concerning the choice of $\varvec{\mathcal {M}}_h(\varvec{\lambda }_h)$, and especially concerning the two most common families of standard and dual Lagrange multipliers, can be found in the abundant literature on this topic. Exemplarily, the reader is referred to [35, 36] for standard Lagrange multiplier interpolation and [17, 49] for dual Lagrange multiplier interpolation within 3D mortar contact formulations. For this contribution, it is of little importance which of the two variants is employed and we will actually show numerical examples for both in Sect. 5. Thus, only a very general notation is given at this point:

$$\begin{aligned} \varvec{\lambda }_h = \sum _{j=1}^{m^{(1)}} \varPhi _j \, {\varvec{\mathsf {\lambda }}}_j, \end{aligned}$$

(16)

with the (standard or dual) shape functions $\varPhi _j$ and the discrete nodal Lagrange $\lambda$ multipliers ${\varvec{\mathsf {\lambda }}}_j$. The total number of slave nodes carrying additional Lagrange multiplier degrees of freedom is $m^{(1)}$. Typically for mortar methods, every slave node also serves as coupling node, and thus in the majority of cases $m^{(1)} = n^{(1)}$ will hold. While this is also assumed for all applications in this paper, we nevertheless point out that it may be favorable to chose $m^{(1)} < n^{(1)}$ in certain cases, e.g. in the context of second-order finite element interpolation, see [31, 37, 51].

Inserting the finite element discretizations (15) and (16) into the weak formulation (13) allows to define the usual mortar matrices ${\varvec{\mathsf {D}}}$ and ${\varvec{\mathsf {M}}}$ with nodal blocks

$$\begin{aligned} {\varvec{\mathsf {D}}}[j,k]&= D_{jk} \, \mathbf {I}_3 = \int _{\gamma _{c,h}^{(1)}} \varPhi _j N_k^{(1)} \mathrm {d} \gamma \, \mathbf {I}_3 \; , \nonumber \\&\quad \quad j=1,\ldots ,n^{(1)}, \;\; k=1,\ldots ,n^{(1)} \; , \end{aligned}$$

(17)

$$\begin{aligned} {\varvec{\mathsf {M}}}[j,l]&= M_{jl} \, \mathbf {I}_3 =\int _{\gamma _{c,h}^{(1)}} \varPhi _j (N_l^{(2)} \circ \chi _h) \, \mathrm {d} \gamma \, \mathbf {I}_3, \nonumber \\&\quad \quad j=1,\ldots ,n^{(1)}, \;\; l=1,\ldots ,n^{(2)}, \end{aligned}$$

(18)

with the identity $\mathbf {I}_3 \in \mathbb {R}^{3 \times 3}$. Moreover, $\chi _h: \gamma _{c,h}^{(1)} \rightarrow \gamma _{c,h}^{(2)}$ defines a discrete approximation of the actual contact mapping $\chi$, see e.g. [8, 33] and Sect. 3.

Similarly, space-discretized forms of the weak non-penetration and frictional sliding constraints can be derived by inserting (15) and (16) into (14). This yields the so-called nodal weighted gaps $\tilde{g}_j$ as well as the nodal relative tangential velocities $(\tilde{{\varvec{\mathsf {v}}}}_{\tau ,{\mathsf {rel}}})_j$, i.e.

$$\begin{aligned}&\tilde{g}_j = {\varvec{\mathsf {n}}}_j \cdot \left[ \sum _{l=1}^{n^{(2)}} {\varvec{\mathsf {M}}}[j,l] \bar{{\varvec{\mathsf {x}}}}_l^{(2)} - \sum _{k=1}^{n^{(1)}} {\varvec{\mathsf {D}}}[j,k] \bar{{\varvec{\mathsf {x}}}}_k^{(1)} \right] , \end{aligned}$$

(19)

$$\begin{aligned}&(\tilde{{\varvec{\mathsf {v}}}}_{\tau ,{\mathsf {rel}}})_j = (\mathbf {I} - {\varvec{\mathsf {n}}}_j \otimes {\varvec{\mathsf {n}}}_j) \nonumber \\&\quad \cdot \left[ \sum _{l=1}^{n^{(2)}} \dot{{\varvec{\mathsf {M}}}}[j,l] \bar{{\varvec{\mathsf {x}}}}_l^{(2)} - \sum _{k=1}^{n^{(1)}} \dot{{\varvec{\mathsf {D}}}}[j,k] \bar{{\varvec{\mathsf {x}}}}_k^{(1)} \right] . \end{aligned}$$

(20)

Herein, ${\varvec{\mathsf {n}}}_j$ is the discrete nodal normal vector at slave node $j$, and $\bar{{\varvec{\mathsf {x}}}}_k^{(1)}$ and $\bar{{\varvec{\mathsf {x}}}}_l^{(2)}$ represent the discrete nodal coordinates on slave and master side, respectively. The discrete relative tangential velocities $(\tilde{{\varvec{\mathsf {v}}}}_{\tau ,rel})_j$ contain time derivatives of mortar matrices, which are discretized in time by introducing a local implicit time stepping procedure of backward Euler type:

$$\begin{aligned} \dot{{\varvec{\mathsf {D}}}}[j,k] \approx \frac{{\varvec{\mathsf {D}}}[j,k](t_n) - {\varvec{\mathsf {D}}}[j,k](t_{n-1})}{\varDelta t}, \nonumber \\ \dot{{\varvec{\mathsf {M}}}}[j,l] \approx \frac{{\varvec{\mathsf {M}}}[j,l](t_n) - {\varvec{\mathsf {M}}}[j,l](t_{n-1})}{\varDelta t}, \end{aligned}$$

(21)

with the discrete time increment ${\varDelta t} = t_n - t_{n-1}$. This formulation allows to satisfy the fundamental requirement of frame indifference of the kinematic measures associated with frictional sliding, see e.g. [13, 55]. Multiplying (21) with the time increment ${\varDelta t}$ yields the so-called discrete nodal slip increment

$$\begin{aligned} (\tilde{{\varvec{\mathsf {u}}}}_{\tau ,{\mathsf {rel}}})_j&= (\mathbf {I} - {\varvec{\mathsf {n}}}_j \otimes {\varvec{\mathsf {n}}}_j)\nonumber \\&\quad \cdot \left[ \sum _{l=1}^{n^{(2)}}\Big ({\varvec{\mathsf {M}}}[j,l](t_n) -{\varvec{\mathsf {M}}}[j,l](t_{n-1})\Big )\bar{{\varvec{\mathsf {x}}}}_l^{(2)}\right. \end{aligned}$$

(22)

$$\begin{aligned}&\quad \left. -\sum _{k=1}^{n^{(1)}} \Big ({\varvec{\mathsf {D}}}[j,k](t_n) - {\varvec{\mathsf {D}}}[j,k](t_{n-1})\Big )\bar{{\varvec{\mathsf {x}}}}_k^{(1)} \right] . \end{aligned}$$

(23)

All details concerning these derivations have been presented in our previous contributions in [13, 29, 30].

Here, we directly proceed with the final semi-discrete problem formulation resulting from mortar finite element discretization, viz.

$$\begin{aligned}&{\varvec{\mathsf {r}}} := {\varvec{\mathsf {f}}}_{kin} (\ddot{{\varvec{\mathsf {d}}}}) + {\varvec{\mathsf {f}}}_{int} ({\varvec{\mathsf {d}}}) - {\varvec{\mathsf {f}}}_{ext} + {\varvec{\mathsf {f}}}_c ({\varvec{\mathsf {d}}},{\varvec{\mathsf {\lambda }}}) = {\varvec{\mathsf {0}}}, \end{aligned}$$

(24)

$$\begin{aligned}&\tilde{g}_{j} \ge 0 \, \quad \lambda _{n,j} \ge 0, \quad \lambda _{n,j} \, \tilde{g}_{j} = 0, \quad j=1,\ldots ,n^{(1)} , \end{aligned}$$

(25)

$$\begin{aligned}&\varPhi _j := \Vert ({\varvec{\mathsf {\uplambda }}}_{\tau })_j \Vert - \mathfrak {F} \vert (\lambda _n)_j \vert \le 0, \nonumber \\&(\tilde{{\varvec{\mathsf {v}}}}_{\tau ,rel})_j + \beta _j ({\varvec{\mathsf {\uplambda }}}_{\tau })_j = {\varvec{\mathsf {0}}}, \quad \beta _j \ge 0 \; , \quad \varPhi _j \beta _j = 0,\nonumber \\&\qquad j=1,\ldots ,n^{(1)}. \end{aligned}$$

(26)

where $\lambda _{n,j}$ and ${\varvec{\mathsf {\lambda }}}_{\tau ,j}$ are the normal and tangential components of the discrete nodal Lagrange multiplier vector ${\varvec{\mathsf {\lambda }}}_j$. The nonlinear force residual ${\varvec{\mathsf {r}}}$ comprises contributions from kinetic, internal and external forces ${\varvec{\mathsf {f}}}_{kin} (\ddot{{\varvec{\mathsf {d}}}})$, ${\varvec{\mathsf {f}}}_{int} ({\varvec{\mathsf {d}}})$ and ${\varvec{\mathsf {f}}}_{ext}$ as well as contact forces ${\varvec{\mathsf {f}}}_c ({\varvec{\mathsf {d}}},{\varvec{\mathsf {\lambda }}})$, which are based on the mortar matrices ${\varvec{\mathsf {D}}}$ and ${\varvec{\mathsf {M}}}$. The discrete contact conditions also depend on ${\varvec{\mathsf {D}}}$ and ${\varvec{\mathsf {M}}}$, as can be seen from (19) and (20). Obviously, the essential computational task associated with mortar finite element discretizations is the actual numerical integration of the mortar matrices ${\varvec{\mathsf {D}}}$ and ${\varvec{\mathsf {M}}}$ defined in (17) and (18). All details on such numerical integration procedures can be found in the main part of this paper, i.e. in Sect. 3.

2.4 Global solution algorithm

The semi-discrete problem formulation in (24)–(26) is eventually discretized in time using implicit time integration schemes well-known from structural dynamics, such as the generalized-$\alpha$ method or the generalized energy-momentum method (GEMM), see e.g. [5, 20, 21, 40]. A velocity-update algorithm as proposed in [22] can be applied to assure both energy conservation and exact constraint enforcement in the context of contact interaction, while however sacrificing second-order accuracy in time.

To solve the introduced contact-specific inequality constraints, which represent an additional source of nonlinearity apart from geometrical and material nonlinearities, we follow the idea of so-called primal-dual active set strategies and split the set of all slave nodes $\mathcal {S}$ into an active set $\mathcal {A}$ and an inactive set $\mathcal {I}$. Furthermore, frictional contact requires to split the active set $\mathcal {A}$ into sets of stick nodes $\mathcal {H}$ and slip nodes $\mathcal {G}$. These sets then allow for a reformulation of the discrete contact and friction laws in (25) and (26) within equality constraints for the corresponding nodal sets. To solve the final nonlinear (and non-smooth) contact problem within each time step by Newton–Raphson iterations, we re-interpret the primal-dual active set strategy as semi-smooth Newton method and introduce so-called nodal nonlinear complementarity (NCP) functions, which are a mathematically equivalent replacement of the two sets of inequality constraints in (25) and (26). The NCP function for the normal constraints in (25) is exemplarily shown in Fig. 2 and reads

$$\begin{aligned} C_{nj}({\varvec{\mathsf {\lambda }}}_j,{\varvec{\mathsf {d}}}) = \lambda _{nj} - \text {max}(0, \lambda _{nj} - c_n \tilde{g}_{nj}), \quad c_n>0. \end{aligned}$$

(27)

The normal contact constraints are exactly fulfilled if

$$\begin{aligned} C_{nj}({\varvec{\mathsf {\lambda }}}_j,{\varvec{\mathsf {d}}}) = 0. \end{aligned}$$

(28)

Here, it becomes obvious that the complementarity parameter $c_n$ does not affect the accuracy of results, but only influences the convergence behavior of the semi-smooth Newton method. For the tangential constraints in (26) we employ a formulation introduced in [18] and extended to finite deformation kinematics in [13]. A simplified 2D version of the NCP function is illustrated in Fig. 3, and the full 3D version reads

$$\begin{aligned} C_{\tau j}({\varvec{\mathsf {\lambda }}}_j,{\varvec{\mathsf {d}}})&= \text {max}(\mathfrak {F} (\lambda _{n,j}-c_n\tilde{g}_{nj}) , \vert \vert {\varvec{\mathsf {\lambda }}}_{\tau j} + c_t (\tilde{{\varvec{\mathsf {u}}}}_{\tau ,{\mathsf {rel}}})_{j} \vert \vert ){\varvec{\mathsf {\lambda }}}_{\tau j} \nonumber \\&\quad -\mathfrak {F}\,\text {max}(0, \lambda _{n,j} - c_n \tilde{g}_{nj})({\varvec{\mathsf {\lambda }}}_{\tau j} + c_t (\tilde{{\varvec{\mathsf {u}}}}_{\tau ,{\mathsf {rel}}})_j), \nonumber \\&\quad c_n, c_t > 0. \end{aligned}$$

(29)

As has been the case for the NCP function corresponding to the non-penetration constraint (28), the solution of the tangential constraints can be equivalently expressed as

$$\begin{aligned} C_{\tau j}({\varvec{\mathsf {\lambda }}}_j,{\varvec{\mathsf {d}}}) = 0. \end{aligned}$$

(30)

Again, the complementarity parameters $c_n$ and $c_{\tau }$ do not have an influence the accuracy of results, but merely on the convergence behavior of the semi-smooth Newton method.

Fig. 2

Nodal NCP function $C_{nj}$ for the normal direction (with $c_n=1$). The constraints are fulfilled for $C_{nj} = 0$

Fig. 3

Nodal NCP function $C_{\tau j}$ for the tangential direction (with $c_{\tau }=1$). The constraints are fulfilled for $C_{\tau j}=0$

For the sake of brevity, we do not discuss the resulting global solution algorithm here, but the interested reader is referred to the numerous recent contributions on this topic, see e.g. [13, 15, 17, 29, 30]. A mathematically more rigorous introduction to semi-smooth Newton methods for constrained optimization problems can be found in [1, 4, 16, 38].

The major advantage of the proposed solution algorithm is that all sources of nonlinearities, i.e. finite deformations, nonlinear material behavior as well as frictional contact itself, can be treated within one single iterative scheme. Numerical investigations, see e.g. [17, 18, 30, 31], have shown that the semi-smooth Newton approach allows for a very efficient treatment of small deformation and finite deformation contact problems, also including frictional sliding. Even for relatively large step sizes and fine contacting meshes, the correct active set is usually found after only a few Newton steps. Once the sets remain constant, quadratic convergence is obtained in the limit due to the underlying consistent linearization.

3 Mortar integration

Accurately and efficiently computing the mortar matrices is one of the main challenges of mortar contact algorithms. This is due to the fact that evaluating the second mortar matrix ${\varvec{\mathsf {M}}}$, and thus also the weighted gap $\tilde{g}_n$ and the relative tangential velocity $\tilde{\varvec{v}}_{\tau ,rel}$, requires an integration over the slave contact surface with an integrand containing quantities from both master and slave side. In the case of non-matching meshes, the integrand represents a non-smooth function which cannot be evaluated exactly by using standard Gauss rules. This non-smoothness stems from the locally supported Lagrange polynomials on master and slave side having kinks at the respective element nodes and edges. Over the last years, two commonly used integration schemes have been established to handle the problems mentioned above.

The first method is named segment-based integration scheme in the following and its general idea was first outlined for the classical segment-to-segment contact formulations [41, 56]. Its application the context of 3D mortar contact formulations was first proposed and elaborated in great detail in [24, 34]. Slight adoptions and extensions can for example be found in [30, 33, 35–37]. The method is based on the prevention of all possibly occuring discontinuities in the integrand of mortar matrix ${\varvec{\mathsf {M}}}$ by creating smooth integrable segments (see again Fig. 1). However, it causes considerable effort for implementation and computation. The second method was firstly introduced in [10, 11] and has been used in many different contact specific contributions since then, e.g. in [6, 46, 47]. In contrast to the segment-based method, it completely ignores the occuring discontinuities and accepts that the integration error may therefore increase significantly. Nevertheless, the implementation effort and especially the associated computational costs are significantly reduced. This is achieved by a slave element-wise evaluation of the mortar integrals, which motivates the denomination as element-based integration used in the following.

To our knowledge, all available contributions on mortar based contact formulations just propagate one of the two ideas without discussing possible shortcomings. Thus, this is the first article that provides a fair and objective comparison of these two methods with regards to both accuracy and computational efficiency. To establish a well-founded basis for such a comparison, the actual process of performing mortar integration is presented for both methods in the following.

3.1 Segment-based mortar integration

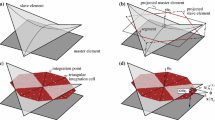
Keeping in mind the idea of integrating just smooth contributions to mortar matrix ${\varvec{\mathsf {M}}}$ over the slave side, we require precise information concerning the position of the involved discontinuities of the integrand. This information is obtained by working with pairs of one slave and master element each. In a first step, both slave and master nodes are projected onto an auxiliary plane. Then, a polygon clipping algorithm is applied in order to determine the overlap of the slave and master element pair, i.e. the region where the integrands in (17) and (18) are $C^1$-continuous. The whole process is illustrated in Fig. 4 and summarized in the algorithm below. Of course, the information which slave and master element pairs have to be considered must first be obtained by an efficient contact search algorithm, see e.g. [53, 54].

Fig. 4

Main steps of the segment-based integration scheme: construct an auxiliary plane (top left), project slave and master nodes onto the auxiliary plane (top right), perform polygon clipping (bottom left), perform Delaunay triangulation and integrate over all created triangular integration cells (bottom right)

Algorithm 1

• 1. Construct an auxiliary plane for numerical integration based on the slave element center ${\varvec{\mathsf {x}}}_0^{(1)}$ and the corresponding unit normal vector ${\varvec{\mathsf {n}}}_0$.

• 2. Project all $n_e^{(1)}$ slave element nodes ${\varvec{\mathsf {x}}}_k^{(1)}$, $k=1,\ldots ,n_e^{(1)}$ along ${\varvec{\mathsf {n}}}_0$ onto the auxiliary plane to create auxiliary slave nodes ${\tilde{{\varvec{\mathsf {x}}}}}_k^{(1)}$.

• 3. Project all $n_e^{(2)}$ master element nodes ${\varvec{\mathsf {x}}}_l^{(1)}$, $l=1,\ldots ,n_e^{(2)}$ along ${\varvec{\mathsf {n}}}_0$ onto the auxiliary plane to create the projected master nodes ${\tilde{{\varvec{\mathsf {x}}}}}_l^{(2)}$.

• 4. Perform polygon clipping in the auxiliary plane to find the overlapping region of projected slave and master element. Clipping algorithms are illustrated in more detail in [12].

• 5. Perform a decomposition of the clip polygon to define easy-to-integrate subdomains which will be used for numerical integration and are therefore called integration cells. If no geometrical subdivision is performed, then the polygon itself represents the sole integration cell.

• 6. Define $n_{int}$ integration points with coordinates $\varvec{\tilde{\xi }}_{g}, \ g=1,\ldots ,n_{int}$ on each integration cell and find the corresponding integration points ${\varvec{\mathsf {\xi }}}_g^{(1)}$ and ${\varvec{\mathsf {\xi }}}_g^{(2)}$ on the slave and master element by an inverse mapping.

• 7. Perform numerical integration of ${\varvec{\mathsf {D}}}[j,k]$ and ${\varvec{\mathsf {M}}}[j,l]$, $j=1,\ldots ,n_e^{(1)}$, $k=1,\ldots ,n_e^{(1)}$ and $l=1,\ldots ,n_e^{(2)}$ on all integration cells

  $$\begin{aligned} {\varvec{\mathsf {D}}}[j,k]&=\sum _{cell=1}^{n_{cell}}\!\left( \sum _{g=1}^{n_{int}} w_g\varPhi _j({\varvec{\mathsf {\xi }}}_g^{(1)}) N_k^{(1)}({\varvec{\mathsf {\xi }}}_g^{(1)})J_{cell}({\varvec{\mathsf {\xi }}}_g^{(1)})\!\right) \!,\\ {\varvec{\mathsf {M}}}[j,l]&=\sum _{cell=1}^{n_{cell}}\!\left( \sum _{g=1}^{n_{int}}w_g \varPhi _j({\varvec{\mathsf {\xi }}}_g^{(1)}) N_l^{(2)}({\varvec{\mathsf {\xi }}}_g^{(2)})J_{cell} ({\varvec{\mathsf {\xi }}}_g^{(1)})\!\right) \!, \end{aligned}$$

  where $J_{cell}, \ cell=1,\ldots ,n_{cell}$ represents the integration cell Jacobian determinant and $n_{cell}$ is the number of integration cells. Furthermore, $n_e^{(i)}$ is the number of the displacement nodes associated with the slave or master element.

The decomposition mentioned in step 5 is carried out to create integration cells with well-known predefined integration rules. To our knowledge, all contributions in the available literature that employ segment-based integration are using some kind of triangulation to create triangular subdomains. Here, the most efficient method is Delaunay triangulation as illustrated exemplarily in Fig. 4. Some other possibilities to create integration cells will be discussed in Sect. 4.1.

3.2 Element-based mortar integration

The element-based approach employs no information about kinks of the mortar matrix integrands due to master side nodes and edges. Therefore, no projection of the master nodes to a slave-related integration domain is required. However, in contrast to the segment-based approach, one may have to deal with integration point projections onto nodes or edges shared by several master elements. Such a projected integration point has to be uniquely assigned to one of the correspondent master elements. However, with the master element displacement shape functions having no strong discontinuities at nodes or edges, the master element to which boundary or node the integration point is assigned can be chosen arbitrarily then. The entire integration procedure for the element-based method is summarized below for one slave element and $n_m$ corresponding master elements determined by a search algorithm.

Algorithm 2

• 1. Define $n_{int}$ integration points ${\varvec{\mathsf {\xi }}}^{(1)}_{int}$ on the slave element parameter space ${\varvec{\mathsf {\xi }}}^{(1)}$.

• 2. Try to map ${\varvec{\mathsf {\xi }}}^{(1)}_{g}$ from the slave element to the master elements to get ${\varvec{\mathsf {\xi }}}_{g}^{(2)}$. If the projection algorithm does not converge for any involved master element or if the integration points lies outside all master element parameter spaces, then this integration point is sorted out.

• 3. Perform numerical integration on the entire slave element of ${\varvec{\mathsf {D}}}[j,k]$ and ${\varvec{\mathsf {M}}}[j,l]$, $j=1,\ldots ,n_e^{1}$, $k=1,\ldots ,n_e^{(1)}$ and $l=1,\ldots ,\tilde{n}_e^{(2)}$

  $$\begin{aligned} {\varvec{\mathsf {D}}}[j,k]&= \sum _{g=1}^{n_{int}} w_g\varPhi _j(\varvec{\xi }_g^{(1)}) N_k^{(1)}(\varvec{\xi }_g^{(1)})J(\varvec{\xi }_g^{(1)}),\\ {\varvec{\mathsf {M}}}[j,l]&= \sum _{g=1}^{n_{int}} w_g\varPhi _j(\varvec{\xi }_g^{(1)}) N_l^{(2)}(\varvec{\xi }^{(2)}(\varvec{\xi }_g^{(1)})) J(\varvec{\xi }_g^{(1)}), \end{aligned}$$

  where $J$ represents the Jacobian determinant of the mapping from physical space to slave element parameter space. In addition, $\tilde{n}_e^{(2)}$ describes the number of master nodes associated with all involved master elements.

It can be seen that the slave element parameter space equals the integration parameter space. Thus, no mapping into an auxiliary space is required.

4 Theoretical comparison of the integration schemes

In this section, the two introduced integration methods are compared with regards to their most important properties. Hence, the advantages and the drawbacks of each scheme are clearly demonstrated and discussed. Remember that all following statements refer to three-dimensional contact problems.

4.1 Choice of integration rule

The first issue we want to highlight is the choice of a suitable integration rule. In principle, there are two different approaches to perform a discrete numerical integration. First, the position and the weighting of each integration point could be calculated for each integration domain individually by using a moment-fitting related approach [26, 27, 52] or by employing methods based on the divergence theorem [42–44]. The second possibility is to use simple predefined integration rules, for example Gauss-Legendre quadrature or Gauss-Lobatto quadrature. Due to the fact that using some algorithm for calculating the integration points for every integration domain individually requires a significantly higher implementational and computational effort than using predefined rules, only predefined quadrature rules are considered in the following.

For the segment-based integration scheme the domain resulting from the polygon clipping procedure (Algorithm 1, step 4) is in general an arbitrary convex polygon. Thus, adopting common quadrature rules first requires some preparation step, in which the polygon is divided into simply shaped domains. The preferred methods for that are triangulation approaches, especially Delaunay triangulation [23] or center-based triangulation (both shown in Fig. 5). As can be seen, using Delaunay triangulation creates the smallest possible number of triangular integration cells, i.e. $N-2$ triangular cells for a convex polygon with $N$ vertices. Here, it should be noted that the Delaunay triangulation is not a unique procedure. Therefore, small errors could occur if different-shaped integration cells are created within one time step. However, in all our simulations we could not detect any negative effect by employing the Delaunay triangulation. Therefore, it is the best triangulation approach for the segment-based integration scheme. However, it would also be possible to subdivide the polygon into quadrilateral and triangular integration cells by adopting the so-called ear-clipping algorithm [25]. In our experience, however, this may lead to strongly distorted quadrilaterals whose Jacobians become rational. Thus, they cannot be integrated with the desired accuracy by a polynomial based integration rule (e.g. any kind of Gauss quadrature). All in all, the preferred procedure is to subdivide the polygon into triangular cells having a constant Jacobian by Delaunay triangulation and to then employ standard Gauss-Legendre quadrature for these triangles. However, note that the highest polynomial degree that can be computed exactly by the integration rule should be chosen somewhat higher than the product of shape functions on slave and master side would indicate. This is due to the nonlinearity of the projections between auxiliary plane and actual contact surfaces. Based on our experiences, we suggest to use seven Gauss points per triangular integration cell, which are able to exactly calculate a polynomial degree of 5.

Fig. 5

Triangulation methods: center-based triangulation (left), Delaunay triangulation (right)

The choice of integration rule for the element-based integration method is simply based on the shape of the slave element, because the slave element parameter space equals the integration domain parameter space. However, for the element-based scheme the choice of the number of integration points is an extremely crucial issue. In many published articles, the authors aim at overcoming the negative influence due to the non-smoothness of the integrand with a very high number of integration points [10, 11]. To analyze the results of using polynomial based Gauss quadrature rules for integrands with weak discontinuities occuring within the contact boundary, a simple academic test case is provided, see Fig. 6. As can be seen, the set of functions $F_1(x)$ are piecewise linear functions in $x\in [-1,1]$ having a kink at $k$ with $F_1(k)=1$ and the boundary values $F_1(-1)=F_1(1)=0$. Varying the kink position from $-1$ to $1$ and performing the numerical integration with 2–5 Gauss–Legendre points gives the error plot also shown in Fig. 6. It is obvious that the maximum integration error indeed decreases with an increasing integration point number. Nevertheless, the integration error strongly depends on the kink position. Therefore, using an increasing integration point number does not necessarily reduce the occuring error for any kink position. In other words, for certain kink positions Gauss rules with few integration points produce smaller errors than much higher Gauss point numbers. Having a closer look at the well-known Gauss point positions, one notices that the kink locations with the largest integration errors actually are the integration point positions. This interesting result can be also transferred to the three-dimensional case. In addition, when having a fine mesh for the master surface and a coarse mesh for the slave surface, the danger of kinks occuring in the integration domain of a slave element significantly increases. Thus, all in all, the element-based integration method is very sensitive to the employed integration point number and also to the mesh size ratio between slave and master surface. Therefore, defining a suitable integration point number is very problem-dependent and requires a certain amount of experience, which is a very crucial drawback compared to the segment-based method.

Fig. 6

Test case to analyze possible integration errors due to weak discontinuities

4.2 Boundary problems

In the following subsection, possible problems at the boundary of the contact interface are discussed, which only arise for the element-based integration scheme.

There exist two characteristic problem settings associated with the boundary of the contact interface, see Fig. 7. Both problem settings share the fact that they introduce strong discontinuities (i.e. jumps) in the integrand of mortar matrix ${\varvec{\mathsf {M}}}$ in addition to the usual weak discontinuities (i.e. kinks). This significantly increases the requirements on the integration rule in terms of accuracy, and thus causes large integration errors in general.

Fig. 7

Two characteristic problem settings of the element-based integration associated with the boundary of the contact interface. Dropping edge situation (left) and small contact search parameter (right)

The two characteristic problem settings shown in Fig. 7 are now analyzed in more detail. For the sake of simplicity, both scenarios are illustrated for two-dimensional mortar contact, but all following considerations can be directly transferred to the three-dimensional case. The first problematic setup is a dropping edge problem, see the left subfigure of Fig. 7. Here, parameter $t$ defines the partition of the slave element which has a zero contribution to the integrand. At the position where the outermost master node $l$ is projected onto the slave element, the integrand jumps from zero to a non-zero value. Thus, a strong discontinuity in the expression to be numerically integrated occurs. A possible remedy in order to avoid excessive integration errors for the element-based scheme will be proposed at the end of this subsection. Obviously, the segment-based approach does not encounter the described problem, since no contact segments are detected in the non-overlapping partition $t$.

Another contact scenario which produces a strong discontinuity is shown in the right subfigure of Fig. 7. The sketch illustrates two boundary meshes being located pretty near to each other and potentially coming into contact. The dashed lines represent the bounding boxes which are typically used for search algorithms. The specific search algorithms employed here are not presented in detail, but the reader is exemplarily referred to [53] instead. Only if the bounding boxes of a slave element and a corresponding master element overlap, then the numerical integration of the mortar matrices will be carried out for these elements. Thus the numerical integration will not be carried out for the master element containing the nodes $l-1$ and $l$. The projection of the integration points from slave element to the master is represented by arrows. Here, the red arrow represents a projection onto the master element that is not considered by the search algorithm. Due to this, the integration point associated with the red arrow has a zero contribution to the mortar integrals. This again leads to a strong discontinuity in the integrand. In contrast to the dropping edge situation, however, this problem can be avoided by an increased search radius. Thus, it does note pose a critical limitation to the accuracy of the element-based integration and will not be considered further.

Nevertheless, the dropping edge situation described above remains to be taken care of. Intuitively, eliminating the impact of strong discontinuities in an integral expression could be achieved by a significantly increased number of integration points. But as will be shown by the numerical results in Sect. 5, this would require so many integration points that the element-based integration scheme becomes very inefficient. Thus, a different solution is needed. Our approach to handle such boundary problems will be termed boundary-segmentation in the following. Herein, the segment-based integration scheme will be employed for problematic slave elements having strong discontinuities in the integrand and for non-critical slave elements within the contact zone the element-based integration is used. The critical slave elements will be identified by detecting integration points whose projection misses all of the master elements associated with this slave element. With this combination of segment-based and element-based integration, boundary problems can be avoided. Therefore, our preferred integration strategy consists of employing the element-based integration wherever possible and only if the problematic boundary scenarios occur, the integration algorithm will be changed to the segment-based scheme.

4.3 Second-order interpolation

The next aspect to be highlighted is mortar integration for higher-order finite element interpolation. Specifically, second-order Lagrangian elements are considered here. For the segment-based integration method, the authors in [37] have suggested a simple, but efficient modification as shown in Fig. 8. This approach can be interpreted as a direct extension to the segment-based integration scheme presented in Sect. 3.

Fig. 8

Subdividing a second-order contact element for the segment-based integration scheme. Exemplarily, a 9-node quadrilateral element is split into four 4-node quadrilateral subelements, to which the segment-based Algorithm 1 can then be applied nearly unchanged

The modification generates linearly interpolated subelements and establishes geometric mappings from parent element space so subsegment space and vice versa. Thus, it is possible to evaluate higher-order shape function products in the integrand of the mortar matrices and the weighted gap without any algorithmic changes. This approach only affects the integration domain itself, which is less accurate in terms of geometry. Compared to the segment-based integration scheme, the element-based method requires no such modification step for second-order interpolation. Numerical integration is still simply carried out in the slave element parameter space without any geometric approximation. However, the impact of weak and strong discontinuities for quadratically interpolated elements is larger than for linearly interpolated elements. Therefore, there exist greater demands on the employed integration formulas. Some examples concerning element-based integration with second-order elements are shown in Sect. 5.

4.4 Frictional contact

As compared with frictionless mortar contact formulations, the frictional version requires not only the discrete weighted gap $(\tilde{g}_n)_j$ but also the discrete relative tangential velocity $(\tilde{{\varvec{\mathsf {v}}}}_{\tau ,{\mathsf {rel}}})_j$ of each slave node $j$ as fundamental kinematic measure. As has been demonstrated in (20), the definition of $(\tilde{{\varvec{\mathsf {v}}}}_{\tau ,{\mathsf {rel}}})_j$ contains time derivatives of the mortar matrices ${\varvec{\mathsf {D}}}$ and ${\varvec{\mathsf {M}}}$, which are then approximated by difference quotients of the mortar matrix entries evaluated at the current time step $t_{n}$ and the last time step $t_{n-1}$, see (21). For the segment-based integration method these differences are in general not problematic because the mortar entries for both time steps are calculated with a high accuracy. In contrast, the element-based integration scheme is in general not able to compute the mortar integrals with a comparable accuracy (unless an excessive number of integration points is used). Thus, at both time steps there occur errors in the mortar expressions which could accumulate. Beside this effect, some entries in the mortar matrices might not even be detected by the element-based integration method. To illustrate this effect, both mortar integration schemes are shown at different time steps, see Fig. 9. Here, the black dashed lines represent four master elements not changing their position during the considered time interval. Additionally, the slave element is defined by blue lines for time step $t_{n-1}$ and by red lines for time step $t_n$. For standard Gauss rules, the integration points are located within the element and not on the element edges. Therefore, there exist element regions where the element-based integration is not able to detect contributions from master elements, see the gray colored area in Fig. 9. The resulting loss of accuracy for frictionless contact is not severe, because the evaluated terms within the element dominate the mortar matrices. In contrast, for frictional contact the non-detected contributions lead to a significantly increased relative error for the relative tangential velocity $(\tilde{{\varvec{\mathsf {v}}}}_{\tau ,{\mathsf {rel}}})_j$, which directly affects the decision, whether a node is in stick or slip state.

Fig. 9

Moving slave surface in time step $t_{n-1}$ (blue) and $t_n$ (red). With segment-based integration (left) and element-based integration (right). (Color figure online)

All in all, for frictional mortar contact the element-based integration is more sensitive than for the frictionless mortar contact. The segment-based integration is the best available integration scheme for this problems with regard to accuracy and ensures the highest possible robustness for a frictional mortar contact algorithm.

4.5 Conservation of linear and angular momentum

Finally, the ability to conserve linear and angular momentum is analyzed and compared for the two integration methods. All investigations are done in the semi-discrete setting, i.e. after spatial discretization but before time discretization. First, as elaborated e.g. in [35] the requirement for linear momentum conservation can be expressed as

$$\begin{aligned} {\varvec{\mathsf {f}}}^{sl}-{\varvec{\mathsf {f}}}^{m}=\sum _{j=1}^{m^{(1)}}\left( \sum _{k=1}^{n^{(1)}} {\varvec{\mathsf {D}}}[j,k]\varvec{\lambda }_j - \sum _{l=1}^{n^{(2)}} {\varvec{\mathsf {M}}}[j,l]\varvec{\lambda }_j \right) =\varvec{0}, \end{aligned}$$

(31)

which can be simplified to

$$\begin{aligned} \sum _{k=1}^{n^{(1)}}{\varvec{\mathsf {D}}}[j,k] - \sum _{l=1}^{n^{(2)}}{\varvec{\mathsf {M}}}[j,l]=\varvec{0}\quad \forall j=1,\ldots ,m^{(1)}. \end{aligned}$$

(32)

Several authors, see e.g. [35], have shown, that this requirement is exactly satisfied for the segment-based integration when integrating both mortar matrices ${\varvec{\mathsf {D}}}$ and ${\varvec{\mathsf {M}}}$ with the same integration procedure. If the mortar integrals were evaluated independently of each other, conservation of linear momentum would not be guaranteed in general. Using the element-based integration scheme inevitably generates additional integration errors for the mortar matrix ${\varvec{\mathsf {M}}}$ and the weighted gap $\tilde{g}_n$. However, these errors interestingly cancel out when evaluating the sum expressions in (32) due to the partition of unity property of the master side shape functions.

$$\begin{aligned}&\sum _{k=1}^{n^{(1)}}\left( \int N_k \varPhi _j d\varOmega \right) - \sum _{l=1}^{n^{(2)}}\left( \int N_l \varPhi _j d\varOmega \right) \nonumber \\&\quad =\int \varPhi _j d\varOmega - \int \varPhi _j d\varOmega = 0 \end{aligned}$$

(33)

Therefore, the element-based integration method also conserves linear momentum exactly. The influence of the generated integration errors could therefore be interpreted as a changed arrangement of the master side forces to the associated nodes. However, summing them up yields the same total force acting on slave and master side.

Enforcing an exact conservation of angular momentum is rather challenging in the context of mortar methods for unilateral contact. The basic requirement for conservation of angular momentum is given as

$$\begin{aligned}&\varvec{0} = {\varvec{\mathsf {m}}}^{sl}-{\varvec{\mathsf {m}}}^{m}\nonumber \\&\quad =\sum _{j=1}^{m^{(1)}}\left[ \sum _{k=1}^{n^{(1)}} {\varvec{\mathsf {x}}}_k^{(1)} \times ({\varvec{\mathsf {D}}}[j,k]\varvec{\lambda }_j) \!-\!\sum _{l=1}^{n^{(2)}} {\varvec{\mathsf {x}}}_l^{(2)}\times ({\varvec{\mathsf {M}}}[j,l]\varvec{\lambda }_j) \!\right] . \end{aligned}$$

(34)

This condition is fulfilled when either the jump vector $\varvec{g}_j$ becomes zero for each active slave node $j$, i.e.

$$\begin{aligned} \varvec{g}_j=\sum _{k=1}^{n^{(1)}}{\varvec{\mathsf {D}}}[j,k]{\varvec{\mathsf {x}}}_k^{(1)} - \sum _{l=1}^{n^{(2)}}{\varvec{\mathsf {M}}}[j,l]{\varvec{\mathsf {x}}}_l^{(2)} =\mathbf {0}, \end{aligned}$$

(35)

or alternatively when the discrete nodal Lagrange multiplier vector $\varvec{\lambda }_j$ and $\varvec{g}_j$ are always collinear. As investigated in [53], both conditions will usually be slightly violated for the segment-based integration. Employing the element-based integration method one can obviously not expect any improvement with regard to angular momentum conservation, but rather a deterioration. However, as the examples in Sect. 5 illustrate, we obtain almost identical results for both integration methods concerning the conservation of angular momentum.

5 Numerical examples

In this section the theoretically discussed properties of the segment-based and element-based integration schemes are verified on the basis of four numerical examples. The first example is a classical contact patch test which is conducted to assess the accuracy of both integration methods and the effect of our newly proposed boundary-segmentation procedure. The second example analyzes the effect of numerical integration on the convergence properties for both first-order and second-order finite element interpolations. Thirdly, a two tori impact example is considered to evaluate the integration methods with regard to efficiency and conservation laws. The fourth example investigates the press fit of two rotating cylinders with regard to possible oscillations of the contact tractions. Finally, an ironing example illustrates the applicability of both integration methods to frictional contact problems.

5.1 Patch test

The first example is supposed to demonstrate the accuracy of the introduced integration schemes and their influence on the consistency of the mortar method. Figure 10 illustrates the problem setting, where a lower block and a smaller upper block are in contact. The lower block is supported at the bottom surface and the upper block’s top surface as well as the free part of the top surface of the lower block are loaded with a constant pressure $p=-0.5$ in vertical direction. Both blocks are defined with equal material parameters based on a Neo-Hookean material model with Young’s modulus $E=100$ and Poisson’s ratio $\nu =0.0$. The discretization consists of linearly interpolated hexahedral elements as shown in Fig. 10. In the following, both possibilities of choosing slave and master surface are tested and compared. Independent from this choice, the mortar method should be able to exactly transmit constant contact pressure across the interface, which characterizes the physically correct solution.

Fig. 10

Initial configuration with finite element discretization of the patch test

The first simulations are carried out with a mortar setting where the lower surface of the upper block is the slave surface and the upper surface of the lower block is the master surface. Thus, all slave elements are covered with master elements causing only weak discontinuities in the integrand of the second mortar matrix and the weighted gap. The resulting Lagrange multiplier (i.e. contact pressure) values are exemplarily plotted along a diagonal line of the mortar surface, see Fig. 11. Here, the results are given for the segment-based integration method employing three Gauss points per triangular integration cell and for the element-based integration scheme employing 9, 64, 100 and 400 Gauss points per slave element. The analytical solution is represented by a constant contact pressure of $-0.5$. The segment-based method passes this patch test. However, the element-based integration method fails the patch test and yields slight deviations of the discrete Lagrange multiplier values. However, even if only nine Gauss points are employed, the errors introduced by the element-based integration scheme are very small as compared with typical engineering accuracies.

Fig. 11

Computed Lagrange multiplier values at the contact interface along a diagonal axis for overlapping master elements with element-based integration and segment-based integration

Now, the slave and master sides are switched, which results in an overlapping slave side. This yields not only weak discontinuities for the integration of slave elements located within the contact zone, but also strong discontinuities in the integrands of overlapping slave elements. Again, the computed Lagrange multiplier values are plotted along a diagonal line of the mortar interface for both segment-based and element-based integration methods, see Fig. 12. It can be seen that the Lagrange multiplier values are again exactly reproduced (to machine precision) for the segment-based integration scheme. The element-based integration method, however, yields unacceptably large errors for all investigated numbers of integration points, even for 400 Gauss points per slave element. The reason for this failure are the strong discontinuities (jumps) which occur in the mortar integrands for this setup. In addition, the results demonstrate how difficult it may be to predict the number of required Gauss points. Employing 64 Gauss points per slave element creates larger errors than nine Gauss points in this case due the fact that to some points of the 64-point rule are located very close to the occuring strong discontinuities. As discussed in Fig. 6 for the two-dimensional case this proximity leads to a significant increase of the overall error level. To handle this problem, the proposed boundary-segmentation is tested, which employs element-based integration for slave elements located fully within the contact interface and segment-based integration scheme for overlapping elements at the boundary of the contact interface. The resulting Lagrange multipliers are much better approximated than for the element-based integration method, which demonstrates why boundary-segmentation is a natural choice in order to prevent excessive integration errors. However, the boundary-segmentation does obviously not reach an accuracy to machine precision, but the error levels are comparable to those of element-based integration for fully projecting slave elements, cf. Fig. 11.

Fig. 12

Computed Lagrange multiplier values at the contact interface along a diagonal axis for overlapping slave elements with element-based integration, segment-based integration and boundary segmentation

5.2 Bending beam

This numerical example is considered to investigate the convergence order of the discretization error measured in the energy norm. The problem setting is a classical domain decomposition setup with non-matching meshes, see Fig. 13. All problem data has been re-used from earlier investigations in [31] to which we refer for further details. The example is based on a small deformation assumption and a linear-elastic material behavior. Therefore, an analytical solution of this problem is well-known [14] and is going to be used as reference result. The following investigations heavily build upon the discretization error $\mathbf {u}-\mathbf {u}_h$ measured in the energy norm, which is defined as

$$\begin{aligned} \vert \vert \mathbf {u}-\mathbf {u}_h\vert \vert _{energy}= \sqrt{\int _{\varOmega }(\varvec{\epsilon }-\varvec{\epsilon }_h): \mathbb {C}:(\varvec{\epsilon }-\varvec{\epsilon }_h)\text {d}\varOmega }, \end{aligned}$$

(36)

with the linearized strain tensor $\varvec{\epsilon }$ and the linear-elastic constitutive tensor $\mathbb {C}$. The mortar interface is defined having a curved shape, with the ratio of the characteristic element sizes between the discretization of slave and master surface being fixed at $\frac{h^{(1)}}{h^{(2)}}=\frac{2}{3}$. Both sub-domains are discretized with hexahedral Lagrangian finite elements of polynomial degree $p=1$ or $p=2$, i.e. typical first- and second-order elements. This yields an expected convergence order of $\mathcal {O}(h^p)$. The interpolation of the Lagrange multipliers is done by dual shape functions of the same order as the displacement interpolation, see [31] for further details.

Fig. 13

Example with bending structure in initial configuration (left) and deformed configuration (right)

To numerically analyze convergence rates of the discretization error, the characteristic mesh size $h$ is uniformly refined and the results are illustrated in Fig. 14. The expected convergence order of $\mathcal {O}(h^p)$ is perfectly represented by the segment-based integration schemes for both linearly and quadratically interpolated elements, as shown by the black dashed lines. For first-order elements, element-based integration gives nearly the same errors as the segment-based method. However, for second-order elements (27-node hexahedra), the element-based scheme fails to deliver an optimal convergence behavior for all employed numbers of Gauss points. The mesh size, below which the element-based method significantly differs from the segment-based solution depends on the number of used Gauss points. Employing more and more integration points reduces the undesirable effect of sub-optimal convergence rates, and the results slowly approach those of the segment-based version. It is very likely that this behavior would also occur for linearly interpolated elements, however only for very small characteristic element sizes, which arguably are irrelevant from a purely practical engineering point of view.

Fig. 14

Convergence of error in the energy norm with uniform mesh refinement for hexahedral meshes (hex8 and hex27 elements) with element-based and segment-based integration

5.3 Two tori contact

The impact of two tori, firstly introduced in the context of contact search algorithms [53], is considered to compare the two integration methods concerning computational efficiency and conservation of linear and angular momentum in a large scale example. The problem setting taken up here is described in [32] and slightly differs from the original example. The employed material is a Neo-Hookean model with $E$ = 5,500, $\nu =0.3$ and a density of $\rho =0.1$ for both bodies. The discretization is equal for both tori and results in a total number of 23.340 linearly interpolated hexahedral elements. For time integration, a generalized-$\alpha$ scheme is employed, see [5] for further details. The calculation of contact interaction is based on 200 time steps, and the numerical solution is performed in parallel on 16 cores. Some characteristic stages of deformation during the impact process are shown in Fig. 15. First, we investigate the efficiency of the introduced integration methods. For this purpose, the average time required for integration for one Newton step within each time step are plotted in the left subfigure of Fig. 16. In addition, the accuracy of the integration schemes is validated by the right subfigure of Fig. 16, which visualizes the deviations of the relative $L^2$-norm of the displacements with respect to a reference solution based on segment-based integration with 12 Gauss points per integration cell. Using 37 or 64 Gauss points per integration cell does not significantly change the displacement norm compared to 12 Gauss points. The relative error of the $L^2$-norm, is given as

$$\begin{aligned} \epsilon _{displ}=\frac{\vert \vert {\varvec{\mathsf {d}}}_{seg12} \vert \vert - \vert \vert {\varvec{\mathsf {d}}}_{n} \vert \vert }{\vert \vert {\varvec{\mathsf {d}}}_{seg12} \vert \vert }, \end{aligned}$$

(37)

where ${\varvec{\mathsf {d}}}_n$ represents the current numerical solution and ${\varvec{\mathsf {d}}}_{seg12}$ the reference solution. For this example, the segment-based integration is tested with three and seven Gauss points per integration cell, and the element-based integration method employs 4–64 Gauss points per slave element. For the segment-based integration, three Gauss points per integration cell is the smallest sensible number of integration points. Thus, it can be seen that compared to the segment-based integration, the element-based integration method has the ability to significantly reduce the number of integration points. In addition, it is obvious that the required integration time scales linearly with the employed number of integration points, which is why all curves in Fig. 16 have a similar shape. The characteristic shape of the curves depends strongly on the active set. Thus, ups and downs of the curves occur due to time steps with a correspondingly high or low number of nodes being in contact. From time step 190 onwards, the curves are zero-valued due to the face that the two tori are not in contact any more. Interestingly, the $L^2$-displacement errors are only small and decrease further with more and more integration points. Even four Gauss points per element are sufficient for the $L^2$-displacement error being negligible. However, with four Gauss points per element, only 7 % of integration time of the segment-based integration employing seven integration points per integration cell are required. All in all, it becomes obvious that the element-based integration scheme allows for dramatic reductions of the computational costs for practical applications, while still maintaining a sufficient level of accuracy.

Fig. 15

Deformation of the two tori during frictionless impact. The time steps 1, 40, 80, 120, 160 and 199 are visualized

Fig. 16

Results for the frictionless tori impact with element-based and segment-based integration: averaged required integration time per Newton step (left) and relative error of computed displacement field (right)

The next aspect to be investigated is the conservation of linear and angular momentum. As described theoretically in Sect. 4, the conservation of linear momentum is guaranteed for both integration methods, but the conservation of angular momentum may be slightly violated. Figure 17 illustrates our numerical results with regard to conservation properties. The left subfigure confirms the exact fulfillment of linear momentum, whereas the right subfigure shows the relative error of the angular momentum. Again, element-based integration produces equally accurate results as segment-based integration. The element-based scheme with nine Gauss points per slave element exhibits the same error level as the segment-based integration scheme. Other Gauss rules for the element-based integration have also been tested and gave equal results with regard to conservation properties.

Fig. 17

Investigation concerning the conservation laws for the large scale two tori impact with element-based and segment-based integration. Plot of linear momentum (left) and Plot of angular momentum (right)

5.4 Cylinder press fit

This example is introduced to investigate the solution quality of normal contact tractions that can be achieved with the different integration strategies. The problem setting is depicted in Fig. 18 and consists of two cylinders that are joined by a press fit. The dimensions of cylinder 1 (the inner cylinder) are given by an outer radius $r_o^1=5.022$ and an inner radius $r_i^1=4.022$, whereas cylinder 2 (the outer cylinder) is defined by an outer radius $r_o^2=6.0$ and an inner radius $r_i^2=5.0$, thus resulting in an initial overlap. The cylinders have the same material properties, which are defined by a Saint Venant–Kirchhoff material model with Young’s modulus $E=500$ and Poisson’s ratio $\nu =0.0$. The outer surface of cylinder 1 acts as slave side, and the inner surface of cylinder 2 is the master side. The cylinders are supported in such a way, that the outer surface of cylinder 2 remains fixed and the inner surface of cylinder 1 is subjected to a rotational load imposed as Dirichlet boundary condition. The mesh ratio between slave and master side is chosen to be $\frac{2}{3}$, and first-order elements (8-node hexahedra) are employed for finite element discretization. The simulation is performed under the assumption, that no displacements in thickness direction will occur. The resulting normal contact traction $\lambda _{n,j}$ of an arbitrarily chosen slave node is monitored over the entire simulation time for both element-based and segment-based integration, see Fig. 19. It can be clearly seen, that the element-based integration procedure exhibits strongly oscillatory behavior of the normal contact tractions, especially for very small numbers of Gauss points. However, by increasing the number of integration points, the element-based integration method converges towards the solution obtained with the segment-based strategy. These observations are in very good agreement with the results from the patch test example in Sect. 5.1. The fact that the normal contact tractions still exhibit slightly oscillatory behavior even for the segment-based integration scheme has nothing to do with numerical integration, but is rather due to the relatively coarse first-order finite element discretization, which generates kinks at every node of the curved contact interface. Thus, for the sake of completeness, a reference solution calculated with second-order finite elements (27-node hexahedra) and corresponding mortar techniques, see [31, 51], is shown in Fig. 20 and obviously reduces oscillations to a level that is negligible. Furthermore, a solution based on a strongly refined mesh with first-order elements (8-node hexahedra) is given in this figure to demonstrate the superior properties of the second-order approach for this example. If deemed necessary, a further smoothing of the contact interface and its associated kinematic and kinetic quantities can be achieved by employing either isogeometric mortar methods [6, 45, 46] or boundary smoothing or enrichment techniques [39, 48].

Fig. 18

Setup of the cylinder press fit example

Fig. 19

Contact tractions for the cylinder press fit example with first-order elements (hex8)

Fig. 20

Contact tractions for the cylinder press fit example with second-order elements (hex27) and first-order elements (hex8, refined mesh)

5.5 Ironing

The last example is a frictional extension to the ironing problem investigated in [30]. The geometric setup is shown in Fig. 21. The upper body is a hollow half cylinder with a Neo-Hookean material model with Young’s modulus $E$ = 1,000 and Poisson ratio $\nu =0.3$. The other body is a block being fixed at the lower surface and has the material parameter $E=1$ and $\nu =0.3$. Frictional contact is modeled by Coulomb’s law with the friction coefficient $\mu =0.2$. At the beginning of the simulation, the cylinder is pressed into the block by a prescribed vertical displacement of $w=1.4$ within 20 steps. After this intrusion, the vertical displacement is held constant and the cylinder slides along the block with a prescribed displacement $u=4.0$ within 130 additional steps. The problem is discretized with 8-node hexahedral elements as shown in Fig. 21. The top surface of the block is chosen as slave side and the bottom surface of the cylinder as master side, thus yielding only weak but no strong discontinuities in the mortar integrands. Typical stages of deformation during contact and associated patterns of tangential forces due to friction can be seen in Fig. 22.

Fig. 21

Setup of the frictional ironing problem

Fig. 22

Deformation and tangential nodal slave forces for the frictional ironing problem

To validate the accuracy of the element-based integration, the segment-based integration scheme is considered as reference solution. Despite the fact that the segment-based integration produces only marginal integration errors, some non-physical effects (e.g. slightly oscillating tractions) occur during the simulation. This could be avoided by well-known surface smoothing procedures, see e.g. [48]. However, for an increasing number of integration points, the element-based solutions should still converge to the segment-based result. This is validated in Fig. 23. The first quantity to be analyzed is the relative error of the displacement field measured in the $L^2$-norm compared to the segment-based reference solution, see the left subfigure in Fig. 23. During the first part of the simulation, the cylinder is pressed into the foundation and starts to slide. After roughly 30 steps all slave nodes are in the slip phase and no sticking effects occur anymore. From step 30 until the end of the calculation, the relative displacement errors of the element-based integration schemes slightly oscillate around the zero-reference. The error magnitude decreases for an increasing number of integration points. The damping effect of the oscillation during the simulation is due to the prescribed movement of the cylinder. Thus, the Dirichlet boundary condition dominates the displacement field for progressing time steps. The peaks of the displacement error are due to the master element edges sliding over parallel slave element edges. For 25 and more Gauss points, this effect vanishes due to the integration points being located near enough to the element edges.

Fig. 23

Relative errors of element-based integration for the $L^2$-norm of the displacements and for the averaged slip increment

The second investigation is concerning the slip increment $\tilde{{\varvec{\mathsf {u}}}}_{\tau ,{\mathsf {rel}}}$ from (23), which represents the most crucial quantity for frictional mortar contact. Here, the slip increment of all slip nodes is summed up and divided by the number of slip nodes, thus yielding an averaged slip increment. This quantity is plotted over step index in the right subfigure of Fig. 23. Again, the relative error in the slip increment decreases with an increasing numbers of Gauss points, but in contrast to the $L^2$-displacement error its magnitude is now considerable.

All in all, with an adequate number of integration points, the calculation of frictional mortar contact problems with the element-based integration scheme is possible, but the error in the slip increment could cause problems with respect to the rather sensitive search for the current stick and slip regions.

6 Conclusion

The two most commonly employed integration methods for mortar contact problems, segment-based and element-based integration, have been compared with each other and their respective advantages and drawbacks have been highlighted. Furthermore, we have proposed a so-called boundary-segmentation method as an ideal compromise for an efficient and accurate integration scheme, because it combines the advantages of both schemes without taking over their deficiencies.

Several numerical examples have demonstrated acceptable results for both integration schemes but with a significantly reduced computation time for the element-based integration. However, for second-order interpolation as well as for frictional problems with very sensitive stick/slip transitions, the quality of the solution is much better for the segment-based integration, which could not be reached by the element-based integration, even for very high numbers of integration points. Therefore, we suggest to employ the segment-based integration as an accurate basis for further mortar-specific method development and the boundary-segmentation scheme together with a thorough error estimation of all relevant quantities (e.g. displacements, contact forces, stick/slip behavior) for large-scale applications with first-order elements.