Keywords

1 Introduction

Teleportation is one of the important applications of quantum information theory. In 1993, the first quantum teleportation scheme was proposed by Bennett [1]. In the scheme, Alice want to transmit an unknown quantum state to Bob with maximally entangled Einstein-Podolsky-Rosen states. Later, Karlsson and Bourennane [2] proposed the first controlled quantum teleportation by using maximally entangled GHZ state as quantum channel. Actually, this schemes of controlled teleportation are the same as quantum state sharing [3,4,5,6,7]. From then on, many theoretical schemes of quantum teleportation [8,9,10,11,12,13,14] have been given by using differently entangled states. At the same time, experimental development of quantum teleportation has also been reported [15, 16]. Recently, Zha [17] demonstrated that some cluster state can be used as quantum channel for bidirectional quantum teleportation. In this type of teleportation schemes, Alice and Bob can simultaneously transmit an single quantum state each other after performing some appropriate locally operators. Up to now, various Bidirectional quantum teleportation schemes have been given with entangled states [18,19,20,21,22,23].

As to teleportation, the entangled qubit states, such as GHZ states [24,25,26], W states [27, 28] and other entangled state [29, 30], play a pivotal role in quantum schemes. In general, those entangled states, which arc used as quantum channel, are maximally entangled. However, those maximally entangled states are difficult to be generated for the coupling of the quantum states. If the quantum states are partially entangled in scheme, this schemes of quantum teleportation are called probabilistic teleportation [31,32,33], which are not almost realized perfect but implemented with a probability less than unit. However, some of partially entangled states [34, 35] are found that they can be utilized as quantum channel for an optimal teleportation just as the biggest entangled states work in the scheme. Now, it is very natural to ask the following question: Whether bidirectional teleportation can also be implemented with probability unit if the quantum states, worked as quantum channel, are partially entangled for some reason? Based on those works, we propose a bidirectional controlled quantum teleportation with non-maximally entangled states in the paper.

The organization of this paper is outlined as follows. In Sect. 2, we firstly illustrate how to generate a 5-qubit entangled state from a normal GHZ state, utilized as quantum channel in the following scheme. In Sect. 3, we propose a scheme of bidirectional controlled quantum teleportation. Finally, discussions and conclusions about our scheme are given.

2 Bidirectional Controlled Teleportation

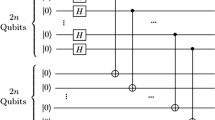
Before describing our scheme, we discuss how to generate the non-maximally entangled GHZ-type state \(|\phi _1\rangle \) (Eq. 1) from a GHZ state, which will be employed in our teleportation scheme. The state \(|\phi _1\rangle \) can be expressed as

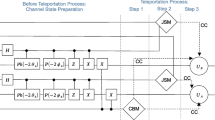
$$\begin{aligned} \begin{aligned} |\phi _1\rangle&=\frac{1}{2}(sin\theta |00000\rangle +sin\theta |00110\rangle +sin\theta |01001\rangle +sin\theta |01111\rangle \\&\ \ \ \ +cos\theta |11100\rangle -cos\theta |11010\rangle -cos\theta |10101\rangle +cos\theta |10011\rangle ). \\ \end{aligned} \end{aligned}$$
(1)

As showed in Fig. 1, the state input into the circuit is GHZ state

$$\begin{aligned} |\phi _0\rangle =sin\theta |00000\rangle +cos\theta |11111\rangle . \end{aligned}$$
(2)

When two Hadamard operations are implemented on the fourth and the fifth qubit of EQ(2), the generalized GHZ state \(|\phi _0\rangle \) is transformed into the following state (Fig. 1)

Fig. 1.
figure 1

A quantum circuit to generate 5-qubit partially entangled GHZ-type states.

Full size image
$$\begin{aligned} \begin{aligned} |\phi _0'\rangle&=sin\theta |000++\rangle +cos\theta |111--\rangle \\&=\frac{1}{2}(sin\theta |00000\rangle +sin\theta |00010\rangle +sin\theta |00001\rangle +sin\theta |00011\rangle \\&+cos\theta |11100\rangle -cos\theta |11110\rangle -cos\theta |11101\rangle +cos\theta |11111\rangle ).\\ \end{aligned} \end{aligned}$$

Then, implementing a CNOT gate on the second qubit with the fifth qubit as the control qubit and another CNOT gate on the third qubit with the fourth qubit as the control qubit, we have generated the partially entangled state \(|\phi _1\rangle \) (Eq. 1). We use the GME-concurrence [36] to analyze the entanglement properties of the state \(|\phi _1\rangle \), which is given as

$$ C_{GME}(|\varOmega \rangle ):=\min \limits _{r_i\in r}\sqrt{2[1-Tr(\rho ^2_{A_{r_i}})]},$$

then we have \(C_{GME}(|\phi _1\rangle )=|sin2\theta |,\) which varies from 0 to 1. When \(C_{GME}=0\), the states

$$\begin{aligned} \begin{aligned} |\phi \rangle =\frac{1}{2}|1\rangle (|1100\rangle -|1010\rangle -|0101\rangle +|0011\rangle ) \end{aligned} \end{aligned}$$

are biseparable. When \(C_{GME}=1\), the states

$$\begin{aligned} \begin{aligned} |\phi _1\rangle =&\frac{1}{2\sqrt{2}}(|00000\rangle +|00110\rangle +|01001\rangle +|01111\rangle \\&\ +|11100\rangle -|11010\rangle -|10101\rangle +|10011\rangle ) \end{aligned} \end{aligned}$$

are maximally entangled.

We supposed the three parties in the scheme are Alice, Bob and Charlie and the 5-qubit partially entangled state \(|\phi _1\rangle \), used as quantum channel, are shared between Alice and Bob. Now, Alice wants to transmit an unknown qubit state \(|\mu _A\rangle \) to Bob, and Bob also wants to transmit an unknown qubit state \(|\mu _B\rangle \) to Alice. Charlie, as a controller, decides whether Alice and Bob, in the scheme, can attain the qubit state successfully from each other. The two qubit states transmitted from Alice and Bob, which are known nothing by everyone, are given by

$$\begin{aligned} \begin{aligned} |\mu _A \rangle =a_0|0\rangle +a_1|1 \rangle , \ \ \ |\mu _B \rangle =b_0|0\rangle +b_1|1 \rangle ,\\ \end{aligned} \end{aligned}$$
(3)

where \(|a_0|^2+|a_1|^2=1,\ \ |b_0|^2+|b_1|^2=1.\) The total state of physical system can be shown as

$$\begin{aligned} |\varOmega \rangle =|\mu _A\rangle _A\otimes |\phi _1\rangle _{12345}\otimes |\mu _B\rangle _B. \end{aligned}$$
(4)

where the qubits A, 3, 5 held by Alice, qubits B, 2, 4 by Bob and the qubit 1 belongs to Charlie. At first, a Bell-states measurement is performed by Alice and Bob on their own qubit respectively. then they public their outcomes each other by sending two bits of classical information. Thus, the whole states (Eq. 4) can be rewritten as

$$\begin{aligned} \begin{aligned} |\varOmega&\rangle _{B2A3145}=|\varPsi ^x\rangle _{B2}|\varPsi ^y\rangle _{A3}[(a_0b_0sin\theta |000\rangle +(-1)^xa_0b_1sin\theta |001\rangle +\\&\ \ \ (-1)^ya_1b_0sin\theta |010\rangle +(-1)^{x+y}a_1b_1sin\theta |011\rangle +a_0b_0cos\theta |111\rangle -\\&\ \ \ (-1)^xa_0b_1cos\theta |110\rangle -(-1)^ya_1b_0cos\theta |101\rangle +(-1)^{x+y}a_1b_1cos\theta |100\rangle ]\\&+|\varPsi ^x\rangle _{B2}|\varPhi ^y\rangle _{A3}[(a_0b_0sin\theta |010\rangle +(-1)^xa_0b_1sin\theta |011\rangle +\\&\ \ \ (-1)^ya_1b_0sin\theta |000\rangle +(-1)^{x+y}a_1b_1sin\theta |001\rangle -a_0b_0cos\theta |101\rangle +\\&\ \ \ (-1)^xa_0b_1cos\theta |100\rangle +(-1)^ya_1b_0cos\theta |111\rangle -(-1)^{x+y} a_1b_1cos\theta |110\rangle ]\\&+|\varPhi ^x\rangle _{B2}|\varPsi ^y\rangle _{A3}[(a_0b_0sin\theta |001\rangle +(-1)^xa_0b_1sin\theta |000\rangle +\\&\ \ \ (-1)^ya_1b_0sin\theta |011\rangle +(-1)^{x+y}a_1b_1sin\theta |010\rangle -a_0b_0cos\theta |110\rangle +\\&\ \ \ (-1)^xa_0b_1cos\theta |111\rangle +(-1)^ya_1b_0cos\theta |100\rangle -(-1)^{x+y}a_1b_1cos\theta |101\rangle ]\\&+|\varPhi ^x\rangle _{B2}|\varPhi ^y\rangle _{A3}[(a_0b_0sin\theta |011\rangle +(-1)^xa_0b_1sin\theta |010\rangle +\\&\ \ \ (-1)^ya_1b_0sin\theta |001\rangle +(-1)^{x+y}a_1b_1sin\theta |000\rangle +a_0b_0cos\theta |100\rangle -\\&\ \ \ (-1)^xa_0b_1cos\theta |101\rangle -(-1)^ya_1b_0cos\theta |110\rangle +(-1)^{x+y}a_1b_1cos\theta |111\rangle ], \end{aligned} \end{aligned}$$
(5)

where \(|\varPsi ^0\rangle =|\varPsi ^+\rangle ,\ |\varPsi ^1\rangle =|\varPsi ^-\rangle ,\ |\varPhi ^0\rangle =|\varPhi ^+\rangle ,|\varPhi ^1\rangle =|\varPhi ^-\rangle ,\) and the four states of \(|\varPsi ^{\pm }\rangle =\frac{1}{\sqrt{2}}(|00\rangle \pm |11\rangle )\) and \( |\varPhi ^{\pm }\rangle =\frac{1}{\sqrt{2}}(|01\rangle \pm |10\rangle )\) are so called Bell-states. It is clear that, when Alice and Bob have finished their measurement, the whole physical states will collapse to one of 16 results. At this time, if Charlie does not want to implement the communication about quantum information between Alice and Bob, she can do nothing on her own particle to terminate this scheme. While she needs to take a measurement on the qubit 1 under bases \(\{ |0\rangle ,\ |1\rangle \}\) and tell the others of her measurement outcome by sending one bit of classical information. Both of Alice and Bob can recover the right states transformed from the other when they receive all of the measurement outcomes informed by the others. For example, supposed the measurement results of Alice and Bob are \(|\varPsi ^1\rangle _{B2}|\varPhi ^0\rangle _{A3}\), the system state collapses into the following state

$$\begin{aligned} \begin{aligned} |\varOmega \rangle _{145}&=a_0b_0sin\theta |010\rangle -a_0b_1sin\theta |011\rangle +a_1b_0sin\theta |000\rangle -a_1b_1sin\theta |001\rangle \\&-a_0b_0cos\theta |101\rangle -a_0b_1cos\theta |100\rangle +a_1b_0cos\theta |111\rangle + a_1b_1cos\theta |110\rangle .\\ \end{aligned} \end{aligned}$$
(6)

Now, we also assume Charlie allows Alice and Bob to exchange their quantum information. Thus, Charlie will take a classical measurement on her qubit 1 and tell Alice and Bob of her outcome. In term of Charlie’s measurement result, the state (Eq. 6) of physic system can be rewritten as follows

$$\begin{aligned} \begin{aligned} |\varOmega \rangle _{145}&=sin\theta |0\rangle ( a_0|1\rangle +a_1|0\rangle )\otimes (b_0|0\rangle -b_1|1\rangle )\\ {}&+cos\theta |1\rangle (a_1|1\rangle -a_0|0\rangle )\otimes (b_0|1\rangle + b_1|0\rangle ).\\ \end{aligned} \end{aligned}$$
(7)

If Charlie’s measurement result is \(|0\rangle \), the composed states hold by Alice and Bob will be

$$\begin{aligned} \begin{aligned} |\varOmega \rangle _{45}&=( a_1|0\rangle +a_0|1\rangle )\otimes (b_0|0\rangle -b_1|1\rangle ),\\ \end{aligned} \end{aligned}$$
(8)

the above state (Eq. 8) hold by Alice and Bob is not absolutely entangled but biseparable states. Thus, it is possible for them to recover the information transmitting from the others by taking some locally unitary operations. Lets come back to the above example, when Alice and Bob have performed the two locally unitary operations \(U_A\) and \(U_B\) on the quibt 5 and qubit 4 respectively, they can recover the states \(|\mu _B\rangle \) and \(|\mu _A\rangle \) , that is \(U_A|\varOmega \rangle _5=|\mu _B\rangle _5\) and \(U_B|\varOmega \rangle _4=|\mu _A\rangle _4\). The two unit operations are given by \(U_A=\sigma _z=|0\rangle \langle 0|-|1\rangle \langle 1|, \ U_B=\sigma _x=|0\rangle \langle 1|+|1\rangle \langle 0|\), where \(\sigma _x, \sigma _z\) are the Pauli operations.

Moreover, if Alice and Bob got any other results of their measurements and Charlie agree they to recover their qubits, Alice and Bob can recover the qubit state too. On the basis of the measuring results, all of the appropriate operations, performed by Alice and Bob, are listed in Table 1.

3 Conclusion

In this paper, a scheme of bidirectional controlled quantum teleportation via a non-maximally entangled GHZ-type state, which can be transformed by the generalized 5-qubit GHZ states, are proposed. As to the mean of technology, our scheme can be implemented deterministically with only two Bell-state measurements and a classical measurement.