Keywords

30.1 Introduction

The goal of this paper is to investigate the possibility of sequentially applying substructure decoupling [1, 2] and constraint addition to the identification of compliant space structures, such as solar panels or array antennas for space applications, under different boundary conditions. Such structures are large thin structures, with the first flexible modes occurring at very low frequencies. They can be attached to the body of the satellite using different types of joints. To predict the dynamic behaviour of such structures under different boundary conditions, it is convenient to start from their dynamic behaviour in free-free conditions. In fact, the effect of different boundary conditions, such as additional constraints or appended structures, can be taken into account starting from the frequency response functions in free-free conditions. In this situation, they would exhibit rigid body modes at zero frequency.

To experimentally simulate free-free boundary conditions, flexible mounts such as soft springs are typically used: with such arrangement, rigid body modes occur at low but non-zero frequencies. Since compliant structures exhibit the first flexible modes at very low frequencies, the two sets of modes become coupled, and measured FRFs do not describe correctly the low frequency dynamics of the free-free structure.

Instead of using raw measurements, the effect of the supports on the measured FRFs can be removed by using substructure decoupling. It consists in the identification of a dynamic model of a structural subsystem, starting from an experimental dynamic model (e.g. FRFs) of the assembled structure and from a dynamic model of a known portion of it (the so-called residual substructure). The structure mounted on the supports plays the role of the assembled structure, whilst the supports alone are the residual substructure. The dynamics of the free-free structure can be finally reconstructed after measuring the FRFs on the assembled structure and, if necessary, on the supports. Since the effect of the supports is going to be removed, one could use stiffer supports than those typically used to simulate free boundary conditions [3], thus making easier the test rig realization procedure. However, when using stiffer supports, the FRF level in the low frequency range decreases and so does the signal to noise ratio [4]. Therefore, the supports should be quite soft. Finally, the FRFs of the structure under different boundary conditions, such as additional kinematic constraints, can be predicted using an FRF condensation procedure detailed in Sect. 30.2.2 and similar to dynamic condensation. The procedure is tested on a reduced scale model of a space solar panel using different support conditions.

30.2 Theoretical Background

30.2.1 Decoupling Technique

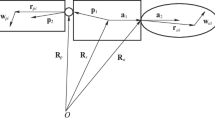
Substructure decoupling represents a special case of experimental dynamic substructuring [5, 6]. A dynamic model of a substructure is identified, starting from an experimental dynamic model (e.g. FRFs) of the assembled structure RU and from a dynamic model of a known portion of it (the so-called residual substructure R). The unknown substructure U (N U DoFs) is joined to the residual substructure R (N R DoFs) by n c coupling DoFs. The degrees of freedom of the assembled structure (N RU DoFs) can be partitioned into coupling DoFs (c), internal DoFs of substructure U (u) and internal DoFs of substructure R (r).

Several assembly techniques can be used, e.g. dual assembly [1, 2] and hybrid assembly [7]. Using dual assembly, the predicted FRF matrix of the unknown substructure U is:

$$\displaystyle{ \begin{array}{ll} \mathbf{H^{U}} =&\left [\begin{array}{*{10}c} \mathbf{H^{RU}}& \mathbf{0} \\ \mathbf{0} &-\mathbf{H^{R}}\\ \end{array} \right ] -\left [\begin{array}{*{10}c} \mathbf{H^{RU}}& \mathbf{0} \\ \mathbf{0} &-\mathbf{H^{R}}\\ \end{array} \right ]\left [\begin{array}{*{10}c} \mathbf{B_{E}^{RU}}^{T} \\ \mathbf{B_{E}^{R}}^{T}\\ \end{array} \right ]\times \\ &\times \left (\left [\begin{array}{*{10}c} \mathbf{B_{C}^{RU}}&\mathbf{B_{C}^{R}}\\ \end{array} \right ]\left [\begin{array}{*{10}c} \mathbf{H^{RU}}& \mathbf{0} \\ \mathbf{0} &-\mathbf{H^{R}}\\ \end{array} \right ]\left [\begin{array}{*{10}c} \mathbf{B_{E}^{RU}}^{T} \\ \mathbf{B_{E}^{R}}^{T}\\ \end{array} \right ]\right )^{+}\times \\ &\times \left [\begin{array}{*{10}c} \mathbf{B_{C}^{RU}}&\mathbf{B_{C}^{R}}\\ \end{array} \right ]\left [\begin{array}{*{10}c} \mathbf{H^{RU}}& \mathbf{0} \\ \mathbf{0} &-\mathbf{H^{R}}\\ \end{array} \right ] \end{array} }$$
(30.1)

where H RU and H R are the FRF matrices of the assembled structure RU and of the residual substructure R, B C = [B C RU B C R] and B E = [B E RU B E R] are signed Boolean matrices used to enforce compatibility and equilibrium at interface DoFs, and the symbol+ denotes the generalized inverse.

As stated in [1], with the dual assembly, the rows and the columns of H U corresponding to compatibility and equilibrium DoFs appear twice. Obviously, only independent entries are retained.

30.2.2 Effect of Additional Constraints

If the dynamic behaviour of a given structure is known through its FRF matrix H, the effect of additional kinematic constraints can be easily considered through an FRF condensation procedure similar to dynamic condensation. DoFs can be partitioned into unconstrained DoFs (master set M) and constrained DoFs (slave set S). It is assumed that the known displacement of the constrained DoFs is zero, i.e. u S = 0 S. It is also assumed that the applied forces f M on the unconstrained DoFs are known. Therefore, the following relation can be written:

$$\displaystyle{ \left [\begin{array}{*{10}c} \mathbf{H_{MM}}&\mathbf{H_{MS}} \\ \mathbf{H_{SM}} & \mathbf{H_{SS}}\\ \end{array} \right ]\left [\begin{array}{*{10}c} \mathbf{f_{M}} \\ \mathbf{f_{S}}\\ \end{array} \right ] = \left [\begin{array}{*{10}c} \mathbf{u_{M}} \\ \mathbf{0_{S}}\\ \end{array} \right ] }$$
(30.2)

By isolating the second row of the Eq. (30.2), it is obtained:

$$\displaystyle{ \mathbf{H_{SM}}\mathbf{f_{M}} + \mathbf{H_{SS}}\mathbf{f_{S}} = \mathbf{0_{S}} }$$
(30.3)

from which the constraint reactions f S are:

$$\displaystyle{ \mathbf{f_{S}} = -\left (\mathbf{H_{SS}}\right )^{-1}\mathbf{H_{ SM}}\mathbf{f_{M}} }$$
(30.4)

By back substituting f S in the first row of Eq. (30.2), it is obtained:

$$\displaystyle{ \left [\mathbf{H_{MM}} -\mathbf{H_{MS}}\left (\mathbf{H_{SS}}\right )^{-1}\mathbf{H_{ SM}}\right ]\mathbf{f_{M}} = \mathbf{u_{M}}\quad \Rightarrow \quad \mathbf{H^{C}}\mathbf{f_{ M}} = \mathbf{u_{M}} }$$
(30.5)

where

$$\displaystyle{ \mathbf{H^{C}} = \mathbf{H_{ MM}} -\mathbf{H_{MS}}\left (\mathbf{H_{SS}}\right )^{-1}\mathbf{H_{ SM}} }$$
(30.6)

represents the FRF matrix of the structure with additional kinematic constraints.

30.2.3 Sequential Application of Substructure Decoupling and Constraint Addition

In order to predict the dynamics of flexible space payloads under different boundary conditions, the following procedure can be applied:

  • the FRFs H RU of the structure of interest mounted on flexible supports (assembled structure) are obtained (measured);

  • the FRFs H U of the structure of interest in free-free conditions (i.e. after removing the effect of flexible supports) are identified using substructure decoupling;

  • the FRFs H C of the structure of interest under different boundary conditions (additional kinematic constraints) are obtained using the FRF condensation procedure, Eq. (30.6), on the FRFs H U in free-free conditions:

    $$\displaystyle{ \mathbf{H^{C}} = \mathbf{H_{ MM}^{U}} -\mathbf{H_{ MS}^{U}}\left (\mathbf{H_{ SS}^{U}}\right )^{-1}\mathbf{H_{ SM}^{U}} }$$
    (30.7)

30.3 Full Scale Structure and Reduced Scale Model

The full scale structure is the solar panel on satellite Sentinel-I. The spacecraft and the solar panel are shown in Figs. 30.1 and 30.2. The size of the solar panel is 7. 36 × 1. 73 × 0. 024 m.

Fig. 30.1
figure 1

Satellite Sentinel-I

Full size image
Fig. 30.2
figure 2

Solar panel on satellite Sentinel-I

Full size image

The cross section characteristics of the solar panel are quite complex as shown in Fig. 30.3. An FE model of the full scale structure is built to determine reference natural frequencies and mode shapes. Due to the large size of the solar panel and to the limited availability and high cost of the materials used to build such systems, the experimental analysis is carried out on an aluminum scale model. The reduced scale model should have a dynamic behavior very close to that of the true solar panel, and specifically very similar natural frequencies and mode shapes.

Fig. 30.3
figure 3

Cross section characteristics of solar panel

Full size image

The aspect ratio (length over width) of the full scale panel is about 4. To avoid possible inversions of natural frequencies corresponding to different mode shapes (e.g. flexural and torsional), the aspect ratio of the reduced scale model is kept around the same value. The thickness is selected so as to minimize the natural frequency error. The size of the reduced scale model is 2. 00 × 0. 50 × 0. 003 m. A visual comparison between the full scale structure and the reduced scale model is shown in Fig. 30.4.

Fig. 30.4
figure 4

Comparison between the full scale structure and the reduced scale model

Full size image

The natural frequencies of the full and reduced scale models are compared in Table 30.1, showing that the scale reduction is acceptable.

Table 30.1 Comparison between natural frequencies of the two models (B = bending; T = torsional)
Full size table

30.4 Simulated Results

30.4.1 Decoupling

In view of the application of decoupling techniques to the identification of the free dynamics of the panel, a fixture to support the panel and to connect it to the ground is also designed.

A very simple choice is to support the panel with four soft springs (see Fig. 30.5), such that the frequency of the first rigid body mode of the panel be lower than that of the first flexible mode of the panel. The springs are non symmetrically located on four points: point 1 is 430 mm from the left edge and 20 mm from the bottom edge; point 2 is 430 mm from the left edge and 30 mm from the top edge; point 3 is 370 mm from the right edge and 30 mm from the top edge; point 4 is 370 mm from the right edge and 20 mm from the bottom edge.

Fig. 30.5
figure 5

Panel supported by four springs

Full size image

By using four commercial springs, with stiffness k = 720 N/m, and considering that the mass of the panel is 8.13 kg, a natural frequency of the heave mode of about 3 Hz is obtained which is lower than the first bending mode at 3.9 Hz. An advantage of using springs with known stiffness instead of a more complicated supporting structure, is that the FRFs of the residual substructure (springs) needs not to be measured. Furthermore, the predicted FRF matrix of the unknown substructure can be explicitly found by considering that the receptance matrix of the residual substructure is:

$$\displaystyle{ \mathbf{H^{R}} = \left [\begin{array}{*{10}c} 1/k& 0 & 0 & 0 \\ 0 &1/k& 0 & 0 \\ 0 & 0 &1/k& 0 \\ 0 & 0 & 0 &1/k\\ \end{array} \right ] }$$
(30.8)

and, by assuming that two internal DoFs of substructure U are measured, the matrices used to enforce compatibility and equilibrium at the four interface DoFs are:

$$\displaystyle{ \mathbf{B_{C}^{RU}} = \mathbf{B_{ E}^{RU}} = [\mathbf{I}_{ 4}\quad \mathbf{O}_{4,2}]\qquad \quad \mathbf{B_{C}^{R}} = \mathbf{B_{ E}^{R}} = -\mathbf{I}_{ 4} }$$
(30.9)

where I n is the n × n identity matrix and O n, m is the n × m matrix of zeros, being m the number of internal DOFs of substructure U. From Eq. (30.1), after some algebraic manipulations, it is found:

$$\displaystyle{ \mathbf{H^{U}} = \left [\begin{array}{*{10}c} \\ \mathbf{H^{RU}} -\mathbf{H^{RU}}\mathbf{B_{E}^{RU}}^{T}(\mathbf{\hat{H}^{RU}} -\mathbf{H^{R}})^{-1}\mathbf{B_{C}^{RU}}\mathbf{H^{RU}}&\quad \quad &-\mathbf{H^{RU}}\mathbf{B_{E}^{RU}}^{T}(\mathbf{\hat{H}^{RU}} -\mathbf{H^{R}})^{-1}\mathbf{H^{R}} \\ -\mathbf{H^{R}}(\mathbf{\hat{H}^{RU}} -\mathbf{H^{R}})^{-1}\mathbf{B_{C}^{RU}}\mathbf{H^{RU}} &\quad \quad & \mathbf{-H^{R}} -\mathbf{H^{R}}(\mathbf{\hat{H}^{RU}} -\mathbf{H^{R}})^{-1}\mathbf{H^{R}}\\ \end{array} \right ] }$$
(30.10)

where \(\mathbf{\hat{H}^{RU}} = \mathbf{B_{C}^{RU}}\mathbf{H^{RU}}\mathbf{B_{E}^{RU}}\) is a 4 × 4 matrix that represents the FRF of the assembled system at the interface DoFs.

To check the feasibility of the idea, an FE model of the assembled structure is built, from which numerical Frequency Response Functions (FRFs) to be used for decoupling are obtained.

To simulate the effect of noise on the FRFs, a random perturbation is generated and it is added to the FRFs \(\hat{H}_{rs}\) computed from the FE model of the assembled structure:

$$\displaystyle{ H_{rs}(\omega _{k}) =\hat{ H}_{rs}(\omega _{k}) + N_{rs}(\omega _{k})\,\sigma _{rs}\,p }$$
(30.11)

where:

  • N rs (ω k ) is the Fourier transform of a band limited white noise n rs (t) having zero mean and unit standard deviation, obtained by low-pass filtering, in the frequency band of interest, a broad band white noise w rs (t);

  • σ rs is an estimate of the standard deviation of the response at DoF r to a unit excitation at DoF s (i.e. H rs );

  • p represents the noise level, i.e. p = 0. 05 stands for 5% noise.

Since the FRFs of the residual substructure are computed from the known stiffness of the four springs, no noise should be added to such FRFs.

First, the decoupling procedure is applied using noise free FRFs. The FRF predicted on point 5 of the unknown substructure is shown in Fig. 30.6 in the frequency range 0–50 Hz, to highlight the low frequency behaviour. As expected, it is completely superimposed to the reference FRF provided by the FE model, showing that the procedure is carried out correctly.

Fig. 30.6
figure 6

H 5z, 5z U: true (0.0,0.00,1.00—), predicted using noise free FRFs (\(1,0.00,0.00_{^{{\ast}{\ast}{\ast}}}\))

Full size image

The decoupling procedure is then applied using FRFs polluted with 3% noise (the noise level is referred to the RMS value of the FRF in the frequency band of interest 0–150 Hz). A typical noise polluted FRF is compared with a noise free FRF in Fig. 30.7. The effect of noise is mostly visible for low values of the FRF.

Fig. 30.7
figure 7

H 5z, 5z RU: noise free (0.0,0.00,1.00—), 3% noise (\(1,0.00,0.00_{^{{\ast}{\ast}{\ast}}}\))

Full size image

The FRF predicted on point 5 of the unknown substructure, from FRFs of the assembled structure polluted with 3% noise, is shown in Fig. 30.8. The very low frequency range shows some scatter but the first natural frequency of the unknown substructure is correctly identified.

Fig. 30.8
figure 8

H 5z, 5z U: true (0.0,0.00,1.00—), predicted using 3% noise (\(1,0.00,0.00_{^{{\ast}{\ast}{\ast}}}\))

Full size image

It is expected that similar or even harder difficulties can be encountered when using experimental data.

30.4.2 Addition of Constraints

Starting from the FRFs of the free-free panel obtained in the previous section using substructure decoupling, the effect of additional constraints is predicted using the FRF condensation procedure.

Results obtained by blocking DoFs 2z, 3z, 4z are shown. Therefore, master DoFs are 1z, 5z, 6z. True FRFs of the panel with DoFs 2z, 3z, 4z blocked are computed using an FE model.

The FRF predicted on point 5 of the additionally constrained structure starting from noise free FRFs is shown in Fig. 30.9. As expected, it is completely superimposed to the true FRF showing that the procedure works correctly.

Fig. 30.9
figure 9

H 5z, 5z C: true (0.0,0.00,1.00—), predicted using noise free FRFs(\(1,0.00,0.00_{^{{\ast}{\ast}{\ast}}}\))

Full size image

The FRF predicted on point 5 of the additionally constrained structure starting from FRFs polluted with 3% noise is shown in Fig. 30.10. As expected, noise in the starting FRFs gets amplified during each step of the procedure: first, at the end of the decoupling procedure used to obtain the FRFs of the free structure; then, at the end of the procedure used to add kinematic constraints. The effect is a significant amount of scatter below 10 Hz that completely hides the first resonance peak which is probably close to a nodal line of the first mode.

Fig. 30.10
figure 10

H 5z, 5z C: true (0.0,0.00,1.00—), predicted using 3% noise (\(1,0.00,0.00_{^{{\ast}{\ast}{\ast}}}\))

Full size image

30.5 Further Developments and Conclusions

An experimental demonstration of the proposed procedure is planned in the near future. To this aim, a reduced scale model of the space solar panel is built, see Fig. 30.11, and it is laid down on soft springs. It will be subjected to laboratory tests to obtain the experimental FRFs to be used for substructure decoupling and for adding different boundary conditions.

Fig. 30.11
figure 11

Reduced scale model of the space solar panel

Full size image

In this paper, the sequential application of substructure decoupling and constraint addition, in order to predict the dynamics of very flexible structures under different boundary conditions, is tested using simulated data. Using noise free data, the procedure provides correct results, i.e. the same FRFs obtained by an FE model with additional constraints. Using noise polluted data, results of substructure decoupling are still acceptable whilst results after adding constraints show a more significant scatter due to error amplification that occurs at each stage of the procedure.