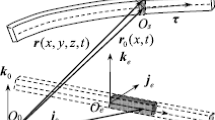Rigid–flexible–thermal coupling dynamics of a hub and multiplate system considering frictional contact

Abstract

A geometric nonlinear modeling approach for strong rigid–flexible–thermal coupling dynamics of a hub and multiplate system considering frictional contact is proposed. Based on the absolute nodal coordinate formulation (ANCF), an ANCF thin-plate element with thermoelasticity is developed, where the temperature field is expressed with Taylor polynomials to yield heat-conduction equations. In contrast to the traditional coupling formulations, the influences of the attitude motion and structural deformation on the intensity of the solar radiation, the geometric nonlinearity of the plate as well as the frictional contact are taken into account. The frictional-contact formulations for a thin plate and a rigid body are presented, which can capture the stick–slip transition and address the multiple-point contact scenarios. To solve the strong rigid–flexible–thermal coupling equations, a novel numerical approach combining the generalized-$\alpha$ method and the modified central-difference method is proposed. Two validations are performed to verify the proposed model, which proves the importance of considering the geometric nonlinearity and reveals the phenomena of thermally induced vibrations. Then, the thermal–dynamic coupling analysis for the satellite and solar-array multibody system in a thermal environment is carried out. The dynamic characteristics of the thermally induced vibration can be successfully revealed by the rigid–flexible–thermal coupling model. Furthermore, it is indicated that the influence of contact and thermal load on the nonlinear behavior of the solar-array deployment is essential, which demonstrates the feasibility of the proposed approach.

1 Introduction

Thermally induced vibrations of flexible spacecraft appendages may be initiated through the rapid changes of thermal loading during the orbital-eclipse transitions. The thermal gradient in the thickness direction is caused by the difference of the heat flux applied on the upper and lower surfaces of the solar arrays, which may induce thermal deformation, thermal vibrations, and even influence the attitude motion of the satellite. Additionally, the thermal–dynamic modeling of the spacecraft in many cases involves contact interaction between flexible appendages undergoing large deformations and overall motions. Therefore, an accurate rigid–flexible–thermal coupling model is essential to guide the practical engineering applications, and this study remains a worthy and challenging area.

Concerning the investigation of the thermal–structural coupling effect, Thornton and Kim [1] developed an analytical approach for determining the dynamic response of a flexible rolled-up solar array due to a sudden increase in external heating, in which the rotational motion of the spacecraft was not taken into account. Johnston and Thornton [2] presented an analytical model to investigate the effects of thermally induced vibrations of the flexible appendages on the rotational motion of the spacecraft, and then further carried out an experimental investigation on the thermal–structural coupling dynamics [3]. Fan and Liu [4] developed a 2D rigid–flexible–thermal coupling model to investigate the thermally induced vibration of a hub–beam system. Shen et al. analyzed the thermal–structural coupling performance for a space thin-walled beam [5] and a spinning spacecraft with an axial boom [6], and further conducted a stability analysis for the thermally induced fluttering phenomena [7]. Čepon et al. [8] proposed a new model for a coupled thermal–structural analysis of the bimetallic strip based on the ANCF. Liu et al. [9–11] carried out a thermal–structural analysis for a flexible spacecraft with a single or double solar panels, in which the coupling effect among attitude motion, structural deformation, and thermal loading are taken into account. Li et al. [12] investigated rigid–flexible–thermal coupling dynamics for a hub–beam system with a clearance joint considering torsional spring, latch mechanism, and attitude controller.

Since the solar arrays are thin plates, it is necessary to extend the thermal–structural coupling investigation to plate structures. Liu et al. [13] investigated the dynamic performance of a hub–plate system. The influence of the rotational motion on the intensity of the heat flux was included in the dynamic model. However, the temperature field expressed by the 3D solid element is complicated, and the geometric nonlinearity as well as the contact between the flexible bodies were not considered.

The Absolute Nodal Coordinate Formulation (ANCF) proposed by Shabana [14] has been widely used for simulation of a plate with large deformation. Since the transverse shear deformable of a thin plate can be neglected, based on Kirchhoff assumptions, Dmitrochenko et al. [15, 16], Dufva [17], and Ren [18] parameterized the plate elements using slopes in the element midsurface direction only. Schwab et al. [19] and Sereshk and Mahmoud [20] compared the thin-plate elements against the plate element based on the conventional finite-element approach. Hyldahl et al. [21] also compared the convergence of rectangular thin-plate elements in different mesh configurations and load conditions. In ANCF, the gradient vectors are used to describe the nodal rotations instead of the rotation parameters, avoiding the singularity problem and the interpolation problem of the finite rotation variables [22–24]. Hence, ANCF is suitable for the geometric nonlinear dynamics modeling of rigid–flexible coupled or rigid–flexible–thermal coupled multibody systems. Based on an ANCF shear-deformable plate element, Shen et al. [25] proposed a coupled thermal–structural model of a laminated composite plate. Cui and Yu proposed a novel method of the thermomechanical coupled analysis based on the unified description [26], and further developed a thermal integrated ANCF thin plate, which depicts the displacement and the temperature field integratedly [27].

Since the contact may occur during the deployment of a hub and multiplate system, it is necessary to consider the effect of frictional contact in the rigid–flexible–thermal coupling modeling. The key to modeling the contact dynamics of multibody systems lies in the treatment of contact-interface nonlinearities, which involves contact detection, contact discretization, enforcement of contact conditions, and a friction-force model [28–31]. In recent years, some researchers have already developed several different formulations for modeling the frictional-contact problem in multibody systems. Konyukhov and Schweizerhof [32, 33] developed a geometrically exact theory for various 3D solid-contact elements, including the normal, the tangential, and the rotational interactions. Yu et al. [34] established the frictional-contact formulation between flexible and rigid bodies through the Hertz contact model and the velocity-based friction model. Shi et al. [35] presented a rotation-free shell formulation and an extended contact discretization for the dynamics of multibody systems with large deformations and frictionless contacts. Sun et al. [36, 37] developed a new 2D segment-to-segment algorithm of contact dynamics based on an ANCF and mortar method, including both frictionless and friction cases. Gay Neto et al. [38] proposed a formulation to handle pointwise frictional-contact interaction of a beam–shell system using the degeneration of the local-contact problem. Tang and Liu [39] modeled the frictional contact in sliding joints with clearances, and generalized the regularized Coulomb friction law into an ANCF beam and rigid hole considering the stick–slip transition. Lei et al. [40] presented a strong coupling modeling method for the rigid bodies and the large deformed beams in contact interaction with the granular matter to simulate the flexible-brush sampling process. To avoid mutual penetration of the plate element with large deformation, a mixed method combining the node-to-surface, edge-to-surface, and surface-to-surface contact elements based on ANCF was proposed by the authors [41, 42]. Nevertheless, few studies have considered the frictional contact interactions in the rigid–flexible–thermal coupling multibody systems.

In this paper, a strong rigid–flexible–thermal coupling dynamic model for a hub and multiplate system is proposed considering the geometric nonlinearity and frictional contact. The remainder of the paper is organized as follows. In Sect. 2, an ANCF thin-plate element with thermoelasticity is developed. Two frictional contact elements based on the ANCF thin-plate element are presented in Sect. 3. In Sect. 4, the heat-conduction equations with solar radiation are derived, and a complete rigid–flexible–thermal coupling model is introduced. In Sect. 5, a new numerical approach combining the generalized-$\alpha$ method and the modified central-difference method is proposed to solve the strong rigid–flexible–thermal coupling equations. Two validations are carried out to confirm the correctness of the proposed thermal–structural coupling model in Sect. 6. Section 7 presents two interesting engineering numerical simulations of the satellite and solar-array multibody system in a thermal environment. Summary and conclusions are presented in Sect. 8.

2 ANCF thin-plate element with thermoelasticity

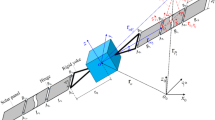
A thin rectangular plate element with length $a_{e}$, width $b_{e}$, and height $h$, is shown in Fig. 1. As shown in the figure, $O$-XYZ and $O_{e}$-$\mathbf{X}_{e}\mathbf{Y}_{e}\mathbf{Z}_{e}$ represent the inertial coordinate system and the element coordinate system, respectively.

Fig. 1

A thin rectangular plate element of ANCF (Color figure online)

The global position vector of an arbitrary point of element $i$ in the midsurface can be defined using the linear combination of the element-shape function matrix $\mathbf{S}$ and the global nodal coordinate vector $\mathbf{q}$, which is given by

$$ \mathbf{r} = \mathbf{S}(x,y) \mathbf{q}_{i},\quad \mathbf{q}_{i} = \mathbf{B}_{i}\mathbf{q}, $$

(1)

where $\mathbf{q}_{i}$ represents the element nodal coordinate vector, and $x$ and $y$ are the spatial coordinates defined in the element coordinate system, respectively. $\mathbf{B}_{i}$ is a Boolean matrix. In the absolute nodal coordinate formulation, $\mathbf{q}_{i}$ contains the global position vectors and slopes that are the spatial derivatives of the position vectors. The element nodal coordinate vector can be written as

$$ \mathbf{q}_{i} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{q}_{i 1}^{\mathrm{T}} & \mathbf{q}_{i2}^{\mathrm{T}} & \mathbf{q}_{i3}^{\mathrm{T}} & \mathbf{q}_{i4}^{\mathrm{T}} \end{array}\displaystyle \right ]^{ \mathrm{T}}, $$

(2)

where $\mathbf{q}_{ij} = [\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \mathbf{r}_{ij}^{\mathrm{T}} & \mathbf{r}_{ij,x}^{\mathrm{T}} & \mathbf{r}_{ij,y}^{\mathrm{T}} & \mathbf{r}_{ij,xy}^{\mathrm{T}} \end{array}]^{ \mathrm{T}}$, $j = 1, \ldots ,4$, and $\mathbf{r}_{ij,x} = \partial \mathbf{r}_{ij}/\partial x$, $\mathbf{r}_{ij,y} = \partial \mathbf{r}_{i j}/\partial y$, $\mathbf{r}_{ij,xy} = \partial ^{2}\mathbf{r}_{ij}/\partial x\partial y$.

In the classical theory of linear thermoelasticity, the thermal strain tensor is a linear relationship with temperature change [43, 44]. For a thin-plate structure, it is assumed that it causes only a positive strain but not a shear strain [45]. Considering a plate element whose temperature is raised from the reference temperature $T_{r}$ at which strains and stresses are zero, to the temperature $T$, the thermal strain of the thin plate due to the temperature change $\Delta T = T - T_{r}$ is [43, 46] given by

$$ \boldsymbol{\varepsilon}_{T} = \boldsymbol{\alpha}_{T}\Delta T = \left [ \textstyle\begin{array}{c} \alpha _{x} \\ \alpha _{y} \\ 0 \end{array}\displaystyle \right ]\Delta T, $$

(3)

where $\alpha _{x}$ and $\alpha _{y}$ are the coefficients of thermal expansion along the $x$ and $y$ directions, respectively.

Based on Kirchhoff assumptions, the virtual work done by the elastic force with thermoelasticity of the ANCF thin element $i$ can be written as

$$ \delta U_{ei} = \int _{0}^{a_{e}} \int _{0}^{b_{e}} \int _{ - h/2}^{h/2} \delta \boldsymbol{\varepsilon}^{\mathrm{T}}\mathbf{D} \left ( \boldsymbol{\varepsilon} - \boldsymbol{\alpha}_{T}\Delta T \right ) \mathrm{d}z\mathrm{d}y\mathrm{d}x, $$

(4)

where $\mathbf{D}$ represents the matrix of modulus, and $\boldsymbol{\varepsilon}$ represents the Green–Lagrange strain vector of an arbitrary point of the plate, which is given by

$$ \boldsymbol{\varepsilon} = \boldsymbol{\varepsilon}_{0} - z\boldsymbol{\kappa}, $$

(5)

where $\boldsymbol{\varepsilon}$ and $\boldsymbol{\kappa}$ represent the inplane Green–Lagrange strain vector and the curvature vector, respectively, which can be given as

$$ \boldsymbol{\varepsilon}_{0} = \left [ \textstyle\begin{array}{c} \frac{1}{2}\left ( \mathbf{r}_{x}^{\mathrm{T}}\mathbf{r}_{x} - 1 \right ) \\ \frac{1}{2}\left ( \mathbf{r}_{y}^{\mathrm{T}}\mathbf{r}_{y} - 1 \right ) \\ \mathbf{r}_{x}^{\mathrm{T}}\mathbf{r}_{y} \end{array}\displaystyle \right ],\quad \boldsymbol{\kappa} = \frac{1}{n}\left [ \textstyle\begin{array}{c} \mathbf{r}_{xx}^{\mathrm{T}}\bar{\mathbf{n}} \\ \mathbf{r}_{yy}^{\mathrm{T}}\bar{\mathbf{n}} \\ 2\mathbf{r}_{xy}^{\mathrm{T}}\bar{\mathbf{n}} \end{array}\displaystyle \right ], $$

(6)

where $\bar{\mathbf{n}}$ is a vector normal to the midsurface of the plate and $n$ is the magnitude of $\bar{\mathbf{n}}$.

For an arbitrary point of the plate, the temperature change $\Delta T$ can be expressed with Taylor polynomials as

$$ \Delta T(x,y,z,t) = T_{0}\left ( x,y,t \right ) + zT_{1}\left ( x,y,t \right ) + \cdots + z^{m}T_{m}\left ( x,y,t \right ), $$

(7)

$$ \textstyle\begin{array}{l} T_{0}\left ( x,y,t \right ) = \Delta T(x,y,0,t), \\ T_{k}\left ( x,y,t \right ) = \displaystyle\left . \frac{\partial ^{k}T\left ( x,y,z,t \right )}{\partial z^{k}} \right |_{z = 0}\left ( k = 1, \ldots ,m \right ). \end{array} $$

(8)

Considering that the thickness of the thin plate is small and the higher-order terms of Eq. (7) can be neglected, $\Delta T$ can be reduced as

$$ \Delta T(x,y,z,t) = T_{0}\left ( x,y,t \right ) + zT_{1}\left ( x,y,t \right ). $$

(9)

Here, $T_{0}$ represents the temperature change of the midsurface of the thin plate and $T_{1}$ represents the temperature gradient along the thickness direction, which are obtained by solving the heat-conduction equations, as discussed later in Sect. 4.

Substituting Eqs. (5) and (9) into Eq. (4), the virtual work done by the elastic force can be rewritten as

$$ \textstyle\begin{array}{l}\displaystyle \delta U_{ei} = \int _{0}^{a_{e}} \int _{0}^{b_{e}} \left ( h\delta \boldsymbol{\varepsilon}_{0}^{\mathrm{T}}\mathbf{D}\boldsymbol{\varepsilon}_{0} + \frac{1}{12}h^{3}\delta \boldsymbol{\kappa}^{\mathrm{T}}\mathbf{D}\boldsymbol{\kappa} \right )\mathrm{d}y\mathrm{d}x \\ \displaystyle\quad \quad - \int _{0}^{a_{e}} \int _{0}^{b_{e}} h\delta \boldsymbol{\varepsilon}_{0}^{\mathrm{T}}\mathbf{D} \boldsymbol{\alpha}_{T}T_{0}\mathrm{d}y\mathrm{d}x - \int _{0}^{a_{e}} \int _{0}^{b_{e}} \frac{1}{12}h^{3}\delta \boldsymbol{\kappa}^{\mathrm{T}}\mathbf{D} \boldsymbol{\alpha}_{T}T_{1}\mathrm{d}y\mathrm{d}x, \end{array} $$

(10)

Variation of $\boldsymbol{\varepsilon}_{0}$ and $\boldsymbol{\kappa}$ leads to

$$ \delta \boldsymbol{\varepsilon}_{0} = \mathbf{H}\delta \mathbf{q}_{i},\quad \delta \boldsymbol{\kappa} = \mathbf{G}\delta \mathbf{q}_{i}, $$

(11)

$$ \mathbf{H} = \left [ \textstyle\begin{array}{c} \mathbf{r}_{x}^{\mathrm{T}}\mathbf{S}_{x} \\ \mathbf{r}_{y}^{\mathrm{T}}\mathbf{S}_{y} \\ \mathbf{r}_{x}^{\mathrm{T}}\mathbf{S}_{y} + \mathbf{r}_{y}^{\mathrm{T}}\mathbf{S}_{x} \end{array}\displaystyle \right ], $$

(12)

$$ \mathbf{G} = \frac{1}{n}\left [ \textstyle\begin{array}{c} \mathbf{r}_{xx}^{\mathrm{T}}\mathbf{Y} \\ \mathbf{r}_{yy}^{T}\mathbf{Y} \\ 2\mathbf{r}_{xy}^{\mathrm{T}}\mathbf{Y} \end{array}\displaystyle \right ] + \frac{1}{n}\left [ \textstyle\begin{array}{c} \bar{\mathbf{n}}^{\mathrm{T}}\mathbf{S}_{xx} \\ \bar{\mathbf{n}}^{\mathrm{T}}\mathbf{S}_{yy} \\ 2\bar{\mathbf{n}}^{\mathrm{T}}\mathbf{S}_{xy} \end{array}\displaystyle \right ] - \frac{1}{n^{2}} \boldsymbol{\kappa} \bar{\mathbf{n}}^{\mathrm{T}}\mathbf{Y}, $$

(13)

$$ \bar{\mathbf{n}} = \tilde{\mathbf{r}}_{x}\mathbf{r}_{y},\quad \mathbf{Y} = \tilde{\mathbf{r}}_{x}\mathbf{S}_{y} - \tilde{\mathbf{r}}_{y}\mathbf{S}_{x}, $$

(14)

in which $\tilde{\mathbf{r}}_{x}$ and $\tilde{\mathbf{r}}_{y}$ are the $3\times3$ skew-symmetric matrices corresponding to $\mathbf{r}_{x}$ and $\mathbf{r}_{y}$, respectively.

Substituting Eq. (11) into Eq. (10), the elastic force of the element is given by

$$ \textstyle\begin{array}{l}\displaystyle \mathbf{Q}_{ei} = \left ( \partial U_{ei}/\partial \mathbf{q}_{i} \right )^{\mathrm{T}} \\ \displaystyle\quad = \int _{0}^{a_{e}} \int _{0}^{b_{e}} \left ( h\mathbf{H}^{\mathrm{T}}\mathbf{D}\boldsymbol{\varepsilon}_{0} + \frac{1}{12}h^{3}\mathbf{G}^{\mathrm{T}}\mathbf{D}\boldsymbol{\kappa} \right )\mathrm{d}y\mathrm{d}x \\ \displaystyle\quad \quad - \int _{0}^{a_{e}} \int _{0}^{b_{e}} \mathbf{H}^{\mathrm{T}}\mathbf{D} \boldsymbol{\alpha}_{T}T_{0}\mathrm{d}y\mathrm{d}x - \frac{1}{12}h^{3}\int _{0}^{a_{e}} \int _{0}^{b_{e}} \mathbf{G}^{\mathrm{T}}\mathbf{D} \boldsymbol{\alpha}_{T}T_{1}\mathrm{d}y\mathrm{d}x. \end{array} $$

(15)

Accordingly, the elastic force can be written as

$$ \mathbf{Q}_{e} = \sum _{i} \mathbf{B}_{i}^{\mathrm{T}}\mathbf{Q}_{ei}. $$

(16)

Defining $\rho$ as the mass density, $\mathbf{g}$ as gravitational acceleration, and $\mu$ as the structural damping coefficient, the variational equations of motion read

$$ \delta \mathbf{q}^{\mathrm{T}}\left ( \mathbf{M}\ddot{\mathbf{q}} + \mathbf{C}\dot{\mathbf{q}} + \mathbf{Q}_{e} - \mathbf{Q}_{g} \right ) = 0, $$

(17)

where $\mathbf{M} = \sum \mathbf{B}_{i}^{\mathrm{T}}(\int _{0}^{a_{e}} \int _{0}^{b_{e}} \rho h\mathbf{S}^{\mathrm{T}}\mathbf{S}\mathrm{d}y\mathrm{d}x )\mathbf{B}_{i}$ is the constant generalized mass matrix, and $\mathbf{C} = \mu \mathbf{M}$ is the damping matrix, and $\mathbf{Q}_{g} = \sum \mathbf{B}_{i}^{\mathrm{T}}(\int _{0}^{a_{e}} \int _{0}^{b_{e}} \rho h\mathbf{S}^{\mathrm{T}}\mathbf{g}\mathrm{d}y\mathrm{d}x )$ is the generalized gravitational force vector.

3 Frictional contact formulations for a thin plate and a rigid body

In this study, two forms of contact are taken into account, i.e., plate-to-plate contact and plate-to-rigid body contact. This section derives two frictional contact elements on the basis of the ANCF thin-plate element, which can address multiple-point contact scenarios with large deformations and overall motions.

The normal contact is formulated using the penalty method [28, 30], and the tangential contact is modeled by the Coulomb friction law with a penalty regularization considering the stick–slip transition [29, 32]. The virtual work of the contact force is

$$ \delta W_{cf} = \textstyle\begin{cases} - \int _{\Omega} \delta \mathbf{u}_{cf}^{\mathrm{T}}\left ( \mathbf{f}_{N} + \mathbf{f}_{T} \right )\mathrm{d}\Omega , & \text{if } g_{N} \le 0,\\ 0,& \text{otherwise} , \end{cases} $$

(18)

where $g_{N}$ is the normal penetration, $\Omega$ is the contact area. $\mathbf{u}_{cf}$ is the relative displacement vector of a contact pair, and $\mathbf{f}_{N}$, $\mathbf{f}_{T}$ are the normal and tangential force vectors of a contact pair, respectively. Contact between the contact pair occurs only if $g_{N} \le 0$.

3.1 Contact between plates

Using the “master–slave” contact-detection approach [29], the contact is checked between each integration points of the slave and the master surfaces, which is named as the STS contact element. As shown in Fig. 2, the nodal vector for the STS contact element can be given by

$$ \mathbf{q}_{ec} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{q}_{ec}^{m \mathrm{T}} & \mathbf{q}_{ec}^{s \mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}}, \mathbf{q}_{ec}^{m} \in \Re ^{48 \times 1}, \mathbf{q}_{ec}^{s} \in \Re ^{48 \times 1}. $$

(19)

Fig. 2

Geometry and kinematics of the STS contact element (Color figure online)

The normal penetration can be defined as

$$ g_{N} = \left ( \mathbf{r}_{S} - \mathbf{r}_{P} \right )^{\mathrm{T}}\mathbf{n} - \frac{h_{M} + h_{S}}{2}, $$

(20)

where $h_{M}$ and $h_{S}$ are the thicknesses of the master and slave surfaces, respectively. Following Eq. (14), the unit normal vector is obtained via the crossproduct of gradient vectors of the master surface, i.e., $\mathbf{n} = \bar{\mathbf{n}} / n$. Here, the direction of the unit normal vector is perpendicular to the master surface and points to the slave node [42, 47]. Thus, the variation of the relative displacement vector of the contact pair $SP$ is written as

$$ \delta \mathbf{u}_{cf} = \delta \mathbf{r}_{S} - \delta \mathbf{r}_{P} = \mathbf{S}_{cf}\delta \mathbf{q}_{ec}, $$

(21)

where $\mathbf{S}_{cf}$ is the shape function matrix of the contact element, which can be defined as

$$ \mathbf{S}_{cf} = \left [ \textstyle\begin{array}{c@{\quad}c} - \mathbf{S}_{m}(\xi ^{M},\eta ^{M}) & \mathbf{S}_{s}(\xi ^{S},\eta ^{S}) \end{array}\displaystyle \right ], $$

(22)

where $\mathbf{S}_{m}$ and $\mathbf{S}_{s}$ are the shape functions of the master and slave surfaces, respectively. $\xi$ and $\eta$ are the convective coordinates defined in the local surface-element coordinate system.

Based on the penalty method [28, 48], the normal contact force of the contact pair $SP$ is formulated as

$$ \mathbf{f}_{N} = \varepsilon _{N}g_{N}\mathbf{n}, $$

(23)

where $\varepsilon _{N}$ is the normal penalty parameter.

In order to describe the stick–slip transition, it requires the history variables from the previous step to describe the incremental nodal displacement [39]. Here, the points related to the previous step are represented by a subscript $(\cdot )_{a}$. As shown in Fig. 2, the contact point of the slave node $S_{a}$ on the master surface is $P_{a}$ in the previous step. Then, the incremental relative displacement vector of the contact pair $SP$ is [42]

$$ \Delta \mathbf{u}_{cf} = \Delta \mathbf{r}_{S} - \Delta \mathbf{r}_{P}, $$

(24)

where

$$ \textstyle\begin{array}{l} \Delta \mathbf{r}_{S} = \mathbf{0}, \\ \Delta \mathbf{r}_{P} = \mathbf{S}_{m}(\xi _{P}^{M},\eta _{P}^{M}) \mathbf{q}_{ec}^{m} - \mathbf{S}_{ma}(\xi _{P_{a}}^{M},\eta _{P_{a}}^{M}) \mathbf{q}_{eca}^{m}. \end{array} $$

(25)

Accordingly, the incremental relative displacement vector on the current tangent plane is

$$ \mathbf{g}_{T} = \left ( \mathbf{I}_{3} - \mathbf{nn}^{\mathrm{T}} \right )\Delta \mathbf{u}_{cf}. $$

(26)

The return-mapping scheme [32] for the Coulomb friction law with a penalty regularization is applied to measure the friction force, it introduces the trial tangential force vector as

$$ \mathbf{f}_{T}^{tr} = \left ( \mathbf{I}_{3} - \mathbf{nn}^{\mathrm{T}} \right ) \mathbf{f}_{Ta} - \varepsilon _{T}\mathbf{g}_{T}, $$

(27)

where $\mathbf{f}_{Ta}$ is the real tangential force vector in the previous step, and $\varepsilon _{T}$ is the tangential penalty parameter. According to the yield function of the Coulomb friction law [29], the real tangential force of the contact pair $SP$ can be determined as

$$ \mathbf{f}_{T} = \textstyle\begin{cases} \mathbf{f}_{T}^{tr},& \text{if } \left \| \mathbf{f}_{T}^{tr} \right \| - \mu _{s}\left \| \mathbf{f}_{N} \right \| \le 0, \text{ sticking}, \\ \displaystyle\mu _{d}\left \| \mathbf{f}_{N} \right \|\frac{\mathbf{f}_{T}^{tr}}{\left \| \mathbf{f}_{T}^{tr} \right \|}, &\text{if } \left \| \mathbf{f}_{T}^{tr} \right \| - \mu _{s}\left \| \mathbf{f}_{N} \right \| > 0, \text{ sliding}, \end{cases} $$

(28)

where $\mu _{s}$ and $\mu _{d}$ are the static and dynamic frictional coefficients, respectively.

Then, the element residual vector of the STS contact element can be summarized as

$$ \mathbf{Q}_{ec}^{STS} = \int _{\Omega} \mathbf{S}_{cf}^{\mathrm{T}}\left ( \mathbf{f}_{N} + \mathbf{f}_{T} \right ) \mathrm{d}\Omega . $$

(29)

3.2 Contact between a plate and a rigid body

As shown in Fig. 3, the contact is checked between each integration points of the slave-plate surface and the master rigid surface, which is named as the STRS contact element. Thus, the nodal vector for the STRS contact element can be given by

$$ \mathbf{q}_{ec} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{q}_{c}^{\mathrm{T}} & \mathbf{q}_{ec}^{s \mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}}, \mathbf{q}_{c} \in \Re ^{6 \times 1}, \mathbf{q}_{ec}^{s} \in \Re ^{48 \times 1}. $$

(30)

Fig. 3

Geometry and kinematics of STRS contact element (Color figure online)

The normal penetration can be obtained by

$$ g_{N} = \left ( \mathbf{r}_{S} - \mathbf{r}_{P} \right )^{\mathrm{T}}\mathbf{n} - \frac{h_{M}}{2}, $$

(31)

where $\mathbf{n} = \mathbf{A}_{c}\mathbf{n}\boldsymbol{'}$ is the unit normal vector of the STRS contact element, and $\mathbf{A}_{c}$ is the direction cosine of the rigid body, and $\mathbf{n}\boldsymbol{'}$ is the unit normal vector of the rigid surface, which is defined in the body-fixed frame $O_{c}$-$\mathbf{X}_{c}\mathbf{Y}_{c}\mathbf{Z}_{c}$. Then, the shape function matrix of the STRS contact element is

$$ \mathbf{S}_{cf} = \left [ \textstyle\begin{array}{c@{\quad}c} - \mathbf{S}_{m}(\xi ^{M},\eta ^{M}) & \mathbf{S}_{s} \end{array}\displaystyle \right ], $$

(32)

where $\mathbf{S}_{s} = [\begin{array}{c@{\quad}c} \mathbf{I}_{3} & - \mathbf{A}_{c}\tilde{\boldsymbol{\rho} \boldsymbol{'}}_{P}\mathbf{K}_{c} \end{array}]$ is the shape function of the slave rigid surface, $\boldsymbol{\rho} \boldsymbol{'}_{P}$ is the position vector of the point $P$, which is defined in $O_{c}$-$\mathbf{X}_{c}\mathbf{Y}_{c}\mathbf{Z}_{c}$, and $\mathbf{K}_{c}$ is a function of the Cardan orientation angle vector of $O_{c}$-$\mathbf{X}_{c}\mathbf{Y}_{c}\mathbf{Z}_{c}$ with respect to the inertial frame [51]. Similar to the STS contact element, the element residual vector of the STRS contact element can be obtained as

$$ \mathbf{Q}_{ec}^{STRS} = \int _{\Omega} \mathbf{S}_{cf}^{\mathrm{T}}\left ( \mathbf{f}_{N} + \mathbf{f}_{T} \right ) \mathrm{d}\Omega . $$

(33)

Therefore, the generalized contact force vector related to Eq. (18) can be assembled as

$$ \mathbf{Q}_{cf} = \sum _{n_{c1}} {\mathbf{B}_{e}^{STS}}^{\mathrm{T}}\mathbf{Q}_{ec}^{STS} + \sum _{n_{c2}} {\mathbf{B}_{e}^{STRS}}^{\mathrm{T}}\mathbf{Q}_{ec}^{STRS}, $$

(34)

where $\mathbf{B}_{e}^{STS}$ and $\mathbf{B}_{e}^{STRS}$ are the connectivity matrices of the STS and STRS contact elements, respectively. $n_{c_{1}}$ and $n_{c_{2}}$ are the numbers corresponding to STS and STRS contact elements, respectively.

4 Heat-conduction equations with solar radiation

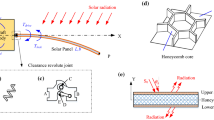
As shown in Fig. 4, the thermal loads due to solar radiation are applied on a thin plate with large deformation and overall motion. According to the first law of thermodynamics and the Fourier law of heat conduction [43–45], the variational heat-conduction equations for the three-dimensional continuum can be given by the authors’ previous study [13], as follows

$$ \textstyle\begin{array}{l}\displaystyle \int _{ V} \left ( \rho c\delta T\dot{T} + \bar{k}\delta T_{x}T_{x} + \bar{k}\delta T_{y}T_{y} + \bar{k}\delta T_{z}T_{z} - Q_{T} \right )\mathrm{d}V \\ \displaystyle- \int _{S^{ +}} \delta Tq^{ +} \mathrm{d}S - \int _{S^{ -}} \delta Tq^{ -} \mathrm{d}S = 0, \end{array} $$

(35)

where $c$ is the specific heat of the material, $\bar{k}$ is the thermal conductivity, $Q_{T}$ is the intensity of the heat source, and $q^{ +}$, $q^{ -}$ represent the heat flux of the upper and lower surfaces, respectively.

Fig. 4

A thin plate with large deformation and overall motion under solar radiation (Color figure online)

Since the distribution of solar-radiation input is affected by various factors, including its position, attitude, and configuration, the absorption of incident solar rays needs to be further evaluated by the heat flux [27]. The solar unit vector is defined as $\vec{s}$, the angle of incidence is $\alpha _{\theta}$, and the initial angle of incidence is $\alpha _{0}$. Taking into account the effect of the shadow region, $q^{ +}$ and $q^{ -}$ can be given by

$$ \textstyle\begin{array}{l} q^{ +} = c_{s}\alpha _{m}^{ +} \xi ^{ +} S_{0} - \sigma \varsigma ^{ +} \left ( T^{ +} \right )^{4}, \\ q^{ -} = c_{s}\alpha _{m}^{ -} \xi ^{ -} S_{0} - \sigma \varsigma ^{ -} \left ( T^{ -} \right )^{4}. \end{array} $$

(36)

where $S_{0}$ is the solar-radiation heat flux, $c_{s}$ is the solar coefficient related to the shadow region, $\alpha _{m}^{ +}$, $\alpha _{m}^{ -}$ represent the effective solar absorptivity of the upper and lower surfaces, respectively, $\xi ^{ +}$, $\xi ^{ -}$ represent the albedo view factors of the upper and lower surfaces, respectively, $\sigma$ represents the Stefan–Boltzmann constant, $\varsigma ^{ +}$, $\varsigma ^{ -}$ represent the emissivity of the upper and lower surfaces, respectively, and $T^{ +} = T_{r} + \Delta T^{ +}$, $T^{ -} = T_{r} + \Delta T^{ -}$ represent the absolute temperature of the upper and lower surfaces, respectively. When the plate is in a shadow region, $c_{s} = 0$.

Considering the influence of rigid-body motion and elastic deformation on the albedo view factors of the upper and lower surfaces, the albedo view factors are given by [2, 13]

$$ \xi ^{ +} = \textstyle\begin{cases} \cos\alpha _{\theta}^{ +}, & 0 \le \alpha _{\theta}^{ +} \le \pi /2, \\ 0,& \pi /2 < \alpha _{\theta}^{ +} \le \pi, \end{cases}\displaystyle \quad \xi ^{ -} = \textstyle\begin{cases} \cos\alpha _{\theta}^{ -}, & 0 \le \alpha _{\theta}^{ -} \le \pi /2, \\ 0,& \pi /2 < \alpha _{\theta}^{ -} \le \pi, \end{cases} $$

(37)

where $\alpha _{\theta}^{ +}$ and $\alpha _{\theta}^{ -}$ are given by

$$ \alpha _{\theta}^{ +} = \arccos \left ( - \frac{1}{n^{ +}} \left ( \bar{\mathbf{n}}^{ +} \right )^{\mathrm{T}}\mathbf{s} \right ), \alpha _{\theta}^{ -} = \arccos \left ( - \frac{1}{n^{ -}} \left (\bar{\mathbf{n}}^{ -} \right )^{\mathrm{T}}\mathbf{s} \right ), $$

(38)

where the normal vectors are

$$ \bar{\mathbf{n}}^{ +} = \tilde{\mathbf{r}}_{x}^{ +} \mathbf{r}_{y}^{ +},\quad \bar{\mathbf{n}}^{ -} = \tilde{\mathbf{r}}_{x}^{ -} \mathbf{r}_{y}^{ -}. $$

(39)

Since $\bar{\mathbf{n}}^{ +}$ and $\bar{\mathbf{n}}^{ -}$ are closely related to the attitude motion of the rigid body as well as the elastic deformation of the plate, the present formulation considers the influence of the attitude motion and the structural deformation on the heat flux $q^{ +}$ and $q^{ -}$, which is a complete rigid–flexible–thermal coupling model.

However, in the conventional formulation, with the neglect of the effects of rigid-body motion and elastic deformation on the heat flux, $\alpha _{\theta}^{ +}$ and $\alpha _{\theta}^{ -}$ are assumed to be constant, which can be expressed as $\alpha _{\theta}^{ +} (t) = \alpha _{\theta}^{ +} (0) = \alpha _{0}$, $\alpha _{\theta}^{ -} (t) = \alpha _{\theta}^{ -} (0) = \pi - \alpha _{0}$. In this case, it is not a complete rigid–flexible–thermal coupling model.

By means of Taylor polynomials, the three-dimensional temperature field of a thin plate can be described by the change of the midsurface temperature $T_{0}$ and the temperature gradient along the thickness direction $T_{1}$. Using a finite-element method, $T_{0}$ and $T_{1}$ can be discretized as [49]

$$ T_{k} = \mathbf{Np}_{ik} \quad (k = 0, 1), $$

(40)

where $\mathbf{p}_{ik}$ ($k = 0, 1$) represent the vectors of temperature variables of plate element $i$, and $\mathbf{N}$ represents the shape-function matrix. Defining $\mathbf{p}_{k}$ ($k = 0, 1$) as the global vectors of temperature variables, the relation between the element vector and the global vector can be given by $\mathbf{p}_{ik} = \mathbf{B}_{ik}\mathbf{p}_{k}$ ($k = 0, 1$). Substituting Eq. (40) into Eq. (9), the absolute temperature in Eq. (35) can be expressed as

$$ T = T_{r} + \Delta T = T_{r} + T_{0} + zT_{1} = T_{r} + \mathbf{NB}_{i0}\mathbf{p}_{0} + \mathbf{NB}_{i1}\mathbf{p}_{1}. $$

(41)

Accordingly, the variational heat-conduction equations can be rewritten as

$$ \delta \mathbf{p}^{\mathrm{T}}\left ( \mathbf{M}_{T}\dot{\mathbf{p}} + \mathbf{K}_{T}\mathbf{p} - \mathbf{F}_{T} \right ) = 0, $$

(42)

where

$$ \mathbf{p} = \left [ \textstyle\begin{array}{c} \mathbf{p}_{0} \\ \mathbf{p}_{1} \end{array}\displaystyle \right ], \mathbf{M}_{T} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{M}_{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{M}_{1} \end{array}\displaystyle \right ], \mathbf{K}_{T} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{K}_{0} & \mathbf{0} \\ \mathbf{0} & \mathbf{K}_{1} \end{array}\displaystyle \right ], \mathbf{F}_{T} = \left [ \textstyle\begin{array}{c} \mathbf{F}_{0} \\ \mathbf{F}_{1} \end{array}\displaystyle \right ], $$

(43)

$$ \mathbf{M}_{k} = b_{k}\int _{0}^{a_{e}} \int _{0}^{b_{e}} \rho c \mathbf{N}^{\mathrm{T}}\mathbf{N}\mathrm{d}y\mathrm{d}x,\quad \left ( k = 0,1 \right ), $$

(44)

$$ \mathbf{K}_{k} = b_{k}\int _{0}^{a_{e}} \int _{0}^{b_{e}} \bar{k} \left ( \mathbf{N}_{x}^{\mathrm{T}}\mathbf{N}_{x} + \mathbf{N}_{y}^{\mathrm{T}}\mathbf{N}_{y} \right )\mathrm{d}y\mathrm{d}x + kh\int _{0}^{a_{e}} \int _{0}^{b_{e}} \bar{k} \mathbf{N}^{\mathrm{T}}\mathbf{N}\mathrm{d}y\mathrm{d}x, \quad \left ( k = 0,1 \right ), $$

(45)

$$ \begin{aligned} \mathbf{F}_{k} &= b_{k}\int _{0}^{a_{e}} \int _{0}^{b_{e}} Q_{T} \mathbf{N}^{\mathrm{T}}\mathrm{d}y\mathrm{d}x + \int _{0}^{a_{e}} \int _{0}^{b_{e}} \left ( 0.5h \right )^{k}q^{ +} \mathbf{N}^{\mathrm{T}}\mathrm{d}y\mathrm{d}x\\ &\quad {} + \int _{0}^{a_{e}} \int _{0}^{b_{e}} \left ( - 0.5h \right )^{k}q^{ -} \mathbf{N}^{\mathrm{T}}\mathrm{d}y\mathrm{d}x,\quad \left ( k = 0,1 \right ), \end{aligned} $$

(46)

$$ b_{k} = \int _{ - h/2}^{h/2} z^{k} \mathrm{d}z,\quad \left ( k = 0,1 \right ). $$

(47)

Considering that the temperature variable vector $\mathbf{p}$ is independent, the heat-conduction equations are given by

$$ \mathbf{M}_{T}\dot{\mathbf{p}} + \mathbf{K}_{T}\mathbf{p} - \mathbf{F}_{T} = \mathbf{0}. $$

(48)

5 Dynamic equations for the rigid–flexible–thermal coupling multibody system

Defining $\mathbf{q}_{c} = [\begin{array}{c@{\quad}c} \mathbf{r}_{c}^{\mathrm{T}} & \boldsymbol{\theta}_{c}^{\mathrm{T}} \end{array}]^{ \mathrm{T}}$ as the generalized coordinate vector of the rigid body, where $\mathbf{r}_{c}$ is the position vector of the centroid defined in the inertial frame, and $\boldsymbol{\theta}_{c}$ is the Cardan orientation angle vector of $O_{c}$-$\mathbf{X}_{c}\mathbf{Y}_{c}\mathbf{Z}_{c}$ with respect to the inertial frame. In addition, the mass matrix $\mathbf{M}_{c}$ and the generalized force vector $\mathbf{Q}_{c}$ of the rigid body are detailed in [50, 51].

Combining the constraint equations $\boldsymbol{\Phi} (\mathbf{q}_{c},\mathbf{q},t) = \mathbf{0}$, the rigid–flexible coupling dynamics equations [52] and the heat-conduction equations, the mixed differential-algebraic equations for the rigid–flexible–thermal coupling multibody system are given by

$$ \boldsymbol{\Psi} = \left [ \textstyle\begin{array}{c} \mathbf{M}_{d}\ddot{\mathbf{q}}_{d} + \mathbf{C}_{d}\dot{\mathbf{q}}_{d} + \boldsymbol{\Phi}_{\mathbf{q}_{d}}^{\mathrm{T}}\boldsymbol{\lambda} - \mathbf{Q}_{d}\left ( \mathbf{p} \right ) \\ \boldsymbol{\Phi} \\ \mathbf{M}_{T}\dot{\mathbf{p}} + \mathbf{K}_{T}\mathbf{p} - \mathbf{F}_{T}\left ( \mathbf{q}_{d} \right ) \end{array}\displaystyle \right ] = \mathbf{0}, $$

(49)

where the generalized coordinate vector of the system is $\mathbf{q}_{d} = [\begin{array}{c@{\quad}c} \mathbf{q}_{c}^{\mathrm{T}} & \mathbf{q}^{\mathrm{T}} \end{array}]^{\mathrm{T}}$, and the generalized mass matrix $\mathbf{M}_{d}$, damping matrix $\mathbf{C}_{d}$, and force matrix $\mathbf{Q}_{d}$ take the form

$$ \mathbf{M}_{d} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{M}_{c} & \mathbf{0}_{6 \times n_{q}} \\ \mathbf{0}_{n_{q} \times 6} & \mathbf{M} \end{array}\displaystyle \right ], $$

(50)

$$ \mathbf{C}_{d} = \left [ \textstyle\begin{array}{c@{\quad}c} \mathbf{0}_{6 \times 6} & \mathbf{0}_{6 \times n_{q}} \\ \mathbf{0}_{n_{q} \times 6} & \mathbf{C} \end{array}\displaystyle \right ], $$

(51)

$$ \mathbf{Q}_{d} = \left [ \textstyle\begin{array}{c} \mathbf{Q}_{c} \\ \mathbf{Q}_{g} - \mathbf{Q}_{e} \end{array}\displaystyle \right ] + \mathbf{Q}_{cf}, $$

(52)

where $n_{q}$ is the number of the generalized coordinates of the plate, and $\boldsymbol{\lambda}$ is the vector of the Lagrange multiplier corresponding to the constraint equations.

A new numerical approach combining the generalized-$\alpha$ method and the modified central-difference method is proposed to solve the strong rigid–flexible–thermal coupling equations. The dynamic equations are solved by the generalized-$\alpha$ method [53, 54], and the heat-conduction equations are solved by a modified central-difference method [49]. Then, the Newton–Raphson algorithm is adopted to solve the combined nonlinear algebraic equations. The solution procedure can be divided into three steps, which are presented in detail in the Appendix.

Figure 5 shows the computational flowchart of the new numerical method proposed in this paper. Compared with the fourth-order Runge–Kutta method used uniformly in the authors’ previous study [13], the computational efficiency of this proposed method is significantly improved. Additionally, compared with the traditional uncoupled method, this method ensures the accuracy of the full coupled simulation by solving the heat-conduction equations and the dynamic equations simultaneously. Considering the geometric nonlinearities (large deformation) and boundary nonlinearities (frictional contact), the variable-step-size control scheme [55] and the preconditioning strategy are employed to improve efficiency.

Fig. 5

Computational flowchart for the proposed numerical approach (Color figure online)

6 Validations

In this section, in order to verify the correctness of the proposed thermal–structural coupling model, simulation experiments of a plate clamped at two sides and a cantilevered plate applied with thermal loads are carried out, while the results from the commercial finite-element software ABAQUS are taken as benchmarks.

6.1 Simulation of a plate clamped at two sides

As shown in Fig. 6, two sides of a plate are fixed on the inertial reference frame $O$ – XYZ, and a constant heat flux $q_{T}$ is applied to the upper surface of the plate. The initial temperature of the whole plate is set at 0 K. The geometric properties and material data of the plate are: length $l = 4\text{ m}$, width $b = 2\text{ m}$, thickness $h = 0.01\text{ m}$, mass density $\rho = 36.8\text{ kg/m}^{3}$, elastic modulus $E = 1.93\times 10^{9}\text{ Pa}$, Poisson ratio $\nu = 0.3$, thermal-expansion coefficient $\alpha _{x} = \alpha _{y} = 2.3\times 10^{-5}\text{ (1/K)}$, conductivity coefficient $\bar{k}=1.5\text{ W}/(\text{m}\cdot\text{K})$, and specific heat $c = 921\text{ J}/(\text{kg}\cdot\text{K})$. In this simulation, the heat flux of the upper and lower surfaces are $q^{+} = q_{T}\cos\alpha _{0}$ and $q^{-} = 0$, respectively, where $q_{T} = 1067\text{ W/m}^{2}$ and $\alpha _{0} = 0$.

Fig. 6

A plate clamped at two sides in a thermal environment (Color figure online)

As shown in Fig. 7, the time histories of the midsurface temperature of point $P$ and the temperature gradient $T_{1} = \partial T/\partial z$ of point $P$ are given, and the results are in good agreement with the comparative results provided by ABAQUS, which demonstrates that the temperature field can be calculated precisely by the proposed method.

Fig. 7

Time histories of (a) midsurface temperature of point $P$; (b) temperature gradient of point $P$ in the $z$ direction (Color figure online)

To further investigate the geometric nonlinear effects, the deflections of point $P$ in the $z$ direction using linear and nonlinear models are compared in Fig. 8. Since the two edges of the plate are fixed, the thermal load leads to compressive thermal stress. It is found that for the nonlinear model, the thermal force causes the softening of the plate, which induces large transverse deformations. However, the results obtained by the linear model are quite different. Due to the neglect of the nonlinear stiffness matrices, the softening effect is not shown and the transverse deformation is small. Furthermore, the results of this paper coincide with the results achieved by ABAQUS, which validates the effectiveness of the proposed thermal integrated ANCF thin-plate element in terms of geometric nonlinearity.

Fig. 8

Time history of the deflection of point $P$ in the $z$ direction (Color figure online)

6.2 Simulation of a cantilevered plate

As shown in Fig. 9, the dynamic simulation of a cantilevered plate applied with thermal loads is performed. The geometric properties and material data of the plate are the same as the numerical example 6.1. The time history of the temperature gradient of point $P$ in the $z$ direction is given in Fig. 10(a), which shows that the results are in accordance with the results obtained by ABAQUS. From the results of the deflections of point $P$ in the $z$ direction shown in Fig. 10(b), we can obtain that the results of the linear and nonlinear models coincide well, it can be concluded that for cantilevered plate without tip constraint, the use of a linear model is computationally accurate and efficient.

Fig. 9

A cantilevered plate in a thermal environment (Color figure online)

Fig. 10

Time histories of (a) temperature gradient; (b) deflection of point $P$ in the $z$ direction (Color figure online)

The thermal–structural analysis for the cantilevered plate applied with thermal loads is further conducted through a comparative study of the thermal–structural coupling model and the constant heat flux model, where $q_{T} = 2525\text{ W/m}^{2}$ and $\alpha _{0} = 65^{\circ}$, which ensures that $q^{+} = 1067\text{ W/m}^{2}$. The time histories of the temperature gradient and the deflection of point $P$ in the $z$ direction are shown in Fig. 11, respectively. As can be seen in the figures, due to the neglect of the elastic deformation of the constant heat-flux model, such a model cannot reveal the thermally induced vibration effect, therefore the vibration amplitude of the temperature gradient and the deflection is constant. On the contrary, since the heat flux varies with the deformation of the plate, the vibration amplitudes of the temperature gradient and the deflection obtained by the thermal–structural coupling model keep increasing. In summary, the proposed model takes into account the coupling effect of the heat flux and the elastic deformation, so that it is able to capture the phenomenon of thermally induced vibration, which is hardly achieved in the commercial finite element software ABAQUS.

Fig. 11

Time histories of (a) temperature gradient; (b) deflection of point $P$ in the $z$ direction (Color figure online)

7 Numerical simulations of a satellite and solar-array multibody system in a thermal environment

Thermal–dynamic analysis of the solar array is of vital importance to the safe operation of spacecraft. In this section, we present two numerical examples to demonstrate the effectiveness of the proposed rigid–flexible–thermal coupling model for the satellite and solar-array multibody system in a thermal environment. The first numerical example focuses on comparing the different coupling models to reveal the dynamic characteristics of thermally induced vibration. The other numerical example is employed to analyze the deployment dynamic performance of the solar array considering contact and thermal loading.

7.1 Numerical simulation of a satellite and solar-array system in a thermal environment

A satellite and solar-array system applied with solar radiation is shown in Fig. 12. The flexible solar array is fully deployed, and its left edge is fixed to the rigid satellite. In this simulation example, the rigid satellite is a cube, and the solar array is an isotropic flexible plate. The inertial reference frame $O -$XYZ is established at the centroid $C$ of the rigid satellite, and the geometric and material properties are given in Table 1.

Fig. 12

A satellite and solar-array system (Color figure online)

Table 1 Geometric and material properties

Defining the initial angel of incidence $\alpha _{0}$ as the solar angle, the coordinate vector of the solar sunlight is given by $\mathbf{s} = \left [ \begin{array}{c@{\quad}c@{\quad}c} \sin \alpha _{0} & 0 & - \cos \alpha _{0} \end{array} \right ]^{\mathrm{T}}$. Initially, the satellite is in a static state, and the body-fixed frame of the satellite is parallel to the global coordinate system. The reference temperature is 273 K.

7.1.1 Dynamic performance of an onorbit satellite and solar-array system

To reveal the advantages of the rigid–flexible–thermal coupling model proposed in this paper for the satellite and solar-array system, two dynamic models are compared: the complete rigid–flexible–thermal coupling model (RFTC) and the rigid–flexible coupling model considering the thermal effect (RFCT). In the RFTC formulation, $\alpha _{\theta}^{ +}$ and $\alpha _{\theta}^{ -}$ are closely related to $\mathbf{q}_{d}^{t + \Delta t}$. However, in the RFCT formulation, $\alpha _{\theta}^{ +}$ and $\alpha _{\theta}^{ -}$ are assumed to be constant, which are equal to $\alpha _{0}$ and $\pi - \alpha _{0}$, respectively, and thus the temperature results are not influenced by the rigid-body motion and the elastic deformation.

For a more intuitive description of the deformation, deflection is introduced. The deflection of an arbitrary point on the plate can be written as

$$ \mathbf{u} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} u & v & w \end{array}\displaystyle \right ]^{\mathrm{T}} = \mathbf{A}_{p}^{\mathrm{T}}\left ( \mathbf{r} - \mathbf{r}_{0} \right ), $$

(53)

where $\mathbf{r}_{0}$ is the origin of the body-fixed frame of the plate, and $\mathbf{A}_{p}$ is the transformation matrix of the body-fixed frame with respect to the inertial frame.

The time histories of the deflection of the corner point $P$ in the $z_{c}$ direction and the temperature gradient $T_{1} = \partial T/\partial z$ of the corner point $P$ are shown in Figs. 13(a) and (b), respectively. As can be seen in the figures, due to ignoring the coupling effect of the solar heat flux, the rigid-body motion, and the elastic deformation, the RFCT model cannot reveal the thermally induced vibration. Accordingly, the vibration amplitude of the deflection is constant. On the contrary, the vibration amplitudes of the deflection and the temperature gradient obtained by the RFTC model keep increasing, which explains the phenomenon of the thermally induced vibration effect.

Fig. 13

Time histories of (a) deflection of point $P$ in the $z_{c}$ direction; (b) temperature gradient of point $P$ in the $z$ direction (Color figure online)

In order to further analyze the effect of thermal load on the motion of the satellite, Fig. 14 gives the time histories of the centroidal velocity of the satellite in the $z$ direction and the angular velocity of the satellite in the $y_{c}$ direction. Due to the coupling of the translational and the rotational motion of the satellite and the elastic deformation of the solar array, the vibration amplitudes of the angular velocity and the centroidal velocity of the satellite obtained by the RFTC model also keep increasing. In summary, it reveals that the thermally induced vibration phenomenon is obvious in practical engineering and needs to be paid attention to.

Fig. 14

Time histories of (a) centroidal velocity of the satellite in the $z$ direction; (b) angular velocity of the satellite in the $y_{c}$ direction (Color figure online)

7.1.2 Parameter analysis of thermally induced vibration

In this section, based on the proposed rigid–flexible–thermal coupling model, some characteristic parameters are investigated: the solar angle $\alpha _{0}$, the specific heat $c$ of the plate, and the damping coefficient $\mu$ of plate on the thermally induced vibration effect.

According to the change of the solar angle, the time history of the angular velocity of the satellite in the $y_{c}$ direction is shown in Fig. 15(a). It is indicated that with the decrease of the solar angle, the average of the deflection increases because of the increase of the intensity of the solar heat flux. However, the variation of the solar heat flux caused by the angular deformation of the plate and the rotation of the satellite becomes less significant, therefore, the thermally induced vibration due to the rigid–flexible–thermal coupling effect also decreases.

Fig. 15

Time histories of the angular velocity of the satellite in the $y_{c}$ direction: under different (a) solar angles $\alpha _{0}$; (b) plate specific heats $c$; (c) plate damping coefficients $\mu$ (Color figure online)

Figure 15(b) depicts the time history of the angular velocity of the satellite in the $y_{c}$ direction at different plate specific heats. As can be seen in the figure, due to the decrease of $c$ and the increase of the thermal coefficient $\bar{k}/(\rho c)$, the thermally induced vibration also weakens.

The time history of the angular velocity of the satellite in the $y_{c}$ direction under different plate damping coefficients is compared, as shown in Fig. 15(c). It can be seen that with the increase of the structural damping coefficient, the vibration amplitude of the deflection attenuates applied with the damping force, which indicates that the increase of the structural damping coefficient contributes to weakening the thermally induced vibration.

7.1.3 Dynamic performance of a maneuvering satellite and solar-array system

In this section, the nonlinear dynamic performance of the maneuvering satellite and solar-array system applied with a thermal load is investigated. Additionally, the solar heat flux is applied on the plate, and the satellite is applied with a translational constraint, which is given by $x_{c} = 0$, $y_{c} = 0$, $z_{c} = 0$, and a rotational constraint, which is given by $\omega _{x} = 0$, $\omega _{z} = 0$, and

$$ \omega _{y} = \textstyle\begin{cases}\displaystyle \frac{\omega _{s}}{t_{s}}\left ( t - \frac{t_{s}}{2\pi} \sin \frac{2\pi t}{t_{s}} \right ), & 0 \le t < t_{s} ,\\ \omega _{s}, & t_{s} \le t < t_{b} - t_{s}, \\ \displaystyle\frac{\omega _{s}}{t_{s}}\left ( t_{b} - t - \frac{t_{s}}{2\pi} \sin \frac{2\pi \left ( t_{b} - t \right )}{t_{s}} \right ), & t_{b} - t_{s} \le t < t_{b}, \\ 0, & t > t_{b}, \end{cases} $$

(54)

where $t_{b} = 200\text{ s}$, $t_{s} = t_{b}/8$, $\omega _{s} = \pi /50$, which is shown in Fig. 16.

Fig. 16

Time history of $\omega _{y}$ (Color figure online)

On the basis of the RFTC model proposed in this paper, the deformed configurations of the satellite and solar-array multibody system as well as the distribution of the von Mises stress of the solar array at some time steps are depicted in Fig. 17. Initially, the satellite rotates with angular velocity around the $y_{c}$-axis, which in turn drives the motion of the solar array. In this situation, the solar array undergoes large deformations and overall motions. It is shown that the stress concentration mainly occurs at the roots of the solar array, and the stress wave gradually spreads toward the free edge of the solar array.

Fig. 17

Motion of the satellite and solar-array system at some time steps (Color figure online)

For the purpose of highlighting the advantages of the rigid–flexible–thermal coupling model for dynamic analysis of the maneuvering satellite and solar-array system with large deformations and overall motions, three dynamic models are compared: the RFTC model, the RFCT model, and the rigid–flexible coupling model without considering the thermal effect (RFC). In the RFC formulation, only rigid–flexible coupling effects are considered, while thermal effects are ignored.

Figure 18 gives the time histories of the deflection $w$ of the corner point $P$ in the $z_{c}$ direction and the temperature gradient $T_{1} = \partial T/\partial z$ of the corner point $P$, respectively. As can be seen in the figure, in the RFC model, except for the acceleration and deceleration phases of $\omega _{y}$, the deflection of point $P$ in the $z_{c}$ direction maintains a small-amplitude vibration due to the rigid–flexible coupling effect. For $t < 200\text{ s}$, the satellite undergoes periodic rotational motion in the $y$ direction, which leads to the periodic deflection in the $z_{c}$ direction and the periodic variation of the temperature gradient in the thickness direction due to the complete rigid–flexible–thermal coupling effect, while the deflection and the temperature gradient obtained by the RFCT model shows neither periodic variation nor amplitude growing. Furthermore, it is shown that for $t > 200\text{ s}$, with the release of the applied angular velocity $\omega _{y}$, the amplitude of vibration obtained by the RFTC model keeps increasing slowly, which reveals the phenomenon of the thermally induced vibration.

Fig. 18

Time histories of (a) deflection of point $P$ in the $z_{c}$ direction; (b) temperature gradient of point $P$ in the $z$ direction (Color figure online)

To further analyze the thermal–dynamic performance of the maneuvering satellite and solar-array system, Fig. 19 gives the phase diagrams of point $P$ in different models. From the phase diagram in the RFC model, it can be seen that the trajectory of the phase diagram exhibits a periodic motion without vibration under the action of $\omega _{y}$. In the RFCT model, the trajectory of the phase diagram can be viewed as the thermal vibrations superimposed on the basis of the RFC model. Since the thermal loads are assumed to be constant in the RFCT model, the thermal vibrations appear as low-frequency oscillations. However, in the RFTC model, it shows low-frequency periodic motion as well as the high-frequency thermally induced vibration, due to the consideration of the influences of rigid-body motion and elastic deformation on the intensity of solar radiation. Therefore, it is necessary to adopt the more precise rigid–flexible–thermal coupling model for dynamic analysis of maneuvering satellite and solar-array systems, which can capture richer nonlinear characteristics.

Fig. 19

Phase diagrams point $P$ in (a) RFTC model; (b) RFCT model; (c) RFC model (Color figure online)

7.2 Deployment dynamics of a solar array in a thermal environment with frictional contact

The second example deals with the deployment of the solar array in a thermal environment considering frictional contact. The simplified model of the satellite and solar-array system in a thermal environment is illustrated by Fig. 20, which consists of four guide wires, eight solar panels, and eight rotational hinges. It is worth mentioning that the translational and attitude motion of the satellite is controlled during the deployment of the solar array, and it can be regarded as points $B$, $D$, $B_{1}$, and $D_{1}$ are restricted to move on the guide wires ignoring the deformation of the guide wires. Since the direction of sunlight is along the negative $z$-axis, and the solar array are symmetrically distributed about the central satellite, it is sufficient to analyze the deployment of the solar panels on one side. $O -$XYZ is the inertial reference frame, which is consistent with the body-fixed frame of the satellite $C -\mathbf{X}_{c}\mathbf{Y}_{c}\mathbf{Z}_{c}$.

Fig. 20

A simplified model of the deployment satellite and solar-array system in a thermal environment: (a) partially deployed configuration; (b) stowed configuration (Color figure online)

The length of one side of the solar array is $L^{P} = 5\text{ m}$, and the solar angle $\alpha _{0} = 0$, and for the other geometric and material properties refer to Table 1. The initial angle between the adjacent solar panels is $\theta _{0} = 2^{\circ}$, as shown in Fig. 20(b). Considering the contact of solar panels and the contact between solar panel and satellite, it requires the STS and STRS contact elements. The normal and tangential penalty parameters for the STS and STRS contact elements are $\varepsilon _{N} =\varepsilon _{T} = 10^{5}\text{ N/m}^{3}$, and the static and dynamic frictional coefficients are $\mu _{s} = \mu _{d} = 0.3$. In addition, the points $D$ and $D_{1}$ are subjected to a prescribed translational displacement vector $\mathbf{d}(t) = [\begin{array}{c@{\quad}c@{\quad}c} d(t) & 0 & 0 \end{array}]^{\mathrm{T}}\text{ m}$. The piecewise function is

$$ d(t) = \textstyle\begin{cases} 0.5a_{d}t^{2} + s_{0}, & 0 \le t < t_{1}, \\ 0.5a_{d}t_{1}^{2} + a_{d}t_{1}(t - t_{1}) + s_{0}, & t_{1} \le t < t_{2}, \\ L^{P} - 0.5a_{d}(t_{3} - t)^{2}, & t_{2} \le t < t_{3}, \\ L^{P}, & t_{3} \le t \le t_{e}, \end{cases} $$

(55)

where $t_{1} = 12\text{ s}$, $t_{2} = 108\text{ s}$, $t_{3} = 120\text{ s}$ and $t_{e} = 200\text{ s}$. $s_{0} = 0.25L^{P}\cos (\theta _{0} / 2)$ is the initial $x$ coordinate, and $a_{d} = (L^{P} - s_{0}) / t_{1}t_{2}$ ensures that the deployment of the solar array ends with a fully deployed configuration, and the maximum velocity of the drive is defined as $v_{m} = v_{c} = a_{d}\ t_{1}$.

Based on the complete rigid–flexible–thermal coupling model proposed in this paper, the changes of configuration at some time steps are shown in Fig. 21, and the color maps represent the distribution of the von Mises stress. The initial stress of the folded solar panels is set to zero, and then the solar panels are gradually deployed applied with the driving constraints. Due to contact, it can be found that the stresses of panels 1 and 2 are greater than those of panels 3 and 4 at $t = 30\text{ s}$ and $t = 60\text{ s}$. As the thermal loads continue, panels 3 and 4 experience greater thermal stress, which can be seen in the configurations at $t = 90\text{ s}$ and $t = 120\text{ s}$. After the solar array is fully deployed, we can observe that the stress distribution of the four solar panels is relatively balanced, accompanied by obvious thermal deflection.

Fig. 21

Configurations and the von Mises stress of the satellite and solar-array system at some time steps (Color figure online)

Figure 22 presents the time history of temperature gradients of the points $P$, $B$, and $Q$ during the deployment of the solar array, and these test points can comprehensively reflect the heating conditions of the solar array. It can be seen that for $t < 50\text{ s}$, the temperature gradient at point $P$ has a zero value, which is due to the fact that point $P$ is in the shadow region at the time of contact and cannot receive solar radiation. Since one of the plates connecting the point $B$ is in the shadow region at the initial stage, the temperature gradient rate at point $B$ is lower than that at point $Q$. This why panels 1 and 2 experience greater thermal stress than panels 3 and 4 during the deployment of the solar array. Finally, the solar panels are fully deployed, and the temperature gradients of the three points are the same. Therefore, the influence of contact and thermal loads on the deployment process of the solar array is essential, which needs to be paid more attention to in engineering.

Fig. 22

Time history of temperature gradients of points $P$, $B$, and $Q$ (see Fig. 20) in the $z$ direction (Color figure online)

7.2.1 Influence of contact

In order to illustrate the necessity of contact, two models are employed. The first one considers the integration of the STS and STRS contact elements, and the other does not consider contact. For the sake of intuitiveness, the configuration of the satellite and solar-array system at $t = 30\text{ s}$ is selected for analysis, as shown in Fig. 23. It can be seen in Fig. 23(a) that the solar array can deploy properly without overpenetration in consideration of contact. On the contrary, it is clearly observed that the large penetration appears not only between the solar panels, but also between the satellite and the solar panels when the contact is not taken into account. In conclusion, for the deployment of the satellite and solar-array system, it requires a combination of STS and STRS contact elements to avoid mutual penetration, thereby ensuring computation accuracy.

Fig. 23

Configurations of the (a) contact model; (b) no contact model at $t = 30\text{ s}$ (Color figure online)

With the view of further analyzing the effect of contact, Fig. 24 depicts the time history of coordinate $x$ of points $B$ and $P$ obtained by the contact and no contact models. It can be seen that the values of the coordinate $x$ of points $B$ and $P$ are less than 1, that is, the solar panels penetrate into the satellite, which violates the real situation. After the contact no longer occurs, the curves of the two contact models gradually tend to be consistent, and the solar array is fully deployed at $t = 120\text{ s}$. Therefore, we can conclude that the contact affects not only the motions of the system, but also the shadow regions, which is related to the intensity of the solar radiation.

Fig. 24

Time history of coordinates $x$ of points $B$ and $P$ in different contact models (Color figure online)

7.2.2 Influence of thermal load

Since the thermal loads have a significant effect on the deployment of the solar array, two different thermal models are compared and analyzed in this section. Figure 25(a) presents the time history of coordinates $z$ of point $Q$ obtained by the thermal and no thermal models, respectively. By observing the coordinates $z_{Q}$ of the two models, it can be seen that when the solar panels 3 and 4 are fully deployed, the thermal model excites high-frequency oscillations with gradually decreasing amplitudes. Combined with the configuration at $t = 55\text{ s}$ in Fig. 25(b), it can be seen that since point $B$ of the no thermal model moves later than that of the thermal model, point $Q$ has a greater vertical velocity as it passes the horizontal position, resulting in a greater offset magnitude. In addition, the final configurations of the thermal and no thermal models at $t = 200\text{ s}$ are also presented in Fig. 25(b), in which we can observe that obvious deflections of the thermal model occur at points $P$ and $Q$ due to the effects of the boundary constraints and the thermal loads, which cannot be obtained by the no thermal model.

Fig. 25

(a) Time history of coordinates $z$ of point $Q$ in different thermal models; (b) Configurations of different thermal models at $t = 55\text{ s}$ and $t = 200\text{ s}$ (Color figure online)

To further analyze the thermal expansion and deflection, the time history of the deflection of point $P$ in different models is given in Fig. 26. Here, $u$, $v$, and $w$ denote the deflection of point $P$ in the $x$, $y$, and $z$ directions, respectively. The values of $u$ and $v$ remain zero in the no thermal model, but eventually exhibit positive expansion in the thermal model. By comparing the curve of $w$ in the two models, it can be observed that when the solar array is fully deployed at $t = 120\text{ s}$, the vibration amplitude of the thermal model is greater than that of the no thermal model, and the decay time is longer. From the results in the figure, it is necessary to pay attention to the phenomenon of thermal deflection during the deployment of the solar array.

Fig. 26

Time history of deflection of point $P$ in different thermal models (Color figure online)

7.2.3 Comparison of different drive speeds

In engineering, the effect of drive speed on the satellite and solar-array system is another issue of concern. In this section, we focus on comparing the results of three different drive speeds acting on the solar array in a thermal environment. As illustrated in Fig. 20, the points $D$ and $D_{1}$ are subjected to a prescribed translational displacement along the $x$ direction. As shown in Fig. 27, the drive-speed curves in different cases have the same displacement at $t = t_{e}$, in which the black curve represents the basic model, and its expression refers to Eq. (55).

Fig. 27

Drive-speed curves in three cases (Color figure online)

Figure 28 plots the dynamic response of point $P$ at three different drive speeds. It can be seen in Fig. 28(a) that the deployment times of the solar array in the three cases are significantly different, and the changes of $x_{P}$ are relatively stable. From the results in Fig. 28(b), we can observe that there are two obvious high-frequency vibrations during the deployment of the solar array. The first occurs when the solar panels 3 and 4 are fully deployed, another occurs when the solar panels 1 and 2 are fully deployed. Since the thermal effect is positively related to the action time of the thermal load, the thermal stress increases with decreasing drive speed, resulting in a greater amplitude of oscillation, especially when the plates are fully deployed.

Fig. 28

Time histories of (a) displacement; (b) velocity of point $P$ in the $x$ direction in different cases (Color figure online)

8 Conclusions

A strong rigid–flexible–thermal coupling dynamic model for a hub and multiplate multibody system with large deformations and frictional contact interactions is proposed. An ANCF thin-plate element with thermoelasticity is developed, and the temperature field is expressed with Taylor polynomials to gain the heat conduction equations. Accounting for the influences of the attitude motion and structural deformation on the intensity of the solar radiation, a complete rigid–flexible–thermal coupling model is created. Subsequently, the STS and STRS frictional contact elements are developed, which can effectively avoid the mutual overpenetration and capture the stick–slip behavior. Furthermore, a new numerical approach combining the generalized-$\alpha$ method and a modified central-difference method is proposed to solve the strong rigid–flexible–thermal coupling equations, which improves the accuracy of the full coupled simulation by solving the heat-conduction equations and the dynamic equations simultaneously.

By setting comparative tests in ABAQUS, the correctness of the proposed thermal–structural coupling model is validated, and the necessary of the geometric nonlinearity is proved. Moreover, the advantages of the proposed model in capturing thermally induced vibration are revealed. To further demonstrate the effectiveness of the proposed rigid–flexible–thermal coupling method, two numerical simulations of the satellite and solar-array multibody system in a thermal environment are conducted. The first example compares the results of three dynamic models: RFTC model, RFCT model, and RFC model. Due to the consideration of the elastic deformation as well as the rigid-body motion on the intensity of heat flux, RFTC model can reveal the phenomena of the thermally induced vibrations, which cannot be achieved by the other two models. Parameter analysis illustrates that the thermally induced vibration effect can be reduced through the decrease of the solar angle and the specific heat or the increase of the damping coefficient. Then, the nonlinear coupling behavior of the maneuvering satellite and solar-array system can be revealed by the proposed RFTC model. The second example is employed to analyze the deployment dynamic performance of the solar array in a thermal environment with frictional contact. It is concluded that the contact affects not only the motions of the system, but also the intensity of the solar radiation because of the shadow regions. Due to the effects of the boundary constraints and the thermal loads, obvious thermal deflection and high-frequency vibration can be induced, especially when the plates are fully deployed. Since the thermal effect is positively related to the action time of the thermal load, the amplitude of thermal vibration increases with the decreasing of the drive speed.

Appendix. Solution scheme for the rigid–flexible–thermal coupling equations

The solution scheme for the rigid–flexible–thermal coupling equations is divided into the following three steps:

• Step1: Prediction of the initial value

Assuming that $\ddot{\mathbf{q}}_{d}^{t + \Delta t} = \mathbf{0}$, we combine Taylor’s formula, the generalized-$\alpha$ method, and a modified central-difference method to predict $\mathbf{a}_{d}^{t + \Delta t}$, $\mathbf{q}_{d}^{t + \Delta t}$, $\dot{\mathbf{q}}_{d}^{t + \Delta t}$, $\boldsymbol{\lambda}^{t + \Delta t}$, $\mathbf{p}^{t + \Delta t}$, as follows:

$$ \mathbf{a}_{d}^{t + \Delta t} = \frac{\alpha _{f}}{1 - \alpha _{m}}\ddot{\mathbf{q}}_{d}^{t} - \frac{\alpha _{m}}{1 - \alpha _{m}}\mathbf{a}_{d}^{t}, $$

(56)

$$ \mathbf{q}_{d}^{t + \Delta t} = \mathbf{q}_{d}^{t} + \Delta t\dot{\mathbf{q}}_{d}^{t} + \Delta t^{2}\left ( 0.5 - \beta \right )\mathbf{a}_{d}^{t} + \Delta t^{2}\beta \mathbf{a}_{d}^{t + \Delta t}, $$

(57)

$$ \dot{\mathbf{q}}_{d}^{t + \Delta t} = \dot{\mathbf{q}}_{d}^{t} + \Delta t\left ( 1 - \gamma \right )\mathbf{a}_{d}^{t} + \Delta t\gamma \mathbf{a}_{d}^{t + \Delta t}, $$

(58)

$$ \boldsymbol{\lambda}^{t + \Delta t} = \boldsymbol{\lambda}^{t}, $$

(59)

$$ \mathbf{p}^{t + \Delta t} = \theta \mathbf{p}^{t + \Delta t} + \left ( 1 - \theta \right )\mathbf{p}^{t}, $$

(60)

where

$$ \alpha _{m} = \frac{2\rho _{\infty} - 1}{\rho _{\infty} + 1},\quad \alpha _{f} = \frac{\rho _{\infty}}{\rho _{\infty} + 1}, $$

(61)

$$ \gamma = 0.5 + \alpha _{f} - \alpha _{m},\quad \beta = 0.25 \left ( \gamma + 0.5 \right )^{2}, $$

(62)

and the numerical parameters $\rho _{\infty}, \theta \in [0, 1]$. The numerical parameters in this paper are taken as $\rho _{\infty} = 0.6$, $\theta = 0.5$.

• Step2: Transformation into nonlinear algebraic equations

The dynamic equations can be transformed into nonlinear algebraic equations using the generalized-$\alpha$ method [53]

$$ \left [ \textstyle\begin{array}{c} \mathbf{M}_{d}\ddot{\mathbf{q}}_{d}^{t + \Delta t} + \mathbf{C}_{d}\dot{\mathbf{q}}_{d}^{t + \Delta t} + \boldsymbol{\Phi}_{\mathbf{q}_{d}}^{\mathrm{T}}\left ( \mathbf{q}_{d}^{t + \Delta t} \right )\boldsymbol{\lambda}^{t + \Delta t} - \mathbf{Q}_{d}(\mathbf{q}_{d}^{t + \Delta t},\mathbf{p}^{t + \Delta t}) \\ \boldsymbol{\Phi} (\mathbf{q}_{d}^{t + \Delta t},t + \Delta t) \end{array}\displaystyle \right ] = \mathbf{0}, $$

(63)

where

$$ \frac{\partial \ddot{\mathbf{q}}_{d}^{t + \Delta t}}{\mathbf{q}_{d}^{t + \Delta t}} = \beta ' \mathbf{I},\quad \frac{\partial \dot{\mathbf{q}}_{d}^{t + \Delta t}}{\mathbf{q}_{d}^{t + \Delta t}} = \gamma ' \mathbf{I}, $$

(64)

$$ \beta ' = \frac{1 - \alpha _{m}}{\left ( 1 - \alpha _{f} \right )\beta \Delta t^{2}},\quad \gamma ' = \frac{\gamma}{\beta \Delta t}. $$

(65)

The heat-conduction equations in Eq. (48) are transformed into nonlinear algebraic equations by a modified central-difference method [49]

$$ \bar{\mathbf{K}} \mathbf{p}^{t + \Delta t} - \bar{\mathbf{Q}}(\mathbf{q}_{d}^{t + \Delta t},\mathbf{p}^{t + \Delta t}) = \mathbf{0}, $$

(66)

where

$$ \bar{\mathbf{K}} = \frac{\mathbf{M}_{T}}{\Delta t} + \theta \mathbf{K}_{T}, $$

(67)

$$ \bar{\mathbf{Q}} = \left [ \frac{\mathbf{M}_{T}}{\Delta t} - \left ( 1 - \theta \right ) \mathbf{K}_{T} \right ]\mathbf{p}^{t} + \left ( 1 - \theta \right )\mathbf{F}_{T}^{t} + \theta \mathbf{F}_{T}^{t + \Delta t}. $$

(68)

• Step3: Solution of the combined nonlinear algebraic equations

According to Eqs. (A8) and (A11), the combined nonlinear algebraic equations are rewritten as

$$ \textstyle\begin{array}{l} \boldsymbol{\Psi} \left ( \mathbf{q}_{d}^{t + \Delta t},\mathbf{p}^{t + \Delta t},\boldsymbol{\lambda}^{t + \Delta t},t + \Delta t \right ) \\ = \left [ \textstyle\begin{array}{c} \mathbf{M}_{d}\ddot{\mathbf{q}}_{d}^{t + \Delta t} + \mathbf{C}_{d}\dot{\mathbf{q}}_{d}^{t + \Delta t} + \boldsymbol{\Phi}_{\mathbf{q}_{d}}^{\mathrm{T}}\left ( \mathbf{q}_{d}^{t + \Delta t} \right )\boldsymbol{\lambda}^{t + \Delta t} - \mathbf{Q}_{d}(\mathbf{q}_{d}^{t + \Delta t},\mathbf{p}^{t + \Delta t}) \\ \boldsymbol{\Phi} (\mathbf{q}_{d}^{t + \Delta t},t + \Delta t) \\ \bar{\mathbf{K}} \mathbf{p}^{t + \Delta t} - \bar{\mathbf{Q}}(\mathbf{q}_{d}^{t + \Delta t},\mathbf{p}^{t + \Delta t}) \end{array}\displaystyle \right ] = \mathbf{0}. \end{array} $$

(69)

The Newton–Raphson algorithm is used to find a solution of Eq. (A14). At an iteration step $k$, the following equation is solved for a correction $\Delta \mathbf{q}_{(k)}^{t + \Delta t}$:

$$ \Delta \mathbf{q}_{(k)}^{t + \Delta t} = \left [ \textstyle\begin{array}{c} \Delta \mathbf{p}_{(k)}^{t + \Delta t} \\ \Delta \mathbf{q}_{d(k)}^{t + \Delta t} \\ \Delta \boldsymbol{\lambda}_{(k)}^{t + \Delta t} \end{array}\displaystyle \right ] = - \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c}\displaystyle \frac{\partial \boldsymbol{\Psi}}{\partial \mathbf{p}^{t + \Delta t}} & \displaystyle\frac{\partial \boldsymbol{\Psi}}{\partial \mathbf{q}_{d}^{t + \Delta t}} &\displaystyle \frac{\partial \boldsymbol{\Psi}}{\partial \boldsymbol{\lambda}^{t + \Delta t}} \end{array}\displaystyle \right ]^{ - 1}\boldsymbol{\Psi}, $$

(70)

where

$$ \frac{\partial \boldsymbol{\Psi}}{\partial \mathbf{p}^{t + \Delta t}} = \left [ \textstyle\begin{array}{c}\displaystyle - \frac{\partial \mathbf{Q}_{d}(\mathbf{q}_{d(k)}^{t + \Delta t},\mathbf{p}_{(k)}^{t + \Delta t})}{\partial \mathbf{p}^{t + \Delta t}} \\ \mathbf{0} \\ \displaystyle\bar{\mathbf{K}} - \frac{\partial \bar{\mathbf{Q}}(\mathbf{q}_{d(k)}^{t + \Delta t},\mathbf{p}_{(k)}^{t + \Delta t})}{\partial \mathbf{p}^{t + \Delta t}} \end{array}\displaystyle \right ], $$

(71)

$$ \frac{\partial \boldsymbol{\Psi}}{\partial \mathbf{q}_{d}^{t + \Delta t}} = \left [ \textstyle\begin{array}{c}\displaystyle \alpha '\mathbf{M}_{d} + \beta '\mathbf{C}_{d} + \frac{\partial \left ( \boldsymbol{\Phi}_{\mathbf{q}_{d}}^{\mathrm{T}}\left ( \mathbf{q}_{d(k)}^{t + \Delta t} \right )\boldsymbol{\lambda}_{(k)}^{t + \Delta t} \right )}{\partial \mathbf{q}_{d}^{t + \Delta t}} - \frac{\partial \left ( \mathbf{Q}_{d}(\mathbf{q}_{d(k)}^{t + \Delta t},\mathbf{p}_{(k)}^{t + \Delta t}) \right )}{\partial \mathbf{q}_{d}^{t + \Delta t}} \\ \boldsymbol{\Phi}_{\mathbf{q}_{d}}\left ( \mathbf{q}_{d(k)}^{t + \Delta t} \right ) \\ \displaystyle- \frac{\partial \bar{\mathbf{Q}}(\mathbf{q}_{d(k)}^{t + \Delta t},\mathbf{p}_{(k)}^{t + \Delta t})}{\partial \mathbf{q}_{d}^{t + \Delta t}} \end{array}\displaystyle \right ], $$

(72)

$$ \frac{\partial \boldsymbol{\Psi}}{\partial \boldsymbol{\lambda}^{t + \Delta t}} = \left [ \textstyle\begin{array}{c}\displaystyle \boldsymbol{\Phi}_{\mathbf{q}_{d}}^{\mathrm{T}}\left ( \mathbf{q}_{d(k)}^{t + \Delta t} \right ) \\ \mathbf{0} \\ \mathbf{0} \end{array}\displaystyle \right ]. $$

(73)

An improved estimate can be obtained as

$$ \mathbf{q}_{(k + 1)}^{t + \Delta t} = \mathbf{q}_{(k)}^{t + \Delta t} + \Delta \mathbf{q}_{(k)}^{t + \Delta t},\quad k = 0, 1,\ldots, $$

(74)

until the precision condition $\left \| \Delta \mathbf{q}_{(k)}^{t + \Delta t} \right \| \le \delta$ is satisfied, in which $\delta$ is the precision error.