Complicated nonlinear oscillations caused by maneuvering of a flexible spacecraft equipped with hinged solar arrays

Abstract

We present a general methodology for the nonlinear dynamical modeling of a three-axis stabilized spacecraft equipped with flexible solar arrays. The large-span multi-panel solar arrays are modeled as flexible thin plates that are connected to the rigid central body of the spacecraft by means of nonlinear flexible hinges. We construct a low-dimensional yet accurate dynamical model by using a Galerkin expansion in terms of global modes of the system that we compute first by using the Rayleigh–Ritz method. The hinged connections between the rigid and flexible parts of the system are imposed employing Lagrange multipliers. The model is used to study the spacecraft response triggered by various maneuvering scenarios. We in particular focus on the coupling between vibrations of the flexible components and the rigid motion of the spacecraft induced by hinge nonlinearities during these orbital and attitude maneuvering operations. In all cases considered, it is found that four global modes are sufficient to accurately compute the system’s response. We also observe other complicated nonlinear dynamical phenomena, such as hysteresis and superharmonic resonance that may be of concern in spacecraft design. Our modeling approach can be applied to other multibody systems directly.

1 Introduction

With the development of the space industry, spacecraft need to accomplish ever-growing tasks, so large-span solar arrays are needed in providing sustainable energy to ensure mission success. Solar arrays of large-scale flexible spacecraft composed of a number of hinges and flexible composite panels tend to become larger, lighter and more flexible (see Fig. 1 for a typical design). Having an accurate coupled rigid-flexible dynamical model that can predict the complicated motion of the system is therefore of great importance in modern spacecraft design. There are several works in the literature concerned with the dynamical modeling of spacecraft. Ji and Li [1] proposed an accurate, freedom-reduced, universally applicable, and fully flexible nonlinear finite element method for modern spacecraft based on continuum mechanics. They overcame the difficulty of structural analysis for spacecraft due to the high number of degrees of freedom of the elements. Zhang et al. [2] developed a nonlinear dynamical model for the flexible spacecraft with external disturbances, inertia uncertainties and input saturation, and investigated the finite-time attitude maneuvering control and vibration suppression. Liu et al. [3] used global analytical modes (GAMs) to develop a rigid-flexible dynamic modeling approach for spacecraft with large flexible appendages and assessed the performance of the controller based on the GAM model. The results reveal that the method can achieve a control index in a shorter time with less input energy than other methods. Azimi et al. [4] presented a novel approach for the modeling and vibration suppression of a flexible spacecraft during a large angle attitude maneuver, and a higher-order theory was used to model the elastic behavior of solar panel appendages with surface-bounded piezoelectric (PZT) patches. Shahravi and Azimi [5] addressed a composite two-time-scale control system for simultaneous three-axis attitude maneuvering and elastic mode stabilization of flexible spacecraft, and the proposed design approach is demonstrated to combine excellent performance in the compensation of residual flexible vibrations for the fully nonlinear system under consideration. Guy et al. [6] described a general framework to generate linearized models of satellites with large flexible appendages, and they considered uncertainties in the characteristic parameters of each substructure by the proposed generic and systematic multibody modeling technique. Azimi et al. [7] applied the homotopy perturbation method (HPM) to investigate the nonlinear free and forced vibration behavior of the rotating cracked beam, and a comparative study was conducted to demonstrate an accurate and effective solution for structures with nonlinear dynamics. Ni et al. [8] developed a time-varying state-space model of a coupled rigid-flexible spacecraft in orbit through the recursive identification method, and an improved identification technique with high efficiency was proposed. Gaite [9] derived the differential equations of lumped-parameter spacecraft models, which considered a satellite thermal model to study the nonlinear oscillations of the system. Liu et al. [10,11,12] considered the honeycomb solar array as a panel with one edge clamped and the other three edges free and established a “Hub-plates” model to obtain the rigid-flexible coupling modes of the spacecraft. In [10,11,12], the flexible hinge that plays a significant role in the dynamic analysis of the solar array is ignored. Then, they established an analytical coupled rigid-flexible model for a flexible spacecraft in analyzing the dynamical response under solar radiation and conducted a comparison study between single and double solar panel arrangements. However, all these dynamical modeling methods ignore the effect of the hinges of the flexible appendages on the dynamical characteristics of the whole spacecraft.

Fig. 1

Model of the three-axis attitude stabilized spacecraft

The various hinges can strongly affect the dynamic behavior of the system. In this paper, we focus on the modeling of these hinges and the effect of their nonlinearities on spacecraft dynamics.

To show the transmission characteristics of the hinges which can strongly affect the dynamical behavior of the whole structure, the parameters of the complex hinges must be confirmed first. The properties of hinges are usually difficult to measure directly. So, identification techniques are effective approaches for determining these important hinge parameters including stiffness, damping and friction. Zhang et al. [13] proposed a new accurate solar array model method by introducing the hinge rolling in order to capture its inner deformation and stress. It is shown that this accurate model can be a good candidate for the engineering application and subsequent control usage.

Lieven [14] proposed a technique to obtain the properties of structural joints, and an experimental investigation was conducted to examine the promise of the proposed method. Kimm and Park [15] presented an identification method to get the nonlinear joint properties based on measured frequency–response functions at the nonlinear joint connection points of the structure. Their investigations overcame the limitations of a time-domain lumped-parameter model. Wu et al. [16] derived differential equations for nonlinear dynamical joint models. Joint parameters for the nonlinear stiffness, friction and damping characteristics of solar arrays in a real spacecraft were identified experimentally. Jalali and Ahmadian [17] used a single-frequency excitation close to the first natural frequency to obtain the force-state mapping from time-domain acceleration records, so that the parameters of the nonlinear joint model could be identified. Ren et al. [18] proposed an identification technique for the dynamical properties of nonlinear joints using dynamical test data, which did not require a theoretical model and only depended on experimental data for the identification. We will use hinge properties (stiffness, damping and friction) as experimentally identified by force-state mapping [19].

In recent decades, there has been a great deal of research on the dynamics of multibody structures taking into account the effect of hinges. Taking the eigenfunctions of the free–free beam as basis functions, the Rayleigh–Ritz method is employed by Cao et al. [12] to obtain the natural frequencies and the corresponding global mode shapes of flexible jointed-panel structures. He et al. [20] proposed an effective way to enhance the computational speed and convergence rate by using characteristic orthogonal polynomials instead of trigonometric functions as basis functions. However, these researches mainly focus on the natural characteristics of hinged substructures of the spacecraft, and the effects of flexible hinges on rigid-flexible coupling phenomena are ignored. Given this, He et al. [21] simplified a three-axis attitude stabilized spacecraft as a rigid central body jointed with four solar panels and analyzed the influence of hinge stiffness on its global natural properties, but they did not study the nonlinear characteristics of hinges and the resulting dynamical behavior. To study the nonlinearity of hinges, Wei et al. [22, 23] proposed a nonlinear analytical model for a spacecraft with flexible jointed multi-beam structures and investigated the nonlinear vibration phenomenon of the system caused by joint nonlinearities during spacecraft maneuvering. However, the past works done by Wei et al. used beam rather than plate modeling.

It is well known that the sudden variation of control force, torque during attitude and orbit maneuvering causes the flexible appendages to shake strongly. Under such conditions, the complicated nonlinear dynamical behavior of the system may be triggered through the nonlinear coupling of the hinges, affecting the attitude stabilization of the whole spacecraft. This paper provides a general methodology for the nonlinear dynamical modeling of a three-axis stabilized spacecraft equipped with flexible solar arrays, which can obtain an analytical and low-dimensional yet accurate dynamical model for such a complicated rigid-flexible coupling system. Different from the assumed mode method, the proposed method expresses the elastic vibrations of all components with only one uniform group of modal coordinates, so that it can deliver accurate and low-dimensional nonlinear dynamical models for complicated systems such as large-scale flexible spacecraft. Different from the finite element method, the proposed method yields analytical models that can be subjected to powerful techniques from nonlinear analysis. Also, the proposed method can be used to derive low-dimensional models for complex systems, thereby reducing computation times to obtain their nonlinear response compared to those typical of finite element approaches. It enables us to conduct the nonlinear analysis for a few degrees of freedom models of the system and study these complicated oscillations induced in various spacecraft maneuvering operations in orbit that may be of concern in spacecraft design. Such an analytical solution for a model consisting of many panels and nonlinear torsional springs has not been investigated in previous studies. This manuscript seeks to fill this gap, which provides a general analytical method for the dynamic modeling of the complex large-scale flexible spacecraft. Our modeling approach can be applied to other multibody systems.

The paper is organized as follows: Section 2 presents the nonlinear modeling of the spacecraft system. The hinges are formulated as matching conditions between the rigid spacecraft hub and the flexible solar panels that are imposed by means of Lagrange multipliers. Past work on spacecraft equipped with solar panels is extended by modeling the panels as plates rather than beams, thereby allowing for additional modes of deformation. Following the work in [26], so-called global modes of the system are computed using the Rayleigh–Ritz approach. These modes are then used to construct a low-dimensional discrete model of the spacecraft by Galerkin truncation. We analyze in detail the spacecraft design shown in Fig. 1, but our approach could equally be applied to other similar spacecraft. The global modes for this particular design are given in Sect. 3. We identify the couplings between the different types of deformations in the various modes of vibration. In Sect. 4, we then investigate the dynamical response of the system triggered by orbit maneuvering forces and three-axis attitude driving torques. Concluding comments are made in Sect. 5.

2 Dynamical modeling of a spacecraft with nonlinear hinges

In this section, we first give a geometrical description of the spacecraft (Sect. 2.1) and a discussion of the numerical modeling of the displacement fields of the solar panels (Sect. 2.2). We then derive the kinetic and potential energies of the system (Sect. 2.3) and formulate the matching conditions for the hinges (Sect. 2.4) to compute the global modes of vibration (Sect. 2.5) and use these modes in a Galerkin expansion to finally obtain our low-dimensional nonlinear dynamical spacecraft model (Sect. 2.6).

2.1 The spacecraft model and its geometrical description

The spacecraft is a typical coupled rigid-flexible system. The central platform can be considered as a rigid hub, and the large-span solar arrays are simplified as two sets of multi-panel structures connected by nonlinear flexible hinges. Because the yokes need sufficient capacity to support the large-span solar arrays, the stiffness of the yoke is generally designed to be very large compared with the flexible solar panels, so yokes can be considered as rigid rods.

Some system assumptions are made to ease the analysis:

• a. When the spacecraft is in orbit, the solar array is fully extended and the hinges are locked.

• b. Flexible hinges are simplified as revolute joints with an extra rotating spring that is ignored in terms of size and mass. Revolute joint only provides a rotational degree of freedom and the connection function for the hinge between two panels. The rotations of revolute joints lead to the rotating of the springs when the solar panels vibrate. So, we just consider the potential energy of the rotational springs in dynamic modeling process.

• c. The system's lateral vibration is solely taken into account, while in-plane vibration is ignored.

The solar array is made up of a honeycomb panel baseboard and solar cells that are covered by glass fiber sheets. Only honeycomb panels are taken into account in this study because they are the primary structures of solar arrays, as shown in Fig. 2.

Fig. 2

Structure diagram of honeycomb panel

The honeycomb panel, of height $2h$, is mainly composed of a honeycomb core with height $2h_{c}$ and face sheets (aluminum plate) with height $h_{f}$ (see Fig. 3). The thickness of coating and adhesives is ignored. The honeycomb core and face sheets are both made of aluminum, so the elastic modulus $E_{f}$, mass density $\rho_{f}$, and shear modulus $G_{f}$ of the face sheet are the same as the elastic modulus $E_{0}$, mass density $\rho_{0}$, and shear modulus $G_{0}$ of the aluminum.

Fig. 3

Equivalent isotropic model for the honeycomb sandwich panel

The cell of honeycomb core is a regular hexagon. $l_{c}$ and $\delta_{c}$ are the length and thickness of the honeycomb wall. $\rho_{c}$ is the mass density of the honeycomb core. Based on equivalent theory proposed in [24], the composite honeycomb panel can be considered equivalent to an isotropic elastic rectangular thin plate, as shown in Fig. 3. The equivalent material properties of honeycomb panel, including Poisson’s ratio $\nu$, equivalent elastic modulus $E_{eq}$, equivalent mass density $\rho_{eq}$, shear modulus $G_{eq}$, and equivalent thickness $t_{eq}$ can be expressed as:

$$ \begin{gathered} t_{eq} = \sqrt {12h_{c}^{2} + 12h_{c} h_{f} + 4h_{f}^{2} } \;,\;\;\;\;\;\;E_{eq} = 2h_{f} E_{f} /t_{eq} \;, \hfill \\ G_{eq} = 2h_{f} G_{f} /t_{eq} \;,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\rho_{eq} = \left( {2h_{f} \rho_{f} + 2h_{c} \rho_{c} } \right)/t_{eq} \;, \hfill \\ \end{gathered} $$

(1)

where $\rho_{c} = \frac{8}{3}\frac{{\delta_{c} }}{{l_{c} }}\rho_{0} \;.$ For convenience, let $t_{eq} = H$ in later expressions.

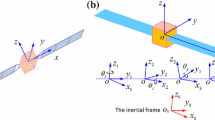
Coordinate systems are defined as shown in Fig. 1. $O_{0} - x_{0} y_{0} z_{0}$ is the inertial reference coordinate system fixed on the orbit around the earth. Point $O$ is the center of the rigid hub. $O - xyz$ is the floating coordinate system fixed on the rigid hub, which is obtained by three successive rotations, as illustrated in Fig. 4. First, we rotate the basis $\left\{ {\xi_{1} ,\xi_{2} ,\xi_{3} } \right\}$ an angle $\theta_{z}$ about the axis aligned with the director $\xi_{3}$. Next, we rotate the basis $\left\{ {\hat{\xi }_{1} ,\hat{\xi }_{2} ,\xi_{3} } \right\}$ an angle $\theta_{x}$ about the axis aligned with the director $\hat{\xi }_{1}$. Finally, we rotate the basis $\left\{ {\hat{\xi }_{1} ,y_{0} ,\hat{\xi }_{3} } \right\}$ an angle $\theta_{y}$ about the axis aligned with the new director $y_{0}$. The transformation matrix from $O - xyz$ to $O_{0} - x_{0} y_{0} z_{0}$ is thus expressed as:

$$ {\mathbf{A}}_{{oo_{0} }} = \left[ {\begin{array}{*{20}c} {\cos \theta_{z} } & { - \sin \theta_{z} } & 0 \\ {\sin \theta_{z} } & {\cos \theta_{z} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \theta_{x} } & { - \sin \theta_{x} } \\ 0 & {\sin \theta_{x} } & {\cos \theta_{x} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\cos \theta_{y} } & 0 & {\sin \theta_{y} } \\ 0 & 1 & 0 \\ { - \sin \theta_{y} } & 0 & {\cos \theta_{y} } \\ \end{array} } \right]\; $$

(2)

Fig. 4

Coordinate transformation process

Point $O_{i}$ is the midpoint of the panel edge. Parallel to $O - xyz$, $O_{i} - x_{i} y_{i} z_{i}$ is the floating coordinate system fixed on the panel, where $i = 1,2, \ldots ,N$ represents the number of the panel. The transformation matrices from $O_{i} - x_{i} y_{i} z_{i}$ to $O - xyz$ are given by:

$$ {\mathbf{A}}_{{o_{i} {\kern 1pt} o}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\; $$

(3)

2.2 Displacement field expressions for the solar panels

The transverse displacements of the solar panels are expressed as:

$$ \left\{ {\begin{array}{*{20}c} {w(x_{{R_{i} }} ,y_{{R_{i} }} ,t) = W(x_{{R_{i} }} ,y_{{R_{i} }} )\sin \omega {\kern 1pt} {\kern 1pt} t,} \\ {w(x_{{L_{i} }} ,y_{{L_{i} }} ,t) = W(x_{{L_{i} }} ,y_{{L_{i} }} )\sin \omega {\kern 1pt} {\kern 1pt} t,} \\ \end{array} } \right.{\text{ for }}i = 1,2, \cdots N $$

(4)

where $\omega$ represent the natural frequency of the whole system (the global mode). $W(x_{{R_{i} }} ,y_{{R_{i} }} )$ and $W(x_{{L_{i} }} ,y_{{L_{i} }} )$ are the modal functions of the solar panels.

Some previous studies of flexible solar panel vibrations adopted eigenfunctions of beams as basic functions [19], but the relatively slow computational speed and convergence rate have significant limitations since the eigenfunctions of beams contain a large number of trigonometric functions. To enhance the speed of computations, we adopt the approach proposed by Bhat [25] and use the more efficient characteristic orthogonal polynomials as basis functions instead of trigonometric functions. So, the modal functions $W(x_{{R_{i} }} ,y_{{R_{i} }} ), \, W(x_{{L_{i} }} ,y_{{L_{i} }} )$ can be written as:

$$ \begin{aligned} W(x_{{R_{i} }} ,y_{{R_{i} }} ) & = \sum\limits_{m = 1}^{{m_{t} }} {\sum\limits_{n = 1}^{{n_{t} }} {A_{{_{mn} {\kern 1pt} }}^{{\left( {R_{i} } \right)}} \varphi_{m} (x_{{R_{i} }} ){\kern 1pt} {\kern 1pt} \varphi_{n} (y_{{R_{i} }} )} } \, \\ W(x_{{L_{i} }} ,y_{{L_{i} }} ) & = \sum\limits_{m = 1}^{{m_{t} }} {\sum\limits_{n = 1}^{{n_{t} }} {A_{{_{mn} {\kern 1pt} }}^{{\left( {L_{i} } \right)}} \varphi_{m} (x_{{L_{i} }} ){\kern 1pt} {\kern 1pt} \varphi_{n} (y_{{L_{i} }} )} } \\ \end{aligned} $$

(5)

where $\varphi_{m} (x_{{R_{i} }} )$, $\varphi_{n} (y_{{R_{i} }} )$, $\varphi_{m} (x_{{L_{i} }} )$, $\varphi_{n} (y_{{L_{i} }} )$ are characteristic orthogonal polynomials in the $x$ and $y$ directions, respectively (for details on these polynomials, see [25]). $m_{t}$ and $n_{t}$ are truncation numbers to be specified for any given model, while $A_{{_{mn} }}^{{\left( {R_{i} } \right)}}$ and $A_{{_{mn} }}^{{\left( {L_{i} } \right)}}$ are unknown coefficients.

2.3 Kinetic and potential energies of the system

With reference to Fig. 1, the position vector of $O$ in inertial coordinate system can be written as:

$$ {\mathbf{r}}_{o} { = }\left[ {\begin{array}{*{20}c} {x_{o} } & {y_{o} } & {z_{o} } \\ \end{array} } \right]^{{\text{T}}} $$

(6)

where $x_{o}$, $y_{o}$ and $z_{o}$ are coordinates of $O$ in $O_{0} - x_{0} y_{0} z_{0}$.

$P_{{0_{i} }}$ is the initial position of an arbitrary point $P$ on the panel. ${\mathbf{r}}_{{o_{i} P_{{0_{i} }} }}$ represents the initial position vector in $O_{i} - x_{i} y_{i} z_{i}$. It can be expressed as:

$$ {\mathbf{r}}_{{o_{i} P_{{0_{i} }} }} { = }\left[ {\begin{array}{*{20}c} {x_{i} } & {y_{i} } & {z_{i} } \\ \end{array} } \right]^{{\text{T}}} {, }i = 1,2, \ldots ,N $$

(7)

${\mathbf{r}}_{{P_{{{0}_{i} }} P_{i} }}$ is the relative position vector of point $P_{i}$ in $O_{i} - x_{i} y_{i} z_{i}$ given by

$$ {\mathbf{r}}_{{P_{{{0}_{i} }} P_{i} }} = \left[ {\begin{array}{*{20}c} { - z_{i} \frac{{\partial w\left( {x_{i} ,y_{i} ,t} \right)}}{{\partial x_{i} }},} & { - z_{i} \frac{{\partial w\left( {x_{i} ,y_{i} ,t} \right)}}{{\partial y_{i} }},} & {w\left( {x_{i} ,y_{i} ,t} \right)} \\ \end{array} } \right]^{{\text{T}}} , \, i = 1,2, \ldots ,N $$

(8)

${\mathbf{r}}_{{oP_{i} }}$ and ${\mathbf{r}}_{{o_{i} P_{i} }}$ denote deformed position vectors of point $P_{i}$ in the floating coordinate system $O - xyz$ and $O_{i} - x_{i} y_{i} z_{i}$, respectively:

$$ {\mathbf{r}}_{{o_{i} P_{i} }} = {\mathbf{r}}_{{o_{i} P_{{0_{i} }} }} + {\mathbf{r}}_{{P_{{{0}_{i} }} P_{i} }} = \left[ {\begin{array}{*{20}c} {x_{i} - z_{i} \frac{{\partial w\left( {x_{i} ,y_{i} ,t} \right)}}{{\partial x_{i} }}} \\ {y_{i} - z_{i} \frac{{\partial w\left( {x_{i} ,y_{i} ,t} \right)}}{{\partial y_{i} }}} \\ {z_{i} + w\left( {x_{i} ,y_{i} ,t} \right)} \\ \end{array} } \right], \, i = 1,2, \ldots ,N $$

(9)

$$ {\mathbf{r}}_{{oP_{i} }} = {\mathbf{r}}_{{oo_{i} }} + {\text{A}}_{{o_{i} {\kern 1pt} o}} {\mathbf{r}}_{{o_{i} P_{i} }} = \left[ {\begin{array}{*{20}c} {r_{0} + a(i - 1) + x - z_{i} \frac{{\partial w\left( {x_{i} ,y_{i} ,t} \right)}}{{\partial x_{i} }}} \\ {y - z_{i} \frac{{\partial w\left( {x_{i} ,y_{i} ,t} \right)}}{{\partial y_{i} }}} \\ {z + w\left( {x_{i} ,y_{i} ,t} \right)} \\ \end{array} } \right], \, i = 1,2, \ldots N $$

(10)

where $w\left( {x_{i} ,y_{i} ,t} \right)$ denotes the transverse displacement of $P_{i}$ on the panel, $a$ is the length of the panel and ${\mathbf{r}}_{{oo_{i} }} = \left[ {\begin{array}{*{20}c} {r_{0} + a(i - 1),} & {0,} & 0 \\ \end{array} } \right]^{T}$. $r_{0}$ is shown in Fig. 1.

Then, using a series of vector operations, the position vector of an arbitrary point $P_{i}$ in $O_{0} - x_{0} y_{0} z_{0}$ can be expressed as:

$$ {\mathbf{r}}_{{P_{i} }} = {\mathbf{r}}_{o} + {\mathbf{A}}_{{oo_{0} }} {\mathbf{r}}_{{oP_{i} }} $$

(11)

Hence, the velocity of the panel can be obtained as:

$$ {\mathbf{v}}_{{P_{i} }} = {\dot{\mathbf{r}}}_{{P_{i} }} = {\dot{\mathbf{r}}}_{o} + {\dot{\mathbf{A}}}_{{oo_{0} }} {\mathbf{r}}_{{oP_{i} }} + {\mathbf{A}}_{{oo_{0} }} {\dot{\mathbf{r}}}_{{oP_{i} }} $$

(12)

where $\left( {\mathop {}\limits^{ \bullet } } \right)$ denotes the time derivative.

The matrix of principal moments of inertia of the central rigid hub is expressed as:

$$ {\text{J}}_{{\text{R}}} = \, \left[ {\begin{array}{*{20}c} {J_{x} } & 0 & 0 \\ 0 & {J_{y} } & 0 \\ 0 & 0 & {J_{z} } \\ \end{array} } \right] $$

(13)

where $J_{x}$, $J_{y}$ and $J_{z}$ are the rigid hub moments of inertia about axes x, y and z.

The kinetic energy of the whole system can then be expressed as:

$$ \begin{aligned} T & = \frac{1}{2}\rho \sum\limits_{i = 1}^{N} {\int\limits_{{V_{{R_{i} }} }} {{\mathbf{v}}_{{P_{{R_{i} }} }} }^{{\text{T}}} \cdot {\mathbf{v}}_{{P_{{R_{i} }} }} dV} + \frac{1}{2}\rho \sum\limits_{i = 1}^{N} {\int\limits_{{V_{{L_{i} }} }} {{\mathbf{v}}_{{P_{{L_{i} }} }} }^{{\text{T}}} \cdot {\mathbf{v}}_{{P_{{L_{i} }} }} dV} \hfill \\ & \quad + \frac{1}{2}m_{R} (\dot{x}_{o}^{2} + \dot{y}_{o}^{2} + \dot{z}_{o}^{2} ) + \frac{1}{2}{{\varvec{\upomega}}}^{{\text{T}}} {\mathbf{J}}_{{\text{R}}} {{\varvec{\upomega}}} \hfill \\ \end{aligned} $$

(14)

where $\rho$ and $m_{R}$ represent the density of the panel and the mass of the central rigid hub, respectively. The angular velocity vector of the spacecraft is derived by:

$$ {{\varvec{\upomega}}} = \left[ {\begin{array}{*{20}c} {\omega_{x} } \\ {\omega_{y} } \\ {\omega_{z} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \theta_{y} } & 0 & { - \cos \theta_{x} \sin \theta_{y} } \\ 0 & 1 & {\sin \theta_{x} } \\ {\sin \theta_{y} } & 0 & {\cos \theta_{x} \cos \theta_{y} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{\theta }_{x} } \\ {\dot{\theta }_{y} } \\ {\dot{\theta }_{z} } \\ \end{array} } \right]\; $$

Because missions always require satellites to reach high-precision orientation, the satellite rotates very slowly at a tiny angle when the attitude adjusts. Consequently, for the vibration analysis we are here interested in, the attitude angles $\theta_{x}$, $\theta_{y}$ and $\theta_{z}$ are assumed to be small. Therefore, Taylor expansion can be used to get the following first-order approximations for trigonometric functions of attitude angles:

$$ \begin{gathered} \sin \theta_{x} = \theta_{x} , \, \sin \theta_{y} = \theta_{y} , \, \sin \theta_{z} = \theta_{z} \hfill \\ \, \cos \theta_{x} = \cos \theta_{y} = \cos \theta_{z} = 1 \hfill \\ \end{gathered} $$

(15)

For simplicity of writing, $w_{{R_{i} }} (x_{{R_{i} }} ,y_{{R_{i} }} ,t)$, $w_{{L_{i} }} (x_{{L_{i} }} ,y_{{L_{i} }} ,t)$, $W_{{R_{i} }} (x_{{R_{i} }} ,y_{{R_{i} }} )$ and $W_{{L_{i} }} (x_{{L_{i} }} ,y_{{L_{i} }} )$ are abbreviated to $w_{{R_{i} }}$, $w_{{L_{i} }}$, $W_{{R_{i} }}$ and $W_{{L_{i} }}$, respectively. It should be pointed out that the third- and higher-order coupling terms involving products of w, θ_x, θ_y, θ_z, x_o, y_o and z_o and/or the partial derivatives respect to time t, x and/or y are neglected in the expression of the kinetic energy. Then, substituting Eqs. (12), (13) and (15) into Eq. (14), the expanded expression of the kinetic energy is obtained as:

$$ \begin{aligned} T &&= \frac{1}{2}\rho \sum\limits_{i = 1}^{N} {\int\limits_{{V_{{R_{i} }} }} {\Re_{T} } } {\text{d}}V_{{R_{i} }} + \frac{1}{2}\rho \sum\limits_{i = 1}^{N} {\int\limits_{{V_{{L_{i} }} }} {\aleph_{T} } } {\text{d}}V_{{L_{i} }} \hfill \\ &\quad + \frac{1}{2}m_{R} (\dot{x}_{o}^{2} + \dot{y}_{o}^{2} + \dot{z}_{o}^{2} ) + \frac{1}{2}\left( {J_{x} \dot{\theta }_{x}^{2} + J_{y} \dot{\theta }_{y}^{2} + J_{z} \dot{\theta }_{z}^{2} } \right) \hfill \\ \end{aligned} $$

(16)

where

$$ \begin{aligned} \Re_{T} & = \left\{ {z_{{R_{i} }}^{2} \left( {\frac{{\partial \dot{w}_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}} \right)^{2} } \right. + z_{{R_{i} }}^{2} \left( {\frac{{\partial \dot{w}_{{R_{i} }} }}{{\partial y_{{R_{i} }} }}} \right)^{2} + \dot{w}_{{R_{i} }}^{2} + \left[ {x_{{R_{i} }} + r_{0} + a(i - 1)} \right]^{2} \left( {\dot{\theta }_{z}^{2} + \dot{\theta }_{y}^{2} } \right) \\ & \quad + y_{{R_{i} }}^{2} \left( {\dot{\theta }_{x}^{2} + \dot{\theta }_{z}^{2} } \right) + z_{{R_{i} }}^{2} \left( {\dot{\theta }_{y}^{2} + \dot{\theta }_{x}^{2} } \right) + 2\left[ {x_{{R_{i} }} + r_{0} + a(i - 1)} \right]\dot{\theta }_{z} \dot{y}_{o} \\ & \quad + \dot{x}_{o}^{2} + \dot{y}_{o}^{2} + \dot{z}_{o}^{2} + 2\dot{z}_{o} \left\{ {\dot{w}_{{R_{i} }} - \left[ {x_{{R_{i} }} + r_{0} + a(i - 1)} \right]\dot{\theta }_{y} + y_{{R_{i} }} \dot{\theta }_{x} } \right\} \\ & \quad - 2\left[ {x_{{R_{i} }} + r_{0} + a(i - 1)} \right]y_{{R_{i} }} \dot{\theta }_{x} \dot{\theta }_{y} - 2y_{{R_{i} }} \dot{\theta }_{z} \dot{x}_{o} - 2\left\{ {\left[ {x_{{R_{i} }} + r_{0} + a(i - 1)} \right]\dot{w}_{{R_{i} }} + z_{{R_{i} }}^{2} \frac{{\partial \dot{w}_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}} \right\}\dot{\theta }_{y} \\ & \quad \left. { + 2\left( {y_{{R_{i} }} \dot{w}_{{R_{i} }} + z_{{R_{i} }}^{2} \frac{{\partial \dot{w}_{{R_{i} }} }}{{\partial y_{{R_{i} }} }}} \right)\dot{\theta }_{x} } \right\} \\ \end{aligned} $$

with $w_{{R_{i} }} = w(x_{{R_{i} }} ,y_{{R_{i} }} ,t)$ the displacement of the ith panel at the right hand defined in (4). The expression of $\aleph_{T}$ can be obtained from $\Re_{T}$ by replacing $r_{0} + a(i - 1)$ and $R_{i}$ with $- r_{0} - a(i - 1)$ and $L_{i}$.

The potential energy of the spacecraft with hinged panels consists of two parts: the strain energy of the panels and the potential energy stored in the rotational springs. The torsional joint is described as a single-degree-of-freedom massless system, and based on experimental parameter identification [16], the torque transmitted by the joint can be represented as a function of the instantaneous state of the joint:

$$ M_{s}^{T} = c\Delta \dot{\theta }_{s} + k\Delta \theta_{s} + k_{n} \left( {\Delta \theta_{s} } \right)^{3} + \mu {\text{sign}}(\Delta \dot{\theta }_{s} ),{ (}s = R_{{A_{i} }} ,R_{{B_{i} }} ,L_{{A_{i} }} ,L_{{B_{i} }} ) $$

(17)

where the terms on the right-hand side represent linear damping, linear spring, nonlinear spring and Coulomb friction, respectively. $c,k,k_{n} ,\mu$ are the linear damping coefficient, linear spring stiffness coefficient, nonlinear spring stiffness coefficient and Coulomb friction torque, respectively. $\Delta \theta_{s}$ denotes the rotational angles of hinges $A_{{R_{i} }}$,$B_{{R_{i} }}$,$A_{{L_{i} }}$ and $B_{{L_{i} }}$ shown in Fig. 1.

The potential energy of the system can be expressed as:

$$ \begin{aligned} U & = \sum\limits_{i = 1}^{N} {\frac{D}{2}\int_{0}^{a} {\int_{ - b}^{b} {\left[ {\left( {\frac{{\partial^{2} w_{{R_{i} }} }}{{\partial x_{{R_{i} }}^{2} }}} \right)^{2} + 2v\frac{{\partial^{2} w_{{R_{i} }} }}{{\partial x_{{R_{i} }}^{2} }}\frac{{\partial^{2} w_{{R_{i} }} }}{{\partial y_{{R_{i} }}^{2} }} + \left( {\frac{{\partial^{2} w_{{R_{i} }} }}{{\partial y_{{R_{i} }}^{2} }}} \right)^{2} + 2\left( {1 - v} \right)\left( {\frac{{\partial^{2} w_{{R_{i} }} }}{{\partial x_{{R_{i} }} \partial y_{{R_{i} }} }}} \right)^{2} } \right]} } dx_{{R_{i} }} dy_{{R_{i} }} } \\ & \quad { + }\sum\limits_{i = 1}^{N} {\frac{D}{2}\int_{ - a}^{0} {\int_{ - b}^{b} {\left[ {\left( {\frac{{\partial^{2} w_{{L_{i} }} }}{{\partial x_{{L_{i} }}^{2} }}} \right)^{2} + 2v\frac{{\partial^{2} w_{{L_{i} }} }}{{\partial x_{{L_{i} }}^{2} }}\frac{{\partial^{2} w_{{L_{i} }} }}{{\partial y_{{L_{i} }}^{2} }} + \left( {\frac{{\partial^{2} w_{{L_{i} }} }}{{\partial y_{{L_{i} }}^{2} }}} \right)^{2} + 2\left( {1 - v} \right)\left( {\frac{{\partial^{2} w_{{L_{i} }} }}{{\partial x_{{L_{i} }} \partial y_{{L_{i} }} }}} \right)^{2} } \right]} } dx_{{L_{i} }} dy_{{L_{i} }} } \\ & \quad + \sum\limits_{i = 1}^{N} {M_{{A_{{R_{i} }} }}^{T} \Delta \theta_{{A_{{R_{i} }} }} } + \sum\limits_{i = 1}^{N} {M_{{B_{{R_{i} }} }}^{T} \Delta \theta_{{B_{{R_{i} }} }} + \sum\limits_{i = 1}^{N} {M_{{A_{{L_{i} }} }}^{T} \Delta \theta_{{A_{{L_{i} }} }} } + \sum\limits_{i = 1}^{N} {M_{{B_{{L_{i} }} }}^{T} \Delta \theta_{{B_{{L_{i} }} }} } } \\ \end{aligned} $$

(18)

where $D = \frac{{E_{eq} t_{eq}^{3} }}{{12\left( {1 - v^{2} } \right)}}$ denotes the flexural rigidity of the panel. $a$ and $b$ are the length and width of the panels, respectively.

2.4 Matching conditions

All panels are formulated independently, so we need to impose matching conditions to ensure the continuity of the structure. As shown in Fig. 1, the structures are connected by hinges $A_{{R_{i} }}$,$B_{{R_{i} }}$,$A_{{L_{i} }}$ and $B_{{L_{i} }}$(i = 1,2,…,N). The flexible hinge is simplified as a revolute joint with a rotational spring, where the size, mass, damping and Coulomb friction are neglected. The rotational angles can be written as $\Delta \theta_{s} \sin \omega t$, where the $\Delta \theta_{s}$ are now independent of time. If we denote $W_{{R_{i} }} = W(x_{{R_{i} }} ,y_{{R_{i} }} )$ and $W_{{L_{i} }} = W(x_{{L_{i} }} ,y_{{L_{i} }} )$, the matching conditions for rotational displacements about each hinge can then be written as:

$$ \Delta \theta_{{A_{{R_{1} }} }} = \left. {\frac{{\partial W_{{R_{1} }} }}{{\partial x_{{R_{1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{1} }} = 0 \\ y_{{R_{1} }} = y{}_{a} \end{subarray} } ,\;\;\Delta \theta_{{B_{{R_{1} }} }} = \left. {\frac{{\partial W_{{R_{1} }} }}{{\partial x_{{R_{1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{1} }} = 0 \\ y_{{R_{1} }} = y{}_{b} \end{subarray} } $$

(19)

$$ \Delta \theta_{{A_{{R_{i} }} }} = \left. {\frac{{\partial W_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i} }} = 0 \\ y_{{R_{i} }} = y_{a} \end{subarray} } - \left. {\frac{{\partial W_{{R_{i - 1} }} }}{{\partial x_{{R_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i - 1} }} = a \\ y_{{R_{i - 1} }} = y_{a} \end{subarray} } ,\;\;\Delta \theta_{{B_{{R_{i} }} }} = \left. {\frac{{\partial W_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i} }} = 0 \\ y_{{R_{i} }} = y_{b} \end{subarray} } - \left. {\frac{{\partial W_{{R_{i - 1} }} }}{{\partial x_{{R_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i - 1} }} = a \\ y_{{R_{i - 1} }} = y_{b} \end{subarray} } ,\;\;i = 2,3, \cdots ,N $$

(20)

$$ \Delta \theta_{{A_{{L_{1} }} }} = \left. {\frac{{\partial W_{{L_{1} }} }}{{\partial x_{{L_{1} }} }}} \right|_{\begin{subarray}{l} x_{{L_{1} }} = 0 \\ y_{{L_{1} }} = y{}_{a} \end{subarray} } ,\;\;\Delta \theta_{{B_{{L_{1} }} }} = \left. {\frac{{\partial W_{{L_{1} }} }}{{\partial x_{{L_{1} }} }}} \right|_{\begin{subarray}{l} x_{{L_{1} }} = 0 \\ y_{{L_{1} }} = y{}_{b} \end{subarray} } $$

(21)

$$ \Delta \theta_{{A_{{L_{i} }} }} = \left. {\frac{{\partial W_{{L_{i} }} }}{{\partial x_{{L_{i} }} }}} \right|_{\begin{subarray}{l} x_{{L_{i} }} = 0 \\ y_{{L_{i} }} = y_{a} \end{subarray} } - \left. {\frac{{\partial W_{{L_{i - 1} }} }}{{\partial x_{{L_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{L_{i - 1} }} = a \\ y_{{L_{i - 1} }} = y_{a} \end{subarray} } ,\;\;\Delta \theta_{{B_{{L_{i} }} }} = \left. {\frac{{\partial W_{{L_{i} }} }}{{\partial x_{{L_{i} }} }}} \right|_{\begin{subarray}{l} x_{{L_{i} }} = 0 \\ y_{{L_{i} }} = y_{b} \end{subarray} } - \left. {\frac{{\partial W_{{L_{i - 1} }} }}{{\partial x_{{L_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{L_{i - 1} }} = a \\ y_{{L_{i - 1} }} = y_{b} \end{subarray} } ,\;\;i = 2,3, \cdots ,N $$

(22)

Hinges are locked when the spacecraft operates in orbit, so there is no relative displacement at the point $A_{{R_{i} }}$,$B_{{R_{i} }}$,$A_{{L_{i} }}$ and $B_{{L_{i} }}$. Then, matching conditions for translation displacements can be derived as:

$$ \Delta W_{{A_{{\,R_{1} }} }} = W_{{\,R_{1} }} \left( {0,y_{a} } \right) = 0,\;\;\Delta W_{{B_{{\,R_{1} }} }} = W_{{\,R_{1} }} \left( {0,y_{b} } \right) = 0, $$

(23)

$$ \Delta W_{{A_{{R_{i} }} }} = W_{{R_{i} }} \left( {0,y_{a} } \right) - W_{{R_{i - 1} }} \left( {a,y_{a} } \right) = 0,\;\;\Delta W_{{B_{{R_{i} }} }} = W_{{R_{i} }} \left( {0,y_{b} } \right) - W_{{R_{i - 1} }} \left( {a,y_{b} } \right) = 0, $$

(24)

$$ \Delta W_{{A_{{\,L_{1} }} }} = W_{{\,L_{1} }} \left( {0,y_{a} } \right) = 0,\;\;\Delta W_{{B_{{\,L_{1} }} }} = W_{{\,L_{1} }} \left( {0,y_{b} } \right) = 0, $$

(25)

$$ \Delta W_{{A_{{L_{i} }} }} = W_{{L_{i} }} \left( {0,y_{a} } \right) - W_{{L_{i - 1} }} \left( {a,y_{a} } \right) = 0,\;\;\Delta W_{{B_{{L_{i} }} }} = W_{{L_{i} }} \left( {0,y_{b} } \right) - W_{{L_{i - 1} }} \left( {a,y_{b} } \right) = 0, $$

(26)

where $y_{a} { = }\frac{{ - b_{0} }}{2}$, $y_{b} = \frac{{b_{0} }}{2}$, $i = 2,3, \cdots ,N$.

2.5 Global natural frequencies and mode shapes

We use the Rayleigh–Ritz method to derive global modes of the system. Lagrange multipliers $\lambda_{{A_{{R_{i} }} }} , \, \lambda_{{B_{{R_{i} }} }} ,\lambda_{{A_{{L_{i} }} }} , \, \lambda_{{B_{{L_{i} }} }}$ ${(}i = 1,2, \cdots ,N)$ are introduced to impose the matching conditions (hinge constraints) derived in Sect. 2.4. The Lagrange function can then be constructed as:

$$ \Pi = U_{\max } - T_{\max } + \sum\limits_{i = 1}^{N} {\lambda_{{A_{{R_{i} }} }} \Delta W_{{A_{{R_{i} }} }} } + \sum\limits_{i = 1}^{N} {\lambda_{{B_{{R_{i} }} }} \Delta W_{{B_{{R_{i} }} }} } + \sum\limits_{i = 1}^{N} {\lambda_{{A_{{L_{i} }} }} \Delta W_{{A_{{L_{i} }} }} } + \sum\limits_{i = 1}^{N} {\lambda_{{B_{{L_{i} }} }} \Delta W_{{B_{{L_{i} }} }} } . $$

(27)

Here, as usual, $U_{\max }$ and $T_{\max }$ are the maximum potential and kinetic energies over a period of the response.

The motion of the spacecraft can be expressed in two parts: large-scale rigid motion without deformation of the solar arrays and small-scale rigid motion synchronously coupled with vibration of the solar arrays. So, the motion of the spacecraft is written as follows:

$$ \left\{ \begin{gathered} x_{o} = x_{or} + x_{ov} ,y_{o} = y_{or} + y_{ov} ,z_{o} = z_{or} + z_{ov} \hfill \\ \theta_{x} = \theta_{xr} + \theta_{xv} ,\theta_{y} = \theta_{yr} + \theta_{yv} ,\theta_{z} = \theta_{zr} + \theta_{zv} \hfill \\ \end{gathered} \right. $$

(28)

where the first term and the second term of each equation denote the rigid motion and vibration, respectively. During the process of solving these modes, the external force is set to zero, so the large-scale rigid motions $x_{or}$,$y_{or}$,$z_{or}$,$\theta_{xr}$,$\theta_{yr}$ and $\theta_{zr}$ are constants and only depend on the initial states, which are time independent.

Following [21], global modes of the system are expressed as rigid motions with superimposed elastic vibrations with only one uniform time dependence. So according to our previous works, we write the displacements and attitude angles of the spacecraft’s central rigid hub as follows:

$$ \begin{aligned} x_{o} &&= x_{or} + X_{o} \sin \omega {\kern 1pt} {\kern 1pt} t,\;\;\; \, y_{o} = y_{or} + Y_{o} \sin \omega {\kern 1pt} {\kern 1pt} t, \, z_{o} = z_{or} + Z_{o} \sin \omega {\kern 1pt} {\kern 1pt} t \hfill \\ \theta_{x} &&= \theta_{xr} + \theta_{0}^{\left( x \right)} \sin \omega {\kern 1pt} {\kern 1pt} t,\;\;\;\theta_{y} = \theta_{yr} + \theta_{0}^{\left( y \right)} \sin \omega {\kern 1pt} {\kern 1pt} t, \, \theta_{z} = \theta_{zr} + \theta_{0}^{\left( z \right)} \sin \omega {\kern 1pt} {\kern 1pt} t \hfill \\ \end{aligned} $$

(29)

where $X_{o}$, $Y_{o}$, $Z_{o}$, $\theta_{0}^{{{\kern 1pt} (x)}}$, $\theta_{{0}}^{{{\kern 1pt} (y)}}$ and $\theta_{{0}}^{{{\kern 1pt} (z)}}$ are unknown coefficients.

Then, the transverse displacement of the solar panel and the rigid displacement of the spacecraft are substituted into the kinetic energy and potential energy. It should be pointed out that the nonlinear terms of the torsional joints are neglected here to find the (linear) natural characteristics of the system.

The Lagrange function is minimized with respect to the unknown coefficients $X_{o}$, $Y_{o}$, $Z_{o}$, $\theta_{0}^{{{\kern 1pt} (x)}}$, $\theta_{{0}}^{{{\kern 1pt} (y)}}$, $\theta_{{0}}^{{{\kern 1pt} (z)}}$,$A_{{_{mn} }}^{{(R_{i} )}}$,$A_{{_{mn} }}^{{(L_{i} )}}$,$\lambda_{{R_{{A_{i} }} }}$,$\lambda_{{R_{{B_{i} }} }}$,$\lambda_{{L_{{A_{i} }} }}$ and $\lambda_{{L_{{B_{i} }} }}$:

$$ \;\frac{\partial \Pi }{{\partial X_{o} }} = 0,\;\; \, \frac{\partial \Pi }{{\partial Y_{o} }} = 0,\;\; \, \frac{\partial \Pi }{{\partial Z_{o} }} = 0 $$

(30)

$$ \;\frac{\partial \Pi }{{\partial \theta_{{_{0} }}^{(x)} }} = 0,\;\; \, \frac{\partial \Pi }{{\partial \theta_{{_{0} }}^{(y)} }} = 0,\;\; \, \frac{\partial \Pi }{{\partial \theta_{{_{0} }}^{(z)} }} = 0 $$

(31)

$$ \frac{\partial \Pi }{{\partial A_{mn}^{{\left( {R_{i} } \right)}} }} = 0, \, \frac{\partial \Pi }{{\partial A_{mn}^{{\left( {L_{i} } \right)}} }} = 0, \, i = 1,2, \ldots ,N $$

(32)

$$ \frac{\partial \Pi }{{\partial \lambda_{{A_{{R_{i} }} }} }} = 0,\;\; \, \frac{\partial \Pi }{{\partial \lambda_{{B_{{R_{i} }} }} }} = 0, \, \frac{\partial \Pi }{{\partial \lambda_{{A_{{L_{i} }} }} }} = 0,\;\; \, \frac{\partial \Pi }{{\partial \lambda_{{B_{{L_{i} }} }} }} = 0, \, i = 1,2, \ldots ,N $$

(33)

From these equations, the characteristic equation of the spacecraft can be obtained as:

$$ \left( {{\mathbf{K}} - \omega^{2} {\mathbf{M}} + {{\varvec{\Lambda}}}} \right){\mathbf{X}} = {\mathbf{0}}\; $$

(34)

where ${\mathbf{X}}$ is the column vector of unknown coefficients expressed as

$$ \begin{gathered} {\mathbf{X}} = [X_{o} ,\;Y_{o} ,\;Z_{o} ,\;\theta_{0}^{{{\kern 1pt} (x)}} ,\;\theta_{0}^{{{\kern 1pt} (y)}} ,\;\theta_{0}^{{{\kern 1pt} (z)}} ,\;A_{{_{11} }}^{{\left( {{\text{R}}_{{1}} } \right)}} ,\;A_{{_{12} }}^{{\left( {{\text{R}}_{{1}} } \right)}} ,\; \cdots ,\;A_{{_{{m_{t} n_{t} }} }}^{{\left( {{\text{R}}_{{1}} } \right)}} , \cdots ,A_{{_{11} }}^{{\left( {{\text{R}}_{{\text{i}}} } \right)}} ,\;A_{{_{12} }}^{{\left( {{\text{R}}_{{\text{i}}} } \right)}} ,\; \cdots ,\;A_{{_{{m_{t} n_{t} }} }}^{{\left( {{\text{R}}_{{\text{i}}} } \right)}} , \cdots , \hfill \\ \, A_{{_{11} }}^{{\left( {{\text{R}}_{{\text{N}}} } \right)}} ,\;A_{{_{12} }}^{{\left( {{\text{R}}_{{\text{N}}} } \right)}} ,\; \cdots ,\;A_{{_{{m_{t} n_{t} }} }}^{{\left( {{\text{R}}_{{\text{N}}} } \right)}} ,\;A_{{_{11} }}^{{\left( {L_{{1}} } \right)}} ,\;A_{{_{12} }}^{{\left( {L_{{1}} } \right)}} ,\; \cdots ,\;A_{{_{{m_{t} n_{t} }} }}^{{\left( {L_{{1}} } \right)}} , \cdots ,A_{{_{11} }}^{{\left( {L_{{\text{i}}} } \right)}} ,\;A_{{_{12} }}^{{\left( {L_{{\text{i}}} } \right)}} ,\; \cdots ,\;A_{{_{{m_{t} n_{t} }} }}^{{\left( {L_{{\text{i}}} } \right)}} , \cdots , \hfill \\ \, A_{{_{11} }}^{{\left( {L_{{\text{N}}} } \right)}} ,\;A_{{_{12} }}^{{\left( {L_{{\text{N}}} } \right)}} ,\; \cdots ,\;A_{{_{{m_{t} n_{t} }} }}^{{\left( {L_{{\text{N}}} } \right)}} ,\lambda_{{A_{{R_{1} }} }} ,\lambda_{{B_{{R_{1} }} }} , \cdots ,\lambda_{{A_{{R_{i} }} }} ,\lambda_{{B_{{R_{i} }} }} , \cdots ,\lambda_{{A_{{R_{N} }} }} ,\lambda_{{B_{{R_{N} }} }} ,\lambda_{{A_{{L_{1} }} }} ,\lambda_{{B_{{L_{1} }} }} , \cdots , \hfill \\ \, \lambda_{{A_{{L_{i} }} }} ,\lambda_{{B_{{L_{i} }} }} , \cdots ,\lambda_{{A_{{L_{N} }} }} ,\lambda_{{B_{{L_{N} }} }} ]^{{\text{T}}} \hfill \\ \end{gathered} $$

(35)

For the detailed form of the matrices ${\text{K}}$, ${\mathbf{M}}$ and ${{\varvec{\Lambda}}}$, we refer to our previous work [26]. Natural frequencies $\omega$ and mode shapes X can then finally be obtained by solving Eq. (34).

2.6 Nonlinear dynamical model of the spacecraft system

The global modes derived in the previous section are employed here to obtain a discrete system of ordinary differential equations (ODEs) for our spacecraft by Galerkin truncation.

For the (k + 6)th-order frequency, the corresponding analytical global modes of the system obtained in Sect. 2.5 can be written as:

$${\varvec{\varPhi}}_{k} = \left[ {X_{o,k} ,Y_{o,k} ,Z_{o,k} ,\theta_{0,k}^{(x)} ,\theta_{0,k}^{(y)} ,\theta_{0,k}^{(z)} ,W_{{R_{1} ,k}} , \cdots ,W_{{R_{N} ,k}} ,W_{{L_{1} ,k}} , \cdots ,W_{{L_{N} ,k}} } \right]^{T} ,k = 1, \ldots n $$

(36)

Based on Eqs. (4) and (28), the displacement of the flexible spacecraft can be expressed by the global modes and a set of generalized coordinates as follows

$$ \begin{gathered} \left[ {x_{o} ,y_{o} ,z_{o} ,\theta_{x} ,\theta_{y} ,\theta_{z} ,w_{{R_{1} }} , \cdots ,w_{{R_{N} }} ,w_{{L_{1} }} , \cdots ,w_{{L_{N} }} } \right]^{{\text{T}}} \hfill \\ = \left[ {x_{or} ,y_{or} ,z_{or} ,\theta_{xr} ,\theta_{yr} ,\theta_{zr} ,{\mathbf{0}}_{1 \times 2N} } \right]^{{\text{T}}} + \user2{\Phi p}\left( t \right) \hfill \\ \end{gathered} $$

(37)

where ${\varvec{\varPhi}}$ is the global modal matrix and p(t) is the vector of generalized coordinates. Then, the first n rigid-flexible coupled modes are expressed as:

$$ \left\{ {\begin{array}{*{20}c} {{\varvec{\varPhi}}= \left[ {{\varvec{\varPhi}}_{1} ,{\varvec{\varPhi}}_{2} , \cdots ,{\varvec{\varPhi}}_{n} } \right] \, } \\ {{\varvec{p}} = \left[ {p_{1} \left( t \right),p_{2} \left( t \right),...,p_{n} \left( t \right)} \right]^{{\text{T}}} } \\ \end{array} } \right. $$

(38)

Equation (37) is substituted into Eqs. (16) and (18), and by employing Hamilton’s principle the following discrete dynamical equations are obtained:

$$ \varvec{M}{\ddot{q}} + \varvec{C}{\dot{q}} + {\varvec{Kq}} + {\varvec{K}}_{n} ({\varvec{q}}) + {{\varvec{\upmu}}}(\dot{\varvec{q}}) = {\varvec{Q}} $$

(39)

where ${\varvec{M}}$,${\varvec{C}}$,${\varvec{K}}$, ${\varvec{K}}_{n}$ and ${{\varvec{\upmu}}}$ are the mass, viscous damping, linear stiffness, nonlinear stiffness and Coulomb friction matrices with dimensions (6 + n) × (6 + n), respectively. ${\varvec{Q}}$ is the maneuvering force vector with dimensions (6 + n) × 1, and ${\varvec{q}}$ is the vector with dimensions (6 + n) × 1 expressed as

$$ {\varvec{q}} = \left[ {x_{or} ,y_{or} ,z_{or} ,\theta_{xr} ,\theta_{yr} ,\theta_{zr} ,{\varvec{p}}^{{\text{T}}} } \right]^{{\text{T}}} $$

(40)

which represents the generalized coordinates. The details of ${\varvec{M}}$,${\varvec{C}}$,${\varvec{K}}$, ${\varvec{K}}_{n}$ and ${{\varvec{\upmu}}}$ are shown in Appendix 1, Appendix 2, Appendix 3 and Appendix 4.

3 Global modes of the spacecraft

In this section, the geometrical and material parameters of our specific spacecraft, shown in Fig. 1, are given and the first twelve global modes calculated and discussed.

The values of the various parameters of our spacecraft model are listed in Table 1.

Table 1 Geometric and material parameters of the LSFS

The truncation numbers $m_{t}$ and $n_{t}$ are chosen based on the accuracy of the solutions obtained. Larger numbers give more accurate solutions. From the convergence study in [26], we conclude that sufficiently accurate results are obtained by taking $m_{t} = n_{t} = 6$.

Frequencies and corresponding mode shapes (eigenvectors) can be derived from the characteristic equation. The elements in the eigenvectors represent the unknown coefficients $A_{{_{mn} }}^{{\left( {R_{i} } \right)}}$, $A_{{_{mn} }}^{{\left( {L_{i} } \right)}}$ and ${{\varvec{\Lambda}}}$. $A_{{_{mn} }}^{{\left( {R_{i} } \right)}}$ and $A_{{_{mn} }}^{{\left( {L_{i} } \right)}}$ are used to determine the amplitudes of the flexible panels; ${{\varvec{\Lambda}}}$ is used to confirm constraint conditions at hinges. The first six frequencies and eigenvectors are relative to the six rigid body motions ($x_{o} ,y_{o} ,z_{o} ,\theta_{x} ,\theta_{y} ,\theta_{z}$), and those six frequencies are zero and neglected in the following analyses. Then, the first twelve rigid-flexible coupling global modes of the system can be obtained and mode shapes are plotted as shown in Fig. 5.

Fig. 5

First twelve global mode shapes of the spacecraft

Some interesting phenomena can be observed in Fig. 5. Different from the mode shapes in Ref. [12], the first six rigid-flexible coupling global modes of the spacecraft appear as the bending modes for multi-panel solar arrays with a large vibration of the rotation springs, but no deformations of the panels, so here the rigid bending modes mean flexible torsional modes for the rotational springs, which mainly reveal the inherent properties of the rotational springs. It proves that the flexible hinges have a great effect on the dynamic properties of the system. If the mode shapes for the two sets of panels are completely symmetric bending, the vibrations of flexible panels will be coupled with the rigid translation $z_{o}$, such as in the 1st, 3rd, 7th and 11th modes. If the mode shapes of the pair of panels are antisymmetric bending, the vibrations of flexible panels will be coupled with the rigid attitude motion $\theta_{y}$, such as in the 2nd, 4th, 8th and 12th modes. If the mode shapes of the two-side panels are symmetric torsion, the vibrations of flexible panels will be coupled with the rigid attitude motion $\theta_{x}$, such as in the 6th and 10th modes. However, if the vibrations for the two sets of panels represent antisymmetric torsion, the flexible vibrations of the panels have no coupling with rigid motions of the central body, such as in the 5th and 9th modes.

4 Nonlinear dynamical response of the spacecraft

Here we present and analyze solutions of the low-dimensional nonlinear spacecraft model derived in Sect. 2.6 under forcing as a result of various maneuvering scenarios, including pulsed excitation, harmonic excitation and periodic pulse excitation. To determine the accuracy of the computational model, we compare results obtained by taking into account different numbers, n, of modes in the Galerkin approximation. We also perform a parametric analysis to assess the effect of the nonlinear flexible hinges on spacecraft dynamics.

4.1 Nonlinear response under an orbital maneuvering force

The orbital maneuvering force F acting on the rigid central module in the z direction is defined as follows:

$$ F = \left\{ \begin{aligned} & F_{0} \sin \left( {\frac{2\pi }{{T_{1} }}} \right), \quad 0 \le t \le T_{1} \\ & F_{0} , \quad T_{1} < t < T_{1} + T_{2} \\ & F_{0} \sin \left[ {\frac{2\pi }{{T_{1} }}\left( {t - \frac{{T_{2} }}{4}} \right)} \right], \quad T_{1} + T_{2} \le t \le 2T_{2} \hfill \\ \end{aligned} \right. $$

(41)

where F₀ is the amplitude of F(t). The time history of F(t) with T₁ = 10 s, T₂ = 20 s and F₀ = 20 N is shown in Fig. 6.

Fig. 6

The orbital maneuvering force F

In this case, ${\varvec{Q}} = \left[ {0,0,F,0,0,0,F{\mathbf{Z}}_{{\mathbf{0}}} } \right]^{{\text{T}}}$. The nonlinear response is calculated by solving Eq. (39), and the results are plotted Figs. 7 and 8.

Fig. 7

Motions of the spacecraft excited by F: a Translation in the z direction; b attitude motion around the x direction; c attitude motion around the y direction; d attitude motion around the z direction

Fig. 8

Deflections of the solar array tip for different hinge linear stiffness: a k = 50 Nm/rad; b k = 100 Nm/rad; c k = 500 Nm/rad; d k = 1000 Nm/rad

In Fig. 7, the motions of the spacecraft are shown when taking two (n = 2) and four (n = 4) rigid-flexible modes into account. The curves for n = 2 and n = 4 agree perfectly, which means that the two-degrees-of-freedom model is already accurate enough to calculate the spacecraft’s motions in this case.

From Fig. 7 (a), we can observe that the orbital maneuvering process causes large displacements in the z direction, and rigid-flexible coupling occurs. According to the mode shapes of the system, the first-order mode is coupled with the translation of the spacecraft in the z direction, and this mode is excited by the orbital maneuvering force. The large amplitudes of the motion at 10 s and 30 s illustrate how a sudden change of the force causes relatively large oscillations of the spacecraft. It can be seen that the orbital maneuvering process has almost no effect on the attitude motions $\theta_{x}$ and $\theta_{z}$ in Fig. 7b, d, but that it causes the oscillations of $\theta_{y}$ in Fig. 7d. According to the global modes of the linear system, the translations and rotations are independent, but we see from Fig. 7c that the hinge nonlinearity couples the motion in the z direction with the rotational vibration in the y direction.

The oscillation response of the solar array’s tip is presented in Fig. 8. For the flexible vibrations of the solar array, it is sufficient to use only two modes to discretize the model. The effect of the hinge linear stiffness k is analyzed in the figure. Due to the increase of hinge stiffness that reduces the flexibility of the whole system, the vibration amplitude of the solar array decreases. However, the increase of hinge stiffness also leads to shorter period and more intensive oscillations of the solar array, especially during 10s–30s. In addition, the larger hinge stiffness may lead to longer residual vibrations and stronger rigid-flexible coupling effects. On account of this, it is necessary to design a vibration controller for the spacecraft when its hinge stiffness is large.

4.2 Nonlinear response under an attitude driving pulse torque

In this case, an attitude driving pulse torque acts on the y axis of the spacecraft’s central module, and Q is defined as ${\varvec{Q}} = \left[ {0,0,0,0,\tau_{y} ,0,\tau_{y} {\uptheta }_{0}^{(y)} } \right]^{{\text{T}}}$.

$$ \tau_{y} = \left\{ \begin{gathered} 2N \cdot {\text{m}} , \, 0 \le t \le 4{\text{s}} \hfill \\ 0, \, 4 < t < 8{\text{s}} , \, t > 12s \hfill \\ - 2N \cdot {\text{m}} , \, 8 \le t \le 12{\text{s}} \hfill \\ \end{gathered} \right. $$

(42)

The time history of $\tau_{y}$ is shown in Fig. 9.

Fig. 9

The attitude driving pulse torque $\tau_{y}$

The nonlinear response under this excitation is shown in Fig. 10. The figure shows that using the first two global modes to discretize the system is not sufficient to accurately calculate the nonlinear response to this type of excitation. More modes should be taken, and the figure shows that the response curves overlap when n = 4 and n = 6. So, the nonlinear model can be truncated as a four-degrees-of-freedom model in this case.

Fig. 10

Motions of the spacecraft under the pulse torque $\tau_{y}$: a Attitude motions around the y axis; b rigid-flexible coupling vibrations; c residual vibrations; d rigid-flexible coupling translations in x, y, z directions (n = 4)

From Fig. 10a, the spacecraft can achieve attitude adjustment through a pulse torque, and the attitude angle is changed from 0 rad to 0.082 rad. The attitude motion $\theta_{y}$ is the sum of the rigid motion $\theta_{yr}$ and the vibration $\theta_{yv}$. Figure 10b illustrates the details of vibrations of the rigid body caused by the attitude driving pulse torque. At the same time, Fig. 11b shows oscillations of the solar array’s tip, which are synchronous with $\theta_{yv}$. So, a clear rigid-flexible coupling phenomenon is revealed by comparing these two figures. It is demonstrated that the attitude maneuvering process excites vibrations of the solar arrays, and conversely the vibrations of the solar arrays also have an effect on the attitude of the spacecraft. The second and fourth modes in Fig. 5 show that the solar array vibrations have an effect on the hub’s attitude motion $\theta_{y}$: the vibrations and the rigid attitude motion are coupled. Comparison of Figs. 10b and 11b gives further evidence of vibrations being synchronous with $\theta_{y}$.

Fig. 11

Deflections of the solar array tip for different hinge linear stiffness: a k = 50 Nm/rad; b k = 100 Nm/rad; c k = 500 Nm/rad; d k = 1000 Nm/rad

Figure 10c shows the residual vibrations $\theta_{y - residual}$ when the attitude torque stops. It can be observed that the rigid-flexible coupling vibrations do not stop instantly when the attitude maneuvering process is over. The residual vibrations will last almost 4s and then decay gradually. It may affect the precision of the attitude adjustment for the spacecraft. So, cooperative controllers of attitude motions and flexible vibrations are essential for the design of spacecraft. As shown in Fig. 10d, the oscillation in the z direction is triggered by the attitude driving pulse torque, and the attitude motions are coupled with the translation, similar to what we saw in Fig. 7c.

Figure 11 shows the deflections of the solar array tip for different hinge linear stiffnesses. With the increase of the hinge stiffness, the vibration responses of the solar array fluctuate extensively, and the oscillation amplitudes become smaller. The stiffnesses of hinges have a great effect on the dynamical characteristics of the spacecraft. The attitude driving pulse torque acted on the rigid central hub may lead to complicated nonlinear oscillations of the solar arrays, especially when the pulse is suddenly applied or stopped. The impact on the system is more likely to arouse the rigid-flexible coupling effect.

4.3 Nonlinear response under a periodic attitude torque

Besides the pulse excitations mentioned before, a periodic torque is also one of the common ways of attitude maneuvering of the spacecraft. Here a periodic attitude torque is taken in the form ${\varvec{Q}} = \left[ {0,0,0,0,\tau_{y} ,0,\tau_{y} {\uptheta }_{0}^{(y)} } \right]^{{\text{T}}}$, shown in Fig. 12. The attitude of the spacecraft is adjusted to the desired goal by applying two cycles of sinusoidal torques in this case.

$$ \tau_{y} = \left\{ \begin{gathered} 2\sin (\frac{\pi }{6}t),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le t \le 24s, \hfill \\ 0{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} t > 24s. \hfill \\ \end{gathered} \right. $$

(43)

Fig. 12

The periodic attitude torque $\tau_{y}$

The nonlinear response is plotted in Fig. 13, where the attitude motion, the vibrations of solar arrays, the residual vibrations of the central platform and the translations of the spacecraft are displayed.

Fig. 13

Motions of the spacecraft under the periodic torque $\tau_{y}$: a Attitude motions around the y axis; b rigid-flexible coupling vibrations; c residual vibrations; d rigid-flexible coupling translations in x, y, z directions (n = 4)

From Fig. 13, we see that only using two modes in this case is not sufficient to guarantee an accurate model. Consequently, the first four rigid-flexible coupling modes of the system are employed to truncate the system of equations. The rigid-flexible coupling response curves of $\theta_{yv}$, similar to the sine form, are shown in Fig. 13b, but there are some small fluctuations at the amplitudes caused by the nonlinearities of the hinges. The residual oscillations of the central body last 2s after the attitude maneuvering process in Fig. 13c, and the damping and friction of the system play important roles for vibration attenuations. As shown in Fig. 13d, due to the nonlinear characteristics of hinges, the oscillation in the z direction is triggered by the attitude maneuvering process, and the attitude motions are closely coupled with the z translation.

Figure 14 analyzes the deflections of the solar array tip for different hinge linear stiffnesses. The flexibilities of hinges have a great effect on nonlinear responses of the system. With the increase of the hinge linear stiffness, the fluctuations in the amplitudes of curves become smaller, which means that increase of linear stiffness can attenuate the nonlinear features of the system. In addition, the curves for n = 2, n = 4 and n = 6 in Fig. 14a and b are very close, but the curves for n = 2 are gradually moving away from the curves for n = 4 and n = 6, as seen in Fig. 14c and d. It shows that the mode numbers for modal truncation should be increased when the hinge stiffness grows.

Fig. 14

Deflections of the solar array tip for different hinge linear stiffness: a k = 50 Nm/rad; b k = 100 Nm/rad; c k = 500 Nm/rad; d k = 1000 Nm/rad

4.4 Nonlinear response under a periodic pulse attitude torque

It is well known that the attitude adjusting process is sometimes not continuous, and it is usually conducted by an intermittent maneuvering with a certain regularity. In this case, the periodic pulse attitude torque is approximated by dividing the sinusoidal curve in Fig. 12 into discrete pulses, and its form is shown in Fig. 15. The forcing is defined as ${\varvec{Q}} = \left[ {0,0,0,0,\tau_{y} ,0,\tau_{y} {\uptheta }_{0}^{(y)} } \right]^{{\text{T}}}$, where $\tau_{y}$ is expressed as:

$$ \tau_{y} = \left\{ \begin{gathered} 2sign(\sin \frac{\pi }{6}t),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [t] \, {\text{is}}\,even, \hfill \\ 0{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \, {\kern 1pt} [t] \, {\text{is}}\,odd. \hfill \\ \end{gathered} \right. $$

(44)

Fig. 15

The periodic pulse attitude torque $\tau_{y}$

Here [] means rounding, and $0 \le t \le 24$.

Compared to the response under the continuous sine excitation with the same period and amplitude in Sect. 4.3, the vibration phenomena are different and more complicated under the periodic pulse excitation. Due to the discontinuity of the attitude driving torque in this case, the attitude motion $\theta_{y}$ in Fig. 16a can only achieve about twice the value of $\theta_{y}$ in Fig. 13a. The fluctuations of curves in Fig. 16b become more remarkable, which means the nonlinear rigid-coupling effect is stronger under the periodic pulse excitation. Besides, the residual vibrations in Fig. 16c last longer than under the continuous sine excitation. In addition, the coupling phenomenon caused by the hinge nonlinearity in Fig. 16d becomes more complicated.

Fig. 16

Motions of the spacecraft under the periodic pulse torque $\tau_{y}$: a Attitude motions around the y axis; b rigid-flexible coupling vibrations; c residual vibrations; d rigid-flexible coupling translations in x, y, z directions (n = 4)

From Fig. 17, we see that the vibration response of the solar arrays is characterized by both periodic excitation and pulse excitation, and the stiffness of hinges has a great effect on the dynamical characteristics of the spacecraft. Comparing Fig. 17a and d, we observe that with the increase of the hinge stiffness, the fluctuations of the solar array vibrations become smaller, and the amplitudes decrease. Compared to the relatively smooth curve in Fig. 14, the fluctuations of the curves are significantly increased, and the attitude periodic pulse torque leads to more complicated nonlinear oscillations of the solar arrays. Especially when the pulse is suddenly applied or stopped, the intermittent impact is more likely to arouse the stronger nonlinear characteristics of hinges.

Fig. 17

Deflections of the solar array tip for different hinge linear stiffness: a k = 50 Nm/rad; b k = 100 Nm/rad; c k = 500 Nm/rad; d k = 1000 Nm/rad

4.5 Nonlinear response under disturbing forces and torques

In general, the complex and longtime maneuvering process of the spacecraft may lead to disturbing forces and torques caused by liquid sloshing or other reasons. In this case, the system may present more complicated nonlinear dynamic behavior due to the nonlinearities of a large number of hinges. The disturbing forces and moments applied to the central rigid body of the spacecraft are expressed as follows:

$$ \left\{ \begin{gathered} F_{z} (t) = F_{d} \cos \Omega {\kern 1pt} {\kern 1pt} t \hfill \\ M_{y} (t) = M_{d} \cos \Omega {\kern 1pt} {\kern 1pt} t \hfill \\ \end{gathered} \right. $$

(45)

So, the forcing can be defined as ${\varvec{Q}} = \left[ {0,0,F_{z} ,0,\tau_{y} ,0,F_{z} {\text{Z}}_{0} + M_{y} {\uptheta }_{0}^{(y)} } \right]^{{\text{T}}}$, where $\Omega$ is the frequency of the periodic disturbance, $F_{d}$ is the amplitude of the disturbance force, and $M_{d}$ is the amplitude of the disturbance torque. We take $F_{d} = 8{\text{N}}$ and $M_{d} = 8\,{\rm Nm}$.

Based on the analysis of the above sections, it can be concluded that employing the first four global modes to discretize the model has been accurate enough to calculate the nonlinear response when a periodic force and torque are applied to the system at the same time. Thus, the response in this case will be calculated from the four-degrees-of-freedom nonlinear model.

The steady-state time-history responses, the phase portraits and the spectra for rigid-flexible coupling translations $z_{ov}$(z₀), rigid-flexible coupling rotations $\theta_{yv}$($\theta_{{y_{1} }}$), rotational displacements of the hinge $B_{{R_{1} }}$ and vibrations of the solar array tips $w_{{R_{3} }}$ are displayed in Fig. 18.

Fig. 18

Response of the system with $k_{n} = 10^{10} {\rm Nm}/{\rm rad}^{3}$, c = 1N ms/rad, μ = 0.01 and $\Omega = 6.3\,{\rm rad}/{\text{s}}$: a–c Rigid-flexible coupling translations of the spacecraft in the z direction; d–f rigid-flexible coupling rotations of the spacecraft around the y axis; g–h rotational displacements of the hinge $B_{{R_{1} }}$; j–k vibrations of the solar array tip; a, d, g and j are steady-state responses; b, e, h and k show the phase portrait; c, f, i and l give the spectrum of the steady-state response

As seen in Fig. 18, the responses of the spacecraft under the disturbing force and torque have strong nonlinear characteristics. The oscillations of the rigid central platform, hinges and solar arrays are in similar patterns, which means all components of the spacecraft are coupled with each other and the hinges have important effects on the dynamical behavior of the spacecraft. In addition, the response amplitudes appear at one third, three and other multiples of the external excitation frequency, and it can be concluded that superharmonic and subharmonic resonances have occurred due to the hinge nonlinearities. These are evident in Fig. 18c, f, i and l.

The role of hinge nonlinearities in spacecraft dynamics is explored further in Fig. 19, which shows frequency–response curves for different values of the nonlinear hinge stiffness. Because the nonlinear hinge stiffness is positive, the curves show hardening characteristic, with curves tilting to the right. As a result, there is multistability for a range of forcing frequencies with jumps at both ends of this range. Hysteresis cycles occur when the frequency is first increased and then decreased (or the other way around) across the main resonance. Under increasing nonlinear stiffness the vibration amplitudes go down, but the hardening characteristic becomes increasingly prominent, and the dynamical behavior of the system becomes much more complicated with superharmonic resonances occurring.

Fig. 19

Frequency–response curves of the system with various values of $k_{n} ({\rm Nm}/{\rm rad}^{3} )$: a–d Rigid-flexible coupling translations of the spacecraft in the z direction with a $k_{n} = 0$, b $k_{n} = 10^{7}$, c $k_{n} = 10^{8}$, d $k_{n} = 10^{9}$; e–h rigid-flexible coupling rotations of the spacecraft around the y axis with e $k_{n} = 0$, f $k_{n} = 10^{7}$, g $k_{n} = 10^{8}$, h $k_{n} = 10^{9}$; i–l rotational displacements of the hinge $B_{{R_{1} }}$ with i $k_{n} = 0$, j $k_{n} = 10^{7}$, k $k_{n} = 10^{8}$, l $k_{n} = 10^{9}$; m–p vibrations of the solar array tip with m $k_{n} = 0$, n $k_{n} = 10^{7}$, o $k_{n} = 10^{8}$, p $k_{n} = 10^{9}$

For a flexible spacecraft with linear hinges, the translation and attitude motion of its rigid central body will not be coupled with each other for the mode shapes of the system, as shown in Fig. 5. At the same time, it can also be observed from Fig. 19a and e that the highest amplitude of the translation and attitude motion of the spacecraft occurs at the first- and second-order natural frequencies, respectively, and $z_{ov}$(z₀), $\theta_{yv}$($\theta_{{y_{1} }}$) are not coupled.

However, that the translations of the rigid central body jump around the first natural frequency of the system can be deduced from Fig. 19b–d. Coincidentally, the attitude motions of the rigid central body jump around the first natural frequency synchronously are shown in Fig. 19f–h. Comparing Fig. 19b–d with f–h, it can be confirmed that the translations and attitude motions of the spacecraft are coupled with each other due to the influence of the nonlinear hinge stiffness. Under increasing nonlinear stiffness, the coupling effect becomes more pronounced. This conclusion explains the phenomena in Figs. 7c, 10d, 13d and 16d.

In order to study the effects of damping and friction of the hinges on the dynamical characteristics of the whole spacecraft system, the frequency–response curves of the system with $k_{n} = 10^{9}$ for various values of c and μ are shown in Figs. 20 and 21, respectively. It is observed that under increasing hinge damping and friction, the oscillation amplitudes of the system decrease gradually, and the stability of the system increases. The superharmonic resonance, however, still appears in Fig. 20 for hinge damping as large as c = 50 Nm·s/rad. In addition, the response curves in Fig. 21 show very complicated, possibly chaotic, behavior when μ = 0 Nm. On the other hand, under increasing hinge friction, the superharmonic resonances gradually diminish until they disappear. We therefore conclude, from comparisons of responses for various values of c and μ, that the characteristics of the hinges have a great effect on the whole system dynamics.

Fig. 20

Response of the system for various values of $c\;({\text{N\,m}}\,{\text{s/rad}})$: a Rigid-flexible coupling translations of the spacecraft in the z direction; b rigid-flexible coupling rotations of the spacecraft around the y axis; c rotational displacements of the hinge $B_{{R_{1} }}$; d vibrations of the solar array tip

Fig. 21

Response of the system for various values of $\mu \;(N\,{\text{m}})$: a rigid-flexible coupling translations of the spacecraft in the z direction; b rigid-flexible coupling rotations of the spacecraft around the y axis; c rotational displacements of the hinge $B_{{R_{1} }}$; d Vibrations of the solar array tip

We end with a comment on an unusual feature of the frequency–response curves in Figs. 19, 20 and 21, where these curves consist of two separate solution branches. One expects there to be a branch of unstable solutions connecting these branches. (These unstable branches are not detected by our numerical method, which only finds stable solutions.) These unstable branches connect folds of the solution curves, i.e., points with vertical tangent. However, it is noticeable from Figs. 19, 20 and 21 that the top (and left) branches in these cases do not quite reach the fold (the bottom branches seem to terminate closer to their fold). This is despite careful stepsize refinement to get closer to the fold. It seems therefore that another bifurcation, causing instability, is encountered under increasing forcing frequency before the fold would induce a jump. We leave further exploration of this phenomenon to future work.

5 Conclusions

In this paper, a low-dimensional nonlinear dynamical model of a large-scale flexible spacecraft has been obtained by exploiting the global modes of the system. Particular attention has been paid to the modeling of nonlinear hinges connecting the rigid central body of the spacecraft to the flexible solar panels. The connections are formulated as matching conditions that are enforced by means of Lagrange multipliers. The model is used to study the complicated nonlinear coupled rigid-flexible vibration phenomena of the spacecraft triggered by various orbit maneuvering forces and three-axis attitude driving torques. A parametric study is also carried out to investigate the dynamical effects of hinge stiffness, damping and friction. The main conclusions of our numerical results can be summarized as follows.

• (1) For such a complex spacecraft system, the nonlinear model established by using the global modes has the advantage of low dimension and high precision. The model discretized by only the first four modes is sufficient to accurately describe the complicated nonlinear characteristics of the system. Moreover, it is a general modeling method that can be applied to other spacecraft designs and indeed to other multibody systems.

• (2) The orbital and attitude maneuvering of the spacecraft causes complicated nonlinear behavior including multistability, jump phenomena, hysteresis and superharmonic resonances. Attitude driving torques acting on the rigid central hub may lead to complicated nonlinear oscillations of the solar arrays, especially when the pulse is suddenly applied or stopped, which is likely to induce nonlinear rigid-flexible coupling. Therefore, the attitude driving torque should be smooth and continuous to avoid more complicated nonlinear vibration phenomena. The residual vibrations may last a period of time before they decay gradually, which may affect the precision of the attitude adjustment of the spacecraft. So, cooperative controllers of attitude motions and flexible vibrations are essential for spacecraft design.

• (3) Hinge design has a great influence on the dynamic characteristics of the system. For a linear spacecraft system, the translational and attitude motions of its rigid central body will not be coupled with each other. However, nonlinear hinge stiffness couples translations and rotations, and the coupling becomes more obvious as the nonlinear stiffness is increased. On the other hand, under increasing hinge damping and friction the system’s response becomes simpler and of lower amplitude.

Appendices

Appendix 1

The mass matrix M is as follows:

$$ {\varvec{M}} = \left[ {\begin{array}{*{20}c} {M_{11} } & 0 & 0 & 0 & 0 & {M_{{1{6}}} } & {{\varvec{M}}_{17} } \\ 0 & {M_{22} } & 0 & 0 & 0 & {M_{{{26}}} } & {{\varvec{M}}_{27} } \\ 0 & 0 & {M_{33} } & {M_{34} } & {M_{{3{5}}} } & 0 & {{\varvec{M}}_{37} } \\ 0 & 0 & {M_{34}^{{}} } & {M_{44} } & {M_{{{45}}} } & 0 & {{\varvec{M}}_{47} } \\ 0 & 0 & {M_{{3{5}}}^{{}} } & {M_{{4{5}}}^{{}} } & {M_{55} } & {0} & {{\varvec{M}}_{57} } \\ {M_{{{16}}}^{{}} } & {M_{{{26}}}^{{}} } & 0 & 0 & {0} & {M_{66} } & {{\varvec{M}}_{67} } \\ {{\varvec{M}}_{17}^{{\text{T}}} } & {{\varvec{M}}_{27}^{{\text{T}}} } & {{\varvec{M}}_{37}^{{\text{T}}} } & {{\varvec{M}}_{47}^{{\text{T}}} } & {{\varvec{M}}_{57}^{{\text{T}}} } & {{\varvec{M}}_{67}^{{\text{T}}} } & {{\varvec{M}}_{77} } \\ \end{array} } \right] $$

The elements of the mass matrix M are as follows:

$$ M_{11} = 2N \cdot 4\rho hab + m_{R} $$

$$ M_{16} = - 2\rho h\sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {y_{{R_{i} }} } } } {\text{d}}y_{{R_{i} }} {\text{d}}x_{{R_{i} }} - 2\rho h\sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {y_{{L_{i} }} } } } {\text{d}}y_{{L_{i} }} {\text{d}}x_{{L_{i} }} $$

$$ M_{22} = 2N \cdot 4\rho hab + m_{R} $$

$$ M_{26} = \rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} [x_{{R_{i} }} + r_{0} { + }a{(}i - 1{\text{)] d}}y_{{R_{i} }} {\text{d}}x_{{R_{i} }} } } + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1){\text{] d}}y_{{L_{i} }} {\text{d}}x_{{L_{i} }} } } $$

$$ M_{33} = 2N \cdot 4\rho hab + m_{R} $$

$$ M_{34} = \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {{2}hy_{{R_{i} }} } {\text{ d}}y_{{R_{i} }} {\text{d}}x_{{R_{i} }} } } + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {{2}hy_{{L_{i} }} } {\text{ d}}y_{{L_{i} }} {\text{d}}x_{{L_{i} }} } } $$

$$ M_{{{35}}} = \rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} { - 2h} [x_{{R_{i} }} + r_{0} + a(i - 1)]{\text{ d}}y_{{R_{i} }} {\text{d}}x_{{R_{i} }} } } + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} { - 2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]{\text{ d}}y_{{L_{i} }} {\text{d}}x_{{L_{i} }} } } $$

$$ M_{44} = \rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{2}{3}h^{3} } { + }2hy_{{R_{i} }}^{2} {\text{d}}y_{{R_{i} }} {\text{d}}x_{{R_{i} }} } } + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {\frac{2}{3}h^{3} } { + }2hy_{{L_{i} }}^{2} {\text{d}}y_{{L_{i} }} {\text{d}}x_{{L_{i} }} } } + J_{x} $$

$$ M_{45} = \rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} { - 2h} y_{{R_{i} }} [x_{{R_{i} }} + r_{0} + a(i - 1)]{\text{ d}}y_{{R_{i} }} {\text{d}}x_{{R_{i} }} } } + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} { - 2hy_{{L_{i} }} [x_{{L_{i} }} - r_{0} - a(i - 1)]} {\text{ d}}y_{{L_{i} }} {\text{d}}x_{{L_{i} }} } } $$

$$ \begin{aligned} M_{55} & = \rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{2}{3}h^{3} + 2h[x_{{R_{i} }} + r_{0} + a(i - 1)]^{2} } {\text{ d}}y_{{R_{i} }} {\text{d}}x_{{R_{i} }} } } \\ & \quad + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {\frac{2}{3}h^{3} + 2h[x_{{L_{i} }} - r_{0} - a(i - 1)]^{2} } {\text{ d}}y_{{L_{i} }} {\text{d}}x_{{L_{i} }} } } { + }J_{y} \, \\ \end{aligned} $$

$$ \begin{aligned} M_{66} & = \rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} \left\{ {[x_{{R_{i} }} + r_{0} + a(i - 1)]^{2} + y_{{R_{i} }}^{2} } \right\}{\text{d}}y_{{R_{i} }} {\text{d}}x_{{R_{i} }} } } \\ & \quad + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h\left\{ {[x_{{L_{i} }} + r_{0} + a(i - 1)]^{2} + y_{{L_{i} }}^{2} } \right\}} {\text{ d}}y_{{L_{i} }} {\text{d}}x_{{L_{i} }} } } { + }J_{z} \, \\ \end{aligned} $$

$$ \begin{aligned} {\varvec{M}}_{17} & = \left( {2N \cdot 4\rho hab + m_{R} } \right){\text{X}}_{0} \\ & \quad - \left( {2\rho h\sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {y_{{R_{i} }} } } } {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} + 2\rho h\sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {y_{{L_{i} }} } } } {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } \right){\uptheta }_{0}^{(z)} \\ \end{aligned} $$

$$ \begin{aligned} {\varvec{M}}_{27} & = \left( {2N \cdot 4\rho hab + m_{R} } \right){\text{Y}}_{0} + \left\{ {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} [x_{{R_{i} }} + r_{0} { + }a{(}i - 1{)] }{\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } } \right. \\ & \quad \left. { + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)] \, {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } } \right\}{\uptheta }_{0}^{(z)} \\ \end{aligned} $$

$$ \begin{aligned} {\varvec{M}}_{37} & = \left( {2N \cdot 4\rho hab + m_{R} } \right){\text{Z}}_{0} \\ & \quad + \left( {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} y_{{R_{i} }} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } } \right.\left. { + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} y_{{L_{i} }} {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } } \right){\uptheta }_{0}^{(x)} \\ & \quad - \left\{ {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)] \, {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } } \right. \\ & \quad \left. { + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]{\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } } \right\}{\uptheta }_{0}^{(y)} \\ & \quad + \rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} {\text{W}}_{{R_{i} }} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} {\text{W}}_{{L_{i} }} {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } \\ \end{aligned} $$

$$ \begin{aligned} {\varvec{M}}_{47} & = \left( {2N \cdot \frac{4}{3}\rho hab^{3} + 2N \cdot \frac{4}{3}\rho h^{3} ab + J_{x} } \right){\uptheta }_{0}^{(x)} \\ & \quad + \left( {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} y_{{R_{i} }} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } } \right.\left. { + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} y_{{L_{i} }} {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } } \right){\text{Z}}_{0} \\ & \quad - \left\{ {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)] \, y_{{R_{i} }} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } } \right. \\ & \quad \left. { + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]y_{{L_{i} }} {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } } \right\}{\uptheta }_{0}^{(y)} \\ & \quad + \rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} y_{{R_{i} }} {\text{W}}_{{R_{i} }} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} y_{{R_{i} }} {\text{W}}_{{L_{i} }} {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } \\ & \quad + \rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{2}{3}h^{3} } \frac{{\partial {\text{W}}_{{R_{i} }} }}{{\partial y_{{R_{i} }} }}{\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {\frac{2}{3}h^{3} } \frac{{\partial {\text{W}}_{{L_{i} }} }}{{\partial y_{{L_{i} }} }}{\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } \\ \end{aligned} $$

$$ \begin{aligned} {\varvec{M}}_{57} & = - \left\{ {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)]{\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } } \right. \\ & \quad \left. { + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]{\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } } \right\}{\text{Z}}_{0} \\ & \quad - \left\{ {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)] \, y_{{R_{i} }} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } } \right. \\ & \quad \left. { + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]y_{{L_{i} }} {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } } \right\}{\uptheta }_{0}^{(x)} \\ & \quad { + }\left\{ {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)]^{2} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } } \right. \\ & \quad \left. { + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]^{2} {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } + 2N \cdot \frac{4}{3}\rho h^{3} ab + J_{y} } \right\}{\uptheta }_{0}^{(y)} \\ & \quad - \left\{ {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)]{\text{ W}}_{{R_{i} }} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } } \right. \\ & \quad \left. { + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]{\text{W}}_{{L_{i} }} {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } } \right\} \\ & \quad + \rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{2}{3}h^{3} } \frac{{\partial {\text{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}{\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {\frac{2}{3}h^{3} } \frac{{\partial {\text{W}}_{{L_{i} }} }}{{\partial x_{{L_{i} }} }}{\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } \\ \end{aligned} $$

$$ \begin{gathered} {\varvec{M}}_{67} = - \left( {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} \, y_{{R_{i} }} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} + } } \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} y_{{L_{i} }} {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } } \right){\text{X}}_{0} \hfill \\ \, - \left\{ {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)]{\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } } \right. \hfill \\ \, \left. { \, + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]{\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } } \right\}{\text{Y}}_{0} \hfill \\ { + }\left\{ {\rho \sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)]^{2} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } } \right. \hfill \\ \, \left. { \, + \rho \sum\limits_{i = 1}^{N} {\int_{ - a}^{0} {\int_{ - b}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]^{2} {\text{d}} y_{{L_{i} }} {\text{d}} x_{{L_{i} }} } } + 2N \cdot \frac{4}{3}\rho hab^{3} + J_{z} } \right\}{\uptheta }_{0}^{(z)} \hfill \\ \end{gathered} $$

$$ \begin{aligned} {M}_{{77}} & = M_{{11}} {\text{X}}_{0}^{T} {\text{X}}_{0} + M_{{22}} {\text{Y}}_{0}^{T} {\text{Y}}_{0} + M_{{33}} {\text{Z}}_{0}^{T} {\text{Z}}_{0} + M_{{44}} {{\theta }}_{0}^{{(x)^{T} }} {{\theta }}_{0}^{{(x)}} + M_{{55}} {{\theta }}_{0}^{{(y)^{T} }} {{\theta }}_{0}^{{(y)}} + M_{{66}} {{\theta }}_{0}^{{(z)^{T} }} {{\theta }}_{0}^{{(z)}} \\ & \quad + \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {\frac{2}{3}h^{3} } \frac{{\partial {\text{W}}_{{R_{i} }}^{T} }}{{\partial x_{{R_{i} }} }}\frac{{\partial {\text{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}\text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } + \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {\frac{2}{3}h^{3} } \frac{{\partial {\text{W}}_{{L_{i} }}^{T} }}{{\partial x_{{L_{i} }} }}\frac{{\partial {\text{W}}_{{L_{i} }} }}{{\partial x_{{L_{i} }} }}\text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \\ & \quad + \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {\frac{2}{3}h^{3} } \frac{{\partial {\text{W}}_{{R_{i} }}^{T} }}{{\partial y_{{R_{i} }} }}\frac{{\partial {\text{W}}_{{R_{i} }} }}{{\partial y_{{R_{i} }} }}\text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } + \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {\frac{2}{3}h^{3} } \frac{{\partial {\text{W}}_{{L_{i} }}^{T} }}{{\partial y_{{L_{i} }} }}\frac{{\partial {\text{W}}_{{L_{i} }} }}{{\partial y_{{L_{i} }} }}\text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \\ & \quad + \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {2h} {\text{W}}_{{R_{i} }}^{T} {\text{W}}_{{R_{i} }} \text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } + \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {2h} {\text{W}}_{{L_{i} }}^{T} {\text{W}}_{{L_{i} }} \text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \\ & \quad + \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)]\text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } \left( {{{\theta }}_{0}^{{(z)^{T} }} {\text{Y}}_{0} + {\text{Y}}_{0}^{T} {{\theta }}_{0}^{{(z)}} } \right) \\ & \quad + \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]\text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \left( {{{\theta }}_{0}^{{(z)^{T} }} {\text{Y}}_{0} + {\text{Y}}_{0}^{T} {{\theta }}_{0}^{{(z)}} } \right) \\ & \quad + \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {2h{\kern 1pt} } \left( {{\text{Z}}_{0}^{T} {\text{W}}_{{R_{i} }} {\text{ + W}}_{{R_{i} }}^{T} {\text{Z}}_{0} } \right)\text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } + \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {2h{\kern 1pt} } \left( {{\text{Z}}_{0}^{T} {\text{W}}_{{L_{i} }} {\text{ + W}}_{{L_{i} }}^{T} {\text{Z}}_{0} } \right)\text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \\ & \quad - \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)]\text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } \left( {{\text{Z}}_{0}^{T} {{\theta }}_{0}^{{(y)}} + {{\theta }}_{0}^{{(y)^{T} }} {\text{Z}}_{0} } \right) \\ & \quad - \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]\text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \left( {{\text{Z}}_{0}^{T} {{\theta }}_{0}^{{(y)}} + {{\theta }}_{0}^{{(y)^{T} }} {\text{Z}}_{0} } \right) \\ & \quad + \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {2h} y_{{R_{i} }} \text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } \left( {{\text{Z}}_{0}^{T} {{\theta }}_{0}^{{(x)}} + {{\theta }}_{0}^{{(x)^{T} }} {\text{Z}}_{0} } \right) + \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {2h} y_{{L_{i} }} \text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \left( {{\text{Z}}_{0}^{T} {{\theta }}_{0}^{{(x)}} + {{\theta }}_{0}^{{(x)^{T} }} {\text{Z}}_{0} } \right) \\ & \quad - \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)]y_{{R_{i} }} \text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } \left( {{{\theta }}_{0}^{{(x)^{T} }} {{\theta }}_{0}^{{(y)}} + {{\theta }}_{0}^{{(y)^{T} }} {{\theta }}_{0}^{{(x)}} } \right) \\ & \quad - \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]y_{{L_{i} }} \text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \left( {{{\theta }}_{0}^{{(x)^{T} }} {{\theta }}_{0}^{{(y)}} + {{\theta }}_{0}^{{(y)^{T} }} {{\theta }}_{0}^{{(x)}} } \right) \\ & \quad - \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {2h} y_{{R_{i} }} \text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } \left( {{{\theta }}_{0}^{{(z)^{T} }} {\text{X}}_{0} + {\text{X}}_{0}^{T} {{\theta }}_{0}^{{(z)}} } \right) - \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {2h} y_{{L_{i} }} \text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \left( {{{\theta }}_{0}^{{(z)^{T} }} {\text{X}}_{0} + {\text{X}}_{0}^{T} {{\theta }}_{0}^{{(z)}} } \right) \\ & \quad - \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {2h} [x_{{R_{i} }} + r_{0} + a(i - 1)]\left( {{\text{W}}_{{_{{R_{i} }} }}^{T} {{\theta }}_{0}^{{(y)}} + {{\theta }}_{0}^{{(y)^{T} }} {\text{W}}_{{R_{i} }} } \right)\text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } \\ & \quad - \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {2h} [x_{{L_{i} }} - r_{0} - a(i - 1)]\left( {{\text{W}}_{{L_{i} }}^{T} {{\theta }}_{0}^{{(y)}} + {{\theta }}_{0}^{{(y)^{T} }} {\text{W}}_{{L_{i} }} } \right)\text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \\ & \quad + \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {2h} y_{{R_{i} }} \left( {{\text{W}}_{{R_{i} }}^{T} {{\theta }}_{0}^{{(x)}} + {{\theta }}_{0}^{{(x)^{T} }} {\text{W}}_{{R_{i} }} } \right)\text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } \\ & \quad + \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {2hy_{{L_{i} }} } \left( {{\text{W}}_{{L_{i} }}^{T} {{\theta }}_{0}^{{(x)}} + {{\theta }}_{0}^{{(x)^{T} }} {\text{W}}_{{L_{i} }} } \right)\text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \\ & \quad - \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {\frac{2}{3}h^{3} } \left( {\frac{{\partial {\text{W}}_{{R_{i} }}^{T} }}{{\partial x_{{R_{i} }} }}{{\theta }}_{0}^{{(y)}} + {{\theta }}_{0}^{{(y)^{T} }} \frac{{\partial {\text{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}} \right)\text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } \\ & \quad - \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {\frac{2}{3}h^{3} } \left( {\frac{{\partial {\text{W}}_{{L_{i} }}^{T} }}{{\partial x_{{L_{i} }} }}{{\theta }}_{0}^{{(y)}} + {{\theta }}_{0}^{{(y)^{T} }} \frac{{\partial {\text{W}}_{{L_{i} }} }}{{\partial x_{{L_{i} }} }}} \right)\text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \\ & \quad + \rho \sum\limits_{{i = 1}}^{N} {\int_{0}^{a} {\int_{{ - b}}^{b} {\frac{2}{3}h^{3} } \left( {\frac{{\partial {\text{W}}_{{R_{i} }}^{T} }}{{\partial y_{{R_{i} }} }}{{\theta }}_{0}^{{(x)}} + {{\theta }}_{0}^{{(x)^{T} }} \frac{{\partial {\text{W}}_{{R_{i} }} }}{{\partial y_{{R_{i} }} }}} \right)\text{d} y_{{R_{i} }} \text{d} x_{{R_{i} }} } } \\ & \quad + \rho \sum\limits_{{i = 1}}^{N} {\int_{{ - a}}^{0} {\int_{{ - b}}^{b} {\frac{2}{3}h^{3} } \left( {\frac{{\partial {\text{W}}_{{L_{i} }}^{T} }}{{\partial y_{{L_{i} }} }}{{\theta }}_{0}^{{(x)}} + {{\theta }}_{0}^{{(x)^{T} }} \frac{{\partial {\text{W}}_{{L_{i} }} }}{{\partial y_{{L_{i} }} }}} \right)\text{d} y_{{L_{i} }} \text{d} x_{{L_{i} }} } } \\ \end{aligned} $$

$$ {\mathbf{W}}_{{R_{i} }} \left( {x_{{R_{i} }} ,y_{{R_{i} }} } \right) = \left[ {W_{{R_{i} ,1}} \left( {x_{{R_{i} }} ,y_{{R_{i} }} } \right), \cdots ,W_{{R_{i} ,n}} \left( {x_{{R_{i} }} ,y_{{R_{i} }} } \right)} \right] $$

where

$$ {\mathbf{W}}_{{L_{i} }} \left( {x_{{L_{i} }} ,y_{{L_{i} }} } \right) = \left[ {W_{{L_{i} ,1}} \left( {x_{{L_{i} }} ,y_{{L_{i} }} } \right), \cdots ,W_{{L_{i} ,n}} \left( {x_{{L_{i} }} ,y_{{L_{i} }} } \right)} \right] $$

$$ {\text{X}}_{0}^{{}} = \left[ {X_{0,1}^{{}} , \ldots ,X_{0,n}^{{}} } \right],\,{\text{Y}}_{0}^{{}} = \left[ {Y_{0,1}^{{}} , \ldots ,Y_{0,n}^{{}} } \right],\,{\text{Z}}_{0}^{{}} = \left[ {Z_{0,1}^{{}} , \ldots ,Z_{0,n}^{{}} } \right] $$

$$ {\uptheta }_{0}^{(x)} = \left[ {\theta_{0,1}^{(x)} , \ldots ,\theta_{0,n}^{(x)} } \right],\,{\uptheta }_{0}^{(y)} = \left[ {\theta_{0,1}^{(y)} , \ldots ,\theta_{0,n}^{(y)} } \right],\,{\uptheta }_{1}^{(z)} = \left[ {\theta_{0,1}^{(z)} , \ldots ,\theta_{0,n}^{(z)} } \right] $$

Appendix 2

The stiffness and damping matrices K and C are as follows:

$$ {\varvec{K}} = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{{{6} \times {6}}} } & {{\mathbf{0}}_{{{6} \times n}} } \\ {{\mathbf{0}}_{{n \times {6}}} } & {{\varvec{K}}_{77} } \\ \end{array} } \right], \, {\varvec{C}} = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{{{6} \times {6}}} } & {{\mathbf{0}}_{{{6} \times n}} } \\ {{\mathbf{0}}_{{n \times {6}}} } & {{\varvec{C}}_{77} } \\ \end{array} } \right] $$

where

$$ \begin{gathered} {\varvec{K}}_{77} = \Re + \ell \hfill \\ \Re = D\sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{{\partial^{2} {\text{W}}_{{R_{i} }}^{T} }}{{\partial x_{{R_{i} }}^{2} }}\frac{{\partial^{2} {\text{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }}^{2} }}} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } \hfill \\ \, + vD\sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{{\partial^{2} {\text{W}}_{{R_{i} }}^{T} }}{{\partial x_{{R_{i} }}^{2} }}\frac{{\partial^{2} {\text{W}}_{{R_{i} }} }}{{\partial y_{{R_{i} }}^{2} }}} + \frac{{\partial^{2} {\text{W}}_{{R_{i} }}^{T} }}{{\partial y_{{R_{i} }}^{2} }}\frac{{\partial^{2} {\text{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }}^{2} }}{\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } \hfill \\ \, + 2\left( {1 - v} \right)D\sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{{\partial^{2} {\text{W}}_{{R_{i} }}^{T} }}{{\partial x_{{R_{i} }} \partial y_{{R_{i} }} }}\frac{{\partial^{2} {\text{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }} \partial y_{{R_{i} }} }}} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } \hfill \\ \, + D\sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{{\partial^{2} {\text{W}}_{{R_{i} }}^{T} }}{{\partial y_{{R_{i} }}^{2} }}\frac{{\partial^{2} {\text{W}}_{{R_{i} }} }}{{\partial y_{{R_{i} }}^{2} }}} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } \hfill \\ \, + k\sum\limits_{i = 1}^{N} {\left( {\Delta \Theta_{{R_{{A_{i} }} }} } \right)^{T} \Delta \Theta_{{R_{{A_{i} }} }} } + k\sum\limits_{i = 1}^{N} {\left( {\Delta \Theta_{{R_{{B_{i} }} }} } \right)^{T} \Delta \Theta_{{R_{{B_{i} }} }} } \hfill \\ \end{gathered} $$

where $\Delta \Theta_{{R_{{A_{1} }} }} = \left. {\frac{{\partial {\text{W}}_{{R_{1} }}^{T} }}{{\partial x_{{R_{1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{1} }} = 0 \\ y_{{R_{1} }} = y{}_{a} \end{subarray} } \left. {\frac{{\partial {\text{W}}_{{R_{1} }} }}{{\partial x_{{R_{1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{1} }} = 0 \\ y_{{R_{1} }} = y{}_{a} \end{subarray} }$, $\Delta \Theta_{{R_{{B_{1} }} }} = \left. {\frac{{\partial {\text{W}}_{{R_{1} }}^{T} }}{{\partial x_{{R_{1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{1} }} = 0 \\ y_{{R_{1} }} = y{}_{b} \end{subarray} } \left. {\frac{{\partial {\text{W}}_{{R_{1} }} }}{{\partial x_{{R_{1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{1} }} = 0 \\ y_{{R_{1} }} = y{}_{b} \end{subarray} }$,

$\Delta \Theta_{{L_{{A_{1} }} }} = \left. {\frac{{\partial {\text{W}}_{{L_{1} }}^{T} }}{{\partial x_{{L_{1} }} }}} \right|_{\begin{subarray}{l} x_{{L_{1} }} = 0 \\ y_{{L_{1} }} = y{}_{a} \end{subarray} } \left. {\frac{{\partial {\text{W}}_{{L_{1} }} }}{{\partial x_{{L_{1} }} }}} \right|_{\begin{subarray}{l} x_{{L_{1} }} = 0 \\ y_{{L_{1} }} = y{}_{a} \end{subarray} }$, $\Delta \Theta_{{L_{{B_{1} }} }} = \left. {\frac{{\partial {\text{W}}_{{L_{1} }}^{T} }}{{\partial x_{{L_{1} }} }}} \right|_{\begin{subarray}{l} x_{{L_{1} }} = 0 \\ y_{{L_{1} }} = y{}_{b} \end{subarray} } \left. {\frac{{\partial {\text{W}}_{{L_{1} }} }}{{\partial x_{{L_{1} }} }}} \right|_{\begin{subarray}{l} x_{{L_{1} }} = 0 \\ y_{{L_{1} }} = y{}_{b} \end{subarray} }$, and when $i = 2,3, \ldots ,N$,

$\Delta \Theta_{{R_{{A_{i} }} }} = \left. {\frac{{\partial {\mathbf{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i} }} = 0 \\ y_{{R_{i} }} = y_{a} \end{subarray} } - \left. {\frac{{\partial {\mathbf{W}}_{{R_{i - 1} }} }}{{\partial x_{{R_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i - 1} }} = a \\ y_{{R_{i - 1} }} = y_{a} \end{subarray} }$, $\Delta \Theta_{{R_{{B_{i} }} }} = \left. {\frac{{\partial {\mathbf{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i} }} = 0 \\ y_{{R_{i} }} = y_{b} \end{subarray} } - \left. {\frac{{\partial {\mathbf{W}}_{{R_{i - 1} }} }}{{\partial x_{{R_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i - 1} }} = a \\ y_{{R_{i - 1} }} = y_{b} \end{subarray} }$,

$\Delta \Theta_{{L_{{A_{i} }} }} = \left. {\frac{{\partial {\mathbf{W}}_{{L_{i} }} }}{{\partial x_{{L_{i} }} }}} \right|_{\begin{subarray}{l} x_{{L_{i} }} = 0 \\ y_{{L_{i} }} = y_{a} \end{subarray} } - \left. {\frac{{\partial {\mathbf{W}}_{{L_{i - 1} }} }}{{\partial x_{{L_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{L_{i - 1} }} = a \\ y_{{L_{i - 1} }} = y_{a} \end{subarray} }$, $\Delta \Theta_{{L_{{B_{i} }} }} = \left. {\frac{{\partial {\mathbf{W}}_{{L_{i} }} }}{{\partial x_{{L_{i} }} }}} \right|_{\begin{subarray}{l} x_{{L_{i} }} = 0 \\ y_{{L_{i} }} = y_{b} \end{subarray} } - \left. {\frac{{\partial {\mathbf{W}}_{{L_{i - 1} }} }}{{\partial x_{{L_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{L_{i - 1} }} = a \\ y_{{L_{i - 1} }} = y_{b} \end{subarray} }$.

The expression for $\ell$ can be obtained from $\Re$ by replacing all instances of $R_{i}$ with $L_{i}$.

The damping matrix C₇₇ is as follows

$$ {\varvec{C}}_{77} = \kappa_{M} {\varvec{M}} + \kappa_{K} {\varvec{K}}_{p} + c{\varvec{C}}_{j} $$

where the coefficients $\kappa_{M}$ and $\kappa_{K}$ are proportionality constants and

$$ \begin{aligned} {\varvec{K}}_{p} & = \Re_{p} + \ell_{p} \\ \Re_{p} & = D\sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{{\partial^{2} {\text{W}}_{{R_{i} }}^{T} }}{{\partial x_{{R_{i} }}^{2} }}\frac{{\partial^{2} {\text{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }}^{2} }}} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } \\ & \quad + vD\sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{{\partial^{2} {\text{W}}_{{R_{i} }}^{T} }}{{\partial x_{{R_{i} }}^{2} }}\frac{{\partial^{2} {\text{W}}_{{R_{i} }} }}{{\partial y_{{R_{i} }}^{2} }}} + \frac{{\partial^{2} {\text{W}}_{{R_{i} }}^{T} }}{{\partial y_{{R_{i} }}^{2} }}\frac{{\partial^{2} {\text{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }}^{2} }}{\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } \\ & \quad + 2\left( {1 - v} \right)D\sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{{\partial^{2} {\text{W}}_{{R_{i} }}^{T} }}{{\partial x_{{R_{i} }} \partial y_{{R_{i} }} }}\frac{{\partial^{2} {\text{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }} \partial y_{{R_{i} }} }}} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } \\ & \quad + D\sum\limits_{i = 1}^{N} {\int_{0}^{a} {\int_{ - b}^{b} {\frac{{\partial^{2} {\text{W}}_{{R_{i} }}^{T} }}{{\partial y_{{R_{i} }}^{2} }}\frac{{\partial^{2} {\text{W}}_{{R_{i} }} }}{{\partial y_{{R_{i} }}^{2} }}} {\text{d}} y_{{R_{i} }} {\text{d}} x_{{R_{i} }} } } \\ \end{aligned} $$

The expression for $\ell_{p}$ can be obtained from $\Re_{p}$ by replacing $R_{i}$ with $L_{i}$.

$$ \begin{aligned} C_{j} & = \sum\limits_{i = 1}^{N} {\left( {\Delta \Theta_{{R_{{A_{i} }} }} } \right)^{T} \Delta \Theta_{{R_{{A_{i} }} }} } + \sum\limits_{i = 1}^{N} {\left( {\Delta \Theta_{{R_{{B_{i} }} }} } \right)^{T} \Delta \Theta_{{R_{{B_{i} }} }} } \\ & \quad + \sum\limits_{i = 1}^{N} {\left( {\Delta \Theta_{{L_{{A_{i} }} }} } \right)^{T} \Delta \Theta_{{L_{{A_{i} }} }} } + \sum\limits_{i = 1}^{N} {\left( {\Delta \Theta_{{L_{{B_{i} }} }} } \right)^{T} \Delta \Theta_{{L_{{B_{i} }} }} } \\ \end{aligned} $$

Appendix 3

The nonlinear stiffness ${\varvec{K}}_{n} \left( {\varvec{q}} \right)$ is as follows:

$$ {\varvec{K}}_{n} ({\varvec{q}}) = \Re_{n} + \ell_{n} $$

$$ \begin{aligned} \Re_{n} & = k_{n} \left. {\frac{{\partial {\text{W}}_{{R_{1} }}^{T} }}{{\partial x_{{R_{1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{1} }} = 0 \\ y_{{R_{1} }} = y{}_{a} \end{subarray} } \left( {\left. {\frac{{\partial w_{{R_{1} }} }}{{\partial x_{{R_{1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{1} }} = 0 \\ y_{{R_{1} }} = y{}_{a} \end{subarray} } } \right)^{3} + k_{n} \left. {\frac{{\partial {\text{W}}_{{R_{1} }}^{T} }}{{\partial x_{{R_{1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{1} }} = 0 \\ y_{{R_{1} }} = y{}_{b} \end{subarray} } \left( {\left. {\frac{{\partial w_{{R_{1} }} }}{{\partial x_{{R_{1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{1} }} = 0 \\ y_{{R_{1} }} = y{}_{b} \end{subarray} } } \right)^{3} \\ & \quad + k_{n} \sum\limits_{i = 2}^{N} {\left( {\left. {\frac{{\partial {\text{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i} }} = 0 \\ y_{{R_{i} }} = y_{a} \end{subarray} } - \left. {\frac{{\partial {\text{W}}_{{R_{i - 1} }} }}{{\partial x_{{R_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i - 1} }} = a \\ y_{{R_{i - 1} }} = y_{a} \end{subarray} } } \right)^{T} \left( {\left. {\frac{{\partial w_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i} }} = 0 \\ y_{{R_{i} }} = y_{a} \end{subarray} } - \left. {\frac{{\partial w_{{R_{i - 1} }} }}{{\partial x_{{R_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i - 1} }} = a \\ y_{{R_{i - 1} }} = y_{a} \end{subarray} } } \right)^{3} } \\ & \quad + k_{n} \sum\limits_{i = 2}^{N} {\left( {\left. {\frac{{\partial {\text{W}}_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i} }} = 0 \\ y_{{R_{i} }} = y_{b} \end{subarray} } - \left. {\frac{{\partial {\text{W}}_{{R_{i - 1} }} }}{{\partial x_{{R_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i - 1} }} = a \\ y_{{R_{i - 1} }} = y_{b} \end{subarray} } } \right)^{T} \left( {\left. {\frac{{\partial w_{{R_{i} }} }}{{\partial x_{{R_{i} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i} }} = 0 \\ y_{{R_{i} }} = y_{a} \end{subarray} } - \left. {\frac{{\partial w_{{R_{i - 1} }} }}{{\partial x_{{R_{i - 1} }} }}} \right|_{\begin{subarray}{l} x_{{R_{i - 1} }} = a \\ y_{{R_{i - 1} }} = y_{b} \end{subarray} } } \right)^{3} } \\ \end{aligned} $$

The expression for $\ell_{n}$ can be obtained from $\Re_{n}$ by replacing $R_{i}$ with $L_{i}$.

Appendix 4

The Coulomb friction matrix is as follows:

$$ {{\varvec{\upmu}}}(\dot{\user2{q}}) = \left[ {\begin{array}{*{20}c} {{0}_{6 \times 1} } \\ {{{\varvec{\upmu}}}(\dot{\user2{p}})} \\ \end{array} } \right] $$

where

$$ \begin{aligned} {{\varvec{\upmu}}}(\dot{\user2{p}}) & = \mu \sum\limits_{i = 1}^{N} {\left\{ {{\text{sign}} \left( {\Delta \Theta_{{R_{{A_{i} }} }} \dot{\user2{p}}} \right)\left( {\Delta \Theta_{{R_{{A_{i} }} }} } \right)^{\text{T}} } \right.} + {\text{sign}} \left( {\Delta \Theta_{{R_{{B_{i} }} }} \dot{\user2{p}}} \right)\left( {\Delta \Theta_{{R_{{B_{i} }} }} } \right)^{\text{T}} \\ & \quad + {\text{sign}} \left( {\Delta \Theta_{{L_{{A_{i} }} }} \dot{\user2{p}}} \right)\left( {\Delta \Theta_{{L_{{A_{i} }} }} } \right)^{\text{T}} \left. { + {\text{sign}} \left( {\Delta \Theta_{{L_{{B_{i} }} }} \dot{\user2{p}}} \right)\left( {\Delta \Theta_{{L_{{B_{i} }} }} } \right)^{\text{T}} } \right\} \\ \end{aligned} $$