INTRODUCTION

One of the primary goals in the spacecraft (SC) control is the problem of stabilization of the SC main body in the desired angular position.

In the development of stabilization algorithms, it is frequently assumed that the SC is a rigid body; however, many vehicles require a different approach to modeling their motion [1, 2]. Telecommunication satellites with large antennas, deep space exploration SC with large solar panels, and SC with robotized manipulators and external booms are examples of such vehicles. A characteristic feature of such an SC is the presence of extended flexible elements (FEs) in their structure, which are often manufactured from light-weight materials. During the orbital and angular maneuvering of the SC, vibrations that occur in the FE may not only reduce the accuracy of the orientation of the whole vehicle but they may even lead to the instability of the required modes of motion. Thus, in the case of an SC with FE, the problem of stabilization of the SC main body is directly related to the problem of damping the vibrations in FEs.

An overview of control methods for an SC with FEs is given in [3–5]. It should be noted that most methods are based on the now classical Lyapunov control and linear-quadratic regulator (LQR).

In the present study, using the model of an SC with FEs as an example, we investigate the possibility of applying the above-mentioned classical control methods to the solution of the problems of the stabilization of the SC main body in the given angular position and vibration reduction in FEs. One of the rapidly developing control methods of nonlinear systems, SDRE control, is also considered [6, 7]. The high dimensionality of the state vector of the system necessitates the use of algorithms that can work with a reduced model of the SC motion. Using the reduction method proposed in [8, 9], the LQR and SDRE control are constructed based on the equations of the angular motion of the SC main body.

It should be noted that the vibration reduction in FE requires, generally speaking, installation of damping devices. For example, these may be piezoelectric actuators [10] mounted on the FEs. However, of practical interest is the problem where the SC control is carried out only by the actuators located on the SC main body. This requirement is the most important property of the SC model considered in the study.

1. STATEMENT OF THE PROBLEM AND MODELS OF MOTION OF AN SC WITH FEs

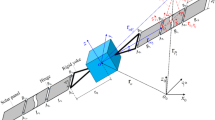
We study the motion of an SC consisting of three bodies: the main body (rigid body) and two FE, which move around the SC’s center of mass in the central Newtonian gravitational field of the Earth. The SC’s center of mass moves in a geostationary orbit. The FEs consist of a panel and antenna. The panel, which is fixed with a one-degree hinge, rotates at a constant angular velocity. The antenna has a single-sided support.

It is required to construct the control that stabilizes the SC main body in the given angular position in inertial frame. The factor that impedes the SC stabilization is the vibrations of the flexible elements; for this reason, in addition to the main problem, it is required to minimize their influence on the accuracy of the SC’s orientation.

The control of the SC is carried out only by means of flywheels located on the SC main body.

1.1. Coordinate Systems

The following right-hand Cartesian reference frames are used in the study:

\(OXYZ\) is the inertial coordinate system with the origin at the Earth’s center of mass \(O\); the \(OZ\) axis is perpendicular to the equatorial plane; and OX is oriented toward the vernal equinox;

\({{O}_{s}}xyz\) is the SC main body-fixed reference frame with the origin in the center of mass of the satellite; the axes of the coordinate system are the principal central axes of the satellite;

\({{O}_{a}}{{x}_{a}}{{y}_{a}}{{z}_{a}}\) is the antenna-fixed reference frame with the origin at the mounting point of the antenna to the satellite body; the axes are the principal axes of inertia for an undeformed antenna;

\({{O}_{p}}{{x}_{p}}{{y}_{p}}{{z}_{p}}\) is the panel-fixed reference frame with the origin at the point of attachment to the hinge; the axes are the principal axes of inertia for an undeformed panel;

\({{O}_{p}}{{\xi }_{p}}{{\eta }_{p}}{{\zeta }_{p}}\) is the coordinate system bound to the hinge; the \({{O}_{p}}{{\xi }_{p}}\) axis is the axis of rotation in the hinge, the other two axes are orthogonal to it.

1.2. The Model of Motion of an SC with FEs

The elementary point-like ith masses of the body, antenna, and panel are specified relative to the Earth’s center of mass by the vectors \({{{\mathbf{R}}}_{{si}}}\), \({{{\mathbf{R}}}_{{ai}}}\), and \({{{\mathbf{R}}}_{{pi}}}\), respectively (the subscript s corresponds to the body of the satellite, a to the antenna, and p to the panel, see Fig. 1):

$$\begin{gathered} {{{\mathbf{R}}}_{{si}}} = {{{\mathbf{R}}}_{s}} + {{{\mathbf{r}}}_{{si}}}, \\ {{{\mathbf{R}}}_{{ai}}} = {{{\mathbf{R}}}_{a}} + {{{\mathbf{r}}}_{{ai}}} + {\mathbf{w}_{{ai}}}, \\ {{{\mathbf{R}}}_{{pi}}} = {{{\mathbf{R}}}_{p}} + {{{\mathbf{r}}}_{{pi}}} + {\mathbf{w}_{{pi}}}, \\ \end{gathered} $$

where \({{{\mathbf{R}}}_{s}}\), \({{{\mathbf{R}}}_{a}}\), and \({{{\mathbf{R}}}_{p}}\) are the selected points of the respective body shown in Fig. 1; \({{{\mathbf{r}}}_{{si}}}\), \({{{\mathbf{r}}}_{{ai}}}\), and \({{{\mathbf{r}}}_{{pi}}}\) are the radius-vectors of the ith points of the respective body relative to the coordinate system bound to the body (the vector origins are the points shown in Fig. 1); \({\mathbf{w}_{{ai}}}\) and \({\mathbf{w}_{{pi}}}\) are the displacements of the ith points of the body caused by elastic deformations.

Fig. 1.
figure 1

Model of SC with FEs.

Full size image

The displacement of the point P of an FE relative to its undeformed position is represented as an infinite series [1]:

$$\mathbf{w}\left( {P,t} \right) = \sum\limits_{r = 1}^\infty {{\boldsymbol{\phi }_{r}}\left( P \right){{q}_{r}}\left( t \right)} ,$$

where \({\boldsymbol{\phi }_{r}}\left( P \right),\; r = \overline {1,\infty } \), are the normal vibrational modes, and \({{q}_{r}}\left( t \right)\), \(r = \overline {1,\infty } \), are the amplitudes of the normal vibrational modes, respectively. In actual systems, FEs are, as a rule, complex structures; for this reason, determining the normal vibrational modes analytically usually does not appear possible. However, as a result of finite-element modeling, the displacement of the FEs’ point relative to its undeformed position specified with the radius-vector \({{{\mathbf{r}}}_{i}}\) can be represented as

$${\mathbf{w}_{i}} = {{{\mathbf{A}}}_{i}}\left( {{{{\mathbf{r}}}_{i}}} \right){\mathbf{q}}\left( t \right),$$

where \({{{\mathbf{A}}}_{i}}({{{\mathbf{r}}}_{i}})\) is the matrix of the normal vibrational modes of an FE, and q(t) is the vector of the amplitudes of the normal vibrational modes [2]. The reduced vibrations corresponds to the situation when all q = 0 and \({\mathbf{\dot {q}}} = 0\).

Since it is natural to specify the values \({{{\mathbf{p}}}_{1}}\) and \({{{\mathbf{a}}}_{1}}\) in the reference frame \({{O}_{s}}xyz\); \({{{\mathbf{p}}}_{2}}\), \({{{\mathbf{r}}}_{{pi}}}\), and \({\mathbf{w}_{{pi}}}\) in the frame \({{O}_{p}}{{x}_{p}}{{y}_{p}}{{z}_{p}}\); and \({{{\mathbf{a}}}_{2}}\), \({{{\mathbf{r}}}_{{ai}}}\), and \({\mathbf{w}_{{ai}}}\) in the frame \({{O}_{a}}{{x}_{a}}{{y}_{a}}{{z}_{a}}\), when deriving the motion equations, all vectors should be written in the same coordinate system, and in this case, the frame \({{O}_{s}}xyz\). The corresponding matrices of transitions are omitted in order not to complicate writing them.

We will use the following notations and formulas: ms is the mass of the SC main body; \({{m}_{{si}}}\) is the mass of the ith point of the SC main body; mp is the mass of the panel; \({{m}_{{pi}}}\) is the mass of the ith point of the panel; \({{m}_{a}}\) is the mass of the antenna; \({{m}_{{ai}}}\) is the mass of the ith point of the antenna; \(m = {{m}_{s}} + {{m}_{p}} + {{m}_{a}}\) is the total mass of the SC with FE; \({{({{\lambda }_{0}},{{{\boldsymbol{\lambda }}}^{\text{T}}})}^{\text{T}}}\) is the orientation quaternion; \({\boldsymbol{\omega }}\) is the absolute angular velocity of the SC main body; \({{{\mathbf{e}}}_{p}}\) is the unit vector of the axis of the hinge; \({{{\boldsymbol{\omega }}}_{p}} = {\boldsymbol{\omega }} + {{{\mathbf{e}}}_{p}}{{\psi }_{0}}\) is the absolute angular velocity of the panel, where \({{\psi }_{0}}\) = const is the angular velocity of rotation of the panel in the hinge; qa and qp are the amplitudes of the normal vibrational modes of the antenna and panel; and \({\mathbf{\tilde {p}}_{2}}\) is the displacement of the center of mass of the panel due to deformation, which is determined via the expression

$${\mathbf{\tilde {p}}_{2}} = \frac{1}{{{{m}_{p}}}}\sum\limits_i {{{m}_{{pi}}}{{{\mathbf{u}}}_{{pi}}}} = \frac{{\sum\limits_i {{{m}_{{pi}}}{{{\mathbf{A}}}_{{pi}}}{\mathbf{q}}} }}{{{{m}_{p}}}},$$

where \({{{\mathbf{A}}}_{{pi}}}({{{\mathbf{r}}}_{{pi}}})\) is the matrix of the normal vibrational modes. The Api values are specified in the reference frame \({{O}_{p}}{{x}_{p}}{{y}_{p}}{{z}_{p}}\). Similarly, \({\mathbf{\tilde {a}}_{2}}\) is the displacement of the center of mass of the antenna due to deformation:

$${\mathbf{\tilde {a}}_{2}} = \frac{1}{{{{m}_{a}}}}\sum\limits_i {{{m}_{{ai}}}{{{\mathbf{u}}}_{{ai}}}} = \frac{{\sum\limits_i {{{m}_{{ai}}}{{{\mathbf{A}}}_{{ai}}}{\mathbf{q}}} }}{{{{m}_{a}}}},$$

where \({{{\mathbf{A}}}_{{ai}}}({{{\mathbf{r}}}_{{ai}}})\) is the matrix of the normal vibrational modes. The Aai values are specified in the reference frame \({{O}_{a}}{{x}_{a}}{{y}_{a}}{{z}_{a}}\); \(\left( {\mathbf{a},{\mathbf{b}}} \right)\) is the scalar product of the vectors a and b; \(\mathbf{a} \times {\mathbf{b}}\) is the vector product of the vectors a and b; \({\mathbf{b}} \times {\mathbf{A}} = {\mathbf{b}} \times \left( {\begin{array}{*{20}{c}} {{{{\mathbf{a}}}_{1}}}&{{{{\mathbf{a}}}_{2}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\mathbf{b}} \times {{{\mathbf{a}}}_{1}}}&{{\mathbf{b}} \times {{{\mathbf{a}}}_{2}}} \end{array}} \right)\) is the multiplication of the vector b by the matrix A, where \({\mathbf{a}_{1}}\) and \({\mathbf{a}_{2}}\) are its columns; and \({\mathbf{K}}({\mathbf{a}},{\mathbf{b}})\) is the matrix of the double-cross vector product, which is introduced in the following way:

$${\mathbf{a}} \times \left( {{\mathbf{y}} \times {\mathbf{b}}} \right) = {\mathbf{K}}({\mathbf{a}},{\mathbf{b}}){\mathbf{y}},{\mathbf{K}}({\mathbf{a}},{\mathbf{b}}) = \left( {\begin{array}{*{20}{c}} {{{a}_{2}}{{b}_{2}} + {{a}_{3}}{{b}_{3}}}&{ - {{a}_{2}}{{b}_{1}}}&{ - {{a}_{3}}{{b}_{1}}} \\ { - {{a}_{1}}{{b}_{2}}}&{{{a}_{1}}{{b}_{1}} + {{a}_{3}}{{b}_{3}}}&{ - {{a}_{3}}{{b}_{2}}} \\ { - {{a}_{1}}{{b}_{3}}}&{ - {{a}_{2}}{{b}_{3}}}&{{{a}_{1}}{{b}_{1}} + {{a}_{2}}{{b}_{2}}} \end{array}} \right).$$

The SC motion equations are derived using the procedure described in [2]. The mathematical model of the vehicle motion has the form

$${\mathbf{S}}\left( {\begin{array}{*{20}{c}} {{\boldsymbol{\dot {\omega }}}} \\ {{{{{\mathbf{\ddot {q}}}}}_{a}}} \\ {{{{{\mathbf{\ddot {q}}}}}_{p}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - {\boldsymbol{\omega }} \times {{{\mathbf{J}}}_{s}}{\boldsymbol{\omega }} + {{{\mathbf{T}}}_{s}} - {{{\mathbf{N}}}_{{\omega a}}} - {{{\mathbf{f}}}_{{\omega a}}} - {{{\mathbf{N}}}_{{\omega p}}} - {{{\mathbf{f}}}_{{\omega p}}}} \\ { - {{{\mathbf{f}}}_{a}} - {{{\mathbf{N}}}_{a}}} \\ { - {{{\mathbf{f}}}_{p}} - {{{\mathbf{N}}}_{p}}} \end{array}} \right),$$
((1.1))

where

$${\mathbf{S}} = \left( {\begin{array}{*{20}{c}} {\mathbf{J}}&{{{{\mathbf{S}}}_{{\omega a}}}}&{{{{\mathbf{S}}}_{{\omega p}}}} \\ {{\mathbf{S}}_{{\omega a}}^{\text{T}}}&{{{{\mathbf{M}}}_{a}}}&{{{{\mathbf{S}}}_{{ap}}}} \\ {{\mathbf{S}}_{{\omega p}}^{\text{T}}}&{{\mathbf{S}}_{{ap}}^{\text{T}}}&{{{{\mathbf{M}}}_{p}}} \end{array}} \right),$$
$$\begin{gathered} {\mathbf{J}} = {{{\mathbf{J}}}_{s}} + {{{{\mathbf{\tilde {J}}}}}_{a}} + {{m}_{a}}{\mathbf{K}}\left( {{\mathbf{a}} + {{{{\mathbf{\tilde {a}}}}}_{2}},{{{\mathbf{a}}}_{1}}} \right) + {{m}_{a}}{\mathbf{K}}\left( {{{{\mathbf{a}}}_{1}},{{{\mathbf{a}}}_{2}} + {{{{\mathbf{\tilde {a}}}}}_{2}}} \right) + {{{{\mathbf{\tilde {J}}}}}_{p}} \\ + \;{{m}_{p}}{\mathbf{K}}\left( {{\mathbf{p}} + {{{{\mathbf{\tilde {p}}}}}_{2}},{{{\mathbf{p}}}_{1}}} \right) + {{m}_{p}}{\mathbf{K}}\left( {{{{\mathbf{p}}}_{1}},{{{\mathbf{p}}}_{2}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right) \\ - \;\frac{1}{m}{\mathbf{K}}\left( {{{m}_{a}}\left( {{\mathbf{a}} + {{{{\mathbf{\tilde {a}}}}}_{2}}} \right) + {{m}_{p}}\left( {{\mathbf{p}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right),\quad {{m}_{a}}\left( {{\mathbf{a}} + {{{{\mathbf{\tilde {a}}}}}_{2}}} \right) + {{m}_{p}}\left( {{\mathbf{p}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right)} \right) \\ \end{gathered} $$

is the tensor of inertia of the SC with FEs.

$$\begin{gathered} {{{\mathbf{S}}}_{{\omega a}}} = \sum\limits_i {{{m}_{{ai}}}\left( {{{{\mathbf{a}}}_{1}} + {{{\mathbf{r}}}_{{ai}}} + {{{\mathbf{u}}}_{{ai}}}} \right) \times {{{\mathbf{A}}}_{{ai}}}} - \frac{1}{m}\left( {{{m}_{a}}\left( {{\mathbf{a}} + {{{{\mathbf{\tilde {a}}}}}_{2}}} \right) + {{m}_{p}}\left( {{\mathbf{p}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right)} \right) \times {{{\mathbf{A}}}_{a}}, \hfill \\ {{{\mathbf{S}}}_{{\omega p}}} = \sum\limits_i {{{m}_{{pi}}}\left( {{{{\mathbf{p}}}_{1}} + {{{\mathbf{r}}}_{{pi}}} + {{{\mathbf{u}}}_{{pi}}}} \right) \times {{{\mathbf{A}}}_{{pi}}}} - \frac{1}{m}\left( {{{m}_{a}}\left( {{\mathbf{a}} + {{{{\mathbf{\tilde {a}}}}}_{2}}} \right) + {{m}_{p}}\left( {{\mathbf{p}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right)} \right) \times {{{\mathbf{A}}}_{p}}, \hfill \\ \end{gathered} $$
$${{{\mathbf{S}}}_{{ap}}} = - \frac{1}{m}{\mathbf{A}}_{a}^{\text{T}}{{{\mathbf{A}}}_{p}},$$
$$\begin{gathered} {{{\mathbf{M}}}_{a}} = \sum\limits_i {{{m}_{{ai}}}{\mathbf{A}}_{{ai}}^{\text{T}}{{{\mathbf{A}}}_{{ai}}}} - \frac{1}{m}{\mathbf{A}}_{a}^{\text{T}}{{{\mathbf{A}}}_{a}}, \hfill \\ {{{\mathbf{M}}}_{p}} = \sum\limits_i {{{m}_{{pi}}}{\mathbf{A}}_{{pi}}^{\text{T}}{{{\mathbf{A}}}_{{pi}}}} - \frac{1}{m}{\mathbf{A}}_{p}^{\text{T}}{{{\mathbf{A}}}_{p}}, \hfill \\ \end{gathered} $$
$${{{\mathbf{T}}}_{s}} = \sum\limits_i {{{{\mathbf{r}}}_{{si}}} \times {\mathbf{F}_{{si}}}} $$

is the external torque acting on the SC main body, where \({\mathbf{F}_{{si}}}\) is the total force applied to the ith point of the SC main body,

$$\begin{gathered} {{{\mathbf{N}}}_{{\omega a}}} = {\boldsymbol{\omega }} \times {{{{\mathbf{\tilde {J}}}}}_{a}}{\boldsymbol{\omega }} + {{m}_{a}}{{{\mathbf{a}}}_{1}} \times {\boldsymbol{\omega }} \times {\boldsymbol{\omega }} \times \left( {{{{\mathbf{a}}}_{2}} + {{{{\mathbf{\tilde {a}}}}}_{2}}} \right) \\ + \;2\sum\limits_i {\left( {{{{\mathbf{a}}}_{1}} + {{{\mathbf{r}}}_{{ai}}} + {{{\mathbf{u}}}_{{ai}}}} \right) \times {\boldsymbol{\omega }} \times {{m}_{{ai}}}{{{{\mathbf{\dot {u}}}}}_{{ai}}}} + {{m}_{a}}\left( {{\mathbf{a}} + {{{{\mathbf{\tilde {a}}}}}_{2}}} \right) \times \left( {{\boldsymbol{\omega }} \times {\boldsymbol{\omega }} \times {{{\mathbf{a}}}_{1}} + {\mathbf{g}}} \right), \\ \end{gathered} $$
$$\begin{gathered} {{{\mathbf{N}}}_{{\omega p}}} = {{m}_{p}}{{{\mathbf{p}}}_{1}} \times \left( {{\boldsymbol{\omega }} \times {{\psi }_{0}}{{{\mathbf{e}}}_{p}}} \right) \times \left( {{{{\mathbf{p}}}_{2}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right) + {{{{\mathbf{\tilde {J}}}}}_{p}}\left( {{\boldsymbol{\omega }} \times {{\psi }_{0}}{{{\mathbf{e}}}_{p}}} \right) \\ + \;2\sum\limits_i {\left( {{{{\mathbf{p}}}_{1}} + {{{\mathbf{r}}}_{{pi}}} + {{{\mathbf{u}}}_{{pi}}}} \right) \times {{{\boldsymbol{\omega }}}_{p}} \times {{m}_{{pi}}}{{{{\mathbf{\dot {u}}}}}_{{pi}}}} + {{{\boldsymbol{\omega }}}_{p}} \times {{{{\mathbf{\tilde {J}}}}}_{p}}{{{\boldsymbol{\omega }}}_{p}} \\ + \;{{m}_{p}}{{{\mathbf{p}}}_{1}} \times {{{\boldsymbol{\omega }}}_{p}} \times {{{\boldsymbol{\omega }}}_{p}} \times \left( {{{{\mathbf{p}}}_{2}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right) + {{m}_{p}}\left( {{\mathbf{p}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right) \times \left( {{\boldsymbol{\omega }} \times {\boldsymbol{\omega }} \times {{{\mathbf{p}}}_{1}} + {\mathbf{g}}} \right), \\ \end{gathered} $$
$${{{\mathbf{N}}}_{a}} = \sum\limits_i {{{m}_{{ai}}}{\mathbf{A}}_{{ai}}^{\text{T}}\left( {{\boldsymbol{\omega }} \times {\boldsymbol{\omega }} \times \left( {{{{\mathbf{r}}}_{{ai}}} + {{{\mathbf{u}}}_{{ai}}}} \right) + 2{\boldsymbol{\omega }} \times {{{{\mathbf{\dot {u}}}}}_{{ai}}} + {\boldsymbol{\omega }} \times {\boldsymbol{\omega }} \times {{{\mathbf{a}}}_{1}} + {\mathbf{g}}} \right)} ,$$
$$\begin{gathered} {{{\mathbf{N}}}_{p}} = \sum\limits_i {{{m}_{{pi}}}{\mathbf{A}}_{{pi}}^{\text{T}}\left( {{\boldsymbol{\omega }} \times {{\psi }_{0}}{{{\mathbf{e}}}_{p}}} \right) \times \left( {{{{\mathbf{r}}}_{{pi}}} + {{{\mathbf{u}}}_{{pi}}}} \right)} \\ + \;\sum\limits_i {{{m}_{{pi}}}{\mathbf{A}}_{{pi}}^{\text{T}}\left( {{{{\boldsymbol{\omega }}}_{p}} \times {{{\boldsymbol{\omega }}}_{p}} \times \left( {{{{\mathbf{r}}}_{{pi}}} + {{{\mathbf{u}}}_{{pi}}}} \right) + 2{{{\boldsymbol{\omega }}}_{p}} \times {{{{\mathbf{\dot {u}}}}}_{{pi}}} + {\boldsymbol{\omega }} \times {\boldsymbol{\omega }} \times {{{\mathbf{p}}}_{1}} + {\mathbf{g}}} \right)} , \\ \end{gathered} $$

and the following notation is introduced:

$${{{\mathbf{A}}}_{a}} = \sum\limits_i {{{m}_{{ai}}}{{{\mathbf{A}}}_{{ai}}}} ,\quad {{{\mathbf{A}}}_{p}} = \sum\limits_i {{{m}_{{pi}}}{{{\mathbf{A}}}_{{pi}}}} ,$$
$$\begin{gathered} {\mathbf{g}} = - \frac{{{{m}_{a}}}}{m}\left( {{\boldsymbol{\omega }} \times {\boldsymbol{\omega }} \times \left( {{\mathbf{a}} + {{{{\mathbf{\tilde {a}}}}}_{2}}} \right) + 2{\boldsymbol{\omega }} \times {{{{\mathbf{\dot {\tilde {a}}}}}}_{2}}} \right) \\ - \;\frac{{{{m}_{p}}}}{m}\left( {{\boldsymbol{\omega }} \times {\boldsymbol{\omega }} \times {{{\mathbf{p}}}_{1}} + {{{\boldsymbol{\omega }}}_{p}} \times {{{\boldsymbol{\omega }}}_{p}} \times \left( {{{{\mathbf{p}}}_{2}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right) + \left( {{\boldsymbol{\omega }} \times {{\psi }_{0}}{{{\mathbf{e}}}_{p}}} \right) \times \left( {{{{\mathbf{p}}}_{2}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right) + 2{{{\boldsymbol{\omega }}}_{p}} \times {{{{\mathbf{\dot {\tilde {p}}}}}}_{2}}} \right). \\ \end{gathered} $$

It is assumed that the SC is affected only by the gravity forces. The addends in (1.1) that describe the action of gravity on the FEs of the SC are represented as

$$\begin{gathered} {{{\mathbf{f}}}_{{\omega a}}} = - 3\omega _{0}^{2}{{m}_{a}}{{{\mathbf{a}}}_{1}} \times {{{\mathbf{e}}}_{3}}\left( {{{{\mathbf{e}}}_{3}},{{{\mathbf{a}}}_{2}} + {{{{\mathbf{\tilde {a}}}}}_{2}}} \right) \\ - \;\omega _{0}^{2}{{m}_{a}}\left( {{\mathbf{a}} + {{{{\mathbf{\tilde {a}}}}}_{2}}} \right) \times \left( {\boldsymbol{\kappa} + 3{{{\mathbf{e}}}_{3}}\left( {{{{\mathbf{e}}}_{3}},\Delta {{{\mathbf{R}}}_{a}}} \right)} \right) - 3\omega _{0}^{2}{{{\mathbf{e}}}_{3}} \times {{{{\mathbf{\tilde {J}}}}}_{a}}{{{\mathbf{e}}}_{3}}, \\ {{{\mathbf{f}}}_{{\omega p}}} = - 3\omega _{0}^{2}{{m}_{p}}{{{\mathbf{p}}}_{1}} \times {{{\mathbf{e}}}_{3}}\left( {{{{\mathbf{e}}}_{3}},{{{\mathbf{p}}}_{2}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right) \\ - \;\omega _{0}^{2}{{m}_{p}}\left( {{\mathbf{p}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right) \times \left( {\boldsymbol{\kappa} + 3{{{\mathbf{e}}}_{3}}\left( {{{{\mathbf{e}}}_{3}},\Delta {{{\mathbf{R}}}_{p}}} \right)} \right) - 3\omega _{0}^{2}{{{\mathbf{e}}}_{3}} \times {{{{\mathbf{\tilde {J}}}}}_{p}}{{{\mathbf{e}}}_{3}}, \\ {{{\mathbf{f}}}_{a}} = {{m}_{a}}\omega _{0}^{2}({\mathbf{A}}_{a}^{\text{T}}\Delta {{{\mathbf{R}}}_{a}} - 3{\mathbf{A}}_{a}^{\text{T}}{{{\mathbf{e}}}_{3}}\left( {{{{\mathbf{e}}}_{3}},\Delta {{{\mathbf{R}}}_{a}}} \right)) \\ + \;\omega _{0}^{2}\left( {\sum\limits_i {{{m}_{{ai}}}{\mathbf{A}}_{{ai}}^{\text{T}}\left( {{{{\mathbf{r}}}_{{ai}}} + {{{\mathbf{A}}}_{{ai}}}{{{\mathbf{q}}}_{a}}} \right) - 3{{m}_{{ai}}}{\mathbf{A}}_{{ai}}^{\text{T}}{{{\mathbf{e}}}_{3}}\left( {{{{\mathbf{e}}}_{3}},{{{\mathbf{r}}}_{{ai}}} + {{{\mathbf{A}}}_{{ai}}}{{{\mathbf{q}}}_{a}}} \right)} } \right), \\ {{{\mathbf{f}}}_{p}} = {{m}_{p}}\omega _{0}^{2}({\mathbf{A}}_{p}^{\text{T}}\Delta {{{\mathbf{R}}}_{p}} - 3{\mathbf{A}}_{p}^{\text{T}}{{{\mathbf{e}}}_{3}}({{{\mathbf{e}}}_{3}},\Delta {{{\mathbf{R}}}_{p}})) \\ + \;\omega _{0}^{2}\left( {\sum\limits_i {{{m}_{{pi}}}{\mathbf{A}}_{{pi}}^{\text{T}}\left( {{{{\mathbf{r}}}_{{pi}}} + {{{\mathbf{A}}}_{{pi}}}{{{\mathbf{q}}}_{p}}} \right) - 3{{m}_{{pi}}}{\mathbf{A}}_{{pi}}^{\text{T}}{{{\mathbf{e}}}_{3}}\left( {{{{\mathbf{e}}}_{3}},{{{\mathbf{r}}}_{{pi}}} + {{{\mathbf{A}}}_{{pi}}}{{{\mathbf{q}}}_{p}}} \right)} } \right), \\ \end{gathered} $$
((1.2))

with the following notations introduced:

$$\begin{gathered} \omega _{0}^{2} = \frac{\mu }{{R_{O}^{3}}},\quad {{{\mathbf{e}}}_{3}} = \frac{{{{{\mathbf{R}}}_{O}}}}{{{{R}_{O}}}}, \\ \boldsymbol{\kappa} = \frac{{{{m}_{a}}}}{m}\left( {{\mathbf{a}} + {{{{\mathbf{\tilde {a}}}}}_{2}}} \right) + \frac{{{{m}_{p}}}}{m}\left( {{\mathbf{p}} + {{{{\mathbf{\tilde {p}}}}}_{2}}} \right),\quad \Delta {{{\mathbf{R}}}_{a}} = {{{\mathbf{a}}}_{1}} - \boldsymbol{\kappa} ,\quad \Delta {{{\mathbf{R}}}_{p}} = {\mathbf{p}_{1}} - \boldsymbol{\kappa} . \\ \end{gathered} $$

The action of gravity on the angular motion of the SC with FEs is determined by the momentum

$${\mathbf{T}} = 3\omega _{0}^{2}{{{\mathbf{e}}}_{3}} \times {{{\mathbf{J}}}_{s}}{{{\mathbf{e}}}_{3}} - {{{\mathbf{f}}}_{{\omega a}}} - {{{\mathbf{f}}}_{{\omega p}}} = 3\omega _{0}^{2}{{{\mathbf{e}}}_{3}} \times {\mathbf{J}}{{{\mathbf{e}}}_{3}}.$$
((1.3))

The orientation of the vehicle’s body is specified with the Rodrigues–Hamilton parameters \({{\left( {{{\lambda }_{0}},{\boldsymbol{\lambda }}} \right)}^{{\text{T}}}}\), which obey the following kinematic relations:

$$\begin{gathered} {{{\dot {\lambda }}}_{0}} = - \frac{1}{2}\left( {{\boldsymbol{\omega }},\,{\boldsymbol{\lambda }}} \right), \\ {\boldsymbol{\dot {\lambda }}} = \frac{1}{2}\left( {{{\lambda }_{0}}{\boldsymbol{\omega }} + {\boldsymbol{\lambda }} \times {\boldsymbol{\omega }}} \right). \\ \end{gathered} $$
((1.4))

The motion equations (1.1) along with kinematic relations (1.4) are used for modeling the motion of the SC with FE.

1.3. Models of Motion used for the Construction of Control

In the construction of the control laws, the value of the control torque is assumed to be much greater than the value of the gravitational torque. Without the influence of the latter taken into consideration, the nonlinear model of motion takes the following form:

$$\begin{gathered} {\boldsymbol{\dot {\omega }}} = - {{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}}{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}^{{ - 1}}}\left( { - {{{\mathbf{N}}}_{q}} - {\mathbf{\Omega q}}} \right) \\ + \;{{{\mathbf{J}}}^{{ - 1}}}({{{\mathbf{E}}}_{{3 \times 3}}} + {{{\mathbf{S}}}_{q}}{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}^{{ - 1}}}{\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}})\left( { - {{{\mathbf{N}}}_{\omega }} + {\mathbf{u}}} \right), \\ {{{{\mathbf{\dot {V}}}}}_{q}} = {{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}^{{ - 1}}}\left( { - {{{\mathbf{N}}}_{q}} - {\mathbf{\Omega q}}} \right) - {{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}^{{ - 1}}}{\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}\left( { - {{{\mathbf{N}}}_{\omega }} + {\mathbf{u}}} \right), \\ {{{\dot {\lambda }}}_{0}} = - \frac{1}{2}\left( {{\boldsymbol{\omega }},{\boldsymbol{\lambda }}} \right), \\ {\boldsymbol{\dot {\lambda }}} = \frac{1}{2}\left( {{{\lambda }_{0}}{\boldsymbol{\omega }} + {\boldsymbol{\lambda }} \times {\boldsymbol{\omega }}} \right), \\ {\mathbf{\dot {q}}} = {{{\mathbf{V}}}_{q}}. \\ \end{gathered} $$
((1.5))

Here, \(\mathbf{u} = {{{\mathbf{T}}}_{s}}\) is the vector that contains only the control, \({\mathbf{q}} = {{({\mathbf{q}}_{a}^{\text{T}},{\mathbf{q}}_{p}^{\text{T}})}^{\text{T}}}\) is the vector of the amplitudes of the vibrational modes of the FE,

$$\begin{gathered} {{{\mathbf{N}}}_{\omega }} = {\boldsymbol{\omega }} \times {{{\mathbf{J}}}_{s}}{\boldsymbol{\omega }} + {{{\mathbf{N}}}_{{\omega a}}} + {{{\mathbf{N}}}_{{\omega p}}},\quad {{{\mathbf{S}}}_{q}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{S}}}_{{\omega a}}}}&{{{{\mathbf{S}}}_{{\omega p}}}} \end{array}} \right), \\ {\mathbf{M}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{M}}}_{a}}}&{{{{\mathbf{S}}}_{{ap}}}} \\ {{\mathbf{S}}_{{ap}}^{\text{T}}}&{{{{\mathbf{M}}}_{p}}} \end{array}} \right),\quad {{{\mathbf{N}}}_{q}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{N}}}_{a}}} \\ {{{{\mathbf{N}}}_{p}}} \end{array}} \right). \\ \end{gathered} $$

The desired angular position is specified by the orientation quaternion, which is set as \({{(1,{\mathbf{0}^{\text{T}}})}^{\text{T}}}\). If the SC is in the vicinity of this position, the control law is constructed using the linearization of Eqs. (1.5); this can be written as the following system:

$${\mathbf{\dot {x}}} = {\mathbf{Ax}} + {\mathbf{Bu}},$$
((1.6))

where \({\mathbf{x}} = {{(\begin{array}{*{20}{c}} {{{{\boldsymbol{\omega }}}^{\text{T}}}}&{{{{\boldsymbol{\lambda }}}^{\text{T}}}}&{{\mathbf{V}}_{q}^{\text{T}}}&{{{q}^{\text{T}}}} \end{array})}^{\text{T}}}\) is the state vector of the SC with FEs, and the constant matrices A and B are

$${\mathbf{A}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{0}}}_{{3 \times 3}}}}&{{{{\mathbf{0}}}_{{3 \times 3}}}}&{{{{\mathbf{0}}}_{{3 \times n}}}}&{{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}}{{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}}^{{ - 1}}}{\mathbf{\Omega }}} \\ {\frac{1}{2}{{{\mathbf{E}}}_{{3 \times 3}}}}&{{{{\mathbf{0}}}_{{3 \times 3}}}}&{{{{\mathbf{0}}}_{{3 \times n}}}}&{{{{\mathbf{0}}}_{{3 \times n}}}} \\ {{{{\mathbf{0}}}_{{n \times 3}}}}&{{{{\mathbf{0}}}_{{n \times 3}}}}&{{{{\mathbf{0}}}_{{n \times n}}}}&{ - {{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}}^{{ - 1}}}{\mathbf{\Omega }}} \\ {{{{\mathbf{0}}}_{{n \times 3}}}}&{{{{\mathbf{0}}}_{{n \times 3}}}}&{{{{\mathbf{E}}}_{{n \times n}}}}&{{{{\mathbf{0}}}_{{n \times n}}}} \end{array}} \right),$$
$${\mathbf{B}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{J}}}^{{ - 1}}}({{{\mathbf{E}}}_{{3x3}}} + {{{\mathbf{S}}}_{q}}{{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}}^{{ - 1}}}{\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}})} \\ {{{{\mathbf{0}}}_{{3 \times 3}}}} \\ { - {{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}}^{{ - 1}}}{\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}} \\ {{{{\mathbf{0}}}_{{n \times 3}}}} \end{array}} \right).$$

The specific feature of the problem of constructing the control of an SC with FEs based on (1.6) is the high dimensionality of the state vector x. Indeed, the vector x has a dimensionality of \(2(3 + {{n}_{a}} + {{n}_{p}})\), where na and np are the number of the vibrational modes of the antenna and panel, respectively, taken into account in the model of an SC with FEs. The higher the dimensionality of the vector q(t), the more accurately the motion model is specified. However, an increase in the dimensionality of the vector q(t) leads to an increase in the computational complexity of the control algorithms that use the system matrix A with a dimensionality of \(2(3 + {{n}_{a}} + {{n}_{p}}) \times 2(3 + {{n}_{a}} + {{n}_{p}})\). The solution to this problem is represented by the algorithms based on the reduced model of motion.

2. CONTROL ALGORITHMS FOR AN SC WITH FES

This section describes the control methods, the primary goal of which is the problem of stabilization of the SC body in the desired angular position. The problem is solved using the control devices located only on the main body of the vehicle, namely, a set of flywheels. In addition to that, it is necessary to take into account the restrictions on the magnitude of the control.

As was noted before, the presence of FEs in the SC structure places additional requirements on the control algorithms. First of all, the algorithms should reduce the vibrations in the FEs (or at least prevent an increase in their amplitudes) that negatively affect the accuracy of the SC’s orientation. Secondly, constructing the laws based on the linear model of motion (1.6) often requires the model to be reduced. Of special interest are the control laws that do not require knowing the amplitudes q(t) of the vibrational modes.

In the first place, we study the possibility of using the classical methods of control: Lyapunov control and LQR for the solution of the stabilization problem.

2.1. Lyapunov Control

The Lyapunov control is constructed based on the nonlinear model of motion of an SC with FEs (1.5). The control law and the corresponding Lyapunov function are chosen in such a way as to the provide the asymptotic stability of the required angular position of the SC main body. The Lyapunov function is considered in the following form:

$$V = \frac{1}{2}{{{\boldsymbol{\omega }}}^{2}} + {{k}_{\lambda }}\left( {1 - {{\lambda }_{0}}} \right),\quad {{k}_{\lambda }} > 0,$$
((2.1))

which takes the kinematic relations (1.4) into account, and its derivative is set with the expression

$$\dot {V} = \left( {{\boldsymbol{\omega }},{\boldsymbol{\dot {\omega }}} + \frac{1}{2}{{k}_{\lambda }}{\boldsymbol{\lambda }}} \right).$$

The Lyapunov control is constructed in such a way that the derivative of the Lyapunov function (2.1), found from the motion equations of system (1.5), would equal \( - {{k}_{\omega }}{{{\boldsymbol{\omega }}}^{2}}\); i.e., it would take on nonpositive values. Then, according to the Barbashin–Krasovskii theorem, the required position of equilibrium is asymptotically stable. Ultimately, the sought control law has the form

$$\begin{gathered} {\mathbf{u}} = {{{\mathbf{N}}}_{\omega }} - {{({{{\mathbf{E}}}_{{3 \times 3}}} + {{{\mathbf{S}}}_{q}}{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}^{{ - 1}}}{\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}})}^{{ - 1}}} \\ \times \;\left( {{\mathbf{J}}\left( {\frac{1}{2}{{k}_{\lambda }}{\boldsymbol{\lambda }} + {{k}_{\omega }}{\boldsymbol{\omega }}} \right) + {{{\mathbf{S}}}_{q}}{{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}}^{{ - 1}}}({{{\mathbf{N}}}_{q}} + {\mathbf{\Omega q}})} \right),\quad {{k}_{\omega }} > 0. \\ \end{gathered} $$
((2.2))

Control (2.2) allows the system to be stabilized at any initial conditions.

The principal moments of inertia of the vehicle under study have an order of 105 kg m2. Therefore, the magnitude of the gravitational moment (1.3) acting on the SC in a geostationary orbit approximately equals 10–5 N m. This is several orders of magnitude less than the maximum control torque of the flywheels, which is assumed to be 0.4 N m.

The numerical illustration of algorithm (2.2) is obtained at the following initial conditions:

(1) Angular velocity \({\boldsymbol{\omega }} = {{\left( {\begin{array}{*{20}{c}} {0.02}&{0.01}&0 \end{array}.03} \right)}^{\text{T}}}\) deg/s;

(2) Orientation quaternion \({{({{\lambda }_{0}},\,{{{\boldsymbol{\lambda }}}^{\text{T}}})}^{\text{T}}}\): vector part \({\boldsymbol{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.5}&{0.5}&{0.5} \end{array}} \right)}^{\text{T}}}\) (corresponds to the rotation at a wide angle) and \({\boldsymbol{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.01}&{0.01}&{0.01} \end{array}} \right)}^{\text{T}}}\) (corresponds to the vicinity of the equilibrium position), and scalar part

$${{\lambda }_{0}} = \sqrt {1 - {{{\boldsymbol{\lambda }}}^{2}}} ;$$

(3) The initial rotation angle of the panel \({{\varphi }_{0}} = 10\) deg;

(4) The angular velocity of the panel’s rotation in the hinge \({{\psi }_{0}} = 7.2 \times {{10}^{{ - 5}}}\) rad/s;

(5) The number of vibrational modes \({{n}_{a}} = 5\), \({{n}_{p}} = 2\);

(6) The amplitudes of vibrational modes

$${{{\mathbf{q}}}_{a}} = {{\underbrace {\left( {\begin{array}{*{20}{c}} {0.1}&{0.1}&{...}&{0.1} \end{array}} \right)}_{{{n}_{a}}}}^{\text{T}}},\quad {{{\mathbf{q}}}_{p}} = {{\underbrace {\left( {\begin{array}{*{20}{c}} {0.1}&{0.1}&{...}&{0.1} \end{array}} \right)}_{{{n}_{p}}}}^{\text{T}}};$$

(7) The rate of change in the amplitudes of the vibrational modes

$${{{\mathbf{V}}}_{{qa}}} = {{\underbrace {\left( {\begin{array}{*{20}{c}} 0&0&{...}&0 \end{array}} \right)}_{{{n}_{a}}}}^{\text{T}}},\,\quad {{{\mathbf{V}}}_{{qp}}} = {{\underbrace {\left( {\begin{array}{*{20}{c}} 0&0&{...}&0 \end{array}} \right)}_{{{n}_{p}}}}^{\text{T}}};$$

(8) Control step \({{\tau }_{{{\text{con}}}}} = 0.25\) s;

(9) Numerical integration is performed using the fourth order Runge–Kutta method with a constant step; the integration step is \({{\tau }_{{{\text{int}}}}} = 0.01\) s;

(10) The maximum control torque of the flywheels is 0.4 N m.

The calculations are performed at two values of the orientation quaternion: \({\boldsymbol{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.01}&{0.01}&{0.01} \end{array}} \right)}^{\text{T}}}\) (Fig. 2) and \({\boldsymbol{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.5}&{0.5}&{0.5} \end{array}} \right)}^{\text{T}}}\)(Fig. 3). The first one specifies the angular position that is in the vicinity of the desired orientation of the SC main body; the second one describes the rotation of the SC with FE at wide angles. As expected, the algorithm in both cases damps the SC rotation (Figs. 2a, 3a) and provides the desired orientation of the body (Figs. 2b, 3b). The parameters of the Lyapunov control were set as follows: \({{k}_{\omega }} = 0.1\) N m s, \({{k}_{\lambda }} = {{10}^{{ - 3}}}\) N m. However, when applied to the problem of control of the SC with FE, the Lyapunov control has three considerable disadvantages.

Fig. 2.
figure 2

Lyapunov control (small angle): (a) angular velocity, (b) vector part of orientation quaternion, (c) amplitudes of vibrational modes of antenna, (d) amplitudes of vibrational modes of panel, and (e) control torque.

Full size image
Fig. 3.
figure 3

Lyapunov control (wide angle): (a) angular velocity, (b) vector part of orientation quaternion, (c) amplitudes of vibrational modes of antenna, (d) amplitudes of vibrational modes of panel, and (e) control torque.

Full size image

1. The magnitude of control is not restricted in any way, which leads to the impossibility of realizing the required control torque (Figs. 2e, 3e). Figure 3e shows that in the case of rotation of the SC at a wide angle, the control torque reaches 4 N m (in the linear case, approximately 2 N m), while the maximum allowable value is 0.4 N m.

2. The influence on the vibrational modes is not restricted as well, which leads to excessive oscillations of the FE (Figs. 2c, 2d, 3c, 3d). In particular, the highest amplitude of one of the vibrational modes of the antenna during transition from position \({\boldsymbol{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.5}&{0.5}&{0.5} \end{array}} \right)}^{\text{T}}}\) to zero exceeded the initial value by a factor of 60 (Fig. 3c), which may surpass allowable deviations.

3. This method requires knowing the amplitudes of the vibrational modes, which sets additional requirements for the procedure of identification of the state of the system [11].

Among the above-mentioned problems, the impossibility of realizing the control laws using onboard actuators needs to be addressed first of all. For this reason, further in the study we consider the methods of control that allow the magnitude of the controlling actions to be restricted.

2.2. Linear Quadratic Requlator

The LQR is a classical type of control that allows us to restrict the magnitude of the controlling actions \({\mathbf{u}}\) [12]. When applied to the linear model of an SC with FEs (1.6), the LQR minimizes the functional

$$J = \int\limits_0^\infty {({{{\mathbf{x}}}^{\text{T}}}{\mathbf{Qx}} + {{{\mathbf{u}}}^{\text{T}}}{\mathbf{Ru}})dt} ,$$
((2.3))

where Q is a nonnegative definite matrix (\({\mathbf{Q}} \geqslant 0\)); i.e., \({{{\mathbf{x}}}^{\text{T}}}{\mathbf{Qx}} \geqslant 0\) holds true for \(\forall {\mathbf{x}} \ne {\mathbf{0}}\) and R is a positive definite matrix (\({\mathbf{R}} > 0\)). Here, \({\mathbf{x}} = {{(\begin{array}{*{20}{c}} {{{{\boldsymbol{\omega }}}^{\text{T}}}}&{{{{\boldsymbol{\lambda }}}^{\text{T}}}}&{{\mathbf{V}}_{q}^{\text{T}}}&{{{q}^{\text{T}}}} \end{array})}^{\text{T}}}\) is the state vector of an SC with FE, and u is the vector of the controlling actions. The magnitude of the controlling actions can be reduced on account of increasing the diagonal elements of the matrix R (the matrices Q and R are the parameters of the algorithm). In turn, increasing the diagonal elements of the matrix Q allows us to minimize the deviation of the state vector x from the required (zero) value. The control law that minimizes (2.3) is set with the expression [12]

$${\mathbf{u}} = - {{{\mathbf{R}}}^{{ - 1}}}{{{\mathbf{B}}}^{\text{T}}}{\mathbf{Px}},$$
((2.4))

where P is the solution of the Riccati matrix equation:

$${{{\mathbf{A}}}^{\text{T}}}{\mathbf{P}} + {\mathbf{PA}} - {\mathbf{PB}}{{{\mathbf{R}}}^{{ - 1}}}{{{\mathbf{B}}}^{\text{T}}}{\mathbf{P}} + {\mathbf{Q}} = 0.$$

The control law (2.4) (under the condition Q > 0) ensures the asymptotic stability of the equilibrium position x = 0 [12]. In other words, using control law (2.4), it is possible not only to stabilize the SC main body in the desired angular position but also to damp the vibrations in the flexible elements of its structure.

A numerical example of the control law (2.4) is given at the same initial conditions as in the case of the Lyapunov control. However, since the LQR is based on the linearized model of the SC with FE, only the case of initial orientation of the SC main body from the vicinity of the required position, i.e., λ = \({{(\begin{array}{*{20}{c}} {0.01}&{0.01}&{0.01} \end{array})}^{\text{T}}}\), is considered.

The LQR parameters were set as

$$\mathbf{Q} = \left( {\begin{array}{*{20}{c}} {{{{10}}^{3}}{\mathbf{E}_{{3 \times 3}}}}&{{\mathbf{0}_{{3 \times 3}}}}&{{\mathbf{0}_{{3 \times 2\left( {{{n}_{a}} + {{n}_{p}}} \right)}}}} \\ {{\mathbf{0}_{{3 \times 3}}}}&{3 \times {{{10}}^{4}}{\mathbf{E}_{{3 \times 3}}}}&{{\mathbf{0}_{{3 \times 2\left( {{{n}_{a}} + {{n}_{p}}} \right)}}}} \\ {{\mathbf{0}_{{2\left( {{{n}_{a}} + {{n}_{p}}} \right) \times 3}}}}&{{\mathbf{0}_{{2\left( {{{n}_{a}} + {{n}_{p}}} \right) \times 3}}}}&{{{{10}}^{4}}{\mathbf{E}_{{2\left( {{{n}_{a}} + {{n}_{p}}} \right) \times 2\left( {{{n}_{a}} + {{n}_{p}}} \right)}}}} \end{array}} \right),\quad \mathbf{R} = {{10}^{5}}{\mathbf{E}_{{3 \times 3}}}.$$

In Figs. 4a and 4b, it can be seen that the control successfully stabilizes the SC main body in the desired angular position. Although, in comparison with the Lyapunov control (2.2), the time required for the stabilization increased, the magnitude of control declined and reached an acceptable level (Fig. 4e). This occurs on account of the addend \({{{\mathbf{u}}}^{\text{T}}}{\mathbf{Ru}}\), which penalizes high values of controlling actions.

Fig. 4.
figure 4

LQR: (a) angular velocity, (b) vector part of orientation quaternion, (c) amplitudes of vibrational modes of antenna, (d) amplitudes of vibrational modes of panel, and (e) control torque.

Full size image

It should be noted that not only the angular velocity and vector part of the quaternion tend to zero but the amplitudes of the elastic vibrations of the FE also decline (Figs. 4a, 4b).

Due to the minimization of the addend \({{{\mathbf{x}}}^{\text{T}}}{\mathbf{Qx}}\) in functional (2.3), there is no significant increase in the amplitudes of the vibrational modes in the FE relative to their initial values during the transition process (Figs. 4c, 4d).

It should be noted that the LQR (2.4), just as the Lyapunov control, requires knowing the amplitudes of the vibrational modes. The solution of this problem is the LQR that is based on a reduced mathematical model that contains only the angular motion of an SC with FEs.

2.3. LQR Based on a Reduced Mathematical Model of an SC with FEs

To construct the LQR based on a reduced model, the linear system (1.6) is represented as two subsystems:

$$\left( {\begin{array}{*{20}{c}} {{\mathbf{\dot {y}}}} \\ \mathbf{\dot {z}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{A}}}_{\omega }}}&{{\mathbf{A}_{{\omega q}}}} \\ \mathbf{0}&{{\mathbf{A}_{{qq}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\mathbf{y}} \\ \mathbf{z} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{\mathbf{B}_{\omega }}} \\ {{\mathbf{B}_{q}}} \end{array}} \right)\mathbf{u}.$$
((2.5))

The vector \({\mathbf{y}} = {{(\begin{array}{*{20}{c}} {{{{\boldsymbol{\omega }}}^{\text{T}}}}&{{{{\boldsymbol{\lambda }}}^{\text{T}}}} \end{array})}^{\text{T}}}\) describes the angular motion of the SC main body, while the vector \(\mathbf{z} = {{(\begin{array}{*{20}{c}} {\mathbf{V}_{q}^{\text{T}}}&{{\mathbf{q}^{\text{T}}}} \end{array})}^{\text{T}}}\) is responsible for the behavior of the FEs. Here,

$${{{\mathbf{A}}}_{\omega }} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{0}}}_{{3 \times 3}}}}&{{{{\mathbf{0}}}_{{3 \times 3}}}} \\ {\frac{1}{2}{{{\mathbf{E}}}_{{3 \times 3}}}}&{{{{\mathbf{0}}}_{{3 \times 3}}}} \end{array}} \right),$$
((2.6))
$$\begin{gathered} {{{\mathbf{A}}}_{{\omega q}}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{0}}}_{{3 \times n}}}}&{{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}}{{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}}^{{ - 1}}}{\mathbf{\Omega }}} \\ {{{{\mathbf{0}}}_{{3 \times n}}}}&{{{{\mathbf{0}}}_{{3 \times n}}}} \end{array}} \right), \\ {{{\mathbf{A}}}_{{qq}}} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{0}}}_{{n \times n}}}}&{ - {{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}}^{{ - 1}}}{\mathbf{\Omega }}} \\ {{{{\mathbf{E}}}_{{n \times n}}}}&{{{{\mathbf{0}}}_{{n \times n}}}} \end{array}} \right), \\ {{{\mathbf{B}}}_{\omega }} = \left( {\begin{array}{*{20}{c}} {{{{\mathbf{J}}}^{{ - 1}}}({{{\mathbf{E}}}_{{3x3}}} + {{{\mathbf{S}}}_{q}}{{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}}^{{ - 1}}}{\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}})} \\ {{{{\mathbf{0}}}_{{3 \times 3}}}} \end{array}} \right), \\ {{{\mathbf{B}}}_{q}} = \left( {\begin{array}{*{20}{c}} { - {{{({\mathbf{M}} - {\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}{{{\mathbf{S}}}_{q}})}}^{{ - 1}}}{\mathbf{S}}_{q}^{\text{T}}{{{\mathbf{J}}}^{{ - 1}}}} \\ {{{{\mathbf{0}}}_{{n \times 3}}}} \end{array}} \right). \\ \end{gathered} $$

As mentioned in [13], if the second equation in system (2.5) is simply discarded and the LQR is constructed based on the reduced part of the system (in our case, the one that describes the angular motion of the SC main body), this leads to undesired disturbances in the flexible elements. The method of constructing the LQR based on a reduced model is considered in [8, 9]. To reduce the disturbances, it is proposed to sum the quality functional with an addend, the minimization of which leads to the reduction.

To implement this method, it is necessary for the second equation of system (2.5) to allow the required equilibrium point; i.e., the following equality should be true:

$$\mathbf{0} = \mathbf{\dot {z}} = {\mathbf{A}_{{qq}}}\mathbf{z} + {\mathbf{B}_{q}}\mathbf{u}.$$
((2.7))

From (2.7), the state vector \(z\) that describes the vibrations of flexible elements is expressed via the control vector

$${\mathbf{z}} = - {\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}{\mathbf{u}}.$$
((2.8))

The first equation of system (2.5), which describes the angular motion of the SC main body, after substitution of (2.8) is rewritten as follows:

$${\mathbf{\dot {y}}} = {{{\mathbf{A}}}_{\omega }}{\mathbf{y}} + ({{{\mathbf{B}}}_{\omega }} - {{{\mathbf{A}}}_{{\omega q}}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}){\mathbf{u}}.$$
((2.9))

Using (2.8), the functional of system (2.5)

$$J = \int\limits_0^\infty {({{{\mathbf{y}}}^{\text{T}}}{{{\mathbf{Q}}}_{{\mathbf{y}}}}{\mathbf{y}} + {{{\mathbf{z}}}^{\text{T}}}{{{\mathbf{Q}}}_{z}}{\mathbf{z}} + {{{\mathbf{u}}}^{\text{T}}}{\mathbf{Ru}})dt} $$

will be rewritten as

$$J = \int\limits_0^\infty {({{{\mathbf{y}}}^{\text{T}}}{{{\mathbf{Q}}}_{{\mathbf{y}}}}{\mathbf{y}} + {{{\mathbf{u}}}^{\text{T}}}({\mathbf{R}} + {{{({\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}})}}^{\text{T}}}{{{\mathbf{Q}}}_{z}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}){\mathbf{u}})dt} .$$
((2.10))

Functional (2.10) contains the addend \({{{\mathbf{u}}}^{\text{T}}}{{({\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}})}^{\text{T}}}{{{\mathbf{Q}}}_{z}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}{\mathbf{u}}\), which minimizes the perturbing influence of the control on the FEs. The LQR based on the reduced model (2.9) and minimizing functional (2.10) has the form

$${\mathbf{u}} = - {\mathbf{R}}_{x}^{{ - 1}}{\mathbf{B}}_{x}^{\text{T}}{\mathbf{Py}},$$
((2.11))

where \({{{\mathbf{R}}}_{x}} = {\mathbf{R}} + {{({\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}})}^{\text{T}}}{{{\mathbf{Q}}}_{z}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}\), \({{{\mathbf{B}}}_{x}} = {{{\mathbf{B}}}_{\omega }} - {{{\mathbf{A}}}_{{\omega q}}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}\), and \(\mathbf{P}\) are the solution of the Riccati equation

$${\mathbf{A}}_{\omega }^{\text{T}}{\mathbf{P}} + {\mathbf{P}}{{{\mathbf{A}}}_{\omega }} - {\mathbf{P}}{{{\mathbf{B}}}_{x}}{\mathbf{R}}_{x}^{{ - 1}}{\mathbf{B}}_{x}^{\text{T}}{\mathbf{P}} + {{{\mathbf{Q}}}_{y}} = \mathbf{0}.$$

Just as LQR (2.4), control (2.11) stabilizes the SC main body in the desired angular position.

The numerical example of algorithm (2.11) uses the same initial conditions as in the case of LQR (2.4). The control parameters were set as

$${\mathbf{Q}_{y}} = \left( {\begin{array}{*{20}{c}} {{{{10}}^{3}}{\mathbf{E}_{{3 \times 3}}}}&0 \\ 0&{3 \times {{{10}}^{4}}{\mathbf{E}_{{3 \times 3}}}} \end{array}} \right),\quad {\mathbf{Q}_{z}} = {{10}^{4}}{\mathbf{E}_{{2\left( {{{n}_{a}} + {{n}_{p}}} \right) \times 2\left( {{{n}_{a}} + {{n}_{p}}} \right)}}},\quad \mathbf{R} = {{10}^{5}}{\mathbf{E}_{{3 \times 3}}}.$$

The numerical results (Fig. 5) show that the conclusions obtained in the modeling of the LQR are also true here. However, in this case, the control is formed without the necessity to determine the amplitudes of the vibrational modes and minimizes the disturbances of the FEs that occur in the process of stabilization of the vehicle body. It should be noted that the information on the forms of vibrations, which is contained in the matrices of system (2.5) is still required for the calculation of the controlling actions.

Fig. 5.
figure 5

Reduced LQR: (a) angular velocity, (b) vector part of orientation quaternion, (c) amplitudes of vibrational modes of antenna, (d) amplitudes of vibrational modes of panel, and (e) control torque.

Full size image

The main disadvantage of the linear-quadratic control laws (2.4) and (2.11) is that they provide the asymptotic stability of the given angular position of the object only in its linear vicinity. One of the rapidly developing methods to project regulators based on a nonlinear model of an object is the SDRE control [6].

2.4. SDRE Control Based on the Reduced Mathematical Model of an SC with FEs

The SDRE control is based on the LQR that uses the Riccati equation, the parameters of which depend on the state of the system [6].

The SDRE control is constructed for an autonomous control-affine nonlinear systems

$$\mathbf{\dot {x}}\left( t \right) = \mathbf{f}\left( \mathbf{x} \right) + \mathbf{B}\left( \mathbf{x} \right)\mathbf{u}\left( t \right),\quad \mathbf{f}\left(\mathbf{0} \right) = \mathbf{0}.$$
((2.12))

Similarly to the LQR, the cost functional is represented as

$$J = \int\limits_0^\infty {({\mathbf{x}^{\text{T}}}\left( t \right)\mathbf{Q}\left( \mathbf{x} \right)\mathbf{x}\left( t \right) + {\mathbf{u}^{\text{T}}}\left( t \right)\mathbf{R}\left( \mathbf{x} \right)\mathbf{u}\left( t \right))dt} ,$$
((2.13))

where the matrices \(\mathbf{Q}\left( \mathbf{x} \right) \geqslant 0,\mathbf{R}\left( \mathbf{x} \right) > 0\) at any value of the state vector x. The matrices Q(x), R(x) depend on the state of the system.

Upon isolating the state vector from the function f(x),

$$\mathbf{f}(\mathbf{x}) = \mathbf{A}(\mathbf{x})\mathbf{x}{\text{,}}$$
((2.14))

system (2.12) is brought to the system of a linear structure with the matrices A(x) and B(x):

$$\dot {\mathbf{x}}\left( t \right) = \mathbf{A}\left( \mathbf{x} \right)\mathbf{x}\left( t \right) + \mathbf{B}\left( \mathbf{x} \right)\mathbf{u}\left( t \right).$$
((2.15))

As follows from [6], the control for the nonlinear system (2.15) with the cost functional (2.13) is represented in the following form:

$$\mathbf{u}\left( t \right) = - \mathbf{K}\left( \mathbf{x} \right)\mathbf{x}\left( t \right) = - {\mathbf{R}^{{ - 1}}}\left( \mathbf{x} \right){\mathbf{B}^{\text{T}}}\left( \mathbf{x} \right)\mathbf{P}\left( \mathbf{x} \right)\mathbf{x}\left( t \right).$$
((2.16))

Here, P(x) is the solution of the algebraic Riccati equation:

$$\mathbf{P}(\mathbf{x})\mathbf{A}(\mathbf{x}) + {\mathbf{A}^{\text{T}}}(\mathbf{x})\mathbf{P}(\mathbf{x}) - \mathbf{P}(\mathbf{x})\mathbf{B}(\mathbf{x}){\mathbf{R}^{{ - 1}}}(\mathbf{x}){\mathbf{B}^{\text{T}}}(\mathbf{x})\mathbf{P}(\mathbf{x}) + \mathbf{Q}(\mathbf{x}) = 0.$$
((2.17))

Thus, the difference of the control law (2.16) from the standard LQR is that the matrices of system (2.15) A(x) and B(x), the control parameters Q(x) and R(x), and, therefore, the solution of the algebraic Riccati equation (2.17) depend on the state of the system. Note that the algebraic Riccati equation should be solved at each step of the control.

In the present study, the SDRE control is constructed based on the reduced model of the system, i.e., on the equations responsible for the angular motion of the SC. The initial values of the angular velocity, as well as amplitudes q of the vibrational modes of the FE and their rates of change \({{{\mathbf{V}}}_{q}}\), are assumed to be sufficiently small, so the model is linearized in all these variables. Only the kinematic relations for the rotation of the vehicle’s body are nonlinear. In this case, Eqs. (1.5) are only nonlinear in the orientation quaternion. The expansion similar to (2.14) leads again to system (2.5) with the only difference that the matrix \({{{\mathbf{A}}}_{\omega }}\) is replaced with the matrix

$${{{\mathbf{A}}}_{{\omega SDRE}}} = {{{\mathbf{A}}}_{\omega }} + \left( {\begin{array}{*{20}{c}} {{{{\mathbf{0}}}_{{3 \times 3}}}}&{{{{\mathbf{0}}}_{{3 \times 3}}}} \\ \Lambda &{{{{\mathbf{0}}}_{{3 \times 3}}}} \end{array}} \right),$$

where

$$\,\Lambda = \left( {\begin{array}{*{20}{c}} 0&{ - {{\lambda }_{3}}}&{{{\lambda }_{2}}} \\ {{{\lambda }_{3}}}&0&{ - {{\lambda }_{1}}} \\ { - {{\lambda }_{2}}}&{{{\lambda }_{1}}}&0 \end{array}} \right).$$

The control law is described by a formula similar to (2.11) and is in the form

$${\mathbf{u}} = - {\mathbf{R}}_{x}^{{ - 1}}\left( y \right){\mathbf{B}}_{x}^{\text{T}}\left( y \right){\mathbf{P}}\left( y \right){\mathbf{y}},$$
((2.18))

where \({{{\mathbf{R}}}_{x}} = {\mathbf{R}} + {{({\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}})}^{\text{T}}}{{{\mathbf{Q}}}_{z}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}\), \({{{\mathbf{B}}}_{x}} = {{{\mathbf{B}}}_{\omega }} - {{{\mathbf{A}}}_{{\omega q}}}{\mathbf{A}}_{{qq}}^{{ - 1}}{{{\mathbf{B}}}_{q}}\), and \(\mathbf{P}\left( \mathbf{y} \right)\) are the solution of the Riccati equation.

$${\mathbf{A}}_{{\omega SDRE}}^{\text{T}}\left( {\mathbf{y}} \right){\mathbf{P}}\left( {\mathbf{y}} \right) + {\mathbf{P}}\left( {\mathbf{y}} \right){{{\mathbf{A}}}_{{\omega SDRE}}}\left( {\mathbf{y}} \right) - {\mathbf{P}}\left( {\mathbf{y}} \right){{{\mathbf{B}}}_{x}}{\mathbf{R}}_{x}^{{ - 1}}{\mathbf{B}}_{x}^{\text{T}}{\mathbf{P}}\left( {\mathbf{y}} \right) + {{{\mathbf{Q}}}_{y}} = \mathbf{0}.$$
((2.19))

Equation (2.19) is solved at each control step by the function that realizes the algorithm that is proposed in [14] and based on the Kleinman algorithm. In [15], it is noted that the solution of the Riccati equation by this algorithm requires \(60{{n}^{3}}\) floating point operations.

Unlike the control law (2.11), the nonlinearity in the quaternion makes it possible to bring the SC main body to the desired position from any initial angular position.

The numerical example of algorithm (2.18) uses the same initial conditions as in the case of the Lyapunov control. Since the study of this algorithm was mainly prompted by the impossibility to rotate the SC main body at wide angles by the linear-quadratic control (2.4) and (2.11), its initial orientation is defined by the quaternion \({\boldsymbol{\lambda }} = {{\left( {\begin{array}{*{20}{c}} {0.5}&{0.5}&{0.5} \end{array}} \right)}^{\text{T}}}\). The control parameters were set as

$${\mathbf{Q}_{y}} = \left( {\begin{array}{*{20}{c}} {{{{10}}^{3}}{\mathbf{E}_{{3 \times 3}}}}&0 \\ 0&{3 \times {{{10}}^{4}}{\mathbf{E}_{{3 \times 3}}}} \end{array}} \right),\quad {\mathbf{Q}_{z}} = {{10}^{4}}{\mathbf{E}_{{2({{n}_{a}} + {{n}_{p}}) \times 2({{n}_{a}} + {{n}_{p}})}}},\quad \mathbf{R} = {{10}^{6}}{\mathbf{E}_{{3 \times 3}}}.$$

It can be seen from the diagrams that the SDRE control successfully stabilizes the SC main body (Figs. 6a, 6b) and reduces the amplitudes of the vibrational modes, preventing the latter from strong deviations from their initial values (Figs. 6c, 6d). Just as in the case of the abovementioned linear-quadratic control laws (2.4) and (2.11), the controlling moment does not exceed the allowable value of 0.4 N m (Fig. 6e).

Fig. 6.
figure 6

SDRE control: (a) angular velocity, (b) vector part of orientation quaternion, (c) amplitudes of vibrational modes of antenna, (d) amplitudes of vibrational modes of panel, and (e) control torque.

Full size image

Unfortunately, the domain of stability of this algorithm is not yet studied. The fact that gives some ground for optimism is that the SDRE control contains all the features of the classical LQR and under the linear approximation coincides with it completely. This question requires further research.

CONCLUSIONS

The control methods with the goal of stabilization of the SC main body and reducing the vibrations in the FEs were tested on the full model of motion of an SC with FEs.

The Lyapunov control solves these problems; the stabilization of the SC main body is possible at any initial orientation and any initial values of the amplitudes of the vibrational modes and their rates of change. However, the absence of the mechanisms to restrict the control and excitation of the vibrational modes leads to difficulties in the implementation of such a type of control in practice. These difficulties can be overcome using the LQR, which, due to the form of the cost functional, allows penalizing the excessive increase in the cost of control resources.

The high dimensionality of the state vector of an SC with FEs and the aim to construct a control algorithm based only on the angular motion of the SC main body led to the construction of an LQR based on a reduced model of motion. This control law not only stabilizes the SC main body in the desired angular position but, due to the modification of the quality functional, also prevents the disturbances in the FE that occur in the process of stabilization of the SC main body.

The main disadvantage of the linear-quadratic methods is that they work only in the vicinity of the required position of the SC.

The SDRE control is apparently the most appropriate method, given the conditions of the problem under study. While retaining the main advantages of the LQR, it is used for the control of nonlinear systems. Unlike the classical LQR, the SDRE control is constructed based on the equations of the relative motion of the SC main body and does not require knowing the vibrational modes of the FEs, thus allowing the rotation of the vehicle at arbitrary angles. The numerical modeling has demonstrated that the use of the SDRE control provides the stabilization of the SC main body with FEs in the desired position and reduces the vibrations in the FEs. The algorithm provides the restriction of the control torque within the prescribed limits. The main disadvantage of the algorithm is the problem of maintaining the global asymptotic stability. This question requires further studies.