1 Introduction

Memristor explains the relationship between charge and magnetic flux, in 1971, Chua [1] firstly proposed the concept of memristor. Memristors are usually divided into two categories: charge-controlled memristor (CCM) [2,3,4] and MFCM [5,6,7]. Chaotic circuit is an important research content in nonlinear circuits, and the nonlinear element is the key for designing chaotic circuits. Memristor is widely used in the field of chaotic circuits because of the nonlinear characteristic and its controllability under external electromagnetic field. For example, Chen et al. [8] designed a mix chaotic circuit by applying a memristor, a capacitor, an induction coil and a memcapacitor. Luo et al. [9] obtained an improved memristive chaotic circuit by replacing the Chua diode in the Chua circuit with a memristor. Peng et al. [10] proposed a new memristive chaotic circuit by replacing the nonlinear term in the Chua circuit with a memristor and a negative conductance. Wang et al. [11] introduced a chaotic circuit by applying an extended memristor and a capacitor. In Ref. [12], a 5D Wien-bridge hyperchaotic memristive circuit was developed from a 4D Wien-bridge chaotic circuit. Memristors have also been studied in discrete maps by introducing different kinds of memristive terms into the mathematical maps. For instance, 2D memristive chaotic maps [13,14,15], 2D memristive hyperchaotic maps [16,17,18], 3D memristive chaotic maps [19, 20], 3D memristive hyperchaotic maps [21,22,23], 4D memristive map [24], higher dimensional memristive map [25] and memristive neuron maps [26,27,28,29,30].

Because the electrical properties of memristors are similar to synapses work [31, 32], memristors are used to simulate the synapses of biological neurons. For instance, Yang et al. [33] investigated the activation and connection of synapses by coupling two functional neurons via memristors. Guo et al. [34] coupled two photoelectric neurons by applying memristive synapse, and explored the synchronization between neurons. Wu et al. [35]confirmed that a memristive synapse can produce similar firing patterns in a neuron encoded with chemical synapse. Hou et al. [36] studied the effect of energy flow on mode selection in neural activities and stochastic resonance in a memristive neuron. In Refs. [37, 38], a memristive neuron was proposed to estimate the external electric field and electromagnetic field, and the self-adaptive regulation mechanism in neural activities under energy flow is explained [39]. In fact, the involvement of Josephson junction [40,41,42,43,44] and other functional electric components [45,46,47,48,49] enable the neural circuits to detect different physical stimuli effectively. Based on these memristive models, the coupling channels and links are tamed to create a variety of memristive neural networks in [50,51,52,53]. In generic way, memristive terms are used to modulate the local kinetics of the neural network, that is, each node of the network has one or two memeristive terms and the collective spatial patterns are affected by the distribution of initials for the memristive variables. On the other hand, memristive channels are created to control the collective behaviors of the network, which indicates high order coupling [54,55,56,57,58] and field coupling [59,60,61] are more effective to control the network behaviors effectively.

When memristor is incorporated into an additive branch circuit of the neural circuit, the memristive term accompanying with the magnetic flux variable can describe the effect of electromagnetic induction of neural activities. On the other hand, the memristive coupling channels become controllable under external field energy injection when memristors are used to couple two or more neural circuits. As mentioned above, activation of memristor into the nonlinear circuits can develop complex dynamics and creation of multistability in the memristive systems and networks. Some memristive systems are used for image encryption [62,63,64,65]. Indeed, one recent work claimed that a memristor can connect two capacitors for building a memristive cell membrane [66], and this memrisive membrane of the biophysical neurons becomes more controllable under energy flow. That is, the physical property of the cell membrane can be discovered from a new aspect, and two capacitive variables are introduced into the neuron model for discerning the effect of membrane flexibility [48, 67, 68]. The electromagnetic induction generated by ion transport inside and outside of the neuron membrane and the influence of external magnetic field on the neuron discharge activity can be explored in a memristor-based nonlinear circuit, and the energy characteristic is discussed for clarifying the self-adaptive property of the memristive neuron.

As is known, Josephson junction can recognize the stimuli from external magnetic field. Therefore, connection of Josesphon Junction [42, 43, 69] to a neural circuit can be used to percieve the effect of electromagnetic field on the neural activities. For example, Zhang et al. [70] suggested a Josephson Junction-coupled neural circuit for detecting mode transition under external magnetic field, and then a memristor is connected to the Josephson junction in parallel [71] to improve the sense ability, which inner and outer magnetic field effect can be desribed synchronously. Besides the model approach and dynamical description, it is more interesting to explore the intrinsic self-daptive property and energy regulation role during changes of neural acticities. In this paper, a memristor-based neuron model is obtained by embedding a MFCM into a simple neuronal circuit. This memristive cicuit can estimate the external magnetic field. The energy function for the memristive circuit is defined and then converted into equivalent Hamilton energy function, which can also be confirmed by using the Helmholtz theorem. An adaptive law is suggested to explain the self-adaptive growth and regulation in the memristive channel because of energy injection. Analog circuit is implemented with exact energy estimation.

2 Model and scheme

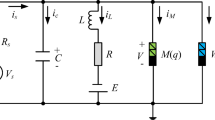
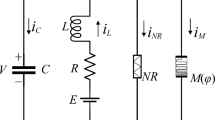
A memristive neural circuit is developped by connecting a MFCM into the fifth branch of the FHN neural circuit. The memristive channel can keep field energy and its channel current will be changed due to external magnetic field, and the circuit approach is displayed in Fig. 1.

Fig. 1
figure 1

Schematic diagram for single memristive neuron model. Vs denotes an external stimulus source, M(φ) is a MFCM, Rs, R and RN are linear and nonlinear resistors, E, L and C represent constant voltage source, induction coil and capacitor, respectively

Full size image

Based on the Kirchhoff's law, the circuit equations for Fig. 1 can be described by

$$ \left\{ \begin{gathered} C\frac{dV}{{dt}} = \frac{{V_{s} - V}}{{R_{s} }} - i_{L} - i_{N} - i_{M} ; \hfill \\ L\frac{{di_{L} }}{dt} = V - Ri_{L} + E. \hfill \\ \end{gathered} \right.{\kern 1pt} $$
(1)

The channel current iN through the nonlinear resistor RN in Fig. 1 can be estimated by

$$ i_{N} = - \frac{1}{\rho }\left( {V - \frac{1}{3}\frac{{V^{3} }}{{V_{0}^{2} }}} \right),{\kern 1pt} $$
(2)

where ρ and V0 represent the normalization parameters, and the memristive channel current iM across the MFCM is given in

$$ i_{M} = M(\varphi )V = \alpha \varphi V,\quad \frac{d\varphi }{{dt}} = \lambda \tanh (\varphi ) - d\varphi + \delta V; $$
(3)

where α, δ and d represent the normalization parameters. As shown in Eq. (3), the M(φ) has a simple form with low order, and its internal state equation is only composed of linear term. Compared with higher-order memristors, the memristor in this paper is easier to implement physically. By imposing simusoidal stimulus Asin(2πωt), where A means the amplitude of stimulus, ω denotes the frequnency of stimulus. The v–i curve for MFCM with different frequnencies ω under A = 3 is shown in Fig. 2a, the v–i curve for MFCM with different amplitude A with ω = 0.8 is shown in Fig. 2b.

Fig. 2
figure 2

The v-i curve for MFCM with different stimulus. For a A = 3; b ω = 0.8

Full size image

The Fig. 2 show that the v–i curve for MFCM exhibites the characteristic of 8-shaped. The 8-shaped area is decreased when the frequnency of stimulus is increased. While the 8-shaped area is increased when the amplitude of stimulus is increased.

The voltage source Vs is selected with periodic form as follows

$$ V_{s} = A_{0} \cos (f_{0} t). $$
(4)

A group of dimensionless variables and parameters are defined by setting scale transformation for the parameters and variables in Eqs. (1)–(4).

$$ \left\{ \begin{gathered} x = \frac{V}{{V_{0} }},y = \frac{{\rho i_{L} }}{{V_{0} }},z = \frac{\varphi }{{\rho CV_{0} }},\tau = \frac{t}{\rho C},a = \frac{E}{{V_{0} }},b = \frac{R}{\rho },c = \frac{{\rho^{2} C}}{L}; \hfill \\ \xi = \frac{\rho }{{R_{s} }},A = \frac{{\rho A_{0} }}{{R_{s} V_{0} }},f = \rho Cf_{0} ,k = \alpha \rho^{2} CV_{0} ,\gamma = d\rho C,\rho = \lambda \rho C. \hfill \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} $$
(5)

A memristive neuron model is obtained by replacing the variables and parameters in Eq. (1) under the scale criterion in Eq. (5) without external electromagnetic radiation. In presence of external magnetic field, the magnetic flux and channel current across the MFCM will be changed; as a result, the memristive current is modified to regulate the excitability and firing modes of the neuron. Therefore, external disturbance term is added to regulate the right side of the formula for magnetic flux variable shown in Eq. (7).

$$ \left\{ \begin{gathered} \frac{dx}{{d\tau }} = x(1 - \xi ) - \frac{1}{3}x^{3} - y - kzx + A\cos (f\tau ); \hfill \\ \frac{dy}{{d\tau }} = c(x - by + a); \hfill \\ \frac{dz}{{d\tau }} = \rho \tanh (z) - \gamma z + \delta x; \hfill \\ \end{gathered} \right.{\kern 1pt} $$
(6)

Both the memristive current (induction current) kzx and the external stimulus Acos(fτ) have impacts on the excitability, and any changes of the two kinds of currents will modify the firing patterns of the neuron. External magnetic field has an impact on the inner magnetic field of the memristor, and then channel current is changed by introducing additive disturbance φext on the third variable for magnetic flux as follows

$$ \left\{ \begin{gathered} \frac{dx}{{d\tau }} = x(1 - \xi ) - \frac{1}{3}x^{3} - y - kzx + A\cos (f\tau ); \hfill \\ \frac{dy}{{d\tau }} = c(x - by + a); \hfill \\ \frac{dz}{{d\tau }} = \rho \tanh (z) - \gamma z + \delta x + \varphi_{ext} , \hfill \\ \end{gathered} \right.{\kern 1pt} $$
(7)

where φext denotes an external magnetic field, here, φext can be considered as a constant for a static magnetic field or a periodic form for a changeable magnetic field, respectively. Furthermore, the physical field energy in the memristive neural circuit in Fig. 1 is calculated by

$$ W = W_{C} + W_{L} + W_{M} = \frac{1}{2}CV^{2} + \frac{1}{2}Li_{L}^{2} + \frac{1}{2}\varphi i_{M} . $$
(8)

By applying the same scale transformation in Eq. (5) on the field energy in Eq. (8), the Hamilton energy function in dimensionless form is obtained by

$$ H = H_{C} + H_{L} + H_{M} = \frac{W}{{CV_{0}^{2} }} = \frac{{W_{C} }}{{CV_{0}^{2} }} + \frac{{W_{L} }}{{CV_{0}^{2} }} + \frac{{W_{M} }}{{CV_{0}^{2} }} = \frac{1}{2}x^{2} + \frac{1}{2c}y^{2} + \frac{1}{2}kz^{2} x. $$
(9)

According to the Eq. (9), the Hamilton energy function of an isolated memristive neuron mainly depends on the variables (x, y, z) and two normalized parameters (c, k). The Hamilton energy function for the memristive neuron in Eq. (6) can also be approached in a theoretical way, based on the Helmholtz theorem, the memristive neuron is written in equivalent vector form in Eqs. (10a, 10b).

$$ \begin{aligned} \left( \begin{gathered} {\dot{x}} \hfill \\ {\dot{y}} \hfill \\ {\dot{z}} \hfill \\ \end{gathered} \right) &= \left( \begin{gathered} x(1 - \xi ) - 1/3x^{3} - y - kzx + A\cos (f\tau ) \hfill \\ c(x + a - by) \hfill \\ \rho \tanh (z) - \gamma z + \delta x \hfill \\ \end{gathered} \right) = F_{c} + F_{d} \\ &= \left( \begin{gathered} - y - \delta kzx \hfill \\ cx + 0.5ckz^{2} \hfill \\ \delta x + 0.5\delta kz^{2} \hfill \\ \end{gathered} \right) + \left( \begin{gathered} x(1 - \xi ) - 1/3x^{3} + A\cos (f\tau ) - (1 - \delta )kzx \hfill \\ c(a - by) - 0.5ckz^{2} \hfill \\ \rho \tanh (z) - \gamma z - 0.5\delta kz^{2} \hfill \\ \end{gathered} \right) \\ & = \left( \begin{gathered} 0\quad - c\quad \quad - \delta \hfill \\ c\quad \quad 0\quad \quad \;0 \hfill \\ \delta \quad 0\quad \quad \;\;0 \hfill \\ \end{gathered} \right)\left( \begin{gathered} x + 0.5kz^{2} \hfill \\ \frac{y}{c} \hfill \\ kzx \hfill \\ \end{gathered} \right) + \left( {\begin{array}{*{20}c} {A_{11} } & 0 & 0 \\ 0 & {A_{22} } & 0 \\ 0 & 0 & {A_{33} } \\ \end{array} } \right)\left( \begin{gathered} x + 0.5kz^{2} \hfill \\ \frac{y}{c} \hfill \\ kzx \hfill \\ \end{gathered} \right)\;. \\ \end{aligned} $$
(10a)
$$ \begin{gathered} A_{11} = \frac{{x(1 - \xi ) - 1/3x^{3} + A\cos (f\tau ) - (1 - \delta )kzx}}{{x + 0.5kz^{2} }}; \\ A_{22} = \frac{{c(c(a - by) - 0.5ckz^{2} )}}{y}; \\ A_{33} = \frac{{\rho \tanh (z) - \gamma z - 0.5\delta kz^{2} }}{kzx}. \\ \end{gathered} $$
(10b)

The Hamilton energy function H meets the following criterion according to the Helmholtz theorem

$$ \nabla H^{T} F_{c} = 0\;;\quad \nabla H^{T} F_{d} = \dot{H} = \frac{dH}{{d\tau }}. $$
(11)

A sole Hamilton energy function can be exact solution for the formula as follows

$$ 0 = \nabla H^{T} F_{c} = ( - y - \delta kzx)\frac{\partial H}{{\partial x}} + \frac{y}{c}\frac{\partial H}{{\partial y}} + (\delta x + 0.5\delta kz^{2} )\frac{\partial H}{{\partial z}}; $$
(12)

Indeed, an exact solution for Eq. (12) can be obtained to be identical to the Hamilton energy function in Eq. (9)

$$ H = \frac{1}{2}x^{2} + \frac{1}{2c}y^{2} + \frac{1}{2}kz^{2} x\;; $$
(13)

That is, the memristive neuron holds exact energy function and the energy can be shunted from the memristive channel considered as energy source (HM = 0.5kxz2 < 0). The first two terms in Eq. (13) always keep positive value, the third term can become negative value, it indicates the memristive channel can release energy and external energy source can be captured.

3 Results and discussions

In this section, the numerical solutions for a single memristive neuron are obtained on the MATLAB platform by applying the four-order Runge–Kutta algorithm with time step h = 0.01. The parameters of the neuron model are selected as a = 0.7, b = 0.8, c = 0.1, ξ = 0.25, k = 0.01, ρ = 0.01, δ = 0.1, γ = 0.1. In Fig. 3, the bifurcation analysis and the largest Lyapunov exponent (LLE) for the memristive neuron are calculated by varying the periodic voltage source.

Fig. 3
figure 3

Bifurcation diagram and LLE for the neuron driven by the periodic voltage source. For a f = 0.8; b A = 0.6. Parameters are chosen as a = 0.7, b = 0.8, c = 0.1, ξ = 0.25, k = 0.01, ρ = 0.01, δ = 0.1, γ = 0.1, and initial value is set as (0.2, 0.1, 0.01). xpeak denotes peak values of membrane potential

Full size image

The results in Fig. 3 show that the memristive neuron can be induced to present bursting, spiking and chaotic firing patterns by adjusting the frequency of external stimulus. In fact, the firing patterns for the memristive neuron can be controlled by applying the periodic voltage source. Furthermore, firing patterns and the changes of Hamilton energy for the memristive neuron are shown in Fig. 4 by changing the frequency for the voltage source.

Fig. 4
figure 4

Sampled time series of membrane potential and evolution of Hamilton energy with different f. For a f = 0.02; b f = 0.2; c f = 0.88. Parameters are chosen as a = 0.7, b = 0.8, c = 0.1, ξ = 0.25, k = 0.01, ρ = 0.01, δ = 0.1, γ = 0.1, A = 0.6, and initials (0.2, 0.1, 0.01). < H > denotes the mean value of Hamilton energy

Full size image

Figure 4 illustrates that the memristive neuron can be excited to show three kinds of firing modes during taming the frequency for external stimulus, and the memristive neuron has higher mean value of Hamilton energy with bursting and spiking firing patterns, while it has lower mean value of Hamilton energy accompanying with chaotic modes.

As shown in Eq. (7), the neuron is placed into a stable magnetic field when φext is considered as a constant signal φc. Changing the intensity of external magnetic field, magnetic flux is regulated synchronously and the results are plotted in Fig. 5 by calculating the distribution of LLE for the memristive neuron under setting different values for φc.

Fig. 5
figure 5

Bifurcation diagram and LLE for the neuron under constant magnetic field φc. For a bifurcation diagram; b LLE. Parameters are chosen as a = 0.7, b = 0.8, c = 0.1, ξ = 0.25, k = 0.01, ρ = 0.01, δ = 0.1, γ = 0.1, A = 0.6, f = 0.8, and initials (0.2, 0.1, 0.01)

Full size image

It is confirmed that a memristive neuron exhibits periodic and chaotic firing modes when an external magnetic field is applied with suitable intensity. Additionally, the memristive neuron undergoes mode transition from a periodic state to a chaotic state through reverse period-doubling bifurcation when the external magnetic field increases from 0 to 1. That is, the strength of the external magnetic field controls the complex firing activities of memristor neurons such as periodic, chaotic patterns. The evolution of membrane potential and changes of Hamilton energy corresponding to periodic and chaotic modes are shown in Fig. 6.

Fig. 6
figure 6

Sampled time series of membrane potential and evolution of Hamilton energy with different external magnetic field φc. For a φc = 0.3; b φc = 0.6. Parameters are chosen as a = 0.7, b = 0.8, c = 0.1, ξ = 0.25, k = 0.01, ρ = 0.01, δ = 0.1, γ = 0.1, A = 0.6, f = 0.8, and initials (0.2, 0.1, 0.01). < H > denotes the mean value of Hamilton energy

Full size image

The results in Fig. 6 show that periodic firing mode has a higher average value of the Hamilton energy, while chaotic pattern has a lower mean value of the Hamilton energy. Furthermore, the effect of periodic magnetic field on the electrical activity of neuron is discussed. The time-varying external magnetic field is considered as φext = Aφsin fφτ, here, Aφ denotes the amplitude and fφ is the frequency of a periodic external magnetic field. The parameters and initial values are kept as above, fφ is fixed at 0.4, the bifurcation diagram and LLE are calculated by changing the value for Aφ, and the results are plotted in Fig. 7.

Fig. 7
figure 7

Bifurcation diagram and LLE for the neuron by changing the amplitude Aφ for external magnetic field. For a bifurcation diagram; b LLE. Parameters are chosen as a = 0.7, b = 0.8, c = 0.1, ξ = 0.25, k = 0.01, ρ = 0.01, δ = 0.1, γ = 0.1, A = 0.6, f = 0.8, fφ = 0.4, and initials (0.2, 0.1, 0.01)

Full size image

The results in Fig. 7 indicate that there are four periodic windows are occurred in the range of amplitude a from 0.6 to 1.2, and the chaotic modes are distributed in a large parameter range. Similar to the case of constant external magnetic field, the firing mode of memristor neurons is completely controlled by periodic external magnetic field. Furthermore, the relation between firing patterns and the Hamilton energy is calculated by selecting different values Aφ, and evolution of membrane potential accompanying with energy changes are displayed in Fig. 8.

Fig. 8
figure 8

Evolution of membrane potential and Hamilton energy for the neuron under periodic external magnetic field. For a Aφ = 0.82; b Aφ = 0.92. Parameters are chosen as a = 0.7, b = 0.8, c = 0.1, ξ = 0.25, k = 0.01, ρ = 0.01, δ = 0.1, γ = 0.1, A = 0.6, f = 0.8, fφ = 0.4, and initial value is set as (0.2, 0.1, 0.01). < H > denotes the mean value of Hamilton energy

Full size image

Similar to the results in Fig. 6, the periodic state exhibits a higher average Hamilton energy value, while the chaotic modes occur a lower average Hamilton energy value. In fact, the applied external magnetic field just injected energy flow into the media and the neural circuit, and the captured energy will be propagated and shared between the capacitive and inductive channels including the capacitor channel, the induction coil channel and the memristor channel. Any changes of energy proportion between these channels and electric components will modify the excitability, and the firing modes are changed even accompanying with parameter shift because of shape deformation in some electric components. To explore the adaptability of the memristor channel in memristive neurons, energy flow is used to control the adaptive growth of the memristor channel. That is, the energy ratio between capacitive and inductive channels will predict possible mode transition, and shape deformation of memristive channels due to large energy injection can be approached by using adaptive parameter shift as follows

$$ \frac{dk}{{d\tau }} = \kappa \cdot k \cdot \theta \left( {\varepsilon - \left| {\frac{{H_{M} }}{{H_{L} }}} \right|} \right),\quad \theta (p) = 1,\quad p \ge 0,\quad \theta (p) = 0,\quad p < 0; $$
(14)

where gain κ controls the growth of the parameter k for the memristive current, the threshold 0 < ε < 1 determines the energy ratio of a memristive channel to inductive channel energy in the neuron. At first, the case of a constant external magnetic field is discussed. Parameters are selected as a = 0.7, b = 0.8, c = 0.1, ξ = 0.25, ρ = 0.01, δ = 0.1, γ = 0.1, A = 0.6, f = 0.8, and the initial values for variables are set as (0.2, 0.1, 0.01). The initial value of parameter k is fixed at 0.001, threshold for ε is fixed as 0.4, and a constant external magnetic field is given as φc = 0.1. The adaptive growth of k, membrane potential and Hamilton energy for different parameter κ are calculated, the results are shown in Fig. 9.

Fig. 9
figure 9

The growth of k, membrane potential and Hamilton energy. For a κ = 0.01; b κ = 0.02

Full size image

It is found that the parameter k reaches a stable value (1.54) aftera transient period (867 time unites). The membrane potential and Hamilton energy also maintain periodic oscillations with time. By setting larger value for the gain κ, k reaches a stable value in a smaller transient period. Chaos theory often emphasizes sensitivity to initial conditions as a defining characteristic. To explore the sensitivity of the memrisve system to initial values, the time sampling sequence of the membrane potential with different initial values are calculated, and the results are shown in Fig. 10.

Fig. 10
figure 10

Sampled time series of membrane potential with different initial values. For a (0.2 + 10–15, 0.1, 0.01), (0.2, 0.1, 0.01); b (0.2, 0.1 + 10–15, 0.01), (0.2, 0.1, 0.01). Parameters are chosen as a = 0.7, b = 0.8, c = 0.1, ξ = 0.25, k = 0.01, ρ = 0.01, δ = 0.1, γ = 0.1, A = 0.6, f = 0.88

Full size image

The results in Fig. 10 illustrate that this memristive neuron model is highly sensitive to initial values. The circuit simulation of the memristive neuron can be realized by applying the Multisim software. The neuron model presented in Eq. (6) is transformed on a time scale by applying τ = 100t, and the Eq. (6) is updated as follows

$$ \left\{ \begin{gathered} \frac{dx}{{dt}} = 100x(1 - \xi ) - \frac{100}{3}x^{3} - 100y - 100kzx + 100A\cos (100f\tau ); \hfill \\ \frac{dy}{{dt}} = 100cx - 100by + 100a; \hfill \\ \frac{dz}{{dt}} = 100\rho \tanh (z) - 100\gamma z + 100\delta x; \hfill \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} $$
(15)

Parameters are chosen as a = 0.7, b = 0.8, c = 0.1, ξ = 0.25, k = 0.01, ρ = 0.01, δ = 0.1, γ = 0.1, A = 0.6, and initial value is set as (0.2, 0.1, 0.01). The corresponding analog circuit is shown in Fig. 11.

Fig. 11
figure 11

The analog circuit of the memristive neuron

Full size image

According to Fig. 11, the state equations can be described by

$$ \left\{ \begin{gathered} C_{1} \frac{{dV_{x} }}{dt} = \frac{1}{{R_{1} }}V_{x} - \frac{1}{{100R_{2} }}V_{x}^{3} - \frac{1}{{R_{3} }}V_{y} - \frac{1}{{10R_{4} }}V_{z} V_{x} + \frac{1}{{R_{5} }}A\cos (2\pi ft); \hfill \\ C_{2} \frac{{dV_{y} }}{dt} = \frac{1}{{R_{6} }}V_{x} - \frac{1}{{R_{7} }}V_{y} + \frac{1}{{R_{8} }}V_{ac} ; \hfill \\ C_{3} \frac{{dV_{z} }}{dt} = \frac{1}{{R_{9} }}\tanh (V_{z} ) - \frac{1}{{R_{10} }}V_{z} + \frac{1}{{R_{11} }}V_{x} ; \hfill \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} $$
(16)

In addition, the energy for the neural circuit is mainly kept in capacitive form as follows

$$ W = \frac{1}{2}C_{1} V_{x}^{2} + \frac{1}{2}C_{2} V_{y}^{2} + \frac{1}{2}C_{3} V_{z}^{2} .{\kern 1pt} {\kern 1pt} $$
(17)

In Fig. 11, the capacitance and resistance parameters are fixed as C1 = C2 = C3 = 10 nF, R1 = 1333.3 kΩ, R2 = 30 kΩ, R3 = R5 = 1000 kΩ, R4 = R6 = R10 = R11 = 10,000 kΩ, R8 = R9 = 100,000 kΩ, R12 = R13 = R14 = R15 = 10 kΩ, and Multiplier is A1 = A2 = A3 = 0.1. The simulation results by applying the oscilloscopes on the Multisim software are displayed in Fig. 12.

Fig. 12
figure 12

Output voltages and formed attractors on the Multisim platform. For a membrane potential and phase diagram for f = 0.318; b membrane potential and phase diagram for f = 3.18; c membrane potential and phase diagram for f = 14.005

Full size image

The results in Fig. 12 confirmed that the memristive neuron can be realized by analog circuits, which will provide a good theoretical basis and experimental guidance for the application of neuron model driven mechanism. Furthermore, according to energy function presented in Eq. (17), the analog circuit for energy function is shown in Fig. 13.

Fig. 13
figure 13

The analog circuit of the memristive neuron

Full size image

The state equation for energy in Fig. 11 can be expressed by

$$ W = \frac{{R_{16} }}{{R_{17} }}V_{x}^{2} + \frac{{R_{16} }}{{R_{18} }}V_{y}^{2} + \frac{{R_{16} }}{{R_{19} }}V_{z}^{2} ;{\kern 1pt} $$
(18)

In Fig. 13, the resistance parameters are fixed as R16 = 50 Ω, R17 = R18 = R19 = 100,000 kΩ, R20 = R21 = 10 kΩ, and Multiplier is A4 = A5 = A6 = 0.1. Based on the anolog circuits in Figs. 11, 13, The energy sequences corresponding to the firing modes in Fig. 13 are displayed in Fig. 14. Due to the small value of W, the results in Fig. 14 are magnified by a factor of 10 in order to observe the output sequence of W significantly in the oscilloscope.

Fig. 14
figure 14

Simulation results for energy on the Multisim platform. For a bursting firing; b spiking firing; c chaotic firing

Full size image

The results indicate that the energy function is dependent on the firing mode, and analog circuit approach is consistent with the results of numerical approach of the memristive neuron model.

In summary, an involvement of memristor into simple FHN neural circuit is effective to detect and describe the effect of external magnetic field on the neural activities. The energy level accounts for mode selection and then external stimuli including electromagnetic radiation can inject energy into the media, as a result, the firing activities of the neuron can be controlled completely. In fact, noisy disturbance on the membrane potential or the magnetic flux due to electromagnetic radiation can be imposed on this memristive neuron, similar coherence resoance and stochastic resonance can be induced, and the cuvre for SNR (signal to noise ratio) and average Hamilton enegry will provide fast way of this prediction. From physical aspect, large energy injection can cause some shape deformation of the electric components even damage, therefore, one or more intrinsic parameters of these electric components will be changed under energy flow. As a result, fast and effective energy shuntering and exchange between different channels and components are crucial for keeping safe running of these neural circuits, and the biophysical neurons release their self-adaptive property by adjusting the intrinsic parameters in adaptive way.

4 Conclusion

A memristive neural circuit sensitive to the magnetic field is proposed. According to the the famous Helmholtz theorem, the Hamilton energy for the memristive neuron is approached in theoretical way, and it is also confirmed by applying scale transformation on the field energy for the neural circuit. The electrical activities and field energy distribution of the memristive neuron under the different types of the magnetic field are investigated in detail. The numerical results show that neuron can be controlled to present suitable firing patterns, in particular, continuous mode transition occurs under the self-adaptive law, which one intrinsic parameter of memristive synapse controls its growth under the energy flow. The potential mechanism is that energy accumulation and external energy injection induce shape deformation of the memristive channels, and one parameter is changed to keep safe energy level in this memristor. It prefers to keep periodic firing patterns when the average field energy maintains a higher level. The memristive neuron can be realized by applying anolog cricuit on the Multisim platform.