Dynamics in a memristive neuron under an electromagnetic field

Abstract

Propagation and exchange of electrical signals between neurons mainly depend on the controllability of synapses. These electrical signals will affect the dynamic characteristics of ion channels on the neuron membrane and the firing activity of neurons can be changes. Polarization and magnetization of media exposed to electromagnetic field encode energy distribution and the neural activities will be changed greatly. The incorporation of memristors is effective to estimate the energy effect from the physical field on neurons. In this work, a charge-controlled memristor (CCM) and a magnetic flux-controlled memristor (MFCF) are connected in parallel to a FitzHugh–Nagumo (FHN) neural circuit for building a new neural circuit, which can perceive modulation from external electric and magnetic fields. Furthermore, the dynamical equation of the memristive neural circuit and the field energy of electrical elements are obtained based on Kirchhoff’s law and Helmholtz’s theorem. The firing patterns of the memristive neuron and energy proportion can be controlled when the external electric and magnetic fields are adjusted. Continuous energy injection into the memristive channels enables memristive synapses to become self-adaptive under energy flow. Noisy disturbance and radiation are applied to discern the occurrence of coherent resonance in this memristive neuron. The results can be used to explore the collective behaviors and creation of heterogeneity in networks in the presence of an electromagnetic field.

1 Introduction

Memristor is regarded as a new type of basic circuit element, and it is used to describe the relationship between magnetic flux and charge [1,2,3,4,5]. Memristor is classified into two kinds, magnetic flux-controlled memristor (MFCM) [6,7,8,9,10] and charge-controlled memristor (CCM) [11,12,13,14,15]. Most memristors have nonlinear characteristics, and then chaotic circuits can be controlled by connecting the memristor and a few circuit components. Exploring the chaotic behavior and generation mechanism of memristor-based chaotic systems has important applications in signal processing and artificial neural networks. By now, many chaotic systems developed from nonlinear circuits coupled with memristors have been suggested and some of them can be used in image encryption applications. For example, continuous memristive chaotic systems [16,17,18], fractional-order memristive chaotic systems [19,20,21], discrete memristive chaotic systems [22,23,24], image encryption algorithms based on the memristive chaotic systems [25,26,27,28,29,30] have been discussed.

The structure and function of the memristor are very similar to the biological synapse, and then synaptic modulation of biological neurons can be reproduced by some memristors. For instance, Guo et al. [31] investigated synchronization between photoelectric neurons with memristive synapse coupling. The creation of a memristive synapse for reaching energy balance between neurons is researched in [32], and it explains the physical mechanism for controllability in the memristive synapse. In addition, an MFCM is used in neurons that can estimate the effect of electromagnetic induction and radiation [33,34,35,36]. A CCM applied in neurons can capture the external electric field [37]. That is, the involvement of memristor in neural circuits and memristive function in neural networks can be effective in neuromorphic computing [38,39,40,41,42]. There are many researches on memristive neural models in [43,44,45,46,47].

When a neuron receives external electrical signals, the membrane potential changes to keep a suitable energy level, and the inner electromagnetic field distribution are also modified. In addition, the neural coding process is affected by an external electromagnetic field, which will affect the firing patterns of neurons. In fact, the application of an external electromagnetic field can inject energy into neurons, and the firing modes can be adjusted synchronously. For biological neurons, the physical energy is often estimated by using the average power (product of channel current and membrane potential) and then the average energy is approached within a certain transient period. For the functional neural circuits, the equivalent Hamilton energy can be obtained in two ways. For example, the physical field energy is mapped into equivalent Hamilton energy by applying scale transformation on the physical variables and parameters for the field energy function. The exact Hamilton energy function [48,49,50,51] for each functional neuron model can be obtained by using the Helmholtz’s theorem [52,53,54].

The neuron acts as an electrically charged body and the electrical activities are changed when it is activated by an external stimulus. As a result, changes in magnetic or electric fields can affect the electrical activity of neurons, and model approach considering these physical effects becomes important. From physical viewpoint, combination of memristive channels is effective to discern the excitation and regulation from external electromagnetic field by developing neural circuits composed of MFCM and CCM synchronously. It is worthy of investigating the firing activities and energy proportion for a neuron under the external electric and magnetic fields when the energy flow is calculated physically. Therefore, a neural circuit connected with a couple of memristors is used to discern the effect of the external electric field and magnetic field on the investigation of the firing patterns and energy proportion. In Sect. 2, the functional neuron model under external electric and magnetic fields is introduced. The numerical simulations of the memristive neural circuit are carried out in Sect. 3. In Sect. 4, an open problem is described. The paper ends with a conclusion in Sect. 5.

2 Model and scheme

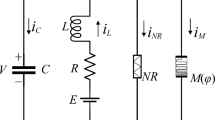
The fourth branch of the FHN neural circuit is replaced by applying a CCM and a MFCM is connected in the fifth branch, and then a functional neuron model is obtained. This neuron can perceive external physical fields, and the schematic diagram of its equivalent circuit is shown in Fig. 1.

Fig. 1

Schematic diagram for memristive neural circuit. V_s denotes an adjustable voltage source, R and R_s are two linear resistors, C and L denote capacitor and induction coil, E is a constant voltage source, M(q) and W(φ) represent memory resistance for CCM and memory conductance for MFCM

The channel current across the CCM in Fig. 1 can be described by

$$ i_{M} = \frac{dq}{{dt}} = \frac{dq}{{d\varphi }}\frac{d\varphi }{{dt}} = \frac{dq}{{d\varphi }}V = \left[k_{1} (\alpha + 3\beta q^{2} ) - \frac{{k_{2} q}}{V}\right]V = k_{1} V(\alpha + 3\beta q^{2} ) - k_{2} q; $$

(1)

where gains (k₁, k₂) are relative to the intrinsic physical property of CCM, which can capture energy from the external electric field. The fifth branch is realized by using an MFCM [55], and the induction current across the memristor with memductance W(φ) can be estimated as follows

$$ \left\{ \begin{array}{l} i_{W} = k_{3} W(\varphi )V = k_{3} \varphi V; \hfill \\ \frac{d\varphi }{{dt}} = \lambda \tanh (\varphi ) - \gamma \varphi + \delta V; \hfill \\ \end{array} \right. $$

(2)

where k₃, λ, γ and δ are relative to the material property of this memristor. According to Kirchhoff’s law, the dynamics of the memristive circuit presented in Fig. 1 can be described by

$$ \left\{\begin{array}{l} C\frac{dV}{{dt}} = \frac{{V_{S} - V}}{{R_{s} }} - i_{L} - k_{1} V(\alpha + 3\beta q^{2} ) + k_{2} q - k_{3} \varphi V; \hfill \\ L\frac{{di_{L} }}{dt} = V - Ri_{L} + E; \hfill \\ \frac{dq}{{dt}} = k_{1} (\alpha + 3\beta q^{2} )V - k_{2} q; \hfill \\ \frac{d\varphi }{{dt}} = \lambda \tanh (\varphi ) - \gamma \varphi + \delta V; \hfill \\ \end{array} \right.{\kern 1pt} $$

(3)

To obtain a dimensionless neuron model and further nonlinear analysis, the scale transformation for the variables and parameters in Eq. (3) are applied as follows

$$ \left\{ \begin{array}{l} x = \frac{V}{E},y = \frac{{Ri_{L} }}{E},\tau = \frac{t}{RC},c = \frac{{R^{2} C}}{L},z = \frac{q}{CE},w = \frac{\varphi }{RCE},\xi = \frac{R}{{R_{s} }},g = k_{2} RC; \hfill \\ u_{s} = \frac{{V_{s} R}}{{R_{s} E}},\alpha^{\prime} = \alpha R,\beta^{\prime} = 3\beta RC^{2} E^{2} ,\mu = k_{3} R^{2} CE,\gamma^{\prime} = \gamma RC,\;\lambda^{\prime} = \lambda RC; \hfill \\ \end{array} \right. $$

(4)

Indeed, the memristive neuron under an external field in the equivalent form can be described by

$$ \left\{ \begin{array}{l} \frac{dx}{{d\tau }} = - \xi x - y + u_{s} - k_{1} (\alpha^{\prime} + \beta^{\prime}z^{2} )x + gz - \mu wx; \hfill \\ \frac{dy}{{d\tau }} = c(x + 1 - y); \hfill \\ \frac{dz}{{d\tau }} = k_{1} x(\alpha^{\prime} + \beta^{\prime}z^{2} ) - gz + E_{ext} ; \hfill \\ \frac{dw}{{d\tau }} = \lambda^{\prime}\tanh (w) - \gamma^{\prime}w + \delta x + \varphi_{ext} ; \hfill \\ \end{array} \right.{\kern 1pt} $$

(5)

where u_s denotes an external stimulus, E_ext and φ_ext describe the equivalent modulation from the external electric field and magnetic field on the memristive neuron. Setting the left-hand side of (5) as 0, it can be easily found that there is no any equilibrium point existing in such the memristive neuron model. Because of no equilibrium point available, the memristive neuron model is a special nonlinear dynamical system owning the specific hidden attractors.

Furthermore, Fig. 2 depicts an enhanced neural circuit built by adding two memristive devices as the fifth and sixth branches of the FHN neural circuit to mimic the effect of the magnetic and electric fields.

Fig. 2

Schematic diagram for memristive neural circuit. R_N represents a nonlinear resistor with cubic relation for the current and voltage

In Fig. 2, the fourth branch uses a nonlinear resistor R_N [56,57,58], and its current is estimated as follows

$$ i_{N} = - \frac{1}{\rho }\left( {V - \frac{{V^{3} }}{{3V_{0}^{2} }}} \right); $$

(6)

where ρ and V₀ are resistance and cutoff voltage. i_M and i_W are estimated in Eqs. (1–2), according to the well-known Kirchhoff’s law, the memristive neural circuit presented in Fig. 2 can be described by

$$ \left\{ \begin{array}{l} C\frac{dV}{{dt}} = \frac{{V_{S} - V}}{{R_{s} }} - i_{L} - i_{N} - k_{1} V(\alpha + 3\beta q^{2} ) + k_{2} q - k_{3} \varphi V; \hfill \\ L\frac{{di_{L} }}{dt} = V - Ri_{L} + E; \hfill \\ \frac{dq}{{dt}} = k_{1} (\alpha + 3\beta q^{2} )V - k_{2} q; \hfill \\ \frac{d\varphi }{{dt}} = \lambda \tanh (\varphi ) - \gamma \varphi + \delta V; \hfill \\ \end{array} \right. $$

(7)

The physical variables and parameters in Eq. (7) are replaced with dimensionless variables

$$ \left\{ \begin{gathered} x = \frac{V}{{V_{0} }},\;y = \frac{{\rho i_{L} }}{{V_{0} }},\;z = \frac{q}{{CV_{0} }},\;w = \frac{\varphi }{{\rho CV_{0} }},\;\tau = \frac{t}{\rho C},\;g = k_{2} \rho C,\;\alpha^{\prime } = \alpha \rho ,\;\beta^{\prime } = 3\beta \rho C^{2} V_{0}^{2} ; \hfill \\ \gamma^{\prime } = \gamma \rho C,\;\lambda^{\prime } = \lambda \rho C,\;a = \frac{E}{{V_{0} }},\;b = \frac{R}{\rho },\;c = \frac{{\rho^{2} C}}{L},\;\xi = \frac{\rho }{{R_{s} }},\;u_{s} = \frac{{V_{s} \rho }}{{R_{s} V_{0} }},\;\mu = k_{3} \rho^{2} CV_{0} ; \hfill \\ \end{gathered} \right. $$

(8)

As a result, a dimensionless memristive neuron can be presented in an improved form

$$ \left\{ \begin{array}{l} \frac{{dx}}{{d\tau }} = (1 - \xi )x - y - \frac{1}{3}x^{3} + u_{s} - k_{1} (\alpha ^{\prime } + \beta ^{\prime } z^{2} )x + gz - \mu xw; \hfill \\ \frac{{dy}}{{d\tau }} = c(x + a - by); \hfill \\ \frac{{dz}}{{d\tau }} = k_{1} x(\alpha ^{\prime } + \beta ^{\prime } z^{2} ) - gz + E_{{ext}} ; \hfill \\ \frac{{dw}}{{d\tau }} = \lambda ^{\prime } \tanh (w) - \gamma ^{\prime } w + \delta x + \varphi _{{ext}} ; \hfill \\ \end{array} \right.{\kern 1pt} $$

(9)

where u_s is an external stimulus, E_ext and φ_ext describe the equivalent radiation from the external electric field and magnetic field on the memristive neuron by regulating the channel variables. Setting the left-hand side of (9) as 0, it can be easily found that there is no any equilibrium point existing in such the memristive neuron model. Because of no equilibrium point available, the memristive neuron model is a special nonlinear dynamical system owning the specific hidden attractors.

The physical energy in the neural circuit presented in (Figs. 1, 2) mainly keeps in capacitor C, induction coil L, two kinds of memristors including MFCM and CCM, and it is estimated by

$$ \left\{\begin{array}{l} W = W_{C} + W_{L} + W_{M} + W_{W} = \frac{1}{2}CV^{2} + \frac{1}{2}Li_{L}^{2} + \frac{1}{2}C_{M} V_{M}^{2} + \frac{1}{2}L_{M} i_{W}^{2} ; \hfill \\ W_{M} = \frac{1}{2}C_{M} V_{M}^{2} = \frac{1}{2}qV_{M} = \frac{1}{2}qV; \hfill \\ W_{W} = \frac{1}{2}L_{M} i_{W}^{2} = \frac{1}{2}\varphi \cdot i_{W} = \frac{1}{2}k_{3} \varphi^{2} V; \hfill \\ H = \frac{W}{{CE^{2} }} = H_{C} + H_{L} + H_{M} + H_{W} = \frac{1}{2}x^{2} + \frac{{y^{2} }}{2c} + \frac{1}{2}xz + \frac{1}{2}\mu w^{2} x; \hfill \\ \end{array} \right. $$

(10)

In fact, a CCM is considered an equivalent capacitor with capacitance C_M and the MFCM is considered an equivalent inductor with inductance L_M. Therefore, the inner energy is described by equivalent electric field energy and magnetic field energy, respectively. For the memristive neuron, the Hamilton energy H is made of four parts, and any energy release or injection will induce changes in energy proportion between these channels. The energy proportion for each channel to total energy H is estimated by

$$ {\kern 1pt} p_{1} = \frac{{H_{C} }}{H},\;{\kern 1pt} p_{2} = \frac{{H_{L} }}{H},\;p_{3} = \left| {\frac{{H_{M} }}{H}} \right|,\;p_{4} = \left| {\frac{{H_{W} }}{H}} \right| $$

(11)

From a physical viewpoint, external noisy electromagnetic radiation can inject energy into the biological neurons and neural circuits. According to Eq. (5) or Eq. (9), external radiation can modulate the physical flows across the two memristive channels, and the memristive currents are changed to shunt the energy propagation. Therefore, the membrane potential and output voltage from the capacitor of the neural circuit will be regulated to present different firing modes. In fact, continuous energy injection and accumulation may induce shape deformation of the cell, and the memristive channel will also be modified with parameter shift for preventing possible damage and safe energy savage. That is, the memristive parameter will show a certain shift when the inner field energy in the memristive channel is beyond a certain proportion value. In this case, we consider the memristive gains (k₁, μ) show certain shift when external electric field and magnetic field are injected to change the energy proportion (|H_M/H_C|, |H_W/H_L|) as follows

$$ \left\{\begin{array}{l}\frac{{dk_{1} }}{d\tau } = r_{1} \cdot k_{1} \vartheta \left( {\varepsilon_{1} - \left| {\frac{{H_{M} }}{{H_{C} }}} \right|} \right); \hfill \\ \frac{d\mu }{{d\tau }} = r_{2} \cdot \mu \vartheta \left( {\varepsilon_{2} - \left| {\frac{{H_{W} }}{{H_{L} }}} \right|} \right); \hfill \\ \vartheta (\eta ) = 1,\;\eta \ge 0;\vartheta (\eta ) = 0,\;\eta < 0; \hfill \\ 0 < \varepsilon_{1} < 1;0 < \varepsilon_{2} < 1; \hfill \\ \end{array} \right. $$

(12)

where the gains (r1, r2) control the growth of memristive parameters (k1, μ), which shows continuous growth when the energy proportion (|HM/HC|, |HW/HL|) for the memristive channel is below a certain threshold (ε1, ε2). On the other hand, the memristive gains can also be adjusted adaptively when its energy level is beyond certain threshold. As a result, the Hamilton energy for this memristive neuron will be changed directly until the parameters (k1, μ) reaches a saturation value. That is, most of the captured energy by this memristive channel is shunted to other channels, and the memristive current is controlled before reaching a saturation value in the presence of external field disturbance.

3 Results and discussion

In this section, the numerical solutions for the neuron model defined in (Eq. (5), Eq. (9), Eq. (12)) are obtained by using the four-order Runge–Kutta algorithm. The time step is selected at h = 0.01, the parameters for the model presented in Eq. (5) are selected as ξ = 0.5, c = 0.5, μ = 0.1, g = 0.1, δ = 0.1, k₁ = 0.1, α´ = 0.1, β´ = 0.01, γ´ = 0.2, λ´ = 0.01, E_ext = 0, φ_ext = 0, the initial values are fixed at (0.2, 0.1, 0.01, 0.01), and external stimulus is selected as u_s = Asin(ωτ). At first, the angular frequency in the external stimulus is fixed at ω = 0.8, the bifurcation diagram by adjusting amplitude is displayed in Fig. 3a. By using the same parameters and initial values, the amplitude is selected as A = 0.6, and the bifurcation diagram by changing angular frequency is calculated in Fig. 3b. The Largest Lyapunov exponent (LLE) are calculated in Fig. 3c, d.

Fig. 3

Bifurcation diagram and LLE for the neuron in Eq. (5) by changing the external forcing current. a, c ω = 0.8; b, d A = 0.6. x_peak represents the maximal value of membrane potential x

Figure 3 confirmed that firing patterns in the memristive neuron present distinct periods, and it seldom shows bursting and chaotic firing patterns because the cubic term is missing. That is, the nonlinear resistor is essential for neural circuits to induce (bursting, spiking, chaotic) firing activities. Furthermore, the parameters and initial values are kept as above, the amplitudes are selected as A = 0.1 and A = 0.6, firing patterns and energy proportion for the memristive neural circuit are calculated in Figs. 4 and 5.

Fig. 4

Firing modes for the memristive neuron in Eq. (5) under different intensities at ω = 0.8. a A = 0.1; b A = 0.6

Fig. 5

Energy proportion for the memristive neuron. a A = 0.1; b A = 0.6. Energy proportion (p₁, p₂, p₃, p₄) is calculated within 1000 time units and angular frequency ω = 0.8

It is found that the neuron presents in periodic modes when capacitive field energy occupies a distinct percentage more than other electric elements. It is interesting to investigate the effect of external electric and magnetic fields on the firing activity of the memristive neuron and the energy proportion of each electric component. The parameters and initial values keep the same as above, the external stimulus u_s = 0.6sin(0.8τ). The bifurcation diagram and LLE by changing the external magnetic field φ_ext and the external electric field E_ext are plotted in Fig. 6.

Fig. 6

Bifurcation diagram and LLE for the neuron presented in Eq. (5) by activating the external electric field or magnetic field. a φ_ext = 0; b E_ext = 0; c φ_ext = 0.5; d E_ext = 0.5. Setting ω = 0.8, A = 0.6. x_peak represents the maximal value of membrane potential x

It is confirmed that the memristive neural circuit shows periodic states by adding an external electric field or magnetic field. In addition, firing patterns and energy proportion are shown in Figs. 7 and 8.

Fig. 7

Firing modes for the memristive neuron in Eq. (5) under the electromagnetic field. a E_ext = 0.01, φ_ext = 0; b φ_ext = 0.01, E_ext = 0; c E_ext = 0.01, φ_ext = 0.01. Setting ω = 0.8, A = 0.6

Fig. 8

Energy proportion for neural circuit presented in Eq. (5) by adding the external electric field or magnetic field. a E_ext = 0.01, φ_ext = 0; b φ_ext = 0.01, E_ext = 0; c E_ext = 0.01, φ_ext = 0.01. Energy proportion (p₁, p₂, p₃, p₄) is calculated within 1000 time units

Figures 7 and 8 show that neuron keeps periodic firing patterns even if disturbance from the electric field or magnetic field is considered, and the capacitive energy is larger than inductive field energy. It is interesting to investigate the same case when the cubic term is considered in this memristive neuron shown in Eq. (9). In this case, the external stimulus u_s = Asin(ωτ). The parameters are selected as a = 0.8, b = 0.7, c = 0.1, ξ = 0.25, μ = 0.01, g = 0.2, δ = 0.1, k₁ = 0.01, α´ = 0.1, β´ = 0.01, γ´ = 0.1, λ´ = 0.01, E_ext = φ_ext = 0. The initials are fixed at the same values (0.2, 0.1, 0.01, 0.01). The bifurcation analysis and LLE are plotted in Fig. 9.

Fig. 9

Bifurcation diagram and LLE for the memristive neuron in Eq. (9) by adjusting the external stimulus. a, c A ∈ [0, 2], ω = 0.8; (b, d) ω ∈ [0, 2], A = 0.6

Due to the nonlinear modulation from the cubic term on the membrane potential, the memristive neuron can present a complete mode transition and keep certain firing patterns (bursting, spiking, periodic, chaotic) when external forcing is changed. In addition, the firing patterns and the relationship between frequency (f) and amplitude (A) are calculated in Fig. 10.

Fig. 10

Firing patterns for the memristive neuron in Eq. (9) at A = 0.6. a bursting for ω = 0.01; b spiking for ω = 0.1; c periodic-I firing for ω = 0.32; d periodic-II firing for ω = 0.4; e periodic-IV firing for ω = 0.72; f chaotic firing for ω = 0.8. f denotes the frequency and A represents the amplitude

The results illustrate that the memristive neuron shows four different firing modes, which are dependent on the exciting frequency. The relationship between frequency and amplitude indicates that chaotic pattern has a continuous power spectrum, periodic modes have corresponding spikes. Obviously, periodic-I pattern has one spike, periodic-II has two spikes, and periodic-IV has four spikes. Furthermore, the energy proportion of the electric elements is calculated in Fig. 11 for sole neurons presenting different firing patterns.

Fig. 11

Energy proportion for the memristive neuron in Eq. (9) showing different firing modes. a bursting firing for ω = 0.01; b spiking firing for ω = 0.1; c periodic-I firing for ω = 0.32; d periodic-II firing for ω = 0.4; e periodic-IV firing for ω = 0.72; f chaotic firing for ω = 0.8. Energy proportion (p₁, p₂, p₃, p₄) is calculated within 1000 time unites and A = 0.6

The results confirmed that the neuron will present periodic (bursting, spiking) firing modes when field energy in the inductor is larger than that of the other element. The neural circuit show periodic (I, II, IV) or chaotic states, when filed energy in the capacitor, is kept the higher proportion. Furthermore, we explore the effect of external electric and magnetic fields on firing activity of memristive neural circuits. The parameters and initial values are chosen as above, and the bifurcation diagram and LLE for this neuron is shown in Fig. 12 by activating the external electric or magnetic field with different intensities.

Fig. 12

Bifurcation diagram and LLE for the neuron by adding different intensities in electric field and magnetic field. a, e E_ext ∈ [0, 1], φ_ext = 0; b, f φ_ext ∈ [0, 1], E_ext = 0; (c, g) E_ext ∈ [0, 1], φ_ext = 0.01; d, h φ_ext ∈ [0, 1], E_ext = 0.01. x_peak represents the maximal value of membrane potential x, A = 0.6, ω = 0.8

From Fig. 12, it is demonstrated that the external physical field has an important impact on mode transition in this memristive neuron. Furthermore, the same case for firing patterns and energy proportion for this neuron is calculated in (Figs. 13, 14) by taming the intensity for the external electric and magnetic field.

Fig. 13

Firing modes for the neuron in Eq. (9) in the presence of the external electric field or magnetic field. a chaotic firing for E_ext = 0.01, φ_ext = 0; b periodic firing for E_ext = 0.05, φ_ext = 0; c chaotic firing for E_ext = 0, φ_ext = 0.01; d periodic firing for E_ext = 0, φ_ext = 0.4; e chaotic firing for E_ext = 0.01, φ_ext = 0.01; f periodic firing for E_ext = 0.01, φ_ext = 0.4. Setting A = 0.6, ω = 0.8

Fig. 14

The energy proportion for the neuron in Eq. (9) when the external electric field or magnetic field is changed. a chaotic firing for E_ext = 0.01, φ_ext = 0; b periodic firing for E_ext = 0.05, φ_ext = 0; c chaotic firing for E_ext = 0, φ_ext = 0.01; d periodic firing for E_ext = 0, φ_ext = 0.4; e chaotic firing for E_ext = 0.01, φ_ext = 0.01; f periodic firing for E_ext = 0.01, φ_ext = 0.4. Energy proportion (p₁, p₂, p₃, p₄) is calculated within 1000 time units, A = 0.6, ω = 0.8

The firing patterns become periodic or chaotic when the external electric field or magnetic field is activated with different intensities. Furthermore, the energy proportion of the neuron under the external electric field or magnetic field is calculated in Fig. 14.

The results in Fig. 14 indicate that memristive neuron mainly keeps the field energy mainly in capacitor, and capacitive energy occupies higher a proportion than inductive field energy. In addition, we explore the case that the external electric and magnetic field fluctuates in periodic form E_ext = A₁sin(0.8τ + 0.1), φ_ext = A₂sin(0.8τ + 0.1). Setting the same values for parameters as a = 0.8, b = 0.7, c = 0.1, ξ = 0.25, μ = 0.01, g = 0.2, δ = 0.1, k₁ = 0.01, α´ = 0.1, β´ = 0.01, γ´ = 0.1, λ´ = 0.01, u_s = 0.6sin(0.8τ), and initials are fixed at (0.2, 0.1, 0.01, 0.01). Figure 15 calculated bifurcation diagram and LLE when the external field is changed.

Fig. 15

The bifurcation diagram and LLE by adjusting the amplitude of the external field at u_s = 0.6sin (0.8τ). For a, e A₁ ∈ [0, 5], φ_ext = 0; b, f A₂ ∈ [0, 6], E_ext = 0; c, g A₁ ∈ [0, 5], A₂ = 0.6; d, h A₂ ∈ [0, 6], A₁ = 0.6

Similar to the case that the external electric and magnetic field is kept as constants, the memristive neuron shows a mode transition from chaotic to periodic firing patterns, and the firing modes and energy proportion are shown in Figs. 16 and 17.

Fig. 16

The firing modes for the neuron in Eq. (9) by applying the external electric and magnetic field in periodic form at u_s = 0.6sin (0.8τ). a A₁ = 0.5, φ_ext = 0; b A₁ = 0.9, φ_ext = 0; c E_ext = 0, A₂ = 0.5; d E_ext = 0, A₂ = 4; e A₁ = 0.6, A₂ = 0.6; f A₁ = 0.9, A₂ = 0.6

Fig. 17

The energy proportion for the neuron in Eq. (9) by applying the external electric and magnetic field in periodic form. a A₁ = 0.5, φ_ext = 0; b A₁ = 0.9, φ_ext = 0; c E_ext = 0, A₂ = 0.5; d E_ext = 0, A₂ = 4; e A₁ = 0.6, A₂ = 0.6; f A₁ = 0.9, A₂ = 0.6. Energy proportion (p₁, p₂, p₃, p₄) is calculated within 1000 time unites and u_s = 0.6sin (0.8τ)

From Fig. 17, the neuron prefers to present (chaotic, periodic) firing patterns when the capacitive field energy proportion is maintained higher level. According to the criterion for growth of memristive parameter presented in Eq. (12), the parameters are kept as a = 0.8, b = 0.7, c = 0.1, ξ = 0.25, μ = 0.01, g = 0.2, δ = 0.1, α´ = 0.1, β´ = 0.01, γ´ = 0.1, λ´ = 0.01, u_s = 0.6sin(0.8τ), ε₁ = 0.5, r₁ = 0.02, φ_ext = 0, external disturbance from electric field is applied to explore the adaptive growth of memristive parameter for CCM in Fig. 18.

Fig. 18

The growth of the memristive parameter k₁ for the neuron exposed to the external electric field E_ext. a E_ext = 0.1; b E_ext = 0.6sin (0.8τ + 0.1); c Noisy E_ext with intensity 0.1. Setting u_s = 0.6sin (0.8τ), ε₁ = 0.5, r₁ = 0.02, φ_ext = 0 and initial value for k₁ = 0.01

As presented in Fig. 18, the memristive parameter k₁ reach a saturation value within a certain transient period and the energy proportion is adjusted to regulate the firing modes in this neuron. Continuous energy injection and absorption can induce finite shape deformation and one of the intrinsic parameters shows finite shift as well. It is interesting to explore the mode transition when the memristive parameter is adjusted, and the firing modes for this neuron are displayed in Fig. 19.

Fig. 19

The firing modes in the memristive neuron with adaptive growth in parameter E_ext. a E_ext = 0.1; b E_ext = 0.6sin (0.8τ + 0.1); c Noisy E_ext with intensity 0.1. Setting u_s = 0.6sin (0.8τ), ε₁ = 0.5, r₁ = 0.02, φ_ext = 0, and initial value for k₁ = 0.01

It is confirmed that the chaotic patterns are suppressed to present periodic modes when the memristive synapse is controlled adaptively by the external electric field. The energy level is dependent on the firing modes, as a result, mode transition predicts a possible jump between energy levels. Therefore, the energy proportion for this neuron showing mode transition is calculated in Fig. 20.

Fig. 20

The energy proportion for the neuron with growth of the memristive parameter under electric field E_ext. a E_ext = 0.1; b E_ext = 0.6sin (0.8τ + 0.1); c Noisy E_ext with intensity 0.1. The initial values are fixed at (0.2, 0.1, 0.01, 0.01, 0.01). Energy proportion (p₁, p₂, p₃, p₄) is calculated within 1000 time unites, and u_s = 0.6sin (0.8τ), ε₁ = 0.5, r₁ = 0.02, φ_ext = 0, initial value for k₁ = 0.01

From Fig. 20, when the external electric field is adjusted, and field energy in mainly kept in capacitive form because the initial firing mode is switched to become periodic type. Furthermore, the growth of memristive parameter γ´ is considered when the external magnetic field is changed with φ_ext in Fig. 21.

Fig. 21

Growth of memristive parameter μ when external magnetic field is disturbed with φ_ext. a φ_ext = 0.01; b φ_ext = 0.6sin (0.8τ + 0.1); c Noisy φ_ext with intensity 0.1. Setting u_s = 0.6sin (0.8τ), ε₂ = 0.5, r₂ = 0.02, E_ext = 0, and initial value for μ = 0.01

Similar to the growth of memristive parameter k₁, the memristive parameter μ presents a steady state within certain transient period. In presence of noisy disturbance from magnetic field, the memristive gain for MFCM shows slight fluctuation when energy in the memristive channel is further increased to occupy more proportion in inductive energy. Mode transition in neural activities is presented in Fig. 22 for this case.

Fig. 22

Firing modes for neuron with growth of memristive parameter under magnetic field φ_ext. a φ_ext = 0.01; b φ_ext = 0.6sin (0.8τ + 0.1); c Noisy φ_ext with intensity 0.1. Setting u_s = 0.6sin (0.8τ), ε₂ = 0.5, r₂ = 0.02, E_ext = 0, and initial value for μ = 0.01

The chaotic patterns in this memristive neuron are controlled to present periodic types during the changes of external magnetic field, which enables adaptive growth of memristive parameter. Furthermore, energy proportion for this memristive neuron exposed to magnetic field is estimated in Fig. 23 considering the adaptive growth and modulation in the memristive synapse/channel.

Fig. 23

Energy proportion for neuron with growth of memristive parameter under magnetic field φ_ext. a φ_ext = 0.01; b φ_ext = 0.6sin (0.8τ + 0.1); c Noisy φ_ext with intensity 0.1. Energy proportion (p₁, p₂, p₃, p₄) is calculated within 2000 time unites, u_s = 0.6sin (0.8τ), ε₂ = 0.5, r₂ = 0.02, E_ext = 0, and initial value for μ = 0.01

In this case, field energy is mainly kept in the inductive channel, and there is a slight difference in the energy proportion of electric components by applying different types of magnetic fields. Furthermore, the growth of memristive parameters (k₁, μ) are calculated in Fig. 24 by applying different types (E_ext, φ_ext), which can estimate the dynamics of this memristive neuron when both electric field and magnetic field are applied to control the energy flow. Evolution of firing patterns and energy proportion for this neuron are shown in Figs. 25 and 26.

Fig. 24

Growth of memristive parameters (k₁, μ) by applying different types (E_ext, φ_ext) for electromagnetic field. a E_ext = 0.1, φ_ext = 0.01; c E_ext = φ_ext = 0.6sin (0.8τ + 0.1). Setting u_s = 0.6sin (0.8τ), ε₁ = 0.5, ε₂ = 0.2 r₁ = 0.01, r₂ = 0.02 and initial values k₁ = 0.01, μ = 0.1

Fig. 25

Firing modes for neuron under electromagnetic field (E_ext, φ_ext). a φ_ext = 0.01, E_ext = 0.1; b φ_ext = 0.6sin (0.8τ + 0.1), E_ext = 0.1sin (0.8τ + 0.1); c Noisy φ_ext and E_ext are selected with intensity 0.1. Setting u_s = 0.6sin (0.8τ), ε₁ = 0.5, ε₂ = 0.2 r₁ = 0.01, r₂ = 0.02 and initial values k₁ = 0.01, μ = 0.1

Fig. 26

Energy proportion for neuron under electromagnetic field (E_ext, φ_ext). a φ_ext = 0.01, E_ext = 0.1; b φ_ext = 0.6sin (0.8τ + 0.1), E_ext = 0.1sin (0.8τ + 0.1); c Noisy φ_ext and E_ext are selected with intensity 0.1. Setting u_s = 0.6sin (0.8τ), ε₁ = 0.5, ε₂ = 0.2 r₁ = 0.01, r₂ = 0.02 and initial values k₁ = 0.01, μ = 0.1. Energy proportion (p₁, p₂, p₃, p₄) is calculated within 1000 time unites

When two kinds of physical fields are applied, energy flow can be absorbed from two memristive channels and the energy is shunted to control the growth of memristive parameters. It is found that these memristive parameters can be increased adaptively for regulating the energy flow in different channels. Furthermore, changes in the membrane potential are presented in Fig. 25 for showing the effect of external fields on mode selection.

The activation and involvement of magnetic field and electric field synchronously can suppress chaotic activities and the neuron prefers to keep periodic oscillation with lower amplitude. In addition, energy shunting between capacitive and inductive channels is plotted in Fig. 26.

It is found that energy is mainly kept in inductive channels and adaptive growth in two memristive channels are effective to trigger mode transition for keeping suitable energy level. In fact, external stimuli can be combination of different periodic signals and then its equivalent stimulus can be approached by using filtered signals from chaotic source. It is interesting to explore the energy distribution of the neural circuit driven by irregular external electric and magnetic fields. However, chaotic signals are similar to random signals; in this case, the output voltage from PR (Pikovskii-Rabinovich) chaotic system [59] is selected as the external electric and magnetic fields, and its dynamics can be estimated by

$$ \left\{\begin{array}{l}\frac{{dx_{1} }}{d\tau } = y_{1} - 0.66z_{1} ; \hfill \\ \frac{{dy_{1} }}{d\tau } = - x_{1} + 0.402y_{1} + 0.165z_{1} \hfill \\ \frac{{dz_{1} }}{d\tau }{ = }\frac{1}{0.047}(x_{1} + z_{1} - z_{1}^{3} ); \hfill \\ \end{array} \right.; $$

(13)

When the initial values are fixed at (0.1, 0.1, 0.1), the chaotic attractor and time series for variable x₁ and x₂ are presented in Fig. 27.

Fig. 27

Phase portrait and time series. a attractor phase in x₁–y₁ space; b time series for the variable x₁; c time series for the variable y₁. The initial values are fixed at (0.1, 0.1, 0.1)

From Fig. 27, the output values of the chaotic system are distributed in (-2, 2). To discern the effect of the irregular electric and magnetic fields on the firing activities and energy proportion of channels in memristive circuit, setting E_ext = x₁ for external electric field, φ_ext = y₁ for magnetic field. The parameters are selected as a = 0.8, b = 0.7, c = 0.1, ξ = 0.25, g = 0.2, δ = 0.1, μ = 0.01, α´ = 0.1, β´ = 0.01, γ´ = 0.1, λ´ = 0.01, u_s = 0.6sin(0.8τ), the firing modes are displayed in Fig. 28.

Fig. 28

Firing modes for memristive neuron in Eq. (9) by imposing irregular external electric and magnetic fields. a φ_ext = 0, E_ext = x₁; b φ_ext = y₁, E_ext = 0; c φ_ext = y₁, E_ext = x₁

The results in Fig. 28 show that the memristive neuron presents the periodic firing patters by imposing the external electric field E_ext = x₁ without the external magnetic field φ_ext = y₁. While the memristive circuit shows chaotic firing patterns when the external magnetic field φ_ext = y₁ is activated. In presence of chaotic form for the external magnetic field and electric field, the neuron is guided to show chaotic patterns. Furthermore, the energy proportion in the neuron under electromagnetic in chaotic form is calculated in Fig. 29.

Fig. 29

Energy proportion for neuron in Eq. (9) excited by irregular external electric and magnetic fields. a φ_ext = 0, E_ext = x₁; b φ_ext = y₁, E_ext = 0; c φ_ext = y₁, E_ext = x₁. Energy proportion (p₁, p₂, p₃, p₄) is calculated within 1000 time unites

It is confirmed in Fig. 29 that field energy mainly keeps in inductor when chaotic disturbance from the electric and magnetic fields are imposed on the neuron. In the nervous system, noise stimulation can increase the human body's observation and reflection of external weak signals under nonlinear resonance. Coherence resonance refers to the phenomenon that when the nervous system is subjected to noise, the intensity of the noise can be carefully adjusted to induce distinct regular states. To investigate whether coherence resonance can occur in this memristive model presented in Eq. (9), for simplicity, the Gaussian white noise is added in the external electric field and magnetic field respectively. The average of Gaussian white noise is < ξ(τ) >  = 0, and the statistical correlation can be represented as < ξ(τ) ξ(τ’) >  = 2Dδ(τ-τ’) with any noise intensity D. To observe the generation of coherent resonance phenomenon, the coefficient of variation (CV) is calculated under different noise intensities, the approach of CV is defined as follows

$$ \left\{\begin{array}{l} CV = \frac{{\sqrt { < T^{2} > - < T >^{2} } }}{ < T > }; \hfill \\ < T > = \frac{1}{N}\sum\limits_{i = 1}^{N} {T_{i} } ;\quad < T^{2} > = \frac{1}{N}\sum\limits_{i = 1}^{N} {T_{i}^{2} } ; \hfill \\ T_{i} = t_{i} - t_{i - 1} \;; \hfill \\ \end{array} \right. $$

(14)

where t_i is time of the ith pulse, T_i denotes the ith interspike interval, N represents total number of action potentials produced by neuron in a given time. The parameters and initial values are kept as above, the CV is calculated by applying different noise intensities, and the results are depicted in Fig. 30.

Fig. 30

Distribution of CV under noisy disturbance in external field. a E_ext; b φ_ext. The parameters are selected as a = 0.8, b = 0.7, c = 0.1, ξ = 0.25, g = 0.2, δ = 0.1, α´ = 0.1, β´ = 0.01, γ´ = 0.1, λ´ = 0.01, k₁ = 0.01, μ = 0.01, u_s = 0.55sin (0.8τ)

From Fig. 30, the CV can detect smallest value when the intensity of noisy field is adjusted carefully, and the memristive neuron can generate coherent resonance phenomenon and prefer to show regular firing patterns.

In a summary, the firing activities of the neuron will be changed under the effect of the external electric field or magnetic field, and the physical field energy is also changed because of external energy injection. The memristive channel and synapse can control its biophysical property adaptively. Neurons show (bursting, spiking) firing modes when field energy is mainly kept in the inductor. Neurons can present (periodic, chaotic) firing patterns when field energy is kept in capacitor. The involvement of MFCM and CCM can enhance the ability of neural circuit to discern external physical effect and the artificial synapses and memristive channels become more controllable.

4 Open problems

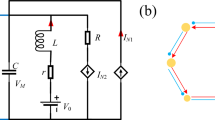
Above all, the physical effect is described by using independent channels, which energy flow for magnetic field and electric field is considered in different channels. In fact, memristive channel has certain dependence of the induced current associated with magnetic field. Therefore, a CCM is used to connect the inductor of the neural circuit and additive memristive channel is also supplied to estimate the energy exchange in the neural circuit in Fig. 31.

Fig. 31

Schematic diagram for a dual memristive neural circuit. V_s denotes an adjustable voltage source, R_s is a linear resistors, C and L denote capacitor and induction coil, E is a constant voltage source, M(q) and W(φ) represent mem-resistance for charge-controlled memristor and memductance for flux-controlled memristor

The channel current across the CCM and MFCM can be described by the same form in Eq. (1), Eq. (2), respectively. The same nonlinear resistor defined in Eq. (6) is also applied to shunt energy between capacitive and inductive field. The dynamics for the neural circuit in Fig. 31 can be described by

$$ \left\{ \begin{array}{l} C\frac{dV}{{dt}} = \frac{{V_{S} - V}}{{R_{s} }} - i_{L} - i_{N} - k_{3} \varphi V; \hfill \\ L\frac{{di_{L} }}{dt} = V - \frac{{i_{L} }}{{k_{1} (\alpha + 3\beta q^{2} )}} + E; \hfill \\ \frac{dq}{{dt}} = i_{L} ; \hfill \\ \frac{d\varphi }{{dt}} = \lambda \tanh (\varphi ) - \gamma \varphi + \delta V; \hfill \\ \end{array} \right.{\kern 1pt} $$

(15)

Similar scale transformation for physical variables in Eq. (15) is applied as follows

$$ \left\{ \begin{array}{l} x = \frac{V}{{V_{0} }},y = \frac{{\rho i_{L} }}{{V_{0} }},z = \frac{q}{{CV_{0} }},w = \frac{\varphi }{{\rho CV_{0} }},\tau = \frac{t}{\rho C},\alpha^{\prime} = \alpha \rho ,\beta^{\prime} = 3\beta \rho C^{2} V_{0}^{2} ; \hfill \\ \gamma^{\prime} = \gamma \rho C,\;\lambda^{\prime} = \lambda \rho C,a = \frac{E}{{V_{0} }},c = \frac{{\rho^{2} C}}{L},\xi = \frac{\rho }{{R_{s} }},u_{s} = \frac{{V_{s} \rho }}{{R_{s} V_{0} }},\mu = k_{3} \rho^{2} CV_{0} ; \hfill \\ \end{array} \right. $$

(16)

As a result, a new memristive neuron is updated as follows

$$ \left\{\begin{array}{l} \frac{dx}{{d\tau }} = (1 - \xi )x - y - \frac{1}{3}x^{3} + u_{s} - \mu xw; \hfill \\ \frac{dy}{{d\tau }} = c(x + a - \frac{y}{{k_{1} (\alpha^{\prime} + \beta^{\prime}z^{2} )}}); \hfill \\ \frac{dz}{{d\tau }} = y + E_{ext} ; \hfill \\ \frac{dw}{{d\tau }} = \lambda^{\prime}\tanh (w) - \gamma^{\prime}w + \delta x + \varphi_{ext} ; \hfill \\ \end{array} \right.{\kern 1pt} $$

(17)

where u_s is an external voltage source, E_ext and φ_ext describe the equivalent radiation from external electric field and magnetic field on the memristive neuron. These intrinsic parameters and external stimuli can be adjusted to find mode transition, stochastic resonance and energy dependence on firing mode even noisy disturbance is applied.

Indeed, the obtained biophysical neuron considers the energy effect from both the electric field and magnetic field, and the energy level is well addressed. In the presence of the distinct firing mode, the energy level becomes stable. Under multiple firing modes, different firing patterns are coexistent with each other and switch between different energy levels are triggered. In particular, the energy function is obtained in a theoretical way. This neuron model can be further used to explore the collective patterns and energy distribution in neural networks, and then the role of energy balance can be further understood [60,61,62,63].

5 Conclusions

A memristive neural circuit sensitive to the electric and magnetic fields is proposed and its energy characteristic is discussed. The field energy of this neural circuit is estimated by using the Hamilton energy based on the famous Helmholtz’s theorem. The electrical activities and field energy distribution of the memristive neural circuit under the different types of the external electric and magnetic fields are analyzed in detail. The numerical results illustrate that neuron show (bursting, spiking) firing modes when field energy mainly keeps in the inductor. It prefers to keep (periodic, chaotic) firing patterns when capacitive field energy maintains a higher level. Energy injection and accommodation can induce shape deformation accompanied by a shift in memristive channels, the neuron shows mixed firing patterns, and the field energy mainly depends on the activation of the inductor. In addition, the neuron model is in (periodic, chaotic) firing states when the external electric and magnetic field are imposed with irregular signal sources. Furthermore, the coherent resonance of the memristive neuron can be induced by selecting the appropriate noise intensity for the external field. This result is helpful to investigate the collective behaviors in the different networks under the external electric and magnetic fields.

Appendices

Appendix A: Approach of energy proportion in memristive neuron model

$$ \left\{ \begin{gathered} p_{1} = \frac{{\int_{0}^{T} {\frac{1}{2}x^{2} d\tau } }}{{\int_{0}^{T} {\left( {\frac{1}{2}x^{2} + \frac{1}{2c}y^{2} } \right)d\tau + \left| {\int_{0}^{T} {\frac{1}{2}xzd\tau } } \right| + \left| {\int_{0}^{T} {\frac{1}{2}\mu w^{2} xd\tau } } \right|} }} \approx \frac{{\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i}^{2} } }}{{\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i}^{2} } + \sum\limits_{i = 1}^{N} {\frac{1}{2c}y_{i}^{2} } + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i} z_{i} } } \right| + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}\mu w_{i}^{2} x_{i} } } \right|}}; \hfill \\ p_{2} = \frac{{\int_{0}^{T} {\frac{1}{2c}y^{2} d\tau } }}{{\int_{0}^{T} {\left( {\frac{1}{2}x^{2} + \frac{1}{2c}y^{2} } \right)d\tau + \left| {\int_{0}^{T} {\frac{1}{2}xzd\tau } } \right| + \left| {\int_{0}^{T} {\frac{1}{2}\mu w^{2} xd\tau } } \right|} }} \approx \frac{{\sum\limits_{i = 1}^{N} {\frac{1}{2c}y_{i}^{2} } }}{{\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i}^{2} } + \sum\limits_{i = 1}^{N} {\frac{1}{2c}y_{i}^{2} } + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i} z_{i} } } \right| + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}\mu w_{i}^{2} x_{i} } } \right|}}; \hfill \\ p_{3} = \frac{{\left| {\int_{0}^{T} {\frac{1}{2}xzd\tau } } \right|}}{{\int_{0}^{T} {\left( {\frac{1}{2}x^{2} + \frac{1}{2c}y^{2} } \right)d\tau + \left| {\int_{0}^{T} {\frac{1}{2}xzd\tau } } \right| + \left| {\int_{0}^{T} {\frac{1}{2}\mu w^{2} xd\tau } } \right|} }} \approx \frac{{\left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i} z_{i} } } \right|}}{{\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i}^{2} } + \sum\limits_{i = 1}^{N} {\frac{1}{2c}y_{i}^{2} } + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i} z_{i} } } \right| + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}\mu w_{i}^{2} x_{i} } } \right|}}; \hfill \\ p_{4} = \frac{{\left| {\int_{0}^{T} {\frac{1}{2}\mu w^{2} xd\tau } } \right|}}{{\int_{0}^{T} {\left( {\frac{1}{2}x^{2} + \frac{1}{2c}y^{2} } \right)d\tau + \left| {\int_{0}^{T} {\frac{1}{2}xzd\tau } } \right| + \left| {\int_{0}^{T} {\frac{1}{2}\mu w^{2} xd\tau } } \right|} }} \approx \frac{{\left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}\mu w_{i}^{2} x_{i} } } \right|}}{{\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i}^{2} } + \sum\limits_{i = 1}^{N} {\frac{1}{2c}y_{i}^{2} } + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}x_{i} z_{i} } } \right| + \left| {\sum\limits_{i = 1}^{N} {\frac{1}{2}\mu w_{i}^{2} x_{i} } } \right|}}; \hfill \\ \end{gathered} \right. $$

(18)

Appendix B: The proof of the Hamilton energy for the memristive neuron by applying a Helmholtz theorem

The memristive neuron model in Eq. (5) is rewritten with equivalent form as follows

$$ \begin{aligned} \left( \begin{gathered} {\dot{x}} \hfill \\ {\dot{y}} \hfill \\ {\dot{z}} \hfill \\ {\dot{w}} \hfill \\ \end{gathered} \right) & = \left( \begin{gathered} u_{s} - \xi x - y - k_{1} x(\alpha^{\prime } + \beta^{\prime } z^{2} ) + gz - \mu wx \hfill \\ c(x + 1 - y) \hfill \\ k_{1} x(\alpha^{\prime } + \beta^{\prime } z^{2} ) - gz + E_{ext} \hfill \\ \lambda^{\prime } \tanh (w) - \gamma^{\prime } w + \delta x + \varphi_{ext} \hfill \\ \end{gathered} \right) = F_{c} + F_{d} \\ & = \left( \begin{array}{c} - y - \frac{1}{2}k_{1} \alpha^{\prime } x - \delta \mu wx \hfill \\ cx \hfill \\ k_{1} \alpha^{\prime } x \hfill \\ \delta x + a_{1} + \frac{1}{2x}wy + a_{2} \hfill \\ \end{array} \right) + \left( \begin{gathered} u_{s} - \xi x - k_{1} x\beta^{\prime } z^{2} + gz + \frac{3}{2}k_{1} \alpha^{\prime } x - \mu wx + \delta \mu wx \hfill \\ c(1 - y) \hfill \\ k_{1} \beta^{\prime } xz^{2} - gz + E_{ext} \hfill \\ \lambda^{\prime } \tanh (w) - \gamma^{\prime } w + \varphi_{ext} - a_{1} - \frac{1}{2x}wy - a_{2} \hfill \\ \end{gathered} \right) \\ & = \left( {\begin{array}{*{20}c} 0 & { - c} & { - k_{1} \alpha^{\prime } } & { - \delta } \\ c & 0 & { - \frac{cz}{x}} & { - \frac{cw}{{2x}}} \\ {k_{1} \alpha^{\prime } } & \frac{cz}{x} & 0 & { - a_{2} } \\ \delta & {\frac{cw}{{2x}}} & {a_{2} } & 0 \\ \end{array} } \right)\left( \begin{gathered} x + \frac{z}{2} + \frac{{\mu w^{2} }}{2} \hfill \\ \frac{y}{c} \hfill \\ \frac{x}{2} \hfill \\ \mu wx \hfill \\ \end{gathered} \right) \\ & \quad + \left( {\begin{array}{*{20}c} {a_{11} } & 0 & 0 & 0 \\ 0 & {c^{2} \left( {\frac{1}{y} - 1} \right)} & 0 & 0 \\ 0 & 0 & {2k_{1} \beta^{\prime } z^{2} - \frac{2}{x}gz + \frac{2}{x}E_{ext} } & 0 \\ 0 & 0 & 0 & {a_{44} } \\ \end{array} } \right)\left( \begin{array}{c} x + \frac{z}{2} + \frac{{\mu w^{2} }}{2} \hfill \\ \frac{y}{c} \hfill \\ \frac{x}{2} \hfill \\ \mu wx \hfill \\ \end{array} \right); \\ \end{aligned} $$

(19)

$$ \begin{gathered} \left\{ \begin{gathered} a_{1} = \delta \left( {\frac{1}{2}z + \frac{1}{2}\mu w^{2} } \right); \hfill \\ a_{2} = \frac{{k_{1} \alpha^{\prime } \left( {\frac{1}{2}z + \frac{1}{2}\mu w^{2} } \right) + \frac{wy}{x}}}{2\mu w}; \hfill \\ a_{11} = \frac{{2(u_{s} - \xi x - k_{1} x\beta^{\prime } z^{2} + gz + \frac{3}{2}k_{1} \alpha^{\prime } x - \mu wx + \delta \mu wx)}}{{2x + z + \mu w^{2} }}; \hfill \\ a_{44} = \frac{{\lambda^{\prime } \tanh (w) - \gamma^{\prime } w + \varphi_{ext} - a_{1} - \frac{1}{2x}wy - a_{2} }}{\mu wx} \hfill \\ \end{gathered} \right. \hfill \\ \quad \; \hfill \\ \end{gathered} $$

(20)

According to the Helmholtz theorem, the dimensionless Hamilton energy H for the neuron model meets the following criterion.

$$ {\kern 1pt} \nabla H^{T} F_{c} (x,y,z,w) = 0;\quad \nabla H^{T} F_{d} (x,y,z,w) = \frac{dH}{{d\tau }}; $$

(21)

Therefore, the energy function can be an exact solution for the formula as follows

$$ {\kern 1pt} \left( { - y - \frac{1}{2}k_{1} \alpha^{\prime } x - \delta \mu wx} \right)\frac{\partial H}{{\partial x}} + (cx)\frac{\partial H}{{\partial y}} + (k_{1} \alpha^{\prime } x)\frac{\partial H}{{\partial z}} + \left( {\delta x + a_{1} + \frac{wy}{{2x}} + a_{2} } \right)\frac{\partial H}{{\partial w}} = 0; $$

(22)

According to Eq. (21), an solution is obtained to match the Hamilton energy function as follows

$$ H = \frac{1}{2}x^{2} + \frac{{y^{2} }}{2c} + \frac{1}{2}xz + \frac{1}{2}\mu w^{2} x; $$

(23)

That is, the energy function for the memristive neuron can be confirmed and changes in the parameters (c, μ) have direct impact on the energy value, and firing mode in electric activities is regulated synchronously.