Synchronization and complex dynamics in locally active threshold memristive neurons with chemical synapses

Abstract

Memristor has been extensively employed to emulate neuron/synapse-inspired behaviors and to characterize the electromagnetic induction generated by ionic flowing. A link between memristive features and neural electrical activities is significantly necessary to be investigated. Thus, we propose a new neuron model with a locally active threshold flux-controlled (LTF) memristor, which depicts the electromagnetic induction. The LTF memristive neuron model can exhibit a regular evolution and transition of various firing patterns dependent upon the negative different conductance of the memristor, through performing the corresponding numerical simulations. It is demonstrated that due to the locally active threshold effect, the obtained model has complex firing behaviors. The memristive neural network is connected via chemical synapses. The memristive neural network under the modulation of excitatory and inhibitory chemical synapses shows different synchronous patterns. The captured results reveal that the locally active threshold effect is crucial for the generation of complex firing modes and the emergence of synchronization behaviors.

1 Introduction

Memristive systems have been investigated intensively since the fourth fundamental passive circuit element in addition to resistor, capacitor, and inductor was postulated by Chua [1]. The memristor is able to store information in different resistances because the resistance of memristive systems can be modulated by the history of its external stimuli. Memristive devices with non-volatile memory are obtained through materials engineering and circuit theory and can maintain their resistance state after the externally applied voltage is removed [2]. The stable resistance state is used to denote stored information. Therefore, memristive systems are suitable for signal storage applications and are employed to mimic neural systems [2,3,4,5].

For emulating biological synapses and neurons, many nonlinear systems as memristive systems offering desirable dynamics have been proposed to clarify intrinsic biophysical mechanism [6,7,8,9,10]. A nanoscale silicon-based memristive system has shown the spike timing-dependent plasticity of biological synapses [11]. A kind of memristive system can reveal rich dynamics of biological neurons, such as excitability, spiking, bursting, and mixed modes [12,13,14]. The photo/thermosensitive neuron models coupled by the memristive synapse exhibit multistability and phase synchronization [15, 16]. Memristive Josephson junction circuits have the ability to reproduce neuron-like excitability, bursting with the same bifurcation mechanism, and synchronous behaviors [17,18,19]. In addition, there are many systems composed of memristors and neural models based on energy perspectives [20,21,22]. On the one hand, a flux-controlled memristor-based neuron model is considered to characterize the electromagnetic induction effect triggered by ionic transmission in cell membranes [23]. Subsequently, the neural systems with flux-controlled memristors are exploited to not only exhibit dynamical and collective behaviors, but also reveal abundant biophysical mechanisms [24,25,26,27,28,29]. A Wilson neuron model with electromagnetic induction effects can display rich electrical activities dependent upon initial conditions and the coexisting electrical activities are verified by implementing an analog circuit on a hardware level [30]. A discrete memristive Rulkov neuron model is able to emulate the electromagnetic induction effects and to better produce the firing activities through a hardware platform [31]. A memristive neural system with an excitatory effect can produce bursting with deceased firing rates [32]. The inhibitory current from the flux-controlled memristor enhances firing rates in the form of bursting, and the bifurcation mechanism is demonstrated by the fast-slow decomposition method [33]. Pattern formation and synchronization stability in the neuron-like network are related to the local kinetics and coupling schemes [34,35,36]. A coupled network with a thermistor can detect the fluctuation of environment temperature and exhibit the phase synchronization [37, 38]. The neural model coupled with the memristor has many rich dynamics such as the wondrous offset-control plane coexisting behaviors, complete synchronizations, coexisting multi-stable patterns, and extreme events [39,40,41,42].

On the other hand, a locally active memristor is used to build a new biophysical system. The locally active memristor has a distinct feature as a negative differential conductance or resistance by observing DC current–voltage curves [43, 44]. Two neurons involving a locally active memristor exhibit coexisting position symmetry for different attractors [45]. The nonlinear systems containing locally-active memristors have more probability to generate complex dynamical behaviors [46,47,48]. Mott memristors with locally active features are suitably useful in certain types of neural-inspired computation [49]. A Hopfield neural network model is constructed by replacing one of the synaptic couplings with a tri-stable locally active memristor [50]. Rulkov neurons coupled with a locally active discrete memristor present multi-stability and phase synchronization [51]. A locally active memristor is proposed to describe electromagnetic induction triggered by action potentials and the memristive neuronal model reveals different threshold values dependent upon the induction effect based on the current-frequency curve [52].

Consequently, memristive systems have attracted significant attention in the past decade as a major enabler of new biophysical paradigms to reproduce abundant brain-inspired behaviors and functions. For instance, an electromagnetic induction current described by a threshold flux-controlled memristor is used to replace the external current in the Hindmarsh-Rose neuron model [53]. The obtained memristive neural model exhibits hidden bursting firing patterns. A coupled FitzHugh-Nagumo model with a local active flux-controlled memristor can reproduce complex firing transitions similar to that of the model with a chemical synapse [54]. However, a combination of threshold and local active features needs to be further reconsidered from the neurodynamics point of view. Thus, we propose a locally-active threshold flux-controlled memristor. The relation between neuronal electrical activity and locally-active threshold feature is explored by bifurcation analysis. Collective behaviors in the memristive neural network are exhibited by modulating excitatory and inhibitory chemical synaptic models.

The rest of the present paper is organized as follows. In Sect. 2, a new memristive neuron model is proposed by introducing a locally threshold electromagnetic induction effect. Meanwhile, the neural network composed of the models and chemical synapses is constructed. In Sect. 3, we analyze the dynamical behaviors in the model based on the bifurcation. Then corresponding collective behaviors have further been demonstrated in the neural network. The conclusion is given in Sect. 4.

2 Model description and method

2.1 Hindmarsh-Rose-type neuron models

Dynamical models that can emphasize important features and downplay the inessential details have been proposed and developed in neuroscience and neurodynamics. For instance, Hindmarsh and Rose reported a second-order neuron model to reduce the complexity of these equations such as the Hodgkin-Huxley model of the nerve impulse composed of four complex nonlinear differential equations, six functions, and seven constants. The second-order Hindmarsh-Rose (labeled as 2D HR) neuron model has few parameters but can predict the frequency-current relationship and may be useful for exploring detailed interactions in small neuronal networks [55]. The mathematical description of the generalized 2D HR neuron model is

$$ \left\{ \begin{gathered} \dot{x} = y - ax^{3} + bx^{2} + I_{ext} , \\ \dot{y} = c - dx^{2} - y, \\ \end{gathered} \right. $$

(1)

where x denotes the membrane potential on neuronal cells, and y is the recovery variable relative to the inward current. While parameters (a, b, c, and d) are the positive constants. And I_ext represents external stimulus current. To explore the complex electrical activities of neurons, modified mathematical models have been proposed to reproduce different bursting and chaotic oscillations dependent upon a variety of bifurcations.

2.2 Modelling of LTF memristor

Neuromorphic circuits are inspired by neurons and synapses in the brain. The circuits have been developed from the physical and mathematical point of view. Novelty, neurons and synapses may be emulated by flux-controlled, charge-controlled, current-controlled, and voltage-controlled memristors. According to the state-dependent Ohm’s law and Chua’s theorem [1, 56], a generic flux-controlled memristor is expressed as follows:

$$ \left\{ \begin{gathered} I_{M} = W(\phi )V_{M} , \\ \frac{d\phi }{{d\tau }} = g(V_{M} ,\phi ), \\ \end{gathered} \right. $$

(2)

where V_M and I_M denote the voltage and current of the memristor, respectively. W(φ) is the memductance function. The state variable ϕ is magnetic flux. The function g(V_M, ϕ) is associated with the device materials and its physical operating mechanism.

Flux-controlled memristors have been used to mimic and describe synapses and neurons with electromagnetic induction. In particular, a threshold flux-controlled memristor was introduced into the 2D HR neuron model, which can generate new firing patterns [53]. A locally-active memristor was introduced into the 2D FHN neuron model to reproduce biophysical functions similar to chemical synapses [54]. Thus, a Locally-active Threshold Flux-controlled memristor (simplified as LTF memristor) is worth proposing and exploring towards its physical realization. The specific forms of LTF memristor are rewritten as follows:

$$ \left\{ \begin{gathered} I_{M} = p\tanh (\phi )V_{M} , \\ \frac{d\phi }{{d\tau }} = \frac{1}{n}(1 - p_{1} \frac{\phi }{{V_{M} }} - p_{2} \phi )V_{M} , \\ \end{gathered} \right. $$

(3)

where p and n are gain to control the magnitude of the memristive current. The inductive potential with linear and nonlinear factors is dependent upon the magnetic flux, due to the existence of complex media in a cell. Two coefficients p₁ and p₂ are deemed as the modulated parameters of the locally-active memristor. Note that the coefficients are able to be chosen, which can be tuned based on the modeling requirement of researchers. For example, when the parameters p₁ and p₂ are set as zero, the model in Eq. (3) is a Threshold Flux-controlled (simplified as TF) memristor.

2.3 Modelling of LTF memristive neuron

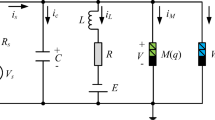
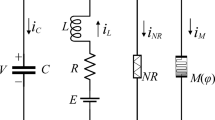
From the physical point of view, the 2D HR neuron model is regarded as a parallel circuit composed of a capacitor, an inductor with internal resistor and voltage source, and two voltage-controlled current sources, as shown in the light-yellow box of Fig. 1a. The two voltage-controlled current sources are defined as

$$ I_{{N_{1} }} (V_{M} ) = V_{M}^{2} - kV_{M}^{3} ,\;I_{{N_{2} }} (V_{M} ) = V_{M}^{2} . $$

(4)

Fig. 1

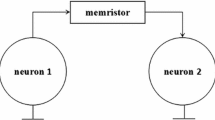
a Schematic diagram of LTF memristive neuron circuit composed of the LTF memristor, capacitor, inductor, and voltage-controlled current sources. b Schematic of neuronal network by using the chemical synapse coupling. The yellow circle, blue line, and red line represent neuron, inhibitory and excitatory chemical synapse, respectively

Inspired by the aforementioned modelling mind, a novel 3D memristive neuron model is reported in here. To better emulate complex dynamical behaviors of the neuronal firings, the 3D HR neuron model was obtained by adding a memristive current. The LTF memristor is employed to emulate the electromagnetic induction. When the memristive current I_M of the LTF memristor is parallel with the neuron model, the new memristive neuron circuit as shown in Fig. 1a.

According to Kirchhoff’s laws, the following equations are described as

$$ \left\{ {\begin{array}{*{20}l} {C\frac{{dV_{M} }}{d\tau } = I + I_{{N_{1} }} (V_{M} ) + I_{M} ,} \hfill \\ {L\frac{dI}{{d\tau }} = V_{0} - rI - RI_{{N_{2} }} (V_{M} ),} \hfill \\ {\frac{d\phi }{{d\tau }} = \frac{1}{n}(1 - p_{1} \frac{\phi }{{V_{M} }} - p_{2} \phi )V_{M} .} \hfill \\ \end{array} } \right. $$

(5)

By using the dimensionless scale transformation,

$$ \begin{aligned} \frac{\tau }{L/r} = & t,\;\frac{I}{{I_{0} }} = y,\;V_{M} = \frac{{LI_{0} }}{rC}x,\;\frac{\phi }{{LI_{0} }} = \varphi , \\ k_{0} = & \frac{pr}{L},k_{1} = LI_{0} p_{2} ,k_{2} = rCp_{1} ,n = \frac{L}{{Cr^{2} }}, \\ a = & \frac{{kL^{3} I_{0}^{2} }}{{r^{3} C^{3} }},\;b = \frac{{L^{2} I_{0} }}{{r^{2} C^{2} }},\;c = \frac{{V_{0} }}{{rI_{0} }},\;d = \frac{{RL^{2} I_{0} }}{{r^{3} C^{2} }}, \\ \end{aligned} $$

(6)

when I₀ = 1/L, the dynamical equation can be simplified and expressed as

$$ \left\{ {\begin{array}{*{20}l} {\frac{dx}{{dt}} = y - ax^{3} + bx^{2} + k_{0} \tanh (\varphi )x,} \hfill \\ {\frac{dy}{{dt}} = c - dx^{2} - y,} \hfill \\ {\frac{d\varphi }{{dt}} = (1 - k_{1} \varphi )x - k_{2} \varphi ,} \hfill \\ \end{array} } \right. $$

(7)

where φ is regarded as the magnetic flux variable associated with the membrane potential x (instead of V_M) in a cell, and the memductance k₀tanh(φ) is used to reflect the electromagnetic induction effect with threshold feature.

The equilibrium point of Eq. (7) is E^* = (x^*, y^*, φ^*). In order to get the equilibrium point E^*, we let the right of Eq. (7) is equal to zero, i.e.

$$ \left\{ \begin{gathered} y^{*} - ax^{*3} + bx^{*2} + k_{0} \tanh (\varphi^{*} )x^{*} = {0,} \hfill \\ c - dx^{*2} - y^{*} = {0,} \hfill \\ (1 - k_{1} \varphi^{*} )x^{*} - k_{2} \varphi^{*} = {0}{\text{.}} \hfill \\ \end{gathered} \right. $$

(8)

We obtain

$$ y^{*} = c - dx^{*2} ,\varphi^{*} = \frac{{x^{*} }}{{k_{1} x^{*} + k_{2} }}, $$

and x^* can be derived from the following equation

$$ - ax^{*3} + (b - d)x^{*2} + k_{0} \tanh \left( {\frac{{x^{*} }}{{k_{1} x^{*} + k_{2} }}} \right)x^{*} + c = 0. $$

(9)

In the appendix, the real roots of Eq. (9) are calculated in detail.

Next, we compute the Jacobian matrix J at E^*, which can be expressed as follows.

$$ J = \left( {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } \\ {a_{21} } & {a_{22} } & {a_{23} } \\ {a_{31} } & {a_{32} } & {a_{33} } \\ \end{array} } \right), $$

(10)

where a₁₁ = –3ax^*2 + 2bx^* + k₀tanh(φ^*), a₁₂ = 1, a₁₃ = k₀x^*(1–tanh²(φ^*)), a₂₁ = –2dx^*, a₂₂ = –1, a₂₃ = 0, a₃₁ = 1–k₁φ^*, a₃₂ = 0, a₃₃ = –k₁x^*–k₂. The characteristic equation of J is given by

$$ \left| {\begin{array}{*{20}c} {\lambda - a_{11} } & { - a_{12} } & { - a_{13} } \\ { - a_{21} } & {\lambda - a_{22} } & { - a_{23} } \\ { - a_{31} } & { - a_{32} } & {\lambda - a_{33} } \\ \end{array} } \right| = 0. $$

(11)

By algebraic simplification, we obtain

$$ \lambda^{3} + b_{2} \lambda^{2} + b_{1} \lambda + b_{0} = 0, $$

(12)

where,

$$ \begin{aligned} b_{2} = & 3ax^{*2} + (k_{1} - 2b)x^{*} - k_{0} \tanh (\varphi^{*} ) + k_{2} + 1, \\ b_{1} = & (3ax^{*2} - 2bx^{*} - k_{0} \tanh (\varphi^{*} ) + 1)(k_{1} x^{*} + k_{2} ) + (k_{1} \varphi^{*} - 1)k_{0} x^{*} (1 - \tanh^{2} (\varphi^{*} )) + 2dx^{*} , \\ b_{0} = & \left( {3ax^{*2} { + }2(d - b)x^{*} - k_{0} \tanh (\varphi^{*} )} \right)\left( {k_{1} x^{*} + k_{2} } \right) + (k_{1} \varphi^{*} - 1)k_{0} x^{*} (1 - \tanh^{2} (\varphi^{*} )). \\ \end{aligned} $$

Then the Routh-Hurwitz criteria is used to determine the stability of E^* = (x^*, y^*, φ^*) and the following theorem is obtained.

Theorem 1

If b₀, b₁, b₂ > 0, and b₂b₁–b₀ > 0, then the equilibrium point E^* = (x^*, y^*, φ^*) is local asymptotic stability.

For instance, if the parameters are fixed at a = 1, b = 3, c = 1, d = 1, k₀ = 0.2, k₁ = 0.01 and k₂ = 2, then the equilibrium point E^* = (2.2660, –1.2660, 1.1203). Correspondingly, the characteristic equation is derived as

$$ \lambda^{{3}} { + 4}{\text{.6694}}\lambda^{{2}} { + 9}{\text{.7296}}\lambda { + 12}{\text{.3417 = 0,}} $$

(13)

and the eigenvalues of Eq. (13) are solved as.

λ₁ = –2.76484, λ₂ = –0.952279–1.88599i, λ₃ = –0.952279 + 1.88599i.

Therefore, the real parts of the characteristic roots are all negative, indicating that the equilibrium point E^* is a stable equilibrium point. Meanwhile, it is evident that b₀, b₁, b₂ > 0, and b₂b₁–b₀ = 33.0899 > 0 are satisfied, which is used to prove the correct of Theorem 1.

2.4 Modelling of LTF memristive neural network with chemical synapses

To better emulate the collective dynamical behaviors of neural systems, we construct a neural network consisting of the LTF memristive HR neurons and chemical synapses. A synaptic coupled model with fast threshold modulation is adopted to characterize the chemical synapse. Thus, corresponding dynamical equations of the LTF memristive neural network as shown in the schematic of Fig. 1b are rewritten as

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{i} = y_{i} - ax_{i}^{3} + bx_{i}^{2} + k_{0} \tanh (\varphi_{i} )x_{i} + g_{c} (E - x_{i} )\Gamma ,} \hfill \\ {\dot{y}_{i} = c - dx_{i}^{2} - y_{i} ,} \hfill \\ {\dot{\varphi }_{i} = (1 - k_{1} \varphi_{i} )x_{i} - k_{2} \varphi_{i} ,} \hfill \\ {\Gamma = \sum\limits_{j = 1}^{n} {k_{ij} \frac{1}{{1 + e^{{ - (x_{j} - \theta )}} }},} } \hfill \\ \end{array} } \right. $$

(14)

here, the LTF memristive neurons are identical. The gain g_c is the coupling strength between the ith neuron and neighbor other neurons j. k_ij is the n × n connectivity matrix. The n is the total number of neurons as n = 20. The sigmoidal function in Eq. (14) is used to describe the chemical synaptic model with a fast threshold θ. For the reversal potential E > x, the synapse is excitatory such as E = 2; while E < x, the synapse is inhibitory such as E =  − 1.

2.5 Method

The bifurcation is used to assess the dynamical behaviors and transition mechanisms of different firing patterns in the LTF memristive neuron model. The numerical integrations to the equations are carried out by using a Brain Dynamics Toolbox in Matlab software [57]. The memristive parameters k₀, k₁, and k₂ can be tamed within a certain range. For convenient numerical simulation, other parameters are fixed at a = 1, b = 3, c = 1, d = 5, based on the consideration in Refs. [32, 33, 58].

3 Results

3.1 Dynamics of the LTF memristor

When the LTF memristor is subjected to a sinusoidal periodic voltage (AC) source as V = Asin(2πft) with changing frequency f while the fixed amplitude A = 1, the voltage-current curves (labeled as AC V-I_M characteristics) are shown in Fig. 2a. It is found that the LTF memristor is able to exhibit a pinched hysteresis loop on the voltage-current plane. The pinched hysteresis loop trends to a linear behavior when the frequency is increased, while to a nonlinear behavior when the frequency is decreased. That is, the memristor becomes a usual (typically linear) resistor at very high frequencies; while a nonlinear resistor at very low frequencies. In addition, when the amplitude is changing and the frequency is fixed at f = 0.02, the voltage-current characteristics are shown in Fig. 2b. It is observed that the pinched hysteresis loop is shrunk in size as the amplitude decreases.

Fig. 2

AC V-I_M characteristics of the LTF memristor. a The pinched hysteresis loops at f = 0.002 (green), 0.02 (red), 0.2 (cyan), and 2 (blue), respectively, while fixed amplitude A = 1; b The pinched hysteresis loops at A = 0.1 (green), 1 (red), and 2 (blue), respectively, while fixed frequency f = 0.02. Other parameters are set as k₀ = 1, k₁ = 1, and k₂ = 0.2, respectively

Figure 3 shows distinct differences between the Threshold Flux-controlled (LF) as k₁ = k₂ = 0 and the Locally-active Threshold Flux-controlled (LTF) memristor in the AC and DC voltage-current planes. When the two memristors are driven by a sinusoidal periodic voltage source V = sin(0.04πt), the pinched hysteresis loop is symmetric for the LF memristor as shown in the blue curve of Fig. 3a, while asymmetric for the LTF memristor as shown in the red curve of Fig. 3a. DC voltage-current plot is used to measure the local activity of a memristor. Thus, when the voltage source is selected as direct current, combined Eqs. (3) and (6), the relationship between voltage and current is rewritten as

$$ \left\{ {\begin{array}{*{20}l} {I_{M} = k_{0} \tanh (\varphi_{c} )V,} \hfill \\ {\varphi_{c} = \frac{V}{{k_{1} V + k_{2} }}.} \hfill \\ \end{array} } \right. $$

(15)

Fig. 3

Difference of the TF and LTF memristor. a AC V-I_M characteristics of the TF (blue k₁ = k₂ = 0) and LTF (red) memristor at f = 0.02, A = 1. b DC V-I_M characteristics of the LTF (red) memristor. Other parameters are set as k₀ = 1, k₁ = 1, and k₂ = 0.2, respectively

If the V in the above equation is a set of constants, a DC voltage-current plane is formed in Fig. 3b. It is found that the V-I_M plane is a point at k₁ = k₂ = 0. However, when k₁ = 1 and k₂ = 0.2, there exists jumping behavior from Q1 to Q2. Then, the slope or differential conductance between Q2 and Q3 is negative as shown in the yellow branches of Fig. 3b. Thus, the modified (LTF) memristor model is a locally-active memristor. Importantly, a kind of circuit with the locally-active memristor may give rise to complex oscillations such as chaotic modes.

3.2 Dynamics of the LTF memristive neuron

To unfold the mechanism of behavioral generation of LTF memristive neurons, complex electrical activities are obtained in the systems by modulating two parameters k₁ and k₂. Based on the parameter modulation in the LTF memristor, it is found that the complex transitions of the model are different by changing k₁ while k₂ is fixed, and vice versa. Thus, we choose two cases: firstly changing k₁ while k₂ = 0.2; secondly changing k₂ while k₁ = 1.

Figure 4 provides the two resulting DC V-I_M curves of the LTF memristor when the above condition is applied, respectively. It is found that the length (L) of the appearance of the negative differential conductance is curtate when k₁ is increased and k₂ = 0.2. While the L becomes long when k₂ is increased and k₁ = 1. For the sake of contrastive analysis, the increasing tendency of parameter k₁ or k₂ is in agreement with that of L1 to L3. Further, dynamical behaviors of the LTF memristive neuron are obtained by modulating parameters k₁ and k₂, as shown in Fig. 5.

Fig. 4

Current–voltage curves of the LTF memristor under DC situation. a Case I: changing k₁ is selected as 0.8 (solid-cyan), 1 (solid-red), 2 (dashed-cyan) while k₂ = 0.2; b Case II: changing k₂ is selected as 0.4 (solid-cyan), 0.2 (solid-red), 0.1 (dashed-cyan) while k₁ = 1. The length of negative differential conductance is marked as L ≈ distance between Q2 and Q3 in Fig. 3b. Other parameters are set as k₀ = 1 and b = 3

Fig. 5

Phase orbits of the LTF memristive neuron. a k₁ = 0, k₂ = 0; b k₁ = 1, k₂ = 0.2; c k₁ = 2, k₂ = 0.2; d k₁ = 0.2, k₂ = 0.2; e k₁ = 1, k₂ = 0.4; f k₁ = 1, k₂ = 0.1. Other parameters are set as k₀ = 1 and b = 3

In Fig. 5a, b, we present different phase orbits of the TF (k₁ = 0, k₂ = 0) and LTF (k₁ = 1, k₂ = 0.2) memristive neuron. The former is curly blue chaotic attractors while the latter is incompact red chaotic attractors. Using the phasing orbit in Fig. 5b as a reference, the red chaotic attractor is chaotic and extended along the negative φ-axis shown in Fig. 5c when the parameter k₁ is enlarged to 2. Nevertheless, the red chaotic attractor becomes a cyan periodical attractor shown in Fig. 5d when the parameter k₁ is diminished to 0.2. At fixed k₁ = 1, by increasing k₂ from 0.2 to 0.4, the red chaotic attractor becomes a green periodical attractor in Fig. 5e. However, by decreasing k₂ from 0.2 to 0.1, the red chaotic attractor is chaotic and extended along the negative φ-axis shown in Fig. 5f. Based on comparisons of Case I shown in Figs. 4a and 5(b–d) and Case II shown in Fig. 4b and Fig. 5b, e, f, it is found that the chaotic feature of the modified neuronal model is associated with the length of negative differential conductance of memristor. That is, the two parameters can control transitions between different dynamical behaviors of the LTF memristive neuron.

In Fig. 6a, b, we compare the bifurcation diagrams (obtained by statistical peak values of negative magnetic flux) with increasing k₁ and k₂. When the parameter k₁ is enhanced, a transition route from simple periodical oscillations into complex chaotic firings is triggered in the LTF memristive neuron. When the parameter k₂ is enhanced, a transition route from complex chaotic firings into simple periodical oscillations occurs. Therefore, increasing k₁ is able to boost the generation of chaotic firings while increasing k₂ can inhibit the occurrence of chaotic oscillations. The largest Lyapunov Exponential curve as shown in the red curve of Fig. 6c, d can also confirm the modulating scheme with increasing k₁ and k₂. Recalling Fig. 4, increasing k₁ for curtate L can enhance firing patterns while increasing k₂ for growing L can inhibit firing patterns of the LTF memristive neuron.

Fig. 6

Bifurcation (upper half panel) and Lyapunov Exponential (lower half panel) diagram of the LTF memristive neuron. a and c Case I: increasing k₁ while k₂ = 0.2; b and d Case II: increasing k₂ while k₁ = 1. Other parameters are set as k₀ = 1 and b = 3. Inserting diagram is a local enlargement of the bifurcation diagram

Figure 7 provides a potential relation diagram between the firing patterns and the changing two parameters (k₁ and k₂), based on the Largest Lyapunov Exponential (LLE) and average frequency (f) diagram. The LLE is greater than zero, indicating that the LTF memristive neuron can produce chaotic behaviors. Thus, the faint yellow district similar to the laminar flow aero-foil profile in Fig. 7a and the starry red district in Fig. 7b are chaotic states.

Fig. 7

Two-parameter panels with changing k₁ and k₂. a Largest Lyapunov Exponential diagram b Average frequency diagram. Other parameters are set as k₀ = 1 and b = 3

Next, we explore a new two-parameter problem using the internal parameter b of the 2D HR model and the gain k₀ of the LTF memristor as two controllable parameters. The goal is to generate different firing patterns in an adaptive way. To achieve this, the bifurcation diagram and Lyapunov Exponential diagram are calculated by increasing the gain k₀ at b = 3 and 2, respectively.

Figure 8a, b illustrate that the LTF memristive neuron has various firing patterns by modulating the gain k₀. It is found that the transition from period-1 to period-2 to period-doubling to chaotic firings can appear. By comparison of Fig. 8a, b, different parameter b leads to different transition routes. Without control at k₀ = 0, the neuron is spiking or resting state. When being controlled as k₀ ≠ 0, the LTF memristive neuron reliably switches to a variety of periodical oscillations involving bursting and chaos. As shown in Fig. 8c, d, when the red largest Lyapunov Exponential is greater than zero, the system pertains to chaotic behaviors. While the red largest Lyapunov Exponential value is close to zero, suggesting that the LTF memristive neuron has multiple periodical oscillation behaviors. By observing time sequences and phase trajectories of the model, Fig. 9 exemplifies three cases involving the periodical, bursting-liking and chaotic firing modes.

Fig. 8

Bifurcation (upper half panel) and Lyapunov Exponential (lower half panel) diagram of the LTF memristive neuron. a and c Case I: increasing k₀ at b = 2.5; b and d Case II: increasing k₀ at b = 2. Other parameters are set as k₁ = 1 and k₂ = 0.2

Fig. 9

Time series (upper half panel) and Phase orbits (lower half panel) of the LTF memristive neuron. a and d k₀ = 1.5, k₁ = 0.1; b and e k₀ = 1, k₁ = 0.1; c and f k₀ = 1, k₁ = 0.2. Other parameters are selected as k₂ = 0.1, and b = 3

Figure 10 portrays a relevancy diagram between the firing patterns and the changing two parameters (k₀ and b), based on the Largest Lyapunov Exponents (LLE) and average frequency (f) diagram. When the LLE is greater than zero, the chaotic behaviors are triggered in the LTF memristive neuron. Thus, the butterfly-wing-like district in Fig. 10a, b involves chaotic firing states.

Fig. 10

Two-parameter panels with changing k₀ and b. a Largest Lyapunov Exponential diagram b Average frequency diagram. Other parameters are set as k₁ = 1 and k₂ = 0.2

3.3 Synchronization of the LTF memristive neuronal network with chemical synapses

Synchronized neural electrical activities have been considered particularly relevant for neuronal signal transmission and coding. Neural systems with various firing patterns can present different forms of synchrony. In this subsection, we concentrate on neural networks of the LTF memristive neurons exhibiting neuron-like bursting patterns. Under the excitatory or inhibitory chemical synaptic effect, the collective dynamical behaviors are explored when the coupling function is activated. The LTF memristive neurons are identical and their initial values are selected as random.

Figure 11 shows a sequence of spatiotemporal and time series diagrams of the neural network (n = 20) with chain-coupling matrix when the excitatory chemical synapses are activated from g_c = 0, to g_c = 0.2, and to g_c = 1.0. The spatiotemporal diagrams exhibit a transition from disorderly and unsystematic states into orderly and vertical stripy states, suggesting that the neural network becomes periodically synchronized when the excitatory chemical synapses are introduced. Moreover, the desynchronized neural network exhibiting neuron-like bursting with random initial values is triggered as complete synchronization states with period-2 bursting and period-1 spiking patterns. Further, a statistical indicator is employed to evaluate the synchronized degree of neural networks. The statistical indicator is calculated by S = std(X(1:n) − X(1)), here X is a vector of x, y, and φ; while the std denotes the standard deviation index based on the Matlab platform. Then, the S is averaged and it is marked as < S > .

Fig. 11

Spatiotemporal diagrams (upper half plane) and Time sequences of membrane potentials (lower half plane) in a chain-coupled LTF memristive neural network when the chemical synapses are excitatory as E = 2. a and d g_c = 0, b and e g_c = 0.2, c and f g_c = 1.0, respectively. Other parameters are set as θ =  − 0.25, k₀ = 1, k₁ = 1 and k₂ = 0.2

Figure 12 provides a synchronized degree of the neural network by modulating the coupling strength g_c. The standard deviation < S > is the average amount of variability of spatiotemporal electrical activities in the neural network. It is found that on average, how far each neuron at time and space lies from the mean firing level. A high standard deviation such as g_c = 0 implies that the neural network is synchronized, while a low standard deviation that is close to zero when g_c ≥ 0.2 indicates that the neural network achieves complete synchronization with periodical firing under the excitatory effect, as shown in Fig. 12b. Therefore, the synchronization behaviors are identified by the scheme. When the key parameter k₁ to control the locally active effect of the LTF memristive model is increased, the threshold of synchronization is different.

Fig. 12

Standard deviation < S > with increasing the coupling strength g_c for the chain LTF memristive neural network when the chemical synapses are excitatory as E = 2. a k₁ = 0.3; b k₁ = 1; k₁ = 3. Other parameters are set as follows: θ =  − 0.25, k₀ = 1, and k₂ = 0.2

Figure 13 presents a sequence of spatiotemporal and time series diagrams of the neural network (n = 20) with a random-coupling matrix when the excitatory chemical synapses are activated from g_c = 0, to g_c = 0.1, to g_c = 0.5, and to g_c = 1.0. The spatiotemporal diagrams exhibit a transition from disorderly states into larger partly orderly states, cluster states, and complete orderly states, suggesting that the neural network becomes synchronized when the excitatory chemical synapses are introduced. It is worth pointing out that in Fig. 13b, c, the partial cluster phase synchronization is triggered. Meanwhile, the spindle-shaped wave is found in Fig. 13g. Further, the standard deviation < S > has a short increasing phase, rapidly lowers to 0.2, and enlarges to an extreme value, and then decreases when g_c > 0.2, lastly becomes zero when the coupling strength g_c > 0.8, 0.72, and 0.65, as shown in Fig. 14a–c. Therefore, the neural network can reach resting multiple states under excitatory effect. When the key parameter k₁ for the LTF memristive model is increased, the threshold of synchronization becomes lower.

Fig. 13

Spatiotemporal diagrams (upper half plane) and Time sequences of membrane potentials (lower half plane) in the random-coupled LTF memristive neural network when the chemical synapses are excitatory as E = 2. a and e g_c = 0, b and f g_c = 0.1, c and g g_c = 0.5, d and h g_c = 1.0, respectively. Other parameters are set as θ =  − 0.25, k₀ = 1, k₁ = 1 and k₂ = 0.2

Fig. 14

Standard deviation < S > with increasing the coupling strength g_c for the LTF memristive neural network when the chemical synapses are excitatory as E = 2. a k₁ = 0.3; b k₁ = 1; b k₁ = 3. Other parameters are set as θ =  − 0.25, k₀ = 1, and k₂ = 0.2

In Fig. 15, a sequence of spatiotemporal and time series diagrams of the neural network (n = 20) with the chain-coupling matrix is depicted when the inhibitory chemical synapses are activated from g_c = 0, to g_c = 0.5, and to g_c = 1.0, respectively. The spatiotemporal behaviors change from partly bursting into chaotic mode and finally tend to a resting mode, suggesting that the neural network becomes a resting synchronization when the inhibitory chemical synapse effect is increased. Moreover, the first and last neurons in the neural network exhibit the same resting states as shown in Fig. 15f. In Fig. 16a–c, the standard deviation < S > is reduced to zero when the coupling strength g_c > 0.72, 0.7, and 0.63, suggesting that the chain-coupled neural network becomes a quiescent state under the inhibitory effect. When the key parameter k₁ of the LTF memristive model is increased, the threshold of synchronization becomes smaller.

Fig. 15

Spatiotemporal diagrams (upper half plane) and Time sequences of membrane potentials (lower half plane) in the chain-coupled LTF memristive neural network when the chemical synapses are inhibitory as E =  − 1. a and d g_c = 0, b and e g_c = 0.5, c and f g_c = 1.0, respectively. Other parameters are set as θ =  − 0.25, k₀ = 1, k₁ = 1 and k₂ = 0.2

Fig. 16

Standard deviation < S > with increasing the coupling strength g_c for the chain-coupled LTF memristive neural network when the chemical synapses are inhibitory as E =  − 1. a k₁ = 0.3; b k₁ = 1; c k₁ = 3. Other parameters are set as θ =  − 0.25, k₀ = 1, and k₂ = 0.2

Figure 17 illustrates collective behaviors of the neural network (n = 20) with a random-coupling matrix when the inhibitory chemical synapses are activated from g_c = 0, to g_c = 0.1, and to g_c = 0.5, via a sequence of spatiotemporal and time series diagrams. The spatiotemporal diagrams exhibit a transition from disorderly states into partly orderly cluster states and horizontal stripy states, suggesting that the neural network becomes multi-resting synchronization when the inhibitory chemical synapses are introduced. Moreover, the first and last neurons in the neural network have different resting states as shown in Fig. 17f. In Fig. 18a–c, the average standard deviation is decreased and lowered to zero when the coupling strength g_c > 0.38, 0.36, and 0.35. Thus, the random-coupled neural network becomes multiple quiescent states under the inhibitory effect. When the key parameter k₁ for the LTF memristive model is increased, the threshold of synchronization is decreased.

Fig. 17

Spatiotemporal diagrams (upper half plane) and Time sequences of membrane potentials (lower half plane) in the random-coupled LTF memristive neural network when the chemical synapses are inhibitory as E =  − 1. a and d g_c = 0, b and e g_c = 0.1, c and f g_c = 0.5, respectively. Other parameters are set as θ =  − 0.25, k₀ = 1, k₁ = 1 and k₂ = 0.2

Fig. 18

Standard deviation < S > with increasing the coupling strength g_c for the random-coupled LTF memristive neural network when the chemical synapses are inhibitory as E =  − 1. a k₁ = 0.1; b k₁ = 0.5; c k₁ = 1. Other parameters are set as θ =  − 0.25, k₀ = 1, and k₂ = 0.2

3.4 Circuit implementation and simulation of the LTF memristive neuron

In this subsection, the LTF memristive neuron model is physically implemented by an analog electronic circuit via employing commercially available components such as resistors, capacitors, operational amplifiers, and analog multipliers. Based on the circuit theory, the implementation circuit of the memristive neuron model is designed in Fig. 19.

Fig. 19

Electronic circuit of the LTF memristive neuron model

The electronic circuit is simulated by the electronic simulation software Multisim. It is possible to reproduce the same dynamical behaviors from the LTF memristive neuron model in Eq. (4). In order to demonstrate this assertion, we provide two cases. First, R24 is selected as 100 kΩ, corresponding to k₁ = 0.1 in the model. Figure 20a, c illustrate the time sequences and phase orbits of bursting firing, consistent with the Fig. 9b, e. Second, R24 is set as 50 kΩ, corresponding to k₁ = 0.2 in the model. For numerical results Fig. 9c, f, the time sequence and phase trajectories of chaotic firing are experimentally captured and shown in Fig. 20b, d.

Fig. 20

Captured bursting-like and chaotic firing under R24 = 100kΩ and 50kΩ, respectively. a and b Time sequences of membrane potential. c and d Phase orbits relative to time sequences

In summary, the numerical and experimental results can exhibit complex dynamical behaviors in the LTF memristive neuron model. And synchronous and collective behaviors can occur in the LTF memristive neural network regardless of excitatory or inhibitory chemical synapses. These collective behaviors have the interesting feature that the different coupling effects can cause major changes in their dynamics. For the excitatory chemical synapses, the transition from neuron-like bursting into periodical firing is triggered in the chain-coupled neural network. For the inhibitory chemical synapses, the electrical activities of the neural network are depressed as resting states. Thus, using the neuron-inspired models, we are able to make distinct predictions about the behaviors of complex biological and artificial neural systems.

4 Conclusions

We report the synchronizations and complex dynamical behaviors of the LTF memristive neural network through chemical synapses. The LTF memristive neuron can exhibit various electrical activities including neuron-like bursting and chaotic firing. The transition between periodical and chaotic firing is dependent upon the negative different conductance. That is, the short occurrence of negative different conductance will be more liable to generate complex firing patterns. In summary, controlling parameters of the LTF memristor is able to obtain different firing patterns in the memristive neuronal model. Meanwhile, the rich dynamical behaviors are identified by calculating the largest Lyapunov Exponential spectrum and two-parameter panel. Further, we focus on the investigation of coupled LTF memristive neurons exhibiting neuron-like bursting. The chemical synapse can be adjusted for complete synchronization with different firing patterns. While oscillation behaviors disappear under the inhibitory chemical synapse in the memristive neural network. The synchronization behaviors and the transitions among them are explored in the LTF memristive neural network with excitatory and inhibitory chemical synapses using the numerically computed approaches.

Appendix

In this section, we calculate in detail the real roots of Eq. (9). Assuming that $x^{*} \ne - \frac{{k_{2} }}{{k_{1} }}$, based on Taylor's expansion, we can get that.

$\tanh \left( {\frac{{x^{*} }}{{k_{1} x^{*} + k_{2} }}} \right) \approx \frac{{x^{*} }}{{k_{1} x^{*} + k_{2} }}$.

Therefore, Eq. (9) can be rewritten as

$$ ak_{1} x^{*4} - ((b - d)k_{1} - ak_{2} )x^{*3} - ((b - d)k_{2} + k_{0} )x^{*2} - ck_{1} x^{*} - ck_{2} = 0. $$

(16)

Let $\begin{aligned} D = & 3((b - d)k_{1} - ak_{2} )^{2} + 8ak_{1} ((b - d)k_{2} + k_{0} ), \\ E = & ((b - d)k_{1} - ak_{2} )^{3} + 4ak_{1} ((b - d)k_{1} - ak_{2} )((b - d)k_{2} + k_{0} ) + 8a^{2} ck_{1}^{3} , \\ F = & 3((b - d)k_{1} - ak_{2} )^{4} + 16a^{2} k_{1}^{2} ((b - d)k_{2} + k_{0} )^{2} + 16ak_{1} ((b - d)k_{1} - ak_{2} )^{2} ((b - d)k_{2} + k_{0} ) \\ & + 16a^{2} ck_{1}^{3} ((b - d)k_{1} - ak_{2} ) + 64a^{3} ck_{1}^{3} k_{2} , \\ A = & D^{2} - 3F,\;B = DF - 9E^{2} ,\;C = F^{2} - 3DE,\;\Delta = B^{2} - 4AC. \\ \end{aligned}$ Then we have seven conditions as following.

(i) When D = E = F, Eq. (16) exhibits a fourfold real root

$$ x_{1}^{*} = x_{2}^{*} = x_{3}^{*} = x_{4}^{*} = \frac{{(b - d)k_{1} - ak_{2} }}{{4ak_{1} }} $$

In this condition, we have.

$$ E^{*} = \left( {\frac{{(b - d)k_{1} - ak_{2} }}{{4ak_{1} }},\;\frac{{16a^{2} ck_{1}^{2} - d((b - d)k_{1} - ak_{2} )^{2} }}{{16a^{2} k_{1}^{2} }},\;\frac{{(b - d)k_{1} - ak_{2} }}{{k_{1} ((b - d)k_{1} + 3ak_{2} )}}} \right). $$

(ii) When $DEF \ne 0,\;A = B = C = 0$, Eq. Equation (16) will have a triple root as well as another real root

$$ x_{1}^{*} = \frac{{((b - d)k_{1} - ak_{2} )D + 9E}}{{4ak_{1} D}},\;x_{2}^{*} = x_{3}^{*} = x_{4}^{*} = \frac{{((b - d)k_{1} - ak_{2} )D - 3E}}{{4ak_{1} D}}. $$

At this moment, it is obvious that.

$E_{1}^{*} = \left( {x_{1}^{*} ,\;c - dx_{1}^{*2} ,\;\frac{{x_{1}^{*} }}{{k_{1} x_{1}^{*} + k_{2} }}} \right),\;E_{2}^{*} = \left( {x_{2}^{*} ,\;c - dx_{2}^{*2} ,\;\frac{{x_{2}^{*} }}{{k_{1} x_{2}^{*} + k_{2} }}} \right)$.

(iii) When D = F = 0, D > 0, Eq. (16) has two double roots

$$ x_{1}^{*} = x_{2}^{*} = \frac{{(b - d)k_{1} - ak_{2} + \sqrt \Delta }}{{4ak_{1} }},\;x_{3}^{*} = x_{4}^{*} = \frac{{(b - d)k_{1} - ak_{2} - \sqrt \Delta }}{{4ak_{1} }}. $$

In this context, it can be gotten that.

$E_{1}^{*} = \left( {x_{1}^{*} ,\;c - dx_{1}^{*2} ,\;\frac{{x_{1}^{*} }}{{k_{1} x_{1}^{*} + k_{2} }}} \right),\;E_{2}^{*} = \left( {x_{3}^{*} ,\;c - dx_{3}^{*2} ,\;\frac{{x_{3}^{*} }}{{k_{1} x_{3}^{*} + k_{2} }}} \right)$.

(iv) When $ABC \ne 0,\;\Delta = 0,\;AB > 0$, Eq. (16) will have a double root and another two real roots

$$ x_{1,2}^{*} = \frac{{(b - d)k_{1} - ak_{2} + \frac{2AE}{B} \pm \sqrt{\frac{2B}{A}} }}{{4ak_{1} }},\;x_{3}^{*} = x_{4}^{*} = \frac{{(b - d)k_{1} - ak_{2} - \frac{2AE}{B}}}{{4ak_{1} }}. $$

Therefore, we can get

$$ \begin{aligned} E_{1}^{*} = & \left( {x_{1}^{*} ,\;c - dx_{1}^{*2} ,\;\frac{{x_{1}^{*} }}{{k_{1} x_{1}^{*} + k_{2} }}} \right),\; \\ E_{2}^{*} = & \left( {x_{2}^{*} ,\;c - dx_{2}^{*2} ,\;\frac{{x_{2}^{*} }}{{k_{1} x_{2}^{*} + k_{2} }}} \right),\; \\ E_{3}^{*} = & \left( {x_{3}^{*} ,\;c - dx_{3}^{*2} ,\;\frac{{x_{3}^{*} }}{{k_{1} x_{3}^{*} + k_{2} }}} \right). \\ \end{aligned} $$

(v) When $ABC \ne 0,\;\Delta = 0,\;AB < 0$, Eq. (16) will have a double real root

$$ x_{1}^{*} = x_{2}^{*} = \frac{{(b - d)k_{1} - ak_{2} - \frac{2AE}{B}}}{{4ak_{1} }}. $$

Meanwhile, it is obtained that

$$ E^{*} = \left( {\frac{{(b - d)k_{1} - ak_{2} - \frac{2AE}{B}}}{{4ak_{1} }},\;\frac{{16a^{2} ck_{1}^{2} - d\left( {(b - d)k_{1} - ak_{2} - \frac{2AE}{B}} \right)}}{{16a^{2} k_{1}^{2} }},\;\frac{{(b - d)k_{1} - ak_{2} - \frac{2AE}{B}}}{{k_{1} \left( {(b - d)k_{1} + 3ak_{2} - \frac{2AE}{B}} \right)}}} \right) $$

(vi) When $\Delta > 0$, Eq. (16) has two real roots. Assuming that

$$ z_{1,2} = AD + 3\left( {\frac{ - B \pm \sqrt \Delta }{2}} \right),\;z = D^{2} - D(\sqrt[3]{{z_{1} }} + \sqrt[3]{{z_{2} }}) + (\sqrt[3]{{z_{1} }} + \sqrt[3]{{z_{2} }})^{2} - 3A, $$

then it is obtained

$$ x_{1,2} = \frac{{(b - d)k_{1} - ak_{2} + {\text{sgn}} (E)\sqrt {\frac{{D + \sqrt[3]{{z_{1} }} + \sqrt[3]{{z_{2} }}}}{3}} \pm \sqrt {\frac{{2D(\sqrt[3]{{z_{1} }} + \sqrt[3]{{z_{2} }}) + 2\sqrt z }}{3}} }}{{4ak_{1} }}. $$

In this condition, we have

$$ E_{1}^{*} = \left( {x_{1}^{*} ,\;c - dx_{1}^{*2} ,\;\frac{{x_{1}^{*} }}{{k_{1} x_{1}^{*} + k_{2} }}} \right),\;E_{2}^{*} = \left( {x_{2}^{*} ,\;c - dx_{2}^{*2} ,\;\frac{{x_{2}^{*} }}{{k_{1} x_{2}^{*} + k_{2} }}} \right) $$

(vii) When $\Delta < 0,\;D > 0,\;F > 0$, Eq. (16) has four real roots.

Assuming that

$$ \theta = \arccos \frac{3B - 2AD}{{2A\sqrt A }},\;\omega_{1} = \frac{{D - 2\sqrt A \cos \frac{\theta }{3}}}{3},\;\omega_{2,3} = \frac{{D - 2\sqrt A \cos \left( {\frac{\theta }{3} \pm \frac{2\pi }{3}} \right)}}{3}, $$

If E = 0, then we obtain

$$ x_{1,2} = \frac{{(b - d)k_{1} - ak_{2} \pm \sqrt {D + 2\sqrt F } }}{{4ak_{1} }},\;x_{3,4} = \frac{{(b - d)k_{1} - ak_{2} \pm \sqrt {D - 2\sqrt F } }}{{4ak_{1} }}. $$

Thus we can get

$$ \begin{aligned} E_{1}^{*} = & \left( {x_{1}^{*} ,\;c - dx_{1}^{*2} ,\;\frac{{x_{1}^{*} }}{{k_{1} x_{1}^{*} + k_{2} }}} \right),\;E_{2}^{*} = \left( {x_{2}^{*} ,\;c - dx_{2}^{*2} ,\;\frac{{x_{2}^{*} }}{{k_{1} x_{2}^{*} + k_{2} }}} \right),\; \\ E_{3}^{*} = & \left( {x_{3}^{*} ,\;c - dx_{3}^{*2} ,\;\frac{{x_{3}^{*} }}{{k_{1} x_{3}^{*} + k_{2} }}} \right),\;E_{4}^{*} = \left( {x_{4}^{*} ,\;c - dx_{4}^{*2} ,\;\frac{{x_{4}^{*} }}{{k_{1} x_{4}^{*} + k_{2} }}} \right). \\ \end{aligned} $$

If E ≠ 0, then we obtain

$$ \begin{gathered} x_{1,2} = \frac{{(b - d)k_{1} - ak_{2} + {\text{sgn}} (E)\sqrt {\omega_{1} } \pm (\sqrt {\omega_{2} } + \sqrt {\omega_{3} } )}}{{4ak_{1} }},\; \hfill \\ x_{3,4} = \frac{{(b - d)k_{1} - ak_{2} + {\text{sgn}} (E)\sqrt {\omega_{1} } \pm (\sqrt {\omega_{2} } - \sqrt {\omega_{3} } )}}{{4ak_{1} }}. \hfill \\ \end{gathered} $$