Analytical Drain Current Modeling and Simulation of Triple Material Gate-All-Around Heterojunction TFETs Considering Depletion Regions

Abstract

This paper deals with electrostatic behavior of triple-material gate-all-around hetero-junction tunneling field-effect transistors (TMGAA-HJTFET) device. The model is advantageous in apprehending a comparative study with the single-material gate-all-around hetero-junction tunneling field-effect transistors (SMGAA-HJTFET) in terms of surface potential, electric field, drain current, transconductance, and threshold voltage. The surface-potential distribution in partition regions along the channel is solved by using two-dimensional Poisson’s equation. By using the drift and diffusion current, drain current is derived, and I_On/I_Off ratio of 10¹¹ is gained from analytical modeling and TCAD simulation. Transconductance and threshold voltage are derived from the tunneling current. The proposed model results are validated by the ATLAS TCAD simulation tool.

1 INTRODUCTION

Tunnel field-effect transistors (TFETs) have drawn attention of semiconductor academic researchers and industry for their loftier performance in subthreshold region. TFET devices operate based on band-to-band tunneling principle, which significantly improves the switching of On and Off states at lower voltages. Compared with the metal oxide–semiconductor field-effect transistor (MOSFETs), TFETs has low subthreshold swing (i.e., below 60 mV/dec), high I_On/I_Off ratio, low Off-state current, low leakage power consumption, and better immunity of short-channel effects [1–3]. The On-current performance of the TFET device is low due to small tunneling efficiency of electrons in larger band gap than the conventional MOSFET devices [4]. Thus, to improve On-current performance many device models are proposed and analytically explored. Based on source, depletion charge and mobile charges are analyzed for the device double-gate TFET (DG-TFET) [5, 6]. Gate engineering with materials having different work function contributed significant control over short-channel effects, some studies dealt with dual material and triple material [7–10] in recent years.

Gate-all-around nanowire TFETs lead to steeper subthreshold slope due to high-level control of gate as field lines get originated from the drain that can’t penetrate into the channel, and get terminated at the gate [11, 12]. Nanowire TFETs with efficient gate along with channel engineering of different work function materials are proposed to improve the On-current performance; steep subthreshold slope, reduced DIBL, and threshold voltage roll-off [13–15]. Hetero-junction TFETs lead to increased On-drain current performance due to shorter tunneling width at source-to-channel junction [16]. The electrostatic parameters such as channel potential, electric field, drain current using band-to-band tunneling generation rate, and shortest channel length, transconductance, and threshold voltage of SiO₂|high-k stacked DG-TFET by considering the depletion regions. High-k is stacked over SiO₂ assumed as the dielectric to avoid the lattice mismatching between silicon and high-k dielectric below the gate electrode [17].

Furthermore, it has been analyzed that I_On current performance can be improved using the nanowire device. Hence, in this view, the proposed device TM GAA-HJTFET has been modeled by using three different materials gate engineering as different regions along with depletion regions. This paper captures the salient features such as surface potential derived from Poisson’s equation using parabolic approximation method, electric field, drain current using Kane’s Model, transconductance, and threshold voltage.

2 DEVICE STRUCTURE

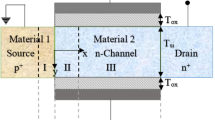
Figure 1 represents the three dimensional structural view of Triple Material GAA-HJTFET (TMGAA-HJTFET).

Fig. 1.

3D structure of triple-material GAA-HJTFET and schematic cross-sectional view of triple-material GAA-HJTFET.

Source length of 20 nm and material used is germanium with a doping concentration of N₁ = 1 × 10²⁰ cm^–3, channel length is 50 nm with a doping concentration of N₂ = 1 × 10¹⁶ cm^–3, drain length is 20 nm and material used is silicon with doping concentration of N₃ = 5 × 10¹⁸ cm^–3, which is assumed in this model. In the cross-sectional schematic view of the TMGAA-HJTFET device, regions are considered for depletion regions and the three materials used for gate which are represented as R₁, R₂, R₃, R₄, and R₅ with respective lengths of L₁, L₂, L₃, L₄, and L₅.

3 MODEL FORMULATION

For analytical modeling, the cross-sectional schematic view of TMGAA-HJTFET is considered due to its potential distribution in r-direction which is same as the DG-TFET shown in Fig. 1. z and r quantities are considered along the channel length; other parameters include oxide thickness (t_ox). Silicon thickness (2t_Si), work functions of three materials (ϕ_m1, ϕ_m2, ϕ_m3). ψ₀, ψ₁, ψ₂, ψ₃, ψ₄, and ψ₅ are the junction potentials are z = 0, z₁ = L₁, z₂ = L₁ + L₂, z₃ = L₁ + L₂ + L₃, z₄ = L₁ + L₂ + L₃ + L₄, and z₅ = L₁ + L₂ + L₃ + L₄ + L₅.

3.1 Analytical Modeling of Surface Potential

The surface potential distribution function along the channel regions R_i is considered as ψ_i(r, z), where i = 1, 2, 3, 4, 5. The two-dimensional (2D) Poisson’s equation for the gate-all-around is given as

$$\begin{gathered} \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{\psi }_{i}}(r,z)}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}{{\psi }_{i}}(r,z)}}{{\partial {{z}^{2}}}} \\ \, = - \frac{{qNi}}{{{{\varepsilon }_{{{\text{Si}}}}}}},\quad i = 1,2,3,4,5. \\ \end{gathered} $$

(1)

The doping concentrations of source (N_Src = 1 × 10²⁰ cm^–3), channel (N_Ch = 1 × 10¹⁶ cm^–3), and drain (N₂ = 5 × 10¹⁸ cm^–3) are assumed, respectively, to improve the I_On/I_Off current ratio. q is the electron charge and ε_Si is the silicon permittivity. 2D potential distribution ψ_i(r, z) in region R_i can be approximated using parabolic approximation method given as

$$\begin{gathered} {{\psi }_{i}}(r,z) = {{a}_{{0i}}}(z) + {{a}_{{1i}}}(z)r + {{a}_{{2i}}}(z){{r}^{2}}, \\ {\text{where}}\quad i = 1,2,3,4,5. \\ \end{gathered} $$

(2)

a_0i(z), a_1i(z) and a_3i(z) are arbitrary functions of z, defined by the boundary conditions [18]:

$$1.\,\,{{\psi }_{i}}(r,z){{{\text{|}}}_{{r = R}}} = {{\psi }_{s}}(z),$$

(3)

$$2.\,\,{{\left. {\frac{{\partial {{\psi }_{i}}(r,z)}}{{\partial r}}} \right|}_{{r = 0}}} = 0,$$

(4)

$$3.\,\,{{\left. {\frac{{\partial {{\psi }_{i}}(r,z)}}{{\partial r}}} \right|}_{{r = R}}} = \frac{{{{\varepsilon }_{{{\text{ox}}}}}}}{{{{\varepsilon }_{{{\text{Si}}}}}R}}\left[ {\frac{{{{\psi }_{G}} - {{\psi }_{s}}(z)}}{{\ln \left( {1 + \frac{{{{t}_{{{\text{ox}}}}}}}{R}} \right)}}} \right],$$

(5)

where ψ_G = V_GS – ϕ_m + χ + E_g/2 and i = 1, 2, 3, 4, 5 for five different regions, gate work function ϕ_m1 = 4.05 eV (Zr), ϕ_m2 = 4.2 eV (Al), and ϕ_m3 = 4.6 eV (Cu), electron affinities χ of 4.0 eV (Ge) and 1.12 eV (Si), energy band gaps E_g are 0.67 eV (Ge) and 1.12 eV (Si), V_GS is the gate-to-source voltage, t_ox is the oxide thickness, t_Si is the silicon thickness (R = t_Si), and ε_ox is the silicon dioxide permittivity.

Using Eq. (3) to solve Eq. (5), we obtain

$${{a}_{{0i}}} = {{\psi }_{s}}(z) - \frac{{{{\varepsilon }_{{{\text{ox}}}}}}}{{2{{\varepsilon }_{{{\text{Si}}}}}}}\left[ {\frac{{{{\psi }_{G}} - {{\psi }_{s}}(z)}}{{\ln \left( {1 + \frac{{{{t}_{{{\text{ox}}}}}}}{R}} \right)}}} \right],$$

(6)

$${{a}_{{1i}}} = 0,$$

(7)

$${{a}_{{2i}}} = \frac{{{{\varepsilon }_{{{\text{ox}}}}}}}{{2{{\varepsilon }_{{{\text{Si}}}}}{{R}^{2}}}}\left[ {\frac{{{{\psi }_{G}} - {{\psi }_{s}}(z)}}{{\ln \left( {1 + \frac{{{{t}_{{{\text{ox}}}}}}}{R}} \right)}}} \right].$$

(8)

The channel potential ψ_i(r, z) and surface potential ψ_s,i(z) are related as ψ_s,i(z) = ψ_i(±t_Si/2, z).

From Eqs. (6)–(8), we can deduce that

$${{\psi }_{i}}(r,z) = {{\psi }_{{0i}}}(z) + \left( {\frac{{{{r}^{2}}}}{{{{\lambda }^{2}}{{R}^{2}}}} - \frac{1}{{{{\lambda }^{2}}}}} \right)({{\psi }_{G}} - {{\psi }_{{0i}}}(z)),$$

(9)

$${{\psi }_{{s,i}}}(z) = {{\psi }_{{0i}}}(z) + \left( {\frac{{t_{{{\text{Si}}}}^{2}}}{{4{{\lambda }^{2}}{{R}^{2}}}} - \frac{1}{{{{\lambda }^{2}}}}} \right)({{\psi }_{G}} - {{\psi }_{{0i}}}(z)),$$

(10)

where ψ_0i(z) = ψ_i(0, z), i.e., when radius r = 0.

At r = 0, 2D Poisson’s equation (1) is written as

$$\frac{1}{r}\frac{\partial }{{\partial r}}{{\left. {\left( {r\frac{{\partial {{\psi }_{i}}(r,z)}}{{\partial r}}} \right)} \right|}_{{r = 0}}} + {{\left. {\frac{{{{\partial }^{2}}{{\psi }_{i}}(r,z)}}{{\partial {{z}^{2}}}}} \right|}_{{r = 0}}} = - {{\left. {\frac{{qNi}}{{{{\varepsilon }_{{{\text{Si}}}}}}}} \right|}_{{r = 0}}}.$$

(11)

Substituting Eq. (2) in Eq. (11), differential equation is gained in terms of center potential as

$$\frac{{{{\partial }^{2}}{{\psi }_{{0i}}}(z)}}{{{{\partial }^{2}}z}} - \eta _{i}^{2}{{\psi }_{{0i}}}(z) = - \eta _{i}^{2}{{P}_{i}},$$

(12)

where

$${{P}_{i}} = \frac{{qNi}}{{\eta _{i}^{2}{{\varepsilon }_{{{\text{Si}}}}}}} + {{\psi }_{G}},$$

and $\eta _{i}^{2} = \frac{4}{{{{\lambda }^{2}}{{R}^{2}}}}$.

The general solution of Eq. (12) is

$$\begin{gathered} {{\psi }_{{0i}}}(z) = {{A}_{i}}\exp ({{\eta }_{i}}(z - {{z}_{{i - 1}}})) \\ \, + {{B}_{i}}\exp ( - {{\eta }_{i}}(z - {{z}_{{i - 1}}})) + {{P}_{i}}, \\ \end{gathered} $$

(13)

where

$$\begin{gathered} {{A}_{i}} = \frac{1}{{2\sinh {{\eta }_{i}}{{L}_{i}}}}[{{\psi }_{{i - 1}}}(z)\exp ( - {{\eta }_{i}}{{L}_{i}}) - {{\psi }_{i}}(z) \\ \, - {{P}_{i}}(\exp ( - {{\eta }_{i}}{{L}_{i}}) + 1)], \\ \end{gathered} $$

(14)

$$\begin{gathered} {{B}_{i}} = \frac{1}{{2\sinh {{\eta }_{i}}{{L}_{i}}}}[{{\psi }_{{i - 1}}}(z)\exp ({{\eta }_{i}}{{L}_{i}}) - {{\psi }_{i}}(z) \\ \, - {{P}_{i}}(\exp ({{\eta }_{i}}{{L}_{i}}) + 1)], \\ \end{gathered} $$

(15)

L_i = z_i – z_{i – 1} is the length of region R_i (i = 1, 2, 3, 4, 5) and i = ψ_s,i(z_i) is surface potential at z = z_i as shown in Fig. 1. By applying the boundary conditions, the surface potential across the regions is obtained [18]

$${{\psi }_{0}} = {{\psi }_{1}}(r,0) = {{V}_{{{\text{bis}}}}},$$

(16)

$${{\psi }_{5}} = {{\psi }_{5}}(r,{{L}_{1}} + {{L}_{2}} + {{L}_{3}} + {{L}_{4}} + {{L}_{5}}) = {{V}_{{{\text{bis}}}}} + {{V}_{{{\text{DS}}}}},$$

(17)

where

$${{V}_{{{\text{bis}}}}} = - \frac{1}{q}[({{\chi }_{1}} - {{\chi }_{2}}) + 0.5({{E}_{{g1}}} - {{E}_{{g2}}}) + q{{V}_{T}}\ln ({{N}_{1}}{\text{/}}{{n}_{i}})]$$

is built-in potential.

ψ₀, ψ₁, ψ₂, ψ₃, and ψ₄ are intermediate surface potentials obtained by using continuity of lateral electric field property such as [18]

$${{\psi }_{{s,i}}}(z){{{\text{|}}}_{{z = {{z}_{i}}}}} = {{\psi }_{{s,i + 1}}}(z){{{\text{|}}}_{{z = {{z}_{i}}}}},$$

(18)

$${{\left. {\frac{{\partial {{\psi }_{{s,i}}}(z)}}{{\partial z}}} \right|}_{{z = {{z}_{i}}}}} = {{\left. {\frac{{\partial {{\psi }_{{s,i + 1}}}(z)}}{{\partial z}}} \right|}_{{z = {{z}_{i}}}}}.$$

(19)

Using Eqs. (18) and (19) in (10) along with (13)–(15), we obtain the intermediate potentials

$$\begin{gathered} {{\psi }_{i}} = \frac{1}{{{{y}_{i}}}}\left[ {\frac{{(x - 1)}}{{\sinh \eta iLi}}\{ {{\eta }_{i}}{{\psi }_{{i - 1}}}} \right. \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}\, + {{\eta }_{i}}{{P}_{i}}(1 + \cosh {{\eta }_{i}}{{L}_{i}}) - {{P}_{{i + 2}}}\sinh {{\eta }_{i}}{{L}_{i}}\} + x{{\psi }_{G}}} \right], \\ \end{gathered} $$

(20)

where

$$x = \left( {\frac{{t_{{{\text{Si}}}}^{2}}}{{4{{\lambda }^{2}}{{R}^{2}}}} - \frac{1}{{{{\lambda }^{2}}}}} \right),$$

$${{y}_{i}} = \left\lfloor {1 - {{\eta }_{i}}(x - 1)\coth {{\eta }_{i}}{{L}_{i}}} \right\rfloor ,\quad i = 1,2,3,4.$$

3.2 Modeling of Electric Field

The vertical and lateral electric field E_ri(r, z) and E_zi(r, z) are obtained by differentiation of potential Eqs. (2) and (13)

$${{E}_{{ri}}}(r,z) = 2r{{a}_{{2i}}}(z),$$

(21)

$$\begin{gathered} {{E}_{{zi}}}(r,z) = - \frac{{\partial {{\psi }_{i}}(r,z)}}{{\partial z}} = {{\eta }_{i}}[ - {{A}_{i}}\exp ({{\eta }_{i}}(z - {{z}_{{i - 1}}})) \\ \, + {{B}_{i}}\exp ( - {{\eta }_{i}}(z - {{z}_{{i - 1}}})]. \\ \end{gathered} $$

(22)

3.3 Lengths of Depletion Regions

The lengths of regions R₁ and R₅ denoted as L₁ and L₅ can be calculated by E_r = 0 at r = r₀ and r = r₂ before deriving potentials ψ₂ and ψ₃. Due to the complexity of the calculations, simple approximation can be done separately by considering source–channel and drain–channel regions shown below using [18] and [20]

$${{L}_{1}} = \sqrt {2{{\varepsilon }_{{{\text{Si}}}}}({{P}_{2}} - {{\psi }_{0}}){\text{/}}(q{{N}_{1}})} ,$$

(23)

$${{L}_{5}} = \sqrt {2{{\varepsilon }_{{{\text{Si}}}}}({{\psi }_{5}} - {{P}_{2}}){\text{/}}(q{{N}_{3}})} .$$

(24)

Since P₂ is dependent on V_GS, L₁ and L₅ values are smaller than the DG-TFET and also dependent on V_GS.

3.4 Modeling of Drain Current

In forward bias condition, the drain current equation can be obtained by Kane’s equation

$${{I}_{D}} = q\int\limits_{{\text{volume}}} {{{A}_{{{\text{Kane}}}}}{{E}_{Z}}(r,z)E_{{{\text{avg}}}}^{{\alpha - 1}} \cdot \exp \left( { - \frac{{{{B}_{{{\text{Kane}}}}}}}{{{{E}_{{{\text{avg}}}}}}}} \right)dV.} $$

(25)

In reverse bias condition, the drain current can be stated as the addition of drift and diffusion current for all the regions [21–23]

$${{I}_{{{\text{Drift}},i}}} = W{{\mu }_{i}}(z){{Q}_{{{\text{I}}i}}}(z)\frac{{d{{\psi }_{{s,i}}}(z)}}{{dz}},$$

(26)

$${{I}_{{{\text{Diff}}i}}} = W{{\mu }_{i}}(z){{V}_{T}}\frac{{d{{Q}_{{{\text{I}}i}}}(z)}}{{dz}},$$

(27)

where V_T, W, Q_Ii(z), and μ_i(z) are thermal voltage, width of the channel, inversion layer charge carriers, and carrier mobility, respectively, for i = 1, 2, 3, 4, 5, given by [21–23].

$${{\mu }_{i}}(z) = \frac{{{{\mu }_{0}}}}{{\sqrt {\left[ {1 + {{{\left( {\frac{{{{E}_{j}}(z)}}{{{{E}_{c}}}}} \right)}}^{2}}} \right]} }},$$

(28)

$${{Q}_{{{\text{I}}i}}}(z) = 2({{Q}_{{{\text{Si}}}}}(z) - {{Q}_{{{\text{D}}i}}}),$$

(29)

$${{E}_{j}}(z) = \frac{{{{C}_{{{\text{ox}}}}}({{\psi }_{D}} - {{\psi }_{{s,i}}}(z))}}{{{{\varepsilon }_{{{\text{Si}}}}}}},$$

(30)

$${{E}_{c}} = 6.01 \times {{10}^{2}}{{T}^{{3/2}}},$$

(31)

$${{Q}_{{si}}}(z) = {{C}_{{{\text{ox}}}}}({{\psi }_{G}} - {{\psi }_{{s,i}}}(z)),$$

(32)

$${{Q}_{{Di}}} = {{C}_{{{\text{ox}}}}}({{\phi }_{{\text{F}}}} - {{V}_{{{\text{Th}}}}} - {{V}_{{{\text{fbi}}}}}),$$

(33)

where E_c, μ₀, E_j(z), Q_si(z), and Q_Di represents critical electric field, low carrier mobility, electric field, surface charge, and depletion layer charge, respectively. Substituting Eqs. (32) and (33) in Eq. (29), the inversion charge is obtained as

$${{Q}_{{{\text{I}}i}}}(z) = 2{{C}_{{{\text{ox}}}}}\left\lfloor {{{V}_{{GS}}} - {{\psi }_{{s,i}}}(z) - {{\phi }_{{\text{F}}}} + {{V}_{{{\text{Th}}}}}} \right\rfloor .$$

(34)

Integrating Eq. (26) on both sides and substituting Eqs. (30) and (34) obtains

$$\begin{gathered} \int\limits_{L_{{i - 1}}^{*}}^{L_{i}^{*}} {{{I}_{{{\text{Drift}}}}}dz} = \int\limits_{{{\psi }_{{s,i - 1}}}}^{{{\psi }_{{s,i}}}} {W{{\mu }_{0}}} \\ \times \;\left[ {\frac{{2{{C}_{{{\text{ox}}}}}({{V}_{{GS}}} - {{\psi }_{{s,i}}}(z) - {{\phi }_{{\text{F}}}} + {{V}_{{{\text{Th}}}}})}}{{\sqrt {\left[ {1 + \left( {\frac{{{{E}_{i}}(z)}}{{{{E}_{c}}}}} \right)} \right]} }}} \right]d{{\psi }_{{s,i}}}, \\ \end{gathered} $$

(35)

where

$${{\psi }_{{s,i - 1}}}(z) = {{\psi }_{{s,i}}}(z){{{\text{|}}}_{{Z = L_{{i - 1}}^{*}}}},\quad {\text{where}}\quad i = 1,2,3,4,5,6,$$

$$\begin{gathered} L_{0}^{*} = 0,\quad L_{1}^{*} = {{L}_{1}},\quad L_{2}^{*} = {{L}_{1}} + {{L}_{2}},\quad \\ L_{3}^{*} = {{L}_{1}} + {{L}_{2}} + {{L}_{3}},\quad L_{4}^{*} = {{L}_{1}} + {{L}_{2}} + {{L}_{3}} + {{L}_{4}}, \\ {\text{and}}\quad L_{5}^{*} = {{L}_{1}} + {{L}_{2}} + {{L}_{3}} + {{L}_{4}} + {{L}_{5}}. \\ \end{gathered} $$

From Eq. (35), we obtain

$$\begin{gathered} {{I}_{{{\text{Drift}}i}}} = - \frac{{{{X}_{4}}}}{{{{L}_{i}} - {{L}_{{i - 1}}}}}\left[ {({{X}_{3}} - {{X}_{1}}){{{\ln }}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}} \right. \\ \times \;\left\{ {\frac{{\sqrt {X_{2}^{2} + {{{({{\psi }_{{s,i}}}(z) - {{X}_{3}})}}^{2}}} + ({{\psi }_{{s,i}}}(z) - {{X}_{3}})}}{{\sqrt {X_{2}^{2} + {{{({{\psi }_{{s,i - 1}}}(z) - {{X}_{3}})}}^{2}}} + ({{\psi }_{{s,i - 1}}}(z) - {{X}_{3}})}}} \right\} \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}\, + \{ \sqrt {X_{2}^{2}\, + \,{{{({{\psi }_{{s,i}}}(z)\, - \,{{X}_{3}})}}^{2}}} \, - \,\sqrt {X_{2}^{2} + {{{({{\psi }_{{s,i - 1}}}(z) - {{X}_{3}})}}^{2}}} \} } \right], \\ \end{gathered} $$

(36)

where

$${{X}_{1}} = {{V}_{{GS}}} + {{V}_{{{\text{Th}}}}} - {{\phi }_{{\text{F}}}},$$

$${{X}_{2}} = \frac{{{{\varepsilon }_{{{\text{Si}}}}} \cdot {{E}_{c}}}}{{{{C}_{{{\text{ox}}}}}}},$$

$${{X}_{3}} = {{V}_{{{\text{fbi}}}}} - {{V}_{{GS}}},$$

$${{X}_{4}} = 2{{\varepsilon }_{{{\text{Si}}}}}{{\mu }_{0}}W{{E}_{c}}.$$

Now, integrating Eq. (27) on both sides

$$\int\limits_{L_{{i - 1}}^{*}}^{L_{i}^{*}} {{{I}_{{{\text{Drift}}i}}}dz} = \int\limits_{{{Q}_{{{\text{I}}i - 1}}}}^{{{Q}_{{{\text{I}}i}}}} {\left[ {\frac{{W{{\mu }_{0}}{{V}_{T}}}}{{\sqrt {\left[ {1 + \left( {\frac{{{{E}_{i}}(z)}}{{{{E}_{c}}}}} \right)} \right]} }}d{{Q}_{{{\text{I}}i}}}} \right]} ,$$

(37)

where

$${{Q}_{{{\text{I}}i - 1}}} = {{Q}_{{{\text{I}}i}}}(z){{{\text{|}}}_{{z = L_{{i - 1}}^{*}}}},\quad {\text{where}}\quad i = 1,2,3,4,5,6,$$

$$\begin{gathered} {{I}_{{{\text{Drift}}i}}} = - \frac{{{{X}_{7}}}}{{{{L}_{i}} - {{L}_{{i - 1}}}}} \\ \times \;\left[ {\ln \left\{ {\frac{{\sqrt {X_{6}^{2} + {{{({{Q}_{{{\text{I}}i}}}(z) - {{X}_{5}})}}^{2}}} + ({{Q}_{{{\text{I}}i}}}(z) - {{X}_{5}})}}{{\sqrt {X_{6}^{2} + {{{({{Q}_{{{\text{I}}i - 1}}}(z) - {{X}_{5}})}}^{2}}} + ({{Q}_{{{\text{I}}i - 1}}}(z) - {{X}_{5}})}}} \right\}} \right], \\ \end{gathered} $$

(38)

where

$${{X}_{5}} = 2{{C}_{{{\text{ox}}}}}[{{\phi }_{{\text{F}}}} + {{V}_{{{\text{Th}}}}} - {{V}_{{{\text{fbi}}}}}],$$

$${{X}_{6}} = 2{{\varepsilon }_{{{\text{Si}}}}} \cdot {{E}_{c}},$$

$${{X}_{7}} = 2{{\varepsilon }_{{{\text{Si}}}}} \cdot {{E}_{c}}W{{V}_{T}} \cdot {{\mu }_{0}}.$$

The drain to source current can be written as [21]

$${{I}_{{DS}}} = \sum\limits_{i = 1}^5 {[{{I}_{{{\text{Drift}}i}}} + {{I}_{{{\text{Diff}}i}}}]} .$$

4 RESULT AND DISCUSSION

The results for the proposed model of surface potential, electric field, drain current, transconductance, and threshold voltage are validated by using the TCAD SILVACO tool. The procedure followed to obtain the results for the device simulation is (1) Defining mMesh points with spacing, (2) Defining regions, (3) Defining physics models, (4) Defining method of solution (Newton), (5) Defining bias voltages (gate and drain voltages), 6) Extracting and plotting the data. The following models are used in defining physics models: BOLTZMANN, FERMI, BGN, CONMOB, CVT, SRH, CONSRH, IMPACT SELB, BBT.STD, KANE, and BBT.KL.

Figure 2 shows the surface potential distribution along the channel comparision plot, the surface potential of TM GAA-HJTFET is high compared to the SM GAA-HJTFET, we observe that the tunneling width across the source–channel junction is less for TM GAA-HJTFET.

Fig. 2.

Comparision of surface potential distribution ψ_s,i along the lateral length of the channel (z) for TM GAA-HJTFET with SM GAA-HJTFET at V_DS = 1 V.

Thus, the surface potential gets increased due to increase in the tunneling rate of electrons at source–channel junction.

Figure 3 represents the surface potential distribution along the channel for different gate biases at V_DS = 1 V.

Fig. 3.

Surface potential distribution ψ_s,i along the lateral length of the channel (z) for different V_GS = 0, 0.5, and 1 V at V_DS = 1 V.

It is observed that when gate bias is applied, surface potential from the source increases linearly and becomes steeper with increase in biasing due to decrease in the tunneling width of the source channel junction. Linear increase at the source channel junction improves the electric field and band-to-band tunneling generation rate.

Figure 4 depicts the surface potential variation along the channel for drain control regime at V_GS = 1 V, it is studied that increase in drain to source voltage increased the potential at drain channel junction, there by increasing the electric field and band to band tunneling generation rate at drain channel junction.

Fig. 4.

Surface potential distribution along the channel for different V_DS = 0.2, 0.6, and 1 V at V_GS = 1 V.

Figure 5 shows the comparison plot of lateral and vertical electric field of the proposed model with SM GAA-TFET, it is observed that the electric field profile of the proposed model device is high at the source channel junction due to the increase in tunneling rate of electrons from valence band to conduction band.

Fig. 5.

Electric field profile comparision plot of TM GAA-HJTFET and SM GAA-HJTFET.

I(V) characteristic of the proposed model is shown in Fig. 6.

Fig. 6.

Comparision of the drain current I_D vs. V_GS of TMGAA-HJTFET and SMGAA-HJTFET.

It is studied that the Off current I_Off is low due to the barrier created by the forbidden gap that prevents the tunneling of electrons at Off state. On-state current is high due to enhanced electrostatic control of cylindrical gate which reduces the short channel effects and subthreshold swing.

5 CONCLUSIONS

A two-dimensional analytical model of TMGAA-HJTFET is modeled for different parameters such as surface potential, electric field, drain current, transconductance, and threshold voltage by derivative method by considering five depletion regions. The surface potential is modeled using parabolic approximation method for five regions. The electric field components are used to calculate drift and diffusion current. It is observed that the I_On/I_Off ratio is improved high compared with SMGAA-HJTFET. The proposed model of TMGAA-HJTFET predicts the device electrostatic characteristics on different parameters to gain intuition on device physics. Results obtained are found to be in good agreement with TCAD ATLAS-based simulation results of the proposed device.