A new analytical approach to threshold voltage modeling of triple material gate-all-around heterojunction tunnel field effect transistor

Abstract

This paper presents a novel threshold voltage model for triple material gate-all-around TFET based on its surface potential that also includes the device depletion regimes. Analytical expressions for surface potential are derived using 2D Poison’s equation and parabolic approximation method. Electric Field and threshold voltage of the device are derived by considering the surface potential of source channel depletion regime. Threshold voltage roll off is then obtained by subtraction between short channel TFET and long channel TFET. Drain-induced barrier lowering of the proposed device is achieved using threshold voltage values for two different drains to source voltage values. Threshold voltage lies in a range between 0.6 and 0.8 V for different doping concentrations as obtained from simulation, which is less in comparison with other available TFET devices. The validity of the device model is tested using TCAD ATLAS Simulation tool.

1 Introduction

In CMOS technology, scaling down of conventional MOSFET device exerts the short channel effects (SCE) and limits subthreshold swing to 60 mV/dec. Tunnel field effect transistor (TFET) is promising device to reduce short channel effects and subthreshold swing due to its high tunneling rate of carriers in reduced tunneling barrier of device energy band diagram. TFET device in general has low OFF-State current (I_OFF) leakage current but also has a drawback of reduced ON-state current (I_ON) performance. In order to improve the I_ON performance of the TFET device a number of new different architectures are reported [1,2,3,4]. Double Gate (DG) TFET has been reported to improve ON current performance with and without considering the influence of mobile charges in potential distribution. Different electrical parameters of the device have been derived and simulated [5, 6]. Dual Material Gate (DMG) TFET has been modeled for electrical parameters such as surface potential, electric field and drain current using shortest tunneling path [7]. Dual Material Double Gate (DM-DG) TFET has two lateral gates with dual work functions, gate closer to drain is termed as auxiliary gate and gate closer to source is termed as tunneling gate. The work function of the tunneling gate is chosen higher than auxiliary gate, such that threshold voltage nearby source is more positive than the drain [8].

Triple Material Double Gate(TM-DG) TFET has three different work functions for dual lateral gate pairing which reduces the tunneling barrier width, due to which the I_ON performance is increased and I_OFF is decreased [9]. In the last few years, nanowire TFET has gained momentum due to its yield in fabrication and potential electrical properties. Gate-all-around (GAA) TFETs have been studied considering their shortest tunneling length over the tunneling volume [10,11,12]. Dual Material Surrounding Gate (DMSG) TFET has been reported in which two work function materials are used in the surrounding gate, which improves the electrostatic performance of the device [13]. Triple Material Surrounding Gate (TMSG) TFET has also been proposed which shows higher I_ON performance [14, 15].

Nanowires of various diverse materials are being dynamically explored for use in TFET structure. Nanowires consisting of various materials may form heterojunctions of a staggered or broken type. Various materials used for heterojunction investigation are silicon, germanium, carbon, InAs, InSb and GaSb. Among these materials germanium has lower direct band gap and high band-to-band tunneling property that improves the carrier mobility. The heterojunction composed of silicon/germanium exploits strain due to lattice mismatch that improves the electrical characteristics of the device. Thus, germanium is used as source and silicon as substrate, to form the heterojunction by alignment of the energy bands such that energy band gap is reduced [16, 17]. Heterojunction based DG TFETs have been previously proposed using superposition principle method [18]. Presently, there are no research papers based on heterojunction nanowire considering depletion regions. Here, we propose a threshold voltage analytical modeling for Triple Material Gate All Around Heterojunction TFET considering depletion regions which provides higher performance compared to the other devices.

Device structure is explained in detail in Sect. 2 of this work. Analytical model of surface potential obtained from 2D Poisson’s equation using parabolic approximation is discussed in Sect. 3. Expressions for the device parameters like electric field, threshold voltage, and threshold voltage roll off are also elaborated. Section 4 presents the results obtained from the mathematical model, and these results are validated using Technology Computer Aided Design (TCAD) ATLAS Tool. Section 5 concludes the paper.

2 Device structure

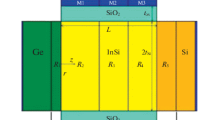
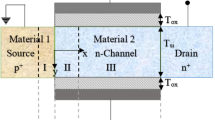
Figure 1a depicts the three-dimensional structural view of Triple Material GAA-HJTFET. Source length is 20 nm and Germanium material is used with p-type doping concentration of $N_{\text{S}} = 1 \times 10^{20} \;{\text{cm}}^{ - 3}$, channel length is 50 nm with a n-type doping concentration of $N_{\text{Ch}} = 1 \times 10^{16} \;{\text{cm}}^{ - 3}$ and drain length is 20 nm and Silicon material is used with n-type doping concentration of $N_{\text{D}} = 5 \times 10^{18} \;{\text{cm}}^{ - 3}$. Figure 1b shows the cross-sectional schematic view of the triple material GAA-HJTFET device. Regions of the device are considered along with depletion regions and three materials used is represented by R₁, R₂, R₃, R₄ and R₅ with respective lengths of $L_{1}$, $L_{2}$,$L_{3}$,$L_{4} \,$ and $L_{5}$.

Fig. 1

(a) 3D structure of triple material GAA-HJTFET (b) schematic cross-sectional view of triple material GAA-HJTFET

Figure 2 shows the energy band diagram of high-k stacked GAA-HJTFET, We observe that at source channel junction the conduction band and valance band are aligned abruptly at heterojunction due to lower band germanium material used. Because of this electrons tunnel at faster rate from the P + source to drain current by drift diffusion technique. Tunneling of electrons occurs due to high electric field formed by increasing the gate bias. The band gap of the heterojunction device is considerably lower than the homojunction device, leading considerable improvement in I_ON, reduced ambipolar behavior and subthreshold swing.

Fig. 2

Energy band diagram of high-k stacked GAA-HJTFET in ON-State (V_G = 1 V) and OFF-State (V_G = 0 V)

3 Model formulation

In TMG-HJTFET it could be seen potential distribution in r-direction which is same as that of DG-TFET shown in Fig. 1b. z and r quantities are considered along the channel length, other parameters include oxide thickness (t_ox). silicon thickness (2t_si), work functions of three materials ($\varphi_{m1}$,$\varphi_{m2}$,$\varphi_{m3}$). $\psi_{0}$,$\psi_{1}$,$\psi_{2}$,$\psi_{3}$,$\psi_{4}$ and $\psi_{5}$ are the junction potentials.

$$\begin{aligned} z & = 0,\;z_{1} = L_{1} ,\;z_{2} = L_{1} + L_{2} ,\;z_{3} = L_{1} + L_{2} + L_{3} , \\ z_{4} & = L_{1} + L_{2} + L_{3} + L_{4} \;{\text{and}}\;z_{5} = L_{1} + L_{2} + L_{3} + L_{4} + L_{5} . \\ \end{aligned}$$

4 Analytical modeling of surface potential

Let $\psi_{i} (r,z)$ be the surface potential distribution function along the channel region R_i where i = 1,2,3,4,5. The two-dimensional (2-D) Poisson’s equation is given as

$$\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial \psi_{i} (r,z)}}{\partial r}} \right) + \frac{{\partial^{2} \psi_{i} (r,z)}}{{\partial z^{2} }} = - \frac{{qN_{i} }}{{\varepsilon_{\text{si}} }}\quad i = 1,2,3,4,5.$$

(1)

The doping concentrations of source ($N_{\text{Src}} = 1 \times 10^{20} \,{\text{cm}}^{ - 3}$), channel ($N_{\text{Ch}} = 1 \times 10^{16} \;{\text{cm}}^{ - 3}$) and Drain ($N_{\text{D}} = 5 \times 10^{18} \;{\text{cm}}^{ - 3}$) are assumed, respectively, to improve the I_ON − I_OFF current ratio. 2-D potential distribution $\psi_{i} (r,z)$ in region R_i can be approximated using parabolic approximation method and given as

$$\psi_{i} (r,z) = a_{0i} (z) + a_{1i} (z)r + a_{2i} (z)r^{2} \;{\text{where}}\quad i = 1,2,3,4,5$$

(2)

where $a_{0i} (z),a_{1i} (z)$ and $a_{3i} (z)$ are arbitrary functions of z, defined by the boundary conditions [10]

$$1.\;\left. {\psi_{i} (r,z)} \right|_{r = R} = \psi_{s} (z)$$

(3)

$$2.\;\left. {\frac{{\partial \psi_{i} (r,z)}}{\partial r}} \right|_{r = 0} = 0$$

(4)

$$3.\;\left. {\frac{{\partial \psi_{i} (r,z)}}{\partial r}} \right|_{r = R} = \frac{{\varepsilon_{\text{ox}} }}{{\varepsilon_{\text{si}} R}}\left[ {\frac{{\psi_{G} - \psi_{s} (z)}}{{\ln \left( {1 + \frac{{t_{\text{ox}} }}{R}} \right)}}} \right]$$

(5)

where $\psi_{G} = V_{\text{GS}} - \varphi_{m} + \chi + \frac{{E_{\text{g}} }}{2}$ and i = 1, 2, 3, 4, 5 for five different regions, gate work function $\varphi_{m1} = 4.05\;{\text{eV}}({\text{Zr}}),$ $\varphi_{m2} = 4.2\;{\text{eV}}({\text{Al}})$, and $\varphi_{m3} = 4.6\;{\text{eV}}({\text{Cu}})$ electron affinity of germanium is 4.0 eV and silicon is 4.05 eV, energy band gap of germanium is 0.67 eV and silicon is 1.12 eV radius of channel R = $t_{\text{si}}$.

Applying boundary conditions Eqs. (3)–(5) in Eq. (2), we obtain

$$a_{0i} = \psi_{s} (z) - \frac{{\varepsilon_{\text{ox}} }}{{2\varepsilon_{\text{si}} }}\left[ {\frac{{\psi_{G} - \psi_{s} (z)}}{{\ln \left( {1 + \frac{{t_{\text{ox}} }}{R}} \right)}}} \right]$$

(6)

$$a_{1i} = 0$$

(7)

$$a_{2i} = \frac{{\varepsilon_{\text{ox}} }}{{2\varepsilon_{\text{si}} R^{2} }}\left[ {\frac{{\psi_{G} - \psi_{S} (z)}}{{\ln \left( {1 + \frac{{t_{\text{ox}} }}{R}} \right)}}} \right].$$

(8)

The relationship between the surface potential and channel potential $\psi_{i} (r,z)$ is defined by $\psi_{s,i} (z) = \psi_{i} \left( {{{ \pm t_{\text{si}} } \mathord{\left/ {\vphantom {{ \pm t_{\text{si}} } 2}} \right. \kern-0pt} 2},z} \right)$.

From Eqs. (6)–(8) we can deduce to obtain potential distribution as below

$$\begin{aligned} \psi_{i} (r,z) & = \psi_{0i} (z) + \left( {\frac{{r^{2} }}{{\lambda^{2} R^{2} }} - \frac{1}{{\lambda^{2} }}} \right) \\ & \quad \times \;\left( {\psi_{G} - \psi_{0i} (z)} \right) \\ \end{aligned}$$

(9)

$$\begin{aligned} \psi_{s,i} (z) & = \psi_{0i} (z) + \left( {\frac{{t_{\text{si}}^{2} }}{{4\lambda^{2} R^{2} }} - \frac{1}{{\lambda^{2} }}} \right) \\ & \quad \times \;\left( {\psi_{G} - \psi_{0i} (z)} \right) \\ \end{aligned}$$

(10)

where $\psi_{0i} (z) = \psi_{i} (0,z)\;{\text{i}}.{\text{e}}\;{\text{when}}\;{\text{radius}}\;r = 0$.

At $r = 0$, 2-D Poisson’s Eq. (1) is written as

$$\left. {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial \psi_{i} (r,z)}}{\partial r}} \right)} \right|_{r = 0} + \left. {\frac{{\partial^{2} \psi_{i} (r,z)}}{{\partial z^{2} }}} \right|_{r = 0} = \left. { - \frac{{qN_{i} }}{{\varepsilon_{\text{si}} }}} \right|_{r = 0} .$$

(11)

Substituting Eq. (2) in Eq. (11), differential equation is gained in terms of center potential as

$$\frac{{\partial^{2} \psi_{0i} (z)}}{{\partial^{2} z}} - \eta_{i}^{2} \psi_{0i} (z) = - \eta_{i}^{2} P_{i}$$

(12)

where $P_{i} = \frac{{qN_{i} }}{{\eta_{i}^{1} \varepsilon_{\text{si}} }} + \psi_{G}$ and $\eta_{i}^{2} = \frac{4}{{\lambda^{2} R^{2} }}$.

The general solution of Eq. (12) is

$$\begin{aligned} \psi_{0i} (z) & = A_{i} \exp (\eta_{i} (z - z_{i - 1} )) \\ & \quad + \;B_{i} \exp ( - \eta_{i} (z - z_{i - 1} )) + P_{i} \\ \end{aligned}$$

(13)

where

$$B_{i} = \frac{1}{{2\sinh \;\eta_{i} L_{i} }}[\psi_{i - 1} (z)\exp (\eta_{i} L_{i} ) - \psi_{i} (z) - P_{i} (\exp (\eta_{i} L_{i} ) + 1)].$$

(14)

Length of region $R_{i}$ is $L_{i} = \,z_{i} - z_{i - 1}$ (i = 1,2,3,4,5) and surface potential at $\,z_{{}} = z_{i}$ is $\psi_{i} = \psi_{s,i} (z_{i} )$ as shown in Fig. 1b. The surface potential across the regions is obtained using the following boundary conditions,

$$\psi_{0} = \psi_{1} (r,0) = V_{\text{bis}}$$

(15)

$$\begin{aligned} \psi_{5} & = \psi_{5} (r,L_{1} + L_{2} + L_{3} + L_{4} + L_{5} ) \\ & = V_{\text{bis}} + V_{\text{DS}} \\ \end{aligned}$$

(16)

where

$$V_{\text{bis}} = - \frac{1}{q}\left[ {\left( {\chi_{1} - \chi_{2} } \right) + 0.5\left( {E_{{{\text{g}}1}} - E_{{{\text{g}}2}} } \right) + qV_{T} \left( {\ln \left( {N_{1} /n_{i} } \right)} \right)} \right].$$

The $\psi_{1}$,$\psi_{2}$,$\psi_{3}$ and $\psi_{4}$ are intermediate surface potentials obtained by using continuity of Lateral electric field property such as

$$\left. {\psi_{s,i} \left( z \right)} \right|_{{z = z_{i} }} = \left. {\psi_{s,i + 1} \left( z \right)} \right|_{{z = z_{i} }}$$

(17)

$$\left. {\frac{{\partial \psi_{s,i} \left( z \right)}}{\partial z}} \right|_{{z = z_{i} }} = \left. {\frac{{\partial \psi_{s,i + 1} \left( z \right)}}{\partial z}} \right|_{{z = z_{i} }} .$$

(18)

The intermediate potentials using Eqs. (17)–(18) in Eq. (10) along with Eqs. (13)–(14) are obtained as,

$$\psi_{1} = \frac{1}{{y_{1} }}\left[ {\frac{{\left( {x - 1} \right)}}{{\sinh \eta_{1} L_{1} }}\left\{ {\eta_{1} \psi_{0} + \eta_{1} P_{1} \left( {1 + \cosh \eta_{1} L_{1} } \right) - P_{2} \sinh \eta_{1} L_{1} } \right\} + x\psi_{G} } \right]$$

(19)

$$\psi_{2} = \frac{1}{{y_{2} }}\left[ {\frac{{\left( {x - 1} \right)}}{{\sinh \eta_{2} L_{2} }}\left\{ {\eta_{2} \psi_{1} + \eta_{2} P_{2} \left( {1 + \cosh \eta_{2} L_{2} } \right) - P_{3} \sinh \eta_{2} L_{2} } \right\} + x\psi_{2} } \right]$$

(20)

$$\psi_{3} = \frac{1}{{y_{3} }}\left[ {\frac{{\left( {x - 1} \right)}}{{\sinh \eta_{3} L_{3} }}\left\{ {\eta_{3} \psi_{2} + \eta_{3} P_{3} \left( {1 + \cosh \eta_{3} L_{3} } \right) - P_{4} \sinh \eta_{3} L_{3} } \right\} + x\psi_{G} } \right]$$

(21)

$$\psi_{4} = \frac{1}{{y_{4} }}\left[ {\frac{{\left( {x - 1} \right)}}{{\sinh \eta_{4} L_{4} }}\left\{ {\eta_{4} \psi_{3} + \eta_{4} P_{4} \left( {1 + \cosh \eta_{4} L_{4} } \right) - P_{5} \sinh \eta_{4} L_{4} } \right\} + x\psi_{G} } \right]$$

(22)

where

$$x = \left( {\frac{{t_{\text{si}}^{2} }}{{4\lambda^{2} R^{2} }} - \frac{1}{{\lambda^{2} }}} \right)$$

$$y_{i} = \left[ {1 - \eta_{i} (x - 1)\coth \eta_{i} L_{i} } \right]\quad i = 1,2,3,4.$$

4.1 Modeling of electric field

The vertical and lateral electric field $E_{ri} (r,z)$ and $E_{zi} (r,z)$ are obtained by differentiation of potential Eqs. (2) and (13) as,

$$E_{ri} (r,z) = 2ra_{2i} (z)$$

(23)

$$E_{zi} (r,z) = - \frac{{\partial \psi_{i} (r,z)}}{\partial z} = \eta_{i} \left[ { - A_{i} \exp \left( {\eta_{i} \left( {z - z_{i - 1} } \right)} \right) + B_{i} \exp \left( { - \eta_{i} \left( {z - z_{i - 1} } \right)} \right)} \right].$$

(24)

4.2 Lengths of depletion regions

$L_{1}$ and $L_{5}$ are determined as the lengths of regions R₁ and R₅ that occur due to source and drain charge depletion regions. TFETs could be contemplated as a gate diode whose potential can be regulated by its gate voltage [19]. To consider the impact of two terminals on each other, $L_{1}$ and $L_{3}$ should be calculated by $E_{r} = \,\,0,\,$ at $r = \,r_{0}$ and $r = \,\,r_{2}$ before deriving potentials $\psi_{2}$ and $\psi_{3}$. To avoid the complexity of these calculations, a simple approximation is made by considering source-channel and drain-channel regions separately as shown below using [20, 21] as,

$$L_{1} = \sqrt {2\varepsilon_{\text{si}} (P_{1} - \psi_{0} )/(qN_{1} )}$$

(25)

$$L_{5} = \sqrt {2\varepsilon_{\text{si}} (\psi_{5} - P_{2} )/(qN_{3} )} .$$

(26)

Since $P_{2}$ is dependent on $V_{\text{GS}}$,$L_{1}$ and $L_{5}$ values are smaller compared with DG-TFET and also dependent on $V_{\text{GS}}$.

4.3 Modeling of threshold voltage

The channel region is made of three metals with three different work functions, the first metal work function near to the source is chosen higher than other metals from Eq. (13). Since the first metal work function is high, the energy barrier level is highest due to which that the surface potential becomes minimum at source-channel region. Unless this energy barrier level is lowered the channel will not conduct. The threshold voltage for the device relies on this channel region. The flat band voltage in region 1 and 2 are same, because they lie under same metal work function. Thus, taking derivative of Eq. (20) related to region 2 and equating it to zero, we find minimum channel position Z_min where the potential distribution is minimum, given by

$$Z_{\hbox{min} } = L_{1} + \frac{1}{{2\beta_{2} }}\ln \left( {\frac{{\beta_{2} }}{{A_{2} }}} \right).$$

(27)

By using Eq. (27), the minimum surface potential distribution can be obtained as

$$\psi_{s,\hbox{min} } = 2\sqrt {A_{2} B_{2} } + \frac{{qN_{\text{S}} }}{{\eta_{2} \varepsilon_{\text{si}} }} + \psi_{G} .$$

(28)

For threshold condition [21]

$$\psi_{s,\hbox{min} } = 2\varphi_{F}$$

(29)

and

$$V_{\text{GS}} = V_{\text{th}} .$$

(30)

The threshold condition can be written using Eqs. (28)–(30), given by

$$2\varphi_{F} = 2\sqrt {A_{2} B_{2} } + \frac{{qN_{\text{s}} }}{{\eta_{2} \varepsilon_{\text{si}} }} + V_{\text{th}} - V_{\text{fb}}$$

(31)

where $V_{\text{fb}} = \varphi_{m2} + \chi + \frac{{E_{\text{g}} }}{2}$.

Using Eq. (31), a quadratic equation for threshold voltage can be approximated as [21]

$$AV_{\text{th}}^{2} + BV_{\text{th}} + C = 0$$

(32)

where

$$A = 1$$

(33)

$$B = - 2V_{\text{thL}}$$

(34)

$$C = - \left( {V_{\text{thL}}^{2} + 4\left( {U_{1} + U_{2} } \right)} \right)$$

(35)

$$\begin{aligned} V_{\text{thL}} & = 2\varphi_{F} + \frac{{qN_{\text{S}} }}{{\eta_{2} \varepsilon_{\text{si}} }} + V_{\text{fb}} \\ U_{1} & = - \frac{1}{{4(\sinh \eta_{2} L_{2} )^{2} }}\left[ {\psi_{1}^{1} - \psi_{1}^{1} - \psi_{1} \psi_{2} 2\cosh \eta_{2} L_{2} } \right] \\ U_{2} & = - \frac{{(1 + \cosh \eta_{{}} L_{2} )}}{{2(\sinh \eta_{2} L_{2} )^{2} }}\left[ {P_{2}^{2} + \psi_{2} P_{2} - \psi_{1} P_{2} } \right]. \\ \end{aligned}$$

From Eq. (32) the threshold voltage expression is found as,

$$V_{\text{th}} = \frac{{ - B + \sqrt {\left( {B^{2} - 4AC} \right)} }}{2A}.$$

(36)

4.4 Threshold voltage roll off

The threshold voltage roll off is difference between the threshold voltage of short channel and threshold voltage of long channel

$$V_{{{\text{th}}\;{\text{roll}}\;{\text{off}}}} = V_{\text{th}} - V_{\text{thL}} .$$

(37)

5 Results and discussion

Here, we discuss the results plotted for potential distribution, lateral and vertical electric field, threshold voltage, threshold voltage roll off and drain induced barrier thinning (DIBT) of proposed model. These are validated by using the TCAD ATLAS tool. Figure 3 shows the comparison plot of surface potential distribution along the channel position; it is observed from the plot that the surface potential value of TM GAA-HJTFET is large compared to the SM GAA-HJTFET. Because of decrease in tunneling width at the source channel junction for TM GAA-HJTFET, the surface potential gets increased due to increase in the tunneling rate of electrons. Figure 4 represents the surface potential distribution plot along the position of channel for different gate voltages at constant drain voltage $V_{\text{DS}} = 1{\text{V}}$. When gate bias is applied surface potential from the source increases linearly and becomes steeper at source channel region and constant across the channel. Because of gradual increase in potential distribution at the source channel junction the electric field and band to band tunneling generation rate improves.

Fig. 3

Comparison of surface potential distribution ($\psi_{s,i}$) along the lateral length of the channel(z) for TM GAA-HJTFET with SM GAA-HJTFET at $V_{\text{DS}}$ = 1 V

Fig. 4

Surface potential distribution($\psi_{s,i}$) along the lateral length of the channel(z) for different, $V_{\text{GS}}$ = 0 V, 0.5 V and 1 V at $V_{\text{DS}}$ = 1 V

Figure 5 depicts the surface potential distribution along the channel for different drain control bias at gate voltage $V_{\text{GS}} = 1{\text{V}}$; it can be deduced that increase in drain to source voltage improves the potential at drain channel junction, further increasing the electric field and band to band tunneling generation rate at drain channel junction. Figure 6 shows the lateral and vertical electric field comparison plot of the proposed device model with SM GAA-TFET; it is observed that the electric field profile of the proposed device is high at the source channel junction due to increase in tunneling rate of electrons from valence band to conduction band.

Fig. 5

Surface potential distribution along the channel for different $V_{\text{DS}}$ = 0.2 V, 0.6 V and 1 V at $V_{\text{GS}}$ = 1 V

Fig. 6

Electric field profile comparison plot for TMGAA-HJTFET and SM GAA-HJTFET

Figure 7 represents the threshold voltage plot along the channel; it can be studied from plot that threshold voltage linearly increases from source to channel until it saturates with respect to gate voltage and remains constant along the channel length. This is due to the impact of maximum electric field at junction and independent of gate length for positive voltage. The threshold voltage shifts are more for higher doping concentration. Figure 8 shows the threshold voltage roll off plot for different silicon thickness. It can be observed that the threshold voltage roll off increases at higher silicon thicknesses, because the gate loses its control over the channel.

Fig. 7

Threshold voltage along the channel for $V_{\text{DS}}$ = 0.5 V and $V_{\text{GS}}$ = 0.8 V

Fig. 8

Threshold voltage roll off along channel length $V_{\text{DS}}$ = 0.1 V, $t_{\text{ox}}$ = 2 nm

6 Conclusion

A threshold voltage analytical modeling and simulation of triple material gate all around heterojunction TFET are proposed. We investigated different TMGAA-HJTFET parameters such as surface potential, electric field, threshold voltage and threshold voltage roll off. The surface potential is modeled initially by 2D Poison Equation then derived using parabolic approximation methodology. The proposed device model exhibits the increased potential distribution and greater electric field at source channel regime which improves the band to band tunneling because of gate engineering compared to previously proposed devices. The threshold voltage is modeled from the surface potential equation. Threshold voltage increases linearly from source to channel junction until it saturates and is constant across the channel. Because of gate engineering the threshold voltage roll off improves, suppresses the hot carrier effect and reduces the DIBT short channel effect. The obtained analytical results are in good agreement with the simulation results.