A full-range dual material gate tunnel field effect transistor drain current model considering both source and drain depletion region band-to-band tunneling

Abstract

In this paper, a 2-D analytical model for the drain current of a dual material gate tunneling field-effect transistor is developed incorporating the effects of source and drain depletion regions. The model can forecast the effects of drain voltage, gate work function, oxide thickness, and silicon film thickness. The proposed model gives analytical expressions for the surface potential, electric field and the band to band generation rate which is numerically integrated to give the drain current. More importantly, our model accurately predicts the ambipolar current and the effects of drain voltage in the saturation region. A semi-empirical approach is used to model the transition from the linear to the saturation region, leading to an infinitely differentiable characteristics. The model is shown to be scalable down to a gate length of 50 nm. The model validation is carried out by a comparison with 2-D numerical simulations.

1 Introduction

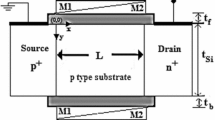
Tunneling field-effect transistors (TFETs) have been extensively studied as an attractive alternative to conventional MOSFETs in ultralow power applications [1–9]. They have been shown to exhibit subthreshold swing (SS) below 60 mV/decade, low OFF-state leakage currents, and diminished short-channel effects (SCEs). However, TFETs also have problems related to ON-state current lower than ITRS requirements [3–8] and DIBL effects [10]; a Dual Material Gate (DMG) TFET had been proposed to address these [11]. The application of DMG is one of the several methods [3, 12, 13] that are being studied to increase the ON-state current of TFETs. Of these methods, the DMG TFET has the advantage of compatibility with the current CMOS fabrication technology. The DMG structures have been shown to give enhanced ON-state current [11, 14]. Therefore, modeling the drain current of the DMG TFET is of great interest. A DMG TFET (see Fig. 1) has a gate made of two different metals, both connected to the same terminal and having the same voltage. The tunneling gate has a lower work function than the auxiliary gate for an n-channel TFET (vice-versa for a p-channel TFET). This leads to a higher ON-state current, lower OFF-state current, and better SS than a conventional TFET [11, 14]. The fabrication of a DMGTFET using a self-aligned symmetric spacer process [15] has been extensively studied [16–18].

Fig. 1

Schematic of the n-channel DMG DG TFET being modeled.

While a number of analytical models have been proposed for the SMGTFET [19–25], most of the studies on a DMGTFET have used TCAD numerical simulations. In the previous models on DMG TFET [26, 27], a single tunneling length was used and therefore, they were not accurate in the subthreshold region. Moreover, as these models did not consider the band to band tunneling simultaneously in the source and the drain depletion regions, they were not able to predict the ambipolar current.

Therefore, this paper develops a 2-D model for the DC drain current of a DMG TFET considering the source and drain depletion regions band to band tunneling. The proposed model is able to predict the drain current accurately in the subthreshold region, the ON-state (strong inversion), and the OFF-state including the ambipolar current. The model results are verified by a comparison with 2-D numerical simulations [28].

2 Model derivation

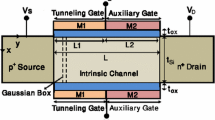
The model is derived for a double gate DMG n-channel TFET (Fig. 1). The corresponding band diagrams for the DG DMG TFET in the (a) OFF-state $(\hbox {V}_{\mathrm{DS}} = 0\,\hbox {V},\,\hbox {V}_{\mathrm{GS}} = 0\,\hbox {V})$ and the (b) ON-state $(\hbox {V}_{\mathrm{DS}} = 0.5\,\hbox {V},\,\hbox {V}_{\mathrm{GS}} = 1.0\,\hbox {V})$ are shown in Fig. 2. Tunneling occurs when the energy barrier separating the valence band of the source and the conduction band of the channel is sufficiently thin. The entire device is divided into separate regions as follows. R1 is the source depletion region and R3 is the drain depletion region. R2 is the channel, which is further sub-divided into R2t, the region under the tunneling gate, and R2a, the region under the auxiliary gate. The device parameters are: channel length $(\hbox {L}_{2}) = 100\,\hbox { nm}$, silicon film thickness $(\hbox {t}_{\mathrm{Si}}) = 10\,\hbox { nm}$, oxide thickness $(\hbox {t}_{\mathrm{ox}}) = 2\,\hbox { nm}$, p-type source doping $(\hbox {N}_{1}) = 10^{20}\,\hbox { cm}^{-3}$, n-type channel doping $(\hbox {N}_{2}) = 10^{17}\,\hbox { cm}^{-3}$, n-type drain doping $(\hbox {N}_{3})=10^{19}\,\hbox { cm}^{-3}$, the tunneling gate work function $(\Phi _{\mathrm{t}}) = 4.0\,\hbox { eV}$, and the auxiliary gate work function $(\Phi _{\mathrm{a}}) = 4.4\,\hbox {eV}$. The length of the tunneling gate $(\hbox {L}_{\mathrm{2t}})$ and the auxiliary gate $(\hbox {L}_{\mathrm{2a}})$ is taken to be 50 nm each in the initial calculations; results for the case of tunneling gate length of 20 nm and auxiliary gate length of 30 nm are also shown. The electron affinity $(\upchi _{\mathrm{Si}}) = 4.17\,\hbox {eV}$ and silicon bandgap $(\hbox {E}_{\mathrm{G}}) = 1.1\,\hbox {eV}$ are taken from the default values used in ATLAS [28].

Fig. 2

Band diagrams for the DG DMG TFET in the a OFF-state $(\hbox {V}_{\mathrm{DS}} = 0\hbox { V},\,\hbox {V}_{\mathrm{GS}} = 0\,\hbox {V})$ and the b ON-state $(\hbox {V}_{\mathrm{DS}} = 0.5\,\hbox {V},\,\hbox {V}_{\mathrm{GS}} = 1.0\,\hbox {V})$.

First, the 2-D Poisson’s equation is solved to obtain a general solution. This solution, the values of the source and drain depletion region lengths, and the appropriate boundary conditions are used to calculate the potential and the electric field throughout the device. The electric field is then substituted into Kane’s model [29] to extract the drain current. In the derivations that follow, all potentials are referenced with respect to the substrate.

2.1 2-D Poisson’s equation

As shown in [25], the mobile charges have negligible effect on the electrostatics of the device as it undergoes a transition from the OFF-state to the ON-state. Since this is the regime that is of primary interest, the Poisson’s equation can be written as

$$\begin{aligned} \frac{\partial ^{2}\psi (x,y)}{\partial x^{2}}+\frac{\partial ^{2}\psi (x,y)}{\partial y^{2}}=-\frac{qN}{\varepsilon _{Si}} \end{aligned}$$

(1)

where $\psi (x,y)$ is the electrostatic potential in the region of consideration, N is the doping, q is the electronic charge, and $\epsilon _{Si}$ is the dielectric constant for silicon.

The potential along Y-direction can be approximated by the second-order polynomial [30]:

$$\begin{aligned} \psi (x,y)=c_{0}(x)+c_{1}(x)y+c_{2}(x)y^{2}. \end{aligned}$$

(2)

To evaluate $\hbox {c}_{0}\hbox {(x)}$, $\hbox {c}_{1}\hbox {(x)}$, and $\hbox {c}_{2}\hbox {(x)}$, four boundary conditions in Y-direction must be imposed. Due to the continuity of potential at the front and back side body-oxide interfaces, respectively, we have two boundary conditions:

$$\begin{aligned}&\!\!\!\psi _{i}(x,0)=\psi _{s}(x) \end{aligned}$$

(3a)

$$\begin{aligned}&\!\!\!\psi _{i}(x,t_{Si})=\psi _{b}(x)=\psi _{s}(x). \end{aligned}$$

(3b)

And due to the continuity of the vertical electric displacement at the front and back side body-oxide interfaces, respectively, we can write two more boundary conditions:

$$\begin{aligned} D_{y}(x,0)&= -\varepsilon _{Si} c_{1}(x)=-\varepsilon _{ox} \frac{\psi _{s}(x)-\psi _{g}}{t_{ox}} \end{aligned}$$

(3c)

$$\begin{aligned} D_{y}(x,t_{Si})&= -\varepsilon _{Si} (c_{1}(x)+2c_{2}(x)y)\nonumber \\&= -\varepsilon _{ox} \frac{\psi _{g}-\psi _{s}(x)}{t_{ox}} \end{aligned}$$

(3d)

where $\psi _{s}(x) =$ the front side surface potential (at $y=0$), $\psi _{b}(x) =$ the back side surface potential (at $y=t_{Si}$), electric displacement $D_{y}=\epsilon _{Si} E_{y}$, and $\hbox {E}_{\mathrm{y}}=$ the electric field in Y-direction. The gate potential is different for both the gates; the tunneling gate potential $\psi _{g2t} =V_{g}-\Phi _{t}+\chi _{Si} +E_{G}/2$, and the auxiliary gate potential $\psi _{g2a} =V_{g}-\Phi _{a}+\chi _{Si} +E_{G}/2$. From the symmetry of the device, we can write $\psi _{s}\left( x\right) =\psi _{b}(x)$.

The eqs. (3a)–(3d) can be solved to give the functions $\hbox {c}_{0}\hbox {(x)}$, $\hbox {c}_{1}\hbox {(x)}$, and $\hbox {c}_{2}\hbox {(x)}$ in terms of the front side surface potential $\psi _{s}(x)$ as

$$\begin{aligned} c_{0}(x)&= \psi _{s}(x) \nonumber \\ c_{1}(x)&= \eta \frac{\psi _{s}(x)-\psi _{g}}{t_{Si}} \nonumber \\ c_{2}(x)&= \eta \frac{\psi _{g}-\psi _{s}(x)}{t_{Si}^{2}} \end{aligned}$$

(4)

where $\eta$ is the capacitance ratio of gate oxide and silicon film, i.e. $\eta =C_{ox} /C_{Si}$. The gate oxide capacitance is $C_{ox} =\epsilon _{ox} /t_{ox}$ for the intrinsic channel region R2. Conformal mapping techniques are used to take into account the fringing field effect of the gate in the depletion regions R1 and R3 [31–33], thereby giving the oxide capacitance as $C_{ox} =2/\pi \times \epsilon _{ox} /t_{ox}$. The silicon film capacitance $C_{Si} =\epsilon _{Si} /t_{Si}$. From (4), $\hbox {c}_{0}\hbox {(x)}$, $\hbox {c}_{1}\hbox {(x)}$, and $\hbox {c}_{2}\hbox {(x)}$ can be substituted into (2). The resultant expression when substituted into the 2-D Poisson’s eq. (1) leads to a 1-D differential equation in $\psi _{s}(x)$:

$$\begin{aligned} \frac{\partial ^{2}\psi _{s}(x)}{\partial x^{2}}-k^{2}\psi _{s}(x)=-k^{2}\psi _{c} \end{aligned}$$

(5)

where

$$\begin{aligned} k&= \sqrt{2\eta /t_{Si}^{2}} \nonumber \\ \psi _{c}&= \psi _{g}-\frac{qN}{k^{2}\varepsilon _{Si}} \end{aligned}$$

(6)

where $1/k$ is the decay length or characteristic length for the surface potential $\psi _{s}(x)$ in each region, and has different values in the source (R1), the channel (R2), and the drain (R3) regions. The parameter $\psi _{c}$ has different values in all the four regions, i.e. the source (R1), the tunneling gate (R2t), the auxiliary gate (R2a), and the drain (R3) regions.

Equation (5) is solved individually for each region (R1, R2a, R2t, and R3). The solution for the $\hbox {i}^{\mathrm{th}}$ region (i=1, 2t, 2a and 3) is

$$\begin{aligned} \psi _{s,i} (x)=a_{i}e^{-k_{i}(x-x_{i-1} )}+b_{i}e^{k_{i}(x-x_{i-1} )}+\psi _{ci} \end{aligned}$$

(7)

where $\hbox {k}_{\mathrm{i}}$ and $\psi _{ci}$ are the parameters defined in (6) for the $\hbox {i}^{\mathrm{th}}$ region. To get the complete solution for the surface potential throughout the device, $\hbox {a}_{\mathrm{i}}$ and $\hbox {b}_{\mathrm{i}}$ need to be solved for.

The surface potential $\psi _{s}(x)$ from (7) is used to find the variation of potential in the Y-direction. This can be done by substituting the surface potential $\psi _{s}(x)$ from (7) into (4), and further substituting the expressions thus obtained for $\hbox {c}_{0}\hbox {(x)}$, $\hbox {c}_{1}\hbox {(x)}$, and $\hbox {c}_{2}\hbox {(x)}$ into (2). The negative of the partial derivatives of the potential with respect to x and y would give the electric fields in the x and y direction respectively.

$$\begin{aligned} E_{x,i}(x,y)&= k_{i}(a_{i}e^{-k_{i}(x-x_{i})}\nonumber \\&-\, b_{i}e^{k_{i}(x-x_{i})})(1+\eta y/t_{Si} -\eta y^{2}/t_{Si}^{2})\end{aligned}$$

(8a)

$$\begin{aligned} E_{y,i} (x,y)&= -c_{1}(x)-2c_{2}(x)y. \end{aligned}$$

(8b)

2.2 Pinning the channel potential

From analytical models that incorporate the effects of drain voltage on the surface potential [14–19], as well as from simulations, it is observed that an inversion charge layer forms in the channel at large positive and negative gate voltages. This inversion charge leads to the ‘pinning’ of the channel potential in both the cases. For an n-channel TFET, the channel potential $\psi _{channel}$ is observed to vary as:

$$\begin{aligned} \Psi _{source} +\Phi _{bi,source} \le \psi _{channel} \le \Psi _{drain} +\Phi _{bi,drain}. \end{aligned}$$

(9)

where $\Psi _{source}$ is the source potential and $\Psi _{drain}$ is the drain potential. $\Phi _{bi}$ is the built-in potential across the respective junction, and can be given as [36]:

$$\begin{aligned}&\!\!\!\Phi _{bi,drain}=\frac{kT}{q}\ln \frac{n_{channel}}{n_{drain}} \end{aligned}$$

(10a)

$$\begin{aligned}&\!\!\!\Phi _{bi,source} =\frac{kT}{q}\ln \frac{n_{channel}}{n_{source}}=-\frac{kT}{q}\ln \frac{p_{channel}}{p_{source}} \end{aligned}$$

(10b)

where $\hbox {n}_{\mathrm{channel}}$ is the electron concentration of the inversion layer formed in the channel when drain side pinning occurs (i.e. when $\psi _{channel} \ge \Psi _{drain})$, and is observed in simulations to be $10^{21}\,\hbox {cm}^{-3}$; $\hbox {n}_{\mathrm{drain}}$ is the electron concentration in the drain. Similarly, $\hbox {p}_{\mathrm{channel}}$ is the hole concentration of the inversion layer formed in the channel when source side pinning occurs (i.e. when $\psi _{channel} \le \Psi _{source}$), and is observed in simulations to be $10^{21}\,\hbox {cm}^{-3}$; $\hbox {p}_{\mathrm{source}}$ is the hole concentration in the source.

In the channel regions, R2t and R2a, the term $\left. {\psi _{ci}} \right| _{i=2t,2a}$ in (7) is the potential solely due to the biasing of the gates. To appropriately capture the behavior of the channel potential as described in (9), a semi-empirical parameter called the “effective gate potential” $\psi _{gi,eff}$ (i = 2t, 2a) is introduced. This parameter varies such that when $\Psi _{source} +\Phi _{bi,source} \le \psi _{gi} \le \Psi _{drain} +\Phi _{bi,drain}$, we have

$$\begin{aligned} \psi _{gi,eff} =\psi _{gi} \end{aligned}$$

(11a)

when $\psi _{gi} \ge \Psi _{drain} +\Phi _{bi,drain}$,

$$\begin{aligned} \psi _{gi,eff} =\Psi _{drain} +\Phi _{bi,drain} \end{aligned}$$

(11b)

and when $\psi _{gi} \le \Psi _{source} +\Phi _{bi,source}$

$$\begin{aligned} \psi _{gi,eff} =\Psi _{source} +\Phi _{bi,source} \end{aligned}$$

(11c)

The parameter $\psi _{gi,eff}$ so defined is used in place of the gate potential $\psi _{gi}$ for calculating the potential and the electric field in the device.

To model the transitions from (11a) to (11c), a semi-empirical approach is adopted by using the following smoothing function [34, 35]:

$$\begin{aligned} \psi _{gi,eff}&= \psi _{gi} -\varphi _{t1} \ln \left( 1+e^{\frac{\psi _{gi} -\Psi _{drain} -\Phi _{bi,drain}}{\varphi _{t1}}}\right) \nonumber \\&+\,\varphi _{t2} \ln \left( 1+e^{\frac{\Psi _{source} +\Phi _{bi,source} -\psi _{gi}}{\varphi _{t2}}}\right) \end{aligned}$$

(12)

where $\phi _{t1}$ and $\phi _{t2}$ are empirical smoothing parameters whose values can be obtained by fitting the simulated and the modeled transfer characteristics. The smoothing parameters must be recalibrated if different doping levels are simulated; they remain constant across variations in gate work-functions and gate lengths. Since most circuit simulators use only a single device structure with fixed parameters and at most vary the size of the device, this should not limit the applicability of the model. The above function ensures the continuity and infinite differentiability of the potential, leading to the continuity and infinite differentiability of all the obtained characteristics.

2.3 Length of depletion regions

To obtain accurate values of the source and drain depletion region lengths, certain boundary conditions need to be imposed. From the continuity of electric field and potential, respectively, at the end of the source depletion region (i.e. $\hbox {x}=\hbox {x}_{0}$):

$$\begin{aligned}&\!\!\!E_{x}(x_{0},y)=0 \end{aligned}$$

(13a)

$$\begin{aligned}&\!\!\!\psi _{s1} (x_{0})=\Psi _{source}. \end{aligned}$$

(13b)

Similarly, from the continuity of electric field and potential, respectively, at the end of the drain depletion region (i.e. $\hbox {x}=\hbox {x}_{1}$):

$$\begin{aligned}&\!\!\!E_{x}(x_{3},y)=0 \end{aligned}$$

(13c)

$$\begin{aligned}&\!\!\!\psi _{s1} (x_{3})=\Psi _{drain}. \end{aligned}$$

(13d)

Since the set of equations (13) are transcendental in nature, solving them is analytically complex and computationally cumbersome.

The source-channel (under the tunneling gate) and channel (under the auxiliary gate)-drain junctions are, therefore, approximated as diodes so that the depletion region length can be modeled using the junction potential [36]. The junction potential is taken to be the difference between the source (or drain) potential and $\psi _{c2t}$ (or $\psi _{c2a}$) which is the potential in the silicon body solely due to the gate voltage. This would give the depletion region lengths as:

$$\begin{aligned} L_{1}&= \sqrt{((2\varepsilon _{Si} \left| {\psi _{c2} \!-\!\Psi _{source}} \right| \!\times \! \left| {N_{2}} \right| )/([q\left| {N_{1}} \right| \!\times \!(\left| {N_{1}} \right| \!+\!\left| {N_{2}}\right| )]))} \nonumber \\ \end{aligned}$$

(14a)

$$\begin{aligned} L_{3}&= \sqrt{((2\varepsilon _{Si} \left| {\Psi _{drain} \!-\!\psi _{c2}} \right| \!\times \! \left| {N_{2}} \right| )/([q\left| {N_{3}}\right| \!\times \!(\left| {N_{1}}\right| \!+\!\left| {N_{3}}\right| )]))}\nonumber \\ \end{aligned}$$

(14b)

where $\hbox {L}_{1}$ and $\hbox {L}_{3}$ are the lengths of the source depletion region (R1) and the drain depletion region (R3), respectively. It should be noted that in (14), the values of $\psi _{c2t}$ and $\psi _{c2a}$ are calculated using $\psi _{g2t,eff}$ and $\psi _{g2a,eff}$, respectively.

2.4 Solution for surface potential

To obtain the coefficients $\hbox {a}_{\mathrm{i}}$ and $\hbox {b}_{\mathrm{i}}$ in (7), the following horizontal boundary conditions need to be imposed. Equations (15a) and (15b) specify the continuity and differentiability, respectively, of the surface potential across the three horizontal interfaces. The interfaces under consideration are: (a) the source-channel (under the tunneling gate) interface for $i=1, j=2t$; (b) the interface between the channel under the tunneling gate and the channel under the auxiliary gate for $i=2t, j=2a$; and (c) the interface between the channel under the auxiliary gate and the drain for $i=2a, j=3$.

$$\begin{aligned} \psi _{s,i} (x_{i})&= \psi _{s,j} (x_{i}) \end{aligned}$$

(15a)

$$\begin{aligned} \psi ^{\prime }_{s,i} (x_{i})&= \psi ^{\prime }_{s,j} (x_{i}). \end{aligned}$$

(15b)

Also, as the surface potential in the source and the drain depletion regions drop to the source potential $(\Psi _{source})$ at $\hbox {x} = \hbox {x}_{0}$ and the drain potential $(\Psi _{drain})$ at $\hbox {x} = \hbox {x}_{3}$, respectively, we must have:

$$\begin{aligned} \psi _{s1} (x_{0})&= \Psi _{source} =V_{source} -\frac{kT}{q}\ln \left| {N_{1}/n_{i}} \right| \end{aligned}$$

(15c)

$$\begin{aligned} \psi _{s3} (x_{3})&= \Psi _{drain} =V_{drain} +\frac{kT}{q}\ln \left| {N_{3}/n_{i}} \right| \end{aligned}$$

(15d)

where $\hbox {V}_{\mathrm{source}}$ is the source voltage and $\hbox {V}_{\mathrm{drain}}$ is the drain voltage.

The terms $\hbox {a}_{\mathrm{i+1}}$ and $\hbox {b}_{\mathrm{i+1}}$ can be written in terms of $\hbox {a}_{\mathrm{i}}$ and $\hbox {b}_{\mathrm{i}}$ by substituting $\psi _{s,i}$ from (7) into (15a) and (15b) and rearranging the resultant equations:

$$\begin{aligned} 2b_{i+1}&= \left( 1-\frac{k_{i}}{k_{i+1}}\right) e^{-k_{i}L_{i}}a_{i} +\left( 1+\frac{k_{i}}{k_{i+1}}\right) e^{k_{i}L_{i}}b_{i}\nonumber \\&+\left( \psi _{ci} -\psi _{ci+1}\right) \end{aligned}$$

(16a)

$$\begin{aligned} 2a_{i+1}&= \left( 1+\frac{k_{i}}{k_{i+1}}\right) e^{-k_{i}L_{i}}a_{i} +\left( 1-\frac{k_{i}}{k_{i+1}}\right) e^{k_{i}L_{i}}b_{i}\nonumber \\&+\left( \psi _{ci} -\psi _{ci+1}\right) . \end{aligned}$$

(16b)

The values for $\hbox {a}_{1}$ and $\hbox {b}_{1}$ are given in the “appendix”, and the other coefficients can be found by substituting those values in (16).

2.5 Drain current

The band-to-band generation rate $G_{btb}$ is numerically integrated throughout the device to give the drain current:

$$\begin{aligned} I_{D}=q\int {G_{btb} dV}. \end{aligned}$$

(17)

$G_{btb}$ is given by Kane’s Model [29] as:

$$\begin{aligned} G_{btb} =A\frac{\left| {E^{2.5}} \right| }{\sqrt{E_{G}}}\exp \left[ {-B\frac{E_{G}^{3/2}}{\left| E \right| }} \right] . \end{aligned}$$

(18)

where $\hbox {E}_{\mathrm{G}}$ is the silicon bandgap and $\left| E \right| =\sqrt{E_{x}^{2}+E_{y}^{2}}$ is the magnitude of the electric field at a given point. The electric fields $\hbox {E}_{\mathrm{x}}$ and $\hbox {E}_{\mathrm{y}}$ are given by (8a) and (8b) respectively.

3 Model validation

The accuracy of the proposed model is verified by comparing the results with 2D numerical simulations. The device structure shown in Fig. 1 is simulated using Silvaco ATLAS [28]. The models used in our simulations are: concentration dependent mobility, electric field dependent mobility, SRH recombination, auger recombination, band gap narrowing, Fermi-Dirac carrier statistics, and Kane’s band to band tunneling, and have been calibrated as described in [27].

The surface potential given by the model and the simulations are compared in Fig. 3 for different values of applied gate and drain voltages, $\hbox {V}_{\mathrm{GS}}$ and $\hbox {V}_{\mathrm{DS}}$, respectively. The model results are in good agreement with the simulation results. In Fig. 4, the electric field along the surface from the model and simulations is compared, and we observe that the results match well. Fig. 5 shows the $\hbox {I}_{\mathrm{D}}$–$\hbox {V}_{\mathrm{GS}}$ curves given by the model and the simulations for $\hbox {V}_{\mathrm{DS}}= 0.5\,\hbox {V}$. It can be seen that the model accurately predicts the drain current in the positive as well as the negative ranges of the gate voltage, both on the logarithmic and linear scale. This is due to the incorporation of the effect of the drain side tunneling, thus leading to the prediction of the ambipolar current. Also, as numerical integration of the band-to-band generation rate has been carried out over the entire device structure rather than using a single tunneling length, the model is able to accurately predict the subthreshold characteristics.

Fig. 3

Surface potential along the channel given by our model (solid lines) and TCAD simulations (dashed lines) for three biasing conditions.

Fig. 4

Electric field (x-direction) at the surface along the channel given by our model (solid lines) and TCAD simulations (dashed lines) for two gate biasing conditions at $\hbox {V}_{\mathrm{DS}}=1\,\hbox {V}$.

Fig. 5

$\hbox {I}_{\mathrm{D}}-\hbox {V}_{\mathrm{GS}}$ given by our model (solid lines) and TCAD simulations (dots) at $\hbox {V}_{\mathrm{DS}} = 0.5\,\hbox {V}$ on a a linear scale, and b a logarithmic scale

In Fig. 6, the surface potentials from our model and TCAD simulations are compared for devices with a fixed total gate length of 100 nm and varying tunneling gate lengths. In Fig. 7, the $\hbox {I}_{\mathrm{D}}$–$\hbox {V}_{\mathrm{GS}}$ characteristics of a TFET with a total gate length of 50 nm and a tunneling gate length of 20 nm are shown. The results shown in Figs. 6 and 7 demonstrate that the proposed model is scalable down to a tunneling gate length of 20 nm and a total gate length of 50 nm.

Fig. 6

Surface potential along the channel given by our model (solid lines) and TCAD simulations (dots) for $\hbox {V}_{\mathrm{DS}} = 1.0\,\hbox {V}$ and $\hbox {V}_{\mathrm{GS}} = 0.5\,\hbox {V}$ for gate length 100 nm, and different tunneling gate lengths: a 20 nm, b 30 nm, c 40 nm, and d 50 nm.

Fig. 7

$\hbox {I}_{\mathrm{D}}-\hbox {V}_{\mathrm{GS}}$ given by our model (solid lines) and TCAD simulations (dots) at $\hbox {V}_{\mathrm{DS}} = 0.5\,\hbox {V}$ for a channel length of 50 nm having a tunneling gate length of 20 nm and an auxiliary gate length of 30 nm.

The transfer characteristics of SMG TFET and DMG TFET are compared in Fig. 8. As can be observed in the figure, an SMG TFET with a gate of lower work function (Fig. 8, curve a) will have a higher ON-state current, but suffers from a low SS due to high OFF-state current. An SMG TFET with a gate of higher work function (Fig. 8, curve b) will have a lower OFF-state current, and thus a better SS, but its ON-state current is also low. A DMG TFET (Fig. 8, curve c) is able to combine the characteristics of both these devices, exhibiting a high ON-state current, a low OFF-state current, and a high SS. Our model can, therefore, be used to vary the gate work functions and achieve the optimal combination of ON-state current and SS as dictated by the design requirements.

Fig. 8

Comparison of transfer characteristics obtained by our model and TCAD simulations for a an SMG TFET (red) with a gate of 50 nm length and 4.0 eV work function, b an SMG TFET (black) with a gate of 50 nm length and 4.4 eV work function, and c a DMG TFET (blue) with a tunneling gate having 25 nm length and 4.0 eV work function, and an auxiliary gate having 25 nm length and 4.4 eV work function.

4 Conclusion

In this work, a model is developed for the surface potential, electric field, and the drain current of a DMG double gate TFET that includes the effects of the source and the drain depletion regions. The variation in the channel potential with gate and drain biases is accurately captured by a semi-empirical approach that gives an infinitely differentiable transfer characteristics. This is needed for circuit design and simulation. The ambipolar current is accurately predicted by our model due to the incorporation of both the source and the drain side depletion region tunneling. The accuracy of the model is validated against calibrated 2-D numerical simulations. The model is accurate in both the subthreshold and the ON-state (strong inversion) regions of operation.

Appendix

The coefficients $\hbox {a}_{1}$ and $\hbox {b}_{1}$ for the source depletion region (R1) are found by applying the boundary conditions as given in (16) and solving the resultant six linear equations in the six variables $\hbox {a}_{\mathrm{i}}$ and $\hbox {b}_{\mathrm{i}}$:

$$\begin{aligned} a_{1}&= e^{-k_{2}L_{2}-k_{3}L_{3}}\nonumber \\&\quad \times \left( { \begin{array}{l} e^{k_{1}L_{1}}\left( {\Psi _{source} -\psi _{c1}}\right) \left( { \begin{array}{l} \Delta k_{23} (\Delta k_{12} e^{2k_{3}L_{3}}-\Sigma k_{12} e^{2k_{2}L_{2}}) \\ +\Sigma k_{23} (\Sigma k_{12} e^{2k_{2}L_{2}+2k_{3}L_{3}}-\Delta k_{12} ) \\ \end{array}} \right) \\ +\,k_{2}\Delta \psi _{1,2t} \left( { \begin{array}{l} \Delta k_{32} (e^{2k_{2}L_{2}}+e^{2k_{3}L_{3}}) \\ +\Sigma k_{32} (1+e^{2k_{2}L_{2}+2k_{3}L_{3}} \\ \end{array}} \right) \\ +\,k_{2}e^{k_{2}L_{2t}}\Delta \psi _{2a,2t} \left( { \begin{array}{l} \Delta k_{23} (e^{2k_{2}L_{2a}}+e^{2k_{3}L_{3}}) \\ -\Sigma k_{23} (1+e^{2k_{2}L_{2a} +2k_{3}L_{3}}) \\ \end{array}} \right) \\ +\,2k_{2}k_{3}e^{k_{2}L_{2}}\Delta \psi _{2a,3} (1+e^{2k_{3}L_{3}})+4(\Psi _{drain} -\psi _{c3} )e^{k_{2}L_{2}+2k_{3}L_{3}} \\ \end{array}} \right) \nonumber \\ b_{1}&= \Psi _{source} -\psi _{c1} -a_{1}. \end{aligned}$$

(19)

Here additional symbols $\Delta \psi _{i,j}$, $\Delta k_{ij}$ and $\Sigma k_{ij}$ have been defined for compact representation of the coefficients $\hbox {a}_{1}$ and $\hbox {b}_{1}$:

$$\begin{aligned}&\Delta \psi _{i,j} =\psi _{ci} -\psi _{cj} \nonumber \\&\Delta k_{ij} = k_{i}-k_{j}\nonumber \\&\Sigma k_{ij} = k_{i}+k_{j} \end{aligned}$$

(20)