Q Function for a Single-Atom Laser Operating in the “Classical” Regime

Abstract

A model of single-atom laser with incoherent pumping is investigated theoretically. In the stationary case, a linear homogeneous differential equation for the phase-averaged Husimi Q function is derived from the equation for the density operator of the system. In the regime in which the coupling of the cavity mode with an atom is much stronger than the coupling of the mode with the reservoir ensuring its damping, the asymptotic solution is obtained to this equation. This solution makes it possible to describe some statistical features of the single-atom laser (in particular, the weak sub-Poissonian photon statistics).

1 INTRODUCTION

At present, sources of nonclassical states of light are required in various branches of physics such as quantum informatics, quantum communications, quantum cryptography, and quantum frequency standards [1–5]. Various investigations are aimed at designing such sources. In particular, in some publications, it is proposed that systems consisting of only one or a few quantum emitters be used for obtaining certain states of light as well as for constructing various elements of quantum devices [6–9]. The properties of a single emitter determine the state of the electromagnetic field, which makes it possible to obtain, for example, sub-Poissonian light [10].

One of fundamental models in quantum optics is the model of a single-atom laser. This model is described in a large number of theoretical [11–27] as well as experimental [28–30] publications. Various effects revealed in these works are mainly associated with a strong manifestation of the Fermi statistics of a single emitter (self-quenching effect, squeezing, sub-Poissonian photon statistics, lasing without inversion, etc.).

A research group from the Stepanov Institute of Physics (Minsk, Belarus), which is headed by S.Ya. Kilin, has made a significant contribution to understanding of single-atom laser physics (see [11, 15–18, 20, 27] and the literature cited therein). One of theoretical approaches used by this group is based on analysis of the equation for the density operator of the system, which is written for quasi-probability distributions such as the Glauber P function and the Husimi Q function; these functions make it possible to determine the normally and antinormally ordered correlation functions of the field operators, respectively.

In [21], a linear homogeneous second-order differential equation for the phase-averaged P function was obtained for the stationary operating regime of a single-atom laser with incoherent pumping. An approximate solution to this equation was obtained in the limiting case, when the interaction between the cavity mode and an atom is much stronger than the coupling between the mode and the reservoir ensuring its damping (the so-called “classical” regime in which the lasing threshold can exist for a single-atom laser [19]). This solution, which is the generating solution in the problem of a small parameter of the senior derivative (boundary-layer problem; see, for example, [31]), provides good agreement with the results of numerical calculations for certain values of laser parameters and, moreover, contains some limiting solutions that have been obtained earlier in [15, 16]. Subsequent analysis of this equation has made it possible to obtain an approximate expression for the P function that, in contrast to previous solutions, demonstrates the essentially nonclassical behavior (becomes negatively definite [22]).

In view of specific features of the P function that can be negative and/or unbounded, analysis of above mentioned equation and its approximate solutions encounters certain difficulties. In particular, the problem of artificial limitation of the domain of definition of the P function appears in this case (see, for example, [15, 21]). In this connection, there emerges a natural incentive to obtain an analogous equation, but for a “good” quasi-probability distribution. In this article, we choose for this distribution a quasi-probability distribution Q, which is non-negatively definite and bounded.

This article has the following structure. In Section 2, a homogeneous differential equation is derived for the phase-averaged Q function for a single-atom laser with incoherent pumping, which generates in the stationary regime. Section 3 is devoted to analysis of the derived equation for the “classical” regime of lasing. An asymptotic solution obtained to this equation is compared with the corresponding solution for the P function [21]. In Section 4, the photon statistics inside the cavity is investigated using the obtained solution. Main attention is paid to the range of values of laser parameters, for which the weak sub-Poissonian photon statistics has been predicted earlier [19]. In Section 5, the obtained asymptotic solution is reduced to the simple Gaussian form for certain values of laser pumping parameters. The Gaussian form of the solution makes it possible to easily determine the relation with the theory that has been developed earlier based on the linearization of the Heisenberg–Langevin equations with respect to small fluctuations in the vicinity of the strong “classical” solution [19]. The results of this study are summarized in Conclusions.

2 MODEL OF SINGLE-ATOM LASER. EQUATION FOR THE PHASE-AVERAGED Q FUNCTION

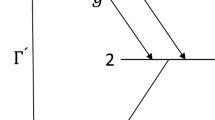
The model of single-atom laser considered here is represented by a single two-level atom interacting with a damping cavity mode. Incoherent pumping of the atoms from lower level |1〉 to upper level |2〉 occurs at rate Γ/2. The spontaneous decay of the atom from upper level |2〉 to lower level |1〉 occurs at rate γ/2. The constant of interaction between the atom and the cavity mode is denoted by g. The cavity mode damping rate is κ/2.

The equation for density operator $\hat {\rho }$ of a single-atom laser has form

$$\begin{gathered} \frac{{\partial \hat {\rho }}}{{\partial t}} = - \frac{i}{\hbar }[\hat {V},\hat {\rho }] + \frac{\kappa }{2}(2\hat {a}\hat {\rho }{{{\hat {a}}}^{\dag }} - {{{\hat {a}}}^{\dag }}\hat {a}\hat {\rho } - \hat {\rho }{{{\hat {a}}}^{\dag }}\hat {a}) \\ + \frac{\gamma }{2}(2\hat {\sigma }\hat {\rho }{{{\hat {\sigma }}}^{\dag }} - {{{\hat {\sigma }}}^{\dag }}\hat {\sigma }\hat {\rho } - \hat {\rho }{{{\hat {\sigma }}}^{\dag }}\hat {\sigma }) \\ + \frac{\Gamma }{2}(2{{{\hat {\sigma }}}^{\dag }}\hat {\rho }\hat {\sigma } - \hat {\sigma }{{{\hat {\sigma }}}^{\dag }}\hat {\rho } - \hat {\rho }\hat {\sigma }{{{\hat {\sigma }}}^{\dag }}), \\ \end{gathered} $$

(1)

where ${{\hat {a}}^{\dag }}$, and $\hat {a}$ are the photon creation and annihilation operators, respectively, in the cavity mode; ${{\hat {\sigma }}^{\dag }}$ = |2〉〈1|, $\hat {\sigma }$ = |1〉〈2| are the atomic flip operators, $\hat {V}$ = $i\hbar g$(${{\hat {a}}^{\dag }}\hat {\sigma }$ + ${{\hat {\sigma }}^{\dag }}\hat {a}$) is the operator of the interaction of the atom with the cavity mode, and $\hbar$ is the reduced Planck constant. The physical meaning of each term on the right-hand side of Eq. (1) is determined by the corresponding rate constant.

We consider the diagonal representation of the antinormally ordered density operator $\hat {\rho }$(z, z*), which is defined as

$$\hat {\rho } = \int {\hat {\rho }(z,z{\text{*}}){\text{|}}z\rangle \langle z{\text{|}}{{d}^{2}}z,} $$

(2)

where |z〉 is the coherent state of the field, d²z ≡ dRe[z]dIm[z], Re[z] and Im[z] being the real and imaginary parts of complex number z. Using familiar transition rules [32]

$$\begin{gathered} {{{\hat {a}}}^{\dag }}\hat {\rho } \to z{\text{*}}\hat {\rho }(z,z{\text{*}}), \\ \hat {a}\hat {\rho } \to \left( {z + \frac{\partial }{{\partial z{\text{*}}}}} \right)\hat {\rho }(z,z{\text{*}}), \\ \hat {\rho }\hat {a} \to z\hat {\rho }(z,z{\text{*}}), \\ \hat {\rho }{{{\hat {a}}}^{\dag }} \to \left( {z{\text{*}} + \frac{\partial }{{\partial z}}} \right)\hat {\rho }(z,z{\text{*}}) \\ \end{gathered} $$

(3)

and introducing functions

$$\begin{gathered} {{\rho }_{{ik}}}(z,z{\text{*}}) = \langle i{\text{|}}\hat {\rho }(z,z{\text{*}}){\text{|}}k\rangle ,\quad i,k = 1,2, \\ D(z,z{\text{*}}) = {{\rho }_{{22}}}(z,z{\text{*}}) - {{\rho }_{{11}}}(z,z{\text{*}}) \\ \end{gathered} $$

as well as the Q function

$$Q(z,z{\text{*}}) = {{\rho }_{{11}}}(z,z{\text{*}}) + {{\rho }_{{22}}}(z,z{\text{*}}),$$

we can easily derive from Eq. (1) the following system of partial differential equations:

$$\begin{gathered} \frac{{\partial Q}}{{\partial t}} = \frac{\partial }{{\partial z}}\left[ {\frac{\kappa }{2}\left( {zQ + \frac{{\partial Q}}{{\partial z{\text{*}}}}} \right) - g{{\rho }_{{21}}}} \right] \\ + \frac{\partial }{{\partial z{\text{*}}}}\left[ {\frac{\kappa }{2}\left( {z{\text{*}}Q + \frac{{\partial Q}}{{\partial z}}} \right) - g{{\rho }_{{12}}}} \right], \\ \frac{{\partial D}}{{\partial t}} = (\Gamma - \gamma )Q - (\Gamma + \gamma )D \\ + \frac{\partial }{{\partial z}}\left[ {\frac{\kappa }{2}zD - g{{\rho }_{{21}}}} \right] + \frac{\partial }{{\partial z{\text{*}}}}\left[ {\frac{\kappa }{2}z{\text{*}}D - g{{\rho }_{{12}}}} \right] \\ - \,2g[z{\text{*}}{{\rho }_{{21}}} + z{{\rho }_{{12}}}] + \kappa \frac{{{{\partial }^{2}}D}}{{\partial z\partial z{\text{*}}}}, \\ \frac{{\partial {{\rho }_{{21}}}}}{{\partial t}} = - \frac{{\Gamma + \gamma }}{2}{{\rho }_{{21}}} + \frac{\kappa }{2}\left[ {\frac{\partial }{{\partial z}}z{{\rho }_{{21}}} + \frac{\partial }{{\partial z{\text{*}}}}z{\text{*}}{{\rho }_{{21}}}} \right] \\ + g\left[ {zD + \frac{1}{2}\frac{\partial }{{\partial z{\text{*}}}}(D - Q)} \right] + \kappa \frac{{{{\partial }^{2}}{{\rho }_{{21}}}}}{{\partial z\partial z{\text{*}}}}. \\ \end{gathered} $$

(4)

Here and below, to avoid cumbersome expressions, we omit the parentheses with complex arguments z and z*.

The physical meaning of additional functions ρ₂₁ and D follows from their mean values:

$$\langle D\rangle = \langle {{\rho }_{{22}}}\rangle - \langle {{\rho }_{{11}}}\rangle \equiv \langle {{\hat {\sigma }}_{z}}\rangle = \int {D{{d}^{2}}z} $$

is the atomic inversion and

$$\langle {{\rho }_{{21}}}\rangle = \langle {{\rho }_{{12}}}\rangle \text{*} \equiv \langle \hat {\sigma }\rangle = \int {{{\rho }_{{21}}}{{d}^{2}}z} $$

is the mean value of the atomic polarization.

The first equation in system (4) can be written in the form of continuity equation

$$\frac{{\partial Q}}{{\partial t}} + {\text{div}}{\mathbf{J}} = q,$$

(5)

where we have defined divergence div = (∂/∂z, ∂/∂z*) and quasi-probability current vector J = (J, J*), J = ‒κ/2(z + ∂/∂z*)Q. Source q = –g(∂ρ₂₁/∂z + ∂ρ₁₂/∂z*) can also be written in terms of the divergence of a certain vector.

We pass to new polar coordinates (I, φ), such that z = $\sqrt I$e^iφ, and define the quasi-probability distributions averaged over phase φ as

$$\begin{gathered} Q(I) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {Q(I,\varphi )d\varphi ,} \\ D(I) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {D(I,\varphi )d\varphi ,} \\ {{\rho }_{{12}}}(I) = \rho _{{21}}^{*}(I) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{e}^{{i\varphi }}}{{\rho }_{{12}}}(I,\varphi )d\varphi .} \\ \end{gathered} $$

(6)

Then, in the stationary case, we can obtain from continuity equation (5) the following relation between Q(I) and the sum of coherencies ρ_Σ(I) = ρ₂₁(I) + ρ₁₂(I):

$${{\rho }_{\Sigma }}(I) = \frac{\kappa }{g}\sqrt I \left[ {Q(I) + \frac{{dQ(I)}}{{dI}}} \right].$$

(7)

The last two equations in system (4) in the stationary case lead to

$$\begin{gathered} (\Gamma - \gamma )Q(I) - (\Gamma + \gamma )D(I) - 2g\sqrt I {{\rho }_{\Sigma }}(I) \\ = \frac{d}{{dI}}\left[ {g\sqrt I {{\rho }_{\Sigma }}(I) - \kappa ID(I) - \kappa I\frac{{dD(I)}}{{dI}}} \right], \\ (\Gamma + \gamma ){{\rho }_{\Sigma }}(I) + \frac{\kappa }{{2I}}{{\rho }_{\Sigma }}(I) \\ - \,2g\sqrt I \left[ {2D(I) + \frac{d}{{dI}}(D(I) - Q(I))} \right] \\ = 2\kappa \frac{d}{{dI}}I\left[ {{{\rho }_{\Sigma }}(I) + \frac{{d{{\rho }_{\Sigma }}(I)}}{{dI}}} \right]. \\ \end{gathered} $$

(8)

Using relation (7), we can exclude function ρ_Σ(I) from system (8) and obtain the system of two differential equations in unknown functions Q(I) and D(I).

Our task is the derivation of a differential equation for function Q(I). However, the first equation in system (8) (we are speaking of system (8) presuming that ρ_Σ(I) is excluded from it with the help of relation (7)) is a second-order differential equation in function D(I), while the second equation is the first-order equation in the same function D(I). Therefore, to exclude functions D(I), dD(I)/dI, and d²D(I)/dI² from system (8), we must supplement this system with one more equation containing the second derivative of function D(I), This equation can be obtained by differentiating the second equation in system (8).

Omitting the intermediate elementary calculations, we write the final result:

$$\sum\limits_{\nu = 0}^5 {{{p}_{\nu }}(I){{Q}^{{(\nu )}}}(I) = 0,} $$

(9)

$${{p}_{5}}(I) = {{b}_{{02}}}{{I}^{2}} + {{b}_{{03}}}{{I}^{3}},$$

$${{p}_{4}}(I) = {{b}_{{11}}}I + {{b}_{{12}}}{{I}^{2}} + {{b}_{{13}}}{{I}^{3}},$$

$${{p}_{3}}(I) = {{b}_{{20}}} + {{b}_{{21}}}I + {{b}_{{22}}}{{I}^{2}} + {{b}_{{23}}}{{I}^{3}},$$

$${{p}_{2}}(I) = {{b}_{{30}}} + {{b}_{{31}}}I + {{b}_{{32}}}{{I}^{2}} + {{b}_{{33}}}{{I}^{3}},$$

$${{p}_{1}}(I) = {{b}_{{40}}} + {{b}_{{41}}}I + {{b}_{{42}}}{{I}^{2}},$$

$${{p}_{0}}(I) = {{b}_{{50}}} + {{b}_{{51}}}I + {{b}_{{52}}}{{I}^{2}},$$

where we have introduced notation Q^(ν)(I) ≡ d^νQ(I)/dI^ν, and coefficients b_ik = b_ik(Γ, γ, κ, g) are given in Appendix.

Thus, the sought equation for the phase-averaged Q function is a homogeneous fifth-order differential equation with polynomial coefficient. It should be recalled that the corresponding equation for the phase-averaged P function is a second-order equation [21].

3 FUNCTION Q(I) FOR A SINGLE-ATOM LASER OPERATING IN THE “CLASSICAL” REGIME

Following [19, 21], we will further use the following three dimensionless parameters: dimensionless pumping rate r = Γ/γ, dimensionless saturation intensity I_s = γ/κ, and dimensionless coupling strength (cooperative parameter) c = 4g²/γκ.

As noted above, the equation for the phase-averaged P function P(I) for our laser is a second-order homogeneous differential equation with polynomial coefficients [21]. In the “classical” regime, when product cI_s ≫ 1 (i.e., g/κ ≫ 1), we can single out in this equation small parameter λ ≈ 1/cI_s appearing at the senior derivative. Using the perturbation theory, the authors of [21] determined generating solution P₀(I) to this equation (formula (50) in [21]), which is the solution to the first-order differential equation.

In the case of a “good-cavity” regime (I_s ≫ 1), function P₀(I) successfully describes the statistical properties of a single-atom laser. In particular, using this function, it is possible to describe some results following from the solution of the system of the Heisenberg–Langevin equations by their linearization with respect to small fluctuations in the vicinity of the strong “classical” solution [19, 21] (henceforth, the “linear” theory). Let us write some results of the linear theory:

$$\begin{gathered} {{I}_{0}}(r,{{I}_{s}},c) = \frac{{{{I}_{s}}}}{2}\left[ {(r - 1) - \frac{{{{{(r + 1)}}^{2}}}}{c}} \right], \\ Q_{f}^{{{\text{lin}}}}(r,c) = \frac{{2{{c}^{2}} - c(r - 5)(r + 1) + 3{{{(r + 1)}}^{3}}}}{{2{{c}^{2}}\left[ {(r - 1) - \frac{{{{{(r + 1)}}^{2}}}}{c}} \right]}}. \\ \end{gathered} $$

(10)

Here, I₀ ≈ 〈$\hat {n}$〉 ≡ 〈${{\hat {a}}^{\dag }}\hat {a}$〉 is the classical intracavity intensity (so-called strong “classical” solution), and $Q_{f}^{{{\text{lin}}}}$ ≈ Q_f = (〈$\hat {n}$²〉 – 〈$\hat {n}$〉²)/〈$\hat {n}$〉 – 1 is the Mandel Q parameter for the field (superscript “lin” indicates that it is the result of the linear theory).

Formulas (10) have sense for c > 8 and for r ∈ (r_th, r_q), where r_th is the threshold value of the pumping rate and r_q is the value of this rate, for which the self-quenching effect occurs. The explicit expressions for r_th and r_q can be obtained from equation I₀ = 0:

$${{r}_{{{\text{th}}}}} = {{r}_{m}} - \frac{c}{2}\sqrt {1 - \frac{8}{c}} ,\quad {{r}_{q}} = {{r}_{m}} + \frac{c}{2}\sqrt {1 - \frac{8}{c}} ,$$

(11)

where r_m = c/2 – 1 is the value of the pumping rate for which I₀ reaches its maximal value I_m = I_s(c/8 – 1).

Results (10) predict an insignificant sub-Poissonian photon statistics in the cavity mode [21]. For c ≈ 200 and higher, and for values of the pumping rate close to r = c/5, the Mandel Q parameter $Q_{f}^{{{\text{lin}}}}$ becomes negative and takes a value of –0.05 for c → ∞. In this range of values of parameters, the P function demonstrates the nonclassical behavior [22]—becomes negative definite and unbounded, and approximate solution P₀(I) acquires an essentially singular point close to I₀, which does not permit the confirmation of the results of the linear theory.

It should be noted that the minimal value of the Mandel Q parameter determined for the model of the single-atom laser considered here is –0.15 [13, 24]. Such a sub-Poissonian statistics is associated with the photon antibunching effect, which is manifested most clearly in the regime of the small number of photons in the cavity mode rI_s ≈ 1 (Γ ≈ κ) [24]. However, in the classical regime considered here (i.e., in the regime in which solutions (10) exist), this effect is suppressed by the presence of a large number of photons randomly accumulated in the mode and characterized by a relatively long stochastic lifetime.

Let us now separate small parameter λ ≈ 1/cI_s in Eq. (9) and try to obtain the corresponding generating solution for the Q function. We will proceed in the same way as in [21]. For this, we write polynomials p_ν(I), separating in them the roots:

$$\begin{gathered} {{p}_{5}}(I) = {{b}_{{03}}}{{I}^{2}}(I - {{I}_{{00}}}), \\ {{p}_{4}}(I) = {{b}_{{13}}}I(I - {{I}_{{11}}})(I - {{I}_{{12}}}), \\ {{p}_{3}}(I) = {{b}_{{23}}}(I - {{I}_{{21}}})(I - {{I}_{{22}}})(I - {{I}_{{23}}}), \\ {{p}_{2}}(I) = {{b}_{{33}}}(I - {{I}_{{31}}})(I - {{I}_{{32}}})(I - {{I}_{{33}}}), \\ {{p}_{1}}(I) = {{b}_{{42}}}(I - {{I}_{{ - 4}}})(I - {{I}_{{ + 4}}}), \\ {{p}_{0}}(I) = {{b}_{{52}}}(I - {{I}_{{ - 5}}})(I - {{I}_{{ + 5}}}), \\ \end{gathered} $$

(12)

where the roots in the last two polynomials are denoted analogously to [21].

The coefficients of the two last polynomials b₄₂, b₅₂ ~ cI_s, while the coefficients of all remaining polynomials are on the order of unity. Therefore, in the regime cI_s ≫ 1, we replace Eq. (9) by the approximate first-order equation

$$\begin{gathered} {{b}_{{42}}}(I - {{I}_{{ - 4}}})(I - {{I}_{{ + 4}}}){{Q}^{{(1)}}}(I) \\ + \,{{b}_{{52}}}(I - {{I}_{{ - 5}}})(I - {{I}_{{ + 5}}})Q(I) = 0. \\ \end{gathered} $$

(13)

The solution to this equation has form

$$\begin{gathered} {{Q}_{0}}(I) = {{N}_{0}}{{\left( {1 - \frac{I}{{{{I}_{{ - 4}}}}}} \right)}^{{{{f}_{1}}}}} \\ \times {{\left| {\left( {1 - \frac{I}{{{{I}_{{ + 4}}}}}} \right)} \right|}^{{{{f}_{2}}}}}\exp \left( { - \frac{{{{b}_{{52}}}}}{{{{b}_{{42}}}}}I} \right), \\ \end{gathered} $$

(14)

$${{f}_{1}} = - \frac{{{{b}_{{52}}}}}{{{{b}_{{42}}}}}\frac{{({{I}_{{ - 4}}} - {{I}_{{ - 5}}})({{I}_{{ - 4}}} - {{I}_{{ + 5}}})}}{{{{I}_{{ - 4}}} - {{I}_{{ + 4}}}}},$$

$${{f}_{2}} = \frac{{{{b}_{{52}}}}}{{{{b}_{{42}}}}}\frac{{({{I}_{{ + 4}}} - {{I}_{{ - 5}}})({{I}_{{ + 4}}} - {{I}_{{ + 5}}})}}{{{{I}_{{ - 4}}} - {{I}_{{ + 4}}}}},$$

where N₀ is the normalization constant, and subscript “0” on the function indicates that this solution is generating in the problem with a small parameter.

The structure of resulting solution (14) almost coincides with that of corresponding generating solution P₀(I) for the P function (see formula (50) in [21]). However, solution (14) has certain advantages associated with the fact that the Q function is non-negatively definite and bounded. For example, the exponential function in (14) decreases upon an increase in argument I in view of positiveness of ratio b₅₂/b₄₂ > 0. Conversely, function P₀(I) determined in [21] increases exponentially as I → ∞, which is one of the reasons for artificial boundedness of its domain of definition.

First parenthesis (1 – I/I_–4) on the right-hand side of relation (14) is always positive since root I_–4 < 0. Second parentheses (1 – I/I₊₄) becomes negative for I > I₊₄ (root I₊₄ > 0); consequently, Q₀(I) takes a complex value, which is inadmissible for the Q function. However, for a “good-cavity” regime (I_s ≫ 1), the value of root I₊₄ is close to values of variable I, for which the Q function is negligibly small. For a “bad-cavity” regime (I_s ~ 1, I_s ≪ 1), the value of root I₊₄ lies in the range of values of variable I, where the Q unction is not small. If, however, we confine the domain of definition of function Q₀(I) to segment [0, I₊₄] as it has been done in [21] for function P₀(I), this can lead to nonphysical results. Therefore, in (14), we take modulo of parentheses (1 – I/I₊₄).

Some features of solution (14), which are also observed for function P₀(I), are worth noting. Root I_‒5 repeats solution (10) for the classical intracavity intensity almost completely (i.e., I_–5 ≈ I₀). In the case of a “good-cavity” regime, approximate equality I₊₄ ≈ I₊₅ holds near the maximum of “classical” solution I₀.

Analysis of Eq. (9) shows that solution (14) cannot be used for describing the laser operation in the case when the pumping rate is much smaller than threshold value r_th. In this case, on account of the fact that main changes in the Q function occur in the range of small values of variable I, we can consider the following equation obtained from Eq. (9) by disregarding all powers of variable I in the polynomials:

$$\begin{gathered} {{b}_{{20}}}{{Q}^{{(3)}}}(I) + {{b}_{{30}}}{{Q}^{{(2)}}}(I) \\ \, + {{b}_{{40}}}{{Q}^{{(1)}}}(I) + {{b}_{{50}}}Q(I) = 0. \\ \end{gathered} $$

(15)

The solution to this equation has form

$$Q(I) = {{N}_{0}}\exp (I{\text{/}}a),$$

(16)

where constant a < 0 is the real-valued root of polynomial equation

$${{b}_{{20}}}{{x}^{3}} + {{b}_{{30}}}{{x}^{2}} + {{b}_{{40}}}x + {{b}_{{50}}} = 0.$$

For r → 0, ∞, this constant tends to –1; i.e., in these limiting cases, the Q function describes the vacuum state of the cavity mode:

$$Q(I) = {{e}^{{ - I}}}{\text{/}}\pi .$$

Therefore, solution (16) describes thermal radiation with average number of photons 〈$\hat {n}$〉 = –(a + 1).

4 RESULTS OF CALCULATIONS

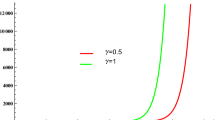
In Fig. 1, the behaviors of functions P₀(I) [21] and Q₀(I) (14) are compared upon a transition to the regime close to strong coupling regime c ≫ I_s (i.e., g ≫ γ, which means that the coupling of an atom with the cavity mode is much stronger than the coupling of the atom with the reservoir, ensuring its spontaneous decay outside the cavity mode). For all curves, r = c/5; i.e., we choose the value of the pumping parameter for which the Mandel Q parameter $Q_{f}^{{{\text{lin}}}}$ (10) takes the minimal value. It can be seen that an increase in coupling constant c for fixed I_s leads to a decrease in the width and an increase in the height of the peak of function P₀(I). For c = 175, the asymmetry of this function associated with the boundedness of its domain of definition is noticeable. For c ≈ 200, function P₀(I) acquires a singularity (analogous to that observed in [24, 25]), which does not allows us to calculate average values of interest. Upon a further increase in coupling constant c, this singularity exceeds the domain of definition of function P₀(I), but the calculation of mean values leads to unrealistic results. Function Q₀(I) has no such singularities as should be expected and permits us to easily calculate the mean values of interest.

Fig. 1.

Comparison of behaviors of functions P₀(I) [21] and Q₀(I) (14): (a) I_s = 100, c = 50; (b) I_s = 100, c = 100; (c) I_s = 100, c = 175. (d) Behavior of function Q₀(I) (14) upon a transition to the strong coupling regime.

Table 1 represents the results of “linear” theory (10) for values of laser parameters corresponding to Figs. 1a–1c (these results are denoted by superscript “lin”), as well as the results obtained with the help of functions P₀(I) and Q₀(I). It can be seen that different approaches lead to close results.

Table 1

Fig. 1a	Is = 100, c = 50
Lin	I0 = 329, $Q_{f}^{{{\text{lin}}}}$ = 0.19
P 0	〈$\hat {n}$〉 = 329.1, Qf = 0.19
Q 0	〈$\hat {n}$〉 = 329.1, Qf = 0.19
Fig. 1b	Is = 100, c = 100
Lin	I0 = 729.5, $Q_{f}^{{{\text{lin}}}}$ = 0.056
P 0	〈$\hat {n}$〉 = 729.6, Qf = 0.056
Q 0	〈$\hat {n}$〉 = 729.6, Qf = 0.057
Fig. 1c	Is = 100, c = 175
Lin	I0 = 1329.7, $Q_{f}^{{{\text{lin}}}}$ = 0.0075
P 0	〈$\hat {n}$〉 = 1329.8, Qf = 0.008
Q 0	〈$\hat {n}$〉 = 1329.8, Qf = 0.0084

Figure 1d illustrates the behavior of function Q₀(I) upon a transition in the strong coupling regime for r = c/5 as before. Parameters c and I_s are chosen so that the classical intracavity intensity is I₀ = 700. The corresponding values of 〈$\hat {n}$〉 and Q_f are given in Table 2.

Table 2

Fig. 1d	Is = 95.95, c = 102
Lin	I0 = 700, $Q_{f}^{{{\text{lin}}}}$ = 0.056
P 0	〈$\hat {n}$〉 = 700.1, Qf = 0.056
Q 0	〈$\hat {n}$〉 = 700.1, Qf = 0.057
Fig. 1d	Is = 8.83, c = 103
Lin	I0 = 700, $Q_{f}^{{{\text{lin}}}}$ = –0.04
P 0	〈$\hat {n}$〉 = UnPh, Qf = UnPh
Q 0	〈$\hat {n}$〉 = 700.1, Qf = –0.039
	Is = 0.87, c = 104
Lin	I0 = 700, $Q_{f}^{{{\text{lin}}}}$ = –0.049
P 0	〈$\hat {n}$〉 = UnPh, Qf = UnPh
Q 0	〈$\hat {n}$〉 = 700.1, Qf = –0.047

In Table 2, only the first two upper blocks correspond to the curves in Fig. 1d. The lower block corresponds to the strong coupling regime and a “bad-cavity” case, I_s = 0.87 (the curve is not shown because it almost coincides with the curve for c = 10³). It can be seen from the values represented in the table that determined Q function Q₀(I) (14) correctly describes the weak sub-Poissonian photon statistics predicted by the “linear” theory. The case of “bad-cavity” regime as well as the cases with c ≈ 200 and c > 200 cannot be described by function P₀(I) (abbreviation UnPh in Table 2 indicates unphysical result).

In Fig. 2, the results of the “linear” theory are compared with the results obtained using solutions (14) and (16). For a good-cavity regime, we have I_s ≫ 1, and both approaches give very close results for values of the pumping rate lying between r_th and r_q (Figs. 2a–2c). The characteristic threshold peak for the Mandel Q parameter [19] and the peak associated with the effect of “trapping” of an atom in the excited state are successfully described by function (14). For values of the pumping rate much lower than classical threshold r_th, solution (14) gives an unphysical result for the Mandel Q parameter. In this case, solution (16) (blue dotted curve) was used for obtaining results.

Fig. 2.

Comparison of the results of “linear” theory (10) with the results obtained using functions Q₀(I) (14). (a, c) Dependences of average number of photons 〈n(r)〉 and the Mandel Q parameter Q_f(r) on pumping rate r; I_s = 40, c = 20. (b, d) Dependences of the Mandel Q parameter Q_f(r) on pumping rate r. Transition to the strong coupling regime; (b) “good-cavity” regime, I_s = 40; (d) “bad-cavity” regime, I_s = 1. Green bullets are the results of numerical calculation.

In Fig. 2b, a transition to the strong coupling regime is illustrated, when the weak sub-Poissonian photon statistics predicted by the linear theory appears. As can be seen from the figure, resulting function Q₀(I) (14) describes this quantum effect comprehensively.

The “bad-cavity” regime I_s ~ 1 is illustrated in Fig. 2d.The curves for the Mandel Q parameter $Q_{f}^{{{\text{lin}}}}$ (10) fully coincide with the curves in Fig. 2b because of its natural dependence only on parameters r and c. Comparison with the results of numerical calculations shows that the results based on “linear” theory (10) better describe a transition to the sub-Poissonian regime. For a “bad-cavity” regime, function Q₀(I) (14) gives only a qualitative result. However, in the limit c → ∞, the results obtained with the help of function Q₀(I) (14) coincide with the results of the “linear” theory.

5 APPROXIMATION OF FUNCTION Q ₀(I) BY THE GAUSSIAN DISTRIBUTION

Let us consider the “good-cavity” regime (I_s ≫ 1) and values of the pumping parameter close to r_m (10), (11). We take into account the fact that I₊₄ ≈ I₊₅ and I_‒5 ≈ I₀ in this case. Hence, f₁ ≈ (b₅₂/b₄₂)(I₀ – I_–4), f₂ ≈ 0, and expression (14) can be written as

$$\begin{gathered} {{Q}_{0}}(I) = {{N}_{0}}{{\left( {1 + \frac{{\Delta I}}{{{{I}_{0}} - {{I}_{{ - 4}}}}}} \right)}^{{({{b}_{{52}}}/{{b}_{{42}}})({{I}_{0}} - {{I}_{{ - 4}}})}}} \\ \times \exp \left( { - \frac{{{{b}_{{52}}}}}{{{{b}_{{42}}}}}\Delta I} \right), \\ \end{gathered} $$

(17)

where ΔI = I – I₀ and I₀ – I_–4 ≫ 1. Function (17) has a maximum corresponding to values of I close to “classical” solution I₀ (i.e., for ΔI ≈ 0). Then in the range of values of variable I, for which the value given by (17) is not negligibly small (i.e., for values of I differing from I₀ not very strongly), we can perform the following expansion of the preexponential factor:

$$\begin{gathered} {{\left( {1 + \frac{{\Delta I}}{{{{I}_{0}} - {{I}_{{ - 4}}}}}} \right)}^{{ - ({{I}_{0}} - {{I}_{{ - 4}}})}}} \\ = \exp \left[ { - ({{I}_{0}} - {{I}_{{ - 4}}})\ln \left( {1 + \frac{{\Delta I}}{{{{I}_{0}} - {{I}_{{ - 4}}}}}} \right)} \right] \\ \approx \exp \left[ { - \Delta I + \frac{{{{{(\Delta I)}}^{2}}}}{{2({{I}_{0}} - {{I}_{{ - 4}}})}}} \right]. \\ \end{gathered} $$

(18)

Substituting this expression into (17), we see that the Q function takes the form of a Gaussian function:

$${{Q}_{0}}(I) = {{N}_{0}}\exp \left[ { - \frac{{{{{(\Delta I)}}^{2}}}}{{2{{\sigma }^{2}}}}} \right],$$

(19)

where variance σ² = (I₀ – I_–4)b₄₂/b₅₂ is defined by solutions (10),

$$\begin{gathered} {{\sigma }^{2}} = \pi \int\limits_0^\infty {{{I}^{2}}{{Q}_{0}}(I)dI - } {{\left( {\pi \int\limits_0^\infty {I{{Q}_{0}}(I)dI} } \right)}^{2}} \\ = 1 + {{I}_{0}}(1 + Q_{f}^{{{\text{lin}}}}). \\ \end{gathered} $$

(20)

Thus, this relation implies that solution (19) describes the weak sub-Poissonian photon statistics in the cavity mode. Indeed, by the definition of the Mandel Q parameter, we obtain

$$\begin{gathered} {{Q}_{f}} = \frac{{\pi \int\limits_0^\infty {{{I}^{2}}Q(I)dI - {{{\left( {\pi \int\limits_0^\infty {IQ(I)dI} } \right)}}^{2}} - \pi \int\limits_0^\infty {IQ(I)dI} } }}{{\pi \int\limits_0^\infty {IQ(I)dI - 1} }} - 1 \\ \approx \frac{{{{\sigma }^{2}} - {{I}_{0}} - 1}}{{{{I}_{0}}}} - 1 = Q_{f}^{{{\text{lin}}}}. \\ \end{gathered} $$

(21)

It should be noted that in [21], a Gaussian expression of type (19) was obtained for function P₀(I) also. However, variance σ² in this case was equal to product I₀$Q_{f}^{{{\text{lin}}}}$, which became negative for the sub-Poissonian photon statistics; this rendered function P₀(I) unbounded.

6 CONCLUSIONS

In this study, the stationary regime of operation of a single-atom laser with incoherent pumping was investigated based on Eq. (9) for phase-averaged Q function. In the “classical” regime (g/κ ≫ 1), approximate solution (14), (16) to this equation was obtained. This solution describes the main features of the single-atom laser, in particular, makes it possible to describe the weak sub-Poissonian statistics of photons in the cavity mode, which has been detected earlier using the approach based on linearization of the Heisenberg–Langevin equation in the vicinity of strong classical solution (10) [19, 21].

Summing up, we can state that analysis of the stationary regime of operation of a single-atom laser with incoherent pumping can be reduced to analysis of a single linear homogeneous differential equation. For example, this is Eq. (41) in [21] in the case of the P function and Eq. (9) of this work for the Q function. In the limiting case considered here and in [21], when g/κ ≫ 1, the aforementioned differential equations acquire a small parameter that makes it possible to obtain approximate solutions to these equations relatively easily.

Concluding this section, we note that Eq. (9) has also been analyzed in [25], where the particular case of Γ ≈ κ (i.e., the case of a small number of photons in the cavity mode) has been considered. For arbitrary values of ratio g/κ, analysis of Eq. (9) was complicated. Exact analytic solutions to Eq. (9), one of which coincided with solution (16), were obtained only in the limiting case g/Γ ≈ g/κ → ∞. For a small number of photons, the approach based on analysis of an infinite system of algebraic equations for different moments of field operators has proved to be more fruitful [24, 25, 33]. It is probably precisely this approach that will make it possible to obtain exact solutions for mean values characterizing a single-atom laser in some particular cases [34].

APPENDIX

Coefficients b_ik from Eq. (9) are given by

$$\begin{gathered} {{b}_{{02}}} = - \frac{1}{2}[1 + {{I}_{s}}(r + 1)],\quad {{b}_{{03}}} = 1; \\ {{b}_{{11}}} = - 3[1 + {{I}_{s}}(r + 1)], \\ {{b}_{{12}}} = \frac{1}{2}[7 - 3{{I}_{s}}(r + 1)],\quad {{b}_{{13}}} = 3; \\ {{b}_{{20}}} = - 3[1 + {{I}_{s}}(r + 1)], \\ {{b}_{{21}}} = \frac{1}{4}[ - 21 - 26{{I}_{s}}(r + 1) + 3I_{s}^{2}{{(r + 1)}^{2}}], \\ \end{gathered} $$

$$\begin{gathered} {{b}_{{22}}} = - 3[ - 4 + {{I}_{s}}(r + 1)],\quad {{b}_{{23}}} = 3; \\ {{b}_{{30}}} = \frac{1}{2}[ - 15 - 8{{I}_{s}}(r + 1) + 3I_{s}^{2}{{(r + 1)}^{2}}], \\ {{b}_{{31}}} = - \frac{1}{2}{{I}_{s}}[c(1 + {{I}_{s}}(r + 1)) - (r + 1)( - 13 + 3{{I}_{s}}(r + 1))], \\ {{b}_{{32}}} = \frac{1}{2}[23 + {{I}_{s}}(2c - 7(r + 1))],\quad {{b}_{{33}}} = 1; \\ {{b}_{{40}}} = \frac{1}{4}[ - 24 + {{I}_{s}}(r + 1 - 3c) - I_{s}^{3}(r + 1)(c + {{(r + 1)}^{2}}) \\ \, + I_{s}^{2}(8{{(r + 1)}^{2}} - c(3r + 4))], \\ \end{gathered} $$

(22)

$$\begin{gathered} {{b}_{{41}}} = \frac{1}{4}[15 - 2{{I}_{s}}(c + 10(r + 1)) \\ \, + I_{s}^{2}(5{{(r + 1)}^{2}} - 2c(2r + 1))], \\ {{b}_{{42}}} = \frac{1}{2}[7 + {{I}_{s}}(4c - 3(r + 1))]; \\ {{b}_{{50}}} = \frac{1}{4}[ - 6 + {{I}_{s}}(5(r + 1) - 3c) + I_{s}^{3}(r + 1)(c(r - 1) \\ \, - {{(r + 1)}^{2}}) + I_{s}^{2}(2{{(r + 1)}^{2}} - 4c)], \\ {{b}_{{51}}} = \frac{1}{2}[3 - 4{{I}_{s}}(r + 1) + I_{s}^{2}({{(r + 1)}^{2}} - 2cr)],\quad {{b}_{{52}}}\, = \,c{{I}_{s}}. \\ \end{gathered} $$