The Dynamical Behaviors of the Two-Atom and the Dynamical Casimir Effect in a Non-Stationary Cavity

Abstract

We study the dynamical Casimir effect and the dynamical behaviors of the two-atom in a non-stationary cavity containing two two-level atoms. By solving the problem in a matrix method, we obtain an analytic solution. The results show that the larger of the atom-field coupling coefficients and the coupling coefficient of atoms, the fewer photons generated, but the probability of double excitation of the two-atom increases with the coupling coefficients. The squeezed coefficient enhances the generation rate of the created photons and the possibility of the atoms in the excited states.

1 Introduction

The dynamical Casimir effect(DCE) is a process of photon creation in an initially empty non-stationary cavity. It was first considered by Moore in 1970 [1, 2]. The experiment on modeling this effect in the superconducting stripline waveguide terminated by a superconducting quantum interference device with a rapidly varying magnetic flux (resulting in time-dependent boundary conditions simulating the motion of some effective boundary) was performed by C.M. Wilson in 2011 [3].

DCE has attracted many researchers to do numerous theoretical studies for a long time, the problem of detecting photons generated by DCE becomes quite actual. It is shown that the presence of detectors can change the statistics of created photons. Previous studies about the influence of field-detector interaction on the rate of photons creation have been performed since 1995 [4]. Based on the early studies, the problem of the back action of detectors on the DCE has been generalised in different schemes and regimes [5,6,7,8,9,10,11]. For instance, it also has been proved that the amount of photons could be created in the ways of changing the dielectric permeability of the medium in the cavity [12]. V. V. Dodonov also proposed that the photons created from the cavity could be registered by coupling the cavity with some detectors. When a harmonic oscillator acts the role of detector, the influence of the coupling strength between the field and the detector on photons creation was pointed out [13, 14]. Analogous to the detector of harmonic oscillator, the situations that the detectors are two-level atoms were also considered [4, 15].

In this paper, the system in an ideal cavity with vibrating walls in the resonance case, taking into account the interaction between the resonant field mode and a detector modeled by two two-level atoms. We suppose the atoms are in the ground states, and the field is in the squeezed vaccum state. We will analyze the influence of the squeezed coefficient, the atom-field coupling coefficients and the coupling coefficient of atoms on the dynamical Casimir effect and the dynamical behavior of the atoms.

This paper is organized as follows: in Section 2 we describe the model and get the Hamiltonian of the system. In Section 3 we will obtain analytical expressions of the number of the photons and the probability of double excitation of the two-atom. In Section 4 we will discussion the results and summarize our results. The last part is the appendix in Appendix.

2 Model

The simplest Hamiltonian in many studies on the dynamical Casimir effects about an ideal single-cavity mode is shown as (we set $\hbar$= 1) [16]

$$ \hat{H_{0}}=\omega (t)\hat{a}^{+}\hat{a}+i\chi (t)(\hat{a}^{+ 2}-\hat{a}^{2}), $$

(1)

where $\hat {a}^{+}(\hat {a})$ is the creation(annihilation) operator of the cavity, $\hat {a}^{+}\hat {a}$ is the photon number operator, and ω(t) is the cavity instantaneous eigenfrequency. We choose the time dependence of the cavity eigenfrequency in the harmonic form

$$ \omega (t)=\omega_{0}[1+\varepsilon \sin (\eta t)], $$

(2)

where ε is the modulation amplitude and η is the frequency of modulation. The relationship between the squeezing coefficientχ(t) and ω(t) is shown as

$$ \chi (t)=\frac{1}{4\omega (t)}\frac{d\omega (t)}{dt}, $$

(3)

Moreover, for |ε| ≪ 1, we write ω(t) ≈ ω₀ and $\chi (t)\approx \frac { \varepsilon \eta }{4}\cos (\eta t)$ for simplicity.

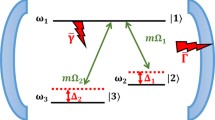
For detecting the cavity DCE, we take the two two-level atoms inserted in the cavity. The interaction of atom-field and the two atoms is described as

$$ \hat{H}_{D}=\lambda_{1}(\hat{ \sigma}_{1}^{+}\hat{a}+\hat{\sigma}_{1}^{-}\hat{a}^{+})+\lambda_{2}(\hat{ \sigma}_{2}^{+}\hat{a}+\hat{\sigma}_{2}^{-}\hat{a}^{+})+J\hat{\sigma}_{1}^{z} \hat{\sigma}_{2}^{z}, $$

(4)

The time-dependent Hamiltonian of the system in the dipole and rotating-wave approximation is given as

$$\begin{array}{@{}rcl@{}} \hat{H}&=&\omega (t)\hat{a}^{+}\hat{a}+i\chi (t)(\hat{a}^{+ 2}-\hat{a}^{2})+\frac{ {\Omega} }{2}(\hat{\sigma}_{1}^{z}+\hat{\sigma}_{2}^{z})+\lambda_{1}(\hat{ \sigma}_{1}^{+}\hat{a}+\hat{\sigma}_{1}^{-}\hat{a}^{+})\\ &&+ \lambda_{2}(\hat{ \sigma}_{2}^{+}\hat{a}+\hat{\sigma}_{2}^{-}\hat{a}^{+})+J\hat{\sigma}_{1}^{z} \hat{\sigma}_{2}^{z}, \end{array} $$

(5)

where Ω is the atomic transition frequency which is assumed to be the same for two atoms, λ₁ and λ₂ are the weak atom-field coupling constants of two atoms, J stands for the coupling constant between two atoms. The Pauli operators $\hat {\sigma }^{\pm }$ and atom operator $\hat {\sigma }^{z}$ are shown as follows

$\hat {\sigma }^{z}=\left (\begin {array}{ll} 1 & 0 \\ 0 & -1 \end {array} \right ) ,$$\hat {\sigma }^{+}=\left (\begin {array}{ll} 0 & 1 \\ 0 & 0 \end {array} \right ) ,$$\hat {\sigma }^{-}=\left (\begin {array}{ll} 0 & 0 \\ 1 & 0 \end {array} \right )$.

3 Analytical Solutions

The aim of this paper is to get the number of the created photons and the dynamical behaviors of the two-atom. As the Hamiltonian is time-dependent, it is difficult for us to solve the Schrö dinger equation and get the formal solution $\left \vert {\Psi } \left (t\right ) \right \rangle =\hat {U}\left \vert {\Psi } \left (0\right ) \right \rangle$$(\hat { U}=e^{-it\hat {H}})$ exactly. The first step in obtaining analytical solutions is to go to the interaction picture by means of the time-dependent unitary transformation $\left \vert {\Psi } \left (t\right ) \right \rangle =\hat {V}\left \vert \psi \left (t\right ) \right \rangle$. We choose the time-dependent transformation operator as

$$ \hat{V}\left( t\right) =\exp \left[ -\frac{it\eta }{2}\left( \hat{N}+\frac{ \hat{\sigma}_{1}^{z}}{2}+\frac{\hat{\sigma}_{2}^{z}}{2}\right) \right] , $$

(6)

utilizing the substitutions mentioned above ω(t) ≈ ω₀ and $\chi (t)\approx \frac {\varepsilon \eta }{4}\cos (\eta t),$ then we can get the new time-independent Hamiltonian

$$ \hat{H}_{I}=\hat{V}^{+}\left( t\right) \hat{H}_{s}\hat{V}\left( t\right) -i \hat{V}^{+}\left( t\right) \frac{d}{dt}\hat{V}\left( t\right) , $$

(7)

under the restriction of rotating wave approximation as

$$\begin{array}{@{}rcl@{}} \hat{H}_{I}&=&\left( \omega_{0}-\frac{\eta }{2}\right) \hat{N}+\frac{i\varepsilon \eta }{8}(\hat{a}^{+ 2}-\hat{a}^{2})+\frac{1}{2}\left( {\Omega} -\frac{\eta }{2} \right) (\hat{\sigma}_{1}^{z}+\hat{\sigma}_{2}^{z})\\ &&+ \lambda_{1}(\hat{\sigma}_{1}^{+}\hat{a}+\hat{\sigma}_{1}^{-}\hat{a}^{+})+\lambda_{2}(\hat{\sigma} _{2}^{+}\hat{a}+\hat{\sigma}_{2}^{-}\hat{a}^{+})+J\hat{\sigma}_{1}^{z}\hat{ \sigma}_{2}^{z}. \end{array} $$

(8)

To obtain the average number of photons, we should caculate the time evolution operator $\hat {U}$. For simplicity we set $-it\hat {H}=-it\hat {A} +-it\hat {B}$ where

$$\begin{array}{@{}rcl@{}} \hat{A} &=&\left( \omega_{0}-\frac{\eta }{2}\right) \hat{N}+\frac{ i\varepsilon \eta }{8}(\hat{a}^{+ 2}-\hat{a}^{2}), \\ \hat{B} &=&\frac{1}{2}\left( {\Omega} -\frac{\eta }{2}\right) (\hat{\sigma} _{1}^{z}+\hat{\sigma}_{2}^{z})+\lambda_{1}(\hat{\sigma}_{1}^{+}\hat{a}+\hat{ \sigma}_{1}^{-}\hat{a}^{+})+\lambda_{2}(\hat{\sigma}_{2}^{+}\hat{a}+\hat{ \sigma}_{2}^{-}\hat{a}^{+})+J\hat{\sigma}_{1}^{z}\hat{\sigma}_{2}^{z}. \end{array} $$

(9)

Using the formula $\hat {U}=e^{-it\hat {H}}\approx e^{-\frac {t^{2}}{2} \left [ \hat {A}\hat {,}\hat {B}\right ] }e^{-it\hat {B}}e^{-it\hat {A}}$, where $\left [ \hat {A},\hat {B}\right ]$ is shown as follow

$$ \left[ \hat{A},\hat{B}\right] =\sum\limits_{j = 1}^{2}\lambda_{j}\left[ \frac{\alpha }{2}\left( -\hat{\sigma}_{j}^{+}\hat{a}+\sigma_{j}^{-}a^{+}\right) -i\beta \left( \hat{\sigma}_{j}^{+}\hat{a}^{+}+\hat{ \sigma}_{j}^{-}\hat{a}\right) \right] , $$

(10)

where $\alpha = 2(\omega _{0}-\frac {\eta }{2}),\beta =\frac {\varepsilon \eta }{4}$. The evolution operator for Hamiltonian (8) could be easily obtained in a form of the matrix. Here we use the basis {|φ₁〉 , |φ₂〉 , |φ₃〉 , |φ₄〉} (|φ₁〉 = |e₁〉 |e₂〉 , |φ₂〉 = |e₁〉 |g₂〉 , |φ₃〉 = |g₁〉 |e₂〉 , |φ₄〉 = |g₁〉 |g₂〉). For simplicity, it is supposed that the initial state is

$$ \left\vert {\Psi} \left( 0\right) \right\rangle =\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ {0_{s}} \end{array} \right) , $$

(11)

where the atoms are in the ground states |g₁〉 |g₂〉. The field is in the squeezed vaccum state |0_s〉which is shown as

$$ {|0_{s}\rangle}=\exp\left( \frac{1}{2}\gamma\hat{a}^{2}-\frac{1}{2}\gamma\hat{a}^{+ 2}\right) |0\rangle, $$

(12)

We assume the squeezed coefficient γ is real for simplicity. The state vector at any time can be expressed as

$$ \left\vert {\Psi} \left( t\right) \right\rangle =\left( \begin{array}{cccc} U_{11} & U_{12} & U_{13} & U_{14} \\ U_{21} & U_{22} & U_{23} & U_{24} \\ U_{31} & U_{32} & U_{33} & U_{34} \\ U_{41} & U_{42} & U_{43} & U_{44} \end{array} \right)\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ {0_{s}} \end{array} \right) , $$

(13)

We mainly put attention to the numbers of the photon generated and the dynamical behaviors of the two-atom. Therefore we just need to caculate the four factors(U₁₄, U₂₄, U₃₄, U₄₄) of the 4 × 4 matrix. The forms of the four factors are given as follows neglecting the terms of the order of ${\lambda _{1}^{m}}{\lambda _{2}^{n}}$ (m + n ≥ 3)

$$\begin{array}{@{}rcl@{}} U_{14} &=&(A_{14}\hat{a}^{2}+B_{14}\hat{a^{+}}\hat{a}+C_{14}\hat{a}^{+ 2})e^{-\frac{1}{2}\beta t\hat{a}^{2}+\frac{1}{2}\beta t\hat{a}^{+ 2}}, \end{array} $$

(14)

$$\begin{array}{@{}rcl@{}} U_{24} &=&\left( A_{24}\hat{a}^{+}+B_{24}\hat{a}\right)e^{-\frac{1}{2}\beta t\hat{a}^{2}+\frac{1}{2}\beta t\hat{a}^{+ 2}}, \end{array} $$

(15)

$$\begin{array}{@{}rcl@{}} U_{34} &=&\left( A_{34}\hat{a}^{+}+B_{34}\hat{a}\right)e^{-\frac{1}{2}\beta t\hat{a}^{2}+\frac{1}{2}\beta t\hat{a}^{+ 2}}, \end{array} $$

(16)

$$\begin{array}{@{}rcl@{}} U_{44} &=&\left( A_{44}\hat{a}^{2}+B_{44}\hat{a}\hat{a}^{+}+C_{44}\hat{a}^{+}\hat{a}+D_{44}\right) e^{-\frac{1}{2}\beta t\hat{a}^{2}+\frac{1}{2}\beta t\hat{a}^{+ 2}}. \end{array} $$

(17)

where

$$\begin{array}{@{}rcl@{}} A_{14} &=&\lambda_{1}\lambda_{2} \left( -t^{2}+it^{3}k_{1}+\frac{ t^{4}}{4}k_{1}k_{2}\right)e^{it(M-J)},\\ B_{14} &=&\lambda_{1}\lambda_{2}\left( \beta t^{3}-\frac{i\beta t^{4}k_{2}}{2}\right) e^{it(M-J)},\\ C_{14} &=&-\lambda_{1}\lambda_{2}\left( \frac{\beta^{2}t^{4}}{4}\right) e^{it(M-J)},\\ A_{24} &=&\frac{i\lambda_{1}\beta t^{2}}{2} e^{it(M-J)},\\ B_{24} &=&-\lambda_{1}\left( it+\frac{ t^{2}k_{2}}{2}\right)e^{it(M-J)},\\ A_{34} &=&\frac{i\lambda_{2}\beta t^{2}}{2} e^{it(M-J)},\\ B_{34} &=&-\lambda_{2}\left( it+\frac{ t^{2}k_{2}}{2}\right)e^{it(M-J)},\\ A_{44} &=&\left( \frac{\beta t^{3}}{2}-\frac{i\beta t^{4}k_{2}}{4}\right)({\lambda_{1}^{2}}+\lambda_{2}^{2}) e^{it(M-J)},\\ B_{44} &=&-({\lambda_{1}^{2}}+{\lambda_{2}^{2}})\left( \frac{ \beta^{2}t^{4}}{8}\right)e^{it(M-J)},\\ C_{44} &=&-({\lambda_{1}^{2}}+{\lambda_{2}^{2}})\left( \frac{it^{3}k_{2}}{2}+\frac{t^{4}{k_{2}^{2}}}{4}+\frac{t^{2}}{2}\right)e^{it(M-J)},\\ D_{44} &=&e^{it(M-J)}. \end{array} $$

(18)

where k₁ = M + 2J, k₂ = M − 2J, $M={\Omega } -\frac {\eta }{2},$α = 0,(here we set $\omega _{0}=\frac {\eta }{2})$. Therefore, the average number of photons $\left \langle \hat {N}\left (t\right ) \right \rangle$ is shown as

$$\begin{array}{@{}rcl@{}} \left\langle \hat{N}\left( t\right) \right\rangle \!&=&\!- 6L_{31}\sinh^{3}\gamma\cosh\gamma+ 2L_{42}(-3\sinh^{3}\gamma\cosh^{3}\gamma-12\sinh^{5}\gamma\cosh\gamma)\\ &&+ 6L_{40}\sinh^{2}\gamma\cosh^{2}\gamma+ 30L_{51}\sinh^{4}\gamma\cosh^{2}\gamma-2L_{20}\sinh\gamma\cosh\gamma\\ &&- 30L_{60}\sinh^{3}\gamma\cosh^{3}\gamma-6M_{31}\sinh^{3}(-\beta t)\cosh(-\beta t)\\ &&+ 2M_{42}[-3\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)-12\sinh^{5}(-\beta t)\cosh(-\beta t)]\\ &&+ 6M_{40}\sinh^{2}(-\beta t)\cosh^{2}(-\beta t)+ 90M_{51}\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)\\ &&- 2M_{20}\sinh(-\beta t)\cosh(-\beta t) + L_{11}\sinh^{2}\gamma + L_{22}(2\sinh^{4}\gamma+\sinh^{2}\gamma\cosh^{2}\gamma)\\ &&+ L_{33}(6\sinh^{6}\gamma + 9\sinh^{4}\gamma\cosh^{2}\gamma) + M_{33}[6\sinh^{6}(-\beta t)\\ &&+ 9\sinh^{4}(-\beta t)\cosh^{2}(- \beta t)]+M_{11}\sinh^{2}(-\beta t)+M_{22}[2\sinh^{4}(-\beta t)\\ &&+ \sinh^{2}(-\beta t)\cosh^{2}(-\beta t)]+M_{00}. \end{array} $$

(19)

The parameters M₃₃, M₃₁, M₄₂, M₄₀, M₅₁, M₁₁, M₂₂, M₂₀, M₀₀, L₃₃, L₃₁, L₄₂, L₅₁, L₆₀, L₂₂, L₄₀, L₂₀ and L₁₁ are in Appendix. We also can obtain the probability of double excitation of the two-atom

$$\begin{array}{@{}rcl@{}} P_{{e_{1},e_{2}}}&\equiv&|\langle e_{1},e_{2}|{\Psi}(t)\rangle|^{2} \\ &=&(2\sinh^{4}\gamma+\sinh^{2}\gamma\cosh^{2}\gamma)(|f_{1}|^{2}+|f_{2}|^{2}+|f_{4}|^{2})\\ &&+ \sinh^{2}\gamma(4|f_{2}|^{2}+|f_{4}|^{2}+f_{4}{f}_{3}^{*}+ {f}_{4}^{*}f_{3})\\ &&+ 3\sinh^{2}\gamma\cosh^{2}\gamma(f_{1}{f}_{2}^{*}+{f}_{1}^{*}f_{2})+ 2|f_{2}|^{2}+|f_{3}|^{2}\\ &&- \sinh\gamma\cosh\gamma(f_{1}{f}_{3}^{*}+{f}_{1}^{*}f_{3}+f_{2}{f}_{3}^{*} + {f}_{2}^{*}f_{3}+ 4f_{2}{f}_{4}^{*}+ 4 {f}_{2}^{*}f_{4})\\ &&- 3\sinh^{3}\gamma\cosh\gamma(f_{1}f_{4}^{*}+f_{1}^{*}f_{4}+f_{2}f_{4}^{*}+f_{2}^{*}f_{4}). \end{array} $$

(20)

where

$$\begin{array}{@{}rcl@{}} f_{1}\!&=&\!A_{14}cosh^{2}(-\beta t)-B_{14}\sinh(-\beta t)\cosh(-\beta t)+C_{14}\sinh^{2}(-\beta t),\\ f_{2}\!&=&\!A_{14}\sinh^{2}(-\beta t)-B_{14}\sinh(-\beta t)\cosh(-\beta t)+C_{14}cosh^{2}(-\beta t),\\ f_{3}\!&=&\!-A_{14}\sinh(-\beta t)\cosh(-\beta t) + B_{14}\sinh^{2}(-\beta t) - C_{14}\sinh(-\beta t)\cosh(-\beta t),\\ f_{4}\!&=&\!-2A_{14}\sinh(-\beta t)\cosh(-\beta t)+B_{14}\cosh(-2\beta t)-2C_{14}\sinh(-\beta t)\cosh(-\beta t). \end{array} $$

(21)

4 Discussion and Conclusions

Via the analytical results in the section II,we can obtain the figures that report the average number of photons and the probability of double excitation of the two-atom as a function of time at different parameters.

In Figs. 1 and 2, it is clear that the number of the photons and the probability of double excitation of the two-atom under three different conditions all experience gradually upward trends. The red lines represent γ = 0.5. The green lines represent γ = 1. In Fig. 1, we can easily find the number of the photons of the red line is fewer,and the number of the photons of the green line is more at the same time. Figure 2 shows the probability of double excitation of the two-atom is always positive. It reveals that the atoms will possibility stay in the double excited states due to the absorption of photons. Figs. 1 and 2 show that the amount of the created photons and the probability of double excitation of the two-atom increase significantly with the increasing of the squeezed coefficient γ at the same time.

Fig. 1

The average number of the created photons of different squeezed coefficients γ. We have taken ε =0.02, β =0.01, ${\Omega } =\frac {\eta }{2}= 1,\lambda _{1}$ = λ₂= 0.0005, J= 0.0001. The red line represents γ= 0.5. The green one represents γ= 1

Fig. 2

The the probability of double excitation of the two-atom of different squeezed coefficients γ.We have taken $\varepsilon = 0.02, \beta = 0.01, {\Omega } =\frac {\eta }{2}= 1,\lambda _{1}=\lambda _{2}= 0.0005, J = 0.0001$. The red line represents γ = 0.5. The green one represents γ = 1

In Figs. 3 and 4, we can see the influence of the weak atom-field coupling constants λ₁, λ₂ on the number of the photons and the probability of double excitation of the two-atom. The red lines denote λ₁ = λ₂ = 0.0005. The green lines denote λ₁ = λ₂ = 0.001. The number of the photons and the probability of double excitation under the different weak atom-field coupling constants are also gradually upward trends. Figure 3 shows the amount of the created photons increases significantly with the decreasing of the weak atom-field coupling constants λ₁, λ₂ at the same time, but Fig. 4 shows the probability of double excitation of the two-atom increases significantly with the increasing of the weak atom-field coupling constants λ₁, λ₂ at the same time.It reveals the greater the atom-field coupling constants are, the more likely the atoms are in the double excited states.

Fig. 3

The average number of the created photons of different weak atom-field coupling constants λ₁, λ₂.We have taken $\varepsilon = 0.02, \beta = 0.01, {\Omega } =\frac {\eta }{2}= 1, \gamma = 0.5, J = 0.0001$. The red line represents λ₁ = λ₂ = 0.0005. The green one represents λ₁ = λ₂ = 0.001

Fig. 4

The probability of double excitation of the two-atom of different weak atom-field coupling constants λ₁, λ₂.We have taken $\varepsilon = 0.02, \beta = 0.01, {\Omega }=\frac {\eta }{2}= 1, \gamma = 0.5, J = 0.0001$. The red line represents λ₁ = λ₂ = 0.0005. The green one represents λ₁ = λ₂ = 0.001

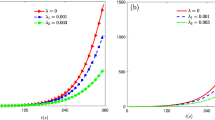
In Figs. 5 and 6, they show the influence of the coupling constant J between the two atoms on the number of the photons and the probability of double excitation of the two-atom. In Fig. 5, we find that the rate of photons creation slightly slows down with the increasing value of the coupling constant J between the two atoms. The larger the value of J selected, the fewer photons generated. That is to say, the interaction between the two atoms restrains the generation of photons in the cavity. In Fig. 6, we find that the probability of double excitation slightly grows up with the increasing value of the coupling constant J between the two atoms. The larger the value of J selected, the more likely the atoms are in the double excited states.

Fig. 5

The average number of the created photons of different coupling constants between atoms J.We have taken $\varepsilon = 0.02, \beta = 0.01, {\Omega } =\frac {\eta }{2}= 1, \lambda _{1}=\lambda _{2}= 0.0005, \gamma = 0.5$. The values of J in these two lines are all 0.00005 and 0.0005 from the red line to the blue line respectively

Fig. 6

The probability of double excitation of the two-atom of different coupling constants between atoms.We have taken $\varepsilon = 0.02, \beta = 0.01, {\Omega } =\frac {\eta }{2}= 1,\lambda _{1}=\lambda _{2}= 0.0005, \gamma = 0.5$. The values of J in these two lines are all 0.00005 and 0.0005 from the red line to the blue line respectively

In conclusion, we obtained closed analytical expressions for the atom-field dynamics generated by the dynamical Casimir effect. It is clear that the number of the photons and the probability of double excitation of the two-atom under the above conditions all experience gradually upward trends. It reveals that the atoms will possibility stay in the double excited states due to the absorption of the photons by the DCE. We also find that the squeezed coefficient γ, the atom-field coupling constants (λ₁, λ₂) and the atom-atom coupling constant J have effect on the generation of the photons and the probability of double excitation of the two-atom. The squeezed coefficient γ promotes the generation rate of the created photons, but both the atom-field coupling constants (λ₁, λ₂) and the atom-atom coupling constant J restrain the generation rate of the created photons. The larger the value of the coupling constants λ₁, λ₂ and J selected, the fewer photons generated. Due to the interaction of the atoms and the field, the probability of double excitation of the two-atom increases with the coupling coefficients λ₁, λ₂, J and the squeezed coefficient γ.

Appendix

A note must be added. The parameters M₃₃, M₃₁, M₄₂, M₄₀, M₅₁, M₁₁, M₂₂, M₂₀, M₀₀, L₃₃, L₃₁, L₄₂, L₅₁, L₆₀, L₂₂, L₄₀, L₂₀ and L₁₁ in (19) can be expressed by

$$\begin{array}{@{}rcl@{}} M_{33}&=&|A_{14}|^{2}+|B_{14}|^{2}+|C_{14}|^{2}+|A_{44}|^{2}+|B_{44}|^{2}+|C_{44}|^{2}+B_{44}^{*}C_{44}+B_{44}C_{44}^{*}, \end{array} $$

(22)

$$\begin{array}{@{}rcl@{}} M_{31}&=& A_{14}^{*}B_{14}+ 5C_{14}B_{14}^{*}+A_{24}B_{24}^{*}+A_{34}B_{34}^{*}+A_{44}^{*}D_{44}+ 2A_{44}^{*}B_{44}+A_{44}^{*}C_{44}, \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}} M_{42}&=& A_{14}^{*}B_{14}+C_{14}B_{14}^{*}+A_{44}^{*}B_{44}+A_{44}^{*}C_{44}, \end{array} $$

(24)

$$\begin{array}{@{}rcl@{}} M_{40}&=& 2A_{14}^{*}C_{14}, \end{array} $$

(25)

$$\begin{array}{@{}rcl@{}} M_{51}&=& A_{14}^{*}C_{14}, \end{array} $$

(26)

$$\begin{array}{@{}rcl@{}} M_{11}&=& |B_{14}|^{2}+ 14|C_{14}|^{2}+ 3|A_{24}|^{2}+ 3|A_{34}|^{2}+|D_{44}|^{2}+ 4|B_{44}|^{2}+|C_{44}|^{2}\\ &&+ 2D_{44}^{*}B_{44}+ 2D_{44}B_{44}^{*}+D_{44}^{*}C_{44}+D_{44}C_{44}^{*}+ 2C_{44}B_{44}^{*}+ 2C_{44}^{*}B_{44}, \end{array} $$

(27)

$$\begin{array}{@{}rcl@{}} M_{22}&=& 3|B_{14}|^{2}+ 8|C_{14}|^{2}+|A_{24}|^{2}+|A_{34}|^{2} + |B_{24}|^{2}+|B_{34}|^{2}+ 5|B_{44}|^{2}+ 3|C_{44}|^{2}\\ &&+ D_{44}^{*}B_{44}+D_{44}B_{44}^{*}+D_{44}^{*}C_{44}+D_{44}C_{44}^{*}+ 4C_{44}B_{44}^{*}+ 4C_{44}^{*}B_{44}, \end{array} $$

(28)

$$\begin{array}{@{}rcl@{}} M_{20}&=& 4B_{14}^{*}C_{14}+A_{24}B_{24}^{*}+A_{34}B_{34}^{*}, \end{array} $$

(29)

$$\begin{array}{@{}rcl@{}} M_{00}&=& 4|C_{14}|^{2}+|A_{24}|^{2}+|A_{34}|^{2} . \end{array} $$

(30)

$$\begin{array}{@{}rcl@{}} L_{33} &=& M_{33}\left[\cosh^{6}(-\beta t)+\sinh^{6}(-\beta t)+ 9\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)\right.\\ &&\left.+ 9\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)\right]\\ &&+ (M_{51}+M_{51}^{*})\left[10\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)+ 10\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)\right]\\ &&+ (M_{42}+M_{42}^{*})\left[-4\sinh(-\beta t)\cosh^{5}(-\beta t)-4\sinh^{5}(-\beta t)\cosh(-\beta t)\right.\\ &&\left.- 12\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)\right], \end{array} $$

(31)

$$\begin{array}{@{}rcl@{}} L_{31} &=& M_{33}\left[-3\cosh^{5}(-\beta t)\sinh(-\beta t)-36\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)\right.\\ &&\left.- 21\sinh^{5}(-\beta t)\cosh(-\beta t)\right] \\ &&+ M_{31}\left[\cosh^{4}(-\beta t)+ 3\sinh^{2}(-\beta t)\cosh^{2}(-\beta t)\right]\\ &&+ M_{31}^{*}\left[\sinh^{4}(-\beta t)+ 3\sinh^{2}(-\beta t)\cosh^{2}(-\beta t)\right]\\ &&- 4M_{40}\sinh(-\beta t)\cosh^{3}(-\beta t)-4M_{40}^{*}\sinh^{3}(-\beta t)\cosh(-\beta t)\\ &&- 2M_{22}[\sinh(-\beta t)\cosh^{3}(-\beta t)+\sinh^{3}(-\beta t)\cosh(-\beta t)]\\ &&- M_{51}[50\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)+ 10\sinh(-\beta t)\cosh^{5}(-\beta t)]\\ &&- M_{51}^{*}[30\sinh^{5}(-\beta t)\cosh(-\beta t)+ 30\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)]\\ &&+ M_{42}[24\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)+ 36\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)] \\ &&+ M_{42}^{*}[40\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)\\ &&+ 12\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)+ 8\sinh^{6}(-\beta t)], \end{array} $$

(32)

$$\begin{array}{@{}rcl@{}} L_{42} &=& M_{33}\left[-3\cosh^{5}(-\beta t)\sinh(-\beta t)-9\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)\right.\\ &&\left.- 3\sinh^{5}(-\beta t)\cosh(-\beta t)\right] \\ &&- M_{51}[10\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)+ 5\sinh(-\beta t)\cosh^{5}(-\beta t)]\\ &&- M_{51}^{*}[5\sinh^{5}(-\beta t)\cosh(-\beta t)+ 10\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)]\\ &&+ M_{42}[\cosh^{6}(-\beta t)+ 8\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)+ 6\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)] \\ &&+ M_{42}^{*}[6\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)\\ &&+ 8\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)+\sinh^{6}(-\beta t)], \end{array} $$

(33)

$$\begin{array}{@{}rcl@{}} L_{51} &=& M_{33}\left[3\cosh^{4}(-\beta t)\sinh^{2}(-\beta t)+ 3\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)\right] \\ &&+ M_{51}\left[\cosh^{6}(-\beta t)+ 5\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)\right]\\ &&+ M_{51}^{*}\left[\sinh^{6}(-\beta t)+ 5\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)\right]\\ &&- M_{42}[2\sinh(-\beta t)\cosh^{5}(-\beta t)+ 4\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)]\\ &&- M_{42}^{*}[2\sinh^{5}(-\beta t)\cosh(-\beta t)+ 4\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)], \end{array} $$

(34)

$$\begin{array}{@{}rcl@{}} L_{60} &=& - M_{51}\sinh(-\beta t)\cosh^{5}(-\beta t)-M_{51}^{*}\sinh^{5}(-\beta t)\cosh(-\beta t)\\ &&+ M_{42}\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)+M_{42}^{*}\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)], \end{array} $$

(35)

$$\begin{array}{@{}rcl@{}} L_{22} &=& M_{33}\left[18\cosh^{4}(-\beta t)\sinh^{2}(-\beta t)+ 54\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)+ 9\sinh^{6}(-\beta t)\right] \\ &&- 3(M_{31}+M_{31}^{*})\left[\cosh^{3}(-\beta t)\sinh(-\beta t)+\sinh^{3}(-\beta t)\cosh(-\beta t)\right]\\ &&+ 6(M_{40}+M_{40}^{*})\cosh^{2}(-\beta t)\sinh^{2}(-\beta t)\\ &&+ M_{22}[\cosh^{4}(-\beta t)+\sinh^{4}(-\beta t)+ 4\sinh^{2}(-\beta t)\cosh^{2}(-\beta t)]\\ &&+ (M_{51}+M_{51}^{*})[60\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)+ 30\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)]\\ &&+ (M_{42}+M_{42}^{*})\left[-54\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)-30\sinh^{5}(-\beta t)\cosh(-\beta t)\right.\\ &&\left.- 6\sinh(-\beta t)\cosh^{5}(-\beta t)\right] , \end{array} $$

(36)

$$\begin{array}{@{}rcl@{}} L_{40} &=& M_{33}\left[3\cosh^{4}(-\beta t)\sinh^{2}(-\beta t)+ 12\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)\right] \\ &&- M_{31}\cosh^{3}(-\beta t)\sinh(-\beta t)-M_{31}^{*}\cosh(-\beta t)\sinh^{3}(-\beta t)\\ &&+ M_{40}\cosh^{4}(-\beta t)+M_{40}^{*}\sinh^{4}(-\beta t)+M_{22}\cosh^{2}(-\beta t)\sinh^{2}(-\beta t)\\ &&+ 15M_{51}\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)\\ &&+ M_{51}^{*}[5\sinh^{6}(-\beta t)+ 10\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)]\\ &&- M_{42}[\sinh(-\beta t)\cosh^{5}(-\beta t)+ 14\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)] \\ &&- M_{42}^{*}[9\sinh^{5}(-\beta t)\cosh(-\beta t)+ 6\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)], \end{array} $$

(37)

$$\begin{array}{@{}rcl@{}} L_{20} &=& M_{33}\left[-18\cosh^{3}(-\beta t)\sinh^{3}(-\beta t)-27\sinh^{5}(-\beta t)\cosh(-\beta t)\right] \\ &&+ 6M_{31}\sinh^{2}(-\beta t)\cosh^{2}(-\beta t) + M_{31}^{*}\left[3\sinh^{4}(-\beta t) + 3\sinh^{2}(-\beta t)\cosh^{2}(-\beta t)\right]\\ &&+ M_{20}\cosh^{2}(-\beta t)+M_{20}^{*}\sinh^{2}(-\beta t)\\ &&- 6M_{40}\sinh(-\beta t)\cosh^{3}(-\beta t)-6M_{40}^{*}\sinh^{3}(-\beta t)\cosh(-\beta t)\\ &&- M_{22}[\sinh(-\beta t)\cosh^{3}(-\beta t)+ 5\sinh^{3}(-\beta t)\cosh(-\beta t)]\\ &&- M_{11}\sinh(-\beta t)\cosh(-\beta t)\\ &&- 45M_{51}\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)\\ &&- 15M_{51}^{*}[2\sinh^{5}(-\beta t)\cosh(-\beta t)+\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)]\\ &&+ M_{42}[39\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)+ 6\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)] \\ &&+ M_{42}^{*}\left[30\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)\right.\\ &&\left.+ 3\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)+ 12\sinh^{6}(-\beta t)\right], \end{array} $$

(38)

$$\begin{array}{@{}rcl@{}} L_{11} &=& M_{33}\left[72\cosh^{2}(-\beta t)\sinh^{4}(-\beta t)+ 18\sinh^{6}(-\beta t)+ 9\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)\right] \\ &&- 3(M_{31}+M_{31}^{*})\left[3\cosh(-\beta t)\sinh^{3}(-\beta t)+\sinh(-\beta t)\cosh^{3}(-\beta t)\right]\\ &&- 2(M_{20}+M_{20}^{*})\sinh(-\beta t)\cosh(-\beta t)+ 12(M_{40}+M_{40}^{*})\cosh^{2}(-\beta t)\sinh^{2}(-\beta t)\\ &&+ M_{22}\left[4\sinh^{4}(-\beta t)+ 8\sinh^{2}(-\beta t)\cosh^{2}(-\beta t)\right]\\ &&+ M_{11}\left[\cosh^{2}(-\beta t)+\sinh^{2}(-\beta t)\right]\\ &&+ (M_{51}+M_{51}^{*})[75\sinh^{4}(-\beta t)\cosh^{2}(-\beta t)+ 15\sinh^{2}(-\beta t)\cosh^{4}(-\beta t)]\\ &&- (M_{42}+M_{42}^{*})[42\sinh^{3}(-\beta t)\cosh^{3}(-\beta t)+ 48\sinh^{5}(-\beta t)\cosh(-\beta t)]. \end{array} $$

(39)