The behavior of a three-level laser in the steady-state regime

Abstract

A system consisting of a three-level atom trapped in a single-mode optical cavity is theoretically investigated. Under different conditions, this system can illustrate the behaviors of a semi-classical laser or quantum treatments. The descriptive master equation of this system is solved numerically in the atom and cavity basis. The results show that near the semi-classical approximation for when a large number of photons are present in the cavity, the system described by the semi-classical laser theory and for when a small number of photons exist in the cavity and in the weak driving limit, the emitted light by the system is antibunching which is a quantum effect.

1 Introduction

Interactions of atoms and electromagnetic modes of an optical cavity form the basic theme of cavity quantum electrodynamics [1]. Cavity quantum electrodynamics has been a subject of many recent studies because of its importance in understanding the fundamental physics of the photon-atom interactions and potential for a wide array of applications in quantum physics and quantum electronics [2,3,4]. The system of an atom or a quantum dot interacting with the quantized field of a high-Q microcavity represents an important tool for the investigation of quantum electrodynamic effects. The possibility of realizing high-Q cavities both in optical and microwave regimes has enabled the observation of a number of remarkable effects, including vacuum Rabi splitting [5], photon antibunching [6], and conditional phase shifts for quantum logic gates [7]. Recently, a one-atom laser consisting of a single atom trapped inside a high-quality factor microcavity and externally pumped has been realized [8]. It was shown that the characteristics of the pumped atom-cavity system are qualitatively different from those of the familiar many-atom lasers. In particular, this one-atom laser produces nonclassical light and can act as an efficient source for deterministic generation of single-photon pulses [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40].

In the previous work [41], to solve the master equation, a combination of the continued fractions method and the quantum optics toolbox approach was used, which did not give an acceptable physical answer for some numerical values. Here, to solve this problem, the master equation is solved in the atom-cavity basis, which does not have the limitations mentioned in the previous methods. On the other hand, usually in the one-atom lasers, due to the self-quenching phenomenon, the lasing occurs in a limited domain [41, 42], while, here, due to the non-occurrence of this effect, the possibility of happening the lasing process exists in larger intervals. Here is a three-level atom enclosed in an optical cavity; the behavior of this system is examined from the perspective of dimensionless parameters. The master equation of the system is solved numerically in the basis of the atom and cavity interactions. It is shown that in the semi-classical approximation, the solution of the equation is independent of the critical photon number $N_{\gamma }$. The problem is then examined from a more general prospect of completely quantum explanation. The quantum model can conclude the conditions under which the semi-classical model is valid. The conclusions show that for large enough $N_{\gamma }$’s, the system behaves like a semi-classical laser, and for small enough values of $N_{\gamma }$ and in the weak driving limit, the system behaves as a two-level atom, under which the quantum effects of photon antibunching can be explained.

A summary of the results of this work is as follows: The three-level atom model confined in the cavity, the master equation of the system, and its solution in the semi-classical approximation are mentioned in Sect. 2. In Sect. 3, the master equation is solved numerically via a more general and complete prospect in the basis of the atom-cavity and comparing its simulations with the outcomes of the semi-classical approximation. The conditions of establishing the semi-classical approximation are discussed in the same section. The requirements for converting the three-level atom to an effective two-level one are given in Sect. 4 to explain the quantum effects. An outline of the results is also written in the last section.

2 Three-level laser

As shown in Fig. 1, the three-level atom is enclosed in the single-mode optical cavity. The 1–3 transition of the atom is driven by an incoherent pump field with the rate ${\varGamma }^\prime$. The coupling of the 2–3 atomic transition with the cavity field mode occurs with the coefficient g. The spontaneous decays of the atom from level 3 to level 2 and level 2 to level 1 occur at the rates $\gamma$ and ${\varGamma }$, respectively. Consider the 2–3 atomic transition frequency is in the resonance with the cavity one. The temporal evolution of this system is demonstrated in terms of the following master equation [43]:

$$\begin{aligned} {\dot{\rho }}=-{{\mathrm{i}}}\left[ g\left( a{\hat{A}}_{32}+{a^\dagger }{\hat{A}}_{23}\right) ,\rho \right] +{{\mathcal {L}}}_{31}\rho +{{\mathcal {L}}}_{23}\rho +{{\mathcal {L}}}_{12}\rho +{{\mathcal {L}}}_{c}\rho , \end{aligned}$$

(1)

where ${\hat{A}}_{ij}=|i\rangle \langle j|$ are the atomic raising and lowering operators. a and $a^{\dagger }$ are the photon annihilation and creation operators of the cavity field mode, and also we have:

$$\begin{aligned}&{{\mathcal {L}}}_{31}\rho =\frac{{\varGamma }^\prime }{2}\left( 2{\hat{A}}_{31}\rho {\hat{A}}_{13}-{\hat{A}}_{11}\rho -\rho {\hat{A}}_{11}\right) , \end{aligned}$$

(2)

$$\begin{aligned}&{{\mathcal {L}}}_{23}\rho =\frac{\gamma }{2}\left( 2{\hat{A}}_{23}\rho {\hat{A}}_{32}-{\hat{A}}_{33}\rho -\rho {\hat{A}}_{33}\right) , \end{aligned}$$

(3)

$$\begin{aligned}&{{\mathcal {L}}}_{12}\rho =\frac{{\varGamma }}{2}\left( 2{\hat{A}}_{12}\rho {\hat{A}}_{21}-{\hat{A}}_{22}\rho -\rho {\hat{A}}_{22}\right) , \end{aligned}$$

(4)

$$\begin{aligned}&{{\mathcal {L}}}_{c}\rho =\frac{\kappa }{2}\left( 2a\rho {a}^{\dagger }-{a}^{\dagger }a\rho -\rho {a}^{\dagger }a\right) , \end{aligned}$$

(5)

where ${{\mathcal {L}}}_{31}\rho$ is related to the incoherent pumping of the 1–3 atomic transition, ${{\mathcal {L}}}_{23}\rho$ and ${{\mathcal {L}}}_{12}\rho$ are associated with the spontaneous emissions of the atom from level 3 to 2 and from level 2 to 1, respectively, and also ${{\mathcal {L}}}_{c}\rho$ is corresponding to the cavity decay with the rate $\kappa$. Now that we have the master equation, the equations are first solved in the semi-classical approximation, then the master equation is written in the basis of the atom and cavity, and from then on, we compare their results. The temporal evolution of some physical quantities can be written as follows:

Fig. 1

The configuration of the energy levels of the three-level atom enclosed in the single-mode optical cavity

$$\begin{aligned}&{\dot{A}}_{11}=-({\varGamma }^\prime +{\varGamma }){A}_{11}-{\varGamma }{A}_{33}+{\varGamma }, \end{aligned}$$

(6)

$$\begin{aligned}&{\dot{A}}_{12}=-{\mathrm{i}}g\langle {\hat{A}}_{13}{a}^{\dagger }\rangle -\frac{1}{2}({\varGamma }+{\varGamma }^\prime ){A}_{12}, \end{aligned}$$

(7)

$$\begin{aligned}&{\dot{A}}_{13}=-{\mathrm{i}}g\langle {\hat{A}}_{12}a\rangle -\frac{1}{2}(\gamma +{\varGamma }^\prime ){A}_{13}, \end{aligned}$$

(8)

$$\begin{aligned}&{\dot{A}}_{23}=-{\mathrm{i}}g\alpha +{\mathrm{i}}g\langle {\hat{A}}_{11}a\rangle +2{\mathrm{i}}g\langle {\hat{A}}_{33}a\rangle -\frac{1}{2}(\gamma +{\varGamma }){A}_{23}, \end{aligned}$$

(9)

$$\begin{aligned}&{\dot{A}}_{33}=-{\mathrm{i}}g\langle {\hat{A}}_{32}a\rangle +{\mathrm{i}}g\langle {\hat{A}}_{23}{a}^{\dagger }\rangle +{\varGamma }^\prime {A}_{11}-\gamma {A}_{33}, \end{aligned}$$

(10)

$$\begin{aligned}&{{\dot{\alpha }}}=-{\mathrm{i}}g{A}_{23}-\frac{\kappa }{2}\alpha , \end{aligned}$$

(11)

due to the appearance of such expected values $\langle {\hat{A}}_{23}{a}^{\dagger }\rangle$, $\langle {\hat{A}}_{33}{a}\rangle$, etc., in Eqs. (7) to (10), these equations do not form a closed set. By applying the semi-classical approximation which assumes that the cavity field a resembles a classical field. This allows us to factorize operator expectation values such that $\langle {a}O\rangle \approx \langle {a}\rangle \langle {O}\rangle$ for any atomic operator O [44,45,46,47,48]. In this approximation the closed form of these equations is obtained as in the following:

$$\begin{aligned}&{\dot{A}}_{11}=-({\varGamma }^\prime +{\varGamma }){A}_{11}-{\varGamma }{A}_{33}+{\varGamma }, \end{aligned}$$

(12)

$$\begin{aligned}&{\dot{A}}_{12}=-{\mathrm{i}}g{A}_{13}{\alpha }^{*}-\frac{1}{2}({\varGamma }+{\varGamma }^\prime ){A}_{12}, \end{aligned}$$

(13)

$$\begin{aligned}&{\dot{A}}_{13}=-{\mathrm{i}}g{A}_{12}\alpha -\frac{1}{2}(\gamma +{\varGamma }^\prime ){A}_{13}, \end{aligned}$$

(14)

$$\begin{aligned}&{\dot{A}}_{23}=-{\mathrm{i}}g\alpha +{\mathrm{i}}g{A}_{11}\alpha +2{\mathrm{i}}g{A}_{33}\alpha -\frac{1}{2}(\gamma +{\varGamma }){A}_{23}, \end{aligned}$$

(15)

$$\begin{aligned}&{\dot{A}}_{33}=-{\mathrm{i}}g{A}_{32}\alpha +{\mathrm{i}}g{A}_{23}{\alpha }^{*}+{\varGamma }^\prime {A}_{11}-\gamma {A}_{33}, \end{aligned}$$

(16)

$$\begin{aligned}&{{\dot{\alpha }}}=-{\mathrm{i}}g{A}_{23}-\frac{\kappa }{2}\alpha , \end{aligned}$$

(17)

after substituting $\alpha =\alpha ^*$, ${A}_{23}={\mathrm{i}}{B}_{23}$, ${A}_{12}={\mathrm{i}}{B}_{12}$ and ${A}_{31}={A}_{13}$, Eqs. (12) to (17) take the following form:

$$\begin{aligned}&{\dot{A}}_{11}=-({\varGamma }^\prime +{\varGamma }){A}_{11}-{\varGamma }{A}_{33}+{\varGamma },\end{aligned}$$

(18)

$$\begin{aligned}&{\dot{B}}_{12}=-g{A}_{13}{\alpha }-\frac{1}{2}({\varGamma }+{\varGamma }^\prime ){B}_{12},\end{aligned}$$

(19)

$$\begin{aligned}&{\dot{A}}_{13}=g{B}_{12}\alpha -\frac{1}{2}(\gamma +{\varGamma }^\prime ){A}_{13},\end{aligned}$$

(20)

$$\begin{aligned}&{\dot{B}}_{23}=-g\alpha +g{A}_{11}\alpha +2g{A}_{33}\alpha -\frac{1}{2}(\gamma +{\varGamma }){B}_{23},\end{aligned}$$

(21)

$$\begin{aligned}&{\dot{A}}_{33}=-2g{B}_{23}\alpha +{\varGamma }^\prime {A}_{11}-\gamma {A}_{33},\end{aligned}$$

(22)

$$\begin{aligned}&{{\dot{\alpha }}}=g{B}_{23}-\frac{\kappa }{2}\alpha , \end{aligned}$$

(23)

after defining the following dimensionless parameters, Eqs. (18) to (23) are solved in the steady-state:

$$\begin{aligned} N_{A}=\frac{\kappa \gamma }{4{g}^{2}},N_{\gamma }=\frac{\gamma ^2}{4{g}^{2}},p=\frac{{\varGamma }^\prime }{\gamma },\eta =\frac{\gamma }{{\varGamma }},m=\frac{n}{N_{\gamma }}, \end{aligned}$$

(24)

where $N_A$ is the critical atom number corresponding to the number of atoms required to have an appreciable effect on the intracavity field, $N_\gamma$ is the critical photon number refers to the number of the photons needed to saturate an intracavity atom, p is the pumping strength, $\eta$ is the ratio of spontaneous emission rates, and m is the scaled photon number and $n={|\alpha |}^{2}$ is the intracavity photon number [49,50,51,52,53]. In the steady-state, two answers are obtained for m, one of which is $m = 0$, and the other is calculated from the following equation:

$$\begin{aligned} m=\frac{(\eta (1-\eta )-(1+\eta )^{2}N_{A})p-N_{A}(1+\eta )}{\eta {N}_{A}(2\eta {p}+1)}, \end{aligned}$$

(25)

since the solution of m is independent of $N_{\gamma }$, in the next section it will be confirmed that for large enough $N_{\gamma }$’s, the semi-classical approximation is established which is also to be expected physically. For sufficiently large amounts of p, the saturated scaled photon number is derived from this equation:

$$\begin{aligned} m_{sat}=\frac{\eta (1-\eta )-(1+\eta )^{2}N_{A}}{2{\eta }^{2}{N}_{A}}, \end{aligned}$$

(26)

the root of m in Eq. (25) is given by:

$$\begin{aligned} {p}_{1}=\frac{{N}_{A}(1+\eta )}{\eta (1-\eta )-(1+\eta )^{2}N_{A}}, \end{aligned}$$

(27)

which characterizes the laser threshold. In Eq. (25), the sign of m is specified by the numerator’s one; if m is negative, then $m=0$ will be the stable solution, defined as the nonlasing regime; if m is positive, below the threshold for $p<{p}_{1}$, the solution of $m=0$ is stable, and above the threshold for $p>{p}_{1}$, the nonzero m is the stable solution which is called the lasing regime [54,55,56]. Physically, m can take zero or positive values. In the parametric space, the plotted $N_A$ curve in terms of $\eta$ in Fig. 2 distinguishes the lasing and nonlasing regimes from one another. The system is on the lasing regime below this curve and the nonlasing regime above the curve. Since ${\tilde{n}}=\kappa n$ is the rate of photon emission out of the cavity, its nonvanishing value as $\kappa$ tends to zero delineates the appearance of a finite laser output even as we get arbitrarily close to a perfect cavity, by a corresponding increase in the photon generation inside. It is physically interpreted as an explosion of stimulated emission, typical for the lasing regime [57]. In this case, it can be shown as:

$$\begin{aligned} \frac{{\tilde{n}}}{\gamma }=\frac{(1-\eta )p}{2\eta {p}+1}, \end{aligned}$$

(28)

Fig. 2

The curve of $N_A$ versus $\eta$ separating the lasing and nonlasing regimes from each other

which is an increasing function of p. Below threshold for $p<{p}_{1}$, we have:

$$\begin{aligned}&{B}_{23}=0, \end{aligned}$$

(29)

$$\begin{aligned}&{A}_{33}=\frac{p}{1+p+\eta {p}}, \end{aligned}$$

(30)

$$\begin{aligned}&{A}_{11}=\frac{{A}_{33}}{p}, \end{aligned}$$

(31)

Fig. 3

The diagrams of population inversion and scaled photon number in terms of p in the semi-classical approximation for $N_{A}=0.01$ and $\eta =0.6$

and above threshold for $p>{p}_{1}$, we have:

$$\begin{aligned}&{B}_{23}={N}_{A}\sqrt{m}, \end{aligned}$$

(32)

$$\begin{aligned}&{A}_{33}=\frac{\eta {p}+{N}_{A}{p}(\eta +1)-\eta {m}{N}_{A}}{\eta (1+2p)}, \end{aligned}$$

(33)

$$\begin{aligned}&{A}_{11}=\frac{{A}_{33}+m{N}_{A}}{p}. \end{aligned}$$

(34)

In Fig. 3, the graphs of the atomic population inversion $A_{33}-A_{22}$ and the scaled photon number m are shown in terms of p for $N_{A}=0.01$ and $\eta =0.6$. The population inversion is the probability difference of finding an electron between the second and third levels. It is clear from the figure that the population inversion is positive, and the m curve shows a distinct laser threshold; with increasing p, the scaled photon number steps up until it finally reaches the saturation value (see also Fig. 5). The following section examines the conditions for which quantities of $N_\gamma$ the semi-classical approximation to hold.

3 Quantum outlook

In the previous section, the solution of equations in the semi-classical approximation and its relations were explained. In this section, the applied constraints in the semi-classical approximation are set aside, and a close model to the real one or the same fully quantum pattern is discussed. The results of the quantum model are compared with the semi-classical predictions, thus identifying cases close to and far from the semi-classical approximation. For this purpose, first, the system’s behavior is studied near the threshold, such as $p=1.3{p}_{1}$; then, the master equation is written in the atom-cavity basis. In Fig. 4, several $N_A$ curves are drawn versus $\eta$ for different values of $m(1.3{p}_{1})$. If we move down from the curve of $m=0$ in this figure, it is obvious that we are moving away from the semi-classical laser theory and the values of $m(1.3{p}_{1})$ grow. In this case, the quantum effects are expected to appear in the system and based on the relation $m(1.3{p}_{1})=n(1.3{p}_{1})/{N}_{\gamma }$, since with the appearance of quantum effects, there is a small number of photons in the cavity, decreasing $n(1.3{p}_{1})$, thus holding this relationship requires smaller $N_{\gamma }$’s. In short, the quantum effects emerge in the system for small enough amounts of $N_{\gamma }$. If we move upward from the curve of $m(1.3{p}_{1})=5$, it is apparent that we are getting closer and closer to the semi-classical approximation; in this case, $m(1.3{p}_{1})$ declines, and the semi-classical effects become visible in the system. Since a large number of photons are present in the cavity as the semi-classical effects appear, $n(1.3{p}_{1})$ increases, and larger $N_{\gamma }$’s are required to establish the relationship $m(1.3{p}_{1})=n(1.3{p}_{1})/{N}_{\gamma }$. In brief, the semi-classical effects occur in the system for large enough values of $N_{\gamma }$. To confirm these claims, it is necessary to solve the master equation numerically and compare the results with the semi-classical approximation in the previous section. The master equation (1) is written as the following in the atom and cavity basis, i.e., $|n,j\rangle$ where $n=0,1,2,\dots$ and $j=1,2,3$ [58,59,60,61,62,63]:

Fig. 4

The curves of $N_A$ in terms of $\eta$ for $m(1.3{p}_{1})=0,0.5,1,1.5,2,3,4,5$. The $m=0$ graph separates the lasing and nonlasing regimes from one another

$$\begin{aligned}&{{\dot{\rho }}}_{n,1;n,1}=-({\varGamma }^{\prime }+\kappa {n})\rho _{n,1;n,1}+{\varGamma }\rho _{n,2;n,2}+\kappa (n+1)\rho _{n+1,1;n+1,1},\end{aligned}$$

(35)

$$\begin{aligned}&{{\dot{\rho }}}_{n,2;n,2}=-{\mathrm{i}}g\sqrt{n}\rho _{n-1,3;n,2}+{\mathrm{i}}g\sqrt{n}\rho _{n,2;n-1,3}-\gamma \rho _{n,3;n,3}-({\varGamma }+\kappa {n})\rho _{n,2;n,2}+\kappa (n+1)\rho _{n+1,2;n+1,2},\end{aligned}$$

(36)

$$\begin{aligned}&{{\dot{\rho }}}_{n-1,3;n,2}=-{\mathrm{i}}g\sqrt{n}\rho _{n,2;n,2}+{\mathrm{i}}g\sqrt{n}\rho _{n-1,3;n-1,3}-\frac{1}{2}\left( \gamma +{\varGamma }+\kappa (2n-1)\right) \rho _{n-1,3;n,2}+\kappa \sqrt{n(n+1)}\rho _{n,3;n+1,2},\end{aligned}$$

(37)

$$\begin{aligned}&{{\dot{\rho }}}_{n,3;n,3}=-{\mathrm{i}}g\sqrt{n+1}\rho _{n+1,2;n,3}+{\mathrm{i}}g\sqrt{n+1}\rho _{n,3;n+1,2}+{\varGamma }^{\prime }\rho _{n,1;n,1}-\left( \gamma +\kappa {n}\right) \rho _{n,3;n,3}+\kappa (n+1)\rho _{n+1,3;n+1,3}, \end{aligned}$$

(38)

and also ${\rho }_{m,i;n,j}^{*}={\rho }_{n,j;m,i}$. The notation $|n,j\rangle$ stands for the state in which n labels the nth Fock state of the cavity mode, and the atom is in its first, second or third level. Equations (35) to (38) and their complex conjugates form a closed set. By applying the condition of $tr(\rho )=1$, these equations can be written as $Ax=b$, which can be solved numerically. For this purpose, it is necessary to truncate the equations at a large enough n like N; in this case, if the truncated x is called as $x_N$, the answer of $x_N$ is acceptable when it does not change any longer by varying n to $N-1$ or $N + 1$. Once the matrix x is specified, the problem is solved, and the desired physical quantities can be obtained. The depicted physical quantities here are as follows:

$$\begin{aligned}&m=\frac{\langle {a}^{\dagger }a\rangle }{N_\gamma }, \end{aligned}$$

(39)

$$\begin{aligned}&{g}^{(2)}(0)=\frac{\langle {{a}^{\dagger }}^{2}{a}^{2}\rangle }{{\langle a^{\dagger }a\rangle }^{2}}, \end{aligned}$$

(40)

$$\begin{aligned}&{A}_{22}=\langle {\hat{A}}_{22}\rangle , \end{aligned}$$

(41)

Fig. 5

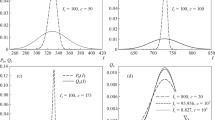
The diagrams of m in terms of p in the semi-classical and quantum models for several $N_{\gamma }$’s in two distinct intervals. In the semi-classical case, the m curve is plotted using Eq. 25

Fig. 6

The graphs of $g^{(2)}(0)$ in terms of p for different $N_\gamma$’s in two separate intervals

in Fig. 5, the graphs of m against p are drawn in the semi-classical approximation and quantum regimes for various values of $N_\gamma$. The curves of m are plotted according to Eq. (39) for different $N_{\gamma }$’s. It is clear that as p increases, the scaled photon number increases until it is eventually saturated. In Fig. 5a, by stepping up $N_{\gamma }$, the diagrams get closer and closer to the semi-classical curve. It can be said that the m curve overlaps the corresponding semi-classical one for $N_{\gamma }=200$. The same curves are depicted near the laser threshold in Fig. 5b. In this figure, for $N_{\gamma }=200$ and at $p=1.3{p}_{1}$, the m graph coincides with the semi-classical one. By dropping $N_\gamma$, the curves gradually move farther and farther away from the semi-classical one. These conclusions verify the description provided in Fig. 4, which means that by enhancing $N_\gamma$, we get nearer and nearer to the semi-classical laser theory. On the other hand, by decreasing it, we gradually get farther and farther away from the semi-classical approximation, and the quantum fluctuations become noticeable in the system.

The correlations are usually studied by using the normalized second-order correlation function $g^{(2)}$, which can have values ranging from zero to infinity. Values of $g^{(2)}<1$ refer to photon antibunching, $1<g^{(2)}<2$ to photon bunching, and $g^{(2)}>2$ to photon superbunching or extrabunching. Photon antibunching, corresponding to the emission of single photons in a regular manner, is a nonclassical phenomenon and has been the subject of intensive theoretical and experimental studies. Photon bunching is characteristic of thermal light, whereas superbunching, indicating strong correlations between photons, has been found characteristic of nonclassical states of light such as squeezed states and entangled Gaussian states [64,65,66,67,68,69,70,71,72,73,74,75,76,77]. According to Eq. (40) in Fig. 6, the graphs of $g^{(2)}(0)$ are depicted versus p at different intervals for some $N_\gamma$’s. In the instance of $N_{\gamma }=200$ and below threshold, the emitted light is thermal, and the coherent light is radiated above the threshold; thus, in this case, the system reveals similar behavior to that of the semi-classical laser. As $N_\gamma$ decreases, the system emits bunched light and for smaller amounts of $N_\gamma$, and in the weak driving limit, the system emits an antibunched beam of photons, a quantum light. Therefore, from the above discussions, it can be concluded that for large enough $N_{\gamma }$’s, the system meets the semi-classical laser theory, and for small enough $N_{\gamma }$’s, the system signifies the quantum effects in the weak driving limit. In the next section, the effect of photon antibunching is explained based on the two-level atom model.

4 Effective two-level atom

In this section, how the three-level atom trapped in the cavity behaves is explained for small $N_{\gamma }$’s and in the weak driving limit and how to explain the antibunching phenomenon. First, it is assumed that $\kappa \gg {2g}$ that is equivalent to the condition $N_{\gamma }\ll {N}_{A}^{2}$. In this case, the transition from level 3 to level 2 happens at the following rate:

Fig. 7

The steps of converting the three-level atom enclosed in the cavity of Fig. 1 to the two-level one

$$\begin{aligned} \gamma _{E}=\frac{4{g}^{2}}{\kappa }, \end{aligned}$$

(42)

next, it is supposed that ${\gamma }\ll {\gamma }_{E}$ which is equivalent to $N_{A}\ll {1}$. Applying these two conditions, the three-level atom confined in the cavity of Fig. 1 is converted to the three-level one of Fig. 7a, which can be further simplified in the weak driving limit ${\varGamma }^{\prime }\ll {\gamma _{E}}$. In the weak driving limit, the third level population is derived from this relation:

$$\begin{aligned} A_{33}=\frac{{\varGamma }^{\prime }}{{\gamma }_{E}}=p{N}_{A}, \end{aligned}$$

(43)

Fig. 8

The curves of the second-level population versus p for different $N_{\gamma }$’s and the two-level atom

since ${\varGamma }^{\prime }\ll {\gamma _{E}}$, so $A_{33}\ll {1}$, the third level can be omitted. In this case, by eliminating the third level, the three-level atom of Fig. 7a turns into the two-level one of Fig. 7b, in which the transition rate from level 1 to level 2 takes place at the rate ${\varGamma }^{\prime }$. By solving the related equations of the two-level atom in the steady-state, it is shown that:

$$\begin{aligned}&A_{22}=\frac{\eta {p}}{\eta {p}+1}, \end{aligned}$$

(44)

$$\begin{aligned}&m=\frac{p}{{N}_{A}(\eta {p}+1)}. \end{aligned}$$

(45)

Fig. 9

The diagrams of m in terms of p for some $N_{\gamma }$’s and the two-level atom

Note that $A_{22}$ and m are independent of $N_{\gamma }$. To see how the utilized approximations to what extent here are valid, the results of Eqs. (44) and (45) can be compared with those of the previous section. For this reason, the curves of $A_{22}$ and m are drawn in Figs. 8 and 9 on several different occasions. In Fig. 8, the second-level population graphs are plotted in terms of p for some values of $N_{\gamma }$. The diagrams of $A_{22}$ are depicted according to eq. (41) for various $N_{\gamma }$’s, and that curve for the two-level atom is drawn based on Eq. (44). The figure shows that with decreasing $N_{\gamma }$, the simulation results get closer and closer to those of the two-level atomic pattern; also, considering the weak driving limit in that $p\ll {100}$, this approximation becomes even better.

In Fig. 9, the diagrams of m against p are plotted for some amounts of $N_{\gamma }$ based on Eq. (39), and that graph for the two-level atom is drawn according to Eq. (45). The smaller the critical photon number is, the closer the outcomes of the quantum model simulations to the values of the two-level atom curve, and the completer the coincidence should be by including the weak driving limit in which $p\ll {100}$. The physical reason for the antibunching effect of light is that once an atom has emitted a photon, it is projected into the lower level and cannot emit a second photon until it is re-excited into the upper level, so that a photon may be emitted again [78, 79]. In short, under applied conditions, the three-level atom confined in the cavity reflects a similar behavior to that of the two-level atom; accordingly, the antibunching phenomenon can be justified. So the results of this section show that under certain conditions, the three-level atom behaves like the two-level one.

5 Conclusions

A theoretical model of a single-atom laser has been examined by trapping a three-level atom inside a single-mode optical cavity. The master equation explains the behavior of the system, the solutions of which are calculated in two different situations: in the semi-classical approximation, the exact solution of the equations has been written, and in the full quantum regime that is closer to the real model, its approximate solution is obtained numerically in the basis of the atom and cavity field. The results show that for a sufficiently large critical photon number, the treatments of the semi-classical laser emerge in the system, and the lasing occurs over a large interval. For small enough critical photon number and in the weak driving limit, the three-level atom behaves similar to the two-level one, and the system radiates an antibunched beam of photons that is a quantum light. In both semi-classical approximation and two-level atomic pattern, the conclusions of the quantum simulations are highly consistent with the separate outcomes of each of those two approximations. The lasing and nonlasing regimes have been specified in the semi-classical model, and all the computations have been implemented in the lasing regime.