1 Introduction

Gradient flows are widely used in mathematical models for problems in materials science and fluid dynamics [3, 4]. A gradient flow is usually determined by an energy functional, and a typical choice of this functional is given by

$$\begin{aligned} E(u):=\int _{\Omega } \left( \frac{1}{2}|\triangledown u|^2+F(u)\right) \mathrm{d}{{\mathbf {x}}}, \end{aligned}$$

where \(\Omega \in {\mathbb {R}}^d \,(d=1,2,3)\) is a bounded domain. For example, in the simulation of two phase dynamics, the unknown variable u represents the concentration of one of the two phases, and F(u) is the nonlinear free energy density. A common choice for the function F(u) is given by \(\frac{1}{4\epsilon ^2} (u^2-1)^2\) with \(\epsilon \) being the inter-facial width.

In this paper, we consider the Allen-Cahn equation which can be interpreted as an \(L^2\) gradient flow:

$$\begin{aligned} u_t&=-M \nu , \\ \nu&=\frac{\delta E}{\delta u}=-\Delta u+F'(u), \end{aligned}$$

where \(M>0\) is the mobility constant and \(\nu \) is the chemical potential. For simplicity of the notations, we denote \(s(u)=-M F'(u)\), then the governing equation can be rewritten into the following general form:

$$\begin{aligned} u_t=M \Delta u+s(u), \end{aligned}$$
(1)

subject to the initial condition

$$\begin{aligned} u({{\mathbf {x}}},0)=u_0({{\mathbf {x}}}), \quad {{\mathbf {x}}}\in \Omega , \end{aligned}$$
(2)

and periodic or homogeneous Neumann/Dirichlet boundary conditions. Here we assume \(s(1)=s(-1)=0\). Roughly speaking, the Allen-Cahn equation describes regions with \(u\approx 1\) and \(u\approx -1\) that grow and decay at the expense of one another.

One important property of the Allen-Cahn equation is that the energy function is decreasing with time:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}E(u)\leqslant 0. \end{aligned}$$
(3)

It is important for numerical schemes to preserve this property. The energy stability for the approximation of Allen-Cahn equations has been investigated intensively. Some popular numerical schemes are convex splitting schemes [36], stabilized schemes [33, 39], invariant energy quadratization methods [41, 42], scalar auxiliary variable (SAV) approach [31, 32], etc.

Besides, the exact solutions of the classical Allen-Cahn equations enjoy the maximum-principle, i.e., the exact solutions are between −1 and 1 if the initial condition satisfies the same property. Most of the previous works focus on the energy stability, and to the best knowledge, the only works in this direction are given in [19, 23, 30, 35], where finite difference methods were discussed. Moreover, the gradient flows may yield a thin transition layer. Therefore, nonuniform meshes are generally useful in capturing these layers. Because of these considerations, we would like to apply the discontinuous Galerkin (DG) method due to its good stability, high-order accuracy, and flexibility on h-p adaptivity and complex geometry. Moreover, in order to preserve the maximum-principle, some slope limiters have to be applied, and the energy stability would be rather difficult to prove. In this paper, we will mainly focus on the maximum-principle-preserving (MPP) techniques and use numerical experiments to demonstrate the energy decay property.

DG methods were first introduced in [28] in the framework of neutron transportation. Subsequently, the Runge-Kutta (RK) discontinuous Galerkin (RKDG) methods for hyperbolic conservation laws were introduced in a series of papers [9,10,11,12]. For convection diffusion equations, the local discontinuous Galerkin (LDG) method was given in [13] motivated by [2], where the Navier-Stokes equations were successfully solved. Besides the above, the ultra-weak DG (UDG) method [6], the staggered DG (SDG) method [8, 14], the direct DG (DDG) method [26], the interior penalty DG (IPDG) methods [1, 29, 37] and the LDG methods on overlapping meshes [18] are also important candidates for solving convection-diffusion equations.

Recently, in [43], genuinely MPP high-order DG methods for scalar conservation laws have been constructed. For parabolic equations, the second-order MPP DG methods were given in [44]. The technique works for IPDG, LDG and UDG methods, see [22, 25] for some applications. However, the extension to high-order schemes seems to be not straightforward. The third-order MPP schemes based on LDG methods on overlapping meshes [16] and DDG method [5] were discussed. Other high-order methods were also investigated in [7, 21, 34, 38, 40] based on the modification of numerical fluxes.

It is well known that the Allen-Cahn equation contains stiff source, leading to extremely small time step size if the time integration is not constructed suitably. Recently, Huang and Shu introduced the modified exponential RK method for hyperbolic equations with stiff source terms [24]. The scheme is weakly asymptotic preserving and overcomes the stiffness. They made some assumptions on the stiff source term in order to design the bound-preserving technique. However, Allen-Cahn equations do not satisfy those assumptions. Moreover, their scheme is not conservative, i.e., if the numerical approximation at the time level n is 1, then it may not be 1 at the time level \(n+1\), hence it is not suitable for Allen-Cahn equations. Later, in [15], two of the authors in this paper introduced the conservative modified exponential RK method and the third-order extension was also given in [17]. Thanks to the conservative time integrations, we can construct the MPP technique for Allen-Cahn equations. Also, the bounds of the numerical approximations will not decay by the time integrations. We will explain this conservative issue in details at the end of Sect. 2.

For simplicity of presentation, we only consider the one- and two-dimensional problems (\(d=1,2\)) in this paper. Yet our method can be extended to problems in three space dimensions (\(d=3\)). Moreover, we only discuss the detailed formulation for second-order LDG schemes coupled with the second-order conservative modified exponential RK method [15] for Allan-Cahn equations. We will theoretically prove the MPP technique for our method and show that the bounds will not decay. The third-order time integration has been given in [17], and high-order spatial discretizations can be obtained following the techniques introduced in [16, 21, 34, 38]. Both second-order and third-order methods will be tested in numerical examples, which demonstrate that the time step size can be larger than the one in the traditional RK method. Moreover, we can observe the energy decays numerically.

The rest of the paper is organized as follows: we will demonstrate the LDG scheme and the time integration for the Allen-Cahn equation in one space dimension in Sect. 2. The MPP property will be proved in Sect. 3. We will extend the idea to problems in two space dimensions in Sect. 4. Numerical experiments will be given in Sect. 5. We will end in Sect. 6 with some concluding remarks.

2 Numerical Scheme in One Space Dimension

In this section, we consider the following one-dimensional Allen-Cahn equation:

$$\begin{aligned} u_t=M u_{xx}+s(u). \end{aligned}$$
(4)

We will review the LDG method for spatial derivative in Sect. 2.1. Then, we adopt the second-order conservative modified exponential RK method in Sect. 2.2 to obtain the fully discretized scheme.

2.1 LDG Spacial Discretization

We first introduce an auxiliary variable p to represent \(u_x\) and rewrite (4) into the following system of first-order equations:

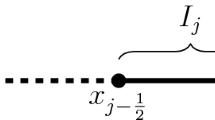
$$\begin{aligned} \left\{ \begin{array}{l} u_t=M p_{x}+s(u), \\ p=u_x. \end{array} \right. \end{aligned}$$
(5)

In order to solve the problem numerically, we decompose the computational domain \(\Omega \) into non-overlapping regular cells and denote the ith cell as

$$\begin{aligned} I_i=\left[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}\right],\quad i=1,\cdots ,N. \end{aligned}$$

The cell center of \(I_i\) is denoted as

$$\begin{aligned} x_i=\frac{1}{2}\left( x_{i-\frac{1}{2}}+x_{i+\frac{1}{2}}\right) . \end{aligned}$$

For simplicity, we consider uniform meshes. However, this assumption is not essential. We denote the cell length as \(\Delta x\):

$$\begin{aligned} \Delta x=x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}. \end{aligned}$$

The finite element space consists of piecewise polynomials which can be discontinuous across cell boundaries:

$$\begin{aligned}&V_h:=\{u_h: u_h|_{I_{i}}\in P^k(I_{i}),\, i=1,\cdots ,N \}, \end{aligned}$$

where \(P^k(I_i)\) is the set of all polynomials of degree up to k defined on the cell \(I_i\). In this paper, we take \(k=1\) and consider the second-order scheme.

We multiply each equation in (5) with test functions in \(V_h\) and integrate the equation on each cell \(I_i\). By using integration by parts, the LDG method is defined as follows: to find \(u_h(\cdot ,t)\in V_h\) and \(p_h\in V_h\), such that for any test functions \(z, q\in V_h\) and any cell \(I_i\), we have

$$\begin{aligned} \int _{I_{i}} (u_h)_t z \mathrm{d}x&= M\left( - \int _{I_{i}} p_h z_x \mathrm{d}x +{\hat{p}}_{i+\frac{1}{2}}z^-_{i+\frac{1}{2}}-{\hat{p}}_{i-\frac{1}{2}}z^+_{i-\frac{1}{2}} \right) +\int _{I_i} s(u_h)z \mathrm{d}x, \end{aligned}$$
(6)
$$\begin{aligned} \int _{I_{i}} p_h q \mathrm{d}x&=-\int _{I_{i}} u_h q_x \mathrm{d}x +{\hat{u}}_{i+\frac{1}{2}}q^-_{i+\frac{1}{2}}-{\hat{u}}_{i-\frac{1}{2}}q^+_{i-\frac{1}{2}}, \end{aligned}$$
(7)

where the notations \(w^-_{i+\frac{1}{2}}\) and \(w^+_{i+\frac{1}{2}}\) are used to represent the values of a function w on the point \(x_{i+\frac{1}{2}}\) obtained from the left and the right of \(x_{i+\frac{1}{2}}\), respectively. \({\hat{p}}_{i+\frac{1}{2}}\) and \({\hat{u}}_{i+\frac{1}{2}}\) are the numerical fluxes and are taken as alternating fluxes

$$\begin{aligned} {\hat{u}}_{i+\frac{1}{2}}={u}_{i+\frac{1}{2}}^-, \quad {\hat{p}}_{i+\frac{1}{2}}={p}_{i+\frac{1}{2}}^+, \end{aligned}$$
(8)

or

$$\begin{aligned} {\hat{u}}_{i+\frac{1}{2}}={u}_{i+\frac{1}{2}}^+, \quad {\hat{p}}_{i+\frac{1}{2}}={p}_{i+\frac{1}{2}}^-. \end{aligned}$$
(9)

In the remaining part of this paper, we adopt (8). The proof for (9) is similar.

2.2 Conservative Modified Exponential RK Temporal Discretization

It is easy to solve for \(p_h\) locally on each cell \(I_i\) by using (7) to get

$$\begin{aligned} p_h(x)|_{I_i}=\frac{u_{i+\frac{1}{2}}^- -u_{i-\frac{1}{2}}^- }{\Delta x}+\frac{6(x-x_i)}{\Delta x^2}\left( u_{i-\frac{1}{2}}^--u_{i-\frac{1}{2}}^+ \right) , \end{aligned}$$

and hence we have

$$\begin{aligned} {\hat{p}}_{i-\frac{1}{2}}={p}_{i-\frac{1}{2}}^+=\frac{u_{i+\frac{1}{2}}^- +3u_{i-\frac{1}{2}}^+ -4u_{i-\frac{1}{2}}^- }{\Delta x}. \end{aligned}$$

Substituting the above equations into (6) and noticing that

$$\begin{aligned} z_x|_{I_i}=\frac{ z_{i+\frac{1}{2}}^- -z_{i-\frac{1}{2}}^+}{\Delta x} \end{aligned}$$

is a constant, we get the following semi-discrete scheme for solving \(u_h(x,t)\) on \(I_i\):

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\int _{I_{i}} u_h(x,t) z(x) \mathrm{d}x&=\frac{M}{\Delta x} \left[ \left( u_{i+\frac{3}{2}}^- +3u_{i+\frac{1}{2}}^+ -5u_{i+\frac{1}{2}}^- +u_{i-\frac{1}{2}}^- \right) z_{i+\frac{1}{2}}^- - 3\left( u_{i-\frac{1}{2}}^+ -u_{i-\frac{1}{2}}^-\right) z_{i-\frac{1}{2}}^+ \right] \\&\quad +\int _{I_i} s(u_h)z(x) \mathrm{d}x, \quad \forall z(x)\in V_h, \, i=1,\cdots ,N. \end{aligned}$$

For simplicity of the formulation, we introduce the notation

$$\begin{aligned} F_i(u_h,z)=\frac{M}{\Delta x} \left[ \left( u_{i+\frac{3}{2}}^- +3u_{i+\frac{1}{2}}^+ -5u_{i+\frac{1}{2}}^- +u_{i-\frac{1}{2}}^- \right) z_{i+\frac{1}{2}}^- - 3\left( u_{i-\frac{1}{2}}^+ -u_{i-\frac{1}{2}}^-\right) z_{i-\frac{1}{2}}^+ \right] , \end{aligned}$$

and use \((\cdot , \cdot )_{I_i}\) to denote the inner product on \(L^2(I_i)\). Then, the semi-discrete scheme becomes

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\left( u_h, z\right) _{I_i} =F_i(u_h,z) +\left( s(u_h), z\right) _{I_i}, \quad \forall z(x)\in V_h, \, i=1,\cdots ,N. \end{aligned}$$
(10)

Since the source term can be stiff, we apply the second-order conservative modified exponential RK method [15] (without the expansion of exponential terms) to get the fully discretized scheme:

$$\begin{aligned} \left( u_h^{(1)}, z\right) _{I_i}= & {} B^1_1\left[ \left( u_h^n, z\right) _{I_i}+\Delta t F_i(u_h^n,z) +\Delta t \left( s(u_h^n)+\mu u_h^n, z\right) _{I_i} \right] , \end{aligned}$$
(11)
$$\begin{aligned} \left( u_h^{n+1}, z\right) _{I_i}= & {} B^1_2\left( u_h^n, z\right) _{I_i}+B^2_2\left[ \left( u_h^{(1)}, z\right) _{I_i} + \Delta t F_i(u_h^{(1)},z) +\Delta t\left( s(u_h^{(1)})+\mu u_h^{(1)}, z\right) _{I_i}\right] , \end{aligned}$$
(12)

where \(u_h^n(x)\) is the numerical approximation of \(u_h(x,t)\) at the time level n, and \(u_h^{(1)}(x)\) is a middle stage approximation. Here \(\mu \) is a constant to be determined in each time step and may depend on the time level n, and

$$\begin{aligned} B_1^1=\frac{1}{1+\mu \Delta t},\quad B_2^1=\frac{{\text{e}}^{-\mu \Delta t}}{{\text{e}}^{-\mu \Delta t}+1+\mu \Delta t},\quad B_2^2=\frac{1}{{\text{e}}^{-\mu \Delta t}+1+\mu \Delta t}. \end{aligned}$$

Numerical examples in Sect. 5 will show that the time step size of this method can be larger than the one used in the traditional RK methods.

We illustrate the conservative property of our method in the following theorem.

Theorem 1

The fully discretized scheme (11) and (12) for solving Allen-Cahn equations is conservative in the sense that: if the numerical solution \(u_h^n\) reaches the upper bound 1 (or the lower bound −1) at the time level n, then \(u_h^{n+1}(x)\) remains 1 (or −1) at the time level \(n+1\).

Proof

It is easy to check the following important property for our method:

$$\begin{aligned} (1+\mu \Delta t)B^1_1=1,\quad B^1_2+ (1+\mu \Delta t)B^2_2 =1. \end{aligned}$$
(13)

By the definition of \(F_i\), we know that \(F_i(u_h,z)=0\) for a constant function \(u_h\). Also, we have assumed that \(s(1)=s(-1)=0\) for the Allen-Cahn equation. Hence, when \(u_h^n=1\) (or −1), we have \(F_i(u_h^n,z)=s(u_h^n)=0\). Then, the property (13) guarantees that

$$\begin{aligned} u_h^{(1)}(x)= u_h^{n}(x). \end{aligned}$$

Subsequently, \(u_h^{(1)}(x)=1\) (or −1) will lead to \(F_i(u_h^{(1)},z)=s(u_h^{(1)})=0\), and (12) together with the property (13) gives

$$\begin{aligned} u_h^{n+1}(x)=u_h^{(1)}(x)= u_h^{n}(x). \end{aligned}$$

Hence, \(u_h^{n+1}(x)\) remains 1 (or −1) at time level \(n+1\).

Remark 1

The major difference between our temporal discretization and the modified exponential RK methods [24] is the design of the coefficients in (11) and (12). The coefficients in [24] do not satisfy the property (13) and hence the magnitudes of the solutions may decay with time due to the dissipation of the source term.

Remark 2

As we see in the next section, the conservative property (13) will also be used for designing the MPP technique. For the non-conservative method in [24], the MPP technique is relatively more complicated and some extra conditions on the source term are needed.

The third-order time integration [17] for solving (10) is

$$\begin{aligned} \left( u_h^{(1)}, z\right) _{I_i}= & {} {\raise0.7ex\hbox{${ \left[ \alpha _{10}\left( u_h^n, z\right) _{I_i}+\beta _{10}\Delta t F_i(u_h^n,z) +\beta _{10}\Delta t \left( s(u_h^n)+\mu u_h^n, z\right) _{I_i} \right]}$} \!\mathord{\left/ {\vphantom {{} {}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${A_1}$}}, \\ \left( u_h^{(2)}, z\right) _{I_i}= & {} {\raise0.7ex\hbox{${\left[ \alpha _{20}\left( u_h^n, z\right) _{I_i}+\beta _{20}\Delta t F_i(u_h^n,z) +\beta _{20}\Delta t \left( s(u_h^n)+\mu u_h^n, z\right) _{I_i} \right]}$} \!\mathord{\left/ {\vphantom {{} {}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${A_2}$}} \\&+{\text{e}}^{\beta _{10}\mu \Delta t}{\raise0.7ex\hbox{${\left[ \alpha _{21}\left( u_h^{(1)}, z\right) _{I_i} + \beta _{21}\Delta t F_i(u_h^{(1)},z) +\beta _{21}\Delta t\left( s(u_h^{(1)})+\mu u_h^{(1)}, z\right) _{I_i}\right]}$} \!\mathord{\left/ {\vphantom {{} {}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${A_2}$}}, \\ \left( u_h^{n+1}, z\right) _{I_i}= & {} {\raise0.7ex\hbox{${\left[ \alpha _{30}\left( u_h^n, z\right) _{I_i}+\beta _{30}\Delta t F_i(u_h^n,z) +\beta _{30}\Delta t \left( s(u_h^n)+\mu u_h^n, z\right) _{I_i} \right]}$} \!\mathord{\left/ {\vphantom {{} {}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${A_3}$}} \\&+{\text{e}}^{\beta _{10}\mu \Delta t}{\raise0.7ex\hbox{${\left[ \alpha _{31}\left( u_h^{(1)}, z\right) _{I_i} + \beta _{31}\Delta t F_i(u_h^{(1)},z) +\beta _{31}\Delta t\left( s(u_h^{(1)})+\mu u_h^{(1)}, z\right) _{I_i}\right]}$} \!\mathord{\left/ {\vphantom {{} {}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${A_3}$}}, \\&+{\text{e}}^{A\mu \Delta t}{\raise0.7ex\hbox{${\left[ \alpha _{32}\left( u_h^{(2)}, z\right) _{I_i} + \beta _{32}\Delta t F_i(u_h^{(2)},z) +\beta _{32}\Delta t\left( s(u_h^{(2)})+\mu u_h^{(2)}, z\right) _{I_i}\right]}$} \!\mathord{\left/ {\vphantom {{} {}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${A_3}$}}, \end{aligned}$$

where

$$\begin{aligned} \alpha _{10}= & {} 1, \quad \beta _{10} = 0.707\,193\,337\,692\,501\,4, \\ \alpha _{20}= & {} 0.668\,689\,293\,307\,440\,4, \quad \beta _{20} =0,\\ \alpha _{21}= & {} 0.331\,310\,706\,692\,559\,6, \quad \beta _{21} = 0.417\,804\,756\,491\,506\,5, \\ \alpha _{30}= & {} 0.348\,741\,943\,025\,609\,0, \quad \beta _{30} =0,\\ \alpha _{31}= & {} 0.203\,957\,613\,878\,089\,8, \quad \beta _{31} =0,\\ \alpha _{32}= & {} 0.447\,300\,443\,096\,301\,1, \quad \beta _{32} =0.564\,075\,463\,710\,043\,9, \end{aligned}$$

and

$$\begin{aligned} A_1= & {} \alpha _{10}+\beta _{10}\mu \Delta t,\qquad A_2=\alpha _{20}+\beta _{20}\mu \Delta t+{\text{e}}^{\beta _{10}\mu \Delta t}\left( \alpha _{21}+\beta _{21}\mu \Delta t\right) , \\ A_3= & {} \alpha _{30}+\beta _{30}\mu \Delta t+{\text{e}}^{\beta _{10}\mu \Delta t}\left( \alpha _{31}+\beta _{31}\mu \Delta t\right) +{\text{e}}^{A\mu \Delta t}\left( \alpha _{32}+\beta _{32}\mu \Delta t\right) . \end{aligned}$$

One can also check that this scheme is conservative. For simplicity, we will only show the MPP technique for the second-order scheme. The idea can be easily extended to the third-order scheme.

3 Maximum-Principle-Preserving Technique

In this section, we design the MPP technique for our method. We will first show that the cell average values can be bounded between −1 and 1 under suitable conditions in Sect. 3.1. Then we adopt a slope limiter to make the entire solutions be bounded between −1 and 1 in Sect. 3.2.

3.1 Maximum-Principle-Preserving of the Cell Averages

We denote the cell integral average values of \(u_h\) and \(s(u_h)\) on cell \(I_i\) as

$$\begin{aligned} {\bar{u}}_i(t)=\frac{1}{\Delta x}\int _{I_i}u_h(x,t)\mathrm{d}x,\quad {\bar{s}}_i(u_h)=\frac{1}{\Delta x}\int _{I_i}s(u_h)\mathrm{d}x. \end{aligned}$$

Taking \(z=1\) in (11) and (12), we get the following equations for updating \({\bar{u}}_i\) in time:

$$\begin{aligned} \bar{{u}}_i^{(1)}= & {} B^1_1\left[ {\bar{u}}_i^{n}+\Delta t f(u_h^n)\right] +\Delta t B^1_1\left[ {\bar{s}}_i(u_h^n)+\mu {\bar{u}}_i^{n}\right] , \end{aligned}$$
(14)
$$\begin{aligned} {\bar{u}}_i^{n+1}= & {} B^1_2{\bar{u}}^{n}_i +B^2_2\left[ {\bar{u}}_i^{(1)} +\Delta tf(u_h^{(1)}) \right] +\Delta t B^2_2\left[ {\bar{s}}_i(u_h^{(1)})+\mu {\bar{u}}_i^{(1)}\right] , \end{aligned}$$
(15)

where \({\bar{u}}_i^n\) and \({\bar{u}}_i^{(1)}\) are the cell averages of \(u_h^n\) and \(u_h^{(1)}\), respectively. Moreover,

$$\begin{aligned} f(\omega )=\frac{1}{\Delta x} F_i(\omega ,1) = \frac{M}{\Delta x^2} \left( \omega _{i+\frac{3}{2}}^- +3\omega _{i+\frac{1}{2}}^+ -5\omega _{i+\frac{1}{2}}^- -3\omega _{i-\frac{1}{2}}^+ +4\omega _{i-\frac{1}{2}}^- \right) \end{aligned}$$

for any function \(\omega \in V_h\).

We first state the property of the spatial discretization operator f in the lemma below following [44].

Lemma 1

For any function \(\omega (x)\in V_h\) with \(\omega (x) \in [-1,1],\,\forall x\in I_i\), \(i=1,\cdots ,N\), we have

$$\begin{aligned} {\bar{\omega }}_i+ \Delta t f(\omega )\in [-1,1] \end{aligned}$$

under the CFL condition \(M\frac{ \Delta t}{\Delta x^2} \leqslant \frac{1}{10}\).

Proof

Notice that \(\omega \) is simply a linear function on each cell \(I_i\), and hence we have

$$\begin{aligned} {\bar{\omega }}_i=\frac{1}{2}\left( \omega _{i+\frac{1}{2}}^-+\omega _{i-\frac{1}{2}}^+\right) . \end{aligned}$$

Then, we obtain

$$\begin{aligned} &{\bar{\omega }}_i+\Delta t f(\omega )= a_1 \omega _{i+\frac{3}{2}}^- +a_2 \omega _{i+\frac{1}{2}}^+ +a_3\omega _{i+\frac{1}{2}}^- +a_4\omega _{i-\frac{1}{2}}^+ +a_5\omega _{i-\frac{1}{2}}^- ,\\ a_1&=\frac{M \Delta t}{\Delta x^2}, \,a_2=3\frac{M \Delta t}{\Delta x^2},\, a_3= \frac{1}{2} -5\frac{M \Delta t}{\Delta x^2} ,\, a_4= \frac{1}{2} -3\frac{M \Delta t}{\Delta x^2} ,\, a_5=4\frac{M \Delta t}{\Delta x^2}. \end{aligned}$$

It is easy to check that \(a_1+a_2+a_3+a_4+a_5=1\). Under the condition \(M\frac{ \Delta t}{\Delta x^2} \leqslant \frac{1}{10}\), all coefficients are non-negative. Hence, we have written \({\bar{\omega }}_i+\Delta t f(\omega )\) as a convex combination of five point values of \(\omega \). Since all point values are bounded between \(-1\) and 1, we can obtain the conclusion of this lemma.

Next, we are able to prove the MPP property for the cell averages. In the following, we consider the L-point Gaussian quadrature rule on the cell \(I_i\), which is exact for the integral of polynomials of degree up to \(2L-1\). We denote the set of these quadrature points on \(I_i\) as

$$\begin{aligned} S_i=\left\{ x^i_1,x^i_2,\cdots ,x^i_L\right\} . \end{aligned}$$

Let \(c_{\alpha }\) be the quadrature weights for the interval \([-0.5,0.5]\) such that \(\sum\limits _{\alpha =1}^Lc_{\alpha }=1\). We choose L large enough such that \({\bar{s}}_i(u_h)\) can be approximated accurately. For the common choice \(s(u)=\frac{M}{\epsilon ^2}(u-u^3)\), we take \(L=2\) since \(u_h\) is a linear polynomial.

Theorem 2

The numerical scheme (14) and (15) is MPP: if \(-1\leqslant u_h^n(x) \leqslant 1\) on each cell \(I_i\), \(i=1,\cdots , N\), then we have \(-1\leqslant {\bar{u}}^{(1)}_i\leqslant 1\) under the conditions

$$\begin{aligned} \mu \geqslant \max \left\{ 0,\, \max _{x\in S_i}{ \frac{s\left( u_h^n(x)\right) }{1-u_h^n(x)}}, \, \max _{x\in S_i}\frac{s\left( u_h^n(x)\right) }{-1-u_h^{n}(x) }\right\} \qquad {and} \qquad M\frac{ \Delta t}{\Delta x^2} \leqslant \frac{1}{10}. \end{aligned}$$

In addition to the above conditions, if \(-1\leqslant u_h^{(1)}(x) \leqslant 1\) on each cell \(I_i\), \(i=1,\cdots , N\), and

$$\begin{aligned} \mu \geqslant \max \left\{ 0, \, \max _{x\in S_i} \frac{s\left( u_h^{(1)}(x)\right) }{1-u_h^{(1)}(x)},\, \max _{x\in S_i} \frac{s\left( u_h^{(1)}(x)\right) }{-1-u_h^{(1)}(x) }\right\} , \end{aligned}$$

then we have \(-1\leqslant {\bar{u}}^{n+1}_i\leqslant 1\).

Proof

We only prove \(-1\leqslant {\bar{u}}^{(1)}_i\leqslant 1\), since the proof for \(-1\leqslant {\bar{u}}^{n+1}_i\leqslant 1\) can be obtained following the same line. From (14), we get

$$\begin{aligned} \bar{{u}}_i^{(1)}=B^1_1 R_1+\mu \Delta t B^1_1 R_2, \end{aligned}$$

where

$$\begin{aligned} R_1= {\bar{u}}_i^{n}+\Delta t f(u_h^n),\qquad R_2=\frac{1}{\mu } {\bar{s}}_i(u_h^{n})+{\bar{u}}_i^{n}. \end{aligned}$$

Next, we estimate the bounds of \(R_1\) and \(R_2\), respectively. Since \(-1\leqslant u_h^n(x) \leqslant 1\) and \(M\frac{ \Delta t}{\Delta x^2} \leqslant \frac{1}{10}\), we can get

$$\begin{aligned} R_1={\bar{u}}_i^n+\Delta t f(u_h^n)\in [-1,1] \end{aligned}$$

by using Lemma 1. Moreover, the condition of \(\mu \) gives

$$\begin{aligned} -1 \leqslant \frac{1}{\mu } s\left( u_h^{n}(x^i_{\alpha })\right) +u_h^{n}(x^i_{\alpha }) \leqslant 1,\quad \alpha =1,\cdots ,L. \end{aligned}$$

Then, by using the Gauss quadrature rule, we get

$$\begin{aligned} R_2=\sum _{\alpha =1}^L c_{\alpha }\left[ \frac{1}{\mu } s\left( u_h^{n}(x^i_{\alpha })\right) +u_h^{n}(x^i_{\alpha })\right] \in [-1,1]. \end{aligned}$$

Recall that our scheme is conservative and \((1+\mu \Delta t)B^1_1=1\). Also, both \(B_1^1\) and \(\mu \Delta t B^1_1 \) are non-negative. Hence, \(\bar{{u}}_i^{(1)}\) is a convex combination of \(R_1\) and \(R_2\). Since \(R_1,\,R_2\in [-1,1]\), we get

$$\begin{aligned} - 1\leqslant {\bar{u}}^{(1)}_i\leqslant 1. \end{aligned}$$

Remark 3

In addition to the assumption \({s}(1)={s}(-1)=0\), we also require the following two limits:

$$\begin{aligned} \lim _{u\rightarrow 1}\frac{s(u)}{1-u},\quad \lim _{u\rightarrow -1}\frac{s(u)}{1+u} \end{aligned}$$

exist. Therefore, the lower bounds of \(\mu \) given in the above theorem are well-defined.

3.2 Maximum-Principle-Preserving Limiter

Based on the theorem in the last section, we can construct physically relevant numerical cell averages \({\bar{u}}_i\). However, the polynomial \(u_h\) may be out of the bounds. Hence, we need to apply suitable limiters to \(u_h^{(1)}(x)\) and \(u_h^{n+1}(x)\), and construct physically relevant numerical approximations in each RK stage.

Assume that we already have \(-1\leqslant u_h^n(x) \leqslant 1\) on each cell on time level n. The full algorithm on each fixed cell \(I_i\) from time level n to time level \(n+1\) is given below.

  1. (i)

    Compute the first stage of the conservative time integration (11) to get \(u_h^{(1)}(x)\). Since \(-1\leqslant u_h^n(x) \leqslant 1\), Theorem 2 shows that \(-1\leqslant {\bar{u}}^{(1)}_i\leqslant 1\) under the suitable conditions on \(\Delta t\) and \(\mu \).

  2. (ii)

    Replace the polynomial \(u_h^{(1)}|_{I_i}\) by a modified polynomial \({\tilde{u}}_h^{(1)}(x)\in P^1(I_i)\):

    $$\begin{aligned} {\tilde{u}}_h^{(1)}(x)=\theta \left( u_h^{(1)}(x)-{\bar{u}}^{(1)}_i\right) +{\bar{u}}^{(1)}_i, \end{aligned}$$

    where

    $$\begin{aligned} \theta =\min \left\{ 1, \frac{1-{\bar{u}}^{(1)}_i}{M_i-{\bar{u}}^{(1)}_i} , \frac{{\bar{u}}^{(1)}_i+1}{{\bar{u}}^{(1)}_i-m_i}\right\} \end{aligned}$$

    with

    $$\begin{aligned} M_i=\max _{x\in I_i}u_h^{(1)}(x),\quad m_i=\min _{x\in I_i}u_h^{(1)}(x). \end{aligned}$$

    In [43], the authors proved that the new polynomial \({\tilde{u}}_h^{(1)}(x)\) is still a second-order accurate approximation with the same cell average and \({\tilde{u}}_h^{(1)}(x)\in [-1,1]\), for all \(x\in I_i\).

  3. (iii)

    Compute the second stage of the conservative time integration (12) to get \(u_h^{n+1}(x)\). Since we have replaced \(u_h^{(1)}(x)\) with \({\tilde{u}}_h^{(1)}(x)\) and \(-1\leqslant {\tilde{u}}_h^{(1)}(x)\leqslant 1\), we can get \(-1\leqslant {\bar{u}}^{n+1}_i\leqslant 1\) under the suitable conditions by using Theorem 2 again.

  4. (iv)

    Replace the polynomial \(u_h^{n+1}\) on \(I_i\) by a modified polynomial \({\tilde{u}}_h^{n+1}(x)\):

    $$\begin{aligned} {\tilde{u}}_h^{n+1}(x)=\theta \left( u_h^{n+1}(x)-{\bar{u}}^{n+1}_i\right) +{\bar{u}}^{n+1}_i, \end{aligned}$$

    where

    $$\begin{aligned} \theta =\min \left\{ 1, \frac{1-{\bar{u}}^{n+1}_i}{M_i-{\bar{u}}^{n+1}_i} , \frac{{\bar{u}}^{n+1}_i+1}{{\bar{u}}^{n+1}_i-m_i}\right\} ,\quad M_i=\max _{x\in I_i}u_h^{n+1}(x),\quad m_i=\min _{x\in I_i}u_h^{n+1}(x). \end{aligned}$$

    Then, we can get \(-1\leqslant {\tilde{u}}_h^{n+1}(x)\leqslant 1\).

4 Two-Dimensional Problem

In this section, we extend the technique to two-dimensional Allen-Cahn problem (1). We first give the numerical scheme in Sect. 4.1 and then design the MPP technique in Sect. 4.2.

4.1 Numerical Scheme

We first use the classical LDG method to discrete the space and get the semi-discrete scheme. For two-dimensional problem, we need to introduce two auxiliary variables p and q to represent \(u_x\) and \(u_y\), respectively. Thus, we can rewrite (1) into the following system:

$$\begin{aligned} \left\{ \begin{array}{l} u_t=M (p_{x}+q_y)+s(u), \\ p=u_x,\\ q=u_y. \end{array} \right. \end{aligned}$$
(16)

Suppose the computational domain is \(\Omega =[a,b]\times [c,d]\). We decompose it into regular rectangular cells. Let \(a=x_{\frac{1}{2}}<x_{\frac{3}{2}}<\cdots <x_{N_x+\frac{1}{2}}=b\) and \(c=y_{\frac{1}{2}}<y_{\frac{3}{2}}<\cdots <y_{N_y+\frac{1}{2}}=d\) be grid points in x and y directions, respectively. We denote the (i, j)th cell as

$$\begin{aligned} I_{i,j}=\left[ x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}\right] \times \left[ y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}\right] ,\quad i=1,\cdots ,N_x,\,\, j=1,\cdots ,N_y . \end{aligned}$$

For simplicity, we also make a non-essential assumption of uniform mesh and denote the cell lengths in x and y directions as \(\Delta x\) and \(\Delta y\), respectively. The finite element space consists of piecewise polynomials which can be discontinuous across cell boundaries:

$$\begin{aligned}&V_h:=\left\{ u_h: u_h|_{I_{i,j}}\in Q^1(I_{i,j}),\, i=1,\cdots ,N_x,\,\,j=1,\cdots ,N_y \right\} . \end{aligned}$$

For any function \(v\in V_h\), we denote \(v_{i-\frac{1}{2},j}^+\), \(v_{i+\frac{1}{2},j}^-\), \(v_{i,j-\frac{1}{2}}^+\) and \(v_{i,j+\frac{1}{2}}^-\) to be the traces of \(v|_{I_{i,j}}\) on the four edges of \(I_{i,j}\), respectively. The LDG method in two-dimensional space is defined as follows: to find \(\left( u_h(\cdot ,t), p_h, q_h\right) \in [V_h]^3\), such that for any test functions \((v,w,z)\in [V_h]^3\) and any cell \(I_{i,j}\), we have

$$\begin{aligned} \int _{I_{i,j}} (u_h)_t v \mathrm{d}x \mathrm{d}y&=- M \int _{I_{i,j}} (p_h v_x+ q_h v_y) \mathrm{d}x \mathrm{d}y+\int _{I_{i,j}} s(u_h)v \mathrm{d}x\mathrm{d}y\nonumber \\&\quad +M\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\left( {\hat{p}}_{i+\frac{1}{2},j}v_{i+\frac{1}{2},j}^- -{\hat{p}}_{i-\frac{1}{2},j}v_{i-\frac{1}{2},j}^+ \right) \mathrm{d}y \nonumber \\&\quad +M\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\left( {\hat{q}}_{i,j+\frac{1}{2}}v_{i,j+\frac{1}{2}}^- -{\hat{q}}_{i,j-\frac{1}{2}}v_{i,j-\frac{1}{2}}^+ \right) \mathrm{d}x, \end{aligned}$$
(17)
$$\begin{aligned} \int _{I_{i,j}} p_h w \mathrm{d}x \mathrm{d}y&=-\int _{I_{i,j}} u_h w_x \mathrm{d}x\mathrm{d}y +\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\left( {\hat{u}}_{i+\frac{1}{2},j}w^-_{i+\frac{1}{2},j}-{\hat{u}}_{i-\frac{1}{2},j}w^+_{i-\frac{1}{2},j}\right) \mathrm{d}y, \end{aligned}$$
(18)
$$\begin{aligned} \int _{I_{i,j}} q_h z \mathrm{d}x \mathrm{d}y&=-\int _{I_{i,j}} u_h z_x \mathrm{d}x\mathrm{d}y +\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\left( {\hat{u}}_{i,j+\frac{1}{2}}z^-_{i,j+\frac{1}{2}}-{\hat{u}}_{i,j-\frac{1}{2}}z^+_{i,j-\frac{1}{2}}\right) \mathrm{d}x, \end{aligned}$$
(19)

where the numerical fluxes are taken as alternating fluxes

$$\begin{aligned} {\hat{u}}_{i+\frac{1}{2},j}={u}_{i+\frac{1}{2},j}^-, \quad {\hat{u}}_{i,j+\frac{1}{2}}={u}_{i,j+\frac{1}{2}}^-,\quad {\hat{p}}_{i+\frac{1}{2},j}={p}_{i+\frac{1}{2},j}^+, \quad {\hat{q}}_{i,j+\frac{1}{2}}={q}_{i,j+\frac{1}{2}}^+. \end{aligned}$$

After we get the semi-discrete scheme by using the LDG method, we still use the second-order conservative modified exponential RK method (11) and (12) to march in time.

4.2 Maximum-Principle-Preserving Technique

We first solve for \(p_h\) locally on each cell \(I_{i,j}\) by using (18). For the integral on \([y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]\), we use the two-point Gaussian quadrature. We denote the two quadrature points on \([y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]\) as \(y^j_1\) and \(y^j_2\) and denote the two quadrature weights on \([-0.5,0.5]\) as \(c_1\) and \(c_2\). Moreover, we denote the linear interpolation basis functions as \(\phi _1(y)\) and \(\phi _2(y)\), \(y\in [y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]\), such that

$$\begin{aligned} \phi _m(y^j_n)=\delta _{mn},\quad m,n\in \{1,2\}. \end{aligned}$$

In (18), we take \(w(x,y)={\tilde{w}}(x)\phi _m(y)\in Q^1(I_{i,j}),\,m=1,2\), where \({\tilde{w}}(x)\) can be any function in \(P^1([x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}])\). Then, we get

$$\begin{aligned}&\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} p_h\left( x,y^j_m\right) {\tilde{w}}(x)\mathrm{d}x \\ = &- \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} u_h\left( x,y^j_m\right) {\tilde{w}}_x(x)\mathrm{d}x +{\hat{u}}_{i+\frac{1}{2},j}\left( y^j_m\right) {\tilde{w}}^-_{i+\frac{1}{2}}-{\hat{u}}_{i-\frac{1}{2},j}\left( y^j_m\right) {\tilde{w}}^+_{i-\frac{1}{2}},\quad m=1,2, \end{aligned}$$

for any test function \({\tilde{w}}(x)\in P^1([x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}])\), which is similar to the one-dimensional problem (7). Following the same idea as in the one-dimensional case, we get

$$\begin{aligned} {\hat{p}}_{i-\frac{1}{2},j}\left( y^j_m\right) ={p}_{i-\frac{1}{2},j}^+\left( y^j_m\right) =\frac{u_{i+\frac{1}{2},j}^-\left( y^j_m\right) +3u_{i-\frac{1}{2},j}^+\left( y^j_m\right) -4u_{i-\frac{1}{2},j}^- \left( y^j_m\right) }{\Delta x}, \quad m=1,2. \end{aligned}$$
(20)

Similarly, we can solve for \(q_h\) locally on each cell \(I_{i,j}\) by using (19) and get

$$\begin{aligned} {\hat{q}}_{i,j-\frac{1}{2}}\left( x^i_m\right) ={q}_{i,j-\frac{1}{2}}^+\left( x^i_m\right) =\frac{u_{i,j+\frac{1}{2}}^-\left( x^i_m\right) +3u_{i,j-\frac{1}{2}}^+\left( x^i_m\right) -4u_{i,j-\frac{1}{2}}^- \left( x^i_m\right) }{\Delta y}, \quad m=1,2, \end{aligned}$$
(21)

where \(x^i_1\) and \(x^i_2\) are the two Gaussian quadrature points on \([x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]\).

Taking \(v=1\) in (17), we get

$$\begin{aligned} \int _{I_{i,j}} (u_h)_t \mathrm{d}x \mathrm{d}y&=M\int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\left( {\hat{p}}_{i+\frac{1}{2},j} -{\hat{p}}_{i-\frac{1}{2},j}\right) \mathrm{d}y +M\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}\left( {\hat{q}}_{i,j+\frac{1}{2}} -{\hat{q}}_{i,j-\frac{1}{2}}\right) \mathrm{d}x \\&\quad +\int _{I_{i,j}} s(u_h)\mathrm{d}x\mathrm{d}y. \end{aligned}$$

By using the two-point Gaussian quadrature rule, we obtain

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} {\bar{u}}_{i,j}&= \frac{M}{\Delta x} \sum _{m=1}^2 c_m \left[ {\hat{p}}_{i+\frac{1}{2},j}\left( y^j_m\right) -{\hat{p}}_{i-\frac{1}{2},j}\left( y^j_m\right) \right] +\frac{M}{\Delta y} \sum _{m=1}^2 c_m \left[ {\hat{q}}_{i,j+\frac{1}{2}}\left( x^i_m\right) -{\hat{q}}_{i,j-\frac{1}{2}}\left( x^i_m\right) \right] \\&\quad +\frac{1}{\Delta x \Delta y}\int _{I_{i,j}} s(u_h)\mathrm{d}x\mathrm{d}y, \end{aligned}$$

where

$$\begin{aligned} {\bar{u}}_{i,j}=\frac{1}{\Delta x \Delta y}\int _{I_{i,j}} u_h \mathrm{d}x \mathrm{d}y. \end{aligned}$$

Substituting (20) and (21) into the above equation, we obtain

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t} {\bar{u}}_{i,j}&= \frac{M}{\Delta x^2} \left.\sum _{m=1}^2 c_m \left( u_{i+\frac{3}{2},j}^-+3u_{i+\frac{1}{2},j}^+ -5u_{i+\frac{1}{2},j}^- -3u_{i-\frac{1}{2},j}^+ +4u_{i-\frac{1}{2},j}^- \right) \right|_{y=y^j_m } \nonumber \\&\quad +\frac{M}{\Delta y^2} \left.\sum _{m=1}^2 c_m \left( u_{i,j+\frac{3}{2}}^- +3u_{i,j+\frac{1}{2}}^+ -5u_{i,j+\frac{1}{2}}^- -3u_{i,j-\frac{1}{2}}^+ +4u_{i,j-\frac{1}{2}}^-\right) \right|_{x=x^i_m } \nonumber \\&\quad +\frac{1}{\Delta x \Delta y}\int _{I_{i,j}} s(u_h)\mathrm{d}x\mathrm{d}y. \end{aligned}$$
(22)

By using the temporal discretization (11) and (12), we get the following equations for updating the cell average value \({\bar{u}}_{i,j}\) in time:

$$\begin{aligned} \bar{{u}}_{i,j}^{(1)}= & {} B^1_1\left[ {\bar{u}}_{i,j}^{n}+\Delta t f\left( u_h^n\right) \right] +\Delta t B^1_1\left[ \frac{1}{\Delta x \Delta y} \int _{I_{i,j}} s\left( u_h^n\right) \mathrm{d}x\mathrm{d}y+\mu {\bar{u}}_{i,j}^{n}\right] , \end{aligned}$$
(23)
$$\begin{aligned} {\bar{u}}_i^{n+1}= & {} B^1_2{\bar{u}}^{n} +B^2_2\left[ {\bar{u}}_{i,j}^{(1)} +\Delta tf(u_h^{(1)}) \right] +\Delta t B^2_2\left[ \frac{1}{ \Delta x \Delta y}\int _{I_{i,j}} s\left( u_h^{(1)}\right) \mathrm{d}x\mathrm{d}y+\mu {\bar{u}}_{i,j}^{(1)}\right] , \end{aligned}$$
(24)

where \({\bar{u}}_{i,j}^n\) and \({\bar{u}}_{i,j}^{(1)}\) are the cell averages of \(u_h^n\) and \(u_h^{(1)}\) on \(I_{i,j}\), respectively. For simplicity of notations, we still use f to denote the spatial discretization operator as in the one-dimensional case. But f has a different definition in the two-dimensional problem:

$$\begin{aligned} f(\omega )&= \frac{M}{\Delta x^2}\left. \sum _{m=1}^2 c_m \left( \omega _{i+\frac{3}{2},j}^-+3\omega _{i+\frac{1}{2},j}^+ -5\omega _{i+\frac{1}{2},j}^- -3\omega _{i-\frac{1}{2},j}^+ +4\omega _{i-\frac{1}{2},j}^- \right) \right|_{y=y^j_m }\\&\quad +\frac{M}{\Delta y^2} \left. \sum _{m=1}^2 c_m \left( \omega _{i,j+\frac{3}{2}}^- +3\omega _{i,j+\frac{1}{2}}^+ -5\omega _{i,j+\frac{1}{2}}^- -3\omega _{i,j-\frac{1}{2}}^+ +4\omega _{i,j-\frac{1}{2}}^-\right) \right|_{x=x^i_m }, \end{aligned}$$

for any function \(\omega \in V_h\). We state the property of f in the following lemma.

Lemma 2

For any function \(\omega (x)\in V_h\) with \(\omega \in [-1,1]\), we have

$$\begin{aligned} {\bar{\omega }}_{i,j}+ \Delta t f(\omega )\in [-1,1], \end{aligned}$$

under the CFL condition \(M\Delta t \leqslant \frac{1}{20} \min \{\Delta x^2,\Delta y^2\}\).

Proof

We divide \(\omega \) into two parts and use the Gaussian quadrature rule in different directions:

$$\begin{aligned} {\bar{\omega }}_{i,j}&=\frac{1}{2}{\bar{\omega }}_{i,j}+\frac{1}{2}{\bar{\omega }}_{i,j}\\&=\frac{1}{2\Delta x}\sum _{m=1}^2c_m\int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} \omega \left( x,y_m^j\right) \mathrm{d}x+\frac{1}{2\Delta y} \sum _{m=1}^2 c_m \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}\omega \left( x_m^i,y\right) \mathrm{d}y\\&=\frac{1}{4}\sum _{m=1}^2c_m \left[ \omega _{i+\frac{1}{2},j}^-\left( y_m^j\right) + \omega _{i-\frac{1}{2},j}^+\left( y_m^j\right) \right] +\frac{1}{4} \sum _{m=1}^2 c_m\left[ \omega _{i,j+\frac{1}{2}}^-\left( x_m^i\right) +\omega _{i,j-\frac{1}{2}}^+\left( x_m^i\right) \right] . \end{aligned}$$

Then, we obtain

$$\begin{aligned}&\quad{\bar{\omega }}_{i,j}+\Delta t f(\omega )\\ =& \left.\sum _{m=1}^2c_m \left( a_1 \omega _{i+\frac{3}{2},j}^- +a_2\omega _{i+\frac{1}{2},j}^+ +a_3\omega _{i+\frac{1}{2},j}^- +a_4\omega _{i-\frac{1}{2},j}^+ +a_5\omega _{i-\frac{1}{2},j}^- \right) \right|_{y=y^j_m } \\&+\left.\sum _{m=1}^2 c_m\left( b_1 \omega _{i,j+\frac{3}{2}}^- +b_2 \omega _{i,j+\frac{1}{2}}^+ +b_3 \omega _{i,j+\frac{1}{2}}^- +b_4 \omega _{i,j-\frac{1}{2}}^+ +b_5 \omega _{i,j-\frac{1}{2}}^- \right) \right|_{x=y^i_m }, \end{aligned}$$

where

$$\begin{aligned}&a_1=\frac{M\Delta t}{\Delta x^2}, \;\, a_2=3\frac{M\Delta t}{\Delta x^2},\;\, a_3= \frac{1}{4} -5\frac{M\Delta t}{\Delta x^2},\;\, a_4= \frac{1}{4}-3\frac{M\Delta t}{\Delta x^2},\;\, a_5=4\frac{M \Delta t}{\Delta x^2},\\&b_1=\frac{M\Delta t}{\Delta y^2},\;\, b_2=3\frac{M\Delta t}{\Delta y^2},\;\, b_3=\frac{1}{4}-5\frac{M\Delta t}{\Delta y^2} ,\;\, b_4=\frac{1}{4}-3\frac{M\Delta t}{\Delta y^2},\;\, b_5=4\frac{M\Delta t}{\Delta y^2} . \end{aligned}$$

Notice that \(c_1+c_2=1\) and hence it is easy to check that

$$\begin{aligned} \sum _{m=1}^2c_m \left( a_1 +a_2+a_3+a_4+a_5\right) +\sum _{m=1}^2 c_m \left( b_1 +b_2+b_3+b_4 +b_5\right) =1. \end{aligned}$$

If we require \(M\Delta t \leqslant \frac{1}{20} \min \{\Delta x^2,\Delta y^2\}\), then all coefficients are non-negative. Hence, we have written \({\bar{\omega }}_{i,j}+\Delta t f(\omega )\) as a convex combination of several point values of \(\omega \). Since all point values are bounded between \(-1\) and 1, we can obtain the conclusion of this lemma.

Finally, we get the following theorem of the maximum-principle-preserving property of the cell average values. The proof is similar to the one-dimensional case and hence we omit it. Here we denote the set of L Gauss quadrature points on \([x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]\) as \(S^x_i\) and denote the set of Gauss quadrature points on \([y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]\) as \(S^y_j\). We still choose L such that the computation for \(\int _{I_{i,j}}s(u_h)\mathrm{d}x\mathrm{d}y \) is accurate enough. Moreover, we let \(S_{i,j}=S^x_i \otimes S^y_j\).

Theorem 3

Consider the ODE (22) of the cell average \({\bar{u}}_{i,j}\), the numerical scheme (23) and (24) is bound-preserving: if \(-1\leqslant u_h^n(x,y) \leqslant 1\) on each cell \(I_{i,j}\), \(i=1,\cdots , N_x\), \(j=1,\cdots , N_y\), then we have \(-1\leqslant {\bar{u}}^{(1)}_{i,j}\leqslant 1\) under the conditions

$$\begin{aligned} \mu \geqslant \max \left\{ 0, \, \max _{(x,y)\in S_{i,j}}\frac{s\left( u_h^n(x,y)\right) }{ 1-u_h^n(x,y)}, \, \max _{(x,y)\in S_{i,j}} \frac{s\left( u_h^n(x,y)\right) }{-1-u_h^{n}(x,y )} \right\} \end{aligned}$$

and

$$\begin{aligned} M\Delta t \leqslant \frac{1}{20} \min \{\Delta x^2,\Delta y^2\}. \end{aligned}$$

In addition to the above conditions, if \(-1\leqslant u_h^{(1)}(x,y) \leqslant 1\) on each cell \(I_{i,j}\), \(i=1,\cdots , N_x\), \(j=1,\cdots ,N_y\) and

$$\begin{aligned} \mu \geqslant \max \left\{ 0, \, \max _{(x,y)\in S_{i,j}}\frac{s\left( u_h^{(1)}(x,y)\right) }{ 1-u_h^{(1)}(x,y)}, \, \max _{(x,y)\in S_{i,j}} \frac{s\left( u_h^{(1)}(x,y)\right) }{-1-u_h^{(1)}(x,y )} \right\} , \end{aligned}$$

then we have \(-1\leqslant {\bar{u}}^{n+1}_{i,j}\leqslant 1\).

Now we can construct physically relevant numerical cell averages \({\bar{u}}_{i,j}\). However, the polynomial \(u_h\) may be out of the bounds. On each stage of the conservative modified exponential RK method, we need to replace the solution with a modified polynomial on each cell. The whole procedure is the same as the one-dimensional limiter described in Sect. 3.2. For simplicity, we only show the formulation at the time level \(n+1\) for the two-dimensional case. On each cell \(I_{i,j}\), after we get the polynomial \(u_h^{n+1}(x,y)\) by using the temporal discretization, we replace it with a modified polynomial \({\tilde{u}}_h^{n+1}(x,y)\):

$$\begin{aligned} {\tilde{u}}_h^{n+1}(x,y)=\theta \left( u_h^{n+1}(x,y)-{\bar{u}}^{n+1}_{i,j}\right) +{\bar{u}}^{n+1}_{i,j}, \end{aligned}$$

where

$$\begin{aligned} \theta =\min \left\{ 1, \frac{1-{\bar{u}}^{n+1}_{i,j}}{M_{i,j}-{\bar{u}}^{n+1}_{i,j}} , \frac{{\bar{u}}^{n+1}_{i,j}+1}{{\bar{u}}^{n+1}_{i,j}-m_{i,j}}\right\} \end{aligned}$$

and

$$\begin{aligned} M_{i,j}=\max _{(x,y)\in I_{i,j}}u_h^{n+1}(x,y),\quad m_i=\min _{(x,y)\in I_{i,j}}u_h^{n+1}(x,y). \end{aligned}$$

Then, we can get \(-1\leqslant {\tilde{u}}_h^{n+1}(x,y)\leqslant 1\).

5 Numerical Examples

In this section, we take the nonlinear free energy density as

$$\begin{aligned} F(u)=\frac{1}{4\epsilon ^2} (u^2-1)^2, \end{aligned}$$

where \(\epsilon \) represents the inter-facial width. In this case, the energy function becomes

$$\begin{aligned} E(u)=\int _{\Omega } \left( \frac{1}{2}|\triangledown u|^2+\frac{1}{4\epsilon ^2} (u^2-1)^2\right) \mathrm{d}{{\mathbf {x}}}. \end{aligned}$$

Also, we have

$$\begin{aligned} s(u)=-M F'(u)= \frac{M}{\epsilon ^2} (u-u^3), \end{aligned}$$

and the Allen-Cahn equation becomes

$$\begin{aligned} u_t=M \left( \Delta u+\frac{1}{\epsilon ^2} (u-u^3)\right) . \end{aligned}$$
(25)

In the one-dimensional case, we have

$$\begin{aligned} u_t=M \left( u_{xx}+\frac{1}{\epsilon ^2} (u-u^3)\right) . \end{aligned}$$
(26)

Although we only show the detailed formulation for the second-order scheme, we also test the third-order scheme in this section. For the spatial discretization, we follow the method in [21]. For the time integration, we adopt the method in [17], which has also been illustrated at the end of Sect. 2. We will numerically show that our method has the MPP property and test whether we can observe the energy decay. In all figures, we use “new RK” to represent the conservative modified exponential RK method and use “RK” to represent the traditional SSP RK method. Also, “without limiter” means that we do not modify the polynomials as in Sect. 3.2. But we still choose a suitable parameter \(\mu \) in the conservative exponential RK method as described in Theorems 2 and 3. This parameter also helps to approach the correct solutions.

Example 1

We first test the stability and accuracy of the ODE solvers, and study the following problem:

$$\begin{aligned} u'(t)=-cu^7, \quad u(0)=u_0, \end{aligned}$$

where c is a parameter that we can adjust. The problem becomes stiff as c increases. The exact solution is

$$\begin{aligned} u(t)=u_0\left( 6ctu_0^6+1\right) ^{-1/6}. \end{aligned}$$

We take the final time to be \(t=0.5\) and denote the total number of time steps as \(N_t\).

We first take \(u_0=0.2\) with \(c=100\). We choose \(c=100\) because in most of the previous works for Allen-Cahn equations, the value of \(1/\epsilon \approx 100\). Numerical results for the second-order and third-order new RK method are listed in Table 1. The initial condition is well-prepared, and we can observe the optimal convergence rates.

Next, we take \(u_0=1\), the results are given in Table 2. For this problem, the initial condition is not well-prepared, and we can observe the optimal convergence rate if the problem is not stiff, e.g., \(c=1\). If the problem is stiff, e.g., \(c=100\), the method may not converge at the expected rate, but our scheme is able to deal with large time steps and we can observe the convergence of the solutions.

Table 1 Accuracy test for ODE solvers with \(u_0=0.2\) with \(c=100\)
Full size table
Table 2 Accuracy test for ODE solvers with \(u_0=1\)
Full size table

Example 2

We consider the one-dimensional Allen-Cahn equation (26) with periodic boundary conditions. We take \(M=1\) and adopt \(N=100\) cells. The computational domain is \([0,2\pi ]\) and the initial condition is taken as

$$\begin{aligned} u(x, 0)=\sin (x). \end{aligned}$$

We first test the second-order schemes. We adopt the new RK method and compare the results with and without the MPP limiter in Fig. 1. Different values of \(\epsilon \) are tested. The time step size \(\Delta t = c\Delta x^2/M\) with \(c=0.1\) is used in all cases. We can see that the energy decays as the time increases. The maximum principle is preserved after we add the MPP limiter.

Next, we take \(\mu =0\), then the new RK method becomes the regular second-order RK method. In this case, the code will blow up with the same choice of \(\Delta t\) as in the new RK method. For comparison, we take \(\epsilon =0.01\) and \(\Delta t = c\Delta x^2/M\) with \(c=0.03\). The results of different methods are shown in Fig. 2. We can see that the traditional RK method will lead to wrong solutions. To obtain correct solutions, \(c=0.01\) is needed. For \(\epsilon =0.001\), \(c=10^{-4}\) is needed in traditional RK method. If we take \(\epsilon =0.000\,1\), then \(c=10^{-6}\) is needed.

Fig. 1
figure 1

Example 2 with different \(\epsilon \). Second-order method with new RK. Comparison of results with and without the MPP limiter. \(\Delta t = c\Delta x^2/M\) with \(c=0.1\)

Full size image
Fig. 2
figure 2

Example 2 with \(\epsilon =0.01\). Second-order schemes with MPP limiters. Comparison between RK and new RK methods. \(\Delta t = c\Delta x^2/M\) with \(c=0.03\)

Full size image

We move on to test the third-order schemes. Firstly, we take \(\epsilon =0.01\) and adopt the new RK method in time. The time step size \(\Delta t = c\Delta x^2/M\) with \(c=0.02\) is used. The numerical methods with and without the MPP limiter are shown in Fig. 3. We can see that the energy decays as the time increases. The maximum principle is preserved after we add the MPP limiter. Next, we still take \(\epsilon =0.01\) and compare our new RK method with the traditional RK method in Fig. 4. The same time step size with \(c=0.02\) is used. We can see that the traditional RK method leads to wrong solutions. To obtain correct solutions with the traditional RK method, we need to take \(c=6\times 10^{-3}\). Finally, we test smaller values of \(\epsilon \). The numerical results of our new RK method are shown in Fig. 5. Here we take with \(c=0.02\) for \(\epsilon =0.001\), and take \(c=6\times 10^{-4}\) for \(\epsilon =0.000\,1\). Again, we can see that the energy decays and the MPP property is preserved. For \(\epsilon =0.001\), if we still use \(c=0.02\) in the traditional RK method, the code will blow up, and \(c=10^{-4}\) is needed to obtain correct solutions. For \(\epsilon =0.000\,1\), \(c=10^{-6}\) is needed in the traditional RK method.

Fig. 3
figure 3

Example 2 with \(\epsilon =0.01\). Third-order method with new RK. Comparison of results with and without the MPP limiter. \(\Delta t = c\Delta x^2/M\) with \(c=0.02\)

Full size image
Fig. 4
figure 4

Example 2 with \(\epsilon =0.01\). Third-order schemes with MPP limiters. Comparison between RK and new RK methods. \(\Delta t = c\Delta x^2/M\) with \(c=0.02\)

Full size image
Fig. 5
figure 5

Example 2 with different \(\epsilon \). Third-order scheme with new RK. \(\Delta t = c\Delta x^2/M\). We take with \(c=0.02\) for \(\epsilon =0.001\), and take \(c=6\times 10^{-4}\) for \(\epsilon =0.000\,1\)

Full size image

Example 3

We consider the one-dimensional Allen-Cahn equation (26) with homogeneous Neumann boundary conditions. We take \(M=1\) and \(\epsilon =0.001\). The computation domain is [0, 1] and the initial condition is chosen as

$$\begin{aligned} u(x,0)=0.9\times \mathrm{rand} (\cdot )+0.05, \end{aligned}$$

where “rand(\(\cdot \))” represents a random number on each point in [0, 1].

From now on, we only test the second-order schemes for simplicity. We take \(N=100\) cells and compare the results with and without the MPP limiter in Fig. 6. The time step size \(\Delta t = c\Delta x^2/M\) with \(c=0.1\) is used. We can observe that the energy decays as the time increases. The maximum principle is preserved after we add the MPP limiter. Again, if we do not add the limiter and further take \(\mu =0\), the code will blow up with the same choice of \(\Delta t\).

Fig. 6
figure 6

Example 3

Full size image

Example 4

We consider the two-dimensional Allen-Cahn equation (25) with periodic boundary conditions. We take \(M=0.01\) and \(\epsilon =0.08\). The computational domain is \([0,1]\times [0,1]\). The initial condition is taken as

$$\begin{aligned} u(x, y, 0)=\cos {(\pi x)}\cos {(\pi y)}. \end{aligned}$$

We divide the computational domain into \(N\times N\) cells, i.e., \(N_x=N_y=N\). The time step size \(\Delta t = 0.02\Delta x^2/M\) is used. Table 3 shows the numerical errors at the time \(T=0.5\). We can observe the second-order convergence rate. Also, the MPP limiter does not harm the original high order of accuracy.

Table 3 Two-dimensional accuracy test
Full size table

Example 5

We solve a benchmark problem for the two-dimensional Allen-Cahn equation (25). Consider a two-dimensional domain \((-128,128)^2\) with a circle of radius \(R_0 = 100\). In other words, the initial condition is given by

$$\begin{aligned} u(x,y,0)=\left\{ \begin{array}{ll} 1, &{}\quad \text {if } x^2+y^2<100^2,\\ -1, &{}\quad \text {otherwise.} \end{array} \right. \end{aligned}$$

The boundary condition is taken as the periodic boundary condition. By mapping the domain to \(\Omega =(-1,1)^2\), the parameters in the two-dimensional Allen-Cahn equation are given by \(M=6.103\,51\times 10^{-5}\) and \(\epsilon =0.007\,8\). In the sharp interface limit (\(\epsilon \rightarrow 0\), which is suitable because the chosen \(\epsilon \) is small), the radius at the time t should be

$$\begin{aligned} R=\sqrt{R_0^2-2t}. \end{aligned}$$

We take \(N_x=N_y=401\). The time step size is \(\Delta t = 0.02\Delta x^2/M\). We add the MPP limiter. Numerical results are shown in Fig. 7. We can see that the energy decays and the maximum principle is preserved. Also, we compare the real radius R with the numerical one. We can see that our method can capture the correct radius.

Fig. 7
figure 7

Example 5

Full size image

Example 6

We consider the two-dimensional Allen-Cahn equation (25) with periodic boundary conditions. We take \(M=1\) and \(\epsilon =0.02\). The computational domain is \([0,2\pi ]^2\). The initial condition is taken as \(u(x,y,0)=0.05\sin (x)\sin (y)\).

We adopt \(N_x=N_y=100\). The time step size is \(\Delta t = 0.02\Delta x^2/M\). We add the MPP limiter. Numerical results are shown in Fig. 8. We can see that the energy decays as the time increases. The maximum principle is preserved. Also, we can observe the phase separation and coarsening process.

Fig. 8
figure 8

Example 6

Full size image

Example 7

We consider the two-dimensional Allen-Cahn equation (25) with periodic boundary conditions. We take \(M=1\) and \(\epsilon =0.02\). The computational domain is \([0,2\pi ]^2\). The initial condition is a random function with values in \([-0.05,0.05]\).

We adopt \(N_x=N_y=100\). The time step size is \(\Delta t = 0.02 \Delta x^2/M\). The MPP limiter is added. The plots of energy and the maximum absolute value are shown in Fig. 9. We can see that the energy decays as the time increases. The maximum principle is preserved. The plots of u at different times are also shown in Fig. 9. We can observe the phase separation and coarsening process.

Fig. 9
figure 9

Example 7

Full size image

6 Conclusion

In this paper, we study the classical Allen-Cahn equations. We apply the LDG method due to its flexibility on the h-p adaptivity and complex geometry. Moreover, since the source given in the equation may be stiff, we use the conservative modified exponential RK methods and thus can use relatively large time step sizes. Thanks to the conservative time integration, we can design the MPP technique for the scheme. Moreover, the physical bounds of the unknown function will not decay. Numerical experiments are also given to demonstrate the good performance of the MPP LDG scheme.

Since the MPP LDG methods require slope limiters, the energy stability may not be easy to obtain. In this paper, we only discuss the MPP technique and use numerical experiments to demonstrate the energy decay property. The proof for the energy decay will be investigated in the future.