Abstract
Staggered grid techniques have been applied successfully to many problems. A distinctive advantage is that physical laws arising from the corresponding partial differential equations are automatically preserved. Recently, a staggered discontinuous Galerkin (SDG) method was developed for the convection–diffusion equation. In this paper, we are interested in solving the steady state convection–diffusion equation with a small diffusion coefficient \(\epsilon \). It is known that the exact solution may have large gradient in some regions and thus a very fine mesh is needed. For convection dominated problems, that is, when \(\epsilon \) is small, exact solutions may contain sharp layers. In these cases, adaptive mesh refinement is crucial in order to reduce the computational cost. In this paper, a new SDG method is proposed and the proof of its stability is provided. In order to construct an adaptive mesh refinement strategy for this new SDG method, we derive an a-posteriori error estimator and prove its efficiency and reliability under a boundedness assumption on \(h/\epsilon \), where h is the mesh size. Moreover, we will present some numerical results with singularities and sharp layers to show the good performance of the proposed error estimator as well as the adaptive mesh refinement strategy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we consider the following steady state convection–diffusion equation
where \(\Omega \subset \mathbb {R}^{d}\) is a polyhedral domain with \(d=2,3\). For simplicity, we only consider the homogeneous Dirichlet boundary condition
Extensions to cases with inhomogeneous Dirichlet boundary condition and other types of boundary conditions are straight-forward. In the above equation, u is the unknown function to be approximated, \(f\in L^{2}(\Omega )\) is the given source term, and \(\mathbf {b}\) is the given vector field which is sufficiently smooth with the divergence free assumption, i.e., \(\nabla \cdot \mathbf {b}=0\). Throughout this paper, vector fields are denoted by bold faces. Moreover, the diffusion coefficient \(\epsilon \) is a constant. We mainly consider the convection dominated case, that is to say, the diffusion is small. Hence, we assume that \(\epsilon \leqslant 1\) throughout this paper.
There have been a number of attempts to solve the convection–diffusion equation numerically. One of the most popular choices is the finite element (FE) method, which uses continuous basis functions. For example, Galerkin/Least Squares methods [27], Continuous Interior Penalty methods [6, 7], and Local Projection Stabilization [1, 2, 4, 33]. Codina’s paper [25] also summarized and compared a few existing variants of FE method, while some new ideas were proposed. Another class of important methods is the discontinuous Galerkin (DG) methods [10, 23, 24, 36, 37], which uses piecewise approximations without enforcing any continuity along cell interfaces. It has several advantages such as high order accuracy, extremely local data structure and high parallel efficiency. There are many successful works in this area, such as [3, 9, 21, 29]. The staggered DG (SDG) method is a relatively new class of DG method in literature, which uses staggered mesh. A distinctive advantage of using staggered mesh is that physical laws arising from the corresponding partial differential equations are automatically preserved. The SDG method can be viewed as a hybrid of the standard DG method and the FE method in the sense that each of the numerical solutions is continuous along some of the faces in the triangulation, but is discontinuous along other faces. The SDG method was first developed by Chung and Enquist [17] in 2006 to solve the wave propagation problem. Since then, there have been a number of successful works on SDG, such as [12, 13, 19, 32]. In 2012, Chung and Lee [20] proposed an SDG scheme for the convection–diffusion equation in which the diffusion coefficient \(\epsilon \) is set to be 1. This SDG method is successful in preserving a number of physical laws. We note that the SDG method is related to the very successful HDG method [14, 15].
It is well-known that the exact solution of the mathematical problem (1.1) may contain singular points. Also, when dealing with the convection dominated case of the convection diffusion equation, that is, when the diffusion coefficient \(\epsilon \) is relevantly small, the exact solution may contain sharp layers. In these cases, numerical computations require a very fine mesh in order to capture the detailed features of the solution near those singular points or sharp layers. Thus, a significant amount of computer memory and time are needed, and the computation of the solution is very challenging. In many cases, adaptively refinement schemes are used for quicker convergence. They refine the mesh locally at suitable locations and thus can reduce the computational cost. Over the past few decades, there are many successful works on adaptive FE or DG methods for solving the convection–diffusion equation, such as [7, 8, 28, 42]. As far as we know, there are only two works on adaptive SDG methods, namely, [22] for the time-harmonic Maxwell’s equation and [16] for the Stokes system, and there is no prior work on adaptive SDG method for convection–diffusion equations.
In this paper, we devote to construct an adaptive SDG method in order to solve the steady state convection–diffusion equation (1.1). The key ingredient is the construction of an efficient and reliable error indicator. Note that there is an extra coefficient \(\epsilon \) in Eq. (1.1) compared to the equation considered in [20]. A straight forward generalization of the SDG method in [20] will lead to a term with coefficient \(\frac{1}{\epsilon }\) in the proof of the reliability of the error indicator. This term will be very large in the convection dominated case. Hence, we make a small modification of the scheme in [20] and provide a new SDG method for solving (1.1). As the exact solution may not be known a priori, we derive a computable error estimator without undetermined variables and use it as an error indicator for the new SDG method. The error indicator is composed of local residuals and jumps of the numerical solution. It can estimate a DG-norm error of the numerical solution locally in each cell of the triangulation. We will then prove the reliability and efficiency of this error indicator. In particular, we will show that the DG-norm error of the numerical solution is both bounded up and bounded below by our computable error estimator up to a data approximation term. Based on the derived error indicator, we can refine the mesh at locations with high estimated error and hence construct an adaptive mesh refinement strategy.
We admit that there is a term with the coefficient \(\frac{h}{\epsilon }\) in our error indicator and the efficiency is proved under the assumption that the ratio \(\frac{h}{\epsilon }\) is bounded. That is, for the convection dominated problem, this error estimator may be much larger than the exact error theoretically at the sparse part of the mesh, and becomes efficient only when the mesh size is small enough locally. However, numerical examples still show that our scheme performs roughly the same as the adaptive refinement scheme using the exact solution as the error indicator. We can see that our adaptive refinement method is much better than the regular uniform refinement method and can reach the optimal rate of convergence. Also, our adaptive SDG method is able to capture the correct locations of singular points and sharp layers and hence can recover the complicated structure of the solution.
This paper is organized as follows. In Sect. 2, we make a small modification of the SDG scheme proposed in [20] and prove the numerical stability of the new SDG method. In Sect. 3, we propose a residual-type a-posteriori error estimator for this new SDG method and prove its reliability and efficiency. An adaptive mesh refinement strategy based on this error estimator is also given. Numerical experiments are performed in Sect. 4 to show the accuracy and efficiency of the proposed error estimator and the adaptive SDG method. Finally, a conclusion is given in Sect. 5.
2 Numerical Scheme
In this section, we briefly show the numerical scheme to solve the steady state convection–diffusion equation (1.1). We follow the basic idea in [20]. However, since there is an extra coefficient \(\epsilon \leqslant 1\) in the diffusion term in this paper, we need to make some modifications. Also, we adjust the notations to make the scheme simpler. We can prove that the stability of this new modified SDG scheme also holds, as in [20].
In the following, we first show a new mixed form of the original convection–diffusion equation and derive the variation form satisfied by the exact solution in Sect. 2.1. Based on the mixed form equations, we show how to construct the new SDG method in Sect. 2.2. For simplicity, we only discuss the two-dimensional case, while its generalization to the three-dimensional case is straight forward.
2.1 A New Mixed Form of the Convection–Diffusion Equation
The key step of the SDG method is to transform the original convection–diffusion equation into a mixed form. Let us first recall the following mixed form used in [20] if we only consider the steady state case:
Notice that \(\mathbf {p}+\frac{1}{2}\mathbf {w}\) in the last equation is in fact \(\nabla u\), deriving from the convection part of the original convection–diffusion equation. However, \(\nabla u\) in the definition of \(\mathbf {p}\) comes from the diffusion part. That is, we need to solve \(\nabla u\) in the convection part by using the diffusion part. Now we consider Eq. (1.1) which contains an coefficient \(\epsilon \) in the diffusion term. A straight forward generalization of the above mixed form leads to
Now we have a coefficient \(\frac{1}{\epsilon }\) in (2.2) which will still appear in the proof of the reliability of the error indicator. Hence, we need a new formulation to eliminate this \(\frac{1}{\epsilon }\) term.
To derive the new formulation, we denote \(\nabla u\) in the convection part as \(\mathbf {s}\) directly and introduce the following two variables:
Then the left hand side of Eq. (1.1) becomes
Since \(\mathbf {b}\) is divergence free, we know that
Hence, Eq. (1.1) becomes
Finally, we obtain the following new mixed form of Eq. (1.1)
which contains no \(\frac{1}{\epsilon }\) term.
Before we proceed, we denote some notations. We simply use \((\cdot ,\cdot )\) to denote the standard \(L^2\) inner product on \(\Omega \). For any domain \(\Lambda \subset \mathbb {R}^{d}\) and functions u and v defined on \(\Lambda \), we define norms as
provided that these norms are well-defined.
By multiplying test functions and using integration by parts, the variational form of Eqs. (2.3) to (2.5) is : find \((\mathbf {p},\mathbf {s},u)\in [L^2(\Omega )]^2\times [L^2(\Omega )]^2 \times H_0^1(\Omega )\), such that
for all test functions \((\mathbf {q},v)\in [L^2(\Omega )]^2 \times H_0^1(\Omega )\).
Now we try to eliminate the auxiliary variables \(\mathbf {p}\) and \(\mathbf {s}\) from the variational form and thus derive the equation satisfied by \(u\in H_0^1(\Omega )\). Note that for any test function \(v \in H_0^1(\Omega )\), by taking \(\mathbf {q}=\nabla v \in [L^2(\Omega )]^2\) and \(\mathbf {q}=\mathbf {b} v \in [L^2(\Omega )]^2\) in Eqs. (2.6) and (2.7), respectively, we have
Substituting the above two equations into Eq. (2.8) and using the fact that \(v \in H_0^1(\Omega )\) and \(\mathbf {b}\) is divergence free, we obtain
If we denote
then the exact solution \(u\in H_0^1(\Omega )\) satisfies
This equation will be used in Sect. 3. Since \(\mathbf {b}\) is divergence free, we can observe that
which shows the following property of \(B_c\)
2.2 The Modified SDG Method
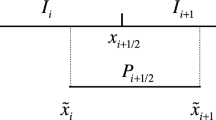
Based on the mixed formulation in the last section, we are ready to construct a new modified SDG method. Following [20], we first define the triangulation. Let \(\mathcal {T}_{0}\) be a shape regular initial triangulation of \(\Omega \), as illustrate by solid lines in Fig. 1. We denote the the collection of all edges in \(\mathcal {T}_{0}\) as \(\mathcal {F}_{u}\) and denote the subset of all interior edges as \(\mathcal {F}_{u}^0\). Next, we construct a staggered mesh by further division of triangles. For each triangle \(\tau \in \mathcal {T}_{0}\), we subdivide it into three small triangles by joining its center with its vertices. Hence, we can obtain a new triangulation consists of all small triangles formed and denote it as \(\mathcal {T}\). As illustrated by dotted lines in Fig. 1, we denote the collection of all new edges formed under \(\mathcal {T}\) as \(\mathcal {F}_{p}\). Moreover, we define the set of all interior edges of \(\mathcal {T}\) as \(\mathcal {F}^0=\mathcal {F}_{p}\bigcup \mathcal {F}_{u}^0\).
For each edge e of \(\mathcal {T}\), we define a unit normal vector \(\mathbf {n}_e\) in the following way. If \(e\in \partial \Omega \), then we define \(\mathbf {n}_e\) as the unit normal vector pointing outside of \(\Omega \). For an interior edge \(e=\partial \tau ^+ \bigcap \partial \tau ^-\), we use notations \(\mathbf {n}^+\) and \(\mathbf {n}^-\) to denote the outward unit normal vectors of e taken from \(\tau ^+\) and \(\tau ^-\), respectively, and fix \(\mathbf {n}_e\) as one of \(\mathbf {n}^{\pm }\). We use notations \(v^+\) and \(v^-\) to denote the values of a function v on e taken from \(\tau ^+\) and \(\tau ^-\), respectively. Then the jump notation [v] over an edge e for a scalar valued function v is defined as
For a vector-valued function \(\mathbf {q}\), the notation \([\mathbf {q}\cdot \mathbf {n}]\) is defined as
Note that \(\mathbf {b}\) is the given vector field, which can be any sufficiently smooth function. In order to solve our problem numerically, we approximate \(\mathbf {b}\) with a piecewise polynomial vector \(\mathbf {b}_h\). In each triangle \(\tau \in \mathcal {T}\), \(\mathbf {b}_h|_{\tau }\) is the Raviart–Thomas projection of \(\mathbf {b}\) onto the Raviart–Thomas space \(RT^k(\tau )\), which is defined as follows
where \(P^{k}(\Lambda )\) denotes the space of polynomials of degree up to k on the domain \(\Lambda \subset \mathbb {R}^{d}\). We all know that \(\mathbf {b}_h|_{\tau }\cdot \mathbf {n}_e\in P^k(e)\) on \(e\in \partial \tau \). Hence, (2.13) shows that \(\mathbf {b}_h|_{\tau }\cdot \mathbf {n}_e\) on \(e\in \partial \tau \) is just the \(L^2\) projection of \(\mathbf {b}\cdot \mathbf {n}_e\) onto \(P^k(e)\). Thus, \(\mathbf {b}_h\cdot \mathbf {n}_e\) is continuous over each interior edge in \(\mathcal {T}\). Another property of the Raviart–Thomas projection is that \(\nabla \cdot \mathbf {b}_h|_{\tau }\) is the \(L^2\) projection of \(\nabla \cdot \mathbf {b}\) onto \(P^k(\tau )\). Since \(\mathbf {b}\) is divergence free, we obtain \(\nabla \cdot \mathbf {b}_h=0\). In the following content of this paper, we denote \(\mathbf {e}_b=\mathbf {b-b}_{h}\) for simplicity. It is well known that the following error estimate holds
Next, we define two finite element spaces on the constructed staggered mesh:
In the space \(U_h\), we define the following norms
where \(h_e\) is the length of e. In the space \(W_h\), we define the following norms
Based on all concepts introduced above, we are ready to construct a new SDG scheme in order to approximate the variational form (2.6)–(2.8) satisfied by the exact solution. In our SDG method, we find the numerical solution \((\mathbf {p}_{h},\mathbf {s}_{h},u_{h})\in W_{h}\times W_{h}\times U_{h}\), such that
for all test functions \(\mathbf {q}\in W_h\) and \(v\in U_h\), where
We remark that the variables \(\mathbf {p}_h\) and \(\mathbf {s}_h\) in (2.16) can be eliminated easily by using (2.14) and (2.15). Thus the scheme consists of one system involving only \(u_h\). Comparing with other types of DG schemes, our SDG scheme has fewer degrees of freedoms due to the additional continuity condition for \(u_h\). On the other hand, it is proved by Chung and Engquist in [18] that
Moreover, the following inf-sup condition holds:
where K is a constant independent of the mesh size.
By using the inf-sup condition of \(B_h^*\), we can prove the following stability of the above modified SDG method.
Theorem 2.1
Let \((\mathbf {p}_{h},\mathbf {s}_{h},u_{h})\in W_{h}\times W_{h}\times U_{h}\) be the solution of the SDG scheme (2.14)–(2.16). Then the following stability holds:
Proof
The inf-sup condition (2.18) for the operator \(B_h^*\) implies that
where we have used the scheme (2.15). Next, we try to compute \(\Vert \mathbf {s}_{h}\Vert _{0;\Omega }^2\). Taking \(\mathbf {q}=\mathbf {s}_h\), \(\mathbf {q}=\mathbf {p}_h\), and \(v=u_h\) in Eqs. (2.14), (2.15), and (2.16), respectively, we have
Combining (2.21) and (2.22), we get
Substituting the above equation into (2.23) and using the property (2.17), we obtain
Combining (2.20) and (2.25), we obtain
Hence, we arrive the conclusion that
\(\square \)
Remark It is noted that the convection term is skew-symmetric and is therefore easy to obtain the following underlying physical law from the original convection–diffusion equation (1.1):
Equation (2.25) is a result of the preservation of the skew-symmetry of the discrete convection operator and shows that our SDG scheme preserves the above physical property in the discrete sense. Such property can also enhance the stability when solving the incompressible Navier–Stokes equations [11]. This is the advantage of using staggered mesh. One can prove that this physical law is not strictly satisfied by using the local DG (LDG) method due to the usage of numerical flux.
By using the definition of \(\Vert u_h\Vert _Z\), the stability of our scheme gives
By combining Eqs. (2.26) and (2.27), we can also derive the following bound of \(\mathbf {s}_h\)
3 An Adaptive SDG Method
In order to develop an adaptive mesh refinement strategy for the new SDG scheme constructed in the last section, we will derive a reliable and efficient a-posteriori error estimator for this SDG scheme in this section. The error estimator can give a computable estimate of the numerical error in each triangle \(\tau \in \mathcal {T}\). Thus, we can use it as an error indicator and refine the mesh adaptively at locations with larger estimated numerical error.
Let \((\mathbf {p},\mathbf {s},u)\in [L^2(\Omega )]^2\times [L^2(\Omega )]^2 \times H_0^1(\Omega )\) be the exact solution of (2.6)–(2.8) and let \((\mathbf {p}_{h},\mathbf {s}_{h},u_{h})\in W_{h}\times W_{h}\times U_{h}\) be the numerical solution of the SDG scheme (2.14)–(2.16). \(\mathbf {b}_h\) is the Raviart–Thomas projection of \(\mathbf {b}\). Then, we denote numerical errors as
Moreover, we define the following DG norm of the numerical error
In Sect. 3.1, we will give an error indicator which gives a locally a-posteriori error estimate of the above DG norm \(\Vert (e_{u}, \mathbf {e}_{bu},\mathbf {e}_{p}, e_{bs})\Vert _{\mathrm {DG}}^2\) and prove the reliability of it. The efficiency of this error indicator will be proved in Sect. 3.2. Based on the error indicator, we will give the adaptive refinement technique in Sect. 3.3.
3.1 Reliability of the Error Indicator
As in the following theorem, we will show that the DG norm of the numerical error defined in (3.1) is bounded above by a computable error indicator \(\eta ^2\), which can be computed locally on each triangle \(\tau \) in the mesh. Throughout the paper, the notation \(\alpha \lesssim \beta \) means that \(\alpha \le C \beta \) for a constant C independent of the mesh size.
Theorem 3.1
Assuming \((\mathbf {p},\mathbf {s},u)\in [L^2(\Omega )]^2\times [L^2(\Omega )]^2 \times H_0^1(\Omega )\) be the the exact solution of (2.6)–(2.8) and denoting the numerical solution of the SDG scheme (2.14)–(2.16) as \((\mathbf {p}_{h},\mathbf {s}_{h},u_{h})\in W_{h}\times W_{h}\times U_{h}\), we can estimate the DG norm of the numerical error defined in Eq. (3.1) as
where for each \(\tau \in \mathcal {T}\),
with
Here, \(h_{\tau }\) denotes the diameter of the circumcircle of a triangle \(\tau \), and \(h_e\) is the length of an edge e. For each \(e\in \partial \tau \), it is obvious that \(h_e\leqslant h_{\tau }\). Through out this paper, we assume that our mesh is regular, that is, \( h_{\tau }\lesssim h_e\) for each \(e\in \partial \tau \).
From the definition of \(\eta ^2\) and the fact that \([u]|_e=0\) on \(e\in \mathcal {F}_p\), we can easily see that the last term of \(\Vert (e_{u}, \mathbf {e}_{bu},\mathbf {e}_{p}, e_{bs})\Vert _{\mathrm {DG}}^{2}\) in Eq. (3.1) is also one term in \(\eta ^2\), and hence is automatically bounded by \(\eta ^2\). Thus we only need to find the upper estimates for the first three terms in \(\Vert (e_{u}, \mathbf {e}_{bu},\mathbf {e}_{p}, e_{bs})\Vert _{\mathrm {DG}}^{2}\). In the following lemma, we first deal with the second and third terms.
Lemma 3.2
Under the assumption of Theorem 3.1, we have the following upper estimates:
Proof
We first prove (3.4). By the variation form (2.6), we know that for any \(\mathbf {q} \in [L^2(\Omega )]^2\), we have
Taking \(\mathbf {q}=\mathbf {e}_p+\frac{1}{2}\mathbf {e}_{bu}\in [L^2(\Omega )]^2\), we obtain
We move on to prove (3.5). Using the fact that \(\mathbf {b}\) and \(\mathbf {b}_h\) are divergence free, we know that for any \(v \in L^2(\Omega )\), we have
From the variation form (2.7), we get
Hence, we obtain
Taking \(v=e_{bs}-\nabla \cdot \mathbf {e}_{bu}\in L^2(\Omega )\), we have
\(\square \)
From the above lemma, we know that the remaining thing is to find an upper bound of \(\epsilon ^2|e_u|_{1;\Omega }^2\), which is also the first term of \(\Vert (e_{u}, \mathbf {e}_{bu},\mathbf {e}_{p}, e_{bs})\Vert _{\mathrm {DG}}^{2}\). For this purpose, we need to introduce an auxiliary variable \(u^{c}\in H_0^1\bigcap U_h\) as in the following lemma on polynomial approximations.
Lemma 3.3
Let \(u_{h}\in U_{h}\). There exists \(u^{c}\in H_0^1(\Omega )\bigcap U_{h}\), such that
Proof
From Theorem 2.2 of [31], we know that there exists \(u^{c}\in H_0^1\bigcap U_{h}\) such that
By the definition of \(U_h\), we know that \(J_1|_{\mathcal {F}_{u}^0}=0\) and \(u_h|_{\partial \Omega }=0\). Hence, we can obtain the conclusion. \(\square \)
Using the triangle inequality, we know that
where the second term on the right hand side is already bounded by a term in our error indicator as shown in the above lemma. Up to this point, only the first term on the right hand side, namely, \(\epsilon ^2|u-u^c|_{1;\Omega }^2 \), dose not have an upper estimate. The following lemma shows that the upper bound of this term is just the “error” obtained by plugging \(u_h\) into Eq. (2.10), which is satisfied by the exact solution u, plus another term in our residual.
Lemma 3.4
For \(u^c\) obtained in Lemma 3.3, we have
where we remark that the gradient operator \(\nabla \) in \(B(u_{h},v)\) means the discrete/broken gradient and \(B(u_{h},v)\) is defined element by element.
Proof
By the definitions of B, \(B_c\), \(B_d\), and the fact that \(B_c(v,v)=0\) for \(v\in H_{0}^{1}(\Omega )\), we know that
and therefore we have
where we have used Eq. (2.10) . Since \(\mathbf {b}\) is divergence free and by using the Cauchy–Schwarz inequality, for any \(v\in H_0^1\) with \(|v|_{1;\Omega }=1\), we obtain
where the last inequality holds because \(\Vert v\Vert _{0;\Omega }\) must be bounded. Using (3.8)–(3.9) and Lemma 3.3, our result follows. \(\square \)
Since the second term in the above lemma is already a term in our error indicator, we just need to further find an upper estimate for \(\displaystyle \sup \nolimits _{v\in H_{0}^{1}(\Omega ),\,|v|_{1;\Omega }=1}\{(f,v)-B(u_{h},v)\}\). Before we proceed, let us state the following lemma, which states some error bounds of polynomial estimations.
Lemma 3.5
Let \(v\in H_0^1(\Omega )\). Then there exists \(v_{h}\in H_0^1(\Omega )\bigcap U_{h}\) such that
for all \(\tau \in \mathcal {T}\).
Recall that our goal is to find an upper estimate for \(\sup _{v\in H_{0}^{1}(\Omega ),\,|v|_{1;\Omega }=1}\{(f,v)-B(u_{h},v)\}\). A usual technique in finding this kind of upper estimate is to break down the test function v into two different parts, namely \(v_{h}\) and \(v-v_{h}\), where \(v_{h}\) is conformal. This technique is useful because we can easily use the numerical scheme to replace the term \((f,v_{h})\) if \(v_{h}\) is conformal, while the term \(v-v_{h}\) usually has some nice approximation properties, as shown in the last lemma. Next, let us first deal with the conformal part \(v_h\). We can prove the following lemma.
Lemma 3.6
Let \(v\in H_0^1(\Omega )\) with \(|v|_{1;\Omega }=1\). Choose \(v_{h}\in H_0^1(\Omega )\bigcap U_{h}\) as in Lemma 3.5. Then,
Proof
By using (2.16) and the fact that \(v_h\in H_0^1(\Omega )\), we know that
Hence, by the definitions of B and \(\mathbf {R}_2\), we have
Using the fact that \(\nabla \cdot \mathbf {b}=0\) and integration by parts, we have
Combining (3.13) and (3.14), we obtain
Now we deal with the term \(\frac{1}{2}(\mathbf {e}_bu_h,\nabla v_h )\). By denoting the cell average value of \(u_h\) on \(\tau \) as \(\bar{u}_{\tau }\), we have
By using the fact that \(\nabla v_h|_{\tau } \in [P^{k-1}(\tau )]^2\) and Eq. (2.12), we know that
and hence
where we have used the Poincaré inequality. By using (2.28) and the fact that \(f\in L^2(\Omega )\) is the given source term, we have
Similarly, for the term \(-\frac{1}{2} (\mathbf {e}_b\cdot \nabla u_h, v_h)\), we have
Substituting (3.16) and (3.17) into (3.15), we obtain
where we have used the Cauchy–Schwarz inequality. Since \(\mathbf {b}\) is the given vector field, we can assume that \(\Vert \mathbf {b}\cdot \mathbf {n}_e\Vert _{\infty ;e}\) is bounded by a constant. By using Lemma 3.5, we know that
Since \(|v|_{1,\Omega }=1\) and hence \(\Vert v\Vert _{1,\Omega }\) is bounded, we know that \(\Vert v_h\Vert _{0;\tau }\) and \(|v_{h}|_{1;\tau }\) have upper bounds too. Hence, we obtain
For the last term in (3.19) on edge \(e=\partial \tau _1 \bigcap \partial \tau _2\), we use the standard trace inequality
where \(\tau _e=\tau _1 \bigcup \tau _2\). Hence, we have
Substituting (3.20) into (3.19), we obtain
\(\square \)
As mentioned before, to find an upper estimate for \(\sup _{v\in H_{0}^{1}(\Omega ),\,|v|_{1;\Omega }=1}\{(f,v)-B(u_{h},v)\}\), we still need to consider the non-conformal case as in the following lemma.
Lemma 3.7
Let \(v\in H_0^1(\Omega )\) with \(|v|_{1;\Omega }=1\). Choose \(v_{h}\in H_0^1(\Omega )\bigcap U_{h}\) as in Lemma 3.5 and denote \(z=v-v_{h}\). Then,
Proof
By definitions, we have
Using integration by parts, we have
Substituting (3.23) into (3.22) and using the definitions of \(\mathbf {R}_2\) and \(R_3\), we can obtain
Using integration by parts and the fact that \(\mathbf {b}_h\) is divergence free, we have
and hence
From Lemma 3.5, we have already known that \(\Vert z\Vert _{0;\tau }\lesssim h_{\tau } \Vert v\Vert _{1;\tau }\) and \(|z|_{1;\tau }\lesssim \Vert v\Vert _{1;\tau }\). Using the fact that \(|v|_{1;\Omega }=1\) and (2.28), we obtain
For \( \Vert z\Vert _{0;e}\) on edge \(e=\partial \tau _1 \bigcap \partial \tau _2\), we employ the following trace inequality [39]
where \(\tau _e=\tau _1 \bigcup \tau _2\). Hence, we obtain
Our lemma follows by substituting the above equation into (3.24). \(\square \)
Combining Lemmas 3.2–3.7, we can prove Theorem 3.1.
Lemma 3.8
Theorem 3.1 holds.
Proof
Combining Lemmas 3.6 and 3.7, we know that
Hence, by Lemma 3.4, we can get
Combining Lemma 3.3 and the above equation, we obtain
From Lemma 3.2, we know that
Combining (3.26)–(3.28), our lemma follows. \(\square \)
Remark 1
Notice that in our error indicator \(\eta ^2\), there is a term with the coefficient \(\frac{h_{\tau }^2}{\epsilon ^2}\). In our computation, we just assume that the ratio \(\frac{h_{\tau }}{\epsilon }\) is bounded above by a constant which is independent of the mesh size, which is a reasonable assumption.
Remark 2
We can easily see that the last term in \(\Vert (e_{u}, \mathbf {e}_{bu},\mathbf {e}_{p}, e_{bs})\Vert _{\mathrm {DG}}^{2}\) is in fact the \(J_1\) term in \(\eta ^2\). We add it in the DG norm in order to prove the efficiency of \(\eta ^2\). It is not hard to find that the \(J_1\) term in \(\eta ^2\) comes from the convection part of the original convection–diffusion equation when we trying to find an upper bound of the diffusion term \(\epsilon ^2 |e_u|_{1;\Omega }^2\). Hence, the first term \(|e_u|_{1;\Omega }^2\) in the DG norm has a coefficient \(\epsilon ^2\) while the last term \(h_e^{-1}\Vert [e_u]\Vert _0^2\) does not have.
3.2 Efficiency of the Error Indicator
In this section, we will prove the efficiency of the error indicator derived in the last section. We use the standard bubble function technique, which was introduced by Verfürth [41] in 1994. Let \(\tau \in \mathcal {T}\) be a triangle and \(e\in \mathcal {F}\) be an edge with \(e=\tau _1 \cap \tau _2\). We denote by \(\beta _{\tau }\) and \(\beta _e\) the standard polynomial bubble functions on \(\tau \) and e, respectively, which are uniquely defined by the following properties:
and
We first state the following lemmas by Houston et al. in [30]. To save space, we combined the scalar case and the vector-valued case together.
Lemma 3.9
(Lemmas 5.1 and 5.2 in [30]) Let v be a scalar/vector-valued polynomial function on \(\tau \). Then
Moreover, let e be an edge shared by two triangles, say \(\tau _{1}\) and \(\tau _{2}\). Let q be a scalar/vector-valued polynomial function on e. Then
Finally, there exists an extension \(Q_{b}\in H_{0}^{1}(\tau _{1}\cup \tau _{2})\) (in the vector-valued case, \(\mathbf {Q}_{b}\in H_{0}^{1}((\tau _{1}\cup \tau _{2}))^{2})\) of \(\beta _{e}q\) such that \(Q_{b}|_{e}=\beta _{e}q\) and
for \(i=1,2\).
Remark For the vector-valued polynomial case, \(\nabla (\beta _{\tau }v)\) in (3.31) and \(\nabla Q_{b}\) in (3.34) mean \(\nabla \cdot (\beta _{\tau }\mathbf {v})\) in (3.31) and \(\nabla \cdot \mathbf {Q}_{b}\), respectively.
Throughout our discussion, we denote the space of all piecewise polynomials of a fixed order \(k_0\) (\(k_0\ge k\)) on \(\mathcal {T}\) by \(P(\mathcal {T})\). For any \(f_{h}\in P(\mathcal {T})\), we denote \(e_f=f-f_h\). Noticing that the error indicator \(\eta ^2\) is defined as the sum of the element-wise error indicator \(\eta _{\tau }^2\), we now define the element-wise norm of the numerical error as
To prove the efficiency, we consider all terms involved in \(\eta _{\tau }^2\) one by one. It turns out that each term can be bounded by the right-hand side of Eq. (3.42). We will first deal with the residual terms.
Lemma 3.10
For the residual terms \(R_1\), \(\mathbf {R}_2\) and \(R_3\), we have
Proof
We define
which are polynomials on each \(\tau \in \mathcal {T}\), and let \(v_{b1}=\beta _{\tau } v_1\), \(\mathbf {v}_{b2}=\beta _{\tau } \mathbf {v}_2\) and \(v_{b3}=\beta _{\tau } v_3\). Then we have \(R_1=v_1+f-f_h\), and hence
Next, we find upper bounds of \(\Vert v_1\Vert _{0;\tau }^2\), \(\Vert \mathbf {v}_2\Vert _{0;\tau }^2\) and \(\Vert v_3\Vert _{0;\tau }^2\). By using the bubble function technique, we know that
Also, the variational form (2.6)–(2.8) gives
Subtracting the above equations from (3.36)–(3.38), we get
where we have used integration by parts and the Cauchy–Schwarz inequality. By using the bubble function technique and by deleting \(\Vert v_1\Vert _{0;\tau }\), \(\Vert \mathbf {v}_2\Vert _{0;\tau }\) and \(\Vert v_3\Vert _{0;\tau }\) from both sides of the above equations respectively, we get
and hence
By using Equation (2.28) and the fact that \(f\in L^2(\Omega )\) is the given source term, we obtain
Our lemma follows by combining the above formula with (3.35). \(\square \)
Now, we proceed to the jump term.
Lemma 3.11
Let \(e\in \mathcal {F}^{0}\) with \(e=\tau _1 \cap \tau _2\). Assume that the exact solution \(\mathbf {p}\cdot \mathbf {n}_e\) is continuous on e, then we have
Proof
Define \(q:=J_2=[(\mathbf {p}_h+\frac{1}{2}\mathbf {b}_h u_h)\cdot \mathbf {n}]\) which is a polynomial on \(e\in \mathcal {F}^{0}\). Since \(u\in H_0^1(\Omega )\), \(\mathbf {b}\in \mathbf {H}(div, \Omega )\) and \(\mathbf {p}\cdot \mathbf {n}_e\) is continuous on each \(e\in \mathcal {F}^{0}\), we have
We define \(Q_b\in H_0^1(\tau _1 \cup \tau _2)\) be the extension of \(\beta _e q\) on \(\tau _1 \cup \tau _2\) such that \(Q_b|_e=\beta _e q\). Again, by using the standard bubble function technique, we have
Since \(Q_b\in H_0^1(\tau _1 \cup \tau _2)\), the variational form (2.8) gives
Adding the above equation with (3.40), we get
where we have used the bubble function technique (3.33) and (3.34). Using (2.28), we know that
Hence, we have
and
\(\square \)
Combing all the lemmas above, we can get the following theorem about the efficiency.
Theorem 3.12
Let \((\mathbf {p},\mathbf {s},u)\in [L^2(\Omega )]^2\times [L^2(\Omega )]^2 \times H_0^1(\Omega )\) be the the exact solution of (2.6)–(2.8) and \((\mathbf {p}_{h},\mathbf {s}_{h},u_{h})\in W_{h}\times W_{h}\times U_{h}\) be the numerical solution of the SDG scheme (2.14)–(2.16). Suppose that the ratio \(\frac{h_{\tau }}{\epsilon }\) is bounded above by a constant which is independent of the mesh size. For any \(f_{h}\in P(\mathcal {T})\), we have
Proof
Since we have assumed that for each cell \(\tau \in \mathcal {T}\), the ratio \(\frac{h_{\tau }}{\epsilon }\) is bounded by a constant, we can obtain the following estimation of \(R_1\) by using Lemma 3.10:
For each edge \(e\in \mathcal {F}_{u}^{0}\) with \(e=\tau _1 \cap \tau _2\), since \(\frac{h_e}{h_{\tau _i}}\leqslant 1\) for both \(i=1\) and \(i=2\). By using Lemma 3.11 and the above inequality, we know that
The remaining proof is trivial by Eqs. (3.43) and (3.44), Lemma 3.10, and the fact that the term about \(J_1\) in \(\eta \) is also a term in \(\Vert (e_{u}, \mathbf {e}_{bu},\mathbf {e}_{p}, e_{bs})\Vert _{\mathrm {DG}}\). \(\square \)
3.3 The Adaptive Refinement Strategy
As proved in Sects. 3.1 and 3.2, we have already known that \(\eta ^2\) is a reliable and efficient local error estimator. Based on well-established ideas for adaptive algorithms [26, 34, 35, 40], now we can get a residual-type adaptive mesh refinement strategy for our SDG method by using \(\eta ^2\) to compute an error indicator.
We should notice that our error estimator \(\eta ^2\) is defined on each element in \(\mathcal {T}\), which is a staggered mesh constructed based on an initial triangulation \(\mathcal {T}_{0}\). The purpose of constructing \(\mathcal {T}\) is to implement our scheme in a staggered way, as described in Sect. 2.2. Our adaptive refinement is constructed based on the initial mesh \(\mathcal {T}_{0}\) instead of the final mesh \(\mathcal {T}\). To define an error indicator on each element \(\rho \) of the initial mesh \(\mathcal {T}_{0}\), we will use the most trivial choice
It is obviously that
Now we present the adaptive refinement strategy. The idea is that we compute the error indicator for each element in the initial mesh, locate elements with larger errors and only refine those elements. After this process, we obtain a new level initial mesh, which can be used to construct a new staggered mesh and the corresponding solution spaces to form the new SDG system. With the j-th level initial mesh denoted as \(\mathcal {T}_{0}^j\), we implement our adaptive refinement scheme by using the following iteration:
-
1.
Subdivide each triangle in \(\mathcal {T}_{0}^j\) to get the staggered mesh. Use the SDG scheme (2.14)–(2.16) to solve for a numerical solution \((\mathbf {p}_{h}^j,\mathbf {s}_{h}^j,u_{h}^j)\in W_{h}\times W_{h}\times U_{h}\).
-
2.
If the total number of triangles in \(\mathcal {T}_{0}^{j}\) is larger than a threshold \(N_0\), we stop the refinement procedure and use \((\mathbf {p}_{h}^j,\mathbf {s}_{h}^j,u_{h}^j)\) as the final result. Otherwise, we evaluate \(\xi _{\rho }^2\) for each element \(\rho \in \mathcal {T}_{0}^{j}\) and thus compute their summation \(\eta ^2\).
-
3.
If the total estimated error \(\eta ^2\) is less than a threshold value \(\delta _0\), we stop the refinement procedure. Otherwise, we use the following two steps to construct a refined mesh \(\mathcal {T}_{0}^{j+1}\).
-
4.
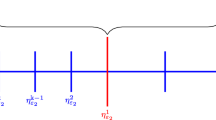
We enumerate all triangles in \(\mathcal {T}_{0}^j\) such that \(\xi _{\rho _{1}}\ge \xi _{\rho _{2}}\ge \xi _{\rho _{3}}\ge \cdots \). Choose \(0<\theta <1\) and find the least possible value of m such that
$$\begin{aligned} \theta \eta ^{2}\le & {} \sum _{i=1}^{m}\xi _{\rho _{i}}^2. \end{aligned}$$ -
5.
Get a new initial mesh \(\mathcal {T}_{0}^{j+1}\) by refining the first m triangles in \(\mathcal {T}_{0}^{j}\) chosen in the last step and any other possible triangles which keep the conformity of \(\mathcal {T}_{0}^{j+1}\).
4 Numerical Examples
In this section, we provide several numerical examples to show the accuracy and the efficiency of the proposed error indicator and the corresponding adaptive refinement technique. We use structured triangular meshes. All the numerical experiments are performed on the square domain \(\Omega =[0,1]\times [0,1]\). The initial mesh consists of two triangles only, by bisecting the domain \(\Omega \) through (0, 0) and (1, 1). The parameter \(\theta \) in our adaptive refinement procedure is chosen to be 0.3. In order to test the ability of our method, we compare our adaptive refinement strategy with two other refinement schemes: (1) uniform refinement; (2) adaptive refinement scheme with the error estimator being replaced by the exact error.
For the space \(U_h\), the degree of freedoms in each triangle \(\tau \in \mathcal {T}\) are taken as function values at \(\frac{(k+1)(k+2)}{2}\) points with the requirement that each edge contains \(k+1\) points. Basis functions are then just interpolation functions at these points. For each edge \(e=\tau _1 \cap \tau _2 \in \mathcal {F}_{u}^0\), \(\tau _1\) and \(\tau _2\) share the same degrees of freedom on e and thus functions in \(U_h\) will be continuous over each edge in \({F}_{u}^0\). For \(W_{h}\), we use the Brezzi–Douglas–Marini (BDM) finite element [5]. The degrees of freedom include the values of the normal component at \(k+1\) points per edge. For \(k > 1\), the degrees of freedom also include integration terms over the triangle. For each edge \(e=\tau _1 \cap \tau _2 \in \mathcal {F}_{p}\), \(\tau _1\) and \(\tau _2\) share the same degrees of freedom on e since functions in \(W_{h}\) should have continuous normal component over each edge in \(\mathcal {F}_{p}\). A detailed description of the basis functions can be found in [38]. For simplicity, we use piecewise linear elements (\(k=1\)) for all examples.
Example 1
For the first example, we take \(\epsilon =1\) and \(\varvec{b}=(1, 1)^T\). We consider the exact solution
which is singular at \((c_1,c_2)\), and hence can compute f. We first consider the case with \(c_1=0.5\) and \(c_2=0.5\). In this case, the singularity is located at the mesh interface. We compare the log-log plots of the numerical error for different refinement schemes in Fig. 2a. We can see that our scheme performs roughly the same as the adaptive refinement scheme using the exact error as the error indicator, which confirms the reliability and efficiency of the proposed error indicator. Also, it is evident that the error of our adaptive refinement scheme is less than the error of the uniform refinement scheme when using the same number of elements. More importantly, we can see that \(\mathrm{log} \Vert (e_{u}, \mathbf {e}_{bu},\mathbf {e}_{p}, e_{bs})\Vert _{\mathrm {DG}}\) declines at a rate of 0.5 against log(number of elements) for our adaptive scheme, which corresponds to order 1 convergence in 2D domains. This shows that our scheme out-performs the uniform refinement scheme and attains an optimal rate of convergence for piecewise linear elements. Our adaptive mesh of level 30 is shown in Fig. 2b. We can see that the refinements are concentrated around the point of singularity as expected. We further consider the case with \(c_1=0.3\) and \(c_2=0.6\). In this case, the singularity is not located at the mesh interface. The numerical results are shown in Fig. 3. We can see that the behavior is largely the same as the previous case, which confirms the robustness of our scheme.
Example 2
For the second example, we consider the solution with a circular internal layer. We take \(\epsilon =10^{-4}\) and \(\varvec{b}=(2, 3)^T\). The exact solution is taken as
We use our adaptive refinement scheme to approximate the solution of this example. Figure 4a shows the adaptive mesh of level 50. We can see that the refinements are more concentrated around the circular internal layer as expected. The largest edge length in this mesh is 0.25 and the smallest edge length near the layer is \(6.51\times 10^{-4}\). Figure 4b, c show the contour plot and also the 3D plot of \(u_h\). We can see that the numerical solution possesses a circular internal layer, which conforms the ability of our scheme to capture the position of the layer.
Example 3
In the third example, we take \(\varvec{b}=(\dfrac{1}{2}, \dfrac{\sqrt{3}}{2})\), \(\epsilon =5\times 10^{-5}\) and \(f=0\). By denoting \(\partial \Omega _1=\left\{ (x,y)\in \partial \Omega :\, x=0\right\} \cup \left\{ (x,y)\in \partial \Omega :\, x\le 0.5,y=0\right\} \), the boundary condition for this example is given by
For this example, the exact solution is unknown, but it should possess both an internal layer and boundary layers. In Fig. 5, we can see that all the layers are recovered by using our adaptive refinement scheme, which conforms the ability of our scheme to capture the positions of the layers. Here we adopt the adaptive mesh level 34. The largest edge length in this mesh is 0.141 and the smallest edge length near the layer is \(5.66\times 10^{-6}\).
5 Conclusion
In this paper, we propose a new SDG method in order to solve the steady state convection–diffusion equation with a small diffusion coefficient \(\epsilon \). A residual-type a-posteriori error estimator for the numerical solutions solved with this new SDG method is derived. The reliability and efficiency of this error estimator are also proved. By using this error estimator as the error indicator, an adaptive mesh refinement technique is proposed. Numerical examples with point singularities and sharp layers are provided, which are computational expensive for regular uniform refinement methods. We can see that the proposed error indicator is close to the exact numerical error. Our adaptive mesh refinement method out-performs the uniform refinement scheme and attains an optimal rate of convergence for piecewise linear elements. Also, the adaptive method can capture the positions of singular points and sharp layers accurately, thus can improve the resolution near these places by making the mesh more dense.
References
Ahmed, N., Matthies, G.: Numerical study of SUPG and LPS methods combined with higher order variational time discretization schemes applied to time-dependent linear convection–diffusion-reaction equations. J. Sci. Comput. 67, 998–1018 (2015)
Ahmed, N., Matthies, G., Tobiska, L., Xie, H.: Discontinuous Galerkin time stepping with local projection stabilization for transient convection–diffusion-reaction problems. Comput. Methods Appl. Mech. Eng. 200, 1747–1756 (2011)
Ayuso, B., Marini, L.D.: Discontinuous Galerkin methods for advection–diffusion-reaction problems. SIAM J. Numer. Anal. 47, 1391–1420 (2009)
Braack, M., Lube, G.: Finite elements with local projection stabilization for incompressible flow problems. J. Comput. Math. 27, 116–147 (2009)
Brezzi, F., Douglas Jr., J., Marini, L.D.: Two families of mixed finite elements for second order elliptic problems. Numer. Math. 47, 217–235 (1985)
Burman, E.: A unified analysis for conforming and nonconforming stabilized finite element methods using interior penalty. SIAM J. Numer. Anal. 43, 2012–2033 (2005)
Burman, E., Ern, A.: Continuous interior penalty hp-finite element methods for advection and advection–diffusion equations. Math. Comput. 76, 1119–1140 (2007)
Cangiani, A., Georgoulis, E.H., Metcalfe, S.: Adaptive discontinuous Galerkin methods for nonstationary convection-diffusion problems. IMA J. Numer. Anal. 34(4), 1578–1597 (2014)
Chen, H., Li, J., Qiu, W.: Robust a posteriori error estimates for HDG method for convection–diffusion equations. IMA J. Numer. Anal. 36, 437–462 (2016)
Chen, H., Qiu, W., Shi, K.: A priori and computable a posteriori error estimates for an HDG method for the coercive Maxwell equations. Comput. Methods Appl. Mech. Eng. 333, 287–310 (2018)
Cheung, S.W., Chung, E., Kim, H.H., Qian, Y.: Staggered discontinuous Galerkin methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 302, 251–266 (2015)
Chung, E.T., Ciarlet Jr., P.: A staggered discontinuous Galerkin method for wave propagation in media with dielectrics and meta-materials. J. Comput. Appl. Math. 239, 189–207 (2013)
Chung, E.T., Ciarlet Jr., P., Yu, T.F.: Convergence and superconvergence of staggered discontinuous Galerkin methods for the three-dimensional Maxwell’s equations on Cartesian grids. J. Comput. Phys. 235, 14–31 (2013)
Chung, E., Cockburn, B., Fu, G.: The staggered DG method is the limit of a hybridizable DG method. SIAM J. Numer. Anal. 52, 915–932 (2014)
Chung, E., Cockburn, B., Fu, G.: The staggered DG method is the limit of a hybridizable DG method. Part II: the Stokes flow. J. Sci. Comput. 66, 870–887 (2016)
Chung, E.T., Du, J., Yuen, M.C.: An adaptive SDG method for the Stokes system. J. Sci. Comput. 70, 766–792 (2017)
Chung, E.T., Engquist, B.: Optimal discontinuous Galerkin methods for wave propagation. SIAM J. Numer. Anal. 44, 2131–2158 (2006)
Chung, E.T., Engquist, B.: Optimal discontinuous Galerkin methods for the acoustic wave equation in higher dimensions. SIAM J. Numer. Anal. 47, 3820–3848 (2009)
Chung, E.T., Kim, H.H., Widlund, O.: Two-level overlapping Schwarz algorithms for a staggered discontinuous Galerkin method. SIAM J. Numer. Anal. 51, 47–67 (2013)
Chung, E.T., Lee, C.S.: A staggered discontinuous Galerkin method for the convection–diffusion equation. J. Numer. Math. 20, 1–31 (2012)
Chung, E.T., Leung, W.T.: A sub-grid structure enhanced discontinuous Galerkin method for multiscale diffusion and convection–diffusion problems. Commun. Comput. Phys. 14, 370–392 (2013)
Chung, E., Yuen, M.C., Zhong, L.: A-posteriori error analysis for a staggered discontinuous Galerkin discretization of the time-harmonic Maxwell’s equations. Appl. Math. Comput. 237, 613–631 (2014)
Cockburn, B., Dong, B., Guzman, J., Restelli, M., Sacco, R.: A hybridizable discontinuous Galerkin method for steady-state convection–diffusion-reaction problems. SIAM J. Sci. Comput. 31, 3827–3846 (2009)
Cockburn, B., Shu, C.-W.: The local discontinuous Galerkin method for time-dependent convection–diffusion systems. SIAM J. Numer. Anal. 35, 2440–2463 (1998)
Codina, R.: Finite element approximation of the convection-diffusion equation: subgrid-scale spaces, local instabilities and anisotropic space-time discretizations. Lecture Notes in Computational Science and Engineering, vol. 81, pp. 85–97 (2011)
Dörfler, W.: A convergent adaptive algorithm for Poissons equation. SIAM J. Numer. Anal. 33, 1106–1124 (1996)
Ern, A., Guermond, J.: Theory and Practice of Finite Elements. Applied mathematical sciences. Springer, New York (2004)
Ern, A., Stephansen, A.F., Vohralik, M.: Guaranteed and robust discontinuous Galerkin a posteriori error estimates for convection–diffusion reaction problems. J. Comput. Appl. Math. 234, 114–130 (2010)
Fu, G., Qiu, W., Zhang, W.: An analysis of HDG methods for convection dominated diffusion problems. ESAIM Math. Model. Numer. Anal. 49, 225–256 (2015)
Houston, P., Perugia, I., Schotzau, D.: An a posteriori error indicator for discontinuous Galerkin discretizations of H(curl)-elliptic partial differential equations. IMA J. Numer. Anal. 27, 122–150 (2007)
Karakashian, O.A., Pascal, F.: A posteriori error estimates for a discontinuous Galerkin approximation of second-order elliptic problems. SIAM J. Numer. Anal. 41, 2374–2399 (2003)
Kim, H.H., Chung, E.T., Lee, C.S.: A staggered discontinuous Galerkin method for the Stokes system. SIAM J. Numer. Anal. 51, 3327–3350 (2013)
Matthies, G., Skrzypacz, P., Tobiska, L.: Stabilization of local projection type applied to convection–diffusion problems with mixed boundary conditions. Electron. Trans. Numer. Anal. 32, 90–105 (2008)
Morin, P., Nochetto, R.H., Siebert, K.G.: Data oscillation and convergence of adaptive FEM. SIAM J. Numer. Anal. 38, 466–488 (2000)
Morin, P., Nochetto, R.H., Siebert, K.G.: Convergence of adaptive finite element methods. SIAM Rev. 44, 631–658 (2002)
Nguyen, N., Peraire, J., Cockburn, B.: An implicit high-order hybridizable discontinuous Galerkin method for linear convection–diffusion equations. J. Comput. Phys. 228, 3232–3254 (2009)
Qiu, W., Shi, K.: An HDG method for convection diffusion equation. J. Sci. Comput. 66, 346–357 (2016)
Rostand, V., Le Roux, D.Y.: Raviart–Thomas and Brezzi–Douglas–Marini finite-element approximations of the shallow-water equations. Int. J. Numer. Methods Fluids 57, 951–976 (2008)
Süli, E., Schwab, C., Houston, P.: hp-DGFEM for partial differential equations with nonnegative characteristic form. In: Cockburn, B., Karniadakis, G. E., Shu, C.-W. (eds.) Discontinuous Galerkin Methods. Lecture Notes in Computational Science and Engineering, vol. . Springer, Berlin, pp. 221–230 (2000)
Stevenson, R.: Optimality of a standard adaptive finite element method. Found. Comput. Math. 7, 245–269 (2007)
Verfürth, R.: A posteriori error estimation and adaptive mesh-refinement techniques. J. Comput. Appl. Math. 50, 67–83 (1994)
Vohralik, M.: A posteriori error estimates for lowest-order mixed finite element discretizations of converction–diffusion-reaction equations. SIAM J. Numer. Anal. 45, 1570–1599 (2007)
Acknowledgements
The work of Eric Chung is partially supported by Hong Kong RGC General Research Fund (Projects: 14317516, 14301314) and CUHK Direct Grant for Research 2016-17.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Du, J., Chung, E. An Adaptive Staggered Discontinuous Galerkin Method for the Steady State Convection–Diffusion Equation. J Sci Comput 77, 1490–1518 (2018). https://doi.org/10.1007/s10915-018-0695-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-0695-9