Local Discontinuous Galerkin Methods for the Two-Dimensional Camassa–Holm Equation

Abstract

In this paper, the local discontinuous Galerkin method is developed to solve the two-dimensional Camassa–Holm equation in rectangular meshes. The idea of LDG methods is to suitably rewrite a higher-order partial differential equations into a first-order system, then apply the discontinuous Galerkin method to the system. A key ingredient for the success of such methods is the correct design of interface numerical fluxes. The energy stability for general solutions of the method is proved. Comparing with the Camassa–Holm equation in one-dimensional case, there are more auxiliary variables which are introduced to handle high-order derivative terms. The proof of the stability is more complicated. The resulting scheme is high-order accuracy and flexible for arbitrary h and p adaptivity. Different types of numerical simulations are provided to illustrate the accuracy and stability of the method.

1 Introduction

In this paper, we consider the two-dimensional Camassa–Holm (2D CH) equation [17, 18, 23]

$$\begin{aligned} \frac{\partial }{\partial t}{} \mathbf m +\mathbf u \cdot \bigtriangledown \mathbf m +\bigtriangledown \mathbf u ^T\cdot \mathbf m +\mathbf m ({\mathbf {Div}}\ \mathbf u )=0, \end{aligned}$$

(1.1)

where $\mathbf u =(u_1,u_2)^T$ is velocity and

$$\begin{aligned} \mathbf m =(m_1,m_2)^T=\mathbf u - {\mathbf {Grad}}\ {\mathbf {Div}}\ \mathbf u \end{aligned}$$

(1.2)

is momentum. In coordinates x, y, the equation reads as follows:

$$\begin{aligned} \frac{\partial m_1}{\partial t}+u_1\frac{\partial m_1}{\partial x}+u_2\frac{\partial m_1}{\partial y}+m_1\frac{\partial u_1}{\partial x}+m_2\frac{\partial u_2}{\partial x}+m_1\left( \frac{\partial u_1}{\partial x}+\frac{\partial u_2}{\partial y}\right)= & {} 0,\qquad \quad \end{aligned}$$

(1.3)

$$\begin{aligned} \frac{\partial m_2}{\partial t}+u_1\frac{\partial m_2}{\partial x}+u_2\frac{\partial m_2}{\partial y}+m_1\frac{\partial u_1}{\partial y}+m_2\frac{\partial u_2}{\partial y}+m_2\left( \frac{\partial u_1}{\partial x}+\frac{\partial u_2}{\partial y}\right)= & {} 0,\qquad \quad \end{aligned}$$

(1.4)

where

$$\begin{aligned} m_1= & {} u_1-\frac{\partial ^2 u_1}{\partial x^2}-\frac{\partial ^2 u_2}{\partial x \partial y}, \end{aligned}$$

(1.5)

$$\begin{aligned} m_2= & {} u_2-\frac{\partial ^2 u_1}{\partial x \partial y}-\frac{\partial ^2 u_2}{\partial y^2}. \end{aligned}$$

(1.6)

The Camassa–Holm (CH) equation was derived as a model to describe the propagation of the gravitational waves in the shallow water. The CH equation has a very intriguing structure, it models wave breaking for a large class of the initial data and is completely integrable. This equation is very important in the literature.

Equation (1.1) is also called Euler–Poincaré equations associated with the diffeomorphism group (EPDiff), which has the same form with the CH equation except for the momentum velocity relationship in two-dimensional case. The CH equation in one-dimensional case is the same as EPDiff equation when the momentum velocity relationship is defined by the Helmholtz equation $m = u - u_{xx}$ [17]. But the EPDiff equations with the Helmholtz relation between velocity and momentum are not quite the CH equations for surface waves in two-dimensional case. The shallow water wave relation in the 2D CH approximation would be:

$$\begin{aligned} \mathbf m =\mathbf u - {\mathbf {Grad}}\ {\mathbf {Div}}\ \mathbf u , \end{aligned}$$

(1.7)

rather than the Helmholtz operator form:

$$\begin{aligned} \mathbf m =\mathbf u - {\mathbf {Div}}\ {\mathbf {Grad}}\ \mathbf u . \end{aligned}$$

(1.8)

The corresponding Lagrangians for the 2D CH equation are:

$$\begin{aligned} L_{\mathrm{CH}}(\mathbf u )=\frac{1}{2}\int \int (|\mathbf u |^2+({\mathbf {Div}}\ \mathbf u )^2)\mathrm{d}x\mathrm{d}y, \end{aligned}$$

(1.9)

instead of Lagrangians for the EPDiff equations

$$\begin{aligned} L_{\mathrm{EPDiff}}(\mathbf u )=\frac{1}{2}\int \int |\mathbf u |^2+({\mathbf {Grad}}\ \mathbf u )^2\mathrm{d}x\mathrm{d}y. \end{aligned}$$

(1.10)

This difference was noted in [17, 23]. Holm and Marsden studied the momentum maps and measure-valued solutions (peakons, filaments, and sheets) for the EPDiff equation in [17]. Kraenkel and Zenchuk studied the two-dimensional integrable generalization of the Camassa–Holm equation in [21], and the Lie symmetry analysis and reductions of a two-dimensional integrable generalization of the Camassa–Holm equation in [22]. Kruse proved the symmetry and perturbation theory of a two-dimensional version of the Camassa–Holm equation in [23].

There are lots of numerical works in the literature to solve the CH equation in one dimension, for example finite difference schemes [3, 5, 8, 9, 13, 16, 20, 24, 27, 35,36,37,38], finite-volume schemes [1], finite element schemes [29, 30], discontinuous Galerkin (DG) schemes [26, 28, 33] and other methods [7, 15, 19, 24, 25, 32]. But there is only a few work for the 2D CH equation. The work in [4, 6, 14, 17] presented the numerical simulations for EPDiff equations.

In this paper, we develop a class of local discontinuous Galerkin (LDG) methods by for the 2D CH equation (1.1)–(1.2), which is using completely discontinuous piecewise polynomial space for the numerical solution and the test functions in the spatial variables. The idea of LDG methods is to suitably rewrite a higher-order partial differential equations into a first-order system, then apply the DG method to the system. A key ingredient for the success of such methods is the correct design of interface numerical fluxes. The resulting scheme is high-order accurate, nonlinear stable and flexible for arbitrary h and p adaptivity. The peakon solution is typical solution for this type nonlinear dispersive equation, which is lack of smoothness, and often causes high-frequency dispersive errors into the calculation. The stable and accurate numerical schemes are very important for solving these equations. Comparing with the LDG scheme for 1D CH equation in [33], the main difference between 1D and 2D is that there are a lot of cross terms in the 2D CH equation and it needs to introduce more auxiliary variables, which brings a lot of trouble for the proof of the stability and numerical test.

The LDG techniques have been developed for nonlinear wave equations with high-order derivatives [34]. The stable LDG methods for general nonlinear wave equations which may be system or multidimensional case have been developed. One of the advantage of DG discretization results in an extremely local, element-based discretization, which is maintaining high-order accuracy on unstructured meshes and is beneficial for parallel computing. Furthermore, the proofs of the nonlinear $L^2$ stability of these methods and successful numerical experiments are also given. These results can prove that the LDG method is an effective tool for nonlinear equations. More detailed information about DG method can be found in [10,11,12].

This paper is organized as follows. We present our LDG method for the 2D CH equation (1.1)–(1.2) and describe the detailed implementation of the method in Sect. 2. In Sect. 3, we prove the energy stability of the LDG method. In Sect. 4, we present the numerical results to demonstrate the capability and the accuracy of the method. Section 5 is concluding remarks.

2 The LDG Method for the 2D CH Equation

2.1 Notation

For a rectangular partition of $[0,L_x]\times [0,L_y]$, we denote the mesh by $I_{i,j}=[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}] \times [y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]$, for $i=1,\ldots ,N_x$ and $j=1,\ldots ,N_y$. The cell lengths are denoted by $h^x_i=x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}$ and $h^y_j=y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}$. We define the piecewise polynomial space $V_{h}$ as the space of piecewise polynomials of degree up to k, i.e.,

$$\begin{aligned} V_{h}=\{v:\; v\in P^k(I_{i,j}),\;\forall \; (x,y)\in I_{i,j}, \; i=1,\ldots ,N_x,\;j=1,\ldots ,N_y\} . \end{aligned}$$

(2.1)

To simplify the notation, we still use u to denote the numerical solution.

We denote by $u^+_{i+\frac{1}{2},y}$ and $u^-_{i+\frac{1}{2},y}$ the values of u at $x_{i+\frac{1}{2}}$, from the right cell $I_{i+1,j}$ and from the left cell $I_{i, j}$ when $y \in [y_{j-\frac{1}{2}},y_{j+\frac{1}{2}}]$, on all vertical edges, respectively. Similarly, we denote by $u^+_{x,j+\frac{1}{2}}$ and $u^-_{x,j+\frac{1}{2}}$ the values of u at $y_{j+\frac{1}{2}}$, from the top cell $I_{i,j+1}$ and from the bottom cell $I_{i,j}$, when $x \in [x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]$, on all horizontal edges, respectively. We use the usual notations

$$\begin{aligned}{}[u]_{{i+\frac{1}{2},y}}=u^+_{{i+\frac{1}{2},y}}-u^-_{{i+\frac{1}{2},y}}, {\quad [u]_{x,{j+\frac{1}{2}}}=u^+_{x, {j+\frac{1}{2}}}-u^-_{x, {j+\frac{1}{2}}}} \end{aligned}$$

to denote the jump of the function u, at each element boundary. Define the inner product over the interval $I_{ij}$ and its sides by:

$$\begin{aligned} (v,w)_{ij}= & {} \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}}vw\mathrm{d}x\mathrm{d}y, \end{aligned}$$

(2.2)

$$\begin{aligned} \langle v,w\rangle _{x,ij}= & {} \int _{y_{j-\frac{1}{2}}}^{y_{j +\frac{1}{2}}}\left( vw^-\mid _{{i+\frac{1}{2}},y}-vw^ +\mid _{{i-\frac{1}{2}},y}\right) \mathrm{d}y, \end{aligned}$$

(2.3)

$$\begin{aligned} \langle v,w\rangle _{y,ij}= & {} \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} \left( vw^-\mid _{x,{j+\frac{1}{2}}}-vw^ +\mid _{x,{j-\frac{1}{2}}}\right) \mathrm{d}x. \end{aligned}$$

(2.4)

For simplicity, we use $(v,w), \langle v,w\rangle _x, \langle v,w\rangle _y$ to replace $(v,w)_{ij}, \langle v,w\rangle _{x,ij}, \langle v,w\rangle _{y,ij}$ in the rest of this paper.

2.2 The LDG Method

In this section, we define our LDG method for the 2D CH equation (1.1)–(1.2), written in the following form:

$$\begin{aligned} m_1= & {} u_1-\frac{\partial ^2 u_1}{\partial x^2}-\frac{\partial ^2 u_2}{\partial x \partial y}, \end{aligned}$$

(2.5)

$$\begin{aligned} m_2= & {} u_2-\frac{\partial ^2 u_1}{\partial x \partial y}-\frac{\partial ^2 u_2}{\partial y^2}, \end{aligned}$$

(2.6)

$$\begin{aligned}&\frac{\partial m_1}{\partial t}+\frac{\partial f(u_1)}{\partial x} - \frac{\partial ^2 }{\partial x^2}\left( u_1\frac{\partial u_1}{\partial x} \right) +\frac{1}{2} \frac{\partial }{\partial x}\left( \frac{\partial u_1}{\partial x} \right) ^2-\frac{\partial ^2 }{\partial x\partial y }\left( \frac{\partial u_1}{\partial x}u_2\right) \nonumber \\&\quad -\,\frac{\partial }{\partial x}\left( u_1 \frac{\partial ^2 u_2 }{\partial x\partial y } \right) +\frac{\partial (u_1u_2)}{\partial y} -\frac{\partial ^2 }{\partial x \partial y}\left( u_2\frac{\partial u_2}{\partial y} \right) \nonumber \\&\quad +\,\frac{1}{2}\frac{\partial u_2^2}{\partial x} +\frac{1}{2} \frac{\partial }{\partial x} \left( \frac{\partial u_2}{\partial y} \right) ^2=0, \end{aligned}$$

(2.7)

$$\begin{aligned}&\frac{\partial m_2}{\partial t}+\frac{\partial f(u_2)}{\partial y} - \frac{\partial ^2 }{\partial y^2}\left( u_2\frac{\partial u_2}{\partial y} \right) +\frac{1}{2} \frac{\partial }{\partial y}\left( \frac{\partial u_2}{\partial y} \right) ^2-\frac{\partial ^2 }{\partial x\partial y }\left( \frac{\partial u_2}{\partial y}u_1\right) \nonumber \\&\quad -\,\frac{\partial }{\partial y}\left( u_2 \frac{\partial ^2 u_1 }{\partial y\partial x } \right) +\frac{\partial (u_1u_2)}{\partial x} -\frac{\partial ^2 }{\partial y \partial x}\left( u_1\frac{\partial u_1}{\partial x} \right) \nonumber \\&\quad +\,\frac{1}{2}\frac{\partial u_1^2}{\partial y} +\frac{1}{2} \frac{\partial }{\partial y} \left( \frac{\partial u_1}{\partial x} \right) ^2=0, \end{aligned}$$

(2.8)

with $f(u)=\displaystyle \frac{3}{2}u^2$, the initial conditions

$$\begin{aligned} u_1(x,y,0)=u_{1,0}(x,y),\quad u_2(x,y,0)=u_{2,0}(x,y) \end{aligned}$$

(2.9)

and periodic boundary conditions. Notice that the assumption of periodic boundary conditions is for simplicity only and is not essential, in fact, the method can be easily designed for nonperiodic boundary conditions.

2.2.1 LDG Schemes for Equations (2.5) and (2.6)

To define the LDG method, we further rewrite (2.5) and (2.6) as a first-order system:

$$\begin{aligned} m_1= & {} u_1- \frac{\partial }{\partial x}(r_1+q_2) , \end{aligned}$$

(2.10)

$$\begin{aligned} m_2= & {} u_2-\frac{\partial }{\partial y}(r_1+q_2) , \end{aligned}$$

(2.11)

$$\begin{aligned} r_1= & {} \frac{\partial u_1}{\partial x} , \end{aligned}$$

(2.12)

$$\begin{aligned} q_2= & {} \frac{\partial u_2}{\partial y} . \end{aligned}$$

(2.13)

The LDG methods for (2.10)–(2.13), where $m_1, m_2$ are assumed known and we would want to solve for $u_1$, $u_2$, are formulated as follows: Find $u_{1}, u_{2}, r_{1}, q_{2} \in V_h$ such that for all test functions $\phi _1, \phi _2, \phi _3, \phi _4 \in V_h$,

$$\begin{aligned} (m_1,\phi _1)= & {} (u_1,\phi _1)-\langle \widehat{r_1}+\widehat{q_2},\phi _1\rangle _{x}+\left( r_1+q_2, \frac{\partial \phi _{1}}{\partial x} \right) , \end{aligned}$$

(2.14)

$$\begin{aligned} (m_2,\phi _2)= & {} (u_2,\phi _2)-\langle \widetilde{r_1}+\widetilde{q_2},\phi _2\rangle _y+\left( r_1+q_2, \frac{\partial \phi _{2}}{\partial y}\right) , \end{aligned}$$

(2.15)

$$\begin{aligned} (r_1,\phi _3)= & {} \langle \widehat{u_1},\phi _3\rangle _x-\left( u_1, \frac{\partial \phi _{3}}{\partial x}\right) , \end{aligned}$$

(2.16)

$$\begin{aligned} (q_2,\phi _4)= & {} \langle \widetilde{u_2},\phi _4\rangle _y-\left( {u_2}, \frac{\partial \phi _{4}}{\partial y}\right) . \end{aligned}$$

(2.17)

The “hat” terms in (2.14)–(2.17) in the cell boundary terms from integration by parts are called numerical fluxes, which are functions defined on the cell edges and should be designed differently for different equations to ensure stability. For (2.14)–(2.17) we can take the choices such that

$$\begin{aligned} \widehat{u_1}|_{{i\pm \frac{1}{2}},y}= & {} u_1^+|_{{i\pm \frac{1}{2}},y}, \quad \widehat{r_1}|_{{i\pm \frac{1}{2}},y}=r_1^-|_{{i\pm \frac{1}{2}},y}, \quad \widehat{q_2}|_{{i\pm \frac{1}{2}},y}=q_2^-|_{{i\pm \frac{1}{2}},y},\nonumber \\ \widetilde{u_2}|_{x,{j\pm \frac{1}{2}}}= & {} u_2^+|_{x,{j\pm \frac{1}{2}}}, \quad \widetilde{r_1}|_{x,{j\pm \frac{1}{2}}}=r_1^-|_{x,{j\pm \frac{1}{2}}}, \quad \widetilde{q_2}|_{x,{j\pm \frac{1}{2}}}=q_2^-|_{x,{j\pm \frac{1}{2}}}.\nonumber \\ \end{aligned}$$

(2.18)

2.2.2 LDG Schemes for Equation (2.7)

For (2.7), we can rewrite it into a first-order system:

$$\begin{aligned}&\frac{\partial m_1}{\partial t}+\frac{\partial }{\partial x}\left( f(u_1)-P-S-L_2\right) + \frac{\partial }{\partial x} (B(r_1)+B(u_2)+B(q_2)) \nonumber \\&\quad +\,\frac{\partial }{\partial y}(A(u_1,u_2)-M)=0, \end{aligned}$$

(2.19)

$$\begin{aligned}&P- \frac{\partial A(u_1,r_1)}{\partial x} =0, \end{aligned}$$

(2.20)

$$\begin{aligned}&S-\frac{\partial A(r_1,u_2)}{\partial y} =0, \end{aligned}$$

(2.21)

$$\begin{aligned}&M-\frac{\partial L_3}{\partial x} =0, \end{aligned}$$

(2.22)

$$\begin{aligned}&q_1-\frac{\partial u_2}{\partial x} =0, \end{aligned}$$

(2.23)

$$\begin{aligned}&t_2-\frac{\partial q_1}{\partial y} =0, \end{aligned}$$

(2.24)

$$\begin{aligned}&L_2-u_1t_2=0, \end{aligned}$$

(2.25)

$$\begin{aligned}&L_3-u_2q_2=0, \end{aligned}$$

(2.26)

where $A(x,y)=xy$, $B(x)=\frac{1}{2}x^2$ and $r_1$, $q_2$ are defined in (2.12)–(2.13).

Now we can define the LDG method for (2.19)–(2.26), resulting in the following scheme: Find $m_1$, P, S, M, $q_1$, $t_2$, $L_2$, $L_3 \in V_h$ such that, for all test functions $\rho _1$, $\varphi _1$, $\varphi _3$, $\varphi _5$, $\psi _3$, $\psi _6$, $\xi _2,$ $\xi _3 \in V_h$,

• Scheme for Equation (2.19)

$$\begin{aligned}&\left( \frac{\partial m_1}{\partial t},\rho _1\right) +\langle \widehat{f(u_1)}-\widehat{P}-\widehat{S}-\widehat{L_2},\rho _1\rangle _x-\left( f(u_1)-P-S-L_2, \frac{\partial \rho _{1}}{\partial x} \right) \nonumber \\&\quad +\,\langle \widehat{B(r_1)}+\widehat{B(u_2)}+\widehat{B(q_2)},\rho _1\rangle _x-\left( B(r_1)+B(u_2)+B(q_2),\frac{\partial \rho _{1}}{\partial x}\right) \nonumber \\&\quad +\,\langle \widetilde{A(u_1,u_2)}-\widehat{M},\rho _1\rangle _y-\left( A(u_1,u_2)-M,\frac{\partial \rho _{1}}{\partial y}\right) =0, \end{aligned}$$

(2.27)

where

$$\begin{aligned} \widehat{P}|_{{i\pm \frac{1}{2}},y}= & {} P^-|_{{i\pm \frac{1}{2}},y},\quad \widehat{S}|_{{i\pm \frac{1}{2}},y}=S^-|_{{i\pm \frac{1}{2}},y},\quad \widehat{L_2}|_{{i\pm \frac{1}{2}},y}=L_2^-|_{{i\pm \frac{1}{2}},y},\nonumber \\ \widehat{B(r_1)}|_{{i\pm \frac{1}{2}},y}= & {} B(r_1^-)|_{{i\pm \frac{1}{2}},y},\quad \widehat{B(u_2)}|_{{i\pm \frac{1}{2}},y}=\frac{1}{2}(u_2^+u_2^-)\Bigl |_{{i\pm \frac{1}{2}},y},\quad \nonumber \\\widehat{B(q_2)}= & {} \frac{1}{2}(q_2^+q_2^-)\Bigl |_{{i\pm \frac{1}{2}},y},\nonumber \\ \widetilde{A(u_1,u_2)}|_{x,{j\pm \frac{1}{2}}}= & {} \frac{1}{2}(u_1^+u_2^++u_1^-u_2^-)\Bigl |_{x,{j\pm \frac{1}{2}}},\quad \widehat{M}|_{x,{j\pm \frac{1}{2}}} =M^-|_{x,{j\pm \frac{1}{2}}}. \end{aligned}$$

(2.28)

Here $\widehat{f}(u_1^-,u_1^+)$ is numerical flux for nonlinear term $f(u_1)$. One can choose monotone numerical flux for solving conservation laws: It is Lipschitz continuous in both arguments, consistent ($\widehat{f}(u_1,u_1)=f(u_1)$), nondecreasing in the first argument, and nonincreasing in the second argument. We could use the simple Lax–Friedrichs flux which is dissipative numerical flux

$$\begin{aligned} \widehat{f(u_1^-,u_1^+)}|_{{i\pm \frac{1}{2}},y}=\frac{1}{2}\left( f(u_1^+) +f(u_1^-)-\alpha (u_1^+-u_1^-)\right) \Bigl |_{{i\pm \frac{1}{2}},y},\alpha =\max |f'(u_1)|. \end{aligned}$$

(2.29)

The other way is to choose conservative numerical flux as in [2]

$$\begin{aligned} \widehat{f(u_1^-,u_1^+)}|_{{i\pm \frac{1}{2}},y}=\frac{1}{2}\left( (u_1^+)^2+u_1^+ u_1^-+(u_1^-)^2\right) \Bigl |_{{i\pm \frac{1}{2}},y}. \end{aligned}$$

(2.30)

• Schemes for Equations (2.20)–(2.26)

$$\begin{aligned} (P,\varphi _1)= & {} \langle \widehat{A(u_1,r_1)},\varphi _1\rangle _x-\left( A(u_1,r_1), \frac{\partial \varphi _{1}}{\partial x}\right) ,\quad \nonumber \\\widehat{A(u_1,r_1)}\Bigl |_{{i\pm \frac{1}{2}},y}= & {} \frac{1}{2}((r_1^++r_1^-)u_1^+)\Bigl |_{{i\pm \frac{1}{2}},y}, \end{aligned}$$

(2.31)

$$\begin{aligned} (S,\varphi _3)= & {} \langle \widehat{A(r_1,u_2)},\varphi _3\rangle _y-\left( A(r_1,u_2),\frac{\partial \varphi _{3}}{\partial y}\right) ,\quad \nonumber \\\widehat{A(u_2,r_1)}\Bigl |_{x,{j\pm \frac{1}{2}}}= & {} \frac{1}{2}(u_2^+r_1^++u_2^-r_1^-)\Bigl |_{x,{j\pm \frac{1}{2}}}, \end{aligned}$$

(2.32)

$$\begin{aligned} (M,\varphi _5)= & {} \langle \widehat{L_3},\varphi _5\rangle _x-\left( L_3,\frac{\partial \varphi _{5}}{\partial x}\right) ,\quad \widehat{L_3}|_{{i\pm \frac{1}{2}},y}=L_3^+|_{{i\pm \frac{1}{2}},y}, \end{aligned}$$

(2.33)

$$\begin{aligned} (q_1,\psi _3)= & {} \langle \widehat{u_2},\psi _3\rangle _x-\left( u_2,\frac{\partial \psi _{3}}{\partial x}\right) ,\quad \widehat{u_2}|_{{i\pm \frac{1}{2}},y}=u_2^+|_{{i\pm \frac{1}{2}},y}, \end{aligned}$$

(2.34)

$$\begin{aligned} (t_2,\psi _6)= & {} \langle \widehat{q_1},\psi _6\rangle _y-\left( q_1,\frac{\partial \psi _{6}}{\partial y}\right) ,\quad \widehat{q_1}|_{x,{j\pm \frac{1}{2}}}=q_1^-|_{x,{j\pm \frac{1}{2}}}, \end{aligned}$$

(2.35)

$$\begin{aligned} (L_2,\xi _2)= & {} (u_1t_2,\xi _2), \end{aligned}$$

(2.36)

$$\begin{aligned} (L_3,\xi _3)= & {} (u_2q_2,\xi _3). \end{aligned}$$

(2.37)

2.2.3 LDG Schemes for Equation (2.8)

For (2.8), we can rewrite it into a first-order system:

$$\begin{aligned}&\frac{\partial m_2}{\partial t}+\frac{\partial }{\partial y}(f(u_2)-Q-T-L_4) + \frac{\partial }{\partial y}(B(r_1)+B(u_1)+B(q_2)) \nonumber \\&\quad + \frac{\partial }{\partial x}(A(u_1,u_2)-N)=0, \end{aligned}$$

(2.38)

$$\begin{aligned}&Q-\frac{\partial A(u_2,q_2)}{\partial y} =0, \end{aligned}$$

(2.39)

$$\begin{aligned}&T-\frac{\partial A(u_1,q_2)}{\partial x} =0, \end{aligned}$$

(2.40)

$$\begin{aligned}&N- \frac{\partial L_1}{\partial y} =0, \end{aligned}$$

(2.41)

$$\begin{aligned}&r_2-\frac{\partial u_1}{\partial y} =0, \end{aligned}$$

(2.42)

$$\begin{aligned}&t_1-\frac{\partial r_2}{\partial x} =0, \end{aligned}$$

(2.43)

$$\begin{aligned}&L_1-u_1r_1=0, \end{aligned}$$

(2.44)

$$\begin{aligned}&L_4-u_2t_1=0, \end{aligned}$$

(2.45)

where $A(x,y)=xy$, $B(x)=\frac{1}{2}x^2$ and $r_1$, $q_2$ are defined in (2.12)–(2.13).

Now we can define the LDG method for (2.38)–(2.45), resulting in the following scheme: Find $m_2$, Q, T, N, $r_2$, $t_1$, $L_1$, $L_4 \in V_h$ such that, for all test functions $\rho _2$, $\varphi _2$, $\varphi _4$, $\varphi _6$, $\psi _2$, $\psi _5$, $\xi _1$, $\xi _4 \in V_h$,

• Scheme for Equation (2.38)

$$\begin{aligned}&\left( \frac{\partial m_2}{\partial t},\rho _2\right) +\langle \widehat{f(u_2)}-\widehat{Q}-\widehat{T}-\widehat{L_4},\rho _2\rangle _y-\left( f(u_2)-Q-T-L_4, \frac{\partial \rho _{2}}{\partial y}\right) \nonumber \\&\quad +\,\langle \widetilde{B(r_1)}+\widehat{B(u_1)}+\widetilde{B(q_2)}, \rho _2\rangle _y-\left( B(r_1)+B(u_1)+B(q_2),\frac{\partial \rho _{2}}{\partial y}\right) \nonumber \\&\quad +\,\langle \widehat{A(u_1,u_2)}-\widehat{N},\rho _2\rangle _x-\left( A(u_1,u_2)-N,\frac{\partial \rho _{2}}{\partial x}\right) =0, \end{aligned}$$

(2.46)

where

$$\begin{aligned} \widehat{Q}|_{x,{j\pm \frac{1}{2}}}= & {} Q^-|_{x,{j\pm \frac{1}{2}}},\quad \widehat{T}|_{x,{j\pm \frac{1}{2}}}=T^-|_{x,{j\pm \frac{1}{2}}},\quad \widehat{L_4}|_{x,{j\pm \frac{1}{2}}}=L_4^-|_{x,{j\pm \frac{1}{2}}},\nonumber \\ \widetilde{B(r_1)}|_{x,{j\pm \frac{1}{2}}}= & {} \frac{1}{2}(r_1^+r_1^-)\Bigl |_{x,{j\pm \frac{1}{2}}},\nonumber \\ \widehat{B(u_1)}|_{x,{j\pm \frac{1}{2}}}= & {} \frac{1}{2}(u_1^+u_1^-)\Bigl |_{x,{j\pm \frac{1}{2}}},\quad \widetilde{B(q_2)}|_{x,{j\pm \frac{1}{2}}}=B(q_2^-)|_{x,{j\pm \frac{1}{2}}},\nonumber \\ \widehat{A(u_1,u_2)}|_{{i\pm \frac{1}{2}},y}= & {} \frac{1}{2}(u_1^+u_2^++u_1^-u_2^-)\Bigl |_{{i\pm \frac{1}{2}},y},\quad \widehat{N}|_{{i\pm \frac{1}{2}},y}=N^-|_{{i\pm \frac{1}{2}},y}. \end{aligned}$$

(2.47)

The numerical flues for $\widehat{f(u_2^-,u_2^+)}$ can be chosen as

• Dissipative numerical flux:

  $$\begin{aligned} \widehat{f(u_2^-,u_2^+)}|_{x,{j\pm \frac{1}{2}}}=\frac{1}{2}(f(u_2^+)+f(u_2^-)-\alpha (u_2^+-u_2^-))\Bigl |_{x,{j\pm \frac{1}{2}}},\alpha =\max |f'(u_2)|. \end{aligned}$$

  (2.48)

• Conservative numerical flux:

  $$\begin{aligned} \widehat{f(u_2^-,u_2^+)}|_{x,{j\pm \frac{1}{2}}}=\frac{1}{2}((u_1^+)^2+u_1^+ u_1^-+(u_1^-)^2)\Bigl |_{x,{j\pm \frac{1}{2}}}. \end{aligned}$$

  (2.49)

• Scheme for Equations (2.39)–(2.45)

$$\begin{aligned} (Q,\varphi _2)= & {} \langle \widehat{A(u_2,q_2)},\varphi _2\rangle _y-\left( A(u_2,q_2),\frac{\partial \varphi _{2}}{\partial y}\right) ,\quad \nonumber \\\widehat{A(u_2,q_2)}\Bigl |_{x,{j\pm \frac{1}{2}}}= & {} \frac{1}{2}((q_2^++q_2^-)u_2^+) \Bigl |_{x,{j\pm \frac{1}{2}}}, \end{aligned}$$

(2.50)

$$\begin{aligned} (T,\varphi _4)= & {} \langle \widehat{A(u_1,q_2)},\varphi _4\rangle _x-\left( A(u_1,q_2),\frac{\partial \varphi _{4}}{\partial x}\right) ,\quad \nonumber \\\widehat{A(u_1,q_2)}\Bigl |_{{i\pm \frac{1}{2}},y}= & {} \frac{1}{2}(u_1^+q_2^++u_1^-q_2^-)\Bigl |_{{i\pm \frac{1}{2}},y}, \end{aligned}$$

(2.51)

$$\begin{aligned} (N,\varphi _6)= & {} \langle \widehat{L_1},\varphi _6\rangle _y-\left( L_1,\frac{\partial \varphi _{6}}{\partial y}\right) ,\quad \widehat{L_1}|_{x,{j\pm \frac{1}{2}}}=L_1^+|_{x,{j\pm \frac{1}{2}}}, \end{aligned}$$

(2.52)

$$\begin{aligned} (r_2,\psi _2)= & {} \langle \widetilde{u_1},\psi _2\rangle _y-\left( u_1,\frac{\partial \psi _{2}}{\partial y}\right) ,\quad \widetilde{u_1}|_{x,{j\pm \frac{1}{2}}}=u_1^+|_{x,{j\pm \frac{1}{2}}}, \end{aligned}$$

(2.53)

$$\begin{aligned} (t_1,\psi _5)= & {} \langle \widehat{r_2},\psi _5\rangle _x-\left( r_2, \frac{\partial \psi _{5}}{\partial x}\right) ,\quad \widehat{r_2}|_{{i\pm \frac{1}{2}},y}=r_2^-|_{{i\pm \frac{1}{2}},y}, \end{aligned}$$

(2.54)

$$\begin{aligned} (L_1,\xi _1)= & {} (u_1r_1,\xi _1), \end{aligned}$$

(2.55)

$$\begin{aligned} (L_4,\xi _4)= & {} (u_2t_1,\xi _4). \end{aligned}$$

(2.56)

We remark that the choices of the fluxes in (2.27)–(2.35) and (2.46)–(2.54) are not unique. There are several choices to ensure the stability.

2.3 Algorithm Flowchart

In this section, we give details related to the implementation of the method.

First, from (2.14)–(2.18), we get $\mathbf m _h$ in the following matrix form:

$$\begin{aligned} \mathbf m _h=\mathbf Au _h, \end{aligned}$$

(2.57)

where $\mathbf m _h=(m_1,m_2)^T$, $\mathbf u _h=(u_1,u_2)^T$.

Second, from (2.27)–(2.37) and (2.46)–(2.56), we obtain the LDG discretization in the following form:

$$\begin{aligned} (\mathbf m _h)_t={\mathbf {res}}(\mathbf u _h). \end{aligned}$$

(2.58)

Then, we combine (2.57) and (2.58) to get

$$\begin{aligned} \mathbf A (\mathbf u _h)_t={\mathbf {res}}(\mathbf u _h). \end{aligned}$$

(2.59)

Finally, we use a time discretization method to solve

$$\begin{aligned} (\mathbf u _h)_t=\mathbf A ^{-1}{\mathbf {res}}(\mathbf u _h). \end{aligned}$$

(2.60)

In this paper, we use the Runge–Kutta methods, in fact any standard ODE solvers can be used here.

3 Energy Stability of the LDG Method

In this section, we prove the energy stability of the LDG method for the 2D CH equation. The Lagrangians for the 2D CH equation are:

$$\begin{aligned} L_{CH}(\mathbf u )=\frac{1}{2}\int \int (|\mathbf u |^2+({\mathbf {Div}}\ \mathbf u )^2)\mathrm{d}x\mathrm{d}y. \end{aligned}$$

(3.1)

More details can be seen in [17]. The energy stability of the 2D CH equation is that:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\int _0^{L_x}\int _0^{L_y}\left( u_1^2+u_2^2 +\left( \frac{\partial u_1}{\partial x} +\frac{\partial u_2}{\partial y} \right) ^2\right) \mathrm{d}x\mathrm{d}y=0. \end{aligned}$$

(3.2)

We will prove energy stability of the corresponding numerical solutions of LDG scheme in the following proposition.

Proposition 3.1

The solution to the schemes (2.27)–(2.37) and (2.46)–(2.56) satisfies the energy stability:

• For dissipative numerical fluxes in (2.29) and (2.48),

  $$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\int _0^{L_x}\int _0^{L_y}\left( u_1^2+u_2^2 +(r_1+q_2)^2\right) \mathrm{d}x\mathrm{d}y\le 0. \end{aligned}$$

  (3.3)

• For conservative numerical fluxes in (2.30) and (2.49),

  $$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}\int _0^{L_x}\int _0^{L_y}\left( u_1^2+u_2^2 +(r_1+q_2)^2\right) \mathrm{d}x\mathrm{d}y=0. \end{aligned}$$

  (3.4)

To prove the energy stability of the LDG method, we need to choose proper test functions in the LDG scheme.

• Test Functions in Schemes (2.14) and (2.17)

For (2.14) and (2.15), we first take the time derivative and get:

$$\begin{aligned} \left( \frac{\partial m_1}{\partial t},\phi _1\right)= & {} \left( \frac{\partial u_1}{\partial t},\phi _1\right) -\left\langle \frac{\partial \widehat{r_1}}{\partial t}+\frac{\partial \widehat{q_2}}{\partial t},\phi _1\right\rangle _x+\left( \frac{\partial {r_1}}{\partial t}+\frac{\partial {q_2}}{\partial t}, \frac{\partial \phi _1}{\partial x} \right) , \end{aligned}$$

(3.5)

$$\begin{aligned} \left( \frac{\partial m_2}{\partial t},\phi _2\right)= & {} \left( \frac{\partial u_2}{\partial t},\phi _2\right) -\left\langle \frac{\partial \widetilde{r_1}}{\partial t}+\frac{\partial \widetilde{q_2}}{\partial t},\phi _2\right\rangle _y+\left( \frac{\partial {r_1}}{\partial t}+\frac{\partial {q_2}}{\partial t}, \frac{\partial \phi _2}{\partial y}\right) .\qquad \end{aligned}$$

(3.6)

We choose the test function as follows: (3.5) with $\phi _1=u_1$, (3.6) with $\phi _2=u_2$, (2.16) with $\phi _3=-\displaystyle \frac{\partial {r_1}}{\partial t}-\displaystyle \frac{\partial {q_2}}{\partial t}-P-S-L_2$, (2.17) with $\phi _4=-\displaystyle \frac{\partial {r_1}}{\partial t}-\displaystyle \frac{\partial {q_2}}{\partial t}-Q-T-L_4$,

$$\begin{aligned} \left( \frac{\partial m_1}{\partial t},u_1\right)= & {} \left( \frac{\partial u_1}{\partial t},u_1\right) -\left\langle \frac{\partial \widehat{r_1}}{\partial t}+\frac{\partial \widehat{q_2}}{\partial t},u_1\right\rangle _x+\left( \frac{\partial {r_1}}{\partial t}+\frac{\partial {q_2}}{\partial t},\frac{\partial u_1}{\partial x}\right) , \qquad \end{aligned}$$

(3.7)

$$\begin{aligned} \left( \frac{\partial m_2}{\partial t},u_2\right)= & {} \left( \frac{\partial u_2}{\partial t},u_2\right) -\left\langle \frac{\partial \widetilde{r_1}}{\partial t}+\frac{\partial \widetilde{q_2}}{\partial t},u_2\right\rangle _y+\left( \frac{\partial {r_1}}{\partial t}+\frac{\partial {q_2}}{\partial t},\frac{\partial u_2}{\partial y}\right) , \end{aligned}$$

(3.8)

$$\begin{aligned}&\quad -\,\left( r_1, \frac{\partial {r_1}}{\partial t}+ \frac{\partial {q_2}}{\partial t}+P+S+L_2\right) \nonumber \\= & {} -\left\langle \widehat{u_1},\frac{\partial {r_1}}{\partial t}+\displaystyle \frac{\partial {q_2}}{\partial t}+P+S+L_2\right\rangle _x\nonumber \\&\quad +\,\left( u_1,\frac{\partial }{\partial x}\left( \frac{\partial {r_1}}{\partial t}+\displaystyle \frac{\partial {q_2}}{\partial t}+P+S+L_2\right) \right) , \end{aligned}$$

(3.9)

$$\begin{aligned}&\quad -\,\left( q_2, \frac{\partial {r_1}}{\partial t}+\displaystyle \frac{\partial {q_2}}{\partial t}+Q+T+L_4\right) \nonumber \\= & {} -\,\left\langle \widetilde{u_2},\frac{\partial {r_1}}{\partial t}+\displaystyle \frac{\partial {q_2}}{\partial t}+Q+T+L_4\right\rangle _y\nonumber \\&\quad +\,\left( {u_2},\frac{\partial }{\partial y}\left( \frac{\partial {r_1}}{\partial t}+ \frac{\partial {q_2}}{\partial t}+Q+T+L_4\right) \right) . \end{aligned}$$

(3.10)

• Test Function in Schemes (2.27)–(2.37)

We choose the test function as follows: (2.27) with $\rho _1=u_1$, (2.31) with $\varphi _1=r_1$, (2.32) with $\varphi _3=r_1$, (2.33) with $\varphi _5=r_2$, (2.34) with $\psi _3=-N$, (2.35) with $\psi _6=L_1$,

$$\begin{aligned}&\left( \frac{\partial m_1}{\partial t},u_1\right) +\langle \widehat{f(u_1)}-\widehat{P}-\widehat{S}-\widehat{L_2},u_1\rangle _x\nonumber \\&\quad -\,\left( f(u_1)-P-S-L_2, \frac{\partial u_1}{\partial x} \right) \nonumber \\&\quad +\,\langle \widehat{B(r_1)}+\widehat{B(u_2)}+\widehat{B(q_2)},u_1 \rangle _x-\left( B(r_1)+B(u_2)+B(q_2),\frac{\partial u_1}{\partial x}\right) \nonumber \\&\quad +\,\langle \widetilde{A(u_2,u_1)}-\widehat{M},u_1\rangle _y-\left( A(u_2,u_1)-M,\frac{\partial u_1}{\partial y}\right) =0, \end{aligned}$$

(3.11)

$$\begin{aligned}&(P,r_1)=\langle \widehat{A(u_1,r_1)},r_1\rangle _x-\left( A(u_1,r_1), \frac{\partial r_{1}}{\partial x}\right) , \end{aligned}$$

(3.12)

$$\begin{aligned}&(S,r_1)=\langle \widehat{A(r_1,u_2)},r_1\rangle _y-\left( A(r_1,u_2),\frac{\partial r_1}{\partial y}\right) , \end{aligned}$$

(3.13)

$$\begin{aligned}&(M,r_2)=\langle \widehat{L_3},r_2\rangle _x-\left( L_3,\frac{\partial r_2}{\partial x}\right) , \end{aligned}$$

(3.14)

$$\begin{aligned}&\quad -\,(q_1,N)=-\langle \widehat{u_2},N\rangle _x+\left( u_2,\frac{\partial N}{\partial x}\right) , \end{aligned}$$

(3.15)

$$\begin{aligned}&(t_2,L_1)=\langle \widehat{q_1},L_1\rangle _y-\left( q_1,\frac{\partial L_1}{\partial y}\right) . \end{aligned}$$

(3.16)

• Test Functions in Schemes (2.46)–(2.56)

(2.46) with $\rho _2=u_2$, (2.50) with $\varphi _2=q_2$, (2.51) with $\varphi _4=q_2$, (2.52) with $\varphi _6=q_1$, (2.53) with $\psi _2=-M$, (2.54) with $\psi _5=L_3$.

$$\begin{aligned}&\left( \frac{\partial m_2}{\partial t},u_2\right) +\langle \widehat{f(u_2)}-\widehat{Q}-\widehat{T}-\widehat{L_4},u_2\rangle _y-\left( f(u_2)-Q-T-L_4, \frac{\partial u_{2}}{\partial y} \right) \nonumber \\&\quad +\,\langle \widetilde{B(r_1)}+\widehat{B(u_1)}+\widetilde{B(q_2)},u_2 \rangle _y-\left( B(r_1)+B(u_1)+B(q_2),\frac{\partial u_{2}}{\partial y}\right) \nonumber \\&\quad +\,\langle \widehat{A(u_1,u_2)}-\widehat{N},u_2\rangle _x-\left( A(u_1,u_2)-N,\frac{\partial u_{2}}{\partial x}\right) =0, \end{aligned}$$

(3.17)

$$\begin{aligned}&(Q,q_2)=\langle \widehat{A(u_2,q_2)},q_2\rangle _y-\left( A(u_2,q_2),\frac{\partial q_{2}}{\partial y}\right) , \end{aligned}$$

(3.18)

$$\begin{aligned}&(T,q_2)=\langle \widehat{A(u_1,q_2)},q_2\rangle _x-\left( A(u_1,q_2),\frac{\partial q_2}{\partial x}\right) , \end{aligned}$$

(3.19)

$$\begin{aligned}&(N,q_1)=\langle \widehat{L_1},q_1\rangle _y-\left( L_1,\frac{\partial q_1}{\partial y}\right) , \end{aligned}$$

(3.20)

$$\begin{aligned}&\quad -\,(r_2,M)=-\langle \widetilde{u_1},M\rangle _y+\left( u_1,\frac{\partial M}{\partial y}\right) , \end{aligned}$$

(3.21)

$$\begin{aligned}&(t_1,L3)=\langle \widehat{r_2},L_3\rangle _x-\left( r_2, \frac{\partial L_3}{\partial x}\right) . \end{aligned}$$

(3.22)

• Main Energy Equation

Adding equations from (3.7) to (3.22), we can get the main energy equation for proving $L^2$ stability.

The left side of the equation is:

$$\begin{aligned}&\left( \frac{\partial m_1}{\partial t},u_1\right) +\left( \frac{\partial m_2}{\partial t},u_2\right) -\left( r_1, \frac{\partial {r_1}}{\partial t}+ \frac{\partial {q_2}}{\partial t}\right) -\left( q_2, \frac{\partial {r_1}}{\partial t}+ \frac{\partial {q_2}}{\partial t}\right) \nonumber \\&\qquad +\,(P,r_1)-(r_1,P)+(S,r_1)-(r_1,S)+(N,q_1)-(q_1,N)\nonumber \\&\qquad +\,(t_2,L_1)-(r_1,L_2)\nonumber \\&\qquad +\,(Q,q_2)-(q_2,Q)+(T,q_2)-(q_2,T)+(M,r_2)-(r_2,M)\nonumber \\&\qquad +(t_1,L_3)-(q_2,L_4)\nonumber \\&\quad =\left( \frac{\partial m_1}{\partial t},u_1\right) +\left( \frac{\partial m_2}{\partial t},u_2\right) -\left( r_1+q_2, \frac{\partial }{\partial t}(r_1+q_2)\right) , \end{aligned}$$

(3.23)

where we use the following equality:

$$\begin{aligned} (t_2,L_1)= & {} (t_2,u_1r_1)=(r_1,u_1t_2)=(r_1,L_2), \end{aligned}$$

(3.24)

$$\begin{aligned} (t_1,L_3)= & {} (t_1,u_2q_2)=(q_2,u_2t_1)=(q_2,L_4). \end{aligned}$$

(3.25)

The right side of the equation is:

$$\begin{aligned}&\left( \frac{\partial u_1}{\partial t},u_1\right) +\left( \frac{\partial u_2}{\partial t},u_2\right) +\left( \frac{\partial m_1}{\partial t},u_1\right) +\left( \frac{\partial m_2}{\partial t},u_2\right) \nonumber \\&\quad +\,\mathbb {A}_{i,j}+\mathbb {B}_{i,j}+\mathbb {C}_{i,j} +\mathbb {D}_{i,j}+\mathbb {E}_{i,j}+\mathbb {F}_{i,j}, \end{aligned}$$

(3.26)

where

$$\begin{aligned} \mathbb {A}_{i,j}= & {} \langle \widehat{f(u_1)},u_1\rangle _x-\left( f(u_1),\frac{\partial u_1}{\partial x}\right) , \end{aligned}$$

(3.27)

$$\begin{aligned} \mathbb {B}_{i,j}= & {} \langle \widehat{f(u_2)},u_2\rangle _y-\left( f(u_2),\frac{\partial u_2}{\partial y}\right) , \end{aligned}$$

(3.28)

$$\begin{aligned} \mathbb {C}_{i,j}= & {} \langle \widehat{A(u_1,r_1)},r_1\rangle _x-\left( A(u_1,r_1),\frac{\partial r_1}{\partial x}\right) +\langle \widehat{B(r_1)},u_1\rangle _x-\left( B(r_1),\frac{\partial u_1}{\partial x}\right) \nonumber \\&+\,\langle \widehat{A(u_1,u_2)},u_2\rangle _x-\left( A(u_1,u_2),\frac{\partial u_2}{\partial x}\right) +\langle \widehat{B(u_2)},u_1\rangle _x-\left( B(u_2),\frac{\partial u_1}{\partial x}\right) \nonumber \\&+\,\langle \widehat{A(u_1,q_2)},q_2\rangle _x-\left( A(u_1,q_2),\frac{\partial q_2}{\partial x}\right) +\langle \widehat{B(q_2)},u_1\rangle _x-\left( B(q_2),\frac{\partial u_1}{\partial x}\right) , \end{aligned}$$

(3.29)

$$\begin{aligned} \mathbb {D}_{i,j}= & {} \langle \widetilde{A(u_2,u_1)},u_1\rangle _y-\left( A(u_2,u_1),\frac{\partial u_1}{\partial y}\right) +\langle \widehat{B(u_1)},u_2\rangle _y-\left( B(u_1),\frac{\partial u_2}{\partial y}\right) \nonumber \\&+\,\langle \widehat{A(u_2,q_2)},q_2\rangle _y-\left( A(u_2,q_2),\frac{\partial q_2}{\partial y}\right) +\langle \widetilde{B(q_2)},u_2\rangle _y-\left( B(q_2),\frac{\partial u_2}{\partial y}\right) \nonumber \\&+\,\langle \widehat{A(u_2,r_1)},r_1\rangle _y-\left( A(u_2,r_1),\frac{\partial r_1}{\partial y}\right) +\langle \widetilde{B(r_1)},u_2\rangle _y-\left( B(r_1),\frac{\partial u_2}{\partial y}\right) , \end{aligned}$$

(3.30)

$$\begin{aligned} \mathbb {E}_{i,j}= & {} -\langle \widehat{P},u_1\rangle _x+\left( P,\frac{\partial u_1}{\partial x}\right) -\langle \widehat{u_1},P\rangle _x+\left( u_1,\frac{\partial P}{\partial x}\right) \nonumber \\&-\,\langle \widehat{S},u_1\rangle _x+\left( S,\frac{\partial u_1}{\partial x}\right) -\langle \widehat{u_1},S\rangle _x+\left( u_1,\frac{\partial S}{\partial x}\right) \nonumber \\&-\,\langle \widehat{L_2},u_1\rangle _x+\left( L_2,\frac{\partial u_1}{\partial x}\right) -\langle \widehat{u_1},L_2\rangle _x+\left( u_1,\frac{\partial L_2}{\partial x}\right) \nonumber \\&-\,\langle \widehat{N},u_2\rangle _x+\left( N,\frac{\partial u_2}{\partial x}\right) -\langle \widehat{u_2},N\rangle _x+\left( u_2,\frac{\partial N}{\partial x}\right) \nonumber \\&+\,\langle \widehat{L_3},r_2\rangle _x-\left( L_3,\frac{\partial r_2}{\partial x}\right) +\langle \widehat{r_2},L_3\rangle _x-\left( r_2,\frac{\partial L_3}{\partial x}\right) \nonumber \\&-\,\left\langle \frac{\partial \widehat{r_1}}{\partial t},u_1\right\rangle _x+\left( \frac{\partial r_1}{\partial t},\frac{\partial u_1}{\partial x}\right) -\left\langle \widehat{u_1},\frac{\partial r_1}{\partial t}\right\rangle _x+\left( u_1,\frac{\partial }{\partial x}\left( \frac{\partial r_1}{\partial t}\right) \right) \nonumber \\&-\,\left\langle \frac{\partial \widehat{q_2}}{\partial t},u_1\right\rangle _x+\left( \frac{\partial q_2}{\partial t},\frac{\partial u_1}{\partial x}\right) -\left\langle \widehat{u_1},\frac{\partial q_2}{\partial t}\right\rangle _x+\left( u_1,\frac{\partial }{\partial x}\left( \frac{\partial q_2}{\partial t}\right) \right) , \end{aligned}$$

(3.31)

$$\begin{aligned} \mathbb {F}_{i,j}= & {} \langle \widehat{L_1},q_1\rangle _y-\left( L_1,\frac{\partial q_1}{\partial y}\right) +\langle \widehat{q_1},L_1\rangle _y-\left( q_1,\frac{\partial L_1}{\partial y}\right) \nonumber \\&-\,\langle \widehat{Q},u_2\rangle _y+\left( Q,\frac{\partial u_2}{\partial y}\right) -\langle \widetilde{u_2},Q\rangle _y+\left( u_2,\frac{\partial Q}{\partial y}\right) \nonumber \\&-\,\langle \widehat{T},u_2\rangle _y+\left( T,\frac{\partial u_2}{\partial y}\right) -\langle \widetilde{u_2},T\rangle _y+\left( u_2,\frac{\partial T}{\partial y}\right) \nonumber \\&-\,\langle \widehat{L_4},u_2\rangle _y+\left( L_4,\frac{\partial u_2}{\partial y}\right) -\langle \widetilde{u_2},L_4\rangle _y+\left( u_2,\frac{\partial L_4}{\partial y}\right) \nonumber \\&-\,\langle \widehat{M},u_1\rangle _y+\left( M,\frac{\partial u_1}{\partial y}\right) -\langle \widetilde{u_1},M\rangle _y+\left( u_1,\frac{\partial M}{\partial y}\right) \nonumber \\&-\,\left\langle \frac{\partial \widetilde{r_1}}{\partial t},u_2\right\rangle _y+\left( \frac{\partial r_1}{\partial t},\frac{\partial u_2}{\partial y}\right) -\left\langle \widetilde{u_2},\frac{\partial r_1}{\partial t}\right\rangle _y+\left( u_2,\frac{\partial }{\partial x}\left( \frac{\partial r_1}{\partial t}\right) \right) \nonumber \\&-\,\left\langle \frac{\partial \widetilde{q_2}}{\partial t},u_2\right\rangle _y+\left( \frac{\partial q_2}{\partial t},\frac{\partial u_2}{\partial y}\right) -\left\langle \widetilde{u_2},\frac{\partial q_2}{\partial t}\right\rangle _y+\left( u_2,\frac{\partial }{\partial x}\left( \frac{\partial q_2}{\partial t}\right) \right) . \end{aligned}$$

(3.32)

Combining Eqs. (3.23) and (3.26), we get the main energy equation

$$\begin{aligned}&\left( \frac{\partial u_1}{\partial t},u_1\right) +\left( \frac{\partial u_2}{\partial t},u_2\right) +\left( r_1+q_2, \frac{\partial }{\partial t}({r_1}+q_2) \right) \nonumber \\&\quad +\,\mathbb {A}_{i,j}+\mathbb {B}_{i,j}+\mathbb {C}_{i,j} +\mathbb {D}_{i,j}+\mathbb {E}_{i,j}+\mathbb {F}_{i,j}=0. \end{aligned}$$

(3.33)

• Proof for $\mathbb {A}_{i,j}+\mathbb {B}_{i,j} +\mathbb {C}_{i,j}+\mathbb {D}_{i,j}+\mathbb {E}_{i,j} +\mathbb {F}_{i,j}$ terms in (3.33)

In the following, we will prove $\mathbb {A}_{i,j}+\mathbb {B}_{i,j} +\mathbb {C}_{i,j}+\mathbb {D}_{i,j}+\mathbb {E}_{i,j}+\mathbb {F}_{i,j}$ terms in (3.33) are nonnegative or zero.

Lemma 3.2

With the dissipative numerical fluxes in (2.29) and (2.48) or conservative numerical fluxes in (2.30) and (2.49), we have

$$\begin{aligned} \sum \limits _{i,j}\mathbb {A}_{i,j}\ge 0, \quad \sum \limits _{i,j}\mathbb {B}_{i,j}\ge 0, \hbox { dissipative numerical fluxes}\mathrm{,} \end{aligned}$$

or

$$\begin{aligned} \sum \limits _{i,j}\mathbb {A}_{i,j}{=} 0, \quad \sum \limits _{i,j}\mathbb {B}_{i,j}= 0, \hbox { conservative numerical fluxes}\mathrm{.} \end{aligned}$$

Proof

Dissipative numerical fluxes

As for $\mathbb A_{i,j}$:

$$\begin{aligned} \mathbb {A}_{i,j}=\Psi _{i+\frac{1}{2},j}-\Psi _{i-\frac{1}{2},j} +\Theta _{i-\frac{1}{2},j}, \end{aligned}$$

(3.34)

where

$$\begin{aligned} \Psi _{i+\frac{1}{2},j}= & {} \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \left( \widehat{f(u_1)}u_1^--F(u_1^-)\right) \mid _{{i+\frac{1}{2}},y}dy, \end{aligned}$$

(3.35)

$$\begin{aligned} \Theta _{i-\frac{1}{2},j}= & {} \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \left( [F(u_1)]-\widehat{f(u_1)}[u_1]\right) \mid _{{i-\frac{1}{2}},y}dy \end{aligned}$$

(3.36)

and $F(u)=\int ^uf(t)\mathrm{d}t$. With the monotonicity of $\widehat{f(u_1)}$, we have

$$\begin{aligned} {[}F(u_1){]}-\widehat{f(u_1)}[u_1]=\int _{u_1^-}^{u_1^+}(f(s) -\widehat{f}(u_1^-,u_1^+))\mathrm{d}s\ge 0. \end{aligned}$$

(3.37)

Then we can finally get $\Theta _{i-\frac{1}{2},j}\ge 0$. Summing up (3.34) over i, j and taking into account the periodic boundary condition, we obtain

$$\begin{aligned} \sum \limits _{i,j}\mathbb {A}_{i,j}\ge 0. \end{aligned}$$

Using the same argument, we immediately know

$$\begin{aligned} \sum \limits _{i,j}\mathbb {B}_{i,j}\ge 0. \end{aligned}$$

Conservative numerical fluxes

Proof is similar to the monotone case and [2], we omit the detail of the proof. $\square$

Lemma 3.3

If the numerical fluxes are chosen as

$$\begin{aligned} \widehat{A(u,v)}\mid _{{i+\frac{1}{2}},y}=\frac{1}{2}(u^+v^+ + u^-v^-)\mid _{{i+\frac{1}{2}},y}, \quad \widehat{B(v)}\mid _{{i+\frac{1}{2}},y} =\frac{1}{2}v^+v^-\mid _{{i+\frac{1}{2}},y}, \end{aligned}$$

(3.38)

or

$$\begin{aligned} \widehat{A(u,v)}\mid _{{i+\frac{1}{2}},y}=\frac{1}{2}(v^+ + v^-)u^+\mid _{{i+\frac{1}{2}},y}, \quad \widehat{B(v)}\mid _{{i+\frac{1}{2}},y} =B(v^-)\mid _{{i+\frac{1}{2}},y}, \end{aligned}$$

(3.39)

then we have

$$\begin{aligned} \sum \limits _{i,j}\left( \langle \widehat{A(u,v)},v\rangle _x-\left( A(u,v),\frac{\partial v}{\partial x}\right) +\langle \widehat{B(v)},u\rangle _x-\left( B(v),\frac{\partial u}{\partial x}\right) \right) =0. \end{aligned}$$

Proof

Similar to the proof in Lemma 3.2.

$$\begin{aligned}&\langle \widehat{A(u,v)},v\rangle _x-\left( A(u,v),\frac{\partial v}{\partial x}\right) +\langle \widehat{B(v)},u\rangle _x-\left( B(v),\frac{\partial u}{\partial x}\right) \nonumber \\&\quad = \Psi _{i+\frac{1}{2},j}-\Psi _{i-\frac{1}{2},j} +\Theta _{i-\frac{1}{2},j}, \end{aligned}$$

(3.40)

where

$$\begin{aligned} \Psi _{i+\frac{1}{2},j}= & {} \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \left( \widehat{A(u,v)}v^-+\widehat{{B}(v)}u^--B(v^-)u^-\right) \mid _{{i+\frac{1}{2}},y}dy, \end{aligned}$$

(3.41)

$$\begin{aligned} \Theta _{i-\frac{1}{2},j}= & {} \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \left( -\widehat{A(u,v)}[v]-\widehat{B(v)}[u]+[B(v)u] \right) \mid _{{i-\frac{1}{2}},y}dy. \end{aligned}$$

(3.42)

With numerical fluxes in (3.38) or (3.39) and algebraic calculation, we easily obtain:

$$\begin{aligned} -\,\widehat{A(u,v)}[v]-\widehat{B(v)}[u]+[B(v)u] =0. \end{aligned}$$

Summing up (3.40) over i, j and taking into account the periodic boundary condition, we obtain

$$\begin{aligned} \sum \limits _{i,j}\left( \langle \widehat{A(u,v)},v\rangle _x-\left( A(u,v),\frac{\partial v}{\partial x}\right) +\langle \widehat{B(v)},u\rangle _x-\left( B(v),\frac{\partial u}{\partial x}\right) \right) =0. \end{aligned}$$

$\square$

Lemma 3.4

If the numerical fluxes are chosen as

$$\begin{aligned} \widehat{A(u,v)}\mid _{x,{j+\frac{1}{2}}}=\frac{1}{2}(u^+v^+ + u^-v^-)\mid _{x,{j+\frac{1}{2}}}, \quad \widehat{B(v)}\mid _{x,{j+\frac{1}{2}}} =\frac{1}{2}v^+v^-\mid _{x,{j+\frac{1}{2}}}, \end{aligned}$$

(3.43)

or

$$\begin{aligned} \widehat{A(u,v)}\mid _{x,{j+\frac{1}{2}}}=\frac{1}{2}(v^+ + v^-)u^+\mid _{x,{j+\frac{1}{2}}}, \quad \widehat{B(v)}\mid _{x,{j+\frac{1}{2}}} =B(v^-)\mid _{x,{j+\frac{1}{2}}}, \end{aligned}$$

(3.44)

then we have

$$\begin{aligned} \sum \limits _{i,j}\left( \langle \widehat{A(u,v)},v\rangle _y-\left( A(u,v),\frac{\partial v}{\partial y}\right) +\langle \widehat{B(v)},u\rangle _y-\left( B(v),\frac{\partial u}{\partial y}\right) \right) =0. \end{aligned}$$

Proof

The proof is similar to Lemma 3.3. $\square$

Corollary 3.5

With the definition of numerical fluxes in schemes (2.27)–(2.35) and (2.46)–(2.54), we have

$$\begin{aligned} \sum \limits _{i,j}\mathbb {C}_{i,j}= 0, \quad \sum \limits _{i,j}\mathbb {D}_{i,j}= 0. \end{aligned}$$

Proof

The results in this Corollary can be obtained by using Lemma 3.3 and Lemma 3.4. $\square$

Lemma 3.6

If the numerical fluxes are chosen as

$$\begin{aligned} \widehat{u}\mid _{{i+\frac{1}{2}},y}=u^-\mid _{{i+\frac{1}{2}},y}, \quad \widehat{v}\mid _{{i+\frac{1}{2}},y}=v^+\mid _{{i+\frac{1}{2}},y}, \end{aligned}$$

(3.45)

or

$$\begin{aligned} \widehat{u}\mid _{{i+\frac{1}{2}},y}=u^+\mid _{{i+\frac{1}{2}},y}, \quad \widehat{v}\mid _{{i+\frac{1}{2}},y}=v^-\mid _{{i+\frac{1}{2}},y}, \end{aligned}$$

(3.46)

then we have

$$\begin{aligned} \sum \limits _{i,j}\left( \langle \widehat{u},v\rangle _x-\left( u,\frac{\partial v}{\partial x}\right) +\langle \widehat{v},u\rangle _x-\left( v,\frac{\partial u}{\partial x}\right) \right) =0. \end{aligned}$$

Table 1 Accuracy test for the 2D CH equation with the exact solutions (4.2), periodic boundary condition. Uniform meshes over $[0,2\pi ]\times [0,2\pi ]$ with $N_x\times N_y$ cells at time $\hbox {t}=0.5$

Fig. 1

Peakon solution $u_1$ for the 2D CH equation (2.5)–(2.8) with the initial conditions (4.5), periodic boundary condition, uniform meshes with $80\times 80$, $P^4$ elements over $[-\,10,10]\times [-\,10,10]$ for Example 4.2. a $u_1, t=0$ b $u_1, t=1$ c $u_1, t=2$ d $u_1, t=4$

Fig. 2

Peakon solution $u_2$ for the 2D CH equation (2.5)–(2.8) with the initial conditions (4.5), periodic boundary condition, uniform meshes with $80\times 80$, $P^4$ elements over $[-\,10,10]\times [-\,10,10]$ for Example 4.2. a $u_2, t=0$ b $u_2, t=1$ c $u_2, t=2$ d $u_2, t=4$

Fig. 3

Peakon solution for the 2D CH equation (2.5)–(2.8) with the initial conditions (4.7). Dirichlet boundary condition. Uniform meshes with $80\times 80$, $P^4$ elements over $[-\,10,10]\times [-\,10,10]$ for Example 4.3. a $t=0$, b $t=\sqrt{2}/2$, c $t=\sqrt{2}$, d $t= 2\sqrt{2}$

Fig. 4

Two-peakon interaction solutions for the 2D CH equation (2.5)–(2.8) with the initial conditions (4.8). Periodic boundary condition. Uniform meshes with $160\times 160$, $P^4$ elements over $[-\,20,20]\times [-\,20,20]$ for Example 4.4. a $t=0$, b $t=1$, c $t=3$, d $t= 8$

Fig. 5

Two-peakon interaction solutions for the 2D CH equation (2.5)–(2.8) with the initial conditions (4.11). Periodic boundary condition. Uniform meshes with $160\times 160$, $P^4$ elements over $[-\,20,20]\times [-\,20,20]$ for Example 4.5. a $t=0$, b $t=1$, c $t=3$, d $t= 8$

Fig. 6

Peakon solution $u_1$ for the 2D CH equation (2.5)–(2.8) with the initial conditions (4.15), Dirichlet boundary condition, uniform meshes with $80\times 80$, $P^4$ elements over $[-\,10,10]\times [-\,10,10]$ for Example 4.6. a $u_1, t=0$, b $u_1, t=1$, c $u_1, t=2$, d $u_1, t=4$

Fig. 7

Peakon solution $u_2$ for the 2D CH equation (2.5)–(2.8) with the initial conditions (4.15), Dirichlet boundary condition, uniform meshes with $80\times 80$, $P^4$ elements over $[-\,10,10]\times [-\,10,10]$ for Example 4.6. a $u_2, t=0$, b $u_2, t=1$, c $u_2, t=2$, d $u_2, t=4$

Fig. 8

Peakon solution $u_1$ for the 2D CH equation (2.5)–(2.8) with the initial conditions (4.17), Dirichlet boundary condition, uniform meshes with $160\times 160$, $P^4$ elements over $[-\,20,20]\times [-\,20,20]$ for Example 4.7. a $u_1, t=0$, b $u_1, t=1$, c $u_1, t=2$, d $u_1, t=4$

Fig. 9

Peakon solution $u_2$ for the 2D CH equation (2.5)–(2.8) with the initial conditions (4.17), Dirichlet boundary condition, uniform meshes with $160\times 160$, $P^4$ elements over $[-\,20,20]\times [-\,20,20]$ for Example 4.7. a $u_2, t=0$, b $u_2, t=1$, c $u_2, t=2$, d $u_2, t=4$

Proof

Similar to the proof in Lemma 3.3

$$\begin{aligned}&\langle \widehat{u},v\rangle _x-\left( u,\frac{\partial v}{\partial x}\right) +\langle \widehat{v},u\rangle _x-\left( v,\frac{\partial u}{\partial x}\right) = \Psi _{i+\frac{1}{2},j}-\Psi _{i-\frac{1}{2},j} +\Theta _{i-\frac{1}{2},j}, \end{aligned}$$

(3.47)

where

$$\begin{aligned} \Psi _{i+\frac{1}{2},j}= & {} \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \left( \widehat{u}v^-+\widehat{v}u^--v^-u^-\right) \mid _{{i+\frac{1}{2}},y}\mathrm{d}y, \end{aligned}$$

(3.48)

$$\begin{aligned} \Theta _{i-\frac{1}{2},j}= & {} \int _{y_{j-\frac{1}{2}}}^{y_{j+\frac{1}{2}}} \left( -\widehat{u}[v]-\widehat{v}[u]+[vu] \right) \mid _{{i-\frac{1}{2}},y}\mathrm{d}y. \end{aligned}$$

(3.49)

With numerical fluxes in (3.45) or (3.46) and algebraic calculation, we easily obtain:

$$\begin{aligned} -\,\widehat{u}[v]-\widehat{v}[u]+[vu] =0. \end{aligned}$$

Summing up (3.47) over ij and taking into account the periodic boundary condition, we obtain

$$\begin{aligned} \sum \limits _{i,j}\left( \langle \widehat{u},v\rangle _x-\left( u,\frac{\partial v}{\partial x}\right) +\langle \widehat{v},u\rangle _x-\left( v,\frac{\partial u}{\partial x}\right) \right) =0. \end{aligned}$$

$\square$

Lemma 3.7

If the numerical fluxes are chosen as

$$\begin{aligned} \widehat{u}\mid _{x,{j+\frac{1}{2}}}=u^-\mid _{x,{j+\frac{1}{2}}}, \quad \widehat{v}\mid _{x,{j+\frac{1}{2}}}=v^+\mid _{x,{i+\frac{1}{2}}}, \end{aligned}$$

(3.50)

or

$$\begin{aligned} \widehat{u}\mid _{x,{j+\frac{1}{2}}}=u^+\mid _{x,{j+\frac{1}{2}}}, \quad \widehat{v}\mid _{x,{j+\frac{1}{2}}}=v^-\mid _{x,{j+\frac{1}{2}}}, \end{aligned}$$

(3.51)

then we have

$$\begin{aligned} \sum \limits _{i,j}\left( \langle \widehat{u},v\rangle _y-\left( u,\frac{\partial v}{\partial y}\right) +\langle \widehat{v},u\rangle _y-\left( v,\frac{\partial u}{\partial y}\right) \right) =0. \end{aligned}$$

Proof

The proof is similar to Lemma 3.6. $\square$

Corollary 3.8

With the definition of numerical fluxes in schemes (2.27)–(2.35) and (2.46)–(2.54), we have

$$\begin{aligned} \sum \limits _{i,j}\mathbb {E}_{i,j}= 0, \quad \sum \limits _{i,j}\mathbb {F}_{i,j}= 0. \end{aligned}$$

Proof

The results in this Corollary can be obtained by using Lemmas 3.6 and 3.7. It is worth to mention that although the terms regarding the derivatives of t in Eqs. (3.31) and (3.32) look a little different from the terms in Lemmas 3.6 and 3.7, we just need to treat the terms regarding the derivatives of t as normal terms, then Lemmas 3.6 and 3.7 also work. $\square$

Summing up the main energy equation (3.33) over ij and taking into account the periodic boundary condition, we obtain the following results by using Lemma 3.2, Corollarys 3.5 and 3.8.

• For dissipative numerical fluxes,

  $$\begin{aligned} \sum \limits _{i,j}\left( \mathbb {A}_{i,j}+\mathbb {B}_{i,j} +\mathbb {C}_{i,j}+\mathbb {D}_{i,j}+\mathbb {E}_{i,j} +\mathbb {F}_{i,j}\right) \ge 0. \end{aligned}$$

  Then we have

  $$\begin{aligned}&\sum \limits _{i,j}\left( \left( \frac{\partial u_1}{\partial t},u_1\right) +\left( \frac{\partial u_2}{\partial t},u_2\right) +\left( r_1+q_2, \frac{\partial }{\partial t}({r_1}+q_2) \right) \right) \nonumber \\&\quad =-\sum \limits _{i,j}\left( \mathbb {A}_{i,j}+\mathbb {B}_{i,j} +\mathbb {C}_{i,j}+\mathbb {D}_{i,j}+\mathbb {E}_{i,j} +\mathbb {F}_{i,j}\right) \nonumber \\&\quad \le 0. \end{aligned}$$

  (3.52)

• For conservative numerical fluxes,

  $$\begin{aligned} \sum \limits _{i,j}\left( \mathbb {A}_{i,j}+\mathbb {B}_{i,j} +\mathbb {C}_{i,j}+\mathbb {D}_{i,j}+\mathbb {E}_{i,j} +\mathbb {F}_{i,j}\right) = 0. \end{aligned}$$

  Then we have

  $$\begin{aligned}&\sum \limits _{i,j}\left( \left( \frac{\partial u_1}{\partial t},u_1\right) +\left( \frac{\partial u_2}{\partial t},u_2\right) +\left( r_1+q_2, \frac{\partial }{\partial t}({r_1}+q_2) \right) \right) \nonumber \\&\quad =-\sum \limits _{i,j}\left( \mathbb {A}_{i,j}+\mathbb {B}_{i,j} +\mathbb {C}_{i,j}+\mathbb {D}_{i,j}+\mathbb {E}_{i,j} +\mathbb {F}_{i,j}\right) \nonumber \\&\quad =0. \end{aligned}$$

  (3.53)

This gives the energy stability results in (3.3) and (3.4). $\square$

4 Numerical Results

In this section, we give numerical solutions for different initial value to demonstrate the accuracy and capability of the LDG method. In this paper, we use the third-order explicit TVD Runge–Kutta method [31] as time discretization. The CFL number is 0.01, and time step is $\bigtriangleup t = 0.01 \bigtriangleup x$.

Example 4.1

Smooth solution

In this example, we test the smooth solution to calculate the order of the LDG scheme for the 2D CH equation with right-hand source terms

$$\begin{aligned} \frac{\partial }{\partial t}{} \mathbf m +\mathbf u \cdot \bigtriangledown \mathbf m +\bigtriangledown \mathbf u ^T\cdot \mathbf m +\mathbf m (\mathrm {div} \mathbf{u })=\mathbf f \end{aligned}$$

(4.1)

with the exact solutions:

$$\begin{aligned} u_1=\mathrm{sin}(x+y+t), \quad u_2=\mathrm{sin}(x-y+t), \end{aligned}$$

(4.2)

initial conditions:

$$\begin{aligned} u_1=\mathrm{sin}(x+y), \quad u_2=\mathrm{sin}(x-y), \end{aligned}$$

(4.3)

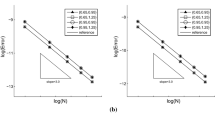
and periodic boundary condition over $[0,2\pi ]\times [0,2\pi ]$ . We can see that the method with $P^k$ elements gives a uniform ($\hbox {k}\,+\,1$)-th order of accuracy for $u_1$ and $u_2$ in Table 1.

Example 4.2

Peakon solution for the simplest case

The peakon solutions of the 2D CH equation are well known and we first display the simplest case that $u_1$ doesn’t have y, and $u_2$ doesn’t have x whose exact solutions read as:

$$\begin{aligned} u_1=e^{-|t-x|}, \quad u_2=e^{-|t-y|} \end{aligned}$$

(4.4)

with the initial conditions:

$$\begin{aligned} u_1=e^{-|x|}, \quad u_2=e^{-|y|} \end{aligned}$$

(4.5)

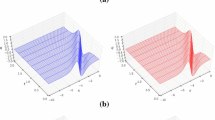
and periodic boundary condition. Uniform meshes with $80\times 80$, $P^4$ elements over $[-\,10,10]\times [-\,10,10]$. We can see the solutions in Figs. 1 and 2. We can find that the peakon is moving evenly over time.

Example 4.3

Peakon solution when the angle is $45^\circ$

In this example, we test the peakon solution for the 2D CH equation (2.5)–(2.8) with exact solutions read as:

$$\begin{aligned} u_1=u_2=e^{-|t-\frac{\sqrt{2}}{2}x-\frac{\sqrt{2}}{2}y|} \end{aligned}$$

(4.6)

and the initial conditions

$$\begin{aligned} u_1=e^{-|\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}y|}, \quad u_2=e^{-|\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}y|} \end{aligned}$$

(4.7)

with Dirichlet boundary condition. Uniform meshes with $80\times 80$, $P^4$ elements over $[-\,10,10]\times [-\,10,10]$. Since the solutions of $u_1$ and $u_2$ are the same, we only present the solution for $u_1$. We can see the solutions in Fig. 3. This kind of one peakon solution will propagate with the velocity in the direction with an angle to the positive x-axis.

Example 4.4

Two-peakon interaction for simplest case

In this example, we consider the two-peakon interaction of the 2D CH equation with the initial conditions:

$$\begin{aligned} u_1=\phi _1(x,y)+\phi _2(x,y), \quad u_2=\varphi _1(x,y)+\varphi _2(x,y), \end{aligned}$$

(4.8)

where

$$\begin{aligned} \phi _1(x,y)= & {} a_1e^{|x+x_1|}, \quad \phi _2(x,y)=a_2e^{|x+x_2|}, \end{aligned}$$

(4.9)

$$\begin{aligned} \varphi _1(x,y)= & {} b_1e^{|y+y_1|}, \quad \varphi _2(x,y)=b_2e^{|y+y_2|}, \end{aligned}$$

(4.10)

where $a_1=2,x_1=5,a_2=1,x_2=0,b_1=2,y_1=5,b_2=1,y_2=0$. Periodic boundary condition. Uniform meshes with $160\times 160$, $P^4$ elements over $[-\,20,20]\times [-\,20,20]$. Since the solutions of $u_1$ and $u_2$ are the same, we only present the solution for $u_1$. The two-peakon interaction at $\hbox {t} = 0, 1, 3$, and 8 is shown in Fig. 4. We can see clearly that the moving peakon interaction is resolved very well.

Example 4.5

Two-peakon interaction when the angle is $45^\circ$

In this example, we also consider the two-peakon interaction of the 2D CH equation with the initial conditions:

$$\begin{aligned} u_1=\phi _1(x,y)+\phi _2(x,y), \quad u_2=\varphi _1(x,y)+\varphi _2(x,y), \end{aligned}$$

(4.11)

where

$$\begin{aligned} \phi _1(x,y)= & {} a_1e^{|\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}y+c_1|}, \quad \phi _2(x,y)=a_2e^{|\frac{\sqrt{2}}{2}x +\frac{\sqrt{2}}{2}y+c_2|}, \end{aligned}$$

(4.12)

$$\begin{aligned} \varphi _1(x,y)= & {} b_1e^{|\frac{\sqrt{2}}{2}x+\frac{\sqrt{2}}{2}y+d_1|}, \quad \varphi _2(x,y)=b_2e^{|\frac{\sqrt{2}}{2}x +\frac{\sqrt{2}}{2}y+d_2|}, \end{aligned}$$

(4.13)

where $a_1=2,c_1=3\sqrt{2},a_2=1,c_2=0,b_1=2,d_1=3 \sqrt{2},b_2=1,d_2=0$. Periodic boundary condition. Uniform meshes with $160\times 160$, $P^4$ elements over $[-\,20,20]\times [-\,20,20]$. Since the solutions of $u_1$ and $u_2$ are the same, we only present the solution for $u_1$. The solutions are shown in Fig. 5 with the two-peakon interaction at t = 0, 1, 3, and 8. We can see clearly that the moving peakon interaction is also resolved very well.

Example 4.6

Peakon solution when $u_1 \ne u_2$

In this example, we display the peakon solutions when $u_1 \ne u_2$ whose exact solutions read as:

$$\begin{aligned} u_1=e^{-|t-\frac{\sqrt{5}}{5}x-\frac{2\sqrt{5}}{5}y|}, u_2=2e^{-|t-\frac{\sqrt{5}}{5}x-\frac{2\sqrt{5}}{5}y|}, \end{aligned}$$

(4.14)

with the initial conditions:

$$\begin{aligned} u_1=e^{-|\frac{\sqrt{5}}{5}x+\frac{2\sqrt{5}}{5}y|}, u_2=2e^{-|\frac{\sqrt{5}}{5}x+\frac{2\sqrt{5}}{5}y|} \end{aligned}$$

(4.15)

and Dirichlet boundary condition. Uniform meshes with $80\times 80$, $P^4$ elements over $[-\,10,10]\times [-10,10]$. We can see the solutions in Figs. 6 and 7. We can find that the peakon is moving evenly over time.

Example 4.7

Two-peakon interaction when $u_1 \ne u_2$

In this example, we display two-peakon interaction when $u_1 \ne u_2$ whose exact solutions read as:

$$\begin{aligned} u_1= & {} 2e^{-|2t-\frac{\sqrt{5}}{5}(x+3)-\frac{2\sqrt{5}}{5}(y+3)|} +e^{-|t-\frac{\sqrt{5}}{5}x-\frac{2\sqrt{5}}{5}y|},\nonumber \\ u_2= & {} 4e^{-|2t-\frac{\sqrt{5}}{5}(x+3)-\frac{2\sqrt{5}}{5}(y+3)|} +2e^{-|t-\frac{\sqrt{5}}{5}x-\frac{2\sqrt{5}}{5}y|}, \end{aligned}$$

(4.16)

with the initial conditions:

$$\begin{aligned} u_1= & {} 2e^{-|\frac{\sqrt{5}}{5}(x+3)+\frac{2\sqrt{5}}{5}(y+3)|} +e^{-|\frac{\sqrt{5}}{5}x+\frac{2\sqrt{5}}{5}y|},\nonumber \\ u_2= & {} 4e^{-|\frac{\sqrt{5}}{5}(x+3)+\frac{2\sqrt{5}}{5}(y+3)|} +2e^{-|\frac{\sqrt{5}}{5}x+\frac{2\sqrt{5}}{5}y|} \end{aligned}$$

(4.17)

and Dirichlet boundary condition. Uniform meshes with $160\times 160$, $P^4$ elements over $[-\,20,20]\times [-\,20,20]$. We can see the solutions in Figs. 8 and 9. We can find that the peakon is moving evenly over time.

5 Conclusion

In this paper, we have developed an LDG method for solving the 2D CH equation and proved the energy stability for this method. The main difference of CH equation between 1D and 2D is there have a lot of cross terms in the 2D CH equation, which brings much trouble for the proof of the stability and numerical test. We have also given several numerical simulation results to illustrate accuracy and capability of the LDG method. In future, the conservative schemes in time and the theoretical analysis for the LDG scheme, such as error estimates, will be our further research topics.