Introduction

Nonlinear system identification is the process of determining the mathematical model of a nonlinear system from input − output data [1, 2]. The goal is to find a mathematical representation of the system that accurately describes its behavior over a range of input conditions [3]. The identified model can then be used for a variety of purposes, such as control, prediction, or simulation of the system’s behavior [4].

The process of nonlinear system identification involves three key steps: detection, characterization, and parameter estimation [5,6,7]. Detection is the first step in building a structural model with accurate predictions [8, 9]. When designing and analyzing a structure, it is essential to consider its nonlinear dynamic characteristics for performance and reliability. Once nonlinear detection is performed, the next step is to determine the mathematical form of the nonlinearity, also known as model selection [10]. Finally, parameter estimation [11, 12] is the final step in creating a structural model with good predictive accuracy. The nonlinear subspace identification (NSI) approach proposed by Marchesiello et al. [13] has opened new possibilities for identifying nonlinear mechanical systems due to its robustness. Further, a negative stiffness oscillator is modeled and tested to exploit its nonlinear dynamical characteristics [14]. However, the model selection remains a crucial step in the identification process, as it is necessary to test the accuracy of candidate models to select the appropriate one. There is currently no universal method for selecting a suitable nonlinear model, and it’s often selected based on the characteristics of the specific identification problem. Improper selection of identification parameters often leads to multiple different models, resulting in an incomplete description of the structure. To find a reasonable model, methods for model selection must be developed to evaluate the model and its parameters. A hybrid nonlinear identification approach [15] is proposed by integrating the restoring force surface (RFS) [16] method and the NSI method. The distinct feature of the presented method is that it has the excellent characterization ability of the RFS and the recognition validity and robustness of the subspace algorithm. Bayesian model selection methods [17] have been developed to evaluate the model and its parameters, taking into account uncertainty in the selection process. These methods can simultaneously consider the impact of multiple models on the prediction of structural response, automatically constrain complex models, and calculate the probability of selecting each model. Based on the evidence obtained, the most likely model can be chosen. Nayek et al. [18] present the use of spike-and-slab (SS) priors [19] for discovering governing differential equations of motion of nonlinear structural dynamic systems, where displacement, velocity, and acceleration response data need to be measured. The use of displacement differentiation or acceleration integration to estimate response data may lead to distorted results due to noise propagation, making it challenging to accurately identify true nonlinear terms.

In this paper, a Spike-and-Slab Priors for Sparse Bayesian Learning is introduced to solve the model selection problem in the nonlinear subspace identification method. Enhanced nonlinear subspace identification (ENSI) is proposed. The method treats nonlinearity as an internal excitation and separates the response caused by it. The type of nonlinearity is then evaluated using Spike-and-Slab Priors for Sparse Bayesian Learning. The selected nonlinear models are then used in subspace identification to determine nonlinear parameters. The paper is structured as follows: “Framework of Enhanced Nonlinear Subspace Identification” introduces the proposed method. “Separate Response Caused by Internal Nonlinear Force Excitation” covers the process of extracting underlying linear characteristics. “Using Spike-and-Slab Priors for Bayesian Basis function Selection” and “Nonlinear Subspace Identification” briefly explain the theory of Spike-and-Slab Priors and nonlinear subspace identification. The numerical simulation and robustness are discussed in “Numerical Simulation”. “Experimental Study” presents an experimental study. The paper concludes in “Conclusion”.

Theory

Framework of Enhanced Nonlinear Subspace Identification

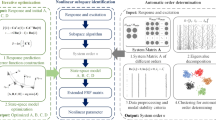
The purpose of this method is to separate the response caused by the internal nonlinear force excitation from the nonlinear structural response, determine the nonlinear basis function model through the Bayesian regression method, and finally bring it into the nonlinear subspace method for parameter identification as shown in Fig. 1. The main steps are: (1) By applying low-level excitation, the response of the structure can be obtained, and the frequency response function can be obtained, from which the unit impulse response function can be obtained through the inverse Fourier transform to obtain the structural characteristics of the underlying system; Apply high-level excitation, to separate the response caused by the internal nonlinear force excitation from the response; (2) Construct a nonlinear unit function library and use Bayesian regression to complete the nonlinear characterization; (3) Substitute the nonlinearity into the nonlinear subspace algorithm for parameter identification.

Fig. 1
figure 1

Schematic diagram of the ENSI

Full size image

Separate Response Caused by Internal Nonlinear Force Excitation

To describe the process, a single Dof system with nonlinearity is written by

$$m\ddot{x} + c\dot{x} + kx + f_{n} \left( t \right) = f\left( t \right)$$
(1)

where m is the mass matrix, c is the damping, k is the linear stiffness, f is the excitation, and fn is the internal nonlinear force. The nonlinear force fn can be shifted to the right, which can be regarded as an internal excitation to the underlying linear system.

$$\underbrace {{m\ddot{x} + c\dot{x} + kx}}_{{\text{Underlying linear part}}} = f\left( t \right) - f_{n} \left( t \right)$$
(2)

When the type of nonlinear function is unknown, the nonlinear restoring forces can be represented by selecting a complete set of candidate nonlinear functions.

$$\begin{aligned} f_{n} & = \left[ {\begin{array}{*{20}c} {G_{1} \left( t \right)} & {G_{2} \left( t \right)} & \cdots & {G_{m_{f}} \left( t \right)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\mu _{1} } & {\mu _{2} } & \cdots & {\mu _{m_{f}} } \\ \end{array} } \right\}^{T} \\ & = \left[ {\begin{array}{*{20}c} {G_{1} } & {G_{2} } & \cdots & {G_{m_{f}} } \\ \end{array} } \right]\mu \\ & = G\mu \\ \end{aligned}$$
(3)

where mf is the number of candidate nonlinear functions, G is the library of nonlinear functions, and μ is the corresponding coefficient vector. Since the number of functions in the nonlinear library exceeds the number of real nonlinearities in the system, only a small number of nonlinearities are active, resulting in a sparse coefficient vector, μ.

When a nonlinear structure is subjected to a low-level excitation flow, the effects of nonlinearities can be generally assumed to be minimal, leading to a response that approximates the linear characteristics of the structure [20]. Therefore, Eq. (2) can be rewritten by

$$m\ddot{x} + c\dot{x} + kx \approx f_{{{\text{low}}}} \left( t \right)$$
(4)

Based on the application of low-level excitation, the response of the structure approximates the linear characteristics of the structure, which allows the linear frequency response function H of the structure to be determined. The unit impulse response function h can then be obtained by performing an inverse Fourier transform [21].

$${\varvec{h}} = \frac{1}{2\pi }\int_{ - \infty }^{ + \infty } {{\varvec{H}}\left( \omega \right)e^{i\omega t} d\omega }$$
(5)

When a high-level excitation fhigh is applied to the structure, the effects of intrinsic nonlinear forces cannot be ignored. The nonlinearity is treated as an additional force applied to the underlying linear structure. The total response of the structure is the result of the combined action of both linear and nonlinear forces. By using the Duhamel integral [22], the response can be expressed as:

$$x\left( t \right) = \underbrace {{h\left( t \right) \otimes f_{{{\text{high}}}} \left( t \right)}}_{{{\text{linear response }}x_{l} }} - h\left( t \right) \otimes f_{n} \left( t \right)$$
(6)

 ⊗ represents the convolution operation. The response of the structure due to the internal nonlinear force fn can be expressed as xn, which is the result of a convolution operation between the unit impulse response function and the nonlinear force

$$x_{n} = h\left( t \right) \otimes f_{n} \left( t \right) = h\left( t \right) \otimes f_{{{\text{high}}}} \left( t \right) - x\left( t \right)$$
(7)

Substituting Eq. (3) into Eq. (7) formula, we can get

$$\begin{gathered} x_{n} = h\left( t \right) \otimes f_{n} \left( t \right) \\ = h\left( t \right) \otimes \left( {\left[ {\begin{array}{*{20}c} {G_{1} \left( t \right)} & {G_{2} \left( t \right)} & \cdots & {G_{m_{f}} \left( t \right)} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\mu_{1} } & {\mu_{2} } & \cdots & {\mu_{m_{f}} } \\ \end{array} } \right\}^{T} } \right) \\ = \mu_{1} \underbrace {{h\left( t \right) \otimes G_{1} \left( t \right)}}_{{G_{1}^{^{\prime}} }} + \mu_{2} \underbrace {{h\left( t \right) \otimes G_{2} \left( t \right)}}_{{G_{2}^{^{\prime}} }} + \cdots + \mu_{m_{f}} \underbrace {{h\left( t \right) \otimes G_{m_{f}} \left( t \right)}}_{{G_{m_{f}}^{^{\prime}} }} \\ = G^{^{\prime}} \mu \\ \end{gathered}$$
(8)

This equation shows that nonlinear representation is a variable selection problem, which can be approached as a regression problem. To estimate the best nonlinear terms in the system, the Bayesian variable selection method based on the spike and slab prior can be used, by calculating the marginal posterior probability through Gibbs sampling [23].

Using Spike-and-Slab Priors for Bayesian Basis Function Selection

In linear regression problems with high-dimensional covariates, the goal is to find a sparse solution to the model by identifying the best subset of relevant covariates. This is done by removing irrelevant covariates and finding a solution that has only a few nonzero coefficients in the regression function.

In the Bayesian framework, variable selection can be achieved by using shrinkage priors. The Spike and slab prior is a common approach that assigns a latent variable to each nonlinear function in the library, indicating whether the function is active in the model. By estimating the posterior probabilities for all possible models and the marginal posterior probabilities for individual functions, the true nonlinear terms in the system can be identified. This approach is useful for high-dimensional covariates, as it tends to find sparse solutions to the model by removing irrelevant functions.

Consider a standard multiple linear regression equation:

$$Y = X\beta + \varepsilon$$
(9)

where Y = (Y1,Y2,…, Yn)T is the n-dimensional target vector, X = (X1,X2,…,Xn)T is the n × p matrix of predictors, β = (β1, β2,…, βp) is the vector of coefficients, and ε = (ε1, ε2,…, εn)T is the error term. Assuming that the elements in the error vector ε are independently and identically distributed following a Gaussian distribution with a mean of 0 and a variance of σ2, the likelihood function of Y can be expressed as

$${\varvec{Y}}|{\mathbf{X}},{{\varvec{\upbeta}}},\sigma^{2} \sim {\mathcal{N}}\left( {{\mathbf{X\beta }},\sigma^{2} {\mathbf{I}}} \right)$$
(10)

where represents the Gaussian distribution and I is the n × n-dimensional identity matrix.

According to the spike and slab prior method, each covariate in the multiple linear regression equation is assigned a latent binary variable, s = (s1,s2,…,sp). This variable, si (where si ∈ {0, 1}), indicates whether the ith covariate is included in the model. When si = 0, the prior distribution of the corresponding regression coefficient (βi) is a spike with a point peak at zero. On the other hand, when si = 1, the prior distribution of βi is a slab with a flat density. In this method, the spike distribution is set to δ(βi), where δ represents the Dirac function. The slab distribution is set to (0, τσ2). Therefore, the prior density of each component (βi) in the coefficient vector β can be expressed as:

$$\beta_{i} |s_{i} \sim \left( {1 - s_{i} } \right)\delta \left( {\beta_{i} } \right) + s_{i} {\mathcal{N}}\left( {0,\tau \sigma^{2} } \right)$$
(11)

Define the following prior distributions for the other parameters:

$$s_{i} |p_{0} \sim {\text{Bernoulli}}\left( {p_{0} } \right)$$
(12)
$$p_{0} \sim {\text{Beta}}\left( {a_{p} ,b_{p} } \right)$$
(13)
$$\tau \sim {\text{Inverse}}\,{\text{Gamma}}\left( {a_{\tau } ,b_{\tau } } \right)$$
(14)
$$\sigma^{2} \sim {\text{Inverse}}\,{\text{Gamma}}\left( {a_{\sigma } ,b_{\sigma } } \right)$$
(15)

The prior distributions for the other parameters in the model are defined as follows: ap and bp for the latent binary variables, aτ and bτ for the slab density, and aσ and bσ for the variance of the error term. These hyperparameters control the shape of their respective priors.

Based on Bayes' theorem, the joint posterior distribution of the parameters can be expressed as:

$$\begin{gathered} p\left( {\beta ,s,p_{0} ,\tau ,\sigma^{2} |Y,X} \right) = \frac{{p\left( {Y|\beta ,\sigma^{2} } \right)p\left( {\beta |s,\tau ,\sigma^{2} } \right)p\left( {s|p_{0} } \right)p\left( {p_{0} } \right)p\left( \tau \right)p\left( {\sigma^{2} } \right)}}{p\left( Y \right)} \\ \propto p\left( {Y|\beta ,\sigma^{2} } \right)p\left( {\beta |s,\tau ,\sigma^{2} } \right)p\left( {s|p_{0} } \right)p\left( {p_{0} } \right)p\left( \tau \right)p\left( {\sigma^{2} } \right) \\ \end{gathered}$$
(16)

To solve this Bayesian inference problem involving multiple hyperparameters, Markov−Monte Carlo techniques are usually used to sample from the posterior. In this case, the Gibbs sampler is used to sample from the posterior distribution described by Eq. (16). The Gibbs sampler requires fully conditional distributions for all random variables, which can be analytically derived using conjugate priors. By using the Gibbs sampler, a Markov chain for the parameters β, σ2, and s can be obtained, and a large number l of samples for variable selection can be obtained by discarding a small number of samples before the burn-in period. The sample of each component si in s indicates the selection of the variable; si = 1 indicates that the variable is selected and si = 0 indicates that the variable is discarded. Therefore, for a large number l of samples of si, the following marginal posterior probability can be defined:

$$p\left( {s_{i} = 1|{\mathbf{Y}},{\mathbf{X}}} \right) = \frac{1}{l}\sum\limits_{j = 1}^{l} {I_{f} \left( {s_{i}^{j} = 1} \right)}$$
(17)

where If is the indicator function. When the marginal posterior probability of a variable, p(si = 1|Y, X) > 0.5 is greater than 0.5, it should be considered for inclusion in the final model.

Nonlinear Subspace Identification

Based on the theory presented in “Using Spike-and-Slab Priors for Bayesian Basis Function Selection”, it is determined that the nonlinear basis functions of the end structure have a total of v items (v < mf). The state-space equation at this time can be expressed as:

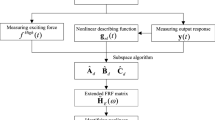
$$\left\{ {\begin{array}{*{20}c} {\dot{x}} \\ {\ddot{x}} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - \frac{k}{m}} & { - \frac{c}{m}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} x \\ {\dot{x}} \\ \end{array} } \right\}{ + }\left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 0 \\ {m^{ - 1} } & {m^{ - 1} \mu_{1} } & \cdots & {m^{ - 1} \mu_{v} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {f\left( t \right)} \\ { - G_{1} \left( t \right)} \\ \vdots \\ { - G_{v} \left( t \right)} \\ \end{array} } \right\}$$
(18)

Based on the authors’ previous work about the nonlinear subspace identification [24], the “extended” frequency response function (FRF) matrix is expressed as

$$H_{E} \left( \omega \right) = \left[ {\begin{array}{*{20}c} H & {H\mu_{1} G_{1} } & \cdots & {H\mu_{q} G_{v} } \\ \end{array} } \right]$$
(19)

where H is the underlying linear system FRF and nonlinear parameters μi can be identified

Numerical Simulation

The system with nonlinear stiffness and damping is investigated. The system parameters are: m = 10 kg, k1 = 800 N/m, c = 2 Ns/m, k3 = 2 × 105 N/m3, cn = 20 Ns2/m2. The dynamic equation is as follows

$$m\ddot{z} + c\dot{z} + k_{1}z + k_{3} z^{3} + c_{n} \dot{z}^{2} { = }\,f\left( t \right)$$
(20)

The system is excited by a low-level force 2Nrms and a high-level force 100Nrms. As shown in Fig. 2, the response is calculated by the Runge– Kutta fourth-order method. The sampling frequency is 1000 Hz, and the acquisition length is t = 50 s.

Fig. 2
figure 2

The displacement under low-level and high-level force

Full size image

It is widely recognized that when structures are subjected to low-level excitations, they display linear characteristics, and the underlying linear system frequency function of the structure can be determined equivalently. As shown in Fig. 3, the frequency response function under low-level excitation is largely consistent with the theoretical linear frequency response function, indicating that nonlinearity is not excited. The estimated impulse response function is calculated.

Fig. 3
figure 3

Underlying linear FRF

Full size image

The estimated unit impulse response function is primarily utilized to distinguish the response caused by nonlinear internal forces and construct a nonlinear function library. Under high-level excitation, the excitation force and the unit impulse response function are convolutionally integrated. Then, the nonlinear response by the internal nonlinear force fn is estimated using Eq. (7), as is depicted in Fig. 4. The results demonstrated that the estimated nonlinear response curve is in close agreement with the true value curve.

Fig. 4
figure 4

Displacement generated by an internal nonlinear force

Full size image

In addition, a nonlinear type construction function library G can be utilized in the construction of a set of systems. In this example, the polynomial type (•)n, the symbol type sgn(•), and the absolute value type |(•)| are considered, as illustrated in Table 1. The function library contains 10 basis functions, and 210 nonlinear functions can be constructed by cross-permutation and combination. The unit impulse response function is convolved with each nonlinear vector in G to construct an extended library of response functions G′.

Table 1 Nonlinear function library
Full size table

Gibbs based on the Bayesian regression is used for sampling, and hyperparameters and initial values of each random variable are set. The hyperparameters are set as follows: ap = 0.1, bp = 1, aτ = 0.5, bτ = 0.5, aσ = 5 × 10–4, bσ = 5 × 10–4. The initial values of β, s, p0, τ, σ2 are set as: p0 (1) = 0.1, τ(1) = 10, σ2 (1) = 0. Utilize the Gibbs sampler method to run two Markov chains simultaneously, each containing 5000 samples, and discard a certain number of samples before the convergence period.

Figure 5 shows the procedure of basis function selection based on the marginal posterior inclusion probability (PIP). When p (si = 1|Y, X) = 1, it implies that the ith basis function had been selected in all Gibbs posterior samples, while p (si = 1|Y, X) = 0 implies the ith basis function had never been selected. As mentioned in “Using Spike-And-Slab Priors For Bayesian Basis Function Selection”, only those basis functions are included in the final estimated model whose corresponding marginal PIPs are greater than the set threshold of 0.5. The results show that x3 is selected with a marginal posterior probability close to 1, another true relevant variable ẋ2 draws marginal PIPs of around 0.9, and the remaining nonlinearities are discarded with a marginal posterior probability less than 0.2, which is consistent with the real situation and verifies the effectiveness of the basis function selection in this paper.

Fig. 5
figure 5

Marginal posterior probability of each nonlinear function without noise

Full size image

When measuring the real structural response, there will inevitably be measurement noise, which may lead to the inaccuracy of the separated nonlinear response and affect the subsequent nonlinear characterization. To further discuss the robustness of the method, 2% and 5% noise were added to the above-mentioned responses under low-level and high-level excitations, respectively. As shown in Fig. 6, in the case of noise, the reconstructed nonlinear response trend is still consistent with the theoretical value. When the noise is large, the curve will show more glitches. Furthermore, the corresponding nonlinear basis function selection results are given in Fig. 7. The results show that in the case of noise, the marginal posterior probability of nonlinear stiffness is still close to 1, while the marginal posterior probability of damping will decrease with the increase of noise, but it is still greater than 0.85, which can accurately determine the nonlinear type of structure, to verify that the model selection has better robustness.

Fig. 6
figure 6

Displacement generated by an internal nonlinear force a with 2% noise; b with 5%noise

Full size image
Fig. 7
figure 7

Marginal posterior probability of each nonlinear function a with 2% noise; b with 5% noise

Full size image

Substituting the above model selection results into the nonlinear subspace, the nonlinear coefficients of the structure can be identified in Table 2. In the case of 5% noise, the absolute value of the identification error is also less than 2%, which verifies that the method has good robustness.

Table 2 Identified nonlinear parameters and errors under different noise levels
Full size table

Experimental Study

To assess the effectiveness of the proposed method in real-world structures, this section presents an experimental test on a negative system. The device being tested consists of a U-shaped frame connected to a central moving mass via rods. The structure is subjected to base motion by a shaking table. The assumption made is that the inertia of the moving parts can be concentrated into a single central point, encompassing the mass of the central bush and the equivalent inertia of the rods. Relevant theoretical findings on this structure have been reported in Ref. [25]. The equation of motion along the vertical direction in the x variable can be expressed as

$$m\ddot{x} + f_{d} - \tilde{k}_{1} x + \tilde{k}_{2} x^{2} + \tilde{k}_{3} x^{3} { + }mg = f\left( t \right)$$
(21)

where \(- \tilde{k}_{1}\) < 0 is the so-called negative stiffness and fd is the nonlinear damping force.

Figure 8 illustrates the experimental setup with two photos, showing the device stable equilibrium positions. The system is excited with a shaking table to provide random excitation. The sampling frequency is 512 Hz, and the acquisition length is 135 s. The equilibrium positions are measured using a laser vibrometer and are found to be \(x_{ - }^{ * }\) =  − 0.0301 m and \(x_{ + }^{ * }\) = 0.0242 m.

Fig. 8
figure 8

Experimental setup. a Negative equilibrium position; b positive equilibrium position [14]

Full size image

A cross-validation method is adopted: the data set is divided into a training set (first 100 s) and a validation set (the last 35 s) to verify the generalization ability of the model in Fig. 9.

Fig. 9
figure 9

Displacement under high-level extraction

Full size image

As previously reported in detail in [25], a new displacement variable z(t) = x(t)-\(x_{ + }^{ * }\) can be defined when a positive reference position \(x_{ + }^{ * }\) is taken into consideration. In this scenario, the system is defined as a stable underlying linear system. Consequently, the equation of motion can be expressed as:

$$m\ddot{z} + c\dot{z} + k_{1} z + k_{2} z^{2} + k_{3} z^{3} + f_{d} = f\left( t \right)$$
(22)

For this experimental system, the nonlinear damping form is challenging to determine a priori. Based on the experimental results in [25], the friction force in this negative stiffness oscillator is dependent on position and velocity. Friction is related to normal force pr, which can be represented by:

$$\begin{gathered} f_{d} \left( {\dot{z},z} \right) = \sum\nolimits_{j = 0}^{{n_{d} }} {c_{j} sign\left( {\dot{z}} \right)} \dot{z}^{j} \left| {\underbrace {{\alpha z^{3} + \beta z^{2} + \gamma z + \delta }}_{{p_{r} \left( z \right)}}} \right| \hfill \\ \, = \sum\nolimits_{j = 0}^{{n_{d} }} {c_{j} sign\left( {\dot{z}} \right)} \dot{z}^{j} \left| {p_{r} \left( z \right)} \right| \hfill \\ \end{gathered}$$
(23)

where the three coefficients (α, β, γ, δ) related to two stable equilibrium positions \(x_{ \pm }^{ * }\) are uniquely determined.

$$\alpha = \frac{{x_{ - }^{3} - x_{ + }^{3} }}{{x_{ - }^{2} - x_{ + }^{2} }} - x_{ + }^{3} - 1$$
(24)
$$\beta = - \alpha \frac{{x_{ - }^{3} - x_{ + }^{3} }}{{x_{ - }^{2} - x_{ + }^{2} }}$$
(25)
$$\gamma = 0,\delta = 1$$
(26)

Based on Ref. [14] or the underlying linear parameter identification method [26], the underlying linear FRFs can be obtained. Then, the nonlinear response by the internal nonlinear force fn is estimated using Eq. (7), as is depicted in Fig. 10.

Fig. 10
figure 10

Displacement generated by an internal nonlinear force with zero-reference shift and reference positive position

Full size image

Then, it is important to determine the nonlinear function. The following set of nonlinear basis functions is considered: z3; z2; \(\sum\nolimits_{j = 0}^{{n_{d} }} {c_{j} sign\left( {\dot{z}} \right)} \dot{z}^{j} \left| {p_{r} \left( z \right)} \right|\), nd = 4; As per the proposed method, the results of basis function selection are illustrated in Fig. 11. The results indicate that the marginal posterior probability of selecting z3 and z2 is close to 1. In terms of the damping term, the marginal PIP of Coulomb and quadratic friction is about 0.7, these two terms dominate the damping, which is in agreement with the results of the previous literature and verifies the effectiveness of the nonlinear basis functions selection of the proposed method.

Fig. 11
figure 11

Marginal posterior probability of each nonlinear function based on the training data

Full size image

By incorporating the results of the model selection into the nonlinear subspace identification method, the estimated coefficients are illustrated in Fig. 12. The results show that the real part of the parameters maintains a horizontal line and is independent of the frequency, thereby verifying the effectiveness and stability of the nonlinear identification. The imaginary parts of the coefficients are consistently lower than the real parts, however, the difference is generally decreased for the damping-related coefficients, indicating that the identified model structure is still impacted by a combination of nonlinear modeling errors and noise. The average ratio between real and imaginary parts E[R/I] is in any case at least one order of magnitude. The complete list of the estimated coefficients is presented in Table 3.

Fig. 12
figure 12

Real and imaginary parts of the identified coefficients based on the training data

Full size image
Table 3 Identified coefficients for the positive reference equilibrium positions
Full size table

The identified restoring force estimated by the proposed method is compared with the experimental value obtained by the restoring force surface method in Fig. 13, and the agreement is good. The friction is related to position and velocity, and a 2D graph like velocity force is unable to evaluate the damping identification. In Fig. 14, the complete restoring surface is obtained to include the damping force in a 3D graph. The experimental restoring surface is calculated by the restoring force surface method, and the experimental restoring surface overlaps with the identified one. The results demonstrate that the proposed method can effectively identify nonlinear stiffness and damping.

Fig. 13
figure 13

Estimation of the restoring force

Full size image
Fig. 14
figure 14

Estimation of the restoring surface

Full size image

Further, the effectiveness of the proposed method is verified by the verification set data. Based on the previous identification results, the response signal of the system is constructed, as shown in Fig. 15. The results show that the estimated response is in good agreement with the experimental signal curve as a whole, but there are some local deviations.

Fig. 15
figure 15

Comparison of experimental and estimated displacement based on the validation set

Full size image

Conclusion

This paper presents an enhanced nonlinear subspace identification method. The proposed method in this paper utilizes Spike-and-Slab Priors for Sparse Bayesian Learning in nonlinear subspace identification to solve the model selection problem. The nonlinear term in the system is treated as an internal excitation. The first step is to extract the impulse response function of the underlying linear system of the structure. This is followed by applying a high-level excitation to the structure, which allows for the separation of the response caused by the nonlinear term from the overall response. The type of nonlinearity is evaluated using Spike-and-Slab Priors for Sparse Bayesian Learning. Then, the nonlinear models are substituted into subspace identification to determine nonlinear parameters. The effectiveness of this method in dealing with nonlinear stiffness and damping is verified by simulation analysis and robustness is further discussed. The method is also shown to have good adaptability in dealing with complex nonlinear damping conditions through experimental study.