1 Introduction

In the field of wind engineering and marine engineering, vortex shedding will occur alternately in the wake on both sides of the bluff body when the fluid flows over the bluff body, which will produce periodically changing fluid force on the transverse direction of the structure. The elastic structure will also generate transverse vibration due to the fluid force acting on the structure, so-called vortex-induced vibration (VIV) [1,2,3,4]. VIV occurs in many engineering systems and has its impact, at times also destructive, on wind turbine tower, offshore structures, high-rise buildings and cables [5, 6], just to name but a few. As the vortex shedding frequency in the wake is close to the natural frequency of the structure, the structure vibrates in a resonance-like phenomenon called “lock-in” [7,8,9]. Under the resonance condition, the vibration amplitude will be much larger than that under normal conditions. Besides, the VIV results in periodic fatigue stress on the structure, and the vibration with large amplitude will lead to fatigue failure and in some cases sudden structural failure [10, 11].

In previous studies, experimental investigations on the VIV [12,13,14,15] have been conducted extensively via solving the problem of a rigid elastically mounted cylinder in the cross-flow direction. Feng [16] firstly carried out experiments of an elastically mounted cylinder with high mass ratio in air and discovered the initial branch and the lower branch of VIV amplitude. Khalak et al. [17, 18] conducted some canonical experiments and found the upper branch of VIV amplitude based on Feng’s research. It also demonstrates that the VIV in underwater structures distinguishes itself from that in air by having wider synchronization regions. In recent years, CFD numerical simulations have been performed to predict the responses of the VIV [19,20,21]. These are very effective tools in the field of computer technologies, and several computational studies have proved that CFD methods could accurately predict the response of the VIV.

To mitigate the effect of the VIV on the fatigue life of high-rise column structure, helical wires and splitter plate are usually added to the structure to destroy vortex structure and coherence and/or change vortex shedding mode [22,23,24]. However, these appendages often increase the drag and cause other forms of vibration. Additionally, installing dampers in the column structure is also an effective method to reduce the vibration of the structure. Nevertheless, conventional dampers such as tuned mass dampers (TMD) and tuned liquid dampers (TLD) often have narrow frequency bandwidth, and their vibration absorption range is small [25,26,27,28]. The nonlinear energy sink (NES) [29,30,31] is a nonlinear vibration absorber which can realize a targeted energy transfer (TET). It has a broadband vibration absorption characteristic. The device is placed in the cylinder, and thus it does not change the shape of the cylinder.

Tumkur et al. [32,33,34] introduced an NES to suppress VIV at a determined flow velocity. Currently, there are two types of NES used in the VIV of a cylinder, translational NES (T-NES), and rotational NES (R-NES). The T-NES consists of a mass linked to the cylinder with a cubic spring and a linear damper, and thus, the nonlinear essence of the T-NES is the strong stiffness nonlinearity. Mehmood et al. [35] used a strong fluid structure coupling model to determine the effects of the initial condition on the system (cylinder and T-NES). Dai et al. [36] established a VIV model of the T-NES-cylinder system by a van der Pol oscillator, which also has high computational efficiency. Chen et al. [37] compared the CFD-coupled FSI model and van der Pol model. These investigations mainly focused on the suppression of VIV without changing the geometry of the cylinder, while it is recently proposed the R-NES can be used for VIV-induced power generation [38]. The R-NES is a rigid bar with a tip-mass attached to the cylinder, where the mass can rotate at a fixed radius about the cylinder axis. This generates an inertial nonlinearity. Tumkur et al. [39] and Blanchard et al. [40] found the R-NES can make a significant difference to the wake. Besides, Selwanis et al. [41] designed the R-NES and experimentally assess the R-NES’s effect on the flow-induced vibration suppression of a square prism.

In light of the NES’s great potentials, in [37, 42] the authors studied the VIV of 1- and 2-DOF cylinders with NES in water at moderate Reynolds number. The NES vibration suppression capacity was evaluated by time-response analysis; however, the energy transfer mechanism of NES was not fully understood. The current literature only described the behavior of a 1-DOF cylinder at low Re numbers under the action of NES, and the influence of the flow direction on the vibration characteristics of the cylinder was not been considered [34]. For the high mass ratio cylinder, the streamwise vibration has little effect on the single-cylinder system. However, under the action of the NES, this small effect may alter the vibration of the whole system and the TET of the NES. This paper addresses both issues and considers the vortex-induced vibration of 2-DOF cylinder in air at low Re numbers. The cylinder’s vibrations in-line and cross-flow directions are considered in the simulation model for higher accuracy. Phase diagrams and time–frequency analysis are presented, and the suppression mechanism of NES is studied in more detail. By calculating the largest Lyapunov exponent, the systemic dynamical state under the action of the NES with different mass ratios is identified.

The rest of the paper is organized as follows. Section 2 presents the FSI simulation method based on CFD. In Sect. 3, the accuracy of the simulation method is discussed. Section 4 illustrates the dynamic behaviors of the 2-DOF VIV of the cylinder under the action of NES at low Re and three suppression mechanisms of the NES with different mass. Finally, in Sect. 5 concluding remarks are offered.

2 Computational approach

2.1 Structural dynamics model

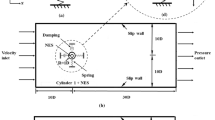
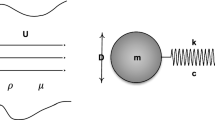
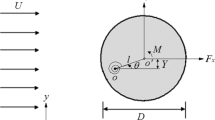
When the fluid moves around the cylinder structure, it will induce a vortex-induced vibration response of the cylinder in both the transverse and in-flow directions. To capture the vibration response in the two directions, the model predicting the vortex-induced vibration of a two-dimensional cylinder with two degrees of freedom is established. The physical model is shown in Fig. 1, which regards the cylinder structure as a mass-spring-damper system. Particularly, in the physical model, the cylinder itself is regarded as the mass block, the elastic modulus as the spring and the structural damping force as the damper. At the same time, the effect of NES is also considered in the proposed model. The NES is located inside the cylinder and is regarded as the mass block, which is connected with the cylinder in the transversal direction of the flow, the y-direction, by the damper and the nonlinear spring. The cylinder is allowed to move in both x- and y-directions. This model can be reduced to a two-dimensional one, because the cylindrical segment and NES mass block can be considered as rigid bodies.

Fig. 1
figure 1

Physical model. a Three-dimensional diagram. b Two-dimensional diagram

Full size image

According to the physical model, the governing equations of 2-DOF elastically mounted cylinder under the action of the NES subjected to the external fluid forces can be cast as:

$$ m\ddot{x}_{1} + c\dot{x}_{1} + kx_{1} = F_{{\rm D}} (t) $$
(1)
$$ (m - m_{{\rm nes}} )\ddot{y}_{1} + c\dot{y}_{1} + ky_{1} + c_{{\rm nes}} (\dot{y}_{1} - \dot{y}_{2} ) + k_{{\rm nes}} (y_{1} - y_{2} )^{3} = F_{{\rm L}} (t) $$
(2)
$$ m_{{\rm nes}} \ddot{y}_{2} + c_{{\rm nes}} (\dot{y}_{1} - \dot{y}_{2} ) + k_{{\rm nes}} (y_{2} - y_{1} )^{3} = 0 $$
(3)

where \(x\) is the displacement of the cylinder in the flow direction, \(y\) is the displacement of the cylinder in the cross-flow direction, (\(\cdot\)) indicates derivative with regard to the dimensional time \(t\), subscript 1 represents the motion parameters of cylinder, and subscript 2 represents the motion parameters of NES; \(m\) is the mass of oscillating system (i.e., the sum of the mass of the single cylinder \(m_{{\rm c}}\) and the mass of NES \(m_{{\rm nes}}\)), \(c\) is damping, \(k\) is stiffness, \(m_{{\rm nes}}\) is the mass of NES, \(c_{{\rm nes}}\) is the damping of NES, \(k_{{\rm nes}}\) is the stiffness of NES. The nonlinear restoring force satisfies the relation, \(F = k_{{\rm nes}} y_{2}^{3}\). It can be seen from the relation that NES has the characteristic of cubic nonlinearity, and restoring force is cubic in the displacement; \(FD\) and \(FL\) are the external fluid forces in the flow direction and cross-flow direction, which can be calculated by CFD.

The above governing equations can be cast in dimensionless form as:

$$ \ddot{x}_{1} + 2\varsigma \omega_{n} \dot{x}_{1} + \omega_{n}^{2} x_{1} = \frac{1}{2}\frac{{C_{{\rm D}} \rho_{{\rm f}} U^{2} D}}{m} $$
(4)
$$ (1 - \beta )\ddot{y}_{1} + 2\varsigma \omega_{n} \dot{y}_{1} + \omega_{n}^{2} y_{1} + 2\varsigma_{{\rm nes}} \omega_{n} (\dot{y}_{1} - \dot{y}_{2} ) + \frac{\gamma }{{D^{2} }}\omega_{n}^{2} (y_{1} - y_{2} )^{3} = \frac{1}{2}\frac{{C_{{\rm L}} \rho_{{\rm f}} U^{2} D}}{m} $$
(5)
$$ \beta \ddot{y}_{2} + 2\varsigma {\rm nes}\omega_{n} (\dot{y}_{2} - \dot{y}_{1} ) + \frac{\gamma }{{D^{2} }}\omega_{n}^{2} (y_{2} - y_{1} )^{3} = 0 $$
(6)

where \(U\) is the inflow velocity, \(\rho_{{\rm f}}\) is the density of fluid, \(D\) is the cylinder’s diameter, \(C_{{\rm L}}\) is the lift coefficient, and \(C_{{\rm D}}\) is the drag coefficient, \(\omega_{n}\) is the natural frequency of cylinder (\(\omega_{n} = \sqrt {{k \mathord{\left/ {\vphantom {k m}} \right. \kern-\nulldelimiterspace} m}}\)), \(\varsigma\) is the cylinder’s damping ratio (\(\varsigma = {c \mathord{\left/ {\vphantom {c {2\sqrt {{\rm km}} }}} \right. \kern-\nulldelimiterspace} {2\sqrt {{\rm km}} }}\)), \(\varsigma_{{\rm nes}}\) is the damping ratio of the NES (\(\varsigma_{{\rm nes}} = {{c_{{\rm nes}} } \mathord{\left/ {\vphantom {{c_{{\rm nes}} } {2\sqrt {{\rm km}} }}} \right. \kern-\nulldelimiterspace} {2\sqrt {{\rm km}} }}\)), \(\beta\) is the mass ratio between the NES and cylinder (\(\beta = {{m_{{\rm nes}} } \mathord{\left/ {\vphantom {{m_{{\rm nes}} } m}} \right. \kern-\nulldelimiterspace} m}\)), \(\gamma\) is the nondimensional stiffness ratio between the NES and cylinder (\(\gamma = {{k_{{\rm nes}} \cdot D^{2} } \mathord{\left/ {\vphantom {{k_{{\rm nes}} \cdot D^{2} } k}} \right. \kern-\nulldelimiterspace} k}\)), and \(\xi\) is the nondimensional damping ratio between the NES and cylinder (\(\xi = {{\varsigma_{{\rm nes}} } \mathord{\left/ {\vphantom {{\varsigma_{{\rm nes}} } \varsigma }} \right. \kern-\nulldelimiterspace} \varsigma }\)).

2.2 Computational fluid dynamics model

In this paper, the flow is treated as unsteady and incompressible with constant fluid properties. It is modeled using the transient, incompressible Reynolds average Navier–Stokes (RANS) solver which uses the generalized \(k - \omega\) (GEKO) turbulence model [43, 44]. The RANS solver adopts the virtual averaging of velocities over an interval of time. As a result, the velocity vector in a RANS solver appears to be constant for a specific interval. To address this shortcoming, an optimized grid is applied to capture the physics of the vortex shedding generated from the cylinder. The RANS solver for transient and incompressible two-dimensional analysis can be found in [37].

In order to close the RANS equations, a generalized \(k - \omega\) (GEKO) model is adopted. The GEKO model is a two-equation turbulence model based on the \(k - \omega\) model. In particular, traditional two-equation turbulence models (\(k - \omega\) and \(k - \varepsilon\)) solve two partial differential equations to obtain two independent scales. Similar to classical turbulence models (\(k - \omega\) and \(k - \varepsilon\)), the GEKO model is capable of accurately predicting flows with the adverse pressure gradients, commencement and intensity of flow separations [45]. However, the coefficients of traditional models cannot be changed casually, because they are interconnected and must satisfy certain conditions. Different from classical models, the GEKO model has more flexibility, whose free parameters can be adjusted for specific types of applications without the negative impact on the basic calibration of the model [44]. The formulations describing the model follow [43, 44]:

$$ \frac{\partial (\rho k)}{{\partial t}} + \frac{{\partial (\rho u_{j} k)}}{{\partial x_{j} }} = P_{k} - \rho C_{\mu } k\omega + \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \frac{{\mu_{t} }}{{\sigma_{k} }}} \right)\frac{\partial k}{{\partial x_{j} }}} \right] $$
(7)
$$ \frac{\partial (\rho \omega )}{{\partial t}} + \frac{{\partial (\rho u_{j} \omega )}}{{\partial x_{j} }} = C_{\omega 1} F_{1} \frac{\omega }{k}P_{k} - C_{\omega 2} F_{2} \rho \omega^{2} + F_{3} \frac{2}{{\sigma_{\omega } }}\frac{\rho }{\omega }\frac{\partial k}{{\partial x_{j} }}\frac{\partial \omega }{{\partial x_{j} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \frac{{\mu_{t} }}{{\sigma_{\omega } }}} \right)\frac{\partial \omega }{{\partial x_{j} }}} \right] $$
(8)

where \(\mu_{t} { = }\rho v_{t}\), \(P_{k} = - \tau_{ij} ({{\partial u_{i} } \mathord{\left/ {\vphantom {{\partial u_{i} } {\partial x_{j} }}} \right. \kern-\nulldelimiterspace} {\partial x_{j} }})\).

A computational domain size of \(40{\text{D}} \times 20{\text{D}}\) is used for the CFD simulation of the VIV of the cylinder. As to the cross-flow direction, the cylinder is in the middle of the domain, which is 10D distant from upstream and downstream boundary. The same computational domain size and boundary conditions in [37] are adopted. The overlapping meshes technology and fully structural mesh are used to perform mesh deformation caused by the cylinder’s motion. The overset mesh for computing is shown in Fig. 2. More details about meshing are also shown in [37, 42].

Fig. 2
figure 2

Computational fluid mesh of 2-DOF spring-supported cylinder

Full size image

2.3 FSI solving process

In this study, an unsteady segregated algorithm is adopted to compute the flow field. A COUPLED algorithm is chosen to solve pressure–velocity coupled equations, and the implicit second-order scheme is used for unsteady terms. In addition, the convection terms are dispersed with upwind second-order scheme. The time step is computed as follows:

$$ t = \frac{D}{{U \cdot (10\;{\text{to}}\;100)}} $$
(9)

and is used in the fluid–structure interaction simulations, where the flow equations and structural equations are solved simultaneously and iteratively. The computational flowchart of fluid–structure interaction is diagrammatically illustrated in Fig. 3. According to the boundary conditions, the pressure and velocity of the two-dimensional cylinder surface are obtained. Subsequently, the force acting on the surface of the cylinder is extracted and then substituted into the structural motion equation of the cylinder. By solving the motion equation of the two-dimensional cylinder, the displacement and velocity of the cylinder at current time step are achieved. At the same time, the computational grid based on overset meshes method is updated according to displacement and instantaneous velocity of cylinder, and then the next time step is calculated. At the end set time, the vibration response of cylinder can be achieved. The numerical simulations are performed by the commercial software ANSYS® FLUENT 2019.

Fig. 3
figure 3

The computational flowchart of fluid–structure interaction

Full size image

3 Model validation

3.1 Validation of 2-DOF model

To assess the effectiveness and accuracy of the CFD computations, the present simulation results have been compared with experimental data from [46]. For this purpose, the VIV response of the cylinder without the NES was considered using the same parameters of the classic 2-DOF experimental work carried out by Jauvtis and Williamson [46]. The mass ratio between the cylinder and water is \(m^{ * } = 2.6\), and \(m^{ * } \varsigma = 0.013\). The simulation is conducted over a reduced velocity range of \(0 \le U_{r} \le 15\). The comparison of VIV results between experimental data from [46] and numerical simulation is depicted in Fig. 4, where Fig. 4a shows nondimensional maximum amplitudes (\(\left| {y_{\max } } \right|/D\)) of the cylinder versus reduced velocity \(U_{r}\) and 4.b shows the frequency ratio in the case of various \(U_{r}\).

Fig. 4
figure 4

The contrast results of VIV with experiment data [46]. a Amplitude distribution at reduced velocity and b frequency ratio versus reduced velocity

Full size image

The simulation model is based on a high-quality structured grid and considers the cylinder vibration both cross-flow and in-flow directions. From Fig. 4a, three different branches can be observed from the current results. The simulation results at the super-upper branch are slightly different from the experimental results. Figure 4b also shows that the synchronization regions of experiment [46] and current results, where \(f_{v} /f_{n} \approx 1\), both occur for \(4 \le U_{r} \le 13\). Overall, the computational results are in a reasonable good agreement with experiment evaluations of [46], which also verifies the accuracy of this established method.

3.2 Mesh convergence study

The vibration response of a single cylinder with NES is investigated and compared with that of a cylinder exposed to a flow at the reduced velocity \(U_{r} = 5.6\) (Re = 100), to observe the effect of NES on suppressing the cylinder VIV. The medium in the flow field is selected as air, and at sea level the air density is \(\rho = 1.225\;{\text{kg/m}}^{3}\) and the kinematic viscosity is \(\upsilon = 1.48 \times 10^{5} \;{\text{m}}^{2} {\text{/s}}\). The other parameters for simulation are from [47]: the inflow velocity \(U = 0.0146\;{\text{m/s}}\), the cylinder diameter \(D = 0.1\;{\text{m}}\), the natural frequency of the cylinder \(f_{n} = 0.0261\;{\text{Hz}}\), the damping ratio of cylinder \(\varsigma = 0.002\), the mass per unit length of the cylinder \(m = 0.1\;{\text{kg/m}}\), and the mass ratio of the cylinder \(m* = 10.4167\). For the high mass ratio cylinder (\(m* > 6\)), the streamwise vibration has little effect on the single-cylinder system. However, under the action of the NES, the vibration characteristics of the cylinder may alter. And the vibration energy in the in-line and cross-flow directions can affect the function of the NES. Thus, the streamwise vibration is also considered in this paper. Though the fluid is laminar flow at Re = 100, GEKO turbulence model is selected in this study in consideration of the vibration-induced turbulence. The time step is 0.5 s. Before simulating the vibration response, mesh independency is assessed.

The grid density has an impact on the simulation accuracy as well as computing efficiency. The analysis of grid convergence is carried out at Re = 98.65. The grid of cylinder’s boundary layer is refined to alter grid quantity, meeting the requirement of y plus (y+) less than 1. Table 1 shows the root-mean-square of lift coefficient \(C_{{\rm L}}^{\prime }\), mean drag coefficient \(\overline{C}_{{\rm D}}\), Strouhal number \(St\) of four groups with different grid density. The comparison of the results of four cases shows that they are close to each other apart from Case 1. Considering the computing efficiency, the mesh of Case 2 is selected as the computational fluid mesh.

Table 1 Sensitivity of the computational mesh
Full size table

4 Results and discussion

4.1 Analysis of the effect of NES on suppressing VIV

To perform comparative analysis with the baseline (without NES) single cylinder, the parameters of NES are selected as \(\beta = 0.2\), \(\gamma = 0.8\), \(\xi = 0.8\). Although not optimal, these parameters have been chosen since have shown good suppressing effect from earlier published work [37]. The optimal parameters of NES to suppressing VIV will be achieved in further investigation. Other parameters for the simulation are shown in Sect. 3.2. At \(U_{r} = 5.6\), lock-in occurs and it vibrates with a large amplitude. It should be noted the total oscillating mass of the cylinder-NES system keeps unchanged, by the means of the reduction of the mass of the cylinder. The system with constant mass can better observe the effect of TET and eliminate the effect of energy dissipation caused by the extra mass of NES. The purpose of this study is to analyze effect of NES at this velocity within the range of synchronization.

The comparison of the VIV response of a cylinder with and without NES is shown in Fig. 5. Figure 5a illustrates the trajectories of the cylinder motion. It can be seen that the trajectories of the cylinder are in the shape of an ‘8,’ indicating that at the current Reynolds number, the vortex shedding is still regular. The long strip indicates that, for the proposed simulation scenario, the transverse vibration amplitude in the cross-flow direction is larger than that in the flow direction. In Fig. 5a, the trajectories of cylinder with/without the NES are depicted. When comparing the two trajectories, the vibration amplitude of the cylinder with NES not only weakens in the cross-flow direction, but also decreases in the streamwise direction. According to the above phenomena, it can be concluded that the NES installed in the transverse direction of the cylinder mainly absorbs the transverse vibration energy; hence, the transverse amplitude decreases. Figure 5b shows the time histories of nondimensional displacements of the cylinder without NES and NES-y1 (the cylinder of the cylinder-NES system) and NES-y2 (the NES of the cylinder-NES system). When comparing these curves, one can note that the vibration amplitude of the cylinder is reduced by more than 50% for the cylinder with NES; hence, we can conclude that the NES has a significant effect on the suppression of the VIV. The amplitude of the NES oscillator is smaller than the radius of the cylinder; hence, it will not collide with the cylinder.

Fig. 5
figure 5

The response of the cylinder with and without NES. a Trajectories of VIV and b time histories of the nondimensional displacements

Full size image

The vorticity contours in one oscillation period of the cylinder are shown in Fig. 6, which indicates the temporal evolution of the vortex shedding of the cylinder. The initial position of the cylinder is shown in the dotted line. Figure 6a shows that the cylinder has a certain displacement relative to the initial position in the cross-flow direction, while the displacement in the flow direction is relatively small. The vortex shedding presents a distinct pattern. In one oscillation period, two vortexes shedding is accompanied, and the wake vortex develops into two rows of vortices at a distance. When the cylinder moves further away to the utmost position from the equilibrium position, the lift coefficient \(C_{{\rm L}}\) acting on the cylinder reaches the maximum value; when the cylinder moves to the equilibrium position, the lift coefficient is negligible, but the velocity of the cylinder in the cross-flow direction is the highest. A period of oscillation is divided into two parts. When the cylinder moves in one side of cross-flow direction, the vortex will shed in the other direction.

Fig. 6
figure 6figure 6

Temporal evolution of vortex formations for flow over a cylinder. a Without NES and b with NES

Full size image

Figure 6b illustrates that the vibration in the cross-flow direction is reduced, and the vortex shedding with the NES is similar to that without the NES. The vortex shedding also develops into two rows of vortices at a distance, but the two rows of vortices are closer than that without the NES. Similar to the situation above, when the cylinder moves to the utmost distance from the equilibrium position, the lift coefficient is the largest. Observing the boundary layer and wake flow, it can be seen that adding the NES to the cylinder delays the separation of boundary layer and narrows the wake vortex area. Accordingly, the pressure drag decreases in the in-flow direction. Although the amplitude of the cylinder in the cross-flow direction becomes smaller, the lift coefficient is larger than that without NES. It is conjectured that the NES transfers the energy of the vibration cylinder to the NES oscillator, which is dissipated by the damping. Therefore, the amplitude is small although the lift is large. In conclusion, the NES with tuned parameters can have a large effect on the suppression of the VIV of the cylinder, without increasing drag.

4.2 Analysis of the effect of NES with different mass ratio \({\varvec{\beta}}\)

To add further insight to the effect of the NES on suppressing the VIV, three different mass ratios between NES and cylinder \(\beta\) are investigated; \(\beta\) is selected as 0.15, 0.2 and 0.3 for simulation, and \(\gamma = 0.8\), \(\xi = 0.8\). In the same way, the cylinder mass is changed to keep total oscillating mass constant. All other conditions are consistent with the above model.

The nondimensional amplitude of oscillations in the cross-flow direction and \(U_{r} = 5.6\) is depicted in Fig. 7. The vibration in the cross-flow direction for all cases is symmetric about zero. By comparing the vibration displacement for different \(\beta\), it can be concluded that the larger the \(\beta\) is, the better the suppression effect on the VIV of cylinder is. When \(\beta = 0.15\), the amplitude does not have any noticeable change. However, for \(\beta > 0.15\), the maximum amplitude reduces by about half, and the beat phenomenon is emerged. Different from other situations, the oscillation for \(\beta = 0.2\) is quite irregular. Clearly, when \(\beta\) is lower than 0.15 for this cylinder system, there is no significant effect on the suppression of VIV.

Fig. 7
figure 7

Time histories of nondimensional displacement. a Without NES. b With NES. \(\beta = 0.15\). c With NES, \(\beta = 0.2\) and d with NES, \(\beta = 0.3\)

Full size image

For the sake of direct comparison between lift coefficient and nondimensional displacement, the time histories of lift coefficient and vibration displacement are depicted in one figure, as shown in Fig. 8. As \(\beta\) increases, it is observed that the lift coefficient also increases, while the nondimensional displacement decreases. Specially double oscillation periods of \(C_{{\rm L}}\) are observed for each oscillation period of \(y/D\) when \(\beta = 0.15\). In other cases, the \(C_{{\rm L}}\) is in phase with the \(y/D\).

Fig. 8
figure 8

Variation \(C_{{\rm L}}\) with \(y/D\) a without NES, b with NES, \(\beta = 0.15\), c with NES, \(\beta = 0.2\) and d with NES, \(\beta = 0.3\)

Full size image

The frequency spectrum curves for vibration in the cross-flow direction in the case of various are depicted in Fig. 9. From a detailed analysis of vibration frequency, the peak frequency of vibration without the NES is identical to the natural frequency. When \(\beta = 0.15\) and \(\beta = 0.2\), the peak frequency is slightly smaller and higher than the natural frequency of cylinder. Particularly when \(\beta = 0.3\), the peak frequency of cylinder displacement response is quite different from the other cases analyzed so far, the coupled system response frequency contrasts the natural frequency of the cylinder is substantially reduced, and the effect of suppressing VIV is enhanced.

Fig. 9
figure 9

Power spectral density a with NES, \(\beta = 0.15\), b with NES, \(\beta = 0.2\) and c with NES, \(\beta = 0.3\)

Full size image

When \(\beta = 0.15\), the ratio of the actual vortex shedding frequency \(f_{v}\) to the natural frequency \(f_{n}\) of the cylinder is 0.9295, and when \(\beta = 0.2\), the ratio is 1.0011. While the mass ratio of the NES to the cylinder is 0.3, that nondimensional ratio \(f_{v} /f_{n}\) is 0.8992, and the amplitude of the cylinder in the cross-flow is minimum.

Contrarily to the observed phenomena above, it can be seen that the fundamental reason why the NES can contain the VIV of the cylinder is that the NES affects the vortex shedding frequency of the cylinder and avoids the synchronization phenomenon. Besides, the larger \(\beta\) is, it becomes very obvious how the vortex shedding frequency changes. As demonstrated in Fig. 9c when \(\beta = 0.3\), the frequency spectrum curves of transverse vibration of cylinder and that of the NES oscillator under the action of the NES are quite similar. This also proves the suppression mechanism of NES transmitting the vibration energy from the cylinder to the NES in the way of resonance capture with the cylinder, and the vibration energy will be dissipated by damping.

Figure 10 shows how the vibration frequency changes with time. The region of high intensity corresponds to the main vibration frequencies. In Fig. 10a, b, the stationary intensity indicates the main frequencies remain constant with time. In this case, the NES has a little impact on energy distribution of the vibration frequencies. This also emphasizes the NES with unsuitable parameters has only minor effects on the VIV. In Fig. 10c, d, the vibration frequency is non stationary, and the form of the fluctuation is similar to the vibration response. This fluctuation is not shown in Fig. 9, which can be inferred as the intermittent function of NES.

Fig. 10
figure 10

Time–frequency spectrum a without NES, b with NES, \(\beta = 0.15\) and c with NES, \(\beta = 0.2\) and d with NES,\(\beta = 0.3\)

Full size image

The time–frequency spectrum reveals three function modes of NES with different mass. With \(\beta = 0.15\), the vibration frequencies remain constant, and the \(C_{{\rm L}}\) is not in phase with the \(y/D\). With the \(\beta = 0.2\), the energy distribution of frequencies fluctuates with time, and VIV suppression can be observed. With \(\beta = 0.3\), the narrow banded is partially constant and partly fluctuating. The period of fluctuation is shorter, and the suppression effect improves.

Differently from galloping, the VIV is a limited amplitude vibration, and its amplitude will not increase without bound with the increase in wind speed. Figure 11 exhibits the phase portrait of cylinder vibration in the cross-flow direction. Figure 11a shows the phase portrait of the VIV without the NES. The vibration of the cylinder is controlled by a limit cycle, when the cylinder is in steady-state vibration and an equilibrium amplitude motion is reached.

Fig. 11
figure 11

Phase-space plot correlated with the time trace of the fluctuating displacement signal. a Without NES, b with NES, \(\beta = 0.15\), c with NES, \(\beta = 0.2\) and d with NES, \(\beta = 0.3\)

Full size image

Figure 11b–d shows the phase portraits of the VIV under the action of the NES with different \(\beta\). There are some regular changes in vibration, which is no longer equal amplitude vibration in these three cases. When \(\beta = 0.15\), the phase portrait curve is limited periodically in three intersecting circles, which corresponds to double oscillation periods of \(C_{{\rm L}}\) in each oscillation period of \(y/D\) in Fig. 8b. The shape of the attractor is a three-loop limit cycle because of the appearance of high-order harmonics. Besides, there is no obvious decrease in vibration when \(\beta = 0.15\). When \(\beta = 0.2\), the phase portrait is an unclosed and nonperiodic curve, where cylinder vibrates randomly in a constrained range. For \(\beta = 0.3\) the results are similar to \(\beta = 0.2\), but the orbit is circular with a certain width. Moreover, the amplitude of VIV is quite smaller in such a situation. As displayed in Fig. 11c, d, the curves are no longer limited to a limit cycle. It can be inferred that the NES is in the state of permanent resonance capture, and the kinetic energy of vortex-induced vibration is kept within a small value. Because of this, the amplitude is also greatly reduced when \(\beta = 0.2\) and \(\beta = 0.3\). Although the vibration of the cylinder is still stable at this time, there are some regular changes in the vibration with different amplitudes.

The Poincare section of the transverse vibration is depicted in Fig. 12. The period of the Poincare section is the main vibration frequency of the cylinder. Without the NES or with \(\beta = 0.15\) NES, the motion of the cylinder is obviously periodic. When \(\beta = 0.15\), there are three points in the Poincare section, corresponding to the triple-period motion. When \(\beta = 0.2\) and \(\beta = 0.3\), the points in Poincare section seem to be random. To further study dynamical behavior for \(\beta = 0.2\) and \(\beta = 0.3\), the largest Lyapunov exponent is estimated by the Rosenstein method [48]. The time series of the cylinder’s vibration are used to reconstructed state space by method of delays. The results with different embedding dimensions are shown in Fig. 13, and the dashed line is plotted by the least-squares fit to the solid curve. Although the results are not completely accurate, they still broadly characterize the time series. The positive Lyapunov exponents for \(\beta = 0.2\) and \(\beta = 0.3\) are displayed in Fig. 13; hence, the cylinder’s vibration can be considered to be under the chaotic state. Under the action of the NES with large mass ratio \(\beta\), the cylinder exhibits more complex dynamics.

Fig. 12
figure 12

Poincare section of the transverse vibration. a Without NES, b with NES, \(\beta = 0.15\), c with NES, \(\beta = 0.2\) and d with NES, \(\beta = 0.3\)

Full size image
Fig. 13
figure 13

Plots of ln(divergence) versus time for a \(\beta = 0.2\), b \(\beta = 0.3\). The slope of the dashed line represents the calculated largest Lyapunov exponent

Full size image

5 Conclusions

In this study, based on computational simulations and adoption of a CFD overset methodology, an FSI model is established to simulate the VIV of a cylinder fitted with a NES damper. Our previous work mainly investigated the effect of different parameters of NES on 1-DOF VIV responses and concluded that the mass ratio between the NES and cylinder \(\beta\) plays a critical role in suppressing the vibration [37]. Thus, based on previous studies, a further detailed research on \(\beta\) is presented herewith. The numerical simulations, validated with experiments from archival literature, provide a wealth of information, represented in the form of vorticity contours, frequency spectrum curves and phase portrait for the VIV of a cylinder exposed to the air environment, and also facilitate observations about the working mechanism and effectiveness of NES. The results show that:

  1. (1)

    the NES with suitable parameters can effectively reduce the VIV of the cylinder, the amplitude in the cross-flow direction, to some extent, and even the vibration amplitude in the streamwise direction;

  2. (2)

    at low Reynolds number, the VIV of the cylinder is a steady and constant amplitude vibration. However, when fitted with the NES, the cylinder vibration shows some regular changes. It is no longer constant amplitude vibration, and it may develop into chaotic motion;

  3. (3)

    there exists a specific range of mass ratio of the NES to the cylinder whereby the NES can affect the frequency of the vortex shedding, and VIV suppression becomes quite effective. When the mass ratio of the NES is unsuitable, the NES VIV capacity is ineffective and the lift coefficient increases;

  4. (4)

    three main function modes of NES with different mass are observed. The three main function modes have different effects on vibration amplitude and frequency.