1 Introduction

Numerous probability distributions are introduced in the literature by mixing, extending and modifying well known distributions and hence provide more flexible hazard rate function for modelling lifetime data. These distributions will then be more suitable for fitting appropriate real data than the base models. Knowledge of the appropriate distribution plays an important role in improving the efficiency of any statistical inference related to data sets. Hence the researchers are more keen to develop new distributions by extending classical distributions to increase model flexibility and adaptability in various aspects of modelling data.

Lindley (1958) introduced in the literature one of the most discussed lifetime distribution, the Lindley distribution, in the context of the Bayesian statistics as a counter example of the fiducial statistics. Lindley distribution (LD) have the probability density function (pdf),

$$\begin{aligned} f_1(x)=\frac{\theta ^2}{1+\theta }(1+x)e^{-\theta x};\, x>0,\, \theta >0, \end{aligned}$$
(1.1)

which is a mixture of exponential \((\theta )\) and gamma \((2,\theta )\) distributions. The corresponding cumulative distribution function (cdf) has been obtained as,

$$\begin{aligned} F_1(x)=1-\frac{\theta +1+\theta x}{1+\theta }e^{-\theta x};\, x>0,\, \theta >0, \end{aligned}$$
(1.2)

where \(\theta\) is the scale parameter.

Mixture models provide a mathematical based, flexible and meaningful approach for the wide variety of classification requirements. There are numerous fields in which mixture models have practical applicability. Lindley itself being a mixture model, it has gained momentum in the theoretical perspective as well as in terms of its applications. Ghitany et al. (2008) have studied various properties of this distribution and showed that (1.1) provides a better model for some applications than the exponential distribution. Mazucheli and Achcar (2011) applied the Lindley distribution to competing risk life time data. A discrete version of this distribution has been suggested by Deniz and Ojeda (2011) having its applications in count data related to insurance. Al-Mutairi et al. (2013) developed the inferential procedure of the stress-strength parameter, when both stress and strength variables follow Lindley distribution. The applicability of Lindley distribution in solving lifetime modelling problems and modelling stress strength model made researchers to develop many generalizations, modifications and extensions of this distribution. Shanker et al. (2013) introduced a two parameter Lindley distribution (\(LD_2\)) for modelling waiting and survival times data with pdf,

$$\begin{aligned} f_2(x;\alpha ,\theta )=\frac{\theta ^2}{\theta +\alpha }(1+\alpha x)e^{-\theta x};\, x>0,\, \theta>0,\,\alpha >-\theta , \end{aligned}$$
(1.3)

where \(f_2(x; \alpha , \theta )\) is a mixture of exponential \((\theta )\) and gamma \((2,\theta )\) with mixing probabilities \(\frac{\theta }{\theta +\alpha }\) and \(\frac{\alpha }{\theta +\alpha }\) respectively. Even though one parameter and two parameter Lindley distributions are mixture of \(E(\theta )\) and \(G(2,\theta )\), most of the further generalizations are based on two gamma models with suitable mixtures. The generalizations that we aware of are:

Zakerzadeh and Dolati (2009) introduced a generalized Lindley distribution (GLD) with pdf,

$$\begin{aligned} f_3(x; \alpha , \theta , \gamma )=\frac{\theta ^2(\theta x)^{\alpha -1}(\alpha +\gamma x)}{(\gamma +\theta )\Gamma (\alpha +1)}e^{-\theta x};\, x>0,\,\alpha ,\theta ,\gamma >0, \end{aligned}$$
(1.4)

\(f_3(x; \alpha , \theta , \gamma )\) is a mixture of gamma \((\alpha ,\theta )\) and gamma \((\alpha +1, \theta )\) with mixing probabilities \(\frac{\theta }{\gamma +\theta }\) and \(\frac{\gamma }{\gamma +\theta }\) respectively.

Ghitany et al. (2011) introduced a weighted Lindley distribution (WLD) with pdf,

$$\begin{aligned} f_4(x;\theta ,\alpha )=\frac{\theta ^{\alpha +1}}{(\theta +\alpha )\Gamma (\alpha )}x^{\alpha -1}(1+x)e^{-\theta x}, \alpha ,\theta ,x>0, \end{aligned}$$
(1.5)

\(f_4(x;\theta ,\alpha )\) can also be expressed as a two component mixture such that

$$\begin{aligned} f_4(x;\theta ,\alpha )=p g_1(x)+(1-p)g_2(x), \end{aligned}$$

where \(p=\frac{\theta }{\theta +\alpha }\) and \(g_i(x)=\frac{\theta ^{\alpha +j-1}}{\Gamma (\alpha +j-1)}x^{\alpha +j-2}e^{-\theta x}, \alpha ,\theta ,x>0, j=1, 2\), is the pdf of the gamma distribution with the shape parameter \(\alpha +j-1\) and scale parameter \(\theta , j=1, 2.\)

Elbatal et al. (2013) proposed a new generalized Lindley distribution (NGLD) with pdf,

$$\begin{aligned} f_5(x;\theta , \alpha ,\beta )=\frac{1}{1+\theta }\left[ \frac{\theta ^{\alpha +1} x^{\alpha -1}}{\Gamma (\alpha )} +\frac{\theta ^{\beta } x^{\beta -1}}{\Gamma (\beta )}\right] e^{-\theta x}; x>0, \alpha , \theta >0, \end{aligned}$$
(1.6)

where \(f_5(x; \alpha , \theta )\) is a mixture of gamma \((\alpha ,\theta )\) and gamma \((\beta , \theta )\) with mixing probabilities \(\frac{\theta }{\theta +1}\) and \(\frac{1}{\theta +1}\) respectively.

Abouammoh et al. (2015) defined another new generalized Lindley distribution (\(NGLD_1\)) with pdf,

$$\begin{aligned} f_6(x; \alpha , \theta )=\frac{\theta ^{\alpha }x^{\alpha -2}}{(\theta +1)\Gamma (\alpha )}(x+\alpha -1) e^{-\theta x}; x>0, \theta \ge 0,\alpha \ge 1, \end{aligned}$$
(1.7)

where \(f_6(x; \alpha , \theta )\) is a mixture of gamma \((\alpha ,\theta )\) and gamma \((\alpha -1, \theta )\) with mixing probabilities \(\frac{1}{\theta +1}\) and \(\frac{\theta }{\theta +1}\) respectively.

All these generalizations play various roles in the literature both in theoretical and applied perspectives. It can be perceived that most of the further developments are based on these six models, which immensely motivates to propose a generalized family, which generalizes the afore mentioned Lindley models. Hence in this work we introduce a wider class of Lindley distribution by mixing binomial probabilities with gamma distribution and name the distribution as binomial mixture Lindley distribution (BMLD).

One of the main peculiarity of the LD is its shape of hazard rate (increasing hazard rate) function compared to the well known exponential distribution. By scrutinizing the flexibility of various variants of Lindley model in terms of the hazard rate function, Lindley-Exponential distribution (Bhati et al. 2015) possess decreasing hazard rate function, GLD possess bathtub shape hazard rate function and inverse Lindley distribution (Sharma et al. 2015) possess upside down bathtub shape hazard rate function. Hence another motivation of this work is to propose a flexible extension of Lindley model which possess all the available shapes of hazard rate function. During the initial stage of this work, we came across several recent articles based on Lindley models. Several authors claim that their model possess bathtub shaped hazard rate but not even a single author attempted to fit a bathtub shaped data. Hence one motivation of this work is to propose a model and successfully apply a well known bathtub shaped data of Aarset (1987). In addition to Aarset data, to prove the superiority of BMLD we also took two other data sets, viz., strength of glass fiber data (see, Smith and Naylor 1987) and survival times of 72 guinea pigs data (see, Bjerkedal 1960) both having increasing hazard rate function.

The rest of the paper is outlined as follows. In Sect. 2 binomial mixture Lindley distribution is defined along with its moments, model identifiability, mean, variance, a recursive relationship for moments and moment generating function. Some of the reliability properties of the model such as hazard rate function, vitality function, mean residual life function, inequality measures and some uncertainty measures are presented in Sect. 3. In Sect. 4, the parameters of the distribution are estimated using method of maximum likelihood and thus obtained observed Fisher information matrix and asymptotic confidence intervals. A simulation study is presented in Sect. 5. Finally in Sect. 6, experimental results of the proposed distribution based on real data sets are illustrated.

2 Binomial Mixture Lindley Distribution

In this section, we present definition and some important properties of the binomial mixture Lindley distribution . Here after we use the short form BMLD for binomial mixture Lindley distribution.

Definition 2.1

A continuous random variable X is said to follow BMLD if its pdf f(x) has the following form,

$$\begin{aligned} f(x)=\sum _{i=0}^{g}p_i\ h_i(x), \end{aligned}$$
(2.1)

where

$$\begin{aligned} h_i(x)=\frac{\theta ^{\alpha _i}}{\Gamma (\alpha _i)}x^{\alpha _i-1}e^{-\theta x}, \end{aligned}$$

for \(\theta >0\), \(\alpha _i > 0\) for \(i=0,1,\cdots ,g\). We define the mixing weights \(p_i\) such that

$$\begin{aligned} p_i= \left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}, \end{aligned}$$
(2.2)

for \(i=0,1,\cdots ,g\) and \(\displaystyle \sum _{i=0}^{g}p_i=1\), \(\beta > 0\), \(\theta > 0\) .

Special cases

  1. (1)

    If g=1, \(\alpha _0\)=1 and \(\alpha _1\)=1, then BMLD becomes the exponential distribution (ED).

  2. (2)

    If g=1, \(\beta\)=1 and \(\alpha _0\)=\(\alpha _1\)=\(\alpha\), then BMLD becomes the gamma distribution (GD).

  3. (3)

    If g=1, \(\beta\)=1, \(\alpha _0\)=2 and \(\alpha _1\)=1, then BMLD becomes the Lindley distribution (LD).

  4. (4)

    If g=1, \(\alpha _0\)=2 and \(\alpha _1\)=1, then BMLD becomes the two parameter Lindley distribution [\(LD_{2}\) (Shanker et al. 2013)].

  5. (5)

    If g=1, \(\alpha _0\)=\(\alpha +1\) and \(\alpha _1\)=\(\alpha\), then BMLD becomes the generalized Lindley distribution [GLD (Zakerzadeh and Dolati 2009)].

  6. (6)

    If g=1 \(\alpha _0=\alpha +1\), \(\alpha _1=\alpha\) and \(\beta =\alpha\), then BMLD becomes the weighted Lindley distribution [\(WLD\,\)(Ghitany et al. 2011)].

  7. (7)

    If g=1 and \(\beta\)=1, then BMLD becomes the new generalized Lindley distribution [\(NGLD\,\)(Elbatal et al. 2013)].

  8. (8)

    If g=1, \(\beta\)=1, \(\alpha _{0}\)=\(\alpha\) and \(\alpha _{2}\)=\(\alpha -1\), then BMLD becomes new generalized Lindley distribution [\(NGLD_{1}\,\)(Abouammoh et al. 2015)].

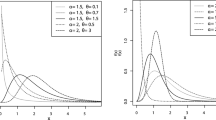
The pdf of the distribution, for different values of parameters, is plotted in Fig. 1.

Fig. 1
figure 1

The pdf of BMLD for g=2 and different values of \(\theta\), \(\beta\), \(\alpha _{0}\), \(\alpha _{1}\), \(\alpha _{2}\)

Full size image

2.1 Identifiability

A set of parameters for a particular model is said to be identifiable if not any two sets of the parameters gives same distribution for the given x.

Result 2.1

The identifiability condition for BMLD with pdf as given in (2.1) is \(\alpha _{i} \ne \alpha _{j}\) for each \(i,j \in {0,1,2,...,g}\) such that \(i\ne j\) .

Proof

For mathematical simplicity, first we consider the case of \(g=2\) and let

$$\begin{aligned} b_{0} B_{0}(x)+b_{1} B_{1}(x)+b_{2} B_{2}(x)=0, \end{aligned}$$
(2.3)

where \(b_{0}\), \(b_{1}\) and \(b_{2}\) are real numbers, \(B_{0}(x)=\int \limits _{u=0}^{x} f(u) d u\), \(B_{1}(x)=\int \limits _{u=0}^{x} g(u) d u\) and \(B_{2}(x)=\int \limits _{u=0}^{x} h(u) d u\) with \(x>0\). Also g(u) and h(u) can be obtained from f(u) by replacing \(\alpha _{i}\) by \(\rho _{i}\) and \(\alpha _{i}\) by \(\mu _{i}\) respectively. Assume that for each \(i=0,1,2\), \(\alpha _{i}\ne \rho _{i}\ne \mu _{i}\),

$$\begin{aligned} B_{0}(x)= & {} \int _{0}^{x}\left[ \left( \frac{\beta }{\theta +\beta }\right) ^{2} \frac{\theta ^{\alpha _{0}}}{\Gamma \left( \alpha _{0}\right) } t^{\alpha _{0}-1} e^{-\theta t}+\frac{2\beta \theta }{(\theta +\beta )^{2}} \frac{\theta ^{\alpha _{1}}}{\Gamma \left( \alpha _{1}\right) } t^{\alpha _{1}-1} e^{-\theta t} \right. \nonumber \\&\left. +\left( \frac{\theta }{\theta +\beta }\right) ^{2} \frac{\theta ^{\alpha _{2}}}{\Gamma \left( \alpha _{2}\right) } t^{\alpha _{2}-1} e^{-\theta t}\right] d t, \end{aligned}$$
(2.4)
$$\begin{aligned} B_{1}(x)= & {} \int _{0}^{x}\left[ \left( \frac{\beta }{\theta +\beta }\right) ^{2} \frac{\theta ^{\rho _{0}}}{\Gamma \left( \rho _{0}\right) } t^{\rho _{0}-1} e^{-\theta t}+\frac{2\beta \theta }{(\theta +\beta )^{2}} \frac{\theta ^{\rho _{1}}}{\Gamma \left( \rho _{1}\right) } t^{\rho _{1}-1} e^{-\theta t} \right. \nonumber \\&\left. +\left( \frac{\theta }{\theta +\beta }\right) ^{2} \frac{\theta ^{\rho _{2}}}{\Gamma \left( \rho _{2}\right) } t^{\rho _{2}-1} e^{-\theta t}\right] d t \end{aligned}$$
(2.5)

and

$$\begin{aligned} B_{2}(x)=\int _{0}^{x}\left[ \left( \frac{\beta }{\theta +\beta }\right) ^{2} \frac{\theta ^{\mu _{0}}}{\Gamma \left( \mu _{0}\right) } t^{\mu _{0}-1} e^{-\theta t}+\frac{2\beta \theta }{(\theta +\beta )^{2}} \frac{\theta ^{\mu _{1}}}{\Gamma \left( \mu _{1}\right) } t^{\mu _{1}-1} e^{-\theta t} \right. \nonumber \\ \left. +\left( \frac{\theta }{\theta +\beta }\right) ^{2} \frac{\theta ^{\mu _{2}}}{\Gamma \left( \mu _{2}\right) } t^{\mu _{2}-1} e^{-\theta t}\right] d t. \end{aligned}$$
(2.6)

Putting the values of \(B_{0}(x)\), \(B_{1}(x)\) and \(B_{2}(x)\) in (2.3) , we obtain the following,

$$\begin{aligned}&\int _{0}^{x}\left[ b_{0} \frac{\theta ^{\alpha _{0}}}{\Gamma \left( \alpha _{0}\right) } t^{\alpha _{0}-1} e^{-\theta t}+b_{1} \frac{\theta ^{\rho _{0}}}{\Gamma \left( \rho _{0}\right) } t^{\rho _{0}-1} e^{-\theta t}+b_{2} \frac{\theta ^{\mu _{0}}}{\Gamma \left( \mu _{0}\right) } t^{\mu _{0}-1} e^{-\theta t}\right] d t=0, \end{aligned}$$
(2.7)
$$\begin{aligned}&\int _{0}^{x}\left[ b_{0} \frac{\theta ^{\alpha _{1}}}{\Gamma \left( \alpha _{1}\right) } t^{\alpha _{1}-1} e^{-\theta t}+b_{1} \frac{\theta ^{\rho _{1}}}{\Gamma \left( \rho _{1}\right) } t^{\rho _{1}-1} e^{-\theta t}+b_{2} \frac{\theta ^{\mu _{1}}}{\Gamma \left( \mu _{1}\right) } t^{\mu _{1}-1} e^{-\theta t}\right] d t=0 \end{aligned}$$
(2.8)

and

$$\begin{aligned} \int _{0}^{x}\left[ b_{0} \frac{\theta ^{\alpha _{2}}}{\Gamma \left( \alpha _{2}\right) } t^{\alpha _{2}-1} e^{-\theta t}+b_{2} \frac{\theta ^{\rho _{2}}}{\Gamma \left( \rho _{2}\right) } t^{\rho _{2}-1} e^{-\theta t}+b_{2} \frac{\theta ^{\mu _{2}}}{\Gamma \left( \mu _{2}\right) } t^{\mu _{2}-1} e^{-\theta t}\right] d t=0. \end{aligned}$$
(2.9)

On combining Eqs. (2.7), (2.8) and (2.9), we get

$$\begin{aligned} Fb=0, \end{aligned}$$
(2.10)

in which, F= \(\begin{bmatrix} f_{\alpha _{0}} &{} f_{\rho _{0}} &{} f_{\mu _{0}} \\ f_{\alpha _{1}} &{} f_{\rho _{1}} &{} f_{\mu _{1}} \\ f_{\alpha _{2}} &{} f_{\rho _{2}} &{} f_{\mu _{2}} \\ \end{bmatrix}\), b= \(\begin{bmatrix} b_{0}\\ b_{1}\\ b_{2} \end{bmatrix}\) and 0= \(\begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}\) and we define \(f_{\alpha _{i}}=\frac{\theta ^{\alpha _{i}}}{\Gamma \alpha _{i}} \int \limits _{0}^{x} t^{\alpha _{i}-1} e^{-\theta t} d t\), \(f_{\rho _{i}}=\frac{\theta ^{\rho _{i}}}{\Gamma \rho _{i}} \int \limits _{0}^{x} t^{\rho _{i}-1} e^{-\theta t} d t\) and \(f_{\mu _{i}}=\frac{\theta ^{\mu _{i}}}{\Gamma \mu _{i}} \int \limits _{0}^{x} t^{\mu _{i}-1} e^{-\theta t} d t\) for \(i=0,1,2\). Obviously det \(F\ne 0\) shows that \(b=0\) and thereby we conclude that the distribution functions \(B_{0}\), \(B_{1}\) and \(B_{2}\) are linearly independent over the set of real numbers ( see, Titterington et al. 1985). In a similar way, the argument can be extended to the case of any positive integer \(g(\ge 3)\) and thus the result follows. \(\square\)

Result 2.2

The cumulative distribution function (cdf) of the BMLD given in (2.1) has the following form,

$$\begin{aligned} F(x)=\sum _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \gamma _{\alpha _i}(\theta x). \end{aligned}$$
(2.11)

Proof

We have

$$\begin{aligned} \begin{aligned} F(x)&=\int \limits _0^x f(t)\ dt\\&=\sum _{i=0}^{g}\frac{p_i}{\Gamma (\alpha _i)}\int \limits _0^x \theta (t\theta )^{\alpha _i-1}e^{-\theta t}dt\\&=\sum _{i=0}^{g} \left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \gamma _{\alpha _i}(\theta x), \end{aligned} \end{aligned}$$

where \(\gamma (s,t)=\int \limits _0^t x^{s-1}e^{-x}dx\) is the lower incomplete gamma function and \(\gamma _{s}(t)=\frac{\gamma (s,t)}{\Gamma (s)}\). \(\square\)

Remark 2.1

The survival function of the BMLD is obtained as

$$\begin{aligned} {\overline{F}}(x)=1-\sum _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \gamma _{\alpha _i}(\theta x). \end{aligned}$$
(2.12)

Result 2.3

The \(r^{th}\) raw moment about origin of the BMLD has been obtained as

$$\begin{aligned} \mu _r^{\prime }=\sum _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \frac{\Gamma (\alpha _i+r)}{\theta ^r \Gamma (\alpha _i)};\,r=1,2,\cdots \end{aligned}$$
(2.13)

Proof

By definition, we have

$$\begin{aligned} \begin{aligned} \mu _r^{\prime }&=\int \limits _0^\infty \sum _{i=0}^{g}p_i\frac{\theta ^{\alpha _i}}{\Gamma (\alpha _i)} x^{\alpha _i+r-1}e^{-\theta x}dx\\&=\sum _{i=0}^{g}\frac{p_i\theta ^{\alpha _i}}{\Gamma (\alpha _i)} \frac{\Gamma (\alpha _i+r)}{\theta ^{\alpha _i+r}}\\&=\sum _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\frac{ \Gamma (\alpha _i+r)}{\theta ^r \Gamma (\alpha _i)}. \end{aligned} \end{aligned}$$

\(\square\)

Remark 2.2

Mean and variance of BMLD is given by

$$\begin{aligned} E(X)=\sum _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \frac{\alpha _i}{\theta } \end{aligned}$$
(2.14)

and

$$\begin{aligned} \begin{aligned} Var(X)&=\frac{1}{\theta ^2}\sum _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\alpha _{i}\Bigg \{1+\alpha _{i}\\&\quad \quad \quad -\sum _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i\left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\alpha _{i}\Bigg \}. \end{aligned} \end{aligned}$$
(2.15)

Result 2.4

The moments of the BMLD can be calculated recursively through the relationship

$$\begin{aligned} \begin{aligned} \mu ^{'}_{r+1} = \mu ^{'}_{r}\frac{\sum \limits _{i=0}^{g} \frac{\left( {\begin{array}{c}g\\ i\end{array}}\right) }{\Gamma (\alpha _i)}\left( \frac{\theta }{\theta +\beta } \right) ^i\left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\Gamma (\alpha _i+r+1)}{\theta \sum \limits _{i=0}^{g}\frac{\left( {\begin{array}{c}g\\ i\end{array}}\right) }{\Gamma (\alpha _i)} \left( \frac{\theta }{\theta +\beta }\right) ^i\left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \Gamma (\alpha _i+r)}. \end{aligned} \end{aligned}$$
(2.16)

Proof

From (2.13), we have

$$\begin{aligned} \theta ^{r}\mu ^{'}_{r}=\sum \limits _{i=0}^{g}\frac{\left( {\begin{array}{c}g\\ i\end{array}}\right) }{\Gamma (\alpha _i)}\left( \frac{\theta }{\theta +\beta }\right) ^i\left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\Gamma (\alpha _i+r) \end{aligned}$$

and

$$\begin{aligned} \theta ^{r+1}\mu ^{'}_{r+1}=\sum \limits _{i=0}^{g}\frac{\left( {\begin{array}{c}g\\ i\end{array}}\right) }{\Gamma (\alpha _i)}\left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\Gamma (\alpha _i+r+1). \end{aligned}$$
$$\begin{aligned} \begin{aligned} \theta \mu ^{'}_{r+1}\sum \limits _{i=0}^{g}\frac{\left( {\begin{array}{c}g\\ i\end{array}}\right) }{\Gamma (\alpha _i)} \left( \frac{\theta }{\theta +\beta }\right) ^i&\left( \frac{\beta }{\theta +\beta } \right) ^{g-i}\Gamma (\alpha _i+r)\\&=\mu ^{'}_{r}\sum \limits _{i=0}^{g}\frac{\left( {\begin{array}{c}g\\ i\end{array}}\right) }{\Gamma (\alpha _i)} \left( \frac{\theta }{\theta +\beta }\right) ^i\left( \frac{\beta }{\theta +\beta } \right) ^{g-i}\Gamma (\alpha _i+r+1). \end{aligned} \end{aligned}$$

By rearranging the above equation, we get (2.16). \(\square\)

Result 2.5

If X has BMLD, then the moment generating function \(M_X(t)\) has the following form,

$$\begin{aligned} M_X(t)=\sum _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \left( \frac{\theta }{\theta -t} \right) ^{\alpha _i}. \end{aligned}$$

Proof

We have

$$\begin{aligned} \begin{aligned} M_X(t)&=E(e^{tX})\\&=\int \limits _0^\infty e^{tx}f(x)dx\\&=\sum _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\frac{\theta ^{\alpha _i} }{\Gamma (\alpha _i)}\int \limits _0^\infty e^{-(\theta -t)x}x^{\alpha _i-1}dx\\&=\sum _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \left( \frac{\theta }{\theta -t} \right) ^{\alpha _i}. \end{aligned} \end{aligned}$$

\(\square\)

Remark 2.3

The characteristic function of the BMLD is \(\Phi _X(t)=M_X(it)\), where \(i=\sqrt{-1}\) is the unit imaginary number.

3 Certain Measures of Reliability, Inequality, Entropy and Extropy

In this section we derived expressions for some reliability measures such as hazard rate function, reversed hazard rate function, cumulative hazard rate function, vitality function and mean residual life function associated with BMLD. Certain inequality measures, entropy and extropy measures are also obtained.

3.1 Reliability Properties

3.1.1 Hazard Rate Function

Let X denote a lifetime variable with cdf \(F(x)=Pr(X\le x)\) and pdf f(x). Then the hazard rate function(hrf) is given by,

$$\begin{aligned} h(x)=\frac{f(x)}{{\overline{F}}(x)}, \end{aligned}$$
(3.1)

where \({\overline{F}}(x)=1-F(x)\) is the survival function of X. That is, h(x)dx represents the instantaneous chance that an individual will die in the interval \((x,x+dx)\) given that this individual is alive at age x.

3.1.2 Reversed Hazard Rate Function

Let X be a non-negative random variable representing lifetimes of individuals having absolutely continuous distribution function F(x) and pdf f(x). Then the reversed hazard rate function is given by

$$\begin{aligned} r(x)=\frac{f(x)}{F(x)}. \end{aligned}$$
(3.2)

3.1.3 Cumulative Hazard Rate Function

Cumulative hazard rate function is the total number of failure or deaths over an interval of time, and it is defined as

$$\begin{aligned} R(x)=-\log {\overline{F}}(x), \text { where } {\overline{F}}(x) \,\text {is the survival function}. \end{aligned}$$
(3.3)

Clearly R(x) is a non-decreasing function of x satisfying; (a) \(R(0)=0\) and (b) \(\mathop {\lim }\limits _{x \rightarrow \infty }R(x)=\infty\).

Result 3.1

If X has the BMLD with density function, cumulative distribution function and survival function given in Eqs. (2.1), (2.11) and (2.12) respectively, then

(a):

Hazard rate function,

$$\begin{aligned} h(x)=\frac{\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\frac{\theta ^{\alpha _i}}{\Gamma (\alpha _i)}x^{\alpha _i-1}e^{-\theta x}}{1-\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\gamma _{\alpha _i}(\theta x)}. \end{aligned}$$
(3.4)
(b):

Cumulative hazard rate function,

$$\begin{aligned} R(x)=-\log \left[ 1-\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\gamma _{\alpha _i} (\theta x)\right] . \end{aligned}$$
(3.5)
(c):

Reversed hazard rate function,

$$\begin{aligned} r(x)=\frac{\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta } \right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\frac{\theta ^{\alpha _i}}{\Gamma (\alpha _i)}x^{\alpha _i-1}e^{-\theta x}}{\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\gamma _{\alpha _i}(\theta x)}. \end{aligned}$$
(3.6)

Proof

By using (2.1), (2.11) and (2.12) in the equations, \(h(x)=\frac{f(x)}{{{\overline{F}}}(x)}\), \(r(x)=\frac{f(x)}{ F(x)}\) and \(R(x)= -\log {{\overline{F}}} (x),\) the hazard rate function, reversed hazard rate function and cumulative hazard rate function are easily obtained.

The hazard rate function for BMLD is plotted for different values of parameters is given in Fig. 2. \(\square\)

Fig. 2
figure 2

The hrf of BMLD for g = 2 and different values of \(\theta\), \(\beta\), \(\alpha _{0}\), \(\alpha _{1}\), \(\alpha _{2}\)

Full size image

The graphs of the hazard function for various combination of parameters show various shapes including increasing, decreasing, bathtub shape (decreasing -stable-increasing) and upside down bathtub shape. This attractive flexibility of the BMLD hazard rate function highly suitable for non-monotone empirical hazard behaviours which are more likely to be encountered in real life situations.

3.1.4 Vitality Function

If X is a non-negative random variable having an absolutely continuous distribution function F(x) with pdf f(x). The vitality function associated with the random variable X is defined as,

$$\begin{aligned} \nu (x)=E[X|X>x]. \end{aligned}$$
(3.7)

In the reliability context (3.7) can be interpreted as the average life span of components whose age exceeds x. It may be noted that the hazard rate reflects the risk of sudden death within a life span, where as the vitality function provides a more direct measure to describe the failure pattern in the sense that it is expressed in terms of increased average life span.

Result 3.2

The vitality function of BMLD has the following form,

$$\begin{aligned} \nu (x)=\frac{\frac{1}{\theta }\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta } \right) ^{g-i}\alpha _i\Gamma _{\alpha _i+1}( \theta x)}{1-\sum \limits _{i=0}^{g} \left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\gamma _{\alpha _i}(\theta x)}. \end{aligned}$$
(3.8)

Proof

The Eq. (3.7) can also be written as,

$$\begin{aligned} \nu (x)=\frac{1}{{\overline{F}}(x)}\int \limits _x^\infty tf(t)dt. \end{aligned}$$
(3.9)

Now

$$\begin{aligned} \begin{aligned} \int \limits _x^\infty tf(t)dt&=\int \limits _x^\infty t\sum _{i=0}^{g}p_i \frac{\theta ^{\alpha _i}}{\Gamma (\alpha _i)}t^{\alpha _i-1}e^{-\theta t}dt\\&=\frac{1}{\theta }\displaystyle \sum _{i=0}^{g}\frac{p_i}{\Gamma (\alpha _i)} \Gamma (\alpha _i+1, \theta x)\\&=\frac{1}{\theta }\displaystyle \sum _{i=0}^{g} \left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \alpha _i\Gamma _{\alpha _i+1}( \theta x), \end{aligned} \end{aligned}$$
(3.10)

where \(\Gamma (s,t)=\int \limits _x^\infty x^{s-1}e^{-x}dx\) is the upper incomplete gamma function and \(\Gamma _{s}(t)=\frac{\Gamma (s,t)}{\Gamma (s)}.\) Substituting (3.10) and (2.12) in (3.9), we get the required result. \(\square\)

3.1.5 Mean Residual Life Function

Mean residual life function or remaining life expectancy function at age x is defined to be the expected remaining life given survival to age x. For a continuous random variable X, with \(E(X)<\infty\), then the mean residual life function (MRLF) is defined as the Borel measurable function,

$$\begin{aligned} \begin{aligned} m(x)&=E[X-x|X>x]\\&=\frac{1}{{\overline{F}}(x)}\int \limits _x^\infty {\overline{F}}(t)dt. \end{aligned} \end{aligned}$$
(3.11)

MRLF is sometimes considered as a superior measure to describe the failure pattern as compared to hazard rate function since the former focuses attention on the average lifetime over a period of time while the latter on instantaneous failure at a point of time. Also MRLF can be expressed in terms of vitality function. That is, Eq. (3.9) can also be written as

$$\begin{aligned} \begin{aligned} \nu (x)&=\frac{1}{{\overline{F}}(x)}\int \limits _x^\infty {\overline{F}}(t)dt+x\\&=m(x)+x. \end{aligned} \end{aligned}$$
(3.12)

Result 3.3

The mean residual life function of BMLD has the following form,

$$\begin{aligned} m(x)=\frac{\frac{1}{\theta }\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta } \right) ^{g-i} \alpha _i\Gamma _{\alpha _i+1}(\theta x)}{1-\sum \limits _{i=0}^{g} \left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\gamma _{\alpha _i}(\theta x)}-x. \end{aligned}$$
(3.13)

Proof

Substituting (3.8) in (3.12), we get (3.13). \(\square\)

3.2 Inequality Measures

Lorenz and Bonferroni curves are income inequality measures that are widely useful and applicable to some other areas including reliability, demography, medicine and insurance (see, Bonferroni 1930). Also Zenga curve introduced by Zenga (2007) is another widely used inequality measure. In this section, we will derive Lorenz, Bonferroni and Zenga curves for the BMLD. The Lorenz, Bonferroni and Zenga curves are respectively given as

\(L_{F}(x) = \frac{\int \limits _{0}^x t f(t) dt }{E(X)}\), \(B_{F}(x) = \frac{\int \limits _{0}^x t f(t) dt }{ F(X)E(X)}\) and \(A_{F}(x)=1-\frac{\mu ^{-}(x)}{\mu ^{+}(x)}\), where \(\mu ^{-}(x)=\frac{\int \limits _{0}^x t f(t) dt }{ F(X)}\) and \(\mu ^{+}(x)=\frac{\int \limits _{x}^\infty t f(t) dt }{ {{\overline{F}}}(X)}.\)

Result 3.4

If X has the BMLD with density function, cumulative distribution function and survival function given in Eqs. (2.1), (2.11) and (2.12) respectively, then

(a):

Lorenz curve,

$$\begin{aligned} L_F(x)=\frac{\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\alpha _i\gamma _{\alpha _i+1}(\theta x)}{\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\alpha _i}. \end{aligned}$$
(3.14)
(b):

Bonferroni curve,

$$\begin{aligned} \begin{aligned} B_{F}(x)&=\frac{\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\alpha _i\gamma _{\alpha _i+1}(\theta x)}{\left\{ \sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\alpha _i \right\} \left\{ \sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \gamma _{\alpha _i}(\theta x)\right\} }. \end{aligned} \end{aligned}$$
(3.15)
(c):

Zenga curve,

$$\begin{aligned} \begin{aligned} A_{F}(x)=1-&\left\{ \frac{\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\alpha _i\gamma _{\alpha _i+1}(\theta x)}{\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \gamma _{\alpha _i}(\theta x)}\right. \\&\quad \times \left. \frac{\Big (1-\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i} \gamma _{\alpha _i}(\theta x)\Big )}{\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\alpha _i\Gamma _{\alpha _i+1}(\theta x)}\right\} . \end{aligned} \end{aligned}$$
(3.16)

Proof

  1. (a)

    By definition

    $$\begin{aligned} \begin{aligned} L_{F}(x)&= \frac{\int \limits _{0}^x t f(t) dt }{E(X)}. \end{aligned} \end{aligned}$$
    (3.17)

    Now

    $$\begin{aligned} \begin{aligned} \int \limits _{ 0 }^x t f(t) dt&= \frac{1}{\theta }\sum \limits _{i=0}^{g} \frac{p_{i}}{\Gamma (\alpha _{i})} \gamma ({\alpha _{i}+1},\theta x)\\&=\frac{1}{\theta }\sum \limits _{i=0}^{g}\left( {\begin{array}{c}g\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{g-i}\alpha _i\gamma _{\alpha _i+1}(\theta x) . \end{aligned} \end{aligned}$$
    (3.18)

    By using (3.18) and (2.14) in (3.17), we get (3.14)

  2. (b)

    By definition

    $$\begin{aligned} \begin{aligned} B_{F}(x) = \frac{\int \limits _{0}^x t f(t) dt }{ F(X)E(X)}. \end{aligned} \end{aligned}$$

    By using (3.18), (2.14) and (2.11), we get (3.15)

  3. (c)

    By definition

    $$\begin{aligned} \begin{aligned} A(x)&=1-\frac{\mu ^{-}(x)}{\mu ^{+}(x)}.\\ \end{aligned} \end{aligned}$$
    (3.19)

By using (3.18) and (2.11), we get \(\mu ^{-}(x)\) and by definition \(\mu ^{+}(x)=\frac{\int \limits _{x}^\infty t f(t) dt }{ {{\overline{F}}}(X)}=\nu (x).\) which is given in (3.8). Substituting \(\mu ^{-}(x)\) and \(\mu ^{+}(x)\) in (3.19), we get (3.16). \(\square\)

3.3 Entropy

Here we derive the expressions for Rényi Entropy and Havrda-Charv\(\acute{a}\)t-Tsallis (HCT) entropy. We are also deriving the expression for a recently developed uncertainty measure, namely extropy and its residual version. For mathematical simplicity these results are derived for \(g=2\).

The concept of entropy was introduced and extensively studied by Shannon (1948). Let X be a non-negative random variable admitting an absolutely continuous cdf F(x) and with pdf f(x). Then the Shannon’s entropy associated with X is defined as \(H(X) = - \int \limits _0^\infty {f(x)\ \log f(x)\ dx}.\) It gives the expected uncertainty contained in f(x) about the predictability of an outcome of X.

Several generalizations of Shannon’s entropy have been put forward by researchers. A generalization which has received much attention subsequently is due to Rényi (1959). The Rényi’s entropy of order \(\nu\) is defined as

$$\begin{aligned} H^{\nu }(X) = \frac{1}{1-\nu } \log \int \limits _{ 0 }^\infty f^{\nu }(x)\ dx,\ \text {for} \ \nu >0, \nu \ne 1. \end{aligned}$$

Another important generalization of Shannon’s entropy is the Havrda-Charv\(\acute{a}\)t-Tsallis (HCT) entropy. It was introduced by Havrda and Charv\(\acute{a}\)t (1967) and further developed by Tsallis (1988) and is given by,

$$\begin{aligned} H^{\xi }(X) = \frac{1}{\xi -1}\left( 1-\int \limits _{ 0 }^\infty f^{\xi }(x)\ dx \right) , \ \text {for} \ \xi >0, \xi \ne 1. \end{aligned}$$

Result 3.5

The R\(\acute{e}\)nyi entropy function for BMLD has the following form,

$$\begin{aligned} \begin{aligned} H^{\nu }(x)&=\frac{1}{1-\nu }\text {log} \left\{ \left( \frac{\beta ^{2}\theta ^{\alpha _{0}}}{(\theta +\beta )^2\Gamma (\alpha _{0})}\right) ^\nu \displaystyle \sum _{j=0}^{\nu } \left( {\begin{array}{c}\nu \\ j\end{array}}\right) \displaystyle \sum _{k=0}^{j}\left( {\begin{array}{c}j\\ k\end{array}}\right) \left( \frac{2\theta ^{\alpha _{1}-\alpha _{2}-1}\Gamma (\alpha _2)}{\Gamma (\alpha _1)}\right) ^k\right. \\&\left. \left( \frac{\theta ^{\alpha _{2}-\alpha _{0}+2}\Gamma (\alpha _0)}{\beta ^{2}\Gamma (\alpha _2)}\right) ^j \right. \\&\times \left. \frac{\Gamma \big ((\alpha _{1}-\alpha _{2})k+(\alpha _{2}-\alpha _{0})j+(\alpha _{0}-1)\nu +1\big )}{(\nu \theta )^{(\alpha _{1}-\alpha _{2})k+(\alpha _{2}-\alpha _{0})j+(\alpha _{0}-1)\nu +1}}\right\} . \end{aligned} \end{aligned}$$
(3.20)

Proof

Using the definition of Rényi entropy, we have

$$\begin{aligned} \begin{aligned} H^{\nu }(x)=&\frac{1}{(1-\nu )} \log \int \limits _ 0^ \infty \left( \frac{1}{(\theta +\beta )^2}\right) ^\nu \left\{ \frac{\beta ^{2}\theta ^{\alpha _{0}}x^{\alpha _{0}-1}}{\Gamma (\alpha _{0})}\right. \\&\left. +\frac{2\theta ^{\alpha _{1}+1}\beta x^{\alpha _{1}-1}\Gamma (\alpha _{2}) +\theta ^{\alpha _{2}+2 }x^{\alpha _{2}-1}\Gamma (\alpha _{1}) }{\Gamma (\alpha _{1})\Gamma (\alpha _{2})}\right\} ^\nu e^{-\nu \theta x}dx \\ =&\frac{1}{(1-\nu )} \log \left\{ \frac{1}{(\theta +\beta )^{2\nu }}\left( \frac{\beta ^{2}\theta ^{\alpha _{0}}}{\Gamma (\alpha _{0})}\right) ^\nu \sum _{j=0}^{\nu } \left( {\begin{array}{c}\nu \\ j\end{array}}\right) \right. \\&\left. \int \limits _0^\infty \left\{ \frac{2\theta ^{\alpha _{1}-\alpha _{0}+1} \Gamma (\alpha _{0})x^{\alpha _{1}-\alpha _{0}}}{\beta \Gamma (\alpha _{1})}+\frac{\theta ^{\alpha _{2}-\alpha _{0}+2}\Gamma (\alpha _{0})x^{\alpha _{2}-\alpha _{0}}}{\beta ^{2} \Gamma (\alpha _{2})}\right\} ^{j}x^{(\alpha _{0}-1)\nu }e^{-\nu \theta x}dx\right\} \\ \end{aligned} \\ \begin{aligned}&=\frac{1}{(1-\nu )} \log \left\{ \left( \frac{\beta ^{2}\theta ^{\alpha _{0}}}{(\theta +\beta )^2\Gamma (\alpha _{0})}\right) ^\nu \sum _{j=0}^{\nu } \left( {\begin{array}{c}\nu \\ j\end{array}}\right) \sum _{k=0}^{j} \left( {\begin{array}{c}j\\ k\end{array}}\right) \left( \frac{2\theta ^{\alpha _{1}-\alpha _{2}-1}\Gamma (\alpha _{2})}{\Gamma (\alpha _{1})}\right) ^k \right. \\&\left. \left( \frac{\theta ^{\alpha _{2}-\alpha _{0}+2}\Gamma (\alpha _{0})}{\beta ^{2}\Gamma (\alpha _{2})}\right) ^j \int \limits _0^\infty x^{(\alpha _{1} -\alpha _{2})k+(\alpha _{2}-\alpha _{0})j+(\alpha _{0}-1)\nu } e^{-\nu \theta x} dx\right\} \\&=\frac{1}{1-\nu }\text {log} \left\{ \left( \frac{\beta ^{2}\theta ^{\alpha _{0}}}{(\theta +\beta )^2\Gamma (\alpha _{0})}\right) ^\nu \displaystyle \sum _{j=0}^{\nu } \left( {\begin{array}{c}\nu \\ j\end{array}}\right) \displaystyle \sum _{k=0}^{j}\left( {\begin{array}{c}j\\ k\end{array}}\right) \left( \frac{2\theta ^{\alpha _{1} -\alpha _{2}-1}\Gamma (\alpha _2)}{\Gamma (\alpha _1)}\right) ^k \left( \frac{\theta ^{\alpha _{2}-\alpha _{0}+2}\Gamma (\alpha _0)}{\beta ^{2} \Gamma (\alpha _2)}\right) ^j \right. \\&\left. \frac{\Gamma \left( (\alpha _{1}-\alpha _{2})k+(\alpha _{2}-\alpha _{0})j +(\alpha _{0}-1)\nu +1\right) }{(\nu \theta )^{(\alpha _{1}-\alpha _{2})k+(\alpha _{2}-\alpha _{0})j+(\alpha _{0}-1)\nu +1}}\right\} . \end{aligned} \end{aligned}$$

\(\square\)

Remark 3.1

When \(\nu \rightarrow 1\) in (3.20), it reduces to Shannon entropy.

Result 3.6

The Havrda-Charv\(\acute{a}\)t-Tsallis entropy of order \(\rho\), for BMLD has the following form,

$$\begin{aligned} \begin{aligned} H^{\xi }(x)=&\frac{1}{(\xi -1)}\left\{ 1- \left( \frac{\beta ^{2}\theta ^{\alpha _{0}}}{(\theta +\beta )^2\Gamma (\alpha _{0})} \right) ^\xi \displaystyle \sum _{j=0}^{\xi } \left( {\begin{array}{c}\xi \\ j\end{array}}\right) \displaystyle \sum _{k=0}^{j}\left( {\begin{array}{c}j\\ k\end{array}}\right) \left( \frac{2\theta ^{\alpha _{1} -\alpha _{2}-1}\Gamma (\alpha _2)}{\Gamma (\alpha _1)}\right) ^k \right. \\&\left. \left( \frac{\theta ^{\alpha _{2}-\alpha _{0}+2}\Gamma (\alpha _0)}{\beta ^{2}\Gamma (\alpha _2)}\right) ^j \frac{\Gamma \left( (\alpha _{1}-\alpha _{2})k+(\alpha _{2}-\alpha _{0})j+(\alpha _{0}-1)\xi +1\right) }{(\xi \theta )^{(\alpha _{1}-\alpha _{2})k+(\alpha _{2}-\alpha _{0})j+(\alpha _{0}-1)\xi +1}}\right\} . \end{aligned} \end{aligned}$$
(3.21)

Proof

Proof is similar to that of Result 3.5 and hence omitted. \(\square\)

3.4 Extropy

Recently, Lad et al. (2015) defined statistically the term extropy as a potential measure of uncertainty, an alternative measure of Shannon entropy. For a random variable X, its extropy is defined as

$$\begin{aligned} J(X) = - \frac{1}{2}\int \limits _0^\infty {f^{2}(x)dx}. \end{aligned}$$
(3.22)

In statistical point of view, the term extropy is used to score the forecasting distributions under the total log scoring rule.

A serious difficulty involved in the application of Shannon’s entropy is that, it is not applicable to a system which has survived for some units of time. In this situation, Ebrahimi (1996) proposed the concept of residual entropy. As in the scenario of introducing the concept of residual entropy, Qiu and Jia (2018) introduced residual extropy to measure the residual uncertainty of a random variable. For a random variable X, its residual extropy is defined as (see, Qiu and Jia 2018)

$$\begin{aligned} J(f;t) = \frac{-1}{2{{\overline{F}}}^{2}(t)}\int \limits _t^\infty {f^{2}(x)dx}, \end{aligned}$$
(3.23)

Result 3.7

The extropy function for BMLD has the following form,

$$\begin{aligned} \begin{aligned} J(X)=&\frac{-1}{2(\theta +\beta )^4}\Bigg \{\frac{\Gamma (2\alpha _{0}-1)}{\Gamma ^2(\alpha _{0})}\beta ^{4}\theta 2^{1-2\alpha _{0}}+\frac{\Gamma (2\alpha _{1}-1)}{\Gamma ^2(\alpha _{1})}\beta ^{2}\theta ^{3}2^{3-2\alpha _{1}}\\&+\frac{\Gamma (2\alpha _{2}-1)}{\Gamma ^2(\alpha _{2})}\theta ^{5}2^{1-2\alpha _{2}} +\frac{\Gamma (\alpha _{0}+\alpha _{1}-1)}{\Gamma (\alpha _{0})\Gamma (\alpha _{1})} \beta ^{3}\theta ^{2}2^{3-\alpha _{0}-\alpha _{1}}\\&+\frac{\Gamma (\alpha _{1}+\alpha _{2}-1)}{\Gamma (\alpha _{1})\Gamma (\alpha _{2})} \beta \theta ^{4}2^{3-\alpha _{1}-\alpha _{2}}+\frac{\Gamma (\alpha _{0}+\alpha _{2}-1)}{\Gamma (\alpha _{0})\Gamma (\alpha _{2})}\beta ^{2}\theta ^{3}2^{2-\alpha _{0}-\alpha _{2}}\Bigg \}. \end{aligned} \end{aligned}$$
(3.24)

Proof

By definition of J(X),

$$\begin{aligned} \begin{aligned} J(X)=&\frac{-1}{2(\theta +\beta )^4}\int \limits _{0}^{\infty } \Bigg \{\frac{\beta ^{2}\theta ^{\alpha _{0}}x^{\alpha _{0}-1}}{\Gamma (\alpha _{0})} +\frac{2\beta \theta ^{\alpha _{1}+1}x^{\alpha _{1}-1}}{\Gamma (\alpha _{1})} +\frac{\theta ^{\alpha _{2}+2}x^{\alpha _{2}-1}}{\Gamma (\alpha _{2})}\Bigg \}^2 e^{-2\theta x} dx\\&= \frac{-1}{2(\theta +\beta )^4} \Bigg \{\frac{\beta ^{4} \theta ^{2\alpha _{0}}}{\Gamma ^{2}(\alpha _{0})}\int \limits _{0}^{\infty }x^{2\alpha _{0}-2}e^{-2\theta x}dx +\frac{4\beta ^{2} \theta ^{2\alpha _{1}+2}}{\Gamma ^{2}(\alpha _{1})}\int \limits _{0}^{\infty }x^{2\alpha _{1}-2}e^{-2\theta x}dx\\&+\frac{\theta ^{2\alpha _{2}+4}}{\Gamma ^{2}(\alpha _{2})} \int \limits _{0}^{\infty }x^{2\alpha _{2}-2}e^{-2\theta x}dx+\frac{4\beta ^{3}\theta ^{\alpha _{0}+\alpha _{1}+1}}{\Gamma (\alpha _{0})\Gamma (\alpha _{1})}\int \limits _{0}^{\infty }x^{\alpha _{0}+\alpha _{1}-2}e^{-2\theta x}dx\\&+\frac{4\beta \theta ^{\alpha _{1}+\alpha _{2}+3}}{\Gamma (\alpha _{1})\Gamma (\alpha _{2})}\int \limits _{0}^{\infty }x^{\alpha _{1}+\alpha _{2}-2}e^{-2\theta x}dx+\frac{2\beta ^{2}\theta ^{\alpha _{0}+\alpha _{2}+2}}{\Gamma (\alpha _{0})\Gamma (\alpha _{2})}\int \limits _{0}^{\infty }x^{\alpha _{0}+\alpha _{2}-2}e^{-2\theta x}dx\Bigg \}. \end{aligned} \end{aligned}$$
(3.25)

By simplifying (3.25), we get (3.24).\(\square\)

Result 3.8

The residual extropy function for BMLD has the following form,

$$\begin{aligned} \begin{aligned} J(f;t)=&\frac{-1}{2\Bigg (1-\sum \limits _{i=0}^{2}\left( {\begin{array}{c}2\\ i\end{array}}\right) \left( \frac{\theta }{\theta +\beta }\right) ^i \left( \frac{\beta }{\theta +\beta }\right) ^{2-i} \gamma _{\alpha _i}(\theta t)\Bigg )^2(\theta +\beta )^4}\Bigg \{\frac{\Gamma (2\alpha _{0}-1,2\theta t)}{\Gamma ^2(\alpha _{0})}\beta ^{4}\theta 2^{1-2\alpha _{0}}\\&+\frac{\Gamma (2\alpha _{1}-1,2\theta t)}{\Gamma ^2(\alpha _{1})}\beta ^{2}\theta ^{3}2^{3-2\alpha _{1}}+\frac{\Gamma (2\alpha _{2}-1,2\theta t)}{\Gamma ^2(\alpha _{2})}\theta ^{5}2^{1-2\alpha _{2}}\\&+\frac{\Gamma (\alpha _{0}+\alpha _{1}-1,2\theta t)}{\Gamma (\alpha _{0})\Gamma (\alpha _{1})}\beta ^{3}\theta ^{2}2^{3-\alpha _{0}-\alpha _{1}}+\frac{\Gamma (\alpha _{1}+\alpha _{2}-1,2\theta t)}{\Gamma (\alpha _{1})\Gamma (\alpha _{2})}\beta \theta ^{4}2^{3-\alpha _{1}-\alpha _{2}}\\&+\frac{\Gamma (\alpha _{0}+\alpha _{2}-1,2\theta t)}{\Gamma (\alpha _{0})\Gamma (\alpha _{2})}\beta ^{2}\theta ^{3}2^{2-\alpha _{0}-\alpha _{2}}\Bigg \},\,\text {for}\,\ g=2. \end{aligned} \end{aligned}$$
(3.26)

Proof

Proof is similar to that of Result 3.7 and hence omitted. \(\square\)

4 Estimation and Ιnference

Estimation of unknown parameters of a distribution is essential in all areas of statistics. In this section, first we obtain the maximum likelihood estimates (MLEs) of the parameters of BMLD for a given random sample. The Fisher information matrix is also computed in this section for the interval estimation. For mathematical simplicity all these inferences are made for \(g=2\).

4.1 Maximum Likelihood Estimation

The method of maximum likelihood is the most frequently used technique for parameter estimation. It’s success stems from its many desirable properties including consistency, asymptotic efficiency, invariance property as well as intuitive appeal.

Let \(X_1, X_2,..., X_n\) be observed values from the BMLD with unknown parameter vector \({\textcircled {{H}}}= \Big (\theta , \beta , \alpha _{0}, \alpha _{1}, \alpha _{2}\Big )\). The likelihood function is given by

$$\begin{aligned} \begin{aligned} l \big ({\textcircled { {H}}}\big ) =&\prod _{i=1}^{n} f_{i} \Big (x; \theta , \beta , \alpha _{0}, \alpha _{1}, \alpha _{2} \Big )\\ =&\left( \frac{1}{(\theta +\beta )^2} \right) ^{n} e^{-\theta \sum \limits _{i=1}^{n}x_{i}} \prod _{i=1}^{n} \Big (\frac{\beta ^{2}\theta ^{\alpha _{0}}x_{i}^{\alpha _0-1}}{\Gamma (\alpha _{0})} +\frac{2\beta \theta ^{\alpha _{1}+1}x_{i}^{\alpha _1-1}}{\Gamma (\alpha _{1})} +\frac{\theta ^{\alpha _{2}+2}x_{i}^{\alpha _2-1}}{\Gamma (\alpha _{2})}\Big ). \end{aligned} \end{aligned}$$

The partial derivatives of \(\log l\big ({\textcircled { {H}}}\big )\) with respect to the parameters are given by

$$\begin{aligned} \begin{aligned}&\frac{\partial \log l}{\partial \theta }= -\frac{2n}{\theta +\beta }-\sum \limits _{i=1}^{n}x_{i}+\frac{1}{\theta }\sum \limits _{i=1}^{n}\left( \frac{\alpha _{0}A_i+(\alpha _1+1)B_i+(\alpha _2+2)C_i}{A_i+B_i+C_i} \right) ,\\&\frac{\partial \log l}{\partial \beta }= -\frac{2n}{\theta +\beta }+ \frac{1}{\beta }\sum \limits _{i=1}^{n}\left( \frac{2A_i+B_i}{A_i+B_i+C_i} \right) ,\\&\frac{\partial \log l}{\partial \alpha _{0}}= \sum \limits _{i=1}^{n}\left( \frac{A_i\Big (\log (\theta x_i)-\psi (\alpha _0)\Big )}{A_i+B_i+C_i} \right) ,\\&\frac{\partial \log l}{\partial \alpha _{1}}= \sum \limits _{i=1}^{n}\left( \frac{B_i\Big (\log (\theta x_i)-\psi (\alpha _1)\Big )}{A_i+B_i+C_i} \right) \end{aligned} \end{aligned}$$
(4.1)

and

$$\begin{aligned} \begin{aligned} \frac{\partial \log l}{\partial \alpha _{2}}= \sum \limits _{i=1}^{n}\left( \frac{C_i\Big (\log (\theta x_i)-\psi (\alpha _2)\Big )}{A_i+B_i+C_i} \right) , \end{aligned} \end{aligned}$$
(4.2)

where \(A_{i}=\frac{\beta ^{2}\theta ^{\alpha _0}x_{i}^{\alpha _0-1}}{\Gamma (\alpha _{0})}\), \(B_{i}=\frac{2\beta \theta ^{\alpha _1+1}x_{i}^{\alpha _1-1}}{\Gamma (\alpha _{1})}\) and \(C_{i}=\frac{\theta ^{\alpha _2+2}x_{i}^{\alpha _2-1}}{\Gamma (\alpha _{2})}.\)

The MLE of the parameters \({\textcircled { {H}}}= \Big (\theta , \beta , \alpha _{0}, \alpha _{1}, \alpha _{2}\Big )\) are obtained by solving the equations \(\frac{\partial \log l}{\partial \theta }=0\), \(\frac{\partial \log l}{\partial \beta }=0\), \(\frac{\partial \log l}{\partial \alpha _{0}}=0\), \(\frac{\partial \log l}{\partial \alpha _{1}}=0\), \(\frac{\partial \log l}{\partial \alpha _{2}}=0\) simultaneously. This can only be achieved by numerical optimization technique such as the Newton-Raphson method and Fisher’s scoring algorithm using mathematical packages like R, Mathematica etc. To avoid local minima problem, we first obtain the moment estimators of the parameters of BMLD and setting these estimators as the initial values to obtain MLEs of the parameters of BMLD.

4.2 Fisher Information Matrix

In order to determine the confidence interval for the parameters of BMLD, we need to find the expected Fisher information matrix \(I({\textcircled { {H}}})\). The expected Fisher information matrix of BMLD is given by,

$$\begin{aligned} I({\textcircled { {H}}}) = \begin{pmatrix} -E\left( \frac{\partial ^{2} \log l}{\partial \theta ^{2}}\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \theta \partial \beta }\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \theta \partial \alpha _0}\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \theta \partial \alpha _1}\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \theta \partial \alpha _2}\right) \\ -E\left( \frac{\partial ^{2} \log l}{\partial \beta \partial \theta }\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \beta ^{2}}\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \beta \partial \alpha _0}\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \beta \partial \alpha _1}\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \beta \partial \alpha _2}\right) \\ -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _0 \partial \theta }\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _0 \partial \beta }\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _0^{2}}\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _0 \partial \alpha _1}\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _0 \partial \alpha _2}\right) \\ -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _1 \partial \theta }\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _1 \partial \beta }\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _1 \partial \alpha _0}\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _1^{2}}\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _1 \partial \alpha _2}\right) \\ -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _2 \partial \theta }\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _2 \partial \beta }\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _2 \partial \alpha _0}\right) &{} -E\left( \frac{\partial ^{2} \log l}{\partial \alpha _2 \partial \alpha _1}\right) &{} -E(\frac{\partial ^{2} \log l}{\partial \alpha _2^{2}})\\ \end{pmatrix} \end{aligned}$$

The expected Fisher information can be approximated by the observed Fisher information matrix \(J\widehat{({\textcircled { {H}}})}\) given by,

$$\begin{aligned} J\widehat{({\textcircled { {H}}})}= \begin{pmatrix} -\frac{\partial ^{2} \log l}{\partial \theta ^{2}} &{} -\frac{\partial ^{2} \log l}{\partial \theta \partial \beta } &{} -\frac{\partial ^{2} \log l}{\partial \theta \partial \alpha _0} &{} -\frac{\partial ^{2} \log l}{\partial \theta \partial \alpha _1} &{} -\frac{\partial ^{2} \log l}{\partial \theta \partial \alpha _2}\\ -\frac{\partial ^{2} \log l}{\partial \beta \partial \theta } &{} -\frac{\partial ^{2} \log l}{\partial \beta ^{2}} &{} -\frac{\partial ^{2} \log l}{\partial \beta \partial \alpha _0} &{} -\frac{\partial ^{2} \log l}{\partial \beta \partial \alpha _1} &{} -\frac{\partial ^{2} \log l}{\partial \beta \partial \alpha _2}\\ -\frac{\partial ^{2} \log l}{\partial \alpha _0 \partial \theta } &{} -\frac{\partial ^{2} \log l}{\partial \alpha _0 \partial \beta } &{} -\frac{\partial ^{2} \log l}{\partial \alpha _0^{2}} &{} -\frac{\partial ^{2} \log l}{\partial \alpha _0 \partial \alpha _1} &{} -\frac{\partial ^{2} \log l}{\partial \alpha _0 \partial \alpha _2}\\ -\frac{\partial ^{2} \log l}{\partial \alpha _1 \partial \theta } &{} -\frac{\partial ^{2} \log l}{\partial \alpha _1 \partial \beta } &{} -\frac{\partial ^{2} \log l}{\partial \alpha _1 \partial \alpha _0}&{} -\frac{\partial ^{2} \log l}{\partial \alpha _1^{2}} &{} -\frac{\partial ^{2} \log l}{\partial \alpha _1 \partial \alpha _2}\\ -\frac{\partial ^{2} \log l}{\partial \alpha _2 \partial \theta } &{} -\frac{\partial ^{2} \log l}{\partial \alpha _2 \partial \beta } &{} -\frac{\partial ^{2} \log l}{\partial \alpha _2 \partial \alpha _0} &{} -\frac{\partial ^{2} \log l}{\partial \alpha _2 \partial \alpha _1} &{} -\frac{\partial ^{2} \log l}{\partial \alpha _2^{2}}\\ \end{pmatrix} \end{aligned}$$

That is,

$$\begin{aligned} \lim \limits _{n \rightarrow \infty } \frac{1}{n}J\widehat{({\textcircled { {H}}})}= I({\textcircled { {H}}}). \end{aligned}$$

For large n, the following approximation can be used,

$$\begin{aligned} J\widehat{({\textcircled { {H}}})}=n I({\textcircled { {H}}}) \end{aligned}$$

The elements of \(J\widehat{({\textcircled { {H}}})}\) are given in APPENDIX.

4.3 Asymptotic Confidence Interval

Here we present the asymptotic confidence intervals for the parameters of BMLD. Let \(\widehat{{\textcircled { {H}}}}=\Big ({\widehat{\theta }}, {\widehat{\beta }}, \widehat{\alpha _0}, \widehat{\alpha _1}, \widehat{\alpha _2}\Big )\) be the maximum likelihood estimator of \({\textcircled { {H}}}=\Big (\theta , \beta , \alpha _0, \alpha _1, \alpha _2\Big )\). Under the usual regularity conditions and that the parameters are in the interior of the parameter space, but not on the boundary, we have \(\sqrt{n} ({\textcircled { {H}}} - \widehat{{\textcircled { {H}}}}) \mathop \rightarrow \limits ^d N_{2}({\underline{0}},I^{-1}({\textcircled { {H}}}))\), where \(I({\textcircled { {H}}})\) is the expected Fisher information matrix. The asymptotic behaviour is still valid if \(I({\textcircled { {H}}})\) is replaced by the observed Fisher information matrix \(J\widehat{({\textcircled { {H}}})}\). The multivariate normal distribution, \(N_{5}\Big ({\underline{0}},I^{-1}({\textcircled { {H}}}) \Big )\) with mean vector \({\underline{0}}=\Big (0, 0, 0, 0, 0\Big )^{\tau }\) can be used to construct confidence interval for the parameters. The approximate \(100(1-\varphi )\%\) two-sided confidence intervals for \(\theta , \beta , \alpha _0, \alpha _1,\) and \(\alpha _2\) are respectively given by, \({\widehat{\theta }} \pm Z_{\frac{\varphi }{2}}\sqrt{I_{\theta \theta }^{-1}({\hat{\theta }}) }\), \({\widehat{\beta }} \pm Z_{\frac{\varphi }{2}}\sqrt{I_{\beta \beta }^{-1}({\hat{\beta }}) },\) \(\widehat{\alpha _0} \pm Z_{\frac{\varphi }{2}}\sqrt{I_{\alpha _{0} \alpha _{0}}^{-1}({\hat{\alpha }}_{0}) },\) \(\widehat{\alpha _1} \pm Z_{\frac{\varphi }{2}}\sqrt{I_{\alpha _{1} \alpha _{1}}^{-1}({\hat{\alpha }}_{1})}\) and \(\widehat{\alpha _2} \pm Z_{\frac{\varphi }{2}}\sqrt{I_{\alpha _{2} \alpha _{2}}^{-1}({\hat{\alpha }}_{2})}\) , where \(I_{\theta \theta }^{-1}({\hat{\theta }})\), \(I_{\beta \beta }^{-1}({\hat{\beta }})\), \(I_{\alpha _{0} \alpha _{0}}^{-1}({\hat{\alpha }}_{0})\), \(I_{\alpha _{1} \alpha _{1}}^{-1}({\hat{\alpha }}_{1})\), \(I_{\alpha _{2} \alpha _{2}}^{-1}({\hat{\alpha }}_{2})\) are diagonal elements of \(J^{-1}\widehat{({\textcircled { {H}}})}\) and \(Z_{\frac{\varphi }{2}}\) is the upper \(\frac{\varphi }{2}^{th}\) percentile of a standard normal distribution.

5 Simulation Study

Here we perform a simulation study to investigate the performance of maximum likelihood estimators of parameters of BMLD. As the model is a general model, we take \(g=2\) in (2.1) and do the Monte Carlo Simulation. The estimates were calculated for true values of parameters (\(\theta =1.5\), \(\beta =3\), \(\alpha _{0}=0.6\), \(\alpha _{1}=1.9\) and \(\alpha _{2}= 1.7\)) and (\(\theta =0.5\), \(\beta =0.01\), \(\alpha _{0}=1.5\), \(\alpha _{1}=1.3\) and \(\alpha _{2}= 1\)) for N = 1000 samples of sizes 25,50,100,200,400 and 800 and the following quantities are computed.

  1. 1.

    Mean of the MLEs, \(\widehat{{\textcircled { {H}}}}\) of parameters \({\textcircled { {H}}}=\Big (\theta , \beta , \alpha _0, \alpha _1, \alpha _2\Big )\) ,

    $$\begin{aligned} \widehat{{\textcircled { {H}}}} =\frac{1}{N}\sum \limits _{i=1}^{N}{\widehat{{\textcircled { {H}}}}_{i}}. \end{aligned}$$
  2. 2.

    Average absolute bias of MLEs of parameters,

    $$\begin{aligned} Bias({\textcircled { {H}}}) = \frac{1}{N}\sum \limits _{i=1}^{N}(\widehat{{\textcircled { {H}}}}_{i}-{\textcircled { {H}}}). \end{aligned}$$
  3. 3.

    Root Mean Square Error (RMSE) of MLEs of parameters:

    $$\begin{aligned} RMSE({\textcircled { {H}}}) =\sqrt{\frac{1}{N}\sum \limits _{i=1}^{N}(\widehat{ {\textcircled { {H}}}}_{i}-{\textcircled { {H}}})^{2}}. \end{aligned}$$

The simulation results are presented in Table 1. From Table 1, one can infer that estimates are quite stable and more precisely close to the true parameter values. Also the estimated biases, MSEs and RMSEs are decreasing when the sample size n is increasing. These results reveal the consistency property of the MLEs.

Table 1 The simulation results for the corresponding values of the parameters
Full size table

6 Data Analysis

In this section we illustrate the superiority of BMLD as compared to some other distributions using three real data sets. The first one is the lifetimes of 50 devices provided by Aarset (1987). Second one is the strength of glass fibres of length 1.5 cm from the National Physical Laboratory in England (see, Smith and Naylor 1987). And the final one is the survival times (in days) of 72 guinea pigs infected with virulent tubercle bacilli, observed and reported by Bjerkedal (1960). A graphical method based on Total Time on Test (TTT) (see, Aarset 1987) is used here to determine the shape of hazard rate function of the datasets we considered. The empirical TTT plot is,

$$\begin{aligned} G\left( \frac{r}{n}\right) =\frac{\sum _{i=1}^{r}X_{(i)}+(n-r)X_{(r)}}{\sum _{i=1}^{n}X_{(i)}},\,\,\,r=1,2,...,n, \end{aligned}$$

where \(X_{(i)}\) denote the ith order statistic of the sample. Figure 3 depicts the empirical TTT plots of the three data sets that we have considered here.

Fig. 3
figure 3

Empirical TTT plots of datas of a Lifetimes of 50 devices, b Strength of glass fibres and c Survival times of 72 guinea pigs

Full size image

For the data set, lifetimes of 50 devices provided by Aarset (1987), the empirical TTT transform is convex then concave, so the hazard function is bathtub shaped. For the other two data sets, the empirical TTT transform is concave, therefore both have increasing hazard function.

For the three data sets we compute model adequacy measures and goodness of fit statistic of BMLD, and compare it with that of classical distributions such as Modified Weibull (MW) (see, Lai et al. 2003), Additive Weibull (AW) (see, Lemonte et al. 2014), Exponentiated Lindley (EL) (see, Nadarajah et al. (2011), Weighted Lindley (WL) (see, Ghitany et al. 2011), Generalized Lindley (GL) (see, Zakerzadeh and Dolati 2009), Lindley Exponential (LE) (see, Bhati et al. 2015), New Generalized Lindley (NGL) (see, Abouammoh et al. 2015), Extended Generalized Lindley (EGL) (see,Ranjbar et al. 2019) and Exponentiated Weibull (EW) (see, Pal et al. 2006).

The estimates of the parameters, -Log Likelihood (− log L), Akaike information criterion (AIC), Bayesian information criterion (BIC), Corrected Akaike information criterion (AICc), Kolmogorov Smirnov (KS) statistic values along with the p value are calculated for these datasets and are given in Tables 2, 3 and 4 respectively. The plots of fitted densities and cumulative densities with respective to the given data sets are also plotted.

Table 2 Estimates, model adequacy measures and KS statistic for the data of lifetimes of 50 devices
Full size table
Table 3 Estimates, model adequacy measures and KS statistic for the data of strength of glass fibres
Full size table
Table 4 Estimates, model adequacy measures and KS statistic for the data of survival times of 72 guinea pigs
Full size table

The best model is the one with lowest AIC, BIC, AICc and KS statistic with largest p value. From the Tables 2,3 and 4 we can clearly observe that BMLD has the smallest value for its model adequacy measures such as AIC, BIC and AICc. Thus one can conclude that BMLD has the better performance compared to the other competing models. Further the Kolmogorv Smirnov (KS) statistic is computed to check the goodness of fit for the data set to BMLD as well as the other models. The value of KS statistic indicates that the BMLD has high fitting ability compared to other models considered here.

The plots of fitted densities and cumulative densities with respective to the datasets are given in Figs. 3, 4 and 5 respectively.

Fig. 4
figure 4

Fitted densities (a) and cumulative densities (b) of data of lifetimes of 50 devices

Full size image
Fig. 5
figure 5

Fitted densities (a) and cumulative densities (b) of data of strength of glass fibres

Full size image
Fig. 6
figure 6

Fitted densities (a) and cumulative densities (b) of data of survival times of 72 guinea pigs

Full size image

Figures 4a, 5a and 6a depicts the empirical histograms of the real data and the fitted densities of the BMLD and other distributions considered here. The fit of BMLD seems to be closer to the histogram of real data sets than other distributions. Also Figs. 4b, 5b and 6b shows the empirical and fitted cumulative density functions of BMLD and other distributions with the real data set. From these plots it is clear that BMLD will give consistently better fits than other competitive models.

7 Conclusion

In this article, we proposed a wider class of Lindley distribution called the binomial mixture Lindley distribution (BMLD), which generalizes ED, GD, LD, \(LD_2\), WLD, GLD, NGLD and \(NGLD_1\). Its flexibility allows increasing, decreasing, bathtub shaped and upside-down bathtub shaped hazard rates. Owing to the attractive feature of hazard rate function of BMLD it can be used to model any type of failure data sets. The estimation of parameters was explored by MLE method and the statistical properties of the estimators are investigated using a simulation study. Finally to establish the potentiality of this model, we use three real data sets in which one among them has bathtub shaped hazard rate and the other two have increasing hazard rate. For all these data sets BMLD performs better when compared to other competing models. Summing up, the BMLD provides a better model for fitting the wide spectrum of positive data sets arising in engineering, survival analysis, hydrology, economics, physics as well as numerous other fields of scientific investigation.