A generalized Lindley distribution

Abstract

A new distribution is proposed for modeling lifetime data. It has better hazard rate properties than the gamma, lognormal and the Weibull distributions. A comprehensive account of the mathematical properties of the new distribution including estimation and simulation issues is presented. A real data example is discussed to illustrate its applicability.

1 Introduction

There are many distributions for modeling lifetime data. Among the known parametric models, the most popular are the gamma, lognormal and the Weibull distributions. The Weibull distribution is more popular than the gamma and lognormal distributions because the survival functions of the latter cannot be expressed in closed forms and one needs numerical integration. The Weibull distribution has closed form survival and hazard rate functions. We refer the readers to Murthy et al. (2004) for details about Weibull distributions.

Gupta and Kundu (1999) introduced the exponentiated exponential distribution as an alternative to the gamma distribution. The exponentiated exponential distribution has many properties similar to those of the gamma and yet has closed form survival and hazard rate functions. See Gupta and Kundu (2007) for a review and some developments on the exponentiated exponential distribution.

However, the above four distributions (gamma, lognormal, Weibull and exponentiated exponential) suffer from a number of drawbacks. Firstly, none of them exhibit bath tub shapes for their hazard rate functions. The four distributions exhibit only monotonically increasing, monotonically decreasing or constant hazard rates. This is a major weakness because most real-life systems exhibit bath tub shapes for their hazard rate functions. Secondly, at least three of the four distributions exhibit constant hazard rates. This is a very unrealistic feature because there are hardly any real-life systems that have constant hazard rates.

The aim of this paper is to introduce a two parameter alternative to the gamma, lognormal, Weibull and the exponentiated exponential distributions that overcomes these mentioned drawbacks. It is most conveniently specified in terms of the cumulative distribution function:

$$ F(x) = \left[ 1 - \frac {1 + \lambda + \lambda x}{1 + \lambda} \exp (-\lambda x) \right]^\alpha$$

(1)

for x > 0, λ > 0 and α > 0. The corresponding probability density function is:

$$ f(x) = \frac {\alpha \lambda^2}{1 + \lambda} (1 + x) \left[ 1 - \frac {1 + \lambda + \lambda x}{1 + \lambda} \exp (-\lambda x) \right]^{\alpha - 1} \exp (-\lambda x). $$

(2)

The corresponding hazard rate function is

$$ h (x) = \frac {\alpha \lambda^2}{1 + \lambda} (1 + x) \left[ 1 - \frac {1 + \lambda + \lambda x}{1 + \lambda} \exp (-\lambda x) \right]^{\alpha - 1} \exp (-\lambda x) \left\{ 1 -V^\alpha (x) \right\}^{-1}, $$

(3)

where

$$ V (x) = 1 - \frac {1 + \lambda + \lambda x}{1 + \lambda} \exp (-\lambda x). $$

(4)

Note that Eq. 2 has two parameters, α and λ, just like the gamma, lognormal, Weibull and exponentiated exponential distributions. Note also that Eq. 2 has closed form survival functions and hazard rate functions just like the Weibull and exponentiated exponential distributions. For α = 1, Eq. 2 reduces to the Lindley distribution (Lindley 1958). As we shall see later, Eq. 2 has the attractive feature of allowing for monotonically decreasing, monotonically increasing and bath tub shaped hazard rate functions while not allowing for constant hazard rate functions.

Another motivation for the new distribution in Eq. 1 can be described as follows. Consider the one parameter Lindley distribution (Lindley 1958) specified by the cumulative distribution function:

$$ F_L (x) = 1 - \frac {1 + \lambda + \lambda x}{1 + \lambda} \exp (-\lambda x) $$

(5)

for x > 0 and λ > 0. This distribution is becoming increasing popular for modeling lifetime data, see Ghitany et al. (2008a, b) and Ghitany and Al-Mutairi (2009). Suppose X ₁, X ₂, ..., X _α are independent random variables distributed according to Eq. 5 and represent the failure times of the components of a series system, assumed to be independent. Then the probability that the system will fail before time x is given by

$$ \begin{array}{rll} \Pr \left( \max \left( X_1, X_2, \ldots, X_\alpha \right) \leq x \right) &=& \Pr \left( X_1 \leq x \right) \Pr \left( X_2 \leq x \right) \cdots \Pr \left( X_\alpha \leq x \right) \\ &=& F_L \left( x \right) F_L \left( x \right) \cdots F_L \left( x \right) \\ &=& \left[ 1 - \frac {1 + \lambda + \lambda x}{1 + \lambda} \exp (-\lambda x) \right]^\alpha. \end{array} $$

So, Eq. 1 gives the distribution of the failure of a series system with independent components.

The contents of this paper are organized as follows. A comprehensive account of mathematical properties of the new distribution is provided in Sections 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15. The properties studied include: relationship to other distributions, stochastic orderings, shapes of the probability density function and the hazard rate function, quantile function, raw moments, conditional moments, L moments, moment generating function, characteristic function, cumulant generating function, mean deviation about the mean, mean deviation about the median, Bonferroni curve, Lorenz curve, Bonferroni index, Gini index, Rényi entropy, Shannon entropy, cumulative residual entropy, order statistics and their moments, asymptotic distribution of the extreme values, and reliability measures. Estimation by the methods of moments and maximum likelihood—including the case of censoring—is presented in Section 16. Two simulation schemes are presented in Section 17. The performances of the two estimation methods are compared by simulation in Section 18. Finally, Section 19 illustrates an application by using a real data set. For additional properties of the new distribution including more details on the derived properties, we refer the readers to Nadarajah et al. (2011).

In the application section (Section 19), the lognormal distribution that we shall consider is a three parameter generalization (Chen 2006) of the usual one given by the probability density function:

$$ f_{LN} (x) = \frac {1}{\sqrt{2 \pi} \sigma (x - \theta)} \exp \left\{ -\frac {\left[ \log (x - \theta) - \mu \right]^2}{2 \sigma^2} \right\} $$

(6)

for x > θ, σ > 0 and − ∞ < μ < ∞. We shall yet note that the proposed two parameter distribution provides better fits than Eq. 6.

2 Related distributions

Note that the cumulative distribution function of a Lindley random variable given by Eq. 5 can be represented as

$$ F_{L} (x) = \theta F_E (x) + (1 - \theta) F_{G2} (x), $$

where θ = λ/(1 + λ), $F_E (x) = 1 - \exp (-\lambda) x$, the cumulative distribution function of an exponential random variable with scale parameter λ, and $F_{G2} (x) = 1 - \{ 1 + \lambda x \} \exp (-\lambda) x$, the cumulative distribution function of a gamma random variable with shape parameter 2 and scale parameter λ. It follows that the cumulative distribution function, Eq. 1, can be represented as

$$ F (x) = \sum\limits_{i = 0}^\infty {\alpha \choose i} \theta^{\alpha - i} (1 - \theta)^i F_E^{\alpha - i} (x) F_{G2}^i (x). $$

So, the proposed distribution can be viewed as an infinite mixture of the products of exponentiated gamma distributions. If α is an integer then the mixture is finite.

For x > 0, λ > m > 0 and β > 0, a gamma distribution has its cumulative distribution function and probability density function specified by

$$ F_{G} (x) = \frac {\gamma (\beta, m x)}{\Gamma (\beta)} $$

and

$$ f_{G} (x) = \frac {m^\beta x^{\beta - 1} \exp (-m x)}{\Gamma (\beta)}, $$

(7)

respectively, where $\gamma (a, x) = \int_0^x t^{a - 1} \exp (-t) dt$ denotes the incomplete gamma function and $\Gamma (a) = \int_0^\infty t^{a - 1} \exp (-t) dt$ denotes the gamma function. It is easy to see that

$$ \frac {F (x)}{F_{G} (x)} \leq M $$

and

$$ \frac {f (x)}{f_{G} (x)} \leq M, $$

where

$$ M = \sup\limits_{x > 0} \frac {f (x)}{f_{G} (x)}, $$

(8)

a finite constant for all 0 < m < λ.

For x > 0, m > 0, α > 0 and β > 0, an exponentiated gamma distribution has its cumulative distribution function and probability density function specified by

$$ F_{EG} (x) = \left[ \frac {\gamma (\beta, m x)}{\Gamma (\beta)} \right]^\alpha $$

(9)

and

$$ f_{EG} (x) = \frac {\alpha m^\beta x^{\beta - 1} \exp (-m x)}{\Gamma (\beta)} \left[ \frac {\gamma (\beta, m x)}{\Gamma (\beta)} \right]^{\alpha - 1}, $$

(10)

respectively. The properties of this distribution have been studied in detail by Nadarajah and Gupta (2007). The particular cases of Eqs. 9 and 10 for β = 2 are

$$ F_{EG2} (x) = \left[ 1 - (1 + m x) \exp (-m x) \right]^\alpha $$

and

$$ f_{EG2} (x) = \alpha m^2 x \exp (-m x) \left[ 1 - (1 + m x) \exp (-m x) \right]^{\alpha - 1}, $$

respectively. It is easy to see that

$$ \frac {F (x)}{F_{EG2} (x)} > 1 $$

for m = λ and m = λ/(1 + λ) and that F _EG2 (x) is a decreasing function of m. If m = λ then

$$ \frac {f (x)}{f_{EG2} (x)} \geq \frac {1 + x}{1 + \lambda} $$

for α ≥ 1 and

$$ \frac {f (x)}{f_{EG2} (x)} \leq \frac {1 + x}{1 + \lambda} $$

for α < 1. If m = λ/(1 + λ) then

$$ \frac {f (x)}{f_{EG2} (x)} \geq (1 + x) (1 + \lambda) \left( 1 - \frac {\lambda^2 x}{1 + \lambda} \right) $$

for α ≥ 1 and

$$ \frac {f (x)}{f_{EG2} (x)} \leq (1 + x) (1 + \lambda) $$

for α < 1.

For x > 0, λ > 0 and β > 0, a Weibull distribution has its cumulative distribution function and probability density function specified by

$$ F_{W} (x) = 1 - \exp \left( - m x^\beta \right) $$

and

$$ f_{W} (x) = m \beta x^{\beta - 1} \exp \left( - m x^\beta \right), $$

(11)

respectively. It is easy to see that

$$ \frac {F (x)}{F_{W} (x)} \leq M^{*} $$

and

$$ \frac {f (x)}{f_{W} (x)} \leq M^{*}, $$

where

$$ M^{*} = \sup_{x > 0} \frac {f (x)}{f_{W} (x)}, $$

(12)

a finite constant for all 0 < β <  min(1, α).

3 Stochastic orders

Suppose X _i is distributed according to Eqs. 1 and 2 with parameters λ _i and α _i for i = 1, 2. Let F _i denote the cumulative distribution function of X _i and let f _i denote the probability density function of X _i . If λ ₁ = λ ₂ then F ₁(x) ≥ F ₂(x) for all x > 0 and for all 0 < α ₁ ≤ α ₂, so X ₂ is stochastically greater than or equal to X ₁. If α ₁ = α ₂ then F ₁(x) ≤ F ₂(x) for all x > 0 and for all 0 < λ ₁ ≤ λ ₂, so X ₁ is stochastically greater than or equal to X ₂. The latter statement follows from the fact that $1 - (1 + \lambda + \lambda x) \exp (-\lambda x)/(1 + \lambda)$ is an increasing function of λ.

We say that X ₂ is stochastically greater than X ₁ with respect to likelihood ratio if f ₂(x)/f ₁(x) is an increasing function of x (Shaked and Shanthikumar 1994). Note that

$$ \begin{array}{rll} \frac {f_2 (x)}{f_1 (x)} &=& \frac {\alpha_2 \lambda_2^2 \left( 1 + \lambda_1 \right)}{\alpha_1 \lambda_1^2 \left( 1 + \lambda_2 \right)} \left[ 1 - \frac {1 + \lambda_2 + \lambda_2 x}{1 + \lambda_2} \exp \left( -\lambda_2 x \right) \right]^{\alpha_2 - 1} \\ && \times \left[ 1 - \frac {1 + \lambda_1 + \lambda_1 x}{1 + \lambda_1} \exp \left( -\lambda_1 x \right) \right]^{1 - \alpha_1} \exp \left( \lambda_1 x - \lambda_2 x \right). \end{array} $$

(13)

So, if λ ₁ = λ ₂ then X ₂ is stochastically greater than X ₁ with respect to likelihood ratio if and only if α ₂ > α ₁. If α ₁ = α ₂ = α then Eq. 13 reduces to

$$ \frac {f_2 (x)}{f_1 (x)} = \frac {\lambda_2^2 \left( 1 + \lambda_1 \right)^\alpha}{\lambda_1^2 \left( 1 + \lambda_2 \right)^\alpha} g^{\alpha - 1} (x), $$

where

$$ g (x) = \frac {1 + \lambda_2 - \left( 1 + \lambda_2 + \lambda_2 x \right) \exp \left( -\lambda_2 x \right)} {1 + \lambda_1 - \left( 1 + \lambda_1 + \lambda_1 x \right) \exp \left( -\lambda_1 x \right)}. $$

We can write

$$ \frac {d \log g (x)}{d x} = (1 + x) \left\{ q \left( \lambda_2 \right) - q \left( \lambda_1 \right) \right\}, $$

where

$$ q (\lambda) = \frac {\lambda^2 \exp (-\lambda x)}{1 + \lambda - (1 + \lambda +\lambda x) \exp (-\lambda x)}. $$

(14)

Note that

$$ \frac {d \log q (\lambda)}{d \lambda} = \frac {2}{\lambda} + \frac {(1 + x) \exp (-\lambda x) - (1 + x + \lambda x)} {1 + \lambda - (1 + \lambda +\lambda x) \exp (-\lambda x)} < 0. $$

(15)

So, if α ₁ = α ₂ = α ≥ 1 then X ₂ is stochastically greater than X ₁ with respect to likelihood ratio if and only if λ ₁ ≥ λ ₂. If α ₁ = α ₂ = α < 1 then X ₂ is stochastically greater than X ₁ with respect to likelihood ratio if and only if λ ₁ ≤ λ ₂.

We say that X ₂ is stochastically greater than X ₁ with respect to reverse hazard rate if f ₁(x) / F ₁(x) ≤ f ₂(x) / F ₂ (x) for all x (Shaked and Shanthikumar 1994). Note that

$$ \frac {f_i (x)}{F_i (x)} = \frac {\alpha_i \lambda_i^2 \left( 1 + x \right) \exp \left( -\lambda_i x \right)} {1 + \lambda_i - \left( 1 + \lambda_i + \lambda_i x \right) \exp \left( -\lambda_i x \right)} = \alpha_i (1 + x) q \left( \lambda_i \right), $$

where q(·) is as defined by Eq. 14. So, if λ ₁ = λ ₂ then X ₂ is stochastically greater than X ₁ with respect to reverse hazard ratio if and only if α ₂ ≥ α ₁. If α ₁ = α ₂ then X ₂ is stochastically greater than X ₁ with respect to reverse hazard ratio if and only if λ ₂ ≤ λ ₁. The latter statement follows from Eq. 15.

4 Shapes

It follows from Eq. 2 that

$$ \frac {d \log f(x)}{d x} = \frac {1}{1 + x} + \frac {(\alpha - 1) \lambda^2 (1 + x) \exp (-\lambda x)}{(1 + \lambda) V(x)} - \lambda $$

and

$$ \frac {d^2 \log f(x)}{d x^2} \!=\! -\frac {1}{(1 + x)^2} \!+\! \frac {(\alpha - 1) \lambda^2}{(1 + \lambda) V^2 (x)} \exp (-\lambda x) \left\{ 1 - \lambda (1 + x) - \frac {\exp (-\lambda x)}{1 + \lambda} \right\}, $$

where V(·) is given by Eq. 4. If α ≥ 1 then, using the fact $\exp (-\lambda x) > 1 - \lambda x$, we can see that d ² log f(x)/dx ² < 0 for all x. So, f is log-concave and has the increasing likelihood ratio property. Also d log f(x)/dx monotonically decreases from ∞ to − λ, so f must attain a unique maximum at x = x ₀ for some 0 < x ₀ < ∞. If α < 1 and λ ≥ 1 then d log f(x)/dx < 0 for all x, so f is monotonically decreasing for all x. If α < 1 and λ < 1 then f could attain a maximum, a minimum or a point of inflection according to whether d ² log f(x)/dx ² < 0, d ² log f(x)/dx ² > 0 or d ² log f(x)/dx ² = 0.

It follows from Eq. 3 that

$$ \frac {d \log h(x)}{d x} = \frac {d \log f(x)}{d x} + \frac {\alpha \lambda^2 (1 + x) V^{\alpha - 1} (x) \exp (-\lambda x)}{(1 + \lambda) \left\{ 1 - V^\alpha (x) \right\}} $$

and

$$ \begin{array}{rll} \frac {d^2 \log h (x)}{d x^2} &=& \frac {d^2 \log f(x)}{d x^2} + \frac {\alpha \lambda^2 V^{\alpha - 1} (x) \exp (-\lambda x)}{1 + \lambda}\\ &&\times \Bigg\{ \left[ 1 \!-\! V^\alpha (x) \right] \left[ 1 - \lambda (1 + x) \right] \!-\!\frac {(\alpha - 1) \lambda}{1 + \lambda} (1 + x)^2 \exp (-\lambda x) V^{-1} (x)\\ &&\qquad- \frac {\lambda}{1 + \lambda} (1 + x)^2 \exp (-\lambda x) V^{\alpha - 1} (x) \Bigg\}. \end{array} $$

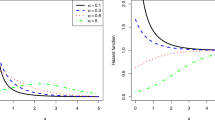
The modes of Eq. 3 are the points x = x ₀ satisfying d log h(x)/dx = 0. These points correspond to a maximum, a minimum and a point of inflection if d ² log h(x)/dx ² < 0, d ² log h(x)/dx ² > 0 and d ² log h(x)/dx ² = 0, respectively. Plots of Eq. 3 presented in Nadarajah et al. (2011) show: the shape of Eq. 3 appears monotonically decreasing or to initially decrease and then increase, a bath-tub shape, if α < 1; the shape appears monotonically increasing if α ≥ 1. So, the proposed distribution allows for monotonically decreasing, monotonically increasing and bath-tub shapes for its hazard rate function. Note that a constant hazard rate is not allowed.

Note that

$$ f (x) \sim \frac {\alpha \lambda^2}{1 + \lambda} x \exp (-\lambda x) $$

(16)

as x → ∞,

$$ f (x) \sim \alpha \left( \frac {\lambda^2}{1 + \lambda} \right)^\alpha x^{\alpha - 1} $$

(17)

as x → 0,

$$ 1 - F (x) \sim \frac {\alpha \lambda}{1 + \lambda} x \exp (-\lambda x) $$

as x → ∞,

$$ F (x) \sim \left( \frac {\lambda^2}{1 + \lambda} \right)^\alpha x^{\alpha} $$

as x → 0,

$$ h (x) \rightarrow \lambda $$

as x → ∞, and

$$ h (x) \sim \alpha \left( \frac {\lambda^2}{1 + \lambda} \right)^\alpha x^{\alpha - 1} $$

as x → 0. So, the lower tail of the probability density function is polynomial while its upper tail decays exponentially. The lower tail of the hazard rate function is polynomial and allows for decreasing, increasing and constant hazard rates. In the upper tail, the hazard rate function approaches a constant.

5 Quantile function

Let X denote a random variable with the probability density function 2. The quantile function, say Q(p), defined by F(Q(p)) = p is the root of the equation

$$ \left[ 1 + \frac {\lambda Q (p)}{1 + \lambda} \right] \exp \left\{ -\lambda Q (p) \right\} = 1 - p^{1/\alpha} $$

(18)

for 0 < p < 1. Substituting Z(p) = − 1 − λ − λQ(p), one can rewrite Eq. 18 as

$$ Z (p) \exp \left\{ Z (p) \right\} = -(1 + \lambda) \exp \left( -1 - \lambda \right) \left( 1 - p^{1/\alpha} \right) $$

for 0 < p < 1. So, the solution for Z(p) is

$$ Z (p) = W \left( -(1 + \lambda) \exp \left( -1 - \lambda \right) \left( 1 - p^{1/\alpha} \right) \right) $$

(19)

for 0 < p < 1, where W(·) is the Lambert W function, see Corless et al. (1996) for detailed properties. Inverting Eq. 19, one obtains

$$ Q (p) = -1 - \frac {1}{\lambda} - \frac {1}{\lambda} W \left( -(1 + \lambda) \exp \left( -1 - \lambda \right) \left( 1 - p^{1/\alpha} \right) \right) $$

(20)

for 0 < p < 1. The particular case of Eq. 20 for α = 1 has been derived recently by Jodrá (2010). Our derivation of the general form here is independent.

A series expansion for Eq. 20 around p = 1 can be obtained as

$$ Q (p) = -1 - \frac {1}{\lambda} - \frac {1}{\lambda} \sum\limits_{i = 1}^\infty \frac {(-i)^{i - 1} x^i}{i!}, $$

(21)

where $x = -(1 + \lambda) ( 1 - p^{1/\alpha} ) \exp (-1 - \lambda)$. However, these expansions may not be needed as in-built routines for computing W(·) are widely available, for example, ProductLog[·] in Mathematica.

6 Moments

Let X denote a random variable with the probability density function 2. Calculating moments of X requires the following lemma.

Lemma 1

Let

$$ K (a, b, c, \delta) = \int_0^\infty x^c (1 + x) \left[ 1 - \frac {1 + b + b x}{1 + b} \exp (-b x) \right]^{a - 1} \exp (-\delta x) dx. $$

We have

$$ K (a, b, c, \delta) = \sum\limits_{i = 0}^\infty \sum\limits_{j = 0}^i \sum\limits_{k = 0}^{j + 1} {a - 1 \choose i} {i \choose j} {j + 1 \choose k} \frac {(-1)^i b^j \Gamma (c + k + 1)}{(1 + b)^i (b i + \delta)^{c + k + 1}}. $$

Proof

Using the series expansion, Eq. 38, one can write

$$ \begin{array}{rll} K (a, b, c, \delta) &=& \sum\limits_{i = 0}^\infty {a - 1 \choose i} \frac {(-1)^i}{(1 + b)^i}\\&& \times\int_0^\infty x^c (1 + x) (1 + b + b x)^i \exp \left( -b i x - \delta x\right) dx \\ &=& \sum\limits_{i = 0}^\infty {a - 1 \choose i} \frac {(-1)^i}{(1 + b)^i} \sum\limits_{j = 0}^i {i \choose j} b^j \\ &&\times\int_0^\infty x^c (1 + x)^{j + 1} \exp \left(-b i x - \delta x\right) dx \\ &=& \sum\limits_{i = 0}^\infty {a - 1 \choose i} \frac {(-1)^i}{(1 + b)^i} \sum\limits_{j = 0}^i {i \choose j} b^j \sum\limits_{k = 0}^{j + 1} {j + 1 \choose k} \\&&\times\int_0^\infty x^{c + k} \exp \left(-b i x - \delta x\right) dx. \end{array} $$

The result of the lemma follows by the definition of the gamma function. □

It follows from Lemma 1 that

$$ E \left( X^n \right)= \frac {\alpha \lambda^2}{1 + \lambda} K (\alpha, \lambda, n, \lambda). $$

In particular, the first four moments of X are

$$ E \left( X \right)= \frac {\alpha \lambda^2}{1 + \lambda} K (\alpha, \lambda, 1, \lambda), $$

$$ E \left( X^2 \right)= \frac {\alpha \lambda^2}{1 + \lambda} K (\alpha, \lambda, 2, \lambda), $$

$$ E \left( X^3 \right)= \frac {\alpha \lambda^2}{1 + \lambda} K (\alpha, \lambda, 3, \lambda) $$

and

$$ E \left( X^4 \right)= \frac {\alpha \lambda^2}{1 + \lambda} K (\alpha, \lambda, 4, \lambda). $$

The variance, skewness and kurtosis of X can now be obtained. Plots of E(X), Var(X), Skewness(X) and Kurtosis(X) versus λ and α presented in Nadarajah et al. (2011) show: E(X) and Var(X) are decreasing functions of λ while Skewness(X) and Kurtosis(X) are increasing functions of λ for every fixed α; E(X) and Var(X) are increasing functions of α while Skewness(X) and Kurtosis(X) are decreasing functions of α for every fixed λ.

7 Conditional moments

For lifetime models, it is also of interest to know what E (X ⁿ | X > x) is. Calculating these moments requires the following lemma.

Lemma 2

Let

$$ L (a, b, c, \delta, t) = \int_t^\infty x^c (1 + x) \left[ 1 - \frac {1 + b + b x}{1 + b} \exp (-b x) \right]^{a - 1} \exp (-\delta x) dx. $$

We have

$$ L (a, b, c, \delta, t) = \sum\limits_{i = 0}^\infty \sum\limits_{j = 0}^i \sum\limits_{k = 0}^{j + 1} {a - 1 \choose i} {i \choose j} {j + 1 \choose k} \frac {(-1)^i b^j \Gamma \left( c + k + 1, (b i + \delta) t \right)}{(1 + b)^i (b i + \delta)^{c + k + 1}}, $$

(22)

where $\Gamma (a, x) = \int_x^{\infty} t^{a - 1} \exp (-t) dt$ denotes the complementary incomplete gamma function. If c is an integer then Eq.  22 can be simplified to

$$ \begin{array}{rll} L (a, b, c, \delta, t) \!&=&\! \sum\limits_{i = 0}^\infty \sum\limits_{j = 0}^i \sum\limits_{k = 0}^{j + 1} {a - 1 \choose i} {i \choose j} {j + 1 \choose k} \frac {(-1)^i b^j (c + k)! \exp \left\{ -(b i + \delta) t \right\}}{(1 + b)^i (b i + \delta)^{c + k + 1}}\\&&\times \sum\limits_{l = 0}^{c + k} \frac {(b i + \delta)^l}{l!}. \end{array} $$

Proof

The proof of Eq. 22 is similar to the proof of Lemma 1, but using the definition of the complementary incomplete gamma function. The final relation follows by using the fact

$$ \Gamma (n, z) = (n - 1)! \exp (-z) \sum\limits_{l = 0}^{n - 1} \frac {z^l}{l!}, $$

see http://functions.wolfram.com/GammaBetaErf/Gamma2/03/01/02/0007/. □

Using Lemma 2, it is easily seen that

$$ E \left( X^n \mid X > x \right) = \frac {\alpha \lambda^2}{(1 + \lambda) \left\{ 1 - V^\alpha (x) \right\}} L (\alpha, \lambda, n, \lambda, x), $$

where V(·) is given by Eq. 4. In particular,

$$ E \left( X \mid X > x \right) = \frac {\alpha \lambda^2}{(1 + \lambda) \left\{ 1 - V^\alpha (x) \right\}} L (\alpha, \lambda, 1, \lambda, x), $$

$$ E \left( X^2 \mid X > x \right) = \frac {\alpha \lambda^2}{(1 + \lambda) \left\{ 1 - V^\alpha (x) \right\}} L (\alpha, \lambda, 2, \lambda, x), $$

$$ E \left( X^3 \mid X > x \right) = \frac {\alpha \lambda^2}{(1 + \lambda) \left\{ 1 - V^\alpha (x) \right\}} L (\alpha, \lambda, 3, \lambda, x) $$

and

$$ E \left( X^4 \mid X > x \right) = \frac {\alpha \lambda^2}{(1 + \lambda) \left\{ 1 - V^\alpha (x) \right\}} L (\alpha, \lambda, 4, \lambda, x). $$

The mean residual lifetime function is E (X | X > x) − x.

8 L moments

Some other important measures useful for lifetime models are the L moments due to Hoskings (1990). It can be shown using Lemma 1 that the kth L moment is

$$ \lambda_k = \sum\limits_{j = 0}^{k - 1} (-1)^{k - 1 - j} {k - 1 \choose j} {k - 1 + j \choose j} \beta_j, $$

where

$$ \beta_k = \frac {\alpha \lambda^2}{1 + \lambda} K \left( \alpha (k + 1), \lambda, 1, \lambda \right). $$

In particular,

$$ \lambda_1 = \beta_0, $$

$$ \lambda_2 = 2 \beta_1 - \beta_0, $$

$$ \lambda_3 = 6 \beta_2 - 6 \beta_1 + \beta_0 $$

and

$$ \lambda_4 = 20 \beta_3 - 30 \beta_2 + 12 \beta_1 - \beta_0, $$

where

$$ \beta_0 = \frac {\alpha \lambda^2}{1 + \lambda} K \left( \alpha, \lambda, 1, \lambda \right), $$

$$ \beta_1 = \frac {\alpha \lambda^2}{1 + \lambda} K \left( 2 \alpha, \lambda, 1, \lambda \right), $$

$$ \beta_2 = \frac {\alpha \lambda^2}{1 + \lambda} K \left( 3 \alpha, \lambda, 1, \lambda \right) $$

and

$$ \beta_3 = \frac {\alpha \lambda^2}{1 + \lambda} K \left( 4 \alpha, \lambda, 1, \lambda \right). $$

The L moments have several advantages over ordinary moments: for example, they apply for any distribution having finite mean; no higher-order moments need be finite.

9 MGF, CHF and CGF

Let X denote a random variable with the probability density function 2. It follows from Lemma 1 that the moment generating function of X, $M (t) = E [\exp (tX)]$, is given by

$$ M (t) = \frac {\alpha \lambda^2}{1 + \lambda} K (\alpha, \lambda, 0, \lambda - t) $$

for t < λ. So, the characteristic function of X, $\phi (t) = E [\exp ({\rm i} tX)]$, and the cumulant generating function of X, K (t) = log ϕ(t), are given by

$$ \phi (t) = \frac {\alpha \lambda^2}{1 + \lambda} K \left(\alpha, \lambda, 0, \lambda - {\rm i} t\right) $$

and

$$ K (t) = \log \frac {\alpha \lambda^2}{1 + \lambda} + \log K \left(\alpha, \lambda, 0, \lambda - {\rm i} t\right), $$

respectively, where ${\rm i} = \sqrt{-1}$.

10 Mean deviations

The amount of scatter in a population is evidently measured to some extent by the totality of deviations from the mean and median. These are known as the mean deviation about the mean and the mean deviation about the median—defined by

$$ \delta_1 (X) = \int_0^{\infty }\left | x - \mu \right | f(x) dx $$

and

$$ \delta_2 (X) = \int_0^{\infty} \left | x - M \right | f(x) dx, $$

respectively, where μ = E(X) and M = Median(X) denotes the median. The measures δ ₁(X) and δ ₂(X) can be calculated using the relationships

$$ \begin{array}{rll} \displaystyle \delta_1 (X) &=& \displaystyle \int_0^\mu (\mu - x) f (x) dx + \int_\mu^\infty (x - \mu) f (x) dx \\ &=& \displaystyle \mu F (\mu) - \int_0^\mu x f (x) dx - \mu \left\{ 1 - F (\mu) \right\} + \int_\mu^\infty x f (x) dx \\ &=& \displaystyle 2 \mu F (\mu) - 2 \mu + 2 \int_\mu^\infty x f (x) dx \end{array} $$

and

$$ \begin{array}{rll} \displaystyle \delta_2 (X) &=& \displaystyle \int_0^M (M - x) f (x) dx + \int_M^\infty (x - M) f (x) dx \\ &=& \displaystyle M F (M) - \int_0^M x f (x) dt - M \left\{ 1 - F (M) \right\} + \int_M^\infty x f (x) dx \\ &=& \displaystyle -\mu + 2 \int_M^\infty x f (x) dx. \end{array} $$

By Lemma 2,

$$ \int_\mu^\infty x f (x) dx = \frac {\alpha \lambda^2}{1 + \lambda} L (\alpha, \lambda, 1, \lambda, \mu) $$

and

$$ \int_M^\infty x f (x) dx = \frac {\alpha \lambda^2}{1 + \lambda} L (\alpha, \lambda, 1, \lambda, M), $$

so it follows that

$$ \displaystyle \delta_1 (T) = 2 \mu F (\mu) - 2 \mu + \frac {2 \alpha \lambda^2}{1 + \lambda} L (\alpha, \lambda, 1, \lambda, \mu) $$

and

$$ \displaystyle \delta_2 (T) = -\mu + \frac {2 \alpha \lambda^2}{1 + \lambda} L (\alpha, \lambda, 1, \lambda, M). $$

11 Bonferroni and Lorenz curves

The Bonferroni and Lorenz curves (Bonferroni 1930) and the Bonferroni and Gini indices have applications not only in economics to study income and poverty, but also in other fields like reliability, demography, insurance and medicine. The Bonferroni and Lorenz curves are defined by

$$ \displaystyle B (p) = \frac {\displaystyle 1}{\displaystyle p \mu} \int_0^q x f (x) dx $$

(23)

and

$$ \displaystyle L (p) = \frac {\displaystyle 1}{\displaystyle \mu} \int_0^q x f (x) dx, $$

(24)

respectively, or equivalently by

$$ \displaystyle B (p) = \frac {1}{p \mu} \int_0^p F^{-1} (x) dx $$

(25)

and

$$ \displaystyle L (p) = \frac {1}{\mu} \int_0^p F^{-1} (x) dx, $$

(26)

respectively, where μ = E (X) and q = F ^− 1 (p). The Bonferroni and Gini indices are defined by

$$ \displaystyle B = 1 - \int_0^1 B (p) dp $$

(27)

and

$$ \displaystyle G = 1 - 2 \int_0^1 L (p) dp, $$

(28)

respectively.

If X has the probability density function, Eq. 2, then, by Lemma 2, one can calculate Eqs. 23 and 24 as

$$ B (p) = \frac {\displaystyle 1}{\displaystyle p \mu} \left\{ \mu - \frac {\alpha \lambda^2}{1 + \lambda} L (\alpha, \lambda, 1, \lambda, q) \right\} $$

(29)

and

$$ L (p) = \frac {\displaystyle 1}{\displaystyle \mu} \left\{ \mu - \frac {\alpha \lambda^2}{1 + \lambda} L (\alpha, \lambda, 1, \lambda, q) \right\}, $$

(30)

respectively. Alternatively, by using Eq. 21, one can calculate Eqs. 25 and 26 as

$$ B (p) = \frac {\displaystyle 1}{\displaystyle \mu} \left[ -1 - \frac {1}{\lambda} + \sum\limits_{i = 1}^\infty \sum\limits_{j = 0}^i \frac {i^{i - 1}}{i!} (1 + \lambda)^i \exp (-i - i \lambda) {i \choose j} \frac {(-1)^j p^{j/\alpha}}{j/\alpha + 1} \right] $$

(31)

and

$$ L (p) = \frac {\displaystyle p}{\displaystyle \mu} \left[ -1 - \frac {1}{\lambda} + \sum\limits_{i = 1}^\infty \sum\limits_{j = 0}^i \frac {i^{i - 1}}{i!} (1 + \lambda)^i \exp (-i - i \lambda) {i \choose j} \frac {(-1)^j p^{j/\alpha}}{j/\alpha + 1} \right], $$

(32)

respectively. Integrating Eqs. 31 and 32 with respect to p, one can calculate the Bonferroni and Gini indices given by Eqs. 27 and 28, respectively, as

$$ B = 1 - \frac {\displaystyle 1}{\displaystyle \mu} \left[ -1 - \frac {1}{\lambda} + \sum\limits_{i = 1}^\infty \sum\limits_{j = 0}^i \frac {i^{i - 1}}{i!} (1 + \lambda)^i \exp (-i - i \lambda) {i \choose j} \frac {(-1)^j}{\left( j/\alpha + 1 \right)^2} \right] $$

(33)

and

$$ G \!=\! 1 \!-\! \frac {\displaystyle 1}{\displaystyle \mu}\!\left[\!-1 \!-\! \frac {1}{\lambda} \!+\! 2 \sum\limits_{i = 1}^\infty \sum\limits_{j = 0}^i \frac {i^{i - 1}}{i!} (1 \!+\! \lambda)^i \exp (-i - i \lambda) {i \choose j} \frac {(-1)^j}{\left( j/\alpha + 1 \right) \left( j/\alpha \!+\! 2 \right)}\!\right]\!, $$

(34)

respectively. Plots of the Bonferroni curve given by Eq. 29 and the Lorenz curve given by Eq. 30 presented in Nadarajah et al. (2011) show that the variability of X—as measured by the area between Bonferroni curve and B (p) = 1 or the area between the Lorenz curve and L(p) = p—decreases as α increases. The area between a Bonferroni curve and B (p) = 1 is the Bonferroni index given by Eq. 33. The area between a Lorenz curve and L(p) = p is known as the area of concentration. The Gini index given by Eq. 34 is twice this area.

12 Entropies

An entropy of a random variable X is a measure of variation of the uncertainty. A popular entropy measure is Rényi entropy (Rényi 1961). If X has the probability density function f(·) then Rényi entropy is defined by

$$ \displaystyle \mathcal{J}_R (\gamma) = \frac {1}{1 - \gamma} \log \left\{ \int f^{\gamma} (x) dx \right\}, $$

(35)

where γ > 0 and γ ≠ 1. Suppose X has the probability density function 2. Then, one can calculate

$$ \begin{array}{rll} \displaystyle \int f^{\gamma} (x) dx &=& \displaystyle \left( \frac {\alpha \lambda^2}{1 + \lambda} \right)^\gamma \int_0^\infty (1 + x)^\gamma V^{\gamma \alpha - \gamma} (x) \exp (-\lambda \gamma x) dx \\&=& \displaystyle \left( \frac {\alpha \lambda^2}{1 + \lambda} \right)^\gamma \sum\limits_{k = 0}^\infty {\gamma \alpha - \gamma \choose k} \frac {(-1)^k}{(1 + \lambda)^k} \\ && \times \int_0^\infty (1 + x)^\gamma \left( 1 + \lambda + \lambda x \right)^k \exp \left\{ -(k + \gamma) \lambda x \right\} dx \\ &=& \displaystyle \left( \frac {\alpha \lambda^2}{1 + \lambda} \right)^\gamma \sum\limits_{k = 0}^\infty {\gamma \alpha - \gamma \choose k} \frac {(-1)^k}{(1 + \lambda)^k} \sum\limits_{j = 0}^k {k \choose j} \lambda^j \\ && \times \int_0^\infty (1 + x)^{\gamma + j} \exp \left\{ -(k + \gamma) \lambda x \right\} dx \\ &=& \displaystyle \left( \frac {\alpha \lambda^2}{1 + \lambda} \right)^\gamma \sum\limits_{k = 0}^\infty {\gamma \alpha - \gamma \choose k} \frac {(-1)^k}{(1 + \lambda)^k} \sum\limits_{j = 0}^k {k \choose j} \lambda^j \exp \left\{ (k + \gamma) \lambda \right\} \\ && \times \int_1^\infty y^{\gamma + j} \exp \left\{ -(k + \gamma) \lambda y \right\} dy \nonumber \\ &=& \displaystyle \left( \frac {\alpha \lambda^2}{1 + \lambda} \right)^\gamma \sum\limits_{k = 0}^\infty {\gamma \alpha - \gamma \choose k} \frac {(-1)^k}{(1 + \lambda)^k}\\&& \times \sum\limits_{j = 0}^k {k \choose j} \lambda^j \exp \left\{ (k \!+\! \gamma) \lambda \right\} \left\{ (k \!+\! \gamma) \lambda \right\}^{-\gamma - j - 1} \Gamma \left( \gamma \!+\! j \!+\! 1, (k \!+\! \gamma) \lambda \right), \end{array} $$

where V(·) is given by Eq. 4 and the final step follows by the definition of the complementary incomplete gamma function. So, one obtains the Rényi entropy as

$$ \begin{array}{rll} \displaystyle \mathcal{J}_R (\gamma) &=& \frac {\gamma}{1 - \gamma} \log \left( \frac {\alpha \lambda^2}{1 + \lambda} \right) \\ && +\frac {1}{1 - \gamma} \log \left\{\sum\limits_{k = 0}^\infty \sum\limits_{j = 0}^k {\gamma \alpha - \gamma \choose k} {k \choose j}\right. \nonumber\\ && \left. \times\vphantom{\sum\limits_{k = 0}^\infty \sum\limits_{j = 0}^k {\gamma \alpha - \gamma \choose k} {k \choose j}} \frac {(-1)^k \lambda^j \exp \left\{ (k + \gamma) \lambda \right\} \Gamma \left( \gamma + j + 1, (k + \gamma) \lambda \right)} {(1 + \lambda)^k \left\{ (k + \gamma) \lambda \right\}^{\gamma + j + 1}} \right\}. \end{array} $$

(36)

Shannon entropy (Shannon 1951) defined by E[ − log f(X)] is the the particular case of Eq. 35 for γ ↑ 1. Limiting γ ↑ 1 in Eq. 36 and using L’Hospital’s rule, one obtains after considerable algebraic manipulation that

$$ \begin{array}{rll} \displaystyle E \left[ -\log f(X) \right] &=& \displaystyle -\log \left( \frac {\alpha \lambda^2}{1 + \lambda} \right) + \lambda E (X) + \sum\limits_{k = 1}^\infty \frac {(-1)^k}{k} E \left( X^k \right) \\ && + (1 - \alpha) \sum\limits_{k = 0}^\infty \sum\limits_{l = 0}^k {k \choose l} \frac {(1 + \lambda)^{k = l} \lambda^l}{k (1 + \lambda)^k} K \left( \alpha, \lambda, l, \lambda + \lambda k \right), \end{array} $$

where K( ⋯ ) is as defined by Lemma 1.

Finally, consider the cumulative residual entropy (Rao et al. 2004) defined by

$$ \displaystyle \mathcal{J}_C = -\int \Pr (X > x) \log \Pr (X > x) dx. $$

(37)

Using the series expansions,

$$ (1 - z)^{a - 1} = \sum\limits_{i = 0}^\infty {a - 1 \choose i} (-1)^i z^i $$

(38)

and

$$ \log (1 - z) = -\sum\limits_{i = 1}^\infty \frac {z^i}{i}, $$

one can calculate Eq. 37 as

$$ \begin{array}{rll} \displaystyle \mathcal{J}_C &=& \sum\limits_{i = 0}^\infty \frac {1}{i} \int_0^\infty V^{\alpha i} (x) \left\{ 1 - V^\alpha (x) \right\} dx \\ &=& -\sum\limits_{i = 0}^\infty \sum\limits_{j = 1}^\infty {\alpha \choose j} \frac {(-1)^j}{i (1 + \lambda)^j} \int_0^\infty (1 + \lambda + \lambda x)^j V^{\alpha i} (x) \exp (-\lambda j x) dx \\ &=& -\sum\limits_{i = 0}^\infty \sum\limits_{j = 1}^\infty \sum\limits_{k = 0}^j {\alpha \choose j} {j \choose k} \frac {(-1)^j \lambda^k}{i (1 + \lambda)^j} \int_0^\infty (1 + x)^k V^{\alpha i} (x) \exp (-\lambda j x) dx \\ &=& -\sum\limits_{i = 0}^\infty \sum\limits_{j = 1}^\infty \sum\limits_{k = 0}^j {\alpha \choose j} {j \choose k} \frac {(-1)^j \lambda^k}{i (1 + \lambda)^j} K \left( \alpha i + 1, \lambda, 0, \lambda j \right), \end{array} $$

where the final step follows by an application of Lemma 1.

13 Order statistics

Suppose X ₁, X ₂, ..., X _n is a random sample from Eq. 2. Let X _{1: n}  < X _{2: n}  < ⋯ < X _{n: n} denote the corresponding order statistics. It is well known that the probability density function and the cumulative distribution function of the kth order statistic, say Y = X _{k: n} , are given by

$$ \begin{array}{rll} \displaystyle f_Y (y) &=& \displaystyle \frac {\displaystyle n!}{\displaystyle (k - 1)! (n - k)!} F^{k - 1} (y) \left\{ 1 - F (y) \right\}^{n - k} f (y) \\ &=& \displaystyle \frac {\displaystyle n!}{\displaystyle (k - 1)! (n - k)!} \sum\limits_{l = 0}^{n - k} {n - k \choose l} (-1)^l F^{k - 1 + l} (y) f (y) \end{array} $$

and

$$ \displaystyle F_Y (y) = \sum\limits_{j = k}^n {n \choose j} F^j (y) \left\{ 1 - F (y) \right\}^{n - j} = \sum\limits_{j = k}^n \sum\limits_{l = 0}^{n - j} {n \choose j} {n - j \choose l} (-1)^l F^{j + l} (y), $$

respectively, for k = 1, 2, ..., n. It follows from Eqs. 1 and 2 that

$$ \displaystyle f_Y (y) = \frac {\displaystyle \alpha \lambda^2 n!}{\displaystyle (1 + \lambda) (k - 1)! (n - k)!} (1 + x) \exp (-\lambda x) \sum\limits_{l = 0}^{n - k} {n - k \choose l} (-1)^l V^{\alpha (k + l) - 1} (y) $$

and

$$ \displaystyle F_Y (y) = \sum\limits_{j = k}^n \sum\limits_{l = 0}^{n - j} {n \choose j} {n - j \choose l} (-1)^l V^{\alpha (j + l)} (y), $$

where V(·) is given by Eq. 4. Using Lemma 1, the qth moment of Y can be expressed as

$$ \displaystyle E \left( Y^q \right) = \frac {\displaystyle \alpha \lambda^2 n!}{\displaystyle (1 + \lambda) (k - 1)! (n - k)!} \sum\limits_{l = 0}^{n - k} {n - k \choose l} (-1)^l K \left( \alpha (k + l), \lambda, m, \lambda \right) $$

for q ≥ 1.

14 Extreme values

If $\overline{X} = (X_1 + \cdots + x_n)/n$ denotes the sample mean then by the usual central limit theorem $\sqrt{n} (\overline{X} - E (X))/\sqrt{Var (X)}$ approaches the standard normal distribution as n → ∞. Sometimes one would be interested in the asymptotics of the extreme values M _n  =  max(X ₁, ..., X _n ) and m _n  =  min(X ₁, ..., X _n ).

Let g (t) = 1/λ. Take the cumulative distribution function and the probability density function as specified by Eqs. 1 and 2, respectively. Note from Eqs. 16 and 17 that

$$ \displaystyle \lim\limits_{t \to \infty} \frac {1 - F (t + x g (t))}{1 - F(t)} = \lim\limits_{t \to \infty} \frac {f (t + x/\lambda)}{f(t)} = \lim\limits_{t \to \infty} \frac {t + x/\lambda}{t} \exp (-x) = \exp (-x) $$

as t → ∞ and

$$ \displaystyle \lim\limits_{t \to 0} \frac {F (tx)}{F(t)} = \lim\limits_{t \to \infty} \frac {x f (t x)}{f(t)} = x^\alpha $$

as t → 0. Hence, it follows from Theorem 1.6.2 in Leadbetter et al. (1987) that there must be norming constants a _n  > 0, b _n , c _n  > 0 and d _n such that

$$ \displaystyle \Pr \left\{ a_n \left( M_n - b_n \right) \leq x \right\} \rightarrow \exp \left\{ -\exp (-x) \right\} $$

and

$$ \displaystyle \Pr \left\{ c_n \left( m_n - d_n \right) \leq x \right\} \rightarrow 1 - \exp \left( -x^\alpha \right) $$

as n → ∞. The form of the norming constants can also be determined. For instance, using Corollary 1.6.3 in Leadbetter et al. (1987), one can see that $b_n = F^{-1} (1 - 1/n)$ and a _n  = λ, where F ^− 1(·) denotes the inverse function of F(·).

15 Reliability

In the context of reliability, the stress-strength model describes the life of a component which has a random strength X ₁ that is subjected to a random stress X ₂. The component fails at the instant that the stress applied to it exceeds the strength, and the component will function satisfactorily whenever X ₁ > X ₂. So, $R = \Pr(X_2 < X_1)$ is a measure of component reliability. It has many applications especially in engineering concepts such as structures, deterioration of rocket motors, static fatigue of ceramic components, fatigue failure of aircraft structures, and the aging of concrete pressure vessels. In the area of stress-strength models there has been a large amount of work as regards estimation of the reliability R when X ₁ and X ₂ are independent random variables belonging to the same univariate family of distributions and its algebraic form has been worked out for the majority of the well-known standard distributions. However, there are still many other distributions (including generalizations of the well-known distributions) for which the form of R has not been investigated. Here, we derive the reliability R when X ₁ and X ₂ are independent random variables distributed according to Eq. 2 with parameters (α ₁, λ ₁) and (α ₂, λ ₂), respectively.

Several representations can be derived for the reliability R. Firstly, note from Eqs. 1 and 2 that

$$ \begin{array}{rll} R &=& \frac {\alpha_1 \lambda_1^2}{1 + \lambda_1} \int_0^\infty (1 + x) \left[ 1 - \frac {1 + \lambda_1 + \lambda_1 x}{1 + \lambda_1} \exp \left(-\lambda_1 x\right) \right]^{\alpha_1 - 1} \\ && \times \left[ 1 - \frac {1 + \lambda_2 + \lambda_2 x}{1 + \lambda_2} \exp \left(-\lambda_2 x\right) \right]^{\alpha_2} \exp \left( -\lambda_1 x \right) dx. \end{array} $$

(39)

Applying the series expansion, Eq. 37, for both the terms within square brackets in Eq. 38, one obtains the representation

$$ \begin{array}{rll} R &=& \frac {\alpha_1 \lambda_1^2}{1 + \lambda_1} \sum\limits_{k = 0}^\infty \sum\limits_{l = 0}^\infty {\alpha_1 - 1 \choose k} {\alpha_2 \choose l} \frac {(-1)^{k + l}}{\left( 1 + \lambda_1 \right)^k \left( 1 + \lambda_2 \right)^l} \\ && \times \int_0^\infty (1 + x) \left( 1 + \lambda_1 + \lambda_1 x \right)^k \left( 1 + \lambda_2 + \lambda_2 x \right)^l \exp \left\{ -\lambda_1 (k + 1) x - \lambda_2 l x\right\} dx \\ &=& \frac {\alpha_1 \lambda_1^2}{1 + \lambda_1} \sum\limits_{k = 0}^\infty \sum\limits_{l = 0}^\infty \sum\limits_{m = 0}^k \sum\limits_{n = 0}^l {\alpha_1 - 1 \choose k} {\alpha_2 \choose l} {k \choose m} {l \choose n} \frac {(-1)^{k + l} \lambda_1^m \lambda_1^n}{\left( 1 + \lambda_1 \right)^m \left( 1 + \lambda_2 \right)^n} \\ && \times \int_0^\infty (1 + x) x^{m + n} \exp \left\{ -\lambda_1 (k + 1) x - \lambda_2 l x\right\} dx \\ &=& \frac {\alpha_1 \lambda_1^2}{1 + \lambda_1} \sum\limits_{k = 0}^\infty \sum\limits_{l = 0}^\infty \sum\limits_{m = 0}^k \sum\limits_{n = 0}^l {\alpha_1 - 1 \choose k} {\alpha_2 \choose l} {k \choose m} {l \choose n} \frac {(-1)^{k + l} \lambda_1^m \lambda_1^n}{\left( 1 + \lambda_1 \right)^m \left( 1 + \lambda_2 \right)^n} \\ && \times \left[ \int_0^\infty x^{m + n} \exp \left(-\lambda_1 k x - \lambda_2 l x\right) dx \right. \\&& \left. \int_0^\infty x^{m + n + 1} \exp \left\{ -\lambda_1 (k + 1) x - \lambda_2 l x\right\} dx \right] \\ &=& \frac {\alpha_1 \lambda_1^2}{1 + \lambda_1} \sum\limits_{k = 0}^\infty \sum\limits_{l = 0}^\infty \sum\limits_{m = 0}^k \sum\limits_{n = 0}^l {\alpha_1 - 1 \choose k} {\alpha_2 \choose l} {k \choose m} {l \choose n} \frac {(-1)^{k + l} \lambda_1^m \lambda_1^n}{\left( 1 + \lambda_1 \right)^m \left( 1 + \lambda_2 \right)^n} \\ && \times \frac {(m + n)!}{\left\{ \lambda_1 (k + 1) + \lambda_2 l \right\}^{m + n + 1}} \left[ 1 + \frac {m + n + 1}{\lambda_1 (k + 1) + \lambda_2 l} \right], \end{array} $$

where the final step follows by the definition of the gamma function. Applying series expansion, Eq. 38, for only the first term within square brackets in Eq. 39, one obtains the representation

$$ \begin{array}{rll} R &=& \frac {\alpha_1 \lambda_1^2}{1 + \lambda_1} \sum\limits_{k = 0}^\infty {\alpha_1 - 1 \choose k} \frac {(-1)^k}{\left( 1 + \lambda_1 \right)^k}\int_0^\infty (1 + x) \left( 1 + \lambda_1 + \lambda_1 x \right)^k\\ &&\times \left[ 1 - \frac {1 + \lambda_2 + \lambda_2 x}{1 + \lambda_2} \exp \left(-\lambda_2 x\right) \right]^{\alpha_2} \exp \left\{ -(k + 1) \lambda_1 x \right\} dx \\ &=& \frac {\alpha_1 \lambda_1^2}{1 + \lambda_1} \sum\limits_{k = 0}^\infty \sum\limits_{l = 0}^k {\alpha_1 - 1 \choose k} {k \choose l} \frac {(-1)^k \lambda_1^l}{\left( 1 + \lambda_1 \right)^l} \\ && \times \Bigg[ \int_0^\infty x^l \left[ 1 - \frac {1 + \lambda_2 + \lambda_2 x}{1 + \lambda_2} \exp \left(-\lambda_2 x\right) \right]^{\alpha_2} \exp \left\{ -(k + 1) \lambda_1 x \right\} dx \\ && \int_0^\infty x^{l + 1} \left[ 1 - \frac {1 + \lambda_2 + \lambda_2 x}{1 + \lambda_2} \exp \left(-\lambda_2 x\right) \right]^{\alpha_2} \exp \left\{ -(k + 1) \lambda_1 x \right\} dx \Bigg] \\ &=& \frac {\alpha_1 \lambda_1^2}{1 + \lambda_1} \sum\limits_{k = 0}^\infty \sum\limits_{l = 0}^k {\alpha_1 - 1 \choose k} {k \choose l} \frac {(-1)^k \lambda_1^l}{\left( 1 + \lambda_1 \right)^l} \\ && \times \left[ K \left( \alpha_2 + 1, \lambda_2, l, (k + 1) \lambda_1 \right) + K \left( \alpha_2 + 1, \lambda_2, l + 1, (k + 1) \lambda_1 \right) \right], \end{array} $$

where the final step follows by an application of Lemma 1. Applying series expansion, Eq. 38, for only the second term within square brackets in Eq. 39, one obtains the representation

$$ \begin{array}{rll} R &=& \frac {\alpha_1 \lambda_1^2}{1 + \lambda_1} \sum\limits_{k = 0}^\infty {\alpha_2 \choose k} \frac {(-1)^k}{\left( 1 + \lambda_2 \right)^k} \int_0^\infty (1 + x) \left( 1 + \lambda_2 + \lambda_2 x \right)^k\\ &&\times \left[ 1 - \frac {1 + \lambda_1 + \lambda_1 x}{1 + \lambda_1} \exp \left(-\lambda_1 x\right) \right]^{\alpha_1 - 1} \exp \left( -k \lambda_2 x - \lambda_1 x \right) dx \\ &=& \frac {\alpha_1 \lambda_1^2}{1 + \lambda_1} \sum\limits_{k = 0}^\infty \sum\limits_{l = 0}^k {\alpha_2 \choose k} {k \choose l} \frac {(-1)^k \lambda_2^l}{\left( 1 + \lambda_2 \right)^l} \\ && \times \int_0^\infty (1 + x) x^l \left[ 1 - \frac {1 + \lambda_1 + \lambda_1 x}{1 + \lambda_1} \exp \left(-\lambda_1 x\right) \right]^{\alpha_1 - 1} \exp \left( -k \lambda_2 x - \lambda_1 x \right) dx \\ &=& \frac {\alpha_1 \lambda_1^2}{1 + \lambda_1} \sum\limits_{k = 0}^\infty \sum\limits_{l = 0}^k {\alpha_2 \choose k} {k \choose l} \frac {(-1)^k \lambda_2^l}{\left( 1 + \lambda_2 \right)^l} K \left( \alpha_1, \lambda_1, l, \lambda_1 + k \lambda_2 \right), \end{array} $$

where the final step follows by an application of Lemma 1. Finally, if λ ₁ = λ ₂ = λ then

$$ R = \frac {\alpha_1 \lambda^2}{1 + \lambda} K \left( \alpha_1 + \alpha_2, \lambda, 0, \lambda_1 \right), $$

which follows by an application of Lemma 1. If in addition α ₁ = α ₂ then R = 1/2. Contours of the Eq. 39 presented in Nadarajah et al. (2011) show that they appear symmetric around the 45° diagonal when λ ₁ and λ ₂ are equal. They become more skewed towards the vertical axis (respectively, the horizontal axis) as the magnitude of λ ₂ − λ ₁ (respectively, λ ₁ − λ ₂) increases.

16 Estimation

Here, we consider estimation by the methods of moments and maximum likelihood and provide expressions for the associated Fisher information matrix. We also consider estimation issues for censored data.

Suppose x ₁, ..., x _n is a random sample from Eq. 2. For the moments estimation, let $m_1 = (1/n) \sum_{j = 1}^n x_j$ and $m_2 = (1/n) \sum_{j = 1}^n x_j^2$. By equating the theoretical moments of Eq. 2 with the sample moments, one obtains the equations:

$$ \frac {\alpha \lambda^2}{1 + \lambda} K (\alpha, \lambda, 1, \lambda) = m_1 $$

(40)

and

$$ \frac {\alpha \lambda^2}{1 + \lambda} K (\alpha, \lambda, 2, \lambda) = m_2. $$

(41)

The method of moments estimators are the simultaneous solutions of these two equations.

Now consider estimation by the method of maximum likelihood. The log likelihood function of the two parameters is:

$$ \log L (\alpha, \lambda)\!=n \log \left( \frac {\alpha\lambda^2}{1\!+\!\lambda} \right)\!+\!\sum\limits_{i=1}^n \log \left( 1\!+\!X_i \right)\!-\!\lambda \sum\limits_{i=1}^n X_i+(\alpha - 1) \sum\limits_{i = 1}^n \log V \left( X_i \right), $$

(42)

where V(·) is given by Eq. 4. It follows that the maximum likelihood estimators, say $\widehat{\alpha}$ and $\widehat{\lambda}$, are the simultaneous solutions of the equations:

$$ \frac {n}{\alpha} = -\sum\limits_{i = 1}^n \log V \left( X_i \right) $$

(43)

and

$$ \frac{n (2 + \lambda)}{\lambda (1 + \lambda)} = \sum\limits_{i = 1}^n X_i + \frac {1 - \alpha}{(1 + \lambda)^2} \sum\limits_{i=1}^n \frac {\exp \left( -\lambda X_i \right)}{V \left( X_i \right)} \left[ \lambda (1 + \lambda) \left( 1 + \lambda + \lambda X_i \right) - X_i \right]. $$

(44)

For interval estimation of (α, λ) and tests of hypothesis, one requires the Fisher information matrix:

$$ {\bf I} = \left( \begin{array}{ll} \displaystyle E \left( -\frac {\partial^2 \log L}{\partial \alpha^2} \right), & \displaystyle E \left( -\frac {\partial^2 \log L}{\partial \alpha \partial \lambda} \right)\\ \displaystyle E \left( -\frac {\partial^2 \log L}{\partial \alpha \partial \lambda} \right) & \displaystyle E \left( -\frac {\partial^2 \log L}{\partial \lambda^2} \right) \end{array} \right). $$

The elements of this matrix for Eq. 42 can be worked out as:

$$ \displaystyle E \left( -\frac {\partial^2 \log L}{\partial \alpha^2} \right) = \frac{n}{\alpha^2}, $$

$$ \displaystyle E \left( \!-\!\frac {\partial^2 \log L}{\partial \alpha \partial \lambda} \right) \!=\! \frac {\alpha \lambda^3}{1 \!+\! \lambda} K \left( \alpha \!-\! 1, \lambda, 0, 2 \lambda \right) \!+\! \frac {\alpha \lambda^2 \left[ \lambda^2 (1 \!+\! \lambda) \!-\! 1 \right]}{(1 \!+\! \lambda)^3} K \left( \alpha \!-\! 1, \lambda, 1, 2 \lambda \right) $$

and

$$ \begin{array}{rll} \displaystyle E \left( -\frac {\partial^2 \log L}{\partial \lambda^2} \right) &=& \frac {2 n}{\lambda^2} - \frac {n}{(1 + \lambda)^2} + \frac {\alpha \lambda^4}{1 + \lambda} K \left( \alpha - 2, \lambda, 0, 3 \lambda \right) \\ && -\frac {2 \alpha \lambda^3 \left[ \lambda^2 (1 + \lambda) - 1 \right]}{(1 + \lambda)^3} K \left( \alpha - 2, \lambda, 1, 3 \lambda \right) \\ && +\frac {\alpha \lambda^2 \left[ \lambda^2 (1 + \lambda) - 1 \right]^2}{(1 + \lambda)^5} K \left( \alpha - 2, \lambda, 2, 3 \lambda \right) \\ && +\frac {\alpha \lambda^2 \left[ \lambda^2 (1 + \lambda) - \lambda - 1 \right]}{(1 + \lambda)^2} K \left( \alpha - 1, \lambda, 0, 2 \lambda \right) \\ && +\frac {\alpha \lambda^2 \left[ 2 - \lambda (1 + \lambda) (1 + 3 \lambda) \right]}{(1 + \lambda)^4} K \left( \alpha - 1, \lambda, 1, 2 \lambda \right), \end{array} $$

where K( ⋯ ) is as defined by Lemma 1. Under regularity conditions, the asymptotic distribution of $(\widehat{\alpha}, \widehat{\lambda})$ as n → ∞ is bivariate normal with zero means and variance co-variance matrix I ^− 1.

Often with lifetime data, one encounters censored data. There are different forms of censoring: type I censoring, type II censoring, etc. Here, we consider the general case of multicensored data: there are n subjects of which

• n ₀ are known to have failed at the times $X_1, \ldots, X_{n_0}$.

• n ₁ are known to have failed in the interval [S _i − 1, S _i ], i = 1, ..., n ₁.

• n ₂ survived to a time R _i , i = 1, ..., n ₂ but not observed any longer.

Note that n = n ₀ + n ₁ + n ₂. Note too that type I censoring and type II censoring are contained as particular cases of multicensoring. The log likelihood function of the two parameters for this multicensoring data is:

$$ \begin{array}{rll} \log L (\alpha, \lambda) &=& n_0 \log \left( \frac {\alpha\lambda^2}{1 + \lambda} \right) \!+\! \sum\limits_{i=1}^{n_0} \log \left( 1 \!+\! X_i \right) \!-\! \lambda \sum\limits_{i=1}^{n_0} X_i \!+\! (\alpha \!-\! 1) \sum\limits_{i = 1}^{n_0} \log V \left( X_i \right) \\ && \!+\!\sum\limits_{i = 1}^{n_1} \log \left[ V^\alpha \left( S_i \right) - V^\alpha \left( S_{i - 1} \right) \right] + \sum\limits_{i = 1}^{n_2} \log \left[ 1 - V^\alpha \left( R_i \right) \right]. \end{array} $$

(45)

It follows that the maximum likelihood estimators are the simultaneous solutions of the equations:

$$ \frac {n}{\alpha} = -\sum\limits_{i = 1}^n \log V \left( X_i \right) - \sum\limits_{i = 1}^{n_1} \frac {U \left( S_i \right) - U \left( S_{i - 1} \right)}{V^\alpha \left( S_i \right) - V^\alpha \left( S_{i - 1} \right)} + \sum\limits_{i = 1}^{n_2} \frac {U \left( R_i \right)}{V^\alpha \left( S_i \right) - V^\alpha \left( S_{i - 1} \right)} $$

and

$$ \begin{array}{rll} \frac{n (2 + \lambda)}{\lambda (1 + \lambda)} &=& \sum\limits_{i = 1}^n X_i + \frac {1 - \alpha}{(1 + \lambda)^2} \sum\limits_{i=1}^n \frac {\exp \left( -\lambda X_i \right)}{V \left( X_i \right)} \left[ \lambda (1 + \lambda) \left( 1 + \lambda + \lambda X_i \right) - X_i \right] \\ && -\alpha \sum\limits_{i = 1}^{n_1} \frac {W \left( S_i \right) - W \left( S_{i - 1} \right)}{V^\alpha \left( S_i \right) - V^\alpha \left( S_{i - 1} \right)} + \sum\limits_{i = 1}^{n_2} \frac {W \left( R_i \right)}{V^\alpha \left( S_i \right) - V^\alpha \left( S_{i - 1} \right)}, \end{array} $$

where U (x) = V ^α(x) log V (x) and $W (x) = (1 + \lambda)^{-2} V^{\alpha - 1} (x) \exp (-\lambda x) \{ \lambda (1 + \lambda) (1 + \lambda + \lambda x) - x \}$. The Fisher information matrix corresponding to Eq. 45 is too complicated to be presented here.

17 Simulation

Here, we consider simulating values of a random variable X with the probability density function 2. Let U denote a uniform random variable on the interval (0, 1). One way to simulate values of X is to set

$$ \left[ 1 + \frac {\lambda X}{1 + \lambda} \right] \exp \left( -\lambda X \right) = 1 - U^{1/\alpha} $$

and solve for X, i.e. use the inversion method. Using Eq. 20, we obtain X as

$$ X = -1 - \frac {1}{\lambda} - \frac {1}{\lambda} W \left( -(1 + \lambda) \exp \left( -1 - \lambda \right) \left( 1 - U^{1/\alpha} \right) \right), $$

where W(·) denotes the Lambert W function. Another way to simulate values of X is by the rejection method with envelope g(·) chosen to be either the gamma probability density function in Eq. 7 or the Weibull probability density function in Eq. 11. It is well known that the rejection scheme for simulating is given by:

• 1. Simulate X = x from the probability density function g(·).

• 2. If g(·) is given by Eq. 7 then simulate Y = U M g(x), where U is an independent uniform random variable on (0, 1) and M is given by Eq. 8; if g(·) is given by Eq. 11 then simulate Y = U M ^* g(x), where U is an independent uniform random variable on (0, 1) and M ^* is given by Eq. 12.

• 3. Accept X = x as a realization of a random variable with the probability density function 2 if Y < f(x). If Y ≥ f(x) return to step 2.

Routines are widely available for simulating from gamma and Weibull distributions (step 1).

18 Maximum likelihood versus moments estimation

In this section, we compare the performances of the two estimation methods presented in Section 16. For this purpose, we generated samples of size n = 10, 20, ..., 50 from Eq. 2 for λ = 1, 2, ..., 6, α = 1, 2, ..., 6 by following the inversion method described in Section 17. For each sample, we computed the moments estimates and the maximum likelihood estimates, by solving the Eqs. 40, 41, 43 and 44 in Section 16. We repeated this process thousand times and computed the bias of the estimates and the mean squared error (MSE). The computer programs NEQNF and GAMIC in IMSL and the computer package R were used for the calculations. The results for n = 20 are reported in Table 1. Those for n = 10, 30, 40, 50 are reported in Nadarajah et al. (2011). logl

Table 1 Maximum likelihood versus moments estimation for n = 20

The following observations can be made:

• for n = 10, the moments estimator is generally superior in terms of bias and mean squared error,

• for n = 20, 30, 40, 50, the moments estimator is generally superior in terms of bias and the maximum likelihood estimator is generally superior in terms of mean squared error,

• the bias of $\widehat{\lambda}$ decreases with increasing n for both maximum likelihood and moments estimators,

• the bias of $\widehat{\alpha}$ decreases with increasing n for both maximum likelihood and moments estimators,

• the mean squared error of $\widehat{\lambda}$ decreases with increasing n for both maximum likelihood and moments estimators,

• the mean squared error of $\widehat{\alpha}$ decreases with increasing n for both maximum likelihood and moments estimators,

• the bias of $\widehat{\lambda}$ generally decreases with increasing α for any given λ and n and for both maximum likelihood and moments estimators,

• the bias of $\widehat{\lambda}$ generally increases with increasing λ for any given α and n and for both maximum likelihood and moments estimators,

• the bias of $\widehat{\alpha}$ generally increases with increasing α for any given λ and n and for both maximum likelihood and moments estimators,

• the mean squared error of $\widehat{\lambda}$ generally decreases with increasing α for any given λ and n and for both maximum likelihood and moments estimators,

• the mean squared error of $\widehat{\lambda}$ generally increases with increasing λ for any given α and n and for both maximum likelihood and moments estimators,

• the mean squared error of $\widehat{\alpha}$ generally increases with increasing α for any given λ and n and for both maximum likelihood and moments estimators.

Because of space limitations, we have only considered n = 10, 20, ..., 50. But the above observations hold also for sample sizes greater than 50.

19 Data analysis

In this section, we illustrate that the new distribution given by Eq. 2 can be a better model than those based on the gamma, lognormal and the Weibull distributions. We use the lifetime data set given by Table 2. This data set is taken from Gross and Clark (1975, p. 105). It shows the relief times of twenty patients receiving an analgesic. We would like to emphasize that the aim here is not to provide a complete statistical modeling or inferences for the data set involved.

Table 2 Relief times of twenty patients

We fitted the models given by Eqs. 2, 7, 6 and 11 to the lifetime data set. The maximum likelihood procedure described by Eqs. 43 and 44 was used. The fitted estimates are given in Table 3. The numbers given within brackets are the standard errors of parameter estimates obtained by the delta method (Rao 1973, pp. 387–389). Also given in the table are the Kolmogorov Smirnov statistics of the fits and the associated p values.

Table 3 Fitted estimates for data in Table 2

The fitted models given by Eqs. 2, 7, 6 and 11 are not nested. So, their comparison should be based on criteria such as the Akaike’s information criterion or the Bayesian information criterion. Table 3 also gives values of these criteria. Note however that if the models have the same number of parameters then these criteria reduce to the usual likelihood ratio test.

Comparing the likelihood values, p values based on the Kolmogorov Smirnov test, AIC and BIC, we see that Eq. 2 provides a significantly better fit than the other three models. We also note from Table 3 that the new model generally yields smaller standard errors than the gamma, lognormal and the Weibull models. This suggests that the new model provides more accurate estimates as well as better fits.