Lindley–Exponential distribution: properties and applications

Abstract

In this paper, we introduce a new class of distributions generated by an integral transform of the probability density function of the Lindley distribution which results in a model that is more flexible in the sense that the derived model spans distributions with increasing failure rate, decreasing failure rate and upside down bathtub shaped hazard rate functions for different choices of parametric values. For this new model, various distributional properties including limiting distribution of extreme order statistics are established. Maximum likelihood estimators and the marginal confidence intervals of the parameters are obtained. The applicability of the proposed distribution is shown through application to real data sets. Through application to two real datasets, it is demonstrated that the proposed model fits better as compared to some other competing models. Further, the model is shown to be useful for analysing stress–strength model.

1 Introduction

Lifetime distribution represents an attempt to describe, statistically, the length of the life of a system, a device, and in general, time-to-event data. Lifetime distributions are frequently used in fields like medicine, biology, engineering, insurance etc. Many parametric models such as exponential, gamma, weibull have been frequently used in statistical literature to analyse lifetime data.

Recently, one parameter Lindley distribution has attracted researchers for its potential in modelling lifetime data, and it has been observed that this distribution has performed excellently in many applications. The Lindley distribution was originally proposed by Lindley [19] in the context of Bayesian statistics, as a counter example to fiducial statistics. The distributon can also be derived as a mixture of exp($\theta$) and gamma(2, $\theta$). More details on the Lindley distribution can be found in Ghitany et al. [7].

A random variable $X$ is said to have the Lindley distribution with parameter $\theta$ if its probability density is defined as:

$$\begin{aligned} f_X(x;\theta )=\frac{\theta ^2}{(\theta +1)}(1+x) e^{-\theta x} ;x > 0,\theta >0. \end{aligned}$$

(1)

The corresponding cumulative distribution function is

$$\begin{aligned} F(x)=1-\frac{e^{-\theta x}(1+\theta +\theta x)}{1+\theta }; x \in \mathbb {R}^+, \theta >0, \end{aligned}$$

Ghitany et al. [6, 7] have introduced a two-parameter weighted Lindley distribution and have pointed out its usefulness, in particular, in modelling biological data from mortality studies. Bakouch et al. [4] have come up with extended Lindley (EL) distribution, Adamidis and Loukas [1] have introduced a new lifetime distribution with decreasing failure rate. Shanker et al. [23] have introduced a two-parameter Lindley distribution. Zakerzadeh and Mahmoudi [24] have proposed a new two parameter lifetime distribution: model and properties. Hassan [11] has introduced convolution of Lindley distribution. Ghitany et al. [8] worked on the estimation of the reliability of a stress-strength system from power lindley distribution. Elbatal et al. [5] has proposed a new generalized Lindley distribution by considering the mixture of two gamma distribution.

Ristić and Balakrishnan [22] have introduced a new family of distributions generated by gamma pdf with survival function given by

$$\begin{aligned} \bar{F}_X(x)= \frac{1}{\Gamma (\alpha )}\int \limits _{0}^{-\log \left( G(x) \right) } t^{\alpha -1}e^{-t} dt, \quad \quad x \in \mathbb {R}^+, \alpha > 0, \end{aligned}$$

where $G(x)$ is a chosen distribution function, called the parent distribution function (df).

In this paper, we introduce a new family of distribution generated by an integral transform of the pdf of a random variable $T$ which follows one parameter Lindley distribution. The survival function of this new family is given as:

$$\begin{aligned} \bar{F}_X(x)= \frac{\theta ^2}{1+\theta }\int \limits _{0}^{-\log (G(x))} (1+t)e^{-\theta t} dt, \quad \quad x\in \mathbb {R}^+, \theta > 0 \end{aligned}$$

(2)

where $\theta > 0$ ,the corresponding probability density function (pdf) is given by

$$\begin{aligned} f(x)=\frac{\theta ^2}{1+\theta }\left( 1-\log G(x)\right) G(x)^{\theta -1} g(x), \end{aligned}$$

(3)

In this formation, we consider $G(x)$ corresponding to exponential distribution with cdf $(1-e^{-\lambda x})$ which yields the survival function of the new distribution is as

$$\begin{aligned} \bar{F}(x)=1-\frac{ \left( 1-e^{-\lambda x}\right) ^{\theta }\left( 1+\theta - \theta \log \left( 1-e^{-\lambda x} \right) \right) }{1+\theta }, \end{aligned}$$

(4)

with corresponding density

$$\begin{aligned} f(x)=\frac{ \theta ^2 \lambda e^{-\lambda x} \left( 1-e^{-\lambda x}\right) ^{ \theta -1} \left( 1-\log \left( 1-e^{-\lambda x}\right) \right) }{(1+\theta )}. \end{aligned}$$

(5)

In this paper, we refer to random variable with survival function (4) as Lindley–Exponential (L–E) distribution with parameters $\theta$ and $\lambda$ and denote it by L–E($\theta ,\lambda$). Motivation for this paper arose from the following observation.

In modelling time-to-event data arising from a new application, the monotonicity nature of the hazard rate function is uncertain and hence an a priori choice of a model becomes challenging. In such cases, one usually resorts to nonparametric methods in general. However, if a parametric model fits the particular application well, it is preferable to choose one such model. There is thus a need to develop a distributional model which would span various monotonicity properties of the hazard rate function, and this paper is an attempt to develop a new model with two parameters model ensuring flexibility of hazard function to posses increasing, decreasing and upside down shapes. Having developed one such distribution, we observe the following properties that connect the new model to known distributions.

• 1. Let $U$ be a random variable with the Log-lindley distribution $LL(\theta ,1)$ proposed by Goméz et al. [10]. Then the random variable $V= G^{-1}(U)$ has distribution with pdf as in (3).

• 2. If $U$ be Lindley distributed random variable, then the random variable $X=G^{-1}(e^{-U})$ has pdf (3).

We now study properties of the L–E distribution and illustrate its applicability. The contents of the proposed work are organized as follows. Various distributional properties like shape of the pdf, quantile function, moment generating function, limiting distribution of sample statistics like maximum and minimum and entropy of L–E distribution are present in Sect. 2. The maximum likelihood estimation is presented in Sect. 3. Performance of the maximum likelihood estimators for small samples is assessed by simulation in Sect. 4. Applicability of the new distribution is shown in Sect. 5. Section 6, gives estimation of stress–strength parameter $(R)$ by using maximum likelihood estimation method.

2 Distributional properties of L–E distribution

2.1 Shape of the density

Theorem 1

The probability density function of the L–E distribution is decreasing for $0<\theta <1$ and uni-modal for $\theta >1$. In the latter case, the mode is the root of the following equation:

$$\begin{aligned} (1-\theta e^{-\lambda x})\left( 1-\log (1-e^{-\lambda x})\right) +e^{-\lambda x}=0 \end{aligned}$$

Proof

The first order derivative of $\log (f(x))$ is

$$\begin{aligned} \frac{d \log (f(x))}{d x}=\frac{\lambda \, r(x)}{\left( 1-e^{-\lambda x}\right) \left( 1-\log \left( 1-e^{-\lambda x}\right) \right) }. \end{aligned}$$

(6)

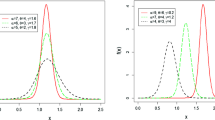
where, $r(x)=\left( \theta e^{-\lambda x}+\left( 1-\theta e^{-\lambda x}\right) \log \left( 1-e^{-\lambda x}\right) -e^{-\lambda x}-1\right)$. For $0<\theta <1$, the function $r(x)$ is negative. So $f'(x)<0$ for all $x>0$. This implies that $f$ is decreasing for $0< \theta <1$. Also note that, $(\log f)'(0)=\infty$ and $(\log f)'(\infty )<0$. This implies that for $\theta >1$, $g(x)$ has a unique mode at $x_0$ such that $r(x) >0$ for $x<x_0$ and $r(x)<0$ for $x>x_0$. So, $g$ is uni-modal function with mode at $x=x_0$. The pdf for various values of $\lambda$ and $\theta$ are plotted in Fig. 1. $\square$

Fig. 1

PDF plot for various values of $\lambda$ and $\theta$

Theorem 2

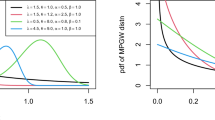
The hazard function of L–E distribution is decreasing, increasing or upside down according as $0<\theta \le 1$, $\theta >2$ and $1<\theta <2$ respectively.

Proof

Considering the hazard rate function (hrf) of the L–E distribution given by

$$\begin{aligned} h(x)=\frac{\theta ^2 \lambda e^{\lambda -x} \left( 1-e^{-\lambda x}\right) ^{\theta -1} \left( 1-\log \left( 1-e^{-\lambda x}\right) \right) }{1+\theta -\left( 1-e^{-\lambda x}\right) ^{\theta } \left( 1+\theta -\theta \log \left( 1-e^{-\lambda x}\right) \right) }, \end{aligned}$$

(7)

and using theorems of Glaser [9], we can discuss the shape characteristics of the hrf of L–E distribution. The function $\eta (x) = -f^{'}(x)/f(x)$ for L–E distribution is given by

$$\begin{aligned} \eta (x) =\lambda \left( \frac{1-\theta e^{-\lambda x}}{1-e^{-\lambda x}}+\frac{e^{-\lambda x}}{\left( 1-e^{-\lambda x}\right) \log \left( 1-e^{-\lambda x}\right) }\right) \end{aligned}$$

and

$$\begin{aligned} \eta ^{'}(x)=\frac{\lambda ^2 e^{-\lambda x} \left( (\theta -2)+(\theta -1) \text {Log}^2\left( 1-e^{-\lambda x}\right) -(2 \theta -3) \log \left( 1-e^{-\lambda x}\right) +e^{-\lambda x}\right) }{\left( 1-e^{-\lambda x}\right) ^2 \left( 1-\log \left( 1-e^{-\lambda x}\right) \right) ^2}. \end{aligned}$$

If $0 < \theta \le 1$, then $\eta ^{'} (x) < 0~ \forall ~ x > 0$. It follows from Theorem (b) of Glaser [9] that the failure rate is decreasing. Whereas, for $\theta > 2, \eta ^{'} (x) > 0 \, \forall \, x > 0$ which indicate increasing failure rate (see Theorem (b) of Glaser [9]. Furthermore, we note that the failure rate can be upside-down bathtub for $1 < \theta < 2$. Moreover, for $\theta > 0$ the hazard rate function follows relation $\lim \nolimits _{x \rightarrow \infty } h(x) = \lambda$. These different failure rate for different values of parameters $\theta$ and $\lambda$ are shown in Fig. 2. $\square$

Fig. 2

Hazard function plot for various values of $\lambda$ and $\theta$

2.2 The quantile function of L–E distribution

The cdf, $F_X(x)=1-\bar{F}(x)$, can be obtained by using Eq. (4). Further, it can be noted that $F_X$ is continuous and strictly increasing so that the quantile function of $X$ is $Q_X(\gamma )=F^{-1}_X(\gamma )$, $0<\gamma <1$. In the following theorem, we give an explicit expression for $Q_X$ in terms of the Lambert $W$ function. For more details on Lambert $W$ function we refer the reader to Joŕda [12] and also to Nair et al. [20] for discussion on quantile functions.

Theorem 3

For any $\theta , \lambda >0$, the quantile function of the L–E distribution $X$ is

$$\begin{aligned} x_{\gamma }=F^{-1}(\gamma )=-\frac{1}{\lambda }\log \left( 1-\left( -\frac{W_{-1} \left( -e^{-\theta -1} (\theta +1) \gamma \right) }{(\theta +1) \gamma }\right) ^{-1/\theta }\right) , \end{aligned}$$

(8)

where $W_{-1}$ denotes the negative branch of the Lambert W function.

Proof

By assume $p=1-e^{-\lambda x}$ the cdf can be written as

$$\begin{aligned} F_X(x)=\frac{p^\theta (1+\theta -\theta \log (p))}{1+\theta } \end{aligned}$$

for fixed $\theta , \lambda >0$ and $\gamma \in (0,1)$, the $\gamma$th quantile function is obtained by solving $F_X(x)=\gamma$. By re-arranging the above, we obtain

$$\begin{aligned} \log (p^{-\theta })-\gamma p^{-\theta }(1+\theta )=-(1+\theta ) \end{aligned}$$

it can be further written as

$$\begin{aligned} -p^{-\theta }(1+\theta )\gamma e^{-p^{-\theta }(1+\theta )\gamma }=-(1+\theta )\gamma e^{-(1+\theta )}. \end{aligned}$$

(9)

We see that $-p^{-\theta } (1+\theta )\gamma$ is the Lambert-W function of real argument $-(1+\theta )\gamma e^{-(1+\theta )}$ .

Thus, we have

$$\begin{aligned} W\left( -(1+\theta )\gamma e^{-(1+\theta )}\right) =-p^{-\theta }(1+\theta )\gamma \end{aligned}$$

(10)

Moreover, for any $\theta$ and $\lambda >0$ it is immediate that $p^{-\theta }(1+\theta )\gamma > 1$, and it can also be checked that $(1+\theta )\gamma e^{-(1+\theta )} \in (-1/e,0)$ since $\gamma \in (0,1)$. Therefore, by taking into account the properties of the negative branch of the Lambert W function, we deduce the following.

$$\begin{aligned} W_{-1}\left( -(1+\theta )\gamma e^{-(1+\theta )}\right) =-p^{-\theta }(1+\theta )\gamma \end{aligned}$$

Again,solving for $x$ by using $p=1-e^{-\lambda x}$, we get

$$\begin{aligned} x_{\gamma }=F^{-1}(\gamma )=-\frac{1}{\lambda }\log \left( 1-\left( -\frac{W_{-1} \left( -e^{-\theta -1} (\theta +1) \gamma \right) }{(\theta +1) \gamma }\right) ^{-1/\theta }\right) . \end{aligned}$$

(11)

$\square$

Further the first three quantiles can be obtained by substituting $\gamma =\frac{1}{4},\frac{1}{2},\frac{3}{4}$ in (11).

$$\begin{aligned} Q_1&=F^{-1}(1/4)= - \frac{1}{\lambda }\log \left( 1-\left( -\frac{4 W_{-1}\left( \frac{-e^{-\theta -1}(1+\theta )}{4} \right) }{(1+\theta )} \right) ^{-\frac{1}{\theta }} \right) \nonumber \\ \text {Median} (M_d)=Q_2&=F^{-1}(1/2)= -\frac{1}{\lambda }\log \left( 1-\left( -\frac{2 W_{-1}\left( \frac{-e^{-\theta -1}(1+\theta )}{2} \right) }{(1+\theta )} \right) ^{-\frac{1}{\theta }} \right) \nonumber \\ Q_3&=F^{-1}(3/4)= -\frac{1}{\lambda }\log \left( 1-\left( -\frac{4 W_{-1}\left( \frac{-3e^{-\theta -1}(1+\theta )}{4} \right) }{3(1+\theta )} \right) ^{-\frac{1}{\theta }} \right) \end{aligned}$$

(12)

2.3 Moments

The Moment Generating function of L–E random variable is given as

$$\begin{aligned} \mathbb {M}_X(t)= \mathbb {E}(e^{Xt})=&\int _0^{\infty } \frac{\theta ^2 \lambda e^{-x(\lambda -t)} \left( 1-e^{-\lambda x}\right) ^{\theta -1} \left( 1-\log \left( 1-e^{-\lambda x}\right) \right) }{\theta +1} \, dx\nonumber \\ =&\frac{\theta \Gamma (\theta +1) \Gamma \left( 1-\frac{t}{\lambda }\right) \left( -\psi ^{(0)}(\theta )+\psi ^{(0)}\left( -\frac{t}{\lambda }+\theta +1\right) +1\right) }{(\theta +1) \Gamma \left( -\frac{t}{\lambda }+\theta +1\right) } \end{aligned}$$

(13)

where, $\psi ^{(n)}(z)=\frac{d^n \psi (z)}{dz^n}$ and $\psi (z)=\frac{\Gamma '(z)}{\Gamma (z)}$ known as digamma function.

Hence the first and second raw moments can be obtained by differentiating the MGF $\left( \frac{d\mathbb {M}_X(t)}{dt}\right) _{t=0}$ and $\left( \frac{d^2\mathbb {M}_X(t)}{dt^2}\right) _{t=0}$ respectively.

$$\begin{aligned} \mathbb {E}(X)=\,&\frac{\upgamma \theta +\frac{1}{\theta }+\theta (-\psi ^{(1)}(\theta +1))+(\theta +1) \psi ^{(0)}(\theta )+\upgamma +1}{(\theta +1) \lambda }\end{aligned}$$

(14)

$$\begin{aligned} \mathbb {E}(X^2)=\,&\frac{1}{\theta ^2(\theta +1)\lambda ^2} \left( (\theta +1) \left( \left( \upgamma ^2+\frac{\pi ^2}{6}\right) \theta ^2+2 \upgamma \theta +1\right) \right. \nonumber \\&\left. +\theta (\theta +1) \psi ^{(0)}(\theta )(2\upgamma \theta +\theta \psi ^{(0)}(\theta )+2) \right. \nonumber \\&\left. -\theta ^2 (\theta +2 \theta (\psi ^{(0)}(\theta )+\upgamma +3) \psi ^{(1)}(\theta +1)+\theta ^3 \psi ^{(2)}(\theta +1)\right) \end{aligned}$$

(15)

where $\upgamma$ is Eulergamma constant $=$ 0.577216.

Table 1 displays the mode, mean and median for L–E distribution for different choices of parameter $\lambda$ and $\theta$. It can be noted from the table that all three measures of central tendency decrease as $\lambda$ increases, and the measures increase as $\theta$ increase. Also for any choice of $\lambda$ and $\theta$ Mean $>$ Median $>$ Mode which is an indication of positive skewness.

Table 1 Mode, mean and median for various value of parameter

2.4 Limiting distribution of sample minimum and maximum

We can derive the asymptotic distribution of the sample minima $X_{1:n}$ by using Theorem 8.3.6 of Arnold et al. [3], it follows that the asymptotic distribution of $X_{1:n}$ is Weibull type with shape parameter $\theta >0$ if

$$\begin{aligned} \lim \limits _{t \rightarrow 0^+}\frac{F(tx)}{F(t)}=x^\theta , \quad \forall x >0 \end{aligned}$$

From (4), $F(X)=1-\bar{F}(X)$, using the identities

$$\begin{aligned} \lim \limits _{t \rightarrow 0^+} \frac{(1-e^{-\lambda t x})^{\theta -1}}{(1-e^{-\lambda t })^{\theta -1}}=x^{\theta -1} \end{aligned}$$

and

$$\begin{aligned} \lim \limits _{t \rightarrow 0^+} \frac{(1-\log (1-e^{-\lambda t x}))}{(1-\log (1-e^{-\lambda t}))}=1 \end{aligned}$$

Thus,we get

$$\begin{aligned} \lim \limits _{t \rightarrow 0^+}\frac{F(tx)}{F(t)}=x \lim \limits _{t \rightarrow 0^+}\frac{f(tx)}{f(t)}= x \lim \limits _{t \rightarrow 0^+} \frac{(1-e^{-\lambda t x})^{\theta -1}(1-\log (1-e^{-\lambda t x}))}{(1-e^{-\lambda t })^{\theta -1}(1-\log (1-e^{-\lambda t}))}=x^{\theta } \end{aligned}$$

Similarly, using the following identity

$$\begin{aligned} \lim \limits _{t \rightarrow \infty } \frac{\left( 1-e^{-\lambda (t+x)}\right) ^{\theta -1}}{\left( 1-e^{-\lambda t}\right) ^{\theta -1}} =e^{-\lambda x(\theta -1)} \end{aligned}$$

and

$$\begin{aligned} \lim \limits _{t \rightarrow \infty } \frac{1-\log \left( 1-e^{-\lambda (t+x)}\right) }{1-\log \left( 1-e^{-\lambda t}\right) } = 1 \end{aligned}$$

It can be seen that

$$\begin{aligned} \lim \limits _{t \rightarrow \infty }\frac{1-F(t+x)}{1-F(t)}=\lim \limits _{t \rightarrow \infty } \frac{(1+\theta )-(1-e^{-\lambda (x+t)})^\theta (1+\theta -\theta \log (1-e^{-\lambda (x+t)}))}{(1+\theta )-(1-e^{-\lambda t})^\theta (1+\theta -\theta \log (1-e^{-\lambda t}))} \end{aligned}$$

by using L-Hópitals rule,

$$\begin{aligned} \lim \limits _{t \rightarrow \infty }\frac{e^{-\lambda x} \left( 1-e^{-\lambda (t+x)}\right) ^{\theta -1} \left( 1-\log \left( 1-e^{-\lambda (t+x)}\right) \right) }{\left( 1-e^{-\lambda t}\right) ^{\theta -1} \left( 1-\log \left( 1-e^{-\lambda t}\right) \right) }=e^{-\lambda \theta x} \end{aligned}$$

Hence, it follows from Theorem 1.6.2 in Leadbetter et al. [17] that there must be norming constants $a_n>0$,  $b_n, c_n>0$ and $d_n$ such that

$$\begin{aligned} \text {Pr}\lbrace a_n(M_n-b_n)\le x \rbrace \rightarrow e^{-e^{-\theta \lambda x}} \end{aligned}$$

(16)

and

$$\begin{aligned} \text {Pr}\lbrace c_n(m_n-d_n)\le x \rbrace \rightarrow 1-e^{-x^\theta } \end{aligned}$$

(17)

as $n \rightarrow \infty$. By following Corollary 1.6.3 in Leadbetter et al. [17], we can determine the form of the norming constants. As an illustration, one can see that $a_n = \theta$ and $b_n=F^{-1}(1-1/n)$, where $F^{-1}(.)$ denotes the inverse function of $F(.)$.

2.5 Entropy

In many fields of science such as communication, physics and probability, entropy is an important concept to measure the amount of uncertainty associated with a random variable $X$. Several entropy measures and information indices are available but among them the most popular entropy called Rényi entropy defined as

$$\begin{aligned} \mathfrak {J}(\zeta )=\frac{1}{1-\zeta } \log \left( \, \int \limits _{\mathbb {R}^+}f^\zeta (x) dx \right) , \quad \text {for} \quad \zeta >1 \quad \text {and} \quad \zeta \ne 1 \end{aligned}$$

(18)

In our case

$$\begin{aligned} \int \limits _{\mathbb {R}^+} f^\zeta dx= \int \limits _{\mathbb {R}^+} \left( \frac{\theta ^2 \lambda }{\theta +1}\right) ^{\zeta }e^{-x \lambda \zeta } \left( 1-e^{-x\lambda }\right) ^{\zeta (\theta -1)} \left( 1-\log \left( 1-e^{-x\lambda }\right) \right) ^\zeta dx \end{aligned}$$

substituting $x=-\frac{1}{\lambda }\log (1-e^{-u})$ and using power series expansion $(1-z)^\alpha =\sum \nolimits _{j=0}^{\infty }(-1)^j \left( {\begin{array}{c}\alpha \\ j\end{array}}\right) z^j$, the above expression reduces to

$$\begin{aligned} \nonumber \int \limits _{\mathbb {R}^+} f^\zeta dx=\,&\frac{\theta ^{2 \zeta } \lambda ^{\zeta -1}}{(\theta +1)^{\zeta }}\int _0^{\infty } (u+1)^{\zeta } \left( 1-e^{-u}\right) ^{\zeta -1} e^{u (-(\zeta (\theta -1)+1))} \, du \nonumber \\ =\,&\frac{\theta ^{2 \zeta } \lambda ^{\zeta -1}}{(\theta +1)^{\zeta }}\int _0^{\infty }\sum _{j=0}^{\infty } (-1)^j \left( {\begin{array}{c}\zeta -1\\ j\end{array}}\right) e^{u(-(\zeta (\theta -1)+j+1))} (u+1)^{\zeta } du \nonumber \\ =\,&\frac{\theta ^{2 \zeta } \lambda ^{\zeta -1}}{(\theta +1)^{\zeta }} \sum _{j=0}^{\infty } (-1)^j \left( {\begin{array}{c}\zeta -1\\ j\end{array}}\right) \int _0^{\infty } (u+1)^{\zeta } e^{u(-(\zeta (\theta -1)+j+1))} \, du \nonumber \\ =\,&\frac{\theta ^{2 \zeta } \lambda ^{\zeta -1}}{(\theta +1)^{\zeta }} \sum _{j=0}^{\infty } (-1)^j e^{\zeta (\theta -1)+j+1} E_{-\zeta }\left[ (j+(\theta -1) \zeta +1)\right] \end{aligned}$$

(19)

where $E_n(z)=\int _1^{\infty }e^{-zt} t^{-n} dt$ known as exponential integral function. For more details see http://functions.wolfram.com/06.34.02.0001.01.

Thus according to (18) the Rényi entropy of L–E$(\theta ,\lambda )$ distribution given as

$$\begin{aligned} \mathfrak {J}(\zeta )=\frac{1}{1-\zeta }\log \left( \frac{\theta ^{2 \zeta } \lambda ^{\zeta -1}}{(\theta +1)^{\zeta }} \sum _{j=0}^{\infty } (-1)^j e^{\zeta (\theta -1)+j+1} E_{-\zeta }\left[ (j+(\theta -1) \zeta +1)\right] \right) \!. \end{aligned}$$

(20)

Moreover, The Shannon entropy defined by $E[\log (f(x))]$ is a special case derived from $\lim \nolimits _{\zeta \rightarrow 1}\mathfrak {J}(\zeta )$

3 Maximum likelihood estimators

In this section we shall discuss the point and interval estimation of the parameters of L–E$(\theta ,\lambda )$. The log-likelihood function $\nonumber l(\Theta )$ of single observation (say $x_i$) for the vector of parameter $\Theta =(\theta , \lambda )^\top$ is

$$\begin{aligned} l_n(x,\Theta )&= 2 \log (\theta )+ \log (\lambda )-\log (\theta +1)+(\theta -1) \log (1-e^{-\lambda x }) \\&+\log (1-\log (1-e^{-\lambda x}))-\lambda x \end{aligned}$$

The associated score function is given by $U_n= \left( \frac{\partial l_n}{\partial \theta }, \frac{\partial l_n}{\partial \lambda } \right) ^\top$, where

$$\begin{aligned} \frac{\partial l_n}{\partial \theta }=\frac{2}{\theta }-\frac{1}{\theta +1}+ \log \left( 1-e^{-\lambda x}\right) \end{aligned}$$

(21)

$$\begin{aligned} \frac{\partial l_n}{\partial \lambda }=\frac{1}{\lambda }-x+(\theta -1)\frac{x e^{-\lambda x}}{1-e^{-\lambda x }}+ \frac{x e^{-\lambda x}}{\left( 1-e^{-\lambda x}\right) (1- \log \left( 1-e^{-\lambda x}\right) )}. \end{aligned}$$

(22)

As we know th expected value of score function equals zero, i.e. $\mathbb {E}(U(\Theta ))$, which implies $\mathbb {E}\left( \log \left( 1-e^{-\lambda x}\right) \right) = \frac{1}{\theta +1}-\frac{2}{\theta }$.

Fig. 3

Contour plot of log-likelihood surface for different values of $\theta$ and $\lambda$

The total log-likelihood of the random sample $x=\left( x_1,\ldots , x_n\right) ^\top$ of size $n$ from $X$ is given by $l_n= \sum \nolimits _{1}^{n}l^{(i)}$ and th total score function is given by $U_n=\sum \nolimits _{i=1}^{n}U^{(i)}$, where $\nonumber l^{(i)}$ is the log-likelihood of $i$th observation and $U^{(i)}$ as given above. The maximum likelihood estimator $\hat{\Theta }$ of $\Theta$ is obtained by solving Eqs. (21) and (22) numerically or this can also obtained easily by using nlm() function in R. The initial guess for the estimators were obtained from the inner region of 3D contour plot of log-likelihood function for a given sample. For example, in Fig. 3, the contour plot of log-likelihood function for different $\theta$ and $\lambda$, the initial estimates were taken from interior. The associated Fisher information matrix is given by

$$\begin{aligned} K=K_n(\Theta )= n \left[ \begin{array}{ll} \kappa _{\theta ,\theta } \quad \kappa _{\theta ,\lambda } \\ \kappa _{\lambda ,\theta } \quad \kappa _{\lambda ,\lambda } \end{array} \right] \end{aligned}$$

(23)

where

$$\begin{aligned} \kappa _{\theta ,\theta }&= \frac{n}{(\theta +1)^2}-\frac{2 n}{\theta ^2}\nonumber \\ \kappa _{\lambda ,\theta }=\kappa _{\theta ,\lambda }&= \mathbb {E} \left( \frac{X e^{-\lambda X}}{1-e^{-\lambda X}}\right) \nonumber \\ \kappa _{\lambda ,\lambda }&=\frac{1}{\lambda ^2}+\mathbb {E}\left( \!\frac{(\theta -1) \left( X^2 e^{-\lambda X}\right) }{\left( 1-e^{-\lambda X}\right) ^2}\!\right) -\mathbb {E}\left( \!\frac{X^2 e^{-\lambda X} \left( -e^{-\lambda X}-\log \left( 1-e^{-\lambda X}\right) +1\right) }{\left( 1-e^{-\lambda X}\right) ^2 \left( 1-\log \left( 1-e^{-\lambda X}\right) \right) ^2}\!\right) \end{aligned}$$

(24)

The above expressions depend on some expectations which can be easily computed using numerical integration. Under the usual regularity conditions, the asymptotic distribution of

$$\begin{aligned} \sqrt{n}\left( \hat{\Theta }-\Theta \right) \, \, \text {is} \, \, N_2(0,K(\Theta )^{-1}) \end{aligned}$$

(25)

where $\lim \nolimits _{n \rightarrow \infty } K_n(\Theta )^{-1}=K(\Theta )^{-1}$. The asymptotic multivariate normal $N_2(0,K(\Theta )^{-1})$ distribution of $\hat{\Theta }$ can be used to construct approximate confidence intervals. An asymptotic confidence interval with significance level $\alpha$ for each parameter $\theta$ and $\lambda$ is

$$\begin{aligned} \text {ACI}\left( \theta ,100(1-\alpha )\,\% \right) \equiv \,&(\hat{\theta }-z_{\alpha /2}\sqrt{\kappa _{(\theta ,\theta )}},\hat{\theta }+z_{\alpha /2}\sqrt{\kappa _{(\theta ,\theta )}}) \nonumber \\ \text {ACI}\left( \lambda ,100(1-\alpha )\,\% \right) \equiv \,&(\hat{\lambda }-z_{\alpha /2}\sqrt{\kappa _{(\lambda ,\lambda )}},\hat{\lambda }+z_{\alpha /2}\sqrt{\kappa _{(\lambda ,\lambda )}}) \end{aligned}$$

(26)

where $z_{1-\alpha /2}$ denotes $1-\alpha /2$ quantile of standard normal random variable.

4 Simulation

In this section, we investigate the behaviour of the ML estimators in finite sample sizes through a simulation study based on different L–E$(\theta ,\lambda )$. The observations are generated using cdf technique presented in Sect. 4 from L–E$(\theta ,\lambda )$ and in the following Sects. 4.1 and 4.2, we investigate the performance of maximum likelihood estimators $(\hat{\theta },\hat{\lambda })$ for various combinations of parameters $(\theta ,\lambda )$ and also with respect to sample size $n$ respectively.

4.1 Performance of estimators for different parametric values

A simulation study consisting of following steps is carried out for each triplet $(\theta ,\lambda ,n)$, where $\theta = 0.5, 1, 2, \lambda = 0.5, 1, 2 ,3$ and $n= 25, 50, 75, 100$.

• 1. Choose the values $\theta _\circ ,\lambda _\circ$ for the corresponding elements of the parameter vector $\Theta =(\theta ,\lambda )$, to specify L–E$(\theta ,\lambda )$ distribution;

• 2. choose sample size $n$;

• 3. generate $N$ independent samples of size $n$ from L–E$(\theta ,\lambda )$;

• 4. compute the ML estimate $\hat{\Theta _n}$ of $\Theta _\circ$ for each of the $N$ samples;

• 5. compute the average bias $= \frac{1}{N} \sum \nolimits _{i=1}^{N}(\Theta _i-\Theta _\circ )$, the average mean square error MSE $(\Theta )= \frac{1}{N} \sum \nolimits _{i=1}^{N}(\Theta _i-\Theta _\circ )^2$ and average width (AW) of 95 % of confidence limit of the obtained estimates over all $N$ samples.

Table 2 Average bias of the simulated estimates

Table 3 Average MSE of the simulated estimates

Table 4 Average Width of 95 % confidence limit

In all three Tables, Tables 2, 3 and 4, it can be clear seen that the value of average bias, MSE and average width decreases with increase in sample size $n$.

4.2 Performance of estimators with respect to sample size $n$

In this subsection, we assess the performance of ML estimators of $\hat{\theta }$ and $\hat{\lambda }$ as sample size $n$, varies from $n = 10, 11,\ldots , 100$, for $\theta =1$ and $\alpha =0.5$. For each of these sample sizes, we generate one thousand samples by using inversion method discussed in Sect. 4 and obtain maximum likelihood estimators and standard errors of ML estimates, $(\hat{\theta }, \hat{\lambda })$ and $(s_{i,\hat{\theta }}, s_{i,\hat{\lambda }})$ for $i=1, 2, \ldots , 1{,}000$ respectively. For each repetition we comput bias, mean squared error and Coverage Lengths (CL):

$$\begin{aligned} bias_{\Theta }(n)&= \frac{1}{1{,}000}\sum \limits _{i=1}^{1,000}\left( \hat{\Theta }_i -\Theta \right) , \textit{MSE}_{\Theta }(n)=\frac{1}{1{,}000}\sum \limits _{i=1}^{1{,}000}\left( \hat{\Theta }_i -\Theta \right) ^2,\\ \text {CL}_{\Theta }(n)&= \frac{2 \cdot 1.956}{1{,}000}\sum \limits _{i=1}^{1,000}s_{i,\hat{\Theta }} \end{aligned}$$

The coverage probabilities (CP) are given by

$$\begin{aligned} \text {CP}_{\Theta }(n)= \frac{1}{1{,}000}\sum \limits _{i=1}^{1{,}000}\mathbb {I}\left( \hat{\Theta }-1.96 s_{i,\hat{\Theta }}< \Theta < \hat{\Theta }-1.96 s_{i,\hat{\Theta }}\right) \end{aligned}$$

for $\Theta =(\theta , \lambda )$ and $\mathbb {I}$ is an indicator function.

Fig. 4

Bias for $\hat{\theta }$ and $\hat{\lambda }$ versus $n$

Fig. 5

MSE for $\hat{\theta }$ and $\hat{\lambda }$ versus $n$

Fig. 6

Converge length for $\hat{\theta }$ and $\hat{\lambda }$ versus $n$

Fig. 7

Converge probabilities for $\hat{\theta }$ and $\hat{\lambda }$ versus $n$

Figures 4, 5, 6 and 7 shows behaviour of bias, mean squared error, coverage length and coverage probability of parameter $(\theta$ and $\lambda )$ as one varies vary $n$. The horizontal lines in Fig. 7 correspond to the coverage probabilities being 0.95.

The following observations can be drawn from the figures: the biases for both the parameter appear generally positive and approach to zero with increasing $n$; the mean squared errors and coverage lengths of $(\theta$ and $\lambda )$ decrease with $n$. The coverage probabilities for $\lambda$ appear generally less than the nominal level but reach the nominal level as sample size increases whereas the coverage probabilities for $\theta$ appear generally closer than the nominal level. These observations are for $\theta = 1$ and $\alpha = 0.5$ and similar observations were noted for other values of parameters.

5 Application to real datasets

In this section, we illustrate, the applicability of L–E Distribution by considering two different datasets used by different researchers. We also fit L–E distribution, Power–Lindley distribution [8], New Generalized Lindley Distribution [5], Lindley Distribution [19], and Exponential distribution. Namely

(i) Power–Lindley distribution (PL$(\alpha ,\beta )$):

$$\begin{aligned} f_1(x)=\frac{\alpha \beta ^2}{1+\beta }(1+x^\alpha ) x^{\alpha -1} e^{-\beta x^\alpha }, \quad \quad x,\alpha ,\beta >0. \end{aligned}$$

(ii) New Generalized Lindley distribution (NGLD($\alpha ,\beta ,\theta$)):

$$\begin{aligned} f_2(x)=\frac{e^{-\theta x}}{1+\theta }\left( \frac{\theta ^{\alpha +1}x^{\alpha -1}}{\Gamma (\alpha )}+\frac{\theta ^{\beta }x^{\beta -1}}{\Gamma (\beta )}\right) , \quad \quad x,\alpha ,\theta ,\beta >0. \end{aligned}$$

(iii) Lindley Distribution (L$(\theta )$)

$$\begin{aligned} f_3(x)=\frac{\theta ^2}{1+\theta }(1+x) e^{-\theta x}, \quad \quad x,\alpha ,\beta >0. \end{aligned}$$

For each of these distributions, the parameters are estimated by using the maximum likelihood method, and for comparison we use Negative LogLikelihood values ($-LL$), the Akaike information criterion (AIC) and Bayesian information criterion (BIC) which are defined by $-2LL+2q$ and $-2LL+q\log (n)$, respectively, where $q$ is the number of parameters estimated and $n$ is the sample size. Further Kolmogorov–Smirnov test (K–S) = $\sup _x|F_n(x)-F(x)|$, where $F_n(x)=\frac{1}{n} \sum \nolimits _{i=1}^{n}\mathbb {I}_{x_i\le x}$ is empirical distribution function and $F(x)$ is cumulative distribution function is calculated and shown for all the datasets.

5.1 Illustration 1: Application to bladder cancer patients

We consider an uncensored data set corresponding to remission times (in months) of a random sample of 128 bladder cancer patients (Lee and Wang [18]) as presented in Appendix A.1 in Table 9. The results for these data are presented in Table 5. We observe that the L–E distribution is a competitive distribution compared with other distributions. In fact, based on the values of the AIC and BIC criteria and K–S test statistic, we observe that the L–E distribution provides the best for these data among all the models considered. The probability density function and empirical distribution function are presented in Fig. 8 for all considered distributions for these data.

Table 5 The estimates of parameters and goodness-of-fit statistics for Illustration 1

Fig. 8

PDF plot for various values of $\lambda$ and $\theta$

5.2 Illustration 2: Application to waiting times in a queue

As second example, we consider 100 observations on waiting time (in minutes) before the customer received service in a bank (see Ghitany et al. [7]). The data sets are presented in Appendix A.2 as Table 10. The results for these data are presented in Table 6. From these results we can observe that L–E distribution provide smallest AIC and BIC values as compare to Power lindley, new generalized Lindley distribution, Lindley and exponential and hence best fits the data among all the models considered. The results are presented in Table 6 and probability density function and empirical distribution function are shown in Fig. 9.

Table 6 The estimates of parameters and goodness-of-fit statistics for Illustration 2

Fig. 9

PDF plot for various values of $\lambda$ and $\theta$

6 Estimation of the reliability of a stress–strength system

The stress–strength parameter $(R)$, defined as $R=P\left( X>Y\right)$, plays an important role in the reliability analysis as it measures the system performance. Some of the significant work on the stress–strength model can be seen in Kundu and Gupta [14, 15], Raqab and Kundu [21], Kundu and Raqab [16], Krishnamoorthy et al. [13], and the references cited therein. Recently Al-Mutairi et al. [2] have presented the estimation of the stress–strength parameter where both strength and stress of the system follow lindley distribution with different shape parameters. In this section, we consider a situation where $X\sim$ L–E$(\theta _1,\lambda )$ and $Y\sim$L–E$(\theta _2,\lambda )$ and are independent of each other. In our case, the stress–strength parameter $R$ is given by

$$\begin{aligned}&R=P\left( X>Y\right) =\int \limits _{0}^{\infty } P\left( X >Y | Y=y\right) f_Y(y) dy \nonumber \\&\quad =\int \limits _{0}^{\infty }S_X(y) f_Y(y) dy \nonumber \\&\quad =1-\int _0^{\infty } \frac{\theta ^2_2 \lambda \left( 1{-}e^{-{\lambda y}}\right) ^{\theta _1{+}\theta _2-1} e^{-\lambda y}\left( 1{-}\log \left( 1{-}e^{-\lambda y}\right) \right) \left( 1{+}\theta _1 (1{-}\log \left( 1{-}e^{-{\lambda y}})\right) \right) }{\left( 1{+}\theta _1\right) \left( 1{+}\theta _2\right) } dy \nonumber \\&\quad =1-\frac{\theta _2^2 \left( \theta _1^3+\left( 2 \theta _2+3\right) \theta _1^2+\left( \theta _2+1\right) \left( \theta _2+3\right) \theta _1+\theta _2^2+\theta _2\right) }{\left( \theta _1+1\right) \left( \theta _2+1\right) \left( \theta _1+\theta _2\right) {}^3} \end{aligned}$$

(27)

Remarks:

• (i) R is independent of $\lambda$

• (ii) When $\theta _1=\theta _2$, R $=$ 0.5. This is intuitive that $X$ and $Y$ are i.i.d. and there is an equal chance that $X$ is bigger than $Y$.

Since R in Eq. (27) is a function of stress–strength parameters $\theta _1$ and $\theta _2$, we need to obtain the maximum likelihood estimators (MLEs) of $\theta _1$ and $\theta _2$ to compute the MLE of R under invariance property of the MLE. Suppose that $X_1,X_2,\ldots ,X_n$ and $Y_1,Y_2,\ldots ,Y_m$ are independent random samples from L–E $(\theta _1, \lambda )$ and L–E $(\theta _2,\lambda )$ respectively, then likelihood function is given by

$$\begin{aligned} L(\theta _1,\theta _2)&=\frac{\theta _2^{2m} \theta _1^{2n} \lambda ^{m+n}}{\left( \theta _1+1\right) \left( \theta _2+1\right) } \prod _{i=1}^n e^{-\lambda x_i} \left( 1-e^{-\lambda x_i}\right) ^{\theta _1-1} \left( 1-\log \left( 1-e^{-\lambda x_i}\right) \right) \\&\quad \cdot \prod _{j=1}^m e^{-\lambda y_j} \left( 1-e^{-\lambda y_j}\right) ^{\theta _2-1} \left( 1-\log \left( 1-e^{-\lambda y_j}\right) \right) . \end{aligned}$$

The log-likelihood function is given by

$$\begin{aligned} \log L(\theta _1,\theta _2) \,&{=}\,2 n \log \left( \theta _1\right) {+}2 m \log \left( \theta _2\right) {+} (m+n)\log (\lambda )-n\log \left( \theta _1+1\right) -m \log \left( \theta _2+1\right) \\&\quad -\left( \theta _1-1\right) s_1-\lambda \sum _{i=1}^n x_i+\sum _{i=1}^n \log (1-\log (1-e^{-\lambda x_i}))-\left( \theta _2-1\right) s_2\\&\quad -\lambda \sum _{j=1}^m y_j +\sum _{j=1}^m \log (1-\log (1-e^{-\lambda y_j})), \end{aligned}$$

where $s_1(\lambda )=- \sum \nolimits _{i=1}^{n} \log \left( 1-e^{-\lambda x_i}\right)$ and $s_2(\lambda )=-\sum \nolimits _{j=1}^{m}\log \left( 1-e^{-\lambda y_j}\right)$.

The MLE of $\hat{\Theta }$ of $\Theta$ is solution of the following non linear equations:

$$\begin{aligned} \frac{\partial \text {logL}}{\partial \alpha }&= \frac{n+m}{\lambda }\!+\!(\theta _1-1)\sum _{i=1}^n \frac{x_i e^{-\lambda x_i}}{\left( 1-e^{-\lambda x_i}\right) }\!+\!(\theta _2-1) \sum _{j=1}^m \frac{y_j e^{-\lambda y_j}}{\left( 1-e^{-\lambda y_j}\right) }-\sum _{i=1}^n x_i-\sum _{j=1}^m y_j \nonumber \\&\quad -\sum _{i=1}^n \frac{x_i e^{-x_i \lambda }}{\left( 1-e^{-x_i \lambda }\right) \left( 1-\log \left( 1-e^{-x_i \lambda }\right) \right) }\nonumber \\&\quad -\sum _{j=1}^m \frac{y_j e^{-y_j \lambda }}{\left( 1-e^{-y_j \lambda }\right) \left( 1- \log \left( 1-e^{-y_j \lambda }\right) \right) }\nonumber \\ \frac{\partial \text {logL}}{\partial \theta _1}&=\frac{2 n}{\theta _1}-\frac{n}{\theta _1+1}-s_1 \nonumber \\ \frac{\partial \text {logL}}{\partial \theta _2}&=\frac{2 m}{\theta _2}-\frac{m}{\theta _2+1}-s_2 \end{aligned}$$

(28)

from above equations, it follows that

$$\begin{aligned} \hat{\theta _1}= \theta _1(\hat{\lambda })\,=\,&\frac{\left( s_1(\hat{\lambda })-n\right) +\sqrt{\left( s_1(\hat{\lambda })-n\right) ^2+8 n s_1(\hat{\lambda })}}{2 s_1(\hat{\lambda })} \nonumber \\ \hat{\theta _2}\,=\,\theta _2(\hat{\lambda })\,=\,&\frac{\left( s_2(\hat{\lambda })-m\right) +\sqrt{\left( s_2(\hat{\lambda })-m\right) ^2+8 m s_2(\hat{\lambda })}}{2 s_2(\hat{\lambda })} \end{aligned}$$

(29)

where $\hat{\lambda }$ is the solution of the non-linear equation:

$$\begin{aligned} H(\lambda )\,=\,&\frac{n+m}{\lambda }+(\theta _1(\lambda )-1)\sum _{i=1}^n \frac{x_i e^{-\lambda x_i}}{\left( 1-e^{-\lambda x_i}\right) }+(\theta _2(\lambda )-1) \nonumber \\&\times \sum _{j=1}^m \frac{y_j e^{-\lambda y_j}}{\left( 1-e^{-\lambda y_j}\right) }-\sum _{i=1}^n x_i-\sum _{j=1}^m y_j \nonumber \\&\!-\!\sum _{i=1}^n \frac{x_i e^{-x_i \lambda }}{\left( 1-e^{-x_i \lambda }\right) \left( 1\!-\!\log \left( 1-e^{-x_i \lambda }\right) \right) }-\sum _{j=1}^m \frac{y_j e^{-y_j \lambda }}{\left( 1-e^{-y_j \lambda }\right) \left( 1- \log \left( 1-e^{-y_j \lambda }\right) \right) }. \end{aligned}$$

(30)

The value of $\hat{\lambda }$ can be substituted in (29) to get $\hat{\theta _1}$ and $\hat{\theta _2}$.

Hence, using the invariance property of the MLE, the maximum likelihood estimator $\hat{R}_{mle}$ of $R$ can be obtained by substituting $\hat{\theta }_k$ for $k$ $=$ 1,2 in Eq. (27).

$$\begin{aligned} \hat{R}_{mle}=1-\frac{\theta _2^2 \left( \theta _1^3+\left( 2 \theta _2+3\right) \theta _1^2+\left( \theta _2+1\right) \left( \theta _2+3\right) \theta _1+\theta _2^2+\theta _2\right) }{\left( \theta _1+1\right) \left( \theta _2+1\right) \left( \theta _1+\theta _2\right) ^3} \bigg |_{\theta _1=\hat{\theta }_1,\theta _2=\hat{\theta }_2}. \end{aligned}$$

(31)

6.1 Asymptotic confidence interval

For an estimator $\hat{\theta }_k$ to be asymptotically efficient for estimating $\theta _k$ for large sample, we should have $\sqrt{n_k} \big ( \hat{\theta }_k-\theta _k\big ) \xrightarrow {\textit{D}} N\left( 0,I(\theta _k)^{-1}\right)$

$$\begin{aligned} I(\theta _k)&=-E\left( \frac{\partial ^2\text {logL}}{\partial \theta _k^2}\right) =-E \left( \frac{n_k}{\left( \theta _k+1\right) {}^2}-\frac{2 n_k}{\theta _k^2}\right) =\frac{2 n_k}{\theta _1^2}-\frac{n_k}{\left( \theta _1+1\right) {}^2} \\ I_1&=I(\theta _1)=-E \left( \frac{n}{\left( \theta _1+1\right) {}^2}-\frac{2 n}{\theta _1^2}\right) =\frac{2 n}{\theta _1^2}-\frac{n}{\left( \theta _1+1\right) {}^2} \\ I_2&=I(\theta _2)=-E \left( \frac{m}{\left( \theta _2+1\right) {}^2}-\frac{2 m}{\theta _2^2}\right) =\frac{2 m}{\theta _2^2}-\frac{m}{\left( \theta _2+1\right) {}^2}\\ \end{aligned}$$

where $n_1 = n$ and $n_2= m$.

Therefore, as easily follows it $n\rightarrow \infty$ and $m \rightarrow \infty$

$$\begin{aligned} \frac{\hat{R}-R}{\sqrt{\frac{d_2^2}{m I_2}+\frac{d_1^2}{n I_1}}}\overset{D}{\longrightarrow }N(0,1) \end{aligned}$$

where

$$\begin{aligned} d_1=&\frac{\partial R}{\partial \theta _1}=\frac{\theta _1 \theta _2^2 \left( \theta _1^3+2 \left( \theta _2+3\right) \theta _1^2+\left( \theta _2^2+8 \theta _2+12\right) \theta _1+2 \left( \theta _2^2+3\theta _2+3\right) \right) }{\left( \theta _1+1\right) ^2 \left( \theta _2+1\right) \left( \theta _1+\theta _2\right) {}^4} \\ d_2=&\frac{\partial R}{\partial \theta _2}=-\frac{\theta _1^2 \theta _2 \left( \theta _2^3+6 \theta _2^2+12 \theta _2+\theta _1^2 \left( \theta _2+2\right) +2 \theta _1 \left( \theta _2^2+4\theta _2+3\right) +6\right) }{\left( \theta _1+1\right) \left( \theta _2+1\right) ^2 \left( \theta _1+\theta _2\right) ^4} \end{aligned}$$

Interval Using the asymptotic distribution of $\hat{R}$, 100$(1-\alpha )$ % confidence interval for R can be easily obtained as

$$\begin{aligned} \hat{R}\mp Z_{\frac{\alpha }{2}} \sqrt{\frac{\hat{d_2^2}}{m\hat{I}_2}+\frac{\hat{d_1^2}}{n \hat{I}_1}}. \end{aligned}$$

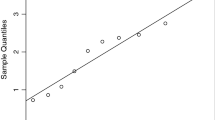
6.2 Illustration 3: Application to stress–strength data

In illustration 3, we present the results obtained from estimation methods of $R$ proposed in Sect. 6, we consider two datasets, reported in Ghitany et al. [7], Al-Mutairi et al. [2], represents the waiting times (in minutes) before customer service in two different banks having 100(n) and 60(m) number of observations respectively. Q–Q plot in Fig. 10 and KS value in Table 7 indicate that LE Distribution fits better than Lindley Distribution (L). Thus, $\hat{R}_{MLE}$ and 95 % confidence interval were computed and presented in Table 8. It is clear that, from the Table 8 that the estimated value of stress–strength parameter obtained from L–E distribution is lower than the one obtained from Lindley distribution. Moreover, standard error of $R$ is also lower for LE distribution compared to Lindley distribution. Hence we recommend, LE distribution for stress-strength analysis also.

Fig. 10

Q–Q plot of the fitted LE and Lindley distribution for Bank A and Bank B data set

Table 7 Kolmogorov–Smirnov distances value for Bank A and Bank B data set

Table 8 The maximum likelihood estimator of $R$ for LE and Lindley model

7 Conclusion

We have proposed a new two parameter class of distribution called Lindley–Exponential (L–E) distribution generated by Lindley distribution possess increasing, decreasing or upside down hazard function for different choices of the parameters. We have derived important properties of the L–E distribution like moments, entropy, asymptotic distribution of sample maximum and sample Minimum. Maximum likelihood of the parameters are obtained which can be used to get asymptotic confidence intervals. We have also illustrated the application of L–E distribution to two real data sets used by researchers earlier and compare it with other popular models. Further the stress–strength analysis were carried out and compared with that of Lindley distribution. Our application to real data set indicate that L–E distribution performs satisfactorily or better than its competitors and can be recommended for lifetime modelling the encountered in engineering, medical science, biological science and other applied sciences.

Appendix

1.1 Appendix A.1: Dataset used in illustration 1

See Table 9.

Table 9 The remission times (in months) of bladder cancer patients

1.2 Appendix A.2: Dataset used in illustration 2

See Table 10.

Table 10 Waiting times (min) of 100 bank customers