Multiattribute group decision-making based on weighted correlation coefficient of linguistic q-rung orthopair fuzzy sets and TOPSIS method

Abstract

Linguistic q-rung orthopair fuzzy number (Lq-ROFN) is a valuable tool for expressing the uncertainty of qualitative information that has received a lot of attention over the last 5 years. In this article, we propose the correlation coefficient to measure the strength of the relationship between two linguistic q-rung orthopair fuzzy sets (Lq-ROFSs). We also provide the various properties of the proposed correlation coefficient of Lq-ROFSs. Moreover, we also propose the weighted correlation coefficient of Lq-ROFSs. Afterward, using the proposed weighted correlation coefficient of Lq-ROFSs and the “technique for order of preference by similarity to ideal solution” (TOPSIS) method, we develop a novel multiattribute group decision-making (MAGDM) method under the Lq-ROFNs environment. We also solve the different MAGDM problems using the proposed MAGDM method and compare the preference order (PO) obtained by the proposed MAGDM method with the POs obtained by the existing MAGDM methods. The comparison analysis shows that the drawbacks of the existing MAGDM methods can be successfully overcome by the proposed MAGDM method, where existing MAGDM methods cannot distinguish the POs of alternatives. In the Lq-ROFNs environment, the proposed MAGDM method provides a useful decision-making method for solving MAGDM problems.

1 Introduction

Multiattribute group decision-making (MAGDM) is a crucial component of decision-making theory. It involves selecting the optimal alternative based on quantitative or qualitative evaluations of each possible attribute by a group of decision-making experts (DMExs). Due to the uncertain information, the most challenging job for the DMEXs is to provide the alternative’s assessment of a MAGDM problem. Therefore, Zadeh (1965) introduced the theory of fuzzy sets (FS) to manage imprecise concepts in quantitative data analysis. Fuzzy set theory has only explored membership degrees (MDs) for decision-making but ignores non-membership degrees (NMDs), which may result in erroneous results in many realistic evaluations. Several applications utilizing FSs have been introduced in previous studies (Chen and Jian 2017; Chen et al. 2019; Zeng et al. 2019; Chen and Hsu 2008; Chen 1996; Chen and Lee 2010; Lin et al. 2006; Chen and Chen 2002; Savita et all. 2024; Akram and Martino 2023; Noor et al. 2023; Muneeza and Abdullah 2023; Farman et al. 2023). To compensate for the inadequacy of the FS, Atanassov (1986) proposed the extension of the FS known as intuitionistic fuzzy sets (IFS) $\langle \theta ,\vartheta \rangle$ that also includes NMD. The IFS satisfies the condition $\theta + \vartheta \le 1$, where $\theta$ is the MD and $\vartheta$ is the NMD. But in some cases, IFS is not able to express the assessments of the DMEXs, where $\theta + \vartheta > 1$. To handle these types of problems, Yager (2013) proposed the pythagorean fuzzy set (PFS) $\langle \theta ,\vartheta \rangle$ which satisfy the condition $\theta ^2 + \vartheta ^2 \le 1$. The PFS provides more space for DMEXs to express their assessment of the alternatives compared to the IFSs. But in some cases, PFS is not also able to express the assessments of the decision-making experts (DMEXs) where $\theta ^2 + \vartheta ^2 > 1$. Therefore, Yager (2017) proposed the generalization of the IFS and PFS known as q-rung orthopair fuzzy set (q-ROFS) $\langle \theta ,\vartheta \rangle$ which satisfies the condition: $\theta ^q + \vartheta ^q \le 1$ and $q\ge 1$, which provides a more range to express the information. Under these environments, different MAGDM approaches (Liu et al. 2020; Kumar and Chen 2023a; Garg and Chen 2020; Pathak et al. 2024; Alcantud 2023; Kumar and Kumar 2023) have been developed by the researchers. Liu et al. (2020) proposed the partitioned Maclaurin symmetric mean AO for MAGDM under the intuitionistic fuzzy number (IFNs) environment. Kumar and Chen (2023a) defined the entropy measure and arithmetic mean aggregation operator (AO) for MAGDM under the PFSs environment. Garg and Chen (2020) defined the neutrality AOs for MAGDM under the q-rung orthopair fuzzy number (q-ROFNs) environment.

However, using IFSs, PFSs, and q-ROFSs, the DMExs can express the assessment information only in numerical terms. In certain circumstances, DMExs may discover that it is challenging to describe their assessment in numerical terms. For instance, DMExs may have challenges when expressing the weather conditions of any city. In that case, the DMExs can use the linguistic phrases like “freezing”, “cold”, “chilly”, “warm”, “hot”, and “burning” to express the weather condition instead of numerical values. First, Zadeh (1975) proposed the concept of linguistic variables (LVs), where various applications (Herrera and Martínez 2001; Xu 2004; Saha et al. 2024; Akram et al. 2023a, b) based on the LVs environment have been developed. Afterward, Chen et al. (2015) defined the idea of linguistic intuitionistic fuzzy sets (LIFS) by combining the features of IFNs and LVs to express the qualitative assessments more conveniently. Some MAGDM approaches (Malik et al. 2024; Kumar and Chen 2023b; Arora and Garg 2019; Kumar and Chen 2022a, b; Rahim 2023) have been developed under the LIFSs environment. Afterward, Garg (2018) defined the concept of the linguistic PFS (LPFS) by combining the features of the PFS and LVs, which is the extension of LIFS. Han et al. (2019) defined the technique for order of preference by similarity to ideal solution (TOPSIS) method based on the entropy measures and distance measures for the LPFSs. Lin et al. (2019) proposed the TOPSIS method based on the correlation coefficient and entropy measures for the LPFSs. In 2019, Liu and Liu (2019a) extended the idea of LIFSs and LPFSs, and defined the idea of linguistic q-rung orthopair fuzzy (Lq-ROF) set (Lq-ROFS) and Lq-ROF number (Lq-ROFN), where the MD and NMD of the Lq-ROFN are indicated by LVs. The Lq-ROFS allows DMExs to provide assessment information across a wider range. Several decision-making applications utilizing Lq-ROFSs have been introduced in previous studies(Neelam et al. 2024; Liu and Liu 2019a, b; Peng et al. 2019; Akram et al. 2021; Bao and Shi 2022; Li and Zhang 2023; Liu et al. 2022; Jana et al. 2023). Liu and Liu (2019a) proposed the power Bonferroni AO of Lq-ROFNs and MAGDM approach based on the proposed AOs under the Lq-ROFNs environment. Liu and Liu (2019b) introduced the power Muirhead mean AO and entropy measures for the MAGDM approach under the Lq-ROFNs environment. Peng et al. (2019) defined the similarity measures of Lq-ROFSs and MAGDM approach using proposed similarity measures under the Lq-ROFNs environment. Akram et al. (2021) defined the MAGDM approach based on the Einstein model in the Lq-ROFNs context. Bao and Shi (2022) proposed the MAGDM approach under the Lq-ROFNs environment based on the ELECTRE method. Liu et al. (2022) defined the point weighted aggregation operators (AOs) for Lq-ROFNs and MAGDM approach based on the proposed AOs of Lq-ROFNs. Li and Zhang (2023) defined the MAGDM approach in the context of the Lq-ROFNs environment based on fuzzy preference relations. Jana et al. (2023) defined the MAGDM approach for evaluation of sustainable strategies for urban parcel delivery under the Lq-ROFNs environment.

In this paper, we find that the majority of existing MAGDM approaches under the Lq-ROFNs environment are based on the AOs of Lq-ROFNs, and there is limited research on the classical MAGDM approaches under the Lq-ROFNs environment. We also find that there is no study on the correlation coefficient of Lq-ROFNs. Moreover, we find that the Liu and Liu’s MAGDM approach (Liu and Liu 2019a) and Liu et al.’s MAGDM approach (Liu et al. 2022) have the shortcomings that they cannot distinguish the preference orders (POs) of alternatives in certain cases. Hence, it is necessary to develop a new classical MAGDM approach under the Lq-ROFNs environment to overcome the limitations of Liu and Liu’s MAGDM approach (Liu and Liu 2019a) and Liu et al.’s MAGDM approach (Liu et al. 2022).

In this paper, we propose the correlation coefficient for the Lq-ROFSs. The proposed correlation coefficient measures the strength of the relationship between two Lq-ROFSs. We also present proofs of the different properties of the proposed correlation coefficient of Lq-ROFSs. We also propose the weighted correlation coefficient of Lq-ROFSs. Afterward, based on the proposed weighted correlation coefficient of Lq-ROFSs and the TOPSIS method, we propose a new classical MAGDM approach to solve the MAGDM problems in the Lq-ROFNs environment. The proposed MAGDM approach can overcome the drawbacks of Liu and Liu’s MAGDM approach (Liu and Liu 2019a) and Liu et al.’s MAGDM approach (Liu et al. 2022), where they cannot distinguish the POs of alternatives in certain cases.

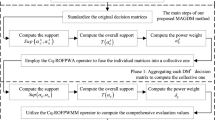
The remaining part of this paper is organized as follows: Sect. 2 provides the fundamental definitions related to this article. In Sect. 3, we develop the correlation coefficient and weighted correlation coefficient for Lq-ROFSs. In Sect. 4, we propose a novel MAGDM approach based on proposed weighted correlation coefficient of Lq-ROFSs and TOPSIS method under the Lq-ROFNs environment. Finally, Sect. 5 gives the conclusion of the paper.

2 Preliminaries

Definition 1

(Herrera and Martínez 2001; Neelam et al. 2023a) A finite linguistic term (LT) set (LTS) $\Upsilon =\Big \{ s_{0}, s_{1},..., s_{h}\Big \}$ of odd cardinality, where LT $s_{t}$ reflects a suitable value for a LV. For example, to express the weather condition, we can consider the LTs as $s_{0}=\text {``freezing''},$ $s_{1}=\text {``cold''}$, $s_{2}= \text {``chilly''}$, $s_{3}= \text {``warm''}$ and $s_{4}= \text {``hot''}$.

The LT $s_{k}$ meets the following criteria:

• (i) $s_{k}\le s_{t} \Leftrightarrow k\le t$;

• (ii) Neg$(s_{k}) = s_{h-k}$;

• (iii) $\max (s_{k},s_{t}) = s_{k} \Leftrightarrow s_{k}\ge s_{t}$;

• (iv) $\min (s_{k},s_{t}) = s_{t} \Leftrightarrow s_{k}\ge s_{t}$.

Later on, the continuous LTS (CLTS) $\Upsilon _{[0,h]}$ is developed by extending the discrete LTS $\Upsilon$ as follows (Xu 2004; Neelam et al. 2023b):

$$\begin{aligned} \Upsilon _{[0,h]}=\Big \{ s_{k} \mid s_{0} \le s_{k} \le s_{h}\Big \}. \end{aligned}$$

Definition 2

(Liu and Liu 2019a) A Lq-ROFS $\zeta$ in a finite universal set G is defined as:

$$\begin{aligned} \zeta = \left\{ \langle x, s_{\theta (g)}, s_{\vartheta (g)} \rangle \mid g \in G\right\} , \end{aligned}$$

(1)

where $s_{\theta (g)}$ and $s_{\vartheta (g)}$ indicate the membership degree (MD) and non-MD (NMD) of g to $\zeta$, respectively, where $s_{\theta }(g)\in \Upsilon _{[0,h]}$, $s_{\vartheta (g)} \in \Upsilon _{[0,h]}$, $0\le (\theta (g))^q+ (\vartheta (g))^q \le h^q$ and $q\ge 1$. The hesitancy degree of g to $\zeta$ is defined as $s_{\pi (g)}= s_{(h^q-(\theta (g))^q-(\vartheta (g))^q)^{1/q}}$.

In Liu and Liu (2019a), Liu and Liu called the pair $\langle s_{\theta }, s_{\vartheta } \rangle$ in the Lq-ROFS $\zeta = \{\langle x, s_{\theta (g)}, s_{\vartheta (g)} \rangle \mid x \in X\}$ a Lq-ROFN.

Let $\Omega _{[0,h]}$ be the set of all Lq-ROFNs in the CLTS $\Upsilon _{[0,h]}$.

Definition 3

(Liu and Liu 2019a) The score function $S(\varrho )$ of the Lq-ROFN $\varrho = \left\langle s_{\theta }, s_{\vartheta }\right\rangle$, where $\varrho \in \Omega _{[0,h]}$, is defined as follows:

$$\begin{aligned} S(\varrho ) = \left( \frac{h^q + \theta ^q - \vartheta ^q}{2}\right) ^{1/q}, \end{aligned}$$

(2)

where $S(\varrho )\in [0,h]$.

Definition 4

(Liu and Liu 2019a) The accuracy function $H(\varrho )$ of the Lq-ROFN $\varrho = \left\langle s_{\theta }, s_{\vartheta }\right\rangle$, where $\varrho \in \Omega _{[0,h]}$, is defined as follows:

$$\begin{aligned} H(\varrho ) = (\theta ^q + \vartheta ^q)^{1/q}, \end{aligned}$$

(3)

where $H(\varrho )\in [0,h]$.

Definition 5

(Liu and Liu 2019a) Let $\varrho _{1} = \langle s_{\theta _{1}} , s_{\vartheta _{1}} \rangle$ and $\varrho _{2} = \langle s_{\theta _{2}} , s_{\vartheta _{2}} \rangle$ be two Lq-ROFNs, then the following rules are defined:

• (a) if $S(\varrho _{1}) > S(\varrho _{2})$ then $\varrho _{1} \succ \varrho _{2}$.

• (b) if $S(\varrho _{1}) < S(\varrho _{2})$ then $\varrho _{1} \prec \varrho _{2}$.

• (c) if $S(\varrho _{1}) = S(\varrho _{2})$ then

• (i) if $H(\varrho _{1}) > H(\varrho _{2})$ then $\varrho _{1} \succ \varrho _{2}$.

• (ii) if $H(\varrho _{1}) < H(\varrho _{2})$ then $\varrho _{1} \prec \varrho _{2}$.

• (iii) if $H(\varrho _{1}) = H(\varrho _{2})$ then $\varrho _{1} = \varrho _{2}$.

3 The proposed correlation coefficient of Lq-ROFSs

In this section, we propose the correlation coefficient of Lq-ROFSs. Let $\varepsilon (G)_{[0,h]}$ be the set of all Lq-ROFSs over the universal set $X=\{g_1, g_2, \ldots , g_n\}$, where MD and NMD of each element $g_i\in G$ belong to the CLTS $\Upsilon _{[0,h]}$.

Definition 6

Let $\zeta _1 = \left\{ \langle g_{i}, s_{\theta _{\zeta _1}(g_{i})}, s_{\vartheta _{\zeta _1}(g_{i})} \rangle \mid g_{i} \in G \right\}$ be a Lq-ROFS, where $\zeta _1 \in \varepsilon (G)_{[0,h]}$. The proposed information energy $T(\zeta _1)$ of the Lq-ROFS $\zeta _1$ is defined as:

$$\begin{aligned} T(\zeta _1) = \frac{1}{nh^{2q}}\sum _{i=1}^{n} \left( \left( \theta _{\zeta _1}(g_{i})\right) ^{2q} + \left( \vartheta _{\zeta _1}(g_{i})\right) ^{2q} + (\pi _{\zeta _1}(g_{i}))^{2q}\right) , \end{aligned}$$

(4)

where $0\le T(\zeta _1)\le 1$, $\pi _{\zeta _1}(g_i)= (h^q-(\theta _{\zeta _1}(g_i))^q-(\vartheta _{\zeta _1}(g_i))^q)^{1/q}$ and $q\ge 1$.

Definition 7

Let $\zeta _1 = \left\{ \langle g_{i}, s_{\theta _{\zeta _1}(g_{i})}, s_{\vartheta _{\zeta _1}(g_{i})} \rangle \mid g_{i} \in G \right\}$ and $\zeta _2 = \left\{ \langle g_{i}, s_{\theta _{\zeta _2}(g_{i})}, s_{\vartheta _{\zeta _2}(g_{i})} \rangle \mid g_{i} \in G \right\}$ be two Lq-ROFSs, where $\zeta _1 \in \varepsilon (G)_{[0,h]}$ and $\zeta _2 \in \varepsilon (G)_{[0,h]}$. The proposed correlation $C(\zeta _1,\zeta _2)$ between the Lq-ROFNs $\zeta _1$ and $\zeta _2$ is defined as follows:

$$\begin{aligned}{} & {} C(\zeta _1,\zeta _2) = \frac{1}{nh^{2q}}\sum _{i=1}^{n} \left( \left( \theta _{\zeta _1}(g_{i})\right) ^{q}\left( \theta _{\zeta _2}(g_{i})\right) ^{q} + \left( \vartheta _{\zeta _1}(g_{i})\right) ^{q}\left( \vartheta _{\zeta _2}(g_{i})\right) ^{q}\right. \nonumber \\{} & {} \quad \left. +(\pi _{\zeta _1}(g_{i}))^{q}(\pi _{\zeta _2}(g_{i}))^{q} \right) , \end{aligned}$$

(5)

where $0\le C(\zeta _1,\zeta _2)\le 1$, $\pi _{\zeta _1}(g_i)= (h^q-(\theta _{\zeta _1}(g_i))^q-(\vartheta _{\zeta _1}(g_i))^q)^{1/q}$, $\pi _{\zeta _2}(g_i)= (h^q-(\theta _{\zeta _2}(g_i))^q-(\vartheta _{\zeta _2}(g_i))^q)^{1/q}$ and $q\ge 1$.

The proposed correlation of Lq-ROFS satisfies the following properties:

• (i) $C(\zeta _1,\zeta _2) = T(\zeta _1)$.

• (ii) $C(\zeta _1,\zeta _2) = C(\zeta _2,\zeta _1)$.

Definition 8

Let $\zeta _1 = \left\{ \langle g_{i}, s_{\theta _{\zeta _1}(g_{i})}, s_{\vartheta _{\zeta _1}(g_{i})} \rangle \mid g_{i} \in G \right\}$ and $\zeta _2 = \left\{ \langle g_{i}, s_{\theta _{\zeta _2}(g_{i})}, s_{\vartheta _{\zeta _2}(g_{i})} \rangle \mid g_{i} \in G \right\}$ be two Lq-ROFSs, where $\zeta _1 \in \varepsilon (G)_{[0,h]}$ and $\zeta _2 \in \varepsilon (G)_{[0,h]}$. The proposed CC $K(\zeta _1,\zeta _2)$ between the Lq-ROFNs $\zeta _1$ and $\zeta _2$ is defined as follows:

$$\begin{aligned}{} & {} K(\zeta _1,\zeta _2) = \frac{C(\zeta _1,\zeta _2)}{\max \{T(\zeta _1),T(\zeta _2)\}}\nonumber \\{} & {} = \tfrac{\sum _{i=1}^{n} \left( (\theta _{\zeta _1}(g_{i}))^{q}\cdot (\theta _{\zeta _2}(g_{i}))^{q} + (\vartheta _{\zeta _1}(g_{i}))^{q}\cdot (\vartheta _{\zeta _2}(g_{i}))^{q} +(\pi _{\zeta _1}(g_{i}))^{q}\cdot (\pi _{\zeta _2}(g_{i}))^{q} \right) }{\max \left\{ \sum _{i=1}^{n} \left( (\theta _{\zeta _1}(g_{i}))^{2q} + (\vartheta _{\zeta _1}(g_{i}))^{2q} + (\pi _{\zeta _1}(g_{i}))^{2q}\right) , \sum _{i=1}^{n} \left( (\theta _{\zeta _2}(g_{i}))^{2q} + (\vartheta _{\zeta _2}(g_{i}))^{2q} + (\pi _{\zeta _2}(g_{i}))^{2q}\right) \right\} }, \end{aligned}$$

(6)

where $0\le K(\zeta _1,\zeta _2) \le 1$, $\pi _{\zeta _1}(g_i)= (h^q-(\theta _{\zeta _1}(g_i))^q-(\vartheta _{\zeta _1}(g_i))^q)^{1/q}$, $\pi _{\zeta _2}(g_i)= (h^q-(\theta _{\zeta _2}(g_i))^q-(\vartheta _{\zeta _2}(g_i))^q)^{1/q}$ and $q\ge 1$.

Example 1

Let $\zeta _1 = \left\{ \langle g_{1},s_5,s_3\rangle , \langle g_{2},s_4,s_4 \rangle , \langle g_{3},s_6,s_1 \rangle \right\}$ and $\zeta _2 = \left\{ \langle g_{1},s_4,s_2 \rangle , \langle g_{2},s_5,s_2 \rangle , \langle g_{3},s_7,s_1\rangle \right\}$ be two Lq-ROFSs, where $\zeta _1 \in \varepsilon (G)_{[0,8]}$ and $\zeta _2 \in \varepsilon (G)_{[0,8]}$.

First, using Eq. (4), we obtain the information energies $T(\zeta _1)$ and $T(\zeta _2)$ of the Lq-ROFSs $\zeta _1$ and $\zeta _2$, respectively, where $q=3$,

$$\begin{aligned}{} & {} T(\zeta _1) = \frac{1}{3h^{2q}}\sum _{i=1}^{3} \left( (\theta _{\zeta _1}(g_{i}))^{2q} + (\vartheta _{\zeta _1}(g_{i}))^{2q} + (\pi _{\zeta _1}(g_{i}))^{2q}\right) \\{} & {} = \frac{1}{3\times 8^{6}}\\{} & {} \left( 5^{6} + 3^{6} + \left( 8^{3}-5^{3}-3^{3}\right) ^2 + 4^{6} + 4^{6} + \left( 8^{3}-4^{3}-4^{3}\right) ^2\right. \\{} & {} \left. + 6^{6} + 1^{6} + \left( 8^{3}-6^{3}-1^{3}\right) ^2 \right) \\{} & {} = 0.5535,\\{} & {} T(\zeta _2) = \frac{1}{3h^{2q}}\sum _{i=1}^{3} \left( (\theta _{\zeta _2}(g_{i}))^{2q} + (\vartheta _{\zeta _2}(g_{i}))^{2q} + (\pi _{\zeta _2}(g_{i}))^{2q}\right) \\{} & {} =\frac{1}{3\times 8^{6}} \left( 4^{6} + 2^{6} + \left( 8^{3}-4^{3}-2^{3}\right) ^2 + 5^{6} + 2^{6}\right. \\{} & {} \left. + \left( 8^{3}-5^{3}-2^{3}\right) ^2 + 7^{6} + 1^{6} + \left( 8^{3}-7^{3}-1^{3}\right) ^2\right) \\= & {} 0.6396. \end{aligned}$$

Now, using Eq. (5), we calculate the correlation $C(\zeta _1,\zeta _2)$ between the Lq-ROFSs $\zeta _1$ and $\zeta _2$, where $q=3$,

$$\begin{aligned}{} & {} C(\zeta _1,\zeta _2) = \frac{1}{3h^{2q}}\sum _{i=1}^{3} \left( (\theta _{\zeta _1}(g_{i}))^{q}\right. \\{} & {} \left. \cdot (\theta _{\zeta _2}(g_{i}))^{q} + (\vartheta _{\zeta _1}(g_{i}))^{q}\cdot (\vartheta _{\zeta _2}(g_{i}))^{q} +(\pi _{\zeta _1}(g_{i}))^{q}\cdot (\pi _{\zeta _2}(g_{i}))^{q} \right) \\{} & {} = \frac{1}{3\times 8^{6}} \left( 5^{3}\cdot 4^{3} + 3^{3}\cdot 2^{3}\right. \\{} & {} \left. + \left( 8^{3}-5^{3}-3^{3}\right) .\left( 8^{3}-4^{3}-2^{3}\right) + 4^{3}\cdot 5^{3} + 4^{3}\cdot 2^{3} \right. \\{} & {} \left. + \left( 8^{3}-4^{3}-4^{3}\right) .\left( 8^{3}-5^{3}-2^{3}\right) + 6^{3}\cdot 7^{3} + 1^{3}\cdot 1^{3} \right. \\{} & {} \left. + \left( 8^{3}-6^{3}-1^{3}\right) .\left( 8^{3}-7^{3}-1^{3}\right) \right) \\= & {} 0.5650. \end{aligned}$$

Hence, using Eq. (6), we get the proposed correlation coefficient $K(\zeta _1,\zeta _2)$ between the Lq-ROFSs $\zeta _1$ and $\zeta _2$, where $q = 3$,

$$\begin{aligned} K(\zeta _1,\zeta _2)= & {} \frac{C(\zeta _1,\zeta _2)}{\max \{T(\zeta _1),T(\zeta _2)\}}\\= & {} 0.8834. \end{aligned}$$

Theorem 1

Let $\zeta _1 = \left\{ \langle g_{i}, s_{\theta _{\zeta _1}(g_{i})}, s_{\vartheta _{\zeta _1}(g_{i})} \rangle \mid g_{i} \in G \right\}$ and $\zeta _2 = \left\{ \langle g_{i}, s_{\theta _{\zeta _2}(g_{i})}, s_{\vartheta _{\zeta _2}(g_{i})} \rangle \mid g_{i} \in G \right\}$ be two Lq-ROFSs, where $\zeta _1 \in \varepsilon (G)_{[0,h]}$ and $\zeta _2 \in \varepsilon (G)_{[0,h]}$. The proposed correlation coefficient $K(\zeta _1,\zeta _2)$ between the Lq-ROFNs $\zeta _1$ and $\zeta _2$, defined in Eq. (6), satisfies the following conditions:

• (P1) $K(\zeta _1,\zeta _2) = K(\zeta _2,\zeta _1)$.

• (P2) $0 \le K(\zeta _1,\zeta _2) \le 1$.

• (P3) $\zeta _1 \zeta _2 \Rightarrow K(\zeta _1,\zeta _2) = 1$.

Proof

Let $\zeta _1 = \left\{ \langle g_{i}, s_{\theta _{\zeta _1}(g_{i})}, s_{\vartheta _{\zeta _1}(g_{i})} \rangle \mid g_{i} \in G \right\}$ and $\zeta _2 = \left\{ \langle g_{i}, s_{\theta _{\zeta _2}(g_{i})}, s_{\vartheta _{\zeta _2}(g_{i})} \rangle \mid g_{i} \in G \right\}$ be two Lq-ROFSs, where $\zeta _1 \in \varepsilon (G)_{[0,h]}$ and $\zeta _2 \in \varepsilon (G)_{[0,h]}$.

• (P1) We have

  $$\begin{aligned} K(\zeta _1,\zeta _2)= & {} \tfrac{\sum _{i=1}^{n} \left( (\theta _{\zeta _1}(g_{i}))^{q}\cdot (\theta _{\zeta _2}(g_{i}))^{q} + (\vartheta _{\zeta _1}(g_{i}))^{q}\cdot (\vartheta _{\zeta _2}(g_{i}))^{q} +(\pi _{\zeta _1}(g_{i}))^{q}\cdot (\pi _{\zeta _2}(g_{i}))^{q} \right) }{\max \left\{ \sum _{i=1}^{n} \left( (\theta _{\zeta _1}(g_{i}))^{2q} + (\vartheta _{\zeta _1}(g_{i}))^{2q} + (\pi _{\zeta _1}(g_{i}))^{2q}\right) , \sum _{i=1}^{n} \left( (\theta _{\zeta _2}(g_{i}))^{2q} + (\vartheta _{\zeta _2}(g_{i}))^{2q} + (\pi _{\zeta _2}(g_{i}))^{2q}\right) \right\} }\\= & {} \tfrac{\sum _{i=1}^{n} \left( (\theta _{\zeta _2}(g_{i}))^{q}\cdot (\theta _{\zeta _1}(g_{i}))^{q} + (\vartheta _{\zeta _2}(g_{i}))^{q}\cdot (\vartheta _{\zeta _1}(g_{i}))^{q} +(\pi _{\zeta _2}(g_{i}))^{q}\cdot (\pi _{\zeta _1}(g_{i}))^{q} \right) }{max \left\{ \sum _{i=1}^{n} \left( (\theta _{\zeta _2}(g_{i}))^{2q} + (\vartheta _{\zeta _2}(g_{i}))^{2q} + (\pi _{\zeta _2}(g_{i}))^{2q}\right) , \sum _{i=1}^{n} \left( (\theta _{\zeta _1}(g_{i}))^{2q} + (\vartheta _{\zeta _1}(g_{i}))^{2q} + (\pi _{\zeta _1}(g_{i}))^{2q}\right) \right\} }\\ {}= & {} K(\zeta _2,\zeta _1). \end{aligned}$$

• (P2) It is obvious $K(\zeta _1,\zeta _2) \ge 0$. Then we will prove $K(\zeta _1,\zeta _2) \le 1$.

  $$\begin{aligned}{} & {} C(\zeta _1,\zeta _2) = \sum _{i=1}^{n} \left( (\theta _{\zeta _1}(g_{i}))^{q}\cdot (\theta _{\zeta _2}(g_{i}))^{q} + (\vartheta _{\zeta _1}(g_{i}))^{q}\cdot (\vartheta _{\zeta _2}(g_{i}))^{q} +(\pi _{\zeta _1}(g_{i}))^{q}\cdot (\pi _{\zeta _2}(g_{i}))^{q} \right) \\{} & {} = \left( (\theta _{\zeta _1}(g_{1}))^{q}\cdot (\theta _{\zeta _2}(g_{1}))^{q} + (\vartheta _{\zeta _1}(g_{1}))^{q}\cdot (\vartheta _{\zeta _2}(g_{1}))^{q} +(\pi _{\zeta _1}(g_{1}))^{q}\cdot (\pi _{\zeta _2}(g_{1}))^{q} \right) \\{} & {} + \left( (\theta _{\zeta _1}(g_{2}))^{q}\cdot (\theta _{\zeta _2}(g_{2}))^{q} + (\vartheta _{\zeta _1}(g_{2}))^{q}\cdot (\vartheta _{\zeta _2}(g_{2}))^{q} +(\pi _{\zeta _1}(g_{2}))^{q}\cdot (\pi _{\zeta _2}(g_{2}))^{q} \right. \\{} & {} + \ldots + \left( (\theta _{\zeta _1}(g_{n}))^{q}\cdot (\theta _{\zeta _2}(g_{n}))^{q} + (\vartheta _{\zeta _1}(g_{n}))^{q}\cdot (\vartheta _{\zeta _2}(g_{n}))^{q} +(\pi _{\zeta _1}(g_{n}))^{q}\cdot (\pi _{\zeta _2}(g_{n}))^{q} \right) . \end{aligned}$$

  According to Cauchy–Schwarz inequality, we have

  $$\begin{aligned}{} & {} \left( g_{1}y_{1} + g_{2}y_{2} + \cdots + g_{n}y_{n}\right) ^2 \le \left( g_{1}^2 + g_{2}^2 + \ldots + g_{n}^2\right) \\{} & {} \cdot \left( y_{1}^2 + y_{2}^2 + \cdots + y_{n}^2\right) . \end{aligned}$$

  Therefore

  $$\begin{aligned}{} & {} (C(\zeta _1,\zeta _2))^2 = \left( \sum _{i=1}^{n} \left( (\theta _{\zeta _1}(g_{i}))^{q}\cdot (\theta _{\zeta _2}(g_{i}))^{q}\right. \right. \\{} & {} \left. \left. +\vartheta _{\zeta _1}(g_{i}))^{q}\cdot (\vartheta _{\zeta _2}(g_{i}))^{q} +(\pi _{\zeta _1}(g_{i}))^{q}\cdot (\pi _{\zeta _2}(g_{i}))^{q} \right) \right) ^2\\{} & {} \le \left( \sum _{i=1}^{n} (\theta _{\zeta _1}(g_{i}))^{q} + (\vartheta _{\zeta _1}(g_{i}))^{q} + (\pi _{\zeta _1}(g_{i}))^{q}\right) ^2 \\{} & {} \cdot \left( \sum _{i=1}^{n} (\theta _{\zeta _2}(g_{i}))^{q} + (\vartheta _{\zeta _2}(g_{i}))^{q} + (\pi _{\zeta _2}(g_{i}))^{q}\right) ^2\\{} & {} \le \sum _{i=1}^{n} (\theta _{\zeta _1}(g_{i}))^{2q} + (\vartheta _{\zeta _1}(g_{i}))^{2q} + (\pi _{\zeta _1}(g_{i}))^{2q} \\{} & {} \cdot \sum _{i=1}^{n} (\theta _{\zeta _2}(g_{i}))^{2q} + (\vartheta _{\zeta _2}(g_{i}))^{2q} + (\pi _{\zeta _2}(g_{i}))^{2q}\\{} & {} = T(\zeta _1) \cdot T(\zeta _2). \end{aligned}$$

  Therefore, $C(\zeta _1,\zeta _2) \le \max \{T(\zeta _1),T(\zeta _2)\}$. Thus, $K(\zeta _1,\zeta _2) \le 1$.

• (P3) Let the Lq-ROFSs $\zeta _1 = \zeta _2$ then $\theta _{\zeta _1}(g_{i})=\theta _{\zeta _2}(g_{i})$, $\vartheta _{\zeta _1}(g_{i})=\vartheta _{\zeta _2}(g_{i})$ and $\pi _{\zeta _1}(g_{i})=\pi _{\zeta _2}(g_{i})$, $\forall g_i \in G$. By using Eq. (6), we have

  $$\begin{aligned} K(\zeta _1,\zeta _2)= & {} \frac{C(\zeta _1,\zeta _2)}{\max \{T(\zeta _1),T(\zeta _1)\}}\\ {}= & {} \tfrac{\sum _{i=1}^{n} \left( (\theta _{\zeta _1}(g_{i}))^{q}\cdot (\theta _{\zeta _1}(g_{i}))^{q} + (\vartheta _{\zeta _1}(g_{i}))^{q}\cdot (\vartheta _{\zeta _1}(g_{i}))^{q} +(\pi _{\zeta _1}(g_{i}))^{q}\cdot (\pi _{\zeta _1}(g_{i}))^{q} \right) }{\max \left\{ \sum _{i=1}^{n} \left( (\theta _{\zeta _1}(g_{i}))^{2q} + (\vartheta _{\zeta _1}(g_{i}))^{2q} + (\pi _{\zeta _1}(g_{i}))^{2q}\right) , \sum _{i=1}^{n} \left( (\theta _{\zeta _1}(g_{i}))^{2q} + (\vartheta _{\zeta _1}(g_{i}))^{2q} + (\pi _{\zeta _1}(g_{i}))^{2q}\right) \right\} }\\= & {} 1. \end{aligned}$$

$\square$

In many practical scenarios, distinct elements $g_1$, $g_2$, $\ldots$, $g_n$ may have varying weights. Therefore, we consider the weights $w_1$, $w_2$, $\ldots$, $w_n$, of the elements $g_1$, $g_2$, $\ldots$, $g_n$, respectively, where $w_{i} \ge 0, i = 1,2,\ldots , n$ and $\sum _{i=1}^{n} w_{i} = 1$. In the following, we propose the weighted correlation coefficient $K_{w}(\zeta _1,\zeta _2)$ between the Lq-ROFNs $\zeta _1$ and $\zeta _2$ as follows:

Definition 9

Let $\zeta _1 = \left\{ \langle g_{i}, s_{\theta _{\zeta _1}(g_{i})}, s_{\vartheta _{\zeta _1}(g_{i})} \rangle \mid g_{i} \in G \right\}$ be a Lq-ROFS, where $\zeta _1 \in \varepsilon (G)_{[0,h]}$. The proposed weighted information energy $T_w(\zeta _1)$ of the Lq-ROFS $\zeta _1$ is defined as:

$$\begin{aligned}{} & {} T_w(\zeta _1) = \frac{1}{h^{2q}}\sum _{i=1}^{n} w_{i}\left( (\theta _{\zeta _1}(g_{i}))^{2q} \right. \nonumber \\{} & {} \quad \left. + (\vartheta _{\zeta _1}(g_{i}))^{2q} + (\pi _{\zeta _1}(g_{i}))^{2q}\right) , \end{aligned}$$

(7)

where $0\le T_w(\zeta _1)\le 1$, $w_{i}$ is the weight of the element $g_i$, $w_{i} \ge 0, i = 1,2,\ldots , n$, $\sum _{i=1}^{n} w_{i} = 1$, $\pi _{\zeta _1}(g_i)= (h^q-(\theta _{\zeta _1}(g_i))^q-(\vartheta _{\zeta _1}(g_i))^q)^{1/q}$ and $q\ge 1$.

Definition 10

Let $\zeta _1 = \left\{ \langle g_{i}, s_{\theta _{\zeta _1}(g_{i})}, s_{\vartheta _{\zeta _1}(g_{i})} \rangle \mid g_{i} \in G \right\}$ and $\zeta _2 = \left\{ \langle g_{i}, s_{\theta _{\zeta _2}(g_{i})}, s_{\vartheta _{\zeta _2}(g_{i})} \rangle \mid g_{i} \in G \right\}$ be two Lq-ROFSs, where $\zeta _1 \in \varepsilon (G)_{[0,h]}$ and $\zeta _2 \in \varepsilon (G)_{[0,h]}$. The proposed weighted correlation $C_w(\zeta _1,\zeta _2)$ between the Lq-ROFNs $\zeta _1$ and $\zeta _2$ is defined as follows:

$$\begin{aligned} C_w(\zeta _1,\zeta _2) = \frac{1}{h^{2q}}\sum _{i=1}^{n}w_{i} \left( (\theta _{\zeta _1}(g_{i}))^{q}(\theta _{\zeta _2}(g_{i}))^{q} + (\vartheta _{\zeta _1}(g_{i}))^{q}(\vartheta _{\zeta _2}(g_{i}))^{q} +(\pi _{\zeta _1}(g_{i}))^{q}(\pi _{\zeta _2}(g_{i}))^{q} \right) , \end{aligned}$$

(8)

where $0\le C_w(\zeta _1,\zeta _2)\le 1$, $w_{i}$ is the weight of the element $g_i$, $w_{i} \ge 0, i = 1,2,\ldots , n$, $\sum _{i=1}^{n} w_{i} = 1$, $\pi _{\zeta _1}(g_i)= (h^q-(\theta _{\zeta _1}(g_i))^q-(\vartheta _{\zeta _1}(g_i))^q)^{1/q}$, $\pi _{\zeta _2}(g_i)= (h^q-(\theta _{\zeta _2}(g_i))^q-(\vartheta _{\zeta _2}(g_i))^q)^{1/q}$ and $q\ge 1$.

Definition 11

Let $\zeta _1 = \left\{ \langle g_{i}, s_{\theta _{\zeta _1}(g_{i})}, s_{\vartheta _{\zeta _1}(g_{i})} \rangle \mid g_{i} \in G \right\}$ and $\zeta _2 = \left\{ \langle g_{i}, s_{\theta _{\zeta _2}(g_{i})}, s_{\vartheta _{\zeta _2}(g_{i})} \rangle \mid g_{i} \in G \right\}$ be two Lq-ROFSs, where $\zeta _1 \in \varepsilon (G)_{[0,h]}$ and $\zeta _2 \in \varepsilon (G)_{[0,h]}$. The proposed weighted correlation coefficient $K_{w}(\zeta _1,\zeta _2)$ between the Lq-ROFNs $\zeta _1$ and $\zeta _2$ is defined as follows:

$$\begin{aligned} K_{w}(\zeta _1,\zeta _2)= & {} \frac{C_{w}(\zeta _1,\zeta _2)}{\max \left\{ T_{w}(\zeta _1),T_{w}(\zeta _2)\right\} }\nonumber \\= & {} \tfrac{\sum _{i=1}^{n} w_i \left( (\theta _{\zeta _1}(g_{i}))^{q}\cdot (\theta _{\zeta _2}(g_{i}))^{q} + (\vartheta _{\zeta _1}(g_{i}))^{q}\cdot (\vartheta _{\zeta _2}(g_{i}))^{q} +(\pi _{\zeta _1}(g_{i}))^{q}\cdot (\pi _{\zeta _2}(g_{i}))^{q} \right) }{\max \left\{ \sum _{i=1}^{n} w_i \left( (\theta _{\zeta _1}(g_{i}))^{2q} + (\vartheta _{\zeta _1}(g_{i}))^{2q} + (\pi _{\zeta _1}(g_{i}))^{2q}\right) , \sum _{i=1}^{n} w_i \left( (\theta _{\zeta _2}(g_{i}))^{2q} + (\vartheta _{\zeta _2}(g_{i}))^{2q} + (\pi _{\zeta _2}(g_{i}))^{2q}\right) \right\} }, \end{aligned}$$

(9)

where $0\le K_{w}(\zeta _1,\zeta _2) \le 1$, $w_{i}$ is the weight of the element $g_i$, $w_{i} \ge 0, i = 1,2,\ldots , n$, $\sum _{i=1}^{n} w_{i} = 1$, $\pi _{\zeta _1}(g_i)= (h^q-(\theta _{\zeta _1}(g_i))^q-(\vartheta _{\zeta _1}(g_i))^q)^{1/q}$, $\pi _{\zeta _2}(g_i)= (h^q-(\theta _{\zeta _2}(g_i))^q-(\vartheta _{\zeta _2}(g_i))^q)^{1/q}$ and $q\ge 1$.

Example 2

Let $\zeta _1 = \left\{ \langle g_{1},s_4,s_3\rangle , \langle g_{2},s_7,s_1 \rangle , \langle g_{3},s_3,s_5 \rangle \right\}$ and $\zeta _2 = \big \{\langle g_{1},s_1,s_5 \rangle , \langle g_{2},s_4,s_3 \rangle , \langle g_{3},s_3,s_2\rangle \big \}$ be two Lq-ROFSs, where $\zeta _1 \in \varepsilon (G)_{[0,8]}$ and $\zeta _2 \in \varepsilon (G)_{[0,8]}$, with weights $w_{1} = 0.3$, $w_{2} = 0.4$ and $w_{3} = 0.3$, respectively.

First, using Eq. (7), we obtain the weighted information energies $T_w(\zeta _1)$ and $T_w(\zeta _2)$ of the Lq-ROFSs $\zeta _1$ and $\zeta _2$, respectively, where $q=3$,

$$\begin{aligned}{} & {} T_w(\zeta _1) = \frac{1}{h^{2q}}\sum _{i=1}^{3} w_{i}\left( (\theta _{\zeta _1}(g_{i}))^{2q} + (\vartheta _{\zeta _1}(g_{i}))^{2q} + (\pi _{\zeta _1}(g_{i}))^{2q}\right) \\{} & {} \quad = \frac{1}{ 8^{6}} \left( 0.3\left( 4^{6} + 3^{6} + (8^{3}-4^{3}-3^{3})^2\right) \right. \\{} & {} \quad \left. + 0.4\left( 7^{6} + 1^{6} + (8^{3}-7^{3}-1^{3})^2\right) \right. \\{} & {} \quad \left. + 0.3\left( 3^{6} + 5^{6} + (8^{3}-3^{3}-5^{3})^2\right) \right) \\{} & {} = 0.5980, \\ T_w(\zeta _2){} & {} \quad = \frac{1}{h^{2q}}\sum _{i=1}^{3} w_{i}\left( (\theta _{\zeta _2}(g_{i}))^{2q} + (\vartheta _{\zeta _2}(g_{i}))^{2q} + (\pi _{\zeta _2}(g_{i}))^{2q}\right) \\{} & {} =\frac{1}{ 8^{6}} \left( 0.3\left( 1^{6} + 5^{6} + (8^{3}-1^{3}-5^{3})^2\right) \right. \\{} & {} \quad \left. +0.4\left( 4^{6} + 3^{6} + (8^{3}-4^{3}-3^{3})^2\right) \right. \\{} & {} \quad \left. + 0.3\left( 3^{6} + 2^{6} + (8^{3}-3^{3}-2^{3})^2\right) \right) \\= & {} 0.7275. \end{aligned}$$

Now, using Eq. (8), we calculate the weighted correlation $C_w(\zeta _1,\zeta _2)$ between the Lq-ROFSs $\zeta _1$ and $\zeta _2$, where $q=3$,

$$\begin{aligned}{} & {} C_{w}(\zeta _1,\zeta _2) = \frac{1}{h^{2q}}\sum _{i=1}^{3} w_{i}\left( (\theta _{\zeta _1}(g_{i}))^{q}\right. \\{} & {} \quad \left. \cdot (\theta _{\zeta _2}(g_{i}))^{q} + (\vartheta _{\zeta _1}(g_{i}))^{q}\cdot (\vartheta _{\zeta _2}(g_{i}))^{q} +(\pi _{\zeta _1}(g_{i}))^{q}\cdot (\pi _{\zeta _2}(g_{i}))^{q} \right) \\{} & {} \quad = \frac{1}{ 8^{6}} \left( 0.3 \left( 4^{3}\cdot 1^{3} + 3^{3}\cdot 5^{3} + \left( 8^{3}-4^{3}-3^{3}\right) .\left( 8^{3}-1^{3}-5^{3}\right) \right) \right. \\{} & {} \quad \left. + 0.4\left( 7^{3}\cdot 4^{3} + 1^{3}\cdot 3^{3}+ \left( 8^{3}-7^{3}-1^{3}\right) .\left( 8^{3}-4^{3}-3^{3}\right) \right) \right. \\{} & {} \quad \left. + 0.3\left( 3^{3}\cdot 3^{3} + 5^{3}\cdot 2^{3} + \left( 8^{3}-3^{3}-5^{3}\right) .\left( 8^{3}-3^{3}-2^{3}\right) \right) \right) \\= & {} 0.5299. \end{aligned}$$

Hence, using Eq. (9), we get the proposed weighted correlation coefficient $K_w(\zeta _1,\zeta _2)$ between the Lq-ROFSs $\zeta _1$ and $\zeta _2$, where $q = 3$,

$$\begin{aligned} K_w(\zeta _1,\zeta _2)= & {} \frac{C\left( \zeta _1,\zeta _2\right) }{\max \{T(\zeta _1),T(\zeta _2)\}}\\= & {} 0.7283. \end{aligned}$$

Theorem 2

Let $\zeta _1 = \left\{ \langle g_{i}, s_{\theta _{\zeta _1}(g_{i})}, s_{\vartheta _{\zeta _1}(g_{i})} \rangle \mid g_{i} \in G \right\}$ and $\zeta _2 = \left\{ \langle g_{i}, s_{\theta _{\zeta _2}(g_{i})}, s_{\vartheta _{\zeta _2}(g_{i})} \rangle \mid g_{i} \in G \right\}$ be two Lq-ROFSs, where $\zeta _1 \in \varepsilon (G)_{[0,h]}$ and $\zeta _2 \in \varepsilon (G)_{[0,h]}$. The proposed weighted correlation coefficient $K_{w}(\zeta _1,\zeta _2)$ between the Lq-ROFNs $\zeta _1$ and $\zeta _2$, defined in Eq. (9), satisfies the following conditions:

• (P1) $K_{w}(\zeta _1,\zeta _2) = K_{w}(\zeta _2,\zeta _1)$.

• (P2) $0 \le K_{w}(\zeta _1,\zeta _2) \le 1$.

• (P3) $\zeta _1 = \zeta _2 \Rightarrow K_{w}(\zeta _1,\zeta _2) = 1$.

Proof

The proof is similar to the proof of Theorem 1. $\square$

4 The proposed MAGDM approach based on the proposed weighted correlation coefficient of Lq-ROFSs and the TOPSIS method

In this section, we propose a new MAGDM approach under the Lq-ROFNs environment based on the proposed weighted correlation coefficient of Lq-ROFSs and the TOPSIS method.

Let $\zeta _{1}, \zeta _{2}, \ldots , \zeta _{p}$ be p alternatives and let $C_{1}, C_{2}, \ldots , C_{r}$ be r attributes. Let $w_{1}, w_{2}, \ldots , w_{r}$ represent the weights of $C_{1}, C_{2}, \ldots , C_{r}$, respectively, where $w_{i} \ge 0, i = 1,2,\ldots , r$ and $\sum _{i=1}^{r} w_{i} = 1$. Let $\xi _{1}, \xi _{2}, \ldots , \xi _{m}$ be the decision-making experts (DMExs) with weights $\varsigma _{1}$, $\varsigma _{2}$, $\ldots$, $\varsigma _{m}$, respectively $\varsigma _{j} \ge 0$, $j = 1,2,\ldots , m$ and $\sum _{j=1}^{m} \varsigma _{j} = 1$. Every DMEx $\xi _{j}$ evaluates the attributes $C_{i}$ of the alternatives $\zeta _{k}$ by utilizing a Lq-ROFN $\tilde{\varrho }_{ki}^{j} = \langle s_{\tilde{\theta }_{ki}^{j}}, s_{\tilde{\vartheta }_{ki}^{j}} \rangle$ to construct the decision matrix (DMx) $\tilde{R}^{j} = (\tilde{\varrho }_{ki}^{j})_{p \times r}$, shown as follows:

• Step 1: Convert the DMxs $\tilde{R}^1 = (\tilde{\varrho }_{ki}^1)_{p \times r}=(\langle s_{\tilde{\theta }_{ki}^1}, s_{\tilde{\vartheta }_{ki}^1}\rangle )_{p \times r}$, $\tilde{R}^2 = (\tilde{\varrho }_{ki}^2)_{p \times r}=(\langle s_{\tilde{\theta }_{ki}^2}, s_{\tilde{\vartheta }_{ki}^2}\rangle )_{p \times r}$, $\ldots$, $\tilde{R}^m = (\tilde{\varrho }_{ki}^m)_{p \times r}=(\langle s_{\tilde{\theta }_{ki}^m}, s_{\tilde{\vartheta }_{ki}^m}\rangle )_{p \times r}$ into the normalize DMx (NDMxs) ${R}^1 = ({\varrho }_{ki}^1)_{p \times r}=(\langle s_{{\theta }_{ki}^1}, s_{{\vartheta }_{ki}^1}\rangle )_{p \times r}$, ${R}^2 = ({\varrho }_{ki}^2)_{p \times r}=(\langle s_{{\theta }_{ki}^2}, s_{{\vartheta }_{ki}^2}\rangle )_{p \times r}$, $\ldots$, ${R}^m = ({\varrho }_{ki}^m)_{p \times r}=(\langle s_{{\theta }_{ki}^m}, s_{{\vartheta }_{ki}^m}\rangle )_{p \times r}$ as follows:

  $$\begin{aligned} {\varrho }_{ki}^j= & {} {\left\{ \begin{array}{ll} \langle s_{\tilde{\theta }_{ki}^j}, s_{\tilde{\vartheta }_{ki}^j}\rangle :&{} \text { for benefit type attribute} \\ \langle s_{\tilde{\vartheta }_{ki}^j}, s_{\tilde{\theta }_{ki}^j}\rangle :&{} \text { for cost type attribute} \end{array}\right. }, \end{aligned}$$

  (10)

  where $k = 1, 2, \ldots , p$, $i= 1,2, \ldots r$ and $j = 1, 2, \ldots , m$.

• Step 2: For each NDMx ${R}^j$, obtain the positive ideal alternative (PIA) $(\zeta ^+)^j$ and the negative ideal alternative (NIA) $(\zeta ^-)^j$, where $j = 1,2,\ldots , m$, shown as follows:

  $$\begin{aligned} (\zeta ^+)^j = \left\{ \langle C_{i}, s_{\left( {\theta _{i}^{+}}\right) ^j}, s_{({\vartheta _{i}^{+}})^j} \rangle , i = 1,2,\ldots , r \right\} , \end{aligned}$$

  (11)
  $$\begin{aligned} (\zeta ^-)^j = \left\{ \langle C_{i}, s_{\left( {\theta _{i}^{-}}\right) ^j}, s_{({\vartheta _{i}^{-}})^j} \rangle , i = 1,2,\ldots , r \right\} , \end{aligned}$$

  (12)

  where $(\theta _{i}^{+})^j = \max _{k}\left\{ \theta _{ki}^j \right\}$, $(\theta _{i}^{-})^j = \min _{k}\left\{ \theta _{ki}^j \right\} , (\vartheta _{i}^{+})^j = \min _{k}\left\{ \theta _{ki}^j \right\} , (\vartheta _{i}^{-})^j = \max _{k}\left\{ \theta _{ki}^j \right\}$, $(\pi _{i}^{+})^j = (h^q-((\theta _{i}^{+})^j)^q-((\vartheta _{i}^{+})^j)^q)^{1/q}$, $(\pi _{i}^{-})^j = (h^q-((\theta _{i}^{-})^j)^q-((\vartheta _{i}^{-})^j)^q)^{1/q}$, $k = 1,2, \ldots , p, i= 1,2, \ldots r$ and $j = 1, 2, \ldots , m$.

• Step 3: Based on Eq. (9), obtain the weighted correlation coefficient $(K_{k}^+)^{j}$ between the alternatives $\zeta _{k}$ and the PIA $(\zeta ^+)^{j}$ and obtain the weighted correlation coefficient $(K_{k}^-)^{j}$ between the alternatives $\zeta _{k}$ and the NIA $(\zeta ^-)^{j}$ for each DMEx $\xi _{j}$, where $j = 1,2,\ldots , m, k = 1,2, \ldots , p$, shown as follows:

  $$\begin{aligned} (K_{k}^+)^{j}= & {} K_{w}^j(\zeta _{k},(\zeta ^+)^{j})\nonumber \\= & {} \tfrac{\sum _{i=1}^{r} w_i \left( (\theta _{ki}^{j})^{q}\cdot ((\theta _{i}^{+})^{j})^{q} + (\vartheta _{ki}^{j})^{q}\cdot ((\vartheta _{i}^{+})^{j})^{q} +(\pi _{ki}^{j})^{q}\cdot ((\pi _{i}^{+})^{j})^{q} \right) }{\max \left\{ \sum _{i=1}^{r} w_i \left( (\theta _{ki}^{j})^{2q} + (\vartheta _{ki}^{j})^{2q} + (\pi _{ki}^{j})^{2q}\right) , \sum _{i=1}^{r} w_i \left( ((\theta _{i}^{+})^{j})^{2q} + ((\vartheta _{i}^{+})^{j})^{2q} + ((\pi _{i}^{+})^{j})^{2q}\right) \right\} }, \end{aligned}$$

  (13)
  $$\begin{aligned} (K_{k}^-)^{j}= & {} K_{w}^j(\zeta _{k},(\zeta ^-)^{j})\nonumber \\= & {} \tfrac{\sum _{i=1}^{r} w_i \left( (\theta _{ki}^{j})^{q}\cdot ((\theta _{i}^{-})^{j})^{q} + (\vartheta _{ki}^{j})^{q}\cdot ((\vartheta _{i}^{-})^{j})^{q} +(\pi _{ki}^{j})^{q}\cdot ((\pi _{i}^{-})^{j})^{q} \right) }{\max \left\{ \sum _{i=1}^{r} w_i \left( (\theta _{ki}^{j})^{2q} + (\vartheta _{ki}^{j})^{2q} + (\pi _{ki}^{j})^{2q}\right) , \sum _{i=1}^{r} w_i \left( ((\theta _{i}^{-})^{j})^{2q} + ((\vartheta _{i}^{-})^{j})^{2q} + ((\pi _{i}^{-})^{j})^{2q}\right) \right\} }, \end{aligned}$$

  (14)

  where $w_{i}$ is the weight of attribute $C_{i}, w_{i} \ge 0,$ and $\sum _{i=1}^{r} w_{i} = 1$.

• Step 4: Calculate the aggregated positive weighted correlation coefficient (PWCC) $(K_{k}^+)$ and negative weighted correlation coefficient (NWCC) $(K_{k}^-)$ for each alternative $\zeta _{k}$, where $k = 1,2, \ldots , p$, shown as follows:

  $$\begin{aligned} K_{k}^+ = \sum _{j=1}^{m} \varsigma _j(K_{k}^+)^{j},\end{aligned}$$

  (15)
  $$\begin{aligned} K_{k}^- = \sum _{j=1}^{m} \varsigma _j(K_{k}^-)^{j}, \end{aligned}$$

  (16)

  where $\varsigma _{j}$ is the weight of DMEx $\xi _{j}, \varsigma _{j} \ge 0,$ and $\sum _{j=1}^{m} \varsigma _{j} = 1$.

• Step 5: Calculate the closeness coefficient $\phi _{k}$ of the alternative $\zeta _{k}$ based on the aggregated PWCC $K_{k}^+$ and aggregated NWCC $K_{k}^-$ of alternatives $\zeta _{k}$, where

  $$\begin{aligned} \phi _{k} = \frac{K_{k}^+}{K_{k}^+ + K_{k}^-} \end{aligned}$$

  (17)

  where $k = 1,2, \ldots , p$.

• Step 6: Rank the alternatives $\zeta _{1}, \zeta _{2}, \ldots , \zeta _{p}$ based on the obtained closeness coefficients $\phi _{1}$, $\phi _{2}$, $\ldots$, $\phi _{p}$.

  A higher closeness coefficient $\phi _{k}$ for alternative $\zeta _{k}$ indicates a superior preference order (PO) for that alternative, where $k = 1,2, \ldots , p$.

Example 3

(Liu and Liu 2019a) We are analyzing a specific postgraduate entrance requirement at a college. There are four potential students denoted as $\zeta _{1}$, $\zeta _{2}$, $\zeta _{3}$, and $\zeta _{4}$, but only two enrollment places are open. The college aims to conduct a comprehensive assessment of the four students and ultimately admit the two most suitable applicants. The college has invited three DMExs named $\xi _1$, $\xi _2$, and $\xi _3$ to evaluate the performance of four students $\zeta _{1}$, $\zeta _{2}$, $\zeta _{3}$, and $\zeta _{4}$. The DMExs $\xi _1$, $\xi _2$, and $\xi _3$ have their weights $\varsigma _{1} = 0.35$, $\varsigma _{2} = 0.4$, and $\varsigma _{3} = 0.25$, respectively. The DMExs $\xi _1$, $\xi _2$ and $\xi _3$ examine the students $\zeta _{1}$, $\zeta _{2}$, $\zeta _{3}$ and $\zeta _{4}$ under the four attributes denoted as $C_1$ (“the score of the written test”), $C_2$ (“the professional relevance”), $C_3$ (“the logical ability”), and $C_4$ (“the learning attitude”), where $w_{1} = 0.25$, $w_{2} = 0.15$, $w_{3} = 0.25$, and $w_{4} = 0.35$ are the weights of the attributes $C_{1}$, $C_{2}$, $C_{3}$ and $C_4$, respectively, using the Lq-ROFNs $\tilde{\varrho }_{ki}^j = \langle s_{\tilde{\theta }_{ki}^j}, s_{{\tilde{\vartheta }}_{ki}^j}\rangle$, where ${\tilde{\varrho }}_{ki}^j \in \Omega _{[0,8]}$, $k=1,2,3,4$; $i=1, 2, 3, 4$ and $j=1,2,3$, to construct the DMxs $\tilde{R}^1 = ({\tilde{\varrho }}_{ki}^1)_{4 \times 4}$, $\tilde{R}^2 = ({\tilde{\varrho }}_{ki}^2)_{4 \times 4}$ and $\tilde{R}^3 = ({\tilde{\varrho }}_{ki}^3)_{4 \times 4}$, respectively, shown as follows:

In the following, we use the proposed MAGDM method to solve this MAGDM problem, shown as follows:

• Step 1: Since all the attributes $C_{1}, C_{2}, C_{3}$ and $C_{4}$ are of benefit type, by using Eq. (10), we get NDMxs ${R}^1 = ({\tilde{\varrho }}_{ki}^1)_{4 \times 4} =({\varrho }_{ki}^1)_{4 \times 4} = (\langle s_{{\theta }_{ki}^1}, s_{{\vartheta }_{ki}^1}\rangle )_{4 \times 4}$, ${R}^2 = ({\tilde{\varrho }}_{ki}^2)_{4 \times 4} =({\varrho }_{ki}^2)_{4 \times 4} = (\langle s_{{\theta }_{ki}^2}, s_{{\vartheta }_{ki}^2}\rangle )_{4 \times 4}$ and ${R}^3 = ({\tilde{\varrho }}_{ki}^3)_{4 \times 4} =({\varrho }_{ki}^3)_{4 \times 4} = (\langle s_{{\theta }_{ki}^3}, s_{{\vartheta }_{ki}^3}\rangle )_{4 \times 4}$.

• Step 2: By using Eqs. (11) and (12), we obtain the PIAs $(\zeta ^+)^1$, $(\zeta ^+)^2$ amd $(\zeta ^+)^3$ and the NIAs $(\zeta ^-)^1$, $(\zeta ^-)^2$ and $(\zeta ^-)^3$ for the DMExs $\xi _1$, $\xi _2$ and $\xi _3$, respectively, as given in Table 1.

• Step 3: By utilizing Eqs. (13) and (14), we obtain the weighted correlation coefficient $(K_{k}^+)^{j}$ between the alternative $\zeta _{k}$ and the PIA $(\zeta ^+)^{j}$ and the weighted correlation coefficient $(K_{k}^-)^{j}$ between the alternatives $\zeta _{k}$ and the NIA $(\zeta ^-)^{j}$, where $q=4$, $j = 1,2,3$, $k = 1,2,3,4$, $(K_{k}^+)^{j} = K_{w}^j(\zeta _{k},(\zeta ^+)^{j})$, $(K_{k}^-)^{j} = K_{w}^j(\zeta _{k},(\zeta ^-)^{j})$, $(K_{1}^+)^{1} = 0.9480, (K_{1}^+)^{2} = 0.8787, (K_{1}^+)^{3} = 0.9452,$ $(K_{2}^+)^{1} = 0.9688, (K_{2}^+)^{2} = 0.9308, (K_{2}^+)^{3} = 0.9620,$ $(K_{3}^+)^{1} = 0.9405, (K_{3}^+)^{2} = 0.8739, (K_{3}^+)^{3} = 0.8633,$ $(K_{4}^+)^{1} = 0.9137, (K_{4}^+)^{2} = 0.9330, (K_{4}^+)^{3} = 0.9099,$ $(K_{1}^-)^{1} = 0.9705, (K_{1}^-)^{2} = 0.9868, (K_{1}^-)^{3} = 0.9224,$ $(K_{2}^-)^{1} = 0.9448, (K_{2}^-)^{2} = 0.9247, (K_{2}^-)^{3} = 0.8826,$ $(K_{3}^-)^{1} = 0.9764, (K_{3}^-)^{2} = 0.9907, (K_{3}^-)^{3} = 0.9827,$ $(K_{4}^-)^{1} = 0.9907, (K_{4}^-)^{2} = 0.9314$ and $(K_{4}^-)^{3} = 0.9568$.

• Step 4: By utilizing Eqs. (15) and (16), we get the PWCC $(K_{k}^+)$ and NWCC $(K_{k}^-)$ for each alternative $\zeta _{k}$, where $k = 1,2,3,4$, $K_{1}^+ = 0.9196, K_{2}^+ = 0.9519, K_{3}^+ = 0.8946, K_{4}^+ = 0.9205, K_{1}^- = 0.9650, K_{2}^- = 0.9212, K_{3}^- = 0.9837, K_{4}^- = 0.9585$.

• Step 5: By using Eq. (17), we get the relative closeness of coefficient $\phi _{1}$, $\phi _{2}$, $\phi _{3}$ and $\phi _{4}$ of the alternative $\zeta _{1}$, $\zeta _{2}$, $\zeta _{3}$ and $\zeta _{4}$, respectively, where $\phi _{1} = 0.4880, \phi _{2} = 0.5082, \phi _{3} = 0.4763$ and $\phi _{4} = 0.4899$.

• Step 6: Because $\phi _{2} \succ \phi _{4} \succ \phi _{1} \succ \phi _{3}$, where $\phi _{1} = 0.4880, \phi _{2} = 0.5082, \phi _{3} = 0.4763$ and $\phi _{4} = 0.4899$, the PO of the alternatives $\zeta _{1}$, $\zeta _{2}$, $\zeta _{3}$ and $\zeta _{4}$ is “$\zeta _{2} \succ \zeta _{4} \succ \zeta _{1} \succ \zeta _{3}$”. Therefore, $\zeta _{2}$ is the best alternative among the alternatives $\zeta _{1}$, $\zeta _{2}$, $\zeta _{3}$ and $\zeta _{4}$.

Table 1 PIA $(\zeta ^+)^j$ and NIA $(\zeta ^-)^j$ for each DMEx $\xi _j$ for Example 3, where $j=1,2,3.$

Table 2 provides a comparison of the POs of the alternatives $\zeta _{1}$, $\zeta _{2}$, $\zeta _{3}$ and $\zeta _{4}$ obtained by the different MAGDM approaches for Example 3. From Table 2, it is clear that the proposed MAGDM approach, the Liu and Liu’s MAGDM approach (Liu and Liu 2019a), and the Liu et al.’s MAGDM approach (Liu et al. 2022) give the same PO “$\zeta _{2} \succ \zeta _{4} \succ \zeta _{1} \succ \zeta _{3}$” of $\zeta _{1}$, $\zeta _{2}$, $\zeta _{3}$ and $\zeta _{4}$.

Table 2 A comparison of the POs of the alternatives obtained by different MAGDM approaches for Example 3

Example 4

Let $\zeta _{1}$, $\zeta _{2}$, and $\zeta _{3}$ be three alternatives, and $C_{1}$, $C_{2}$, and $C_{3}$ be three attributes, where $w_{1} = 0.3$, $w_{2} = 0.3$, and $w_{3} = 0.4$ are the weights of $C_{1}$, $C_{2}$, and $C_{3}$, respectively. The weight of DMExs $\xi _1$, $\xi _2$ and $\xi _3$ are $\varsigma _{1} = 0.3$, $\varsigma _{2} = 0.4$ and $\varsigma _{3} = 0.3$, respectively. The DMExs $\xi _1$, $\xi _2$ and $\xi _3$ evaluate the attribute $C_{i}$ of the alternative $\zeta _{k}$ by using a Lq-ROFN ${\tilde{\varrho }}_{ki}^j = \langle s_{{\tilde{\theta }}_{ki}^j}, s_{{\tilde{\vartheta }}_{ki}^j}\rangle$, where ${\tilde{\varrho }}_{ki}^j \in \Omega _{[0,8]}$, to construct the DMxs $\tilde{R}^1 = ({\tilde{\varrho }}_{ki}^1)_{3 \times 3}$, $\tilde{R}^2 = ({\tilde{\varrho }}_{ki}^2)_{3 \times 3}$ and $\tilde{R}^3 = ({\tilde{\varrho }}_{ki}^3)_{3 \times 3}$, respectively, shown as follows:

In the following, we use the proposed MAGDM method to solve this MAGDM problem, shown as follows:

• Step 1: Since all the attributes $C_{1}, C_{2}$ and $C_{3}$ are of benefit type, using Eq. (10), we get NDMxs ${R}^1 = ({\tilde{\varrho }}_{ki}^1)_{3 \times 3} =({\varrho }_{ki}^1)_{3 \times 3} = (\langle s_{{\theta }_{ki}^1}, s_{{\vartheta }_{ki}^1}\rangle )_{3 \times 3}$, ${R}^2 = ({\tilde{\varrho }}_{ki}^2)_{3 \times 3} =({\varrho }_{ki}^2)_{3 \times 3} = (\langle s_{{\theta }_{ki}^2}, s_{{\vartheta }_{ki}^2}\rangle )_{3 \times 3}$ and ${R}^3 = ({\tilde{\varrho }}_{ki}^3)_{3 \times 3} =({\varrho }_{ki}^3)_{3 \times 3} = (\langle s_{{\theta }_{ki}^3}, s_{{\vartheta }_{ki}^3}\rangle )_{3 \times 3}$.

• Step 2: By utilizing Eqs. (11) and (12), we obtain the PIAs $(\zeta ^+)^1$, $(\zeta ^+)^2$, amd $(\zeta ^+)^3$ and the NIAs $(\zeta ^-)^1$, $(\zeta ^-)^2$, and $(\zeta ^-)^3$ for the DMExs $\xi _1$, $\xi _2$, and $\xi _3$, respectively, as given in Table 3.

• Step 3: By utilizing Eqs. (13) and (14), we obtain the weighted correlation coefficient $(K_{k}^+)^{j}$ between the alternative $\zeta _{k}$ and the PIA $(\zeta ^+)^{j}$ and the weighted correlation coefficient $(K_{k}^-)^{j}$ between the alternatives $\zeta _{k}$ and the NIA $(\zeta ^-)^{j}$, where $q=4$, $j = 1,2,3$, $k = 1,2,3$, $(K_{k}^+)^{j} = K_{w}^j(\zeta _{k},(\zeta ^+)^{j})$, $(K_{k}^-)^{j} = K_{w}^j(\zeta _{k},(\zeta ^-)^{j})$, $(K_{1}^+)^{1} = 0.9623, (K_{1}^+)^{2} = 0.9947, (K_{1}^+)^{3} = 0.6731, (K_{2}^+)^{1} = 0.6899, (K_{2}^+)^{2} = 0.9719, (K_{2}^+)^{3} = 0.9838, (K_{3}^+)^{1} = 0.6356, (K_{3}^+)^{2} = 0.9257, (K_{3}^+)^{3} = 0.7300, (K_{1}^-)^{1} = 0.6570, (K_{1}^-)^{2} = 0.9368, (K_{1}^-)^{3} = 0.9217, (K_{2}^-)^{1} = 0.9393, (K_{2}^-)^{2} = 0.9560, (K_{2}^-)^{3} = 0.6098, (K_{3}^-)^{1} = 0.9920, (K_{3}^-)^{2} = 0.9937$ and $(K_{3}^-)^{3} = 0.9349$.

• Step 4: By utilizing Eq. (15) and (16), we get the PWCC $(K_{k}^+)$ and NWCC $(K_{k}^-)$ for each alternative $\zeta _{k}$, where $k = 1,2,3$, $K_{1}^+ = 0.8885, K_{2}^+ = 0.8909, K_{3}^+ = 0.7800, K_{1}^- = 0.8483, K_{2}^- = 0.8471, K_{3}^- = 0.9756$.

• Step 5: By utilizing Eq. (17), we get the relative closeness of coefficient $\phi _{1}$, $\phi _{2}$, and $\phi _{3}$ of the alternative $\zeta _{1}$, $\zeta _{2}$, and $\zeta _{3}$, respectively, where $\phi _{1} = 0.5116, \phi _{2} = 0.5126$, and $\phi _{3} = 0.4443$.

• Step 6: Because $\phi _{2} \succ \phi _{1} \succ \phi _{3}$ where $\phi _{1} = 0.5116, \phi _{2} = 0.5126$, and $\phi _{3} = 0.4443$, the PO of the alternatives $\zeta _{1}$, $\zeta _{2}$, and $\zeta _{3}$ is “$\zeta _{2} \succ \zeta _{1} \succ \zeta _{3}$”. Therefore, $\zeta _{2}$ is the best alternative among the alternatives $\zeta _{1}$, $\zeta _{2}$, and $\zeta _{3}$.

Table 3 PIA $(\zeta ^+)^j$ and NIA $(\zeta ^-)^j$ for each DMEx $\xi _j$ for Example 4, where $j=1,2,3.$

Table 4 provides a comparison of the POs of the alternatives $\zeta _{1}$, $\zeta _{2}$ and $\zeta _{3}$ obtained by the different MAGDM methods for Example 4. From Table 4, it is clear that the Liu et al.’s MAGDM approach (Liu et al. 2022) gets the PO “$\zeta _{1} = \zeta _{2} \succ \zeta _{3}$” of the alternatives $\zeta _{1}$, $\zeta _{2}$ and $\zeta _{3}$, where it has the shortcomings that it cannot distinguish the PO of alternatives $\zeta _1$ and $\zeta _2$ in this case. Furthermore, it is also clear that the proposed MAGDM approach and the Liu and Liu’s MAGDM approach (Liu and Liu 2019a) obtain the same PO “$\zeta _{2} \succ \zeta _{1} \succ \zeta _{3}$” of $\zeta _{1}$, $\zeta _{2}$ and $\zeta _{3}$. Hence, the proposed MAGDM approach can overcome the shortcomings of Liu et al.’s MAGDM approach (Liu et al. 2022) in this case.

Table 4 A comparison of the POs of the alternatives obtained by different MAGDM approaches for Example 4

Example 5

Let $\zeta _{1}$, $\zeta _{2}$, $\zeta _{3}$, and $\zeta _{4}$ be four alternatives and $C_{1}$, $C_{2}$, $C_{3}$, and $C_{4}$ be four attributes where $w_{1} = 0.2$, $w_{2} = 0.3$, $w_{3} = 0.2$, and $w_{4} = 0.3$ are the weights of the $C_{1}$, $C_{2}$, $C_{3}$, and $C_{4}$, respectively. The weight of DMExs $\xi _1$, $\xi _2$, and $\xi _3$ is $\varsigma _{1} = 0.25$, $\varsigma _{2} = 0.35$, and $\varsigma _{3} = 0.4$, respectively. The DMExs $\xi _1$, $\xi _2$ and $\xi _3$ evaluate the attribute $C_{i}$ of the alternative $\zeta _{k}$ using a Lq-ROFN ${\tilde{\varrho }}_{ki}^j = \langle s_{{\tilde{\theta }}_{ki}^j}, s_{{\tilde{\vartheta }}_{ki}^j}\rangle$, where ${\tilde{\varrho }}_{ki}^j \in \Omega _{[0,8]}$, $k=1,2,3,4$; $i=1, 2, 3,4$ and $j=1,2,3$, to construct the DMxs $\tilde{R}^1 = ({\tilde{\varrho }}_{ki}^1)_{4 \times 4}$, $\tilde{R}^2 = ({\tilde{\varrho }}_{ki}^2)_{4 \times 4}$ and $\tilde{R}^3 = ({\tilde{\varrho }}_{ki}^3)_{4 \times 4}$, respectively, shown as follows:

In the following, we use the proposed MAGDM method to solve this MAGDM problem, shown as follows:

• Step 1: Since all the attributes $C_{1}, C_{2}, C_{3}$ and $C_{4}$ are of benefit type, using Eq. (10), we get NDMxs ${R}^1 = ({\tilde{\varrho }}_{ki}^1)_{4 \times 4} =({\varrho }_{ki}^1)_{4 \times 4} = (\langle s_{{\theta }_{ki}^1}, s_{{\vartheta }_{ki}^1}\rangle )_{4 \times 4}$, ${R}^2 = ({\tilde{\varrho }}_{ki}^2)_{4 \times 4} =({\varrho }_{ki}^2)_{4 \times 4} = (\langle s_{{\theta }_{ki}^2}, s_{{\vartheta }_{ki}^2}\rangle )_{4 \times 4}$ and ${R}^3 = ({\tilde{\varrho }}_{ki}^3)_{4 \times 4} =({\varrho }_{ki}^3)_{4 \times 4} = (\langle s_{{\theta }_{ki}^3}, s_{{\vartheta }_{ki}^3}\rangle )_{4 \times 4}$.

• Step 2: By utilizing Eqs. (11) and (12), we obtain the PIAs $(\zeta ^+)^1$, $(\zeta ^+)^2$, amd $(\zeta ^+)^3$ and the NIAs $(\zeta ^-)^1$, $(\zeta ^-)^2$, and $(\zeta ^-)^3$ for the DMExs $\xi _1$, $\xi _2$, and $\xi _3$, respectively, as given in Table 5.

• Step 3: By utilizing Eqs. (13) and (14), we obtain the weighted correlation coefficient $(K_{k}^+)^{j}$ between the alternative $\zeta _{k}$ and the PIA $(\zeta ^+)^{j}$ and the weighted correlation coefficient $(K_{k}^-)^{j}$ between the alternatives $\zeta _{k}$ and the NIA $(\zeta ^-)^{j}$, where $q=2$, $j = 1,2,3$, $k = 1,2,3,4$, $(K_{k}^+)^{j} = K_{w}^j(\zeta _{k},(\zeta ^+)^{j})$, $(K_{k}^-)^{j} = K_{w}^j(\zeta _{k},(\zeta ^-)^{j})$, $(K_{1}^+)^{1} = 0.4568, (K_{1}^+)^{2} = 0.7657, (K_{1}^+)^{3} = 0.6953, (K_{2}^+)^{1} = 0.5307, (K_{2}^+)^{2} = 0.5445$, $(K_{2}^+)^{3} = 0.9824, (K_{3}^+)^{1} = 0.7401, (K_{3}^+)^{2} = 0.3540$, $(K_{3}^+)^{3} = 0.4186, (K_{4}^+)^{1} = 0.3177, (K_{4}^+)^{2} = 0.3752$, $(K_{4}^+)^{3} = 0.5082, (K_{1}^-)^{1} = 0.6600, (K_{1}^-)^{2} = 0.4133, (K_{1}^-)^{3} = 0.5843, (K_{2}^-)^{1} = 0.5623, (K_{2}^-)^{2} = 0.6008, (K_{2}^-)^{3} = 0.3674, (K_{3}^-)^{1} = 0.4242, (K_{3}^-)^{2} = 0.8513$, $(K_{3}^-)^{3} = 0.9623$, $(K_{4}^-)^{1} = 0.8402, (K_{4}^-)^{2} = 0.8935$ and $(K_{4}^-)^{3} = 0.9047.$

• Step 4: By utilizing Eqs. (15) and (16), we get the PWCC $(K_{k}^+)$ and NWCC $(K_{k}^-)$ for each alternative $\zeta _{k}$, where $k = 1,2,3,4$, $K_{1}^+ = 0.6603, K_{2}^+ = 0.7162, K_{3}^+ = 0.4764, K_{4}^+ = 0.4140, K_{1}^- = 0.5434, K_{2}^- = 0.4978, K_{3}^- = 0.7889, K_{4}^- = 0.8846$.

• Step 5: By utilizing Eq. (17), we get the relative closeness of coefficient $\phi _{1}$, $\phi _{2}$, $\phi _{3}$, and $\phi _{4}$ of the alternative $\zeta _{1}$, $\zeta _{2}$, $\zeta _{3}$, and $\zeta _{4}$, respectively, where $\phi _{1} = 0.5486, \phi _{2} = 0.5899, \phi _{3} = 0.3765$, and $\phi _{4} = 0.3188$.

• Step 6: Because $\phi _{2} \succ \phi _{1} \succ \phi _{3} \succ \phi _{4}$ where $\phi _{1} = 0.5486, \phi _{2} = 0.5899, \phi _{3} = 0.3765$, and $\phi _{4} = 0.3188$, the ranking order of the alternatives $\zeta _{1}, \zeta _{2}, \zeta _{3}$, and $\zeta _{4}$ is “$\zeta _{2} \succ \zeta _{1} \succ \zeta _{3} \succ \zeta _{4}$”. Therefore, $\zeta _{2}$ is the best alternative among the alternatives $\zeta _{1}, \zeta _{2}, \zeta _{3}$, and $\zeta _{4}$.

Table 5 PIA $(\zeta ^+)^j$ and NIA $(\zeta ^-)^j$ for each DMEx $\xi _j$ for Example 5, where $j=1,2,3.$

Table 6 provides a comparison of the POs of the alternatives $\zeta _{1}, \zeta _{2}, \zeta _{3}$, and $\zeta _{4}$ obtained by the different MAGDM approaches for Example5. From Table 6, it is clear that the MAGDM approach by Liu and Liu (2019a) gets the PO “$\zeta _{1} = \zeta _{2} \succ \zeta _{3} \succ \zeta _{4}$” of the alternatives $\zeta _{1}, \zeta _{2}, \zeta _{3}$ a,nd $\zeta _{4}$, it has the shortcomings that it cannot distinguish the PO of alternatives $\zeta _1$ and $\zeta _2$ in this case. Furthermore, it is also clear that the proposed MAGDM approach and the Liu et al.’s MAGDM method (Liu et al. 2022) obtain the same PO “$\zeta _{2} \succ \zeta _{1} \succ \zeta _{3} \succ \zeta _{4}$” of $\zeta _{1}, \zeta _{2}, \zeta _{3}$ and $\zeta _{4}$. Hence, the proposed MAGDM approach can overcome the limitations of Liu and Liu’s MAGDM approach (Liu and Liu 2019a) in this case.

Table 6 A comparison of the POs of the alternatives obtained by different MAGDM approaches for Example 5

5 Conclusion

In this paper, we have developed a multiattribute group decision making (MAGDM) approach based on the proposed weighted correlation coefficient of linguistic q-rung orthopair fuzzy sets (Lq-ROFSs) and the TOPSIS method under linguistic q-rung orthopair fuzzy numbers (Lq-ROFNs) environment. For this, first, we have proposed the correlation coefficient and weighted correlation coefficient of Lq-ROFSs, which measure the strength of the relationship between two Lq-ROFSs. We have also provided the various properties of the proposed correlation coefficient and weighted correlation coefficient of Lq-ROFSs. Furthermore, we have developed the MAGDM approach under the Lq-ROFNs environment, which is based on the TOPSIS method and the proposed weighted correlation coefficient of Lq-ROFSs. We have also solved the different MAGDM problems by utilizing the proposed MAGDM approach to illustrate the applicability and practicality of the proposed MAGDM approach. The results of Example 3, Example 4, and Example 5 show that the proposed MAGDM approach can overcome the shortcomings of the Liu and Liu’s MAGDM approach (Liu and Liu 2019a) and Liu et al.’s MAGDM approach (Liu et al. 2022), where they cannot distinguish the preference orders of alternatives in some situations. The proposed MAGDM approach provides a valuable tools for tackling MAGDM problems in the context of Lq-ROFNs.