Abstract
Pythagorean cubic fuzzy is a relatively new improvement in the field of fuzzy set (FS) theory. It is a mathematical framework that allows decision-makers to effectively evaluate and select the best course of action when faced with uncertainty and ambiguity. The theory is built on the idea of a Pythagorean FS (PFS), which is a generality of the traditional FS. It also includes a cubical structure, which allows for more flexibility in representing complex relationships. The Pythagorean cubic fuzzy (PCF) sets (PCFSs) provide a way to model and handle uncertainty more precisely and accurately, giving decision-makers the ability to make better-informed decisions in uncertain and fuzzy environments. This study aims to investigate the use of Frank operations, which are a type of mathematical operation, to aggregate PCF numbers (PCFNs) and provide a powerful tool for decision-making in uncertain and fuzzy environments. We introduce new operations for PCF environments, including the Frank sum, product, scalar multiplication and exponentiation. Using these operations, we develop new a series of aggregation operators (AOs) such as the PCF Frank weighted averaging (PCFFWA) and PCF Frank weighted geometric (PCFFWG) operator. We establish various properties of these operators, provide examples of them, and examine the connections between these operators. Furthermore, we utilize these operators to devise a method for handling group decision-making with CPF information. To demonstrate the usefulness and efficiency of the operators and method, we present a numerical example. Finally, we compare the results of the proposed method with existing methods to demonstrate its applicability and feasibility.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Multi-criteria decision-making (MCDM) is a method of evaluating and choosing alternatives based on multiple, often conflicting, criteria. MCDM involves evaluating alternatives based on multiple criteria (e.g. cost, feasibility, impact) and weighing them with mathematical models to find the optimal solution. MCDM is useful in situations where traditional single-criteria decision-making is insufficient, such as when multiple objectives need to be optimized or trade-offs between objectives must be made. With the progression of society and the economy, practical decision-making problems have become increasingly complex. As a result, it has become challenging for decision-makers (DMs) to make decisions based solely on precise numerical values. The complexity of these problems requires a more nuanced approach to decision-making, taking into account multiple factors and variables, rather than relying solely on clear-cut numerical data. This has led to the need for MCDM methods that can help DMs weigh and evaluate different factors to arrive at a more informed and optimal decision. The concept of FSs introduced by Zadeh (1965) allows for the representation of ambiguous, vague, and uncertain elements in a set. This is achieved through the use of a membership degree, which serves as a measure of the extent to which a specific element belongs to a particular set. The membership degree ranges from 0 to 1, where 0 indicates that an element does not belong to the set and 1 indicates full membership. This concept provides a flexible and precise way to deal with the uncertain or vague aspects of data. Atanassov (1986) proposed a solution to address the limitations of FS by introducing the concept of intuitionistic fuzzy sets (IFSs). The key difference between FS and IFS is that IFS considers both the degree of membership and the degree of non-membership for each element within the set. In real-world decision-making scenarios, it is common for DMs to encounter situations where the sum of their membership and non-membership degrees is greater than one, even though the sum of their squares is less than or equal to one. To address this issue, Yager (2013) introduced the concept of PFSs, which is an extension of the IFS model. PFS provides a framework for dealing with these complex situations by considering both the membership and non-membership degrees in a more nuanced and sophisticated manner. This allows for a more accurate representation of uncertainty and vagueness in decision-making processes. Zhang (2016) introduced the concept of interval-valued PFS (IVPFS) to address the challenges faced in MCDM problems. IVPFS is an extension of the PFS model and represents the membership and non-membership degrees as intervals rather than single values. This approach allows for a more comprehensive understanding of the degree of membership and non-membership, providing a more accurate representation of uncertainty and vagueness in MCDM problems.
The existing literature shows that previous studies primarily concentrate on FSs, interval fuzzy sets, IFS, PFS, and their practical applications. Jun et al. (2012) later introduced the concept of cubic sets (CSs), which combines interval-valued fuzzy numbers and fuzzy numbers, and defined logic operations for them. In this set, Khan et al. (2016) proposed cubic aggregation operators, while Mahmood et al. (2016) introduced the concept of cubic hesitant fuzzy sets and their aggregation operators in decision-making. Garg and Kaur (2019) introduced the concept of cubic intuitionistic fuzzy sets (CIFSs) and specified several desirable properties for these operations. Kaur and Garg (2018) introduced the concept of Bonferroni Mean Operators for use with cubic IFSs (CIFSs) and developed a decision-making method utilizing these operators.
Khan et al. (2019a) introduced the concept of Pythagorean cubic fuzzy sets, which represents a noteworthy advancement in the field of FS theory. This new idea represents a more effective and innovative approach to solving problems and making decisions in uncertain environments. Khan et al. (2019b) investigated a series averaging and geometric operators by utilizing the information PCFSs and the idea of confidence levels. Khan et al. (2020) presented a technique for MCDM that uses the technique for order of preference by similarity to ideal solution (TOPSIS) method with limited weight information. Wang and Zhao (2021) transformed the PCFS into a geometric form and suggested the utilization of PCFS geometric-distance measurements. The utilization of the cubic intuitionistic fuzzy set has become increasingly important in handling uncertainty and fuzziness during the decision-making process. This is because it allows for the simultaneous expression of interval-valued intuitionistic fuzzy numbers and intuitionistic fuzzy values, thus providing a more comprehensive approach to representing complex and uncertain information. By employing the cubic intuitionistic fuzzy set, decision-makers can better capture the nuances and ambiguities that arise in real-world scenarios. The set offers a more flexible and powerful tool for modeling uncertain information, as it provides a more accurate representation of the decision-making environment.
Frank t-conorm and t-norm are currently the only class of t-conorm and t-norm that possess the features of general t-conorm and t-norm, including algebraic, Einstein, and Hamacher t-conorm and t-norm. Additionally, they are the only t-conorm and t-norm that abide by the compatibility law. Frank t-conorms and t-norms offer greater versatility than their counterparts due to the presence of an additional parameter that modulates the magnitude of the argument values being raised. This added degree of control allows for a greater range of results, providing greater flexibility to the user. When we make various selections for the parameter, it leads to the emergence of specific instances or scenarios. These instances, also referred to as special cases, result from the distinct choices made for the parameter. Over the past several decades, there has been extensive research and exploration into Frank t-conorms and t-norms. This area of study has produced a significant amount of results and advancements, with many noteworthy achievements having been documented and reported. For example, Yager (2004) introduced two novel methods for computing the Frank t-conorm and t-norm and utilized them for approximate reasoning. Sarkoci (2005) compared the Frank t-norms to the Hamacher t-norms in terms of domination through inspection and showed that both t-norms originate from the same family. Mahnaz et al. (2021) developed general operational laws, known as Frank operational laws, for T-spherical fuzzy numbers using the Frank t-norm and t-conorm. Seikh and Mandal (2022) created aggregation operators based on the Frank t-norm and t-conorm for merging q-rung orthopair fuzzy (q-ROF) information. Seikh and Mandal (2021) introduced some operations and aggregation operators for Picture Fuzzy Sets.
1.1 Motivation
Based on the previous discussion, it is evident that there is a lack of research on the utilization of Frank T-norm and T-conorm in the context of Pythagorean Cubic Fuzzy sets. This research gap presents an opportunity for further investigation and exploration of the potential applications and benefits of utilizing these operators in PCF-based decision-making frameworks. Such studies may lead to new insights and a deeper understanding of the capabilities and limitations of Pythagorean cubic fuzzy sets, and help to expand their applicability to a wider range of real-world problems. In this communication, we aim to introduce a new approach to aggregate the preferences decision-makers. Our proposal is based on the concept of the Frank operations and leverages the benefits of the PCFS in expressing uncertainty. The new operators we present are known as the PCFFWA and the PCFFWG. These operators offer a fresh perspective on aggregation and aim to improve decision-making processes. The desirable features of these operators have been thoroughly analyzed, with a focus on their key advantage of considering the interconnections among aggregated values. Additionally, the properties of the proposed operator have been investigated and specific cases have been developed. The proposed operator has been shown to be more comprehensive compared to previous studies, as previous work can be derived from the proposed operator. Lastly, a methodology for ranking various alternatives based on the proposed operators has been presented for making informed decisions.
2 Preliminaries
In this section, we provide a comprehensive review of definitions and concepts related cubic sets, Pythagorean fuzzy sets, interval-valued Pythagorean fuzzy sets, Pythagorean cubic fuzzy sets, and their associated operational principles and laws.
2.1 Pythagorean fuzzy sets
Definition 1
(Yager 2013) Let \(T\) represent a non-empty set. A PFS of an element \(t\) that belongs to the set \(T\) is formally defined as follows
The membership function of an element \(t\) in \(T\) is represented by \({\mu }_{P}\left(t\right)\) which maps to the interval \(\left[\mathrm{0,1}\right]\). Meanwhile, the non-membership grade of \(t\) is represented by \({\vartheta }_{P}(t)\) which also maps to the interval \(\left[\mathrm{0,1}\right]\).
Definition 2
(Yager and Abbasov 2013) For any Pythagorean fuzzy number \(P=({\mu }_{P},{\vartheta }_{P})\), score function of \(P\) can be calculated as:
where \(-1\preccurlyeq \mathrm{Sc}\left(p\right)\preccurlyeq 1\). The accuracy function of \(P\) is defined as follows:
where \(0\preccurlyeq \mathrm{Ac}\left(p\right)\preccurlyeq 1\).
For any two Pythagorean fuzzy numbers \({P}_{1},{P}_{2}\), if \(\mathrm{Sc}\left({P}_{1}\right)\prec \mathrm{Sc}\left({P}_{2}\right)\) or \(\mathrm{Ac}\left({P}_{1}\right)\prec \mathrm{Ac}({P}_{2})\), then \({P}_{1}\prec {P}_{2}\). If \(\mathrm{Sc}\left({P}_{1}\right)\succ \mathrm{Sc}({P}_{2})\) or \(\mathrm{Ac}\left({P}_{1}\right)\succ \mathrm{Ac}\left({p}_{2}\right),\) then \({P}_{1}\succ {P}_{2}\). If \(\mathrm{Sc}\left({P}_{1}\right)=\mathrm{Sc}({P}_{2})\) and \(\mathrm{Ac}\left({P}_{1}\right)=\mathrm{Ac}({P}_{2})\) then \({P}_{1}={P}_{2}\).
Definition 3
(Zhang and Xu 2014) Let \(P=({\mu }_{P},{\vartheta }_{P})\), \({p}_{1}=({\mu }_{{P}_{1}},{\vartheta }_{{P}_{1}})\) and \({p}_{2}=({\mu }_{{P}_{2}}{\vartheta }_{{P}_{2}})\) be any three PFNs, and \(\varphi \) is any positive real number, then
-
1.
\({P}_{1}\oplus {P}_{2}=\left(\langle \sqrt{{\mu }_{{P}_{1}}^{2}{+\mu }_{{P}_{2}}^{2}{-\mu }_{{P}_{1}}^{2}{\mu }_{{P}_{2}}^{2}},{\vartheta }_{{P}_{1}}{\vartheta }_{{P}_{2}}\rangle \right)\),
-
2.
\({P}_{1}\otimes {P}_{2}=\left(\langle {\mu }_{{P}_{1}}{\mu }_{{P}_{2}},\sqrt{{\vartheta }_{{P}_{1}}^{2}{+\vartheta }_{{P}_{2}}^{2}{-\vartheta }_{{P}_{1}}^{2}{\vartheta }_{{P}_{2}}^{2}}\rangle \right)\),
-
3.
\({P}^{\varphi }=\left({\mu }_{P}^{\varphi },\sqrt{{1-(1-{\vartheta }_{P}^{2})}^{\varphi }}\right)\),
-
4.
\(\varphi P=\left(\langle \sqrt{{1-(1-{\mu }_{P}^{2})}^{\varphi }},{\vartheta }_{P}^{\varphi }\rangle \right)\).
2.2 Interval-valued Pythagorean fuzzy sets
Definition 4
(Zhang 2016) Let \(T\) be a non-empty finite set. An IVPFS \(Q\) in element \(t\in T\) is defined as follows:
where \({\mu }_{Q}\left(x\right)\) interval-valued fuzzy membership grade and can be represented as \({\mu }_{Q}\left(x\right)=\left[{\mu }_{Q}^{-}\left(t\right),{\mu }_{Q}^{+}(t)\right]\) and \({\vartheta }_{Q}(t)\) interval-valued non-membership grade and can be represented as \({\vartheta }_{Q}\left(x\right)=\left[{\vartheta }_{Q}^{-}\left(t\right),{\vartheta }_{Q}^{+}(t)\right]\) of set \(Q\) such that \({\mu }_{Q}^{+}(t)+{\vartheta }_{Q}^{+}(t)\preccurlyeq 1\).
Definition 5
(Zhang 2016) Let \(Q=(\left[a,b\right],\left[c,d\right])\) be an interval-valued Pythagorean fuzzy number. The score function of \(Q\) is defined as:
where \(-1\preccurlyeq \mathrm{Sc}\left(Q\right)\preccurlyeq 1\). The accuracy function of \(Q\) is defined as:
where \(0\preccurlyeq \mathrm{Ac}\left(\delta \right)\preccurlyeq 1.\)
For any two interval-valued Pythagorean numbers \({Q}_{1}\) and \({Q}_{2}\), if \(\mathrm{Sc}\left({Q}_{1}\right)\prec \mathrm{Sc}\left({Q}_{2}\right)\) or \(\mathrm{Ac}\left({Q}_{1}\right)\prec \mathrm{Ac}({Q}_{2})\), then \({Q}_{1}\prec {Q}_{2}\). If \(\mathrm{Sc}\left({Q}_{1}\right)\succ \mathrm{Sc}\left({Q}_{2}\right)\) or \(\mathrm{Ac}\left({Q}_{1}\right)\succ \mathrm{Ac}\left({Q}_{2}\right)\), then \({Q}_{1}\succ {Q}_{2}\). If \(\mathrm{Sc}\left({Q}_{1}\right)=\mathrm{Sc}({Q}_{2})\) and \(\mathrm{Ac}\left({\delta }_{1}\right)=\mathrm{Ac}({Q}_{2})\), then \({Q}_{1}={Q}_{2}\).
Definition 6
(Zhang 2016) Let \(Q=(\left[a,b\right],[c,d])\), \({Q}_{1}=(\left[{a}_{1},{b}_{2}\right],[{c}_{1},{d}_{1}])\) and \({Q}_{2}=(\left[{a}_{2},{b}_{2}\right],[{c}_{2},{d}_{2}])\), be three interval-valued Pythagorean fuzzy numbers and \(\varphi \) is any positive integer then,
-
1.
\({Q}_{1}\oplus {Q}_{2}=\left(\left[\begin{array}{c}\sqrt{{a}_{1}^{2}+{a}_{2}^{2}-{a}_{1}^{2}{a}_{2}^{2}},\\ \sqrt{{b}_{1}^{2}+{b}_{2}^{2}+{b}_{1}^{2}{b}_{2}^{2}}\end{array}\right],\left[\begin{array}{c}{c}_{1}{c}_{2},\\ {d}_{1}{d}_{2}\end{array}\right]\right)\),
-
2.
\({Q}_{1}\otimes {Q}_{2}=\left(\left[\begin{array}{c}{a}_{1}{a}_{2},\\ {b}_{1}{b}_{2}\end{array}\right],\left[\begin{array}{c}\sqrt{{c}_{1}^{2}+{c}_{2}^{2}-{c}_{1}^{2}{c}_{2}^{2}},\\ \sqrt{{d}_{1}^{2}+{d}_{1}^{2}-{d}_{1}^{2}{d}_{2}^{2}}\end{array}\right]\right)\),
-
3.
\(\varphi Q=\left(\left[\begin{array}{c}\sqrt{1-{\left(1-{a}^{2}\right)}^{\varphi }},\\ \sqrt{{1-\left(1-{b}^{2}\right)}^{\varphi }}\end{array}\right],\left[\begin{array}{c}{c}^{\varphi },\\ {d}^{\varphi }\end{array}\right]\right)\),
-
4.
\({Q}^{\varphi }=\left(\left[\begin{array}{c}{a}^{\varphi },\\ {b}^{\varphi }\end{array}\right],\left[\begin{array}{c}\sqrt{{1-\left(1-{c}^{2}\right)}^{\varphi }},\\ \sqrt{{1-(1-{d}^{2})}^{\varphi }}\end{array}\right]\right)\).
The complement of PFNS \(Q\) is denoted by \({Q}^{c}\) and defined as \({Q}^{c}=(\left[c,d\right],[a,b])\).
Let \({\varphi }_{1}\) and \({\varphi }_{2}\) are any positive real numbers, then the following properties for interval-valued Pythagorean fuzzy numbers \(Q\), \({Q}_{1}\) and \({Q}_{2}\) holds.
-
1.
\({Q}_{1}{\oplus Q}_{2}={Q}_{1}\oplus {Q}_{2}\),
-
2.
\({Q}_{1}\otimes {Q}_{2}={Q}_{1}\otimes {Q}_{2}\),
-
3.
\(\varphi \left({Q}_{1}{\oplus Q}_{2}\right)=\varphi {Q}_{1}\oplus \varphi {Q}_{2}\),
-
4.
\(\left({\varphi }_{1}+{\varphi }_{2}\right)Q={\varphi }_{1}Q{\oplus \varphi }_{2}Q\),
-
5.
\({({Q}_{1}{\otimes Q}_{2})}^{\varphi }={Q}_{1}^{\varphi }\otimes {Q}_{2}^{\varphi }\),
-
6.
\(\left({Q}^{{\varphi }_{1}}{\otimes Q}^{{\varphi }_{2}}\right)={Q}^{{\varphi }_{1}+{\varphi }_{2}}\).
2.3 Cubic sets
Definition 7
(Jun et al. 2012) Let \(T\) be a non-empty finite set. A cubic set over an element \(t\in T\) is defined as follows:
where \(\mathcal{R}(t)\) is interval-valued fuzzy set and \(\mu (t)\) is a fuzzy set of an element \(t\in T\). A cubic set \(R=\left\{\langle t,\mathcal{R}\left(t\right),\mu (t)\rangle \left|t\in T\right.\right\}\) is simply denoted by \(R=\langle \mathcal{R},\mu \rangle .\) Let \(R\left(t\right)=[a,b]\), then a cubic set \(R=\langle \mathcal{R},\mu \rangle \) is said to be internal cubic set if \(\mu \in [a,b]\), on the other hand a cubic set \(R=\langle \mathcal{R},\mu \rangle \) is said to be external cubic set if \(\mu \notin \left[a,b\right].\)
Definition 8
(Jun et al. 2012) Let \(R=\langle \mathcal{R},\mu \rangle \) and \(S=\langle \mathcal{S},\nu \rangle \) be two cubic sets in \(T\). Then the following properties holds.
-
1.
(Equality). If \(\mathcal{R}=\mathcal{S}\) and \(\mu =\nu \), then \(R=S\),
-
2.
(P-order) \(R{\subseteq }_{P}S\Leftrightarrow \mathcal{R}\subseteq \mathcal{S}\) and \(\mu \preccurlyeq \nu \),
-
3.
(R-order) \({R\subseteq }_{R}S\iff \mathcal{R}\subseteq \mathcal{S}\) and \(\mu \succcurlyeq \nu .\)
Definition 9
(Jun et al. 2012) For any \({R}_{i}=\left(t,\langle {\mathcal{R}}_{i}\left(t\right),{\mu }_{i}(t)\rangle \left|t\in T\right.\right)\) where \(i\epsilon \Delta \). Then,
P-Union
R-Union
P-Intersection
R-Intersection
2.4 Pythagorean cubic fuzzy sets
Definition 10
(Khan et al. 2019a, b) Let \(T\) be a non-empty finite set. A PCFS \(D\) of an element \(t\in T\) is defined as:
where \({\mathcal{C}}_{D}\left(t\right)=\langle {Z}_{D}\left(t\right);{\mu }_{D}(t)\rangle \) membership grade, while \({\mathcal{D}}_{D}\left(t\right)=\langle {\widetilde{Z}}_{D}\left(t\right);{\nu }_{D}(t)\rangle \) represent the non-membership grade. Furthermore \({Z}_{D}\left(t\right)\) and \({\widetilde{Z}}_{D}(t)\) are interval-valued fuzzy sets while \({\mu }_{D}(t)\) and \({\nu }_{D}(t)\) represent fuzzy sets. Let \({Z}_{D}\left(t\right)=[{\mu }_{D}^{-}\left(t\right),{\mu }_{D}^{+}(t)]\) and \({\widetilde{Z}}_{D}\left(t\right)=[{\vartheta }_{D}^{-}\left(t\right),{\vartheta }_{1}^{+}(t)]\), then \({\mathcal{C}}_{D}\left(t\right)=\left(\langle [{\mu }_{D}^{-}\left(t\right),{\mu }_{D}^{+}(t);{\mu }_{D}(t)\rangle \right)\) describes the degree of membership, while \({\mathcal{D}}_{D}\left(t\right)=\left(\langle [{\vartheta }_{D}^{-}\left(x\right),{{\vartheta }_{D}^{+}}_{\widehat{p}}(t)];{\nu }_{D}(t)\rangle \right)\) represent non-membership degree of an element \(t\in T\), such that \({0\preccurlyeq \left({\mu }_{D}^{+}(t)\right)}^{2}+\left({\vartheta }_{D}^{+}(t)\right)\preccurlyeq 1\) and \({0\preccurlyeq \left({\mu }_{D}(t)\right)}^{2}+{\left({\vartheta }_{D}(t)\right)}^{2}\preccurlyeq 1\). For simplicity we call \(\left(\langle Z(t);\mu (t)\rangle ,\langle \widetilde{Z}(t);\vartheta (t)\rangle \right)\) a CPF number (PCFN) denoted by \(\beta =\left(\langle Z;\mu \rangle ,\langle \widetilde{Z},\vartheta \rangle \right).\)
Definition 11
(Khan et al. 2019a, b) Let \(\beta =\left(\langle Z;\xi \rangle ,\langle \widetilde{Z},\tau \rangle \right)\), \({\beta }_{1}=\left(\langle {Z}_{1};{\mu }_{1}\rangle ,\langle {\widetilde{Z}}_{1},{\vartheta }_{1}\rangle \right)\) and \({\beta }_{2}=\left(\langle {Z}_{2};{\mu }_{2}\rangle ,{\widetilde{Z}}_{2};{\vartheta }_{2}\right)\) be three PCFNs, and \(\varphi \) is any positive real number, where \({Z}_{1}=[{\mu }_{1}^{-}\left(t\right),{\mu }_{1}^{+}(t)]\), \({\widetilde{Z}}_{1}=[{\vartheta }_{1}^{-}\left(t\right),{\vartheta }_{1}^{+}(t)]\), \({Z}_{2}=[{\mu }_{2}^{-}\left(t\right),{\mu }_{2}^{+}(t)]\), \({\widetilde{Z}}_{2}=[{\vartheta }_{2}^{-}\left(t\right),{\vartheta }_{2}^{+}(t)]\), \(Z=[{\mu }^{-}\left(t\right),{\mu }^{+}(t)]\) and \(\widetilde{Z}=[{\vartheta }^{-}\left(t\right),{\vartheta }^{+}(t)]\) then the operational laws are defined as.
-
1.
\({\beta }_{1}\oplus {\beta }_{2}=\left(\begin{array}{c}\langle \begin{array}{c}\left[\begin{array}{c}\sqrt{{\left({\mu }_{1}^{-}\right)}^{2}+{\left({\mu }_{2}^{-}\right)}^{2}-{\left({\mu }_{1}^{-}\right)}^{2}{\left({\mu }_{2}^{-}\right)}^{2}},\\ \sqrt{{\left({\mu }_{1}^{+}\right)}^{2}+{\left({\mu }_{1}^{+}\right)}^{2}-{\left({\mu }_{1}^{+}\right)}^{2}{\left({\mu }_{1}^{+}\right)}^{2}}\end{array}\right];\\ \sqrt{{\mu }_{1}^{2}+{\mu }_{2}^{2}-{\mu }_{1}^{2}{\mu }_{2}^{2}}\end{array}\rangle ,\\ \langle \left[{\vartheta }_{1}^{-}{\vartheta }_{2}^{-},{\vartheta }_{1}^{+}{\vartheta }_{2}^{+}\right];{\vartheta }_{1}{\vartheta }_{2}\rangle \end{array}\right)\),
-
2.
\({\beta }_{1}\otimes {\beta }_{2}=\left(\begin{array}{c}\langle \left[{\mu }_{1}^{-}{\mu }_{2}^{-},{\mu }_{1}^{+}{\mu }_{2}^{+}\right];{\mu }_{1}{\mu }_{2}\rangle ,\\ \langle \begin{array}{c}\left[\begin{array}{c}\sqrt{{\left({\vartheta }_{1}^{-}\right)}^{2}+{\left({\vartheta }_{2}^{-}\right)}^{2}-{\left({\vartheta }_{1}^{-}\right)}^{2}{\left({\vartheta }_{2}^{-}\right)}^{2}},\\ \sqrt{{\left({\vartheta }_{1}^{+}\right)}^{2}+{\left({\vartheta }_{1}^{+}\right)}^{2}-{\left({\vartheta }_{1}^{+}\right)}^{2}{\left({\vartheta }_{1}^{+}\right)}^{2}}\end{array}\right];\\ \sqrt{{\vartheta }_{1}^{2}+{\vartheta }_{2}^{2}-{\vartheta }_{1}^{2}{\vartheta }_{2}^{2}}\end{array}\rangle \end{array}\right)\),
-
3.
\(\varphi \beta =\left(\begin{array}{c}\langle \begin{array}{c}\left[\begin{array}{c}\sqrt{{1-\left(1-{\left({\mu }^{-}\right)}^{2}\right)}^{\varphi }},\\ \sqrt{1-{\left(1-{\left({\mu }^{+}\right)}^{2}\right)}^{\varphi }}\end{array}\right];\\ \sqrt{1-{\left(1-{\mu }^{2}\right)}^{\varphi }}\end{array}\rangle ,\\ \langle \left[{\left({\vartheta }^{-}\right)}^{\varphi },{\left({\vartheta }^{+}\right)}^{\varphi }\right];{\vartheta }^{\varphi }\rangle \end{array}\right)\),
-
4.
\({\beta }^{\varphi }=\left(\begin{array}{c}\langle \left[{\left({\mu }^{-}\right)}^{\varphi },{\left({\mu }^{+}\right)}^{\varphi }\right];{\mu }^{\varphi }\rangle ,\\ \langle \begin{array}{c}\left[\begin{array}{c}\sqrt{{1-\left(1-{\left({\vartheta }^{-}\right)}^{2}\right)}^{\varphi }},\\ \sqrt{1-{\left(1-{\left({\vartheta }^{+}\right)}^{2}\right)}^{\varphi }}\end{array}\right];\\ \sqrt{1-{\left(1-{\vartheta }^{2}\right)}^{\varphi }}\end{array}\rangle \end{array}\right)\).
Definition 12
(Khan et al. 2019a, b) Let \(\beta =\left(\langle Z;\mu \rangle ,\langle \widetilde{Z};\vartheta \rangle \right)\) be a PCFN, where \(Z=[{\mu }^{-},{\mu }^{+}]\) and \(\widetilde{Z}=[{\vartheta }^{-},{\vartheta }^{+}]\) then the score function \(Sc(\rho )\) is defined as follows:
while the accuracy function is defined as follows:
where \(-1\preccurlyeq \mathrm{Sc}\left(\beta \right)\preccurlyeq 1\) and \(0\preccurlyeq \mathrm{Ac}\left(\beta \right)\preccurlyeq 1\). Let \({\beta }_{1}=\left(\langle {Z}_{1};{\mu }_{1}\rangle ,\langle {\widetilde{Z}}_{1}{,\vartheta }_{1}\rangle \right)\) and \({\beta }_{1}=\left(\langle {Z}_{2},{\mu }_{2}\rangle ,\langle {\widetilde{Z}}_{2},{\vartheta }_{2}\rangle \right)\) be two PCFNs. If \(\mathrm{Sc}({\beta }_{1})\prec \mathrm{Sc}({\beta }_{2})\) or \(\mathrm{Ac}({\beta }_{1})\prec \mathrm{Ac}\left({\beta }_{2}\right)\) then \({\beta }_{1}\) \(\prec {\beta }_{2}\). If \(\mathrm{Sc}({\beta }_{1})\succ \mathrm{Sc}({\beta }_{2})\) or \(\mathrm{Ac}({\beta }_{1})\succ \mathrm{Ac}({\beta }_{2})\) then \({\beta }_{1}\succ {\beta }_{2}\). If \(Sc\left({\beta }_{1}\right)=\mathrm{Sc}({\beta }_{2})\) and \(\mathrm{Ac}\left({\beta }_{1}\right)=\mathrm{Ac}({\beta }_{2})\) then \({\beta }_{1}={\beta }_{2}\).
Definition 13
(Khan et al. 2019a, b) Let \(\beta \), \({\beta }_{1}\) and \({\beta }_{2}\) be any three PCFNs and \(\varphi \), \({\varphi }_{1}\) and \({\varphi }_{2}\) are positive real numbers then following properties holds.
-
1.
\({\beta }_{1}\oplus {\beta }_{2}={\beta }_{2}{\oplus \beta }_{1}\),
-
2.
\({\beta }_{1}\otimes {\beta }_{2}={\beta }_{2}\otimes {\beta }_{1}\),
-
3.
\(\varphi \left({\beta }_{1}\oplus {\beta }_{2}\right)={\varphi \beta }_{1}\oplus {\varphi \beta }_{2}\),
-
4.
\(\left({\varphi }_{1}{+\varphi }_{2}\right)\beta ={\varphi }_{1}\beta {\oplus \varphi }_{2}\beta \),
-
5.
\({\left({\beta }_{1}\otimes {\beta }_{2}\right)}^{\zeta }={\beta }_{1}^{\varphi }\otimes {\beta }_{2}^{\varphi }\),
-
6.
\({\beta }^{\left({\varphi }_{1}+{\varphi }_{2}\right)}={\beta }^{{\varphi }_{1}}{\otimes \beta }^{{\varphi }_{2}}\).
2.5 Frank operations
Definition 14
(Frank 1979) Let \(\delta \) be a positive real and \(\left(a, b\right)\in {[\mathrm{0,1}]}^{2}\). Then, Frank product \({\otimes }_{F}\) and Frank sum \({\oplus }_{F}\) are defined as follows:
Properties of the Frank product and Frank sum are as follows:
-
1.
\(\left(a{\oplus }_{F}b\right)+\left(a{\otimes }_{F}b\right)=a+b\),
-
2.
\(\frac{\partial (a{\oplus }_{F}b)}{\partial a}+\frac{\partial (a{\otimes }_{F}b)}{\partial b}=1\).
Based on the limit theory see (Wang and He 2009),
-
1.
If \(\delta \to 0\), then \(a{\oplus }_{F}b\to a+b-ab\), Then Frank sum being transformed into a probabilistic sum..
-
2.
If \(\delta \to 0\) then \(a{\otimes }_{F}b\to ab\), then Frank product transformed into a probabilistic product.
-
3.
If \(\delta \to \infty \) then \(a{\oplus }_{F}b\to \mathrm{min}\left(a+b,1\right)\), then Frank sum transformed into a Lukasiewicz sum.
-
4.
If \(\delta \to \infty \) then \(a{\otimes }_{F}b\to \mathrm{max}(0,a+b-1)\), then Frank product transformed into a Lukasiewicz product.
3 Frank operations in Pythagorean cubic fuzzy environment
This section presents the Frank operations on PCFSs and examines several key properties of these operations.
Definition 15
Let \(\beta =\left(\langle [{\mu }^{-},{\mu }^{+}];\mu \rangle ,\langle \left[{\vartheta }^{-},{\vartheta }^{+}\right];\vartheta \rangle \right)\), \({\beta }_{1}=\left(\langle \left[{\mu }_{1}^{-},{\mu }_{1}^{+}\right];{\mu }_{1}\rangle ,\langle \left[{\vartheta }_{1}^{-},{\vartheta }_{1}^{+}\right]\rangle ;{\vartheta }_{1}\right)\) and \({\beta }_{2}=\left(\langle \left[{\mu }_{2}^{-},{\mu }_{2}^{-}\right];{\mu }_{2}\rangle ,\langle \left[{\vartheta }_{2}^{-},{\vartheta }_{2}^{-}\right];{\vartheta }_{2}\rangle \right)\) be any three PCFNs and \(\varphi \) is any positive real number, then
-
1.
\({\beta }_{1}{\oplus }_{F}{\beta }_{2}=\left(\langle \begin{array}{c}\left[\begin{array}{c}\sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{\left({\delta }^{1-{\left({\mu }_{1}^{-}\right)}^{2}}-1\right)\left({\delta }^{1-{\left({\mu }_{1}^{-}\right)}^{2}}-1\right)}{\delta -1}\right)},\\ \sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{\left({\delta }^{{1-\left({\mu }_{1}^{+}\right)}^{2}}-1\right)\left({\delta }^{{1-\left({\mu }_{2}^{+}\right)}^{2}}-1\right)}{\delta -1}\right)}\end{array}\right];\\ \sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{\left({\delta }^{1-{\mu }_{1}^{2}}-1\right)\left({\delta }^{1-{\mu }_{2}^{2}}-1\right)}{\delta -1}\right)}\\ \langle \begin{array}{c}\left[\begin{array}{c}{\mathrm{log}}_{\delta }\left(1+\frac{\left({\delta }^{{\left({\vartheta }_{1}^{-}\right)}^{2}}-1\right)\left({\delta }^{{\left({\vartheta }_{2}^{-}\right)}^{2}}-1\right)}{\delta -1}\right),\\ {\mathrm{log}}_{\delta }\left(1+\frac{\left({\delta }^{{\left({\vartheta }_{1}^{+}\right)}^{2}}-1\right)\left({\delta }^{{\left({\vartheta }_{2}^{+}\right)}^{2}}-1\right)}{\gamma -1}\right)\end{array}\right];\\ {\mathrm{log}}_{\delta }\left(1+\frac{\left({\delta }^{{\vartheta }_{1}^{2}}-1\right)\left({\delta }^{{\vartheta }_{2}^{2}}-1\right)}{\delta -1}\right)\end{array}\rangle \end{array}\rangle ,\right)\)
-
2.
\({\beta }_{1}{\otimes }_{F}{\beta }_{2}=\left(\begin{array}{c}\langle \begin{array}{c}\left[\begin{array}{c}{\mathrm{log}}_{\delta }\left(1+\frac{\left({\delta }^{{\left({\mu }_{1}^{-}\right)}^{2}}-1\right)\left({\delta }^{{\left({\mu }_{2}^{-}\right)}^{2}}-1\right)}{\delta -1}\right),\\ {\mathrm{ log}}_{\delta }\left(1+\frac{\left({\delta }^{{\left({\mu }_{1}^{+}\right)}^{2}}-1\right)\left({\delta }^{{\left({\mu }_{2}^{+}\right)}^{2}}-1\right)}{\delta -1}\right)\end{array}\right];\\ {\mathrm{log}}_{\updelta }\left(1+\frac{\left({\delta }^{{\mu }_{1}^{2}}-1\right)\left({\delta }^{{\mu }_{2}^{2}}-1\right)}{\delta -1}\right)\end{array}\rangle \\ \langle \begin{array}{c}\left[\begin{array}{c}\sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{\left({\delta }^{1-{\left({\vartheta }_{1}^{-}\right)}^{2}}-1\right)\left({\delta }^{1-{\left({\vartheta }_{2}^{-}\right)}^{2}}-1\right)}{\delta -1}\right)},\\ \sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{\left({\delta }^{1-{\left({\vartheta }_{1}^{+}\right)}^{2}}-1\right)\left({\delta }^{1-{\left({\vartheta }_{2}^{+}\right)}^{2}}-1\right)}{\delta -1}\right)}\end{array}\right];\\ \sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{\left({\delta }^{1-{\vartheta }_{1}^{2}}-1\right)\left({\delta }^{1-{\vartheta }_{2}^{2}}-1\right)}{\delta -1}\right)}\end{array}\rangle \end{array}\right)\)
-
3.
\({\beta }^{\varphi }=\left(\begin{array}{c}\langle \begin{array}{c}\left[\begin{array}{c}{\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{{\left({\mu }^{-}\right)}^{2}}-1\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right),\\ {\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{{\left({\mu }^{+}\right)}^{2}}-1\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right)\end{array}\right];\\ {\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{{\mu }^{2}}-1\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right)\end{array}\rangle ,\\ \langle \begin{array}{c}\left[\begin{array}{c}\sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{1-{\left({\vartheta }^{-}\right)}^{2}}-1\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right)},\\ \sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{1-{\left({\vartheta }^{+}\right)}^{2}}\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right)}\end{array}\right];\\ \sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{1-{\vartheta }^{2}}-1\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right)}\end{array}\rangle \end{array}\right),\)
-
4.
\(\varphi \beta =\left(\begin{array}{c}\langle \begin{array}{c}\left[\begin{array}{c}\sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{1-{\left({\mu }^{-}\right)}^{2}}-1\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right)},\\ \sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{1-{\left({\mu }^{+}\right)}^{2}}-1\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right)}\end{array}\right];\\ \sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{1-{\mu }^{2}}-1\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right)}\end{array}\rangle ,\\ \langle \begin{array}{c}\left[\begin{array}{c}{\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{{\left({\vartheta }^{-}\right)}^{2}}-1\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right),\\ {\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{{\left({\vartheta }^{+}\right)}^{2}}-1\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right)\end{array}\right];\\ {\mathrm{log}}_{\delta }\left(1+\frac{{\left({\delta }^{{\vartheta }^{2}}-1\right)}^{\varphi }}{{\left(\delta -1\right)}^{\varphi -1}}\right)\end{array}\rangle \end{array}\right),\)
Theorem 1
Let \(\beta =\left(\langle \left[{\mu }^{-}, {\mu }^{+}\right];\mu \rangle ,\langle \left[{\vartheta }^{-},{\vartheta }^{+}\right];\vartheta \rangle \right)\), \({\beta }_{1}=\left(\langle \left[{\mu }_{1}^{-},{\mu }_{1}^{+}\right]{;\mu }_{1}\rangle ,\langle \left[{\vartheta }_{1}^{-},{\vartheta }_{1}^{+}\right];{\vartheta }_{1}\rangle \right)\) and \({\beta }_{2}=\left(\langle \left[{\mu }_{2}^{-},{\mu }_{2}^{+}\right]{;\mu }_{2}\rangle ,\langle \left[{\vartheta }_{2}^{-},{\vartheta }_{2}^{+}\right];{\vartheta }_{2}\rangle \right)\) be any three CPFNs. Then the operational laws \({\beta }_{1}{\oplus }_{F}{\beta }_{2}\), \({\beta }_{1}{\otimes }_{F}{\beta }_{2}\), \(\varphi \beta \) and \({\beta }^{\varphi }\) are also PCFNs.
Proof
Proof Since \(\left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right],\left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right]\in [{\mathrm{0,1}]}^{2}\) and \({\mu }_{i}{, \vartheta }_{i}\epsilon [\mathrm{0,1}]\) for \(i=\mathrm{1,2}\), then
On the other hand, we have \(\sqrt{1-{\mathrm{log}}_{\delta }\left(1+\frac{\left({\delta }^{1-0}-1\right)\left({\delta }^{1-0}\right)}{\delta -1}\right)}\)
Similarly, we can prove that \(0\preccurlyeq {\xi }_{i}^{2}\preccurlyeq 1\) and \(0\preccurlyeq {\tau }_{i}^{2}\preccurlyeq 1.\)
Now, in order to show that \({\left({\mu }_{i}^{+}\right)}^{2}+{\left({\vartheta }_{i}^{+}\right)}^{2}\preccurlyeq 1\) and \({\mu }_{i}^{2}+{\vartheta }_{i}^{2}\preccurlyeq 1\), we will proceeds as follows:
Similarly, we can prove that \({\mu }_{i}^{2}+{\vartheta }_{i}^{2}\preccurlyeq 1\).Hence \({\beta }_{1}{\otimes }_{F}{\beta }_{2}\) is PCFN. Similarly, we can prove that \({\beta }_{1}\oplus {\beta }_{2}\), \(\varphi \beta \) and \({\beta }^{\varphi }\) are also PCFNs.
Theorem 2
For any three PCFNs \(\beta =\left(\langle \left[{\mu }^{-},{\mu }^{+}\right];\mu \rangle ,\langle \left[{\mu }^{-},{\mu }^{+}\right];\vartheta \rangle \right)\), \({\beta }_{1}=\left(\langle \left[{\mu }_{1}^{-},{\mu }_{1}^{+}\right];{\mu }_{1}\rangle ,\langle \left[{\vartheta }_{1}^{+},{\vartheta }_{1}^{+}\right];{\vartheta }_{1}\rangle \right)\) and \({\beta }_{2}=\left(\langle \left[{\mu }_{2}^{-},{\mu }_{2}^{+}\right];{\mu }_{2}\rangle ,\langle \left[{\vartheta }_{2}^{-},{\vartheta }_{2}^{+}\right];{\vartheta }_{2}\rangle \right)\) and \(\varphi \), \({\varphi }_{1}\) and \({\varphi }_{2}\) are any positive real numbers then the following properties holds.
-
1.
\({\beta }_{1}{\oplus }_{F}{\beta }_{2}={\beta }_{2}{\oplus }_{F}{\beta }_{1}\),
-
2.
\(\beta_{1} \otimes_{F} \beta_{2} = \beta_{2} \otimes_{F} \beta_{1}\),
-
3.
\(\varphi \left({\beta }_{1}{\oplus }_{F}{\beta }_{2}\right)=\varphi {\beta }_{1}{\oplus }_{F}\varphi {\beta }_{2}\),
-
4.
\({\left({\beta }_{1}{\otimes }_{F}{\beta }_{2}\right)}^{\varphi }={\beta }_{1}^{\varphi }{\otimes }_{F}{\beta }_{2}^{\varphi }\),
-
5.
\({\beta }^{{\varphi }_{1}+{\varphi }_{2}}={\beta }^{{\varphi }_{1}}{\otimes }_{F}{\beta }^{{\varphi }_{2}}\),
-
6.
\(\left({\varphi }_{1}+{\varphi }_{2}\right)\beta ={\varphi }_{1}\beta {\oplus }_{F}{\varphi }_{2}\beta \).
Proof 1
1. By Definition 15, we have
2. Similarly, By Definition 15, we have
3. According to the Definition 15, we get
As stated in Definition 15, it can be concluded that
The rest of the proof can be carried out in a similar manner.
4 PCF Frank operators
In this section, we present the creation of two new aggregation techniques, derived from Frank t-norm and Frank t-conorm, aimed at reducing any uncertainties present in the decision values during decision-making processes. Additionally, we have also explored some of their key characteristics.
Definition 16
Let \({\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right]{;\mu }_{i}\rangle ,\langle \left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right];{\vartheta }_{i}\rangle \right)\) \((i=\mathrm{1,2},\ldots ,n)\) be a collection of PCFNs and \(\eta ={{(\eta }_{1}{,\eta }_{2},\ldots ,{\eta }_{n})}^{T}\) be the weight vector such that \({\eta }_{i}\in [\mathrm{0,1}]\), and \({\sum }_{i=1}^{n}{\eta }_{i}=1\). The PCFFWA operator is a mapping \(\mathrm{PCFFWA}:{\Gamma }^{n}\to\Gamma \) and defined as follows:
Definition 17
Let \({\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right]{;\mu }_{i}\rangle ,\langle \left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right];{\vartheta }_{i}\rangle \right)\) \((i=\mathrm{1,2}\ldots ,n)\) be the collection of PCFNs and \(\eta ={({\eta }_{1},{\eta }_{2},\ldots ,{\eta }_{n})}^{T}\) be the weight vector such that \({\eta }_{i}\epsilon [\mathrm{0,1}]\) and \({\sum }_{i=1}^{n}{\eta }_{i}=1\). PCFFWG operator is a mapping \(\mathrm{PCFFWG}:{\Gamma }^{n}\to\Gamma \) and defined as follows:
Definition 18
As the value of \(\delta \) approaches \(1\), the PCFFWA operator gradually transforms into the CPFWA operator
In the same way, as the value of \(\delta \) approaches \(1\), the PCFFWG operator converges to the CPFWG operator
Definition 19
For any collection \({\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right]{;\mu }_{i}\rangle ,\langle \left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right];{\vartheta }_{i}\rangle \right)\) of CPFNs we have
Definition 20
Let be a collection of PCFNs \({\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right]{;\mu }_{i}\rangle ,\langle \left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right];{\vartheta }_{i}\rangle \right)\). Then complement of \({\beta }_{i}\) is denoted by \({\beta }_{i}^{C}\) and defined as follows:
Theorem 3
Given \({\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right]{;\mu }_{i}\rangle ,\langle \left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right];{\vartheta }_{i}\rangle \right)\) \((i=\mathrm{1,2},\ldots ,n)\) as the set of PCFNs, the aggregated values obtained through the application of the PCFFWA operator are also considered to be a PCFN.
Proof.
According to the principle of mathematical induction and the operational law outlined in Definition 15, it can be concluded that
Step 1. If \(n=2\), then, we get
As \({\sum }_{i=1}^{2}{\eta }_{i}-1=0\),
This implies that Eq. (14) is valid for \(n=2\).
Step 2. Assuming that Eq. (14) holds true for the value of \(n\) being equal to \(k\), meaning that
For \(n=k+1\), we have
This implies that Eq. (14) is valid for \(n = k +1\).
Consequently, Eq. (14) holds for all values of \(n\), which concludes the proof of Theorem 3.
Theorem 4
Let \({\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right]{;\mu }_{i}\rangle ,\langle \left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right];{\vartheta }_{i}\rangle \right)\) \((i=\mathrm{1,2},\ldots ,n)\) be a collection of PCFNs and \(\upeta ={({\upeta }_{1},{\upeta }_{2},\ldots ,{\upeta }_{\mathrm{n}})}^{\mathrm{T}}\) be a weight vector with \({\eta }_{i}\in [\mathrm{0,1}]\) and \({\sum }_{i=1}^{n}{\eta }_{i}=1\), then the aggregated values obtained by PCFFWG operator is also PCFN.
Proof
The proof is simple and can be easily understood, therefore we have chosen not to include it in this discussion.
Theorem 6
Let \({\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right]{;\mu }_{i}\rangle ,\langle \left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right];{\vartheta }_{i}\rangle \right)\) and \({\widetilde{\beta }}_{i}=\left(\langle \left[{\widetilde{\mu }}_{i}^{-},{\widetilde{\mu }}_{i}^{+}\right]{;\widetilde{\mu }}_{i}\rangle ,\langle \left[{\widetilde{\vartheta }}_{i}^{-},{\widetilde{\vartheta }}_{i}^{+}\right];{\widetilde{\vartheta }}_{i}\rangle \right)(i=1, 2, \ldots ,n)\) be two collections of PCFNs. If \({\mu }_{i}^{-}\preccurlyeq {\widetilde{\mu }}_{i}^{-}\), \({\mu }_{i}^{+}\preccurlyeq {\widetilde{\mu }}_{i}^{+}\), \({\vartheta }_{i}^{-}\succcurlyeq {\widetilde{\vartheta }}_{i}^{-}\), \({\vartheta }_{i}^{+}\succcurlyeq {\widetilde{\vartheta }}_{i}^{+}\), \({\mu }_{i}\preccurlyeq {\widetilde{\mu }}_{i}\) and \({\vartheta }_{i}\succcurlyeq {\widetilde{\vartheta }}_{i}\) then
Proof
As \({\mu }_{i}^{-}\preccurlyeq {\widetilde{\mu }}_{i}^{-}\) then
In the same way,
By Definition 9, we have
Theorem 7
The results obtained by applying the PCFFWA method, which is a representation of PCFFWG, on a group of PCFNs \({\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right]{;\mu }_{i}\rangle ,\langle \left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right];{\vartheta }_{i}\rangle \right)\), have limitations and are confined to certain boundaries i.e.,
Proof
The demonstration of this proof follows a similar process as the proof for Theorem 6, therefore, for the sake of brevity, we have chosen not to include it here.
Theorem 8
Let \({\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right]{;\mu }_{i}\rangle ,\langle \left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right];{\vartheta }_{i}\rangle \right)\) be a collection of PCFNs and \({\beta }_{i}^{C}=\left(\langle {\left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right];\mu }_{i}\rangle ,\langle \left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right];{\vartheta }_{i}\rangle \right)\), then we have \(\mathrm{PCFFWG}\left({\beta }_{1},{\beta }_{2},\ldots ,{\beta }_{n}\right)=\mathrm{PCFFWA}{({\beta }_{1}^{C},{\beta }_{2}^{C},\ldots ,{\beta }_{n}^{C})}^{C}\) and
Proof
By Definition 20, \({\beta }_{i}^{C}=\left(\langle {\left[{\vartheta }_{i}^{-},{\vartheta }_{i}^{+}\right];\mu }_{i}\rangle ,\langle \left[{\mu }_{i}^{-},{\mu }_{i}^{+}\right];{\vartheta }_{i}\rangle \right)\). Then, by Theorem 3, we have
This implies that
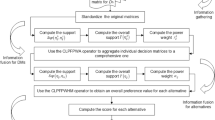
5 A revised approach to MCGDM based on proposed operators
In this article, a solution to multi-criteria group decision-making (MAGDM) problems has been presented. This approach is based on the use of Pythagorean cubic fuzzy information and two specific operators: the PCFFWA and the PCFFWG. These operators enable a more comprehensive and accurate evaluation of the available alternatives and help arrive at a well-informed group decision. Let \(A=\left\{{A}_{1},{A}_{2},\ldots ,{A}_{m}\right\}\) be a set of possible alternatives, while \(G=\left\{{G}_{1},{G}_{2},\ldots ,{G}_{n}\right\}\) be a set of features (attributes) that help differentiate each alternative in the set \(A\). It is important to note that both sets \(A\) and \(G\) are finite, meaning that there is a specific, limited number of elements in each set. The decision-makers evaluate the information related to alternative \({A}_{i}\) with respect to attribute \({G}_{j}\), (where \(i\) ranges from \(1\) to \(m\) and \(j\) ranges from \(1\) to \(n\)) and it is assumed that these evaluations are represented by PCFNs. It is assumed that the Pythagorean cubic fuzzy decision matrix referred to as "\(E\left(h\right)={\left({e}_{ij}^{\left(h\right)}\right)}_{m\times n}(h=\mathrm{1,2},\ldots ,t)\) " has been provided by an expert \({\mathcal{e}}_{\mathcal{h}}\). The weight vector assigned to the attributes is \(\eta ={({\eta }_{1},{\eta }_{2},\ldots ,{\eta }_{j})}^{T}\). This vector is used to measure the importance or significance of each attribute in a specific context or application. The values in the vector \(\eta \) determine the relative weight of each attribute, allowing for a more informed decision-making process based on the weighted analysis of all relevant attributes. In order to create a solution for this issue, an approach will be developed that incorporates the proposed aggregation operators. This approach consists of several steps that include:
Step 1. Formulate the PCF decision matrix \(E\left(h\right)={\left({e}_{ij}^{\left(h\right)}\right)}_{m\times n}\) where \({d}_{ij}=\left(\langle \left[{\mu }_{ij}^{-},{\mu }_{ij}^{+}\right]{;\mu }_{ij}\rangle ,\langle \left[{\vartheta }_{ij}^{-},{\vartheta }_{ij}^{+}\right];{\vartheta }_{ij}\rangle \right)\) characterize the PCFN with respect to the alternative \({X}_{i}\).
Step 2. Categorize the attributes into two groups:
-
1.
Cost attributes which refer to the expenses incurred and
-
2.
Benefit attributes which refer to the advantages or positive outcomes gained.
The first category, "Cost attributes," refers to attributes that represent the costs or expenses involved. The second category, "Benefit attributes," refers to attributes that represent the benefits or positive outcomes that are gained.
Normalization of the rating values is required if the attributes are of two different types, using the following formula. However, if all the attributes are of the same type, normalization is not necessary.
Step 3. Make use of the recommended aggregation operators in order to calculate the complete and final appraisals of the available alternatives. These operators will be used to bring together and investigate different pieces of information and data, in order to determine the value of each alternative and arrive at a single, overall valuation.
Step 4. To compute the score or accuracy value for each alternative, use Eqs. (9) and (10). These equations provide a numerical representation of the accuracy of each alternative and will be used to determine which alternative is the most accurate.
Step 5. To determine the best and most desirable alternative(s), it is necessary to rank all of the alternatives based on their score or accuracy. This process involves evaluating each alternative and comparing it to the others to determine its position in terms of effectiveness and performance. Once all the alternatives have been ranked, the top-performing alternative(s) can then be selected as the best and most desirable alternative(s).
5.1 Numerical example
Let us consider an investment company that has a significant amount of funds at their disposal and is actively searching for the most advantageous investment alternative to put their money in (taken from the study of Khan et al. (2019a, b)). They want to ensure that they make the best use of their funds by investing in a choice that promises maximum returns while minimizing the risk involved. The investment firm has been given a set of five distinct investment alternatives, labelled as \(\left\{{A}_{1},{A}_{2},{A}_{3},{A}_{4},{A}_{5}\right\}\), from which they must carefully select the most suitable one to allocate their funds towards. \({A}_{1}\) is a car company, \({A}_{2}\) is a food company, \({A}_{3}\) is a computer company, \({A}_{4}\) is a arms company, and \({A}_{5}\) TV company.
Four criteria are considered when making a decision. These include: \({G}_{1}\) risk analysis—an examination of potential risks involved in a particular situation. \({G}_{2}\) growth analysis—an evaluation of the potential for growth and expansion. \({G}_{3}\) social-political impact analysis—a study of the effects on society and politics. \({G}_{4}\) environmental impact analysis—an examination of the impact on the natural environment. Three decision-makers \(\left\{{E}^{1},{E}^{2},{E}^{3}\right\}\) form a committee to evaluate the five alternatives \({A}_{i}\) (\(i=\mathrm{1,2},\mathrm{3,4},5\)) based on the four criteria \({G}_{j}\) (\(j=\mathrm{1,2},\mathrm{3,4}\)). The decision makers have evaluated the five possible alternatives based on four attributes and the resulting information is recorded in Tables 1, 2 and 3.
The ranking of these decision matrices was obtained by applying the score function specified in Eq. (9). The normalized decision matrices that have been arranged in order are summarized in Tables 4, 5 and 6.
Transform the preference values into their overall score values using the score function outlined in Eq. (9). The score values for each alternative are summarized in Table 7.
The aggregation of the preference value of each alternative \({A}_{i}\) (where \(i\) ranges from \(1\) to \(5\)) can be achieved by utilizing the PCFFWA operator defined in Eq. (13).
The PCFFWG operator, which is defined in Eq. (13), can be applied to gather the performance metrics of various alternatives, with a \(\delta \) value of \(2\). This results in a combined evaluation that provides an overall assessment of the alternatives' performances.
Calculating the score values of each alternative using Eq. (9), as displayed in Table 8.
The order in which the alternatives are ranked, as determined by their respective score values, has been determined to be \({A}_{5}\succ {A}_{3}\succ {A}_{1}\succ {A}_{4}\succ {A}_{2}\).
5.2 Evaluating the effect of \(\delta \) on alternative ordering in rankings
The aggregation operators that have been suggested possess symmetry in terms of the parameter \(\delta \). However, in order to understand the influence of the parameter on the ultimate ranking of the alternatives, a study was conducted by altering parameter \(\delta \). The results of the investigation, including the score values and the ranking order, have been presented in Table 9. This table demonstrates that while the score values of the aggregated numbers change with different values assigned to the parameter \(\delta \), the relative rankings of the alternatives remain unchanged. The significance of this aspect of the proposed operators is particularly important in actual decision-making scenarios. For example, as the number of parameter \(\delta \) increases, the scores of the alternatives also rise, providing a positive outlook for decision makers.
5.3 A comparative examination of various approaches
5.3.1 Comparison with existing PCF operators
To validate the superiority of our proposed aggregation operators over existing operators, as described by Khan et al. (2019a, b), a comprehensive examination was carried out to determine the best alternative. The scores and rankings of the various options are summarized in Table 10. Based on the results, it is evident that \({A}_{5}\) is the best choice. Table 10 provides evidence that the ranking of alternatives determined through approach (Khan et al. 2019a, b) is identical to the ranking suggested by our approach. One of the key advantages of the PCFFWA and PCFFWG methods is their ability to minimize computational complexity costs while preserving the consistency of the aggregate results in uncertain conditions. Furthermore, our proposed approach includes a parameter that allows for modifications to the aggregate value based on actual decision-making needs and reflects the personal preferences of the decision-maker. As a result, the suggested operators are more versatile and adaptable. Additionally, the study highlights that the computational process of the proposed approach differs from the existing approaches under different conditions. However, the results obtained from the proposed method in this paper are more in line with reality in the decision-making process because they take into account the consistent priority degree between the pairs of arguments.
5.4 Comparison with existing IVPFS operators
In order to assess the performance of the proposed method in comparison to existing theories within an interval-valued Pythagorean fuzzy environment, we established the fuzzy judgments of the PCFNs to be zero. As a result, the obtained information was transformed into IVPFS. Subsequently, the transformed data undergoes the application of multiple available optimization algorithms such as averaging operator (Peng and Yang 2016), geometric operator (Rahman and Abdullah 2019), Frank power AOs (Yang et al. 2018), Einstein AOs (Rahman et al. 2018), and Muirhead mean operators (Tang et al.2019). The aim of this step is to identify the most appropriate alternative(s) among the available options. The outcome of this process is presented in Table 11, which also includes the order of ranking for each alternative. Based on these results, it has been observed that alternative \({A}_{5}\) remains the best option. However, the worst alternative has changed for all cases. The reason for this is that in previous studies, only the initial preferences of the alternatives have been taken into account. This means that these existing theories are unable to handle situations where the evaluator or decision maker must consider the degree of falsehood associated with their earlier assigned truth degree across a range. Thus, the methods used in IVPFSs may overlook valuable information from IVPFNs, which could impact the decision outcome. Finally, it can be concluded that the proposed operators take into account the decision maker's parameter "\(\delta \)", which offers them more options to choose from and select their preferred alternative based on the varying score values of the alternatives for different values of "\(\delta \)". This provides decision makers with the flexibility to make choices that best align with their preferences.
6 Conclusion
In the current study, we have made an advancement by extending the Frank t-conorm and t-norm to encompass PCF environments. Additionally, we have established multiple new operational laws specifically for PCFNs and conducted a thorough examination of their properties and relationships. As a result of these new operational laws, new aggregation operators such as the CPFFWA and CPFFWG have been created to handle cases where the inputs are PCFNs. An in-depth investigation has been conducted on the desirable properties and specific instances of these operators, and the connections between them have been explored as well. In conclusion, the newly created operators have been utilized to address group decision-making problems with interval-valued intuitionistic fuzzy information. A numerical example has been provided to demonstrate the process. However, the current paper does not cover the determination of the parameter \(\delta \) in the proposed operators for practical situations, which is a crucial and intriguing aspect that deserves further investigation in future studies. We plan to implement the suggested operators and method in various practical applications such as game theory, image processing, cluster analysis, pattern recognition, and uncertain programming in the future.
Data availability statement
This article does not require data sharing as no datasets were used or generated during the current study.
References
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Frank MJ (1979) On the simultaneous associativity ofF (x, y) andx+ y− F (x, y). Aequ Math 19(1):194–226
Garg H, Kaur G (2019) Cubic intuitionistic fuzzy sets and its fundamental properties. J Mult Valued Logic Soft Comput 33(6)
Jun YB, Kim CS, Yang KO (2012) Cubic sets. Ann Fuzzy Math Inform 4(1):83–98
Kaur G, Garg H (2018) Multi-attribute decision-making based on Bonferroni mean operators under cubic intuitionistic fuzzy set environment. Entropy 20(1):65
Khan M, Abdullah S, Zeb A, Majid A (2016) CUCBIC aggregation operators. Int J Comput Sci Inf Secur 14(8):670
Khan F, Abdullah S, Mahmood T, Shakeel M, Rahim M (2019a) Pythagorean cubic fuzzy aggregation information based on confidence levels and its application to multi-criteria decision making process. J Intell Fuzzy Syst 36(6):5669–5683
Khan F, Khan MSA, Shahzad M, Abdullah S (2019b) Pythagorean cubic fuzzy aggregation operators and their application to multi-criteria decision making problems. J Intell Fuzzy Syst 36(1):595–607
Khan MSA, Khan F, Lemley J, Abdullah S, Hussain F (2020) Extended topsis method based on Pythagorean cubic fuzzy multi-criteria decision making with incomplete weight information. J Intell Fuzzy Syst 38(2):2285–2296
Mahmood T, Mehmood F, Khan Q (2016) Cubic hesitant fuzzy sets and their applications to multi criteria decision making. Int J Algebra Stat 5(1):19–51
Mahnaz S, Ali J, Malik MA, Bashir Z (2021) T-spherical fuzzy Frank aggregation operators and their application to decision making with unknown weight information. IEEE Access 10:7408–7438
Peng X, Yang Y (2016) Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators. Int J Intell Syst 31(5):444–487
Rahman K, Abdullah S (2019) Generalized interval-valued Pythagorean fuzzy aggregation operators and their application to group decision-making. Granul Comput 4:15–25
Rahman K, Abdullah S, Khan MSA (2018) Some interval-valued Pythagorean fuzzy Einstein weighted averaging aggregation operators and their application to group decision making. J Intell Syst 29(1):393–408
Sarkoci P (2005) Domination in the families of Frank and Hamacher t-norms. Kybernetika 41(3):349–360
Seikh MR, Mandal U (2021) Some picture fuzzy aggregation operators based on Frank t-norm and t-conorm: application to MADM process. Informatica 45(3)
Seikh MR, Mandal U (2022) Q-rung orthopair fuzzy Frank aggregation operators and its application in multiple attribute decision-making with unknown attribute weights. Granul Comput 1–22
Tang X, Wei G, Gao H (2019) Models for multiple attribute decision making with interval-valued Pythagorean fuzzy Muirhead mean operators and their application to green suppliers selection. Informatica 30(1):153–186
Wang W, He H (2009) Research on flexible probability logic operator based on Frank T/S norms. Acta Electron Sin 37(5):1141–1145
Wang F, Zhao X (2021) Prospect-theory and geometric distance measure-based Pythagorean cubic fuzzy multicriteria decision-making. Int J Intell Syst 36(8):4117–4142
Yager RR (2004) On some new classes of implication operators and their role in approximate reasoning. Inf Sci 167(1–4):193–216
Yager RR, Abbasov AM (2013) Pythagorean membership grades, complex numbers, and decision making. Int J Intell Syst 28(5):436–452
Yager RR (2013) Pythagorean fuzzy subsets. In: Paper presented at the 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS)
Yang Y, Chen ZS, Chen YH, Chin KS (2018) Interval-valued Pythagorean fuzzy frank power aggregation operators based on an isomorphic frank dual triple. Int J Comput Intell Syst 11(1):1091–1110
Zadeh LA (1965) Information and control. Fuzzy Sets 8(3):338–353
Zhang X (2016) Multicriteria Pythagorean fuzzy decision analysis: a hierarchical QUALIFLEX approach with the closeness index-based ranking methods. Inf Sci 330:104–124
Zhang X, Xu Z (2014) Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst 29(12):1061–1078
Funding
The authors of this manuscript wish to disclose that the research and preparation of this manuscript was self-funded and no external funding sources were utilized.
Author information
Authors and Affiliations
Contributions
M. R wrote and prepared the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors state that they have no conflicts of interest.
Ethical approval
The authors did not conduct any studies involving human or animal participants for this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Rahim, M. Multi-criteria group decision-making based on frank aggregation operators under Pythagorean cubic fuzzy sets. Granul. Comput. 8, 1429–1449 (2023). https://doi.org/10.1007/s41066-023-00376-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41066-023-00376-z