Analysis of domination in the environment of picture fuzzy information

Abstract

Picture fuzzy graph (PFG) is a useful tool in fuzzy graph theory that can be used to model a variety of real-world problems involving uncertainty caused by unknown, changing, and indeterminate data. PFG might be more fruitful at solving confusing problems than fuzzy graph (FG) and intuitionistic fuzzy graph (IFG). In this study, some interesting properties and results for the PFGs have been presented by using the concepts of strong arcs. The notions of covering in a PFG, strong node covering, strong arc covering, strong independent set, and matching number have been introduced for PFG. Moreover, we also devised the conception of paired domination, strong paired domination, and strong paired dominating set for a PFG. Furthermore, many interesting properties of these conceptions are established. Additionally, the strong paired domination numbers of complete PFG and complete bipartite PFG have been worked out. In addition, many various intriguing aspects of strong paired domination have been examined.

1 Introduction

In many fields, the graphical framework is important because graphs conveniently describe data. Due to their usefulness, graphs have got significant importance in many fields, besides mathematics. Several serious issues are easily solved by describing them graphically. Graph theory is one of the most significant branches of mathematics and combinatorics. Chartrand and Zang (2006). Introduction to graph theory, Tata McGraw-Hill Edition. It is useful in a variety of domains, including networking, set theory, economics, data mining, image segmentation, grouping, image processing, and so on. Picture fuzzy set (PFS) is an extension fuzzy set (FS), an intuitionistic fuzzy set (IFS), When comparing the fuzzy models, the picture fuzzy models provide more accuracy, consistency, and reliability.

Zadeh (1965) presented the idea of the fuzzy set (FS) that is useful in a wide range of research fields. The fuzzy set’s structure consists of a membership function that describes the truth value of an entity in the fuzzy set. This truth value is also called the value of membership. Atanassov (1986) initialized the concept of an intuitionistic fuzzy set (IFS) as a generalization of the FS. An IFS involves the value of membership as well as the value of non-membership. Coung and Kreinovich (2013) initialized the concepts of picture fuzzy set (PFS) that adds in the neutral value to the structure of IFS. Thus, a PFS consists of three mappings; value of membership, neutral value, value of non-membership, that take on values from the interval $[\text{0,1}]$ given that their sum also belongs to the unit interval.

Rosenfield (1975) introduced the idea of the fuzzy graph (FG), which was first initiated by Kauffman (1973). Rosenfeld also found the fuzzy relationships between the FSs. As a special case of Atanassov’s IFG, Karunambigai and Parvathi (2006) developed an intuitionistic fuzzy graph.

The definition of intuitionistic fuzzy relation (IFR) was introduced by Atanassov (2012). The notion of an intuitionistic fuzzy competition graph was discussed by Sahoo and Pal (2015). Cen Zuo et al. (2019) introduced the idea of picture fuzzy graphs (PFG). PFG is an enhanced version of IFG that is used to model uncertain real-world problems that IFG might not be able to adequately model. PFG has been used in different areas, including computer science, chemistry, engineering, economics, statistics, and many more.

After Rosenfield (1975) the FG theory has been worked out by many researches, such as fuzzy tolerance graphs by Samanta and Pal (2011), fuzzy threshold graphs by Samanta and Pal (2011), bipolar fuzzy graphs by Rashmanlou et al. (2015), Dubois and Prade (2005) described interval-valued Fuzzy Sets. (a) Mendel et al. (2006) made the interval type-2 fuzzy (IT2F) logic system simple. Based on T2FSs. (b) Chen et al. (2012) describes Fuzzy rules interpolation for sparse fuzzy rule-based systems. (c) Chen and Hong (2014) described the TOPSIS method and fuzzy multiple attribute decision making established on IT2FSs’ ranking. (d) Chen and Lee (2011) proposed the fuzzy interpolative reasoning for sparse fuzzy rule-based systems. Akram et al. (2011) proposed interval-valued fuzzy graphs. Pramanik et al. (2016a, b) interval-valued fuzzy planar graphs, highly irregular interval-valued fuzzy graphs by Rashmanlou and Pal (2013a, b), isometry and interval-valued fuzzy graphs by Rashmanlou and Pal (2014). Balanced interval-valued fuzzy graph by Rashmanlou and Pal (2013a, b). Nasir et al. (2021a, b) applied the interval-valued fuzzy sets and interval-valued intuitionistic fuzzy sets for medical diagnosis and cyber security in industrial control systems, respectively. Jan et al. (2021) introduced the complex intuitionistic fuzzy sets and applied them to investigate the cyber security and cyber-threats in petroleum sectors. Knyazeva et al. (2018) worked out the topological ordering on IT2FG. Samanta and Pal (2013), worked out Fuzzy k-competition and p-competition fuzzy graph. New concept of fuzzy planner graph by Samanta et al. (2014) and Samanta and Pal (2015) Fuzzy planar graph, bipolar fuzzy hypergraph and Irregular bipolar fuzzy graphs by, Samanta and Pal (2012a, b), m-set fuzzy competition graph by Samanta et al. (2015a, b), completeness and regularity graph of generalization fuzzy graph by Samanta et al. (2016), fuzzy phi- tolerance completion fuzzy graph by Pramanik et al. (2016a, b) and so on. Presents the new idea of fuzzy coloring is given by Samanta et al. (2015a, b). Nayeem and Pal (2005) proposed the shortest path problem on a network with imprecise arc weights. Strong intuitionistic fuzzy graphs were defined by Akram and Davvaz (2012). Akram and Dudek (2013) also talked about intuitionistic fuzzy hypergraphs and their applications. Intuitionistic fuzzy graph structures were defined by Akmal and Akram (2017). The idea of covering, matching, and paired domination plays a significant role in both applied and theoretical picture fuzzy graphs. Sahoo et al. (2017) introduced the concept of covering and paired domination in IFG. Khan et al. (2021) carried out the graphical analysis of covering and paired domination in the environment of neutrosophic information.

The main contributions of this paper are the introduction of concepts of covering and paired domination in PFGs. This study describes the strong arcs and then used this concept to introduce the innovative conceptions of covering; strong arc covering and strong node covering. In addition, the strong independent set, strong matching, matching number, and independent numbers have been formulated. These concepts have been supported by suitable examples and graphical illustrations. Many intriguing results have also been presented. Moreover, we also developed the idea of paired domination using strong arcs. In addition, the strong paired domination, strong paired dominating set, and strong paired domination number are defined. The idea of defining a strong modeling technique motivated me to write this research article. We chose the PFG for our study because it is the most generalized structure. The picture fuzzy information is based on three mappings, membership, neutral, and non-membership. Thus, we prioritized to use a structure that has a broader domain and covers all of the other structures in fuzzy set and fuzzy graph theory. On the other hand, the FGs only discuss the membership values, IFG talk about the membership and non-membership values. These structures have certain limitations. Therefore, PFGs are the best among the other contenders. Henceforth, we defined all the innovative concepts for the PFGs.

This article is arranged as; Sect. 2 covers the essential definitions and illustrations of FG, IFG, PFS, and PFG. In Sect. 3, strong node cover (SNC), strong arc (SA), strong independent set (SIS), strong matching (SM) utilizing SAs, and numerous interesting properties are defined. In Sect. 4, we introduced paired domination (PD) and strong paired domination (SPD) in PFGs. The investigation is finally concluded in Sect. 5.

2 Preliminaries

In this section, we will review some essential definitions of graphs are examined with illustrations, including fuzzy graph (FG), intuitionistic fuzzy graph (IFG), picture fuzzy set (PFS), and picture fuzzy graph (PFG).

Definition 1

(Chartrand and Zang 2006). The collection of nodes and arcs is called a graph and it’s denoted by

$$\bar{G}=\left( {U,\hat{E}} \right),$$

where $U$ represents the collection of nodes and $\hat{E}$ shows the set of arcs.

Example 1

Let a graph $\bar{G} =\left( U, \hat{E} \right)$ where $U=\left({ u}_{1},{ u}_{2}{, u}_{3 },{u}_{4}\right)$ are the collections of nodes and $\hat{E} =\left\{{c}_{1}, {c}_{2}{ , c}_{3},{c}_{4}\right\}$ are the set of arc, shown in Fig. 1.

Fig. 1

Crisp graph

Definition 2

(Rosenfield 1975) A FG is of the form $\bar{G}=\left(U, \hat{E} \right)$ where

• i. ${U\to \{{u}_{1},{u}_{2},{u}_{3}\dots ., u}_{ n}\}$ such that ${\alpha }_{1}: U\to \left[\text{0,1}\right]$ where ${\alpha }_{1}$ represents the value of membership,

• ii. $\hat{E} \subseteq U\times U$ where ${\alpha }_{2}: U\times U\to \left[\text{0,1}\right]$ are such that

$${\alpha }_{2}\left({u}_{i}, {u}_{j}\right)\le \,\,\text{min }\,\, \left[{\alpha }_{1} \left(u\right), {\alpha }_{1}\left({u}_{j}\right)\right].$$

(1)

And satisfy the condition,

$$0 \le {\alpha }_{2} \left({u}_{i}, u\right)\le 1.$$

(2)

Example 2

Let $\bar{G}=(U, \hat{E} )$ be a FG, where $U=\left\{{u}_{1},{u}_{2},{u}_{3}\right\}$ are nodes and $\hat{E} = \left\{ {c}_{1}, {c}_{2}{, c}_{3}\right\}$ is the set of arcs then fuzzy graph shown in Fig. 2.

Fig. 2

Fuzzy graph

Definition 3

(Parvathi and Karunambigai 2006) An IFG is of the form $\bar{G}=\left(U, \hat{E} \right)$ where

• (i) $U{\to \{{u}_{1},{u}_{2},{u}_{3}\dots ., u}_{ n}\}$ such that ${\alpha }_{1}: U \to \left[\text{0,1}\right]$ and ${\beta }_{1}: U\to \left[\text{0,1}\right]$ show the value of membership and nonmembership of the factor ${u}_{i}\epsilon U$,$i=(\text{1,2},\dots ..n)$ correspondingly and

$$0 \le {\alpha }_{1} \left(u{}_{i}\right) + {\beta }_{1} \left({u}_{i}\right) \le 1,$$

(3)

For every ${u}_{i} \epsilon U i =(1, 2,\dots ..n)$

• (ii) ${\hat{E} } \subseteq U \times U$ where ${\alpha }_{2}: U \times u \to \left[\text{0,1}\right]$ and ${\beta }_{2}:U\times U\to \left[\text{0,1}\right]$ are in the such that

$${\alpha }_{2}\left({u}_{{\varvec{i}}}, {u}_{j}\right)\le \,\,\text{min }\,\, \left[{\alpha }_{1}\left({u}_{i}\right), {\alpha }_{1}\left({u}_{j} \right)\right],$$

(4)

$${\beta }_{2}\left({u}_{i}, {u}_{j}\right)\le \,\,\text{max}\,\, \left[{\beta }_{1}\left({u}_{i}\right), {\beta }_{1}\left({u}_{j}\right)\right],$$

(5)

and

$$0 \le {\alpha }_{2} \left({u}_{i}, {u}_{j}\right)+ {\beta }_{2} \left({u}_{i}, {u}_{j}\right)\le 1.$$

(6)

Note: $\bar{G}$ is not an IFG if one or more of the inequalities (3), (4), (5), or (6) are not fulfilled.

Example 3

Let $\bar{G}=\left(U, \hat{E} \right)$ be an IFG, where $U={\{u}_{1}, { u}_{2}, { u}_{3}\}$ are nodes and $\hat{E} =\left\{ {c}_{1},{c}_{2}, { c}_{3} \right\}$ is the set of arcs then IFG shown in Fig. 3.

Fig. 3

IFG

Definition 4

(Cuong and Kreinovich 2013) Let $C$ be a PFS. $C$ in $L$ is defined by ${C}= \left\{l, { \alpha }_{1} (l),{ \gamma }_{1} (l),{ \beta }_{1} (l) | l \epsilon {L}\right\}$ where ${\alpha }_{1}\left(l\right)\in \left[\text{0,1}\right]$ is called the membership value, ${\gamma }_{1}\left(l\right)\in \left[\text{0,1}\right]$ is called neutral value and ${ \beta }_{1}\left(l\right)\in \left[\text{0,1}\right]$ is called the nonmembership value of $l$ in $C$ and satisfies the following condition.

$$\forall l\, \epsilon {L}, 0\,\le {\alpha }_{1} \left(l\right)+ { \gamma }_{1} \left(l\right)+ {\beta }_{1} \left(l\right)\le 1.$$

(7)

Now, $1-( {\alpha }_{1} (l) + {\gamma }_{1} (l) + {\beta }_{1} (l)$ is said to be the refusal value.

Definition 5

(Zuo et al. 2019) A PFG is of the form $\bar{G}=\left(U, \hat{E} \right)$, here

• (i) $U\to \left\{{u}_{1}, {u}_{2} , {u}_{3},\dots ., {u}_{n}\right\}$ such that ${\alpha }_{1}: U \to \left[\text{0,1}\right]$ and ${\gamma }_{1}: U\to \left[\text{0,1}\right]$ and ${\beta }_{1}: U \to \left[\text{0,1}\right]$ show the membership value, neutral value, and nonmembership value of the factor ${u}_{i} \epsilon U$, correspondingly

$$0 \le {\alpha }_{1}({u}_{i}) +{ \gamma }_{1}\left({u}_{i}\right) + {\beta }_{1}\left({u}_{i}\right) \le 1.$$

• (ii) ${\hat{E} } \subseteq U\times U$ where ${\alpha }_{2}: U\times U \to \left[\text{0,1}\right]$_, ${\gamma }_{2}: U\times U \to \left[\text{0,1}\right]$ and ${\beta }_{2}: U\times U\to \left[\text{0,1}\right]$ such that

  $${\alpha }_{2}\left({u}_{i},{u}_{j}\right)\le \,\,\text{min }\,\,\left[ {\alpha }_{1}\left({u}_{i}\right), { \alpha }_{1}\left({u}_{j}\right)\right],$$

  (8)
  $${\gamma }_{2}\left(u,{u}_{j}\right)\le \,\,\text{min }\,\, \left[{ \gamma }_{1}\left({u}_{i}\right),\left({u}_{j}\right)\right],$$

  (9)
  $${\beta }_{2}\left({u}_{i}, {u}_{j}\right)\le \,\,\text{max}\,\, \left[{\beta }_{1}\left({u}_{i}\right),{ \beta }_{1}\left({u}_{j}\right)\right],$$

  (10)

  and satisfy the condition,

$$0\le {\alpha }_{2} \left({u}_{i}, {u}_{j}\right)+ {\gamma }_{2} \left({u}_{i}, {u}_{j}\right)+ {\beta }_{2} \left({u}_{i}, {u}_{j}\right)\le 1,$$

(11)

For any $\left({u}_{i}, u{}_{j}\right) \epsilon \hat{E}$.

Example 4

Let $\bar{G}=\left(U, \hat{E} \right)$ be a PFG where $U=\left\{{u}_{1}, {u}_{2}, {u}_{3}, {u}_{4}\right\}$ are the set of nodes and $\hat{E} =\left\{{c}_{1}, {c}_{2}{, c}_{3},{c}_{4}\right\}$ is the set of arcs then PFG shown in Fig. 4.

Fig. 4

PFG

3 Covering and matching in picture fuzzy graph

The definition of covering and matching are discussed in this section. Strong arcs are used in picture fuzzy graphs (PFGs). Many interesting results were discussed and developed. Initially, we define strong node cover (SNC) in PFG.

Definition 6

Let $\bar{G} = \left(U, \hat{E} \right)$ be a PFG. A node and a strong arc occurrence to it are said to strong cover each other. The set $\acute{Z}$ of the node that envelops all strong arcs (SAs) of PFG $\bar{G}$ is called SNC in $\bar{G}.$The membership value of SNC $\acute{Z}$ is defined a $\acute{M}_1\left(\acute{Z}\right)={\sum }_{\grave{u} \epsilon \acute{Z}}{ \alpha }_{1}\left(\grave{u} ,u\right)$, the neutral value of SNC $\acute{Z}$ is defined as $\acute{M}_2\left(\acute{Z}\right)={\sum }_{\grave{u} { \epsilon \acute{Z}}}{ \gamma }_{1}\left(\grave{u} ,u\right)$ and nonmembership value of SNC $\acute{Z}$ is defined as $\acute{M}_3 \left(\acute{Z}\right)={\sum }_{\grave{u} { \epsilon \acute{Z} }}{\beta }_{1} \left(\grave{u} ,u\right)$, where ${\alpha }_{1}\left(\grave{u} ,u\right) is$ the least value of membership, ${\gamma }_{1}\left(\grave{u} ,u\right)$ is the least value of neutral and ${\beta }_{1}\left(\grave{u} ,u\right)$ is the greatest value of nonmembership. The strong node covering the number of PFG $\bar{G}$ is defined by ${X}_{0 }\left(\bar{G}\right)= {X}_{0 }= \left({X}_{10 }, {X}_{20 }, {X}_{30 }\right),$ where (${X}_{10 }, {X}_{20}$) are the least membership and least neutral value of SNC of $\bar{G}$ and ${X}_{30}$ is the greatest non-membership value of SNC of$\bar{G}$. A SNC with the least membership value, least neutral value, and greatest nonmembership value in a PFG $\bar{G}$ are said to be the least strong node cove.

Theorem 1

Suppose $\bar{G}=(U, \hat{E} )$ be a complete PFG where ${X}_{10}, {X}_{20}, {X}_{30}$ are defined as ${X}_{10 }=\left(\tilde{n} -1\right) {\alpha }_{2}\left(\grave{u} ,u\right)$, ${X}_{20}=\left(\tilde{n} -1\right) {\gamma }_{2} \left(\grave{u} ,u\right)$ and, ${X}_{30}=\left(\tilde{n} -1\right) {\beta }_{2} \left(\grave{u} ,u\right),$ where $\tilde{n}$ shows the number of nodes in $\bar{G}$. Where ${\alpha }_{2}(\grave{u} ,u)$, ${\upgamma }_{2}(\grave{u} ,u)$ is membership value, neutral value, and ${\beta }_{2}\left(\grave{u} ,u\right)$ is nonmembership value of the weakest arc in $\bar{G}$.

Proof

Since $\bar{G}= (U, \hat{E} )$ is a complete PFG then every node is associated in $\bar{G}$ and all of its arcs are strong. Hence, the strong cover node of $\bar{G}$ is shaped by any set of $(n-1)$ nodes. Let $\grave{u}$ be a node in $\bar{G}$ having the least membership value, neutral value, and greatest nonmembership value. Let ${ u}_{1}, {u}_{2}\dots {u}_{n-1}$ be the node connected to$\grave{u}$. The arc is $\left(\grave{u} ,{u}_{1}\right), \left(\grave{u} ,{u}_{2} \right),\dots (\grave{u} , {\upsilon }_{n-1})$ of all weakest arc of $\bar{G}$ with membership strength is ${\alpha }_{2}\left(\grave{u} ,u\right),$ neutral strength is ${\gamma }_{2}\left(\grave{u} ,u\right)$ and nonmembership strength of each arc is equal to ${\beta }_{2} \left(\grave{u} ,u\right)$ where $\acute{Z} \epsilon \left\{{u}_{1},{u}_{2}\dots {u}_{n}\right\}.$ Hence the set of $U$ is $U= \left\{{u}_{1},{u}_{2}\dots ..{u}_{n-1}\right\}$ nodes from SNC of $\bar{G}$ with $\acute{M}_{1}\left(\acute{Z}\right)=\sum_{{u}_{i} {\epsilon }_{ \acute{Z}}}{\alpha }_{2}\left(\grave{u} ,{u}_{i}\right),$ $i = 1, 2, \dots$ is the least value of membership of SE incident on ${u}_{1}$ then ${X}_{10 }= {\alpha }_{2}\left(\grave{u} ,u\right)+ {\alpha }_{2}\left(\grave{u} ,u\right)\dots ..+ {\alpha }_{2}\left(\grave{u} ,u\right)\left[\left(n-1\right)\text{time}\right]$ where ${\alpha }_{2}\left(\grave{u} ,u\right)$ is the weakest arc in $\bar{G}{^{\prime}}$ s membership value. Hence ${X}_{10} = \left(n -1\right) {\alpha }_{2}\left( \grave{u} ,u\right).$

Similar to that.

$\acute{M}_{2}\left(\acute{Z}\right)=\sum_{{u}_{i} {\epsilon }_{ \acute{M}}}{ \gamma }_{2}\left(\grave{u} ,{u}_{i}\right)$, $i = \text{1,2},3,\dots n,$ is the least neutral value of strong arc occurrence on ${u}_{1}$ then ${X}_{20}= {\gamma }_{2} (\grave{u} ,u) + {\gamma }_{2} (\grave{u} ,u )\dots .+ {\gamma }_{2} (\grave{u} ,u) [(n-1)$ $\text{time}].$

Where ${\gamma }_{2}\left(\grave{u} ,u\right)$ is the neutral value of the weakest arc in $\bar{G}$. Hence ${X}_{20}=\left(n-1\right){ \gamma }_{2}\left(\grave{u} ,u\right).$

Similar to that,

$\acute{M}_{3} \left(\acute{Z}\right)={\sum }_{{u}_{i} {\epsilon }_{ \acute{Z}} }{\beta }_{2} \left({\grave{u} },u\right) ,$ $i =\text{ 1,2},3,\dots ..n,$ is the greatest value of nonmembership of strong arc incident on ${u}_{1}$ then ${X}_{30}= {\beta }_{2} ({\grave{u} },u), {\beta }_{2} ({\grave{u} },u)\dots . {\beta }_{2}({\grave{u} },u) [\left(n-1\right)\text{time}]$ where ${\beta }_{2}\left({\grave{u} },u\right)$ is the nonmembership value of the weakest arc in $\bar{G}.$Hence ${X}_{30}=\left(n-1\right){ \beta }_{1}\left({\grave{u} },u\right).$

Theorem 2

$\acute{\kappa}$ is complete bipartite PFG with partite set ${\check{U}}_{1}$ and ${\check{U}}_{2}$ then

$${X}_{10} \left(\acute{\kappa}\right)=\,\,\text{min }\,\, \left\{\acute{M}_{1}\left({\check{U}}_{1}\right), \acute{M}_{1}\left({\check{U}}_{2}\right)\right\},$$

$${X}_{20}\left(\acute{\kappa}\right)=\,\,\text{min }\,\, \left\{ \acute{M}_{2} \left({\check{U}}_{1}\right), \acute{M}_{1}\left({\check{U}}_{2}\right)\right\},$$

$${X}_{30} \left(\acute{\kappa}\right)=\,\,\text{max}\,\, \left\{ \acute{M}_{3} \left({\check{U}}_{1}\right), \acute{M}_{3}\left({\check{U}}_{2}\right)\right\}.$$

Proof

Since $\acute{\kappa}$ is a complete bipartite PFG. Consequently, all of its arcs are strong. Furthermore, each of the nodes in ${\check{U}}_{1}$ is associated with all of the nodes in ${\check{U}}_{2}$, and vice versa. The collection of all arcs of $\acute{\kappa}$ is the union of a set of all arcs occurrence to every node in ${\check{U}}_{1}$ and the collection of all arcs occurrence to every node in ${\check{U}}_{2}.$Also, ${\check{U}}_{1}, {\check{U}}_{2}$_, and ${\check{U}}_{1}\cup {\check{U}}_{2}$ are PFG in $\acute{\kappa}.$ It’s clear that,

$$\acute{M}_{1} \left( {\check{U}}_{1}\cup {\check{U}}_{2} \right)> \acute{M}_{1}\left( {\check{U}}_{1}\right) \text{and} \acute{M}_{1}\left( {\check{U}}_{1}\cup {\check{U}}_{2}\right)> {M}_{1}\left({\check{U}}_{2}\right).$$

Therefore,

$${X}_{10} \left(\acute{\kappa}\right)=\,\,\text{min }\,\, \left\{ \acute{M}_{1}\left({\check{U}}_{1}\right), \acute{M}_{1}\left({\check{U}}_{2}\right)\right\}.$$

And,

$$\acute{M}_{2} \left({\check{U}}_{1}\cup {\check{U}}_{2}\right)> \acute{M}_{2} \left({\check{U}}_{1}\right) \text{and} \acute{M}_{2} \left({\check{U}}_{1}\cup {\check{U}}_{2}\right)> \acute{M}_{2} \left({\check{U}}_{2}\right).$$

Therefore,

$${X}_{20} \left(\acute{\kappa}\right)=\,\,\text{min }\,\, \left\{ \acute{M}_{2}\left({\check{U}}_{1}\right), \acute{M}_{2} \left({\check{U}}_{2}\right)\right\}.$$

Similarly

$$\acute{M}_{3} \left({\check{U}}_{1}\cup {\check{U}}_{2}\right)> \acute{M}_{3} \left({\check{U}}_{1}\right) \text{and} \acute{M}_{3} {(\check{U}}_{1}\cup {\check{U}}_{2}) > \acute{M}_{3} ({\check{U}}_{2}).$$

And

$${X}_{30} \left(\acute{\kappa}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{3}\left({\check{U}}_{1}\right), \acute{M}_{3}\left({\check{U}}_{2}\right)\right\}.$$

Theorem 3

If $\bar{G}=\left(U, \hat{E} \right)$ is a picture fuzzy cycle (PFC) and $g$ is a crisp cycle (CC) then

$${X}_{10} \left(\bar{G}\right) =\,\,\text{min }\,\,\left\{\acute{M}_{1} (\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, |\acute{Z} |\ge \lceil\frac{\tilde{n} }{2}\rceil \right\},$$

$${X}_{20} \left(\bar{G}\right)=\,\,\text{min }\,\,\left\{ \acute{M}_{2}(\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, | X |\ge \lceil\frac{\tilde{n} }{2}\rceil\right\},$$

and

$${X}_{30} \left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{3} (\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, | \acute{Z} |\ge \lceil\frac{\tilde{n} }{2}\rceil\right\}.$$

Proof

Every arc in a PFC is strong. The SNC number of $\bar{G}$ is $\lceil\frac{\tilde{n} }{2}\rceil$ because every arc is strong; while the number of strong nodes in PFG and CC $g$ are the same, since every arc is strong in both graph. Consequently in the SNC of $\bar{G}$ $\lceil\frac{\tilde{n} }{2}\rceil$ is the smallest number of nodes so,

$${X}_{10}\left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{1}(\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, |\acute{Z} |\ge \lceil\frac{\tilde{n} }{2}\rceil \right\},$$

$${X}_{20}\left(\bar{G}\right)=\,\,\text{min }\,\, \left\{ \acute{M}_{2}(\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, | \acute{Z} |\ge \lceil\frac{\tilde{n} }{2}\rceil\right\},$$

and

$${X}_{30}\left(\bar{G}\right)=\,\,\text{max}\,\, \left\{\acute{M}_{3}(\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, | \acute{Z} |\ge \lceil\frac{\tilde{n} }{2}\rceil\right\}.$$

Definition 7

If there is no strong arc between two nodes in PFG $\bar{G},$ then they are said to be strongly independent. A strong independent set (SIS) is defined as any collection in $\bar{G}$ that contains at least two strongly independent nodes.

Definition 8

In a PFG $\bar{G}$ the membership value of SIS $D$ is defined as $\acute{M}_{1}\left(D\right)={\Sigma }_{\grave{u} \epsilon \text{D} } {\alpha }_{2} \left(\grave{u} ,u\right)$ where ${\alpha }_{2}\left(\grave{u} ,u\right)$ shows the least value among the membership values of strong arcs occurrence on $\grave{u}$ and neutral value of an SIS $D$ in a PFG $\bar{G}$ is defined as $\acute{M}_{2}\left( D \right)={\Sigma }_{\grave{u} \epsilon \text{D}} {\gamma }_{2}\left(\grave{u} ,u\right)$ where ${\gamma }_{2}\left(\grave{u} ,u\right)$ denotes the least value among the neutral values of strong arcs occurrence on $\grave{u}$ and nonmembership value of an SIS $D$ in a PFG $\bar{G}$ is defined as $\acute{M}_{3}\left(D\right)={{\Sigma }_{\grave{u} \epsilon {D}} \beta }_{2}\left(\grave{u} ,u\right)$ where ${\beta }_{2}\left(\grave{u} ,u\right)$ denotes the greatest value among the non-membership values of strong arcs occurrence on $\grave{u}$. ${A}_{0} \left( \bar{G} \right)= {A}_{0}= \left({A}_{10}, { A}_{20}, { A}_{30}\right)$ represents and defines the strong independent number of a PFG $\bar{G}$ where $\left({A}_{20}, { A}_{30}\right)$ greatest membership values and greatest neutral values of $D$ in $\bar{G}$ and ${A}_{30}$ is least nonmembership values of $D$ in $\bar{G}.$The strong independent set within the greatest membership values, neutral values, and least nonmembership values in a PFG $\bar{G}$ is known as the greatest strong SIS of nodes.

Theorem 4

If PFG $\bar{G}=\left(U, \hat{E} \right)$ is complete. Then ${A}_{10} = {\alpha }_{2}\left(\grave{u} ,u\right), {A}_{20} = {\upgamma }_{2}\left(\grave{u} ,u\right)$ and ${A}_{30}= {\beta }_{2}\left(\grave{u} ,u\right)$ where ${\alpha }_{2}\left(\grave{u} ,u\right),$ ${\upgamma }_{2}\left(\grave{u} ,u\right)$ and ${\beta }_{2}\left(\grave{u} ,u\right)$ are the membership, neutral, and nonmembership values of the weakest arc in $\bar{G}$.

Proof

Since $\bar{G}=\left(U, \hat{E} \right)$ is a complete PFG. Therefore, all of the nodes are associated with each other vertices in $\bar{G}$, and all of its arcs are strong. So, there is single SIS, which is $D=\left\{\grave{u} \right\}.$ Therefore the result follows.

Theorem 5

$\acute{\kappa}$ is complete bipartite PFG with partite sets $\check{U}$ ₁ and $\check{U}$ ₂ then,

$${A}_{10} \left(\acute{\kappa}\right)= \,\,\text{max}\,\, \left\{\acute{M}_{1} \left({\check{U}}_{1} \right), \acute{M}_{1} \left({{\check{U}}}_{2} \right)\right\},$$

$${A}_{20} \left(\acute{\kappa}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{2}\left({\check{U}}_{1}\right), \acute{M}_{2}\left({\check{U}}_{2}\right)\right\},$$

$${A}_{30} \left(\acute{\kappa}\right)=\,\,\text{min }\,\, \left\{\acute{M}_{3}\left({\check{U}}_{1}\right), \acute{M}_{3}\left({\check{U}}_{2}\right)\right\}.$$

Proof

Since $\acute{\kappa}$ is a complete bipartite PFG. Consequently, all of its arcs are strong Furthermore, each of the nodes in $\check{U}$₁ is linked to all the nodes in $\check{U}$₂, and each of the nodes in $\check{U}$₂ is linked to all of the nodes in $\check{U}$₁. Therefore $\check{U}$₁ and $\check{U}$₂ SISs in $\acute{\kappa}.$Hence

$${A}_{10} \left(\acute{\kappa}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{1} \left({\check{U}}_{1} \right), \acute{M}_{1} \left({\check{U}}_{2} \right)\right\},$$

$${A}_{20} \left(\acute{\kappa}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{2}\left({\check{U}}_{1}\right), \acute{M}_{2}\left({\check{U}}_{2}\right)\right\},$$

and

$${A}_{30} \left({\acute{\kappa}}\right)=\text{min }\left\{\acute{M}_{3}\left({{\check{U}}}_{1}\right), \acute{M}_{3}\left({{\check{U}}}_{2}\right)\right\}.$$

Theorem 6

Let $\bar{G}=(U, \hat{E} )$ is a PFC and $g$ represents a crisp cycle (CC) then

$${A}_{10} \left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{1} (\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, | \acute{Z} | \le \left[\frac{\tilde{n} }{2}\right]\right\},$$

$${A}_{20} \left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{2} (\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, | \acute{Z} | \le \left[\frac{\tilde{n} }{2}\right]\right\},$$

and

$${A}_{30} \left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{3} (\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, | \acute{Z} | \le \left[\frac{\tilde{n} }{2}\right]\right\}.$$

Proof

As so every arc in a PFC is strong. The SNC number of $\bar{G}$ is $\left[\frac{\tilde{n} }{2}\right]$ because the number of nodes is SIS in $g$ and $\bar{G}$ are the same. After all, in both graphs, each arc is a strong arc. So, in the SNC in $\bar{G}$ $\left[\frac{\tilde{n} }{2}\right]$ is the greatest number of nodes. Thus,

$${A}_{10} \left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{1} (\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, | \acute{Z} | \le \left[\frac{\tilde{n} }{2}\right]\right\},$$

$${A}_{20} \left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{2} (\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, | \acute{Z} | \le \left[\frac{\tilde{n} }{2}\right]\right\},$$

and

$${A}_{30} \left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{3} (\acute{Z} )| \acute{Z} \text{ is an SNC in } \bar{G} \,\,\text{with}\,\, | \acute{Z} | \le \left[\frac{\tilde{n} }{2}\right]\right\}.$$

Definition 9

Let $\bar{G}=(U \hat{E} )$ be an associated PFG. The collection $\tilde{N}$ of strong arcs (SAs) that envelops all the nodes of PFG $\bar{G}$ is known as SAC in $\bar{G}.$ $\acute{M}_{1}\left(\tilde{N} \right)={\sum }_{\left(\grave{u} , u\right) \in { \tilde{N} } }{\alpha }_{2} (\grave{u} ,u),$ $\acute{M}_{2}\left(\tilde{N} \right)={\sum }_{\left(\grave{u} , u\right) \in { \tilde{N} } }{\gamma }_{2} (\grave{u} ,u)$ and, $\acute{M}_{3} (\tilde{N} )={\sum }_{\left(\grave{u} , u \right) \in \tilde{N} }{ \beta }_{2} (\grave{u} , u)$ where${\alpha }_{2} (\grave{u} ,u )$, ${\gamma }_{2}(\grave{u} ,u)$ show the membership, neutral values of SAC and ${\beta }_{2} (\grave{u} ,u )$ shows the non-membership values of SAC $\tilde{N}$ respectively.

${X}_{1} (\bar{G}) = {X}_{1} = ({X}_{11}, {X}_{21},{X}_{31})$ is the SAC number of a PFG $\bar{G}$, where ${X}_{11}, {X}_{21}$ are the least values of membership, least values of neutral in the SAC of PFG $\bar{G}$ and ${X}_{31}$ is the greatest value of non-membership in SAC of PFG $\bar{G}.$ A SAC with the least membership value, neutral value, and greatest non-membership value in a PFG $\bar{G}$ is said to be the least strong arc cover (SAC).

Theorem 7

If $\bar{G} = \left(U, \hat{E} \right)$ is a complete PFG then

$${X}_{11}(\bar{G})=\,\,\text{min }\,\,\left\{\acute{M}_{1}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \bar{G} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right]\right\},$$

$${X}_{21}\left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{2}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \bar{G} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right]\right\},$$

and

$${X}_{31}\left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{3}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \bar{G} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right]\right\}.$$

Proof

Every node in complete PFG $\bar{G}$ is linked to each node of $\bar{G},$ as well as its arcs are strong. Furthermore, the SAC of number $\bar{G}$ is $\lceil\frac{\tilde{n} }{2}\rceil,$ because all arcs are strong in complete PFG and the crisp graph, so the number of strong arcs in both graphs is the same. Thus, the smallest number of arcs in $\bar{G}$ is $\left[\frac{\tilde{n} }{2}\right]$. Therefore,

$${X}_{11}\left(\bar{G}\right)=\,\,\text{min }\,\, \left\{\acute{M}_{1}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \bar{G} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right]\right\},$$

$${X}_{21}\left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{2}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \bar{G} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right]\right\},$$

and

$${X}_{31}\left(\bar{G}\right)=\,\,\text{max}\,\, \left\{\acute{M}_{3}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \bar{G} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right]\right\}.$$

Theorem 8

$\acute{\kappa}$ is complete bipartite PFG with a partite set $\check{U}$₁ and $\check{U}$₂, then

$${X}_{11}\left(\acute{\kappa}\right)=\,\,\text{min }\,\, \left\{\acute{M}_{1} (\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \,\,\text{max}\,\,\ge \left\{ \left|{\check{U}}_{1}\right|| {\check{U}}_{2}\right\}\right\},$$

$${X}_{21}\left(\acute{\kappa}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{2} (\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \,\,\text{max}\,\,\ge \left\{ \left|{\check{U}}_{1}\right|| {\check{U}}_{2}\right\}\right\},$$

and

$${X}_{31}\left(\acute{\kappa}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{3} (\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \,\,\text{max}\,\,\ge \left\{ \left|{\check{U}}_{1}\right|| {\check{U}}_{2}\right\}\right\}.$$

Proof

Since $\acute{\kappa}$ is a complete bipartite PFG. Consequently, all of its arcs are strong. Furthermore, all of the nodes in $\check{U}$₁ is associated to all of the nodes in $\check{U}$₂, and each of the nodes $\check{U}$₂ is associated to all of the nodes in $\check{U}$ ₁. The arc covering a number of $\acute{\kappa}$ is $\left\{\left|{\check{U}}_{1}\left|,\right|{\check{U}}_{2}\right| \right\},$ since every arc is strong in a complete bipartite PFG; in both graphs the number of strong arcs is the same. As a result, the smallest number of arcs in the SAC in $\acute{\kappa}$ is $\{| \check{U}1|,| \check{U}2|\}.$ Thus,

$${X}_{11}\left(\acute{\kappa}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{1} (\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \,\,\text{max}\,\,\ge \left\{ \left|{\check{U}}_{1}\right|| {\check{U}}_{2}\right\}\right\},$$

$${X}_{21} \left(\acute{\kappa}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{2} (\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \,\,\text{max}\,\,\ge \left\{ \left|{\check{U}}_{1}\right|| {\check{U}}_{2}\right\}\right\},$$

and

$${X}_{31}\left(\acute{\kappa}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{3} (\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \,\,\text{max}\,\,\ge \left\{ \left|{\check{U}}_{1}\right|| {\check{U}}_{2}\right\}\right\}.$$

Theorem 9

Let $\bar{G} = (U, \hat{E} )$ be a PFG and $\bar{g}$ is a crisp cycle (CC), then

$${X}_{11}\left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{1}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right] \right\},$$

$${X}_{21}\left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{2}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right] \right\},$$

and

$${X}_{31}\left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{3}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right] \right\}.$$

Proof

Since every arc in a PFG is strong. Furthermore, while the number of SAs in PFG and the CC $\bar{g}$ are the same, as each arc is strong in both graphs, so the SAC of $\bar{G}$ is $\lceil\frac{\tilde{n} }{2}\rceil.$ As a result, in the SAC of $\lceil\frac{\tilde{n} }{2}\rceil$ is the least number of arcs. Hence

$${X}_{21}\left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{1}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right] \right\},$$

$${X}_{21}\left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{2}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right] \right\},$$

and

$${X}_{31}\left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{3}(\tilde{N} )| \tilde{N} \text{ is a SAC in } \acute{\kappa} \,\,\text{with}\,\, | \tilde{N} | \ge \left[\frac{\tilde{n} }{2}\right] \right\}.$$

Definition 10

A set of strong arcs is denoted by $Q$ in a PFG $\bar{G}=(U, \hat{E} ),$ is known as SIS of arcs since none of its arcs allocates a node, in $\bar{G}=(U, \hat{E} ) Q$ is also known as strong matching (SM).

Definition 11

If $({\grave{u} },u)\in Q$, here $Q$ is SM in a PFG $\bar{G}=(U, \hat{E} ).$ Then it is stated that $\grave{u}$ is strongly matched to $u$ by $Q$. $\acute{M}_{1}\left(Q\right)={\sum }_{ \grave{u} ,u \in Q }{\alpha }_{2} \left( \grave{u} ,u\right), \acute{M}_{2}\left(Q\right)= {\sum }_{{ \grave{u} }, u \in { Q }}{\gamma }_{2} \left({ \grave{u} },u\right),$ and $\acute{M}_{3}(Q)= {\sum }_{ \grave{u} ,u \in Q }{\beta }_{2} (\grave{u} ,u )$ are the membership, neutral, and non-membership values of the SAC $Q,$ correspondingly.

${A}_{1} (\bar{G})= {A}_{1}=( {A}_{11}, {A}_{21}, {A}_{31})$ is the SA independent number or SM number of PFG $\bar{G} = (U, \hat{E} ),$ where ${A}_{11}$ and ${A}_{21}$ are the greatest membership and neutral values of the SMs of $\bar{G}$ and ${A}_{31}$ represents the least non-membership value. An SM with the greatest membership value, greatest neutral value, and least nonmembership value in a PFG $\bar{G}$ is said to be the greatest SM.

Theorem 10

Let $\bar{G} = (U, \hat{E} )$ be a complete PFG then

$${A}_{11}\left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{1}(Q)| Q \text{ is an SM in } \bar{G} \,\,\text{with}\,\, | Q | \le \left[\frac{ \tilde{n} }{2}\right]\right\},$$

$${A}_{21}\left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{2}(Q)| Q \text{ is an SM in }\bar{G} \,\,\text{with}\,\, | Q | \le \left[\frac{ \tilde{n} }{2}\right]\right\},$$

and

$${A}_{31}\left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{3}(Q)| Q \text{ is an SM in } \bar{G} \,\,\text{with}\,\, | Q | \le \left[\frac{ \tilde{n} }{2}\right]\right\}.$$

where ${\tilde{n} }$ denotes the number of nodes in $\bar{G}$.

Proof

Every node in complete PFG is associated to each other in $\bar{G}$, and all of its arcs are strong. Furthermore, the SM number $\bar{G}$ is $\left[\frac{\tilde{n} }{2}\right]$. Because each arc is strong in complete PFG and the crisp graph. So, in both graphs, the SM number is the same. Thus in the SM $\bar{G}$ is $\left[\frac{\tilde{n} }{2}\right]$ the greatest number of arcs. Thus.

$${A}_{11}\left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{1}(Q)| Q \text{ is an SM in } \bar{G} \,\,\text{with}\,\, | Q | \le \left[\frac{ \tilde{n} }{2}\right]\right\},$$

$${A}_{21}\left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{2}(Q)| Q \text{ is an SM in } \bar{G} \,\,\text{with}\,\, | Q | \le \left[\frac{ \tilde{n} }{2}\right]\right\}$$

and

$${A}_{31}\left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{3}(Q)| Q \text{ is an SM in } \bar{G} \,\,\text{with}\,\, | Q | \le \left[\frac{ \tilde{n} }{2}\right]\right\}.$$

Theorem 11

$\acute{\kappa}$ is complete bipartite PFG with a partite set $\check{U}$ ₁ and $\check{U}$ ₂ then

$${A}_{11}\left(\acute{\kappa}\right)=\,\,\text{max}\,\, \left\{\acute{M}_{1} (\text{Q})| Q \text{ is an SM in } \acute{\kappa} \,\,\text{with}\,\, | Q |\le \,\,\text{min }\,\,\{{\check{U}}_{1}|,| {\check{U}}_{2}|\}\right\},$$

$${A}_{21}\left(\acute{\kappa}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{2} (\text{Q})| Q \text{ is an SM in } \acute{\kappa} \,\,\text{with}\,\, | Q |\le \,\,\text{min }\,\,\{{\check{U}}_{1}|,| {\check{U}}_{2}|\}\right\},$$

and

$${A}_{31}\left(\acute{\kappa}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{3} (\text{Q})| Q \text{ is an SM in } \acute{\kappa} \,\,\text{with}\,\, | Q | \le \,\,\text{min }\,\,\{{\check{U}}_{1}|,| {\check{U}}_{2}|\}\right\}.$$

Proof

Since $\acute{\kappa}$ is a complete bipartite PFG. Consequently, every one of the arcs is strong. Furthermore, every node in $\check{U}$ ₁ is associated to every node in $\check{U}$ ₂, and all of the nodes in ${\check{U}}_{2}$ are associated with all of the nodes in $\check{U}$ ₁. The Matching number of $\acute{\kappa}$ is $\left\{\left|{\check{U}}_{1}\right|,\left|{\check{U}}_{2}\right|\right\}$, because all arcs are strong in complete bipartite PFG and the complete bipartite crisp graphs; consequently both graphs have the same number of SM. Hence, in the SM of $\acute{\kappa}$ is $\left\{\left|{\check{U}}_{1}\right|,\left|{\check{U}}_{2}\right|\right\}$ the greatest number of arcs. Thus.

$${A}_{11}\left(\acute{\kappa}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{1} (\text{Q})| Q \text{ is an SM in } \acute{\kappa} \,\,\text{with}\,\, | Q | \le \,\,\text{min }\,\,\{{\check{U}}_{1}|,| {\check{U}}_{2}|\}\right\},$$

$${A}_{21}\left(\acute{\kappa}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{2} (\text{Q})| Q \text{ is an SM in } \acute{\kappa} \,\,\text{with}\,\, | Q | \le \,\,\text{min }\,\,{\check{U}}_{1}|,| {\check{U}}_{2}|\}\right\},$$

and

$${A}_{31}\left(\acute{\kappa}\right)=\,\,\text{min }\,\, \left\{\acute{M}_{3} (\text{Q})| Q \text{ is an SM in } \acute{\kappa} \,\,\text{with}\,\, | Q | \le \,\,\text{min }\,\,\{{\check{U}}_{1}|,| {\check{U}}_{2}|\}\right\}.$$

Theorem 12

Let $\bar{G}=(U, \hat{E} )$ be a PFG and $g$ is a crisp cycle (CC), then

$${A}_{11} \left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{1} (Q)| Q \text{ is an SM in } \bar{G} \,\,\text{with}\,\, |Q| \le \left[\frac{\tilde{n} }{2}\right]\right\},$$

$${A}_{21} \left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{2} (Q)| Q \text{ is an SM in } \bar{G} \,\,\text{with}\,\, |Q| \le \left[\frac{\tilde{n} }{2}\right]\right\},$$

and

$${A}_{31}\left(\bar{G}\right)=\,\,\text{min }\,\,\left\{ \acute{M}_{3} (Q)| Q \text{ is an SM in } \bar{G} \,\,\text{with}\,\, |Q| \le \left[\frac{\tilde{n} }{2}\right]\right\}.$$

Proof

Since each arc in a PFG is strong. Furthermore,$\left[ \frac{\tilde{n} }{2}\right]$ is the SM number of $\bar{G}$, because every arc is strong in both graphs $\bar{G}$ and $g$, since the number of SM in PFG and the crisp cycle $g$ are the same. Thus, in the SM of $\bar{G}$ is $\left[\frac{\tilde{n} }{2} \right]$ is the greatest number of arcs. Hence

$${A}_{11}\left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{1} (Q)| Q \text{ is an SM in } \bar{G} \,\,\text{with}\,\, |Q| \le \left[\frac{\tilde{n} }{2}\right]\right\},$$

$${A}_{21}\left(\bar{G}\right)=\,\,\text{max}\,\,\left\{\acute{M}_{2} (Q)| Q \text{ is an SM in } \bar{G} \,\,\text{with}\,\, |Q| \le \left[\frac{\tilde{n} }{2}\right]\right\},$$

and

$${A}_{31}\left(\bar{G}\right)=\,\,\text{min }\,\,\left\{\acute{M}_{3}(Q)| Q \text{ is an SM in } \bar{G} \,\,\text{with}\,\, |Q| \le \left[\frac{\tilde{n} }{2}\right]\right\}.$$

Example 5

Figure 5 shows PFG$\bar{G}=(U, \hat{E} )$. In PFG $\bar{G}$ arcs show the solid lines $(u, \tilde{n} ), (\tilde{n} , \grave{u} )$ and $(\hat{w}, u)$ are strong arcs while $(\hat{w}, u)$ is not SE. So SNCs are ${ \check{H}}_{1}=\left(u, \tilde{n} \right), {\check{H}}_{2}= \left(u, \grave{u} \right),{\check{H}}_{3}=(\hat{w}, \tilde{n} )$,${\check{H}}_{4} =(u,\hat{w}, \tilde{n} )$,${\check{H}}_{5}=(u, \tilde{n} , \grave{u} )$,${\check{H} }_{6}=(u ,\hat{w}, \check{U})$,${\check{H}}_{7}=(\hat{w}, \tilde{n} , \grave{u}$) and ${\check{H}}_{8}=(u ,\hat{w},\tilde{n} , \grave{u} ).$

Fig. 5

Strong covering in PFG

The following outcomes we get for each SNC, $\acute{M}\left({\check{H}}_{1}\right)=0.1+0.1, 0.2+0.1, 0.6+0.5=\left(0.2, 0.3, 1.1\right)$, $\acute{M}\left({{\check{H}}}_{2} \right)=\left(0.2, 0.3, 1.1\right),\acute{M}\left({{\check{H}}}_{3}\right)=\left(0.4, 0.3, 1\right),$ $\acute{M}\left({{\check{H}}}_{4}\right)=\left(0.5, 0.5, 1.7\right)$, $\acute{M}({{\check{H}}}_{5})=(0.3, 0.4, 1.7)$, $\acute{M}\left({{\check{H}}}_{6}\right)=\left(0.5, 0.5, 1.6\right),\text{ MMM }\left({{\check{H}}}_{7} \right)=\left(0.5, 0.4, 1.6\right),\text{ MMM }\left({{\check{H}}}_{8}\right)= \left(0.6, 0.6, 2.2\right).$

Now SNC number of $\bar{G}$ is ${X}_{0} (\bar{G}) = {X}_{0}=({X}_{10}, { X}_{20}, {X}_{30}) = (0.2, 0.3, 2.2).$

In this case, there are no minimum strong independent covers and no minimum SNCs.

The nodes $\hat{w}$ and $\grave{u}$ are strongly independent because they are not connected by strong arcs. However, they are not independent because they are neighbors.

The SISs are ${\check{H}}_{1} =(u, \grave{u} ),$${\check{H}}_{2}=( \hat{w}, \tilde{n} ),$ ${\check{H}}_{3}=(\hat{w}, \grave{u} ),$ Now we find the strong independent number. $\acute{M} ({\check{H}}_{1})=(0.3+0.3, 0.2+0.4, 0.5+0.3)=(0.6, 0.6, 0.8),$ $\acute{M} \left({\check{H}}_{2}\right)=\left(0.6, 0.4, 1\right)$, $M ({\check{H}}_{3})=(0.6, 0.6, 0.8).$ Strong independent number of $\bar{G}$ is ${A}_{0} (\bar{G})= {A}_{0}=({A}_{10}, {A}_{20}, {A}_{30})=(0.6, 0.6, 0.8),$ the greatest values of strong independent set is $(0.6, 0.6, 0.8).$

The SACs are ${\tilde{N} }_{1} =\{(u, \hat{w}), ( \tilde{n} , \grave{u} )\}$,${\tilde{N} }_{2}=\{(u, \hat{w}),( \tilde{n} , ),( u, \tilde{n} )\}$. Now we find the number of SACs. $\acute{M} \left({\tilde{N} }_{1}\right)=\left(0.3+0.3, 0.2+0.4, 0.5+0.3\right)=\left(0.6, 0.6, 0.8\right).$ Similarly $\acute{M} ({\tilde{N} }_{2})=(0.9, 0.8, 1.13$).

By definition of SAC numbers is ${A}_{1}(\bar{G}) ={A}_{1}=( {A}_{11} , {A}_{21}, {A}_{31}) = (0.6, 0.6, 1.13),$ there is no least SAC in any of the strong node covers.

The only strong matching (SM) of $\bar{G}$ is $Q = (u, \hat{w}),( \tilde{n} , \grave{u} ).$

By definition of SM, we find SM number, that is

$$\acute{M} \left(Q\right)=\left(0.3+0.3, 0.2+0.4, 0.5+0.3\right)=\left(0.6, 0.6, 0.8\right).$$

Theorem 13

Let $\bar{G}=(U, \hat{E} )$ be a PFG of order $(m,\tilde{n} )$ such that there are no isolated vertices in $\bar{G}$. Then for each graph of this type,

• ${X}_{0}+ {A}_{0}=\acute{M}\left(U\right)\le m.$

• (ii)${ X}_{1} + {A}_{1} \ge { \tilde{n} }.$

Proof

Let ${X}_{0} = \acute{M} (\hat{R}_{0})$, where ${\hat{R}}_{0}$ the least SNC of $\bar{G}$. Then $U-{\hat{R}}_{0}$ is an SIS of the nodes. That mean node in $U-{\hat{R}}_{0}$ are incident on strong arcs in ${\bar{G}}.$

Therefore,

$$\begin{aligned}&{X}_{0} \ge \acute{M} \left(U - {N}_{0} \right)= \acute{M} \left(U\right)-{A}_{0 },\\& \quad\text{i}.\text{e}. {X}_{0}+ {A}_{0}\ge \acute{M} \left(U\right).\end{aligned}$$

(12)

Let ${X}_{0} = \acute{M} ({\gamma}_{0} )$, where ${\gamma}_{0}$ the greatest SIS of the node in is $\bar{G}$. That is no nodes in $\gamma$₀ are connected by a strong arc, so the node in $U-\gamma$₀ strongly covers all the nodes in ${\gamma}_{0}.$Hence,

$U-\gamma$₀ is an SNC of \bar{G} and ${X}_{0}$ is the least value of such SNCs. Thus,

$$\begin{aligned}&{A}_{0} \le \acute{ M}\left({U}-{{\gamma}}_{0} \right)=\acute{M}\left({U}\right)-{A}_{0},\\ & \quad\text{i}.\text{e}., {X}_{0} + {A}_{0} \le \acute{M}\left(\text{U}\right).\end{aligned}$$

(13)

From (12) and (13), we have ${X}_{0} + {A}_{0} = \acute{M} (U).$

Since $\acute{M} \left(U\right)\le m$ according to the definition of $\acute{M} (U).$

Hence,

$${X}_{0} + {A }_{0} =\acute{M} \left(U\right)\le m.$$

(14)

Since the value of the SA is taken into consideration when determining ${X}_{0}, {A}_{0}$. The second inequality follows immediately since $m$ is the sum of the node values.

Definition 12

Let $\bar{G} = (U, \hat{E} )$ be a PFG and $Q$ be an SM in $\bar{G}.$If $Q$ strongly matches every node of $\bar{G}$ to some node of \bar{G}. Then $Q$ is called perfect strong matching (PSM).

Example 6

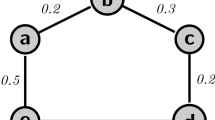
In the PFG $\bar{G}$ of Fig. 6, all arcs are strong. The set ${\text{Q}}_{1}=(a,b), (c, d)\},$ ${\text{Q}}_{2}=\left\{\left(a,c\right),\left(b,d\right)\right\},$ and ${\text{Q}}_{3} =\left\{\left(a,d\right)\left(b,c\right)\right\}$ are PSM with values $\acute{M} \left({\text{Q}}_{1}\right)= \left(0.3+\text{0.2,0.3}+\text{0.1,0.4}+0.4\right)= \left(\text{0.5,0.4,0.8}\right),$ $\acute{M} \left({\text{Q}}_{2}\right)=\left(0.3+\text{0.2,0.1}+\text{0.1,0.4}+0.5\right)= \left(\text{0.5,0.2,0.9}\right)$ and $\acute{M} ({\text{Q}}_{3})= (0.2+\text{0.4,0.1}+\text{0.3,0.2}+0.5)= \text{0.6,0.4,0.7}.$

Fig. 6

Perfect strong matching

4 Paired domination in picture fuzzy graph

In this part, we will discuss paired domination (PD), strong paired domination (SPD), and perfect paired domination using strong arcs based on perfect strong matching (PSM) and proof well-known results.

Definition 13

In a PFG $\bar{G} = \left(U, \hat{E} \right),$ a node $u$ is said to strongly dominate itself and each of its strong neighbors of $u$. i.e., $u$ has strongly dominated the node in $\hat{R} \left[u \right].$If any node of $\grave{u} (\bar{G})-\acute{Z}$ is a strong neighbor of several nodes in the $\acute{Z}$ nodes of $\bar{G}$, then that set of nodes is a strong dominating set of$\bar{G}$.

Definition 14

${\acute{M} }_{1}(\acute{Z}) = {\sum }_{\grave{u} \in \acute{Z} }{\acute{\alpha}}_{2}(\grave{u} ,u)$ is the membership value, ${\acute{M} }_{2}(\acute{Z}) = {\sum }_{\grave{u} \in \acute{Z} }{\gamma }_{2}(\grave{u} ,u)$ is the neutral value and ${\acute{M} }_{3}(\acute{Z})={\sum }_{\grave{u} \in \acute{Z} } {\beta }_{2}(\grave{u} ,u)$ is non-membership value of the strong dominating set (SDS) $\acute{Z}$, where ${\alpha }_{2}(\grave{u} ,u)$ and ${\gamma }_{2}(\grave{u} ,u)$ denote the least value of membership and neutral value of the SAs occurrence on $\grave{u}$ while ${\beta }_{2}(\grave{u} ,u)$ denotes the greatest values of non-membership of such arcs. The SD number of a PFG $\bar{G}$ denotes and defines as $B(\bar{G})=B=({B}_{1}, {B}_{2}, {B}_{3})$ where ${B}_{1}, {B}_{2}$ denote the least membership value and neutral value of the SD set of $\bar{G}.$ and ${B}_{3}$ denotes the greatest non-membership value of such sets.

Definition 15

Let $\bar{G} = (U, \hat{E} )$ be a PFG. If $\acute{Z}$ is a strong dominating set and the induced picture fuzzy subgraph (PFSG) $\acute{Z}$ contains a perfect strong matching (PSM), the set ${\acute{Z} } \subseteq U$ of nodes is called a strong paired domination (SPD) set. The SPD set $\acute{Z}$ membership value is defined as $\acute{M}_{1} \left({\acute{Z} }\right)= {\sum }_{\grave{u} \in \check{Z}} {\acute{\alpha}}_{2} (\grave{u} ,u ),$ where ${\acute{\alpha}}_{2} (\grave{u} ,u )$ is the least values of membership of the SAs occurrence on$\grave{u}$, and neutral value of the SD set $\acute{Z}$ is defined as $\acute{M}_{2} ({\acute{Z} }) ={\sum }_{\grave{u} \in \check{Z} }{\gamma }_{2} ( \grave{u} ,u)$ where ${\gamma }_{2} (\grave{u} ,u )$ is the least neutral value of the SAs occurrence on ù and non-membership value of the SD set $\check{Z}$ is defined as.

$\acute{M}_{3}({\acute{Z} })={\sum }_{\grave{u} \in \check{Z}} {\beta }_{2}(\grave{u} ,u),$ where ${\beta }_{2}(\grave{u} ,u)$ is the greatest value of the non-membership of the SAs occurrence on $\grave{u} .$ The SPD number of a PFG $\bar{G}$ is denoted by ${\rm P} (\bar{G})={\rm P}=( {\rm P}_{1}, {\rm P}_{2}, {\rm P}_{3})$ where ${\rm P}$₁ and ${\rm P}$₂ show the least value of membership and the least neutral value of SPD sets of $\bar{G}$ while ${\rm P}$₃ denotes the greatest value of non-membership of such set.

Example 7

Let PFG $\bar{G} = (U, \hat{E} )$ strong arcs are $(u, \tilde{n} ), (\tilde{n} , \grave{u} ), ( \hat{w}, \grave{u} )$ while $( \hat{w}, u)$ is not the strong arc in PFG $\bar{G}$.

${{\acute{Z} }}_{1}=\left(u, \tilde{n} \right), {{\acute{Z} }}_{2}= \left(\hat{w}, \grave{u} \right),$ ${{\acute{Z} }}_{3}=\left(u, \tilde{n} , \hat{w}, \grave{u} \right)$ are paired dominating sets. Now we found the values of strong dominating.

$$\acute{M} \left({{\acute{Z} }}_{1}\right)=\left(0.3+0.1, 0.2+0.2, 0.4+0.4\right)= \left(0.4, 0.4, 0.8\right),$$

$$\acute{M} \left({{\acute{Z} }}_{2}\right)=\left(0.2, 0.4, 0.9\right),$$

and

$$\acute{M} ({{\acute{Z} }}_{3}) = (0.6, 0.8, 1.8).$$

By definition of SPD number is defined ${\rm P} (\bar{G})= {\rm P}=( {\rm P}_{1}, {\rm P}_{2}, {\rm P}_{3})= (\text{0.2,0.4,1.8})$ is SPD number in Fig. 7

Fig. 7

Paired domination in PFG

Theorem 14

If $\bar{G} = \left(U, \hat{E} \right)$ be a complete PFG then ${\rm P}_{1} \left(\bar{G}\right)= 2{\alpha }_{2} \left(\grave{u} ,u\right), {\rm P}_{2} \left(\bar{G}\right)= 2{\gamma }_{2} \left(\grave{u} ,u\right)$ and ${\rm P}_{3}\left(\bar{G}\right)= 2{\beta }_{2} \left(\grave{u} ,u\right)$ where ${\alpha }_{2}\left(\grave{u} ,u\right)$ is membership values, ${\gamma }_{2}\left(\grave{u} ,u\right)$ are neutral values ${\beta }_{2}\left(\grave{u} ,u\right)$ is nonmembership values of the weakest arc in $\bar{G}.$

Proof

Because $\bar{G}=\left(U, \hat{E} \right)$ be a complete PFG, all of its nodes are associated with the others, and all of its arcs are solid. If $\left\{\grave{u} ,u\right\}$ is two nodes in any set of $\bar{G}$, then such set forms a strong paired dominant collection. In this manner

$${\rm P}_{1 }\left(\bar{G} \right)= {\alpha }_{2}\left(\grave{u} ,u\right)+ {\alpha }_{2}\left(\grave{u} ,u\right)= 2{\alpha }_{2} \left(\grave{u} ,u \right),$$

$${\rm P}_{2} \left(\bar{G}\right)= {\gamma }_{2}\left(\grave{u} ,u\right)+ {\gamma }_{2}\left(\grave{u} ,u\right)= 2{\gamma }_{2}\left(\grave{u} ,u\right),$$

and

$${\rm P}_{3} \left({\bar{G}}\right)= {\beta }_{2} \left({\grave{u} },u\right)+ {\beta }_{2} \left({\grave{u} },u\right)= 2{\beta }_{2} \left({\grave{u} },u\right).$$

Theorem 15

SPD numbers for complete bipartite PFG $\acute{\kappa}$ are ${\rm P}_{1}\left(\acute{\kappa}\right)= 2{\alpha }_{2} \left(\grave{u} ,u\right), {\rm P}_{2} \left(\acute{\kappa}\right)= 2{\gamma }_{2} \left(\grave{u} ,u\right)$ and ${\rm P}_{3} (\acute{\kappa} ) = 2{\beta }_{2} (\grave{u} ,u$) where ${\alpha }_{2} (\grave{u} ,u), {\gamma }_{2} (\grave{u} ,u )$ and ${\beta }_{2} \left(\grave{u} ,u\right)$ are membership, neutral, and nonmembership value of weakest arc in $K.$

Proof

By definition of complete bipartite PFG$\acute{\kappa}$, all of its arcs are strong. Furthermore, every one of the nodes in $U$₁ is linked to all the nodes in $U$₂. Therefore, any collection in $\acute{\kappa}$ that includes two nodes, one in $U$₁ and different in $U$₂ is an SPD set. Let $\left\{\grave{u} ,u\right\}$ end nodes of any weakest arc in $( \grave{u} ,u )$ in $\acute{\kappa}$ such that $\grave{u} \epsilon {U}_{1}$ and $u \epsilon {U}_{2}$ after that $\{ \grave{u} ,u \}$ create an SPD set. In this manner

$${\rm P}_{1 }\left(\acute{\kappa} \right)= {\alpha }_{2} \left(\grave{u} ,u \right)+ {\alpha }_{2} \left(\grave{u} ,u \right)= 2{\alpha }_{2} \left(\grave{u} ,u \right),$$

$${\rm P}_{2} \left(\acute{\kappa}\right)= {\gamma }_{2} \left(\grave{u} ,u \right)+ {\gamma }_{2} \left(\grave{u} ,u \right)= 2{\gamma }_{2} \left(\grave{u} ,u\right),$$

and

$${\rm P}_{3} \left(\acute{\kappa} \right)= {\beta }_{2} \left(\grave{u} ,u \right)+ {\beta }_{2} \left(\grave{u} ,u \right)= 2{\beta }_{2} \left(\grave{u} ,u \right).$$

5 Conclusion

This study used the concept of strong arcs in a picture fuzzy graph (PFG) to define some innovative notions of covering and paired domination in PFG. Since the PFG is a generalization of FGs and IFGs, so we considered this extended structure for our study. The FGs and IFGs have certain limitations that are covered by PFGs. Three fuzzy valued mappings defining the PFG are membership value, neutral value, and nonmembership value. The relation between the concepts of strong node cover, strong independent number, strong arc cover, and strong matching in PFGs using strong arcs are determined. Moreover, we implemented the paired domination, strong paired dominating set, and strong paired domination number in PFGs using strong arcs. Additionally, the complete PFG and complete bipartite PFG have been worked out to find the strong paired domination number. Every definition is supported by graphical and theoretical examples. Also, several interesting properties of the proposed concepts are investigated.