Domination of Bipolar Fuzzy Graphs in Various Settings

Abstract

Bipolar fuzzy sets are used to describe the positive and negative of the uncertainty of objects, and the bipolar fuzzy graphs are used to characterize the structural relationship between uncertain concepts in which the vertices and edges are assigned positive and negative membership function values to feature the opposite uncertainty elevation. The dominating set is the control set of vertices in the graph structure and it occupies a critical position in graph analysis. This paper mainly contributes to extending the concept of domination in the fuzzy graph to the bipolar frameworks and obtaining the related expanded concepts of a variety of bipolar fuzzy graphs. Meanwhile, the approaches to obtain the specific dominating sets are presented. Finally, a numeral example on city data in Yunnan Province is presented to explain the computing of domination in bipolar fuzzy graph in the specific application.

1 Introduction

Fuzzy sets are used to describe the uncertainty of things, and are widely used in fuzzy reasoning, fuzzy intelligent decision-making systems and other fields, and thus have received widespread attention (see Bera and Pal [1] and [2], Islam and Pal [3], Samanta1 et al. [4], Amanathulla et al. [5], Pal et al. [6], Prabakaran et al. [7], Bagherinia et al. [8], Gonzalez et al. [9], and Maldonado et al. [10]). On the other hand, graphs are an effective tool to describe the structured data. Edges are used to measure the hierarchical and subordinate relationships between concepts, and the entire data set can be stored as graphs. Knowledge graphs and ontology graphs are typical examples. Therefore, fuzzy graphs are defined and used to represent the structure of fuzzy data, and are applied in various engineering applications which involve uncertainty issues.

Recently, bipolar fuzzy graphs have raised much attention from researchers. Akram et al. [11] aggregated the decisions of all experts by means of the performance of alternatives, traits of the attributes and the tricks of bipolar fuzzy N-soft weighted average operator. Fahmi and Amin [12] constructed several bipolar neutrosophic fuzzy (BNF) operators in terms of prioritized muirhead mean aggregation operations. Ozcelik and Nalkiran [13] introduced TrBF-EDAS which is a tool to evaluate the alternatives in any system in which there is fuzzy bipolar information. Yiarayong [14] generalized the concept of interval-valued bipolar fuzzy sets and defined interval-valued bipolar fuzzy subsemigroups and interval-valued bipolar fuzzy left ideals over semigroups. Cornejo et al. [15] obtained a characterization of the solvability of bipolar max-product fuzzy equations with the standard negation. Xiang et al. [16] performed a work in terms of permutation fuzzy entropy to analyze the brain complexity of bipolar disorder patients. Sindhu et al. [17] introduced the aggregation operators for the novel extension of PcFSs which was named as bipolar picture fuzzy sets. Shirzadi et al. [18] developed a fuzzy programming by bipolar approach. Sarwar et al. [19] applied Bipolar fuzzy soft information in hypergraph setting. Muhiuddin and Al-Kadi [20] introduced the notion of bipolar fuzzy implicative ideals of a BCK-algebra and determined several properties.

Since bipolar fuzzy sets can be used to represent the uncertain attributes of both positive and negative sides of things, they are widely used in fuzzy decision-making systems. To structurally express the fuzzy attributes with bipolar features, a bipolar fuzzy graph is defined, and the concepts of path, connectivity, and topological indices of the fuzzy graph are also defined successively (for more details on graph, fuzzy graph in various settings, see Santiago et al. [21], Ali et al. [22], Bozhenyuk et al. [23], Das et al. [24], Akram et al. [25], Das et al. [26], Kalathian et al. [27], Gao et al. [28] and [29], and Gong and Hua [30]). Although the bipolar fuzzy graph framework is successfully applied in some fields, its fuzzy characteristics and related attributes still need to be studied in most settings. Inspired by these facts, this paper does further research on bipolar fuzzy graphs.

The main contribution of this work is to study the domination of bipolar fuzzy graphs. Since there are various framework settings for fuzzy graphs, we need to discuss bipolar fuzzy graphs in different settings separately, and to summarize and classify the different definitions of the existing domination sets.

The organization of the rest sections are arranged as follows. First, we review the concept of bipolar fuzzy graph settings, including bipolar fuzzy incidence graph setting and bipolar intuitionistic fuzzy graph setting. Then, in the third section, we mainly extend the dominating set and domination number to these bipolar graph settings. Specially, there are more than one definition of domination in normal bipolar graph setting, and we introduce them in detail.

2 Definitions in Bipolar Fuzzy Graph Setting

Let V be a universal set (i.e., it denotes the vertex set of fuzzy graph without membership function values). The set $A = \{ (v,\mu_{A}^{P} (v),\mu_{A}^{N} (v)):v \in V\}$ is a bipolar fuzzy set in V if two maps satisfy $\mu_{A}^{P} :V \to [0,1]$ and $\mu_{A}^{N} :V \to [ - 1,0]$. Generalized bipolar fuzzy graph was introduced by Yang et al. [31]. If $A = \{ (v,\mu_{A}^{P} (v),\mu_{A}^{N} (v)):v \in V\}$ is a bipolar fuzzy set on an underlying set V and $B = (\mu_{B}^{P} ,\mu_{B}^{N} )$ is a bipolar fuzzy set in $\tilde{V}^{2}$ where $\mu_{B}^{P} (v,{v^{\prime}}) \le min\{ \mu_{A}^{P} (v),\mu_{A}^{P} ({v^{\prime}})\}$, $\mu_{B}^{N} (v,{v^{\prime}}) \ge \max \{ \mu_{A}^{N} (v),\mu_{A}^{N} ({v^{\prime}})\}$ for any $(v,{v^{\prime}}) \in \tilde{V}^{2}$, and $\mu_{B}^{P} (v,{v^{\prime}}) = \mu_{B}^{N} (v,{v^{\prime}}) = 0$ for any $(v,{v^{\prime}}) \in \tilde{V}^{2} - E$, then $G = (V,A,B)$ is a bipolar fuzzy graph (BFG) of the graph $G* = (V,E)$ (the corresponding originally graph is called a crisp graph of fuzzy graph). In what follows, we always use $\wedge$ and $\vee$ instead of minimum and maximum operations, respectively. More related concepts were introduced by Mathew et al. [32], Akram [33], Akram and Karunambigal [34], Karunambigai et al. [35], Akram and Farooq [36], Singh and Kumar [37], and Yang et al. [31].

Verty recently, Poulik and Ghorai [38] revised the concepts of order, neighborhood, neighborhood degree, irregular and subdigraph of bipolar fuzzy graphs which were first defined by Akram [38]. The order of a bipolar fuzzy graph $G = (V,A,B)$ is denoted by

$$O(G) = (O^{P} (G),O^{N} (G)) = \left(\sum\limits_{v \in V} {\mu_{A}^{P} (v)} ,\sum\limits_{v \in V} {\mu_{A}^{N} (v)} \right)$$

The size of a bipolar fuzzy graph is formulated by

$$S(G) = (S^{P} (G),S^{N} (G)) = \left(\sum\limits_{{(v,{v^{\prime}}) \in \tilde{V}^{2} }} {\mu_{B}^{P} (v,{v^{\prime}})} ,\sum\limits_{{(v,{v^{\prime}}) \in \tilde{V}^{2} }} {\mu_{B}^{N} (v,{v^{\prime}})} \right)$$

For a subset vertex set $S \subseteq V$, the fuzzy cardinality of S is denoted by

$$\left| S \right| = \left(\sum\limits_{v \in S} {\mu_{A}^{P} (v)} ,\sum\limits_{v \in S} {\mu_{A}^{N} (v)} \right)$$

The open neighborhood of a vertex v in bipolar fuzzy graph $G = (V,A,B)$ is

$$N(v) = \{ {v^{\prime}} \in V:\mu_{B}^{P} (v,{v^{\prime}}) > 0{\text{ or }}\mu_{B}^{N} (v,{v^{\prime}}) < 0\}$$

The close neighborhood of a vertex v is denoted by $N[v] = N(v) \cup \{ v\}$. The open neighborhood degree of a vertex v in bipolar fuzzy graph is then determined by

$$d(v) = (d^{P} (v),d^{N} (v)) =\left(\sum\limits_{{(v,{v^{\prime}}) \in \tilde{V}^{2} }} {\mu_{B}^{P} (v,{v^{\prime}})} ,\sum\limits_{{(v,{v^{\prime}}) \in \tilde{V}^{2} }} {\mu_{B}^{N} (v,{v^{\prime}})} \right)$$

A fuzzy incidence graph $G = (\eta ,\theta ,\Psi )$ is defined as follows: $\eta :V \to [0,1]$, $\theta :E \to [0,1]$, $\Psi :V \times E \to [0,1]$, and these membership functions satisfy $\Psi (v,e) \le \eta (v) \wedge \theta (e)$ and for any $v \in V$ and $e \in E$. Gong and Hua [39] extended the definition of fuzzy incidence to bipolar fuzzy incidence graph which is described as follows. Let $G = (V,E)$ be a graph, $\eta^{P} :V \to [0,1]$, $\eta^{N} :V \to [ - 1,0]$, $\theta^{P} :E \to [0,1]$, $\theta^{N} :E \to [ - 1,0]$, $\Psi^{P} :V \times E \to [0,1]$, $\Psi^{N} :V \times E \to [ - 1,0]$. If $\Psi^{P} (v,e) \le \eta^{P} (v) \wedge \theta^{P} (e)$ and $\Psi^{N} (v,e) \ge \eta^{N} (v) \vee \theta^{N} (e)$ for any $v \in V$ and $e \in E$, then $(\Psi^{P} ,\Psi^{N} )$ is called a bipolar fuzzy incidence of G. Change an other word, let $G = (V,E)$ be a graph, and $(\eta^{P} ,\eta^{N} ,\theta^{P} ,\theta^{N} )$ be a bipolar fuzzy subgraph of G. If $(\Psi^{P} ,\Psi^{N} )$ is a bipolar fuzzy incidence of G, then $G = (\eta^{P} ,\eta^{N} ,\theta^{P} ,\theta^{N} ,\Psi^{P} ,\Psi^{N} )$ is called a bipolar fuzzy incidence graph of G.

An intuitionistic fuzzy set A in V is formulated by

$$A = \{ (v,\mu_{A} (v),\eta_{A} (v)):v \in V\}$$

where functions $\mu_{A} ,\eta_{A} :V \to [0,1]$ represent the degree of membership and degree of non-membership of the elements v in V and satisfies $\mu_{A} (v) + \eta_{A} (v) \le 1$ for any $v \in V$. Moreover, value $\pi_{A} (v) = 1 - (\mu_{A} (v) + \eta_{A} (v))$ is called the intuitionistic fuzzy set index or hesitation margin of v in A, where $\pi_{A} (v)$ is the degree of indeterminacy of v in the intuitionistic fuzzy set.

The intuitionistic fuzzy relation $R$ on the set $X \times Y$ is an intuitionistic fuzzy set with the following version:

$$R = \{ ((x,y),\mu_{R} (x,y),\eta_{R} (x,y))|(x,y) \in X \times Y\}$$

where $\mu_{R} ,\eta_{R} :X \times Y \to [0,1]$ which satisfies $\mu_{R} (x,y) + \eta_{R} (x,y) \le 1$ for any $(x,y) \in X \times Y$. Atanassov and Gargov [40] introduced the operation on intuitionistic fuzzy variables.

Shannon and Atanassov [41] and [42] introduced intuitionistic fuzzy graph as $G = (V,A,B)$, where $A = (V,\mu_{A} ,\eta_{A} )$ is an intuitionistic fuzzy set on vertex set V, $B = (V \times V,\mu_{B} ,\eta_{B} )$ is an intuitionistic fuzzy set on $V \times V$ such that $\mu_{B} (v,{v^{\prime}}) \le \mu_{A} (v) \wedge \mu_{A} ({v^{\prime}})$, $\eta_{B} (v,{v^{\prime}}) \le \eta_{A} (v) \vee \eta_{A} ({v^{\prime}})$ and the property $\mu_{B} (v,{v^{\prime}}) + \eta_{B} (v,{v^{\prime}}) \le 1$ holds for any $v,{v^{\prime}} \in V$. Note that an intuitionistic fuzzy graph can be re-written as $G = (V,E)$, where $E = (V \times V,\mu ,\eta )$ is intuitionistic fuzzy edges with $\mu (v,{v^{\prime}}) + \eta (v,{v^{\prime}}) \le 1$ holds for any $v,{v^{\prime}} \in V.$

Ezhilmaran and Sankar [43] introduced bipolar intuitionistic fuzzy set and bipolar intuitionistic fuzzy graph. A bipolar intuitionistic fuzzy set on universal set V is denoted by

$$A = \{ (v,\mu_{A}^{P} (v),\mu_{A}^{N} (v),\eta_{A}^{P} (v),\eta_{A}^{N} (v)):v \in V\}$$

where the positive membership degree $\mu_{A}^{P} :V \to [0,1]$ expresses the satisfaction degree of element v to the property corresponding to a bipolar intuitionistic fuzzy set A; the negative membership degree $\mu_{A}^{N} :V \to [ - 1,0]$ denotes the satisfaction degree of an element v to the certain implicit counter property corresponding to a bipolar intuitionistic fuzzy set; the positive non-membership degree $\eta_{A}^{P} :V \to [0,1]$ is used to imply the satisfaction degree of v to the property corresponding to A; the negative non-membership degree $\eta_{A}^{N} :V \to [ - 1,0]$ denotes the satisfaction degree of v to certain implicit counter property corresponding to a bipolar intuitionistic fuzzy set A. Furthermore, we have $0 \le \mu_{A}^{P} (v) + \eta_{A}^{P} (v) \le 1$ and $- 1 \le \mu_{A}^{N} (v) + \eta_{A}^{N} (v) \le 0$ for any $v \in V$. A mapping $B = (\mu_{B}^{P} ,\mu_{B}^{N} ,\eta_{B}^{P} ,\eta_{B}^{N} ):V \times V \to ([0,1] \times [ - 1,0] \times [0,1] \times [ - 1,0])$ a bipolar intuitionistic fuzzy relation such that $\mu_{B}^{P} (v,{v^{\prime}}) \in [0,1]$, $\mu_{B}^{N} (v,{v^{\prime}}) \in [ - 1,0]$, $\eta_{B}^{P} (v,{v^{\prime}}) \in [0,1]$ and $\eta_{B}^{N} (v,{v^{\prime}}) \in [ - 1,0]$ (there are all symmetric functions).

A bipolar intuitionistic fuzzy graph $G = (V,A,B)$ with $A = (\mu_{A}^{P} ,\mu_{A}^{N} ,\eta_{A}^{P} ,\eta_{A}^{N} )$ and $B = (\mu_{B}^{P} ,\mu_{B}^{N} ,\eta_{B}^{P} ,\eta_{B}^{N} )$ is a bipolar intuitionistic fuzzy relation such that

$$\mu_{B}^{P} (v,{v^{\prime}}) \le \mu_{A}^{P} (v) \wedge \mu_{A}^{P} ({v^{\prime}}), \quad \mu_{B}^{N} (v,{v^{\prime}}) \ge \mu_{A}^{N} (v) \vee \mu_{A}^{N} ({v^{\prime}}), \quad \eta_{B}^{P} (v,{v^{\prime}}) \ge \eta_{A}^{P} (v) \vee \eta_{A}^{P} ({v^{\prime}}) , \quad \eta_{B}^{N} (v,{v^{\prime}}) \le \eta_{A}^{N} (v) \wedge \eta_{A}^{N} ({v^{\prime}}),$$

$\mu_{B}^{P} (v,{v^{\prime}}) + \eta_{B}^{P} (v,{v^{\prime}}) \le 1$ and $\mu_{B}^{N} (v,{v^{\prime}}) + \eta_{B}^{N} (v,{v^{\prime}}) \ge - 1$ for any $(v,{v^{\prime}}) \in V \times V$, and $\mu_{B}^{P} (v,{v^{\prime}}) = \mu_{B}^{N} (v,{v^{\prime}}) = 0,\eta_{B}^{P} (v,{v^{\prime}}) = 1,\eta_{B}^{N} (v,{v^{\prime}}) = - 1$ for any $(v,{v^{\prime}}) \in V \times V - E$. Based on these definitions, Sankar and Ezhilmaran [44] introduced more concepts on bipolar intuitionistic fuzzy graphs, and Alnaser et al. [45] defined the concepts of incidence intuitionistic bipolar fuzzy matrix and line intuitionistic bipolar fuzzy graph.

3 Dominating Set and Domination Number of Fuzzy Graphs

Recall that in classical graph setting, dominating set D is a subset of V such that for any $x \in V - D$, there is a vertex $y \in D$ satisfying $xy \in E$. Accordingly, the domination number of G is denoted by $\gamma (G)$ which is the minimum cardinality of all dominating sets of G. When it comes to the fuzzy graphs, the definition of dominating set is determined by the various definition of fuzzy edges. In this section, we aim to extend these domination related concepts to bipolar fuzzy graph settings.

3.1 Effective Edge-Based Domination in Bipolar Fuzzy Graphs

In fuzzy graph $G = (V,A,B)$, the edge vv' is called effective if $\mu_{B} (v,{v^{\prime}}) = \mu_{A} (v) \wedge \mu_{A} ({v^{\prime}})$. Then, a fuzzy graph G is strong if all edges in E are effective, and G is complete if for all $v,{v^{\prime}} \in V$, we have $\mu_{B} (v,{v^{\prime}}) = \mu_{A} (v) \wedge \mu_{A} ({v^{\prime}})$. Somasundaram and Somasundaram [46] introduced the domination of fuzzy graphs in terms of effective edges, that is, $D \subseteq V$ is a dominating set of G if for every $v \in V - D$, there is a ${v^{\prime}} \in D$ such that $v{v^{\prime}}$ is an effective edge. The domination number of fuzzy graph G is the minimum fuzzy cardinality of dominating sets. Formally,

$$\gamma (G) = \min \left\{ \sum\limits_{v \in D} {\mu_{A} (v)} |D{\text{ is a dominating set}}\right\}.$$

In bipolar graph setting, the edge vv' is called effective if $\mu_{B}^{P} (v,{v^{\prime}}) = \mu_{A}^{P} (v) \wedge \mu_{A}^{P} ({v^{\prime}})$ or $\mu_{B}^{N} (v,{v^{\prime}}) = \mu_{A}^{N} (v) \vee \mu_{A}^{N} ({v^{\prime}})$ (Here, we need explain more. According to the revised definitions on bipolar fuzzy graphs by Poulik and Ghorai [38], the neighborhood-related concepts only need one membership function hold, for example, the open neighborhood of a vertex v inquires one of its positive relation membership value and negative relation membership value not equal to zero, which is not necessary to satisfy both of them not equal to zero. Similarly, here for effective edge in bipolar graph, it is sufficient only one of $\mu_{B}^{P} (v,{v^{\prime}}) = \mu_{A}^{P} (v) \wedge \mu_{A}^{P} ({v^{\prime}})$ and $\mu_{B}^{N} (v,{v^{\prime}}) = \mu_{A}^{N} (v) \vee \mu_{A}^{N} ({v^{\prime}})$ to be satisfied). Then, a bipolar fuzzy graph G is strong if all edges in E are effective, and G is complete if for all $v,{v^{\prime}} \in V$, we have $\mu_{B}^{P} (v,{v^{\prime}}) = \mu_{A}^{P} (v) \wedge \mu_{A}^{P} ({v^{\prime}})$ or $\mu_{B}^{N} (v,{v^{\prime}}) = \mu_{A}^{N} (v) \vee \mu_{A}^{N} ({v^{\prime}})$. $D \subseteq V$ is a dominating set of bipolar fuzzy G if for every $v \in V - D$, there is a ${v^{\prime}} \in D$ such that $v{v^{\prime}}$ is an effective edge. We call this kind of dominating set as the first class dominating set of bipolar fuzzy graph. The domination number of bipolar fuzzy graph G is formulated by

$$\gamma_{1} (G) = \min \left\{ \sum\limits_{v \in D} {\mu_{A}^{P} (v)} + \left| {\sum\limits_{v \in D} {\mu_{A}^{N} (v)} } \right||D{\text{ is a first class dominating set}}\right\} .$$

We call $\gamma_{1} (G)$ the first class of domination number of bipolar fuzzy graph.

3.2 Valid Edge-Based Domination in Bipolar Fuzzy Graphs

In terms of neighborhood definitions by Poulik and Ghorai [38], we introduce the bipolar fuzzy bipartite graph. A bipolar fuzzy graph $G = (V,A,B)$ is said to be bipartite if its vertex set V can be partitioned into two non-empty sets $V_{1}$ and $V_{2}$ such that $\mu_{B}^{P} (v,{v^{\prime}}) = \mu_{B}^{N} (v,{v^{\prime}}) = 0$ if $v,{v^{\prime}} \in V_{1}$ or $v,{v^{\prime}} \in V_{2}$. If $\mu_{B}^{P} (v,{v^{\prime}}) = \mu_{A}^{P} (v) \wedge \mu_{A}^{P} ({v^{\prime}})$ and $\mu_{B}^{N} (v,{v^{\prime}}) = \mu_{A}^{N} (v) \vee \mu_{A}^{N} ({v^{\prime}})$ for any $v \in V_{1}$ and ${v^{\prime}} \in V_{2}$, then G is called complete bipolar fuzzy bipartite graph.

For a fuzzy graph $G = (V,A,B)$, Afsharmanesh and Borzooei [47] introduced the validity of edge $uv \in E$ by

$$I(v,{v^{\prime}}) = \frac{{\mu_{B} (v,{v^{\prime}})}}{{\mu_{A} (v) \wedge \mu_{A} ({v^{\prime}})}} .$$

(Note that in some literatures (see Samanta et al. [48], and Mahapatra et al. [49] and [50]) on the coloring of fuzzy graph, the above formulation is called the strength of edge.) The edge $uv$ is valid if $I(v,{v^{\prime}}) \ge \frac{1}{2}$, and otherwise call invalid. Furthermore, valid edge-based domination concepts are defined by Afsharmanesh and Borzooei [47]: $D \subseteq V$ is a dominating set of G if for every $v \in V - D$, there is a ${v^{\prime}} \in D$ such that $v{v^{\prime}}$ is a valid edge. The domination number of fuzzy graph G is the minimum fuzzy cardinality of valid edge-based dominating sets.

Now, we extend it in bipolar fuzzy setting. The validity of edge $uv \in E$ in bipolar graph G is denoted by

$$I(v,{v^{\prime}}) = (I^{P} (v,{v^{\prime}}),I^{N} (v,{v^{\prime}})) = (\frac{{\mu_{B}^{P} (v,{v^{\prime}})}}{{\mu_{A}^{P} (v) \wedge \mu_{A}^{P} ({v^{\prime}})}},\frac{{\mu_{B}^{N} (v,{v^{\prime}})}}{{\mu_{A}^{N} (v) \vee \mu_{A}^{N} ({v^{\prime}})}}) .$$

The edge $uv$ is valid if $I^{P} (v,{v^{\prime}}) \ge \frac{1}{2}$ or $I^{N} (v,{v^{\prime}}) \ge \frac{1}{2}$, and otherwise call invalid. $D \subseteq V$ is a dominating set of bipolar fuzzy G if for every $v \in V - D$, there is a ${v^{\prime}} \in D$ such that $v{v^{\prime}}$ is a valid edge. We call this kind of dominating set as the second-class dominating set of bipolar fuzzy graph. The domination number of bipolar fuzzy graph G is formulated by

$\gamma_{2} (G) = \min \left\{ \sum\limits_{v \in D} {\mu_{A}^{P} (v)} + \left| {\sum\limits_{v \in D} {\mu_{A}^{N} (v)} } \right||D{\text{ is a second class dominating set}}\right\},$.

We call $\gamma_{2} (G)$ the second class of domination number of bipolar fuzzy graph.

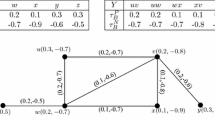
Example 1. Let $G = (V,A,B)$ be a bipolar fuzzy graph with $V = \{ v_{1} ,v_{2} ,v_{3} ,v_{4} ,v_{5} \}$ and $E = \{ v_{1} v_{2} ,v_{2} v_{3} ,v_{3} v_{4} ,v_{4} v_{5} ,v_{5} v_{1} ,v_{2} v_{4} \}$. The values of membership function are presented in Fig. 1, and by simple computing, we confirm that $v_{1} v_{5} ,v_{2} v_{3} ,v_{3} v_{4} ,v_{4} v_{2}$ are valid edges, $v_{1} v_{2} ,v_{4} v_{5}$ are invalid. The critical dominating sets (a dominating set D is critical if deleting any vertex v from D, $D - \{ v\}$ is not a dominating set) are $D_{1} = \{ v_{1} ,v_{2} \}$, $D_{2} = \{ v_{1} ,v_{3} \}$, $D_{3} = \{ v_{1} ,v_{4} \}$, $D_{4} = \{ v_{5} ,v_{2} \}$, $D_{5} = \{ v_{5} ,v_{3} \}$, $D_{6} = \{ v_{5} ,v_{4} \}$.

Fig. 1

A bipolar fuzzy graph and its valid edges

In light of their membership function values, we get

$$\sum\limits_{{v \in D_{1} }} {\mu_{A}^{P} (v)} + \left| {\sum\limits_{{v \in D_{1} }} {\mu_{A}^{N} (v)} } \right| = 1.1,$$

$$\sum\limits_{{v \in D_{2} }} {\mu_{A}^{P} (v)} + \left| {\sum\limits_{{v \in D_{2} }} {\mu_{A}^{N} (v)} } \right| = 1.8,$$

$$\sum\limits_{{v \in D_{3} }} {\mu_{A}^{P} (v)} + \left| {\sum\limits_{{v \in D_{3} }} {\mu_{A}^{N} (v)} } \right| = 1.4,$$

$$\sum\limits_{{v \in D_{4} }} {\mu_{A}^{P} (v)} + \left| {\sum\limits_{{v \in D_{4} }} {\mu_{A}^{N} (v)} } \right| = 1.7,$$

$$\sum\limits_{{v \in D_{5} }} {\mu_{A}^{P} (v)} + \left| {\sum\limits_{{v \in D_{5} }} {\mu_{A}^{N} (v)} } \right| = 2.4,$$

$$\sum\limits_{{v \in D_{6} }} {\mu_{A}^{P} (v)} + \left| {\sum\limits_{{v \in D_{6} }} {\mu_{A}^{N} (v)} } \right| = 2.$$

Therefore, we check that $D_{1} = \{ v_{1} ,v_{2} \}$ is the minimum dominating set and $\gamma_{2} (G) = 1.1$.

For a bipolar fuzzy graph G, if G is complete, then any vertex is a dominating set, and thus $\gamma_{2} (G) = \min \{ \mu_{A}^{P} (v) + \left| {\mu_{A}^{N} (v)} \right||v \in V\}$. On the contrary, if all the edges in G are invalid, then the unique dominating set contains all vertices and $\gamma_{2} (G) = \sum\limits_{v \in V} {(\mu_{A}^{P} (v) + \left| {\mu_{A}^{N} (v)} \right|)}$. Moreover, if G is a complete bipolar fuzzy bipartite graph, then we have (it vertex set partitioned into $V_{1}$ and $V_{2}$)

$$\gamma_{2} (G) = \min \{ \sum\limits_{{v \in V_{1} }} {(\mu_{A}^{P} (v) + \left| {\mu_{A}^{N} (v)} \right|)} ,\sum\limits_{{v \in V_{2} }} {(\mu_{A}^{P} (v) + \left| {\mu_{A}^{N} (v)} \right|)} ,$$

$\mathop {\min }\nolimits_{{v \in V_{1} }} (\mu_{A}^{P} (v) + \left| {\mu_{A}^{N} (v)} \right|) + \mathop {\min }\nolimits_{{v \in V_{2} }} (\mu_{A}^{P} (v) + \left| {\mu_{A}^{N} (v)} \right|)\}.$.

3.3 Valid Edge-Based Domination Set in Bipolar Fuzzy Incidence Graphs

For a fuzzy incidence graph $G = (\eta ,\theta ,\Psi )$, the pair $(v,e)$ is effective if $\Psi (v,e) = \eta (v) \wedge \theta (e)$, and G is complete if all edges are effective. Afsharmanesh and Borzooei [47] contributed in the following concepts. The incidence edge $v{v^{\prime}}$ of G is an incidence valid edge if $I(v,{v^{\prime}}) = \frac{\theta (v{v^{\prime}})}{{\eta (v) \wedge \eta ({v^{\prime}})}} \ge \frac{1}{2}$, $\Psi (v,v{v^{\prime}}) \ge \frac{\theta (v{v^{\prime}})}{2}$ and $\Psi ({v^{\prime}},{v^{\prime}}v) \ge \frac{\theta (v{v^{\prime}})}{2}$. Otherwise, it is called an incidence invalid edge. The open incidence valid neighborhood of vertex $v \in V$ is denoted by

$$N_{{IV}} (v) = \{ v^{\prime } \in V|vv^{\prime } \,{\text{is}}\,{\text{an}}\,{\text{incidence}}\,{\text{valid}}\;{\text{edge}}\} .$$

Accordingly, the close incidence valid neighborhood of vertex $v \in V$ is $N_{{{\text{IV}}}} [v] = N_{{{\text{IV}}}} (v) \cup \{ v\}$. For $\emptyset \ne D \subseteq V$, $N_{{{\text{IV}}}} (D) = \sum\nolimits_{v \in D} {N_{{{\text{IV}}}} (v)}$ and $N_{{{\text{IV}}}} [D] = N_{{{\text{IV}}}} (D) \cup D$. The incidence valid neighborhood degree of vertex v is denoted by $\sum\nolimits_{{{v^{\prime}} \in N_{{{\text{IV}}}} (v)}} {\eta ({v^{\prime}})}$. $D \subseteq V$ is an incidence dominating set of G if for every $v \in V - D$, there is a ${v^{\prime}} \in D$ such that $v{v^{\prime}}$ is an incidence valid edge. The domination number of fuzzy incidence graph G is the minimum fuzzy cardinality of incidence valid edge-based incidence dominating sets.

Next, we extend the concepts to bipolar setting. Let $G = (\eta^{P} ,\eta^{N} ,\theta^{P} ,\theta^{N} ,\Psi^{P} ,\Psi^{N} )$ be a bipolar fuzzy incidence graph. The pair $(v,e)$ is effective if $\Psi^{P} (v,e) = \eta^{P} (v) \wedge \theta^{P} (e)$ and $\Psi^{N} (v,e) = \eta^{N} (v) \vee \theta^{N} (e)$, and G is said to be complete if all edges are effective. The incidence edge $v{v^{\prime}}$ of bipolar fuzzy incidence graph G is an incidence valid edge if (i)$I^{P} (v,{v^{\prime}}) = \frac{{\theta^{P} (v{v^{\prime}})}}{{\eta^{P} (v) \wedge \eta^{P} ({v^{\prime}})}} \ge \frac{1}{2}$, $\Psi^{P} (v,v{v^{\prime}}) \ge \frac{{\theta^{P} (v{v^{\prime}})}}{2}$, $\Psi^{P} ({v^{\prime}},{v^{\prime}}v) \ge \frac{{\theta^{P} (v{v^{\prime}})}}{2}$; or (ii)$I^{N} (v,{v^{\prime}}) = \frac{{\theta^{N} (v{v^{\prime}})}}{{\eta^{N} (v) \vee \eta^{N} ({v^{\prime}})}} \ge \frac{1}{2}$, $\Psi^{N} (v,v{v^{\prime}}) \le \frac{{\theta^{N} (v{v^{\prime}})}}{2}$, $\Psi^{N} ({v^{\prime}},{v^{\prime}}v) \le \frac{{\theta^{N} (v{v^{\prime}})}}{2}$. Otherwise, it is called a bipolar incidence invalid edge. The open bipolar incidence valid neighborhood of vertex $v \in V$ is denoted by

$$N_{\text{BIV}} (v) = \{ v^{\prime } \in V|vv^{\prime } \;{\text{is}}\;{\text{a}}\;{\text{bipolar}}\;{\text{incidence}}\;{\text{valid}}\;{\text{edge}}\} .$$

Accordingly, the close bipolar incidence valid neighborhood of vertex $v \in V$ is denoted by $N_{{{\text{BIV}}}} [v] = N_{{{\text{BIV}}}} (v) \cup \{ v\}$. For $\emptyset \ne D \subseteq V$, $N_{{{\text{BIV}}}} (D) = \sum\nolimits_{v \in D} {N_{{{\text{BIV}}}} (v)}$ and $N_{{{\text{BIV}}}} [D] = N_{{{\text{BIV}}}} (D) \cup D$. The bipolar incidence valid neighborhood degree of vertex v is denoted by $\sum\nolimits_{{{v^{\prime}} \in N_{{{\text{BIV}}}} (v)}} {\eta ({v^{\prime}})}$. $D \subseteq V$ is a bipolar incidence dominating set of G if for every $v \in V - D$, there is a ${v^{\prime}} \in D$ such that $v{v^{\prime}}$ is a bipolar incidence valid edge. The domination number of bipolar fuzzy incidence graph G is formulated by.

$\gamma_{{{\text{BI}}}} (G) = \min \{ \sum\nolimits_{v \in D} {\eta^{P} (v)} + \left| {\sum\nolimits_{v \in D} {\eta^{N} (v)} } \right||D{\text{ is a bipolar incidence dominating set}}\}$.

Clearly, if G is a complete bipolar fuzzy incidence graph, then $\gamma_{{{\text{BI}}}} (G) = \mathop {\min }\nolimits_{v \in V} \{ \eta^{P} (v) + \left| {\eta^{N} (v)} \right||$.

Example 2.

A bipolar fuzzy incidence graph G is presented in Fig. 2. It is shown that $V = \{ v_{1} ,v_{2} ,v_{3} ,v_{4} ,v_{5} ,v_{6} \}$, $E = \{ v_{1} v_{2} ,v_{2} v_{3} ,v_{3} v_{4} ,v_{4} v_{1} ,v_{5} v_{1} ,v_{5} v_{4} ,v_{5} v_{6} ,v_{6} v_{2} ,v_{6} v_{3} \}$, $\eta^{P} (v_{1} ) = 0.8$, $\eta^{N} (v_{1} ) = - 0.9$, $\eta^{P} (v_{2} ) = 0.6$, $\eta^{N} (v_{2} ) = - 0.5$, $\eta^{P} (v_{3} ) = 0.4$, $\eta^{N} (v_{3} ) = - 0.4$, $\eta^{P} (v_{4} ) = 0.7$, $\eta^{N} (v_{4} ) = - 0.6$, $\eta^{P} (v_{5} ) = 0.9$, $\eta^{N} (v_{5} ) = - 0.7$, $\eta^{P} (v_{6} ) = 0.4$, $\eta^{N} (v_{6} ) = - 0.5$, $\theta^{P} (v_{1} v_{2} ) = 0.6$, $\theta^{N} (v_{1} v_{2} ) = - 0.5$, $\theta^{P} (v_{2} v_{3} ) = 0.4$, $\theta^{N} (v_{2} v_{3} ) = - 0.2$, $\theta^{P} (v_{3} v_{4} ) = 0.4$, $\theta^{N} (v_{3} v_{4} ) = - 0.4$, $\theta^{P} (v_{4} v_{1} ) = 0.6$, $\theta^{N} (v_{4} v_{1} ) = - 0.6$, $\theta^{P} (v_{5} v_{1} ) = 0.8$, $\theta^{N} (v_{5} v_{1} ) = - 0.6$, $\theta^{P} (v_{5} v_{4} ) = 0.7$, $\theta^{N} (v_{5} v_{4} ) = - 0.6$, $\theta^{P} (v_{5} v_{6} ) = 0.3$, $\theta^{N} (v_{5} v_{6} ) = - 0.3$, $\theta^{P} (v_{6} v_{2} ) = 0.4$, $\theta^{N} (v_{6} v_{2} ) = - 0.3$, $\theta^{P} (v_{6} v_{3} ) = 0.4$, $\theta^{N} (v_{6} v_{3} ) = - 0.3$,

Fig. 2

A bipolar fuzzy incidence graph

$\Psi^{P} (v_{1} ,v_{1} v_{2} ) = 0.5$, $\Psi^{N} (v_{1} ,v_{1} v_{2} ) = - 0.5$, $\Psi^{P} (v_{2} ,v_{2} v_{1} ) = 0.4$, $\Psi^{N} (v_{2} ,v_{2} v_{1} ) = - 0.3$,

$\Psi^{P} (v_{2} ,v_{2} v_{3} ) = 0.3$, $\Psi^{N} (v_{2} ,v_{2} v_{3} ) = - 0.2$, $\Psi^{P} (v_{3} ,v_{3} v_{2} ) = 0.1$, $\Psi^{N} (v_{3} ,v_{3} v_{2} ) = - 0.1$, $\Psi^{P} (v_{3} ,v_{3} v_{4} ) = 0.2$, $\Psi^{N} (v_{3} ,v_{3} v_{4} ) = - 0.1$, $\Psi^{P} (v_{4} ,v_{4} v_{3} ) = 0.3$, $\Psi^{N} (v_{4} ,v_{4} v_{3} ) = - 0.4$, $\Psi^{P} (v_{4} ,v_{4} v_{1} ) = 0.4$, $\Psi^{N} (v_{4} ,v_{4} v_{1} ) = - 0.5$, $\Psi^{P} (v_{1} ,v_{1} v_{4} ) = 0.5$, $\Psi^{N} (v_{1} ,v_{1} v_{4} ) = - 0.5$, $\Psi^{P} (v_{5} ,v_{5} v_{1} ) = 0.3$, $\Psi^{N} (v_{5} ,v_{5} v_{1} ) = - 0.1$, $\Psi^{P} (v_{1} ,v_{1} v_{5} ) = 0.2$, $\Psi^{N} (v_{1} ,v_{1} v_{5} ) = - 0.2$, $\Psi^{P} (v_{5} ,v_{5} v_{4} ) = 0.5$, $\Psi^{N} (v_{5} ,v_{5} v_{4} ) = - 0.6$, $\Psi^{P} (v_{4} ,v_{4} v_{5} ) = 0.6$, $\Psi^{N} (v_{4} ,v_{4} v_{5} ) = - 0.6$,

$\Psi^{P} (v_{5} ,v_{5} v_{6} ) = 0.1$, $\Psi^{N} (v_{5} ,v_{5} v_{6} ) = - 0.1$, $\Psi^{P} (v_{6} ,v_{6} v_{5} ) = 0.1$, $\Psi^{N} (v_{6} ,v_{6} v_{5} ) = - 0.1$, $\Psi^{P} (v_{6} ,v_{6} v_{2} ) = 0.1$, $\Psi^{N} (v_{6} ,v_{6} v_{2} ) = - 0.2$, $\Psi^{P} (v_{2} ,v_{2} v_{6} ) = 0.1$, $\Psi^{N} (v_{2} ,v_{2} v_{6} ) = - 0.1$,

$\Psi^{P} (v_{6} ,v_{6} v_{3} ) = 0.3$, $\Psi^{N} (v_{6} ,v_{6} v_{3} ) = - 0.2$, $\Psi^{P} (v_{3} ,v_{3} v_{6} ) = 0.2$, and $\Psi^{N} (v_{3} ,v_{3} v_{6} ) = - 0.1$.

By the definition of bipolar incidence valid edge, we infer that $v_{1} v_{2} ,v_{2} v_{3} ,v_{3} v_{4} ,v_{4} v_{1} ,v_{5} v_{4} ,v_{6} v_{3}$ are incidence valid edges and $v_{5} v_{1} ,v_{5} v_{6} ,v_{6} v_{2}$ are bipolar incidence invalid edges. Thus, all the critical bipolar incidence dominating sets (a bipolar incidence dominating set D is critical if deleting any vertex v from D, $D - \{ v\}$ is not a bipolar incidence dominating set) are $D_{1} = \{ v_{1} ,v_{3} ,v_{5} \}$, $D_{1} = \{ v_{1} ,v_{5} ,v_{6} \}$, $D_{3} = \{ v_{2} ,v_{4} ,v_{6} \}$, $D_{4} = \{ v_{2} ,v_{5} ,v_{6} \}$, and furthermore.

$\sum\nolimits_{{v \in D_{1} }} {\eta^{P} (v)} + \left| {\sum\nolimits_{{v \in D_{1} }} {\eta^{N} (v)} } \right| = 4.1$,

$\sum\nolimits_{{v \in D_{2} }} {\eta^{P} (v)} + \left| {\sum\nolimits_{{v \in D_{2} }} {\eta^{N} (v)} } \right| = 4.2$,

$\sum\nolimits_{{v \in D_{3} }} {\eta^{P} (v)} + \left| {\sum\nolimits_{{v \in D_{3} }} {\eta^{N} (v)} } \right| = 3.3$,

$\sum\nolimits_{{v \in D_{4} }} {\eta^{P} (v)} + \left| {\sum\nolimits_{{v \in D_{4} }} {\eta^{N} (v)} } \right| = 3.6$.

Therefore, we conclude that $\gamma_{{{\text{BI}}}} (G) = 3.3$.

Theorem 1.

Let $G = (\eta^{P} ,\eta^{N} ,\theta^{P} ,\theta^{N} ,\Psi^{P} ,\Psi^{N} )$ be a bipolar fuzzy incidence graph. Then,

$\gamma_{{{\text{BI}}}} (G) \le \sum\nolimits_{v \in V} {(\eta^{P} (v) + \left| {\eta^{N} (v)} \right|)} - \mathop {\max }\nolimits_{v \in V} \{ \sum\nolimits_{{{v^{\prime}} \in N_{{{\text{BIV}}}} (v)}} {(\eta^{P} ({v^{\prime}}) + \left| {\eta^{N} ({v^{\prime}})} \right|)} \}.$

Proof.

The result follows from the fact that for any $v \in V$, $V - N_{{{\text{BIV}}}} (v)$ is a bipolar incidence dominating set of G.

A vertex $v \in V$ in a bipolar fuzzy incidence graph G is called an isolated vertex if $N_{{{\text{BIV}}}} (v) = \emptyset$. For a given vertex subset $S \subseteq V$, we say $v \in S$ is an isolated vertex in S if $N_{{{\text{BIV}}}} (v) \cap S = \emptyset$. All vertices in V are isolated $\Leftrightarrow \gamma_{{{\text{BI}}}} (G) = \sum\nolimits_{v \in V} {(\eta^{P} (v) + \left| {\eta^{N} (v)} \right|)}$. On the contrary, if G has no isolated vertex, then $\gamma_{{{\text{BI}}}} (G) \le \frac{{\sum\nolimits_{v \in V} {(\eta^{P} (v) + \left| {\eta^{N} (v)} \right|)} }}{2}$. In addition, the characteristics of critical bipolar incidence dominating set can be stated in the following theorem (an extension of Theorem 3.27 and Theorem 3.28 in Afsharmanesh and Borzooei [47]).

Theorem 2.

A bipolar incidence dominating set D in bipolar fuzzy incidence graph G. We have the following facts.

• D is critical if and only if for arbitrary $v \in D$, v is isolated in D or there is ${v^{\prime}} \in V - D$ satisfying $N_{{{\text{BIV}}}} ({v^{\prime}}) \cap S = \{ v\}$.

• If D is critical and G has no isolated vertices, then $V - D$ is a bipolar incidence dominating set.

A vertex subset $I \subseteq V$ is called a bipolar incidence independence set if there is no bipolar incidence valid edge between any two vertices in I, i.e., for any $v \in I$, v is a isolated vertex in I. A bipolar incidence independent set I of bipolar fuzzy incidence graph G is maximal if for any $v \in V - I$, the set $I \cup \{ v\}$ is not bipolar incidence independent.

Theorem 3.

Let $G = (\eta^{P} ,\eta^{N} ,\theta^{P} ,\theta^{N} ,\Psi^{P} ,\Psi^{N} )$ be a bipolar fuzzy incidence graph. $I \subseteq V$ is a maximal bipolar incidence independence set if and only if I is a critical bipolar incident dominating set. Furthermore, we have $\gamma_{{{\text{BI}}}} (G) = \min \{ \sum\nolimits_{v \in I} {\eta^{P} (v)} + \left| {\sum\nolimits_{v \in I} {\eta^{N} (v)} } \right||I{\text{ is a maximal bipolar incidence independence set}}\}.$

Let $G = (\eta^{P} ,\eta^{N} ,\theta^{P} ,\theta^{N} ,\Psi^{P} ,\Psi^{N} )$ be a bipolar fuzzy incidence graph, S be a non-empty subset of its vertex set and $u \in S$. The vertex v is a bipolar incidence valid private neighbor of u w.r.t. S if $N_{{{\text{BIV}}}} [v] \cap S = \{ u\}$. Denote

$$BIPN_{{{\text{BIV}}}} (u,S) = \,N_{{{\text{BIV}}}} [u] - \bigcup\nolimits_{{v \in S\backslash \{ u\} }} {N_{{{\text{BIV}}}} [v]} = N_{{{\text{BIV}}}} [u] - N_{{{\text{BIV}}}} [S - \{ u\} ]$$

by the bipolar valid private neighbor set of u w.r.t. S. Clearly, u is an isolated vertex in G[S] if $u \in BIPN_{{{\text{BIV}}}} (u,S)$. If $BIPN_{{{\text{BIV}}}} (u,S) \ne \emptyset$ for any $u \in S$, then S is a bipolar incidence irredundant set. If $S \cup \{ u\}$ is not a bipolar incidence irredundant set for any $u \in V\backslash S$, then S is a maximal bipolar incidence irredundant set. The bipolar incidence irredundance number is denoted by.

$i\gamma_{{{\text{BI}}}} (G) = \min \{ \sum\nolimits_{v \in I} {\eta^{P} (v)} + \left| {\sum\nolimits_{v \in I} {\eta^{N} (v)} } \right||I{\text{ is a maximal bipolar incidence irredundant set}}\}.$

Moreover, the upper bipolar incidence irredundance number is denoted by

$I\gamma_{{{\text{BI}}}} (G) = \max \{ \sum\nolimits_{v \in I} {\eta^{P} (v)} + \left| {\sum\nolimits_{v \in I} {\eta^{N} (v)} } \right||I{\text{ is a maximal bipolar incidence irredundant set}}\}$.

The following conclusion can be viewed as the extension of Theorem 3.35 and Theorem 3.36 in Afsharmanesh and Borzooei [47], and we skip the detailed proof.

Theorem 4. A bipolar incidence dominating set in the bipolar fuzzy incidence graph is a minimal bipolar incidence dominating set if and only if it is a bipolar incidence irredundant set. Furthermore, any minimal bipolar incidence dominating set in the bipolar fuzzy incidence graph G is a maximal bipolar incidence irredundant set in G.

3.4 Domination in Bipolar Intuitionistic Fuzzy Graphs

Bozhenyuk et al. [23] introduced the domination set of intuitionistic fuzzy graph, and let us review this trick first. Let $G = (V,A,B)$ be an intuitionistic fuzzy graph with $A = (V,\mu_{A} ,\eta_{A} )$ and $B = (V \times V,\mu_{B} ,\eta_{B} )$. A vertex subset $X \subseteq V$ is an intuitionistic dominating vertex set of G with the intuitionistic degree of domination.

$\beta (X) = \mathop \wedge \nolimits_{{v^{\prime}} \in V - X} \mathop \vee \nolimits_{v \in X} (\mu_{B} (v,{v^{\prime}}),\eta_{B} (v,{v^{\prime}}))$,

where the operations $\wedge$ and $\vee$ are specially formulated by

$$(\mu_{B} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B} (v_{1} ,v_{1}^{{\prime}} )) \wedge (\mu_{B} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B} (v_{2} ,v_{2}^{{\prime}} )),$$

$$= (\min\{ \mu_{B} (v_{1} ,v_{1}^{{\prime}} ),\mu_{B} (v_{2} ,v_{2}^{{\prime}} )\} ,\max\{ \eta_{B} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B} (v_{2} ,v_{2}^{{\prime}} )\} ),$$

$= ((\mu_{B} (v_{1} ,v_{1}^{{\prime}} ) \wedge \mu_{B} (v_{2} ,v_{2}^{{\prime}} )),(\eta_{B} (v_{1} ,v_{1}^{{\prime}} ) \vee \eta_{B} (v_{2} ,v_{2}^{{\prime}} ))).$,

$$(\mu_{B} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B} (v_{1} ,v_{1}^{{\prime}} )) \vee (\mu_{B} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B} (v_{2} ,v_{2}^{{\prime}} ))$$

$$= (\max \{ \mu_{B} (v_{1} ,v_{1}^{{\prime}} ),\mu_{B} (v_{2} ,v_{2}^{{\prime}} )\} ,\min \{ \eta_{B} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B} (v_{2} ,v_{2}^{{\prime}} )\} )$$

$= ((\mu_{B} (v_{1} ,v_{1}^{{\prime}} ) \vee \mu_{B} (v_{2} ,v_{2}^{{\prime}} )),(\eta_{B} (v_{1} ,v_{1}^{{\prime}} ) \wedge \eta_{B} (v_{2} ,v_{2}^{{\prime}} )))$.

Assume that $(\mu_{B} (v,v),\eta_{B} (v,v)) = (1,0)$ for any $v \in V$. Hence, the expression $\beta (X)$ can be re-written as.

$\beta (X) = \mathop \wedge \nolimits_{{v^{\prime}} \in V} \mathop \vee \nolimits_{v \in X} (\mu_{B} (v,{v^{\prime}}),\eta_{B} (v,{v^{\prime}}))$.

Assume that $\beta (X_{1} ) = (\mu_{B} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B} (v_{1} ,v_{1}^{{\prime}} ))$ and $\beta (X_{2} ) = (\mu_{B} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B} (v_{2} ,v_{2}^{{\prime}} ))$, then $\beta (X_{1} ) < \beta (X_{2} )$ implies $\mu_{B} (v_{1} ,v_{1}^{{\prime}} ) < \mu_{B} (v_{2} ,v_{2}^{{\prime}} )$ and $\eta_{B} (v_{1} ,v_{1}^{{\prime}} ) > \eta_{B} (v_{2} ,v_{2}^{{\prime}} )$. A subset $X \subseteq V$ is a minimal intuitionistic dominating vertex subset with degree $\beta (X)$ if $\beta (X^{\prime}) < \beta (X)$ for any subset $X^{\prime} \subseteq X$. Let $Y_{k} = \{ X_{k1} ,X_{k2} , \cdots ,X_{kl} \}$ be the family of all minimal intuitionistic dominating vertex subset with k vertices, $\beta (X_{ki} ) = \beta_{ki}$ for $i = 1, \cdots ,l$ and $\beta_{k}^{0} = \mathop \vee \nolimits_{i = 1, \cdots ,l} \beta_{ki}$. Then, an intuitionistic fuzzy set $D = \{ (1,\beta_{1}^{0} ),(2,\beta_{2}^{0} ), \cdots ,(n,\beta_{n}^{0} )\}$ is a domination set of intuitionistic fuzzy graph G.

The purpose of this subsection is to extend the Bozhenyuk’s domination set concept to bipolar setting. Let $G = (V,A,B)$ be a bipolar intuitionistic fuzzy graph with $A = (\mu_{A}^{P} ,\mu_{A}^{N} ,\eta_{A}^{P} ,\eta_{A}^{N} )$ and $B = (\mu_{B}^{P} ,\mu_{B}^{N} ,\eta_{B}^{P} ,\eta_{B}^{N} )$. A vertex subset $X \subseteq V$ is a bipolar intuitionistic dominating vertex set of G with the bipolar intuitionistic degree of domination

$\beta (X) = \mathop \wedge \nolimits_{{v^{\prime}} \in V - X} \mathop \vee \nolimits_{v \in X} (\mu_{B}^{P} (v,{v^{\prime}}),\mu_{B}^{N} (v,{v^{\prime}}),\eta_{B}^{P} (v,{v^{\prime}}),\eta_{B}^{N} (v,{v^{\prime}}))$,

where the operations $\wedge$ and $\vee$ are specially formulated by

$$(\mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} )) \wedge (\mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} ),\mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} ))$$

$$= (min\{ \mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )\} ,\max \{ \mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ),\mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )\} ,max\{ \eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )\} ,$$

$$\min \{ \eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )\} )$$

$$= ((\mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) \wedge \mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )),(\mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) \vee \mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )),(\eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) \vee \eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )),$$

$(\eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) \wedge \eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )))$,

$$(\mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} )) \vee (\mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} ),\mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} ))$$

$$= (\max \{ \mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )\} ,\min \{ \mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ),\mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )\} ,\min \{ \eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )\} ,$$

$$\max \{ \eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )\} )$$

$$= ((\mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) \vee \mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )),(\mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) \wedge \mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )),(\eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) \wedge \eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )),$$

$(\eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) \vee \eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )))$.

Assume that $(\mu_{B}^{P} (v,v),\mu_{B}^{N} (v,v),\eta_{B}^{P} (v,v),\eta_{B}^{N} (v,v)) = (1,0,0,1)$ for any $v \in V$. Hence, the expression $\beta (X)$ can be re-stated by

$\beta (X) = \mathop \wedge \nolimits_{{v^{\prime}} \in V} \mathop \vee \nolimits_{v \in X} (\mu_{B}^{P} (v,{v^{\prime}}),\mu_{B}^{N} (v,{v^{\prime}}),\eta_{B}^{P} (v,{v^{\prime}}),\eta_{B}^{N} (v,{v^{\prime}}))$.

Assume that $\beta (X_{1} ) = (\mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ))$ and $\beta (X_{2} ) = (\mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} ),\mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} ))$, then $\beta (X_{1} ) < \beta (X_{2} )$ implies $\mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) < \mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )$, $\mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) > \mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )$, $\eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) > \eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )$ and $\eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) < \eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )$. A subset $X \subseteq V$ is a minimal bipolar intuitionistic dominating vertex subset with degree $\beta (X)$ if $\beta (X^{\prime}) < \beta (X)$ for any subset $X^{\prime} \subset X$. Let $Y_{k} = \{ X_{k1} ,X_{k2} , \cdots ,X_{kl} \}$ be the family of all minimal bipolar intuitionistic dominating vertex subset with k vertices, $\beta (X_{ki} ) = \beta_{ki}$ for $i = 1, \cdots ,l$ and $\beta_{k}^{0} = \mathop \vee \nolimits_{i = 1, \cdots ,l} \beta_{ki}$. Then an intuitionistic fuzzy set $D = \{ (1,\beta_{1}^{0} ),(2,\beta_{2}^{0} ), \cdots ,(n,\beta_{n}^{0} )\}$ is a domination set of bipolar intuitionistic fuzzy graph G.

Let G be a crisp graph (classical graph). We get

$(\mu_{B}^{P} (v,{v^{\prime}}),\mu_{B}^{N} (v,{v^{\prime}}),\eta_{B}^{P} (v,{v^{\prime}}),\eta_{B}^{N} (v,{v^{\prime}})) = \left\{ \begin{gathered} (1, - 1,0,0),{\text{ if }}v{v^{\prime}} \in E \hfill \\ (0,0,1, - 1),{\text{ if }}v{v^{\prime}} \notin E \hfill \\ \end{gathered} \right.$,

$\beta (X) = \left\{ \begin{gathered} (1, - 1,0,0),{\text{ if }}X \subseteq V{\text{ is a dominating set of crisp graph }}G \hfill \\ (0,0,1, - 1),{\text{ otherwise}} \hfill \\ \end{gathered} \right.$.

Example 3.

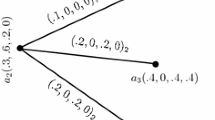
A bipolar intuitionistic fuzzy graph is presented in Fig. 3. If set $X_{1} = \{ v_{1} ,v_{2} \}$, then we have

Fig. 3

A bipolar intuitionistic fuzzy graph

$\mathop \vee \nolimits_{{v \in X_{1} }} (\mu_{B}^{P} (v,v_{3} ),\mu_{B}^{N} (v,v_{3} ),\eta_{B}^{P} (v,v_{3} ),\eta_{B}^{N} (v,v_{3} )) = (0.4, - 0.6,0.4, - 0.4)$,

$\mathop \vee \nolimits_{{v \in X_{1} }} (\mu_{B}^{P} (v,v_{4} ),\mu_{B}^{N} (v,v_{4} ),\eta_{B}^{P} (v,v_{4} ),\eta_{B}^{N} (v,v_{4} )) = (0.2, - 0.3,0.3, - 0.2)$,

$\mathop \vee \nolimits_{{v \in X_{1} }} (\mu_{B}^{P} (v,v_{5} ),\mu_{B}^{N} (v,v_{5} ),\eta_{B}^{P} (v,v_{5} ),\eta_{B}^{N} (v,v_{5} )) = (0.6, - 0.4,0.2, - 0.5)$,

and hence the bipolar intuitionistic degree is $\beta (X_{1} ) = (0.2, - 0.3,0.4, - 0.5)$. If we set $X_{2} = \{ v_{1} \}$ and $X_{3} = \{ v_{2} \}$, then we get $\beta (X_{2} ) = (0,0,1, - 1)$ and $\beta (X_{3} ) = (0,0,1, - 1)$. Clearly, in terms of its definition $X_{1}$, $X_{2}$ and $X_{3}$ are all minimal bipolar intuitionistic dominating vertex subsets.

To determine the bipolar intuitionistic fuzzy set D of bipolar intuitionistic fuzzy graph G, we need compute more intermediate results:

$\beta (\{ v_{1} \} ) = (0,0,1, - 1)$,

$\beta (\{ v_{2} \} ) = (0,0,1, - 1)$,

$\beta (\{ v_{3} \} ) = (0,0,1, - 1)$,

$\beta (\{ v_{4} \} ) = (0,0,1, - 1)$,

$\beta (\{ v_{5} \} ) = (0,0,1, - 1)$,

$\beta (\{ v_{1} ,v_{2} \} ) = (0.2, - 0.3,0.4, - 0.5)$,

$\beta (\{ v_{1} ,v_{3} \} ) = (0,0,1, - 1)$,

$\beta (\{ v_{1} ,v_{4} \} ) = (0,0,1, - 1)$,

$\beta (\{ v_{1} ,v_{5} \} ) = (0.2, - 0.1,0.4, - 0.4)$,

$\beta (\{ v_{2} ,v_{3} \} ) = (0.2, - 0.3,0.4, - 0.5)$,

$\beta (\{ v_{2} ,v_{4} \} ) = (0.2, - 0.3,0.5, - 0.5)$,

$\beta (\{ v_{2} ,v_{5} \} ) = (0.2, - 0.3,0.5, - 0.5)$,

$\beta (\{ v_{3} ,v_{4} \} ) = (0,0,1, - 1)$,

$\beta (\{ v_{3} ,v_{5} \} ) = (0,0,1, - 1)$,

$\beta (\{ v_{4} ,v_{5} \} ) = (0,0,1, - 1)$,

$\beta (\{ v_{3} ,v_{4} ,v_{5} \} ) = (0.4, - 0.4,0.3, - 0.5)$,

$\beta (\{ v_{2} ,v_{4} ,v_{5} \} ) = (0.2, - 0.3,0.5, - 0.5)$,

$\beta (\{ v_{2} ,v_{3} ,v_{5} \} ) = (0.2, - 0.3,0.4, - 0.5)$,

$\beta (\{ v_{2} ,v_{3} ,v_{4} \} ) = (0.4, - 0.4,0.3, - 0.5)$,

$\beta (\{ v_{1} ,v_{4} ,v_{5} \} ) = (0.4, - 0.4,0.4, - 0.4)$,

$\beta (\{ v_{1} ,v_{3} ,v_{5} \} ) = (0.2, - 0.1,0.3, - 0.2)$,

$\beta (\{ v_{1} ,v_{3} ,v_{4} \} ) = (0,0,1, - 1)$,

$\beta (\{ v_{1} ,v_{2} ,v_{5} \} ) = (0.2, - 0.3,0.4, - 0.4)$,

$\beta (\{ v_{1} ,v_{2} ,v_{4} \} ) = (0.4, - 0.4,0.4, - 0.5)$,

$\beta (\{ v_{1} ,v_{2} ,v_{3} \} ) = (0.2, - 0.3,0.3, - 0.5)$,

$\beta (\{ v_{2} ,v_{3} ,v_{4} ,v_{5} \} ) = (0.4, - 0.6,0.3, - 0.2)$,

$\beta (\{ v_{1} ,v_{3} ,v_{4} ,v_{5} \} ) = (0.6, - 0.4,0.2, - 0.2)$,

$\beta (\{ v_{1} ,v_{2} ,v_{4} ,v_{5} \} ) = (0.4, - 0.6,0.4, - 0.4)$,

$\beta (\{ v_{1} ,v_{2} ,v_{3} ,v_{5} \} ) = (0.2, - 0.3,0.3, - 0.2)$,

$\beta (\{ v_{1} ,v_{2} ,v_{3} ,v_{4} \} ) = (0.6, - 0.4,0.2, - 0.5)$,

$\beta (\{ v_{1} ,v_{2} ,v_{3} ,v_{4} ,v_{5} \} ) = (1, - 1,0,0)$.

Thus, the bipolar minimal bipolar intuitionistic dominating vertex subsets are $\{ v_{1} \}$, $\{ v_{2} \}$, $\{ v_{3} \}$, $\{ v_{4} \}$, $\{ v_{5} \}$, $\{ v_{1} ,v_{2} \}$, $\{ v_{1} ,v_{5} \}$, $\{ v_{2} ,v_{3} \}$, $\{ v_{2} ,v_{4} \}$, $\{ v_{2} ,v_{5} \}$, $\{ v_{3} ,v_{4} ,v_{5} \}$, and $\{ v_{1} ,v_{2} ,v_{3} ,v_{4} ,v_{5} \}$. Hence,

$Y_{1} = \{ \{ v_{1} \} ,\{ v_{2} \} ,\{ v_{3} \} ,\{ v_{4} \} ,\{ v_{5} \} \}$,

$Y_{2} = \{ \{ v_{1} ,v_{2} \} ,\{ v_{1} ,v_{5} \} ,\{ v_{2} ,v_{3} \} ,\{ v_{2} ,v_{4} \} ,\{ v_{2} ,v_{5} \} \}$,

$Y_{3} = \{ \{ v_{3} ,v_{4} ,v_{5} \} \}$,

$Y_{4} = \{ \emptyset \}$,

$Y_{5} = \{ \{ v_{1} ,v_{2} ,v_{3} ,v_{4} ,v_{5} \} \}$.

Accordingly, define $\beta (\emptyset ) = (0,0,1, - 1)$, we get.

$\beta_{1}^{0} = \beta (\{ v_{1} \} ) \vee \beta (\{ v_{2} \} ) \vee \beta (\{ v_{3} \} ) \vee \beta (\{ v_{4} \} ) \vee \beta (\{ v_{5} \} ) = (0,0,1, - 1),\beta_{2}^{0} = \beta (\{ v_{1} ,v_{2} \} ) \vee \beta (\{ v_{1} ,v_{5} \} ) \vee \beta (\{ v_{2} ,v_{3} \} ) \vee \beta (\{ v_{2} ,v_{4} \} ) \vee \beta (\{ v_{2} ,v_{5} \} )$$= (0.2, - 0.3,0.4, - 0.4)$,

$\beta_{3}^{0} = \beta (\{ v_{2} ,v_{3} ,v_{4} \} ) = (0.4, - 0.4,0.3, - 0.5)$,

$\beta_{4}^{0} = \beta (\emptyset ) = (0,0,1, - 1)$,

$\beta_{5}^{0} = \beta (\{ v_{1} ,v_{2} ,v_{3} ,v_{4} ,v_{5} \} ) = (1, - 1,0,0)$.

Finally, we conclude that.

$D = \{ (1,\beta_{1}^{0} ),(2,\beta_{2}^{0} ),(3,\beta_{3}^{0} ),(4,\beta_{4}^{0} ),(5,\beta_{5}^{0} )\} = \{ (1,0,0,1, - 1),(2,0.2, - 0,3,0.4, - 0.4),(3,0.4, - 0.4,0.3, - 0.5),\;(4,0,0,1, - 1),(5,1, - 1,0,0)\} .$

4 A Numerical Experiment

Yunnan Province is one of the provinces with frequent earthquakes in China. There are two well-known geological plate fault zones “Xiaojiang Fault Zone:” and “Honghe Fault Zone” located in Yunnan Province. This has caused areas along the fault zone to become a high-risk area for earthquakes, such as “Dali”, “Tonghai”, “Lijiang”, “Honghe”, “Ludian” and so on. In recent 10 years, earthquakes above 5-level scale that occurred in Yunnan are shown in Table 1.

Table 1 Earthquakes of magnitude 5 and above in Yunnan Province in the past 10 years

Therefore, the Yunnan Provincial Natural Resources Bureau established the Emergency Disaster Department, which specializes in the emergency management of natural disasters including earthquake relief. Now, suppose we need to choose several cities from Yunnan Province to build earthquake-resistant warehouses that can store food, machinery and sanitary materials, and can use land transportation. Fast transportation between cities in the event of an earthquake above the scale becomes essential in the earthquake rescue and relief. We use bipolar fuzzy graph domination set theory to select these cities. The map of various cities in Yunnan Province is shown in Fig. 4.

Fig. 4

City distribution map of Yunnan Province (copy from the internet)

Based on Fig. 4, we can get the following structure in Fig. 5, where each vertex represents a prefecture-level city, and there is an edge between two cities if and only if they are adjacent.

Fig. 5

Graph corresponding to Fig. 4

The correspondence between cities and vertices is presented in Table 2.

Table 2 Vertex and city comparison

It should be noted that the cities represented by the vertices in Fig. 5 are prefecture-level cities, and prefecture-level cities are in charge of many small cities, and we will not use other vertices to represent them. In other words, we use a vertex to represent the central city of a district, while ignoring the surrounding counties.

We need to use a bipolar membership function to express the uncertainty to blur the graph. These uncertainties include the different conditions of cities in the construction of emergency warehouses, such as distance between cities, quality, safety, roadblocks, and traffic. The existence of and other aspects are different. For cost-saving considerations, the city where the emergency center is located should choose the least number and the most ideal city, so that the remaining cities are adjacent to at least one of them through suitable roads, so that the stored items can be transferred as soon as possible in the event of an incident. Therefore, we use the concept of dominance to select cities in the fuzzy graph. Cities to be chosen to build emergency warehouses should consider the following criteria.

• 1. The city is of high grade, with sufficient resources and manpower to dispatch, and the level of management personnel is high.

• 2. The city is not on the “Xiaojiang Fault Zone” and “Honghe Fault Zone”, that is, the city itself is relatively safe.

• 3. Convenient transportation in the city.

• 4. Take account of various urban agglomerations. According to the national overall plan, the entire Yunnan can be divided into 6 major urban agglomerations: Central Yunnan, Northeast Yunnan, Southwest Yunnan, West Yunnan, Northwest Yunnan, and Southeast Yunnan. The choice of cities needs to take these six urban agglomerations into account.

Correspondingly, we invite an expert group to assign a pair of values in the intervals $[0,1] \times [ - 1,0]$ to each city, to score the city. For each of the items mentioned above, there is a function from V to $[0,1] \times [ - 1,0]$, denoted as $s_{1} = (s_{1}^{P} ,s_{1}^{N} )$,$s_{2} = (s_{2}^{P} ,s_{2}^{N} )$,$s_{3} = (s_{3}^{P} ,s_{3}^{N} )$ and $s_{4} = (s_{4}^{P} ,s_{4}^{N} )$, respectively. Consider the bipolar membership function $\eta^{P} ,\eta^{N}$ on V as the average of these scores. We set a weighting coefficient for each item, respectively, 0.3, 0.2, 0.3 and 0.2. Therefore, for any $v \in V$, we use the following weighting formula to calculate the positive and negative scores:

$$\eta^{P} = 0.3s_{1}^{P} + 0.2s_{2}^{P} + 0.3s_{3}^{P} + 0.2s_{4}^{P}$$

$$\eta^{N} = 0.3s_{1}^{N} + 0.2s_{2}^{N} + 0.3s_{3}^{N} + 0.2s_{4}^{N}$$

The specific values are shown in Table 3 (in fact, Diqing, Nujiang, Lijiang, Dali, Baoshan, Chuxiong, Lincang, Yuxi, Honghe, and even the provincial capital Kunming are all on the seismic fault zone).

Table 3 Score of each city

The following factors are considered for each edge to determine the bipolar membership of roads between cities.

• 1. The length of road

• 2. Road quality, including infrastructure, safety, condition of mountain roads along the way, and convenience facilities along the route.

For each of the above, we have a function from E to $[0,1] \times [ - 1,0]$, denoted by $e_{1} = (e_{1}^{P} ,e_{1}^{N} )$ and $e_{2} = (e_{2}^{P} ,e_{2}^{N} )$, respectively. The weighted average of these two functions (since Yunnan is a mountainous province, most of the mountain roads are steep, so relative to the length of the road, the quality of the road plays a decisive role. Therefore, the proportion of the first and second terms is set to 0.3 and 0.7) form the membership function $e^{P} ,e^{N} :E \to [0,1] \times [ - 1,0]$ of the edge in the bipolar fuzzy graph. which is

$$e^{P} = 0.3e_{1}^{P} + 0.7e_{2}^{P}$$

$$e^{N} = 0.3e_{1}^{N} + 0.7e_{2}^{N}$$

For any $uv \in E(G)$, suppose $\theta^{P} (uv) = \min \{ e^{P} (uv),\eta^{P} (u),\eta^{P} (v)\}$ and $\theta^{N} (uv) = \max \{ e^{N} (uv),\eta^{N} (u),\eta^{N} (v)\}$. Since $\theta^{P} (uv) \le \eta^{P} (u) \wedge \eta^{P} (v)$ and $\theta^{N} (uv) \ge \eta^{N} (u) \vee \eta^{N} (v)$, it conforms to the relationship between the membership functions of the vertices and edges of the fuzzy graph, that is, $G = (V,\eta^{P} ,\eta^{N} ,\theta^{P} ,\theta^{N} )$ is a bipolar fuzzy graph. The data of the edge membership function are shown in Table 4.

Table 4 Calculation of edge membership function of bipolar fuzzy graph in Fig. 5

Table 5 Computing the values of $\Psi^{P}$ and $\Psi^{N}$

According to the definition, all the above edges are valid edges of $G = (V,\eta^{P} ,\eta^{N} ,\theta^{P} ,\theta^{N} )$. Now, suppose that a city meets the conditions required to build an earthquake-resistant warehouse and can enter another city through suitable roads (Table 5). If the city entrances and exits become crowded, especially during a crisis, when road traffic increases, the city cannot be considered Candidates to build warehouses. Therefore, construct a bipolar incidence graph to describe the uncertainty of the quality of urban entrances and exits through the functions $\Psi^{P} :V \times E \to [0,1]$ and $\Psi^{N} :V \times E \to [ - 1,0]$ as follows:

Therefore, $G = (V,\eta^{P} ,\eta^{N} ,\theta^{P} ,\theta^{N} ,\Psi^{P} ,\Psi^{N} )$ is a bipolar fuzzy incidence graph. By calculating, it can be known that except for $v_{12} v_{14}$, $v_{11} v_{14}$ and $v_{14} v_{16}$, the others are all valid edges. We list the domination sets determined by several approaches in Table 6.

Table 6 Calculation results of bipolar fuzzy graph domination set

It can be seen from Table 6 that for the example of earthquake-resistant warehouse construction in Yunnan Province, the same calculation results can be obtained using the three methods given in this article. We believe that the reason is that there are two hanging points in the figure, leading to and being selected at the same time. In addition, we believe that this choice is reasonable for this particular application. Intuitively, Kunming is the capital city of Yunnan Province and should be selected, but in fact, it is located on the fault zone and is not suitable for material storage. We have given the calculation results of the method to exclude Kunming. In summary, the earthquake-resistant warehouses in Yunnan Province should be built in the four cities of “Diqing”, “Baoshan”, “Pu’er” and “Qujing”.

5 Discussion

For intuitionistic fuzzy graph, Bozhenyuk et al. [23] determined that the intuitionistic dominating sets have property $(0,1,) \le \beta_{1}^{0} \le \beta_{2}^{0} \le \cdots \le \beta_{n}^{0} \le (1,0)$. When it comes to bipolar setting, if we expand it directly, then it will become $(0,0,1, - 1) \le \beta_{1}^{0} \le \beta_{2}^{0} \le \cdots \le \beta_{n}^{0} \le (1, - 1,0,0)$. However, it is obvious that for bipolar intuitionistic fuzzy graph and bipolar intuitionistic dominating set, this property is not hold any more. In Bozhenyuk et al. [23], the authors gave more discussions, algorithm and numerical examples on how to compute the domination set in intuitionistic fuzzy graph, and unfortunately, these statement can be extended to bipolar setting.

The main reason for this phenomenon is that the definition of minimal bipolar intuitionistic dominating vertex subset is too strict, and the deeper reason in the definition of $\beta (X_{1} ) < \beta (X_{2} )$ is too harsh. Recall that in Bozhenyuk et al. [23], for $\beta (X_{1} ) = (\mu_{B} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B} (v_{1} ,v_{1}^{{\prime}} ))$ and $\beta (X_{2} ) = (\mu_{B} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B} (v_{2} ,v_{2}^{{\prime}} ))$,$\beta (X_{1} ) < \beta (X_{2} )$ implies $\mu_{B} (v_{1} ,v_{1}^{{\prime}} ) < \mu_{B} (v_{2} ,v_{2}^{{\prime}} )$ and $\eta_{B} (v_{1} ,v_{1}^{{\prime}} ) > \eta_{B} (v_{2} ,v_{2}^{{\prime}} )$. In this paper, we directly extend it to bipolar setting, for $\beta (X_{1} ) = (\mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ))$ and $\beta (X_{2} ) = (\mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} ),\mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} ))$, $\beta (X_{1} ) < \beta (X_{2} )$ implies $\mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) < \mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )$, $\mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) > \mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )$, $\eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) > \eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )$ and $\eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) < \eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )$. Then, $X \subseteq V$ is a minimal bipolar intuitionistic dominating vertex subset with degree $\beta (X)$ if $\beta (X^{\prime}) < \beta (X)$ for any subset $X^{\prime} \subset X$. Here, we see that to meet $\beta (X^{\prime}) < \beta (X)$, the corresponding value of four membership functions should be strict “ < ” or “ > ”. It leads that to be that a minimal bipolar intuitionistic dominating vertex subset is a difficult condition. As depicted in above example, when k = 4, there is no subset with four vertices meeting this demand.

To solve this problem, the definition of $\beta (X^{\prime}) < \beta (X)$ may be revised in the future. An alternative solution is described as follows.

Possible modified definition: Assume $\beta (X_{1} ) = (\mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ),\eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ))$ and $\beta (X_{2} ) = (\mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} ),\mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} ),\eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} ))$. Then, $\beta (X_{1} ) < \beta (X_{2} )$ if the following two conditions are established:

(1) $\mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) \le \mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )$, $\mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) \ge \mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )$ or $\eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) \ge \eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )$ or $\eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) \le \eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )$.

(2)$\mu_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) < \mu_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )$ or $\mu_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) > \mu_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )$ or $\eta_{B}^{P} (v_{1} ,v_{1}^{{\prime}} ) > \eta_{B}^{P} (v_{2} ,v_{2}^{{\prime}} )$ or $\eta_{B}^{N} (v_{1} ,v_{1}^{{\prime}} ) < \eta_{B}^{N} (v_{2} ,v_{2}^{{\prime}} )$.

The definition of this replacement needs to be discussed in the future work.

6 Conclusion

In this paper, we mainly study the dominating sets in various kinds of bipolar graphs, including traditional bipolar fuzzy graph, bipolar fuzzy incidence graph and bipolar intuitionistic fuzzy graph. In particular, in normal bipolar fuzzy graph framework, we consider two kinds of dominating set and domination number: effective edge based and valid edge based. The tricks on how to compute these dominating sets are presented and several related features are determined.