Interval-valued fuzzy planar graphs

Abstract

In this paper, interval-valued fuzzy planar graphs are defined and several properties are studied. The interval-valued fuzzy graphs are more efficient than fuzzy graphs, since the degree of membership of vertices and edges lie within the interval [0, 1] instead at a point in fuzzy graphs. We also use the term ‘degree of planarity’ to measures the nature of planarity of an interval-valued fuzzy graph. The other relevant terms such as strong edges, interval-valued fuzzy faces, strong interval-valued fuzzy faces are defined here. The interval-valued fuzzy dual graph which is closely associated to the interval-valued fuzzy planar graph is defined. Several properties of interval-valued fuzzy dual graph are also studied. An example of interval-valued fuzzy planar graph is given.

1 Introduction

Graph theory is applied in most of the research areas of real life applications such as data mining, image segmentation, clustering, image capturing, networking, communication, planning, scheduling, etc. There are many practical applications with a graph structure in which crossing between edges is a nuisance such as design problems for circuits, subways, utility lines, etc. Crossing of two connections normally means that the communication lines must be run at different heights. This is not a big issue for electrical wires, but it creates extra expenses for some types of lines, e.g. burying one subway tunnel under another. Circuits, in particular, are easier to manufacture if their connections can be constructed in fewer layers. These applications are designed by the concept of planar graphs. In a city planning, subway tunnels, pipelines, metro lines are essential in twenty first century. Due to crossing, there are chances of accident. Also the cost of crossing of routes in underground is high. But, underground routes reduce the traffic jam. In a city planning, routes without crossing are perfect for safety. But, due to lack of space, crossing of such lines is allowed. It is easy to observe that the crossing between one congested and one non-congested route is better than the crossing between two congested routes. The term ‘congested’ have no definite meaning. We generally use the terms ‘congested’, ‘very congested’, ‘highly congested’ routes, etc. These terms are called linguistic terms and they can be defined by some membership degrees (generally by an interval in [0, 1]). A congested route may be referred as strong route and low congested route may be called as weak route. Thus crossing between strong route and weak route is more safe than the crossing between two strong routes. That is, crossing between strong route and weak route may be allowed in city planning with certain amount of safety. The terms ‘strong route’ and ‘weak route’ lead strong edge and weak edge of an interval-valued fuzzy graph respectively. And the permission of crossing between strong and weak edges leads to the concept of interval-valued fuzzy planar graph. After development of fuzzy graph theory by Rosenfeld [18], this topic has been increased with a large number of branches. Many works have been done on fuzzy sets as well as on fuzzy graphs [4, 5, 7–17, 19–34, 36, 37]. Abdul jabbar et al. [1] introduced the concept of fuzzy planar graph. Also, Samanta and Pal [25] introduced fuzzy planar graph in a different way. In this paper, they also introduced fuzzy faces, strong fuzzy planar graphs and fuzzy dual graphs. In 1975, Zadeh [38] introduced the notion of interval-valued fuzzy sets and related properties. Interval-valued fuzzy sets are the extension of fuzzy sets and represent uncertainty more perfectly. In recent time, Akram [3] introduced the interval-valued fuzzy graphs. Some useful research in these topics are found in [2, 3].

In this paper, interval-valued fuzzy planar graphs, interval-valued fuzzy dual graphs are defined and some important properties are established. Here, the ‘degree of planarity’ is used to measure the nature of planarity of an interval-valued fuzzy graph. Also, we introduced some terms like interval-valued fuzzy multiset, interval-valued fuzzy multigraph, interval-valued fuzzy dual graph. Some theorems have been proved on degree of planarity. Depending on the degree of planarity, the considerable edge has been introduced. A real life application of interval-valued fuzzy planar graph has been demonstrated.

2 Preliminaries and notations

A finite graph is a graph $G = (V,E)$ such that V and E are finite sets. An infinite graph is one with an infinite set of vertices or edges or both. Most commonly in graph theory, it is implied that the graphs discussed are finite. A multigraph is a graph that may contain multiple edges between any two vertices, but it does not contain any self loops. A graph can be drawn in many different ways. A graph may or may not be drawn on a plane without crossing of edges. A geometric representation of a graph on any plane surface such that no edges intersect is called embedding. A graph G is planar if it can be drawn in the plane with its edges only intersecting at vertices of G. So the graph is non-planar if it can not be drawn without crossing. A planar graph with cycles divides the plane into a set of regions, also called faces. The length of a face in a planar graph G is the number of edges bounding the face. The portion of the plane lying outside a graph embedded in a plane is infinite region. In graph theory, the dual graph of a given planar graph G is a graph which has a vertex corresponding to each plane region of G, and the graph has an edge joining two neighbouring regions for each edge in G, for a certain embedding of G.

A fuzzy set A on an universal set X is defined by a mapping $m:X\rightarrow [0,1]$, which is called the membership function. A fuzzy set is denoted by $A = (X,m)$. A fuzzy graph [31] $\xi =(V,\sigma , \mu )$ is a non-empty set V together with a pair of functions $\sigma : V\rightarrow [0,1]$ and $\mu : V\times V \rightarrow [0,1]$ such that for all $x,y\in V, \mu (x,y)\,\le\, \min \{\sigma (x),\sigma (y)\}$, where $\sigma (x)$ and $\mu (x,y)$ represent the membership values of the vertex x and of the edge $(x,y)$ in $\xi$ respectively. A loop at a vertex x in a fuzzy graph is represented by $\mu (x,x)\ne 0$. An edge is non-trivial if $\mu (x,y)\ne 0$. A fuzzy graph $\xi =(V,\sigma , \mu )$ is complete if $\mu (x,y)=\min \{\sigma (x),\sigma (y)\}$ for all $x,y\in V$.

Several definitions of strong edge are available in literature. Among them the definition of [6] is more suitable for our purpose. For the fuzzy graph $\xi =(V,\sigma , \mu )$, an edge $(x,y)$ is called strong if $\displaystyle \frac{1}{2}\min \{\sigma (x),\sigma (y)\}\,\le\,\mu (x,y)$ and weak otherwise.

By an interval-valued fuzzy graph [3], we mean a pair $\xi =(A,B)$, where $A = (V, [\sigma ^-, \sigma ^+])$ is an interval-valued fuzzy set on V and $B = (V\times V, [\mu ^-,\mu ^+])$ is an interval-valued fuzzy set on $V\times V$, such that $\mu ^-(x,y)\,\le\,\min \{\sigma ^-(x),\sigma ^-(y)\}$ and $\mu ^+(x,y)\,\le\,\min \{\sigma ^+(x),\sigma ^+(y)\}$ for all $(x,y)\in E$. We call A as the interval-valued fuzzy vertex set of $\xi$ and B as the interval-valued fuzzy edge set of $\xi$ respectively.

An interval-valued fuzzy graph $\xi = (A,B)$ is said to be complete interval-valued fuzzy graph [19] if $\mu ^-(x,y)\,=\,\min \{\sigma ^-(a),\sigma ^-(b)\}$ and $\mu ^+(x,y)\,=\,\min \{\sigma ^+(x),\sigma ^+(y)\}$, for all $x, y \in V$. An interval-valued fuzzy graph is said to be bipartite if the vertex set V can be partitioned into two independent sets $V_1$ and $V_2$ such that $\mu ^+\,(v_1, v_2) > 0$ if $v_1\in V_1$ (or $V_2$) and $v_2 \in V_2$ (or $V_1$). This definition does not mention about any condition for $\mu ^-\,(v_1, v_2)$. If $\mu ^+\,(v_1, v_2)>0$, then the edge $(v_1, v_2)$ exists even when $\mu ^-\,(v_1, v_2)=0$.

Throughout this paper the following notations are used.

G :

an arbitrary graph

V :

set of vertices of G

N :

set of natural numbers

E :

set of edges of G

X :

universal set

m :

membership function from a crisp set into [0, 1]

A :

a fuzzy set

ξ :

a interval-valued fuzzy graph

σ :

membership function of the vertices

μ :

membership function of the edges

$[{\sigma }^{-}, {\sigma }^{+}]$ :

the membership value of a vertex, $\sigma ^{-}$ and $\sigma ^{+}$ represents the left end and right end points respectively

$[\mu ^{-}, \mu ^{+}]$ :

the membership value of an edge, $\mu ^{-}$ and $\mu ^{+}$ represents the left end and right end points respectively

$[\sigma _i^{-}, \sigma _{i}^{+}]$ :

the ith membership value of a vertex, $\sigma _i^-$ and $\sigma _i^+$ represents the left end and right end points respectively

$[\mu _{j}^{-}, \mu _{j}^{+}]$ :

the membership value of jth edge between two vertices, $\mu _j^-$ and $\mu _j^+$ represents the left end and right end points respectively

$D_1, D_2$ :

subintervals of the interval [0,1]

$I_{(a,b)}$ :

strength of the edge $(a,b)$, which is an interval number whose left end point is $\displaystyle I_{(a,b)}^- = \frac{\mu ^-(a,b)}{\min \{\sigma ^+(a), \sigma ^+(b)\}}$ and right end point is $\displaystyle I_{(a,b)}^+ = \frac{\mu ^+(a,b)}{\min \{\sigma ^+(a), \sigma ^+(b)\}}$

${\mathcal {I}}_P$ :

intersecting number at the point of crossing of two edges $(a,b)$ and $(c,d)$, which is an interval number whose left end point is $\displaystyle {\mathcal {I}}_P^- = \frac{I_{(a,b)}^- + I_{(c,d)}^-}{2}$ and the right end point is $\displaystyle {\mathcal {I}}_P^+ = \frac{I_{(a,b)}^+ + I_{(c,d)}^+}{2}$

f :

degree of planarity of a interval-valued fuzzy graph, which is an interval number whose left end point is $\displaystyle f^-= \frac{1}{1+\{{\mathcal {I}}_{P_1}^+ + {\mathcal {I}}_{P_2}^+ + \cdots + {\mathcal {I}}_{P_k}^+\}}$ and the right end point is $\displaystyle f^+= \frac{1}{1+\{{\mathcal {I}}_{P_1}^- + {\mathcal {I}}_{P_2}^- + \cdots + {\mathcal {I}}_{P_k}^-\}}$, k being the number of point of intersections

$N_p$ :

number of point of intersections between the edges in a fuzzy graph

c :

considerable number

Now, we define interval-valued fuzzy multiset.

3 Interval-valued fuzzy multiset

A (crisp) multiset over a non-empty set V is simply a mapping $d : V \rightarrow N$, where N is the set of natural numbers. An element of non-empty set V may occur more than once with possibly the same or different natural numbers. A natural generalization of this interpretation of multiset leads to the notion of fuzzy multiset, or fuzzy bag, over a nonempty set V as a mapping $C :V\times [0,1]\rightarrow N$. The membership values of $v \in V$ are denoted as $\sigma ^j(v),$ $j=1,2,\cdots , p$ where $p\,=\,\max \{j : \sigma ^j(v)\ne 0\}$. So the fuzzy multiset can be denoted as $M = \left\{ \left( v, \sigma ^j(v)\right) , j = 1, 2, \cdots , p| v \in V\right\}$. Interval-valued fuzzy multiset (IVFMS) is another generalisation of multiset. The definition is given below.

Definition 1

(Interval-valued fuzzy multiset). Let V be a non-empty set. Also, let $\sigma _i^- : V \rightarrow [0, 1]$ and $\sigma ^+_i : V \rightarrow [0, 1]$ be the mappings such that $\sigma _i^- (x) \le \sigma ^+_i (x)$ for all $x \in V$ and $i = 1, 2,\cdots , p$. The interval-valued fuzzy multiset on V is denoted as $(V, [\sigma _i^-, \sigma ^+_i ])$ and is defined as $(V, [\sigma _i^-, \sigma ^+_i ]) =\{(x, [\sigma _i^-, \sigma ^+_i ])| x \in V, i = 1, 2, \cdots , p\}$.

Example 1

Let $V\,=\,\{a, b, c, d\}$. Then one of the interval-valued fuzzy multisets on V is $\{(a, [0.3, 0.5])$, $(a, [0.4, 0.6])$, $(b, [0.6, 0.8])$, $(c, [0.6, 0.9])$, $(d, [0.2, 0.4])$, $(d, [0.4, 0.5])$, $(d, [0.3, 0.5])\}$. Here $\sigma _1^- (a) = 0.3, \sigma ^+_1 (a) = 0.5$ and $\sigma _2^- (a) = 0.4, \sigma ^+_2 (a) = 0.6$, etc.

4 Interval-valued fuzzy multigraph

Now, we introduced the interval-valued fuzzy multigraph (IVFMG) using the notion of interval-valued fuzzy multiset. Let V be a non-empty set. Also let $\sigma _i^- : V \rightarrow [0,1]$ and $\sigma _i^+ : V \rightarrow [0,1]$ be the mappings such that $A\,=\,\{(V, [\sigma _i^-, \sigma ^+_i ]), i=1,2,\cdots , p\}$ be an IVFMS on V. Let $\mu ^-_j: V\times V\rightarrow [0,1]$, $\mu ^+_j: V\times V\rightarrow [0,1]$ be the mappings such that $B\,=\,\{(V\times V, [\mu ^-_j,\mu ^+_j]),j=1,2,\cdots , q\}$ be an IVFMS on $V\times V$. $(A,B)$ is said to be IVFMG if $\mu ^-_j(x,y)\,\le\,\min \{\sigma ^-_i(x),\sigma ^-_i(y)\}$ and $\mu ^+_j(x,y)\,\le\,\min \{\sigma ^+_i(x),\sigma ^+_i(y)\}$, $i=1,2,\cdots , p$, $j=1,2,\cdots , q$ for all $x,y\in V$.

An example of interval-valued fuzzy multigraph is given below.

Example 2

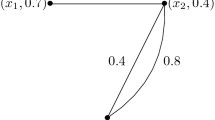
Let $V\,=\,\{a, b\}$ be a set of vertices. Let $\sigma ^-(a)\,=\,0.6,\, \sigma ^+(a)\,=\,0.8,\, \sigma ^-(b)\,=\,0.4,\, \sigma ^+(b)=0.5$ and $\mu _1^- (a, b) = 0.3,\, \mu ^+_1 (a, b) = 0.4,\, \mu ^-_2 (a, b) = 0.2,\, \mu ^+_2 (a, b) = 0.4,\, \mu _3^- (a, b) = 0.2,\, \mu ^+_3(a,b)= 0.3.$ Then $A = \{(a, [0.6, 0.8]), (b, [0.4, 0.5])\}$ and $B = \{((a, b), [0.3, 0.4])$, $((a, b), [0.2, 0.4])$, $((a, b), [0.2, 0.3])\}$. Therefore, $(A,B)$ is an IVFMG (see Fig. 1).

Fig. 1

An example of IVFMG

Underlying crisp graph of an IVFMG $\xi = (A,B)$, is denoted by $G = (V,E)$ where $V = \{x|\sigma ^-(x) > 0\}$ and $E = \{(x, y)| \mu ^-(x, y) > 0\}$. A special type of IVFMG is discussed below.

5 Interval-valued fuzzy planar graphs

Planarity is important in connection with the wire lines, gas lines, water lines, printed circuit designs, etc. But, sometimes little crossing may be accepted to these designs of such lines or circuits. So the concept of interval-valued fuzzy planar graph (IVFPG) is an important topic for these connections. A crisp graph is called non-planar graph if there is at least one crossing between the edges for all possible geometrical representations of the graph. Let a crisp graph G has a crossing for a certain geometrical representation between two edges $(a, b)$ and $(c, d)$ and has another crossing between the edges $(u,v)$ and $(w,x)$. Now, when we think about the strength of the edges of a graph in real phenomenon, some crossing causes a big problem and some are not. Here we assumed that $(a, b)$, $(c, d)$ and $(u,v)$ are strong edges and $(w,x)$ is a weak edge of the graph G stated above. In realistic view, the crossing between two strong edges $(a, b)$ and $(c, d)$ can not be taken in a planar graph, whereas the crossing between one strong edge $(u,v)$ and one weak edge $(w,x)$ may be acceptable. These linguistic words can be stated in a well-defined manner as follows:

In IVF concept, we say that each of the three strong edges $(a, b)$, $(c, d)$ and $(u,v)$ have membership values near to [1, 1] and the weak edge $(w,x)$ has membership value near to [0, 0]. If we remove the edge $(c, d)$, then the membership value of the edge $(c, d)$ in the graph is taken as [0, 0].

Let $\xi = (A,B)$ be an IVFMG and for a certain geometric representation, the graph has only one crossing between two edges $((w, x), [\mu ^-(w, x), \mu ^+(w, x)])$ and $((y, z)$, $[\mu ^-(y, z)$, $\mu ^+(y, z)])$. If $\mu ^-(w, x) = 1$ (obviously $\mu ^+(w, x) = 1$) and $\mu ^-(y, z) = 0 = \mu ^+(y, z)$, then we say that the graph has no crossing. Similarly, if $\mu ^-(w, x)$ has value near to 1 (obviously $\mu ^+(w, x) > \mu ^-(w, x)$ has value near to 1) and $\mu ^-(y, z)$ and $\mu ^+(y, z)$ have value near to 0, the crossing will not be important for the planarity. If $\mu ^-(w, x)$ has value near to 1 and $\mu ^-(y, z)$ has value near to 1, then the crossing becomes very important for the planarity. So, left end value of the membership degree (interval) is important for calculation. Before going to the main definition, some co-related terms are discussed below.

Addition: Let $D_1=[a^-, a^+]$ and $D_2=[b^-, b^+]$ be two subintervals of [0, 1]. Then the sum of $D_1$ and $D_2$ is denoted by $D_1+D_2$ and is defined by $\displaystyle D_1+D_2=[a^-, a^+] +[b^-, b^+]=[a^-+b^-, a^++b^+]$.

Comparability: Let $D_1=[a^-, a^+]$ and $D_2=[b^-, b^+]$ be two interval numbers in [0, 1]. Then $D_1$ is greater than or equal to $D_2$ i.e., $D_1\ge D_2$ if and only if $a^-\ge b^-$ and $a^+\ge b^+$. Also, $D_1$ is less than or equal to $D_2$ i.e., $D_1\le D_2$ if and only if $a^-\le b^-$ and $a^+\,\le\, b^+$. And, $D_1\,=\,D_2$ if and only if $a^-\,=\,b^-$ and $a^+\,=\,b^+$.

5.1 Intersecting value in IVFMG

In this paper, strength of an edge $(a, b)$ is defined by an interval number $\displaystyle I_{(a,b)}=\left[ I_{(a,b)}^-, I_{(a,b)}^+\right]$, where $\displaystyle I_{(a,b)}^- = \frac{\mu ^-(a,b)}{\min \{\sigma ^+(a),\sigma ^+(b)\}}$ and $\displaystyle I_{(a,b)}^+ = \frac{\mu ^+(a,b)}{\min \{\sigma ^+(a),\sigma ^+(b)\}}$. An edge $(a, b)$ is non-trivial if $I_{(a,b)}^- > 0$.

Now, we define strong edge in IVFMG as follows.

Definition 2

(Interval-valued fuzzy strong edge) Let $\xi = (A,B)$ be an IVFMG. An edge $(a, b)$ in $\xi$ is said to be interval-valued fuzzy strong if $I_{(a,b)}\ge [0.5,0.5]$ and interval-valued fuzzy weak otherwise.

In IVFMG, when two edges intersect at a point, an interval number is assigned to that point in the following way.

Let in IVFMG, $\xi = (A,B)$, B contains two edges $((a, b), [\mu ^-(a, b), \mu ^+(a, b)])$ and $((c, d), [\mu ^-(c, d), \mu ^+(c, d)])$ which are intersected at a point P. Now, we calculate the interval numbers $I_{(a,b)}$ and $I_{(c,d)}$ for the respective edges. We define the intersecting number at the point P by

$$\begin{aligned} {{\mathcal {I}}_P =[{\mathcal {I}}_P^-, {\mathcal {I}}_P^+]= \left[ \frac{I_{(a,b)}^-+I_{(c,d)}^-}{2}, \frac{I_{(a,b)}^+ +I_{(c,d)}^+}{2}\right] }. \end{aligned}$$

It is noted that ${\mathcal {I}}_P$ is an interval number in [0, 1]. Now, we recall the term ‘planarity’. In crisp sense, the planar graph has no crossing of edges, i.e. there is no intersection of edges. So, the ‘planarity’ of the planar graph is ‘full’. Therefore, if the number of points of intersection in an IVFMG increases, ‘planarity’ decreases. So for IVFMG, ${\mathcal {I}}_P$ is inversely proportional to the ‘planarity’. Based on this concept, a new terminology is introduced below for IVFMG.

Definition 3

(Planarity of an IVFMG) Let $\xi$ be an IVFMG and for a certain geometrical representation $P_1, P_2, \cdots , P_k$ (k being an integer) be the points of intersections between the edges. Then $\xi$ is said to be interval-valued fuzzy planar graph (IVFPG) with degree of planarity $f=[f^-, f^+]$, where

$$\begin{aligned} f^- =\frac{1}{1 + \{{\mathcal {I}}_{P_1}^+ + {\mathcal {I}}_{P_2}^+ + \cdots + {\mathcal {I}}_{P_k}^+\}}, \end{aligned}$$

$$\begin{aligned} and\, f^+= \frac{1}{1 + \{{\mathcal {I}}_{P_1}^- + {\mathcal {I}}_{P_2}^- + \cdots + {\mathcal {I}}_{P_k}^-\}}. \end{aligned}$$

It is obvious that f is bounded and $f\in D[0,1]$, where $D[0,1]$ is the set of all subintervals of the interval [0, 1].

If there is no point of intersection for a certain geometrical representation of an IVFPG, then its degree of planarity is [1, 1]. In this case, the underlying crisp graph of this IVFPG is the crisp planar graph. According our definition every IVFG is an IVFPG with some degree of planarity.

Example 3

Let us consider an IVFPG with one point of intersection between two edges $(a, b)$ and $(c, d)$. Here the membership degree of the vertices are given as $(a, [0.2, 0.4])$, $(b, [0.4, 0.5])$, $(c, [0.7, 0.8])$, $(d, [0.8, 0.9])$. The membership degree of the edges are $((a, b), [0.1, 0.3])$, $((c, d), [0.5, 0.6])$, $((a,c), [0.2, 0.05])$, $((b,d), [0.3,0.4])$. Now, $I_{(a,b)} = [0.25,0.75]$ and $I_{(c,d)} = [0.625,0.75]$. Hence, the intersecting number of the point of intersection is $\displaystyle \left[ \frac{0.25+0.625}{2}, \frac{0.75+0.75}{2}\right] = [0.4375, 0.75]$. So, the degree of planarity of the IVFPG is $\displaystyle \left[ \frac{1}{1+0.675}, \frac{1}{1+0.4375}\right] =[0.597, 0.697]$.

Fig. 2

An example of IVFPG with degree of planarity [0.571, 0.622]

The degree of planarity of a complete IVFG is calculated in the following theorem.

Theorem 1

Let $\xi$ be a complete IVFG. The degree of planarity f of $\xi$ is given by $\displaystyle f = [f^-, f^+]$, where $\displaystyle f^- = \frac{1}{1+N_p}$ and $\displaystyle \frac{1}{1+N_p}\le f^+ \le 1$, where $N_p$ is the number of points of intersection between the edges in $\xi$.

Proof

Let $\xi = (A,B)$ be an IVFG. For the complete IVFG, $\mu ^-(x,y)=\min \{ \sigma ^-(x), \sigma ^-(y)\}$ and $\mu ^+(x,y)=\min \{\sigma ^+(x), \sigma ^+(y)\}$ for all $x,y\in V$.

Let $P_1, P_2, \cdots , P_k$ be the points of intersections between the edges in $\xi$, k being an integer. For any edge $(a, b)$ in a complete IVFG, $\displaystyle I_{(a,b)}^- =\frac{\mu ^- (a,b)}{\min \{\sigma ^+(a),\sigma ^+(b)\}} \le 1$ and $\displaystyle I_{(a,b)}^+=\frac{\mu ^+ (a,b)}{\min \{\sigma ^+(a),\sigma ^+(b)\}} = 1$. Therefore, for the point $P_1$, the point of intersection between the edges $(a, b)$ and $(c, d)$, ${\mathcal {I}}_{P_1}^+$ is equals to $\frac{1+1}{2}=1$ and ${\mathcal {I}}_{P_1}^-\le \frac{1+1}{2}=1$. Hence ${\mathcal {I}}_{P_i}^+ = 1$ and ${\mathcal {I}}_{P_i}^-\le 1$ for $i = 1, 2, \cdots , k$.

Now, $\displaystyle f^- = \frac{1}{1+{\mathcal {I}}_{P_1}^+ +{\mathcal {I}}_{P_2}^+ +\cdots +{\mathcal {I}}_{P_k}^+}=\frac{1}{1+(1+1+\cdots +1)}=\frac{1}{1+N_p}$ and it is obvious that, where $N_p$ is the number of point of intersections between the edges in $\xi$. Therefore, the degree of planarity f is given by $f=[f^-,f^+]$ where, $\displaystyle f^-=\frac{1}{1+N_p}$ and $\displaystyle \frac{1}{1+N_p}\le f^+ \le 1$. $\square$

Theorem 2

Let $\xi$ be an IVFG with $f> [0.5,0.5]$.The number of point of intersections between interval-valued strong edges in $\xi$ is at most one.

Proof

Let $\xi = (A,B)$ be an IVFG with degree of planarity $f = [f^-, f^+]$ where, $f^->0.5$ and $f^+> 0.5$. Let, if possible, $\xi$ has at least two point of intersections $P_1$ and $P_2$ between two interval-valued strong edges in $\xi$.

For any interval-valued strong edge $((a, b), [\mu ^- (a, b), \mu ^+ (a, b)])$, $I_{(a,b)}^- \ge 0.5$ and $I_{(a,b)}^+ \ge 0.5$. Thus for two intersecting interval-valued strong edges $((a, b)$, $[\mu ^- (a, b)$, $\mu ^+ (a, b)])$ and $((c, d)$, $[\mu ^- (c, d)$, $\mu ^+ (c, d)])$, $\frac{I_{(a,b)}^- +I_{(c,d)}^-}{2} \ge 0.5$ and $\frac{I_{(a,b)}^+ +I_{(c,d)}^+}{2} \ge 0.5$, that is, ${\mathcal {I}}_{P_1}^- \ge 0.5$ and ${\mathcal {I}}_{P_1}^+ \ge 0.5$. Similarly, ${\mathcal {I}}_{P_2}^- \ge 0.5$ and ${\mathcal {I}}_{P_2}^+ \ge 0.5$. Then, $1 + {\mathcal {I}}_{P_1}^+ + {\mathcal {I}}_{P_2}^+ \ge 2$ and $1 + {\mathcal {I}}_{P_1}^- + {\mathcal {I}}_{P_2}^- \ge 2$. Therefore, $\displaystyle f^- = \frac{1}{1 + {\mathcal {I}}_{P_1}^+ + {\mathcal {I}}_{P_2}^+ }\le 0.5$ and $\displaystyle f^+ = \frac{1}{1 + {\mathcal {I}}_{P_1}^- + {\mathcal {I}}_{P_2}^- }\le 0.5$. It contradicts the fact that $f >[ 0.5,0.5]$.

So, the number of points of intersections between interval-valued strong edges can not be two. It is clear that if the number of point of intersections of interval-valued strong fuzzy edges increases, the fuzzy degree of planarity decreases. Similarly, if the number of point of intersection of interval-valued strong edges is one, then the degree of planarity f is given in such a way that $f> [0.5,0.5]$. Any IVFG without any crossing between edges has degree of planarity $f> [0.5,0.5]$. Thus, we conclude that the maximum number of point of intersections between the interval-valued strong edges in $\xi$ is one. $\square$

The above theorem is justified by the following example.

Example 4

Let us consider two IVFPGs shown in Fig. 3. In Fig. 3a, an IVFPG is considered with one crossing between two interval-valued strong edges $(a, d)$ and $(b, e)$. Let $\sigma _1^-(a) =\sigma _1^-(b) = \sigma _1^-(d) = \sigma _1^-(e) = 0.3$ and $\sigma _1^+(a) =\sigma _1^+(b) = \sigma _1^+(d) = \sigma _1^+(e) = 1$ and $\mu ^-(a, d) = 0.99, \mu ^-(b, e) = 0.99, \mu ^+(a, d) = 1, \mu ^+(b, e) = 1$ (only required membership values are mentioned). The degree of planarity of this graph is $[0.5,0.5025]\ge [0.5,0.5]$. Therefore, for this planar graph $f\ge [0.5,0.5]$ and the number of point of intersection is 1. In Fig. 3b, an IVFPG is considered with two crossing between interval-valued strong edges $(a, d), (b, e)$ and $(a, d), (c, e)$. For this IVFPG, let $\sigma _1^-(a) =\sigma _1^-(b) = \sigma _1^-(d) = \sigma _1^-(e) = 1$ and $\sigma _1^+(a) =\sigma _1^+(b)$ $= \sigma _1^+(d)$ $= \sigma _1^+(e) = 1$ and $\mu ^-_1 (a, d) = 0.5, \mu ^-_1 (b, e) = 0.5, \mu ^-_2 (a, d) = 0.5, \mu ^-_1 (c, e) = 0.5$ and $\mu ^+_1 (a, d) = 0.5, \mu ^+_1 (b, e) = 0.5, \mu ^+_2 (a, d) = 0.5, \mu ^+_1 (c, e) = 0.5$ (only required membership values are mentioned). The degree of planarity of this graph is $[0.5, 0.5]$. Also, it is easy to observe that if there is no crossing, then the IVFPG must have degree of planarity greater than $[0.5,0.5]$. This observation and above two examples support the statement of Theorem 2.

Fig. 3

IVFPGs with one and two crossings

One fundamental theorem of IVFPG is discussed below.

Theorem 3

Let $\xi$ be an IVFPG with degree of planarity f. If $f \ge [0.67,0.67]$, $\xi$ does not contain any point of intersection between two interval-valued strong edges.

Proof

Let $\xi = (A,B)$ be an IVFPG with fuzzy degree of planarity f, where $f \ge [0.67,0.67]$. Let, if possible, P be a point of intersection between two interval-valued strong edges $((a, b), [\mu ^- (a, b), \mu ^+ (a, b)])$ and $((c, d), [\mu ^- (c, d),$

$\mu ^+ (c, d)])$.

For any interval-valued strong edge $((a, b), [\mu ^- (a, b), \mu ^+ (a, b)])$, $I_{(a,b)}^-\ge 0.5$ and $I_{(a,b)}^+\ge 0.5$. For the minimum value of $I_{(a,b)}^-$, $I_{(c,d)}^-$, $I_{(a,b)}^+$ and $I_{(c,d)}^+$, ${\mathcal {I}}_P^- = 0.5$ and ${\mathcal {I}}_P^+ = 0.5$ then $f^- = \frac{1}{1+0.5}< 0.67$ and $f^+ = \frac{1}{1+0.5}< 0.67$, a contradiction. Hence, $\xi$ does not contain any point of intersection between interval-valued strong edges. $\square$

Motivated from this theorem, we introduce a special type of IVFPG called interval-valued strong IVFPG whose degree of planarity is more than or equal to $[0.67,0.67]$. As in mentioned earlier, if the degree of planarity is [1, 1], then the geometrical representation of IVFPG is similar to the crisp planar graph. It is shown in Theorem 3, if the degree of planarity is $[0.67,0.67]$, then there is no crossing between interval-valued strong edges. For this case, if there is any point of intersection between edges, that is the crossing between the interval-valued weak edge and any other edge. Again, the significance of interval-valued weak edge is less compared to interval-valued strong edges. Thus, interval-valued strong IVFPG is more significant. If the degree of planarity increases, then the geometrical structure of planar graph tends to crisp planar graph.

Here we give the definition of strong IVFPG.

Definition 4

(Strong IVFPG) An IVFPG $\xi$ is called strong IVFPG if the degree of planarity is greater than or equal to $[0.67,0.67]$.

The IVFPG of Example 4 is not strong IVFPG as its degree of planarity is less than $[0.67,0.67]$.

Thus, depending on the degree of planarity, the IVFPGs are divided into two groups namely, strong IVFPG and weak IVFPG.

Strength of an edge plays an important role to model some types of projects. If the strength of an edge is very small, the edge should not be considered to design a project. So the edges with sufficient strengths are useful to design such projects. We call these edges as considerable edges, the formal definition is given below.

Definition 5

(Considerable edge) Let $\xi =(A,B)$ be an IVFPG. Let $0 < c < 0.5$ be a rational number. An edge $(x, y)$ is said to considerable edge if $\displaystyle \left[ \frac{\mu ^-(x,y)}{\min \{\sigma ^+ (x), \sigma ^+(y)\}}\right.$, $\displaystyle \left. \frac{\mu ^+(x,y)}{\min \{\sigma ^+ (x), \sigma ^+(y)\}}\right] \ge [c,c]$. If an edge is not considerable, it is called non-considerable edge. For IVFMG $\xi =(A,B)$, a multi-edge $(x, y)$ is said to be considerable edge if $\displaystyle I_{(x,y)}\ge [c,c]$ for each $(x,y)$ in $\xi$.

Here $0 < c < 0.5$ is a rational number. If $\displaystyle \frac{\mu ^-(x,y)}{\min \{\sigma ^+(a),\sigma ^+(b)\}} \ge c$ for all edges $(x, y)$ of an IVFPG, then the number c is said to be considerable number of the IVFPG. Considerable number of an IVFPG may not be unique.

Obviously, for a specific value of c, a set of considerable edges is obtained and for different values of c, one can obtain different sets of considerable edges. Actually, c is a pre-assigned number for a specific application. For example, a social network is viewed as IVFPG, where a social unit (people, organisation, etc.) is taken as a vertex and the relation between them is represented by an edge. The amount of relationship (measure within unit scale) is taken as membership degree of the edge. Now for this network, if we choose c = 0.25, then we get a set of considerable edges, say $\mathcal {C}$. This set gives a group of people who have some considerable amount of relationship. The number of point of intersections between considerable edges can be determined from the following theorem.

Theorem 4

Let $\xi$ be a strong IVFPG with considerable number c. The number of point of intersections between considerable edges in $\xi$ is at most $\left[ \frac{0.49}{c} \right]$ ($[x]$ represents greatest integer not exceeding x).

Proof

Let $\xi = (A,B)$ be a strong IVFPG. Also, let $0 < c < 0.5$ be a considerable number and f be the degree of planarity. For any considerable edge $((a, b), \mu ^- (a, b))$, it is seen that $\mu ^- (a, b) \ge c$ $\times \min \{\sigma ^+(a),\sigma ^+(b)\}$. In this case $I_{(a,b)}^- \ge c$. Similarly, $I_{(a,b)}^+ \ge c$.

Let $P_1, P_2, \cdots , P_k$ be the k point of intersections between the considerable edges. Let $P_1$ be the point of intersection between the considerable edges $((a,b), [\mu ^-(a,b),\mu ^+(a,b)])$ and $((c,d),[\mu ^-(c,d),\mu ^+(c,d)])$. Then $\displaystyle {\mathcal {I}}_{P_1}^- = \frac{I_{(a,b)}^-+I_{(c,d)}^-}{2} \ge c$. So $\displaystyle \sum ^k_{i=1} {\mathcal {I}}_{P_i}^- \ge kc$ and $\displaystyle \sum ^k_{i=1} {\mathcal {I}}_{P_i}^+ \ge kc$. Hence $\displaystyle f^+ \le \frac{1}{1+kc}$ and $\displaystyle f^- \le \frac{1}{1+kc}$. As $\xi$ is a strong IVFPG, then we have, $[0.67,0.67] \le f \le \left[ \frac{1}{1+kc},\frac{1}{1+kc}\right]$. Hence $\displaystyle 0.67 \le \frac{1}{1+kc}$. This implies $\displaystyle k \le \frac{0.49}{c}$. This inequality will be satisfied for $\displaystyle k = \left[ \frac{0.49}{c} \right]$.$\square$

In the crisp sense, the complete graph with five vertices $K_5$ and the complete bipartite graph of six vertices $K_{3,3}$ cannot be drawn without crossings. So any graph containing $K_5$ or $K_{3,3}$ as subgraph is non-planar, in crisp sense.

Theorem 5

A complete IVFG of five vertices $K_5$ or complete bipartite IVFG of six vertices $K_{3,3}$ are not strong IVFPG.

Proof

Let $\xi = (A,B)$ be a complete IVFG of five vertices where $V = \{a, b, c, d, e\}$ and $E = \{((x, y),[ \mu ^-(x, y), \mu ^+(x,y)])| x,y \in V \}$. For all $x, y \in V , \mu ^-(x, y) = \min \{\sigma ^-(x), \sigma ^-(y)\}$ and $\mu ^+(x,y)=\min \{\sigma ^+(x), \sigma ^+(y)\}$.

From Theorem 1, it is known that the degree of planarity of a complete IVFG is $\displaystyle f = [f^-, f^+]$ where, $\displaystyle f^-=\frac{1}{1+N_p}$, $N_p$ is the number of point of intersections of the edges in $\xi$. We know that the geometric representation of the underlying crisp graph of a fuzzy complete graph of five vertices is non-planar and one point of intersection can not be avoided for any representation. So $\displaystyle f^- =0.5$. Hence $\xi$ is not strong IVFPG.

Similarly, it can be shown that a complete bipartite interval-valued fuzzy graph $K_{3,3}$ is not a strong IVFPG.$\square$

An IVFPG with five vertices and each pair of vertices connected by an edge may or may not be strong IVFPG. In Fig. 4, there is one point of intersection between two edges $((v_2, v_4), [0.15, 0.5])$, $((v_1, v_3), [0.45, 0.5])$. This is an example of strong IVFPG with degree of planarity $[0.52,0.63]$, which has five vertices and each pair of vertices are connected by an edge. Again from Theorem 5, one can say that a complete IVFPG of five vertices is not a strong IVFPG.

Fig. 4

Example of a strong IVFPG

A bipartite IVFPG of six vertices partitioned in two subsets containing three vertices each and all pairs of vertices between two partitioned sets are connected by edges may or may not be a strong IVFPG. The graph of Fig. 5, contains only one point of intersection between two edges $((a, f), [0.5, 0.7])$ and $((c, d), [0.2, 0.3])$ and it is a strong IVFPG with degree of planarity $[0.59,0.64]$. Now from Theorem 5, we know that a complete IVFPG of six vertices is not a strong IVFPG. Hence this conclusion is true.

6 Face of IVFPG

Face of a planar graph is an important parameter. In this section, we consider an IVFPG with degree of planarity [1, 1] to define face. That is, the IVFPG does not contain any pair of intersecting edges.

Face in an IVFPG is a region bounded by edges. Every face is characterized by edges in its boundary. If the membership values of all the edges in the boundary of a face are [1,1], it becomes crisp face. If one of such edges is removed or if we assign membership value of any edge to [0,0] then, the face does not exist. So the existence of a face depends on the minimum strength of the edges in its boundary.

A face and its strength are defined below.

Definition 6

Let $\xi = (A,B)$ be a strong IVFPG, whose degree of planarity is [1,1] on V. A face of $\xi$ is a region, bounded by the set of edges $E' \subset V\times V$, of a geometric representation of $\xi$. The strength of the face is

$$\begin{aligned} \left\{ \left[ \min \{I_{(x,y)}^-\}, \min \{I_{(x,y)}^+\}\right] | (x, y) \in E'\right\} . \end{aligned}$$

A face is called interval-valued strong fuzzy face if its strength is greater than [0.5,0.5], and interval-valued weak fuzzy face otherwise. Every interval-valued strong IVFPG has an infinite region which is called outer face. Other faces are called inner faces.

Fig. 5

An example of strong IVFPG with fuzzy degree of planarity [0.59,0.64]

Example 5

In Fig. 6, we consider an IVFPG with degree of planarity [1,1]. Here $F_1, F_2$ and $F_3$ are three fuzzy faces. $F_1$ is bounded by the edges $((v_1, v_2),$ $[0.5, 0.55])$, $((v_2, v_3)$, $[0.6, 0.7])$, $((v_1, v_3)$, $[0.55, 0.6])$ with strength $[0.833, 0.917]$. Similarly, $F_3$ is a face bounded by the edges $((v_1, v_2)$, $[0.5, 0.55])$, $((v_2, v_4)$, $[0.6, 0.65])$, $((v_1, v_4)$, $[0.2, 0.5])$ with strength $[0.333, 0.833]$. $F_2$ is the outer face with strength $[0.857,0.928]$. So $F_1, F_2$ are interval-valued strong fuzzy faces while $F_3$ is an interval-valued weak fuzzy face.

Fig. 6

An example of IVFPG with three faces

Every interval-valued strong fuzzy face has membership value greater than [0.5,0.5]. So every edge of an interval-valued strong fuzzy face is an interval-valued fuzzy strong edge.

Any IVFPG without any point of intersection of edges is an IVFPG with degree of planarity [1, 1]. Therefore, it is a strong IVFPG.

7 Interval-valued fuzzy dual graph

We now introduce the dual of IVFPG whose degree of planarity is [1, 1]. In interval-valued fuzzy dual graph (IVFDG), vertices are corresponding to the interval-valued strong faces and each edge in dual graph between two vertices is corresponding to each edge in the boundary between two interval-valued fuzzy faces. The formal definition is given below.

Definition 7

(Interval-valued fuzzy dual graph). Let $\xi = (A,B)$ be an IVFPG whose degree of planarity is [1,1]. Let $F_1, F_2, \cdots , F_k$ be the interval-valued strong faces of $\xi$. The IVFDG of $\xi$ is an IVFPG $\xi _1 = (A_1,B_1)$, where $A_1 = \{(V_1, [\tau ^- , \tau ^+ ])$, $B_1 = \{(V_1 \times V_1, [\nu ^-_l , \nu ^+_l ])$ and $V_1 = \{x_i, i =1, 2, \cdots , k\}$, the vertex $x_i$ of $\xi _1$ is correspond to the face $F_i$ of $\xi$.

The membership values of vertices are given by the mappings $\tau ^- : V_1 \rightarrow [0, 1]$ such that $\tau ^- (x_i) = \max \{\mu ^- (u, v)|(u, v)$ is an edge of the boundary of the interval-valued fuzzy face $F_i\}$. Also, $\tau ^+ : V_1 \rightarrow [0,1]$ such that $\tau ^+ (x_i) = \max \{\mu ^+ (u, v)|(u, v)$ is an edge of the boundary of the interval-valued fuzzy face $F_i\}$.

Fig. 7

An example of IVFDG

Between two interval-valued fuzzy faces $F_i$ and $F_j$ of $\xi$, there may exist more than one common edges. Thus between two vertices $x_i$ and $x_j$ in IVFDG $\xi _1$, there may be more than one edges. We denote $[\nu ^-_l (x_i, x_j)$, $\nu ^+_l (x_i, x_j)]$ be the membership degree of the lth edge between $x_i$ and $x_j$. The membership degrees of the edges of the IVFDG are given by $\nu ^-_l (x_i, x_j) = \mu ^- (u, v)$ and $\nu ^+_l (x_i, x_j) = \mu ^+ (u, v)$ where $(u, v)$ is a common edge between two interval-valued fuzzy faces $F_i$ and $F_j$ and $l = 1, 2, \cdots , s$, where s is the number of common edges in the boundary between $F_i$ and $F_j$ or the number of edges between $x_i$ and $x_j$.

If there be any interval-valued strong pendant edge in the strong IVFDG, then there exists a self loop in $\xi _1$ corresponding to this pendant edge. The edge membership degree of the self loop is equal to the membership degree of the pendant edge. IVFDG of strong IVFPG with degree of planarity [1, 1] does not contain any point of intersection of edges for a certain representation, so it is an IVFPG with degree of planarity [1, 1].

Here we give an example of IVFDG of an IVFPG which are shown in Fig. 7. Filled circles represents the vertices of IVFPG and lines represents the edges of that graph whereas the empty circles represents the vertices of IVFDG and dotted lines represent the edges of IVFDG corresponding to the IVFPG of Fig. 7.

Example 6

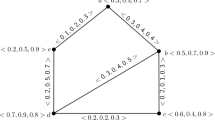
In Fig. 7, a strong IVFPG $\xi = (A,B)$ where $V = \{a, b, c, d\}$ is given. For this graph, let $\sigma ^-(a) = 0.6, \sigma ^+(a) = 0.8$, $\sigma ^-(b) = 0.7, \sigma ^+(b) = 0.9$, $\sigma ^-(c) = 0.8, \sigma ^+(c) = 0.9$, $\sigma ^-(d) = 0.9, \sigma ^+(d) = 0.95$ and $B = \{((a, b)$, $[0.5, 0.55])$, $((a, c), [0.4, 0.5])$, $((a, d), [0.55, 0.6])$, $((b, d), [0.45, 0.5])$,

$((b, d), [0.6, 0.65])$, $((c, d), [0.7, 0.75])\}$. Thus, the strong IVFPG has the following faces:

• 1. $F_1$ is bounded by $((a, b), [0.5, 0.55])$, $((a, d), [0.55, 0.6])$, $((b, d), [0.45, 0.5])$,

• 2. $F_2$ is bounded by $((a, d)$, $[0.55, 0.6])$, $((c, d)$, $[0.7, 0.75])$, $((a, c)$, $[0.4, 0.5]))$,

• 3. $F_3$ is bounded by $((b, d), [0.45, 0.5])$, $((b, d), [0.6, 0.65]))$ and outer fuzzy face

• 4. $F_4$ is surrounded by $((a, b)$, $[0.5, 0.55])$, $((b, d)$, $[0.6, 0.65])$, $((c, d)$, $[0.7, 0.75])$, $((a, c)$, $[0.4, 0.5])$.

Since all the faces are interval-valued strong faces, for each interval-valued strong fuzzy face, we consider a vertex for the IVFDG. Thus the vertex set $V_1 = \{x_1, x_2, x_3, x_4\}$ where each vertex $x_i$ corresponds to the interval-valued strong fuzzy face $F_i$, $i = 1, 2, 3, 4$. So $\tau ^- (x_1) = \max \{0.5, 0.55, 0.45\} = 0.55$, $\tau ^+ (x_1) = \max \{0.55, 0.6, 0.5\} = 0.6$, $\tau ^- (x_2)$ $= \max \{0.55, 0.7, 0.4\}$ $= 0.7$, $\tau ^+ (x_2)$ $= \max \{0.6, 0.75, 0.5\}$ $= 0.75$, $\tau ^- (x_3)$ $= \max \{0.45, 0.6\} = 0.6$, $\tau ^+ (x_3) = \max \{0.5, 0.65\} = 0.65$ and $\tau ^- (x_4)=$ $\max \{0.5, 0.6, 0.7, 0.4\} = 0.7$, $\tau ^+ (x_4)$ $= \max \{0.55, 0.65, 0.75, 0.5\} = 0.75$.

There are two common edges $(a, c)$ and $(c, d)$ between the faces $F_2$ and $F_4$ in $\xi$. Hence, between the vertices $x_2$ and $x_4$, there are two edges in the IVFDG. Here the membership degrees of these edges are given by $\nu ^-_1 (x_2, x_4) = \mu ^-_1 (c, d) = 0.7$, $\nu ^+_1 (x_2, x_4) = \mu ^+_1(c, d) =0.75$, $\nu ^-_2 (x_2, x_4) = \mu ^-_1 (a, c) = 0.4$, $\nu ^+_2 (x_2, x_4) = \mu ^+_1(a, c) = 0.5$.

The membership values of other edges of the IVFDG are calculated as $\nu ^-_1 (x_1, x_3) =\mu ^-_1 (b, d) = 0.45$, $\nu ^+_1 (x_1, x_3) = \mu ^+_1(b, d) = 0.5$, $\nu ^-_1 (x_1, x_2) = \mu ^-_1 (a, d) = 0.55$, $\nu ^+_1 (x_1, x_2) =\mu ^+_1(a, d) = 0.6$, $\nu ^-_1 (x_1, x_4) = \mu ^-_1 (a, b) = 0.5$, $\nu ^+_1 (x_1, x_4) = \mu ^+_1(a, b) = 0.55$, $\nu ^-_1 (x_3, x_4) =\mu ^-_2 (b, d) = 0.6$, $\nu ^+_1 (x_3, x_4) = \mu ^+_2(b, d) = 0.65$.

Thus the edge set of IVFDG is $B_1 = \{((x_1, x_3), [0.45, 0.5])$, $((x_1, x_2)$, $[0.55, 0.6])$, $((x_1, x_4)$, $[0.5, 0.55])$, $((x_3, x_4)$, $[0.6, 0.65])$, $((x_2, x_4)$, $[0.7, 0.75])$, $((x_2, x_4)$, $[0.4, 0.5])\}$.

In Fig. 7, the edges of IVFDG $\xi ' = (A_1,B_1)$ of $\xi$ are drawn by dotted line.

Theorem 6

Let $\xi$ be a strong IVFDG whose number of vertices, number of edges and number of interval-valued strong fuzzy faces are denoted by n, p and m respectively. Also, let $\xi _1$ be the IVFDG of $\xi$. Then

• 1. the number of vertices of $\xi _1$ is equal to m,

• 2. the number of edges of $\xi _1$ is equal to p and

• 3. the number of fuzzy faces of $\xi _1$ is equal to n.

Proof

Proof of (i), (ii) and (iii) are obvious from the definition of fuzzy dual graph. $\square$

The number of interval-valued strong fuzzy faces in IVFDG of a strong IVFPG is less than or equal to the number of vertices of IVFPG, as all faces of IVFDG may not be interval-valued strong fuzzy faces.

Fig. 8

An example of a fuzzy dual graph with interval-valued strong fuzzy face

Theorem 7

Let $\xi = (A,B)$ be a strong IVFPG without interval-valued weak edges and the IVFDG of $\xi$ be $\xi _1 = (A_1,B_1)$. The membership degrees of edges of $\xi _1$ are equal to membership degrees of the IVFPG of $\xi$.

Proof

Let $\xi = (A,B)$ be a strong IVFPG without interval-valued weak edges. The IVFDG of $\xi$ is $\xi _1 = (A_1,B_1)$ which is a strong IVFPG as there is no point of intersection between any edges. Let $\{F_1, F_2, \cdots , F_k\}$ be the set of strong faces of $\xi$.

From the definition of IVFDG, we know that $\nu ^-_l (u, v) = \mu ^-_l (u, v)_l$ and $\nu ^+_l (u, v) =\mu ^+_l (u, v)_l$, where $(u, v)_l$ is an edge in the boundary between two interval-valued strong fuzzy faces $F_i$ and $F_j$ and $l = 1, 2, \cdots , s$, where s represents the number of common edges in the boundary between $F_i$ and $F_j$.

The numbers of fuzzy edges of two fuzzy graphs $\xi$ and $\xi _1$ are same as $\xi$ has no interval-valued weak fuzzy edges. For each fuzzy edge of $\xi$ there is a fuzzy edge in $\xi _1$ with same membership value. $\square$

8 Application of interval-valued fuzzy planar graph

We consider a network consisting of five important cities (vertices) in a country. They are interconnected by roads (edges). The network is shown in Fig. 9.

The number adjacent to an edge represents the distance between the cities (vertices). The above network can be represented with the help of a classical matrix $M=[a_{ij}],\, i,j=1,2,\ldots , n$ where, n is the total number of nodes. The ijth element $a_{ij}$ of M is defined as

$$\begin{aligned} a_{ij} = \left\{ \begin{array}{ll} 0, &{} \text {if }\;i=j\\ \infty , &{} \text {the\;vertices}\; i\; \text { and }\;j\;\text { are\;not\;directly\;connected\;by\;an\;edge}\\ w_{ij}, &{} w_{ij}\;\text { is\;the\;distance\;of\;the\;road\;connecting\;{\it i}\;and\;{\it j}.} \end{array} \right. \end{aligned}$$

Fig. 9

A network

Since the distance between the two vertices are known, precisely, so the matrix M is obviously a classical matrix. Generally, the distance between two cities are crisp value, so the corresponding matrix is crisp matrix.

Now, we consider the crowdness of the roads connecting cities. It is clear that the crowdness of a road obviously, is a fuzzy quantity. The amount of crowdness depends on the decision makers mentality, habits, natures, etc, i.e., completely depends on the decision maker. The measurement of crowdness as a point is a difficult task for the decision maker. So, here we consider amount of crowdness as an interval instead of a point (Table 1).

For illustration, we consider the crowdness of the road $(i,j)$ connecting the places i and j as follows:

Table 1 The crowdness of the network of the Fig. 9

As the crossing road increases, the possibility of crowdness increases and kill time, so the travelling cost increases. Thus, construct the roads in such a way that the number of crossing decreases, i.e., the degree of planarity increases. Therefore, the measurement of degree of planarity is important. In the network of Fig. 9, there are only two crossings, one between the roads (1, 4) and (3, 5) and other between the roads (2, 4) and (3, 5).

To model up the given network as an interval-valued fuzzy planar graph we consider the membership values of each vertices as interval number [1, 1]. Then the following computations have been made.

$\displaystyle I_{(1,4)}^- = \frac{\mu ^-(1,4)}{\min \{\sigma ^+ (1), \sigma ^+(4)\}}=\frac{0.3}{1}=0.3$

Similarly,

$\displaystyle I_{(1,4)}^+ = \frac{\mu ^+(1,4)}{\min \{\sigma ^+ (1), \sigma ^+(4)\}}=\frac{0.6}{1}=0.6$

$\displaystyle I_{(3,5)}^- = 0.4 ; \quad I_{(3,5)}^+ = 0.5$

$\displaystyle I_{(2,4)}^- = 0.5 ; \quad I_{(2,4)}^+ = 0.6$.

Therefore, the intersecting number at the point $P_1$, the intersection between the roads (2, 4) and (3, 5) is

$$\begin{aligned} {\mathcal {I}}_{P_1}&= \left[ \frac{I_{(2,4)}^- +I_{(3,5)}^- }{2}, \frac{I_{(2,4)}^+ + I_{(3,5)}^+}{2}\right] \\&= \left[ \frac{0.5+0.4}{2}, \frac{0.6+ 0.5}{2}\right] \\&= [0.45, 0.55] \end{aligned}$$

and the intersecting number at the point $P_2$, the intersection between the roads (1,4) and (3,5) is

$$\begin{aligned} {\mathcal {I}}_{P_2}&= \left[ \frac{I_{(1,4)}^- +I_{(3,5)}^- }{2}, \frac{I_{(1,4)}^+ + I_{(3,5)}^+}{2}\right] \\&= \left[ \frac{0.3+0.4}{2}, \frac{0.6+ 0.5}{2}\right] \\&= [0.35, 0.55] \end{aligned}$$

So, the degree of planarity $f=[f^-, f^+]$ is given by

$$\begin{aligned} f^- = \frac{1}{1+0.55+0.55}=0.48\\ f^+ = \frac{1}{1+0.35+0.45}=0.56. \end{aligned}$$

Therefore, the degree of planarity of the network of Fig. 9 is [0.48, 0.56], which is far from the degree of planarity [0.67, 0.67] hence it is likely to be crowded. Obviously, this crowdness occurs due to the crossing of roads.

9 Conclusion

Our study describes the IVFMG, IVFPG, and a very important consequence of IVFPG is IVFDG. In crisp planar graph, no edge intersects other. But, the edges of any IVFG may be interval-valued fuzzy weak or interval-valued fuzzy strong. Using the concept of interval-valued fuzzy weak edge, we define IVFPG in such a way that an edge may intersect other edges. But, this facility violates the definition of planarity of graph. Since the role of interval-valued fuzzy weak edge is insignificant, the intersection between an interval-valued fuzzy weak edge with any edge is less important. Motivating from this idea, we allow the intersection of edges in IVFPG. It is well known that if the membership values of all edges become one, the graph becomes crisp graph. Keeping this idea in mind, we define a new term called degree of planarity of an IVFG. If the degree of planarity of an IVFG is [1,1], then no edge crosses other. This leads to the crisp planar graph. Thus, the planarity value measures the degree of planarity of an IVFG. This is a very interesting concept of interval-valued fuzzy graph theory. Strong IVFPG has been exemplified. Another important term of planar graph is ‘face’ which is redefined in IVFPG. In this paper, new theories have been investigated for IVFPG. The IVFDG is defined for the IVFPG whose degree of planarity is [1,1]. These theories will be helpful to improve algorithms in different fields including computer vision, image segmentation, etc. This idea can be extended to the other types of fuzzy graphs such as intuitionistic fuzzy planar graph, bipolar fuzzy planar graph, etc. At present we are working on bipolar fuzzy planar graphs.