The Progressive Wave Approach Analyzing the Evolution of Shock Waves in Dusty Gas

Abstract

In the present paper the theory of progressive waves is used to analyze the finite amplitude disturbances, moderately small amplitude disturbances in a dusty gas for generalized geometry. The conditions, under which a complete history of the evolutionary behavior of shock waves including weak shock can be traced out, are determined. It is also assessed as to how the presence of dust particles in the gas affects the existence of shock or no shock. Further the effect of variation of mass fraction of the dust particles on the growth and decay behavior of shock in cylindrically symmetric and spherically symmetric flows are discussed.

Introduction

The ideal gas model has played an important role to study the shock wave phenomena. Many important and interesting results have been worked out using the ideal gas model while real gases are not exactly described by ideal gas model; there is always certain deviation, from the ideal gas model, in the behaviour of real fluids. The shock wave phenomena in real fluid exhibits richer behaviour than that of ideal gas model. In the last few decades, in non linear waves the theory of progressive wave has received a great attention from mathematical as well as physical points of view as it is associated with sonic boom problem in the field of aerodynamics. Several approaches have been developed to investigate the asymptotic properties of weakly nonlinear waves and for the derivation of transport equation describing the wave phenomena governed by a hyperbolic system see [1,2,3,4]. The theory of relatively undistorted waves was first presented by Varley and Cumberbatch [5] in which they have studied the nonlinear wave phenomenon governed by nonlinear system of equations. The theory of relatively undistorted waves depends on a scheme of successive approximations to the system of hyperbolic equations, which makes no assumption on the magnitude of the disturbance, it also gives an asymptotic expansion of the flow variable for outward going wave. This method was further discussed in detail by Seymour and Mortell [6] in which they have proposed an expansion scheme which generalizes the earlier study and was used in linear geometrical acoustics to account for the amplitude dispersion and shock formation. Again Seymour and Mortell [6] have proved that the representation of high frequency waves in terms of modulated simple wave with slowly changing Riemann invariants, the parameter expansion technique of geometrical optics can be modified to finite amplitude waves. Further, the theory of simple modulated waves has been used by few authors such as Varley and Cumberbatch [5], Varley and Rogers [7] and Gupta et al. [8] to discuss high frequency waves in different material media. The necessary idea underlying the theory of progressive waves may be found in [9,10,11,12]. Also a parallel attempt, in the field of perturbation method has been done by Asano, T. Taniuti and some other associated authors see [13,14,15]. Zhao et al. [16] has presented a complete classification of shock waves in van der Waals fluids in which a theoretical understanding of shock related phenomena is developed in real fluids which cannot be accounted by the ideal gas model. A remarkable attention on evolution and propagation of weak shock waves in different material media has been drawn by Singh et al. [17,18,19]. Radha et al. [20] have studied the interaction of shock waves with weak discontinuities. Ambika et al. [21] have used the theory of progressive waves to study the finite and moderately small amplitude waves in non-ideal gas.

The dusty gas is a mixture of gas and small solid particles where solid particles do not occupy more than 5% volume of the total volume of the mixture. The study of shock waves in dusty gas is of great importance due to its wide application in industry, lunar ash flow, nozzle flow, bomb blast, propellant rocket, supersonic flight in polluted air and many other engineering problems see (Miura and Glass [22], Pai et.al [23, 24]). Anand [25] have derived the Shock jump relations for the dusty gas atmosphere. When a shock wave is propagated through a gas which contains an appropriate amount of dust particles, the thickness of the wave, the pressure changes across the shock and the other features of the flow differ greatly from those which arise when the shock passes through dust free gas. Further Carrier [26] has studied the feature of shock waves in dusty gases in which the plane steady decelerated flow of a dusty gas mixture is analyzed in an appropriate manner. The main motivation of the present work is to study the planar and radially symmetric flow of finite amplitude disturbances, small amplitude disturbances and evolution of shock waves in a dusty gas by using the theory of progressive waves. Further some specific cases, in which the initial disturbance is either a pulse or periodic wave, are considered to trace out the complete history of shock decay after its formation in a dusty gas.

Basic Equations

The governing equations describing a one dimensional planar (m $=$ 0), cylindrically symmetric (m $=$ 1) or spherically symmetric (m $=$ 2) flow of an ideal compressible fluid with dust particles may be written in the following form [22,23,24, 27]

$$\begin{aligned}&\rho _t +u\rho _x +\rho u_x +{m\rho u}/x=0, \end{aligned}$$

(1)

$$\begin{aligned}&u_t +uu_x +{p_x }/\rho =0, \end{aligned}$$

(2)

$$\begin{aligned}&E_t +uE_x -p/{\rho ^{2}\left( {\rho _t +u\rho _x } \right) =0}, \end{aligned}$$

(3)

where $\rho$ is the density, u is the velocity, p is the pressure, t is the time and x is the spatial coordinate. The subscripts denote partial differentiation unless stated otherwise. The internal energy E per unit mass of the mixture is given as

$$\begin{aligned} E=\frac{\left( {1-Z} \right) p}{\left( {\Gamma -1} \right) \rho }, \end{aligned}$$

(4)

where $Z={V_{sp} }/{V_g }$ is the volume fraction and $k_p ={m_{sp} }/{m_g }$ is the mass fraction of the solid particles in the mixture while $m_{sp}$ and $V_{sp}$ are the total mass and volumetric extension of the solid particles respectively, $V_g$ and $m_g$ are the total volume and total mass of the mixture respectively, $\Gamma$ is called Grüneisen coefficient and is defined as $\Gamma ={\gamma \left( {1+\lambda \beta } \right) }/{\left( {1+\lambda \beta \gamma } \right) }$, $\lambda ={k_p }/{\left( {1-k_p } \right) }$, $\beta ={c_{sp} }/{c_p }$ and $\gamma ={c_p }/{c_v }$, where $c_{sp}$ is the specific heat of the solid particles, $c_p$ is the specific heat of the gas at constant pressure and $c_v$ is the specific heat of the gas at constant volume. The entities Z and $k_p$ are related via the expression$Z=\theta \rho$, where $\theta ={k_p }/{\rho _{sp} }$ with $\rho _{sp}$ is the specific density of the solid particles. If we set $Z=0$ in Eq. (4) (i.e. the gas is free from dust particles) then Eq. (4) turns to the equation of state for an ideal gas.

Using Eq. (4) in Eq. (3) we get

$$\begin{aligned} p_t +up_x +\rho C^{2}\left( {u_x +{mu}/x} \right) =0, \end{aligned}$$

(5)

where C is the sound velocity and is given by $C=\sqrt{{\Gamma p}/{\left( {1-Z} \right) \rho }}$.

Now Eq. (1), (2) and (5) can be written in matrix form as

$$\begin{aligned} V_t +MV_x +N=0, \end{aligned}$$

(6)

where $V=\left[ {\begin{array}{c} \rho \\ u \\ p \\ \end{array}} \right]$, $M=\left[ {\begin{array}{ccc} u &{}\quad \rho &{}\quad 0 \\ 0 &{}\quad u &{}\quad { 1}/\rho \\ 0 &{}\quad \rho C^{2} &{}\quad u \\ \end{array}} \right]$ and $N=\left[ {\begin{array}{c} { m\rho u}/x \\ 0 \\ {\rho C^{2}mu}/x \\ \end{array}} \right]$.

The eigenvalues of the matrix M are $u+C$, u and $u-C$. Since all the eigenvalues of the coefficient matrix M are real and distinct therefore the system of equations (6) is strictly hyperbolic in nature.

Progressive Wave Approximations

The solution vector V of Eq. (6) is said to define a progressive wave if there exist a family of propagating surfaces $\Omega \left( {x,t} \right) =\alpha$, called wavelets, such that the magnitude of rate of change of fluid flow parameters $\rho$, u and p with respect to x for fixed wavelet $\Omega \left( {x,t} \right) =\alpha$ is very small as compared with the magnitude of the variation of the flow parameters with respect to x for a fixed time t [10]. Such type of motion is clearly an extension of the theory of simple wave, where we can find a variables $\Omega \left( {x,t} \right)$ such that the flow variables $\rho$, u and p can be expressed only in terms of $\Omega$. This shows that the progressive waves, which we consider here, treated as slowly modulated simple waves. In order to determine a progressive wave solution, let us suppose a transformation from $\left( {x,t} \right)$ to $\left( {x,\Omega } \right)$ through $t=T\left( {x,\Omega } \right)$. Then equations (1), (2) and (5) may be transformed in terms of ${\bar{{\rho }}}$, ${\bar{{u}}}$ and ${\bar{{p}}}$ through $\rho \left( {x,t} \right) ={\bar{{\rho }}}\left( {x,\Omega } \right)$, $u\left( {x,t} \right) ={\bar{{u}}}\left( {x,\Omega } \right)$ and $p\left( {x,t} \right) ={\bar{{p}}}\left( {x,\Omega } \right)$ respectively.

$$\begin{aligned}&\left( {1-uT_x } \right) \rho _t -\rho u_t T_x +{\bar{{u}}} {\bar{{\rho }}}_x +{\bar{{\rho }}} {\bar{{u}}}_x +{m{\bar{{\rho }}} {\bar{{u}}}}/x=0, \end{aligned}$$

(7)

$$\begin{aligned}&\left( {1-uT_x } \right) u_t -{T_x p_t }/\rho +{\bar{{u}}} {\bar{{u}}}_x +{{\bar{{p}}}_x }/{{\bar{{\rho }}}}=0,\end{aligned}$$

(8)

$$\begin{aligned}&\left( {1-uT_x } \right) p_t -\rho C^{2}T_x u_t +{\bar{{u}}}{\bar{{p}}}_x +{\bar{{\rho }}}{\bar{{C}}}^{2}\left( {{\bar{{u}}}_x +{m{\bar{{u}}}}/x} \right) =0, \end{aligned}$$

(9)

where ${\bar{{C}}}^{2}={\Gamma {\bar{{p}}}}/{\left( {1-\bar{{Z}}} \right) }{\bar{{\rho }}}$.

Since the solution is supposed to be a progressive wave therefore, we have$\left| {{\partial {\bar{{\rho }}}}/{\partial x}} \right|<<\left| {{\partial \rho }/{\partial x}} \right|$.

But in a progressive wave $\rho _x \simeq \rho _t T_x$, therefore above equation becomes

$$\begin{aligned} \left| {{\partial {\bar{{\rho }}}}/{\partial x}} \right|<<\left| {{\partial \rho }/{\partial t}} \right| . \end{aligned}$$

(10)

Similarly as above, we can write

$$\begin{aligned}&\left| {{\partial {\bar{{u}}}}/{\partial x}} \right|<<\left| {{\partial u}/{\partial t}} \right| , \end{aligned}$$

(11)

$$\begin{aligned}&\left| {{\partial {\bar{{p}}}}/{\partial x}} \right|<<\left| {{\partial p}/{\partial t}} \right| . \end{aligned}$$

(12)

Further if ${\bar{{\rho }}}_x =O\left( {{\bar{{\rho }}}/x} \right)$, ${\bar{{u}}}_x =O\left( {{\bar{{u}}} /x} \right)$ and ${\bar{{p}}}_x =O\left( {{\bar{{p}}}/x} \right)$ then Eqs. (7)–(9) can be written in a more convenient form as

$$\begin{aligned}&\left( {1-uT_x } \right) \rho _t -\rho u_t T_x =0, \end{aligned}$$

(13)

$$\begin{aligned}&\left( {1-uT_x } \right) u_t -{T_x p_t }/{\rho =0}, \end{aligned}$$

(14)

$$\begin{aligned}&\left( {1-uT_x } \right) p_t -\rho C^{2}T_x u_t =0, \end{aligned}$$

(15)

which, on simplification gives us

$$\begin{aligned} T_x =\left( {u+C} \right) ^{-1}. \end{aligned}$$

(16)

From Eq. (16) we observe that the wavelets are nothing but the characteristic curves of system of partial differential equations (6). Using Eq. (16) in (13)–(15) we have

$$\begin{aligned} {\bar{{C}}}^{2}{\bar{{\rho }}}_\Omega ={\bar{{p}}}_\Omega ={\bar{{\rho }}} {\bar{{C}}} {\bar{{u}}}_\Omega . \end{aligned}$$

(17)

Now in order to find the compatibility condition of system of Eqs. (7)–(9), multiplying equation (8) by ${\bar{{\rho }}} {\bar{{C}}}$ and then adding to Eq. (9), which gives the compatibility condition containing ${\bar{{\rho }}}$, ${\bar{{u}}}$, ${\bar{{p}}}$ and their derivatives as

$$\begin{aligned} \left( {{\bar{{\rho }}} {\bar{{C}}} {\bar{{u}}}_x +{\bar{{p}}}_x } \right) \left( {{\bar{{u}}}+{\bar{{C}}}} \right) +{m{\bar{{\rho }}} {\bar{{u}}} {\bar{{C}}}^{2}}/x=0\quad . \end{aligned}$$

(18)

Let us suppose the region, in which the disturbance is propagating, is uniform and at rest characterizing as $\rho =\rho _0$, $u=0$ and $p=p_0$. It is possible to choose the label of each wavelet $\Omega$ so that $\Omega =t$ at $x=x_0$; consequently assuming the boundary condition for ${\bar{{\rho }}}$ and T to be

$$\begin{aligned} {\bar{{\rho }}}=g\left( \Omega \right) , \quad T=\Omega ,\hbox { at }\, x=x_0, \end{aligned}$$

(19)

where g is a smooth bounded function i.e. $\left| g \right| =O\left( 1 \right)$. In the progressive wave approximation, in view of Eq. (17) we have

$$\begin{aligned} {\bar{{u}}}\left( {x,\Omega } \right) =U\left( {{\bar{{\rho }}}\left( {x,\Omega } \right) } \right) , \quad {\bar{{p}}}\left( {x,\Omega } \right) =P\left( {{\bar{{\rho }}}\left( {x,\Omega } \right) } \right) . \end{aligned}$$

(20)

Using Eqs. (20), (16) can be solved for $t=T\left( {x,\Omega } \right)$ as

$$\begin{aligned} T=\Omega +\int _{x_0 }^x {\frac{1}{U\left( {{\bar{{\rho }}}} \right) +F\left( {{\bar{{\rho }}}} \right) }dx} . \end{aligned}$$

(21)

Also, in view of Eqs. (20), (18) can be solved for ${\bar{{\rho }}}$ as a function of x and $\Omega$

$$\begin{aligned} {\bar{{\rho }}} U\left( {{\bar{{\rho }}}} \right) =g\left( \Omega \right) U\left( {g\left( \Omega \right) } \right) \left( {x/{x_0 }} \right) ^{-m/2}, \end{aligned}$$

(22)

where $U\left( {{\bar{{\rho }}}} \right) =\int \limits _{\rho _0 }^{{\bar{{\rho }}}} {\frac{F\left( s \right) }{s}} ds$, $P\left( {{\bar{{\rho }}}} \right) =p_0 \left( {\frac{1-Z_0 }{\rho _0 }} \right) ^{\Gamma }\left( {\frac{{\bar{{\rho }}}}{1-\bar{{Z}}}} \right) ^{\Gamma }$ and $F\left( s \right) =\left( {\frac{\Gamma P\left( s \right) }{\left( {1-\theta s} \right) s}} \right) ^{1/2}$.

where $Z_0 =\theta \rho _0$. From Eq. (21) it follows immediately that a shock first forms at a point $x=x_s$ on the wavelets $\Omega _s$, where $x_s$ can be found from the solution of

$$\begin{aligned} 1-\int \limits _{x_0 }^{x_s } {\frac{\Gamma \left( {\Gamma +1} \right) P\left( {{\bar{{\rho }}}} \right) }{2{\bar{{\rho }}}^{2}F\left( {{\bar{{\rho }}}} \right) \left( {1-\bar{{Z}}} \right) ^{2}\left[ {U\left( {{\bar{{\rho }}}} \right) +F\left( {{\bar{{\rho }}}} \right) } \right] ^{2}}\left( {\frac{\partial {\bar{{\rho }}}}{\partial \Omega }} \right) _{\Omega =\Omega _s } dx=0} , \end{aligned}$$

(23)

Equations (20)–(23) construct the desired modulated simple wave solution. Indeed the disturbance that propagates into a uniform region $\rho =\rho _0$, $u=0$, $p=p_0$ and is expressed by equations (20)–(23), can be obtained from Eqs. (21), (22) and further density ${\bar{{\rho }}}$ can be found. With the help of ${\bar{{\rho }}}$, velocity ${\bar{{u}}}$ and pressure ${\bar{{p}}}$ can be obtained from Eq. (20). It is also evident from the equation (23) that the solution may break after running a finite length $x_s$ depending on the dust particles $\theta$. Now we shall investigate shock wave propagation into an undisturbed region with $u=0$ ahead of the shock.

Small Amplitude Disturbances

For studying the flow pattern and its distortions explicitly, let us consider the disturbed flow as a perturbation of the uniform state, which is of the form ${\bar{{\rho }}}=\rho _0 +\rho _1$ where the perturbed density $\rho _1$ is taken to be very small. Therefore from Eq. (20) we have

$$\begin{aligned} {\bar{{p}}}\left( {x,\Omega } \right) =p_0 +\rho _1 \left( {x,\Omega } \right) F_0 ^{2}, \quad {\bar{{u}}}\left( {x,\Omega } \right) =\rho _1 \left( {x,\Omega } \right) {F_0 }/{\rho _0 }. \end{aligned}$$

(24)

With the assumption $\left| {g\left( \Omega \right) -\rho _0 } \right|<<1$, the perturbed density $\rho _1$ is given by

$$\begin{aligned} \rho _1 \left( {x,\Omega } \right) =g\left( \Omega \right) \left( {x/{x_0 }} \right) ^{-m/2}. \end{aligned}$$

(25)

Now Eq. (21) on integration, yields the perturbed wavelet as

$$\begin{aligned} T\left( {x,\Omega } \right) =\Omega +{\left( {x-x_0 } \right) }/{F_0 -\psi _1 g\left( \Omega \right) \omega \left( x \right) }, \end{aligned}$$

(26)

where $\psi _1 =\frac{\Gamma \left( {\Gamma +1} \right) p_0 }{2\rho _0^2 F_0 ^{3}\left( {1-Z_0 } \right) ^{2}}$,

and

$$\begin{aligned} \omega \left( x \right) =\left\{ {\begin{array}{ll} x-x_0 , &{}\hbox {if }\,\, m=0, \\ 2x_0 \left( {\left( {\frac{x}{x_0 }} \right) ^{1/2}-1} \right) , &{} \hbox {if }\,\, m=1, \\ x_0 \log \left( {\frac{x}{x_0 }} \right) , &{}\hbox {if } \,\, m=2. \\ \end{array}} \right. \end{aligned}$$

From Eq. (26) we observe that for $\psi _1 >0$, a shock forms on a compression wavelet $\left( {{dg\left( \Omega \right) }/{d\Omega }>0} \right)$ at a distances $x_s$, given by

$$\begin{aligned} \psi _1 \omega \left( {x_s } \right) \left( {\frac{dg\left( \Omega \right) }{d\Omega }} \right) _{\hbox {at} \Omega =\Omega _s } =1. \end{aligned}$$

(27)

Equation (25) represents that, along the wavelets the perturbed density $\rho _1$ is constant for planar flow ($m=0$) and decay according to the power law in case of cylindrically symmetric ($m=1$) and spherically symmetric ($m=2$) flows.

When a shock wave is formed it will separate the portions of the continuous region. Here we can use the following equal area rule to determine the location of the weak shock wave, see [9]

$$\begin{aligned} \int \limits _{\Omega _1 }^{\Omega _2 } {g\left( \zeta \right) d\zeta } =\left( {\Omega _2 -\Omega _1 } \right) \left( {\frac{g\left( {\Omega _1 } \right) +g\left( {\Omega _2 } \right) }{2}} \right) , \end{aligned}$$

(28)

where $\Omega _1$ and $\Omega _2$ are the wavelets ahead of the shock and behind of the shock respectively.

Evolution of Shocks

To study the early history of shock decay after its formation on the leading wave front $\Omega =0$, consider a special case in which the disturbance at the boundary $x=x_0$ is a pulse defined as

$$\begin{aligned} g\left( \Omega \right) =\left\{ {\begin{array}{ll} 0 , &{}\hbox { if }\,\, \Omega<0, \\ \rho _0 \delta \sin \left( {\frac{\Omega F_0 }{x_0 }} \right) , &{} \hbox { if }\,\, 0<\Omega <\frac{\pi x_0 }{F_0 } \\ 0 , &{}\hbox { if }\,\, \Omega \hbox {>}\frac{\pi x_0 }{F_0 }. \\ \end{array}} \right. , \end{aligned}$$

(29)

So with the help of Eq. (29), the progressive wave solution for a moderately small amplitude disturbance can be obtained from Eqs. (24) and (25) as

$$\begin{aligned}&{\bar{{p}}}\left( {x,\Omega } \right) =p_0 +F_0^2 \rho _0 \delta \sin \left( {\frac{\Omega F_0 }{x_0 }} \right) \left( {\frac{x}{x_0 }} \right) ^{-m/2}, \end{aligned}$$

(30)

$$\begin{aligned}&{\bar{{u}}}\left( {x,\Omega } \right) =F_0 \delta \sin \left( {\frac{\Omega F_0 }{x_0 }} \right) \left( {\frac{x}{x_0 }} \right) ^{-m/2}, \end{aligned}$$

(31)

and

$$\begin{aligned} {\bar{{\rho }}}\left( {x,\Omega } \right) =\rho _0 +\rho _0 \delta \sin \left( {\frac{\Omega F_0 }{x_0 }} \right) \left( {\frac{x}{x_0 }} \right) ^{-m/2}. \end{aligned}$$

(32)

Also, from Eq. (26) we have

$$\begin{aligned} T\left( {x,\Omega } \right) =\Omega +\frac{1}{F_0 }\left( {x-x_0 } \right) -\frac{1}{\psi _{11} F_0 }\sin \left( {\frac{\Omega F_0 }{x_0 }} \right) \omega \left( x \right) . \end{aligned}$$

(33)

While, the shock formation distance ${x_s }/{x_0 }$ can be obtained from Eq. (27) as

$$\begin{aligned} \frac{x_s }{x_0 }=\left\{ {\begin{array}{ll} 1+\frac{\psi _{11} }{\cos \left( {{\Omega F_0 }/{x_0 }} \right) } , &{}\hbox {if }\,\, m=0, \\ \left( {1+\frac{\psi _{11} }{2\cos \left( {{\Omega F_0 }/{x_0 }} \right) }} \right) ^{2} , &{}\hbox {if }\,\, m=1, \\ \exp \left( {\frac{\psi _{11} }{\cos \left( {{\Omega F_0 }/{x_0 }} \right) }} \right) , &{} \hbox {if }\,\, m=2, \\ \end{array}} \right. \end{aligned}$$

(34)

where $\psi _{11}$ is a dimensionless constant quantity and is given by

$$\begin{aligned} \psi _{11} =\frac{2\left( {1-Z_0 } \right) }{\delta \left( {\Gamma +1} \right) }, \end{aligned}$$

(35)

with $Z_0 =\theta \rho _0$. In view of Eq. (35) we observe that $\psi _{11}$ will be positive for given $\theta$ and $\rho _0$ if $\theta \rho _0 <1$ and will be negative if $\theta \rho _0 >1$, thus a shock forms (since $x_s >x_0 )$ on the leading wave front $\Omega =0$ (respectively on the trailing wave front $\Omega =\pi )$. From Eq. (35) we have

$$\begin{aligned} \frac{\partial \psi _{11} }{\partial Z_0 }=\frac{-2}{\delta \left( {\Gamma +1} \right) }. \end{aligned}$$

(36)

Further for a shock of small strength i.e. for weak shock propagating into the disturbed region where $g\left( {\Omega _1 } \right) =0$ for $\Omega _1 \le 0$, in view of Eq. (29) and (33) we have from Eq. (28) as

$$\begin{aligned} \sin \left( {\frac{\Omega _2 F_0 }{2x_0 }} \right) =\left( {1-\frac{\psi _{11} x_0 }{\omega \left( x \right) }} \right) ^{1/2}. \end{aligned}$$

(37)

On using Eq. (37) in Eq. (32), the shock strength means i.e. jump in density can be obtained as

$$\begin{aligned} \left[ \rho \right] =2\rho _0 \delta \left( {\frac{x}{x_0 }} \right) ^{-m/2}\left( {\frac{\psi _{11} x_0 }{\omega \left( x \right) }\left( {1-\frac{\psi _{11} x_0 }{\omega \left( x \right) }} \right) } \right) ^{1/2}. \end{aligned}$$

(38)

From Eq. (38) we observe that the shock after its formation on $\Omega =0$ at the point $x=x_s >x_0$ rises to a maximum strength at the point $x=x_1 >x_s$, where $x_1$ can be obtained from the solution of the following equation:

$$\begin{aligned} \frac{\omega \left( x \right) }{x_0 }+m\left( {\frac{x}{x_0 }} \right) ^{-1+m/2}\left( {\frac{\omega \left( {x_1 } \right) }{x_0 }-\psi _{11} } \right) \frac{\omega \left( x \right) }{x_0 }-2\psi _{11} =0, \end{aligned}$$

(39)

and then decays ultimately in proportion to $x^{-m/2}$.

Let us consider a special case in which a small disturbance is taken at the boundary $x=x_0$ having a periodic wave front which is given as

$$\begin{aligned} g\left( \Omega \right) =\delta \rho _0 \sin \left( {{\hat{{\Omega }}}} \right) , \end{aligned}$$

(40)

where $\delta <0$ and ${\hat{{\Omega }}}$ is defined as ${\hat{{\Omega }}}={F_0 \Omega }/{x_0 }$ and suppose the growth over one cycle $0\le {\hat{{\Omega }}}\le 2\pi$ so that in this case shock will first form on the wavelet ${\hat{{\Omega }}}=\pi$ at a distance $x=x_s$ close to $x_0$ which is obtained from the solution of Eq. (27). Here Eqs. (26) and (28) are satisfied on the shock if ${\hat{{\Omega }}}_1 +{\hat{{\Omega }}}_2 =2\pi$ and ${\hat{{\Omega }}}_1 -{\hat{{\Omega }}}_2 =2\mu$, where $\mu$ can be obtained from the solution of the following equation:

$$\begin{aligned} \frac{\sin \mu }{\mu }=\frac{\psi _{11} x_0 }{\omega \left( x \right) }. \end{aligned}$$

(41)

Therefore the discontinuity in $\rho$ at the shock is given by

$$\begin{aligned} \left[ \rho \right] =2\delta \rho _0 \sin \mu \left( {x/{x_0 }} \right) ^{-m/2}, \end{aligned}$$

(42)

where x and $\mu$ satisfies the Eq. (41). From Eq. (42) we observe that the shock begins with zero strength corresponding to $\mu$ which tends to zero at $x=x_s$. Here $x_s$ can be obtained from the solution of equation (27). The shock strength increases to maximum for $\mu \rightarrow \mu _m$ at a point $x=x_m$ satisfying by following relation

$$\begin{aligned} \sin \left( {2\mu _m } \right) -m\psi _{11} \left( {\sin \left( {\mu _m } \right) } \right) -\mu _m \cos \left( {\mu _m } \right) \left( {{x_m }/{x_0 }} \right) ^{-1+m/2}=0. \end{aligned}$$

(43)

Fig. 1

Variation of $\psi _{11}$ versus $k_p$ for different values of $Z_0$

Fig. 2

Variation of the dimensionless density $\hat{{\rho }}={\left( {\rho _0 +\rho _1 } \right) }/{\rho _0 }$ with the dimensionless variable $\xi ={\left( {x-F_0 t} \right) }/{x_0 }$ on the leading wavelet $\Omega =0$ for $m=1$

Fig. 3

Variation of the dimensionless density $\hat{{\rho }}={\left( {\rho _0 +\rho _1 } \right) }/{\rho _0 }$ with the dimensionless variable $\xi ={\left( {x-F_0 t} \right) }/{x_0 }$ on the leading wavelet $\Omega =0$ for $m=2$

Fig. 4

Variation of the dimensionless density $\hat{{\rho }}={\left( {\rho _0 +\rho _1 } \right) }/{\rho _0 }$ with the dimensionless variable $\xi ={\left( {x-F_0 t} \right) }/{x_0 }$ on the wavelet ${\hat{{\Omega }}}=\pi$ in cylindrically symmetric flow

Fig. 5

Variation of the dimensionless density $\hat{{\rho }}={\left( {\rho _0 +\rho _1 } \right) }/{\rho _0 }$ with the dimensionless variable $\xi ={\left( {x-F_0 t} \right) }/{x_0 }$ on the wavelet ${\hat{{\Omega }}}=\pi$ in spherically symmetric flow

Fig. 6

Effect of variation of mass fractions on the growth and decay behaviour of shock in cylindrically symmetric flow

Fig. 7

Effect of variation of mass fractions on the growth and decay behaviour of shock in spherically symmetric flow

Results and Discussion

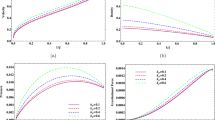
From Eq. (36) it is observed that $\psi _{11}$ is a decreasing function of $Z_0$. Further from Fig. 1, which is plotted by using Eq. (35), we observe that when $\psi _{11}>0$, then for a given value of mass fraction of dust particles in the gas (i.e. $k_p$) an increase in $Z_0$ causes to decrease in $\psi _{11}$, as a result the shock formation distance decreases i.e. shock forms earlier which is also evident from Eq. (34). Also from Eq. (34) it is observed that in case of nonplanar flow the shock formation is delayed as compared to the corresponding planar case. The distortion of the pulse, which is given by Eq. (29), is shown in Figs. 2 and 3 for three sets of values of mass fraction of the dust particles (i) $k_p =0.0$ (ii) $k_p =0.3$ and (iii) $k_p =0.6$. The value of the constants involved in the computation are chosen as $\gamma =1.4$, $\beta =0.8$, $Z=0.04$ and $\delta =0.35$. The effect of variation of mass fraction on the density for cylindrically symmetric and spherically symmetric flows is shown in the Figs. 2 and 3 respectively. From the Figs. 2 and 3 we infer that an increasing (decreasing) value of the mass fraction of the dust particles causes to slow down (enhance) the flattening of the wave profiles as a result the shock formation distance decreases (increases) i.e. early (delayed) shock formation. Also the shock formation distance increases in the case of nonplanar flows as compared to the corresponding planar flows. The evolution of shock waves governed by Eq. (40) are shown in Figs. 4 and 5 for cylindrically symmetric and spherically symmetric flows respectively. From these figures we observe that the shock first forms on the wavelet ${\hat{{\Omega }}}=\pi$ and then grows up to a maximum strength at a point $x=x_m$ and then decays according to the power law $x^{-m/2}$ given by Eq. (39). Further from Figs. 6 and 7 it is observed that, an increase in the value of mass fraction of the dust particles causes to decrease the shock strength and vice versa. Also it may be noted here that an increase in the mass fraction of dust particles causes to decrease the shock curvature.

Conclusions

Present paper uses the progressive wave approach to analyze the propagation of finite amplitude disturbances and moderately small amplitude disturbances in a dusty gas for generalized geometry. The influence of presence of dust particles in the mixture on the growth and decay behaviour of shock including weak shock are elucidated. It was observed that the amplitude dispersion depends on the amplitude of the wavelets which is dependent on the values of the mass fraction of dust particles. Also the shock formation distance varies according to variation of mass fraction of dust particles i.e. an increase (decrease) in the value of mass fraction of dust particles causes to decrease (increase) in the shock formation distance respectively. Further, in case of small amplitude disturbances, the condition which leads to shock or no shock depends strongly on the mass fraction of the dust particles. In order to trace out the early decay of shock after its formation, we have analyzed two different cases in which small amplitude disturbance is either a pulse or a periodic wave. The effect of increasing/decreasing value of mass fraction on the profile of shock strength is also presented.