1 Introduction

Many fields including mathematics as well as physics implements the evolutionary behavior of shock waves. The study of shock waves propagation in a mixture of non-ideal gas and small solid particles has become crucial because there are several applications of it, in fields like environmental and industrial. A few applications include nozzle flow, black hole theory, lunar ash flow and phenomena like nuclear blasts, volcanic explosion, dusty crystals formation, supersonic flight in dusty air etc. This literature is quite vast as it is concerned with the study of shock waves propagation in dusty gas [1, 2]. Strong shock waves consequentially produce high pressure and high temperature at the center of convergence, which is one of the prominent reason for it being a field of continuous research interest. This property of converging shocks further adds on to the several engrossing applications in different aspects such as fusion initiation, detonation. Shock waves is the most common treatment for kidney stones in the medical field and in laboratories, these waves are used to manage the high temperature to observe and analyse the numerous processes that occur in a gas medium. In past few decades, the researchers gave more attention to the shock wave because of its theoretical and practical involvement in the various fields such as material science, aerodynamics, astrophysics, medical science. Guderley [3], Zeldovich and Raizer [4], Hafner [5], Zhao et al. [6], Ramsey et al. [7], Pandey and Sharma [8] and Lazarus [9] investigated a theoretical study of converging shock waves in a gaseous medium.

The shock wave propagation in interstellar models has immense significance from astrophysical point of view and become an interesting topic for both physicists and astronomers. In the context of formation of stars, the collapse of interstellar gas clouds and the analytical and numerical studies have been made by many authors, some of them are worth mentioning [10,11,12]. In the past few decades, within the framework of Einstein’s theory of gravity, many extensive investigations on the gravitational collapse models were made which provided useful insights into the final fate of massive stars [13]. The acceleration waves, the formation of shocks, and their stability in the atmosphere involving gravity are studied by Muracchini and Ruggeri [14].

The non-linear discontinuity waves propagation theory has been applied to study the gravitational collapse of a spherically symmetric interstellar gas cloud by Ferraioli et al. [15]. Later, the study of gravitational collapse in self-gravitating gaseous systems were made by Virgopia and Ferraioli [16] by using an asymptotic wave approach. In order to understand how structure within interstellar gas is shaped and created, supersonic turbulence is an essential element. Gas components in interstellar medium have highly supersonic velocity dispersion which indicates that shock is already appearing in the medium. A crucial role is played by shock waves in a number of astrophysical phenomenon [17].

In this present work, we examined the study of propagation of converging shock waves in a spherical interstellar cloud of an non-ideal gas (van der Waals type) with dust particles using Lie group theoretic technique. Sophus Lie developed the group theoretic method which is one of the powerful and systematic methods for studying and obtaining the similarity solutions of systems of non-linear PDEs. The study of continuous symmetries in mathematics, theoretical physics and mechanics uses the Lie group of transformation frequently because it helps in simplifying the complicated problems into solvable equations. Generally, without approximations, it is tedious to find a solution for a system of non-linear PDEs. In Lie group of point transformations, there exists a solution of basic equation with respect to the Rankine-Hugoniot jump conditions along a set of curves, called the similarity curves, through which, the system of PDEs can be converted into the system of ODEs (see [18,19,20,21,22,23]). Thereafter, the system of ODEs can be solved conveniently by using some numerical techniques. A theoretical study for imploding shock was first performed by Guderley [3]. Logan and Perez [23] applied Lie group analysis to determine the entire class of self-similar solutions for one-dimensional, time-dependent shock hydrodynamics in which a chemical reaction takes place behind the shock front. To obtain the entire class of similarity solutions to a problem concerning radially and plane symmetric flows of a relaxing gas, Sharma and Radha [24] applied the Lie group method described in the works of Bluman and Cole [21], Bluman and Kumei [22] and Logan and Perez [23]. The method enables us to characterize the medium for which the problem is invariant and admits similarity solutions. Chadda and Jena [2] obtained the similarity solutions to the non-ideal dusty gas using Group theoretic technique. Yadav et al. [25] have studied the strong shock propagation in a non-ideal gas with rotational effect with the help of similarity method. Nath [26] investigated the flow behind an exponential shock wave in a perfectly conducting mixture of micro size small solid particles and non-ideal gas with azimuthal magnetic field. Sahu obtained the similarity solutions using Lie group theoretic method and the influence of magnetic and gravitational fields in a non-ideal dusty gas with heat conduction and radiation heat flux is analysed in [27]. Some other important works related to Lie group theoretic method are presented in [28,29,30,31]. The problem of converging shock wave in different material medium has been solved by many researchers [32,33,34,35,36,37] by using the perturbation series method. Also, the other remarkable recent works have been presented in the literature [38,39,40,41,42].

An interstellar gas cloud is composed of a mixture of atomic hydrogen in large percentage, molecular hydrogen, and in a minor percentage carbon, oxygen, heavy elements, some of which ionized. It is also important to mention that in the interstellar medium different types of grains and dust exist [43]. Many physical phenomena in cosmology and astrophysics, which involve the gravitational collapse in interstellar gas clouds, are of great importance because of the description of star formation. Therefore, the study of the collapse of a self-gravitating interstellar gas clouds in the spiral arms of the galaxy has grabbed the attention of the astronomers and physicists. From the authors’ studies so far, the considered problem has not been addressed in any of the previous research publications using the method of Lie group of invariance, which distinguishes this work from the previously published studies and makes this work novel. The present work can be significant to confirm the correctness of the solution obtained by using the theory of self-similarity and computational methods. In the present work, we consider the one dimensional flow in a spherical interstellar, self gravitating cloud with dust particles in Sect. 2. We have adopted the model of van der Waals gas with dust particles to discover how the deviations from the ideal gas to non-ideal gas can affect the flow parameters behind the shock wave. This system is more complex than the Euler equations in ordinary gas dynamics and it is quite difficult to obtain the exact analytical solution to the problem without approximation. By writing the system of PDEs (1) in its conservative form, we derive the Rankine-Hugoniot jump conditions in Sect. 3. The motivation behind the present study comes from the work presented by Logan and Perez [23] and Logan [29]. They investigated a problem in shock hydrodynamics by using the similarity method and determined all possible class of self-similar solutions. In Sect. 4, we determine the similarity solutions to the one-dimensional, unsteady, spherically symmetric flow in an interstellar non-ideal dusty gas clouds by using the method mentioned in Bluman and Cole [21], Bluman and Kumei [22], Logan and Perez [23] and Logan [29]. In Sect. 5, The collapse of imploding shock for the spherically symmetric flow with power law shock path is worked out in detail and numerical calculations have been performed to estimate the leading similarity exponents. In Sect. 6, the comparison of the obtained similarity exponent is made with the results obtained by the characteristic method and listed in Table 1 for various values of \(k_{p}, \beta , \Psi\) and b. Flow profiles behind the shock have been shown graphically. In Sect. 7, all the observations are discussed in detail. Section 8 concludes the paper.

2 Basic equations

We consider the one dimensional flow in a spherical interstellar, self gravitating cloud with dust particles under the following main assumptions: the dust particles are spherical, uniform in size, taking up less than \(5\%\) of the total volume, incompressible, their adiabatic index is constant, and within each particle, the temperature is uniform, the interaction between different size particles is neglected, dust particles are uniformly distributed, mass transfer and heat transfer are not considered into account between two phases. The effect of particles on gas appears at the first in the wake of the particles and then distributed over the rest of the gas by mixing, and the external forces are not applied on the mixture of gas.

The system of equations describing the one-dimensional, spherically symmetric flow in an invicid, self-gravitating, interstellar non-ideal dusty gas cloud can be expressed as follows [12, 15]

$$\begin{aligned} & \frac{{\partial \rho }}{{\partial t}} + u\frac{{\partial \rho }}{{\partial r}} + \rho \frac{{\partial u}}{{\partial r}} + \frac{{2\rho u}}{r} = 0, \\ & \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial r}} + \frac{1}{\rho }\frac{{\partial p}}{{\partial r}} = g, \\ & \frac{{\partial p}}{{\partial t}} + u\frac{{\partial p}}{{\partial r}} + \rho a^{2} \left( {\frac{{\partial u}}{{\partial r}} + \frac{{2u}}{r}} \right) = - \frac{{(\Gamma - 1)(1 + \bar{b}\rho )\rho }}{{(1 - z)}}L(p,\rho ), \\ & \frac{{\partial g}}{{\partial t}} + u\frac{{\partial g}}{{\partial r}} + \frac{{2gu}}{r} = 0, \\ \end{aligned}$$
(1)

where \(\rho , u, p\), t, r, g represent the density, fluid velocity, pressure, time, spatial coordinate which is radial in spherically symmetric flows, gravitational force per unit mass, respectively. L is the cooling-heating function. \(\varGamma\) (Gr\(\ddot{u}\)neisen coefficient) is defined as

$$\begin{aligned} \varGamma =\dfrac{\gamma (1+\lambda \beta )}{(1+\lambda \beta \gamma )}, \end{aligned}$$

with \(\lambda =k_{p}/(1-k_{p})\), \(\gamma =c_{p}/c_{v}\), \(\beta =c_{sp}/c_{p}\), where \(c_{sp}\) is the specific heat of solid particle, \(c_{v}\) and \(c_{p}\) are the specific heats of gas at constant volume and constant pressure, respectively. \({\bar{b}}=b(1-k_{p})\), where \(k_{p}\) is mass fraction of the solid particles in the mixture defined as \(k_{p}=m_{sp}/m_{g},\) with \(m_{g}\) and \(m_{sp}\) as the total mass of the mixture and total mass of solid particles, respectively and b \((0.9\times 10^{-3}\le b\le 1.1\times 10^{-3})\) is the van der Waals excluded volume [44]. We have a relation between the mass fraction \(k_{p}\) and the volume fraction z given by the expression \(z=\vartheta \rho ,\) where \(\vartheta =k_{p}/\rho _{sp}\), with \(\rho _{sp}\) as the density of solid particles. We introduce the ratio of density of solid particles to the species density of the gas as \(\Psi =\rho _{sp}/\rho _{g}\). The equation of state for the mixture of non-ideal gas [44] and dust particles [2] is of the form:

$$\begin{aligned} p=\frac{(1-k_{p})(1+{\bar{b}}\rho )}{(1-z)}\rho {\mathcal {R}}{\mathcal {T}}, \end{aligned}$$
(2)

where \({\mathcal {R}}\) is the specific gas constant and \({\mathcal {T}}\) is the absolute temperature of the gas and the solid particles, provided the equilibrium flow conditions are maintained.

Also, for isentropic flow the speed of sound is given by

$$\begin{aligned} \begin{aligned} a^{2}&=\Big (\frac{\partial p}{\partial \rho }\Big )_{{\textbf {S}}}\\&=\Big (\frac{(\varGamma -\vartheta {\bar{b}}\rho ^{2}+2\varGamma {\bar{b}}\rho +(\varGamma -1){\bar{b}}^{2}\rho ^{2}) p}{(1-z)(1+{\bar{b}}\rho )\rho }\Big )^{1/2}, \end{aligned} \end{aligned}$$
(3)

where \({\textbf {S}}\) refers to the process of constant entropy, and a depends on the parameters \(\vartheta\) and \({\bar{b}}\), which are defined above. The above system (1) can be written in matrix notation, as

$$\begin{aligned} {\mathcal {F}}_{t}(r,t,{\mathcal {W}})+{\mathcal {G}}_{r}(r,t,{\mathcal {W}})={\mathcal {H}}(r,t,{\mathcal {W}}), \end{aligned}$$
(4)

where \({\mathcal {W}}=(\rho , u, p, g)^{tr}\), \({\mathcal {F}}=(\rho , \rho u, \rho e, \rho g)^{tr}\), \({\mathcal {G}}=(\rho u,(p+\rho u^{2}), u(p+\rho e),\rho ug)\),

\({\mathcal {H}}=(-\frac{2\rho u}{r}, g\rho -\frac{2\rho u^{2}}{r},-\frac{2u(p+\rho e)}{r},-\frac{4\rho ug}{r})\) with “tr" denoting the transpose. and e is the total energy defined as below

$$\begin{aligned} e=\frac{(1-\vartheta \rho ) p}{(\varGamma -1)(1+{\bar{b}}\rho )\rho }+L+\frac{u^{2}}{2}, \end{aligned}$$
(5)

where \(L(p,\rho )\) represents the energy variation per unit mass which is positive or negative depending upon the cooling or heating of dusty gas clouds, respectively. Initially, we assume that \(L=0,\) i.e, there is no net gain or loss of energy. The cooling-heating function given in Eq. (1) is determined as

\(L=C_{ei}+C_g+C_{H_2}-H_{CR}-H_{ph}+C_{H}+A\) (erg cm\(^3\,s^{-1}),\) where \(C_{ei}=\dfrac{10^{-23}n_{H}n_e}{T^{1/2}}\left( 0.64 e^{-92/T}+1.7e^{-554/T}+6.4e^{413/T}+2.2e^{-961/T}\right)\) (iconic cooling),

$$C_{g} = \left\{ {\begin{array}{*{20}l} {1.37 \times 10^{{ - 29}} \epsilon n_{H}^{2} T^{{1/2}} ,} \hfill & {T > 180^{0} } \hfill \\ {7.33 \times 10^{{ - 32}} \epsilon n_{H}^{2} T^{{1/2}} (T - T_{g} ),} \hfill & {T \le 180^{0} K\,{\text{(inelastic collisions)}}} \hfill \\ {{\text{or}}} \hfill & {} \hfill \\ 0 \hfill & {{\text{(elastic collisions)}},} \hfill \\ \end{array} } \right.$$

\(C_{H_2}=\dfrac{8.45\times 10^{-24}n_{H_2}e^{-502/T}}{\left\{ 1+\dfrac{42}{n_{H}T^{1/2}(1+0.1n_{H_2}/n_{H})} \right\} }\) (\(H_2\) cooling),

\(H_{CR}=1.6\times 10^{-11}Fn_{H}\left( 1+2\frac{n_{H_2}}{n_H} \right) \; (\text{cosmic\,ray\,heating}),\)

\(H_{ph}=4.82\times 10^{-26}n_{H}n_{e}T^{0.6548} \quad (\text{photo-ionization\,heating}),\)

\(C_{H}=\dfrac{3\times 10^{-24}}{T^{1/2}}e^{-227/T}n_{H}n_{e} \quad (\text{hydrogen\,atom\,cooling}),\)

\(A=-\dfrac{3.8\times 10^{-29}}{T^{1/2}}(n_{H})^2e^{-23.6/T} \quad(\text{other\,atomic\,cooling\,processes}).\)

Here \(n_{H},\) \(n_{e},\) and \(n_g\) denote the hydrogen, electron, and grain number density, respectively. \(r_{r}\) is the radius of the grains and \(T_{g}\) is the temprature of the radius. F is the cosmic ray flux and \(\epsilon\) is the free parameter.

3 Rankine–Hugoniot conditions

The Rankine-Hugoniot jump relation [45] is given by the following

$$\begin{aligned}{}[{\mathcal {F}}_{k}]V=[{\mathcal {G}}],\, k=1,2,3,4, \end{aligned}$$
(6)

where V and \([Y]=Y-Y_{0}\) represent the shock velocity and jump in variable Y, respectively. The medium ahead of shock ( i.e upstream condition ) is denoted by the subscript o while the medium behind the shock (i.e downstream condition) is denoted by without the subscript. Consider the shock front \(r=Q(t)\) is moving forward with velocity V into the inhomogeneous medium which is given by \(u_{0} =0,\quad p_{0}\) = constant,    \(\rho _{0}= \rho _{0}(r)\),    \(g_{0} = g_{0}(r)\).

In view of Eqs.(3) and (6), the boundary conditions just behind the shock front can be obtained from the following relations:

$$\begin{aligned} \rho (V-u)=\, & {} \rho _{0}(V-u_{0}),\nonumber \\ p+\rho (V-u)^{2}=\, & {} p_{0}+\rho _{0}(V-u_{0})^{2},\\ h+\frac{(V-u)^{2}}{2}=\, & {} h_{0}+\frac{(V-u_{0})^{2}}{2},\nonumber \\ g=\,g_{0},\nonumber \end{aligned}$$
(7)

Here, \(v=V - u\) represents the particle speed relative to the shock speed behind the wavefront, \(h=\varepsilon +p/\rho\) denotes the enthalpy, where \(\varepsilon =L+((1-\vartheta \rho ) p)/((\varGamma -1)(1+{\bar{b}}\rho )\rho )\) is the internal energy per unit mass of the system.

Equations(7)\(_{1}\) and (7)\(_{2}\) imply

$$\begin{aligned} v=\frac{\rho _{0}V}{\rho }, \quad p=p_{0}+\rho _{0}V^{2}-\frac{\rho _{0}^{2}V^{2}}{\rho }. \end{aligned}$$
(8)

Using (9) into (8)\(_{3}\), we obtain the following cubic equation in density \(\rho\) across the shock

$$\begin{aligned}{} & {} \Big (2p_{0}{\bar{b}}(1-\vartheta \rho _{0})+\Omega \Big )\rho ^{3}-\nonumber \\{} & {} \Big ((2p_{0}{\bar{b}}(1-\vartheta \rho _{0})+\Omega )\rho _{0}+\Theta \Big )\rho ^{2}\nonumber \\{} & {} \quad +\Big (\Theta \rho _{0}-(\varGamma +1)(1+{\bar{b}}\rho _{0})\rho _{0}^{2}V^{2}\Big )\rho \nonumber \\{} & {} \quad +(\varGamma +1)(1+{\bar{b}}\rho _{0})\rho _{0}^{3}V^{2}=0, \end{aligned}$$
(9)

where \(\Omega =(\varGamma -1){\bar{b}}(1+{\bar{b}}\rho _{0})(2p_{0}+\rho _{0}V^{2})\) and \(\Theta =(1+{\bar{b}}\rho _{0})\Big (-2p_{0}\varGamma +\rho _{0}V^{2}(1-\varGamma -2\vartheta \rho _{0}+\rho _{0}{\bar{b}}(\varGamma -1))\Big ).\)

Rankine-Hugoniot Jump conditions on the basis of parameter \(\vartheta\) and b: One can easily solve the Eq.(9) for density \(\rho (Q(t))\) in terms of flow variables just ahead of the shock and thereafter other flow variables u(Q(t)), p(Q(t)) and g(Q(t)) at shock front can be obtained from Eqs. (7), (8) as follows:

Case (i):If \(\vartheta \ne 0\) and \(b\ne 0\) i.e. the mixture is a non-ideal gas with dust particle. On solving (9), we get the following boundary conditions at shock front:

$$\begin{aligned} \rho =\frac{\rho _{0}}{\mu },\quad u=(1-\mu )V, \quad p=p_{0}+(1-\mu )\rho _{0}V^{2},\quad g= & {} g_{o}(Q(t)), \end{aligned}$$
(10)

with

$$\begin{aligned} \mu =\frac{2\rho _{0}(\Omega +2{\bar{b}}p_{0}(1-\vartheta \rho _{0}))}{\Theta \pm \sqrt{\Theta ^{2}+4\rho _{0}^{2}V^{2}(\varGamma +1)(1+{\bar{b}}\rho _{0})(\Omega +2{\bar{b}}p_{0}(1-\vartheta \rho _{0}))}}. \end{aligned}$$

The conditions for strong shocks, in Eqs (10) reduce to

$$\begin{aligned} \rho =\frac{\rho _{0}}{\mu ^{*}},\quad u=(1-\mu ^{*})V, \quad p=(1-\mu ^{*})\rho _{0}V^{2},\quad g= & {} g_{o}(Q(t)), \end{aligned}$$
(11)

with

$$\begin{aligned} \begin{aligned} \mu ^{*}&=\frac{2{\bar{b}}\rho _{0}(\varGamma -1)(1+{\bar{b}}\rho _{0})}{\Theta ^{*}\pm \sqrt{(\Theta ^{*})^{2}+4\rho _{0}{\bar{b}}(\varGamma ^{2}-1)(1+{\bar{b}}\rho _{0})^{2}}},\\ \Theta ^{*}&=(1+{\bar{b}}\rho _{0})\Big (1-\varGamma -2\vartheta \rho _{0}+(\varGamma -1)\rho _{0}{\bar{b}}\Big ). \end{aligned} \end{aligned}$$

Case (ii): If \(\vartheta =0\) and \(b=0\) i.e. the mixture is a ideal gas (i.e. ideal in the sense that there is no interaction between the gas molecules ), then \(\varGamma =\gamma ,\) \(a^{2}=\gamma p/\rho\) and boundary conditions (10), (11) become:

at shock front,

$$\begin{aligned} \begin{aligned} \rho= & {} \frac{(\gamma +1)\rho _{0}^{2}V^{2}}{(\gamma -1)\rho _{0}V^{2}+2\gamma p_{0}},\quad u=\frac{2}{(\gamma +1)}\frac{\rho _{0}V^{2}-\gamma p_{0}}{\rho _{0}V},\\ p= & {} \frac{2\rho _{0}V^{2}-(\gamma -1)p_{0}}{(\gamma +1)},\quad g = g_{o}(Q(t)), \end{aligned} \end{aligned}$$
(12)

for strong shock,

$$\begin{aligned} \begin{aligned} \rho= & {} \frac{(\gamma +1)}{(\gamma -1)}\rho _{0},\quad u=\frac{2}{(\gamma +1)}V,\\ p= & {} \frac{2}{(\gamma +1)}\rho _{0}V^{2},\quad g= g_{o}. \end{aligned} \end{aligned}$$
(13)

Case (iii): If \(\vartheta =0\) and \(b\ne 0\) i.e. the mixture is a non-ideal gas, then \(\varGamma =\gamma\), \(a^{2}=((\gamma +2\gamma {\bar{b}}\rho +(\gamma -1){\bar{b}}^{2}\rho ^{2}) p)/(\rho (1+{\bar{b}}\rho ))\) and boundary conditions (10)-(11) become:

at shock front,

$$\begin{aligned} \rho= & {} \frac{\rho _{0}}{\mu _{1}},\quad u=(1-\mu _{1})V, \quad p=p_{0}\nonumber \\{} & {} \quad +(1-\mu _{1})\rho _{0}V^{2},\quad g= g_{o}(Q(t)), \end{aligned}$$
(14)

with

$$\begin{aligned} \begin{aligned} \mu _{1}&=\frac{2\rho _{0}(\Omega _{1}+2{\bar{b}}p_{0})}{\Theta _{1}\pm \sqrt{\Theta _{1}^{2}+4\rho _{0}^{2}V^{2}(\gamma +1)(1+{\bar{b}}\rho _{0})(\Omega _{1}+2{\bar{b}}\rho _{0})}},\\ \Omega _{1}&=(\gamma -1){\bar{b}}(1+{\bar{b}}\rho _{0})(2p_{0}+\rho _{0}V^{2}),\\ \Theta _{1}&=(1+{\bar{b}}\rho _{0})\Big (-2p_{0}\gamma +\rho _{0}V^{2}(1-\gamma +\rho _{0}{\bar{b}}(\gamma -1))\Big ), \end{aligned} \end{aligned}$$

and for strong shocks,

$$\begin{aligned} \rho =\frac{\rho _{0}}{\mu _{1}^{*}},\quad u=(1-\mu _{1}^{*})V, \quad p=(1-\mu _{1}^{*})\rho _{0}V^{2},\quad g= & {} g_{o}(Q(t)), \end{aligned}$$
(15)

with

$$\begin{aligned} \begin{aligned} \mu _{1}^{*}&=\frac{2{\bar{b}}\rho _{0}(\gamma -1)(1+{\bar{b}}\rho _{0})}{\Theta ^{*}_{1}\pm \sqrt{(\Theta ^{*}_{1})^{2}+4\rho _{0}{\bar{b}}(\gamma ^{2}-1)(1+{\bar{b}}\rho _{0})^{2}}},\\ \Theta _{1}^{*}&=(1-\gamma )(1-\bar{b^{2}}\rho _{0}^{2}). \end{aligned} \end{aligned}$$

Case (iv): If \(\vartheta \ne 0\) and \(b=0\), i.e., the mixture of an ideal gas with dust particles, then \(a^{2}=(\varGamma p)/\rho (1-\vartheta \rho )\) and boundary conditions (10)-(11) become:

at shock front,

$$\begin{aligned} \begin{aligned} \rho=&\frac{(\varGamma +1)\rho _{0}^{2}V^{2}}{(\varGamma -1+2\vartheta \rho _{0})\rho _{0}V^{2}+2\varGamma p_{0}},\quad u=\frac{2}{(\varGamma +1)}\frac{(1-\vartheta \rho _{0})\rho _{0}V^{2}-\varGamma p_{0}}{\rho _{0}V},\\ p=&\frac{2(1-\vartheta \rho _{0})\rho _{0}V^{2}-(\varGamma -1)p_{0}}{(\gamma +1)},\quad g= g_{o}(Q(t)), \end{aligned} \end{aligned}$$
(16)

and for strong shock,

$$\begin{aligned} \begin{aligned} \rho&=\frac{(\varGamma +1)}{(\varGamma -1+2\vartheta \rho _{0})}\rho _{0},\quad u=\frac{2(1-\vartheta \rho _{0})}{(\varGamma +1)}V,\\ p=&\frac{2(1-\vartheta \rho _{0})}{(\varGamma +1)}\rho _{0}V^{2},\quad g= g_{o}. \end{aligned} \end{aligned}$$
(17)

4 Self-similar solution using lie group invariance analysis

Similarity method for finding the similarity solutions of PDEs is usually based on the property that it reduces the number of independent variables in the model equations to be reduced by one. In case of multi-dimensional problem dealing with similarity method by means of one-parameter Lie group of point transformations reduces one independent variable at each step and gives a new equation with one independent variable less than the previous step. The obtained new equation at each step must remain invariant under the Lie group of transformations. One parameter group of transformations that leaves invariant a given PDEs, we can construct a solution that is remains unchanged under the transformation. We study the motion of converging shock wave in a self-gravitating, interstellar non-ideal dusty gas cloud by using the similarity method.

“In order to obtain the similarity solutions for the system of PDEs (1), we consider one-parameter (\(\epsilon\)) Lie group of point transformations (see [21, 23, 29]) under which the system of PDEs (1) reduces to the system of ODEs in terms of new variable \(\xi\), which is called the similarity variable”. For simplicity, let us take \(r_1 = t, r_2 = r, u_1 = \rho , u_2 = u, u_3 = p, u_4 = g\), and then the one-parameter (\(\epsilon\)) Lie group of point transformations for system (1) is given by

$$\begin{aligned} \begin{aligned} r^*_{l} = r_{l} + \epsilon \, \xi ^{l}_{r}(r_{1},r_{2},u_{1},u_{2},u_{3},u_{4})+O(\epsilon ^{2}), \\ u^*_{n} = u_{n} + \epsilon \, \xi ^{n}_{u}(r_{1},r_{2},u_{1},u_{2},u_{3},u_{4})+O(\epsilon ^{2}), \end{aligned} \end{aligned}$$
(18)

where \(l=1,2\); \(n=1,2,3,4\); and \(\epsilon\) is a very small parameter. The functions \(\xi ^{l}_{r}\) and \(\xi ^{n}_{u}\) are the infinitesimal generators of Lie group of transformations which will be determined later.

By using \(p^n_l = \frac{\partial u_n}{\partial r_l}\), the system of  Eq. (1) can be written in the following form

$$\begin{aligned} H_k(r_l,u_n,p^n_l) = 0, k=1,2,3,4, \end{aligned}$$

the system of equations (1) remains unchanged under the transformation (18), if there exist constants \(s_{ka}(k,a = 1,2,3,4)\) such that

$$\begin{aligned} {\mathcal {L}}H_k = s_{ka} H_{a}, \end{aligned}$$
(19)

Here, \({\mathcal {L}}\) denotes the Lie derivative and can be defined as

$$\begin{aligned} {\mathcal {L}} = \xi _r^l \frac{\partial }{\partial r_l} + \xi _u^n \frac{\partial }{\partial u_n} + \xi _{p_{l}}^n \frac{\partial }{\partial p_l^n}, \end{aligned}$$
(20)

with \(\xi _r^1 = T, \xi _r^2 = \chi , \xi _u^1 = F, \xi _u^2 = U, \xi _u^3 = P, \xi _u^4 = G\) and \(\xi _{p_l}^n\) is defined as

$$\begin{aligned} \xi _{p_{l}}^n = \frac{\partial \xi _u^n}{\partial r_l} + \frac{\partial \xi _u^n}{\partial u_k} p_l^k - \frac{\partial \xi _r^i}{\partial r_l} p_{i}^{n} - \frac{\partial \xi _r^i}{\partial u_j} p_i^n p_l^j, \end{aligned}$$
(21)

where \(i = 1,2; j = 1,2,3,4\).

In view of Eqs. (19)-(21), the system (1) implies

$$\begin{aligned}{} & {} \xi _r^l \frac{\partial H_k}{\partial r_l} + \xi _u^n \frac{\partial H_k}{\partial u_n} + \xi _{p_{l}}^n \frac{\partial H_k}{\partial p_l^n} = s_{ka} H_a, \quad k = 1,2,3,4; \quad a = 1,2,3,4. \end{aligned}$$
(22)

Using Eq. (21) into (22), we get a polynomial in \(p_l^n\). Setting the coefficients of \(p_l^n\) and the terms free from derivatives of dependent variables to zero gives system of first-order linear PDEs in infinitesimal generators \(T,\chi ,F,U,P,G\) which are given in the Appendix. These first order linear PDEs are known as determining equations whose consistency gives rise to determining the infinitesimals \(T,\chi ,F,U,P,G\) as follows:

For convenience, let \(s=b+\vartheta\)

$$\begin{gathered} T = a_{1} t + b_{1} ,\quad \chi = (s_{{22}} + 2a_{1} )r + c, \hfill \\ F = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {(s_{{11}} + a_{1} )\rho } \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right.\quad U = (s_{{22}} + a_{1} )u, \quad P = \left\{ {\begin{array}{*{20}l} {\left( {2s_{{22}} + 2a_{1} } \right)p} \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {\left( {2s_{{22}} + s_{{11}} + 3a_{1} } \right)\rho } \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right. \hfill \\ G = s_{{22}} g + d,\quad FL_{\rho } + PL_{p} = (2s_{{22}} + a_{1} )L, \hfill \\ \end{gathered}$$
(23)

where \(a_{1}, b_{1}, c, d, k_{1}, s_{11},s_{22}\) are all arbitrary constants. On the basis of arbitrary constants occurring in the expression for the infinitesimals generator, there arise two different possible cases of solutions which is discussed as follows:

Case 1: \(a_{1} \ne 0\) and \((s_{22}+2a_{1}) \ne 0\). Let us take the following translational invariance from (r, t, g) to \(({\tilde{r}}, {\tilde{t}},{\tilde{g}})\) defined as

$$\begin{aligned} {\tilde{r}}=r+\frac{c}{s_{22}+2a_{1}},\quad {\tilde{t}} = t + \frac{b_{1}}{a_{1}},\quad {\tilde{g}}=g+\frac{d}{s_{22}}, \end{aligned}$$
(24)

under which all the basic equations remain unchanged. On suppressing the tilde sign, the set of infinitesimal generators in Eq.(23) can be written as:

$$\begin{gathered} T = a_{1} t,\quad \chi = (s_{{22}} + 2a_{1} )r + c, \hfill \\ F = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {(s_{{11}} + a_{1} )\rho } \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right.\quad U = (s_{{22}} + a_{1} )u, \hfill \\ P = \left\{ {\begin{array}{*{20}l} {(2s_{{22}} + 2a_{1} )p} \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {(2s_{{22}} + s_{{11}} + 3a_{1} )p} \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right.\quad G = s_{{22}} g + d,\quad FL_{\rho } + PL_{p} = (2s_{{22}} + a_{1} )L. \hfill \\ \end{gathered}$$
(25)

The invariant surface condition yields:

$$\begin{aligned} \begin{aligned} \chi \rho _r + T \rho _t = F, \qquad \chi u_r + T u_t = U,\\ \chi p_r + T p_t = P, \qquad \chi g_r + T g_t = G, \end{aligned} \end{aligned}$$
(26)

which on integrating together with Eq.(25), yield the following forms of flow variables \(\rho , u, p, g\) and L:

$$\begin{aligned} \rho & = \left\{ {\begin{array}{*{20}l} {\hat{F}(\xi )} \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {t^{{1 + \frac{{s_{{11}} }}{{a_{1} }}}} \hat{F}(\xi )} \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right.\quad u = t^{{\delta - 1}} \hat{U}(\xi ), \\ p & = \left\{ {\begin{array}{*{20}l} {t^{{2\delta - 2}} \hat{P}(\xi )} \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {t^{{2\delta - 1 + \frac{{s_{{11}} }}{{a_{1} }}}} \hat{P}(\xi )} \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right. \\ g & = t^{{(\delta - 2)}} \hat{G}(\xi ),L = \left\{ {\begin{array}{*{20}l} {p^{{\frac{{2\delta - 3}}{{2(\delta - 1)}}}} \quad q(\eta )} \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {p^{{\frac{{(2\delta - 3)a_{1} }}{{(2\delta - 1)a_{1} + s_{{11}} }}}} \quad q(\eta )} \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right. \\ \end{aligned}$$
(27)

where \(\delta = \frac{s_{22}+2a_{1}}{a_{1}}\). The form of L in terms of arbitrary function of \(\eta\) is the general form for which similarity solution exists, where

$$\eta = \left\{ {\begin{array}{*{20}l} {\rho ,} \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {\rho p^{{\frac{{ - (s_{{11}} + a_{1} )}}{{((2\delta - 1)a_{1} + s_{{11}} )}}}} ,} \hfill & {{\text{if}}\quad s = 0.} \hfill \\ \end{array} } \right.$$
(28)

The functions \({\hat{U}}, {\hat{P}}, {\hat{F}}\) and \({\hat{G}}\) depend on the similarity variable \(\xi\), which is given as

$$\begin{aligned} \xi =\frac{r}{ t^\delta }. \end{aligned}$$
(29)

let the position of the shock front be \(\xi = 1,\) then the shock path Q and shock speed V are given as

$$\begin{aligned} Q= t^\delta , \quad V= \frac{\delta Q}{t}. \end{aligned}$$
(30)

At the shock, we have the following conditions on flow variables \(\rho , u, p\) and g

$$\begin{array}{*{20}l} {\rho |_{{\xi = 1}} = \left\{ {\begin{array}{*{20}l} {\hat{F}(1)} \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {t^{{(1 + \frac{{s_{{11}} }}{{a_{1} }})}} \hat{F}(1)} \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right.} \hfill & {u|_{{\xi = 1}} = t^{{(\delta - 1)}} \hat{U}(1),} \hfill \\ {p|_{{\xi = 1}} = \left\{ {\begin{array}{*{20}l} {t^{{2(\delta - 1)}} \hat{P}(1)} \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {t^{{(2\delta - 1 + \frac{{s_{{11}} }}{{a_{1} }})}} \hat{P}(1)} \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right.} \hfill & {g|_{{\xi = 1}} = t^{{(\delta - 2)}} \hat{G}(1).} \hfill \\ \end{array}$$
(31)

For invariance of jump condition, Eq.(12) yields the following forms of \(\rho _0(r)\) and \(g_0(r)\)

$$\begin{aligned} \begin{aligned} \rho _0(r)= {\left\{ \begin{array}{ll} \rho _c &{} \text {if} \quad s \ne 0,\\ \rho _c r^\nu &{} \text {if} \quad s = 0, \end{array}\right. } \qquad g_0(r)=g_{0c} r^\sigma . \end{aligned} \end{aligned}$$
(32)

Using Eqs. (31) and (32), the jump conditions (11), (13), (15) and (17) for strong shock reduce as follows

$$\begin{gathered} \hat{F}(1) = \left\{ {\begin{array}{*{20}l} {\frac{{\rho _{c} }}{{\beta _{1} }}} \hfill & {{\text{if}}\quad \vartheta \ne 0,b \ne 0,} \hfill \\ {\frac{{\rho _{c} }}{{\beta _{2} }}} \hfill & {{\text{if}}\quad \vartheta = 0,b \ne 0,} \hfill \\ {\frac{{\varvec{\varGamma } + 1}}{{(\varvec{\varGamma } - 1 + 2\vartheta \rho _{c} )}}\rho _{c} ,} \hfill & {{\text{if}}\quad \vartheta \ne 0,b = 0,} \hfill \\ {\frac{{\gamma + 1}}{{\gamma - 1}}\rho _{c} } \hfill & {{\text{if}}\quad \vartheta = 0,b = 0,} \hfill \\ \end{array} } \right. \hfill \\ \hat{U}(1) = \left\{ {\begin{array}{*{20}l} {\delta (1 - \beta _{1} )} \hfill & {{\text{if}}\quad \vartheta \ne 0,b \ne 0,} \hfill \\ {\delta (1 - \beta _{2} )} \hfill & {{\text{if}}\quad \vartheta = 0,b \ne 0,} \hfill \\ {\frac{{2\delta (1 - \vartheta \rho _{c} )}}{{\varvec{\varGamma } + 1}},} \hfill & {{\text{if}}\quad \vartheta \ne 0,b = 0,} \hfill \\ {\frac{{2\delta }}{{\gamma + 1}},} \hfill & {{\text{if}}\quad \vartheta = 0,b = 0,} \hfill \\ \end{array} } \right. \hfill \\ \hat{P}(1) = \left\{ {\begin{array}{*{20}l} {\rho _{c} \delta ^{2} (1 - \beta _{1} )} \hfill & {{\text{if}}\quad \vartheta \ne 0,b \ne 0,} \hfill \\ {\rho _{c} \delta ^{2} (1 - \beta _{2} )} \hfill & {{\text{if}}\quad \vartheta = 0,b \ne 0,} \hfill \\ {\frac{{2\rho _{c} \delta ^{2} (1 - \vartheta \rho _{c} )}}{{\varvec{\varGamma } + 1}},} \hfill & {{\text{if}}\quad \vartheta \ne 0,b = 0,} \hfill \\ {\frac{{2\rho _{c} \delta ^{2} }}{{\gamma + 1}},} \hfill & {{\text{if}}\quad \vartheta = 0,b = 0,} \hfill \\ \end{array} } \right. \hfill \\ \hat{G}(1) = g_{{0c}} \hfill \\ \end{gathered}$$
(33)

together with

$$\begin{aligned} \begin{aligned}&\sigma =\frac{\delta -2}{\delta }, \quad \nu =\frac{s_{11}+a_{1}}{\delta a_{1}}, \\&\beta _{1}=\frac{2{\bar{b}}\rho _{c}(1+{\bar{b}}\rho _{c})(\varGamma -1)}{\Theta ^{**}\pm \sqrt{(\Theta ^{**})^{2}+4\rho _{c}{\bar{b}}(\varGamma ^{2}-1)(1+{\bar{b}}\rho _{c})^{2}}},\\&\beta _{2}=\frac{2{\bar{b}}\rho _{c}(1+{\bar{b}}\rho _{c})(\gamma -1)}{\Theta _{1}^{**}\pm \sqrt{(\Theta _{1}^{**})^{2}+4\rho _{c}{\bar{b}}(\gamma ^{2}-1)(1+{\bar{b}}\rho _{c})^{2}}},\\&\Theta ^{**}=\Big (1-2\vartheta \rho _{c}-\varGamma +(\varGamma -1)\rho _{c}{\bar{b}}\Big )(1+{\bar{b}}\rho _{c}),\\&\Theta _{1}^{**}=(1-\gamma )(1-{\bar{b}}^{2}\rho _{c}^{2}), \end{aligned} \end{aligned}$$
(34)

where \(\rho _{c}, g_{c}\) and \(g_{0c}\) are some reference constants. In view of Eq. (28)-(30), (32) and (34), all the flow variables in Eq. (27) can be written as

$$\begin{array}{*{20}l} {\rho = \left\{ {\begin{array}{*{20}l} {\rho _{c} F^{*} (\xi )} \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {\rho _{0} (Q(t))F^{*} (\xi )} \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right.} \hfill & {u = VU^{*} (\xi ),} \hfill \\ {p = \left\{ {\begin{array}{*{20}l} {\rho _{c} V^{2} P^{*} (\xi ),} \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {\rho _{0} (Q(t))V^{2} P^{*} (\xi ),} \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right.} \hfill & {g = \frac{V}{t}G^{*} (\xi ),} \hfill \\ {L = \left\{ {\begin{array}{*{20}l} {p^{{\frac{{(2\delta - 3)}}{{2(\delta - 1)}}}} \quad q(\eta ),} \hfill & {{\text{if}}\quad s \ne 0,} \hfill \\ {p^{{\frac{{(2\delta - 3)}}{{(2(\delta - 1) + \delta \nu )}}}} \quad q(\eta ),} \hfill & {{\text{if}}\quad s = 0,} \hfill \\ \end{array} } \right.} \hfill & {\eta = \left\{ {\begin{array}{*{20}c} {\rho ,} & {{\text{if}}\quad s \ne 0,} \\ \rho & {p^{{\frac{{ - \delta \nu }}{{(2(\delta - 1) + \delta \nu )}}}} {\text{if}}\quad s = 0,} \\ \end{array} } \right.} \hfill \\ \end{array}$$
(35)

where \(F^{*}=\frac{{\hat{F}}}{\rho _{c}}, U^{*}=\frac{{\hat{U}}}{\delta }, P^{*}=\frac{{\hat{P}}}{\rho _{c}\delta ^{2}}, G^{*}=\frac{{\hat{G}}}{\delta }.\)

Using Eq. (35) in the system (1) and then using (29), (30), (32) and (34)\(_{1}\), we get the following system of ODEs in \(F^*, V^*, P^*\) and \(G^*\) (For simplicity we suppressed asterisk sign)

for \(s \ne 0\):

$$\begin{aligned} U - \xi )F^{\prime} + F\left( {U^{\prime} + \frac{{2U}}{\xi }} \right) & = 0,\left( {\frac{{\delta - 1}}{\delta }} \right)U + (U - \xi )U^{\prime} + \frac{{P^{\prime}}}{F} = \frac{G}{\delta },2\left( {\frac{{\delta - 1}}{\delta }} \right)P + (U - \xi )P^{\prime} \\ & \quad + \frac{{\left( {\varvec{\varGamma } - \vartheta \bar{b}\rho _{c}^{2} F^{2} + 2\varvec{\varGamma }\bar{b}\rho _{c} F + (\varvec{\varGamma } - 1)\bar{b}^{2} \rho _{c}^{2} F^{2} } \right)P}}{{(1 - \vartheta \rho _{c} F)(1 + \bar{b}\rho _{c} )F}}\left( {U^{\prime} + \frac{{2U}}{\xi }} \right) \\ & \quad + \frac{{\left( {\varvec{\varGamma } - 1)(1 + \bar{b}\rho _{c} F} \right)FL_{*} }}{{(1 - \vartheta \rho _{c} F)}} = 0,\left( {\frac{{\delta - 2}}{\delta }} \right)G \\ & \quad + (U - \xi )G^{\prime} + \frac{{2UG}}{\xi } = 0, \\ \end{aligned}$$
(36)

and for \(s = 0\):

$$\begin{aligned} \begin{aligned}&(U-\xi )F' + F\Big (\nu + U' + \frac{2U}{\xi }\Big ) = 0,\\&\Big (\frac{\delta -1}{\delta }\Big ) U + (U-\xi )U' + \frac{P'}{F}=\frac{G}{\delta },\\&(U-\xi )P'+ \left( 2\Big (\frac{\delta -1}{\delta }\Big ) + \nu \right. \\&\quad \left. + \gamma \Big (U' + \frac{2U}{\xi }\Big )\right) P + (\gamma -1)FL_* = 0,\\&\Big (\frac{\delta -2}{\delta }\Big ) G + (U-\xi ) G' + \frac{2UG}{\xi } = 0, \end{aligned} \end{aligned}$$
(37)

where

$$\begin{aligned} \begin{aligned} L_*= {\left\{ \begin{array}{ll} \rho _{c}^{\frac{4\delta -5}{2(\delta -1)}}\delta ^{\frac{-\delta }{\delta -1}}FP^{\frac{2\delta -3}{2(\delta -1)}}, &{} \text {if} \quad s \ne 0,\\ \rho _{c}^{\frac{(4\delta -5)}{(2(\delta -1)+\delta \nu )}}\delta ^{\frac{-(2\delta +5\delta \nu )}{(2(\delta -1)+\delta \nu )}}FP^{\frac{(2\delta -3-\delta \nu )}{(2(\delta -1)+\delta \nu )}}, &{} \text {if} \quad s=0. \end{array}\right. } \end{aligned} \end{aligned}$$

The above system of ODEs (36) and (37) together with boundary conditions is solved numerically in Sect. 5.

Case 2: \(a_{1}=0\) and \(s_{22} \ne 0\). Let us take the following translational invariance from (r, t, g) to \(({\tilde{r}}, {\tilde{t}},{\tilde{g}})\) defined as

$$\begin{aligned} {\tilde{r}}=r + c(s_{22})^{-1}, \quad {\tilde{t}} = t,\quad {\tilde{g}}=g+\frac{d}{s_{22}}, \end{aligned}$$
(38)

under which all the basic equations remain unchanged. In view of equation (23) and (26) together with (38), after suppressing the tilde sign, all the flow variables can be written as

$$\begin{array}{*{20}l} {\rho = \left\{ {\begin{array}{*{20}l} {\rho _{c} F^{*} (\xi ),} \hfill & {{\text{if}}\;s \ne 0,} \hfill \\ {\rho _{0} (Q(t))F^{*} (\xi ),} \hfill & {{\text{if}}\;s = 0,} \hfill \\ \end{array} } \right.} \hfill & {u = VU^{*} (\xi ),} \hfill \\ {{\text{p = }}\left\{ {\begin{array}{*{20}l} {\rho _{{\text{c}}} {\text{V}}^{{\text{2}}} {\text{P}}^{{\text{*}}} (\xi ),} \hfill & {{\text{if}}\;{\text{s}} \ne {\text{0}},} \hfill \\ {\rho _{{\text{0}}} ({\text{Q}}({\text{t}})){\text{V}}^{{\text{2}}} {\text{P}}^{{\text{*}}} (\xi ),} \hfill & {{\text{if}}\;{\text{s}} = {\text{0}},} \hfill \\ \end{array} } \right.} \hfill & {{\text{g}} = {\text{VG}}^{{\text{*}}} (\xi ),} \hfill \\ {{\text{L = }}\left\{ {\begin{array}{*{20}l} {{\text{pq}}(\eta ),} \hfill & {\quad {\text{if}}\;{\text{s}} \ne {\text{0}},} \hfill \\ {{\text{p}}^{{\frac{{\text{2}}}{{\nu {\text{ + 2}}}}}} {\text{q}}(\eta ),} \hfill & {\quad {\text{if}}\;{\text{s}} = {\text{0}},} \hfill \\ \end{array} } \right.} \hfill & {\eta = \left\{ {\begin{array}{*{20}l} {\rho ,} \hfill & {\quad {\text{if}}\;{\text{s}} \ne {\text{0}},} \hfill \\ {\rho {\text{p}}^{{\frac{{ - \nu }}{{\nu {\text{ + 2}}}}}} ,} \hfill & {\quad {\text{if}}\;{\text{s}} = {\text{0}},} \hfill \\ \end{array} } \right.} \hfill \\ {\rho _{{\text{0}}} ({\text{r}}){\text{ = }}\left\{ {\begin{array}{*{20}l} {\rho _{{\text{c}}} ,} \hfill & {\quad {\text{if}}\;{\text{s}} \ne {\text{0}},} \hfill \\ {\rho _{{\text{c}}} ({\text{r/r}}_{{\text{0}}} )^{\nu } ,} \hfill & {\quad {\text{if}}\;{\text{s}} = {\text{0}},} \hfill \\ \end{array} } \right.} \hfill & {{\text{g}}_{{\text{0}}} ({\text{r}}) = {\text{g}}_{{{\text{c0}}}} ({\text{r/r}}_{{\text{0}}} ),} \hfill \\ \end{array}$$
(39)

where \(\nu =s_{11}/s_{22}, \delta = s_{22}/b_{1}, F^{*}=\frac{{\hat{F}}}{\rho _{c}}, U^{*}=\frac{{\hat{U}}}{\delta }, P^{*}=\frac{{\hat{P}}}{\rho _{c}\delta ^{2}}, G^{*}=\frac{{\hat{G}}}{\delta }\).

Shock can be normalized at \(\xi\) = 1. The shock path Q and the shock velocity V as follows:

$$\begin{aligned} \xi = r e^{- \delta t}, \qquad Q = e^{ \delta t}, \qquad V = \delta e^{\delta t}, \end{aligned}$$
(40)

Using Eqs. (39) and (40) in the system (1), we get the system of ODEs in terms \(F^*, V^*, P^*\) and \(G^*\) as follows (For simplicity we suppressed asterisk sign)

for \(s \ne 0\):

$$\begin{aligned} \begin{aligned}&(U-\xi )F' + F\Big (U' + \frac{2U}{\xi }\Big ) = 0,\\&U + (U-\xi )U' + \frac{P'}{F} = \frac{G}{\delta },\\&(U-\xi )P' + 2P \\&\quad + \frac{(\varGamma -{\bar{b}}\vartheta \rho _{c}^{2}F^{2}+2\varGamma {\bar{b}}\rho _{c}F+(\varGamma -1){\bar{b}}^{2}\rho _{c}^{2}F^{2})P}{(1-\vartheta \rho _c F)(1+{\bar{b}}\rho _{c}F)}\Big (U' + \frac{2U}{\xi }\Big )\\&+ \frac{(\varGamma -1)(1+{\bar{b}}\rho _{c}F)FL_*}{(1-\vartheta \rho _{c}F)} = 0,\\&G + (U-\xi ) G' +\frac{2GU}{\xi } = 0, \end{aligned} \end{aligned}$$
(41)

and for \(s = 0\):

$$\begin{aligned} \begin{aligned}&(U-\xi )F' + F\Big (\nu + U' + \frac{2U}{\xi }\big ) = 0,\\&U + (U-\xi )U' + \frac{P'}{F} = \frac{G}{\delta },\\&P(2+\nu )+ (U-\xi )P' + \gamma P\Big (U' + \frac{2U}{\xi }\Big ) + (\gamma -1)FL_* = 0,\\&G + (U-\xi ) G' +\frac{2UG}{\xi } = 0, \end{aligned} \end{aligned}$$
(42)

where

$$\begin{aligned} \begin{aligned} L_*= {\left\{ \begin{array}{ll} \rho _{c}^{2}\delta ^{-1} FP, &{} \text {if} \quad s \ne 0,\\ \rho _{c}^{\frac{4}{(2+\nu )}}\delta ^{\frac{-(2+5\nu )}{(2+\nu )}}FP^{\frac{(2-\nu )}{(2+\nu )}}, &{} \text {if} \quad s=0. \end{array}\right. } \end{aligned} \end{aligned}$$

In this case, the boundary conditions for strong shock remain the same as in Case 1 given by Eq.(33).

5 Imploding shocks

We consider an imploding shock for Case 1 and discuss in detail. For the existence of an imploding shock, \(V \gg a_0\) in the neighborhood of implosion. For an imploding shock collapsing at the center, we assume the origin of time t to be the instant at which the shock falls at the center so that \(t \le 0\) in (36)-(37). Thus, in this regard, we slightly modify the expression of similarity variable by setting

$$\begin{aligned} Q = (-t)^\delta ,\quad \xi = r/(-t)^\delta , \end{aligned}$$

so that the intervals of flow variables become \(0 \le r\le Q\), \(- \infty < t \le 0\) and \(1 \le \xi < \infty\). At time \(t=0\), we observe that sound speed at any finite radius r and all the flow variables are bounded and \(\xi = \infty\). For the boundedness of variables \(\rho , p, u\) and g for \(t=0\) and finite r, the following boundary conditions must be satisfied at \(\xi = \infty\):

$$\begin{aligned}{} & {} U(\infty ) \nonumber \\{} & {} \quad = 0, \quad {\left\{ \begin{array}{ll} \frac{(\varGamma -\vartheta {\bar{b}}F^{2}(\infty )+2\varGamma {\bar{b}}F(\infty )+(\varGamma -1){\bar{b}}^{2}F^{2}(\infty ))P(\infty )}{(1 - \vartheta F(\infty ))F(\infty )(1+{\bar{b}}F(\infty ))F(\infty )} =0, &{}\quad s \ne 0,\\ \frac{\gamma P(\infty )}{F(\infty )} =0, &{}\quad s = 0, \end{array}\right. } \quad G(\infty ) = 0. \end{aligned}$$
(43)

We rewrite system of equations (36) and (37) in the matrix form as:

$$\begin{aligned} ES' = N, \end{aligned}$$
(44)

where \(S = (U, F, P, G)^{tr}\); the matrix E and the column vector N can be obtained from equations (36) and (37). The system of equation (44) together with (33) and (43), constitute a boundary value problem that can be solved for the flow variables behind the shock. But for this purpose, first we need to determine the unknown parameter \(\delta\) appearing in (44), known as the similarity exponent. The value of \(\delta\) can only be determined by solving a non-linear eigenvalue problem for imploding shock. We solve the system (44) for \(U', F', P'\) and \(G'\) in the following forms:

$$\begin{aligned} U' = \frac{\Lambda _1}{\Lambda }, \quad F' = \frac{\Lambda _2}{\Lambda }, \quad P' = \frac{\Lambda _3}{\Lambda }, \quad G' = \frac{\Lambda _4}{\Lambda }, \end{aligned}$$
(45)

where \(\Lambda\) is the determinant of the matrix E and given by:

$$\begin{aligned} \begin{aligned} \Lambda = {\left\{ \begin{array}{ll} -(U- \xi )^2\Big ((U- \xi )^{2} - \frac{(\varGamma -\vartheta {\bar{b}}\rho _{c}^{2}F^{2}+2\varGamma {\bar{b}}\rho _{c}F+(\varGamma -1){\bar{b}}^{2}\rho _{c}^{2}F^{2}) P}{F(1- \vartheta \rho _c F)(1+{\bar{b}}\rho _{c}F)}\Big ), &{}\quad \text {if }s\ne 0,\\ -(U- \xi )^2\Big ((U- \xi )^{2}-\frac{\gamma P}{F}\Big )=0, &{} \quad \text {if }s=0. \end{array}\right. } \end{aligned} \end{aligned}$$
(46)

The determinants \(\Lambda _i (i=1,2,3,4)\) are obtained from \(\Lambda\) by replacing the ith column of E by the column vector N.

In the interval \([1,\infty )\), we may note that \(U < \xi\), whereas

$$\begin{aligned} \begin{aligned} \Lambda = {\left\{ \begin{array}{ll} > 0, &{}\quad \text {at }\xi =1,\\ <0, &{}\quad \text {at }\xi =\infty , \end{array}\right. } \end{aligned} \end{aligned}$$
(47)

which shows that \(\exists\) a point \(\xi _{c} \in [1,\infty )\) at which \(\Lambda =0\), thus the solutions become singular at \(\xi _{c}\). In order to determine a non-singular solution of (44) in the interval \([1,\infty )\), we choose the value of the \(\delta\) in such a manner at the points where \(\Lambda\) and \(\Lambda _1\) vanish simultaneously. Without any difficulty, it can be checked that the determinants \(\Lambda _2, \Lambda _3\) and \(\Lambda _4\) also vanish simultaneously for the points at which \(\Lambda\) and \(\Lambda _1\) are vanish. For the determination of such \(\delta\), we introduce a variable Z of the following form

$$\begin{aligned}{} & {} Z(\xi )\nonumber \\{} & {} \quad = {\left\{ \begin{array}{ll} (U-\xi )^2 - \frac{(\varGamma -\vartheta {\bar{b}}\rho _{c}^{2}F^{2}+2\varGamma {\bar{b}}\rho _{c}F+(\varGamma -1){\bar{b}}^{2}\rho _{c}^{2}F^{2}) P}{F(1- \vartheta \rho _c F)(1+{\bar{b}}\rho _{c}F)}, &{}\quad \text {if }s\ne 0,\\ (U-\xi )^{2}-\frac{\gamma P}{F}, &{}\quad \text {if }s=0, \end{array}\right. } \end{aligned}$$
(48)

whose first derivative is

$$\begin{aligned} \frac{dZ}{d \xi }=\frac{\Lambda _{5}}{\Lambda }, \end{aligned}$$
(49)

where

$$\begin{aligned}{} & {} \Lambda _5 \\ {}{} & {} \quad = {\left\{ \begin{array}{ll} 2(U-\xi )(\Lambda _{1}-\Lambda ) - \zeta _{1} \Lambda _{3}+\frac{\zeta _{1}P\Lambda _{2}}{F} -\zeta _{2}P\Lambda _{2}-\zeta _{1} P\Lambda _{2}\Big (\frac{\vartheta \rho _{c}}{(1-\vartheta \rho _{c}F)}-\frac{{\bar{b}}\rho _{c}}{(1+{\bar{b}}\rho _{c}F)}\Big ), &{}\quad \text {if }s\ne 0,\\ 2(U-\xi )(\Lambda _{1}-\Lambda )-\frac{\gamma \Lambda _{3}}{F}+\frac{\gamma P\Lambda _{2}}{F^{2}}, &{}\quad \text {if }s=0,\\ \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \xi = {\left\{ \begin{array}{ll} U + \sqrt{Z + P\zeta _{1}}, &{}\quad \text {if }s\ne 0,\\ U + \sqrt{Z + \frac{\gamma P}{F}}, &{}\quad \text {if }s=0,\\ \end{array}\right. } \end{aligned}$$

where \(\zeta _{1}=\frac{\Big (\varGamma -\vartheta {\bar{b}}\rho _{c}^{2}F^{2}+2\varGamma {\bar{b}}\rho _{c}F+(\varGamma -1){\bar{b}}^{2}\rho _{c}^{2}F^{2}\Big )}{(1- \vartheta \rho _c F)(1+{\bar{b}}\rho _{c}F)F}\) and \(\zeta _{2}=\frac{\Big (-2\vartheta {\bar{b}}\rho _{c}^{2}F+2\varGamma {\bar{b}}\rho _{c}+2(\varGamma -1){\bar{b}}^{2}\rho _{c}^{2}F\Big )}{(1- \vartheta \rho _c F)(1+{\bar{b}}\rho _{c}F)F}\).

In view of Eq.(48), Eq.(45) becomes

$$\begin{aligned} \frac{dU}{dZ} = \frac{\Lambda _1}{\Lambda _5}, \quad \frac{dF}{dZ} = \frac{\Lambda _2}{\Lambda _5}, \quad \frac{dP}{dZ} = \frac{\Lambda _3}{\Lambda _5}, \quad \frac{dG}{dZ} = \frac{\Lambda _4}{\Lambda _5}. \end{aligned}$$
(50)

6 Characteristic method

“In the Whitham’s rule [45], the structure of the solution is unaffected by the characteristics behind the shock. It inculcates the application of the differential relation which is true along with a characteristic to the flow variables just behind the blast wave. The method is useful in writing a characteristic equation for the characteristics moving along the direction of shock”, which results in a differential equation of the following form:

$$\begin{aligned}{} & {} \frac{D p}{D r} + \rho a \frac{D u}{D r} \nonumber \\ {}{} & {} \quad + \frac{1}{u+a}\left( \frac{(\varGamma -1)(1+b\rho )\rho L}{1-\vartheta \rho }+\frac{2a^2 \rho u}{r}-ag\rho \right) = 0, \end{aligned}$$
(51)

where

$$\begin{aligned} \frac{D }{D r} = \frac{\partial }{\partial r} + (u + a)^{-1}\frac{\partial }{\partial t} \end{aligned}$$

with characteristic \(\frac{D r}{D t} = u + a\). By using Eq. (51) along with the Eq. (11) for the strong shock and (4) for the speed of sound a in the mixture, we get the evolutionary equation for the shock as follows:

$$\begin{aligned} \frac{1}{V}\frac{d V}{d r} + \frac{2W}{r} = 0, \end{aligned}$$
(52)

where

\(W = \frac{(1 - \mu ^{*})(W^{*})^{2}}{\big (\mu ^{*}(1 - \mu ^{*}) + \mu ^{*} W^{*}\big )\big (2(1-\mu ^{*})+\frac{1 - \mu ^{*}}{\mu ^{*}} W^{*}\big )}\), \(W^{*} = \sqrt{\Big (}\frac{(\varGamma (\mu ^{*})^2-\vartheta {\bar{b}}\rho _{0}^{2}+2\varGamma {\bar{b}}^{2}\rho _{0}\mu ^{*}+(\varGamma -1){\bar{b}}^{2}\rho _{0}^{2}) \mu ^{*}(1 - \mu ^{*})}{(\mu ^{*} - \vartheta \rho _{0})(\mu ^{*}+{\bar{b}}\rho _{0})}\Big )\) and \(\mu ^{*}\) is same as in Eq.(11).

We get the following relation after integrating the Eq.(52),

$$\begin{aligned} V \sim r^{-2W}. \end{aligned}$$
(53)

As per the Guderley’s hypothesis, the shock location in the neighborhood of the collapse is given by

$$\begin{aligned} Q = A(-t)^{\delta }, \end{aligned}$$
(54)

where t is the time which is taken to be negative upto the instant of collapse, A is a constant, which measures the strength of shock and \(\delta\) is the similarity exponent. By using Eqs. (53) and (54), we determine the similarity exponent \(\delta\) as follows

$$\begin{aligned} \delta = \frac{1}{1 + 2W}. \end{aligned}$$
(55)
Table 1 Comparison of the similarity exponent \(\delta\) calculated in this work and those calculated by CCW rule [45]
Full size table
Fig. 1
figure 1

Flow pattern in the region behind the shock front: (a) radial fluid velocity (b) density (c) pressure (d) gravitational force; \(\gamma =7/5, \Psi = 100, \beta = 0.5, b = 0.0011\)

Full size image
Fig. 2
figure 2

Flow pattern in the region behind the shock front: (a) radial fluid velocity (b) density (c) pressure (d) gravitational force; \(\gamma =7/5, \Psi = 100, k_{p}= 0.4, b=0.0009\)

Full size image
Fig. 3
figure 3

Flow pattern in the region behind the shock front: (a) radial fluid velocity (b) density (c) pressure (d) gravitational force; \(\gamma =7/5, 5/3, \Psi = 100, k_{p}= 0.6, \beta =1.0\)

Full size image
Fig. 4
figure 4

Flow pattern in the region behind the shock front: (a) radial fluid velocity (b) density (c) pressure (d) gravitational force; \(\gamma =7/5,5/3, k_{p}= 0.6, \beta =1.5, b=0.0009\)

Full size image

7 Numerical results and discussion

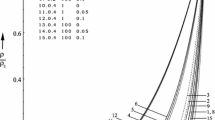
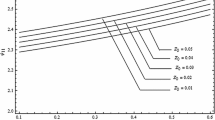
Using the Runga-Kutta 4-th order method, we estimate the value of leading similarity exponent \((\delta )\) numerically by solving the system (50) along with the Eq. (33). The entire computational process is carried out by writing a program in the software package “Mathematica 7”. The exponent \(\delta\) is calculated in such a way that for a trial value of \(\delta\), we integrate the system (50) from the shock, \(Z=Z[1]\) to \(Z=0\) and calculate U, F, P, G and \(\Lambda _1\) at singular point \(Z=0\). The value of \(\delta\) is improved by successive approximations in such a manner that for its final value, the determinant \(\Lambda _1\) vanishes at \(Z=0.\) For the purpose of numerical integration, the values of the physical parameters involved in the computation are taken as \(\gamma =7/5, 5/3,\)  (see [46, 47])       \(k_p=0.2,0.4,0.6;\)       \(\beta =0.5, 1.0, 1.5;\)       \(\Psi =100, 1000,\)       \(b=0.0009, 0.0011.\) (see [48])

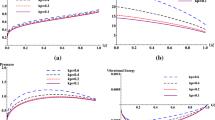
Table 1 lists the numerical values of similarity exponent \(\delta\) obtained in Eq.(55) by Whitham’s rule. We see that all the values of the similarity exponent estimated by using both the methods are in excellent agreement upto 3 decimal places. It is worth noting that the value of \(\delta\) is less than 1, indicating that the shock is constantly accelerating, indeed, the shock velocity V becomes infinite as \(Q\rightarrow 0\). From Table 1, we observe that the values of \(\delta\) decreases with the decrement in the values of parameters \(k_{p}, \beta\) and \(\Psi\) and with the increment in value of van der Waals excluded gas volume b. Consequently, the shock velocity increases and becomes unbounded as it reaches the center of implosion. Thus, the shock velocity decreases due to the presence of the dust particles while the non-ideal parameter b has an opposite effect on the shock velocity. The values of the flow variables before collapse and at the instant of collapse are shown graphically by integrating Eq.(50) along with the boundary conditions (33) numerically for \(1\le \xi <\infty\). The effects of various parameters \(k_{p}, \beta , \gamma , b, \Psi\) on the flow velocity, density, pressure and gravitational force are shown by the typical flow profiles in Figs. 1, 2, 3 and 4. From Figs. 1a, b, 2a, b, 3a, b and 4a, b, we observe that the fluid velocity decreases and density increases monotonically in the region behind the shock as we go nearer to the axis of collapse, this increase in density may be attributed to the geometrical convergence or the area contraction of the shock wave. There is decrement in the velocity behind the shock wave because of the gas particle passing through the shock is subjected to a shock compression. Also, it is clear from the Figs. 1a, 2a, 3a and 4a, that this decrement in the velocity is further reinforced with the decrement in \(k_{p}, \beta , \Psi\) and increment in \(\gamma , b\). The increment in density is also further enhanced with the increment in \(k_{p}, \beta , \Psi\) and decrement in \(\gamma , b\). From Figs. 1c, 2c, 3c and 4c, we found complicated behavior of pressure profiles; behind the shock, pressure profiles exhibit non-monotonic variations. As we go nearer to the center of collapse, we see that pressure first increases, attains its maximum value and then starts decreasing. As the value of dusty gas parameter \(k_{p}\) increases, the particles collide more frequently and in turn generate high pressure as can be seen in Fig. 1c. From Figs. 1d, 2d, 3d and 4d, we see that the gravitational force reduces behind the shock as we go nearer to the center of implosion. With the increment of \(k_{p}\), gravitational force increases too (see Fig. 1d). These results describe the physical phenomena well.

8 Conclusions

In the present paper, an imploding shock wave problem in an interstellar non-ideal dusty gas clouds has been studied. By using the method of Lie group of transformation, whole range of similarity solutions to a problem involving spherically symmetric flows in an interstellar non-ideal dusty cloud involving strong converging shocks have been determined. All invariance properties associated with the ambient gas are presented and the general form of heating-cooling function for which the similarity solutions exist is obtained. The infinitesimal generators of the Lie group transformations associated with the system of partial differential equations are determined by using the invariance surface conditions. Taking into consideration the constants arising in the expressions for the infinitesimal generators, two different cases, involving similarity solutions following the power-law and exponential shock paths are obtained. A detailed study has been made for a particular case of the collapse of an imploding shock following the power-law shock path for the spherically symmetric flow. The similarity exponents are calculated numerically for the different values of dusty gas parameters and van der Waals excluded volume. The comparison of the calculated values of the similarity exponents has been made with those obtained by the characteristic method. The effects of the mass fraction of the dust particle, relative specific heat, ratio of density of dust particle to the density of gas and van der Waals excluded volume have been shown on the flow variables. The patterns of all the flow variables in the flow-field region behind the shock are analyzed graphically.

In future, the present work can be extended with the rotational effect and magnetic field effect and the solutions by using the theory of self-similarity and computational methods can be obtained.