Hall Current and Viscous Dissipation Effects on Boundary Layer Flow of Heat Transfer Past a Stretching Sheet

Abstract

The effect of Hall current and viscous dissipation on MHD natural convective heat transfer flow of a compressible viscous fluid past a stretching surface in the presence of strong magnetic field has been considered in the present work. A magnetic field is applied transversely to the direction of the flow. By means of similarity transformation the governing equations are transformed into nonlinear ordinary flow and heat transfer characteristics which are evaluated by making the use of Nachtsheim–Swigert iteration technique along with the sixth order Runge–Kutta integration scheme. Validation is achieved through the use of Mathematica software as well. The influence of various parameters is then presented graphically in the form of non-dimensional velocity (primary and secondary) and temperature within the boundary layer entering into the problem. Also the effects of the pertinent parameters on the skin-friction coefficients and rate of heat transfer in terms of the Nusselt number, which are of physical interest, are sorted out and presented in the form of table and the conclusion is drawn that the flow field and other quantities of physical interest are significantly influenced by these parameters.

Introduction

Laminar boundary layer flow, a significant type of flow, in presence of magnetic field and under the viscous dissipation effect over a moving continuous surface has been receiving wide attention due to its applications in engineering and industries. Ostrach [1] analyzed a similarity solution of transient free convection flow past a semi infinite vertical plate by an integral method. Goody [2], one of the initiator of free convection problem, considered a neutral fluid. Sakiadis [3] analyzed the boundary layer flow over a solid surface moving with a constant velocity. This boundary layer flow situation is quite different from the classical Blasius problem of boundary flow over a semi-infinite flat plate due to entrainment of ambient fluid. Cess [4] analyzed the effect of thermal radiation on absorbing emitting gray fluids with black vertical plate. Soundalgekar [5] made analytical study on the MHD forced and free convection flow past a vertical porous plate. Ferdows [6] introduced a similarity analysis for the forced and free convection boundary layer flow in a semi-infinite expanse of an electrically conducting viscous incompressible fluid past a semi-infinite non-conducting porous plate with suction applying a uniform magnetic field normal to the plate.

Crane [7] noted that usually the sheet is assumed to be inextensible, but situations may arise in the polymer industry in which it is necessary to deal with a stretching plastic sheet. For examples, materials manufactured by aerodynamic extrusion processes and heat-treated materials traveling between a feed roll and a wind-up roll or on a conveyor belt possess the characteristics of a moving continuous stretching surface. Moreover lots of metallurgical processes occupy the system of cooling of continuous strips or filaments by drawing them through a quiescent fluid and that in the process of drawing, these strips are sometimes stretched. Gorla [8] depicted the application of linearly stretched surface in electro-chemistry. Banks [9] discussed the flow field of a stretching wall with a power-law velocity variation. McLeod and Rajagopal [10] investigated the uniqueness of the flow of a Navier Stokes fluid due to a linear stretching boundary.

Another important matter is that the final product depends to a great extent on the rate of cooling. By drawing such strips in an electrically conducting fluid subjected to a magnetic field, the rate of cooling can be controlled and a final product of desired characteristics can be achieved. The study of heat and mass transfer is necessary for determining the quality of the final product. Sparrow [11] explained a parameter named Rosseland approximation to describe the radiation heat flux in the energy equation in his book. Soundalgekar and Takhar [12] studied radiation effects on free convection flow of a gas past a semi infinite flat plate using the Cogley–Vincentine–Giles equilibrium model. Anderson [13] studied of the diffusion of a chemically reactive species from a linearly stretching sheet. Samad and Mohebujjaman [14] exposed the effect of a chemical reaction on the flow over a linearly stretching vertical sheet in the presence of heat and mass transfer as well as a uniform magnetic field with heat generation/absorption. Samad [15] calculated numerically the effect of thermal radiation on steady MHD free convectoin flow taking into account the Rosseland diffusion approximaion.

Sattar and Hossain [16] investigated the unsteady free convective flow, with Hall currents and mass transfer, past an accelerated vertical porous plate in the presence of a transverse magnetic field while assuming the plate temperature and concentration to be functions of time. Bég [17] examined the steady double-diffusive free convective heat and mass transfer of a chemically-reacting micropolar fluid flowing through a Darcian porous regime adjacent to a vertical stretching plane including viscous dissipation effects in the energy equation. Devi and Ganga [18] considered viscous and Joule dissipation effects on MHD nonlinear flow and heat transfer past a stretching porous surface embedded in a porous medium under a transverse magnetic field.

Very recently, Mahatha [19] studied the two dimensional steady hydromagnetic boundary layer flow of a viscous, incompressible, and electrically conducting nanofluid past a stretching sheet with Newtonian heating, in the presence of viscous and Joule dissipations. In their study included in the transport equations the combined effects of Brownian motion and thermophoresis. Pal [20] studied the unsteady mixed convection boundary layer flow of an electrically conducting fluid over an stretching permeable sheet in the presence of transverse magnetic field, thermal radiation and non-uniform heat source/sink effects. Hayat and Hendi [21] investigated the effects of thermal-diffusion and diffusion-thermo on MHD three-dimensional axisymmetric flow of a viscous fluid between radially stretching sheets in the presence of Hall and ion-slip currents, viscous dissipation, Joule heating and first order chemical reaction by applying homotopy analysis method (HAM). Motsa and Shateyi [22] considered the problem of magnetomicropolar fluid flow, heat, and mass transfer with suction through a porous medium is numerically analyzed. By introducing successive linearization method (SLM) together with Chebyshev collocation method the problem was studied under the effects of chemical reaction, Hall, ion-slip currents, and variable thermal diffusivity. Comprehensive reviews on thermoelasticity of micropolar bodies and materials have been made by researchers including Marin [23,24,25].

In this paper boundary layer flow and heat transfer analysis has been undertaken in order to clarify the parametric behavior of free convection saturated strong magnetic field over a stretching sheet in the presence of dynamic effects of Hall current and viscous dissipation.

Mathematical Model

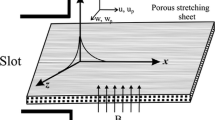
We consider a steady, incompressible and electrically conducting viscous fluid flowing over a vertical plate in the x-direction under the influence of heat transfer. The flow under consideration is also subject to a strong transverse magnetic field $B_{0}$ with a constant intensity along the y-axis see Fig. 1. The velocity component u on a stretching sheet is proportional to its distance from the leading edge.

Fig. 1

Model Geometry

Generally, Hall current has an effect on an electrically conducting fluid in the presence of a magnetic field. The effect of Hall current gives rise to a force in the z-direction, which induces a cross-flow in the z-direction and hence the flow becomes three dimensional. The equation of conservation of Charge $\nabla \cdot \overline{J} =0$ gives $\hbox {J}_{\mathrm{y}}=$ constant, where the current density $\overline{J} =\left( {J_x ,J_y , J_z } \right)$. Since the plate is non-conducting this constant is zero, $\hbox {J}_{\mathrm{y}}= 0$ at the plate and hence everywhere. The expressions for the current density components $\hbox {J}_{\mathrm{x}}$ and $\hbox {J}_{\mathrm{z}}$ as obtained from the generalized ohm’s law, see Cowling [26].

Fig. 2

Primary Velocity profiles for different step sizes $\Delta \eta$

Fig. 3

Secondary Velocity profiles for different step sizes $\Delta \eta$

Fig. 4

Temperature profiles for different step sizes $\Delta \eta$

Table 1 Variation of physical parameters

Fig. 5

Primary Velocity profiles for $\updelta$ (Pr $=$ 0.72, Gr $=$ 5, $M=0.2$, $m=3.0$ and Ec $=$ 0. 22)

Fig. 6

Secondary Velocity profiles for $\updelta$ (Pr $=$ 0.72, Gr $=$ 5, $M=0.2$, $m=3.0$ and Ec $=$ 0. 22)

Fig. 7

Temperature profiles for $\updelta$ (Pr $=$ 0.72, Gr $=$ 5, $M=0.2$, $m=3.0$ and Ec $=$ 0. 22)

Fig. 8

Primary Velocity profiles for Pr (Gr $=$ 5.0, $M=0.2$, $m=3.0$ and Ec $=$ 0. 22)

Fig. 9

Secondary Velocity profiles for Pr (Gr $=$ 5.0, $M=0.2$, $m=3.0$ and Ec $=$ 0. 22)

Fig. 10

Temperature profiles for Pr (Gr $=$ 5.0, $M = 0.2$, $m=3.0$ and Ec $=$ 0. 22)

$J=\frac{\sigma }{1+m^{2}}\left( {\overline{E} +\overline{V} \times \overline{B} -\frac{1}{en_e }\overline{J} \times \overline{B} } \right)$ in the absence of electric field are given by $J_x =\frac{\sigma \mu _e B_0 \lambda }{1+m^{2}\lambda ^{2}}(m\lambda u-w)$ and $J_z =\frac{\sigma \mu _e B_0 \lambda }{1+m^{2}\lambda ^{2}}(u+m\lambda w)$.

To simplify the problem, we assume that there is no variation of flow or heat transfer quantities in the z-direction. Under the usual boundary layer and Boussinesq approximations, the governing equations in (x, y, z) coordinate for the problem under consideration can be written as follows:

$$\begin{aligned}&\displaystyle \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 \end{aligned}$$

(1)

$$\begin{aligned}&\displaystyle u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\upsilon \frac{\partial ^{2}u}{\partial y^{2}}+u_e \frac{du_e }{dx}+g\beta \left( {T-T_\infty } \right) -\frac{B_0 }{\rho }J_z \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}=\upsilon \frac{\partial ^{2}w}{\partial y^{2}}+\frac{B_0 }{\rho }J_x \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{\kappa }{\rho C_p }\frac{\partial ^{2}T}{\partial y^{2}}+\frac{v}{C_p }\left( {\left( {\frac{\partial u}{\partial y}} \right) ^{2}+\left( {\frac{\partial w}{\partial y}} \right) ^{2}} \right) +\frac{\sigma \mu _e B_0 ^{2}\lambda }{\rho C_p (1+m^{2}\lambda ^{2})}(u^{2}+w^{2})\nonumber \\ \end{aligned}$$

(4)

The boundary conditions are

$$\begin{aligned} \left. {\begin{array}{ll} u=u_0 =Bx,\;v=0,\;w=0, T=T_\mathrm{w} =T_\infty +A\left( {x/l} \right) &{}\hbox { at } y=0 \\ {u}\rightarrow u_e \left( x \right) =Cx, w\rightarrow 0,\;T\rightarrow T_\infty &{}\hbox { as } y\rightarrow \infty \\ \end{array}} \right\} \end{aligned}$$

(5)

Here $\hbox {V} = (u, v, w)$ are the fluid velocity components in the x, y, z-directions respectively, $J_x =\frac{\sigma \mu _e B_0 \lambda }{1+m^{2}\lambda ^{2}}(m\lambda u-w)$ and $J_z =\frac{\sigma \mu _e B_0 \lambda }{1+m^{2}\lambda ^{2}}(u+m\lambda w)$ are the currents only to x- and z-axis respectively, $\sigma$is the electric conductivity, $\mu _e$ is the viscosity of fluid, $B_0$ is the uniform magnetic field strength, $m=\omega _e \tau _e$is the Hall parameter and $\lambda =\cos \alpha$ where $\alpha$ is the angle between the direction of the strong uniform magnetic field $\mathop B\limits ^\rightarrow$and the plane transverse to the plate which is assumed to be electrically non-conducting, E is the intensity of electric field, $\hbox {n}_{\mathrm{e}}$ is the electron number density, $\upsilon$ is the kinematic viscosity, $u_{e}(x)$ is the external velocity, $\beta$ is the volumetric coefficient of thermal expansion, $\rho$ is the fluid density, $\kappa$ is the thermal conductivity of the fluid, $C_{p}$ the specific heat at constant pressure, A is a constant and l is the length.

Similarity Analysis

In order to obtain similarity solution for the problem under consideration, we may take the following suitable similarity variables

$$\begin{aligned} \eta= & {} y\left( {\frac{B}{\upsilon }} \right) ^{\frac{1}{2}}, \quad u=B x {f}'\left( \eta \right) , \quad v=-\left( {B\upsilon } \right) ^{\frac{1}{2}}f\left( \eta \right) , \quad w=B x g\left( \eta \right) \hbox { and } \quad \theta \left( \eta \right) \nonumber \\= & {} \frac{T-T_\infty }{T_w-T_\infty }. \end{aligned}$$

(6)

Therefore the transformed equation using the above parameter becomes:

$$\begin{aligned} {f}'''+\delta ^{2}+f {f}''-{f}'^{2}+Gr\theta -\frac{M\lambda }{1+m^{2}\lambda ^{2}}\left( {{f}'+m\lambda g} \right)= & {} 0 \end{aligned}$$

(7)

$$\begin{aligned} {g}''+f {g}'+{f}' g+\frac{M\lambda }{1+m^{2}\lambda ^{2}}\left( {m\lambda {f}'-g} \right)= & {} 0 \end{aligned}$$

(8)

$$\begin{aligned} {\theta }''+\Pr f {\theta }'-\Pr {f}' \theta +\frac{M\lambda }{1+m^{2}\lambda ^{2}}\Pr .Ec \left( {{f}'^{2}+g^{2}} \right)= & {} 0 \end{aligned}$$

(9)

The corresponding boundary conditions are

$$\begin{aligned} \left. {\begin{array}{ll} f=0, {f}'=1, g=0, \theta =1 &{}\quad \hbox {at }\eta =0 \\ {f}'\rightarrow \delta , g\rightarrow 0, \theta \rightarrow 0 &{}\quad \hbox {as } \eta \rightarrow \infty \\ \end{array}} \right\} \end{aligned}$$

(10)

Here, $\delta =\frac{C}{B}$ is the velocity parameter, $Gr=\frac{g\beta \left( {T_w -T_\infty } \right) x}{u_0 ^{2}}$ is the local Grashof number, $M=\frac{\sigma \mu _e B_0 ^{2}x}{\rho u_0 }$ is the local magnetic parameter and $B_0 =\frac{B}{\sqrt{x}}$ is the magnetic field, $\Pr =\frac{\rho \upsilon C_p }{\kappa }$ is the Prandtl number and $Ec=\frac{u_0 ^{2}}{C_p \left( {T_w -T_\infty } \right) }$ is the Eckert number.

The parameters of engineering interest for the present problem are the wall skin-friction components for the primary and secondary velocities, and the local Nusselt number (Nu). The non-dimensional shear stress components due to the primary and secondary velocity are given by

$$\begin{aligned} C_{fx} =\frac{\tau _{wx} }{\frac{1}{2}\rho u_0 ^{2}}\hbox { and }C_{fz} =\frac{\tau _{wz} }{\frac{1}{2}\rho u_0 ^{2}} \end{aligned}$$

(11)

The skin-friction $\tau _{wx}$ and $\tau _{wz}$ are given by, $\tau _{wx} =\mu \left. {\frac{\partial u}{\partial y}} \right| _{y=0} =\mu u_0 \left( {\frac{B}{\upsilon }} \right) ^{\frac{1}{2}}{f}''\left( 0 \right)$

and $\tau _{wz} =\mu \left. {\frac{\partial w}{\partial y}} \right| _{y=0} =\mu u_0 \left( {\frac{B}{\upsilon }} \right) ^{\frac{1}{2}}{g}'\left( 0 \right)$ respectively.

Substitute these values in (11), we get

$$\begin{aligned} C_{fx}= & {} \frac{\tau _{wx} }{\frac{1}{2}\rho u_0 ^{2}}=\frac{2\left( {B\upsilon } \right) ^{\frac{1}{2}}}{u_0 }{f}''\left( 0 \right) \end{aligned}$$

(12)

$$\begin{aligned} C_{fz}= & {} \frac{\tau _{wz} }{\frac{1}{2}\rho u_0 ^{2}}=\frac{2\left( {B\upsilon } \right) ^{\frac{1}{2}}}{u_0 }{g}'\left( 0 \right) \end{aligned}$$

(13)

Now introducing dimensionless quantities, we obtain a local dimensionless coefficient of heat transfer which is known as the local Nusselt number, the local Nusselt number $Nu_x$ and is proportional to the temperature gradient at the plate. It is defined as

$$\begin{aligned} Nu_x =\frac{xq_w }{k\left( {T_w -T_\infty } \right) } \end{aligned}$$

Heat transfer from the plate $q_w$ is given by $q_w =-k\left( {\frac{\partial T}{\partial y}} \right) _{y=0}$

Thus,

$$\begin{aligned} Nu_x =\frac{x}{\left( {T_w -T_\infty } \right) }\left. {\frac{\partial T}{\partial y}} \right| _{y=0} =-u_0 \left( {B\upsilon } \right) ^{- \frac{1}{2}}{\theta }'\left( 0 \right) \end{aligned}$$

(14)

Thus from the above definition we have $C_{fx} \propto {f}^{{\prime }{\prime }}\left( 0 \right)$, $C_{fz} \propto {g}^{\prime }\left( 0 \right)$ and $Nu_x \propto -{\theta }^{\prime }\left( 0 \right)$.

Fig. 11

Primary Velocity profiles for Gr ($\updelta$ = 0.1, Pr = 0.72, $M=0.2$, $m=3.0$ and Ec $=$ 0. 22)

Fig. 12

Secondary Velocity profiles for Gr ($\updelta$ $=$ 0.1, Pr $=$ 0.72, $M=0.2$, $m=3.0$ and Ec $=$ 0. 22)

Fig. 13

Temperature profiles for Gr ($\updelta$ $=$ 0.1, Pr $=$ 0.72, $M=0.2$, $m=3.0$ and Ec $=$ 0. 22)

Fig. 14

Primary Velocity profiles for M ($\updelta$ $=$ 0.1, Pr $=$ 0.72, Gr $=$ 5, $m =3.0$ and Ec $=$ 0.22)

Fig. 15

Secondary Velocity profiles for M ($\updelta = 0.1$, Pr $=$ 0.72, Gr $=$ 5, $m=3.0$ and Ec $=$ 0.22)

Fig. 16

Temperature profiles for M ($\updelta$ $=$ 0.1, Pr $=$ 0.72, Gr $=$ 5, $m=3.0$ and Ec $=$ 0.22)

Numerical Computation

The numerical solutions of the non-linear differential equations (7)–(9) under the boundary conditions (10) have been performed by applying a shooting method namely Nachtsheim and Swigert [27] iteration technique (guessing the missing values) along with sixth order Runge–Kutta iteration scheme. We have chosen a step size $\Delta \eta =0.01$ to satisfy the convergence criterion of $10^{-5}$ in all cases. The value of $\eta _\infty$ has been found to each iteration loop by $\eta _\infty =\eta _\infty +\Delta \eta$. The maximum value of $\eta _\infty$ to each group of parameters $\updelta$, Pr, Gr, M, m and Ec has been determined when the values of the unknown boundary conditions at $\eta =0$ not change to successful loop with error less than $10^{-5}$. In order to verify the effects of the step size $\Delta \eta$, we have run the code for our model with three different step sizes as $\Delta \eta =0.01, \Delta \eta =0.005$ and $\Delta \eta =0.001,$ and in each case we have found excellent agreement among them shown in Figs. 2, 3 and 4. Table 1 also compare the Mathematica solution, Wolfram [28] with the Nachtsheim and Swigert iteration technique solutions for the skin friction and temperature gradient functions at selected values of the parameters. In all cases, excellent agreement is observed. Confidence in the present Nachtsheim and Swigert iteration computations, which are used for all graphical depictions, is therefore very high.

Fig. 17

Primary Velocity profiles for m ($\updelta$ $=$ 0.1, Pr $=$ 0.72, Gr $=$ 5, $M=0.2$ and Ec $=$ 0.22)

Fig. 18

Secondary Velocity profiles for m ($\updelta$ $=$ 0.1, Pr $=$ 0.72, Gr $=$ 5, $M=0.2$ and Ec $=$ 0.22)

Fig. 19

Temperature profiles for m ($\updelta$ $=$ 0.1, Pr $=$ 0.72, Gr $=$ 5, $M=0.2$ and Ec $=$ 0.22)

Fig. 20

Primary Velocity profiles for Ec ($\updelta$ $=$ 0.1, Pr $=$ 0.71, Gr $=$ 5, $M=0.2$ and $m=3.0$)

Fig. 21

Secondary Velocity profiles for Ec ($\updelta$ $=$ 0.1, Pr $=$ 0.71, Gr $=$ 5, $M=0.2$ and $m=3.0$)

Fig. 22

Temperature profiles for Ec ($\updelta$ $=$ 0.5, Pr $=$ 0.71, Gr $=$ 5, $M=0.2$ and $m=3.0$)

Results and Discussion

Nachtsheim–Swigert iteration technique along with the sixth order Runge–Kutta integration scheme have been performed to investigate the non-dimensional primary $\left( {{f}'} \right)$, secondary velocity $\left( g \right)$ and temperature $\left( \theta \right)$ variations for the effects of velocity parameter ($\updelta )$, Prandtl number (Pr), Grashof number (Gr), magnetic field parameter (M), hall parameter (m) and Eckert number (Ec). The values of buoyancy parameter Gr is taken to be positive to represent cooling of the plate. The parameters are chosen arbitrarily where Pr = 0.71 corresponds physically to air at $20^{\circ }\hbox {C}, \hbox {Pr}\,=\,1.0$ corresponds to electrolyte solution such as salt water and Pr  $=$  7.0 corresponds to water, consider M, m, Ec and $\updelta$ are chosen arbitrarily. As demonstrated in this model, the angle between the direction of the strong uniform magnetic field and the plane transverse to the plate is zero i.e., $\alpha =0^{\circ }$, hence the value of the parameter $\lambda$ is set at 1. In order to illustrate the results graphically, the numerical values are plotted in Figs. 5, 6, 7. 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 and 22. Representative results for the physical parameters have been presented in Table 1.

Figures 5, 6 and 7 illustrate the primary velocity, secondary velocity and temperature profiles for different velocity parameter. As $\updelta$ increases the thickness of the momentum boundary layer increases for both the primary and secondary velocities. Evidently in Fig. 5, the greatest velocity is achieved for primary velocity than in Fig. 6. Asymptotically smooth behavior of all profiles is obtained at the edge of the momentum and thermal layer adjusting the convergence solutions. As with the temperature distribution (Fig. 7), due to the heat convection in the fluid flow, the temperature profile decreases as $\updelta$ increases.

Figures 8, 9 and 10 shows the effect of Prandtl number on velocity and temperature profiles. The Prandtl number effect on the primary velocity profile is shown in Fig. 8. It is seen that with the increase of Pr the primary velocity reduces which is observed in each case of $\updelta =0.1, 0.5$ and 1.2. But increasing effect is seen in secondary profile for the Prandtl number. When $\updelta = 0.1$ the effect is apparent for large Pr. But for higher $\updelta$ there is no significant effect of Pr on secondary velocity profile (Fig. 9). Figure 10 finally shows that there is uniform temperature profile across the thermal boundary layer for Pr.

Figures 11, 12 and 13 present the influence of Grashof number on the profiles of velocity and temperature. Near the plate there is very noteworthy effect of the Grashof number Gr on primary velocity profile. At the beginning primary velocity profile increases with the increase of Gr but profile overlaps and Gr has tiny decreasing effect after $\eta = 2.07$ as in Fig. 11. Figure 12 shows that in the vicinity of the plate ($\eta <0.92$) secondary velocity profile increases with the rising of the value of Gr but away from the plate Gr affects reversely on the secondary velocity profiles. For $G_r \rangle 1$ buoyancy force dominates the viscous force. Increasing Gr therefore attain falling outcome to the temperature profile closer to the plate surface.

Figures 14, 15 and 16 depict the effect of present the influence of magnetic field parameter on the profiles of velocity and temperature. Trivial effect associated with primary velocity and temperature where as the vastly affected corresponds to secondary velocity. Due to slight mounting deviation in M the secondary profile enhances to a very large extent.

Figures 17, 18 and 19 depict the effects of the Hall current parameter m on the velocity and temperature distributions. We observe that there is no influence of m on the primary velocity as well as on the temperature profile. Secondary velocity profile is affected enormously by the Hall current parameter m. The temperature distribution decreases at a great extent as m increases as shown in Fig. 18.

Figures 20, 21 and 22 depict the effect of present the influence of Eckert number on the profiles of velocity and temperature. Figure 20 demonstrates the effects of the Eckert number Ec on primary velocity profile for some values of $\updelta$ (0.1, 0.5 and 1.2). For small velocity parameter ($\updelta$ = 0.1) there is not so remarkable effect of Ec. But when $\updelta$ $=$ 0.5 the effect of Ec is very patent. Primary velocity profile increases with the increase of Ec. When the value of $\updelta$ is getting large the effect of Ec on primary velocity profile is lessening. The secondary velocity profile increases when the value of Ec increases as shown in Fig. 21. Figure 22 demonstrates that Ec has increasing influence on the temperature profile.

Finally, the effects of various physical quantities at the plate surface appeared in problem such as the skin frictions $C_{fx} \propto {f}^{{\prime }{\prime }}\left( 0 \right)$ & $C_{fz} \propto {g}'\left( 0 \right)$ and local Nusselt number $Nu_x \propto -{\theta }'\left( 0 \right)$ are shown in the Table 1.

Conclusions

In the current paper, the steady three-dimensional MHD natural convection heat transfer of an electrically conducting fluid past a stretching surface in the presence of Hall currents, viscous dissipation and Joule heating effects was studied. The governing equations were reduced to a system of ordinary differential equations and then the results were carried out numerically. The effects of velocity parameter ($\updelta )$, Prandtl number (Pr), Grashof number (Gr), magnetic field parameter (M), hall parameter (m) and Eckert number (Ec) on the primary and secondary velocity (momentum) and temperature (Thermal) profiles are investigated through the use of graphs and table. The main results of the present analysis are listed below:

• 1. Both the primary and secondary velocities increase whereas the temperature distributions decreases with increasing velocity parameter $\updelta$.

• 2. Both the primary and secondary velocities profiles increase for increasing Gr near to the plate while the trend is reversed far from the plate. The Grashof numberGr is to decelerate the temperature profiles.

• 3. Both the primary velocity and temperature profiles are insensible to change with magnetic parameter M. Further, Increasing magnetic parameter M tends to increase the secondary velocity profiles.

• 4. Both the primary velocity and temperature profiles are insensible to change with Hall current parameter m. Further, Increasing Hall current parameter m tends to diminish the secondary velocity profiles.

• 5. Both the secondary velocity and temperature profiles boost with a rise in the Eckert number Ec. Further, Primary velocity is intangible to change Eckert number Ec for lower value of ($\updelta$ = 0.1) while it increases moderately with the higher value of ($\updelta$ $=$ 0.5 and 1.2).