MHD Flow and Heat Transfer Over a Slender Elastic Permeable Sheet in a Rotating Fluid with Hall Current

Abstract

Magnetohydrodynamic flow and heat transfer over a stretching sheet with a variable thickness in a rotating fluid with Hall current is investigated. Both analytical and numerical methods are employed to solve the governing coupled nonlinear differential equations. The analytical solutions are obtained through the optimal homotopy analysis method where the numerical solutions are computed by a second-order finite difference scheme. The solutions for the non-dimensional velocity and temperature fields are obtained and presented graphically for various physical parameters. The accuracy of the analytical solution is verified by plotting the residual errors and by comparing solutions with available results in the literature for some special cases. The Hall current gives rise to a cross flow. The rotating fluid frame and the wall transpiration (suction/injection) can have strong effects on the shear stress and the Nusselt number.

Introduction

The study of boundary layer flow and heat transfer over a stretching sheet is of interest as it occurs in a variety of engineering and technological processes. These processes include cooling of an infinite metallic plate in a cooling bath, extrusion of polymers involving cooling of a molten liquid, drawing and tinning of copper wires, paper production, glass blowing, and heat treatment of materials travelling on conveyor belts. Some considerations must be made to accomplish the desired quality in such processes, namely, selection of the liquid to be used to cool the object of interest and the rate of stretching applied to the material. Processes involving sudden solidification focus heavily on the rate of stretching. In these processes, we come across nonlinear relations between stress and rate of strain. In science and technological industries, frequently we find systems of coupled nonlinear boundary value problems. The analysis of such systems of nonlinear boundary value problems is usually coupled and poses challenges to mathematicians and physicists. Because of such complexities, there are many problems still open in the literature and one such problem is the Navier–Stokes equations. Traditionally, solutions of nonlinear boundary value problems strongly depend on the type of nonlinearity, physical parameters, and the employed techniques. Crane [1] considered the stretching sheet problem and presented the exact solutions. Later, various extensions were carried out by Wang [2], Miklavcic and Wang [3], and Fang and Zhang [4]. There are several analytical techniques available in the literature to solve nonlinear boundary value problems. Some of the classical analytical techniques are Adomian’s decomposition method (ADM), Lyapunov’s artificial small parameter method, the $\delta$-expansion method, Chebyshev spectral collocation method, Padé approximation, homotopy perturbation method (HPM), Laplace decomposition method (LDM), homotopy analysis method (HAM), spectral-homotopy analysis method (SHAM), differential transformation method (DTM) and variational iteration method (VIM), optimal homotopy analysis method (OHAM). Details of these methods can be found in Dehghan et al. [5], Dehghan and Shakeri [6], Lyapunov [7], Karmishin et al. [8], Khater et al. [9], John [10], Hayat et al. [11], He [12], Khan [13], Tan and Abbasbandy [14], Liao [15,16,17,18], Fan and You [19], Hayat et al. [20,21,22,23], Shehzad et al. [24], Farooq et al. [25] and Motsa et al. [26]. In particular, the homotopy analysis method logically contains traditional non-perturbation techniques, such as Adomian’s decomposition method, Lyapunov’s artificial small parameter method, and the $\delta$-expansion method. Hence it can be regarded as a unified or generalized theory of these three methods. This method also provides a special way to control and adjust the convergence region and rate of solution series of nonlinear problems. Liao [17] observed that HAM cannot always guarantee the convergence of approximation series of nonlinear equations in general and to overcome this restriction, he introduced non-zero auxiliary parameter $c_{0 }$ (convergence-control parameter) to construct a two-parameter family of equations to gain better approximations and the method is called OHAM. Further, Motsa et al. [26] proposed a spectral-homotopy analysis method (SHAM) which is a modification of the homotopy analysis method (HAM) and the basic idea of this method is to blend in HAM with the Chebyshev spectral collocation method.

In contrast to the above-mentioned analytical/semi-analytical methods for finding stable solutions, for certain class of systems, researchers have developed many prominent numerical methods. To mention a few, the shooting method, finite difference approximations, finite element method, Crank–Nicolson method and Keller-box method have been employed (see Meade et al. [27], Cebeci and Bradshaw [28], Keller [29], Vajravelu and Prasad [30], Abbasi et al. [31], Sheikholeslami et al. [32], and Hayat et al. [33]). One of the notable advantages of the Keller-box method over the other methods is that it allows easy programming for finding the solution of a large number of coupled equations with second-order accuracy along with arbitrary (non-uniform) spacing for discretization in the x- and y-directions.

The main objective of this paper is to solve the system of coupled nonlinear boundary value problem which arises in the mathematical modeling of MHD flow and heat transfer over a slender permeable elastic sheet in a rotating fluid with Hall current. The semi-analytical method OHAM and the second-order finite difference scheme known as the Keller-box method are used. The study of the MHD flow in a rotating environment includes the effect of Coriolis forces, thermal convection current, and Hall current. It is generally admitted that the Coriolis force due to the earth’s rotation has a strong influence on the hydromagnetic flow in the earth’s liquid core. Several authors have examined the fluid dynamics of rotating systems under different geometry due to its various applications such as the compressor, wind turbine, jet engine, pumps, large-scale atmospheric and oceanic flows (see Wang [34], Abbas et al. [35]). The present work aims to look into the enhancement in the transport phenomena due to an increase in temperature (e.g. Grubka and Bobba [36], Ali [37] and Chen [38], Chaudhary and Kumar Jha [39]) by considering a special type of nonlinear stretching $u_w \left( x \right) =U_0 \left( {x+b} \right) ^{n}$ at $y=A\left( {x+b} \right) ^{{\left( {1-n} \right) }/2}$ for different values of n. That is, a stretching sheet with a variable thickness, as in Fang et al. [40], Khader and Megahed [41] and Hayat et al. [42, 43]. This study is also pertinent to vibration of orthotropic plates. The governing nonlinear coupled equations for flow and heat transfer are reduced to a set of nonlinear coupled differential equations through a suitable similarity transformation and are solved for various values of physical parameters by the OHAM and Keller-box method. We may find out from the numerical results that under what conditions the fluid flow can be appreciably influenced by the physical parameters. The present findings will not only be useful to industrial applications but also help a basic understanding of the physics of the problem.

Mathematical Formulation

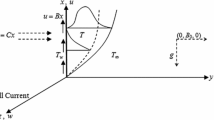
Consider a steady, laminar boundary layer flow of a viscous, incompressible and electrically conducting fluid induced by permeable stretching of a surface in the x-direction with a variable thickness. The surface coincides with the plane at $y=A\left( {x+b} \right) ^{{( {1-n} )}/2}$, and is being stretched with a nonlinear velocity $U_w (x)$ and temperature $T_w ( x )$. The fluid is rotating with a constant angular velocity $\Omega$ about the y-axis. The sheet is in the plane $z = 0$. Initially, the fluid and the plate rotate synchronously with uniform angular velocity $\Omega$. The fluid is then set into motion with uniform acceleration along the x-axis. The stretching nonlinear distance x is also rotating with the fluid. The flow is three dimensional due to the presence of the Coriolis force. The positive x-coordinate is measured along the stretching sheet in the direction of motion and the positive y-coordinate is measured normal to the sheet in the upward direction (see Fig. 1 for details).

Fig. 1

a Schematic diagram of the stretching sheet with variable thickness model; b schematic representation of the physical model and co-ordinate system

An external magnetic field is applied in the positive y-direction with a constant flux density $B_{0}$. In general, for an electrically conducting fluid, Hall current affects the flow in the presence of a strong magnetic field. The effect of Hall current gives rise to a cross flow and hence the flow becomes three-dimensional. We assume that there is no variation of flow quantities in the z-direction. This assumption is valid for a surface of infinite extent. The generalized Ohm’s law including Hall currents in the usual notation is given by

$$\begin{aligned} \mathbf{J}=\sigma \left( {\mathbf{E}+\mathbf{V}\times \mathbf{B}-\frac{1}{en_e }{} \mathbf{J}\times \mathbf{B}+\frac{1}{en_e }\nabla p_e } \right) . \end{aligned}$$

(1)

Here $\mathbf{J} =\left( {J_x ,J_y ,J_z } \right)$ is the current density vector, $\mathbf{E}$ is the intensity vector of the electric field, $\mathbf{V}$ is the velocity vector, $\mathbf{B} =\left( {0,B_0 ,0} \right)$ is the magnetic induction vector, $\sigma$ is the electrical conductivity, and $p_e$ is the electronic pressure. Since there is no applied or polarization voltage is imposed on the flow we have, $\mathbf{E}=0$. For weakly ionized gases, the electron pressure gradient and the ion slip effects can be neglected. The generalized Ohm’s law under the above conditions for electrically non-conducting sheet $J_y =0$. Hence Eq. (1) reduces to

$$\begin{aligned} J_x =\frac{\sigma B_0 \left( x \right) }{\left( {1+m^{2}} \right) }\left( {mu-w} \right) \quad \hbox {and}\quad J_z =\frac{\sigma B_0 \left( x \right) }{\left( {1+m^{2}} \right) }\left( {u+mw} \right) . \end{aligned}$$

(2)

Here u, v and w are the x-, y- and z-components of the velocity vector $\mathbf{V}$, and m is the Hall parameter. The following assumptions are made.

• 1. Joule heating and viscous dissipation are neglected.

• 2. The fluid is isotropic, homogeneous, and has constant viscosity and electric conductivity.

• 3. The wall is impermeable $(v_w =0)$.

• 4. The sheet is being stretched with a velocity $U_w (x)=U_0 \left( {x+b} \right) ^{n}\;\hbox {where}\;U_0$ is constant, b is the physical parameter related to stretching sheet, and n is the velocity exponent parameter.

• 5. The sheet is not flat and is defined as $y=A\left( {x+b} \right) ^{{\left( {1-n} \right) }/2}{,}$ where the coefficient A is chosen as small so that the sheet is sufficiently thin, to avoid pressure gradient along the sheet $(\partial p/\partial x=0)$.

Under these assumptions, along with the boundary layer approximations, the governing equations can be written as (for details see Abbas et al. [35] and Chaudhary and Kumar Jha [39]):

$$\begin{aligned}&u_x +v_y =0, \end{aligned}$$

(3)

$$\begin{aligned}&\rho \left( {u u_x +vu_y } \right) -2\Omega w=\mu u_{yy} -\frac{\sigma B_0^2 \left( x \right) }{\left( {1+m^{2}} \right) }\left( {u+mw} \right) , \end{aligned}$$

(4)

$$\begin{aligned}&\rho \left( {u w_x +vw_y } \right) +2\Omega u= \mu w_{yy} +\frac{\sigma B_0^2 \left( x \right) }{\left( {1+m^{2}} \right) }\left( {mu-w} \right) , \end{aligned}$$

(5)

$$\begin{aligned}&\rho c_p \left( {uT_x +v T_y } \right) =kT_{yy} . \end{aligned}$$

(6)

Here, the subscript denotes partial differentiation with respect to the independent variable, $\rho$ is fluid density, $\mu$ dynamic viscosity, $C_p$ is the specific heat at constant pressure, T is the temperature, k thermal conductivity. A special form of a magnetic field $B_0^2 \left( x \right) =B_0^2 \left( {x+b} \right) ^{n-1}$ is considered to facilitate the similarity transformation. The appropriate boundary conditions for the problem are

$$\begin{aligned}&\left. {{\begin{array}{l} {u(x,y)=U_w =U_0 (x+b)^{n},v(x,y)=0} \\ {w(x,y)=0,T(x,y)=T_w =\frac{C}{l}\left( {x+b} \right) ^{r}} \\ \end{array} }} \right\} \quad \hbox {at}\;y=A(x+b)^{1-n/2}, \nonumber \\&u(x,y)\rightarrow 0,w(x,y)\rightarrow 0,T(x,y)\rightarrow T_\infty \quad \hbox {as}\;y\rightarrow \infty , \end{aligned}$$

(7)

where C is a constant and r is the wall temperature. It should be noted that the positive and negative value of n indicate cases of surface stretching and surface shrinking, respectively. Now we transform the system of Eqs. (3)–(6) into a dimensionless form. To this end, let us introduce a dimensionless similarity variable

$$\begin{aligned} \eta = y\sqrt{\frac{n+1}{2 }\frac{U_0 }{\nu }}(x+b)^{\frac{n-1}{2}}. \end{aligned}$$

(8)

Now in terms of $\eta$, we define the dimensionless stream function $\psi (x,y)$ and the dimensionless temperature distribution $\theta \left( \eta \right)$ as

$$\begin{aligned} \psi (x,y) = f(\eta ) \sqrt{\frac{2}{n+1 }\nu U_0 \left( {x+b} \right) ^{n+1}}, \quad \theta \left( \eta \right) =\frac{T-T_\infty }{T_w -T_\infty }, \end{aligned}$$

(9)

where $\psi (x,y)$ identically satisfies the continuity Eq. (3). With the help of Eq. (9), the velocity components can be written as

$$\begin{aligned} u=U_w {f}'(\eta ), v=-\sqrt{\nu \frac{n+1}{2}U_0 (x+b)^{n-1}}\left[ {f(\eta )+\eta {f}'(\eta )\left( {\frac{n-1}{n+1}} \right) } \right] , w=U_w h(\eta ). \end{aligned}$$

(10)

Here a prime denotes differentiation with respect to $\eta$. With the use of Eqs. (8)–(10), Eqs. (4)–(6) and (7) can be reduced to

$$\begin{aligned}&{f}'''+f {f}''-\frac{2n}{(n+1)}{f}'^{2}+\beta h-\frac{2Mn}{\left( {1+m^{2}} \right) \left( {1+n} \right) }\left( {{f}'+mh} \right) =0, \end{aligned}$$

(11)

$$\begin{aligned}&{h}''+f {h}'-\frac{2n}{n+1}{f}' h-\beta {f}'+\frac{2Mn}{\left( {1+m^{2}} \right) \left( {1+n} \right) }\left( {m {f}'-h} \right) =0, \end{aligned}$$

(12)

$$\begin{aligned}&{\theta }'' +\Pr \left( {f{\theta }'-\frac{2r}{n+1}\theta {f}'} \right) = 0, \end{aligned}$$

(13)

$$\begin{aligned}&f\left( \alpha \right) = \alpha \frac{1-n}{1+n},\quad {f}'\left( \alpha \right) = 1 ,\quad h\left( \alpha \right) =0, \theta \left( \alpha \right) =1, \theta (\infty )=0 , \quad {f}'(\infty )=0,h(\infty )=0.\nonumber \\ \end{aligned}$$

(14)

The non-dimensional parameters Mn, $\beta$ and Pr, respectively denote the magnetic parameter, the fluid rotation parameter, and the Prandtl number and are defined as follows:

$$\begin{aligned} Mn=\frac{\sigma B_0 ^{2}}{\rho U_0 }, \quad \beta =\frac{4\Omega }{\left( {n+1} \right) \rho U_0 }\quad \text { and }\quad \hbox {Pr}=\frac{\nu }{\alpha }. \end{aligned}$$

Here, $\alpha =A\sqrt{(n+1)U_0 /(2\nu )}$ is the wall thickness parameter and $\eta =\alpha = A\sqrt{(n+1)U_0 /(2\nu )}$ indicates the plate surface. In order to facilitate the computation, we define $f(\xi )=f\left( {\eta -\alpha } \right) =f\left( \eta \right) ,h(\xi )=h\left( {\eta -\alpha } \right) =h( \eta )$ and $\theta (\xi )=\theta (\eta -\alpha )=\theta (\eta )$. Now Eqs. (11)–(13) become

$$\begin{aligned}&{f}'''+f{f}''-\frac{2n}{(n+1)}{f}'^{2}+\beta h-\frac{2Mn}{\left( {1+m^{2}} \right) \left( {1+n} \right) }\left( {{f}'+mh} \right) =0, \end{aligned}$$

(15)

$$\begin{aligned}&{h}''+f {h}'-\frac{2n}{\left( {n+1} \right) }{f}' h-\beta {f}'+\frac{2Mn}{\left( {1+m^{2}} \right) \left( {1+n} \right) }\left( {m {f}'-h} \right) =0, \end{aligned}$$

(16)

$$\begin{aligned}&{\theta }'' +\Pr \left( {f{\theta }'-\frac{2r}{n+1}\theta {f}'} \right) = 0, \end{aligned}$$

(17)

and the corresponding boundary conditions are $\left( {n\ne -1} \right)$

$$\begin{aligned} f(0)= & {} \alpha \frac{1-n}{1+n},\quad {f}'(0)=1 ,\quad h(0)=0,\quad \theta (0)=1,\quad \theta (\infty )=0 ,\quad \nonumber \\ h(\infty )= & {} 0,\quad {f}'(\infty )=0 \end{aligned}$$

(18)

where the prime denotes differentiation with respect to $\xi .$ When $\left( {\alpha<0\hbox { and }n<1} \right)$ or $\left( {\alpha>0\hbox { and }n>1} \right)$, the surface is of a suction case, and when $\left( {\alpha <0\hbox { and }n>1} \right)$ or $\left( {\alpha >0\hbox { and }n<1} \right)$, the surface is of injection (blowing) case. In general, injection (blowing) tends to decrease the skin friction and Nusselt number, whereas suction acts in the opposite manner. For all practical purposes, the important physical quantities of interest are the horizontal skin friction $C_{fx}$, transverse skin friction $C_{fz}$ and the Nusselt number $Nu_x$ defined by

$$\begin{aligned} C_{f_x}= & {} \frac{2 \nu \left( {u_y } \right) _{ y =A\left( {x+b} \right) ^{\frac{1-n}{2}}} }{U_w^2 }=2\sqrt{\frac{n+1}{2 \hbox {Re}_x }} {f}''(0), \nonumber \\ C_{f_z }= & {} \frac{2 \nu \left( {w_y } \right) _{ y =A\left( {x+b} \right) ^{\frac{1-n}{2}}} }{U_w^2 }=2\sqrt{\frac{n+1}{2 \hbox {Re}_x }}{h}'(0), \nonumber \\ Nu_x= & {} \frac{\left( {x+b} \right) \left( {T_y } \right) _{ y =A\left( {x+b} \right) ^{\frac{1-n}{2}}} }{\left( {T_w -T_\infty } \right) }=-\sqrt{\frac{n+1}{2 \hbox {Re}_x }}{\theta }'(0), \end{aligned}$$

(19)

where $\hbox {Re}_x = U_w (x+b)/\nu$ is the local Reynolds number.

Method of Solution

Semi-analytical Solution: Optimal Homotopy Analysis Method (OHAM)

Optimal homotopy analysis method has been employed to solve the nonlinear, system of Eqs. (15)–(17) with boundary conditions (18). The OHAM scheme breaks down a nonlinear differential equation into infinitely many linear ordinary differential equations whose solutions are found analytically. In the framework of the OHAM, the nonlinear equations are decomposed into their linear and nonlinear parts described as follows.

In accordance with the boundary conditions (18), consider the base functions as $\{ {\exp \left( {-n\xi } \right) \hbox {for}\,n\ge 0} \}$, then the dimensionless velocities $f(\xi ),h(\xi )$ and temperature $\theta (\xi )$ can be expressed in a series form as follows

$$\begin{aligned} f(\xi )=\sum _{n=0}^\infty {a_n e^{\left( {-n\xi } \right) }} , \quad h(\xi )=\sum _{n=0}^\infty {b_n e^{\left( {-n\xi } \right) }} \quad \hbox {and}\quad \theta (\xi )=\sum _{n=1}^\infty {c_n e^{\left( {-n\xi } \right) }} \end{aligned}$$

where $a_n , b_n$ and $c_n$ are the coefficients. According to the solution expression and boundary conditions (18), we assume the following.

• a. Initial guesses for dimensionless velocities $f(\xi ), h(\xi )$ and temperature $\theta (\xi )$ (for detail see Liao [18] and Fan and You [19]):

  $$\begin{aligned} f_0 (\xi )=1-e^{-\xi }+\alpha \frac{1-n}{1+n}, \quad h_0 (\xi )=0 \quad \hbox {and}\quad \theta _0 (\xi )=e^{-\xi }. \end{aligned}$$

  (20)

• b. Choose linear operators $L_f, L_h$ and $L_\theta$ as follows:

  $$\begin{aligned} L_f =\frac{d^{3}}{d\xi ^{3}}-\frac{d}{d\xi } ,\quad L_h =\frac{d^{2}}{d\xi ^{2}}-\frac{d}{d\xi } \quad \hbox {and} \quad L_\theta =\frac{d^{2}}{d\xi ^{2}}-\frac{d}{d\xi } \end{aligned}$$

  (21)

  such that

  $$\begin{aligned} L_f [c_1 +c_2 e^{\xi }+c_3 e^{-\xi }]=0 ,\quad L_h [c_4 +c_5 e^{-\xi }]=0 \quad \hbox {and}\quad L_\theta [c_6 +c_7 e^{-\xi }]=0, \end{aligned}$$

  where $c_i'\hbox {s}\,(i=1,2,3,4,5,6,7)$ are arbitrary constants.

• c. Choose the auxiliary function as $H_f (\xi )=e^{-\xi }, H_h (\xi )=e^{-\xi } \hbox { and } H_\theta (\xi )=e^{-\xi }$. Let us consider the so-called zero-th order deformation equations as

  $$\begin{aligned} (1-q)L_f \left[ {\hat{{f}}(\xi ,q)-f_0 (\xi )} \right]= & {} qH_f (\xi )\overline{h} N_f \left[ {\hat{{f}}(\xi ,q),\hat{h}(\xi ,q)} \right] ,\end{aligned}$$

  (22)
  $$\begin{aligned} (1-q)L_h \left[ {\hat{h}(\eta ,q)-h_0 (\eta )} \right]= & {} qH_h (\xi )\bar{{h}}N_h \left[ {\hat{h}(\xi ,q),\hat{{f}}(\xi ,q)} \right] ,\end{aligned}$$

  (23)
  $$\begin{aligned} (1-q)L_\theta \left[ {\hat{{\theta }}(\xi ,q)-\theta _0 (\xi )} \right]= & {} qH_\theta (\xi )\bar{{h}}N_\theta \left[ {\hat{{\theta }}(\xi ,q),\hat{{f}}(\xi ,q)} \right] , \end{aligned}$$

  (24)

  with conditions

  $\hat{{f}}(0,q)=\alpha \frac{1-n}{1+n}, {\hat{{f}}}'(0,q)=1, {\hat{{f}}}'(\infty ,q)=0; \hat{h}(0,q)=0, \hat{h}(\infty ,q)=0; \hat{{\theta }}(0,q)=1, \hat{{\theta }}(\infty ,q)=0,$ where $q\in [0,1]$ is an embedding parameter, $\bar{{h}}\ne 0$ is the convergence control parameter and $N_f ,N_h$ and $N_\theta$ are nonlinear operators defined as

  $$\begin{aligned} N_f= & {} \hat{{{f}'''}}(\xi ,q)+\hat{{f}}(\xi ,q){\hat{{f}}}''(\xi ,q) -\left( {\frac{2n}{n+1}} \right) {\hat{{f}}}'^{2}(\xi ,q)+\beta \hat{h}(\xi ,q) \\&-\,\frac{2Mn}{\left( {1+m^{2}} \right) \left( {1+n} \right) }\left( {{\hat{{f}}}'(\xi ,q)+m\hat{h}(\xi ,q)} \right) , \\ N_h= & {} \hat{{{h}''}}(\xi ,q)+\hat{{f}}(\xi ,q)\hat{{{h}'}}(\xi ,q)-\left( {\frac{2n}{n+1}} \right) {\hat{{f}}}'(\xi ,q)\hat{{h}}(\xi ,q)-\beta {\hat{{f}}}'(\xi ,q) \\&+\,\frac{2Mn}{\left( {1+m^{2}} \right) \left( {1+n} \right) }\left( {m{\hat{{f}}}'(\xi ,q)-\hat{h}(\xi ,q)} \right) \\ N_\theta= & {} \hat{{{\theta }''}}(\xi ,q)+\Pr \left( {\hat{{f}}(\xi ,q)\hat{{{\theta }'}}(\xi ,q)-\frac{2r}{n+1}\hat{{\theta }}(\xi ,q){\hat{{f}}}'(\xi ,q)} \right) . \end{aligned}$$

  From Eqs. (22)–(24), at $q=0$ we have

  $L_f \left[ {\hat{{f}}(\xi ,0)-f_0 (\xi )} \right] =0, \quad L_h \left[ {\hat{{h}}(\xi ,0)-h_0 (\xi )} \right] =0$ and $L_\theta \left[ {\hat{{\theta }}(\xi ,0)-\theta _0 (\xi )} \right] =0$, which imply that $\hat{{f}}(\xi ,0)=f_0 (\xi ), \hat{{h}}(\xi ,0)=h_0 (\xi )$ and $\hat{{\theta }}(\xi ,0)=\hat{{\theta }}_0 (\xi )$, respectively. Whereas at $q=1$ we have $N_f \left[ {\hat{{f}}(\xi ,1),\hat{{h}}(\xi ,1),\hat{{\theta }}(\xi ,1)} \right] =0, N_h \left[ {\hat{{h}}(\xi ,1),\hat{{f}}(\xi ,1)} \right] =0$ and $N_\theta \left[ {\hat{{\theta }}(\xi ,1),\hat{{f}}(\xi ,1)} \right] =0$ which implies that $\hat{{f}}(\xi ,1)=f(\xi ), \hat{{h}}(\xi ,1)=h(\xi )$ and $\hat{{\theta }}(\xi ,1)=\theta (\xi )$ respectively. Hence, by defining

  $$\begin{aligned} f_m (\eta )= & {} \left. \frac{1}{m!}\frac{d^{m}f(\xi ,q)}{d\xi ^{m}} \right| _{q=0} , \quad \left. {h_m (\xi )=\frac{1}{m!}\frac{d^{m}h(\xi ,q)}{d\xi ^{m}}} \right| _{q=0} , \quad \\ \theta _m (\xi )= & {} \left. \frac{1}{m!}\frac{d^{m}\theta (\xi ,q)}{d\xi ^{m}} \right| _{q=0} . \end{aligned}$$

  We expand $\hat{{f}}(\xi ,q), \hat{{h}}(\xi ,q)$ and $\hat{{\theta }}(\xi ,q)$ by means of Taylor’s series as

  $$\begin{aligned}&\hat{{f}}(\xi ,q)=f_0 (\xi )+\sum _{m=1}^\infty {f_m (\xi )q^{m}} ,\quad \hat{{h}}(\eta ,q)=h_0 (\xi )+\sum _{m=1}^\infty {h_m (\xi )q^{m}} \nonumber \\&\hbox {and }\hat{{\theta }}(\xi ,q)=\theta _0 (\xi )+\sum _{m=1}^\infty {\theta _m (\xi )q^{m}}. \end{aligned}$$

  (25)

  If the series (25) converges at $q=1,$ we get the homotopy series solution as

  $$\begin{aligned} f(\xi )= & {} f_0 (\xi )+\sum _{m=1}^\infty {f_m (\xi )} ,\quad h(\xi )=h_0 (\xi )+\sum _{m=1}^\infty {h_m (\xi )}\quad \hbox {and}\quad \nonumber \\ \theta (\xi )= & {} \theta _0 (\xi )+\sum _{m=1}^\infty {\theta _m (\xi )} . \end{aligned}$$

  (26)

  It should be noted that $f(\xi ), h(\xi )$ and $\theta (\xi )$ in Eq. (26) contain an unknown convergence control parameter $\bar{{h}}\ne 0$, which can be used to adjust and control the convergence region and the rate of convergence of the homotopy series solution. The mth order deformation equations and the conditions are

  $$\begin{aligned} L_f \left[ {f_m (\xi )-\chi _m f_{m-1} (\xi )}\right]= & {} H_f (\xi ) \bar{{h}} R_m ^{f}(\xi ), L_h \left[ {h_m (\xi )-\chi _m h_{m-1} (\xi )} \right] \nonumber \\= & {} H_h (\xi ) \bar{{h}} R_m ^{h}(\xi ), \hbox { and } \\ L_\theta \left[ {\theta _m (\xi )-\chi _m \theta _{m-1} (\xi )} \right]= & {} H_\theta (\xi ) \bar{{h}} R_m ^{\theta }(\xi ). \end{aligned}$$

  Here $f_m (0)=0,f_m^{\prime }(0)=0,f_m^{\prime }(\infty )=0,h_m (0)=0,\theta _m (\infty )=0, h_m (\infty )=0,{f}'_m (\infty )=0$, with

  $$\begin{aligned} R_m ^{f}= & {} {f}'''_{m-1} (\xi )+\sum _{k=0}^{m-1} {{f}''_{m-1-k} f_k } -\left( {\frac{2n}{n+1}} \right) \sum _{k=0}^{m-1} {{f}'_{m-1-k} {f}'_k } +\beta h_{m-1} \\&-\,\frac{2Mn}{\left( {1+m^{2}} \right) \left( {1+n} \right) }{f}'_{m-1}-\frac{2mMn}{\left( {1+m^{2}} \right) \left( {1+n} \right) }h_{m-1} \\ R_m ^{h}= & {} {h}''_{m-1} (\xi )+\sum _{k=0}^{m-1} {{h}'_{m-1-k} f_k } -\left( {\frac{2n}{n+1}} \right) \sum _{k=0}^{m-1} {{f}'_{m-1-k} h_k } -\beta {f}'_{m-1} \\&+\,\frac{2mMn}{\left( {1+m^{2}} \right) \left( {1+n} \right) }{f}'_{m-1}-\frac{2Mn}{\left( {1+m^{2}} \right) \left( {1+n} \right) }h_{m-1} \\ R_m ^{\theta }= & {} {\theta }''_{m-1} (\xi )+\Pr \sum _{k=0}^{m-1} {{\theta }'_{m-1-k} f_k -\left( {\frac{2r}{n+1}} \right) \Pr } \sum _{k=0}^{m-1} {{f}'_{m-1-k} \theta _k } \hbox { and }\chi _m =\left\{ {{\begin{array}{l} {0,m\le 1} \\ {1,m>1} \\ \end{array} }} \right. . \end{aligned}$$

  Now, we evaluate the error and minimize it over $\overline{h}$ in order to obtain the optimal value of $\overline{h}$ with the least possible error. In the process of error analyses two different methods are employed, namely, the exact residual error and the average residual error. For different order approximations, the CPU time required for evaluation of ${f}''(0)$ is noted. It is evident that the values of ${f}''(0)$ evaluated using the two methods are almost the same (for details see Table 1). As for CPU time is concerned, the average residual error needs much less time compared with that for the exact residual error.

  At the mth order deformation equation, the exact residual error is given by

  $$\begin{aligned} \hat{{E}}_m^f \left( {\bar{{h}}} \right)= & {} \int \limits _0^\infty {\left( {N_f \left[ {\sum _{n=0}^m {f_n (\xi )} } \right] } \right) ^{2}} d\xi , \quad \hat{{E}}_m^h \left( {\bar{{h}}} \right) =\int \limits _0^\infty {\left( {N_h \left[ {\sum _{n=0}^m {h_n (\xi )} } \right] } \right) ^{2}} d\xi ,\hbox { and}\\ \hat{{E}}_m^\theta \left( {\bar{{h}}} \right)= & {} \int \limits _0^\infty {\left( {N_\theta \left[ {\sum _{n=0}^m {\theta _n (\xi )} } \right] } \right) ^{2}} d\xi . \end{aligned}$$

  But in practice the evaluation of $\hat{{E}}_m^f (\bar{{h}}), \hat{{E}}_m^h (\bar{{h}})$ and $\hat{{E}}_m^\theta (\bar{{h}})$ is much time consuming so instead of the exact residual error, we use the average residual error, which is defined as

  $$\begin{aligned} E_m^f \left( {\bar{{h}}} \right)= & {} \frac{1}{M+1}\sum _{k=0}^M {\left( {N_f \left[ {\sum _{n=0}^m {f_n (\xi _k )} } \right] } \right) ^{2}} ,\\ E_m^h \left( {\bar{{h}}} \right)= & {} \frac{1}{M+1}\sum _{k=0}^M {\left( {N_h \left[ {\sum _{n=0}^m {h_n (\xi _k )} } \right] } \right) ^{2}} \hbox { and}\\ E_m^\theta \left( {\bar{{h}}} \right)= & {} \frac{1}{M+1}\sum _{k=0}^M {\left( {N_\theta \left[ {\sum _{n=0}^m {\theta _n (\xi _k )}} \right] } \right) ^{2}} \end{aligned}$$

  where $\xi _k =k\Delta \xi =k/M,k=0,1,2,\ldots , M$. Now the error function $E_m^f \left( {\bar{{h}}} \right) , E_m^h \left( {\bar{{h}}} \right)$ and $E_m^\theta \left( {\bar{{h}}} \right)$ is minimized with respect to $\bar{{h}}$ to obtain the optimal value of $\bar{{h}}$. For the mth order approximation the optimal value of $\bar{{h}}$ for f, h and $\theta$ is given by $dE_m^f \left( {\bar{{h}}} \right) /dh=0, dE_m^h \left( {\bar{{h}}} \right) /dh=0$ and $dE_m^\theta \left( {\bar{{h}}} \right) /dh=0,$ respectively. Evidently,$\mathop {\lim }\limits _{m\rightarrow \infty } E_m^f \left( {\bar{{h}}} \right) =0, \mathop {\lim }\limits _{m\rightarrow \infty } E_m^h \left( {\bar{{h}}} \right) =0$ and $\mathop {\lim }\limits _{m\rightarrow \infty } E_m^\theta \left( {\bar{{h}}} \right) =0$ correspond to a convergent series solution. Substituting this optimal value of $\bar{{h}}$ into Eq. (26), we get the approximate solutions of Eqs. (15)–(17), which satisfy the conditions given in Eq. (18).

Table 1 Comparison of ${f}''(0)$ and CPU time (s) incurred to evaluate the mth order approximation by exact residual error and average residual error when $\beta =0.2,r=1.0,m=1.0,\alpha =0.5,n=1.0$

Numerical Procedure

For accuracy of the OHAM solution, the highly nonlinear and coupled ordinary differential equations with variable coefficients are solved numerically via the Keller-box technique. The boundary value problem given in Eqs. (15)–(17) is reduced to a system of seven simultaneous ordinary differential equations of first order for seven unknowns. To solve this system of first-order equations, we require seven initial conditions while we have only two initial conditions on f and one initial condition for each of $\theta$ and h. The three initial conditions ${f}''(0), {h}'(0)$ and ${\theta }'(0)$ are not known. However, the values of ${f}'(\xi ), h(\xi )$ and $\theta (\xi )$ are known as $\xi \rightarrow \infty$. We employ the Keller-box scheme where these three boundary conditions are utilized to produce three unknown initial conditions at $\xi =0$. To select $\xi _\infty$, we begin with some initial guess value of the unknown initial conditions and solve the boundary value problem to obtain ${f}''(0) , {h}'(0)$ and ${\theta }'(0) .$ Let $\alpha _0 , \beta _0$ and $\gamma _0$ be the correct values of $f_3 (0), h_2 (0)$ and $\theta _2 (0) ,$ respectively, and integrate the system using the fourth order Runge–Kutta method and denote the values of $f_3 (0), h_2 (0)$ and $\theta _2 (0)$, respectively. The solution process is repeated with another larger value of $\xi _\infty$ until two successive values differ only by a small quantity within the desired accuracy. The last value of $\xi _\infty$ is chosen as an appropriate value for that particular set of parameters. Then solve the system of equations by the Keller-box method; for details see Cebeci and Bradshaw [28], Keller [29], and Vajravelu and Prasad [30]. For the sake of brevity, the details of the numerical solution procedure are not presented here. For numerical calculations, a uniform step size of $\Delta \xi =0.01$ is found to be satisfactory and the shooting error is controlled with an error tolerance of $10^{-6}$ in all cases.

In order to validate the two methods used in this study and to judge the accuracy of the present analysis, the horizontal skin friction ${f}''(0),$ the transverse skin friction ${h}'(0)$ and wall temperature gradient ${\theta }'(0)$ are compared with the previously published results of Andersson et al. [44] and Fang et al. [40], Khader and Megahed [41], Grubka and Bobba [36], Ali [37], Chen [38], Wang [34], and Abbas et al. [35] for several special cases and the results are all found to be in good agreement: The results are presented in Tables 2, 3, 4 and 5. Results obtained from this method are discussed and compared with OHAM in “Results and Discussion” section.

Table 2 Comparison of skin friction $-{f}''(0)$ for different values of Mn with $\beta = r=m=\alpha =0.0,n=1.0$

Table 3 Comparison of skin friction $-{f}''(0)$ for different values of n and $\alpha$ with $\beta =Mn = r=m=0.0$

Table 4 Comparison of skin friction $-{f}''(0)$ and $-{h}'(0)$ for different values of $\beta$ with $Mn= \alpha = r=m=0.0$

Table 5 Comparison of wall temperature gradient $-{\theta }'(0)$ for different values of Pr and $\beta$ when $Mn= r=m=\alpha =0.0,n=1.0$

Exact Solutions for Some Special Cases

Here we present the exact solutions for certain special cases and these solutions serve as a baseline for computing general solutions through numerical schemes. We note that in the absence of rotation, magnetic field, and Hall current, Eq. (15) reduces to those of Fang et al. [40].

Absence of Rotation and Hall Current for the Case of a Flat Plate $\left( { \hbox {i.e.}\, n=1.0,\beta =m=0.0\hbox { and }b=0.0} \right)$

In the limiting case of $n=1$ and $m=0,$ the boundary layer flow and heat transfer problem degenerates. The solution for the velocity in the presence of a magnetic field turns out to be $f\left( { \xi } \right) =\frac{1-e^{-\lambda \xi }}{\lambda }\hbox { and }{f}'\left( { \xi } \right) =e^{-\lambda \xi }$ where $\lambda =\sqrt{1+Mn}$ and the solution for the temperature field can be written as a two-parameter solution in terms of confluent hypergeometric series, namely, Kummer’s function, $\phi ,$ as:

$$\begin{aligned} \theta (\xi )=e^{-\frac{\Pr }{\beta } \xi }\frac{\phi \left( {a_1 ,b_1 ,z} \right) }{\phi \left( {a_1 ,b_1 ,-a_0 } \right) }, \hbox {where }a_0 = \frac{\Pr }{\beta ^{2}}, a_1 =a_0 -r, b_1 =1+a_0 , z=-a_0 e^{-\beta \xi }. \end{aligned}$$

Absence of Rotation, Magnetic Field, Hall Currents, Heat Transfer But in the Presence of Variable Boundary Thickness $\left( {\hbox {i.e.}\, \beta =0.0,Mn=m=0.0, n\ne 1,r=0.0} \right)$

When $n=-1/3,$ Eq. (15) becomes ${f}'''+f{f}''+{f}'^{2}=0$ with the boundary conditions $f(0)=2\alpha , {f}'(0)=1$ and ${f}'(\infty )=0.$ The solution is

$$\begin{aligned} f(\xi )=\sqrt{2+4\alpha ^{2}}\hbox {tanh}\left[ {\frac{\sqrt{2+4\alpha ^{2}}}{2}\xi +\hbox {tanh}^{-1}\left( {\frac{2\alpha }{\sqrt{2+4\alpha ^{2}}}} \right) } \right] . \end{aligned}$$

When $n=-1/2,$ Eq. (15) becomes ${f}'''+f{f}''+2{f}'^{2}=0$ with the boundary conditions $f(0)=3\alpha , {f}'(0)=1,$ and ${f}'(\infty )=0.$ This equation is equivalent to $\frac{1}{f}\frac{d}{d\xi }\left[ {f^{3/2}\frac{d}{d\xi }\left( {f^{-1/2}{f}'+\frac{2}{3}f^{3/2}} \right) } \right] =0,$ of which the solution is

$$\begin{aligned} \eta +D= & {} \frac{1}{2d^{2}}\ln \left[ {\frac{f+d\sqrt{f}+d^{2}}{\left( {d-\sqrt{f}} \right) ^{2}}} \right] +\frac{\sqrt{3}}{d^{2}}\tan ^{-1}\left( {\frac{2\sqrt{f}+d}{d\sqrt{3}}} \right) ,\\ \hbox {where }d= & {} \left[ {\left( {3\alpha } \right) ^{3/2}+\frac{3}{2\sqrt{3\alpha }}} \right] ^{1/3}\hbox { and }D=\frac{1}{2d^{2}}\ln \frac{\left( {3\alpha +d\sqrt{3\alpha }+d^{2}} \right) }{\left( {d-\sqrt{3\alpha }} \right) ^{2}}\\&+\,\frac{\sqrt{3}}{d^{2}}\tan ^{-1}\left( {\frac{2\sqrt{3\alpha }+d}{d\sqrt{3}}} \right) . \end{aligned}$$

Results and Discussion

The problem of MHD flow and heat transfer over a slender elastic sheet in a rotating fluid with Hall effect is solved analytically as well as numerically. The analytical solutions of the system of ordinary differential equations subject to the boundary conditions are obtained through the optimal homotopy analysis method (OHAM) and Keller-box method. Here the OHAM has been used as a benchmark tool to test the accuracy, and hence the reliability of the Keller-box results.

Fig. 2

a Horizontal velocity profiles for different values of n and $\alpha$ with $\hbox {Pr} = 2.0$, ${Mn} = 0.5$, $B = 0.2$, $m = 1.0$, and $r = 1.0$; b temperature profiles for different values of n and $\alpha$ with $\hbox {Pr} = 2.0, Mn = 0.5$, $\beta = 0.2, m = 1.0$, and $r = 1.0$; c transverse velocity profiles for different values of $\alpha$ and n with $\hbox {Pr} = 2.0, \beta = 0.2, m = 1.0, r = 1.0$, and ${Mn} = 0.5$

Fig. 3

a Horizontal velocity profiles for different values of $\beta$ and n with $\hbox {Pr} = 2.0, m = 1.0\, \alpha = 0.2, r = 1.0$, and $Mn = 1.0$; b temperature profiles for different values of n and $\beta$ with $\hbox {Pr} = 2.0, m = 1.0$, $Mn = 0.5$, $\alpha = 0.2$, and $r = 1.0$; c transverse velocity profiles for different values of $\beta$ and n with $\hbox {Pr} = 2.0$, $\alpha = 0.2, m = 1.0, r = 1.0$, and ${Mn} = 1.0$

Fig. 4

a Horizontal velocity profiles for different values of Mn with $\hbox {Pr} = 2.0$, $m = 1.0, \beta = 0.2, \alpha = 0.2, r = 1.0$, and $n = 2.0$; b temperature profiles for different values of Mn with $\hbox {Pr} = 2.0$, $m = 1.0, \beta = 0.2, \alpha = 0.2, r = 1.0$, and $n = 2.0$; c transverse velocity profiles for different values of Mn and m with $\hbox {Pr} = 2.0$, $\beta = 0.2, \alpha = 0.2, r = 1.0$, and $n = 2.0$

Fig. 5

a Horizontal velocity profiles for different values of m with $\hbox {Pr} = 2.0, {Mn} = 0.5, \beta = 0.2, \alpha = 0.2, r = 1.0$, and $n = 2.0$; b temperature profiles for different values of m and n with $\hbox {Pr} = 2.0, {Mn} = 0.5, \beta = 0.0$, $\alpha = 0.2, r = 1.0$; c transverse velocity profiles for different values of $\beta$ and m with $\hbox {Pr} = 2.0, {Mn} = 0.5$, $\alpha = 0.2, r = 1.0$, and $n = 2.0$

Fig. 6

Temperature profiles for different values of r and Pr with $m = 1.5, \beta = 0.2, \alpha = 0.2$, ${Mn} = 0.5$, and $n = 2.0$

Fig. 7

Comparison of OHAM and Keller-Box method for $f '(\xi )$ for different values of $\beta$ with $\hbox {Pr} = 2.0$, $m = 1.0, \alpha = 0.2, r = 1.0$, ${Mn} = 1.0$, and $n = 2.0$

Fig. 8

a Residual error of horizontal velocity profile at $\hbox {Pr} = 5.09$, $\beta = 0.5, r = 2.0, \alpha = 2.0$, ${Mn} = 0.2$, $m = 0.5$, and $n = 2.0$; b residual error of transverse velocity profile at $\hbox {Pr} = 5.09$, $\beta = 0.5, r = 2.0, \alpha = 2.0$, ${Mn} = 0.2, m = 0.5, n = 2.0$; c residual error of temperature profile for different values of Pr at $\beta = 0.5, r = 2.0, \alpha = 2.0$, ${Mn} = 0.2, m = 0.5$, and $n = 2.0$

In order to get clear a insight into the physical problem, numerical computations have been carried out for different values of flow parameters such as the Hall parameter m, the fluid rotation parameter $\beta$, the power index parameter n, the variable thickness $\alpha$, the wall temperature parameter r, the Prandtl number Pr, and the magnetic parameter Mn. Exact solutions are obtained for the special cases, such as the absence of rotation and Hall current for the case of a flat surface (i.e. $n=1,\beta =m=b=0)$. The graphical representation of the numerical results for the horizontal velocity profile ${f}'(\xi ),$ the transverse velocity profile $h(\xi ),$ and the temperature field $\theta (\xi )$ for different values of physical parameters are presented in Figs. 2, 3, 4, 5, 6 and 7, and residual error profiles are shown for ${f}'(\xi ), h(\xi )$ and $\theta (\xi )$ in Fig. 8. It can be seen that both ${f}'(\xi )$ and $\theta (\xi )$ decrease monotonically and tend to zero asymptotically as the distance from the boundary increases. In the case of $h(\xi ),$ we find negative profiles which indicate that this component is transverse to the main flow in a clockwise direction. The computed numerical values for the horizontal skin friction ${f}''(0),$ the transverse skin friction ${h}'(0)$ and the rate of heat transfer ${\theta }'(0)$ are tabulated in Table 6. From the experimental studies it has been noted that at $20{^{\circ }}\hbox {C}$ the Prandtl number for air is 0.72, at $300{^{\circ }}\hbox {C}$ the Prandtl number for water is 1.09, at $40{^{\circ }}\hbox {C}$ the Prandtl number for ammonia is 2.0 and at $417{^{\circ }}\hbox {C}$ the Prandtl number for molten salt is 5.09 (see for details Kothandaraman and Subramanyan [45]). Therefore, the values of Pr chosen in Table 6 range from 0.01 to 1000, which supports the experimental study; the values of other physical parameter are chosen arbitrarily.

Figure 2a–c exhibit the effects of $\alpha$ and n on ${f}'(\xi ), \theta (\xi )$ and $h(\xi )$. It is observed that both the fluid velocity and the temperature rise as $\alpha$ and n increase, and as a result, both the momentum boundary layer and thermal boundary layer thicknesses increase and the opposite is true for cross flow. As n increases, the stretching velocity of the sheet increases, which produces deformation in the fluid causing the fluid velocity to increase as well. This shows that there is a significant effect of $\alpha$ and n (for all values of n, positive, zero or negative) on the flow pattern. Here, it may be observed that the sheet is shrinking along the axis for negative n, and is stretching for positive n. Moreover, the variation of ${f}''(0)$ mainly depends on both $\alpha$ and n. For given values of $\alpha$ and n in the range of $\left( {\alpha<0\hbox { and }n<1} \right)$ or $\left( {\alpha>0\hbox { and }n>1} \right)$, the skin friction ${f}''(0)$ and wall temperature gradient ${\theta }'(0)$ decreases when $\alpha =-0.5,-1.0$ and $n=2.0, 5.0$. In other words, $\left| {{f}''(0)} \right|$ and $\left| {{\theta }'(0)} \right|$ become higher for smaller values of $\alpha$ and higher values of n in the range of $\left( {\alpha <0\hbox { and }n>1} \right)$ or $\left( {\alpha >0\hbox { and }n<1} \right)$. This can be explained by the boundary condition $f(0)=\alpha \left( {1-n} \right) /\left( {1+n} \right)$. In this case we obtained $f(0)>0$ (injection/blowing process) when $\alpha =-0.5,-1.0$ and $n=2.0,\hbox { 5}.0$, opposite results may be obtained in the case of $f(0)<0$ (suction process) when $\alpha =2.0,5.0$ and $n=2.0,5.0$ (see Table 6 for details). In addition to this, for $\alpha =0$ or $n=1$ the boundary condition reduces to $f(0)=0$, which indicates an impermeable surface.

Figure 3a–c illustrate the effect of $\beta$ on ${f}'(\xi ), \theta (\xi )$ and $h(\xi ).$ As $\beta$ increases, the velocity decreases and the reverse trend is observed in the case of $\theta (\xi )$; see Fig. 3a, b. Influence of the rotation parameter on the flow reversal is presented in Fig. 3c. Here, the profiles are parabolic in nature, in particular, as the value of $\beta$ is increased, the transverse velocity profiles maintain their form, but are shifted downward. Figure 4a–c elucidate the effect of Mn on ${f}'(\xi ), \theta (\xi )$ and $h(\xi )$. Figure 4a shows the effect of Mn on the fluid velocity. It is well known that the velocity will decrease with an increase in the magnetic field parameter owing to an increase in the Lorentz drag force that opposes the fluid motion, and is quite opposite in the case of heat transfer; see Fig. 4b. Here, the thickness of the momentum boundary layer decreases while the thermal boundary layer increases with an increase in the strength of the appliedmagnetic field. It is interesting to note from Fig. 4c that the cause of the transverse velocity spikes near the origin is the parameter Mn. As Mn increases, the transverse velocity profiles vary steadily from negative to positive and shift upwards. We explore the effect of increasing values of m on ${f}'(\xi ), \theta (\xi )$ and $h(\xi )$ in Fig. 5a–c. Figure 5a shows the increase in ${f}'(\xi )$ and decrease in $\theta (\xi )$ as shown in Fig. 5b. This is attributed to the fact that the effective conductivity $\left[ {\sigma /{\left( {1+m^{2}} \right) }} \right]$ diminishes as m increases. This in turn reduces the magnetic damping force on ${f}'(\xi )$ and hence increases the propelling effect on ${f}'(\xi ).$ Furthermore, the spikes near the origin are observed in Fig. 5c. The transverse flow in the z-direction initially increases with m and reaches maximum when $m = 1.5$ and then dips in the absence of rotation effect. For large values of m, the term $\left[ {1/{\left( {1+m^{2}} \right) }} \right]$ becomes very small and hence the resistive effect of the magnetic field is diminished. The presence of rotation effect results in a downward shift in the transverse velocity profiles and reaches nadir at $m = 5.0$. The impact of Pr and r on $\theta (\xi )$ is presented in Fig. 6. It is found that $\theta (\xi )$ is a decreasing function of Pr implying a decrease in the thermal conductivity k; consequently a decrease in the thermal boundary layer is observed. Therefore, cooling of the heated sheet can be improved by choosing a coolant with a larger Pr. Similar phenomenon is observed for increasing values of r and this is because when $r > 0$, heat flows from the stretching sheet into the ambient medium and, when $r < 0$, the temperature gradient is positive and heat flows into the stretching sheet from the ambient medium.

Figure 7 presents evidence to support the agreement of the OHAM and Keller box method. It is clear from the figure that the solutions by both methods are compatible. Further evidence is provided in Tables 2, 3, 4 and 5.

Finally, the residual errors for ${f}'(\xi ), h(\xi )$ and $\theta (\xi )$ are presented in Fig. 8a–c, which demonstrate the accuracy and convergence of the OHAM. These figures show that an eighth-order approximation may yield the best accuracy for the present model.

Table 6 Values of skin friction, transverse skin friction and wall temperature gradient for different values of the physical parameters

Table 6 shows the results for ${f}''(0), {h}'(0)$ and ${\theta }'(0)$ corresponding to different values of the physical parameters. It is interesting to note that ${f}''(0)$ decreases for negative values of $\alpha$ and increases for positive values. This is because of the induced momentum transfer, which will accelerate fluid particles downstream. This phenomenon is true even in the case of ${h}'(0)$ and ${\theta }'(0)$.

Conclusions

Steady MHD flow and heat transfer over a slender permeable elastic sheet in a rotating fluid with Hall current has been examined. Optimal homotopy analytic solutions (OHAM) of the boundary value problem were obtained with the aid of the package Mathematica. An efficient implicit finite difference scheme based on the Keller box method was employed to compute the numerical solutions. A few interesting conclusions have been observed as summarized below.

• 1. The analytic and numerical solutions are found to be in excellent agreement. The solutions also agree with some of the results available in the literature and with the exact solution for the special case of a flat sheet.

• 2. The nature of the elastic sheet depends on a variable thickness parameter, and a velocity power index parameter n, which leads to wall transpiration (suction or injection).

• 3. The elastic sheet with a variable thickness has a direct impact on the physical properties of the sheet such as shrinking and stretching along the axis, corresponding to negative and positive n.

• 4. An increase in the wall thickness parameter leads to an increase in the skin-friction coefficient in the x-direction and the Nusselt number for $n>1$.

• 5. Hall current can have a significant effect on the shear stress and the Nusselt number. For large values of the Hall parameter m, the resistive effect of the magnetic field is reduced, as a result, the skin-friction coefficient in the x-direction increases and the wall temperature gradient decreases.