Combined Influence of Radiation Absorption and Hall Current on MHD Free Convective Heat and Mass Transfer Flow Past a Stretching Sheet

Abstract

The present article investigates the combined influence of thermal radiation, radiation absorption, Soret and Dufour effect, and non-uniform heat source on the steady convective heat and mass transfer flow of a viscous incompressible fluid past a stretching sheet. The non-linear equations governing the flow, heat and mass transfer have been solved by using a Runge–Kutta fifth-order together with shooting technique. The influence of Sr/Du, A₁, B₁ on all flow characteristics has been analysed.

1 Introduction

The analysis of boundary layer heat and flow transfer of fluids over a continuous stretching surface has gained much attention from numerous researchers. Stretching brings a one-sided direction to the extradite; due to this, the end product significantly relies upon the stream and heat and mass process. Many researchers have studied the flows with temperature-dependent viscosity in different geometries and under various flow conditions with Hall effects (1–8). Some of its applications in Industrial and Engineering domains are in polymeric sheets extraction, insulating materials, fine fiber matters, production of glass fibre and sticking of labels on surface of hot bodies. Some of the other applications are drawing of hot rolling wire, drawing of thin films of plastic and the study of crude oil spilling over the surface of seawater. In liquids-based applications such as petroleum, oils, glycerin, glycols and many more, viscosity exhibits a considerable variation with temperature. The viscosity of the water decreases by 240% when the temperature increases from 10 ℃ (μ = 0.0131 g/cm) to 50 ℃ (μ = 0.00548 g/cm). To estimate the heat transfer rate accurately, it is necessary to take the variation of viscosity with temperature into consideration.

2 Formulation of the Problem

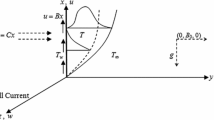
The consequent equations, which are highly non-linear, are explained by using the fifth-order Runge–Kutta–Fehlberg method (denoted by RKF method) with shooting technique. Figure 1 explains the problem configuration of a stretching sheet having momentous convective stream of Nu and Sh of a viscous and electrically conducting liquid. A constant magnetic field B₀ is introduced across the y-axis considering Hall current effect. The temperature and the species concentration are maintained at prescribed constant values $T_{w} ,C_{w}$ at the sheet and $T_{\infty } ,C_{\infty }$ are the fixed values far away from the sheet.

Fig. 1

Physical sketch of the problem

Taking Lai and Kulacki [1] proposition, μ the liquid viscosity is assumed to change as inversely proportional to the linear function of temperature is provided by

$$ \frac{1}{\mu } = \frac{1}{{\mu_{\infty } }}\left[ {1 + \gamma_{0} (T - T_{\infty } )} \right] \Rightarrow \frac{1}{{\mu_{\infty } }} = \alpha (T - T_{\infty } ) $$

(1)

where $\alpha = \frac{{\gamma_{0} }}{{\mu_{\infty } }}$ and $T_{r} = T_{\infty } - \frac{1}{{\gamma_{0} }}$ in which $\alpha$ and $T_{r}$ are constants, and their respective values are based on the liquid’s thermal characteristic. Generally, $\alpha > 0$, $\alpha < 0$ represent for liquids and gases, respectively. The governing equations taking thermal radiating approximated by Rosseland approximation (Pal [2]) are

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0, $$

(2)

$$ \left. \begin{aligned} \rho_{m} \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) & = \frac{\partial }{\partial y}\left( {\mu \frac{\partial u}{\partial y}} \right) + \rho_{m} g_{0} \beta_{\tau } \left( {T - T_{\infty } } \right) \\ & \quad + \rho_{m} g_{0} \beta_{c} \left( {C - C_{\infty } } \right) - \frac{{\sigma B_{0}^{2} }}{{1 + m^{2} }}(u + m\,w) \\ \end{aligned} \right\} $$

(3)

$$ \rho_{m} \left( {u\frac{\partial w}{\partial x} + v\frac{\partial w}{\partial y}} \right) = \frac{\partial }{\partial y}\left( {\mu \frac{\partial w}{\partial y}} \right) + \frac{{\sigma B_{0}^{2} }}{{1 + m^{2} }}(m\,u - w) $$

(4)

$$ \begin{aligned} \rho C_{p} \left( {u\frac{\partial T}{\partial x} + w\frac{\partial T}{\partial z}} \right) & = k_{f} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \mu \left( {\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)^{2} \\ & \quad + \frac{{k_{f} u_{w} (x)}}{vx}\left( {A_{1} (T_{w} - T_{\infty } )u + B_{1} (T_{w} - T_{\infty } )} \right) \\ & \quad + \frac{{D_{m} K_{T} }}{{C_{s} C_{p} }}\frac{{\partial^{2} C}}{{\partial y^{2} }} + Q_{1}^{1} (C_{w} - C_{\infty } ) + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3\beta_{R} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} \\ \end{aligned} $$

(5)

$$ u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{m} \frac{{\partial^{2} C}}{{\partial y^{2} }} - k_{0} \left( {C - C_{\infty } } \right) + \frac{{D_{m} K_{T} }}{{T_{m} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} $$

(6)

The pertinent boundary conditions are

$$ u\,(0) = u_{w\,\,} (x) = bx\,,\quad v\,(0) = w\,(0) = 0,\quad T\,(0) = T_{w} ,\quad C\,(0) = C_{w\,\,} $$

(7)

$$ u\,(\infty ) \to 0\,,\quad w\,(\infty ) \to 0,\quad T\,(\infty ) \to T_{\infty } ,\quad C\,(\infty ) \to C_{\infty } $$

(8)

where $D_{m}$, $K_{T}$, $K_{f}$, $C_{s}$ and $C_{p}$ denotes Mass diffusivity coefficient, thermal diffusion ratio, thermal conductivity coefficient, concentration susceptibility and specific heat at constant pressure. The below similarity transformations are introduced to study the stream adjoining the sheet.

$$ \begin{aligned} u & = bxf^{\prime}(\eta );v = - \sqrt {bv} f(\eta );w = bxg(\eta ) \\ \eta & = \sqrt {\frac{b}{v}} \,y;\theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }};\varphi = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }} \\ \end{aligned} $$

(9)

where $f$, $h$, $\theta$ and $\emptyset$ are non-dimensional stream function, similarity space variable and non-dimensional temperature and concentration, respectively. Equation (9) is satisfied by u and v in the continuity equation (Eq. 2). Substituting Eq. (9), Eqs. (2)–(6) reduce to

$$ \begin{aligned} & \left( {\frac{{\theta - \theta_{r} }}{{\theta_{r} }}} \right)\left( {f^{\prime } - ff^{\prime } } \right) + f^{\prime \prime } - \left( {\frac{{\theta^{\prime}}}{{\theta - \theta_{r} }}} \right)f^{\prime } \\ & \quad - \left( {\frac{{\theta - \theta_{r} }}{{\theta_{r} }}} \right)G(\theta + N\varphi ) + M^{2} \left( {\frac{{\theta^{\prime } - \theta_{r} }}{{\theta_{r} }}} \right)\left( {\frac{{f^{\prime } + mg}}{{1 + m^{2} }}} \right) = 0 \\ \end{aligned} $$

(10)

$$ \left( {\frac{{\theta - \theta_{r} }}{{\theta_{r} }}} \right)\left( {f^{{\prime }} g - fg^{{\prime }} } \right) + g^{{\prime \prime }} - \left( {\frac{{\theta^{{\prime }} }}{{\theta - \theta_{r} }}} \right)g^{{\prime }} - M^{2} \left( {\frac{{\theta - \theta_{r} }}{{\theta_{r} }}} \right)\left( {\frac{{mf^{{\prime }} - g}}{{1 + m^{2} }}} \right) = 0 $$

(11)

$$ \left( {1 + \frac{{4N_{{r_{r} }} }}{3}} \right)\theta^{{\prime \prime }} + \Pr {\text{Ec}}(f^{{\prime \prime }} )^{{^{2} }} + \left( {A_{1} f^{{\prime }} + B_{1} \theta } \right) + {\text{PrDu}}\emptyset^{{\prime \prime }} + Q_{1} \emptyset = 0 $$

(12)

$$ \varphi^{{\prime \prime }} - {\text{Sc}}(f\varphi^{{\prime }} - \gamma \varphi ) = - {\text{ScSr}}\theta^{{\prime \prime }} $$

(13)

Similarly, the transformed boundary conditions are given by

$$ f^{\prime } (\eta ) = 1, \, f(\eta ) = 0, \, g(\eta ) = 0,\,\theta (\eta ) = 1,\varphi (\eta ) = 1{\text{ at }}\eta = 0 $$

(14)

$$ f^{\prime } (\eta ) \to 1,\,g(\eta ) \to 0,\theta (\eta ) \to 1,\varphi (\eta ) \to 0\,{\text{as}}\,\eta \to \infty $$

(15)

3 Formulation of the Problem

The non-linear ordinary differential Eqs. (10–13) with boundary conditions (14–15) are solved numerically using Runge–Kutta–Fehlberg integration coupled with shooting technique. This method involves, transforming the equation into a set of initial value problems (IVP) which contain unknown initial values that need to be determined by first guessing, after which the Runge–Kutta–Fehlberg iteration scheme is employed to integrate the set of IVPs until the given boundary conditions are satisfied. The initial guess can be easily improved using the Newton–Raphson method.

4 Comparison

The results of this chapter are compared with the results of previously published paper of Shit et al. [3] as shown in Table 1, and the outcomes are in good concurrence.

Table 1 Comparison of Nu and Sh at η = 0 with Shit et al. [3] with Sr = 0, Du = 0, A₁ = 0, B₁ = 0, Ec = 0, Q₁ = 0

5 Results and Discussion

An increase in heat source (A₁, B₁ > 0) generates energy in the thermal boundary layer, and as a consequence, the axial velocity rises. In the case of heat absorption (A₁, B₁ < 0), the axial velocity falls with decreasing values of A₁, B₁ < 0, an increase in the space-dependent/temperature-dependent heat generating source (A₁, B₁ > 0), and reduces in the case of heat absorbing source. The concentration increases with the increase of space-dependent heat/temperature-dependent generating source (A₁, B₁ > 0) and reduces in the case of heat absorbing source (A₁, B₁ < 0). And an increase in A₁, B₁ enhances the skin friction component |τ_x| (Figs. 2, 3, 4, 5, 6, 7, 8 and 9).

Fig. 2

Variation of f′ with A₁, B₁: G = 5, N = 1, Nr = 0.5, Sc = 1.3, Sr = 2, Du = 0.04, θ_r = −2, Q₁ = 0.5

Fig. 3

Variation of f′ with Sr and Du: A₁ = 0.1, B₁ = 0.1, G = 5, N = 1, Nr = 0.5, Sc = 1.3, θ_r = −2, Q₁ = 0.5

Fig. 4

Variation of g with A₁, B₁: G = 5, N = 1, Nr = 0.5, Sc = 1.3, Sr = 2, Du = 0.04, θ_r = −2, Q₁ = 0.5

Fig. 5

Variation of g with Sr and Du: A₁ = 0.1, B₁ = 0.1, G  = 5, N = 1, Nr = 0.5, Sc = 1.3, θ_r = −2, Q₁ = 0.5

Fig. 6

Variation of θ with A₁, B₁ G = 5, N = 1, Nr = 0.5, Sc = 1.3, Sr = 2, Du = 0.04, θ_r = −2, Q₁ = 0.5

Fig. 7

Variation of θ with Sr and Du: A₁ = 0.1, B₁ = 0.1, G = 5, N = 1, Nr = 0.5, Sc = 1.3, θ_r = −2, Q₁ = 0.5

Fig. 8

Variation of θ with A₁, B₁: G = 5, N = 1, Nr = 0.5, Sc = 1.3, Sr = 2, Du = 0.04, θ_r = −2, Q₁ = 0.5

Fig. 9

Variation of ϕ with Sr and Du: A₁ = 0.1, B₁ = 0.1, G = 5, N = 1, Nr = 0.5, Sc = 1.3, θ_r = −2, Q₁ = 0

An increase in the strength of space-dependent/temperature-dependent heat generating source (A₁, B₁ > 0) results in an enhancement in |Nu| at η = 0 and we find that Sherwood number grows with A₁, B₁ > 0 and reduces with A₁, B₁ < 0 in the case of heat source absorption. It can be observed from the profiles that increase in Sr (or decrease in Du) smaller the axial velocity and cross flow velocity in the boundary layer. It is also found that higher the radiative heat flux smaller the axial velocity in the flow region and larger the cross flow velocity. It can be observed from the profiles that increase in Sr (or decreasing Du) reduces the temperature and concentration in the boundary layer. Increasing Soret parameter Sr (or decreasing Dufour parameter Du) leads to an enhancement in |τ_x| at the wall. |τ_z|, |Nu| and |Sh| at η = 0 (Table 2).

Table 2 Shear stress, Nusselt number and Sherwood number at h = 0

6 Conclusions

This paper studies the influence of Soret and Dufour effects, non-uniform heat source, dissipation and radiation absorption and variable viscosity on mixed convective heat and mass transfer flow past stretching sheet. Influence of Soret and Dufour parameter on uniform heat source, dissipation and radiation absorption parameter on mixed convective heat and mass transfer flow has been explored in detail. Increasing Sr (or decreasing Du) reduces $\left| {Nu} \right|$ and $\left| {Sh} \right|$ at $\eta = 0$. $\left| {Nu} \right|$ reduces and $\left| {Sh} \right|$ enhances the increase in Ec. $Nu$ and $Sh$ at the wall grow with increase in the strength of A₁/B₁ and reduce with that of absorbing source. Excellent agreement with the present study and Shit et al. [3] has been obtained.