Introduction

Flow between nonparallel plane walls, commonly known as the Jeffery–Hamel flow, is of paramount importance in many engineering disciplines such as: fluid mechanics, mechanical, chemical and bio-mechanical engineering. One can mention, for example, flow through blood arteries, diffusers, nozzles and reducers. The theory of flow through convergent–divergent channels has also been successfully used in understanding rivers and canals.

The steady two-dimensional flow between two inclined plates is highly considered as one of the rare exact solutions of the Navier–Stokes equations. The mathematical investigations of this type of flow were pioneered by Jeffery [1] and Hamel [2]. Thereafter, several authors studied and discussed the Jeffery–Hamel flow. Rosenhead [3] expressed the solution of the classical Jeffery–Hamel flow in terms of jacobian elliptic functions. Millsaps and Pohlhausen [4] established the exact solutions of the energy equation governing the heat transfer problem in Jeffery–Hamel flow. The stability problem of classical Jeffery–Hamel flow has been also much attracted by the researchers [6–10]. In fact, due to the inflectional behaviour of velocity (i.e. presence of backflow regions in diverging flow), authors concluded that the diverging flow is unstable.

The problem of stretching–shrinking surfaces has also attracted the attention of researcher’s community and finds applications in fluid mechanics, biomechanics and chemical engineering as well as in manufacturing process from industry such as the aerodynamic extrusion of plastic sheets, the extrusion process of polymers and the heat-treated materials. In fact, in literature we can find a large number of studies dealing with the effect of stretching/shrinking surfaces on the flow and heat transfer of viscous incompressible fluids. For example, Blasius flow past stretching plate was studied by Crane [11]. In this contribution, heat conduction in the linear stretching case, skin friction coefficient and heat transfer rate were explored and discussed. An overall mathematical analysis of the heat and mass transfer in the boundary layer over a stretching sheet under the effect of suction and blowing was given by Gupta et al. [12]. The effect of stretching sheet issued from thin slit on the temperature evolution of a viscous incompressible fluid flow was studied by Dutta et al. [13]. They showed that the temperature decreases with the increase of Prandtl number. Fang et al. [14] solved analytically the magnetohydrodynamic (MHD) flow under slip conditions over a shrinking sheet. They explored the effects of mass transfer, slip and magnetic parameters. On the other hand, Fang and Zhang [15] also studied heat transfer over a shrinking sheet with mass transfer. They investigated the effects of the Prandtl number, the wall mass transfer parameter and the power index on the wall heat flux, the wall temperature and the temperature evolution. The effect of stretchable/shrinkable walls on the flow and heat transfer in classical Jeffery–Hamel flow was studied by Turkyilmazoglu [16]. The obtained results show that the stretching walls leads to production of more heat in the flow; however, more cooling is achieved in the case of shrinking walls. Asad Mahmood et al. [17] investigated hydromagnetic stagnation point flow and heat transfer over a nonlinearly stretching/shrinking surface of micropolar fluid. They reported the dual solutions for different values of magnetic and material parameters against the limited range of stretching/shrinking parameter.

Nowadays, the so-called nanofluids, created by dispersing micro-sized solid particles (less than 100 nm) like Cu, CuO, \(\hbox {Al}_{2}\hbox {O}_{3}\) and SiC in a conventional base fluid such as: water, ethylene glycol and engine oil, are considered as a highly efficient class of solid–liquid suspensions. The first use of nanofluid term is proposed by Choi [18], of the Argonne National Laboratory, USA. Since then, nanofluids have received much attention and studied intensively by many authors due to their anomalously high thermal conductivities. In fact, numerous experimental and theoretical investigations on the nanofluids were undertaken. Experimentally, thermal conductivity of nanofluids was measured by several researchers [19–22]. The obtained results show that the nanofluids exhibit significantly higher thermal conductivities than base fluids.

By numerical means, the effect of suspended nanoparticles in a conventional base fluid on heat transfer characteristics has been also investigated by many researchers. For example, Khanafer et al. [23] developed a model to analyze heat transfer performance of nanofluids inside an enclosure taking into account the solid particle dispersion. This study gives a heat transfer correlation of the average Nusselt number for various Grashof numbers and volume fractions. Obtained results showed that the nanoparticles enhance significantly the heat transfer rate at any Grashof number. Kuznetsov and Nield [24] investigated analytically the natural convection of nanofluid flow past a vertical semi-infinite plate. They showed that the solution mainly depends on a Lewis number, a buoyancy-ratio number, a Brownian motion number, and a thermophoresis number. Sheikholeslami and Ganji [25] investigated heat transfer of a nanofluid flow which is squeezed between parallel plates. This investigation uses the Homogony perturbation method (HPM) and results show that the Nusselt number increases with the increase of nanoparticle volume fraction and the squeeze number when two plates are separated, while it decreases with the increase of the squeeze number when two plates are squeezed. Raza et al. [26] studied the hydro-magnetic three-dimensional flow of a nanofluid in a rotating channel. They consider, on the one hand, simultaneous effects of energy and concentration of the nanoparticles. On the other hand, they utilized velocity, thermal and concentration slip conditions in order to make the analysis more interesting. Sun et al. [27] studied the flow and convective heat transfer characteristics of the nanofluids inside a plate heat exchanger. They demonstrated that, at the same Reynolds number, the overall heat transfer coefficient and resistance coefficient are enhanced with the addition of nanoparticles. Also, they showed that the overall heat transfer coefficient was improved significantly with the increase of the mass fraction of nanoparticles, while the resistance coefficient did not significantly increase. Alam et al. [28] investigated the magnetohydrodynamic stability of Jeffery–Hamel flow using different nanoparticles. They studied numerically the effect of nanoparticles volume fraction on critical values and bifurcation diagrams of channel angle and flow Reynolds number. This investigation also shows the critical relationships among the physical parameters of the studied problem.

On the other hand, many authors considered the nanofluids as random processes and consequently use concepts from probabilities theory in order to obtain models of nanoparticles and the thermal conductivity of nanofluids. With this intent, by considering the fractal character of solid nanoparticles in the nanofluids, Feng et al. [29] developed the probability model for nanoparticle size distribution and the effective thermal conductivity model. In this research work, the Monte Carlo simulations were performed and compared with the available experimental data for nanofluids. Kaminski and Ossowski [30] have used a variety of statistical and probabilistic methods to find numerically the effective physical properties of nanofluids. They investigated a new problem of homogenization of the fluids filled with a random volume fraction of nanoparticles using a probabilistic approach in the form of a higher order stochastic perturbation method. Usocwicz et al. [31] developed a new physical–statistical model for predicting the effective thermal conductivity of nanofluids. The proposed model shows a good agreement with the available experimental results and gives an efficient prediction for the effective thermal conductivity of nanofluids compared to existing models.

In recent decades, several methods were developed in order to solve analytically the nonlinear initial or boundary values problems, such as the homotopy analysis method (HAM) and the variational iteration method (VIM). Same as the HAM and the VIM, the Adomian decomposition method (ADM) [32] developed since 1980s provides the solution of nonlinear problems in the form of a polynomial series and can be applied directly to nonlinear differential equations without requiring perturbation or discretization. These analytical methods have been extensively used by several authors. In fact, they give the approximate solutions to a wide variety of linear or nonlinear differential equations [33–37]. Also, these methods were successfully applied [38–40] to solve the traditional nonlinear problem of Jeffery–Hamel flow and results show that the obtained solutions match perfectly with numerical Runge–Kutta solution used as a guide, thus justifying the validity, the applicability and the effectiveness of the analytical methods.

Motivated by the conducted investigations on the nanofluids, the present paper considers the problem of flow of Al\(_{2}\)O\(_{3}\)–water nanofluid between stretchable/shrinkable nonparallel plane walls. In this study, the resulting nonlinear ordinary differential equations governing the velocity and temperature fields are solved analytically and numerically. The analytic solution is investigated by an efficient technique of computation, called Adomian decomposition method, while the numerical solution is obtained via fourth order Runge–Kutta method. It should also be pointed out that the effect of nanoparticles on the flow and heat transfer characteristics in such configurations is not addressed yet. The effects of various physical parameters on velocity and temperature profiles as well as on skin friction and Nusselt number are tabulated, plotted and therefore discussed. The principal aim is, on the one hand, to find an approximate analytical solution of the studied problem, and, on the other hand, to investigate the effects of nanoparticle volume fraction on the flow and heat transfer characteristics between stretchable/shrinkable inclined walls.

Basic Equations

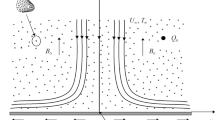
In this research, the steady two-dimensional flow and heat transfer of Al\(_{2}\)O\(_{3}\)–water nanofluid between two stretchable or shrinkable nonparallel plates are investigated analytically using Adomian decomposition method. As for the traditional case, we assume that the nanofluid flow is symmetric and has (Fig. 1) a purely radial motion. Due to this assumption, the nanofluid velocity is only along radial direction and mainly depends on r and \(\uptheta \). Consequently, we have: (\(V_r =V\left( {r,\theta } \right) ;V_\theta =V_z =0)\).

Fig. 1
figure 1

Geometry of Jeffery–Hamel flow of nanofluids

Full size image

On the other hand, the walls could radially stretch or shrink and consequently we have:

$$\begin{aligned} V_r =V_w =\frac{s}{r} \end{aligned}$$
(1)

where, s: is the stretching/shrinking rate. \(V_{w}\): Velocity of the wall.

In cylindrical coordinates \(({r, \theta , z})\), the continuity equation, Navier–Stokes equation and energy equation for stretchable/shrinkable Jeffery–Hamel flow of nanofluids are expressed as:

$$\begin{aligned}&\displaystyle \frac{\rho _{nf} }{r}\cdot \frac{\partial }{\partial r}\left( {r\cdot V_r } \right) =0 \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle V_r \cdot \frac{\partial V_r }{\partial r}=-\frac{1}{\rho _{nf} }\cdot \frac{\partial P}{\partial r}+ \quad \nu _{nf} \cdot \left[ {\frac{\partial ^{2}V_r }{\partial r^{2}}+\frac{1}{r}\cdot \frac{\partial V_r }{\partial r}+\frac{1}{r^{2}}\cdot \frac{\partial ^{2}V_r }{\partial \theta ^{2}}-\frac{V_r }{r^{2}}} \right] \end{aligned}$$
(3)
$$\begin{aligned}&\displaystyle \quad -\frac{1}{\rho _{nf} \cdot r}\cdot \frac{\partial P}{\partial \theta }+\frac{2\cdot \nu _{nf} }{r^{2}}\cdot \frac{\partial V_r }{\partial \theta }=0 \end{aligned}$$
(4)
$$\begin{aligned}&\displaystyle \left( {\rho .c_p } \right) _{nf} V_r \frac{\partial T}{\partial r}=K_{nf} \left[ {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial T}{\partial r}} \right) +\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}}} \right] \nonumber \\&\displaystyle \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad +\,\mu _{nf} \left[ {2.\left( {\left( {\frac{\partial V_r }{\partial r}} \right) ^{2}+\left( {\frac{V_r }{r}} \right) ^{2}} \right) +\left( {\frac{1}{r}\frac{\partial V_r }{\partial r}} \right) ^{2}} \right] \nonumber \\ \end{aligned}$$
(5)

where \(V_r\) is the radial velocity, T is the temperature, \(\rho _{nf}\) is the effective nanofluid density, \({\upmu }_{\mathrm{nf}}\) is the effective dynamic viscosity of nanofluid, \(\nu _{nf} \) is the effective kinematic viscosity of nanofluid, P is fluid pressure, \({c_p}_{nf} \) is the effective specific heat of nanofluid at constant pressure and \(K_{nf}\) is the effective nanofluid thermal conductivity.

The boundary conditions are expressed as follows:

  • At the centerline of channel:

    $$\begin{aligned} \frac{\partial V_r }{\partial \theta }=0, \frac{\partial T}{\partial \theta }=0,\, V_r =\frac{V_C }{r} \end{aligned}$$
    (6)

  • At the body of channel: due to the stretching/shrinking of the convergent–divergent channels, we have:

    $$\begin{aligned} V_r =V_w =\frac{s}{r}, \quad T=\frac{T_w }{r^{2}} \end{aligned}$$
    (7)

where \(T_w\): is the constant wall temperature. \(V_c\): rate of movement in the radial direction (\(V_c =r \cdot V_{max})\).

On the other hand, the effective density \(\rho _{nf} \), the effective dynamic viscosity \(\mu _{nf} \), the effective heat capacity \(\left( {\rho \cdot c_p } \right) _{nf} \) and the effective thermal conductivity \(K_{nf} \) of the nanofluid are given as [41]:

$$\begin{aligned} \rho _{nf}= & {} \left( {1-\psi } \right) \rho _f +\psi \cdot \rho _s , \quad \mu _{nf} =\frac{\mu _f }{\left( {1-\psi } \right) ^{2.5}}, \quad \left( {\rho \cdot c_p } \right) _{nf}\nonumber \\= & {} \left( {1-\psi } \right) \cdot \left( {\rho \cdot c_p } \right) _f +\psi \cdot \left( {\rho \cdot c_p } \right) _s ,\nonumber \\ \frac{K_{nf} }{K_f }= & {} \frac{\left( {k_s +2k_f } \right) -2\psi \left( {k_f -k_s } \right) }{\left( {k_s +2k_f } \right) +\psi \left( {k_f -k_s } \right) } \end{aligned}$$
(8)

where \(\psi \) is the volume fraction of nanoparticles. The subscript f denotes the base fluid and s the solid nanoparticles.

Now by introducing the dimensionless parameters [16]:

$$\begin{aligned} F\left( \eta \right) =\frac{f\left( \theta \right) }{V_c }, \quad \eta =\theta /\alpha \end{aligned}$$
(9)

together with a transformation:

$$\begin{aligned} \frac{T}{T_w }=\frac{G\left( \theta \right) }{r^{2}} \end{aligned}$$
(10)

And eliminating the pressure term between (3) and (4), we obtain:

$$\begin{aligned}&{F}^{'''}+2R_{e} \cdot \alpha \cdot \left[ (1-\psi )|^{2.5}\cdot \left( (1-\psi )+\psi \cdot \frac{\rho s}{\rho f}\right) \right] \cdot FF^{'}+ 4\alpha ^{2} F^{'} = 0 \end{aligned}$$
(11)
$$\begin{aligned}&G^{''} + 4{\alpha ^2}G + \frac{{{C_1}}}{{{C_2}}}2{\alpha ^2}{P_r}FG + \frac{{{P_r}\cdot {E_c}}}{{{R_e}\cdot {C_2}\cdot {{\left( {1 - \psi } \right) }^{2.5}}}}\left( {4{\alpha ^2}{F^2} + {F^{'2}}} \right) = 0 \end{aligned}$$
(12)

With:

$$\begin{aligned} C_1= & {} \left( {1-\psi } \right) +\psi \cdot \frac{{\rho _s}\cdot {c_{p}}_s}{{\rho _{f}} \cdot {c_{p}}_{f}} \end{aligned}$$
(13)
$$\begin{aligned} C_2= & {} \frac{\left( {k_s +2k_f } \right) -2\psi \left( {k_f -k_s } \right) }{\left( {k_s +2k_f } \right) +\psi \left( {k_f -k_s } \right) } \end{aligned}$$
(14)

The Reynolds, Prandtl and Eckert numbers of the Jeffery–Hamel flow of nanofluids are introduced as:

$$\begin{aligned} R_e= & {} \frac{V_c \cdot \alpha }{\nu _f } \quad \left\{ {{\begin{array}{l} {V_c>0,\,\alpha >0\quad Divergent\, channel } \\ {V_c<0, \alpha <0\quad Convergent\, channel} \\ \end{array} }} \right. \end{aligned}$$
(15)
$$\begin{aligned} P_r= & {} \frac{{\rho _{f}} \cdot {C_{p}}_{f} \cdot V_c }{K_f } \end{aligned}$$
(16)
$$\begin{aligned} E_c= & {} \frac{\alpha \cdot V_c ^{2}}{{C_{p}}_f \cdot T_w } \end{aligned}$$
(17)

Accordingly, in terms of \(F\left( \eta \right) \) and \(G\left( \eta \right) \), the boundary conditions are converted into:

$$\begin{aligned} \hbox {At the centerline of channel}:F(0)= & {} 1, \, F^{'}(0)=0,\, {G}^{'}(0) = 0\end{aligned}$$
(18)
$$\begin{aligned} \hbox {At the body of channel}: F(1)= & {} C,\, G(1)=1 \end{aligned}$$
(19)

where \(C=\frac{s}{V_c}\) is the shrinking \((C<0)\) or stretching \((C>0)\) parameters.

The quantities of engineering interest for the studied problem are the skin friction coefficient and the Nusselt number that give an indication of the physical wall shear stress and the rate of heat transfer, respectively. In fact, the Skin friction coefficient \(C_f \) can be expressed as:

$$\begin{aligned} C_f =\frac{\tau _w }{\rho \cdot V_c^2 } \end{aligned}$$
(20)

where the wall shear stress is expressed as

$$\begin{aligned} \tau _w =\left. {\mu _{nf} \left( {\frac{1}{r}\cdot \frac{\partial u}{\partial \theta }} \right) } \right| _{\theta =\alpha } \end{aligned}$$
(21)

By substituting Eq. (21) into Eq. (20), and using the dimensionless quantities (9) and (10), the Skin friction coefficient is written as:

$$\begin{aligned} C_f =\frac{1}{R_{e\cdot } \cdot \left( {1-\psi } \right) ^{2.5}}\cdot {F}^{'} (1) \end{aligned}$$
(22)

On the other hand, the Nusselt number is defined as follows:

$$\begin{aligned} Nu=\frac{r\cdot \left. {q_w } \right| _{\theta =\alpha } }{K\cdot T_w } \end{aligned}$$
(23)

where, the heat flux \(q_w \) is expressed as:

$$\begin{aligned} q_w =-K_{nf} \cdot \left( {\frac{\partial T}{\partial r}+\frac{1}{r}\cdot \frac{\partial T}{\partial \theta }} \right) \end{aligned}$$
(24)

Finally, by substituting Eq. (24) into Eq. (23), and using the dimensionless quantities (9) and (10), the Nusselt number is written as:

$$\begin{aligned} Nu=\frac{K_{nf}}{K_{f} }\cdot \left[ 2-\frac{{G}^{'}(1)}{\alpha } \right] \end{aligned}$$
(25)

Adomian Decomposition Method

In this section, we present the basic principle of Adomian decomposition method. Consider the following nonlinear differential equation:

$$\begin{aligned} L\left( y \right) +N\left( y \right) =f\left( t \right) \end{aligned}$$
(26)

where \(L=\frac{d^{n}}{dx^{n}}\) is the n-order derivative operator, N is a nonlinear operator and f is a given function.

Assume that \(L^{-1}\) is an inverse operator that represents n-fold integration for an n-th order of the derivative operator L. Applying the inverse operator \(L^{-1}\) to both sides of (26) yields:

$$\begin{aligned} L^{-1}L\left( y \right) =L^{-1}f-L^{-1}N\left( y \right) \end{aligned}$$
(27)

As a result, we obtain:

$$\begin{aligned} y=\beta +L^{-1}f-L^{-1}N\left( y \right) \end{aligned}$$
(28)

where \(\beta \) is a constant determined from the boundary or initial conditions.

Now based on the Adomian decomposition procedure, the solution y of the Eq. (26) can be constructed by a sum of components defined by the following infinite series:

$$\begin{aligned} y={\mathop {\sum }\limits _{n=0}^\infty } y_n \end{aligned}$$
(29)

Also, the nonlinear term is given as follows:

$$\begin{aligned} Ny={\mathop {\sum }\limits _{n=0}^{+\infty }} A_n \left( {y_0 ,y_1 ,\ldots ,y_n } \right) \end{aligned}$$
(30)

where

$$\begin{aligned} y_0 =\beta +L^{-1}f, \quad y_{n+1} =-L^{-1}\left( {A_n } \right) . \end{aligned}$$
(31)

\(A_{n} {}^{\prime }s\) are called the Adomian polynomials. The recursive formula that defines the Adomian polynomials [32] is given as follows:

$$\begin{aligned} A_n \left( {y_0 ,y_1 ,\ldots ,y_n } \right) =\frac{1}{n!}\left[ {\frac{d^{n}}{d\lambda ^{n}}\left[ {N\left( {{\mathop {\sum }\limits _{n=0}^{\infty }} \lambda ^{i} y_i } \right) } \right] } \right] _{\lambda =0}, n=0,1,2,\ldots . \end{aligned}$$
(32)

Finally, after some iterations, the solution of the studied equation can be given as an infinite series by:

$$\begin{aligned} y\cong y_0 +y_1 +y_2 +y_3 +\cdots +y_n . \end{aligned}$$
(33)

The Adomian decomposition method (ADM) is a powerful technique which provides efficient algorithms for several real applications in engineering and applied sciences. The main advantage of this method is to obtain the solution of both nonlinear initial value problems (IVPs) and boundary value problems (BVPs) as fast convergent series with elegantly computable terms and does not need linearization, discretization or any perturbation.

Implementation of Adomian Decomposition Method

In this study, the Adomian decomposition method is applied to the ordinary nonlinear differential equations (11) and (12) governing dimensionless velocity and temperature profile of nanofluid flow between nonparallel plates. In order to apply the Adomian decomposition method, the linear operators are given as follows:

$$\begin{aligned} L_1= & {} \frac{d^{3}}{d\eta ^{3}} \end{aligned}$$
(34)
$$\begin{aligned} L_2= & {} \frac{d^{2}}{d\eta ^{2}} \end{aligned}$$
(35)

Differential equations of Jeffery–Hamel nanofluid flow (11) and (12), after applying Eqs. (34) and (35) become:

$$\begin{aligned}&L_1 F=-2R_e \cdot \alpha \cdot \left[ {\left( {1-\psi } \right) ^{2.5}\cdot \left( {\left( {1-\psi } \right) +\psi \cdot \frac{\rho _S }{\rho _f }} \right) } \right] \cdot {FF}^{'} + 4\alpha ^{2} F^{'} \end{aligned}$$
(36)
$$\begin{aligned}&L_2 G+\frac{P_r \cdot E_c }{R_e \cdot C_2 \cdot \left( {1-\psi } \right) ^{2.5}}\left( {4\alpha ^{2}F^{2}+F^{{\prime }2}} \right) =-4\alpha ^{2}G-2\alpha ^{2}\frac{C_1 }{C_2 }P_r FG \end{aligned}$$
(37)

The inverse of the operators \(L_{1}\) and \(L_{2}\) can be expressed as follows:

$$\begin{aligned}&L_1^{-1} ={\mathop {\int }\nolimits _{0}^{\eta }} {\mathop {\int } \nolimits _{{\varvec{0}}}^{\varvec{\eta }}} {\mathop {\int }\nolimits _{{\varvec{0}}}^{\varvec{\eta }}} d\eta \, d\eta \, d\eta \end{aligned}$$
(38)
$$\begin{aligned}&L_2^{-1} ={\mathop {\int }\nolimits _{0}^{\eta }} {\mathop {\int } \nolimits _{0}^{\eta }} d\eta \, d\eta \end{aligned}$$
(39)

Operating with \(L_1^{-1} \) and \(L_2^{-1} \) on Eqs. (36) and (37) and after applying boundary conditions, we obtain:

$$\begin{aligned} F\left( \eta \right)= & {} F\left( 0 \right) +{F}^{'} (0)\eta + F^{''} (0) \frac{\eta ^{2}}{2}+ L^{-1} (Nu1) \end{aligned}$$
(40)
$$\begin{aligned} G\left( \eta \right)= & {} G\left( 0 \right) +L^{-1}\left( {Nu2} \right) \end{aligned}$$
(41)

where

$$\begin{aligned} Nu1= & {} 2R_e \cdot \alpha \cdot \left[ {\left( {1-\psi } \right) ^{2.5}\cdot \left( {\left( {1-\psi } \right) +\psi \cdot \frac{\rho _S }{\rho _f }} \right) } \right] \cdot FF^{'}+ 4\alpha ^{2} F^{'} \end{aligned}$$
(42)
$$\begin{aligned} Nu2= & {} -4\alpha ^{2}G-2\alpha ^{2}\frac{C_1 }{C_2 }P_r FG \end{aligned}$$
(43)

On the other hand, the application of boundary conditions leads to the following expressions:

$$\begin{aligned} F\left( \eta \right)= & {} {\mathop {\sum }\limits _{n=0}^\infty } F_n =F_0 + L^{-1}\left( {Nu1} \right) \end{aligned}$$
(44)
$$\begin{aligned} G\left( \eta \right)= & {} {\mathop {\sum }\limits _{n=0}^\infty } G_n =G_0 +L^{-1}\left( {Nu2} \right) \end{aligned}$$
(45)

where \(F_0 \) and \(G_0 \) are expressed as follows:

$$\begin{aligned} F_0= & {} 1+a\frac{\eta ^{2}}{2} \end{aligned}$$
(46)
$$\begin{aligned} G_0= & {} b+\frac{1}{2\hbox {Re}\left( {1-\psi } \right) ^{2.5}\cdot C_2 }\hbox {Ec Pr}\left( {F}^{'2}+ {4\upalpha }^{2} F^{2} \right) \eta ^{2} \end{aligned}$$
(47)

By applying the recursive formula (31), the terms of Adomian polynomials for the nanofluid flow are expressed as:

$$\begin{aligned} A_0= & {} -2a\left( {\left( {1-\psi } \right) +\psi \cdot \frac{\rho _S }{\rho _f }} \right) \left( {1-\psi } \right) ^{2.5}\hbox {Re}\alpha \eta -4a\alpha ^{2}\eta -\hbox {C}_2 \left( {1-\psi } \right) ^{2.5}\hbox {Re}\alpha \eta ^{3} \end{aligned}$$
(48)
$$\begin{aligned} {A_1}= & {} ~\frac{2}{3}a{\left( {\left( {\left( {1 - \psi } \right) + \psi .\frac{{{\rho _S}}}{{{\rho _f}}}} \right) {{\left( {1 - \psi } \right) }^{2.5}}} \right) ^2}\mathrm{{R}}{\mathrm{{e}}^2}{\alpha ^2}{\eta ^3}\nonumber \\&+\, \frac{8}{3}a\left( {\left( {1 - \psi } \right) + \psi \cdot \frac{{{\rho _S}}}{{{\rho _f}}}} \right) {\left( {1 - \psi } \right) ^{2.5}}\mathrm{{Re}}{\alpha ^3}{\eta ^3} + \frac{8}{3}a{\alpha ^4}{\eta ^3} \nonumber \\&+\,\frac{3}{5}{a^2}{\left( {\left( {\left( {1 - \psi } \right) + \psi \cdot \frac{{{\rho _S}}}{{{\rho _f}}}} \right) {{\left( {1 - \psi } \right) }^{2.5}}} \right) ^2}\mathrm{{R}}{\mathrm{{e}}^2}{\alpha ^2}{\eta ^5}\nonumber \\&+\, \frac{6}{5}{a^2}\left( {\left( {1 - \psi } \right) + \psi .\frac{{{\rho _S}}}{{{\rho _f}}}} \right) {\left( {1 - \psi } \right) ^{2.5}}\mathrm{{Re}}{\alpha ^3}{\eta ^5} \nonumber \\&+\, \frac{1}{{15}}{a^3}{\left( {\left( {\left( {1 - \psi } \right) + \psi .\frac{{{\rho _S}}}{{{\rho _f}}}} \right) {{\left( {1 - \psi } \right) }^{2.5}}} \right) ^2}\mathrm{{R}}{\mathrm{{e}}^2}{\alpha ^2}{\eta ^7} \end{aligned}$$
(49)

\(\vdots \)

Therefore, the first iterations of solution are given as:

$$\begin{aligned} F_0= & {} 1+\frac{a\eta ^{2}}{2} \end{aligned}$$
(50)
$$\begin{aligned} F_1= & {} -\frac{1}{12}a\left( {\left( {1-\psi } \right) +\psi \cdot \frac{\rho _S }{\rho _f }} \right) \left( {1-\psi } \right) ^{2.5}\hbox {Re}\alpha \eta ^{4}\nonumber \\&-\frac{1}{6}a\alpha ^{2}\eta ^{4}-\frac{1}{120}a^{2}\left( {\left( {1-\psi } \right) +\psi \cdot \frac{\rho _S }{\rho _f }} \right) \left( {1-\psi } \right) ^{2.5}\hbox {Re}\alpha \eta ^{6} \end{aligned}$$
(51)

\(\vdots \)

The application of the recursive formula (31) on heat transfer problem leads to the following expressions:

$$\begin{aligned} B_0= & {} \left( {-4{\upalpha }^{2}-\frac{2}{\hbox {C}_2 }\left( {FC_1 \hbox { Pr } \upalpha ^{2}} \right) } \right) \left( \hbox {b}-\frac{1}{2\hbox {Re}\left( {1-\psi } \right) ^{2.5}\hbox {C}_2 }\left( {\hbox {Ec Pr }\left( F^{'2}+4\upalpha ^{2} F^{2}\right) \eta ^{2}} \right) \right. \nonumber \\ \end{aligned}$$
(52)
$$\begin{aligned} {B_1}= & {} - \frac{1}{{\mathrm{{~Re}}{{\left( {1 - \psi } \right) }^{2.5}}{\mathrm{{C}}_2}^3}}\left( {2\cdot {\mathrm{{C}}_2} + F {C_1}\mathrm{{~Pr}}} \right) {\mathrm{{\alpha }}^2} {\eta ^2} \left( {{F'}^2}{\mathrm{Ec\,Pr }}\left( 0.166667 F {C_1}{\mathrm{Pr }}{{{\upalpha }}^2} {\eta ^{2}}\right. \right. \nonumber \\&\quad \left. \left. +\,{\mathrm{{C}}_2} \left( { - 1. + 0.333333 {{{\upalpha }}^2} {\eta ^2}} \right) \right) \right. \nonumber \\&\quad \left. +\,{{{\upalpha }}^2}\left( \mathrm{{b~}}{{\left( {1 - \psi } \right) }^{2.5}} {\mathrm{{C}}_2} \left( { - 4\cdot {\mathrm{{C}}_2} - 2\cdot F{C_1}\mathrm{{Pr}}} \right) \mathrm{{~Re}} + {\mathrm{Ec }} {F^2}\mathrm{{~Pr~}}\left( - 4\cdot {\mathrm{{C}}_2}\right. \right. \right. \nonumber \\&\quad \left. \left. \left. +\,1.33333\mathrm{{~A~}}{{{\upalpha }}^2} {\eta ^2} + 0.666667 F{C_1}\mathrm{{~Pr~}}{{{\upalpha }}^2} {\eta ^2} \right) \right) \right) . \end{aligned}$$
(53)

\(\vdots \)

$$\begin{aligned} G_0= & {} b+\frac{1}{2\hbox {Re}\left( {1-\psi } \right) ^{2.5}\cdot C_2 }\hbox { Ec Pr }\left( {F}^{'2} + 4\upalpha ^{2} F^{2} \right) \eta ^{2} \end{aligned}$$
(54)
$$\begin{aligned} {G_1}= & {} \mathrm{{~}} - \left( {\frac{1}{{2\mathrm{{Re}}{{\left( {1 - \psi } \right) }^{2.5}}{\mathrm{{C}}_2}}}} \right) {F'^2}\mathrm{{~Ec~Pr~}}{\eta ^2}\nonumber \\&\quad -\,2\mathrm{{~b~}}{{{\upalpha }}^2}\mathrm{{~}}{\eta ^2} - \frac{1}{{{\mathrm{{C}}_2}}}\mathrm{{b~}}F\mathrm{{~}}{C_1}\mathrm{{Pr}}{{{\upalpha }}^2}\mathrm{{~}}{\eta ^2} - \frac{{2\mathrm{{~}}}}{{\mathrm{{Re}}{{\left( {1 - \psi } \right) }^{2.5}}{\mathrm{{C}}_2}}}\mathrm{{Ec~}}{F^2}2\mathrm{{Pr}}{{{\upalpha }}^2}\mathrm{{~}}{\eta ^2} \nonumber \\&\quad +\,\frac{0.166667}{{{\mathrm{Re}}{{\left( {1 - \psi } \right) }^{2.5}}{\mathrm{C}}_2}} F^{'2} \hbox { EcPr} \upalpha ^{4} \eta ^{4} \nonumber \\&\quad +\,\frac{{0.0833333\mathrm{{~}}}}{{\mathrm{{Re}}{{\left( {1 - \psi } \right) }^{2.5}}\mathrm{{C}}_2^2}}{F'^2}\mathrm{{~Ec~}}F\mathrm{{~}}{C_1}2\mathrm{{Pr~}}{{{\upalpha }}^2}\mathrm{{~}}{\eta ^4} + \frac{{0.666667\mathrm{{~}}}}{{\mathrm{{Re}}{{\left( {1 - \psi } \right) }^{2.5}}{\mathrm{{C}}_2}}}\mathrm{{Ec~}}{F^2}\mathrm{{Pr}}{{{\upalpha }}^4}\mathrm{{~}}{\eta ^4}\nonumber \\&\quad + \frac{{0.333333\mathrm{{~}}}}{{\mathrm{{Re}}{{\left( {1 - \psi } \right) }^{2.5}}\mathrm{{C}}_2^2}}\mathrm{{Ec~}}{F^3}{C_1}\mathrm{{~P}}{\mathrm{{r}}^2}\mathrm{{~}}{{{\upalpha }}^4}\mathrm{{~}}{\eta ^4}\nonumber \\ \end{aligned}$$
(55)

\(\vdots \)

Finally, the approximate solutions for the studied problem are:

$$\begin{aligned} F\left( \eta \right)= & {} F_0 +F_1 +F_2 +F_3 +\cdots +F_n \end{aligned}$$
(56)
$$\begin{aligned} G\left( \eta \right)= & {} G_0 +G_1 +G_2 +G_3 +\cdots +G_n \end{aligned}$$
(57)

The accuracy of ADM solution increases by increasing iterations number (n). Also, the constants a and b can be easily determined with the boundary conditions (18) and (19).

Results and Discussions

Nanofluid flow and heat transfer between two stretchable or shrinkable walls coinciding at an angle 2\(\upalpha \) are investigated analytically and numerically. The main goal of this study is to have an insight on the nanofluid flow behaviour and the heat transfer performances. The analytic solution is developed using an efficient method of computation, called Adomian decomposition method; while the Numerical solution is obtained with mathematica package. In fact, this software uses a Runge–Kutta method as default to solve the boundary value problems (BVPs) numerically.

According to the Adomian decomposition method (ADM), we can obtain an elevate order of series solutions. In this paper, we have only presented the expression of the second approximate solution because the results are too long.

Fig. 2
figure 2

Effect of stretching parameter on velocity profiles in convergent channel

Full size image
Fig. 3
figure 3

Effect of shrinking parameter on velocity profiles in convergent channel

Full size image
Fig. 4
figure 4

Effect of stretching parameter on velocity profiles in divergent channel

Full size image
Fig. 5
figure 5

Effect of shrinking parameter on velocity profiles in divergent channel

Full size image
Fig. 6
figure 6

Effect of nanoparticle volume fraction on velocity profile in diverging channel

Full size image
Fig. 7
figure 7

Effect of nanoparticle volume fraction on velocity profile in diverging channel

Full size image
Fig. 8
figure 8

Effect of stretching of the convergent channel on the evolution of temperature

Full size image
Fig. 9
figure 9

Effect of stretching of the divergent channel on the evolution of temperature

Full size image
Fig. 10
figure 10

Effect of shrinking of the convergent channel on the evolution of temperature

Full size image

Numerical and analytical results of the present study are drawn in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 and 17. These figures display velocity and temperature profiles, Nusselt number and Enhancement parameter through convergent–divergent channels. On the other hand, the thermo-physical properties of the studied nanofluid flow are given in Table 1.

The analytical ADM results in this investigation are compared with numerical results used as a guide (Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and Tables 2, 3, 4, 5, 6, 7). It is found that the results are similar to each other, thus justifying validity, applicability and the higher accuracy of Adomian decomposition method.

Nanofluid Flow Behaviour

The effects of stretching/shrinking of the convergent–divergent channels on the behaviour of fluid velocity are depicted in Figs. 2, 3, 4, 5. For the stretching case, it is clear that the wall moves in the direction of flow; however, the wall has an opposite movement in the case of shrinking. On the other hand, at a fixed value of the stretching parameter (i.e. \(C=1\)), it should be pointed out that the wall and the nanofluid flow have a same velocity, which is physically expected.

As drawn in Figs. 2, 3, 4, 5 in the case of stationary rigid walls (i.e. \(C=0\)), we notice that the fluid velocity appeared as an increasing function from \(F(1)=0\) at the body of channel to \(F(0)=1\) at the centerline of channel. On the other hand, as displayed in Fig. 2, it is clear that the increase of stretching of a convergent channel (i.e. after \(C = 1\)) intensifies the presence of particles near the walls. In this zone, the entire fluid moves faster and consequently the velocity shows a higher magnitude in comparison with the centerline velocity \(V_{c}\). From a practical viewpoint, this means that particles will intensify near the wall, for example, in polymer science, the polymers will concentrate near the convergent channels and show a reverse behaviour to that observed in the classical Jeffery–Hamel flow (i.e. nonstretched rigid walls) where the velocity is concentrated at the centerline of the channel.

As depicted in Table 2, the skin friction coefficient increases with the stretching of a convergent channel. This can be explained by the higher wall shear stress near the walls.

Fig. 11
figure 11

Effect of shrinking of the divergent channel on the evolution of temperature

Full size image
Fig. 12
figure 12

Effects of shrinking parameter and nanoparticle volume fraction on the Nusselt number

Full size image
Fig. 13
figure 13

Effects of stretching parameter and nanoparticle volume fraction on the Nusselt number

Full size image
Fig. 14
figure 14

Heat transfer enhancement En versus shrinking diverging channel for different values of nanoparticle volume fraction

Full size image
Fig. 15
figure 15

Heat transfer enhancement En versus stretching diverging channel for different values of nanoparticle volume fraction

Full size image
Fig. 16
figure 16

Heat transfer enhancement En versus stretching converging channel for different values of nanoparticle volume fraction

Full size image
Fig. 17
figure 17

Heat transfer enhancement En versus shrinking converging channel for different values of nanoparticle volume fraction

Full size image

Figure 3 shows the effect of shrinking of a convergent channel on the fluid velocity behaviour. In this case, we notice a reverse behaviour to that observed in the case of stretching (Fig. 2). In fact, due to the opposite movement of the wall, it is clear that the fluid particles are obliged to reverse near the wall. Consequently the velocity profile tends to show an inflectional behaviour at high values of shrinking parameter. On the other hand, we notice that the high velocity is occurred near the wall. As displayed in Table 3, the skin friction, in a convergent channel, is a decreasing function at the low values of the shrinking parameter (C < 1); however, it is an increasing function after a certain critical value of the shrinking parameter. In this case, the decrease in fluid velocity and the negative skin friction coefficient are mainly due to the opposite movement of the wall.

As shown in Figs. 4 and 5, we observe that the effect of stretching of a divergent channel (Fig. 4) on fluid velocity is similar to that observed in the case of stretching of a convergent channel. The shrinking of a divergent channel (Fig. 5) shows also a similar behaviour as noticed in the case of a shrinking of convergent channel. On the other hand, it is well clear that the velocity profile (Fig. 4), shows an inflectional behaviour after a critical value of the stretching parameter. According to this behaviour, the backflow phenomenon may occur for large values of stretching of the divergent channel, thus signalling the start of separation.

As drawn in Table 4, we notice that the skin friction increases for low values of stretching of the divergent channel; however, it decreases after a certain critical value of stretching parameter. This decrease clearly indicates on the beginning of the backflow phenomenon. In Table 5, we notice a decrease in skin friction coefficient with the increase of shrinking of a divergent channel.

Effects of the nanoparticle volume fraction on velocity profile in the case of stretching of a diverging channel are depicted in Figs. 6 and 7. In fact, we notice that the fluid velocity increases with the increase of nanoparticle volume fraction and consequently the backflow phenomenon starts. On the other hand, after a certain critical value of nanoparticle volume fraction, it can be seen that increasing nanoparticle volume fraction causes fluid velocity to decrease. As consequence the backflow is slowed.

Thermal Distributions

To visualize the effects of stretching/shrinking of convergent–divergent channels on the temperature profile in Jeffery–Hamel flow of nanofluids, Figs. 8, 9, 10 and 11 are drawn with \(\alpha =\pm 3^{\circ }, {Re}=50\), \(\uppsi =0.1\) and Ec \(=\) 0.5. As mentioned above, the stretching of convergent–divergent channels generates more shear stress near the walls. In fact, this shearing leads to the increased thermal boundary layer as depicted in Figs. 8, 9. According to Figs. 10, 11, shrinking leads to reducing of thermal boundary layer for both converging–diverging channels. On the other hand, as depicted in Table 6, it is clear that the stretching enhances the heat transfer rate between nonparallel plates; however, the shrinking generates less heat in converging/diverging channels and consequently the heat transfer rate will be decreased as presented in Table 7.

The Nusselt number is known as the ratio of convective to conductive heat transfer. It is also well known that the convection terms include both advection and diffusion. Also the presence of nanoparticles in a base fluid leads to increased thermal conductivity of the nanofluids. This increase is accompanied by an increase in thermal diffusivity; consequently a drop in temperature gradients is occurred, thus leading to increase in the thickness of thermal boundary layer. Increased thermal boundary layer reduces the Nusselt number; however, as presented in Eq.  25, the Nusselt number is defined as a multiplication of thermal conductivity ratio \(\left( \frac{K_{nf} }{K_f }\right) \) and the temperature gradient. According to Figs. 12, 13, the Nusselt number increases with the increase of volume fraction of Alumina nanoparticles. In fact, with the presence of nanoparticles, thermal conductivity ratio is higher than reduction in temperature gradient; therefore an enhancement in Nusselt number is taking place with the increase of nanoparticle volume fraction.

Table 1 Thermophysical properties of \(\hbox {Al}_{2}\hbox {O}_{3}\)–water nanofluid
Full size table
Table 2 Effect of stretching on Skin friction coefficient in convergent channel Re \(=50\), \(\upalpha =-3{^{\circ }}\) and \(\psi =0.1\)
Full size table
Table 3 Effect of shrinking on Skin friction coefficient in convergent channel Re \(=\) 50, \(\upalpha = - 3{^{\circ }}\) and \(\psi =0.1\)
Full size table
Table 4 Effect of stretching on Skin friction coefficient in divergent channel when: Re \(=\) 50, \(\upalpha =3{^{\circ }}\) and \(\psi =0.1\)
Full size table

As displayed in Fig. 12, an increase in Nusselt number is well observed when the shrinking parameter increases. Also, as shown in Fig. 13, it is clear that the Nusselt number decreases with the increase of the stretching parameter (C \(\in \) [0–1]). After a certain critical value of the stretching parameter \((\hbox {C}\cong \, 1\) in our case), we notice that the Nusselt number increases as the stretching parameter increases. In Tables 8 and 9 we visualize the critical Nusselt number and the corresponding critical stretching parameter. The results shown are depicted versus Reynolds number (Re) and the nanoparticles volume fraction \((\psi )\). We notice, that the magnitude of \({Nu}_{critical}\) and \(C_{critical}\) decreases with the increase of Reynolds number; however, it increases with the increase of nanoparticle volume fraction.

On the other hand, the presence of Al\(_{2}\)O\(_{3}\) nanoparticles in a base fluid leads to the increased in thermal conductivity and enhances significantly the Nusselt number for both stretching and shrinking of convergent–divergent channels as displayed in Figs. 12 and 13.

Table 5 Effect of shrinking on Skin friction coefficient in divergent channel Re \(=\) 50, \(\upalpha =3^{\circ }\) and \(\psi =0.1\)
Full size table
Table 6 Effect of stretching on heat transfer rate in converging/diverging channel
Full size table
Table 7 Effect of shrinking on heat transfer rate in converging/diverging channel
Full size table
Table 8 Critical values of Nusselt number and stretching parameter in the classical flow \((\uppsi =0)\)
Full size table
Table 9 Critical values of Nusselt number and Stretching parameter in nanofluid flow (\(\uppsi =0.1\))
Full size table

As mentioned above, the presence of nanoparticles plays a significant role on the evolution of Nusselt number. The enhancement in heat transfer due to the presence of alumina nanoparticles in a water base fluid was evaluated. In fact, the enhancement parameter “\({{\varvec{En}}}\)” is calculated between the cases of \(\uppsi =0.1\), 0.2 and 0.3 and the pure fluid case as follows:

$$\begin{aligned} E_n =\frac{Nu_{\left( {nanofluid} \right) } -Nu_{\left( {base fluid} \right) } }{Nu_{\left( {base fluid} \right) } }\times 100 \end{aligned}$$
(58)

The enhancement evolution versus the stretching/shrinking parameters for different values of nanoparticle volume fraction, \(\uppsi \), is displayed in Figs. 14, 15, 16, 17. In the case of stretching/shrinking of a divergent channel, the enhancement in heat transfer increases as the shrinking increases but it decreases with the increase of the stretching parameter. A reverse behaviour is observed in the case of stretching/shrinking of a convergent channel. In fact, the enhancement decreases as the shrinking increases, while it increases with the increase of the stretching values. Also, it is well observed that the enhancement increases with the increase of nanoparticle volume fraction.

Note on the Correspondence Between Nanofluid Flow and Standard Fluid Flow

As given above, Eqs. (11) and (12) with the boundary conditions (18) and (19) consider a steady two-dimensional nanofluid flow between stretchable–shrinkable nonparallel plane walls. It should be mentioned that these equations depend explicitly upon the nanoparticle volume fraction parameter (\(\psi )\).

Now, we propose the following transformations:

$$\begin{aligned} F\left( \eta \right) =\frac{1}{C_\psi }\cdot F\left( \zeta \right) , \quad G\left( \eta \right) =\phi \left( \zeta \right) , \quad \zeta =\eta \end{aligned}$$
(59)

with

$$\begin{aligned} C_\psi =\left( {1-\psi } \right) ^{2.5}\cdot \left( {\left( {1-\psi } \right) +\psi \cdot \frac{\rho _S }{\rho _f }} \right) \end{aligned}$$
(60)

Which leads to the rescaled system:

$$\begin{aligned}&F^{'''}\left( \zeta \right) + 2{R_e}\cdot \alpha \cdot F\left( \zeta \right) \cdot F'\left( \zeta \right) + 4{\alpha ^2}F'\left( \zeta \right) = 0\end{aligned}$$
(61)
$$\begin{aligned}&\phi ^{''}\left( \zeta \right) + 4{\alpha ^2}\phi \left( \zeta \right) + P_r^*\cdot 2{\alpha ^2}\cdot F\left( \zeta \right) \cdot \phi \left( \zeta \right) + \frac{{P_r^*\cdot {E_c}}}{{{R_e}}}\cdot \left[ {4{\alpha ^2}{F^2}\left( \zeta \right) + {F^{'2}}\left( \zeta \right) } \right] = 0\nonumber \\ \end{aligned}$$
(62)

where 

$$\begin{aligned} P_r^*=\frac{P_r }{C_2 \cdot C_3 } \end{aligned}$$
(63)

with

$$\begin{aligned} C_2 =\frac{\left( {k_s +2k_f } \right) -2\psi \left( {k_f -k_s } \right) }{\left( {k_s +2k_f } \right) +\psi \left( {k_f -k_s } \right) } \end{aligned}$$
(64)
$$\begin{aligned} C_3 =\left( {1-\psi } \right) ^{2.5} \end{aligned}$$
(65)

In this situation, the boundary conditions can be expressed as follows:

$$\begin{aligned}&\hbox {At the centerline of channel } (\zeta =0): F\left( \zeta \right) =1,\quad F^{'}\left( \zeta \right) = 0, \quad \phi ^{'}\left( \zeta \right) = 0\end{aligned}$$
(66)
$$\begin{aligned}&\hbox {At the body of channel } (\zeta =1): F\left( \zeta \right) =C, \quad \phi \left( \zeta \right) = 1 \end{aligned}$$
(67)

Equation (61) is not explicitly dependent on the nanoparticle volume fraction \((\psi )\). In fact, this equation is equivalent to Eq. (11) in the case of regular fluid when the parameter \(\psi \) is equal zero (i.e. \(\psi =0\)). Moreover, Eq. (62) can be also considered independent from \(\psi \) for a fixed \(P_{r}^{*}\).

Physical parameters of interest which are the skin friction coefficient \(C_f \) and the Nusselt number Nu can also be easily evaluated by using Eq. (59). In fact, the quantities \({F}^{'}(1)\) and \({G}^{'}(1)\), for \(\eta =\zeta =1\), can be replaced by the following expressions:

$$\begin{aligned}&{F}^{'}(\eta )=\frac{1}{c_{\psi }}F^{'}(\zeta ) \end{aligned}$$
(68)
$$\begin{aligned}&G^{\prime }\left( \eta \right) =\phi ^{\prime }\left( \zeta \right) \end{aligned}$$
(69)

Conclusions

In this research, effects of stretching/shrinking of convergent/divergent channels and nanoparticle volume fraction on the flow and heat transfer characteristics have been investigated analytically and numerically.

The main conclusions, which we can draw from this study, are:

  • Near the walls, the entire fluid moves faster. Consequently, fluid velocity is higher for both stretching and shrinking of convergent/divergent channels when compared to that observed at the centerline of channel.

  • Skin friction coefficient increases with the stretching of a convergent channel. This can be explained by the high shear stress near the walls.

  • Skin friction coefficient in a convergent channel is a decreasing function at the low values of the shrinking parameter; however, it is an increasing function after a certain critical value of the shrinking parameter.

  • A decrease in skin friction coefficient may occur with the increase of shrinking of a divergent channel.

  • Skin friction coefficient increases at low values of the stretching parameter of a divergent channel; however, it decreases after a certain critical value of this parameter.

  • Backflow phenomenon may occur at large values of the stretching parameter of a divergent channel, thus signalling the start of separation.

  • Stretching of both converging–diverging channels lead to an increase in thermal boundary layer, generate more heat and act for improving heat transfer rate.

  • Shrinking leads to reducing of thermal boundary layer for both converging–diverging channels.

  • Nusselt number increases as the magnitude of shrinking increases; however, it increases after a certain critical value of the stretching parameter.

  • The magnitude of \({Nu}_{critical}\) and \(C_{critical}\) decreases with the increase in Reynolds number; however, it increases with the increase of nanoparticle volume fraction.

  • The presence of Al\(_{2}\)O\(_{3}\) nanoparticles in a water base fluid enhances significantly heat transfer characteristics and consequently the Nusselt number increases with the increase of nanoparticle volume fraction.

  • Analytical results match perfectly with those of numerical Runge–Kutta method, thus justifying the efficiency and the higher accuracy of the used Adomian decomposition method.

  • A detailed discussion was given whether the nanofluid problem can be interpreted in terms of regular fluid.