1 Introduction

The flow past a static sheet is a classic problem in fluid dynamics, studied by many researchers in the past (see, e.g., [1,2,3,4] where this problem can be seen among the classic fluid dynamics problems). Crane was the one who first considered the flow past a stretching sheet and further presented a closed-form solution for the flow under consideration [5]. Undeniably, the stretching/shrinking sheet flows appear in various and sundry industrial applications pertinent to the extrusion of plastic sheets, the boundary layer along a liquid film, condensation process of metallic plate in cooling bath and glass as well as the extrusion of molten polymers. This elucidates the importance of the present subject. In this respect, so far, many researchers have explored features associated with the stagnation-point flow of Newtonian and/or non-Newtonian fluids subject to specific conditions (see, e.g., [6,7,8,9,10,11,12,13,14]). In [6], authors have considered, generally the wedge flow of a viscous fluid subject to a nonlinearly stretching/shrinking wall, being proportional to the free stream flow. This proportionality allows a similarity transformation for the problem, in particular including the stagnation-point flow. It has been numerically shown that the problem possesses dual solutions with respect to the shrinking case for the nonlinearity exponent greater than a specific value. Kolomenskiy and Moffatt presented the unsteady similarity solutions for the stagnation-point flow for the first time accounting a specific unsteadiness for the free stream (irrotational) flow [7]. In [8], authors have studied the mixed convection flow near the stagnation point of a vertical surface. The governing partial differential equations were reduced to the ordinary ones employing Lie-point symmetry analysis and then the resulting equations were tackled numerically. References [9,10,11,12,13,14] are a few examples of the studies with respect to the stagnation-point flow of non-Newtonian fluids; for example, in [9], authors have considered the magnetohydrodynamics (MHD) double stratified stagnation-point flow of Carreau fluid toward a nonlinear stretchable surface with radiation. Employing Homotopy Analysis Method (HAM), the effects of the various involved parameters have been studied in an analytic manner. Gorla et al. [10] presented similarity solutions for the 3D flow and heat transfer of a power-law fluid near a stagnation point of an isothermal surface and specifically explored the effect of the power-law index on the evolution of the main quantities of interest.

The emergence of nanofuids as an alternative to most traditional approaches in heat transfer issue was presumably promising enough to attract interest of many researchers to explore the position of nanofluids mainly in the heat transfer enhancement. In this respect, stagnation-point flow of nanofluids has been extensively investigated and some novel conclusions have been established. Normally, nanofluids are modeled through single-phase or two-phase modeling frameworks. In fact, the latter provides us with a more in-depth insight into the involved phenomena; however, as pointed out in [15], the diffusion factors associated with thermophoresis and Brownian effects are still vague in the literature and in this respect; one may find the single-phase modeling more preferable subject to the more rigorous physical basis. Here we list some recent studies on the stagnation-point flow of nanofluids and highlight some findings. Najib et al. [16] presented the similarity solutions for the stagnation-point flow of nanofluids toward an impermeable stretching/shrinking sheet employing a two-phase mathematical framework with second slip order and a modified boundary condition for the concentration equation being typical of the steady-state sense [17]. In particular, they found dual solutions for the shrinking case starting from a certain shrinking ratio, extended to a critical point. Stability analysis revealed that the solutions associated with the lower case are not physically realizable. In addition, it was found that an increase in the slip parameters leads to a decrease in the normalized skin friction coefficient. This was while an increase in slip parameters resulted in an enhancement in the normalized heat transfer coefficient. Moreover, an increment of Soret effect (a decrement of Dufour effect) gave rise to a decrease in the heat transfer coefficient. Hamad and Ferdows [18] conducted a numerical analysis of the stagnation-point flow of nanofluids toward a stretching sheet in porous medium accounting a two-phase modeling framework. In particular, they showed that the stretching ratio plays a significant role in the evolution of Nusselt number and Sherwood number. Interested readers are referred to Refs. [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34] for more information upon the subject.

According to the literature, it becomes clear that a good deal of the studies on the stagnation-point flow of nanofluids are constructed on the basis of two-phase modeling framework with some unknown factors regarding Brownian and thermophoresis effects, chosen arbitrarily on almost no basis subject to a rigorous physical ground. Nevertheless, these studies are of mathematical interest with the promise to understand the structure of solutions subject to the two-phase modeling framework. Besides, the existing studies accounting a single-phase modeling framework mostly lack an appropriate model for the target nanofluids. In other words, for a given nanofluid, the volumetric fraction of nanoparticles is almost the only variable which plays role in the evolution of temperature and velocity fields as well as the main quantities of engineering interest.

In this paper, a contemporary and realistic nanofluid model is employed to specifically target the stagnation-point flow of copper/water nanofluids. The model has been developed in [35]. This model contains empirical information regarding some practical nanofluids including Cu/water, being regarded as a promising nanofluid for thermal applications in the pertinent industries. For that reason, the literature contains some experimental efforts regarding this specific type of nanofluids, mainly investigating the convective heat transfer in pipes/tubes in both laminar and turbulent regimes (see, e.g., [36,37,38,39]).

Moreover, following a critical paper, we notice that for Cu/water nanofuids, a single-phase modeling framework is more appreciated since the effects of Brownian motion and thermophoresis are almost negligible for low volume fraction of nanoparticles, meaning that the copper nanoparticles migration in the media of water due to the significant slip mechanisms can be ignored for this specific nanofluid (see [40] for more information). The new deployed model provides us with the information regarding the impact of nanoparticles size and the heat transfer direction in addition to the volume concentration of nanoparticles on the evolution of velocity and temperature fields as well as the main quantities of engineering interest.

Therefore, implementation of this new model for the stagnation-point flow of nanofluids with porous and stretching/shrinking wall is the untapped and novel consideration which is to be studied here, hopefully, for a better understanding of the concealed features of stagnation-point flow of Cu/water nanofluids.

1.1 The New Model

The model proposed in [35] is brought into account to study the stagnation-point flow of Cu/water nanofluids. We notice that the correlated relations for thermal conductivity and viscosity in [35] cover a wide range of nanofluids; however, some restrictions exist. First of all, the correlations are on the basis of some certain base fluids with various nanoparticles. Moreover, the valid intervals for temperature, nanoparticles diameter and volumetric fraction of nanoparticles should be also noted. Implementation of this new model requires a combination of the valid intervals for the correlated thermal conductivity and viscosity. This gives a range of 25–150 nm for nanoparticles size, 294–323 K for temperature and 0.002–0.071 for the volumetric fraction of nanoparticles. Having this in mind, thermo-physical properties of nanofluids can be written as [35]:

$$ \begin{aligned} \rho_{\text{nf}} & = \phi \rho_{\text{np}} + (1 - \phi )\rho_{\text{bf}} \\ C_{{p_{\text{nf}} }} & = \frac{{\phi (\rho C_{\text{p}} )_{\text{np}} + (1 - \phi )(\rho C_{\text{p}} )_{\text{bf}} }}{{\rho_{\text{nf}} }} \\ k_{\text{nf}} (T) & = k_{\text{bf}} \left( {1 + 4.4\text{Re}^{0.4} \Pr^{0.66} \left( {\frac{T}{{T_{\text{fr}} }}} \right)^{10} \left( {\frac{{k_{\text{np}} }}{{k_{\text{bf}} }}} \right)^{0.03} \phi^{0.66} } \right) \\ \text{Re} & = \frac{{2\rho_{\text{bf}} k_{\text{Bo}} T}}{{\pi \mu_{\text{bf}}^{2} d_{\text{np}} }} \\ \mu_{\text{nf}} & = \mu_{\text{bf}} \left( {1 - 34.87\left( {\frac{{d_{\text{np}} }}{{d_{\text{bf}} }}} \right)^{ - 0.3} \phi^{1.03} } \right)^{ - 1} \\ d_{\text{bf}} & = \frac{1}{10}\left( {\frac{6M}{{N_{\text{A}} \pi \rho_{\text{bfo}} }}} \right) \\ \end{aligned} $$
(1)

In the above, \( \rho \) is density, \( \phi \) is the volumetric fraction of nanoparticles, \( C_{\text{p}} \) is the specific heat capacity, \( k \) is thermal conductivity, \( T \) is temperature, \( \Pr \) is the Prandtl number of base fluid, \( T_{\text{fr}} \) is the freezing temperature of the base fluid, \( k_{\text{Bo}} \) is the Boltzmann’s constant, \( \mu \) is the dynamic viscosity, \( d \) is diameter, \( M \) is the molecular weight of the base fluid, \( N_{\text{A}} \) is Avogadro number, and \( \rho_{\text{bfo}} \) is the density of the base fluid calculated at \( T_{0} = 293\;{\text{K}} \). The subscribes ‘\( bf \)’, ‘\( nf \)’ and ‘\( np \)’ denote base fluids, nanofluids and nanoparticles, respectively.

In the context of this model, one is able to consider the thermal conductivity as:

$$ \begin{aligned} k_{\text{nf}} & = k_{\text{bf}} (1 + AT^{10.4} ) \\ A & = 4.4\left( {\frac{{2\rho_{\text{bf}} k_{\text{Bo}} }}{{\pi \mu_{\text{bf}}^{2} d_{\text{np}} }}} \right)^{0.4} \Pr^{0.66} \left( {\frac{1}{{T_{\text{fr}} }}} \right)^{10} \left( {\frac{{k_{\text{np}} }}{{k_{\text{bf}} }}} \right)^{0.03} \phi^{0.66} \\ \end{aligned} $$
(2)

2 Stagnation-Point Flow of Cu/Water Nanofluids

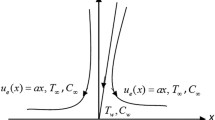
Consider 2D stagnation-point flow of nanofluids subject to a stretching/shrinking wall with possible transpiration velocity. As for the thermal condition, the wall is subjected to a uniform temperature, different from the free stream temperature (see Fig. 1).

Fig. 1
figure 1

Schematic of the problem: the solution in SI unit for the stream function (\( \psi \)); left: Q = 0, a/c = 2 (stretching), pure water; right: Q = 0, a/c = − 1 (shrinking), pure water

Full size image

The flow is assumed to be steady and incompressible, and the flowing nanofluid is assumed to follow the aforementioned model. Therefore, the conservative equations of mass, momentum and energy are:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$
(3)
$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = u_{\text{e}} \frac{\text{d}}{{{\text{d}}x}}(u_{\text{e}} ) + \upsilon_{\text{nf}} \frac{{\partial^{2} u}}{{\partial y^{2} }} $$
(4)
$$ (\rho C_{\text{p}} )_{\text{nf}} \left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}} \right) = \frac{\partial }{\partial y}\left( {k_{\text{nf}} \frac{\partial T}{\partial y}} \right) $$
(5)

The associated boundary conditions are:

$$ \begin{aligned} u(x,0) & = ax,\,\,\,\,v(x,0) = - \sqrt {c\upsilon_{\text{bf}} } Q,\,\,\,T(x,0) = T_{\text{w}} \\ u(x,\infty ) & = cx,\,\,\,T(x,\infty ) = T_{\infty } \\ \end{aligned} $$
(6)

In the above, \( a \) is the stretching/shrinking ratio, \( u_{\text{e}} = cx \) with \( c \) being a constant, \( \upsilon \) is the kinematic viscosity, \( Q \) is a constant (positive Q indicates suction, while the negative values denote injection), \( T_{\text{w}} \) and \( T_{\infty } \) are the wall and the ambient temperatures, respectively.

Figure 1 shows a schematic of the problem under consideration, showing stream lines in the hydrodynamics boundary layer, forming near the stretching/shrinking wall.

Here, we introduce the following variables [41]:

$$ \frac{u}{{u_{\text{e}} }} = f^{\prime } (\eta ),\,\,\,\,\theta = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},\,\,\,\,\eta = \sqrt {\frac{c}{{\upsilon_{\text{bf}} }}} y $$
(7)

Upon substitution into Eqs. 3–5, one gets:

$$ \frac{{\upsilon_{\text{nf}} }}{{\upsilon_{\text{bf}} }}f^{\prime \prime \prime } (\eta ) + f(\eta )f^{\prime \prime } (\eta ) - f^{\prime } (\eta )^{2} + 1 = 0 $$
(8)
$$ \frac{\text{d}}{{{\text{d}}\eta }}\left( {\left( {1 + A\left( {\Delta T_{0} \theta (\eta ) + T_{\infty } } \right)^{10.4} } \right)\theta^{\prime } (\eta )} \right) + \Pr \frac{{(\rho C_{\text{p}} )_{\text{nf}} }}{{(\rho C_{\text{p}} )_{\text{bf}} }}f(\eta )\theta^{\prime } (\eta ) = 0 $$
(9)

In Eq. 9, \( \Delta T_{0} = T_{\text{w}} - T_{\infty } \). The similarity boundary conditions become:

$$ \begin{aligned} f(0) & = Q,\,\,\,\,f^{\prime } (0) = \frac{a}{c} = P,\,\,\,\,f^{\prime } (\infty ) = 1 \\ \theta (0) & = 1,\,\,\,\,\,\theta (\infty ) = 0 \\ \end{aligned} $$
(10)

For the main quantities of engineering interest, we get:

$$ C_{\text{f}} \text{Re}_{x}^{{\frac{1}{2}}} \frac{{\mu_{\text{bf}} }}{{\mu_{\text{nf}} }} = f^{\prime \prime } (0),\,\,\, - Nu_{x} \text{Re}_{x}^{{ - \frac{1}{2}}} \frac{{k_{\text{bf}} }}{{k_{\text{nf}} \left| {_{{T = T_{\text{w}} }} } \right.}} = \theta^{\prime } (0) $$
(11)

In the above, \( C_{\text{f}} \) is the skin friction coefficient, \( {\text{Nu}} \) is Nusselt number, and \( \text{Re}_{x} = \frac{{u_{\text{e}} x}}{{\upsilon_{\text{bf}} }} \)

For Cu/water nanofluids, the involved properties are as listed in Table 1.

Table 1 Properties of copper and water [41]
Full size table

In this work, we investigate the most distinct stages with respect to the present nanofluids model. This means that the nanoparticles size is assumed to be 25 nm and 150 nm. Moreover, as for the thermal boundary conditions, it is assumed that \( T_{\text{w}} = 323 \), \( T_{\infty } = 294 \) (regarded as the Cooling case), and vice versa; \( T_{\text{w}} = 294 \), \( T_{\infty } = 323 \) (regarded as the Heating case). Table 2 shows \( \frac{{\upsilon_{\text{nf}} }}{{\upsilon_{\text{bf}} }} \) and \( A \) for the selected stages.

Table 2 \( \frac{{\upsilon_{\text{nf}} }}{{\upsilon_{\text{bf}} }} \) and \( A \) for the selected stages
Full size table

3 Results and Findings

3.1 Comparison

There exist various algorithms to tackle nonlinear partial and ordinary differential equations, each of which with some certain advantages and restrictions (drawbacks) (e.g., see [42,43,44]). Here, the nonlinear Eqs. 8 and 9 were discretized employing a Runge–Kutta scheme, namely Runge–Kutta–Fehlberg (RKF45), and were solved with a proper shooting technique satisfying a suitable predefined error tolerance at the infinity.

In this section, we first present a validation table in order to verify the present RKF45 numerical solution. For this purpose, for \( Q = 0,\,\,\,\phi = 0 \) and the shrinking case, the results in various P for \( f^{\prime \prime } (0) \) are compared with those available in the literature (Table 3).

Table 3 Comparison of the RKF45 results for \( f^{\prime \prime } (0) \) with \( Q = 0,\,\,\,\phi = 0 \)
Full size table

3.2 Velocity and Temperature Fields

Figures 2 and 3 show the velocity field for Cu/water nanofluids with dp = 150 nm and dp = 25 nm, respectively (Q = 1). From these figures, it is clear that the lower solutions are not much affected by the variation of volumetric fraction of nanoparticles; besides, for dp = 150 nm, the upper solutions are more distinct compared with those for dp = 25 nm. Figures 4 and 5 display the temperature field for Cu/water nanofluids with dp = 150 nm and dp = 25 nm, respectively (Q = 1: the Cooling case). From Figs. 4 and 5, it is again confirmed that the upper solutions with dp = 150 nm are more sensitive to the volumetric fraction of nanoparticles.

Fig. 2
figure 2

\( f^{\prime } (\eta ) \) as a function of \( \eta \) for some stages with dual solutions (\( Q = 1,\,\,\,d_{\text{p}} = 150\;{\text{nm}} \))

Full size image
Fig. 3
figure 3

\( f^{\prime } (\eta ) \) as a function of \( \eta \) for some stages with dual solutions (\( Q = 1,\,\,\,d_{\text{p}} = 25\;{\text{nm}} \))

Full size image
Fig. 4
figure 4

\( \theta (\eta ) \) as a function of \( \eta \) for some stages with dual solutions (\( Q = 1,\,\,\,d_{\text{p}} = 150\;{\text{nm}} \), Cooling)

Full size image
Fig. 5
figure 5

\( \theta (\eta ) \) as a function of \( \eta \) for some stages with dual solutions (\( Q = 1,\,\,\,d_{\text{p}} = 25\;{\text{nm}} \), Cooling)

Full size image

3.3 Quantities of Interest

In this section, we mainly visualize the numerical results for the main quantities of engineering interest being proportional to the mathematical quantities of \( f^{\prime \prime } (0) \) and \( \theta^{\prime } (0) \). It is shown how the nanoparticles size and the heat transfer direction affect these quantities. Figures 6, 7, 8, 9 and 10 exhibit some sample plots, showing \( f^{\prime \prime } (0) \) as a function of P for several stages with Q = 1:0.5:3, respectively. These figures follow an analogous topological behavior. In other words, for dp = 25 nm, the solutions associated with the Cu/water nanofluids with vol. = 0.035 are placed above the nanofluids with vol. = 0.071. Therefore, for the upper solutions and in each P, \( f^{\prime\prime}(0) \) associated with dp = 25 nm and vol. = 0.035 is higher than that for vol. = 0.071. However, for dp = 150 nm, the solutions with the nanofluids with vol. = 0.035 are positioned below those connected to vol. = 0.071. This discrepancy should be followed by the functionality of the new model to the nanoparticles size. It should be pointed out that this behavior is also governing with varying Q. In addition, we recorded that with the increase in Q, the graphs become enlarged containing a broader domain and the lower solutions become extended. This behavior is perhaps connected to the proportionality of the suction to the normalized skin friction coefficient; as the suction parameter increases, the hydrodynamics boundary layer shrinks (due to the suppression of the upward vertical component of the velocity field) and hence an increase in the normalized skin friction coefficient is normally expected. However, later, we perform a temporal stability analysis to show that the lower solutions are instable and hence, for the stable solutions we plot some results for the main quantities of engineering interest to develop some new findings regarding the nanofluids under considerations. Figures 11, 12 and 13 show some sample plots for \( \theta^{\prime } (0) \) as a function of P in various stages with Q = 1:0.5:2, respectively. According to these figures, it is vivid that the nanoparticles size and the heat transfer direction (Cooling or Heating) considerably affect the mathematical quantity \( \theta^{\prime } (0) \). In addition, the lower solutions approach the upper solutions (a contracting behavior) as Q increases. In the last section, it is shown how the sensitivity of \( \theta^{\prime } (0) \) to the heat transfer direction and nanoparticles size appears in the local Nusselt number for the stable region of the acquired solutions.

Fig. 6
figure 6

\( f^{\prime \prime } (0) \) as a function of P with Q = 1 for several stages: dashed black lines indicate upper solutions; dashed red lines indicate lower solutions

Full size image
Fig. 7
figure 7

\( f^{\prime \prime } (0) \) as a function of P with Q = 1.5 for several stages: dashed black lines indicate upper solutions; dashed red lines indicate lower solutions

Full size image
Fig. 8
figure 8

\( f^{\prime \prime } (0) \) as a function of P with Q = 2 for several stages: dashed black lines indicate upper solutions; dashed red lines indicate lower solutions

Full size image
Fig. 9
figure 9

\( f^{\prime \prime } (0) \) as a function of P with Q = 2.5 for several stages: dashed black lines indicate upper solutions; dashed red lines indicate lower solutions

Full size image
Fig. 10
figure 10

\( f^{\prime \prime } (0) \) as a function of P with Q = 3 for several stages: dashed black lines indicate upper solutions; dashed red lines indicate lower solutions

Full size image
Fig. 11
figure 11

\( \theta^{\prime } (0) \) as a function of P with Q = 1 for several stages: dashed black lines indicate upper solutions; dashed red lines indicate lower solutions

Full size image
Fig. 12
figure 12

\( \theta^{\prime } (0) \) as a function of P with Q = 1.5 for several stages: dashed black lines indicate upper solutions; dashed red lines indicate lower solutions

Full size image
Fig. 13
figure 13

\( \theta^{\prime } (0) \) as a function of P with Q = 2 for several stages: dashed black lines indicate upper solutions; dashed red lines indicate lower solutions

Full size image

3.4 Stability Analysis

In this section, a temporal stability analysis is performed to assess the physical validity of the obtained dual solutions. For this purpose, the momentum equation undergoes the stability check. In this respect, the instable momentum solutions indicate that the corresponding thermal solutions are also not physically realizable. Similar to some previous works by the present author (see [45–47]) for the temporal stability analysis, the momentum equation is replaced by:

$$ \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = u_{\text{e}} \frac{d}{dx}(u_{\text{e}} ) + \upsilon_{\text{nf}} \frac{{\partial^{2} u}}{{\partial y^{2} }} $$
(12)

The new variables are now defined as:

$$ \frac{u}{{u_{\text{e}} }} = \frac{\partial f}{\partial \eta }(\eta ,\tau ),\,\,\,\,\,\eta = \sqrt {\frac{c}{{\upsilon_{\text{bf}} }}} y,\,\,\,\tau = ct $$
(13)

With these, Eq. 12 is reconstructed as:

$$ \frac{{\upsilon_{\text{nf}} }}{{\upsilon_{\text{bf}} }}\frac{{\partial^{3} f}}{{\partial \eta^{3} }} + f(\eta ,\tau )\frac{{\partial^{2} f}}{{\partial \eta^{2} }} - \left( {\frac{\partial f}{\partial \eta }} \right)^{2} + 1 - \frac{{\partial^{2} f}}{\partial \eta \partial \tau } = 0 $$
(14)

Together with the following boundary conditions:

$$ f(0,\tau ) = Q,\,\,\,\frac{\partial f}{\partial \eta }(0,\tau ) = P,\,\,\,\frac{\partial f}{\partial \eta }(\infty ,\tau ) = 1 $$
(15)

In order to check the stability of the steady solutions, we assume:

$$ f(\eta ,\tau ) = f_{0} (\eta ) + {\text{e}}^{ - \lambda \tau } F(\eta ) $$
(16)

In the above, \( f_{0} (\eta ) \) is the steady solutions, \( \lambda \) is an unknown eigenvalue, and \( F(\eta ) \) is the eigenfunction.

Upon substitution of Eq. 16 into Eq. 14 and ignoring nonlinear terms with respect to the perturbation principle (linearization [45–47]—the disturbance function \( F(\eta ) \) can be assumed to be small; this is equivalent to assume that the first-order perturbed equation has been captured), we obtain:

$$ \frac{{\upsilon_{\text{nf}} }}{{\upsilon_{\text{bf}} }}F^{\prime \prime \prime } (\eta ) + f_{0} (\eta )F^{\prime \prime } (\eta ) + f^{\prime \prime }_{0} \,(\eta )F(\eta ) - 2f_{\text{o}}^{\prime } (\eta )F^{\prime } (\eta ) + \lambda F^{\prime } (\eta ) = 0 $$
(17)

Together with:

$$ F(0) = F^{\prime } (0) = F^{\prime } (\infty ) = 0 $$
(18)

If \( F(\eta ) \) is a solution for Eq. 17 with the boundary conditions denoted in (18), so also is \( CF(\eta ) \), with \( C \) being an arbitrary constant. Hence, without loss of generality, one is able to assume \( F^{\prime \prime } (0) = c \), e.g., \( c = 1 \).

For each given steady solution, there exist a spectrum of eigenvalues, all of which satisfy Eq. 17 with its boundary conditions. Since it is expected that as \( \tau \to \infty \), the unsteady solution approaches to the steady stage; for a stable solution, the smallest eigenvalue should be positive. Therefore, negative eigenvalues can be regarded as the identification of the instability. Equation 17 was solved employing RKF45 with the modified boundary conditions discussed above. Tables 4 and 5 show the stability results for several stages. According to these tables, it is confirmed that the lower solutions are not likely to reside in actual physics and are mainly of mathematical interest.

Table 4 Q = 1: stability results (smallest \( \lambda \)) for some stages
Full size table
Table 5 Q = 1.5: stability results (smallest \( \lambda \)) for some stages
Full size table

3.5 Practical Findings

In this section, we consider a case with Q = 0, and − 1 < P < 1. This case seems to be more practical in related industries compared with those having \( Q \ne 0 \). Moreover, only the physically stable solutions are visualized for the main quantities of engineering interest to specifically indicate the effects of the nanoparticles size and the heat transfer direction on these significant quantities. To this end, Figs. 14 and 15 show \( \text{Re}_{x}^{{\frac{1}{2}}} C_{\text{f}} \) and \( \text{Re}_{x}^{{ - \frac{1}{2}}} {\text{Nu}}_{x} \) for several stages. According to Fig. 14, Cu/water nanofluids with dp = 25 nm show greater friction at the wall for − 1 < P < 1. Figure 15 indicates that Cu/water nanofluids with dp = 25 nm are more promising for heat transfer enhancement. Moreover, a higher enhancement was observed with respect to the Cooling case. Therefore, in practical applications, the influence of these concealed factors should be brought into account.

Fig. 14
figure 14

\( C_{\text{f}} \text{Re}_{x}^{{\frac{1}{2}}} \) as a function of P with Q = 0 for several stages

Full size image
Fig. 15
figure 15

\( {\text{Nu}}_{x} \text{Re}_{x}^{{ - \frac{1}{2}}} \) as a function of P with Q = 0 for several stages

Full size image

4 Conclusion

The stagnation-point flow of Cu/water nanofluids over a permeable stretching/shrinking wall was studied numerically employing RKF45 algorithm. For this purpose, a realistic nanofluid model was deployed. In the context of the new model, one would be able to track the impact of nanoparticles size and the heat transfer direction on the evolution of the main quantities of engineering interest. The impact of these effects on the mathematical quantities \( f^{\prime \prime } (0) \) and \( \theta^{\prime } (0) \) in an extensive manner was shown. Later on, a temporal stability analysis revealed that only the upper class of the obtained solutions is likely to be regarded physically stable. Eventually, for a practical region for the stretching/shrinking ratio, the main quantities of interest were visualized for the stable solutions. In particular, it was found that Cu/water nanofluids with smaller nanoparticles are more promising for heat transfer purpose. In addition, the deviation in Nusselt number regarding the Cooling and Heating applications should be taken into account.