1 Introduction

In view of numerous physical problems such as endothermic chemical reactions or fluid undergoing exothermic reactions, analysis of the effect of heat generation on the moving fluid is important. Exact modelling of internal heat generation is very crucial. Heat generation can be temperature-dependent, space-dependent and constant. Heat generation can be used in manufacturing, microelectronics, transportation and thermal power plants. Patil and Roy [1] studied the effect of heat generation on the unsteady flow over a moving vertical sheet. After that, Mahapatra et al [2], Chaudhary et al [3] and Eid [4] studied the influence of heat generation on magnetohydrodynamic (MHD) flow. Recently, some of the associated studies are explored by Sun and Wu [5] and Hayat et al [6].

Thermal radiation is the key factor of heat transfer, which is due to the thermal motion of the charged particles in the material. It is transmitted in the form of electromagnetic radiations. This type of radiation is identical to the light speed and there is no need for any kind of medium for its breeding. The applications of radiation heat transfer are important in turbid water bodies, power technology, design of furnace, nuclear reactor safety and power plants. Moreover, it has several applications in space technology, where devices should have high thermal efficiency, as the devices are handled at high level of temperature. Investigation of thermal radiation effect on MHD flow is carried out by Raptis et al [7]. Since then, Jat and Chaudhary [8], Pal and Mondal [9], Sinha and Shit [10], Bhatti et al [11], Khan et al [12], Chaudhary and Choudhary [13] and Kumar et al [14] have published on this topic of thermal radiation heat transfer.

The interaction of electromagnetic forces and electrically conducting liquids is known as MHD. Impacts of MHD can be seen in numerous man-made and natural flows. Fluid flows under the influence of magnetic field have many engineering and industrial applications, especially in flow-meter, measurement of blood flow, nuclear reactor, production of polymers, hydromagnetic generators and pumping and heating of fluids. MHD flows have captivated enough attentions both experimentaly and theoretically. Abdelkhalek [15] initiated the study on MHD flow with heat and mass transfer. A computational investigation of MHD flow in vertical channel was done by Liu and Lo [16]. In the numerical analysis, some researchers like Pekmen and Tezer-Sezgin [17], Hayat et al [18], Chen et al [19], Chaudhary and Choudhary [20] and Khan et al [21] presented the impact of magnetic field on the flow problems with various configurations.

Solid nanosized particles with 1–100 nm diameter are suspended in the engineered colloidal fluids to enhance heat transfer and thermal transport and this mixture of nanoparticles and fluid is known as nonofluid.

Nanoparticles are generally composed of oxides, metals, carbides or carbon nanotubes, while base fluids typically used are water and organic fluid particularly, ethylene glycol, ethanol and oil. The size of the nanoparticles is approximately equal to the size of the molecules of the base fluid. Particle shape, type and size affect the thermal conductivity of the nanofluid. Carbon nanotubes (CNTs) have greater thermal conductivity than other nanotubes. CNTs have some prominent features such as torsion capability, superb flexibility and extremely high resistance. There are two types of CNTs, namely the single-wall carbon nanotube (SWCNT) and the multiple-wall carbon nanotube (MWCNT). Conclusively, SWCNT is built by Bethune by adding transition term. CNTs can be used in frames of helicopters and veneer of the tennis rackets owing to their resistance and they can be used in fuselage in transmission industry, electronics industry and also in the production of athletic equipments. Nanofluid material concept is elaborated by Akbarinia and Laur [22]. Further, Moghari et al [23] addressed the two-phase mixed convection nanofluid flow in an annulus. In recent years, a few models with good performance of nanofluid flow for numerous physical situations are given by Dib et al [24], Wang and Su [25], Al-Sayegh [26], Chaudhary and Kanika [27] and Ghosh and Mukhopadhyay [28].

Fluid flow towards a stretching plate with heat and mass transfer has attracted the attention of researchers in various areas because of its applications in industries and engineering processes. Cooling of electronic components, designing of buildings, thermal insulation, fibre spinning, glass blowing and polymer sheets’ aerodynamic extrusion are the most useful applications of the stretching sheet flow. Moreover, this type of flow have promising considerations in the polymer plate extrusion by a die or in the plastic flows drawing. Mechanical characteristics of the final product stringently depend on the cooling and stretching rates in the procedure. Ariel [29] introduced the three-dimensional flow towards a stretched sheet. Additionally, Jat and Chaudhary [30], Turkyilmazoglu and Pop [31] and Weidman [32] studied the fluid flow due to the stretchable plate. In the last few decades, many researchers and scientists like Chaudhary et al [33] and Mahapatra and Sidui [34] showed the effects of stretching surface under different conditions.

Main focus of this article is the effect of SWCNT with water as the base fluid, steady MHD nanofluid flow past a stretched plate in the existence of heat generation and thermal radiation. The nanofluid flow is studied along with the effects of viscous dissipation and Joule heating. Further, the Galerkin finite-element method is applied to find numerical solution of the problem. The confirmation of parameters for the analysis is executed and authorised by comparing between previous and present results. It is elaborated that the results will award towards better compassionating of CNT–water nanofluid. At last the effects of specified parameters are computed and presented in graphical and tabular forms.

Fig. 1
figure 1

Physical sketch of the problem.

Full size image

2 Modelling

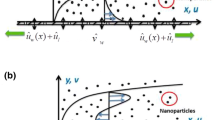
An electrically conducting incompressible, viscous SWCNT–water nanofluid towards a stretched surface along with the impacts of heat generation and thermal radiation is considered. The stretching velocity is taken as \(U_\mathrm {w}=ax\) and the velocity of free stream is assumed to be \(U_{\infty }=bx\), where a is a positive constant, b is the free stream parameter and x is the coordinate measured parallel to the sheet. \(T_\mathrm {w}\) and \(T_{\infty }\) are the wall temperature and the temperature of free stream respectively. In the normal direction of flow, a magnetic field of strength \(B_0\) is applied as shown in figure 1. The induced magnetic field is negligible because a very small magnetic Reynolds number is taken. By invoking the aforementioned assumptions, the governing equations for the present analysis can be given as (Bansal [35])

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y} =0 \end{aligned}$$
(1)
$$\begin{aligned}&u\frac{\partial u}{\partial x}+ v\frac{\partial u}{\partial y}=U_{\infty }\frac{\mathrm {d}U_{\infty }}{\mathrm {d}x}+\nu _{\mathrm {nf}}\frac{\partial ^{2}{u}}{\partial y^2}\nonumber \\&~~~~~~~~~~~~~~~~~~~~\quad -\frac{{(\sigma _e)_{\mathrm {nf}}}{{B_0^2}}}{\rho _{\mathrm {nf}}}{(u-U_{\infty })} \end{aligned}$$
(2)
$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha _{\mathrm {nf}} \frac{\partial ^{2}T }{\partial y^2}+\frac{Q_0}{({\rho }{C_\mathrm {p}})_{\mathrm {nf}}}(T-T_{\infty })\nonumber \\&~~~~~~~~~~~~~~~~~~~~\quad -\frac{1}{({\rho }{C_\mathrm {p}})_{\mathrm {nf}}}\frac{\partial q_\mathrm{r}}{\partial y}+\frac{\mu _{\mathrm {nf}}}{({\rho }{C_\mathrm {p}})_{\mathrm {nf}}}\left( \frac{\partial u}{\partial y}\right) ^{2}\nonumber \\&~~~~~~~~~~~~~~~~~~~~\quad +\frac{{(\sigma _e)_{\mathrm {nf}}}{B_{0}^{2}}}{({\rho }{C_\mathrm {p}})_{\mathrm {nf}}}{(u-U_{\infty })^2} \end{aligned}$$
(3)

with the corresponding boundary conditions

$$\begin{aligned}&y=0:\quad u=U_\mathrm{w},\quad v=0,\quad T=T_\mathrm {w} \nonumber \\&y\rightarrow \infty :\quad u\rightarrow U_\infty , \quad T \rightarrow T_\infty , \end{aligned}$$
(4)

where the subscript ‘nf’ stands for the nanofluid, u and v are the velocity factors parallel to the x- and y-axes respectively, \(\nu ={\mu }/{\rho }\) is the kinematic viscosity, \( \mu \) is the coefficient of viscosity, \( \rho \) is the density, \( \sigma _e\) is the electrical conductivity, T is the temperature of the nanofluid, \(\alpha ={\kappa }/{\rho C_\mathrm {p}} \) is the thermal diffusivity, \(\kappa \) is the thermal conductivity, \(C_\mathrm {p}\) is the specific heat at constant pressure, \(Q_0\) is the heat generation coefficient, \(q_\mathrm {r}=-({4\sigma ^*}/{3k^*})({\partial T^4}/{\partial y})\) is the radiative heat flux by the Rosseland approximation, \(\sigma ^*\) is the Stefan–Boltzmann constant and \(k^*\) is the mean absorption coefficient. The temperature difference in the flow can be expressed in a Taylor series about \(T_{\infty }\) neglecting higher order terms

$$\begin{aligned} T^4\cong 4{T_{\infty }^3}T-3{T_{\infty }^4}. \end{aligned}$$
(5)

Moreover, thermophysical characteristics of SWCNT–water nanofluid such as coefficient of viscosity, density, electrical conductivity, thermal conductivity and heat capacitance given by from Khalid et al [36] are mentioned as

$$\begin{aligned}&\frac{\mu _{\mathrm {nf}}}{\mu _{\mathrm {f}}}=\frac{1}{(1-\phi )^{5/2}}, \end{aligned}$$
(6)
$$\begin{aligned}&\frac{\rho _{\mathrm {nf}}}{\rho _{\mathrm {f}}} =1-\phi +\phi \frac{\rho _{\mathrm {CNT}}}{\rho _{\mathrm {f}}}, \end{aligned}$$
(7)
$$\begin{aligned}&\frac{(\sigma _e)_{\mathrm {nf}}}{(\sigma _e)_\mathrm {f}}\nonumber \\&\quad =1+\frac{3\phi \left\{ [(\sigma _e)_{\mathrm {CNT}}/{(\sigma _e)_\mathrm {f}}]-1\right\} }{\left[ ({(\sigma _e)_{\mathrm {CNT}}}/{(\sigma _e)_\mathrm {f}}) +2\right] -\phi \left[ ({(\sigma _e)_{\mathrm {CNT}}}/{(\sigma _e)_\mathrm {f}})-1\right] }, \end{aligned}$$
(8)
$$\begin{aligned}&\frac{\kappa _{\mathrm {nf}}}{\kappa _{\mathrm {f}}}=\frac{1-\phi +2\phi \frac{\kappa _{\mathrm {CNT}}}{\kappa _{\mathrm {CNT}}-\kappa _{\mathrm {f}}}\ln \frac{\kappa _{\mathrm {CNT}} +\kappa _{\mathrm {f}}}{2\kappa _{\mathrm {f}}}}{1-\phi +2\phi \frac{\kappa _{\mathrm {f}}}{\kappa _{\mathrm {CNT}}-\kappa _{\mathrm {f}}}\ln \frac{\kappa _{\mathrm {CNT}}+\kappa _{\mathrm {f}}}{2\kappa _{\mathrm {f}}}}, \end{aligned}$$
(9)
$$\begin{aligned}&\frac{(\rho C_\mathrm {p})_{\mathrm {nf}}}{(\rho C_\mathrm{p})_{\mathrm {f}}}=1-\phi +\phi \frac{(\rho C_\mathrm {p})_{\mathrm {CNT}}}{(\rho C_\mathrm {p})_{\mathrm {f}}}, \end{aligned}$$
(10)

where subscripts ‘f’ and ‘CNT’ indicate the fluid and carbon nanotubes respectively, and \(\phi \) is the solid volume fraction. Moreover, table 1 followed by Khalid et al [36] shows the values for the above-represented physical properties of the conventional fluid and CNTs.

Table 1 Values of material properties.
Full size table

3 Similarity variables

The following similarity variables are imported to convert the governing equations into ordinary differential equations as followed by Valipour et al [37]:

$$\begin{aligned}&\psi =(a\nu _{\mathrm {nf}})^{1/2}xf(\eta ),\quad \eta =\left( \frac{a}{\nu _{\mathrm {nf}}}\right) ^{1/2}y,\nonumber \\&T=T_{\infty }+(T_\mathrm {w}-T_{\infty })\theta (\eta ), \end{aligned}$$
(11)

where \( \psi (x,y) \) is the stream function, which is used in the usual manner as \( u={\partial \psi }/{\partial y} \) and \( v=-{\partial \psi }/{\partial x} \) and symmetrically satisfies the continuity equation (1), \( f(\eta ) \) is the dimensionless stream function, \( \eta \) is the similarity variable and \( \theta (\eta ) \) is the dimensionless temperature.

Substituting the dimensionless similarity variables equation (11) into eqs (2)–(4) gives

$$\begin{aligned}&f^{\prime \prime \prime }+ff^{\prime \prime }-f^{\prime 2}\nonumber \\&\quad -\frac{1}{E_1}\frac{(\sigma _e)_{\mathrm {nf}}}{(\sigma _e)_\mathrm {f}}M(f^{\prime }-\lambda )+{\lambda }^2=0 \end{aligned}$$
(12)
$$\begin{aligned}&E_1E_2\left( \frac{\kappa _{\mathrm {nf}}}{\kappa _\mathrm {f}}+Nr\right) \theta ^{\prime \prime }+E_3{\mathrm {Pr}}f\theta ^{\prime }+\mathrm {Pr} S\theta \nonumber \\&\quad +E_1\mathrm {Br}\left[ f^{{\prime \prime }2}+\frac{1}{E_1}\frac{(\sigma _e)_{\mathrm {nf}}}{(\sigma _e)_{\mathrm {f}}}M{(f^{\prime }-\lambda )}^2\right] =0 \end{aligned}$$
(13)

with the transformed boundary conditions

$$\begin{aligned}&\eta =0{:} \, f=0,\quad f^{\prime }=1,\quad {\theta }=1,\nonumber \\&\eta \rightarrow \infty {:}\, f^{\prime }\rightarrow \lambda ,\quad \theta \rightarrow 0, \end{aligned}$$
(14)

where prime (\(\prime \)) represents the differentiation with respect to \( \eta \), \(E_1=1-\phi +\phi ({\rho _{\mathrm {CNT}}}/{\rho _\mathrm {f}})\), \(E_2=(1-\phi )^{5/2}\), \(E_3=1-\phi +\phi [{(\rho C_\mathrm {p})_{\mathrm {CNT}}}/{(\rho C_\mathrm {p})_\mathrm {f}}]\), \( M={(\sigma _e)_{\mathrm {f}}{B_0^2}}/{a\rho _\mathrm {f}}\) is the magnetic parameter, \(\lambda ={b}/{a}\) is the velocity ratio parameter, \(Nr={16\sigma ^*T_{\infty }^{3}}/{3k^*\kappa _{\mathrm {f}}}\) is the radiation parameter, \(\hbox {Pr}={\nu _\mathrm {f}}/{\alpha _\mathrm {f}} \) is the Prandtl number, \(S={Q_0}/{a(\rho C_\mathrm {p})_\mathrm {f}}\) is the heat generation parameter and Br\(\, ={\nu _\mathrm {f}{U_{\mathrm {w}}^2}}/[{\alpha _\mathrm {f}(C_\mathrm {p})_\mathrm {f}(T_\mathrm {w}-T_{\infty })]} \) is the Brinkmann number.

4 Physical quantities of primary interest

The local skin friction coefficient \((C_\mathrm {f}\)) and the local Nusselt number (Nu\(_x\)) at the wall are defined as

$$\begin{aligned}&C_\mathrm {f}=\frac{\mu _{\mathrm {nf}}\left( {\partial u}/{\partial y}\right) _{y=0}}{{\rho _\mathrm {f} {U_\mathrm {w}^2}}/{2}},\nonumber \\&\mathrm {Nu}_x = \frac{x\left[ -\kappa _{\mathrm {nf}}({\partial T}/{\partial y})+q_\mathrm{r}\right] _{y=0}}{\kappa _\mathrm {f}(T_\mathrm {w}-T_{\infty })}. \end{aligned}$$
(15)

By applying the non-dimensional variable equation (11), eq. (15) can be given as

$$\begin{aligned}&{\mathrm {Re}_x^{1/2}}C_\mathrm {f} =2\left( \frac{E_1}{E_2}\right) ^{1/2}f^{\prime \prime }(0),\nonumber \\&\frac{1}{{\mathrm {Re}_x^{1/2}}}{\mathrm {Nu}_x}=-\left( E_1E_2\right) ^{1/2}\left( \frac{\kappa _{\mathrm {nf}}}{\kappa _{\mathrm {f}}}+Nr\right) \theta ^{\prime }(0), \end{aligned}$$
(16)

where Re\(_x={U_\mathrm {w} {x}}/{\nu _\mathrm {f}} \) is the local Reynolds number.

5 Numerical method for the solution

An authoritative technique like Galerkin finite-element method is used to solve the ordinary differential equations (12) and (13) along with boundary condition equation (14). In this scheme, the whole region is split into smaller finite-dimensional elements. This numerical technique is the most adaptable in the studies of diverse analysis of fluid mechanics, electrical system, solid mechanics and heat transfer. Assuming

$$\begin{aligned} f^{\prime }=g \end{aligned}$$
(17)

then eqs (12) and (13) are reduced to

$$\begin{aligned}&g^{\prime \prime }+fg^{\prime }-g^{2}\nonumber \\&\quad -\frac{1}{E_1} \frac{(\sigma _e)_{\mathrm {nf}}}{(\sigma _e)_\mathrm {f}}M(g-\lambda )+{\lambda }^2=0 \end{aligned}$$
(18)
$$\begin{aligned}&E_1E_2\left( \frac{\kappa _{\mathrm {nf}}}{\kappa _\mathrm {f}}+Nr\right) \theta ^{\prime \prime }+E_3{\mathrm {Pr}}f\theta ^{\prime }\nonumber \\&\quad +\mathrm {Pr} S\theta +E_1\mathrm {Br}\left[ g^{{\prime }2}+\frac{1}{E_1}\frac{(\sigma _e)_{\mathrm {nf}}}{(\sigma _e)_{\mathrm {f}}}M{(g-\lambda )}^2\right] =0\nonumber \\ \end{aligned}$$
(19)

and the associated boundary conditions become

$$\begin{aligned}&\eta =0{:}\, f=0,\quad g=1,\quad {\theta }=1,\nonumber \\&\eta \rightarrow \infty {:}\, \, g\rightarrow \lambda ,\quad \theta \rightarrow 0. \end{aligned}$$
(20)

For the computational process, \(\eta \rightarrow \infty \) is shifted to \(\eta =5\), without any loss of generalisation and the domain is split into 1000 linear elements, while every element has two nodes.

The variational formulation correlated with eqs (17)–(19) along a typical linear element \((\eta _{e}, \eta _{e+1})\) is given by

$$\begin{aligned}&\int _{\eta _e}^{\eta _{e+1}}w_{1}(f^{\prime }-g)\,\mathrm {d}\eta =0, \end{aligned}$$
(21)
$$\begin{aligned}&\int _{\eta _e}^{\eta _{e+1}}w_{2}\left[ g^{\prime \prime }+fg^{\prime }-g^{2}\right. \nonumber \\&\quad \left. -\,\frac{1}{E_1}\frac{(\sigma _e)_{\mathrm {nf}}}{(\sigma _e)_\mathrm {f}}M(g-\lambda )+{\lambda }^2\right] \,\mathrm {d}\eta =0, \end{aligned}$$
(22)
$$\begin{aligned}&\int _{\eta _e}^{\eta _{e+1}}w_{3}\left\{ E_1E_2\left( \frac{\kappa _{\mathrm {nf}}}{\kappa _\mathrm {f}}+Nr\right) \theta ^{\prime \prime }\right. \nonumber \\&\quad \left. +\,E_3{\mathrm {\mathrm {Pr}}}f\theta ^{\prime }+\mathrm {Pr} S\theta \right. \nonumber \\&\quad \left. +\,E_1\mathrm {Br}\left[ g^{{\prime }2}+\frac{1}{E_1}\frac{(\sigma _e)_{\mathrm {nf}}}{(\sigma _e)_{\mathrm {f}}}M{(g-\lambda )}^2\right] \right\} \mathrm {d}\eta =0,\nonumber \\ \end{aligned}$$
(23)

where \(w_{1}\), \(w_{2}\) and \(w_{3}\) are weight functions and can be viewed as the variations in f, g and \(\theta \) respectively.

The finite-element approximations of the functions f, g and \(\theta \) are considered as

$$\begin{aligned} \begin{aligned}&f=\sum _{j=1}^{2}{f_{j}\varphi _{j}},\quad g=\sum _{j=1}^{2}g_j\varphi _j,\quad \theta =\sum _{j=1}^{2}{\theta _{j}\varphi _{j}}\quad \\&\text {with}\;\\ {}&w_{1}=w_{2}=w_{3}=\varphi _{i}\;(i=1,2), \end{aligned} \end{aligned}$$

where \(\varphi _i\) are the shape functions for a typical linear element \((\eta _e, \eta _{e +1})\) and are summarised as

$$\begin{aligned}&\varphi _{1}^{(e)}=\frac{\eta _{e+1}-\eta }{\eta _{e+1}-\eta _{e}},\\&\varphi _{2}^{(e)} =\frac{\eta -\eta _{e}}{\eta _{e+1}-\eta _{e}},\quad \eta _{e}\leqslant \eta \leqslant \eta _{e+1}. \end{aligned}$$
Table 2 Comparison of values of \(f^{\prime \prime }(0)\) and \(\theta ^{\prime }(0)\) between the previous studies and the present study for different values of \(\lambda \) when \(\phi =M=Nr=0\), \(\mathrm{Pr}=1\), \(S=0\) and \(\mathrm{Br}=0\).
Full size table

The finite-element model of eqs (21)–(23) is given by

$$\begin{aligned} \begin{bmatrix} [H^{11}] &{} \quad [H^{12}] &{}\quad [H^{13}]\\ [H^{21}] &{}\quad [H^{22}] &{}\quad [H^{23}]\\ [H^{31}] &{}\quad [H^{32}] &{}\quad [H^{33}] \end{bmatrix} \begin{bmatrix} \{f\}\\ \{g\}\\ \{\theta \} \end{bmatrix} = \begin{bmatrix} \{b^{1}\}\\ \{b^{2}\}\\ \{b^{3}\} \end{bmatrix}, \end{aligned}$$
(24)

where \([H^{mn}]\) and \([b^m]\) \((m= 1,2\; \mathrm {and}\; n= 1,2)\) are given as

$$\begin{aligned}&H_{ij}^{11}=\int _{\eta _e}^{\eta _{e+1}}\varphi _{i}\frac{\mathrm {d}\varphi _j}{\mathrm {d}\eta }\mathrm {d}\eta ,\\&H_{ij}^{12}=-\int _{\eta _e}^{\eta _{e+1}}\varphi _{i}\varphi _{j}\,\mathrm {d}\eta ,\\&H_{ij}^{13}=0,\\&H_{ij}^{21}=0,\\&H_{ij}^{22}=\int _{\eta _e}^{\eta _{e+1}}\left\{ -\frac{\mathrm {d}\varphi _{i}}{\mathrm {d}\eta }\frac{\mathrm {d}\varphi _{j}}{\mathrm {d}\eta }+\bar{f} \varphi _i \frac{\mathrm {d}\varphi _j}{\mathrm {d}\eta }\right. \\&\quad ~~~~\left. -\left[ \bar{g}+\frac{1}{E_1}\frac{(\sigma _e)_{\mathrm {nf}}}{(\sigma _e)_\mathrm {f}}M\right] \varphi _i\varphi _j\right\} \mathrm {d}\eta ,\\&H_{ij}^{23}=0,\\&H_{ij}^{31}=0,\\&H_{ij}^{32}=\int _{\eta _{e}}^{\eta _{e+1}}\left[ E_1\mathrm {Br} \bar{g}\varphi _i \frac{\mathrm {d}\varphi _j}{\mathrm {d}\eta }\right. \\&\quad ~~~~~~~~ \left. +\frac{(\sigma _e)_{\mathrm {nf}}}{(\sigma _e)_\mathrm {f}}M\mathrm {Br}(\bar{g}-2\lambda )\varphi _i\varphi _j\right] \mathrm {d}\eta ,\\&H_{ij}^{33}=\int _{\eta _e}^{\eta _{e+1}}\left\{ -E_1E_2\left( \frac{\kappa _{\mathrm {nf}}}{\kappa _\mathrm {f}}+Nr\right) \frac{\mathrm {d}\varphi _{i}}{\mathrm {d}\eta }\frac{\mathrm {d}\varphi _{j}}{\mathrm {d}\eta }\right. \\&\quad ~~~~~~~~ \left. +E_3\mathrm {Pr}\bar{f} \varphi _i \frac{\mathrm {d}\varphi _j}{\mathrm {d}\eta }+\mathrm {Pr} S\varphi _i\varphi _j\right\} \mathrm {d}\eta ,\\&b_{i}^{1}=0,\\&b_{i}^{2}=-\left( \varphi _i\frac{\mathrm {d}g}{\mathrm {d}\eta }\right) _{\eta _{e}}^{\eta _{e+1}}\\&\quad ~~~+\int _{\eta _{e}}^{\eta _{e+1}}\left[ \frac{1}{E_1}\frac{(\sigma _e)_{\mathrm {nf}}}{(\sigma _e)_\mathrm {f}}M\lambda +{\lambda }^2\right] \varphi _i \,\mathrm {d}\eta \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} b_{i}^{3}=&E_1E_2\left( \frac{\kappa _{\mathrm {nf}}}{\kappa _\mathrm {f}} +Nr\right) \left( \varphi _i\frac{\mathrm {d}\theta }{\mathrm {d}\eta }\right) _{\eta _{e}}^{\eta _{e+1}}\\&+\int _{\eta _{e}}^{\eta _{e+1}} \frac{(\sigma _e)_{\mathrm {nf}}}{(\sigma _e)_\mathrm {f}}M\mathrm {Br}{\lambda }^2\varphi _i \,\mathrm {d}\eta \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \bar{f}=\sum _{i=1}^{2}{\bar{f_i}\varphi _i},\quad \bar{g}=\sum _{i=1}^{2}{\bar{g_i}\varphi _i}. \end{aligned}$$

The entire flow region is partitioned into 1000 linear elements of equal size. Every element is two-nodded and three functions can be evaluated at each node. So a matrix of order \( 3003\times 3003 \) is found after assembling all element equations. For solving the system, an iterative scheme must be applied. After imposing the boundary conditions, a set of 2998 equations remain, which are solved by using the Newton–Raphson method while maintaining an accuracy of \( 10^{-7} \).

6 Validation of computational algorithm

The achieved data of the present investigation are compared with those of Mahapatra and Gupta [38] for different values of \(\lambda \) in non-magnetic case that can be observed in table 2. The comparison indicates that the numerical results in this study are highly accurate and acceptable.

7 Discussion of physical outcomes

After finding the solutions of the governing equations of the present study with the Galerkin finite-element method, effects of \(\lambda \), \(\phi \), M, Nr, S and Br on the velocity (\(f^{\prime }(\eta ))\) and the temperature (\(\theta (\eta ))\) distributions for the SWCNT–water nanofluid are shown in graphical forms. Also the influences of variable parameters on the surface shear stress \((f^{\prime \prime }(0)\)) and the surface heat flux \((\theta ^{\prime }(0)\)) are presented in table form in SWCNT–water nanofluid. Further, to find the effect of a specified parameter, the remaining controlling parameters are taken as constants.

Ascending changes in \(\lambda \) on \(f^{\prime }(\eta )\) and \(\theta (\eta )\) are shown in figures 2 and 3 respectively. Observations indicate that the fluid velocity increases by rising \(\lambda \), whereas opposite phenomenon can be seen in temperature field. If the velocity of free stream is greater than the stretching velocity, then retarding force reduces. So the fluid velocity increases and the fluid temperature decreases.

Fig. 2
figure 2

Variation of velocity by enhancing \(\lambda \) when \(\phi =0.07\) and \(M=0.1\).

Full size image
Fig. 3
figure 3

Variation of temperature by enhancing \(\lambda \) when \(\phi \,{=}\,0.07\), \(M\,{=}\,0.1\), \(Nr\,{=}\,1\), \(\mathrm{Pr} \,{=}\,6.2\), \(S\,{=}\,0.1\) and \(\mathrm{Br}\,{=}\,1\).

Full size image
Fig. 4
figure 4

Variation of velocity by enhancing \(\phi \) when \(\lambda =0.2\) and \(M=0.1\).

Full size image
Fig. 5
figure 5

Variation of temperature by enhancing \(\phi \) when \(\lambda =0.2\), \(M=0.1\), \(Nr=1\), \(\mathrm{Pr}=6.2\), \(S=0.1\) and \(\mathrm{Br}=1\).

Full size image

Figures 4 and 5 demonstrate the effects of \(\phi \) on \(f^{\prime }(\eta )\) and \(\theta (\eta )\) respectively. An increment in the value of \(\phi \) causes negligible change in the momentum boundary layer. Further, thermal boundary layer thickness increases due to the increase in \(\phi \) value. It occurs because an enhancement in volume fraction of solids leads to enhancement in \(\kappa \) of the nanofluid. But as SWCNTs are suspended as nanoparticles in the base fluid, there is no effect in fluid velocity.

Fig. 6
figure 6

Variation of velocity by enhancing M when \(\lambda =0.2\) and \(\phi =0.07\).

Full size image
Fig. 7
figure 7

Variation of temperature by enhancing M when \(\lambda =0.2\), \(\phi =0.07\), \(Nr=1\), \(\mathrm{Pr}=6.2\), \(S=0.1\) and \(\mathrm{Br}=1\).

Full size image

\(f^{\prime }(\eta )\) and \(\theta (\eta )\) fields are sketched in figures 6 and 7 respectively for several values of M. It can be noted from these figures that an increment in M reduces \(f^{\prime }(\eta )\) and enhances \(\theta (\eta )\) because the increase in M generates Lorentz force which gives resistance to the flow. This causes fall in \(f^{\prime }(\eta )\). This in turn causes enlargement of \(\theta (\eta )\).

Fig. 8
figure 8

Variation of temperature by enhancing Nr when \(\lambda =0.2\), \(\phi =0.07\), \(M=0.1\), Pr \(=6.2\), \(S=0.1\) and Br \(=1\).

Full size image

Figure 8 plots the behaviour of \(\theta (\eta )\) distribution under the influence of Nr. This figure shows that the thermal boundary layer enlarges as Nr increases. This is due to the fact that huge heat transformation in the occupied fluid causes increase in temperature of the fluid.

Fig. 9
figure 9

Variation of temperature by enhancing S when \(\lambda =0.2\), \(\phi =0.07\), \(M=0.1\), \(Nr=1\), Pr \(=6.2\) and Br \(=1\).

Full size image

Behavior of \(\theta (\eta )\) for various values of S is demonstrated in figure 9. This figure shows that as S increases, the temperature of the fluid increases. This is because there is greater flow towards the surface due to the thermal buoyancy effect.

Fig. 10
figure 10

Variation of temperature by enhancing Br when \(\lambda =0.2\), \(\phi =0.07\), \(M=0.1\), \(Nr=1\), Pr \(=6.2\) and \(S=0.1\).

Full size image
Table 3 Numerical values of \(f^{\prime \prime }(0) \) and \( \theta ^{\prime }(0) \) for various values of the specified parameters for SWCNT–water nanofluid when Pr \(=6.2\).
Full size table

Figure 10 presents the variation in \(\theta (\eta )\) under the influence of Br. This figure shows that the thermal boundary layer increases with the enhancement in Br, because viscous dissipation influences the flow area to increase the energy, thereby causing higher temperature of the fluid and higher buoyancy force.

The roles of \(\lambda \), \(\phi \), M, Nr, S and Br on \(f^{\prime \prime }(0)\) and \(\theta ^{\prime }(0)\) are addressed in table 3. Accordingly, \(C_\mathrm {f}\) increases and Nu\(_x\) decreases with a step-up of \(\lambda \), while reversed scenario is found for \(\phi \) and M. Subsequently, the surface heat flux evolves over to the increasing values of Nr, S and Br. From the practical point of view, the negative values of the shear stress and the heat transfer rate for all values of the associated parameters are the reason that fluid utilises a drag force from the surface and heat flow on the surface respectively.

8 Conclusions

In the present investigation, radiation heat transfer and MHD flow of SWCNT–water nanofluid along a stretched surface under the influence of heat generation have been examined by Galerkin finite-element scheme. Some main consequences are noted as follows:

  • It is observed that speed of the flow as well as \(C_\mathrm {f}\) increase when \(\lambda \) increases, although \(\theta (\eta )\) as well as the rate of heat transfer decline due to increment in \(\lambda \). However, reversal impact is found in the velocity, temperature, \(f''(0)\) and \(\theta '(0)\) for increasing values of M.

  • Negligible effect is found in the momentum boundary layer due to the rising values of \(\phi \). Further, increasing \(\phi \) tends to reduce \(f''(0)\) and increase the thermal boundary layer thickness and \(\theta '(0)\).

  • On the other hand, \(\theta (\eta )\) and Nu\(_x\) increase with the increase in Nr, S and Br.