1 Introduction

Uncertainties and nonlinearities have been studied extensively in systems and control theory. Among them, models that involve the input’s time derivatives present considerable challenge. Such dynamics appear in various applications such as cranes [1], cars with trailers [1], piezoelectric actuators [2], capacitor loops connected with voltage sources [3], inductor cut-sets connected with current sources [3], transducers in setting the reference inputs [3], active suspension systems with vibration control [3], descriptor variable systems [3], flat systems [1], and biological processes [4]. Controlling such models is challenging since they do not directly conform to the conventional state-space models, and inputs are not independent. Even if the input derivatives are alternated with state variables [3, 5, 6], this method faces two problems. First, these added states lead to the added controller complexity and its stability analysis. Second, as state variables describe the system behavior without external forces affecting the system, alternating the input derivatives with the states leads to less physical interpretation. Alternatively, directly handling such dynamics could be a valuable framework for such a problem, but few works have addressed it.

There are considerably fewer works on controlling the mentioned dynamics without converting to the conventional state-space form. Among the few, Zhang et al. offered indirect and direct adaptive first-order Takagi–Sugeno (TS) fuzzy controllers with state observers for models affine with the input and its first derivative [7, 8]. The fuzzy systems were used to estimate three unknown nonlinear functions. They later showed that converting the nonaffine nonlinear pure feedback dynamics to a form with the input derivative and input–output nonlinear relationships might also reach better tracking and avoid the backstepping structure with virtual inputs [9]. Furthermore, the work of [10] simplified the mentioned method through a low-pass filter driven by a control input. However, the mentioned papers only studied systems with the first-order derivative of the input.

TS fuzzy approaches have been developed over the past 30 years, particularly following the seminal works of Wang. As mentioned before, there are only four references on TS fuzzy approaches of uncertain nonlinear systems with the time derivative of the input. However, no fuzzy controller exists on unknown nonlinear systems, including higher-order input derivatives. In other words, to study a broader range of existing systems, we consider uncertain nonlinear systems, where the order of input derivatives is extended, and the model is nonaffine in the input and its derivatives. The aim is to design a simpler and more robust controller for handling different categories of uncertainties. As a result, we propose an observer-based \({H}_{\infty }\) indirect adaptive zero-order TS fuzzy controller (\(\hbox {OH}_{\infty }\)IAZTSFC). In other words, the investigation’s contributions are as follows:

  • To study a broader range of existing systems, we consider uncertain nonlinear systems, where the input derivatives are extended to mth order and the model is nonaffine in not only u but also \(\dot{u}\),\(\ldots\),\(u^{(m-1)}\).

  • We propose zero-order TS fuzzy systems, whose inputs are the states, the dynamical system input, and its derivatives, to improve transparency and simplicity and reduce the amount of online adjustable parameters.

  • We propose a \({H}_\infty\) controller and a compensation control for such augmented systems to guarantee asymptotic stability and improve robustness under uncertainties.

  • We avoid solving the Riccati equation to define the \({\varvec{P}}\) matrix and \({\varvec {B_c}}\) vector in adaptive rules.

Note that the proposed method lowers tracking errors, observer errors, adjustable parameters, and consumed energies, besides improving the convergence speed under realistic uncertainties, such as unmeasured states, disturbances, measurement noise, data loss, and dead-zone.

This paper contains the following sections. Section 2 includes research in different categories. Section 3 describes the dynamics. Section 4 explains the proposed methodology. Section 5 investigates stability and convergence. Section 6 demonstrates the simulation results compared with a recent competing approach. Ultimately, Sect. 7 provides the conclusions.

Notation The superscripts “T” and “-1” show the transposition and inverse, respectively. \(R^n\) denotes n-dimensional Euclidean space. \(\Vert .\Vert\) indicates the Euclidean norm, \(\Vert A\Vert ^2_B\) means \(A^T BA\) and \(\mid .\mid\) shows the absolute value. For any derivable signal such as u, \(\dot{u}\) is the first derivative, \(\ddot{u}\) is the second derivative, and \(u^{(m)}\) is the mth derivative. For any ideal C, \(C^*\) is the optimization, \({\hat{C}}\) is the estimation, and \({\tilde{C}}=C-{\hat{C}}\). Besides that, \(D^{'}=L^{-1}(s)D\) for any D.

2 Related Works

Fuzzy logic systems (FLSs) have universal approximation properties [11] to handle uncertainties. The literature is abundant, with excellent examples of applying fuzzy logic to control complex systems. One may refer to some seminal works, such as by Mamdani in 1975 [12], which was improved by online adaptive rules [13] and observer design [14] to handle model and external uncertainties. Recently, the observer-based adaptive fuzzy approach was developed to control different types of nonlinear systems, such as stochastic systems [15], fractional-order systems [16], large-scale systems [17], multi-agent systems [18], strict-feedback systems [19], nonstrict-feedback systems [20], rigorous feedback cascade systems [21], singular systems [22], stochastic systems [23], switched systems [24], nontriangular systems [25], and networked systems [26]. As a result, even the more recent works on fuzzy control generally assume the nonlinear systems in the standard and conventional state-space models.

\({H}_{\infty }\) analysis [27] has been merged into the fuzzy controllers to improve robustness and semi-global stabilization. The fruitful results occur by attenuating the errors and the influence of environmental effects on an arbitrary level [28]. A combined observer-based \({H}_{\infty }\) adaptive fuzzy approach is an excellent candidate for creating a comprehensible controller. For instance, an \({H}_{\infty }\) controller with a PD form was employed in [29] for stable and robust tracking in the indirect adaptive fuzzy method. In [30], the composite learning based on a serial–parallel identifier promoted the mentioned combined method. The \({H}_{\infty }\) controller compensated the residual errors of the fuzzy system and the observer to the desired level. In [31], an \({H}_{\infty }\)-\({H}_2\) strategy enhanced the trade-off between energy consumption and control performances. In [32], an adaptive event-triggered scheme reduced resource consumption and output variation. A networked TS fuzzy filter improved the design flexibility, guaranteeing stability with the desired \({H}_{\infty }\) disturbance attenuation performance. Falla-Gh [33] considered the \({H}_{\infty }\) controller to compensate uncertainties for different nonlinear systems in an adaptive fuzzy method. However, the strategies mentioned above focused on nonlinear systems with conventional state-space representation without any input derivates.

3 Problem Description

Consider nth-order unknown nonlinear systems with mth-order input derivatives and nonlinear input–output relationships as

$${\left\{ \begin{array}{ll} {\dot{x}}_i=x_{i+1},\quad \; 1\le {i}\le {n-1},\\ {\dot{x}}_n=f({\varvec{x}},u,{\dot{u}},\ldots ,u^{(m-1)})+g({\varvec{x}},u,{\dot{u}},\ldots \\,u^{(m-1)})u^{(m)}+d(t),\\ y=x_1, \end{array}\right. }$$
(1)

where \({\varvec{x}}=(x_1,x_2,\ldots ,x_n )^{T}=(x,{\dot{x}},\ldots ,x^{n-1}) ^{T}\in {R^{n}}\) is the unavailable state vector of the plant, f(.) and g(.) are the unknown nonlinear functions, \(y\in {R}\) is the output of the system, \(u\in {R}\) is the system input to which its derivatives also contribute, and d(t) is the unknown external disturbance. Because of the appearance of the derivatives of u in the dynamic equations, (1) does not have the conventional state-space representation. f(.) and g(.) relate to \({\varvec{u}}=(u,\dot{u},\ldots ,u^{(m-1)})\); which causes the nonlinearity of the input–output relationship.

Equation (1) is represented in the following form by \({\varvec {A_0}}= \begin{bmatrix} 0 &{} 1 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} 1 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 1 \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 \end{bmatrix}\), \({\varvec{B}}= \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{bmatrix}\), and \({\varvec{C}}= \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \\ 0 \end{bmatrix}\):

$${\left\{ \begin{array}{ll} \dot{{\varvec{x}}}&{}={\varvec {A_0}}{\varvec{x}}+{\varvec{B}}\big (f({\varvec{x}},{\varvec{u}})+g({\varvec{x}},{\varvec{u}})u^{(m)}+d\big ),\\ y&{}={\varvec{C}}^T. \end{array}\right. }$$
(2)

Assumption 1

f(.) and g(.) are unknown, nonlinear, bounded, smooth, and continuous functions for \({\varvec{x}}\in {R^n}\) and \({\varvec{u}}\in R^m\). It is assumed that \(0<|f(.)|\le {F^U}\), where \(F^U\) is an unknown upper bound of f(.). As the system (1) should be controllable, \(g^{-1}(.)\) exists which means \(g(.)\ne {0}\). There are unknown constants \(G_L\) and \(G^U\) such that \(0<{G_L}\le {|g(.)|}\le {G^U}\), where \(G_L\) and \(G^U\) show the lower and upper bound, respectively.

Assumption 2

u(t) is a continuous input which is m-times differentiable.

Assumption 3

\(y_d(t)\) is the reference signal which is n-times differentiable, bounded, smooth, and known.

Assumption 4

d(t) is the unknown bounded disturbance, i.e., \(|d|\le {D}\) and D is the unknown upper bound.

Control Objectives This paper’s main goals are to track the reference trajectory and to achieve high robustness against uncertainties, whereas all signals involved are bounded.

4 Proposed Controller Design

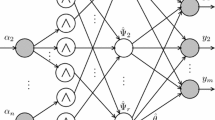
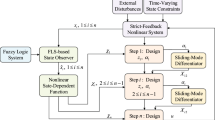
Figure 1 shows the proposed method of this section.

4.1 Proposed Adaptive Fuzzy Controller

By knowing f(.), g(.), and all the elements of \({\varvec{x}}\) with \(d(t)=0\), we propose the control law for the maximal order of the input derivatives as

$$\begin{aligned} u^{*^{(m)}}(t)=&\frac{1}{g({\varvec{x}},{\varvec{u}}^*)}\Big [-f({\varvec{x}},{\varvec{u}}^*)+y_m^{(n)}(t)+{\varvec{K}}^T{\varvec{e}}\Big ], \end{aligned}$$
(3)

where \({\varvec{u}}^*=\left( u^*,\dot{u}^*,\ldots ,u^{*^{(m-1)}}\right)\), \({\varvec{e}}=[e,{\dot{e}},\ldots ,e^{n-1}]^T\) , \(e=y_d-y\) is the tracking error, \({\varvec{K}}=[k_n,k_{n-1},\ldots ,k_1]^T\) which yields all roots of \(s^n+k_1s^{n-1}+\cdots +k_n=0\) in the open left half of the complex s-plane and guarantees \({\varvec {A_1}}={\varvec {A_0}}-{\varvec{B}}{\varvec{K}}^T\) to be strictly Hurwitz in Lyapunov equation as

$$\begin{aligned} ({\varvec {A_0}}-{\varvec{B}}{\varvec{K}}^T)^T{\varvec {P_0}}+{\varvec {P_0}}({\varvec {A_0}}-{{\varvec{B}}}{\varvec{K}}^T)=-{\varvec {Q_0}}, \end{aligned}$$
(4)

where \({\varvec {P_0}}\) and \({\varvec {Q_0}}\) are positive definite matrices.

Substituting (3) into (1), the closed-loop control system is given as

$$\begin{aligned} e^{(n)}+k_1e^{(n-1)}+\cdots +k_ne=0, \end{aligned}$$
(5)

where it means e converges to zero as \({t\rightarrow \infty }\).

Fig. 1
figure 1

Scheme of the proposed \(\hbox {OH}_\infty\)IAZTSFC method

Full size image

Unfortunately, f(.) and g(.) are unknown, all the states are not available, and the disturbances exist in real applications. Therefore, FLSs are used for the estimation.

Lemma 1

[11] FLS can approximate any continuous function on a compact set.

We use zero-order TS FLSs to identify the unknown functions in the dynamical system such that the adaptive laws adjust the fuzzy controller parameters based on the Lyapunov synthesis approach. We describe the lth rule as

$$\begin{aligned}&\text{ IF }\;\hat{x}_1\,\text{ is }\,A^l_1\,\text{ and }\,\hat{x}_2\,\text{ is }\,A^l_2\,\text{ and }\cdots \text{ and }\,\hat{x}_n\,\text{ is }\,A^l_n\,\text{ and }\, \\&u\,\text{ is }\,B^l_1\, \text{ and }\,{\dot{u}}\,\text{ is }\, B^l_2\, \text{ and }\cdots \text{ and }\,u^{(m-1)}\,\text{ is }\,B^l_m\,;\\&\text{ THEN }\; y_l=a^l, \end{aligned}$$

where \(l=(1,\ldots ,M)\), M is the number of rules; \({\hat{\varvec{x}}}=[{\hat{x}}_1,{\hat{x}}_2,\ldots ,{\hat{x}}_n]^T\) is the estimation of \({\varvec{x}}=[x_1,x_2,\ldots ,x_n]^T\) based on the observer design; \({\hat{\varvec{x}}}\) and \({\varvec{u}}\) are the fuzzy inputs; \(A_i^l\) is the fuzzy set of \(\hat{x}_i\), \(i=1,\ldots ,n\); \(B_{i^\prime }^l\) is the fuzzy set of \(u^{({i^\prime }-1)}\), \(i^\prime =1,\ldots ,m\); \(y_l\) is the output of lth rule; and \(a^l\) is the constant coefficient of the lth output function.

The FLS’s output is obtained as

$$\begin{aligned} y&={\frac{\displaystyle \sum\nolimits_{l=1}^M y_l\displaystyle \prod\nolimits_{i=1}^n \exp \left(-\left(\frac{{\hat{x}}_i - \bar{x}_i^l}{\delta _{1,i}^l}\right)^2\right)\displaystyle \prod\nolimits_{i^\prime =1}^m \exp \left(-\left(\frac{{u}^{(i^\prime -1)} - \bar{u}_{i^\prime }^l}{\delta _{2,i^\prime }^l}\right)^2\right)}{\displaystyle \sum\nolimits_{l=1}^M \displaystyle \prod\nolimits_{i=1}^n \exp \left(-\left(\frac{\hat{x}_i - \bar{{x}}_i^l}{\delta _{i}^l}\right)^2\right)\displaystyle \prod\nolimits_{i^\prime =1}^m \exp \left(-\left(\frac{{u}^{(i^\prime -1)} - \bar{u}_{i^\prime }^l}{\delta _{2,i^\prime }^l}\right)^2\right)}} \nonumber \\&=\theta ^T \, \xi ({{\hat{\varvec{x}}}},{\varvec{u}}), \end{aligned}$$
(6)

and

$$\begin{aligned} \begin{array}{c} \displaystyle \theta =\left( a^1,a^2,\ldots ,a^M \right) ^T,\\ \displaystyle \xi ({{\hat{\varvec{x}}}},{\varvec{u}})=[\xi _1,\xi _2,\ldots ,\xi _M]^T,\\ \displaystyle \xi _l= {\frac{\displaystyle \prod\nolimits _{i=1}^n \exp \left(-\left(\frac{{{\hat{x}}}_i-\bar{{x}}_i^l}{\delta _{1,i}^l}\right)^2\right)\displaystyle \prod\nolimits _{i^\prime =1}^m \exp \left(-\left(\frac{{u}^{(i^\prime -1)} - \bar{u}_{i^\prime }^l}{\delta _{2,i^\prime }^l}\right)^2\right)}{\displaystyle \sum\nolimits _{l=1}^M \displaystyle \prod\nolimits _{i=1}^n \exp \left(-\left(\frac{{{\hat{x}}}_i-\bar{{x}}_i^l}{\delta _{1,i}^l}\right)^2\right)\displaystyle \prod\nolimits _{i^\prime =1}^m \exp \left(-\left(\frac{{u}^{(i^\prime -1)} - \bar{u}_{i^\prime }^l}{\delta _{2,i^\prime }^l}\right)^2\right)}}, \end{array} \end{aligned}$$
(7)

where the fuzzifier is singleton, the membership functions are Gaussian with the center \(\bar{x}_i^l\) and the width \(\delta _{1,i}^l\) for \({{\hat{x}}}_i\) and also with the center \(\bar{u}_{i^ \prime }^l\) and the width \(\delta _{2,i^\prime }^l\) for \(u^{(i^\prime -1)}\), the inference engine is product, and the defuzzifier is center-average.

Therefore, f(.) and g(.) are approximated as

$$\begin{aligned} \begin{array}{c} \hat{f}(\hat{{\varvec{x}}},{\varvec{u}}|\theta _f)=\theta _f^T\xi _f(\hat{{\varvec{x}}},{\varvec{u}}),\\ \hat{g}(\hat{{\varvec{x}}},{\varvec{u}}|\theta _g)=\theta _g^T\xi _g(\hat{{\varvec{x}}},{\varvec{u}}), \end{array} \end{aligned}$$
(8)

where \(\xi _f\), \(\xi _g\) are the fuzzy basis function vectors, and \(\theta _f\), \(\theta _g\) are the adjustable parameters vectors.

Definition 1

The optimal parameters’ vectors are described as

$$\begin{aligned} \begin{array}{c} \theta _f^*=\arg \min _{\theta _f\in \Omega _f}\left[ \sup \big |\hat{f}-f\big |\right] ,\\ \theta _g^*=\arg \min _{\theta _g\in \Omega _g}\left[ \sup \big |\hat{g}-g\big |\right] , \end{array} \end{aligned}$$
(9)

where \(\Omega _f\triangleq \left\{ \theta _f\in R^{N_f}\Big ||\theta _f|\le M_f \right\}\) and \(\Omega _g\triangleq \left\{ \theta _g\in R^{N_g}\Big |0<\varepsilon <\vert \theta _g\vert \le M_g \right\}\) are the constraint sets, and the constants of \(M_f\), \(M_g\) , and \(\varepsilon\) are unknown.

Definition 2

The minimum approximation error is defined as follows:

$$\begin{aligned}&\omega _1\triangleq {\hat{f}} (\hat{{\varvec{x}}},{\varvec{u}}|\theta _f^*)-f({\varvec{x}},{\varvec{u}})+({\hat{g}}(\hat{{\varvec{x}}},{\varvec{u}}|\theta _g^*) -g({\varvec{x}},{\varvec{u}})) u_c^{(m)}. \end{aligned}$$
(10)

Definition 3

The observer error vector is written as

$$\begin{aligned} {\hat{{\varvec{e}}}}=\left( {\hat{e}},\hat{\dot{e}},\ldots ,{\hat{e}} ^{(n-1)} \right) ^T, \end{aligned}$$
(11)

where \({\hat{e}}=y_d-{\hat{x}}\).

The proposed fuzzy control is given by feedback linearization method as

$$\begin{aligned} u_c^{(m)}=\frac{1}{{\hat{g}}(\hat{{\varvec{x}}},{\varvec{u}}|\theta _g)} [&-{\hat{f}}({\hat{{\varvec{x}}}},{\varvec{u}}|\theta _f)+y_m^{(n)}(t)+{\varvec{K}}^T {\hat{{\varvec{e}}}}\\ \nonumber&-u_h -u_s], \end{aligned}$$
(12)

where \(\hat{f}(.)\) and \({\hat{g}} (.)\) are the FLSs’ outputs; \(u_h\) is an \({H}_\infty\) control term to attenuate the uncertainties effect; \(u_s\) is a linear combination of the error estimates; \(u_h\) and \(u_s\) ensure the stability of the closed-loop system.

By (12) and (1), the dynamics is rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{{\varvec{e}}}&{}={\varvec {A_1}} {\varvec{e}}+{\varvec{B}} [({\hat{f}} ({\hat{{\varvec{x}}}},{\varvec{u}}|\theta _f)-{\hat{f}} ({\hat{\varvec{x}}},{\varvec{u}}|\theta _f^*) )+\\ {} &{}({\hat{g}} ({\hat{{\varvec{x}}}},{\varvec{u}}|\theta _g)- {\hat{g}} ({\hat{{\varvec{x}}}},{\varvec{u}}|\theta _g^*)) u_c^{(m)}+u_h+u_s+\omega ] , \\ e&{}={\varvec{C}}^T {\varvec{e}}, \end{array}\right. } \end{aligned}$$
(13)

where \(\omega =\omega _1-d\).

4.2 Designing the Observer

The concerns over the cost of sensors lead to using observers for estimating unavailable states. The observer error equation is written as follows [34]:

$$\left\{ {\begin{array}{ll} {\dot{\hat{\varvec{e}}}} = {\varvec{A}}_{1} {\hat{\varvec{e}}} - {\varvec{BK}}^{T} {\hat{\varvec{e}}} + {\varvec{K}}_{0} (e - {\hat{e}}), \hfill \\ {\hat{e}} = {\varvec{C}}^{T} {\hat{\varvec{e}}}, \hfill \\ \end{array} } \right.$$
(14)

where \({\varvec {K_0}}=[k_{01},k_{02},\ldots ,k_{0n}]^T\) is the observer gain vector satisfying \({\varvec {A_2}}={\varvec {A_1}}-{\varvec {K_0}}{\varvec{C}}^T\) to be a strict Hurwitz matrices.

By defining \({\tilde{{\varvec{e}}}}={\varvec{e}}-{\hat{\varvec{e}}}={\hat{{\varvec{x}}}}-{\varvec{x}}\in R^n\), the observation state-space equation is calculated as

$${\left\{ \begin{array}{ll} {\dot{\tilde{{\varvec{e}}}}}&={\varvec {A_2}}{\tilde{{\varvec{e}}}}+{\varvec{B}} [({\hat{f}} ({\hat{{\varvec{x}}}},{\varvec{u}}|\theta _f)- {\hat{f}}({\hat{{\varvec{x}}}},{\varvec{u}}|\theta _f^*) )+\\ &({\hat{g}} ({\hat{{\varvec{x}}}},{\varvec{u}}|\theta _g)-{\hat{g}}({\hat{\varvec{x}}},{\varvec{u}}|\theta _g^*)) u_c^{(m)}+u_h+u_s+\omega ] , \\ {\tilde{e}}&={\varvec{C}}^T {\tilde{{\varvec{e}}}}. \end{array}\right.}$$
(15)

As only y is measurable, \({\tilde{e}}\) is available. Therefore, the strictly positive real (SPR) Lyapunov design method is employed to analyze the system stability and one has

$$\begin{aligned}&{\dot{\tilde{{\varvec{e}}}}}=H(s)L(s)L^{-1}(s)\Big [({\hat{f}} ({\hat{{\varvec{x}}}},{\varvec{u}}|\theta _f)-{\hat{f}} ({\hat{\varvec{x}}},{\varvec{u}}|\theta _f^*))+\nonumber \\ &({\hat{g}} ({\hat{\varvec{x}}},{\varvec{u}}|\theta g)-{\hat{g}} ({\hat{{\varvec{x}}}},{\varvec{u}}|\theta _g^*)) u_c^{(m)}+u_h+u_s+\omega \Big ], \end{aligned}$$
(16)

where \(H(s)={\varvec{C}}^T (sI-{\varvec {A_2}})^{-1} {\varvec{B}}\) is in stable; \(L(s)=s^{(n-1)}+C_{n-1}^1 \alpha s^{n-2}+\cdots +C_{n-1}^{n-2} \alpha ^{n-2} s+\alpha ^{n-1}={(s+\alpha )}^{n-1}\), \(\alpha >0\), where \(L^{-1}(s)\) is a proper stable transfer function and H(s)L(s) is a proper SPR transfer function.

By defining \({\tilde{\theta }} _f=\theta _f-\theta _f^*\) and \(\tilde{\theta }_g=\theta _g-\theta _g^*\), (15) is represented as follows:

$${\left\{ \begin{array}{ll} \dot{\tilde{{\varvec{e}}}}&{}={\varvec {A_2}}{\tilde{{\varvec{e}}}}+{\varvec {B_c}} ({\tilde{\theta }} _f\xi _f^\prime +{\tilde{\theta }} _g\xi _g^\prime u_c^{(m)}+u_h^\prime +u_s^\prime +\omega ^\prime )\\ {\tilde{e}}&{}={\varvec{C}}^T {\tilde{{\varvec{e}}}}, \end{array}\right. }$$
(17)

where \({\varvec {B_c}}=\left[ 1,C_{n-1}^1 \alpha ,\ldots ,C_{n-1}^{n-2} \alpha ^{n-2},\alpha ^{n-1}\right] ^T\); \(\xi _f^\prime (.)=L^{-1}(s)\xi _f (.)\); \(\xi _g^\prime (.)=L^{-1} (s)\xi _g (.)\); \({u}_h^\prime =L^{-1} (s)u_h\); \({u}_s^\prime =L^{-1} (s)u_s\); and \(\omega ^\prime =L^{-1} (s) \omega\).

4.3 Proposed Robust Controllers and Adaptive Laws

The \({H}_\infty\) control term, the compensation control term, and adaptive laws are described in this section. The Lyapunov function proves the validity of these equations.

As H(s)L(s) is a proper SPR transfer function, there are \({\varvec{P}}>0\) and \({\varvec{Q}}>0\) in the Riccati equation such that [35]

$$\begin{aligned}&{\varvec {A_2}}^T{\varvec{P}}+{\varvec{P}}{\varvec {A_2}}-{\varvec{P}} {\varvec {B_c}} \left( \frac{2}{\lambda }-\frac{1}{\rho ^2}\right) {\varvec {B_c}}^T{\varvec{P}}=-{\varvec{Q}},\nonumber \\&{\varvec{P}}{\varvec {B_c}}={\varvec{C}}, \end{aligned}$$
(18)

where \((0<\lambda \le 2\rho ^2)\).

The \({H}_\infty\) controller compensates for the approximation error. Lowering \(\rho\) improves the tracking performance while it could saturate the control input and cause higher frequency chattering.

Since \({\tilde{{\varvec{e}}}}\) is measurable, we define the \({H}_\infty\) control term as follows:

$$\begin{aligned} {u}_h^\prime =-\frac{1}{\lambda }{\varvec {B_c}}^T{\varvec{P}}{\tilde{\varvec{e}}}. \end{aligned}$$
(19)

By \({\varvec{P}}{\varvec{B}}_c={\varvec{C}}\) (18), we can simplify (19) as

$$\begin{aligned} {u}_h^\prime =-\frac{1}{\lambda }{\varvec{C}}^T{\tilde{\varvec{e}}}=-\frac{\tilde{e}}{\lambda }. \end{aligned}$$
(20)

The above equation is considered without needing for finding \(n\times n\)-matrix \({\varvec{P}}\) and \(n\times 1\)-vector \({\varvec {B_c}}\). Therefore, we describe the robust term by only one designing parameter as \(\lambda\).

The compensation control term is defined as

$$\begin{aligned} {u}_s^\prime =-{\varvec{K}}_{\varvec{0}}^T{\varvec{P}}_{\varvec{0}}{\hat{\varvec{e}}}. \end{aligned}$$
(21)

Lemma 2

The adaptive laws are defined as

$$\begin{aligned} {\dot{\theta }} _f&=-\gamma _1 {\tilde{ {\varvec{e}}}}^T {\varvec{P}} {\varvec {B_c}} \xi _f^\prime ({\hat{\varvec{x}}},{\varvec{u}})=-\gamma _1 {\tilde{e}} \xi _f^\prime ({\hat{\varvec{x}}},{\varvec{u}}), \nonumber \\ {\dot{\theta }} _g&=-\gamma _2 {\tilde{{\varvec{e}}}}^T {\varvec{P}} {\varvec {B_c}} \xi _g^\prime ({\hat{\varvec{x}}},{\varvec{u}}) u_c^{(m)}=-\gamma _2 {\tilde{e}} \xi _g^\prime ({\hat{\varvec{x}}},{\varvec{u}}) u_c^{(m)}, \end{aligned}$$
(22)

where \(\pmb \gamma =[\gamma _1\),\(\gamma _2] > 0\) regulate the convergence of the adaptive parameters. According to \({\varvec{P}}{\varvec {B_c}}={\varvec{C}}\) (18), the control law and adaptive laws are simplified to be free of designing \({\varvec{P}}\) matrix and \({\varvec {B_c}}\) vector.

Lemma 3

[13] The projection method restricts \(\theta _f\) and \(\theta _g\) to be in the sets of \(\Omega _f\) and \(\Omega _g\), respectively. As a result, \({\dot{\theta }} _f\) is modified as

$$\begin{aligned} {\dot{\theta }} _f= {\left\{ \begin{array}{ll} -\gamma _1 {\tilde{e}} \xi _f^\prime \left( \hat{{\varvec{x}}},{\varvec{u}}\right) \\ \text{ if } \left( \Vert \theta _f\Vert< M_f\right) \text{ or } (\Vert \theta _f\Vert =M_f \text{ and } {\tilde{e}} \theta _f^T\xi _f^\prime \ge 0), \\ -\gamma _1 {\tilde{e}}\xi _f^\prime ({\hat{\varvec{x}}},{\varvec{u}}) +\gamma _1 {\tilde{e}}\frac{\theta _f \theta _f^T \xi _f^\prime ({\hat{\varvec{x}}},{\varvec{u}})}{\Vert \theta _f\Vert ^ 2},\\ \text{ if }(\Vert \theta _f\Vert =M_f \text{ and }{\tilde{e}}\theta _f^ T \xi _f^\prime < 0), \end{array}\right. } \end{aligned}$$
(23)

and \({\dot{\theta }} _g\) is rewritten as follows:

a. For an element \(\theta _{gi}=\varepsilon\) of \(\theta _g\), one has

$$\begin{aligned} {\dot{\theta }} _{gi}= {\left\{ \begin{array}{ll} -\gamma _2 {\tilde{e}} \xi _g^\prime ({\hat{\varvec{x}}},{\varvec{u}}) u_c^{(m)},&{}\text{ if }\quad {\tilde{e}} \xi _{gi}^\prime u_c^m< 0, \\ 0, &{} \text{ if }\quad {\tilde{e}} \xi _{gi}^\prime u_c^m\ge 0, \end{array}\right. } \end{aligned}$$
(24)

to guarantee \(|\theta _g|\ge \varepsilon\).

b. Otherwise,

$$\begin{aligned} {\dot{\theta }} _g= {\left\{ \begin{array}{ll} -\gamma _2 {\tilde{e}} \xi _g^\prime \left( \hat{{\varvec{x}}},{\varvec{u}}\right) u_c^{(m)},\\ \text{ if } \left( \Vert \theta _g\Vert< M_g\right) \text{ or }\Big (\Vert \theta _g\Vert =M_g \text{ and }{\tilde{e}} \theta _g^T\xi _g^\prime u_c^{(m)} \ge 0 \Big ). \\ -\gamma _2 {\tilde{e}}\xi _g^\prime ({\hat{\varvec{x}}},{\varvec{u}}) u_c^{(m)}+\gamma _2 {\tilde{e}}\frac{\theta _g \theta _g^T\xi _g^\prime ({\hat{\varvec{x}}},{\varvec{u}}) u_c^{(m)}}{\Vert \theta _g\Vert ^ 2},\\ \text{ if } \Big (\Vert \theta _g\Vert =M_g \text{ and } {\tilde{e}} \theta _g^T\xi _g^\prime u_c^{(m)} < 0 \Big ), \end{array}\right. } \end{aligned}$$
(25)

which guarantees \(|\theta _g|\le M_g\).

By the above Lemma, it is proved that \(\theta _f\) and \(\theta _g\) are bounded and also \({\tilde{\theta }} _f\) and \({\tilde{\theta }} _g\) ultimately converge to compact residual sets around zero.

5 Stability Analysis

The stability of the closed-loop system in the proposed scheme is proven by the following theorem.

Theorem 1

By considering Assumptions 1–4 for the plant (1) with the control law (12), the robust controllers (20), (21), and the adaptive laws (23)–(25), the following results are obtained:

  • The asymptotic stability is proved, and the system output y follows the reference signal \(y_d\).

  • All the signals of the closed-loop system, i.e., \({\varvec{x}}(t)\), \({\hat{ {\varvec{x}}}}(t)\), \(\theta _f(t)\), \(\theta _g(t)\), \(u_c(t)\), \(\dot{u}_c(t)\),\(\ldots\), and \(u_c^{(m)}\) are bounded for all \(t\ge 0\).

  • The \({H}_\infty\) tracking criterion is achieved for a prescribed attenuation level \(\rho >0\).

Proof

The Lyapunov function is considered as

$$\begin{aligned} V=&\frac{1}{2}{\hat{{\varvec{e}}}}^T{\varvec {P_0}}{\hat{ \varvec{e}}}+\frac{1}{2}{\tilde{ {\varvec{e}}}}^T {\varvec{P}} {\tilde{ \varvec{e}}}+\frac{1}{2\gamma _1}{\tilde{\theta }} _f^T{\tilde{\theta }} _f+\frac{1}{2\gamma _2}{\tilde{\theta }} _g^T{\tilde{\theta }} _g, \end{aligned}$$
(26)

The time derivative of V is computed as

$$\begin{aligned}\dot{V}&=-\frac{1}{2}{\hat{{\varvec{e}}}}^T{\varvec {Q_0}}{\hat{ \varvec{e}}}-\frac{1}{2}{\tilde{ {\varvec{e}}}}^T {\varvec{Q}} {\tilde{ \varvec{e}}}+\frac{1}{2}{\tilde{ {\varvec{e}}}}^T{\varvec{P}}{\varvec {B_c}}\left( \frac{2}{\lambda }-\frac{1}{\rho ^2}\right) \\ &{\varvec {B_c}}^T{\varvec{P}}\tilde{ {\varvec{e}}}+\tilde{ {\varvec{e}}}{\varvec{C}} {\varvec {K_0}}^T\varvec {P_0}{\hat{{\varvec{e}}}}\\&\quad+\tilde{ {\varvec{e}}}{\varvec{P}}{\varvec {B_c}}\left( {\tilde{\theta }}_f^T\xi ^\prime +{\tilde{\theta }}_g^T\xi _g^\prime u_c^{(m)}+u_h^\prime +u_s^\prime +\omega ^\prime \right) \\&\quad+ \frac{1}{\gamma _1}{\tilde{\theta }}_f^T{\dot{\theta }} _f+\frac{1}{\gamma _2}{\tilde{\theta }}_g^T{\dot{\theta }} _g. \end{aligned}$$
(27)

According to \({\varvec{C}}={\varvec{P}}\varvec {B_c}\) in the third line of Eq. (18), we have

$$\begin{aligned} \dot{V}&=-\frac{1}{2}{\hat{{\varvec{e}}}}^T{\varvec {Q_0}}{\hat{ \varvec{e}}}-\frac{1}{2}{\tilde{ {\varvec{e}}}}^T {\varvec{Q}} {\tilde{ \varvec{e}}}+\frac{1}{2}{\tilde{ {\varvec{e}}}}^T{\varvec{P}}{\varvec {B_c}}\left( -\frac{1}{\rho ^2}\right) {\varvec {B_c}}^T{\varvec{P}}\tilde{ {\varvec{e}}}\\&\quad+{\tilde{ \varvec{e}}}^T{\varvec {PB_c}}\left( \frac{1}{\lambda }{\varvec {B_c}}^T{\varvec{P}}{\tilde{{\varvec{e}}}}+{\varvec {K_0}}^T{\varvec {P_0}}{\hat{e}}+u_h^\prime +u_s^\prime +\omega ^\prime \right) \\&\quad+ \frac{1}{\gamma _1}{\tilde{\theta }}_f^T\left( {\dot{\theta }} _f+\gamma _1 \tilde{ {\varvec{e}}}^T{\varvec{P}}{\varvec {B_c}}\xi _f^\prime \right) \\&\quad+ \frac{1}{\gamma _2}{\tilde{\theta }}_g^T\left( {\dot{\theta }} _g+\gamma _2 \tilde{ {\varvec{e}}}^T{\varvec{P}}\varvec {B_c}\xi _g^\prime u_c^{(m)}\right) . \end{aligned}$$
(28)

By replacing \(u_s^\prime =-\varvec {K_0}^T{\varvec {P_0}}{\hat{\varvec{e}}}\), \(u_h^\prime =-\frac{1}{\lambda } \varvec {B_c}^T{\varvec{P}}\tilde{{\varvec{e}}}\), \(\dot{\theta _f}=-\gamma _1 \tilde{ {\varvec{e}}}^T{\varvec{P}}{\varvec {B_c}}\xi _f^\prime\) and \({\dot{\theta }} _g=-\gamma _2 \tilde{ {\varvec{e}}}^T{\varvec{P}}{\varvec {B_c}}\xi _g^\prime u_c^{(m)}\), the result is realized as

$$\begin{aligned} \begin{aligned} \dot{V}&=-\frac{1}{2}{\hat{{\varvec{e}}}}^T{\varvec {Q_0}}{\hat{ \varvec{e}}}-\frac{1}{2}{\tilde{ {\varvec{e}}}}^T {\varvec{Q}} {\tilde{ \varvec{e}}}-\frac{1}{2\rho ^2}{\tilde{ {\varvec{e}}}}^T{\varvec{P}}{\varvec {B_c}}{\varvec {B_c}}^T{\varvec{P}}{\tilde{{\varvec{e}}}}+ \\&{\tilde{ {\varvec{e}}}}^T{\varvec{P}} {\varvec {B_c}}\omega ^\prime . \end{aligned} \end{aligned}$$
(29)

By considering \(a={\omega }^\prime\) and \(b={\tilde{{\varvec{e}}}}^T{\varvec{P}}{\varvec {B_c}}\) in Young’s inequality, which holds \(ab-\frac{1}{2\rho ^2} b^2\le \frac{1}{2} \rho ^2 a^2\), the asymptotic stability is proved as follows:

$$\begin{aligned} \dot{V}&\le -\frac{1}{2}{\hat{{\varvec{e}}}}^T{\varvec {Q_0}}{\hat{ \varvec{e}}}-\frac{1}{2}\tilde{ {\varvec{e}}}^T {\varvec{Q}} {\tilde{ \varvec{e}}}+\frac{1}{2}\rho ^2{\omega ^\prime }^T\omega ^\prime . \end{aligned}$$
(30)

Hence \(\dot{V}\) is negative semi-definite when \(\omega ^\prime\) is too small.

The integration of the above equation from 0 to T gives

$$\begin{aligned} \begin{aligned} \int _{0}^{T} \dot{V} (t)\le&-\frac{1}{2}\int _{0}^{T}{\hat{ \varvec{e}}}^T{\varvec {Q_0}}{\hat{{\varvec{e}}}}\, \mathrm dt-\frac{1}{2}\int _{0}^{T}{\tilde{ \varvec{e}}}^T{\varvec{Q}}{\tilde{{\varvec{e}}}}\, \mathrm dt+\\&\frac{1}{2}\rho ^2 \int _{0}^{T} {\omega ^ \prime }^T{\omega ^\prime }\, \mathrm dt. \end{aligned} \end{aligned}$$
(31)

By the Euclidean norm and \(\Vert A\Vert ^2_B=A^{T}BA\), we have

$$\begin{aligned} \begin{aligned} \int _{0}^{T} \dot{V} (t)\le&-\frac{1}{2}\int _{0}^{T}\Vert {\hat{ \varvec{e}}}\Vert _{\varvec {Q_0}}^2\, \mathrm dt-\frac{1}{2}\int _{0}^{T}\Vert \tilde{ {\varvec{e}}}\Vert _{{\varvec{Q}}}^2\, \mathrm dt+\\&\frac{1}{2}\rho ^2\int _{0}^{T}\Vert \omega ^\prime \Vert ^2\, \mathrm dt. \end{aligned} \end{aligned}$$
(32)

By considering \({\varvec {Q_1}}=diag\left[ \varvec {Q_0},\varvec{Q}\right]\) and \({{\varvec{e}}}_{{\varvec{1}}}=\left[ {\hat{ \varvec{e}}},\tilde{ {\varvec{e}}}\right] ^T\), we have

$$\begin{aligned} 2\left( V(T)-V(0) \right) \le -\int _{0}^{T}\Vert { {\varvec{e}}}_{\varvec{1}}\Vert _{{\varvec {Q_1}}}^2\, \mathrm dt+\rho ^2\int _{0}^{T}\Vert \omega ^\prime \Vert ^2\, \mathrm dt. \end{aligned}$$
(33)

Assuming a positive constant \(M_\omega >0\) such that \(\int _{0}^{\infty }\Vert \omega ^\prime \Vert ^2\, dt\le M_\omega\), we have

$$\begin{aligned} 2\left( V(T)-V(0) \right) \le -\int _{0}^{T}\Vert { {\varvec{e}}}_{\varvec{1}}\Vert _{{\varvec {Q_1}}}^2\, \mathrm dt+\rho ^2 M_\omega . \end{aligned}$$
(34)

As \(V(T)\ge 0\), we get

$$\begin{aligned} \int _{0}^{\infty }\Vert { {\varvec{e}}}_{{\varvec{1}}}\Vert _{{\varvec {Q_1}}}^2\, \mathrm dt \le 2V(0)+\rho ^2 M_\omega . \end{aligned}$$
(35)

Therefore, the integral \(\int _{0}^{T}\Vert \bar{ \varvec{e}}\Vert _{{\varvec {Q_1}}}^2\, dt\) is bounded. By Barbalat’s lemma, it is proved that \(\lim _{t\rightarrow \infty }\tilde{{\varvec{e}}}=0\), and \(\lim _{t\rightarrow \infty }{\hat{{\varvec{e}}}}=0\), which yield \(\lim _{t\rightarrow \infty }{\varvec{e}}=0\). It shows that y asymptotically tracks \(y_d\). The boundedness of the errors also guarantees the boundedness of \({\hat{ {\varvec{x}}}}\), \({\varvec{x}}\), and \(u_c^{(m)}\). As the signals of u,\(\dot{u}\),\(\ldots\), and \(u^{(m-1)}\) are obtained through the integration of \(u_c^{(m)}\) signal, their boundedness is proved. Moreover, by Lemma 3, the parameters of \(\theta _f\) and \(\theta _g\) can reach their optimal values.

By defining \({\varvec {P_1}}=diag[{\varvec {P_0}},{\varvec{P}}]\), we have

$$\begin{aligned} \begin{aligned} \int _{0}^{\infty } \Vert \bar{{\varvec{e}}}\Vert _{{\varvec {Q_1}}} ^2 \, \mathrm dt&\le \bar{ {\varvec{e}}}^T(0){ \varvec {P_1}}\bar{ \varvec{e}}(0)+\frac{1}{\gamma _1} {\tilde{\theta }}_f^T(0){\tilde{\theta }}_f(0)\\&+\frac{1}{\gamma _2} {\tilde{\theta }}_g^T(0){\tilde{\theta }}_g(0)+\rho ^2 M_\omega . \end{aligned} \end{aligned}$$
(36)

The above shows the following \({H}_\infty\) tracking performance is met. \(\square\)

6 Simulation Results

We apply two uncertain nonlinear systems with inputs derivative under various uncertainties for evaluation.

Fig. 2
figure 2

The spring-mass-damper trolley system

Full size image

6.1 Second-Order System

Example 1

The spring-mass-damper system is used in different architectures, e.g., cars, trains, screw presses in forging processes, seismically excited multi-story buildings, and human structure [36,37,38,39,40]. The spring-mass-damper trolley system is expressed as [7, 41]

$$\begin{aligned} m\ddot{y}_2 +f\left( \dot{y}_2-\dot{y}_1\right) +k\exp ^{-\left( y_2-y_1 \right) }\left( y_2-y_1\right) =0, \end{aligned}$$
(37)

where \(y_1\) is the displacement input, \(y_2\) is the mass displacement output, m is the mass, and f and k are the coefficients of the viscous friction and the stiffness spring, respectively (see Fig. 2).

By defining \(x_1=y_2\), \(x_2=\dot{y}_2\) , \(u=y_1\) , \(\dot{u}=\dot{y}_1\) [7, 8], (37) is described as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_1=x_2,\\ \dot{x}_2=\frac{-fx_2-k\exp ^{-(x_1-u)}(x_1-u)-bx_1^3}{m}+\frac{f}{m}\dot{u}+d,\\ y\,\,\,=\,x_1+\nu , \end{array}\right. } \end{aligned}$$
(38)

where d and \(\nu\) are a disturbance and a measurement noise, respectively.

Fig. 3
figure 3

Comparison of the proposed method (\(\hbox {OH}_\infty\)IAZTSFC) with OIAFTSFC [7] in Case A. a Trajectory of y. b \({\hat{x}}_1\). c \(\dot{u}\). d u. e \(f-{\hat{f}}\). f \(g-{\hat{g}}\)

Full size image
Table 1 Comparison of the proposed method (\(\hbox {OH}_\infty\)IAZTSFC) with OIAFTSFC [7] for Example 1 by mean squared errors (MSE and \(MS{\hat{E}}\)), the consumed control energies (\(J_1\) and \(J_2\)), the settling time (\(T_s\)), and the number of the adaptive parameters
Full size table

Physical parameters are \(m = 1\, \text {k}g\), \(k = 10\, {\text {N}}/{\text {m}}\), \(f=200\, {\text {N}\text {s}}/{\text {m}}\) [7, 8]. The reference trajectory is a unit step function. 4\(^{th}\)-order Runge–Kutta method is taken to solve equations in the numerical simulations in which the step time of the simulation experiments is \(0.0001 \text {s}\). The initial values are \({\varvec{x}}(0)=[2,1.3]^T\), \({\hat{\varvec{x}}}(0)=[1.5,1.2]^T\), \(u(0)=0\). The control parameters are assigned by trial and error to attain reasonable tracking error and control energy consumption. Therefore, \({\varvec{K}}=[1000,60]^T\), \({\varvec {K_0}}=[1,2]^T\), \(\gamma _1=1, \gamma _2=2\), \(L(s)=(s+20)\), and \(\lambda =0.01\). The Gaussian functions are used in the estimation of f(.) and g(.) with \(\delta =0.5\) for all membership functions. Furthermore, the centers of the fuzzy membership functions are equally spaced in the range of \({\hat{x}}_1\), \({\hat{x}}_2\), and u. The universe of discourse of each FLS’s input variable is defined by three fuzzy sets; therefore, the number of fuzzy rules equals 27 (\(3\times 3\times 3=27\)). Hence, each of \(\xi _f\), \(\xi _g\), \(\theta _f\), and \(\theta _g\) includes 27 parameters. For comparison results, the method of [7] is considered, which employs observer-based indirect adaptive first-order TS fuzzy controllers (OIAFTSFC). By defining three fuzzy sets for each input in the first-order TS, the dimension of the fuzzy basis functions and the adaptive parameters increases to 36 elements (\(3\times 3\times 4=36\)) in OIAFTSFC. The simulation time equals \(1\, \text {s}\) in Fig. 3 and Table 1. We investigate different conditions in the following case studies (A-G).

Case A. Ideal Condition Here, we consider the trolley when there are no environmental effects. Figure 3 shows the tracking of the reference signal and the estimated state, the boundedness of the system inputs, the estimations of the unknown nonlinear functions, and the better transient response. Table 1 shows that the proposed method lowers the mean squared tracking error \(e_1\) (MSE), the mean squared observer error \({\hat{e}}_1\) (\(MS{\hat{E}}\)), the consumed control energy measurement criteria by u (\(J_1\)), the consumed control energy measurement criteria by \(\dot{u}\) (\(J_2\)), and the settling time (\(T_s\)) by \(60.3\%\), \(32.7\%\), \(2.9\%\), \(75\%\), and \(48.6\%\), respectively.

Case B. Sinusoidal Disturbance The trolley is considered in the presence of a fast external sinusoidal disturbance \(d(t)=3\sin (20t)\). The comparison results between the two methods are shown in Table 1. \(\hbox {OH}_\infty\)IAZTSFC lowers MSE by \(60.3\%\), \(MS{\hat{E}}\) by \(32.7\%\), \(J_1\) by \(2.9\%\), \(J_2\) by \(74.9\%\), and \(T_s\) by \(48.6\%\).

Case C. Pulse Disturbance Here, we apply an external pulse disturbance \(d(t)={\left\{ \begin{array}{ll} 1,\quad 0.3\le t\le 0.6\\ 0,\quad otherwise \end{array}\right. }\). Table 1 shows that \(\hbox {OH}_\infty\)IAZTSFC lowers MSE by \(60.3\%\), \(MS{\hat{E}}\) by \(32.7\%\), \(J_1\) by \(2.8\%\), \(J_2\) by \(75\%\), and \(T_s\) by \(48.1\%\).

Case D. Noise Under the measurement noise (\(SNR=40\,\mathrm dB\)), MSE, \(MS{\hat{E}}\), \(J_1\), \(J_2\), and \(T_s\) are improved in the proposed method by \(60.2\%\), \(32.7\%\), \(2.9\%\), \(79.3\%\), and \(48.1\%\), respectively (see Table 1).

Case E. Data Loss Data loss is in networked control systems with negative effects on system stability. The stochastic data losses effect in the trolley system is shown as [42]

$$\begin{aligned} {x_i}_c(t)=\alpha x_i(t)+(1-\alpha )x_i(t-1), \end{aligned}$$
(39)

where \({x_i}_c(t)\) is the ith states used in the control, \(x_i(t)\) is the ith state to be transmitted through the communication network, and \(0<\alpha <1\) is the constant data loss probability. By supposing \(\alpha =0.65\), Table 1 shows that \(\hbox {OH}_\infty\)IAZTSFC lowers MSE (by \(98.2\%\)), \(MS{\hat{E}}\) (by \(29.6\%\)), \(J_1\) (by \(62.7\%\)), \(J_2\) (by \(88.1\%\)), and \(T_s\) (by \(29\%\)).

Case F. Dead-Zone The dead-zone nonlinearities of the actuators negatively affect the control systems. The output of the dead-zone with input u(t) is considered as

$$\begin{aligned} \phi (u(t))= {\left\{ \begin{array}{ll} m_r\left( u(t)-b_r\right) ,&{}\text{ if }\; u(t)\ge b_r,\\ 0,\quad &{}\text{ if }\; -b_l<u(t)<b_r,\\ m_l(u(t)-b_l),&{}\text{ if }\; u(t)\le -b_l, \end{array}\right. } \end{aligned}$$
(40)

where \(m_r\) and \(m_l\) are the slope of the dead-zone, and \(b_r\) and \(b_l\) are the right and left dead-zone breakpoints, respectively.

We consider the asymmetric dead-zone by \(m_r=m_l=0.4\), \(b_r=0.5\), and \(b_l=-0.9\) (see Table 1). \(\hbox {OH}_\infty\)IAZTSFC improves all of the comparison criteria, e.g., MSE, \(J_1\), and \(J_2\) by \(88.5\%\), \(29.5\%\), and \(86.3\%\), respectively. The proposed method also shows a fast convergence rate, as \(T_s\) improves by \(95.7\%\) compared with OIAFTSFC, whereas the mean squared observer error has no significant change (\(1.9\%\)).

Case G. Sensitivity Analysis The sensitivity of the proposed method to variations of the controller’s parameters is studied here. We calculate performance change with respect to lowering the controller’s parameters by \(10\%\) (\({\varvec {K_0}}\), \({\varvec{K}}\), \(\pmb {\gamma }\), \(\alpha\), and \(\lambda\)) from the designed values. Table 1 shows that the proposed method maintains its advantage in terms of the comparison criteria, e.g., MSE (by \(59.7\%\)), \(MS{\hat{E}}\) (by \(29.5\%\)), \(J_1\) (by \(13.4\%\)), \(J_2\) (by \(73.6\%\)), and \(T_s\) (by \(97.2\%\)).

6.2 Third-Order System

Example 2

Consider the following third-order system as [9]:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}_1=x_2,\\ \dot{x}_2=x_3,\\ \dot{x}_3=F\left( x_1,x_2,u\right) +G\left( x_1,x_2,u\right) \dot{u}+d\\ y=x_1+\nu ,\\ \end{array}\right. } \end{aligned}$$
(41)

and

$$\begin{aligned} F(x_1,x_2,&u)=2\left( 1-x_1^2\right) \Big ( -x_1+2x_2+\frac{u}{\sqrt{|u|+0.1}}\nonumber \\&-\qquad 2x_1^2x_2\Big ) -x_2-\frac{1}{2u\left( |u|+0.1 \right) \sqrt{|u|+0.1}},\nonumber \\ G(x_1,x_2,&u)=\frac{\sqrt{|u|+0.1}}{|u|+0.1}, \end{aligned}$$
(42)

where \({\varvec{x}}=[x_1,x_2,x_3 ]^T\) is the state vector, y is the system output, u and \(\dot{u}\) are the system inputs, d is an external disturbance, and \(\nu\) is a measurement noise.

In this example, the reference trajectory \(y_d\) is a step function. The numerical simulation method is a fourth-order Rung-Kutta with the simulation step time \(0.001\, \text {s}ec\). The initial states are supposed to be \({\varvec{x}}(0)=[0.2,0,0]^T\) and \({\hat{ \varvec{x}}}(0)=[0.1,0.1,0.1]^T\). The control parameters are assigned by trial and error to attain reasonable tracking error and control energy consumption, e.g., \({\varvec{K}}=[600,400,100]^T\), \({\varvec {K_0}}=[50,300,1500]^T\), \(\gamma _1=1\), \(\gamma _2=1\), \(L(s)=(s^2+14s+49)\), and \(\lambda =0.00004\). The basic fuzzy functions are the Gaussian membership function with \(\delta =0.5\). Furthermore, the centers of the fuzzy membership functions are equally spaced in the range of the inputs of the fuzzy system \({\hat{x}}_1\), \({\hat{x}}_2\), \({\hat{x}}_3\), and u. The universe of discourse of each input variable consists of three fuzzy sets, so there are 81 fuzzy rules (\(3\times 3\times 3\times 3=81\)) and 81 adaptive parameters. But, in OIAFTSFC, \(\xi _f\), \(\xi _g\), \(\theta _f\), and \(\theta _g\) include 135 (\(27\times 5=135\)) parameters because first-order TS increases the dimension burden. The following seven cases (A–G) express the better performance of the proposed method compared with OIAFTSFC in all the evaluation criteria.

Fig. 4
figure 4

Comparison of \(\hbox {OH}_\infty\)IAZTSFC with (OIAFTSFC) [7] in Case A. of Example 2. a Trajectory of output. b Trajectory of \({\hat{x}}_1\). c Designed Controller (\(\dot{u}\)). d Input (u). e Trajectory of \({\hat{x}}_2\). f Trajectory of \({\hat{x}}_3\)

Full size image

Case A. Ideal Condition By considering the system (38) without any environmental effects, the better results of the tracking performance and the transient response are shown in Fig. 4. Table 2 also expresses the proposed approach lowers MSE by \(36.6\%\), \(MS{\hat{E}}\) by \(35.9\%\), \(J_1\) by \(70\%\), \(J_2\) by \(85.4\%\), and \(T_s\) by \(36.3\%\) compared to OIAFTSFC.

Table 2 Comparison of the proposed method (\(\hbox {OH}_\infty\)IAZTSFC) with OIAFTSFC [7] for Example 2 by mean squared errors (MSE and \(MS{\hat{E}}\)), the consumed control energies (\(J_1\) and \(J_2\)), the settling time (\(T_s\)), and the number of the adaptive parameters
Full size table

Case B. Sinusoidal Disturbance The effect of a disturbance signal \(d(t)=3\sin (20t)\) is discussed. \(\hbox {OH}_\infty\)IAZTSFC lowers MSE by \(37.9\%\), \(MS{\hat{E}}\) by \(37\%\), \(J_1\) by \(23.7\%\), \(J_2\) by \(68.4\%\), and \(T_s\) by \(40.5\%\) in comparison with OIAFTSFC (see Table 2).

Case C. Pulse Disturbance In the presence of \(d(t)={\left\{ \begin{array}{ll} 1\qquad 0.5\le t\le 2.5\\ 0\qquad otherwise \end{array}\right. }\), \(\hbox {OH}_\infty\)IAZTSFC lowers MSE by \(36.4\%\), \(MS{\hat{E}}\) by \(35.5\%\), \(J_1\) by \(79.4\%\), \(J_2\) by \(85.4\%\), and \(T_s\) by \(53.1\%\) in comparison with OIAFTSFC (see Table 2).

Case D. Measurement Noise Under noise with \(SNR=45\, \text {d}B\), Table 2 shows that \(\hbox {OH}_\infty\)IAZTSFC lowers MSE by \(30.5\%\), \(MS{\hat{E}}\) by \(30.1\%\), \(J_1\) by \(68.6\%\), \(J_2\) by \(53.3\%\), and \(T_s\) by \(49.8\%\).

Case E. Data Loss By supposing \(\alpha =0.98\) in (39), Table 2 shows that \(\hbox {OH}_\infty\)IAZTSFC lowers MSE by \(33.3\%\), \(MS{\hat{E}}\) by \(32.7\%\), \(J_1\) by \(42.8\%\), \(J_2\) by \(78.5\%\), and \(T_s\) by \(48.3\%\).

Case F. Dead-Zone Under the asymmetric dead-zone with \(m_r=m_l=0.3\), \(b_r=0.5\), \(b_l=-0.8\), Table 2 reveals that the proposed method lowers MSE by \(23.4\%\), \(MS{\hat{E}}\) by \(23.1\%\), \(J_1\) by \(18.7\%\), \(J_2\) by \(36\%\), and \(T_s\) by \(53.5\%\) compared with OIAFTSFC.

Case G. Sensitivity Analysis The sensitivity of the introduced method to variations of the controller’s parameters is analyzed here. We calculate performance with respect to lowering the controller’s parameters by \(10\%\) (\({\varvec {K_0}}\), \({\varvec{K}}\), \(\pmb {\gamma }\), \(\alpha\), and \(\lambda\)) from the designed values. Table 2 shows that \(\hbox {OH}_\infty\)IAZTSFC improves MSE (by \(35.2\%\)), \(MS{\hat{E}}\) (by \(34.4\%\)), \(J_1\) (by \(69.5\%\)), \(J_2\) (by \(91.7\%\)), and \(T_s\) (by \(48.9\%\)).The results show the better performance of the proposed method in all criteria.

7 Conclusion

This paper studies nonlinear systems with high-order input derivatives and nonlinear input–output relationships. The dynamics are investigated without converting them to standard state-space forms to increase simplicity and interpretability. The proposed controller guarantees robust stability and trajectory tracking under uncertainties. The proposed method utilizes the simple structure of the zero-order TS fuzzy systems to increase transparency and estimate unknown nonlinear functions. The state observer approximates the unmeasured states to decrease the cost. The \({H}_\infty\) controller tries to compensate for the residual errors. The adaptive rules and the \({H}_\infty\) controller have simplified which their equations are expressed without determining \({\varvec {P_0}}\), \({\varvec {Q_0}}\), \({\varvec{P}}\), \({\varvec{Q}}\) matrixes, and \({\varvec {B_c}}\) vector. Compensation control is appended to ensure stability. The asymptotic stability of the closed-loop system and the parameters’ convergence are proved with the Lyapunov theory. Finally, the effectiveness of the proposed method is revealed via simulations of the second-order trolley system and the third-order SISO system in the presence of unmeasured states, disturbances, measurement noises, data loss, and asymmetric dead-zone. The results show that the proposed approach has better tracking behavior and lower energy consumption with a fast response. Our future research directions in this research will be as follows:

  • Use optimal controllers to adjust the parameters we obtain with trial and error.

  • Study various uncertainties, such as hysteresis, delay, and saturation in the model, to check the robustness.

  • Study more expressions of uncertainties in fuzzy systems, such as in type-2 fuzzy systems, to reach higher performance levels.