1 Introduction

Stability is a crucial aspect in control systems. By definition, the stability of a dynamic system usually evaluates whether a system reaches equilibrium state after being subjected to a disturbance. Therefore, stability is defined so that when a system starts from an initial condition close to the origin, its trajectory will stay within its vicinity. Contrarily, the system is considered as unstable. But, since nonlinear systems are driven by complex dynamics, more detailed stability concepts like asymptotic, exponential, and global asymptotic stability are introduced. For instance, even though the system is stable, the principal challenge in some applications is the trajectory’s convergence speed. In other words, how fast the trajectory gets to the origin which is captured by the concept of exponential stability.

In the research literature, control system design methodologies can be separated into three classes. The first class uses classical linear control techniques by linearizing nonlinear systems dynamics at an operating point of the states (Pathak et al. 2005). This methodology is known for its simplicity. However, designing a controller for an approximated system does not guarantee the performance and stability of the overall system. Hence, the second category consists of control design based on nonlinear systems dynamics, which preserves the characteristics of nonlinear systems (Chaoui and Sicard 2012; Wai et al. 2008; Xu et al. 2014; Huang et al. 2015; Park and Chwa 2009; Santiesteban et al. 2007). But, design complexity increases with the order of the nonlinear systems since an accurate mathematical system model is needed (Li and Luo 2009; Fukushima et al. 2013; Huang et al. 2013; Kwon et al. 2015). These approaches mainly consider parametric uncertainties and tend to show good performance in theory. However, their capability gets affected in the face of unstructured uncertainties like friction and disturbance. In real-world applications, formulating such model for complicated industrial systems may be a difficult undertaking because of varying operating conditions (Chaoui and Gueaieb 2008; Chaoui et al. 2013). Additionally, various elements may also be uncertain such as, temperature and noise. Thus, the system’s dynamics cannot be efficiently based on presumptively precise mathematical models. The third class deals with nonlinear control design based on soft-computing tools such as, artificial neural networks (ANNs) and fuzzy logic systems (FLSs) (Chaoui et al. 2009, 2010; Ali et al. 2008; Chang et al. 2009). These intelligent techniques have been considered in numerous applications as powerful tools for robust approximation of systems suffering from structured and unstructured uncertainties (de Silva 1995). Several models are available for the control of nonlinear systems, leading to a suitable performance and hence providing an alternative to conventional control methods (Ali et al. 2008; Huang et al. 2011; Orozco et al. 2015; Wai et al. 2008; Jung and Kim 2008; Chen et al. 2009; Li and Yang 2012; Tao et al. 2008; Yang et al. 2014). However, FLSs are unsuited for incorporating any learning and neural networks are also inadequate for aggregating any human-like expertise previously captured about the system dynamics. Additionally, these methodologies are based on heuristic, which makes tuning difficult especially for complex systems. Furthermore, many controllers based on these methods lack stability proofs in various applications.

Stability of FLSs has received an increasing interest in control applications, i.e., fuzzy logic controllers and observers (Sharma et al. 2010; Zhang et al. 2008; Biglarbegian et al. 2010; Barkat et al. 2011; Aliev and Pedrycz 2009; Pan et al. 2011). However, they suffer from too restrictive assumptions made for the control design and stability analysis (Boulkroune et al. 2011). Without these assumptions, their stability analysis is not trivial since nonlinear controller/observer design is difficult in general. Since most real-life systems are nonlinear, an advanced controller is often required to compensate for these nonlinearities. In some cases, the nonlinear system can be reasonably approximated by its linearized counterpart when the range of operation of a given nonlinear system is small. Then, the application of a variety of powerful linear control methods can be possible. But, nonlinearities can be discontinuous, called hard nonlinearities, and cannot be handled by linear systems. This paper aims to propose a stability analysis for adaptive FLSs without states measurement or estimation. The proposed scheme makes use of adaptive control theory to propose a Lyapunov-based adaptation law. Hence, the proposed approach stability is guaranteed by Lyapunov direct method. Several adaptive FLSs with stability proofs are available in the literature (Tong et al. 2013; Liu et al. 2013; Pan and Er 2013; Boulkroune et al. 2011). Backstepping is a popular technique used to design stable adaptive FLSs. However, this method is known for issues of “explosion of complexity” when dealing with nonlinear systems with unmodeled dynamics (Tong et al. 2013). To reduce complexity, a decentralized adaptive fuzzy output feedback approach is proposed in Liu et al. (2013) for a class of large-scale nonlinear systems using a reduced-order observer. Despite of complexity reduction, states estimation remains as a requirement. In an effort to relax constraint conditions of existing methods, an enhanced adaptive fuzzy controller, presented in Pan and Er (2013), achieves partial asymptotic tracking providing a more flexible solution. However, fuzzy approximation requires high-gain adaptation which is not practical due to measurement noise. Thus, fast adaptation and robustness is yet an issue not solved in Pan and Er (2013). On the other hand, adaptive fuzzy sliding mode controllers have also been proposed for various nonlinear systems (Saghafinia et al. 2015; Ho and Ahn 2012). However, robustness to disturbance and other uncertainties can be obtained only when sliding mode truly occurs. Moreover, discontinuous control action combined with limited switching frequency in real-life applications leads to the well-known chattering problem. To overcome this issue, the boundary solution approximates the sign function in a boundary layer of sliding mode manifold. This solution preserves partially the invariance property of sliding mode where states are confined to a small vicinity of the manifold, and convergence to zero cannot be guaranteed. In Nekoukar and Erfanian (2011), a continuous terminal sliding mode controller is presented for a class of nonlinear uncertain systems. Again, large gains are required to increase the stability boundary which lead to sensitivity to noise depleting the robustness properties associated with FLSs.

Unlike the aforementioned design methodologies, the proposed approach yields reduced complexity and does not require states measurement or estimation to reconstruct the regression vector. In this paper, stability and tracking problems of a class of nonlinear dynamic systems is addressed in the presence of both structured and unstructured uncertainties without states measurement or estimation unlike several adaptive FLSs available in the literature. First, stability is derived for an adaptive controller and then extended to adaptive FLSs. Thus, robustness to structured/unstructured uncertainties is obtained as opposed to adaptive control. Henceforth, the proposed Lyapunov-based adaptive FLS can be used as an alternative approach for a class of uncertain affine nonlinear systems operating in varying conditions. Implementation details are provided through a numeric illustrative example and results illustrate the performance and effectiveness of the proposed strategy. This paper is organized as follows: the developed adaptive control strategy is detailed in Sect. 2 and Sect. 3 outlines its extension to adaptive FLSs. A numeric example is presented and discussed in Sect. 4. Results are also reported and analyzed with some remarks pertaining to this problem.

2 Adaptive Control

In here, an adaptive control strategy is designed for a general nonaffine nonlinear system whose dynamics can be expressed in the following form,

$$\begin{aligned}&\dot{x}_i(t) = x_{i+1}(t)\qquad \qquad {{i}={1},\ldots ,{n-1}}\nonumber \\&\dot{x}_n(t) = f(x_n(t),u(t)) \end{aligned}$$
(1)

where \(x(t) \in {\mathbb {R}}^{n} \triangleq [x_1(t),\ldots ,x_n(t)]^\mathrm{T}\) denotes the state vector of the system, f is a continuous nonlinear function such that, \(f(x_n(t),u(t)) = a_n f_n(x_n(t)) + \cdots + a_1 f_1(x_1(t)) + b~u(t)\), where \(f_1\), \(\ldots \), and \(f_n\) are nonaffine nonlinear functions, \(a_1\), \(\ldots \), \(a_n\) and b are unknown constant parameters, and u is the control input. For clarity, the argument (t) is dropped when no ambiguity arises. The system’s dynamics can also be expressed in a linear parametric regression form as,

$$\begin{aligned} u = \frac{1}{b} \dot{x}_n - a_n f_n(x_n) - \cdots - a_1 f_1(x_1) = \varPsi ^\mathrm{T} \varTheta \end{aligned}$$
(2)

where \(\varPsi \in {\mathbb {R}}^{n+1}\) is a vector of known nonlinear functions (regressor), and \(\varTheta \in {\mathbb {R}}^{n+1}\) is a vector of unknown constant parameters. Define \(e \in {\mathbb {R}}^{n} \triangleq [e_1,\ldots ,e_n]^\mathrm{T}\) as the tracking error vector,

$$\begin{aligned} \left[ \begin{array}{c} e_1 \\ \vdots \\ e_n \end{array} \right] = \left[ \begin{array}{c} x_1 - x^*_1 \\ \vdots \\ x_n - x^*_n \end{array} \right] \end{aligned}$$

where \(x^* \in {\mathbb {R}}^{n} \triangleq [x^*_1,\ldots ,x^*_n]^\mathrm{T}\) is the desired time-dependent vector. Therefore, the control law can be defined as,

$$\begin{aligned} u = \frac{1}{\hat{b}} \dot{\bar{x}}_n - \hat{a}_n f_n(x_n) - \cdots - \hat{a}_1 f_1(x_1) \end{aligned}$$
(3)

where, \(\dot{\bar{x}}_n = \dot{x}_n - k^{\prime }_n e_n - \cdots - k^{\prime }_1 e_1\). The symbol \(\hat{\bullet }\) denotes the parameter estimate. Substituting for \(\dot{\bar{x}}_n\) in the control law (3) yields,

$$\begin{aligned} u = \frac{1}{\hat{b}} (\dot{x}_n - k^{\prime }_n e_n - \cdots - k^{\prime }_1 e_1) - \hat{a}_n f_n(x_n) - \cdots - \hat{a}_1 f_1(x_1) \end{aligned}$$
(4)

Substituting u from (2) and add and subtract \(({}^{1}\!/_{\hat{b}}) \dot{x}^*_n\) leads to,

$$\begin{aligned} \dot{e}_n + k_n e_n + \cdots + k_1 e_1 = \hat{b} \varPsi ^\mathrm{T} \tilde{\varTheta } \end{aligned}$$
(5)

where, \(\tilde{\varTheta } = \varTheta - \hat{\varTheta }\) is the parameter vector estimation error and \(k = k^{\prime } \hat{b}\). This way, the control law (3) leads to the following closed-loop dynamics,

$$\begin{aligned} \dot{e}_n + k_n e_n + \cdots + k_1 e_1 = 0 \end{aligned}$$

Formulation (5) can be written in a state-space form as,

$$\begin{aligned} \dot{E} = A~E + B~U \end{aligned}$$
(6)

where \(E \in {\mathbb {R}}^n = [e_1, \ldots , e_n]^\mathrm{T}\) is the state vector and \(U~\in ~{\mathbb {R}}~=~\varPsi ^\mathrm{T} \tilde{\varTheta }\) is the state-space input. \(A \in {\mathbb {R}}^{n \times n}\) is a stable matrix, and \(B \in {\mathbb {R}}^{n}\), are given by:

$$\begin{aligned}&A = \left[ \begin{array}{ccccc} 0 &{}\quad 1 &{}\quad 0 &{}\quad \ldots &{}\quad 0 \\ \vdots &{}\quad &{}\quad &{}\quad \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \ldots &{}\quad 1\\ -k_n &{}\quad -k_{n-1} &{}\quad -k_{n-2} &{}\quad \ldots &{}\quad -k_1 \end{array} \right] \\&B = \left[ \begin{array}{c} 0 \\ \vdots \\ \hat{b} \end{array} \right] \end{aligned}$$

Henceforth, the gain vector \(k \in {\mathbb {R}}^n\) can be chosen to place the closed-loop poles at their desired locations by using a pole placement technique or by solving the algebraic Riccati equation.

Theorem 1

Consider a nonlinear system in the form of (1) with the control law (3). The closed-loop system’s asymptotic stability and error convergence to zero are guaranteed with the following adaptation law:

$$\begin{aligned} \dot{\hat{\varTheta }} = - \Gamma \varPsi E_1 \end{aligned}$$
(7)

where \(E_1 = B^\mathrm{T} P E\) and \(\Gamma =\text {diag}(\gamma _1,\ldots ,\gamma _n)\) with \(\gamma _{i}\) is a positive constant. P is a symmetric positive definite matrix chosen to satisfy the following Lyapunov equation:

$$\begin{aligned} A^\mathrm{T} P + P A = -Q \end{aligned}$$
(8)

with Q is a positive definite matrix.

Proof

Choose the following Lyapunov candidate:

$$\begin{aligned} V = E^\mathrm{T} P E + \tilde{\varTheta }^\mathrm{T} \Gamma ^{-1} \tilde{\varTheta } \end{aligned}$$

Taking the derivative of V yields:

$$\begin{aligned} \dot{V} = \dot{E}^\mathrm{T} P E + E^\mathrm{T} P \dot{E} + 2 \tilde{\varTheta }^\mathrm{T} \Gamma ^{-1} \dot{\hat{\varTheta }} \end{aligned}$$
(9)

Since the parameter vector \(\varTheta \) is considered to be constant, therefore, \(\dot{\tilde{\varTheta }} = \dot{\hat{\varTheta }}\). Substituting \(\dot{E}\) from (6) yields,

$$\begin{aligned} \dot{V} = [A E + B U]^\mathrm{T} P E + E^\mathrm{T} P [A E + B U] + 2 \tilde{\varTheta }^\mathrm{T} \Gamma ^{-1} \dot{\hat{\varTheta }} \end{aligned}$$

Therefore, setting \(U = \varPsi ^\mathrm{T} \tilde{\varTheta }\) implies that,

$$\begin{aligned} \dot{V} = E^\mathrm{T} [A^\mathrm{T} P + P A] E + 2 \tilde{\varTheta }^\mathrm{T} \varPsi E_1 + 2 \tilde{\varTheta }^\mathrm{T} \Gamma ^{-1} \dot{\hat{\varTheta }} \end{aligned}$$

Setting \(A^\mathrm{T} P + P A = -Q\) as in (8) leads to,

$$\begin{aligned} \dot{V} = -E^\mathrm{T} Q E + 2 \tilde{\varTheta }^\mathrm{T} [\varPsi ^\mathrm{T} E_1 + \Gamma ^{-1} \dot{\hat{\varTheta }}] \end{aligned}$$

Setting the adaptation law as defined in (7) implies that,

$$\begin{aligned} \dot{V} = -E^\mathrm{T} Q E < 0 {} \square \end{aligned}$$

Since Q is positive definite, so \(\dot{V} < 0\) \(\forall E \ne 0\) such that \(E = 0\) is considered as a globally asymptotically stable equilibrium point. Since the positive Lyapunov function V is decreasing \((\dot{V}~<~0)\), then it must converge to a finite limit. Hence, E and so, e and \(\tilde{\varTheta }\) are also bounded and converge to finite values. Since \(\varPsi \) is bounded, it implies from (6) that \(\dot{E}\) is also bounded. Henceforth, \(\ddot{V}\) is also bounded.

Lemma 1

(Barbalat) If the differentiable function V(t) has a finite limit as \(t \rightarrow \infty \), and if \(\dot{V}(t)\) is uniformly continuous, then \(\dot{V}(t) \rightarrow 0\) as \(t \rightarrow \infty \).

From Lemma 1, V has a finite limit as \(t \rightarrow \infty \) and \(\dot{V}\) is uniformly continuous. Henceforth, the system is asymptotically stable in the sense of Lyapunov. Therefore, \(\lim _{t \rightarrow \infty } \dot{V} = 0\), and hence, \(\lim _{t \rightarrow \infty } E = 0\). It shows that \(\lim _{t \rightarrow \infty } e = 0\) and \(\lim _{t \rightarrow \infty } \dot{e} = 0\). Therefore, \(\lim _{t \rightarrow \infty } x = x^*\).

Remark 1

The goal in adaptive control is to achieve tracking error convergence to zero. However, it gives a false impression that parameter convergence is attained. Persistent excitation condition ensures parameter convergence if the following condition:

$$\begin{aligned} \alpha _0 I_n \le \int _{t_0}^{t_0+\delta } \varPsi \varPsi ^\mathrm{T} \hbox {d}t \le \alpha _1 I_n \end{aligned}$$

is met for all \(t_0\), where \(\alpha _0\), \(\alpha _1\) and \(\delta \) are all positive. Note that the integral of \(\varPsi \varPsi ^\mathrm{T}\) must be positive definite and bounded over all intervals of length \(\delta \). In other word, \(\varPsi \) must vary sufficiently over the interval \(\delta \) so that the entire dimensional space is spanned.

3 Adaptive Fuzzy Logic Systems

Several classical methodologies fail to provide good performance since they are heavily dependent on accurate mathematical models. In real-life, the derivation of a precise model is not trivial because of the presence of uncertainties and high nonlinearities. Opportunely, these limitations are nonexistent in soft-computing methods due to their independence from a mathematical model and therefore, higher performance can be achieved. In the reality, these tools are mainly used in a large number of applications where accurate mathematical models cannot be guaranteed due to large signals noise magnitudes, and dynamically changing parameters (Karray and Silva 2004; Lin and Lee 1996; Chaoui and Gueaieb 2008). The computational intelligence tool of interest in this work is FLSs. This section proposes an extension of the developed adaptive control theory to FLSs.

FLSs have the ability to uniformly approximate, to any degree of accuracy, any well-defined nonlinear function over a compact set U.

Theorem 2

(universal approximation theorem) For any given real continuous function g on the compact set \(U \subset {{\mathbb {R}}}^n\) and arbitrary \(\xi >0\), there exists a function \(f(\zeta )\) in the form of (10) such that

$$\begin{aligned} \sup _{\zeta \in U} \parallel g(\zeta ) - f(\zeta ) \parallel < \xi \nonumber \end{aligned}$$

The above theorem (Wang 1994) reveals the power of FLSs in achieving a high approximation of continuous nonlinear functions providing a rational substitute to dealing with complex ill-defined dynamic systems. A FLS maps crisp inputs into crisp outputs using generally three stages: fuzzification, inference fuzzy rule engine, and defuzzification.

Fuzzy sets can be defined by a membership function \(\mu _A\) in which each element \(\alpha \) of the universe of discourse X is associated with a membership grade \(\mu _A(\alpha )\) in the interval [0,1]. As such, the fuzzification stage consists of mapping a crisp input \(\alpha \in X\) into a fuzzified value \(A\in U\) (Universe). Singleton fuzzification: fuzzy set A with support \(\alpha _i\), where \(\mu _A(\alpha _i) = 1\), for \(\alpha = \alpha _i\) and \(\mu _A(\alpha _i) = 0\), for \(\alpha \ne \alpha _i\). Non-singleton fuzzification: \(\mu _A(\alpha _i) = 1\), for \(\alpha = \alpha _i\) and gradually dropped from 1 to 0 when moving away from \(\alpha = \alpha _i\).

The inference engine is instrumental for any FLS as it gathers the knowledge base IF–THEN rules with the fuzzy sets provided by the fuzzification stage to produce an overall output fuzzy set. In other words, it generates a mapping from the input fuzzy sets to the output ones. The t-norm and t-conorm operators are then used, respectively, for the intersection of multiple rule antecedents and their union. Each rule l in the knowledge base is taken as a fuzzy implication, which when combined with the fuzzified inputs, it leads to a fuzzy set \(B^{l}\) such that:

$$\begin{aligned} \mu _{B^{l}}(\beta ) = \sqcup _{\alpha \in X} [\mu _{A_{\alpha }}(\alpha ) \sqcap \mu _{R^{l}}(\alpha ,\beta )] . \end{aligned}$$
(10)

where \(\sqcup \) and \(\sqcap \) are the t-norm and t-conorm operators, respectively.

Fig. 1
figure 1

Adaptive fuzzy logic control structure

Full size image

The fuzzy rule base is formed of numerous IF–THEN rules. The lth rule has the following form:

\(R^{l}\) : IF \(\alpha _{1}\) is \(F^{l}_{1}\) and \(\alpha _{2}\) is \(F^{l}_{2}\) and \(\ldots \) and \(\alpha _{p}\) is \(F^{l}_{p}\)

THEN \(\beta _1\) is \(G_{1}^{l}\) and \(\beta _2\) is \(G_{2}^{l}\) and \(\ldots \) and \(\beta _m\) is \(G_{q}^{l}\)

where \(\alpha _{1} \in X_{1},\ldots ,\alpha _{p} \in X_{p}\), and \(\beta _1 \in Y_1,\ldots , \beta _m \in Y_m\), are the input/output fuzzy linguistic variables, respectively. \(F^{l}_{i}\) and \(G^{l}_{j}\), \(i=1,\ldots ,p, j=1,\ldots ,q\), are the input/output fuzzy labels, respectively. \(R^{l}\) is a fuzzy relation mapping fuzzy input sets X to fuzzy output sets Y, p and q are the number of the inputs and outputs of the FLS, respectively.

To calculate the final output crisp value, a defuzzification step is needed. Various defuzzification techniques are available for FLSs, such as the centroid, centre-of-sets, and centre-of-sums defuzzifiers. By using a commonly used defuzzification such as centroid, the output at instant k can be expressed as:

$$\begin{aligned} y_j(k) = \frac{\sum ^{r}_{l=1} \theta _{l}~\mu _{B^{l}}(\beta )}{\sum ^{r}_{l=1} \mu _{B^{l}}(\beta )} \end{aligned}$$
(11)

where, \(l=1,\ldots ,r\) and r is the number of the fuzzy rules.

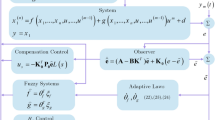
The adaptive FLS scheme is shown in Fig. 1. It is composed of four layers: layers 1 and 2 form the antecedent part of the fuzzy rules and consist of the input and the fuzzification nodes, respectively; layers 3 and 4 represent the consequent part of the fuzzy rules constructed with the fuzzy rule and the output nodes, respectively. These layers are linked by the parameter matrix \(\varTheta \).

The FLS’s output in (11) is described as,

$$\begin{aligned} Y = \varPsi ^\mathrm{T} \varTheta + \epsilon = \hat{\varPsi }^\mathrm{T} \hat{\varTheta } \end{aligned}$$
(12)

where, \(\epsilon = \hat{\varPsi }^\mathrm{T} \hat{\varTheta } - \varPsi ^\mathrm{T} \varTheta \) is the fuzzy logic output error, \(\hat{\varTheta } \in {\mathbb {R}}^{r \times q}\) is the fuzzy logic consequent part parameter matrix, i.e., singleton output membership functions, which is adapted online using a Lyapunov-based adaptation law, and \(\hat{\varPsi } \in {\mathbb {R}}^r\) is the r-dimensional fuzzy logic antecedent part vector of known functions (regressor) defined as:

$$\begin{aligned} \hat{\varPsi } = \frac{\mu _{B^{l}}(\beta )}{\sum ^{r}_{l=1} \mu _{B^{l}}(\beta )} \end{aligned}$$
(13)

In this work, the FLS consists of a single output system, i.e., (\(q=1\)), the matrix \(\hat{\varTheta } \in {\mathbb {R}}^{r \times q}\) is reduced to a vector \(\hat{\varTheta } \in {\mathbb {R}}^{r \times 1}=[\theta _1,\theta _2,\ldots ,\theta _r]\), where \(\theta _l\) is the fuzzy logic consequent part of the lth rule as shown in (11), \({{l}={1},\ldots ,{r}}\). Setting \(r=n\) makes the dimension of vectors \(\hat{\varPsi }\) and \(\hat{\varTheta }\) equal to dimension of vectors \(\varPsi \) and \(\varTheta \) in (2). Therefore, define the fuzzy logic control law as,

$$\begin{aligned} u = \hat{\varPsi }^\mathrm{T} \hat{\varTheta } \end{aligned}$$
(14)

Since the regression vector \(\varPsi \) is assumed to unknown and only an approximation \(\hat{\varPsi }\) is possible with the adaptive fuzzy logic controller, the error dynamics Eq. (5) can be written as,

$$\begin{aligned} \dot{e}_n + k_n e_n + \cdots + k_1 e_1 = \hat{b} \epsilon \end{aligned}$$
(15)

Therefore, the adaptive fuzzy logic closed-loop dynamics can also be written in a state-space form as in (6), where \(U~\in ~{\mathbb {R}}~=~\epsilon \) is the state-space input and \(\epsilon = \hat{\Phi }^\mathrm{T} \hat{\varTheta } - \varPsi ^\mathrm{T} \varTheta \).

Theorem 3

Consider a nonlinear system in the form (1) with the control law (14). The closed-loop system’s stability is achieved with the following adaptation law:

$$\begin{aligned} \dot{\hat{\varTheta }} = - \Gamma \hat{\varPsi } E_1 \end{aligned}$$
(16)

where \(E_1 = B^\mathrm{T} P E\) and \(\Gamma =\text {diag}(\gamma _1,\ldots ,\gamma _n)\) with \(\gamma _{i}\) is a positive constant. P is a symmetric positive definite matrix chosen to satisfy the Riccati equation (8).

Proof

Choose the following Lyapunov candidate:

$$\begin{aligned} V = \frac{1}{2} E^\mathrm{T} P E + \frac{1}{2} \tilde{\varTheta }^\mathrm{T} \Gamma ^{-1} \tilde{\varTheta } \end{aligned}$$
(17)

Taking the derivative of V:

$$\begin{aligned} \dot{V} = \frac{1}{2} \dot{E}^\mathrm{T} P E + \frac{1}{2} E^\mathrm{T} P \dot{E} + \tilde{\varTheta }^\mathrm{T} \Gamma ^{-1} \dot{\hat{\varTheta }} \end{aligned}$$
(18)

Substitute \(\dot{E}\):

$$\begin{aligned} \dot{V} = -\frac{1}{2} E^\mathrm{T} Q E + \epsilon ^\mathrm{T} E_1 + \tilde{\varTheta }^\mathrm{T} \Gamma ^{-1} \dot{\hat{\varTheta }} \end{aligned}$$
(19)

where \(E_1 = B^\mathrm{T} P E\). Add and subtract \(\hat{\Phi }^\mathrm{T} \varTheta \) from \(\epsilon = \hat{\Phi }^\mathrm{T} \hat{\varTheta } - \varPsi ^\mathrm{T} \varTheta \),

$$\begin{aligned} \epsilon = \hat{\Phi }^\mathrm{T} \varTheta - \hat{\Phi }^\mathrm{T} \hat{\varTheta } + \varPsi ^\mathrm{T} \varTheta - \hat{\varPsi }^\mathrm{T} \varTheta \end{aligned}$$
(20)

Therefore, \(\epsilon = \hat{\varPsi }^\mathrm{T} \tilde{\varTheta } + \tilde{\varPsi }^\mathrm{T} \varTheta \). Substitute \(\epsilon \) in (19):

$$\begin{aligned} \dot{V} = -\frac{1}{2} E^\mathrm{T} Q E + \tilde{\varPsi }^\mathrm{T} \varTheta E_1 + \tilde{\varTheta }^\mathrm{T} \left[ \hat{\varPsi } E_1 + \Gamma ^{-1} \dot{\hat{\varTheta }} \right] \end{aligned}$$
(21)

Setting the adaptation law as \(\dot{\hat{\varTheta }} = -\Gamma \hat{\varPsi } E_1\) implies that,

$$\begin{aligned} \dot{V} = -\frac{1}{2} E^\mathrm{T} Q E + \tilde{\varPsi }^\mathrm{T} \varTheta E_1 \end{aligned}$$
(22)

Therefore,

$$\begin{aligned} \dot{V} \le -\frac{1}{2} E^\mathrm{T} Q E + |\tilde{\varPsi }^\mathrm{T} \varTheta E_1| \end{aligned}$$
(23)

Henceforth, it is possible to choose the gain vector k so that \(\dot{V} \le 0\), \(\forall E \ne 0\). Then, the system is stable in the sense of Lyapunov. The neighborhood of \(E = 0\) is a region defined by the fuzzy logic approximation error \(\tilde{\varPsi }\) and gets smaller as \(\tilde{\varPsi } \rightarrow 0\).

The adaptive fuzzy logic algorithm is shown in Algorithm 1.

figure a

4 Numeric Example and Discussion

Inverted pendulums have been abundantly utilized to validate various kinds of control systems. They are viewed as a well-established point of comparison for several control systems (El-Hawwary et al. 2006; Uyanik et al. 2015; Phan and Gale 2007; Muralidharan and Mahindrakar 2014; Hsueh et al. 2010; Yang et al. 2013). The hard nonlinearities combined with external disturbances and varying operating conditions makes the control of such complex nonlinear unstable systems extremely challenging. These systems are single-input multiple-output (SIMO) and therefore, are underactuated since only a single control input is available to control both the pendulum’s angle and the cart’s motion. Moreover, inverted pendulums are driven by highly nonlinear dynamics and are unstable non-minimum phase systems. The inverted pendulum system, shown in Fig. 2, is used as an illustrative example to validate the proposed control scheme. The pendulum is mounted on a cart that uses a dc servomotor in order to move along a track (Phan and Gale 2007; Hsueh et al. 2010). Based on Euler–Lagrange equation, the system’s dynamics can be written in a general form of (1) as described in (24) (Pan et al. 2011), where \(x_1\) and \(x_2\) are the angular position and velocity of the pendulum, respectively, \(m_\mathrm{c}\) is the mass of the cart, \(m_\mathrm{p}\) is the mass of the pole, L is the length of the pole, \(g = 9.8~m/s^2\) is the gravitational constant acceleration, u is the force applied to the cart, and d is the disturbance. The control aim is to design a control law u to make the inverted pendulum position \(x_1\) and velocity \(x_2\) track their pre-defined time-dependent trajectories in the presence of external disturbances. The inverted pendulum parameters, \(m_\mathrm{c}\), \(m_\mathrm{p}\), L, and g are assumed to be unknown.

$$\begin{aligned} \dot{x}_1&= x_2 \nonumber \\ \dot{x}_2&= \left( g \text {sin}(x_1) - \frac{m_\mathrm{p} L x^2 \text {cos}(x_1) \text {sin}(x_1)}{m_\mathrm{c} + m_\mathrm{p}} \right) \nonumber \\&\quad \times \Biggm / \left( \frac{4L}{3} - \frac{m_\mathrm{p} L \text {cos}^2(x_1)}{m_\mathrm{c} + m_\mathrm{p}}\right) \nonumber \\&\qquad + \frac{\text {cos}(x_1)}{m_\mathrm{c} + m_\mathrm{p}} \Biggm / \left( \frac{4L}{3} - \frac{m_\mathrm{p} L \text {cos}^2(x_1)}{m_\mathrm{c} + m_\mathrm{p}}\right) u + d \end{aligned}$$
(24)
Fig. 2
figure 2

Inverted pendulum system

Full size image

Assumption 1

The system’s body is considered symmetric along the y axis.

Coulomb, viscous, and static friction elements are considered in the following nonlinear a priori unknown friction model to increase the complexity of system (24) (Armstrong and de Wit 1996),

$$\begin{aligned} F = F_\mathrm{c} ~\text {sign}(\dot{\sigma }) + F_\mathrm{v} ~\dot{\sigma } + F_\mathrm{s} ~\text {sign}(\dot{\sigma }) ~\hbox {e}^{-(\dot{\sigma }/ \eta _\mathrm{s})^2} \end{aligned}$$
(25)

where \(F_\mathrm{c}\), \(F_\mathrm{v}\) and \(F_\mathrm{s}\) are the Coulomb, viscous and static friction parameters, respectively, \(\sigma \) is a displacement, \(\eta _\mathrm{s}\) is the rate of decay of the static friction term. This friction model is used to represent friction at the hinge and the wheels (Fig. 3).

Fig. 3
figure 3

Results of friction experiment Stribeck friction model

Full size image
Fig. 4
figure 4

Adaptive fuzzy logic control scheme

Full size image

Let us define the tracking errors as \(e_1 = x_1 - x_1^*\) and \(e_2 = x_2 - x_2^*\). The resultant control scheme is depicted in Fig. 4. Given the tracking error \(e_1\) and its derivative \(e_2\), the FLS produces a control force u. The rules are defined such as the control action is large when both errors move away from their respective nominal zero-valued surfaces. This control output is gradually decreased for a smoother approach as input signals approach the surfaces. Then, it is set to zero once the error signals are on their nominal surfaces. This way, the FLS defines an equilibrium on the nominal zero-valued surfaces of the input signals and forces the system’s errors \(e_1\) and \(e_2\) to approach zero. In this demonstration, triangular membership functions are used for their low computational requirements (Fig. 5). The fuzzy rules are described in Table 1, which can be adjusted to get the best control performance. As such, an offline empirical study is performed to determine the optimal input membership function parameters and the fuzzy inference engine rules. The control scheme aims the stabilization of the inverted pendulum. However, if the system’s initial condition is irrecoverable, e.g., rest position of the inverted pendulum, a swing-up strategy is needed to drive the pendulum to the upright region.

Fig. 5
figure 5

Fuzzy logic input membership functions

Full size image
Table 1 Fuzzy logic rules
Full size table
Table 2 Systems’s parameters
Full size table
Fig. 6
figure 6

System response: a angular position; b angular velocity; c tracking errors; and d control input u

Full size image

To demonstrate the capabilities of the proposed control method, the inverted pendulum dynamics in (24) and Algorithm 1 are implemented in MATLAB/Simulink. The reference trajectory is taken as \(\pi /6~\text {sin}(t)\). A simulation is performed to study the proposed controller’s response taking into account the angular position and velocity, tracking errors, and the control signal u. Table 2 outlines the system’s parameters along with their respective values that are used for the simulation of the system’s dynamics. The initial state x(0) is set to [\(\pi /12, 0\)] to evaluate the controller’s convergence properties from a nonzero initial position. The vector of parameters estimate \(\hat{\varTheta }\) is set to small random values. The benefit of the use of the adaptive fuzzy logic control scheme can be clearly observed in (Fig. 6) by the tracking performance. The system starts with a nonzero initial condition, which causes an initial tracking error. The proposed controller achieves fast and precise convergence while providing a smooth control signal. It is important to note how easily the friction nonlinearities were compensated by the adaptive fuzzy logic controller.

5 Conclusion

In this paper, stability analysis is investigated for adaptive FLSs. The proposed scheme makes use of adaptive control theory to propose a Lyapunov-based adaptation law for FLSs. For clarity, stability analysis is presented first for an adaptive controller. Then, these findings are extended to adaptive FLSs. Moreover, a numeric illustrative example shows implementation details on an inverted pendulum system with nonlinear friction. The proposed adaptive fuzzy control strategy is capable of coping with structured/unstructured uncertainties. Henceforth, it can be considered as a long-lasting alternative for systems subjected to uncertainties and external disturbances. Unlike other adaptive FLSs, no a priori offline training or parameter initialization is required. Results show good performance in tracking convergence and precision. Furthermore, the adaptive FLS capabilities are a key in obtaining the control accuracy needed for high-performance applications.