1 Introduction

State feedback control, the structure of most modern control algorithms, is based on the availability of the full state. However, more often than not, the full state is not measurable. State observers have then been introduced in order to deal with this obstacle (Luenberger, 1971). For linear systems, the design of Luenberger state observers is relatively easy. This may not be, in general, the case for nonlinear systems. Indeed, the proposed approaches are based on particular model structures usually affine in the control or in the state (Besançon, 2008). Takagi–Sugeno, TS, fuzzy model with consequences in linear state space form has been used to design state feedback fuzzy controllers (Coutinho et al., 2019; Esfahani (2020); Guerra et al., 2009; Johansson et al., 1999; Kruszewski et al., 2008; Lendek & Lauber, 2022; Sala & Arino, 2007). On the other hand, fuzzy observers have been extensively studied in the last two decades. Two situations have been identified according to the type of the premise variables of the fuzzy model (Tanaka et al., 1998). When the premise variables are measurable, the design of the fuzzy observer does not involve difficulties. In this case, the main steam of research has been to reduce the conservatism inherent to the Lyapunov function-based design, e.g., (Bouyahya et al., 2020; Guerra et al., 2011; Ku et al., 2021; Xie et al., 2021, Xie et al., 2022, Xie et al. 2022b, Gong et al., 2022). On the other hand, when the premise variables of the fuzzy model include the unmeasurable variables, the fuzzy observer design has been recognized to be more difficult (Tanaka et al., 1998). This is due to the error term between the normalized weight of the measurable and unmeasurable variables. This is a severe limitation as many nonlinear systems are modeled with measurable and unmeasurable premise variables. Nonetheless, a number of approaches have been developed in order to deal with this problem for continuous and discrete TS systems. These can be classified into direct and indirect approaches. Direct approaches consider the usual TS fuzzy model with unmeasurable premise variables and linear consequences. Various techniques are then used to deal with the error term. An early approach was introduced in Bergsten (2002) whereby the error term is assumed to be Lipschitz. As a result, the sufficient condition yields LMIs depending on the Lipschitz constant. However, it was quickly recognized that the method is very conservative. Some improvements to the approach were proposed (Ichalal et al., 2010, Lendek et al., 2009). In other approaches, the TS model is rewritten as an uncertain system with the error term as the uncertainty. The observer design is then posed as an \({H}_{\infty }\) disturbance attenuation (Yoneyama et al., 2000; Yoneyama, 2008; Yoneyama, 2000). The differential mean value theorem (DMVT) was proposed as an alternative to the Lipschitz constant approach (Ichalal et al., 2011). The main drawback of this approach is its complexity due to the large number of LMI to be solved. Indirect approaches use alternative TS fuzzy models in which the unmeasurable variables are separated from the measured ones in order to reduce conservatism and complexity of the design (Dong et al., 2010, Dong and Yang, 2017, Guerra et al., 2018, Ichalal et al., 2010, Ichalal et al., 2018, Nagy et al., 2022, Pan et al., 2021). This model was first introduced in Dong et al. (2010) where the premises depend only on measurable variables. The consequences are formed by the sum of a linear term that depends on the measurable variables and a nonlinear term that is a function of the unmeasurable variables. The Lipschitz condition on the error is associated with the membership functions of the measurable variables. This yields a TS model with fewer rules. In Guerra et al., (2018), the premise vector is separated into measured and unmeasured variables, and the DMTV deals only with the unmeasured part. The procedure is recognized to be quite complex. The DMTV path was further pursued in Pan et al., (2021) with a model similar to the one introduced in Dong et al., (2010). This latter model is also exploited in Nagy et al., (2022) where the nonlinear part, which contains the unmeasurable variables, must satisfy a slope-restricted condition. The immersion technique and the so-called auxiliary dynamics generation are used in Ichalal et al., (2018) to transform a TS fuzzy system with unmeasured premise variables into a system with weight functions that depend on the measured variables. As mentioned therein, the algorithm may fail in some case. The authors in Maalej et al., (2017) present an alternative method utilizing the input to state stability analysis and the small gain theorem.

The objective of this work is to introduce a less conservative and less complex method for the design of a fuzzy observer and observer-based output feedback fuzzy controller within the framework of the matrix norms approach introduced in Belarbi, (2019). This approach was introduced for the stability and stabilization of discrete time based on the assumption that all the states are measurable. However, this assumption is not always fulfilled, as some states may not be available for measurement. Henceforth, in this work, we extend the application of this approach to the stabilization of such system through observer-based output feedback. In this respect, we develop the design of a fuzzy observer and then observer-based output feedback fuzzy controllers. Our contributions are as follows:

-As mentioned above, whenever the premise variables depend only on the measurable variables, the main issue in fuzzy TS observer design is in reducing the conservatism. We show that by using the matrix norms approach it is possible not only to reduce the conservatism but also the complexity of the design.

-For the case where the premises depend on the unmeasurable variables, on the contrary to previous indirect approaches that used specific nonlinear TS fuzzy models, we first consider a TS model with measurable and unmeasurable premise variables and linear consequences. The designer can then freely choose the premise variables. Then using the model reduction procedure of Taniguchi et al., (2001), we obtain a reduced-order model with measurable premise variables and uncertainties that compensate for the reduction error and using these results, we first show that the separation principle holds then we introduce an observer-based output feedback fuzzy controller.

The rest of this paper is organized as follows. The second section introduces the discrete TS fuzzy model and the main results of the matrix norms stability results of Belarbi, (2019). In the third section, convergence conditions and design methods are presented for measurable and unmeasurable premise variables. The fourth section describes the design of an observer-based output feedback fuzzy controller. The last section presents two examples to illustrate the application of the proposed approaches.

2 Background

In this section, we briefly recall the TS fuzzy model used in the sequel and the main results of Belarbi, (2019).

2.1 Discrete Takagi–Sugeno Fuzzy Model

As usual a rule \({R}_{i}\),\(i=1\dots r\), of the TS fuzzy model with linear consequences is given by. if \({z}_{1}\, is\, {M}_{i1}\) AND \({z}_{2} \,is \,{M}_{i2}\,\) …AND \({z}_{p} \,is\, {M}_{ip}\,\)then

$$x\left(t+1\right)={A}_{i}x\left(t\right)+{B}_{i}u\left(t\right)$$
(1)
$$y\left(t\right)={C}_{i}x(t)$$

\(x(t)\in {R}^{n}\), \(z(t)\in {R}^{{n}_{z}}\) \(u(t)\in {R}^{{m}_{u}}\) \(y\left(t\right)\in {R}^{{m}_{y}}\) are, respectively, the state and premise variables, and the control and the output vectors, \({M}_{ij},\) are fuzzy sets. Fusion of the rules gives the overall model

$$x\left(t+1\right)=\sum_{i=1}^{r}{h}_{i}\left(z\left(t\right)\right)\left({A}_{i}x\left(t\right)+{B}_{i}u\left(t\right)\right)$$
(2)
$$y\left(t\right)=\sum_{i=1}^{r}{h}_{i}(z(t){C}_{i}x(t)):$$

with

$${h}_{i}\left(z\left(t\right)\right)=\frac{{\mu }_{{R}_{i}}(z(t))}{\sum_{i}^{r}{\mu }_{i}(z(t))}$$
$${\sum_{i=1}^{r}{h}_{i}\left(z\left(t\right)\right)=1,0\le h}_{i}\left(z\left(t\right)\right)\le 1, i=1\dots r$$
(3)

and

$${\mu }_{i}\left(z\left(t\right)\right)=\prod_{i=1}^{p}{\mu }_{{M}_{ij}}({z}_{i}),$$
(4)

2.2 Stability Conditions Based on the Matrices Norms

The following lemma introduced in Belarbi (2019) gives the conditions for global stability of the discrete TS system (2) with \(u\left(t\right)=0\).

Lemma 1

(Sufficient condition for global stability of discrete Takagi–Sugeno fuzzy systems (Belarbi, 2019)) The fuzzy system (2) with \(u\left(t\right)=0\) and \({h}_{i}\left(z\left(t\right)\right)\) satisfying the convex sum property (3) is globally asymptotically stable if there exists a finite integer k such that.

$$\begin{aligned}\Vert {A}_{{i}_{1}}{A}_{{i}_{2}}\dots {A}_{{i}_{l}}\Vert <1 {i}_{1}&=1\dots r, {i}_{2}=1\dots r,\\ & \quad {i}_{l}=1\dots r, l=2\dots k\end{aligned}$$
(5)

\(\Vert \, \Vert \) can be the ∞-norm, 1-norm, or the 2-norm.

On the other hand, the following lemma provides condition for local stability:

Lemma 2

(Local stability of discrete TS fuzzy systems) System (1) with \(u\left(t\right)=0\) and (3) is locally asymptotically stable in a region \({S}_{o}\) around the origin, if and only if there exists a finite integer k and \({\alpha }_{i}, {\alpha }_{i}={\overline{\alpha }}_{i} \,or\, {\alpha }_{i}= \underline{{\alpha _{i} }} , i=1\dots r\) with.

$$0< {\overline{\alpha }}_{i}<1, 0< \underline{{\alpha _{i} }}<1$$
(6)

such that:

$$\begin{aligned}\Vert {A}_{{i}_{1}}^{^{\prime}} &\times {A}_{{i}_{2} }^{^{\prime}}\times \dots {\times A}_{{i}_{l}}^{^{\prime}}\Vert <1\,{i}_{1}=1\dots r,\\&\quad {i}_{2}=1\dots r,{i}_{l}=1\dots r, l=2\dots k\end{aligned}$$
(7)

where \({A}_{i}^{^{\prime}}={\alpha }_{i}{A}_{i}\).

Remark: The proof is based on the fact that if (6) is satisfied, then there must exist \(\overline{z}\) and \(\underline{z}\) such that \({\overline{\alpha }}_{i}={h}_{i}(\overline{z})\) and \(\underline{{\alpha _{i} }} ={h}_{i}\left(\underline{z}\right).\) The region of local stability is then limited by \(\overline{z}\) and \(\underline{z}\).

3 TS Fuzzy Observer Design

The usual parallel distributed compensation, PDC, structure is considered for the TS fuzzy observer with local Luenberger observers. As it is well known, two different cases arise (Tanaka et al., 1998) according to whether the premises variables are measurable or unmeasurable.

3.1 TS Fuzzy Observer with Measurable Premise Variables

When the premises of the TS fuzzy model depend only on the measurable variables, the classical fuzzy observer for the discrete time fuzzy model is

$$\begin{aligned}\widehat{x}\left(t+1\right)&=\sum_{i=1}^{r}{h}_{i}\left(z\left(t\right)\right)\left({A}_{i}\widehat{x}\left(t\right)+{B}_{i}u\left(t\right)\right.\\&\quad\left.+{L}_{i}\left(y\left(t\right)-\widehat{y}\left(t\right)\right)\right)\end{aligned}$$
(8)
$$\widehat{y}\left(t\right)=\sum_{i=1}^{r}{h}_{i}\left(z\left(t\right)\right){C}_{i}\widehat{x}\left(t\right);$$

Given the estimation error \(e\left(t\right)=x\left(t\right)-\widehat{x}\left(t\right)\), the fuzzy observer should satisfy \(e\left(t\right)\to 0 \,as\, t\to \mathrm{ \infty }.\)

From (8) and (2), the estimation error is given by

$$e\left(t+1\right)=\sum_{i=1}^{r}\sum_{j=1}^{r}{h}_{i}\left(z\left(t\right)\right){h}_{j}\left(z\left(t\right)\right)\left({A}_{i}-{L}_{i}{C}_{j}\right)e(t)$$
(9)
$${0\le h}_{i}{\left(z\left(t\right)\right)h}_{j}\left(z\left(t\right)\right)<1 \forall i,j$$

Setting \({{\mathcal{A}}_{ij}=A}_{i}-{L}_{i}{C}_{j}, i=1\dots r,j=1,\dots ,r\) the estimation error (9) is rewritten as

$$e\left(t+1\right)=\sum_{i}^{r}\sum_{j}^{r}{h}_{i}{\left(z\left(t\right)\right)h}_{j}\left(z\left(t\right)\right){\mathcal{A}}_{ij}e(t)$$
(10)

The error equation can be written in compact form as

$$e\left(t+1\right)=\sum_{i=1}^{r\times r}{\widetilde{h}}_{i}\left(z\left(t\right)\right){\mathcal{A}}_{i}e(t),$$
(11)
$$0<{\widetilde{h}}_{i}\left(z\left(t\right)\right)\le 1\, i=1\dots r\times r, \sum_{i=1}^{r\times r}{\widetilde{h}}_{i}\left(z\left(t\right)\right)=1$$
(12)

The following theorem gives the sufficient condition for the global convergence of the estimation error (11):

Theorem 1

The observer error given by (11) with (12) converges globally asymptotically to the origin if there exists \({L}_{i}\) in (10) and a finite integer \(k\) such that.

$$\begin{aligned}&\Vert {\mathcal{A}}_{{i}_{1}}{\mathcal{A}}_{{i}_{2}}\dots {\mathcal{A}}_{{i}_{l}}\Vert <1 \quad {i}_{1}=1\dots r\times r,\\&\quad {i}_{2}=1\dots r\times r,{i}_{l}=1\dots r\times r, l=2\dots k\end{aligned}$$
(13)

Proof

Since \({\widetilde{h}}_{i}\left(z\left(t\right)\right)\) in (12) satisfy the convex sum property, the proof is a direct application of lemma 1.

Likewise, local convergence of the fuzzy observer error is given by the following theorem:

Theorem 2

The observer error given by (11) with (12) converges locally asymptotically to the origin if and only if there exist \({L}_{i}\) in (10), a finite integer k and \({\alpha }_{i}, {\alpha }_{i}={\overline{\alpha }}_{i} or {\alpha }_{i}=\underline{{\alpha _{i} }} , i=1\dots r \) with

$$0< {\overline{\alpha }}_{i}<\mathrm{1,0}< \underline{{\alpha _{i} }} <1$$
(14)

such that

$$\begin{aligned}&\Vert {\mathcal{A}\mathrm{^{\prime}} }_{{i}_{1}}{\mathcal{A}\mathrm{^{\prime}}}_{{i}_{2}}\dots {\mathcal{A}\mathrm{^{\prime}}}_{{i}_{l}}\Vert <1 {i}_{1}=1\dots r\times r,\\&\quad {i}_{2}=1\dots r\times r, l=2\dots k\end{aligned}$$
(15)

where \({\mathcal{A}}_{i}^{\prime } = \alpha_{i} {\mathcal{A}}_{i}\).

Proof

As for Theorem 1, the proof is a direct application of lemma 2

Theorems 1 and 2 allow us to develop a fuzzy observer design procedure for measurable premise variables.

It was shown in Belarbi (2019) that the design of the fuzzy controller can be cast as a norm minimization problem. Using this result and the fact that the design of the fuzzy observer is dual to that of the controller and considering global convergence as given by Theorem 1, the design can be cast as the following norm minimization problem (Belarbi, 2019):

$$\underset{{L}_{i}}{\mathrm{min}}\Vert {A}_{i}-{L}_{i}{C}_{j}\Vert i=1\dots r, j=1 \dots r$$
(16)

Alternatively, this can be rewritten implicitly as.

Find \({L}_{i}\) with

$$\Vert {A}_{i}-{L}_{i}{C}_{j}\Vert <1, i=1\dots r, j=1\dots r$$
(17)

This problem is equivalent to the following LMIs in the observer gains \({L}_{i}\) (Bouyahya et al., 2020):

$$ \left( {\begin{array}{*{20}c} I & {amp;A_{i} - L_{i} C_{j} } \\ {(A_{i} - L_{i} C_{j} )^{\prime } } & {amp;I} \\ \end{array} } \right){\text{ }};{\mkern 1mu} 0\,i = 1...r,j = 1...r $$
(18)

It is clear that if for some \(i,j \in \{1\dots r\}\) (18) is not satisfied, (16) is implicitly satisfied since the associated minimum norm cannot be less than one.

However, unless all norms in the solution of (18) are less than one, there is no guarantee that this norm minimization implies convergence of the observer. A second step is thus necessary to verify that global convergence using (13) or local convergence using (13) is satisfied.

3.2 Case 2: TS Fuzzy Observer with Unmeasurable Premise Variables

In this paragraph, we consider the design of a robust fuzzy observer for a nonlinear system whose TS fuzzy model includes unmeasurable premise variables. This TS fuzzy model is transformed into one with only measurable premises variables using the model reduction procedure of Taniguchi et al., (2001). Parameters uncertainties are then introduced into the reduced-order model to compensate for the reduction error.

The reduced-order model with uncertainties is written as

$$\begin{aligned}x\left(t+1\right)&=\sum_{i=1}^{{r}_{d}}{h}_{i}\left(z\left(t\right)\right)\\&\left(\left({A}_{{d}_{i}}+{D}_{i}{\Delta A}_{i} {E}_{i}\right)x\left(t\right)+\left({B}_{{d}_{i}}+{\Delta B}_{i}\right)u\left(t\right)\right)\end{aligned}$$
(19)

where \({r}_{d}\) is the reduced number of rules, and \({\Delta A}_{i}\), \({\Delta B}_{i}\) are the upper bound on the uncertainties computed as in Taniguchi (2001), with

$${D}_{i}= \left[\begin{array}{c}\begin{array}{c}0\\ .\end{array}\\ \begin{array}{c}0\\ 1\\ 0\end{array}\\ \begin{array}{c}.\\ 0\end{array}\end{array}\right]{ E}_{i}=\left[\begin{array}{ccc}0& \dots & \begin{array}{ccc}0& 1& \begin{array}{ccc}0& \dots & 0\end{array}\end{array}\end{array}\right]$$

The position of the ones corresponds to the indices of the reduced variable. The robust fuzzy observer with respect to reduced-order fuzzy model (19) is given by

$$\begin{aligned}\widehat{x}\left(t+1\right)&=\sum_{i=1}^{{r}_{d}}{h}_{i}\left(z\left(t\right)\right)\left(\left(\left({A}_{{d}_{i}}+{{D}_{i}\Delta A}_{i}{E}_{i}\right)\widehat{x}\left(t\right)\right.\right. \\ & \quad\left.\left. +{(B}_{{d}_{i}}+{\Delta B}_{i}\right)u\left(t\right)+{L}_{i}\left(y\left(t\right)-\widehat{y}\left(t\right)\right)\right)\end{aligned}$$
(20)
$$\widehat{y}\left(t\right)=\sum_{i=1}^{{r}_{d}}{h}_{i}\left(z\left(t\right)\right){C}_{{d}_{i}}\widehat{x}\left(t\right)$$

From this definition, the estimation error is computed as

$$\begin{aligned}e\left(t+1\right)&=\sum_{i=1}^{{r}_{d}}\sum_{j=1}^{{r}_{d}}{h}_{i}\left(z\left(t\right)\right){h}_{j}\left(z\left(t\right)\right)\\ & \left(\left({A}_{{d}_{i}}+{{D}_{i}\Delta A}_{i}\left(t\right){E}_{i}\right)-{L}_{i}{C}_{{d}_{j}}\right)e(t)\end{aligned}$$
(21)

with

$${0\le h}_{i}{\left(z\left(t\right)\right)h}_{j}\left(z\left(t\right)\right)<1 \forall i,j$$

This can be rewritten as

$$e\left(t+1\right)=\sum_{i=1}^{r\times r}{\widetilde{h}}_{i}\left(z\left(t\right)\right)\left(\left({A}_{{d}_{i}}+{{D}_{i}\Delta A}_{i}{E}_{i}\right)-{L}_{i}{C}_{{d}_{j}}\right)e(t),$$
(22)
$$0<{\widetilde{h}}_{i}\left(z\left(t\right)\right)\le 1 i=1\dots r\times r, \sum_{i=1}^{r\times r}{\widetilde{h}}_{i}\left(z\left(t\right)\right)=1$$
(23)

The fuzzy observer design is carried out as in the case of the measurable premise variables replacing \({A}_{i}-{L}_{i}{C}_{j}\) by.

\({A}_{{d}_{i}}+\Delta {A}_{i}-{L}_{i}{C}_{{d}_{j}}\) in (16), (17) and (18), that is

$$ \mathop {\min }\limits_{{L_{i} }} \left\| {A_{{d_{i} }} + A_{i} - L_{i} C_{{d_{j} }} } \right\|, i = 1...r, j = 1...r $$
(24)

and

$$ \begin{aligned}&\left( {\begin{array}{*{20}c} I & {A_{{d_{i} }} + \Delta A_{i} - L_{i} C_{{d_{j} }} } \\ {\left( {A_{{d_{i} }} + \Delta A_{i} - L_{i} C_{{d_{j} }} } \right)^{\prime } } & I \\ \end{array} } \right)\\& > 0\quad i = 1...r, j = 1...r \end{aligned}$$
(25)

3.3 Reduced-Order Fuzzy Observer

The above full-order fuzzy observer estimates all states whether they are measurable or not. The reduced-order observer estimates only the unmeasurable variables. The basic formulation of the reduced-order observer separates the state variables into measurable and unmeasurable. For the TS fuzzy model, this is written as

$${x}_{a}\left(t+1\right)=\sum_{i=1}^{r}{h}_{i}\left(z\left(t\right)\right)\left({{A}_{aa}}_{i}{x}_{a}\left(t\right)+{A}_{{ab}_{i}}{x}_{b}\left(t\right)+{B}_{{a}_{i}}u\left(t\right)\right)$$
(26)
$${x}_{b}\left(t+1\right)=\sum_{i=1}^{r}{h}_{i}\left(z\left(t\right)\right)\left({{A}_{ba}}_{i}{x}_{a}\left(t\right)+{A}_{{bb}_{i}}{x}_{b}\left(t\right)+{B}_{{b}_{i}}u(t)\right)$$
(27)
$$y\left(t\right)={x}_{a}\left(t\right)$$

with \({x}_{a}\left(t\right)\) the measurable variables and \({x}_{b}\left(t\right)\) the unmeasurable variables to be observed.

This representation is reformulated as

$${x}_{b}\left(t+1\right)=\sum_{i=1}^{r}{h}_{i}\left(z\left(t\right)\right)\left({A}_{{bb}_{i}}{x}_{b}\left(t\right)+{B}_{{d}_{i}}{u}_{d}\left(t\right)\right)$$
(28)

with \({u}_{d}(t)=\left(\begin{array}{c}{x}_{a}\left(t\right)\\ u(t)\end{array}\right)\)

and \({B}_{{d}_{i}}=\left(\begin{array}{c}{A}_{{ba}_{i}}\\ {B}_{{b}_{i}}\end{array}\right)\)

and

$$\begin{aligned}{}&{x}_{a}\left(t+1\right)-\sum_{i=1}^{r}{h}_{i}\left(z\left(t\right)\right)\left({{A}_{aa}}_{i}{x}_{a}\left(t\right)+{B}_{{a}_{i}}u\left(t\right)\right)\\& ={A}_{{ab}_{i}}{x}_{b}\left(t\right)={C}_{{d}_{i}}{x}_{b}\left(t\right) \end{aligned}$$
(29)

The measured output for the reduced-order observer is

$${y}_{d}\left(t+1\right)= \sum_{i=1}^{r}{h}_{i}\left(z\left(t\right)\right)\left({x}_{a}\left(t+1\right)-{A}_{{aa}_{i}}{x}_{a}\left(t\right)-{B}_{{a}_{i}}u\left(t\right)\right)$$
(30)

The estimation error of the reduced-order fuzzy observer with the measurable premise variables is

$${e}_{b}\left(t+1\right)=\sum_{i=1}^{r}\sum_{j=1}^{r}{h}_{i}\left(z\left(t\right)\right){h}_{j}\left(z\left(t\right)\right)\left({A}_{{bb}_{i}}-{L}_{i}{C}_{{d}_{k}}\right){e}_{b}(t)$$

The results of the preceding section on the full-order fuzzy observer are applied directly to the reduced-order observer by making the adequate substitutions.

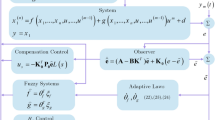
4 Observer-Based Output Feedback Fuzzy Controller

In this section, we consider a system controlled with a PDC fuzzy controller together with the PDC fuzzy observer developed in the previous sections. In this case, the control signal depends on the observed states:

$$u\left(t\right)=-\sum_{i}^{r}{{h}_{i}\left(z\left(t\right)\right)K}_{i}\widehat{x}(t)$$
(31)

We first study the case of a fuzzy observer with measurable premise variables and the PDC control law. The closed loop is obtained as

$$x\left(t+1\right)=\sum_{i}^{r}{h}_{i}\left(z\left(t\right)\right)\left({A}_{i}x\left(t\right)-{B}_{i}\sum_{j}^{r}{{h}_{j}\left(z\left(t\right)\right)K}_{j}\widehat{x}(t)\right)$$
(32)

Setting \({x}_{a}(k)=\left(\begin{array}{c}x(t)\\ e(t)\end{array}\right),\) as the augmented system equation yields

$$\begin{aligned}{x}_{a}\left(t+1\right)&=\sum_{i=1}^{r}\sum_{j=1}^{r}{h}_{i}\left(z\right){h}_{j}\left(z\right)\left(\begin{array}{cc}{A}_{i}-{B}_{i}{K}_{j}& {B}_{i}{K}_{j}\\ 0& {A}_{i}-{L}_{i}{C}_{j}\end{array}\right)\\ & {x}_{a}(t)\end{aligned}$$
(33)

Using the same formalism as in the previous section, this equation is rewritten as

$${x}_{a}\left(t+1\right)=\sum_{i=1}^{r\times r}{\widetilde{h}}_{i}\left(z\right){\mathbb{A}}_{i}x(t), {\widetilde{h}}_{i}\in \left[0, 1\right], i=1\dots \times r$$
(34)
$$0<{\widetilde{h}}_{i}\left(z\right)\le 1 \sum_{i=1}^{r\times r}{\widetilde{h}}_{i}\left(z\right)=1$$
(35)

with

$${\mathbb{A}}_{l}\equiv \left(\begin{array}{cc}{A}_{i}-{B}_{i}{K}_{j}& {B}_{i}{K}_{j}\\ 0& {A}_{i}{-L}_{i}{C}_{k}\end{array}\right)$$
(36)

For the case of the reduced-order model with the uncertainties, the augmented system equation is given by (34) with

$${\mathbb{A}}_{l}\equiv \left(\begin{array}{cc}{A}_{i}+\Delta {A}_{i}-{(B}_{i}+\Delta {B}_{i}){K}_{j}& ({B}_{i}+{\Delta {B}_{i})K}_{j}\\ 0& {A}_{{d}_{i}}+\Delta {A}_{i}-{L}_{i}{C}_{{d}_{j}}\end{array}\right)$$
(37)

Given the equations of the augmented systems, the following theorem provides the sufficient conditions for global stability of the closed-loop system with the PDC fuzzy control and fuzzy observer.

Theorem 3

The augmented system given by (34) with (35) in the case of the measurable premise variables converges globally asymptotically to the origin if there exists \({L}_{i,} i=1\dots n\) \({K}_{j}, j=1\dots n\) and an integer \(k\) such that:

$$\begin{aligned}&\Vert {\mathbb{A}}_{{i}_{1}}{\mathbb{A}}_{{i}_{2}}\dots {\mathbb{A}}_{{i}_{l}}\Vert <1 {i}_{1}=1\dots r\times r, {i}_{2}=1\dots r\times r,\\ & {i}_{s}=1\dots r\times r , l=2\dots k\end{aligned}$$
(38)

\({\mathbb{A}}_{i}\) is given by (38).

Proof

As in the previous section, since \({\widetilde{h}}_{i}\left(z\left(t\right)\right)\) in (34) satisfy the convex sum property, the proof follows from Lemma 1.

Local convergence of the augmented system to zero is obtained by application of lemma 2.

Theorem 4

The state of the augmented system given by (33) with (34) converges locally asymptotically to the origin if and only if there exists a finite k and \({\alpha }_{i}, {\alpha }_{i}={\overline{\alpha }}_{i} or {\alpha }_{i}=\underline{{\alpha _{i} }} , i=1\dots r \) with

\(0< {\overline{\alpha }}_{i}<1, 0< \underline{{\alpha _{i} }} <1\)

such that:

$$ \left\| {{{\mathbb{A}}^{\prime}}_{{i_{1} }} {{\mathbb{A}}^{\prime}}_{{i_{2} }} \ldots {{\mathbb{A}}^{\prime}}_{{i_{l} }} } \right\| < 1 i_{1} = 1...r \times r, i_{2} = 1...r \times r, l = 2...k $$
(39)
$$ {{\mathbb{A}}^{\prime}}_{i} = \alpha_{i} {\mathbb{A}}_{i} $$

with \({\mathbb{A}}_{i}\) given by (36).

Proof

The proof is a direct application of lemma 2

The condition of stability of the augmented system for the case of unmeasurable variables is obtained by replacing \({\mathbb{A}}_{i}\) in (38) by \({\mathbb{A}}_{l}\) of (39). The proofs follow from Theorems 3 and 4.

It can be noticed from the structure of the matrices \({\mathbb{A}}_{l}\) in (38) and (39); by the definition of 1-norm and the ∞-norm, the separation principle holds. Consequently, it is possible to design separately the TS fuzzy controller and the observer.

5 Examples

In this section, two design problems are described to demonstrate the application of the proposed approaches for TS fuzzy observer design for discrete time case. In order to allow for comparison, these examples are taken from the literature.

Example 1

TS Fuzzy Observer with Measurable Premise Variables

In this first example, we describe the design of a TS fuzzy observer for the tunnel diode considered previously (Xie et al., 2015, 2018, Wang et al., 2020) which is considered to be a difficult problem. The following state space model gives the nonlinear model of this component:

$${\dot{x}}_{1}\left(t\right)=\left(-0.002{0x}_{1}\left(t\right)-0.010{x}_{1}^{3}\left(t\right)+{x}_{2}\left(t\right)\right)/C$$
$${\dot{x}}_{2}\left(t\right)=\left(-{x}_{1}\left(t\right)-R{x}_{2}\left(t\right)\right)/L$$
$$y(t)={x}_{1}\left(t\right)$$

where \({x}_{1}\left(t\right)\) and \({x}_{2}\left(t\right)\) are, respectively, the voltage and the current across the diode. The two-rule discrete TS fuzzy model given in Xie et al., (2015) with the measurable premise variable \({x}_{1}\) and sampling \(T=0.02\) has the following local matrices:

$${A}_{1}=\left(\begin{array}{cc}0.9886& 0.9023\\ -0.0180& 0.810\end{array}\right){A}_{2}=\left(\begin{array}{cc}0.9034& 0.8616\\ -0.0172& 0.8104\end{array}\right)$$
$${C}_{1}={C}_{2}=\left(\begin{array}{cc}1& 0\end{array}\right)$$

with normalized membership functions

$${h}_{1}({x}_{1}\left(t\right))=\left\{\begin{array}{c}\begin{array}{c}\frac{{x}_{1}\left(t\right)+3}{3}\,for\,-3\le {x}_{1}(t)\le 0\\ 0 \,for\, {x}_{1}\left(t\right)<-3 \end{array} \\ \begin{array}{c}\frac{-{x}_{1}(t)+3}{3} \,for\, 0\le {x}_{1}(t)\le 3 \\ 0 \,for\, {x}_{1}(t)>3\end{array}\end{array}\right.$$
$${h}_{2}\left({x}_{1}\left(t\right)\right)=1-{h}_{1}\left({x}_{1}\left(t\right)\right)$$

The fuzzy observer is set as

$$\widehat{x}(t+1)=\sum_{i=1}^{2}{h}_{i}\left({x}_{1}\left(t\right)\right)\left({A}_{i}\widehat{x}\left(t\right)+{L}_{i}\left(y\left(t\right)-\widehat{y}\left(t\right)\right)\right)$$

The design is cast as in Eq. (19). Since \({C}_{1}={C}_{2},\) we obtain the following:

$$\ \mathop {{\text{min}}}\limits_{{L_{1} }} \left\| {A_{1} - L_{1} C_{1} } \right\|\,{\text{and}}\,\mathop {{\text{min}}}\limits_{{L_{2} }} \left\| {A_{2} - L_{2} C_{2} } \right\| $$

Choosing the infinity norm with \({L}_{1}=\left(\begin{array}{c}{L}_{11}\\ {L}_{12}\end{array}\right)\) and \({L}_{2}=\left(\begin{array}{c}{L}_{21}\\ {L}_{22}\end{array}\right)\), these can be written explicitly as

$$ \mathop {{\text{min}}}\limits_{{L_{1} }} \left\| {\begin{array}{*{20}c} {0.9887 - L_{{11}} } & {0.9024} \\ { - 0.0180 - L_{{12}} } & {0.810} \\ \end{array} } \right\|_{\infty } $$

and

$$ \mathop {{\text{min}}}\limits_{{L_{2} }} \left\| {\begin{array}{*{20}c} {0.9033 - L_{{21}} } & {0.8617} \\ { - 0.0172 - L_{{22}} } & {0.8103} \\ \end{array} } \right\|_{\infty } $$

This problem can be solved easily by hand to give.

\({L}_{1}=\left(\begin{array}{c}0.9887\\ -0.0180\end{array}\right)\) and \({L}_{2}=\left(\begin{array}{c}0.9033\\ -0.0172\end{array}\right)\)with the norms

\({\Vert {A}_{1}-{L}_{1}{C}_{1}\Vert }_{\infty }\)= 0.9024 and \({\Vert {A}_{2}-{L}_{2}{C}_{2}\Vert }_{\infty }\)= 0.8617.

Since the norms are less than one, Theorem 1 is satisfied with \(k=2\) and the estimation error is globally asymptotically convergent to zero.

The results of simulations are shown in Fig. 1 in dotted red lines, for the following initial conditions:\(x(\mathrm{0,0})=(1.5, 1.5)\) and \(x(\mathrm{0,0})=(-1.5, -1.5)\)with \(\widehat{x}(\mathrm{0,0})=(0, 0)\)

Fig. 1
figure 1

Example 1: error 1 with original gains and error 2 with altered gains

Full size image
$$x\left(\mathrm{0,0}\right)=\left(3, 3\right) \widehat{x}(\mathrm{0,0})=(3, -3)$$
$$x(\mathrm{0,0})=(3, -3)\widehat{x}=\left(3, 3\right)$$

The errors convergences are quite sluggish. Noting that \({L}_{12}\) and \({L}_{22}\) can be increased up to 0.172 with the infinity norm remaining less than one. These gains are altered to \({L}_{12}={L}_{22}=0.170\) with the resulting norms \({\Vert {A}_{1}-{L}_{1}{C}_{1}\Vert }_{\infty }=0.9980\) and \({\Vert {A}_{2}-{L}_{2}{C}_{2}\Vert }_{\infty }=0.9975\). The results of the simulations are shown in Fig. 1 in continuous blue line. The improvement is quite significant, and the errors show much better transient.

As a comparison, the results obtained in Xie et al., (2018) and Wang et al., (2020) involve quite complicated procedures involving the solution of no less than fifteen LMIs, while the approach of Xie et al., (2015) fails to provide a solution.

Example 2

Observer-Based Output Feedback Fuzzy Controller

As a second example, we consider an open-loop unstable system that was studied in Dong et al., (2010), Zhang et al., (2015), Pan et al., (2021). The discrete model of this system with a discretization step \(T=0.5\) is given by:

$$\begin{aligned}{x}_{1}\left(t+1\right)&=(1+T){x}_{1}(t)+{Tx}_{2}(t)+T\mathrm{sin}{x}_{3}(t)+0.1T{x}_{4}(t)\\&\quad+T(1+{x}_{1}^{2}(t))u(t)\end{aligned}$$
$${x}_{2}(t+1)=T{x}_{1}(t)+(1-2T){x}_{2}(t)$$
$${x}_{3}\left(t+1\right)=T{x}_{1}\left(t\right)+(1-0.3T){x}_{3}\left(t\right)+T{x}_{1}^{2}(t){x}_{2}(t)$$
$${x}_{4}\left(t+1\right)=\left(1-T\right){x}_{4}\left(t\right)+T\mathrm{sin}{x}_{3}(t)$$
$${y}_{1}\left(t\right)={x}_{2}(t)+\left(1+{x}_{1}^{2}\left(t\right)\right){x}_{4}(t)$$
$${y}_{2}\left(t\right)={x}_{1}(t)$$

The objective is to design an observer-based output feedback fuzzy controller using the method described in this paper. This implies the following steps:

  • Obtain a fuzzy model of the system using the sector nonlinearity approach.

  • Construct a reduced-order model with measurable variables and parameters uncertainties.

  • Design separately a robust TS reduced-order robust fuzzy observers and fuzzy controllers.

The sector nonlinearity approach used in the sector\({x}_{1}\left(t\right)\in \left[-a ,+a\right]\), \({x}_{3}\left(t\right)\in \left[-b ,+b\right]\) with the premise variables.\({z}_{1}={x}_{1}^{2}\) and \({z}_{2}=\frac{\mathrm{sin}{x}_{3}}{{x}_{3}}\) yields the following four-rule TS fuzzy model

$$x\left(t+1\right)=\sum_{i=1}^{4}{h}_{i}\left(z\left(t\right)\right)\left({A}_{i}x\left(t\right)+{B}_{i}u\left(t\right)\right)$$
$$\mathrm{y}\left(t\right)=\sum_{i}^{4}{h}_{i}\left(z\left(t\right)\right){C}_{i}\mathrm{x}\left(t\right);$$

with

$${A}_{1}=\left(\begin{array}{cc}\begin{array}{cc}\begin{array}{c}\begin{array}{c}1+T\\ T\end{array}\\ \begin{array}{c}T\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{c}T\\ 1-2T\end{array}\\ \begin{array}{c}T{a}^{2}\\ 0\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\begin{array}{c}T\\ 0\end{array}\\ \begin{array}{c}1-0.3T\\ T\end{array}\end{array}& \begin{array}{c}\begin{array}{c}0.1T\\ 0\end{array}\\ \begin{array}{c}0\\ 1-T\end{array}\end{array}\end{array}\end{array}\right)$$
$${A}_{2}=\left(\begin{array}{cc}\begin{array}{cc}\begin{array}{c}\begin{array}{c}1+T\\ T\end{array}\\ \begin{array}{c}T\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{c}T\\ 1-2T\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\begin{array}{c}T\\ 0\end{array}\\ \begin{array}{c}1-0.3T\\ T\end{array}\end{array}& \begin{array}{c}\begin{array}{c}0.1T\\ 0\end{array}\\ \begin{array}{c}0\\ 1-T\end{array}\end{array}\end{array}\end{array}\right)$$
$${A}_{3}=\left(\begin{array}{cc}\begin{array}{cc}\begin{array}{c}\begin{array}{c}1+T\\ T\end{array}\\ \begin{array}{c}T\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{c}T\\ 1-2T\end{array}\\ \begin{array}{c}T{a}^{2}\\ 0\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\begin{array}{c}T\frac{\mathrm{sin}b}{b}\\ 0\end{array}\\ \begin{array}{c}1-0.3T\\ T\frac{\mathrm{sin}b}{b}\end{array}\end{array}& \begin{array}{c}\begin{array}{c}0.1T\\ 0\end{array}\\ \begin{array}{c}0\\ 1-T\end{array}\end{array}\end{array}\end{array}\right)$$
$${A}_{4}=\left(\begin{array}{cc}\begin{array}{cc}\begin{array}{c}\begin{array}{c}1+T\\ T\end{array}\\ \begin{array}{c}T\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{c}T\\ 1-2T\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\begin{array}{c}T\frac{\mathrm{sin}b}{b}\\ 0\end{array}\\ \begin{array}{c}1-0.3T\\ T\frac{\mathrm{sin}b}{b}\end{array}\end{array}& \begin{array}{c}\begin{array}{c}0.1T\\ 0\end{array}\\ \begin{array}{c}0\\ 1-T\end{array}\end{array}\end{array}\end{array}\right)$$
$${C}_{1}={C}_{3}=\left(\begin{array}{cc}\begin{array}{cc}\begin{array}{c}0\\ 1\end{array}& \begin{array}{c}1\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}1+{a}^{2}\\ 0\end{array}\end{array}\end{array}\right){C}_{2}={C}_{4}=\left(\begin{array}{cc}\begin{array}{cc}\begin{array}{c}0\\ 1\end{array}& \begin{array}{c}1\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}\right)$$
$${B}_{1}={B}_{3}=\left(\begin{array}{c}\begin{array}{c}1+T{a}^{2}\\ 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right){B}_{2}={B}_{4}=\left(\begin{array}{c}\begin{array}{c}T\\ 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right)$$

The variable \({z}_{1}\) is measurable, while \({z}_{2}\) is unmeasurable with the membership functions:

$${h}_{1}\left({z}_{1}\right)=\frac{{x}_{1}^{2}}{{a}^{2}}, {h}_{2}\left({z}_{1}\right)=1-{h}_{1}\left({z}_{1}\right)$$

\( h_{1} \left( {z_{2} } \right) = \frac{{\sin x_{3} /x_{3} - \sin b/b}}{{1 - \sin b/b}},h_{2} \left( {z_{2} } \right) = 1 - h_{1} \left( {z_{2} } \right) \) and \({h}_{1}\left(z\right)={h}_{1}\left({z}_{1}\right){h}_{1}\left({z}_{2}\right); {h}_{2}\left(z\right)={h}_{1}\left({z}_{1}\right){h}_{2}\left({z}_{2}\right)\)

$${h}_{3}\left(z\right)={h}_{2}\left({z}_{1}\right){h}_{1}\left({z}_{2}\right) {h}_{4}\left(z\right)={h}_{2}\left({z}_{1}\right){h}_{2}\left({z}_{2}\right)$$

From the above TS fuzzy model, a two-rule reduced-order TS fuzzy model with parameters uncertainties is obtained with the measurable premise variable \({z}_{1}={x}_{1}^{2}\). The uncertainty \(\Delta A\) with respect to the reduced variable is computed as in Taniguchi (2001) and then slightly increased to obtain \(\Delta A\) =0.95.

$$A_{{d_{1} }} = \left( {\begin{array}{*{20}c} {1 + T} & T & {\frac{T}{2}\left( {\frac{b + \sin b}{b}} \right) + \Delta A} & { - 0.1 T} \\ T & {1 - 2T} & 0 & 0 \\ T & {T \cdot a} & {1 - 0.3 T} & 0 \\ 0 & 0 & {\frac{T}{2}\left( {\frac{b + \sin b}{b}} \right) + \Delta A} & {1 - T} \\ \end{array} } \right) $$

The corresponding local matrices are

$$ A_{{d_{2} }} = \left( {\begin{array}{*{20}c} {1 + T} & T & {\frac{T}{2}\left( {\frac{b + \sin b}{b}} \right) + \Delta A} & { - 0.1 T} \\ T & {1 - 2T} & 0 & 0 \\ T & 0 & {1 - 0.3 T} & 0 \\ 0 & 0 & {\frac{T}{2}\left( {\frac{b + \sin b}{b}} \right) + \Delta A} & {1 - T} \\ \end{array} } \right) $$
$${B}_{{d}_{1}}=\left(\begin{array}{c}\begin{array}{c}1+T{a}^{2}\\ 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right){B}_{{d}_{2}}=\left(\begin{array}{c}\begin{array}{c}1\\ 0\end{array}\\ \begin{array}{c}0\\ 0\end{array}\end{array}\right)$$
$${C}_{{d}_{1}}=\left(\begin{array}{cc}\begin{array}{cc}\begin{array}{c}0\\ 1\end{array}& \begin{array}{c}1\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}1+{a}^{2}\\ 0\end{array}\end{array}\end{array}\right) {C}_{{d}_{2}}=\left(\begin{array}{cc}\begin{array}{cc}\begin{array}{c}0\\ 1\end{array}& \begin{array}{c}1\\ 0\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}\right)$$

Based on Theorem 7, the design of the observer-based output feedback controller is performed separately for the fuzzy observer and fuzzy controller. Since \({x}_{1}(t)={y}_{2}(t),\) a reduced-order fuzzy observer is designed with premise variables \({z}_{1}(t)\). In order to be able to compare with previous design in terms of conservatism, we sought the maximum value of \(a\) for which both the observer and controller design can yield a solution. This was found to be \({a}^{*}=40000\); the largest value so far was \({a}^{*}=2084.90\) obtained in Pan et al. (2021). The following controller gains are obtained using the method introduced in (Belarbi 2019):

$${K}_{1}={10}^{-8}\left(\begin{array}{ccc}0.1875& \begin{array}{cc}0.0625& 0.1762\end{array}& -0.0062\end{array}\right)$$
$${K}_{2}=\left(\begin{array}{ccc}3& 1& \begin{array}{cc}2.85& -0.1\end{array}\end{array}\right).$$

On the other hand, the following gains of the reduced-order fuzzy observer are obtained using (31) with the results of Sect. 3.3:

$${L}_{1}={10}^{8}\left(\begin{array}{c}0\\ 1.6231\\ 0\end{array}\right){L}_{2}=\left(\begin{array}{c}0\\ 0.5351\\ 0.8762\end{array}\right)$$

The gain \({K}_{2}\) was altered to \({K}_{2}=\left(\begin{array}{ccc}0.8& 1& \begin{array}{cc}2.85& -0.1\end{array}\end{array}\right)\). The test of local stability of Theorem 4 was successful for \(k=6\). The results of the simulations are shown in Fig. 2 for a variety of initial conditions. We remark that asymptotic stability of the closed loop is guaranteed by the proposed observer-based output controller designed using the separation principle introduced in Sect. 4.

Fig. 2
figure 2

Example 2: Time responses of the states

Full size image

6 Conclusion

In this work, simple design procedures have been presented for TS fuzzy observers for both measurable and unmeasurable premise variables. These are based on a condition of stability of TS fuzzy systems that uses matrices norms instead of Lyapunov theory. As in previous studies, the case of TS fuzzy observers based on a model with measurable premise variables does not present major difficulties. However, the approach introduced here is simpler and less conservative. The case of a TS model with unmeasurable premise variables was tackled by transforming this model into a reduced-order model with measurable variables and parameters uncertainties that account for the reduction error. This procedure yields a simple solution similar to the case of measurable variables. Using these results and the separation principle, we have developed an observer-based output feedback fuzzy controller for nonlinear systems. Two examples are given to show the simplicity and effectiveness of the proposed approaches.