1 Introduction

Singular systems have been widely applied to discuss control issues for tunnel diodes circuit system [1], bio−economic system [2, 3], DC motor system [4] and so on, because possessing physical signification is more general than one of normal systems. In contrast to normal systems, singular systems consist of differential equations and algebraic equations which effects the existence of the unique solution. Referring to [5], there exists the strong impulse behavior when the considered system has the infinite poles. The behavior may stop the system from working or even destroy the system. Thus, it is necessary to point out that the singular system has a unique solution because the impulse terms are not expected to appear in general. In the literature [6], the definitions concerning the matrix rank condition of the singular system were provided via decomposing the original matrix of the system. Those definitions ensure that the singular system is impulse−free and regular. Furthermore, according to the viewpoint of [6], the singular system can be stabilized if the system has unique solution, or the impulse behavior is eliminated by a controller. Based on those definitions, several control theories have been developed on linear singular systems including passive control [7], delay−dependent control [8] and robust control [9]. Those control theories also can overcome some negative effects, such as external disturbance, time−delay and uncertainty, respectively.

Generally, nonlinearity exists in most practical systems and increases the difficulty of stability analysis and controller synthesis. Thus, nonlinear singular systems have been attracted attention from scholars of control community. To analyze the nonlinearity, the nonlinear singular systems were usually represented by Takagi–Sugeno (T−S) fuzzy model [10]. According to IF–THEN rules [10], the nonlinear singular systems are separated into several linear subsystems representing the local dynamics. By blending several linear subsystems and fuzzy membership functions, the final T−S fuzzy model is obtained to represent the nonlinear systems. Besides, the uncertainty is naturally arisen in the modeling for representing modeling errors or aging components of practical systems. It may cause inaccurate control signals such that the system cannot be stabilized by the controller. Thus, robust performance became an important issue concerning the stability of practical systems in the past decades [11,12,13]. According to the concept of Parallel Distributed Compensation (PDC) [14], a state feedback fuzzy controller was furtherly constructed in [15,16,17] for stabilizing the uncertain T−S Fuzzy Singular Systems (T−SFSS). The idea of the PDC method is that each linear controller is designed for each local linear model, respectively. Thus, several linear control methods can be used to deal with the control problems of nonlinear singular systems [18,19,20]. However, referring to Remark 1 of [21], one can easily know that the singularities are mainly caused by the derivative matrix. Also, the infinite poles and the impulse behaviors cannot be well eliminated by state feedback controller which only alters the system matrix.

Generally, the methods as state feedback control [16, 22, 23] and output feedback control [24, 25] are usually applied for the stability analysis of T−SFSS. Referring to those methods [16, 22,23,24,25], two portions were focused on discussing the stability analysis. The first one is to ensure the regularity and impulse free for that T−SFSS has unique solution and non−impulsive behavior. Another is to analyze the stability of T−SFSS based on Lyapunov theory. As the generally known, it is complex and difficult to guarantee the first portion. For reducing the complexity, Proportional−Derivative (PD) control method was proposed by [26,27,28,29] to be an effective feedback control scheme for the singular systems. From those researches [26, 28, 29], the free−weighting matrix technique was extensively applied for decoupling the state feedback gain and derivative state feedback gain. Referring to [26,27,28,29], the derivative feedback in PD controller is applied to effectively eliminate the impulse behavior and change the dynamical order [26]. Thus, the procedure of ensuring the regularity and non−impulsiveness is successfully simplified through inversing the derivative term of PD controller.

However, the completely information of the states is a practical problem for designing the PD controller because of the derivative term. According to the existence of all states, a PD fuzzy observer for nonlinear singular systems was investigated by [30, 31] via the T−S fuzzy approach. Unfortunately, the controller design issue has not been discussed in [30, 31] to ensure the stability of T−SFSS. According to the above works, an observer−based PD fuzzy controller design method [32, 33] was proposed by the PDC concept for T−SFSS. And, the stability conditions of [32] were derived by an inequality and projection lemma [34] into Linear Matrix Inequality (LMI) form. Nevertheless, a conservatism in the stability criterion of [32] is produced by the diagonal positive definite matrix in their Lyapunov function. Generally, the off−diagonal in the positive definite matrix is as zeros that reduces the freedom in the calculation. Moreover, the inequality also brings the conservatism result in discussing the observer−based PD fuzzy control problem Thus, an interested issue for developing the less conservative stability criterion of T−SFSS is investigated by this paper.

According to the above motivations, this paper proposes a relaxed observer−based controller design method such that the nonlinear singular system achieves robustness and asymptotical stability. Based on the modeling approach, the uncertain nonlinear singular systems can be described by uncertain T−SFSS. To avoid the complex derivatives of discussing the regularity and non−impulsiveness, the PD control scheme and PDC concept are applied to structure the observer−based PD fuzzy controller. During the development of stability criterion, the positive definite matrix in Lyapunov function is not required as diagonal case to derive the less conservative sufficient conditions Furthermore, the technologies as Singular Value Decomposition (SVD) [23], Schur complement and projection lemma [34] are employed such that the sufficient conditions can be converted into LMI form. Thus, the proposed design method can directly apply the convex optimization algorithm [35] to find the feasible solutions for establishing the observer−based PD fuzzy controller. The contributions of this paper can be summarized as follows. (1) The proposed control design method is more general than one in [32] due to the consideration of robust control. (2) The proposed control method is less conservative than [32] because the positive definite matrix in this paper is not limited as diagonal case. Finally, a bio−economic singular system is presented to validate the effectiveness and application of the proposed control method.

This paper is organized as follows. In Sect. 2, the uncertain nonlinear singular system is expressed as the T−S fuzzy model. In Sect. 3, some sufficient are derived to ensure robust stability. In Sect. 4, an example is provided to demonstrate the applicability of the proposed method. At last, the conclusion is stated in Sect. 5.


Notation \(\Re^{{n_{x} }}\) and \(\Re^{{n_{x} \times n_{u} }}\) represent the \(n_{x}\)-dimensional vector and the \(n_{x} \times n_{u}\)-dimensional matrix, respectively. \({\mathbf{I}}\) represents the identity matrix with approximate dimension. \(sym\left\{ \varphi \right\}\) denotes the shorthand of \(\varphi { + }\varphi^{{\text{T}}}\). \(*\) denotes the symmetric term in the matrix. \({\mathbf{\aleph }}_{ \bot }\) represents the null-space matrix of \({\mathbf{\aleph }}\). \({\mathbf{\aleph }}^{\text{T}} = {\mathbf{\aleph }}^{ - 1}\) denotes orthogonal matrix.

2 System Descriptions and Problem Statements

In this section, a class of nonlinear singular system with perturbations is described by the following uncertain T–SFSS.


Plant Rule i:

IF \(q_{1} \left( t \right)\) is \({\text{M}}_{i1}\) and … and \(q_{r} \left( t \right)\) is \({\text{M}}_{ir}\) THEN

$${\mathbf{E}}\dot{x}\left( t \right) = \left( {{\mathbf{A}}_{i} + {\mathbf{\Delta A}}_{i} \left( t \right)} \right)x\left( t \right) + \left( {{\mathbf{B}}_{i} + {\mathbf{\Delta B}}_{i} \left( t \right)} \right)u\left( t \right)$$
(1a)
$$y\left( t \right) = {\mathbf{C}}x\left( t \right)$$
(1b)

where \(q\left( t \right) = \left[ {\begin{array}{*{20}c} {q_{1} \left( t \right)} & {q_{{2}} \left( t \right)} & \cdots & {q_{r} \left( t \right)} \\ \end{array} } \right]\) are premise variables, \(M_{ir}\) is the fuzzy set, \(r\) is the number of premise variables, \(i = 1,2 \, ..., \, m\), \(m\) is the number of rules, \(x\left( t \right) \in \Re^{{n_{x} }}\) is the state vector, \(u\left( t \right) \in \Re^{{n_{u} }}\) is the control input vector and \(y\left( t \right) \in \Re^{{n_{y} }}\) is output vector. \({\mathbf{A}}_{i} \in \Re^{{n_{x} \times n_{x} }}\), \({\mathbf{B}}_{i} \in \Re^{{n_{x} \times n_{u} }}\) and \({\mathbf{C}} \in \Re^{{n_{y} \times n_{x} }}\) are constant matrices with compatible dimensions. \({\mathbf{E}}\) is a constant matrix with \(rank({\mathbf{E}}) < n_{x}\). \({\mathbf{\Delta A}}_{i} \left( t \right) \in \Re^{{n_{x} \times n_{x} }}\) and \({\mathbf{\Delta B}}_{i} \left( t \right) \in \Re^{{n_{x} \times n_{u} }}\) are considered as the time-varying perturbation matrix for the system state and input, which are represented as \({\mathbf{\Delta A}}_{i}\) and \({\mathbf{\Delta B}}_{i}\) in the following context for simplicity. Moreover, \({\mathbf{\Delta A}}_{i}\) and \({\mathbf{\Delta B}}_{i}\) can be described as

$$\left[ {\begin{array}{*{20}c} {{\mathbf{\Delta A}}_{i} } & {{\mathbf{\Delta B}}_{i} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{H}}_{Ai} {{\varvec{\Delta}}}\left( t \right){\mathbf{W}}_{Ai} } & {{\mathbf{H}}_{Bi} {{\varvec{\Delta}}}\left( t \right){\mathbf{W}}_{Bi} } \\ \end{array} } \right]$$
(2)

where \({\mathbf{H}}_{Ai}\), \({\mathbf{H}}_{Bi}\), \({\mathbf{W}}_{Ai}\) and \({\mathbf{W}}_{Bi}\) are real constant matrices with appropriate dimensions, and \({{\varvec{\Delta}}}\left( t \right)\) is unknown time-varying function satisfying \({{\varvec{\Delta}}}^{{\text{T}}} \left( t \right){{\varvec{\Delta}}}\left( t \right) \le {\mathbf{I}}\). Furthermore, the overall T–S fuzzy model is constructed as follows:

$${\mathbf{E}}\dot{x}\left( t \right) = \sum\limits_{{i = {1}}}^{m} {h_{i} \left( {q\left( t \right)} \right)\left\{ {\left( {{\mathbf{A}}_{i} + {\mathbf{\Delta A}}_{i} } \right)x\left( t \right){ + }\left( {{\mathbf{B}}_{i} + {\mathbf{\Delta B}}_{i} } \right)u\left( t \right)} \right\}}$$
(3a)
$$y\left( t \right) = {\mathbf{C}}x\left( t \right)$$
(3b)

where \(h_{i} \left( {q\left( t \right)} \right) = \frac{{\prod\nolimits_{l = 1}^{r} {{\text{M}}_{il} \left( {q_{l} \left( t \right)} \right)} }}{{\sum\nolimits_{i = 1}^{m} {\prod\nolimits_{l = 1}^{r} {{\text{M}}_{il} } } \left( {q_{l} \left( t \right)} \right)}}\), \(h_{i} \left( {q\left( t \right)} \right) \ge 0\) and \(\sum\nolimits_{i = 1}^{m} {h_{i} \left( {q\left( t \right)} \right) = 1}\).

Assumption 1

[23] The system (1) is completely controllable and completely observable if the following equalities are satisfied.

\(rank\left( {\left[ {\begin{array}{*{20}c} {s{\mathbf{E}} - {\mathbf{A}}_{i} } & {{\mathbf{B}}_{i} } \\ \end{array} } \right]} \right) = rank\left( {\left[ {\begin{array}{*{20}c} {\mathbf{E}} & {{\mathbf{B}}_{i} } \\ \end{array} } \right]} \right) = n_{x}\) and \(rank\left( {\left[ {\begin{array}{*{20}c} {s{\mathbf{E}} - {\mathbf{A}}_{i} } \\ {\mathbf{C}} \\ \end{array} } \right]} \right) = rank\left( {\left[ {\begin{array}{*{20}c} {\mathbf{E}} \\ {\mathbf{C}} \\ \end{array} } \right]} \right) = n_{x}.\) where \(\forall s \in {\mathbb{C}}_{ + }\), \({\mathbb{C}}_{ + }\) is the open right-half of the complex plane.

Assumption 2

Suppose that the matrix \({\mathbf{C}} \in \Re^{{n_{y} \times n_{x} }}\) has full row rank, the singular value decomposition of matrix \({\mathbf{C}}\) can be described as follows:

$${\mathbf{C}} = {\mathbf{U}}\left[ {\begin{array}{*{20}c} {\mathbf{S}} & {\mathbf{0}} \\ \end{array} } \right]{\mathbf{V}}^{{\text{T}}}$$

where \({\mathbf{U}} \in \Re^{{n_{y} \times n_{y} }}\) and \({\mathbf{V}} \in \Re^{{n_{x} \times n_{x} }}\) are orthogonal matrices and \({\mathbf{S}} \in \Re^{{n_{y} \times n_{y} }}\) is a diagonal matrix with positive diagonal elements.

For simplification, \(h_{i} \left( {q\left( t \right)} \right) \triangleq h_{i}\) is used in the following context. Since the consideration of unmeasurable states, the following PD fuzzy observer is constructed.


Observer Rule i:

IF \(q_{1} \left( t \right)\) is \({\text{M}}_{i1}\) and … and \(q_{r} \left( t \right)\) is \({\text{M}}_{ir}\) THEN

$${\mathbf{E}}\dot{\hat{x}}\left( t \right) = {\mathbf{A}}_{i} \hat{x}\left( t \right) + {\mathbf{B}}_{i} u\left( t \right) + {\mathbf{L}}_{pi} \left( {y\left( t \right) - \hat{y}\left( t \right)} \right) + {\mathbf{L}}_{di} \left( {\dot{y}\left( t \right) - \dot{\hat{y}}\left( t \right)} \right)$$
(4a)
$$\hat{y}\left( t \right) = {\mathbf{C}}\hat{x}\left( t \right)$$
(4b)

where \(\hat{x}\left( t \right) \in \Re^{{n_{x} }}\) is the estimated state vector and \(\hat{y}\left( t \right) \in \Re^{{n_{y} }}\) is the estimated output vector. The matrices \({\mathbf{L}}_{pi}\) and \({\mathbf{L}}_{di}\) are the observer gains. Also, the overall fuzzy observer can be furtherly represented as follows:

$${\mathbf{E}}\dot{\hat{x}}\left( t \right) = \sum\limits_{i = 1}^{m} {h_{i} \left\{ {{\mathbf{A}}_{i} \hat{x}\left( t \right) + {\mathbf{B}}_{i} u\left( t \right) + {\mathbf{L}}_{pi} \left( {y\left( t \right) - \hat{y}\left( t \right)} \right) + {\mathbf{L}}_{di} \left( {\dot{y}\left( t \right) - \dot{\hat{y}}\left( t \right)} \right)} \right\}}$$
(5a)
$$\hat{y}\left( t \right) = {\mathbf{C}}\hat{x}\left( t \right)$$
(5b)

Based on the concept of PDC, the following observer-based PD fuzzy controller is designed.


Controller Rule i:

IF \(q_{1} \left( t \right)\) is \({\text{M}}_{i1}\) and … and \(q_{r} \left( t \right)\) is \({\text{M}}_{ir}\) THEN

$$u\left( t \right) = - {\mathbf{F}}_{pi} \hat{x}\left( t \right) - {\mathbf{F}}_{di} \dot{\hat{x}}\left( t \right)$$
(6)

where \({\mathbf{F}}_{pi}\) and \({\mathbf{F}}_{di}\) are controller gains. The overall fuzzy controller can be represented as follows:

$$u\left( t \right) = \sum\limits_{i = 1}^{m} {h_{i} \left\{ { - {\mathbf{F}}_{pi} \hat{x}\left( t \right) - {\mathbf{F}}_{di} \dot{\hat{x}}\left( t \right)} \right\}}$$
(7)

In order to discuss the stabilization issue of the system (3a, 3b), the following system is inferred by introducing (7) to (5a).

$${\mathbf{E}}\dot{\hat{x}}\left( t \right) = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{m} {h_{i} h_{j} \left\{ {\left( {{\mathbf{A}}_{i} - {\mathbf{B}}_{i} {\mathbf{F}}_{pj} } \right)\hat{x}\left( t \right) + {\mathbf{L}}_{pi} {\mathbf{C}}e\left( t \right) - {\mathbf{B}}_{i} {\mathbf{F}}_{dj} \dot{\hat{x}}\left( t \right) + {\mathbf{L}}_{di} {\mathbf{C}}\dot{e}\left( t \right)} \right\}} }$$
(8)

Remark 1

Because the dynamic states and derivative states are not always measurable in reality, the PD control scheme usually assumes all the states are measurable [29]. The conclusion in [21], the author proposed that the observer-based control is a solution such that the derivative feedback signals are employed reasonably. Thus, the observer-based control issue seems meaningful and is the one of motivations of this paper.

Defining an error function \(e\left( t \right) = x\left( t \right) - \hat{x}\left( t \right)\), the following relationship is easily found using (3a, 3b), (7) and (8).

$${\mathbf{E}}\dot{e}\left( t \right) = {\mathbf{E}}\dot{x}\left( t \right) - {\mathbf{E}}\dot{\hat{x}}\left( t \right)$$
$$= \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{m} {h_{i} h_{j} \left\{ {\left( {{\mathbf{A}}_{i} + {\mathbf{\Delta A}}_{i} } \right)x\left( t \right) + \left( {{\mathbf{B}}_{i} { + }{\mathbf{\Delta B}}_{i} } \right)u\left( t \right)} \right.} }$$
$$\left. { - \left( {{\mathbf{A}}_{i} \hat{x}\left( t \right) + {\mathbf{B}}_{i} u\left( t \right) + {\mathbf{L}}_{pi} \left( {y\left( t \right) - {\mathbf{C}}\hat{x}\left( t \right)} \right) + {\mathbf{L}}_{di} \left( {\dot{y}\left( t \right) - {\mathbf{C}}\dot{\hat{x}}\left( t \right)} \right)} \right)} \right\}$$
$$= \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{m} {h_{i} h_{j} \left\{ {\left( {{\mathbf{\Delta A}}_{i} - {\mathbf{\Delta B}}_{i} {\mathbf{F}}_{pj} } \right)\hat{x}\left( t \right) + \left( {{\mathbf{A}}_{i} + {\mathbf{\Delta A}}_{i} - {\mathbf{L}}_{pi} {\mathbf{C}}} \right)e\left( t \right) - {\mathbf{\Delta B}}_{i} {\mathbf{F}}_{dj} \dot{\hat{x}}\left( t \right) - {\mathbf{L}}_{di} {\mathbf{C}}\dot{e}\left( t \right)} \right\}} }$$
(9)

Based on (8) and (9), the following augmented system is obtained for discussing observer-based PD control problem of (3a, 3b).

$$\left[ {\begin{array}{*{20}c} {\mathbf{E}} & 0 \\ 0 & {\mathbf{E}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{\hat{x}}\left( t \right)} \\ {\dot{e}\left( t \right)} \\ \end{array} } \right] = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{m} {h_{i} h_{j} \left\{ {\left[ {\begin{array}{*{20}c} {{\mathbf{A}}_{i} - {\mathbf{B}}_{i} {\mathbf{F}}_{pj} } & {{\mathbf{L}}_{pi} {\mathbf{C}}} \\ {{\mathbf{\Delta A}}_{i} - {\mathbf{\Delta B}}_{i} {\mathbf{F}}_{pj} } & {{\mathbf{A}}_{i} + {\mathbf{\Delta A}}_{i} - {\mathbf{L}}_{pi} {\mathbf{C}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\hat{x}\left( t \right)} \\ {e\left( t \right)} \\ \end{array} } \right]} \right.} }$$
$$\left. { + \left[ {\begin{array}{*{20}c} { - {\mathbf{B}}_{i} {\mathbf{F}}_{dj} } & {{\mathbf{L}}_{di} {\mathbf{C}}} \\ { - {\mathbf{\Delta B}}_{i} {\mathbf{F}}_{dj} } & { - {\mathbf{L}}_{di} {\mathbf{C}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{\hat{x}}\left( t \right)} \\ {\dot{e}\left( t \right)} \\ \end{array} } \right]} \right\}$$
(10)

Arranging (10), one can furtherly find the following equation.

$${\tilde{\mathbf{E}}}_{Rij} \left( h \right)\dot{\tilde{x}}\left( t \right) = {\tilde{\mathbf{A}}}_{Rij} \left( h \right)\tilde{x}\left( t \right)$$
(11)

where \(\tilde{x}\left( t \right) = \left[ {\begin{array}{*{20}c} {\hat{x}^{{\text{T}}} \left( t \right)} & {e^{{\text{T}}} \left( t \right)} \\ \end{array} } \right]^{{\text{T}}}\), \({\tilde{\mathbf{E}}}_{Rij} \left( h \right) = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{m} {h_{i} h_{j} \left\{ {{\tilde{\mathbf{E}}}_{Rij} } \right\}} }\), \({\tilde{\mathbf{A}}}_{Rij} \left( h \right) = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{m} {h_{i} h_{j} \left\{ {{\tilde{\mathbf{A}}}_{Rij} } \right\}} }\),\({\tilde{\mathbf{E}}}_{Rij} = {\mathbf{E}}_{Rij} + {\tilde{\mathbf{H}}}_{Bi} {{\varvec{\Delta}}}\left( t \right){\tilde{\mathbf{W}}}_{BDij}\), \({\mathbf{E}}_{Rij} = \left[ {\begin{array}{*{20}c} {{\mathbf{E}} + {\mathbf{B}}_{i} {\mathbf{F}}_{dj} } & { - {\mathbf{L}}_{di} {\mathbf{C}}} \\ 0 & {{\mathbf{E}} + {\mathbf{L}}_{di} {\mathbf{C}}} \\ \end{array} } \right]\), \({\tilde{\mathbf{H}}}_{Bi} = \left[ {\begin{array}{*{20}c} 0 \\ {{\mathbf{H}}_{Bi} } \\ \end{array} } \right]\), \({\tilde{\mathbf{W}}}_{BDij} = \left[ {\begin{array}{*{20}c} {{\mathbf{W}}_{Bi} {\mathbf{F}}_{dj} } & 0 \\ \end{array} } \right]\), \({\tilde{\mathbf{A}}}_{Rij} = {\mathbf{A}}_{Rij} + {\tilde{\mathbf{H}}}_{Ai} {{\varvec{\Delta}}}\left( t \right){\tilde{\mathbf{W}}}_{Ai} + {\tilde{\mathbf{H}}}_{Bi} {{\varvec{\Delta}}}\left( t \right){\tilde{\mathbf{W}}}_{BPij}\), \({\mathbf{A}}_{Rij} = \left[ {\begin{array}{*{20}c} {{\mathbf{A}}_{i} - {\mathbf{B}}_{i} {\mathbf{F}}_{pj} } & {{\mathbf{L}}_{pi} {\mathbf{C}}} \\ 0 & {{\mathbf{A}}_{i} - {\mathbf{L}}_{pi} {\mathbf{C}}} \\ \end{array} } \right]\), \({\tilde{\mathbf{H}}}_{Ai} = \left[ {\begin{array}{*{20}c} 0 \\ {{\mathbf{H}}_{Ai} } \\ \end{array} } \right]\), \({\tilde{\mathbf{W}}}_{Ai} = \left[ {\begin{array}{*{20}c} {{\mathbf{W}}_{Ai} } & {{\mathbf{W}}_{Ai} } \\ \end{array} } \right]\) and \({\tilde{\mathbf{W}}}_{BPij} = \left[ {\begin{array}{*{20}c} { - {\mathbf{W}}_{Bi} {\mathbf{F}}_{pj} } & 0 \\ \end{array} } \right]\).

Based on Assumption 2, there exists the controller gains \({\mathbf{F}}_{dj}\) and observer gains \({\mathbf{L}}_{di}\) such that \({\mathbf{E}}_{Rij}^{{}}\) is full rank and invertible. Therefore, the Eq. (11) is easily rewritten as follows:

$$\dot{\tilde{x}}\left( t \right) = {\tilde{\mathbf{E}}}_{Rij}^{ - 1} \left( h \right){\tilde{\mathbf{A}}}_{Rij} \left( h \right)\tilde{x}\left( t \right)$$
(12)

From (12), it should be mentioned that the argument system (10) is regular and impulse-free based on [6]. Furthermore, the system (12) is used to discuss the stability and stabilization problem of (10) for guaranteeing the convergences of \(\hat{x}\left( t \right)\) and \(e\left( t \right)\).

The following Fig. 1 is provided to clearly show the structure of the closed-loop system (12). Based on Fig. 1, the gains are required to design the fuzzy controller and fuzzy observer.

Fig. 1
figure 1

Block diagram for the closed-loop system (12)

Full size image

Definition 1 [17]

The following unforced system inferred from (3a) is robust asymptotically stable if it is asymptotically stable for any admissible uncertainty matrices \({\mathbf{\Delta A}}_{i}\).

$${\mathbf{E}}\dot{x}\left( t \right) = \sum\limits_{{i = {1}}}^{m} {h_{i} \left( {q\left( t \right)} \right)\left\{ {\left( {{\mathbf{A}}_{i} + {\mathbf{\Delta A}}_{i} } \right)x\left( t \right)} \right\}}$$

For dealing with the robust stability problem of (12), the following lemmas are employed to derive some sufficient conditions.

Lemma 1 [27]

Give the matrices \({\mathbf{H}}\) and \({\mathbf{W}}\) with appropriate dimensions, and \({{\varvec{\Delta}}}\left( t \right)\) satisfying \({{\varvec{\Delta}}}^{{\text{T}}} \left( t \right){{\varvec{\Delta}}}\left( t \right) \le {\mathbf{I}}\), one can find results with a scalar \(\varepsilon > 0\) as follows:

$${\mathbf{H}}^{{\text{T}}} {{\varvec{\Delta}}}^{{\text{T}}} \left( t \right){\mathbf{W}}{ + }{\mathbf{W}}^{{\text{T}}} {{\varvec{\Delta}}}\left( t \right){\mathbf{H}} \le \varepsilon {\mathbf{H}}^{{\text{T}}} {\mathbf{H}}{ + }\varepsilon^{{ - {1}}} {\mathbf{W}}^{{\text{T}}} {\mathbf{W}}$$
(13)

Lemma 2 [34]

Given the matrices \({{\varvec{\Psi}}} \in \Re^{{n_{{{\varvec{\Psi}}}} \times n_{{{\varvec{\Xi}}}} }}\), \({{\varvec{\Lambda}}} \in \Re^{{n_{{{\varvec{\Lambda}}}} \times n_{{{\varvec{\Xi}}}} }}\) and symmetric matrix \({{\varvec{\Xi}}} \in \Re^{{n_{{{\varvec{\Xi}}}} \times n_{{{\varvec{\Xi}}}} }}\) which satisfies \(rank\left( {{\varvec{\Psi}}} \right) < n_{{{\varvec{\Xi}}}}\) and \(rank\left( {{\varvec{\Lambda}}} \right) < n_{{{\varvec{\Xi}}}}\), if and only if there exists any matrix \({{\varvec{\Pi}}}\) such that

$${{\varvec{\Xi}}} + {{\varvec{\Psi}}}^{{\text{T}}} {\mathbf{\Pi \Lambda }} + {{\varvec{\Lambda}}}^{{\text{T}}} {{\varvec{\Pi}}}{}^{{\text{T}}}{{\varvec{\Psi}}}{ < 0}$$
(14a)

then, the following inequalities are held.

$${{\varvec{\Psi}}}_{ \bot }^{{\text{T}}} {\mathbf{\Xi \Psi }}_{ \bot } < 0 {\text{and}} {{\varvec{\Lambda}}}_{ \bot }^{{\text{T}}} {\mathbf{\Xi \Lambda }}_{ \bot } { < 0}$$
(14b)

where \({{\varvec{\Psi}}}_{ \bot }\) and \({{\varvec{\Lambda}}}_{ \bot }\) are the null-space matrices of \({{\varvec{\Psi}}}\) and \({{\varvec{\Lambda}}}\), respectively.

The stability criterion for nonlinear singular system (3a, 3b) under unmeasurable states is developed in the next section. Moreover, the sufficient conditions are converted into LMI form for applying the convex optimization algorithm.

3 Robust Criterion for T–S Fuzzy Singular System

In this section, a Lyapunov function is chosen to derived the sufficient condition. To reduce the conservatism of condition, the positive definite matrix of the function is not required as diagonal matrix.

Theorem 1

Given the matrices \({\mathbf{F}}_{pj}\), \({\mathbf{F}}_{dj}\), \({\mathbf{L}}_{pi}\), \({\mathbf{L}}_{di}\), \({\mathbf{R}}_{1}\) and \({\mathbf{R}}_{2}\), the closed-loop system (12) is robust asymptotically stable if there exists the matrices \({\mathbf{P}} = {\mathbf{P}}^{{\text{T}}} > 0\) and a scalar \(\varepsilon\) such that

$$\left[ {\begin{array}{*{20}c} {sym\left\{ { - {\mathbf{E}}_{Rij} {{\varvec{\Pi}}}^{ - 1} } \right\} + {{\varvec{\Gamma}}}_{11} } & {{\mathbf{P}} + {{\varvec{\Pi}}}^{{ - {\text{T}} }} {\mathbf{A}}_{Rij} + {{\varvec{\Pi}}}^{{ - {\text{T}} }} {\mathbf{E}}_{Rij} + {{\varvec{\Gamma}}}_{12} } \\ * & { - 2{\mathbf{P}} + {{\varvec{\Gamma}}}_{22} } \\ \end{array} } \right] < 0$$
(15)

where \({{\varvec{\Gamma}}}_{11} = \varepsilon {{\varvec{\Pi}}}^{{ - {\text{T}} }} {\tilde{\mathbf{H}}}_{Bi} {\tilde{\mathbf{H}}}_{Bi}^{\text{T}} {{\varvec{\Pi}}}^{ - 1} + \varepsilon {{\varvec{\Pi}}}^{{ - {\text{T}} }} {\tilde{\mathbf{H}}}_{Ai} {\tilde{\mathbf{H}}}_{Ai}^{\text{T}} {{\varvec{\Pi}}}^{ - 1} + \varepsilon^{ - 1} {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} {\tilde{\mathbf{W}}}_{BDij}^{{}}\), \({{\varvec{\Gamma}}}_{22} = \varepsilon^{ - 1} {\tilde{\mathbf{W}}}_{BPij}^{\text{T}} {\tilde{\mathbf{W}}}_{BPij}^{{}} + \varepsilon^{ - 1} {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} {\tilde{\mathbf{W}}}_{BPij}^{{}} + \varepsilon^{ - 1} {\tilde{\mathbf{W}}}_{BPij}^{\text{T}} {\tilde{\mathbf{W}}}_{BDij}^{{}} + \varepsilon^{ - 1} {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} {\tilde{\mathbf{W}}}_{BDij}^{{}} + \varepsilon^{ - 1} {\tilde{\mathbf{W}}}_{Ai}^{\text{T}} {\tilde{\mathbf{W}}}_{Ai}^{{}}\), \({{\varvec{\Gamma}}}_{12} = - \varepsilon^{ - 1} {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} {\tilde{\mathbf{W}}}_{BPij}^{{}} - \varepsilon^{ - 1} {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} {\tilde{\mathbf{W}}}_{BDij}^{{}}\), \({\mathbf{P}} = \left[ {\begin{array}{*{20}c} {{\mathbf{P}}_{1} } & {{\mathbf{P}}_{3} } \\ * & {{\mathbf{P}}_{2} } \\ \end{array} } \right]\) and \({{\varvec{\Pi}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{R}}_{{1}} } & 0 \\ * & {{\mathbf{VR}}_{{2}} {\mathbf{V}}^{{\text{T}}} } \\ \end{array} } \right]\).

Proof:

Let choose the following Lyapunov function.

$$V\left( {\tilde{x}\left( t \right)} \right) = \tilde{x}^{{\text{T}}} \left( t \right){\mathbf{P}}\tilde{x}\left( t \right)$$
(16)

The derivative of (16) along the trajectory of (12) is inferred as follows.

$$\dot{V}\left( {\tilde{x}\left( t \right)} \right) = \dot{\tilde{x}}^{{\text{T}}} \left( t \right){\mathbf{P}}\tilde{x}\left( t \right) + \tilde{x}^{{\text{T}}} \left( t \right){\mathbf{P}}\dot{\tilde{x}}\left( t \right)$$
$$= \left( {{\tilde{\mathbf{E}}}_{Rij}^{ - 1} \left( h \right){\tilde{\mathbf{A}}}_{Rij} \left( h \right)\tilde{x}\left( t \right)} \right)^{{\text{T}}} {\mathbf{P}}\tilde{x}\left( t \right) + \tilde{x}^{{\text{T}}} \left( t \right){\mathbf{P}}\left( {{\tilde{\mathbf{E}}}_{Rij}^{ - 1} \left( h \right){\tilde{\mathbf{A}}}_{Rij} \left( h \right)\tilde{x}\left( t \right)} \right)$$
$$= \tilde{x}^{{\text{T}}} \left( t \right)\left( {{\tilde{\mathbf{A}}}_{Rij}^{{\text{T}}} \left( h \right){\tilde{\mathbf{E}}}_{Rij}^{{ - {\text{T}}}} \left( h \right){\mathbf{P}} + {\mathbf{P\tilde{E}}}_{Rij}^{ - 1} \left( h \right){\tilde{\mathbf{A}}}_{Rij} \left( h \right)} \right)\tilde{x}\left( t \right)$$
(17)

It is easy to find the following inequality through arranging the condition (15).

$$\left[ {\begin{array}{*{20}c} {sym\left\{ { - {\mathbf{E}}_{Rij} {{\varvec{\Pi}}}^{ - 1} } \right\}} & {{\mathbf{P}}{ + }{{\varvec{\Pi}}}^{{ - {\text{T}} }} {\mathbf{A}}_{Rij} + {{\varvec{\Pi}}}^{{ - {\text{T}} }} {\mathbf{E}}_{Rij} } \\ * & { - 2{\mathbf{P}}} \\ \end{array} } \right]$$
$$+ \varepsilon \left[ {\begin{array}{*{20}c} {{{\varvec{\Pi}}}^{{ - {\text{T}} }} {\tilde{\mathbf{H}}}_{Bi} } \\ 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{{\varvec{\Pi}}}^{{ - {\text{T}} }} {\tilde{\mathbf{H}}}_{Bi} } \\ 0 \\ \end{array} } \right]^{\text{T}} + \varepsilon^{ - 1} \left[ {\begin{array}{*{20}c} { - {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} } \\ {{\tilde{\mathbf{W}}}_{BPij}^{\text{T}} + {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} { - {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} } \\ {{\tilde{\mathbf{W}}}_{BPij}^{\text{T}} + {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} } \\ \end{array} } \right]^{\text{T}}$$
$$+ \varepsilon \left[ {\begin{array}{*{20}c} {{{\varvec{\Pi}}}^{{ - {\text{T}} }} {\tilde{\mathbf{H}}}_{Ai} } \\ 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{{\varvec{\Pi}}}^{{ - {\text{T}} }} {\tilde{\mathbf{H}}}_{Ai} } \\ 0 \\ \end{array} } \right]^{\text{T}} + \varepsilon^{ - 1} \left[ {\begin{array}{*{20}c} 0 \\ {{\tilde{\mathbf{W}}}_{Ai}^{\text{T}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 \\ {{\tilde{\mathbf{W}}}_{Ai}^{\text{T}} } \\ \end{array} } \right]^{\text{T}} < 0$$
(18)

Based on Lemma 1, \(\sum\limits_{i = 1}^{m} {h_{i} } = 1\) and \(0 \le h_{i} \le 1\), the following inequality is deduced from (18).

$$\left[ {\begin{array}{*{20}c} {sym\left\{ { - {\mathbf{E}}_{Rij} \left( h \right){{\varvec{\Pi}}}^{ - 1} } \right\}} & {{\mathbf{P}}{ + }{{\varvec{\Pi}}}^{{ - {\text{T}} }} {\mathbf{A}}_{Rij} \left( h \right) + {{\varvec{\Pi}}}^{{ - {\text{T}} }} {\mathbf{E}}_{Rij} \left( h \right)} \\ * & { - 2{\tilde{\mathbf{P}}}} \\ \end{array} } \right]$$
$$+ \left[ {\begin{array}{*{20}c} {{{\varvec{\Pi}}}^{{ - {\text{T}} }} {\tilde{\mathbf{H}}}_{Bi} \left( h \right)} \\ 0 \\ \end{array} } \right]{{\varvec{\Delta}}}\left( t \right)\left[ {\begin{array}{*{20}c} { - {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} \left( h \right)} \\ {{\tilde{\mathbf{W}}}_{BPij}^{\text{T}} \left( h \right) + {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} \left( h \right)} \\ \end{array} } \right]^{\text{T}} + \left[ {\begin{array}{*{20}c} {{{\varvec{\Pi}}}^{{ - {\text{T}} }} {\tilde{\mathbf{H}}}_{Ai} \left( h \right)} \\ 0 \\ \end{array} } \right]{{\varvec{\Delta}}}\left( t \right)\left[ {\begin{array}{*{20}c} 0 \\ {{\tilde{\mathbf{W}}}_{Ai}^{\text{T}} \left( h \right)} \\ \end{array} } \right]^{\text{T}}$$
$$+ \left[ {\begin{array}{*{20}c} { - {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} \left( h \right)} \\ {{\tilde{\mathbf{W}}}_{BPij}^{\text{T}} \left( h \right) + {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} \left( h \right)} \\ \end{array} } \right]{{\varvec{\Delta}}}^{\text{T}} \left( t \right)\left[ {\begin{array}{*{20}c} {{{\varvec{\Pi}}}^{{ - {\text{T}} }} {\tilde{\mathbf{H}}}_{Bi} \left( h \right)} \\ 0 \\ \end{array} } \right]^{\text{T}} + \left[ {\begin{array}{*{20}c} 0 \\ {{\tilde{\mathbf{W}}}_{Ai}^{\text{T}} \left( h \right)} \\ \end{array} } \right]{{\varvec{\Delta}}}^{\text{T}} \left( t \right)\left[ {\begin{array}{*{20}c} {{{\varvec{\Pi}}}^{{ - {\text{T}} }} {\tilde{\mathbf{H}}}_{Ai} \left( h \right)} \\ 0 \\ \end{array} } \right]^{\text{T}}$$
$$= {{\varvec{\Xi}}} + sym\left\{ {{{\varvec{\Psi}}}^{\text{T}} {\mathbf{\Pi \Lambda }}} \right\} < 0$$
(19)

where \({{\varvec{\Psi}}} = \left[ { - \begin{array}{*{20}c} {{\tilde{\mathbf{E}}}_{Rij} \left( h \right)} & {{\tilde{\mathbf{A}}}_{Rij}^{{}} \left( h \right)} \\ \end{array} + {\tilde{\mathbf{E}}}_{Rij}^{{}} \left( h \right)} \right]\), \({{\varvec{\Lambda}}} = \left[ {\begin{array}{*{20}c} {\mathbf{I}} & 0 \\ \end{array} } \right]\) and \({{\varvec{\Xi}}} = \left[ {\begin{array}{*{20}c} 0 & {\mathbf{P}} \\ * & { - 2{\mathbf{P}}} \\ \end{array} } \right]\).

According to Lemmas 2 and (19), \({{\varvec{\Psi}}}_{ \bot }^{{\text{T}}} = \left[ {\begin{array}{*{20}c} {{\tilde{\mathbf{A}}}_{Rij}^{{\text{T}}} \left( h \right){\tilde{\mathbf{E}}}_{Rij}^{{ - {\text{T}}}} \left( h \right) + {\mathbf{I}}} & {\mathbf{I}} \\ \end{array} } \right]\) and \({{\varvec{\Lambda}}}_{ \bot }^{{\text{T}}} = \left[ {\begin{array}{*{20}c} 0 & {\mathbf{I}} \\ \end{array} } \right]\) are chosen to hold the existence of the following inequalities.

$${\tilde{\mathbf{A}}}_{Rij}^{{\text{T}}} \left( h \right){\tilde{\mathbf{E}}}_{Rij}^{{ - {\text{T}}}} \left( h \right){\mathbf{P}} + {\mathbf{P\tilde{E}}}_{Rij}^{ - 1} \left( h \right){\tilde{\mathbf{A}}}_{Rij} \left( h \right) = {{\varvec{\Psi}}}_{ \bot }^{{\text{T}}} {\mathbf{\Xi \Psi }}_{ \bot } < 0$$
(20a)

and

$$- 2{\mathbf{P}} = {{\varvec{\Lambda}}}_{ \bot }^{{\text{T}}} {\mathbf{\Xi \Lambda }}_{ \bot } < 0$$
(20b)

Obviously, \({{\varvec{\Psi}}}_{ \bot }^{{\text{T}}} {\mathbf{\Xi \Psi }}_{ \bot } < 0\) and \({{\varvec{\Lambda}}}_{ \bot }^{{\text{T}}} {\mathbf{\Xi \Lambda }}_{ \bot } < 0\) can be guaranteed if the condition (15) is satisfied. Moreover, the \({{\varvec{\Psi}}}_{ \bot }^{{\text{T}}} {\mathbf{\Xi \Psi }}_{ \bot } < 0\) furtherly holds \(\dot{V}\left( {\tilde{x}\left( t \right)} \right) < 0\) according to the (17). Therefore, the system (12) is stable on the basis of Lyapunov theory such as \(\dot{V}\left( {\tilde{x}\left( t \right)} \right) < 0\). The proof of Theorem 1 is completed.

To design the observer-based PD fuzzy controller (7), Theorem 1 cannot be directly applied with using the convex optimization algorithm. Thus, some conditions are derived in the following theorem by converting (15) and converted into strict LMI form.

Theorem 2:

Given the matrices \({\mathbf{U}}\), \({\mathbf{S}}\) and \({\mathbf{V}}\) satisfying Assumption 2, the closed-loop system (12) is robust asymptotically stable if there exists matrices \({\mathbf{Y}}_{dj}\), \({\mathbf{Y}}_{pj}\), \({\mathbf{K}}_{di}\), \({\mathbf{K}}_{pi}\), \({\tilde{\mathbf{P}}}_{1} = {\tilde{\mathbf{P}}}_{1}^{{\text{T}}} > 0\), \({\tilde{\mathbf{P}}}_{2} = {\tilde{\mathbf{P}}}_{2}^{{\text{T}}} > 0\), \({\tilde{\mathbf{P}}}_{3}\), \({\mathbf{R}}_{{1}}\) and \({\mathbf{R}}_{{2}} { = }\left[ {\begin{array}{*{20}c} {{\mathbf{Z}}_{11} } & 0 \\ {{\mathbf{Z}}_{21} } & {{\mathbf{Z}}_{22} } \\ \end{array} } \right]\), and a scalar \(\varepsilon\) such that

$$\left[ {\begin{array}{*{20}c} {{{\varvec{\Phi}}}_{11} } & {{\mathbf{K}}_{di} {\mathbf{C}}} & {{{\varvec{\Phi}}}_{13} } & {{{\varvec{\Phi}}}_{14} } & 0 & 0 & { - {\mathbf{Y}}_{dj}^{\text{T}} {\mathbf{W}}_{Bi}^{\text{T}} } & 0 \\ * & {{{\varvec{\Phi}}}_{22} } & {{\tilde{\mathbf{P}}}_{3}^{\text{T}} } & {{{\varvec{\Phi}}}_{24} } & {\varepsilon {\mathbf{H}}_{Bi} } & {\varepsilon {\mathbf{H}}_{Ai} } & 0 & 0 \\ * & * & { - 2{\tilde{\mathbf{P}}}_{1} } & { - 2{\tilde{\mathbf{P}}}_{3} } & 0 & 0 & {{{\varvec{\Phi}}}_{37} } & {{\mathbf{R}}_{{1}}^{{\text{T}}} {\mathbf{W}}_{Ai}^{\text{T}} } \\ * & * & * & { - 2{\tilde{\mathbf{P}}}_{2} } & 0 & 0 & 0 & {{\mathbf{VR}}_{{2}}^{{\text{T}}} {\mathbf{V}}^{{\text{T}}} {\mathbf{W}}_{Ai}^{\text{T}} } \\ * & * & * & * & { - \varepsilon {\mathbf{I}}} & 0 & 0 & 0 \\ * & * & * & * & * & { - \varepsilon {\mathbf{I}}} & 0 & 0 \\ * & * & * & * & * & * & { - \varepsilon {\mathbf{I}}} & 0 \\ * & * & * & * & * & * & * & { - \varepsilon {\mathbf{I}}} \\ \end{array} } \right] < 0 \; {\text{for}} \; i,j = 1,2, \ldots ,n$$
(21)

where \({{\varvec{\Phi}}}_{11} = - sym\left\{ {{\mathbf{ER}}_{1} + {\mathbf{B}}_{i} {\mathbf{Y}}_{dj} } \right\}\), \({{\varvec{\Phi}}}_{13} = {\tilde{\mathbf{P}}}_{1} + {\mathbf{A}}_{i} {\mathbf{R}}_{1} - {\mathbf{B}}_{i} {\mathbf{Y}}_{pj} + {\mathbf{ER}}_{1} + {\mathbf{B}}_{i} {\mathbf{Y}}_{dj}\), \({{\varvec{\Phi}}}_{14} = {\tilde{\mathbf{P}}}_{3} + {\mathbf{K}}_{pi} {\mathbf{C}} - {\mathbf{K}}_{di} {\mathbf{C}}\), \({{\varvec{\Phi}}}_{22} = - sym\left\{ {{\mathbf{EVR}}_{{2}} {\mathbf{V}}^{{\text{T}}} + {\mathbf{K}}_{di} {\mathbf{C}}} \right\}\), \({{\varvec{\Phi}}}_{24} = {\tilde{\mathbf{P}}}_{2} + {\mathbf{A}}_{i} {\mathbf{VR}}_{{2}} {\mathbf{V}}^{{\text{T}}} + {\mathbf{EVR}}_{{2}} {\mathbf{V}}^{{\text{T}}} - {\mathbf{K}}_{pi} {\mathbf{C}} + {\mathbf{K}}_{di} {\mathbf{C}}\) and \({{\varvec{\Phi}}}_{37} = - {\mathbf{Y}}_{pj}^{\text{T}} {\mathbf{W}}_{Bi}^{\text{T}} - {\mathbf{Y}}_{dj}^{\text{T}} {\mathbf{W}}_{Bi}^{\text{T}}\).

Proof

By applying Schur complement to (18), one can obtain the following inequality.

$$\left[ {\begin{array}{*{20}c} {sym\left\{ { - {\mathbf{E}}_{Rij} {{\varvec{\Pi}}}^{ - 1} } \right\}} & {{\mathbf{P}} + {{\varvec{\Pi}}}^{ - T} {\mathbf{A}}_{Rij} + {{\varvec{\Pi}}}^{ - T} {\mathbf{E}}_{Rij} } & {\varepsilon {{\varvec{\Pi}}}^{ - T} {\tilde{\mathbf{H}}}_{Bi} } & {\varepsilon {{\varvec{\Pi}}}^{ - T} {\tilde{\mathbf{H}}}_{Ai} } & { - {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} } & 0 \\ * & { - 2{\mathbf{P}}} & 0 & 0 & {{\tilde{\mathbf{W}}}_{BPij}^{\text{T}} + {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} } & {{\tilde{\mathbf{W}}}_{Ai}^{\text{T}} } \\ * & * & { - \varepsilon {\mathbf{I}}} & 0 & 0 & 0 \\ * & * & * & { - \varepsilon {\mathbf{I}}} & 0 & 0 \\ * & * & * & * & { - \varepsilon {\mathbf{I}}} & 0 \\ * & * & * & * & * & { - \varepsilon {\mathbf{I}}} \\ \end{array} } \right] < 0$$
(22)

Pre- and post-multiplying (22) by \(diag\left\{ {{{\varvec{\Pi}}}^{{\text{T}}} ,{{\varvec{\Pi}}}^{{\text{T}}} ,{\mathbf{I}},{\mathbf{I}},{\mathbf{I}},{\mathbf{I}}} \right\}\) and its transpose, the following inequality can be inferred.

$$\left[ {\begin{array}{*{20}c} {sym\left\{ { - {\mathbf{E}}_{Rij} {{\varvec{\Pi}}}} \right\}} & {{\tilde{\mathbf{P}}} + {\mathbf{A}}_{Rij} {{\varvec{\Pi}}} + {\mathbf{E}}_{Rij} {{\varvec{\Pi}}}} & {\varepsilon {\tilde{\mathbf{H}}}_{Bi} } & {\varepsilon {\tilde{\mathbf{H}}}_{Ai} } & { - {{\varvec{\Pi}}}^{T} {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} } & 0 \\ * & { - 2{\tilde{\mathbf{P}}}} & 0 & 0 & {{{\varvec{\Pi}}}^{T} \left( {{\tilde{\mathbf{W}}}_{BPij}^{\text{T}} + {\tilde{\mathbf{W}}}_{BDij}^{\text{T}} } \right)} & {{{\varvec{\Pi}}}^{T} {\tilde{\mathbf{W}}}_{Ai}^{\text{T}} } \\ * & * & { - \varepsilon {\mathbf{I}}} & 0 & 0 & 0 \\ * & * & * & { - \varepsilon {\mathbf{I}}} & 0 & 0 \\ * & * & * & * & { - \varepsilon {\mathbf{I}}} & 0 \\ * & * & * & * & * & { - \varepsilon {\mathbf{I}}} \\ \end{array} } \right] < 0$$
(23)

where \({\tilde{\mathbf{P}}} = {{\varvec{\Pi}}}^{{\text{T}}} {\mathbf{P\Pi }}\) and \({\tilde{\mathbf{P}}} = \left[ {\begin{array}{*{20}c} {{\tilde{\mathbf{P}}}_{1} } & {{\tilde{\mathbf{P}}}_{3} } \\ * & {{\tilde{\mathbf{P}}}_{2} } \\ \end{array} } \right]\). By defining \({\mathbf{Y}}_{dj} = {\mathbf{F}}_{dj} {\mathbf{R}}_{{1}}\) and \({\mathbf{Y}}_{pj} = {\mathbf{F}}_{pj} {\mathbf{R}}_{{1}}\), the inequality (23) can be rewritten as follows:

$$\left[ {\begin{array}{*{20}c} {{{\varvec{\Phi}}}_{11} } & {{\mathbf{L}}_{di} {\mathbf{CVR}}_{2} {\mathbf{V}}^{{\text{T}}} } & {{{\varvec{\Phi}}}_{13} } & {{\tilde{\mathbf{\Phi }}}_{14} } & 0 & 0 & { - {\mathbf{Y}}_{dj}^{\text{T}} {\mathbf{W}}_{Bi}^{\text{T}} } & 0 \\ * & {{\tilde{\mathbf{\Phi }}}_{22} } & {{\tilde{\mathbf{P}}}_{3}^{\text{T}} } & {{\tilde{\mathbf{\Phi }}}_{24} } & {\varepsilon {\mathbf{H}}_{Bi} } & {\varepsilon {\mathbf{H}}_{Ai} } & 0 & 0 \\ * & * & { - 2{\tilde{\mathbf{P}}}_{1} } & { - 2{\tilde{\mathbf{P}}}_{3} } & 0 & 0 & {{{\varvec{\Phi}}}_{37} } & {{\mathbf{R}}_{{1}}^{{\text{T}}} {\mathbf{W}}_{Ai}^{\text{T}} } \\ * & * & * & { - 2{\tilde{\mathbf{P}}}_{2} } & 0 & 0 & 0 & {{\mathbf{VR}}_{{2}}^{{\text{T}}} {\mathbf{V}}^{{\text{T}}} {\mathbf{W}}_{Ai}^{\text{T}} } \\ * & * & * & * & { - \varepsilon {\mathbf{I}}} & 0 & 0 & 0 \\ * & * & * & * & * & { - \varepsilon {\mathbf{I}}} & 0 & 0 \\ * & * & * & * & * & * & { - \varepsilon {\mathbf{I}}} & 0 \\ * & * & * & * & * & * & * & { - \varepsilon {\mathbf{I}}} \\ \end{array} } \right] < 0$$
(24)

where \({\tilde{\mathbf{\Phi }}}_{14} = {\tilde{\mathbf{P}}}_{3} + {\mathbf{L}}_{pi} {\mathbf{CVR}}_{2} {\mathbf{V}}^{{\text{T}}} - {\mathbf{L}}_{di} {\mathbf{CVR}}_{2} {\mathbf{V}}^{{\text{T}}}\), \({\tilde{\mathbf{\Phi }}}_{22} = - sym\left\{ {{\mathbf{EVR}}_{{2}} {\mathbf{V}}^{{\text{T}}} + {\mathbf{L}}_{di} {\mathbf{CVR}}_{2} {\mathbf{V}}^{{\text{T}}} } \right\}\) and \({\tilde{\mathbf{\Phi }}}_{24} = {\tilde{\mathbf{P}}}_{2} + {\mathbf{A}}_{i} {\mathbf{VR}}_{{2}} {\mathbf{V}}^{{\text{T}}} + {\mathbf{EVR}}_{{2}} {\mathbf{V}}^{{\text{T}}} - {\mathbf{L}}_{pi} {\mathbf{CVR}}_{2} {\mathbf{V}}^{{\text{T}}} + {\mathbf{L}}_{di} {\mathbf{CVR}}_{2} {\mathbf{V}}^{{\text{T}}}\).

According to Assumption 2, the following relationship can be derived. Noted that the \({\mathbf{V}}\) and \({\mathbf{U}}\) are the orthogonal matrices.

$${\mathbf{CVR}}_{2} {\mathbf{V}}^{{\text{T}}} = {\mathbf{U}}\left[ {\begin{array}{*{20}c} {\mathbf{S}} & 0 \\ \end{array} } \right]{\mathbf{V}}^{{\text{T}}} {\mathbf{V}}\left[ {\begin{array}{*{20}c} {{\mathbf{Z}}_{11} } & 0 \\ {{\mathbf{Z}}_{21} } & {{\mathbf{Z}}_{22} } \\ \end{array} } \right]{\mathbf{V}}^{{\text{T}}} = {\hat{\mathbf{R}}}_{{2}} {\mathbf{C}}$$
(25)

where \({\hat{\mathbf{R}}}_{{2}} = {\mathbf{USZ}}_{11} {\mathbf{S}}^{ - 1} {\mathbf{U}}^{{\text{T}}}\). Based on (25), \({\tilde{\mathbf{\Phi }}}_{14} = {\tilde{\mathbf{P}}}_{3} + {\mathbf{L}}_{pi} {\hat{\mathbf{R}}}_{{2}} {\mathbf{C}} - {\mathbf{L}}_{di} {\hat{\mathbf{R}}}_{{2}} {\mathbf{C}}\), \({\tilde{\mathbf{\Phi }}}_{22} = - sym\left\{ {{\mathbf{EVR}}_{{2}} {\mathbf{V}}^{{\text{T}}} + {\mathbf{L}}_{di} {\hat{\mathbf{R}}}_{{2}} {\mathbf{C}}} \right\}\) and \({\tilde{\mathbf{\Phi }}}_{24} = {\tilde{\mathbf{P}}}_{2} + {\mathbf{A}}_{i} {\mathbf{VR}}_{{2}} {\mathbf{V}}^{{\text{T}}} + {\mathbf{EVR}}_{{2}} {\mathbf{V}}^{{\text{T}}} - {\mathbf{L}}_{pi} {\hat{\mathbf{R}}}_{{2}} {\mathbf{C}} + {\mathbf{L}}_{di} {\hat{\mathbf{R}}}_{{2}} {\mathbf{C}}\) can be furtherly inferred. Then, the following inequality can be thus obtained from (24) and (25) by defining \({\mathbf{K}}_{di} = {\mathbf{L}}_{di} {\hat{\mathbf{R}}}_{{2}}\) and \({\mathbf{K}}_{pi} = {\mathbf{L}}_{pi} {\hat{\mathbf{R}}}_{{2}}\).

$$\left[ {\begin{array}{*{20}c} {{{\varvec{\Phi}}}_{11} } & {{\mathbf{K}}_{di} {\mathbf{C}}} & {{{\varvec{\Phi}}}_{13} } & {{{\varvec{\Phi}}}_{14} } & 0 & 0 & { - {\mathbf{Y}}_{dj}^{\text{T}} {\mathbf{W}}_{Bi}^{\text{T}} } & 0 \\ * & {{{\varvec{\Phi}}}_{22} } & {{\tilde{\mathbf{P}}}_{3}^{\text{T}} } & {{{\varvec{\Phi}}}_{24} } & {\varepsilon {\mathbf{H}}_{Bi} } & {\varepsilon {\mathbf{H}}_{Ai} } & 0 & 0 \\ * & * & { - 2{\tilde{\mathbf{P}}}_{1} } & { - 2{\tilde{\mathbf{P}}}_{3} } & 0 & 0 & {{{\varvec{\Phi}}}_{37} } & {{\mathbf{R}}_{{1}}^{{\text{T}}} {\mathbf{W}}_{Ai}^{\text{T}} } \\ * & * & * & { - 2{\tilde{\mathbf{P}}}_{2} } & 0 & 0 & 0 & {{\mathbf{VR}}_{{2}}^{{\text{T}}} {\mathbf{V}}^{{\text{T}}} {\mathbf{W}}_{Ai}^{\text{T}} } \\ * & * & * & * & { - \varepsilon {\mathbf{I}}} & 0 & 0 & 0 \\ * & * & * & * & * & { - \varepsilon {\mathbf{I}}} & 0 & 0 \\ * & * & * & * & * & * & { - \varepsilon {\mathbf{I}}} & 0 \\ * & * & * & * & * & * & * & { - \varepsilon {\mathbf{I}}} \\ \end{array} } \right] < 0$$
(26)

Then, one can find that (26) is equivalent to the condition of Theorem 2. The proof of Theorem 2 is completed.

Obviously, the feasible solutions of the conditions in Theorem 2 can be found using convex optimization algorithm. Based on the solutions, the condition in Theorem 1 can also be satisfied. To clarify the design process of this paper, the following procedure is proposed using Theorem 2 to search the feasible solutions and to establish the observer-based PD fuzzy controller (7).

3.1 Design Procedure

  1. Step 1:

    Check the satisfactions in Assumption 1.

  2. Step 2:

    Setting the constant matrices \({\mathbf{H}}_{Ai}\), \({\mathbf{H}}_{Bi}\), \({\mathbf{W}}_{Ai}\) and \({\mathbf{W}}_{Bi}\) based on (2).

  3. Step 3:

    Decomposing the output matrix \({\mathbf{C}}\) to find the matrices \({\mathbf{U}}\), \({\mathbf{S}}\) and \({\mathbf{V}}\) satisfying Assumption 2.

  4. Step 4:

    Based on the matrices \({\mathbf{U}}\), \({\mathbf{S}}\) and \({\mathbf{V}}\) obtained in Step 3, the variables \({\mathbf{Y}}_{pi}\), \({\mathbf{Y}}_{di}\), \({\mathbf{K}}_{pi}\), \({\mathbf{K}}_{di}\), \({\tilde{\mathbf{P}}}_{{1}} = {\tilde{\mathbf{P}}}_{{1}}^{{\text{T}}} > 0\), \({\tilde{\mathbf{P}}}_{{2}} = {\tilde{\mathbf{P}}}_{{2}}^{{\text{T}}} > 0\), \({\tilde{\mathbf{P}}}_{{3}}\), \({\mathbf{R}}_{{1}}\) and \({\mathbf{R}}_{{2}} { = }\left[ {\begin{array}{*{20}c} {{\mathbf{Z}}_{11} } & 0 \\ {{\mathbf{Z}}_{21} } & {{\mathbf{Z}}_{22} } \\ \end{array} } \right]\) are searched to satisfy Theorem 2 by convex optimization algorithm.

  5. Step 5:

    With \({\hat{\mathbf{R}}}_{{2}} = {\mathbf{USZ}}_{11} {\mathbf{S}}^{ - 1} {\mathbf{U}}^{{\text{T}}}\), the gains can be obtained by \({\mathbf{F}}_{pj} = {\mathbf{Y}}_{pj} {\mathbf{R}}_{1}^{ - 1}\), \({\mathbf{F}}_{dj} = {\mathbf{Y}}_{dj} {\mathbf{R}}_{{1}}^{ - 1}\), \({\mathbf{L}}_{pi} = {\mathbf{K}}_{pi} {\hat{\mathbf{R}}}_{2}^{ - 1}\) and \({\mathbf{L}}_{di} = {\mathbf{K}}_{di} {\hat{\mathbf{R}}}_{2}^{ - 1}\).

  6. Step 6:

    Based on the gains in Step 5, the observer-based PD fuzzy controller (7) can be established.

Based on the above procedure, the observer-based PD fuzzy controller (7) can be design for ensuring the stability of the closed-loop system (12). Besides, the following remark is provided to show the contribution of this paper.

Remark 2

Although PD control scheme [26] is widely applied for control problem of nonlinear singular systems, only few works [31, 32] focused on the observer design method. Referring to [31], the problem of unmeasurable states was discussed to design an observer for nonlinear singular systems. The controller design method was not proposed by [31] to guarantee the stability. Thus, the observer-based fuzzy control problem [32] was discussed using PD control scheme for the systems. To extend the application of [32], the uncertainty is considered by this paper to achieve the robustness of the closed-loop system (12). Through the chosen Lyapunov function and SVD technology, the conservatism of the condition (21) in Theorem 2 can be furtherly reduced to increase the applicability of the proposed design method. Thus, this paper provides more general and less conservative stability criterion than [32]. To clarify the contribution of this paper, Table 1 shows the comparisons with the works [26, 28, 32].

Table 1 The comparison between the proposed method and the other methods
Full size table

In the next section, two examples are applied to verify the usefulness and effectivity of the proposed design method.

4 Numerical Example

Two examples are provided in this section to show the availability and effectiveness of the proposed observer-based PD fuzzy controller design method. The first example is to discuss the stabilization problem of real bio-economic system [2]. Through this example, the relaxation of the proposed design method is verified by comparing with the method of [32]. Moreover, some extreme uncertainties are added to the bio-economic system to interpret the robust asymptotical stability in Definition 1. Besides, a complicated numerical example is provided in Example 2 to show the importance of robust performance. Also, the method without robustness in [32] is applied to show the importance.

Example 1

Referring to [2], the following nonlinear single-species bio-economic system was considered for the economic interest of harvest effort on the immature population.

$$\dot{x}_{{1}} \left( t \right) = - 0.79x_{{1}} \left( t \right) + 0.15x_{{2}} \left( t \right) - 40x_{{3}} \left( t \right) - 0.001x_{{1}}^{{2}} \left( t \right) - x_{{1}} \left( t \right)x_{{3}} \left( t \right)$$
(27a)
$$\dot{x}_{{2}} \left( t \right) = 0.5x_{{1}} \left( t \right) - 0.1x_{{2}} \left( t \right)$$
(27b)
$${0} = 0.01x_{{1}} \left( t \right) + x_{{1}} \left( t \right)x_{{3}} \left( t \right) - m + u\left( t \right)$$
(27c)

From (27a, 27b, 27c), \(x_{{1}} \left( t \right) \in \left[ { - {10},\;{10}} \right]\) is chosen for population density. Through the modeling approach [10], the following T–S fuzzy model for (27a, 27b, 27c) can be expressed.

$${\mathbf{E}}\dot{x}\left( t \right) = \sum\limits_{{i = {1}}}^{{2}} {h_{i} \left( {x\left( t \right)} \right)\left\{ {{\mathbf{A}}_{i} x\left( t \right) + {\mathbf{B}}u\left( t \right)} \right\}}$$
(28a)
$$y\left( t \right) = {\mathbf{C}}x\left( t \right)$$
(28b)

where \({\mathbf{E}} = \left[ {\begin{array}{*{20}c} {1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {0} & {0} \\ \end{array} } \right]\), \({\mathbf{A}}_{{1}} = \left[ {\begin{array}{*{20}c} { - 0.78 + g} & {0.15} & { - 30} \\ {0.5} & { - 0.1} & {0} \\ {0.01} & {0} & { - 10} \\ \end{array} } \right]\), \({\mathbf{A}}_{{2}} = \left[ {\begin{array}{*{20}c} { - 0.8 - g} & {0.15} & { - 50} \\ {0.5} & { - 0.1} & {0} \\ {0.01} & {0} & {10} \\ \end{array} } \right]\), \({\mathbf{B}} = \left[ {\begin{array}{*{20}c} {0} \\ {0} \\ {1} \\ \end{array} } \right]\) and \({\mathbf{C}} = \left[ {\begin{array}{*{20}c} 1 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\). The membership functions are \(h_{{1}} \left( {x\left( t \right)} \right) = {{\left( {{1} - \frac{{x_{{1}} \left( t \right)}}{10}} \right)} \mathord{\left/ {\vphantom {{\left( {{1} - \frac{{x_{{1}} \left( t \right)}}{10}} \right)} {2}}} \right. \kern-\nulldelimiterspace} {2}}\) and \(h_{{2}} \left( {x\left( t \right)} \right) = {1} - h_{{1}} \left( {x\left( t \right)} \right)\). To show the relaxation and effectiveness of the proposed design method, the following cases are provided for the stabilization problem of (28a, 28b).


Case 1

In this case, the proposed design method and the method of [32] are respectively applied to find the maximum value of \(g\). It is well known that the relaxed method allows the bigger value of \(g\) than the conservative method. To applying the proposed design method, the \(rank\left( {\left[ {\begin{array}{*{20}c} {\mathbf{E}} & {\mathbf{B}} \\ \end{array} } \right]} \right) = 3\) and \(rank\left( {\left[ {\begin{array}{*{20}c} {\mathbf{E}} \\ {\mathbf{C}} \\ \end{array} } \right]} \right) = 3\) can be checked by Step 1 of Design Procedure to satisfy Assumption 1. Because none uncertainty exists in this case, Step 2 is therefore ignored. In Step 3, the matrices \({\mathbf{U}}\), \({\mathbf{S}}\) and \({\mathbf{V}}\) satisfying Assumption 2 are given in Table 2 from decomposing the output matrix \({\mathbf{C}}\).

Table 2 The used parameters
Full size table

Following Step 4 and Step 5, one can find the feasible solutions to satisfy Theorem 2. Also, the obtained solutions hold the achievement of Theorem 1. Repeating the procedure, the maximum value of \(g = 1.5\) is allowed to find the feasible solutions.

In this case, the maximum value of \(g = 1.3\) is allowed to use the method of [32] for finding feasible solutions of the stabilization problem of (28a, 28b). All values of \(g\) found by the methods are concluded in Table 3. Obviously, the value of \(g\) found by the proposed design method is bigger than one found by the method of [32]. The reasons causing the conservatism in [32] are the zero elements in positive definite matrix of Lyapunov function and the inequality used to obtain LMI conditions. Based on the result in this case, the proposed design method is less conservative than the method of [32].

Table 3 Comparison for proposed design method and the design method of [32]
Full size table

Case 2

To discuss the robust asymptotical stability in Definition 1, some extreme uncertainties are added to (28a, 28b) and \(g = 0\) is set in this case. Thus, the system (28a, 28b) with uncertainties are as follows.

$${\mathbf{E}}\dot{x}\left( t \right) = \sum\limits_{{i = {1}}}^{{2}} {h_{i} \left( {x\left( t \right)} \right)\left\{ {\left( {{\mathbf{A}}_{i} + {\mathbf{\Delta A}}_{i} } \right)x\left( t \right) + \left( {{\mathbf{B}}_{i} + {\mathbf{\Delta B}}_{i} } \right)u\left( t \right)} \right\}}$$
(29)

where \({\mathbf{\Delta A}}_{{1}} = \left[ {\begin{array}{*{20}c} {{\text{sin}}\left( {50t} \right)} & 0 & 0 \\ { - 0.4{\text{sin}}\left( {50t} \right)} & 0 & {0} \\ 0 & {0} & 0 \\ \end{array} } \right]\), \({\mathbf{\Delta A}}_{2} = \left[ {\begin{array}{*{20}c} {0.6{\text{sin}}\left( {50t} \right)} & 0 & 0 \\ { - 0.2{\text{sin}}\left( {50t} \right)} & 0 & {0} \\ 0 & {0} & 0 \\ \end{array} } \right]\), \({\mathbf{\Delta B}}_{1} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - 0.3{\text{sin}}\left( {50t} \right)} \\ \end{array} } \right]\) and \({\mathbf{\Delta B}}_{2} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {0.4{\text{sin}}\left( {50t} \right)} \\ \end{array} } \right]\).

According to the added uncertainties, the constant matrices in Step 2 are assigned as Table 4.

Besides the uncertainty, Step 1 and Step 3 can be avoided by the same results obtained by the above case. Through Design procedure, the feasible solutions in Step 4 can be found by the convex optimization algorithm.

\({\tilde{\mathbf{P}}}_{1} { = }\left[ {\begin{array}{*{20}c} {18.5589} & {0.3589} & {1.2372} \\ {0.3589} & {15.8891} & {0.0445} \\ {1.2372} & {0.0445} & {6.2014} \\ \end{array} } \right]\), \({\tilde{\mathbf{P}}}_{2} { = }\left[ {\begin{array}{*{20}c} {14.5404} & { - 2.0594} & {0.0291} \\ { - 2.0594} & {13.6171} & {0.1896} \\ {0.0291} & {0.1896} & {3.9279} \\ \end{array} } \right]\), \({\tilde{\mathbf{P}}}_{3} { = }\left[ {\begin{array}{*{20}c} { - 0.0071} & { - 2.3883} & { - 0.2832} \\ { - 1.2335} & {0.9976} & {0.0046} \\ {0.1056} & { - 0.0311} & { - 2.4340} \\ \end{array} } \right]\), \({\mathbf{R}}_{1} = \left[ {\begin{array}{*{20}c} {7.0586} & { - 2.4681} & { - 0.0884} \\ {0.3982} & {18.0941} & {0.0875} \\ {0.4654} & {0.1074} & {0.0434} \\ \end{array} } \right]\), \({\mathbf{R}}_{2} = \left[ {\begin{array}{*{20}c} {6.1128} & { - 0.2017} & 0 \\ {0.1302} & { - 0.0115} & 0 \\ {0.1928} & {0.2097} & {18.1534} \\ \end{array} } \right]\), \({\mathbf{K}}_{p1} = \left[ {\begin{array}{*{20}c} {4.1089} & {0.3496} \\ {2.4982} & {0.1826} \\ {0.3073} & {2.6903} \\ \end{array} } \right]\), \({\mathbf{K}}_{p2} = \left[ {\begin{array}{*{20}c} {4.1520} & {0.8118} \\ {3.4829} & { - 0.0396} \\ { - 0.1333} & {4.7496} \\ \end{array} } \right]\), \({\mathbf{K}}_{d1} = \left[ {\begin{array}{*{20}c} {4.8576} & {0.5830} \\ {0.4665} & {0.0893} \\ {0.2883} & {1.9454} \\ \end{array} } \right]\), \({\mathbf{K}}_{d2} = \left[ {\begin{array}{*{20}c} {2.4684} & { - 0.2438} \\ {2.0260} & { - 0.1348} \\ {0.0277} & {4.0220} \\ \end{array} } \right]\), \({\mathbf{Y}}_{p1}^{\text{T}} = \left[ {\begin{array}{*{20}c} { - 2.7256} \\ { - 1.1171} \\ {5.6100} \\ \end{array} } \right]\), \({\mathbf{Y}}_{p2}^{\text{T}} = \left[ {\begin{array}{*{20}c} {5.1933} \\ {0.9740} \\ {7.8066} \\ \end{array} } \right]\), \({\mathbf{Y}}_{d1}^{\text{T}} = \left[ {\begin{array}{*{20}c} {1.7270} \\ {0.5833} \\ {1.0386} \\ \end{array} } \right]\), \({\mathbf{Y}}_{d2}^{\text{T}} = \left[ {\begin{array}{*{20}c} { - 0.9565} \\ { - 0.6106} \\ {2.2969} \\ \end{array} } \right]\) and \(\varepsilon = 60.7512\).

Following Step 5, the following gains can be inferred to design the observer-based PD fuzzy controller (7).

\({\mathbf{F}}_{p1} = \left[ {\begin{array}{*{20}c} { - 7.9783} & { - 1.8428} & {116.7187} \\ \end{array} } \right]\), \({\mathbf{F}}_{p2} = \left[ {\begin{array}{*{20}c} { - 9.9607} & { - 2.2793} & {164.1716} \\ \end{array} } \right]\), \({\mathbf{F}}_{d1} = \left[ {\begin{array}{*{20}c} { - 1.1929} & { - 0.2612} & {22.0254} \\ \end{array} } \right]\), \({\mathbf{F}}_{d2} = \left[ {\begin{array}{*{20}c} { - 3.2471} & { - 0.7606} & {47.8407} \\ \end{array} } \right]\), \({\mathbf{L}}_{p1} = \left[ {\begin{array}{*{20}c} {1.7977} & { - 74.7475} \\ {1.0308} & { - 41.3165} \\ {5.6739} & { - 373.4598} \\ \end{array} } \right]\), \({\mathbf{L}}_{p2} = \left[ {\begin{array}{*{20}c} {2.7700} & { - 138.8451} \\ {0.8253} & { - 16.9715} \\ {9.8407} & { - 654.9540} \\ \end{array} } \right]\), \({\mathbf{L}}_{d1} = \left[ {\begin{array}{*{20}c} {2.4782} & { - 111.8035} \\ {0.3072} & { - 15.3300} \\ {4.1200} & { - 270.4708} \\ \end{array} } \right]\) and \({\mathbf{L}}_{d2} = \left[ {\begin{array}{*{20}c} {0.1365} & {17.7549} \\ {0.2479} & {5.5502} \\ {8.3698} & { - 555.5267} \\ \end{array} } \right]\).

Based on the designed controller, the responses of (29) are provided in Figs. 2, 3 and 4 with initial conditions as \(x\left( 0 \right) = \left[ {\begin{array}{*{20}c} {0.5} & {0.7} & 0 \\ \end{array} } \right]^{{\text{T}}}\) and \(\hat{x}\left( 0 \right) = \left[ {\begin{array}{*{20}c} 0 & {0} & 0 \\ \end{array} } \right]^{{\text{T}}}\). Based on those figures, some vibrations caused by the uncertainties shows that the effect of uncertainties on the system (29). Though the vibrations exist, \(x\left( t \right) \to 0\) and \(e\left( t \right) \to 0\) implying \(\hat{x}\left( t \right) \to x\left( t \right)\) are achieved for satisfying \(\dot{V}\left( {\tilde{x}\left( t \right)} \right) < 0\) as \(t \to \infty\). Therefore, the robust asymptotical stability in Definition 1 is achieved by the design observer-based PD fuzzy controller in this case. In this example, one can easily find that the proposed design method is less conservative than the method of [32] from Case 1. And, the effectiveness of the proposed method is demonstrated by Case 2 for guaranteeing the robust asymptotical stability of uncertain nonlinear singular systems. To emphasize the importance of considering robust performance, a stabilization problem of the complicated numerical example is provided in the following example.

Fig. 2
figure 2

Responses of \(x_{1} \left( t \right)\) for Example 1

Full size image
Fig. 3
figure 3

Responses of \(x_{2} \left( t \right)\) for Example 1

Full size image
Fig. 4
figure 4

Responses of \(x_{3} \left( t \right)\) for Example 1

Full size image

Example 2

In this example, the method of [32] is applied to describe the effect of uncertainty on the system. Let us consider the following uncertain nonlinear singular system.

$$\dot{x}_{{1}} \left( t \right) = \left( { - 4 - 0.5{{\sin}}\left( t \right)} \right)x_{{1}} \left( t \right) + \left( {{2} - {0.5}{{\sin}}\left( t \right)} \right)x_{{2}} \left( t \right){ + }x_{{3}} \left( t \right){ + 2}x_{{4}} \left( t \right)$$
(30a)
$$\dot{x}_{2} \left( t \right) = \left( { - 2 + 0.1{\text{sin}}\left( t \right)} \right)x_{{1}} \left( t \right) + \left( {3 + 0.1{\text{sin}}\left( t \right)} \right)x_{{2}} \left( t \right) - {\text{sin}}\left( {x_{{1}} \left( t \right)} \right)x_{{3}} \left( t \right) - \left( {{2 \mathord{\left/ {\vphantom {2 {{\text{cos}}\left( {x_{{1}} \left( t \right)} \right)}}} \right. \kern-\nulldelimiterspace} {{\text{cos}}\left( {x_{{1}} \left( t \right)} \right)}} + 1} \right)u\left( t \right)$$
(30b)
$$\dot{x}_{3} \left( t \right) = {\text{sin}}\left( {x_{{1}} \left( t \right)} \right) - 2x_{{2}} \left( t \right) - {\text{cos}}\left( {x_{{1}} \left( t \right)} \right)x_{{3}} \left( t \right) + x_{4} \left( t \right)$$
(30c)
$$0 = 5x_{{2}} \left( t \right) - 3x_{{3}} \left( t \right) - 2x_{4} \left( t \right) + \left( {1 - 0.2{\text{sin}}\left( t \right)} \right)u\left( t \right)$$
(30d)
$$y_{{1}} \left( t \right) = x_{1} \left( t \right)$$
(30e)
$$y_{{2}} \left( t \right) = x_{2} \left( t \right)$$
(30f)
$$y_{{3}} \left( t \right) = x_{{4}} \left( t \right)$$
(30g)

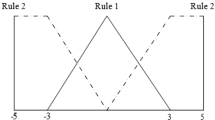
Based on the modeling approach, the uncertain nonlinear singular system (30) can be represented as the following T–S fuzzy model with the membership function in Fig. 5.

$${\mathbf{E}}\dot{x}\left( t \right) = \sum\limits_{{i = {1}}}^{{2}} {h_{i} \left( {x\left( t \right)} \right)\left\{ {\left( {{\mathbf{A}}_{i} + {\mathbf{\Delta A}}} \right)x\left( t \right) + \left( {{\mathbf{B}}_{i} + {\mathbf{\Delta B}}} \right)u\left( t \right)} \right\}}$$
(31a)
$$y\left( t \right) = {\mathbf{C}}x\left( t \right)$$
(31b)
Fig. 5
figure 5

Membership function of \(x_{1} \left( t \right)\) for Example 2

Full size image

where \({\mathbf{E}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]\), \({\mathbf{A}}_{1} = \left[ {\begin{array}{*{20}c} { - 4} & 2 & 1 & 2 \\ { - 2} & 3 & 0 & 0 \\ 0 & { - 2} & { - 1} & 1 \\ 0 & 5 & { - 3} & { - 2} \\ \end{array} } \right]\), \({\mathbf{A}}_{2} = \left[ {\begin{array}{*{20}c} { - 4} & 2 & 1 & 2 \\ { - 2} & 3 & { - 1} & 0 \\ {\frac{2}{\pi }} & { - 2} & { - \beta } & 1 \\ 0 & 5 & { - 3} & { - 2} \\ \end{array} } \right]\), \({\mathbf{B}}_{1} = \left[ {\begin{array}{*{20}c} 0 \\ { - 1} \\ 0 \\ 1 \\ \end{array} } \right]\), \({\mathbf{B}}_{2} = \left[ {\begin{array}{*{20}c} 0 \\ {\frac{ - 2}{{\beta + 1}}} \\ 0 \\ 1 \\ \end{array} } \right]\), \({\mathbf{\Delta A}} = \left[ {\begin{array}{*{20}c} 0 & { - 0.5\sin \left( t \right)} & { - 0.5\sin \left( t \right)} & 0 \\ 0 & 0 & 0 & 0 \\ 0 & {0.1\sin \left( t \right)} & {0.1\sin \left( t \right)} & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]\), \({\mathbf{\Delta B}} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ { - 0.2\sin \left( t \right)} \\ \end{array} } \right]\),

\({\mathbf{C}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]\) and \(\beta = {\text{cos}} \left( {88^{ \circ } } \right)\).

According to Step 1 in Design Procedure, Assumption 1 is checked by \(rank\left( {\left[ {\begin{array}{*{20}c} {\mathbf{E}} & {{\mathbf{B}}_{1} } \\ \end{array} } \right]} \right) = 4\), \(rank\left( {\left[ {\begin{array}{*{20}c} {\mathbf{E}} & {{\mathbf{B}}_{2} } \\ \end{array} } \right]} \right) = 4\) and \(rank\left( {\left[ {\begin{array}{*{20}c} {\mathbf{E}} \\ {\mathbf{C}} \\ \end{array} } \right]} \right) = 4\). In Step 2 and Step 3, the parameters in Table 5 are assigned to satisfy (2) and Assumption 2.

Table 4 The used parameters
Full size table
Table 5 The used parameters
Full size table

Based on Step 4, the following solutions are obtained by the convex optimization algorithm.

\({\tilde{\mathbf{P}}}_{1} { = }\left[ {\begin{array}{*{20}c} {2.7501} & {0.1011} & {0.4126} & { - 0.7019} \\ {0.1011} & {0.7302} & { - 0.0384} & {0.0080} \\ {0.4126} & { - 0.0384} & {1.1830} & { - 0.2800} \\ { - 0.7019} & {0.0080} & { - 0.2800} & {1.0910} \\ \end{array} } \right]\), \({\tilde{\mathbf{P}}}_{2} { = }\left[ {\begin{array}{*{20}c} {1.3405} & {0.1373} & { - 0.0501} & { - 0.4682} \\ {0.1373} & {0.4964} & {0.0652} & {0.1531} \\ { - 0.0501} & {0.0652} & {0.1421} & {0.2809} \\ { - 0.4682} & {0.1531} & {0.2809} & {1.3967} \\ \end{array} } \right]\), \({\tilde{\mathbf{P}}}_{3} { = }\left[ {\begin{array}{*{20}c} {0.3194} & {0.1223} & {0.0075} & { - 0.1920} \\ {0.1786} & { - 0.1122} & {0.0011} & {0.0821} \\ {0.1304} & { - 0.0565} & {0.0088} & { - 0.0609} \\ { - 0.1781} & {0.0640} & {0.0064} & {0.0239} \\ \end{array} } \right]\), \({\mathbf{R}}_{1} { = }\left[ {\begin{array}{*{20}c} {1.0805} & {0.6027} & { - 0.2492} & {0.0154} \\ {0.1405} & {0.2985} & { - 0.0381} & {0.1549} \\ {0.4322} & {0.1829} & {0.7527} & {0.0365} \\ { - 0.9540} & {0.5744} & { - 1.3293} & {0.8779} \\ \end{array} } \right]\), \({\mathbf{R}}_{2} { = }\left[ {\begin{array}{*{20}c} {0.5858} & {0.2513} & { - 0.0021} & 0 \\ {0.1070} & {0.0978} & { - 0.0579} & 0 \\ {0.5864} & { - 0.2448} & {0.7862} & 0 \\ { - 0.3167} & { - 0.0876} & {0.0494} & {0.1167} \\ \end{array} } \right]\), \({\mathbf{Y}}_{p1}^{{\text{T}}} = \left[ {\begin{array}{*{20}c} {0.7179} \\ { - 0.3797} \\ { - 0.2167} \\ {0.1460} \\ \end{array} } \right]\), \({\mathbf{Y}}_{p2}^{{\text{T}}} = \left[ {\begin{array}{*{20}c} {0.6098} \\ { - 0.2724} \\ {0.0952} \\ {0.1073} \\ \end{array} } \right]\), \({\mathbf{Y}}_{d1}^{{\text{T}}} = \left[ {\begin{array}{*{20}c} { - 0.0192} \\ { - 0.0307} \\ {0.1552} \\ {0.1947} \\ \end{array} } \right]\), \({\mathbf{Y}}_{d2}^{{\text{T}}} = \left[ {\begin{array}{*{20}c} {0.0350} \\ { - 0.0958} \\ {0.0386} \\ {0.1505} \\ \end{array} } \right]\), \({\mathbf{K}}_{p1} = \left[ {\begin{array}{*{20}c} { - 0.2877} & { - 0.0403} & {0.5880} \\ { - 0.2157} & {0.2250} & { - 0.0052} \\ { - 0.9903} & { - 0.0051} & {0.5493} \\ {0.1571} & { - 0.1370} & {0.2410} \\ \end{array} } \right]\), \({\mathbf{K}}_{p2} = \left[ {\begin{array}{*{20}c} { - 0.3707} & { - 0.1414} & {0.6471} \\ { - 0.5293} & {0.5249} & {0.0365} \\ { - 0.3389} & {0.1098} & {0.3901} \\ {0.2426} & { - 0.1304} & {0.1636} \\ \end{array} } \right]\), \({\mathbf{K}}_{d1} = \left[ {\begin{array}{*{20}c} {0.4659} & { - 0.0622} & { - 0.0137} \\ {0.0310} & {0.2118} & { - 0.1277} \\ { - 0.2453} & { - 0.0498} & { - 0.0594} \\ { - 0.0021} & { - 0.0681} & {0.2453} \\ \end{array} } \right]\), \({\mathbf{K}}_{d2} = \left[ {\begin{array}{*{20}c} {0.4547} & { - 0.1203} & { - 0.0248} \\ { - 0.0529} & {0.4101} & { - 0.1405} \\ { - 0.2559} & { - 0.1341} & { - 0.1074} \\ {0.0587} & { - 0.1389} & {0.2001} \\ \end{array} } \right]\) and \(\varepsilon = 2.6413\).

Following Step 5, the following gains can be derived from the solutions in Step 4.

\({\mathbf{F}}_{p1} = \left[ {\begin{array}{*{20}c} {3.2471} & { - 16.0564} & {4.8172} & {2.7422} \\ \end{array} } \right]\), \({\mathbf{F}}_{p2} = \left[ {\begin{array}{*{20}c} {2.3573} & { - 11.9582} & {3.8855} & {2.0294} \\ \end{array} } \right]\), \({\mathbf{F}}_{d1} = \left[ {\begin{array}{*{20}c} {0.5165} & { - 3.6328} & {1.5847} & {0.7879} \\ \end{array} } \right]\), \({\mathbf{F}}_{d2} = \left[ {\begin{array}{*{20}c} {0.7690} & { - 4.6477} & {1.6748} & {0.9084} \\ \end{array} } \right]\),

\({\mathbf{L}}_{p1} = \left[ {\begin{array}{*{20}c} {4.9535} & { - 18.3600} & {2.0875} \\ { - 5.6023} & {20.4385} & { - 1.4977} \\ { - 2.1591} & {4.5758} & {0.3673} \\ {6.3806} & { - 22.7005} & {1.9622} \\ \end{array} } \right]\), \({\mathbf{L}}_{p2} = \left[ {\begin{array}{*{20}c} {6.5686} & { - 24.9321} & {2.6427} \\ { - 12.7348} & {46.4402} & { - 3.3415} \\ { - 0.2242} & {0.5575} & {0.4557} \\ {6.1215} & { - 21.5032} & {1.7762} \\ \end{array} } \right]\), \({\mathbf{L}}_{d1} = \left[ {\begin{array}{*{20}c} {4.8961} & { - 16.1071} & {1.1563} \\ { - 4.6647} & {17.8068} & { - 1.4621} \\ { - 2.0004} & {5.8919} & { - 0.5044} \\ {3.9269} & { - 14.1469} & {1.3439} \\ \end{array} } \right]\) and \({\mathbf{L}}_{d2} = \left[ {\begin{array}{*{20}c} {5.6193} & { - 19.0633} & {1.3581} \\ { - 8.7763} & {33.2577} & { - 2.6059} \\ { - 1.2698} & {2.7274} & { - 0.3343} \\ {5.0859} & { - 18.4977} & {1.6039} \\ \end{array} } \right]\).

According to Step 6, the observer-based PD fuzzy controller (7) can be established. Based on the design controller, the response of (30) are stated in Figs. 6, 7, 8 and 9 with the initial conditions as \(x\left( 0 \right) = \left[ {\begin{array}{*{20}c} {0.3} & {0.5} & { - 0.5} & {0.5} \\ \end{array} } \right]^{\text{T}}\) and \(\hat{x}\left( 0 \right) = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ \end{array} } \right]^{\text{T}}\). It is obvious that \(x\left( t \right) \to 0\) and \(\hat{x}\left( t \right) \to x\left( t \right)\) with \(t \to \infty\) that achieves robust asymptotical stability in Definition 1.

Fig. 6
figure 6

Responses of \(x_{1} \left( t \right)\) for Example 2

Full size image
Fig. 7
figure 7

Responses of \(x_{2} \left( t \right)\) for Example 2

Full size image
Fig. 8
figure 8

Responses of \(x_{3} \left( t \right)\) for Example 2

Full size image
Fig. 9
figure 9

Responses of \(x_{4} \left( t \right)\) for Example 2

Full size image

By applying the method in [32], the following gains can be obtained by the convex optimization algorithm for (31) without uncertainties.

\({\mathbf{F}}_{p1} = \left[ {\begin{array}{*{20}c} {1.5967} & { - 5.5300} & {1.1141} & {0.7900} \\ \end{array} } \right]\), \({\mathbf{F}}_{p2} = \left[ {\begin{array}{*{20}c} {0.9577} & { - 3.1842} & {1.0972} & {0.4703} \\ \end{array} } \right]\), \({\mathbf{F}}_{d1} = \left[ {\begin{array}{*{20}c} {0.7869} & { - 3.0010} & {0.8267} & {0.3569} \\ \end{array} } \right]\), \({\mathbf{F}}_{d2} = \left[ {\begin{array}{*{20}c} {0.4116} & { - 1.6968} & {0.5585} & {0.2096} \\ \end{array} } \right]\),

\({\mathbf{L}}_{p1} = \left[ {\begin{array}{*{20}c} {18.3588} & {13.8048} & {27.0341} \\ {617.7153} & {443.4477} & {952.7203} \\ { - 576.5891} & { - 412.5907} & { - 891.5177} \\ { - 31.4543} & { - 25.2292} & { - 40.6696} \\ \end{array} } \right]\), \({\mathbf{L}}_{p2} = \left[ {\begin{array}{*{20}c} {18.8686} & {14.3036} & {26.5415} \\ {636.1224} & {457.8134} & {940.5807} \\ { - 593.2377} & { - 425.9614} & { - 880.2819} \\ { - 31.9561} & { - 25.9466} & { - 39.9944} \\ \end{array} } \right]\), \({\mathbf{L}}_{d1} = \left[ {\begin{array}{*{20}c} {9.4613} & {5.9723} & {11.5323} \\ {282.1270} & {206.5731} & {450.4091} \\ { - 262.5442} & { - 193.3040} & { - 421.9625} \\ { - 14.3907} & { - 14.9146} & { - 17.9430} \\ \end{array} } \right]\) and \({\mathbf{L}}_{d2} = \left[ {\begin{array}{*{20}c} {9.9413} & {6.4724} & {10.9506} \\ {299.1701} & {220.5872} & {434.7562} \\ { - 278.5444} & { - 206.3352} & { - 407.4295} \\ { - 14.8450} & { - 15.6308} & { - 17.1248} \\ \end{array} } \right]\).

With the above gains, the corresponding observer-based PD fuzzy controller can be designed. Based on the same initial conditions, the responses of (30) derived by the controller designed by [32] are also shown in Figs. 6, 7, 8 and 9. Referring to those figures, the system (30) driven by the controller designed by [32] is also stable since the robustness of fuzzy controller. However, the control performances including overshoot and settling time of (30) driven by the observer-based fuzzy controller designed via the proposed design method are better than one designed via the method of [32]. Besides, according to the uncertainty, some strange responses of system (30) driven by the controller design by [32] are caused by the uncertainty. Therefore, the robustness is worth considered in the practical dynamic systems. Based on those examples, the proposed design method is more general and less conservative than the method of [32].

5 Conclusions

In this paper, the observer-based PD fuzzy controller design method was proposed for uncertain nonlinear singular systems. According to the designed observer, the current states can be estimated to guarantee the existence of derivative term in controller. Therefore, the PD fuzzy controller can be realized to guarantee the robust asymptotical stability of the considered systems. To develop the method, the Lyapunov function whose positive definite matrix is not required as diagonal case was chosen to derive the sufficient conditions. The SVD technology was applied to decompose the constant output matrix into a convertible term. The projection lemma is used to transfer the conditions into LMI form that can be directly solved by the convex optimization algorithm. Based on the chosen Lyapunov function and the converting technologies, the less conservative stability criterion for nonlinear singular systems was proposed by this paper. Furthermore, the proposed is more general and less conservative than the existing method related to observer-based PD fuzzy control issue due to the consideration of robust performance. To demonstrate the application and effectiveness of this paper, two numerical examples were proposed to compare with the relaxed work. According to the SVD technology, a limitation in the proposed method is to require linear output. Thus, it is interested issue of avoiding the limitation in investigating the observer-based PD fuzzy control problem.