1 Introduction

Since Takagi and Sugeno put forward the Takagi–Sugeno (T–S) fuzzy model [1], there has been a growing interest in the control design for nonlinear systems based on the T–S fuzzy model, because the T–S fuzzy model can provide an effective way to present the complex nonlinear systems [2–4]. In recent years, many important researching results have been obtained, for example see [5–12]. Among them, [5] proposed a novel polynomial event-triggered scheme to determine the transmission of the signal and designed a fault detection filter to guarantee that the control system is asymptotically stable. The works in [6, 7] proposed an unknown input observer design approach for the T–S systems and an output feedback controller was developed for stabilizing the uncertain nonlinear systems. [8] investigated the problem of the fuzzy control for a class of nonlinear networked control systems via T–S fuzzy models, and [9] proposed LMI formulations to analyze the local stability and local stabilization of discrete-time nonlinear T–S fuzzy systems. A stability and tracking control of nonlinear systems via T–S fuzzy modeling is developed in [10], and [11] provided a fuzzy state feedback controller approach to guarantee systems stability based on nonlinear discrete-time T–S fuzzy system. [12] designed a new adaptive sliding mode controller to guarantee that the closed-loop system is uniformly ultimately bounded. In addition, the Lyapunov stability theory is a powerful approach to deal with the stability analysis for T–S fuzzy models. Various Lyapunov functions have been used to solve stability analysis problem. Based on the PDC design method, the papers in [13–15] proposed some relaxed stability conditions, and [16] studied an analysis for local stability and designed controllers for T–S fuzzy nonlinear systems, where the corresponding conditions are given in form of LMI. By using fuzzy and non-fuzzy multiple Lyapunov function, [17] discussed the method of controller synthesis for T–S fuzzy singularly perturbed systems. [18] considered the robust stabilization for T–S fuzzy systems. However, the aforementioned fuzzy controller design and stability analysis theories are only for nonswitched fuzzy systems, not the switched fuzzy systems.

Switched systems are a special class of hybrid systems, which consist of a family of continuous or discrete subsystems called modes and rules orchestrating the switching among the modes [19– 21]. In fact, many practical physical and engineering [22–26] can be described as the switched systems, such as the automotive industry, chemical industry process control systems, the plane control systems, vehicle speed change systems, air traffic control, navigation systems. Recently, various results about the stability analysis and control design have been reported for switched fuzzy systems [25–32]. The works in [27–29] investigated the stabilization problems for a class of discrete and continuous switched T–S fuzzy systems. To guarantee the stabilization of the control systems, [30, 31] designed a robust controller and a switching control law for a class of switched fuzzy systems. [32, 33] proposed the stability conditions of the switched stochastic systems with time-varying delay. By using a common Lyapunov function and the average dwell time method, [34] developed a controller for a class of fuzzy systems with asynchronous switching. However, the aforementioned results are only limited to the fuzzy systems with measurable premise variables, and to the best of our knowledge, there are no results on the switched nonlinear fuzzy systems with the immeasurable premise variables. Because the premise variables are usually the functions of the state variables, they are estimated by a state observer; this makes it difficult to guarantee the stability of the switched fuzzy system.

Motivated by the aforementioned analysis, this paper studies the output feedback robust stabilization problem for a class of switched fuzzy nonlinear systems, where the premise variables and the state variables are not available for feedback control design. By using PDC design and the Multiple Lyapunov function methods, an output feedback state controller and the sufficient conditions of ensuring the control system stability are developed. To obtain the feasible solutions of the control and observer gain matrixes, a novel decoupled method is proposed to transform the non-LMI conditions into some LMI forms. Compared with the existing literature, the main contributions of this paper can be summarized as follows:

  1. (1)

    This paper first studied the observer-based fuzzy control design problem for a class of switched fuzzy systems. The addressed control plants contain the immeasurable premise variables and the state variables. Note that the literatures [35, 36] also studied the same problem; however, the considered switched plants in [35, 36] are simple fuzzy system, instead of switched fuzzy systems with the immeasurable premise variables. To the best of our knowledge, to date, there are not any results reported on the immeasurable state switched fuzzy nonlinear systems.

  2. (2)

    This paper first investigated a decoupled method for a class of switched nonlinear fuzzy systems. Although the previous literatures [34, 37] also studied the decoupled methods, these control methods are suitable for the nonswitching fuzzy systems. It should be mentioned that the switched control design has a major difference from non-switched control design. The former is much more difficult and challenging than the latter.

2 System Description

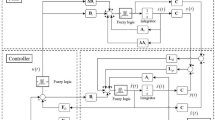
Consider the following switched nonlinear fuzzy system, which is composed of l fuzzy subsystems as follows:

$$R_{\sigma }^{i} \;:{\text{ If}}\;z_{1} \;{\text{is}}\;F_{{\sigma {\kern 1pt} 1}}^{i} ,\;z_{2} \;{\text{is}}\;F_{{\sigma {\kern 1pt} 2}}^{i} , \ldots ,\;z_{p} \;F_{\sigma p}^{i} ,{\text{ then}}$$
$$\left\{ \begin{array}{ll} \dot{x} = A_{{\sigma {\kern 1pt} i}} x + B_{{\sigma {\kern 1pt} i}} u_{\sigma } \hfill \\ y = C_{{\sigma {\kern 1pt} i}} x \hfill \\ \end{array} \right.,\quad i = 1,2, \ldots ,N_{\sigma } ,$$
(1)

where \(z = [z_{1} ,z_{2} \cdots z_{p} ]^{\text{T}}\) are the immeasurable premise variables, and \(F_{\sigma j}^{i}\) are the fuzzy sets; \(\sigma \in M = \{ 1,2, \ldots ,l\}\) is a switching signal, which is a piecewise constant function; \(A_{{\sigma {\kern 1pt} i}}\), \(B_{{\sigma {\kern 1pt} i}}\) and \(C_{{\sigma {\kern 1pt} i}}\) are known real constant matrices with appropriate dimensions; \(u_{\sigma }\) is the control input vector; \(x \in R^{n}\) is the immeasurable state variable vector; \(y\) is the output of the switched system.

Using the center-average defuzzification, product inference, and singleton fuzzifier, the input–output relation in the lth switched system (1) is represented as

$$\left\{ \begin{array}{ll} \dot{x} = \sum\limits_{i = 1}^{{N_{\sigma } }} {\mu_{{\sigma {\kern 1pt} i}} } (z)\left[ {A_{{\sigma {\kern 1pt} i}} x + B_{{\sigma {\kern 1pt} i}} u_{\sigma } } \right] \hfill \\ y = \sum\limits_{i = 1}^{{N_{\sigma } }} {\mu_{{\sigma {\kern 1pt} i}} } (z)C_{{\sigma {\kern 1pt} i}} x \hfill \\ \end{array} \right.$$
(2)

where the lth switched system (2) is equivalent to

$$\left\{ \begin{array}{ll} \dot{x} = A_{\sigma } (\mu_{\sigma } )x + B_{\sigma } (\mu_{\sigma } )u_{\sigma } \hfill \\ y = C_{\sigma } (\mu_{\sigma } )x \hfill \\ \end{array} \right.$$

\(\mu_{{\sigma {\kern 1pt} i}} (z) = \omega_{{\sigma {\kern 1pt} i}} (z)/\sum\limits_{i = 1}^{{N_{\sigma } }} {\omega_{{\sigma {\kern 1pt} i}} } (z),\;\omega_{\sigma \,i} (z) = \prod\limits_{p = 1}^{q} {F_{{\sigma {\kern 1pt} p}} (z_{p} )}\).

\(F_{{\sigma {\kern 1pt} p}} (z_{p} )\) is the fuzzy membership grade of \(z_{p}\) in \(F_{p}\), \(N_{\sigma }\) is the number of If-Then rules, \(\mu_{{\sigma {\kern 1pt} i}} (z)\) satisfies the following conditions:

$$0 < \mu_{{\sigma {\kern 1pt} i}} (z) < 1,\;\sum\limits_{i = 1}^{{N_{\sigma } }} {\mu_{{\sigma {\kern 1pt} i}} (z) = 1} ,$$

Lemma 1

[36] For any real matrices \(X_{i} ,Y_{i} (1 \le i \le n)\), and D > 0 with appropriate dimensions, we have,

$$\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {\sum\limits_{l = 1}^{n} {h_{i} } } } } h_{j} h_{k} h_{l} X_{ij}^{\rm T} DY_{kl} \le {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {h_{i} h_{j} } } \left( {X_{ij}^{\rm T} DX_{ij} + Y_{ij}^{\rm T} DY_{ij} } \right)$$
(3)

where \(0 < h_{i} < 1,\;\sum\nolimits_{i = 1}^{n} {h_{i} } = 1,\;(1 \le i \le n)\).

Lemma 2

[38] Given constant matrices \(X\) and \(Y\), for arbitrary \(\varpi > 0\), the following inequality holds:

$$X^{\rm T} Y + Y^{\rm T} X \le \varpi X^{\rm T} X + \varpi^{ - 1} Y^{\rm T} Y$$
(4)

The control objective of this paper is to design an output feedback fuzzy controller for the fuzzy system ( 2 ) and a switching law \(\sigma\) such that the switched fuzzy nonlinear system is robustly asymptotically stable.

3 Fuzzy Controller Design and Stability Analysis

This section will give the output feedback control design for the switched fuzzy system, and the stability of the closed-loop switched fuzzy system will be proved by using multiple Lyapunov function method.

Since the states in (2) are unavailable for the control design, a fuzzy state observer is first established for estimating the immeasurable states.

Design the switched fuzzy observer for switched fuzzy system (2) as

$$\left\{ \begin{array}{ll} \dot{\hat{x}} = \sum\limits_{i = 1}^{{N_{\sigma } }} {\mu_{{\sigma {\kern 1pt} i}} (\hat{z})(A_{{\sigma {\kern 1pt} i}} \hat{x} + B_{{\sigma {\kern 1pt} i}} u_{\sigma } + L_{{\sigma {\kern 1pt} i}} (y - \hat{y}))} \hfill \\ \hat{y} = \sum\limits_{i = 1}^{{N_{\sigma } }} {\mu_{{\sigma {\kern 1pt} i}} (\hat{z})C_{{\sigma {\kern 1pt} i}} \hat{x}} \hfill \\ \end{array} \right.$$
(5)

The switched fuzzy observer (5) is equivalent to

$$\left\{ \begin{array}{ll} \dot{\hat{x}} = A_{\sigma } (\hat{\mu }_{\sigma } )\hat{x} + B_{\sigma } (\hat{\mu }_{\sigma } )u_{\sigma } + L_{\sigma } (\hat{\mu }_{\sigma } )(y - \hat{y}) \hfill \\ \hat{y} = C_{\sigma } (\hat{\mu }_{\sigma } )\hat{x} \hfill \\ \end{array} \right.$$

where \(\hat{x} \in R^{n}\) is the estimate of \(x\), \(\hat{z}\) is the estimate of immeasurable premise variables \({\kern 1pt} z\), \(\hat{\mu }_{\sigma }\) is the estimate of membership functions \(\mu_{\sigma }\), \(L_{{\sigma {\kern 1pt} i}}\) is the observer gain matrix for the \(\sigma {\text{th}}\) switched fuzzy subsystem; \(L_{\sigma } (\hat{\mu }_{\sigma } ) = \sum\limits_{i = 1}^{{N_{\sigma } }} {\mu_{{\sigma {\kern 1pt} i}} (\hat{z})} L_{{\sigma {\kern 1pt} i}}\).

Next, we consider the switching signal in the state-dependent form \(\sigma = \sigma (\hat{x})\) [39], suppose that \(\tilde{\varOmega }_{1} ,\tilde{\varOmega }_{2} , \ldots ,\tilde{\varOmega }_{l - 1}\) and \(\tilde{\varOmega }_{l}\) is a segmentation of \(R^{n}\), i.e., \(\mathop \cup \limits_{i = 1}^{l} \tilde{\varOmega }_{i} = R^{n} \backslash \{ 0\} ,\) and \(\tilde{\varOmega }_{i} \cap \tilde{\varOmega }_{j} = \phi\), \(i \ne j\), the switching signal is chosen as \(\sigma = \sigma (\hat{x}) = r\) , which depends on \(\tilde{\varOmega }_{1} ,\tilde{\varOmega }_{2} , \ldots ,\tilde{\varOmega }_{l - 1}\) and \(\tilde{\varOmega }_{l}\). When \(\hat{x} \in \tilde{\varOmega }_{l}\), the switching signal \(\sigma (\hat{x})\) can be described by function \(\nu_{r} (\hat{x})\).

$$\nu_{r} (\hat{x}) = \left\{ \begin{array}{ll} 1 \quad \hat{x} \in \tilde{\varOmega }_{r} \hfill \\ 0\quad \hat{x} \notin \tilde{\varOmega }_{r}, \hfill \\ \end{array} \right. \quad r \in M = \{ 1,2, \ldots ,l\}$$
(6)

That is, if and only if \(\sigma = \sigma (\hat{x}) = r\), \(\nu_{r} (\hat{x}) = 1\). We will show how to construct \(\tilde{\varOmega }_{1} ,\tilde{\varOmega }_{2} , \ldots ,\tilde{\varOmega }_{l - 1}\) and \(\tilde{\varOmega }_{l}\), thus the switching law \(\sigma\) will be designed later.

The overall switched fuzzy observer (5) can be rewritten as

$$\left\{ \begin{array}{ll} \dot{\hat{x}} = \sum\limits_{r = 1}^{l} {\sum\limits_{i = 1}^{{N_{r} }} {v_{r} (\hat{x})\mu_{ri} (\hat{z})[A_{ri} \hat{x} + B_{ri} u_{r} + L_{ri} (y - \hat{y})]} } \hfill \\ \hat{y} = \sum\limits_{r = 1}^{l} {\sum\limits_{i = 1}^{{N_{r} }} {v_{r} (\hat{x})\mu_{ri} (\hat{z})} C_{ri} \hat{x}} \hfill \\ \end{array} \right.$$
(7)

The equivalent form of (7) is

$$\left\{ \begin{array}{ll} \dot{\hat{x}} = \sum\limits_{r = 1}^{l} {v_{r} (\hat{x})[A_{r} (\hat{\mu }_{r} )\hat{x} + B_{r} (\hat{\mu }_{r} )u_{r} + L_{r} (\hat{\mu }_{r} )(y - \hat{y})]} \hfill \\ \hat{y} = \sum\limits_{r = 1}^{l} {v_{r} (\hat{x})C_{r} (\hat{\mu }_{r} )\hat{x}} \hfill \\ \end{array} \right.$$
(8)

where \(A_{r} (\hat{\mu }_{r} ) = \sum\limits_{j = 1}^{{N_{r} }} {\mu_{rj} } (\hat{z})A_{rj}\), \(B_{r} (\hat{\mu }_{r} ) = \sum\limits_{j = 1}^{{N_{r} }} {\mu_{rj} } (\hat{z})B_{rj}\) and \({\kern 1pt} C_{r} (\hat{\mu }_{r} ) = \sum\limits_{j = 1}^{{N_{r} }} {\mu_{rj} } (\hat{z})C_{rj} {\kern 1pt}\) are known matrices;\({\kern 1pt} v_{r} (\hat{x})\) is the membership function of switching signal \(\sigma (\hat{x})\).

Based on the PDC scheme, the fuzzy control law for the switched fuzzy systems (2) is

$$u_{r} = \sum\limits_{r = 1}^{l} {\sum\limits_{i = 1}^{{N_{r} }} {v_{r} (\hat{x})\mu_{ri} (\hat{z}_{r} )} K_{ri} \hat{x}}$$
(9)

or

$$u_{r} = \sum\limits_{r = 1}^{l} {v_{r} (\hat{x})K_{r} (\hat{\mu }_{r} )\hat{x}}$$
(10)

where \({\kern 1pt} K_{r}\) is the control gain matrix of the \(\sigma\) th switching mode; \(K_{r} (\mu_{r} ) = \sum\limits_{s = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} s}} (\hat{z}_{r} )} K_{{r{\kern 1pt} s}}\).

Substituting (9) into (2), the closed-loop switched fuzzy system is represented as follows:

$$\left\{ \begin{array}{ll} \dot{x} = \sum\limits_{r = 1}^{l} {v_{r} (\hat{x})} \sum\limits_{i = 1}^{{N_{r} }} {\mu_{ri} (z)\sum\limits_{s = 1}^{{N_{r} }} {\mu_{rs} (\hat{z})} } [A_{ri} x + B_{ri} K_{rs} \hat{x}] \hfill \\ y = \sum\limits_{r = 1}^{l} {v_{r} } (\hat{x})\sum\limits_{i = 1}^{{N_{r} }} {\mu_{ri} (\hat{z})} C_{ri} x \hfill \\ \end{array} \right.$$
(11)

The equivalent form of (11) is

$$\left\{ \begin{array}{ll} \dot{x} = \sum\limits_{r = 1}^{l} {v_{r} } (\hat{x})[A_{r} (\mu_{r} )x + B_{r} (\mu_{r} )K_{r} (\hat{\mu }_{r} )\hat{x}] \hfill \\ y = \sum\limits_{r = 1}^{l} {\nu_{r} (\hat{x})} C_{r} (\mu_{r} )x \hfill \\ \end{array} \right.$$
(12)

where \({\kern 1pt} A_{r} (\mu_{r} ) = \sum\limits_{i = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} i}} } (z)A_{{r{\kern 1pt} i}}\), \(B_{r} (\mu_{r} ) = \sum\limits_{i = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} i}} } (z)B_{{r{\kern 1pt} i}}\), and \(C_{r} (\mu_{r} ) = \sum\limits_{i = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} i}} } (z)C_{{r{\kern 1pt} i}}\) are known matrices.

Let \(e = x - \hat{x}\). From (7), (9) and (11), we get the dynamic equation of estimation error \(e\).

$$\begin{array}{lll} \dot{e} = \dot{x} - \dot{\hat{x}} = \sum\limits_{r = 1}^{l} {v_{r} } (\hat{x})\sum\limits_{i = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} i}} (z)\sum\limits_{j = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} j}} (\hat{z})} \sum\limits_{s = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} s}} (\hat{z})} } [((A_{ri} - A_{rj} ) \, + (B_{ri} - B_{rj} )K_{rs} {\kern 1pt} - L_{rj} (C_{ri} - C_{rs} ))\hat{x} + (A_{ri} - L_{rj} C_{ri} )e] \end{array}$$
(13)

Eq. (13) can be expressed as follows:

$$\begin{aligned} \dot{e} = \sum\limits_{r = 1}^{l} {v_{r} (\hat{x})} [((A_{r} (\mu_{r} ) - A_{r} (\hat{\mu }_{r} )) + (B_{r} (\mu_{r} ) - B_{r} (\hat{\mu }_{r} ))K_{r} (\hat{\mu }_{r} ) \hfill - L_{r} (\hat{\mu }_{r} )(C_{r} (\mu_{r} ) - C_{r} (\hat{\mu }_{r} )))\hat{x} + (A_{r} (\mu_{r} ) - L_{r} (\hat{\mu }_{r} )C_{r} (\mu_{r} ))e] \hfill \end{aligned}$$
(14)

where

$${\kern 1pt} A_{r} (\mu_{r} ) - A_{r} (\hat{\mu }_{r} ) = \sum\limits_{i = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} i}} (z)A_{{r{\kern 1pt} i}} } - \sum\limits_{j = 1}^{{N_{r} }} {\mu_{rj} (\hat{z})A_{rj} } ;$$
$${\kern 1pt} B_{r} (\mu_{r} ) - B_{r} (\hat{\mu }_{r} ) = \sum\limits_{i = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} i}} (z)B_{{r{\kern 1pt} i}} } - \sum\limits_{j = 1}^{{N_{r} }} {\mu_{rj} (\hat{z})B_{rj} } ;$$
$${\kern 1pt} C_{r} (\mu_{r} ) - C_{r} (\hat{\mu }_{r} ) = \sum\limits_{i = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} i}} (z)C_{{r{\kern 1pt} i}} } - \sum\limits_{j = 1}^{{N_{r} }} {\mu_{rj} (\hat{z})C_{rj} } ;$$
$$A_{r} (\mu_{r} ) - L_{r} (\hat{\mu }_{r} )C_{r} (\mu_{r} ) = \sum\limits_{i = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} i}} (z)A_{{r{\kern 1pt} i}} } - \sum\limits_{j = 1}^{{N_{r} }} {\mu_{rj} (\hat{z})} \sum\limits_{i = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} i}} (z)} L_{rj} C_{{r{\kern 1pt} i}}.$$

The sufficient stabilization conditions of the closed-loop switched fuzzy systems are provided in the following theorem.

Theorem 1

For the switched fuzzy system (12), if there exist non-positive (non-negative) \(\gamma_{r\lambda } \in R\;(r,\;\lambda = 1,\;2, \cdots l,\;r \ne \lambda )\), positive definite matrices \(P_{r}\), \(Q_{r}\) and \(P_{\lambda }\) with appropriate dimensions and \(\delta > \alpha > 0,\beta > 0\), satisfying the following conditions

$$\varPi_{r} + \beta^{ - 1} Q_{r} Q_{r} < 0$$
(15)
$$\varLambda_{r} + \sum\limits_{\lambda = 1,\;\lambda \ne r}^{l} {\gamma_{r\lambda } } (P_{\lambda } - P_{r} ) < 0$$
(16)

with

$$\varPi_{r} = A_{ri}^{\rm T} Q_{r} - C_{ri}^{\rm T} L_{rj}^{\rm T} Q_{r} + Q_{r} A_{ri} - Q_{r} L_{rj} C_{ri} + (\alpha^{ - 1} - \delta^{ - 1} )I$$
$$\begin{array}{lll} \varLambda_{r} = \left( {A_{rj}^{\rm T} + K_{rs}^{\rm T} B_{rj}^{\rm T} + \left( {C_{ri}^{\rm T} - C_{rs}^{\rm T} } \right)L_{rj}^{\rm T} } \right)P_{r} + P_{r} \left( {A_{ri} + B_{rj} K_{rs} + L_{rj} (C_{ri} - C_{rs} )} \right) \hfill \quad+ \alpha P_{r} L_{rj} C_{ri} C_{ri}^{\rm T} L_{rj}^{\rm T} P_{r} + \beta \left( {A_{ri}^{\rm T} - A_{rj}^{\rm T} + K_{rs}^{\rm T} \left( {B_{ri}^{\rm T} - B_{rj}^{\rm T} } \right)} \right)(A_{ri} - A_{rj} + (B_{ri} - B_{rj} ) \hfill \quad \times K_{rs} ) - \delta \left( {C_{ri}^{\rm T} - C_{rs}^{\rm T} } \right)L_{rj}^{\rm T} Q_{r} Q_{r} L_{rj} (C_{ri} - C_{rs} ) \hfill \end{array}$$

Then the output feedback controller (9) with the switching law \(\sigma = \sigma (\hat{x})\) can guarantee the closed-loop switched fuzzy system (12) to be asymptotical stable.

Proof

Consider the Lyapunov function candidate

$$V = \hat{x}^{\rm T} P_{r} \hat{x} + e^{\rm T} Q_{r} e$$
(17)

where \(P_{r}\) and \(Q_{r}\) are two positive definite matrices. For any \(e \ne 0\), it follows from (15) that

$$\varPi_{r} + \beta^{ - 1} Q_{r} Q_{r} < 0$$
(18)

(15) means that under designing switching law, the observer error \(e\) asymptotically converges to zero.

Without loss of generality, we assume \(\gamma_{{r{\kern 1pt} \lambda }} \ge 0\). Obviously, for every \(\hat{x} \in R^{n} \backslash \{ 0\}\), there exists a \(r\) such that \(\hat{x}^{\rm T} (P_{\lambda } - P_{r} )\hat{x} > 0\), \(\forall \lambda \in M\), then from the matrix inequality (16), we have

$$\varLambda_{r} + \sum\limits_{\lambda = 1,\lambda \ne r}^{l} {\gamma_{r\lambda } } (P_{\lambda } - P_{r} ) < 0$$
(19)

For an arbitrary \(r \in M = \{ 1,2, \ldots ,l\}\), let

$$\varOmega_{r} = \{ \hat{x} \in R^{n} |\hat{x}^{\rm T} [\varLambda_{r} + \sum\limits_{\lambda = 1,\lambda \ne r}^{l} {\gamma_{r\lambda } } (P_{\lambda } - P_{r} )]\hat{x} < 0,\forall \hat{x} \ne 0\}$$

Then \(\varOmega_{r} = R^{n} \backslash \{ 0\}\). Constructing the sets \(\tilde{\varOmega }_{r} = \varOmega_{r} \backslash \mathop \cup \limits_{i = 1}^{r - 1} \tilde{\varOmega }_{r}\), it is easy to see that \(\mathop \cup \limits_{i = 1}^{r - 1} \tilde{\varOmega }_{i} = R^{n} \backslash \{ 0\}\), and \(\tilde{\varOmega }_{i} \cap \tilde{\varOmega }_{j} = \phi\), \(i \ne j\).

Therefore, the switching law is

$$\sigma (\hat{x}) = r\;{\text{when}}\;\hat{x} \in \tilde{\varOmega }_{r}$$
(20)

Let \(V_{1} = \hat{x}^{\rm T} P_{r} \hat{x}\) and \(V_{2} = e^{\rm T} Q_{r} e\).

  1. (i)

    The time derivative of \(V_{1}\) satisfies

    $$\begin{array}{lllll} \dot{V}_{1} = \dot{\hat{x}}^{\text{T}} P_{r} \hat{x} + \hat{x}^{\text{T}} P_{r} \dot{\hat{x}} = \sum\limits_{r = 1}^{l} {v_{r} } (\hat{x})\sum\limits_{i = 1}^{{N_{r} }} {\mu_{ri} (z)\sum\limits_{j = 1}^{{N_{r} }} {\mu_{rj} (\hat{z})} \sum\limits_{s = 1}^{{N_{r} }} {\mu_{rs} (\hat{z})} } [\hat{x}^{\text{T}} (A_{ri}^{\text{T}} P_{r} + P_{r} A_{ri} )\hat{x} + (u_{r}^{\text{T}} B_{ri}^{\text{T}} + (y - \hat{y})^{\text{T}} L_{rj}^{\text{T}} )P_{r} \hat{x} + \hat{x}^{\text{T}} P_{r} (A_{ri} \hat{x} + B_{rj} u_{r} + L_{rj} (y - \hat{y}))] = \sum\limits_{r = 1}^{l} {v_{r} } (\hat{x})\sum\limits_{i = 1}^{{N_{r} }} {\mu_{ri} (z)\sum\limits_{j = 1}^{{N_{r} }} {\mu_{rj} (\hat{z})} \sum\limits_{s = 1}^{{N_{r} }} {\mu_{rs} (\hat{z})} } [\hat{x}^{\text{T}} ((A_{rj}^{\text{T}} + K_{rs}^{\text{T}} B_{rj}^{\text{T}} + (C_{ri}^{\text{T}} - C_{rs}^{\text{T}} )L_{rj}^{\text{T}} ) P_{r} + P_{r} (A_{ri} + B_{rj} K_{rs} + L_{rj} (C_{ri} - C_{rs} )))\hat{x} + e^{\text{T}} C_{ri}^{\text{T}} L_{rj}^{\text{T}} P_{r} \hat{x} + \hat{x}^{\text{T}} P_{r} L_{rj} C_{ri} e] \end{array}$$
    (21)

    According to Lemma 2, we have

    $$e^{\rm T} C_{ri}^{\rm T} L_{rj}^{\rm T} P_{r} \hat{x} + \hat{x}^{\rm T} P_{r} L_{rj} C_{ri} e \le \alpha \hat{x}^{\rm T} P_{r} L_{rj} C_{ri} C_{ri}^{\rm T} L_{rj}^{\rm T} P_{r} \hat{x} + \alpha^{ - 1} e^{\rm T} e$$
    (22)

    Applying (22) to (21) yields

    $$\begin{aligned} \dot{V}_{1} \le \sum\limits_{r = 1}^{l} {v_{r} } (\hat{x})\sum\limits_{i = 1}^{{N_{r} }} {\mu_{ri} (z)\sum\limits_{j = 1}^{{N_{r} }} {\mu_{rj} (\hat{z})} \sum\limits_{s = 1}^{{N_{r} }} {\mu_{rs} (\hat{z})} } [\hat{x}^{\rm T} ((A_{rj}^{\rm T} + K_{rs}^{\rm T} B_{rj}^{\rm T} + (C_{ri}^{\rm T} - C_{rs}^{\rm T} )L_{rj}^{\rm T} ) \hfill \times P_{r} + P_{r} (A_{ri} + B_{rj} K_{rs} + L_{rj} (C_{ri} - C_{rs} )) + \alpha P_{r} L_{rj} C_{ri} C_{ri}^{\rm T} L_{rj}^{\rm T} P_{r} )\hat{x} + \alpha^{ - 1} e^{\rm T} e]\, \hfill \end{aligned}$$
    (23)
  2. (ii)

    The time derivative of \(V_{2}\) is

    $$\begin{array}{lllllll} \dot{V}_{2} = \dot{e}^{\rm T} Q_{r} e + e^{\rm T} Q_{r} \dot{e} = \sum\limits_{r = 1}^{l} {v_{r} } (\hat{x})\sum\limits_{i = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} i}} (z)\sum\limits_{j = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} j}} (\hat{z})} \sum\limits_{s = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} s}} (\hat{z})} } [(((A_{ri} - A_{rj} ) + (B_{ri} - B_{rj} )K_{rs} {\kern 1pt} - L_{rj} \quad \times (C_{ri} - C_{rs} ))\hat{x} + (A_{ri} - L_{rj} C_{ri} )e)^{\rm T} Q_{r} e + e^{\rm T} Q_{r} (((A_{ri} - A_{rj} ) + (B_{ri} - B_{rj} )K_{rs} \quad - L_{rj} (C_{ri} - C_{rs} ))\hat{x} + (A_{ri} - L_{rj} C_{ri} )e] = \sum\limits_{r = 1}^{l} {v_{r} } (\hat{x})\sum\limits_{i = 1}^{{N_{r} }} {\mu_{ri} (z_{r} )\sum\limits_{j = 1}^{{N_{r} }} {\mu_{rj} (\hat{z}_{r} )} \sum\limits_{s = 1}^{{N_{r} }} {\mu_{rs} (\hat{z}_{r} )} } [\hat{x}^{\rm T} (A_{ri}^{\rm T} - A_{rj}^{\rm T} + K_{rs}^{\rm T} (B_{ri}^{\rm T} - B_{rj}^{\rm T} ))Q_{r} \quad\times e + e^{\rm T} Q_{r} (A_{ri} - A_{rj} + (B_{ri} - B_{rj} )K_{rs} )\hat{x} - e^{\rm T} Q_{r} L_{rj} (C_{ri} - C_{rs} )\hat{x} - \hat{x}^{\rm T} (C_{ri}^{\rm T} - C_{rs}^{\rm T} ) \quad\times L_{rj}^{\rm T} Q_{r} e + e^{\rm T} [(A_{ri}^{\rm T} - C_{ri}^{\rm T} L_{rj}^{\rm T} )Q_{r} + Q_{r} (A_{ri} - L_{rj} C_{ri} )]e \\ \end{array}$$
    (24)

By using the Lemma 2 and (24), we can obtain

$$\begin{array}{lll}\dot{V}_{2} &\le \sum\limits_{r = 1}^{l} {v_{r} } (\hat{x})[e^{\rm T} ((A_{ri}^{\rm T} - C_{ri}^{\rm T} L_{rj}^{\rm T} )Q_{r} + Q_{r} (A_{ri} - L_{rj} C_{ri} ) - \delta^{ - 1} I + \beta^{ - 1} \hfill \\& \quad \times Q_{r} Q_{r} )e + \hat{x}^{\rm T} (\beta (A_{ri}^{\rm T} - A_{rj}^{\rm T} + K_{rs}^{\rm T} (B_{ri}^{\rm T} - B_{rj}^{\rm T} ))(A_{ri} - A_{rj} + (B_{ri} \hfill \\ &\quad- B_{rj} )K_{rs} ) - \delta (C_{ri}^{\rm T} - C_{rs}^{\rm T} )L_{rj}^{\rm T} Q_{r} Q_{r} L_{rj} (C_{ri} - C_{rs} ))\hat{x}] \hfill \\ \end{array}$$
(25)

In view of (23), (25), and (17), we have

$$\begin{array}{lllll} \dot{V} = \dot{V}_{1} + \dot{V}_{2} \hfill \le \sum\limits_{r = 1}^{l} {v_{r} } (\hat{x})\sum\limits_{i = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} i}} (z)\sum\limits_{j = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} j}} (\hat{z})} \sum\limits_{s = 1}^{{N_{r} }} {\mu_{{r{\kern 1pt} s}} (\hat{z})} } [\hat{x}^{\rm T} ((A_{rj}^{\rm T} + K_{rs}^{\rm T} B_{rj}^{\rm T} + (C_{ri}^{\rm T} - C_{rs}^{\rm T} )L_{rj}^{\rm T} )P_{r} \hfill \quad + P_{r} (A_{ri} + B_{rj} K_{rs} + L_{rj} (C_{ri} - C_{rs} )) + \alpha P_{r} L_{rj} C_{ri} C_{ri}^{\rm T} L_{rj}^{\rm T} P_{r} + \beta (A_{ri}^{\rm T} - A_{rj}^{\rm T} + K_{rs}^{\rm T} (B_{ri}^{\rm T} \hfill \quad - B_{rj}^{\rm T} ))(A_{ri} - A_{rj} + (B_{ri} - B_{rj} )K_{rs} ) - \delta (C_{ri}^{\rm T} - C_{rs}^{\rm T} )L_{rj}^{\rm T} Q_{r} Q_{r} L_{rj} (C_{ri} - C_{rs} ))\hat{x} + e^{\rm T} \hfill \quad \times ((A_{ri}^{\rm T} - C_{ri}^{\rm T} L_{rj}^{\rm T} )Q_{r} + Q_{r} (A_{ri} - L_{rj} C_{ri} ) + (\alpha^{ - 1} - \delta^{ - 1} )I + \beta^{ - 1} Q_{r} Q_{r} )e] \hfill \end{array}$$
(26)

Further, we have

$$\begin{aligned} \dot{V} \le \sum\limits_{r = 1}^{l} {v_{r} (\hat{x})} [\hat{x}^{\rm T} ((A_{r}^{\rm T} (\hat{\mu }_{r} ) + K_{r}^{\rm T} (\hat{\mu }_{r} )B_{r}^{\rm T} (\hat{\mu }_{r} ) + (C_{r}^{\rm T} (\mu_{r} ) - C_{r}^{\rm T} (\hat{\mu }_{r} ))L_{r}^{\rm T} (\hat{\mu }_{r} )) \hfill \quad \times P_{r} + P_{r} (A_{r} (\mu_{r} ) + B_{r} (\hat{\mu }_{r} )K_{r} (\hat{\mu }_{r} ) + L_{r} (\hat{\mu }_{r} )(C_{r} (\mu_{r} ) - C_{r} (\hat{\mu }_{r} ))) + \alpha P_{r} \hfill \quad\times L_{r} (\hat{\mu }_{r} )C_{r} (\mu_{r} )C_{r}^{\rm T} (\mu_{r} )L_{r}^{\rm T} (\hat{\mu }_{r} )P_{r} + \beta (A_{r}^{\rm T} (\mu_{r} ) - A_{r}^{\rm T} (\hat{\mu }_{r} ) + K_{r}^{\rm T} (\hat{\mu }_{r} ) \hfill \quad \times (B_{r}^{\rm T} (\mu_{r} ) - B_{r}^{\rm T} (\hat{\mu }_{r} )))(A_{r} (\mu_{r} ) - A_{r} (\hat{\mu }_{r} ) + (B_{r} (\mu_{r} ) - B_{r} (\hat{\mu }_{r} ))K_{r} (\hat{\mu }_{r} )) \hfill \\&\quad - \delta (C_{r}^{\rm T} (\mu_{r} ) - C_{r}^{\rm T} (\hat{\mu }_{r} ))L_{r}^{\rm T} (\hat{\mu }_{r} )Q_{r} Q_{r} L_{r} (\hat{\mu }_{r} )(C_{r} (\mu_{r} ) - C_{r} (\hat{\mu }_{r} )))\hat{x} + e^{\rm T} \hfill \quad \times ((A_{r}^{\rm T} (\mu_{r} ) - C_{r}^{\rm T} (\mu_{r} )L_{r}^{\rm T} (\hat{\mu }_{r} ))Q_{r} + Q_{r} (A_{r} (\mu_{r} ) - L_{r} (\hat{\mu }_{r} )C_{r} (\hat{\mu }_{r} )) + (\alpha^{ - 1} \hfill \, - \delta^{ - 1} )I + \beta^{ - 1} Q_{r} Q_{r} )e] \hfill \end{aligned}$$
(27)

According to Lemma 1, there exists a symmetric matrix \(Y_{rijj}\) and a matrix \(Y_{rijs}\) such that the following inequalities are satisfied [36]:

$$\begin{aligned} (A_{rj}^{\rm T} + K_{rj}^{\rm T} B_{rj}^{\rm T} + (C_{ri}^{\rm T} - C_{rj}^{\rm T} )L_{rj}^{\rm T} )P_{r} + P_{r} (A_{ri} + B_{rj} K_{rj} + L_{rj} (C_{ri} - C_{rj} )) \hfill \quad + \alpha P_{r} L_{rj} C_{ri} C_{ri}^{\rm T} L_{rj}^{\rm T} P_{r} + \beta (A_{ri}^{\rm T} - A_{rj}^{\rm T} + K_{rj}^{\rm T} (B_{ri}^{\rm T} - B_{rj}^{\rm T} ))(A_{ri} - A_{rj} + (B_{ri} \hfill \quad - B_{rj} )K_{rj} ) - \delta (C_{ri}^{\rm T} - C_{rj}^{\rm T} )L_{rj}^{\rm T} Q_{r} Q_{r} L_{rj} (C_{ri} - C_{rj} ) + \sum\limits_{\lambda = 1,\lambda \ne r}^{l} {\gamma_{r\lambda } } (P_{\lambda } - P_{r} ) < Y_{rijj} \hfill \end{aligned}$$
(28)
$$\begin{aligned} 2[(A_{rj}^{\rm T} + K_{rs}^{\rm T} B_{rj}^{\rm T} + C_{ri}^{\rm T} L_{rs}^{\rm T} )P_{r} + P_{r} (A_{ri} + B_{rj} K_{rs} + L_{rs} C_{ri} ) + \alpha P_{r} L_{rj} C_{ri} C_{ri}^{\rm T} L_{rj}^{\rm T} \hfill \quad\times P_{r} + \beta (A_{ri}^{\rm T} - A_{rj}^{\rm T} + K_{rs}^{\rm T} (B_{ri}^{\rm T} - B_{rj}^{\rm T} ))(A_{ri} - A_{rj} + (B_{ri} - B_{rj} ) \times K_{rs} )] - (C_{rj}^{\rm T} \hfill \quad \times L_{rs}^{\rm T} + C_{rs}^{\rm T} L_{rj}^{\rm T} )P_{r} - P_{r} (L_{rs} C_{rj} + L_{rj} C_{rs} ) - \delta (C_{ri}^{\rm T} - C_{rj}^{\rm T} )L_{rs}^{\rm T} Q_{r} Q_{r} L_{rs} (C_{ri} - C_{rj} ) \hfill \,+ \sum\limits_{\lambda = 1,\lambda \ne r}^{l} {\gamma_{r\lambda } } (P_{\lambda } - P_{r} ) < Y_{rijs} + Y_{{_{risj} }}^{\rm T} \hfill \end{aligned}$$
(29)

By using Lemma 1 again, there exist a symmetric matrix \(Z_{rijj}\) and a matrix \(Z_{risj}\) such that the following inequalities are satisfied for the estimation error:

$$(A_{ri}^{\rm T} - C_{ri}^{\rm T} L_{rj}^{\rm T} )Q_{r} + Q_{r} (A_{ri} - L_{rj} C_{ri} ) + (\alpha^{ - 1} - \delta^{ - 1} )I + \beta^{ - 1} Q_{r} Q_{r} < Z_{rijj}$$
(30)
$$2[(A_{ri}^{\rm T} - C_{ri}^{\rm T} L_{rj}^{\rm T} )Q_{r} + Q_{r} (A_{ri} - L_{rj} C_{ri} ) + (\alpha^{ - 1} - \delta^{ - 1} )I + \beta^{ - 1} Q_{r} Q_{r} ] < Z_{rijs} + Z_{{_{risj} }}^{\rm T}$$
(31)

Similar to [40], the time derivative of (26) is expressed by

$$\begin{aligned} \dot{V} \le \sum\limits_{r = 1}^{l} {\sum\limits_{i = 1}^{f} {v_{r} (\hat{x})\hat{\mu }_{ri} } \left\{ {\left[ \begin{aligned} \hat{\mu }_{r1} I \hfill \\ \hat{\mu }_{r2} I \hfill \\ \vdots \hfill \\ \hat{\mu }_{rf} I \hfill \\ \end{aligned} \right]^{\rm T} \left[ {\begin{array}{cccc} {Y_{ri11} {\kern 1pt} {\kern 1pt} } &\quad * &\quad \ldots &\quad * \\ {(Y_{ri12} )^{\rm T} } &\quad {(Y_{ri22} )^{\rm T} } &\quad \ldots &\quad * \\ \vdots &\quad {{\kern 1pt} \vdots {\kern 1pt} } &\quad \ddots &\quad \vdots \\ {(Y_{ri1f} )^{\rm T} } &\quad * &\quad \cdots &\quad {Z_{riff} } \\ \end{array} } \right]\left[ \begin{aligned} \hat{\mu }_{r1} I \hfill \\ \hat{\mu }_{r2} I \hfill \\ \vdots \hfill \\ \hat{\mu }_{rf} I \hfill \\ \end{aligned} \right]} \right.} \hfill \quad \left. { + \left[ \begin{aligned} \hat{\mu }_{rf} I \hfill \\ \hat{\mu }_{rf} I \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \hfill \\ \hat{\mu }_{rf} I \hfill \\ \end{aligned} \right]^{\rm T} \left[ {\begin{array}{cccc} {Z_{ri11} } &\quad * &\quad \cdots &\quad * \\ {(Z_{ri12} )^{\rm T} } &\quad {{\kern 1pt} (Z_{ri22} )^{\rm T} {\kern 1pt} } &\quad \cdots &\quad * \\ \vdots &\quad \vdots &\quad \ddots &\quad \vdots \\ {(Z_{ri1f} )^{\rm T} } &\quad * &\quad \cdots &\quad {Z_{riff} } \\ \end{array} } \right]\left[ \begin{aligned} \hat{\mu }_{rf} I \hfill \\ \hat{\mu }_{rf} I \hfill \\ \vdots \hfill \\ \hat{\mu }_{rf} I \hfill \\ \end{aligned} \right]} \right\} < 0 \hfill \\ \end{aligned}$$
(32)

From (15) and (16), we know that under the switching law (20), for arbitrary \(\hat{x} \ne 0\) and \(e \ne 0\), i.e.,\(x \ne 0\), \(\dot{V} < 0\) holds.

Therefore, the closed-loop switched fuzzy system is asymptotically stable, and the observer error \(e\) asymptotically converges to zero.

Note that matrix inequalities \(\Re_{r} = \varLambda_{r} + \sum\limits_{\lambda = 1,\lambda \ne r}^{l} {\gamma_{r\lambda } } (P_{\lambda } - P_{r} ) < 0\) are not linear matrix inequalities. Therefore, we should transform \(\Re_{r} < 0\) into LMI and obtain positive definite matrices \(P_{r}\), control gain matrices \(K_{rs}\) and observer gain matrices \(L_{rj}\).

Now, using Schur’s complement, and letting \(M_{rj} = P_{r} L_{rj}\) and \(W_{rj} = K_{rs} P_{r}\), we obtain the following LMIs

$$\left[ {\begin{array}{*{20}c} {\varXi_{r} + {\rm T}_{r} } & {\psi_{r} } & {N_{rj} (C_{ri} - C_{rs} )} & {M_{rj} C_{ri} } \\ * & { - \beta^{ - 1} I} & 0 & 0 \\ * & * & {\delta^{ - 1} I} & 0 \\ * & * & * & { - \alpha^{ - 1} I} \\ \end{array} } \right] < 0$$
(33)

with

$$\varXi_{r} = (A_{rj}^{\rm T} + K_{rs}^{\rm T} B_{rj}^{\rm T} )P_{r} + P_{r} (A_{ri} + B_{rj} K_{rs} ) + \sum\limits_{\lambda = 1,\lambda \ne r}^{l} {\gamma_{r\lambda } } (P_{\lambda } - P_{r} )$$
$$\psi_{r} = A_{ri} - A_{rj} + (B_{ri} - B_{rj} )K_{rs}$$
$${\rm T}_{r} = (C_{ri}^{\rm T} - C_{rs}^{\rm T} )L_{rj}^{\rm T} P_{r} + P_{r} L_{rj} (C_{ri} - C_{rs} )) = (C_{ri}^{\rm T} - C_{rs}^{\rm T} )M_{rj}^{\rm T} + M_{rj} (C_{ri} - C_{rs} ))$$

Since three parameters \(P_{r}\), \(K_{rs}\) and \(L_{rj}\) for system \(R\) should be determined from (30), there is no effective method for solving them simultaneously. In the following, a decoupled method is provided to solve \(P_{r}\), \(K_{rs}\) and \(L_{rj}\) simultaneously. To this end, the following useful theorem is first introduced.

Theorem 2

[34] If two symmetric matrices are satisfied

$$\left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } \\ * & {a_{22} } & {a_{23} } \\ * & * & {a_{33} } \\ \end{array} } \right] < 0$$
(34)

and

$$\left[ {\begin{array}{*{20}c} {b_{11} } & {b_{12} } \\ * & {b_{22} } \\ \end{array} } \right] < 0$$
(35)

Then we will get

$$\left[ {\begin{array}{*{20}c} {a_{11} } & 0 & {a_{12} } & {a_{13} } \\ * & 0 & 0 & 0 \\ * & * & {a_{21} } & {a_{22} } \\ * & * & * & {a_{33} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {b_{11} } & {b_{12} } & 0 & 0 \\ * & {b_{22} } & 0 & 0 \\ * & * & 0 & 0 \\ * & * & * & 0 \\ \end{array} } \right] < 0$$
(36)

Proof

For any \([\begin{array}{*{20}c} {g_{1} } & {g_{2} } & {g_{3} } & {g_{4} } \\ \end{array} ] \ne 0\), if (34) and (35) hold, then

$$\left[ {\begin{array}{*{20}c} {g_{1} } \\ {g_{2} } \\ {g_{3} } \\ {g_{4} } \\ \end{array} } \right]^{\rm T} \left\{ {\left[ {\begin{array}{*{20}c} {a_{11} } & 0 & {a_{12} } & {a_{13} } \\ * & 0 & 0 & 0 \\ * & * & {a_{21} } & {a_{22} } \\ * & * & * & {a_{33} } \\ \end{array} } \right] + } \right.\left. {\left[ {\begin{array}{*{20}c} {b_{11} } & {b_{12} } & 0 & 0 \\ * & {b_{22} } & 0 & 0 \\ * & * & 0 & 0 \\ * & * & * & 0 \\ \end{array} } \right]} \right\}\left[ {\begin{array}{*{20}c} {g_{1} } \\ {g_{2} } \\ {g_{3} } \\ {g_{4} } \\ \end{array} } \right] \hfill \quad = \left[ {\begin{array}{*{20}c} {g_{1} } \\ {g_{2} } \\ {g_{3} } \\ \end{array} } \right]^{\rm T} \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } & {a_{13} } \\ * & {a_{22} } & {a_{23} } \\ * & * & {a_{33} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {g_{1} } \\ {g_{2} } \\ {g_{3} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {g_{1} } \\ {g_{2} } \\ \end{array} } \right]^{\rm T} \left[ {\begin{array}{*{20}c} {b_{11} } & {b_{12} } \\ * & {b_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {g_{1} } \\ {g_{2} } \\ \end{array} } \right] < 0$$
(37)

This implies that (37) holds. Therefore, the proof is completed.

Note that (33) can be decoupled as (38), then, we have

$$\left[ {\begin{array}{*{20}c} {\varXi_{r} + {\rm T}_{r} } & {\psi_{r} } & {N_{rj} (C_{ri} - C_{rs} )} & {M_{rj} C_{ri} } \\ * & { - \beta^{ - 1} I} & 0 & 0 \\ * & * & {\delta^{ - 1} I} & 0 \\ * & * & * & { - \alpha^{ - 1} I} \\ \end{array} } \right] \hfill = \left[ {\begin{array}{*{20}c} {{\rm T}_{r} } & 0 & {N_{rj} (C_{ri} - C_{rs} )} & {M_{rj} C_{ri} } \\ * & 0 & 0 & 0 \\ * & * & {\delta^{ - 1} I} & 0 \\ * & * & * & { - \alpha^{ - 1} I} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\varXi_{r} } & {\psi_{r} } & 0 & 0 \\ * & { - \beta^{ - 1} I} & 0 & 0 \\ * & * & 0 & 0 \\ * & * & * & 0 \\ \end{array} } \right] < 0$$
(38)

The equivalent expressions of the two decoupled matrices are

$$\left[ {\begin{array}{*{20}c} {{\rm T}_{r} } & 0 & {N_{rj} (C_{ri} - C_{rs} )} & {M_{rj} C_{ri} } \\ * & 0 & 0 & 0 \\ * & * & {\delta^{ - 1} I} & 0 \\ * & * & * & { - \alpha^{ - 1} I} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\rm T}_{r} } & {N_{rj} (C_{ri} - C_{rs} )} & {M_{rj} C_{ri} } \\ * & {\delta^{ - 1} I} & 0 \\ * & * & { - \alpha^{ - 1} I} \\ \end{array} } \right] < 0$$
(39)
$$\left[ {\begin{array}{*{20}c} {\varXi_{r} } & {\psi_{r} } & 0 & 0 \\ * & { - \beta^{ - 1} I} & 0 & 0 \\ * & * & 0 & 0 \\ * & * & * & 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varXi_{r} } & {\psi_{r} } \\ * & { - \beta^{ - 1} I} \\ \end{array} } \right] < 0$$
(40)

Pre-and post-multiplying both side of (40) by matrix diag \(\{ P_{r}^{ - 1} ,I\}\) and by using Schur’s complement, then we have

$$\left[ {\begin{array}{*{20}c} {\varGamma_{r} } & {X_{r} } & \cdots & {X_{r} } & {{\rm H}_{r} } \\ * & { - \gamma_{r1}^{ - 1} X_{1} } & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ * & * & \cdots & { - \gamma_{rl}^{ - 1} X_{l} } & 0 \\ * & * & * & * & { - \beta^{ - 1} I} \\ \end{array} } \right] < 0$$
(41)

with \(X_{r} = P_{r}^{ - 1} ,\;\varGamma_{r} = X_{r} A_{rj}^{\rm T} + W_{rs}^{\rm T} B_{rj}^{\rm T} + A_{ri} X_{r} + B_{rj} W_{rs} - \sum\limits_{\lambda = 1,\lambda \ne r}^{l} {\gamma_{r\lambda } } X_{r}\), \(X_{\lambda } = P_{\lambda }^{ - 1} ,\lambda = 1,2, \ldots l,\;{\rm H}_{r} = (A_{ri} - A_{rj} )X_{r} + (B_{ri} - B_{rj} )W_{rs}\).

We need to transform the inequality (18) into LMI. Now, by using Schur’s complement, and letting \(N_{rj} = Q_{r} L_{rj}\), we obtain the following LMI

$$\left[ {\begin{array}{*{20}c} {\varPi_{r} } & {Q_{r} } \\ * & { - \beta } \\ \end{array} } \right] < 0$$
(42)

Solving the LMIs (39), (41), and (42), we can obtain the positive definite matrices \(Q_{r}\) and \(X_{r}\) (thus \(X_{r} = P_{r}^{ - 1}\)), the control gain matrices \(W_{rs}\) (thus \(K_{rs} = W_{rs} X_{r}\)), the observer gain matrices \(N_{rj}\) (thus \(L_{rj} = Q_{r} N_{rj}\)).

4 Simulation Study

In order to illustrate the effectiveness of the proposed method, two simulation examples are given as follows:

Example 1

Consider a switched fuzzy system with immeasurable premise variables.

$$\left\{ \begin{array}{ll} \dot{x} = \left[ {\begin{array}{*{20}c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ \end{array} } \right] = \sum\limits_{i = 1}^{2} {\mu_{\sigma i} } (z_{1} )[A_{\sigma i} x_{1} + B_{\sigma i} u_{\sigma } ] \hfill \\ y = \left[ {\begin{array}{ll} {y_{1} } \\ {y_{2} } \\ \end{array} } \right] = \sum\limits_{i = 1}^{2} {\mu_{\sigma i} } (z_{1} )C_{\sigma i} x_{1} \hfill \\ \end{array} \right.$$

where \(A_{11} = \left[ {\begin{array}{*{20}c} { - 0.32} & 0 \\ {0.1} & {0.08} \\ \end{array} } \right],\;A_{12} = \left[ {\begin{array}{*{20}c} {0.2} & { - 0.8} \\ {2.6} & { - 0.77} \\ \end{array} } \right],\;A_{21} = \left[ {\begin{array}{*{20}c} { - 0.9} & { - 1} \\ { - 0.05} & { - 0.5} \\ \end{array} } \right]\), \(A_{22} = \left[ {\begin{array}{*{20}c} {0.27} & 1 \\ { - 0.1} & { - 0.5} \\ \end{array} } \right],\;B_{11} = \left[ \begin{aligned} - 0.39 \hfill \\ 0.78 \hfill \\ \end{aligned} \right],\;B_{12} = \left[ \begin{aligned} 0.58 \hfill \\ 1.67 \hfill \\ \end{aligned} \right],\;B_{21} = \left[ \begin{aligned} 0.13 \hfill \\ 1.21 \hfill \\ \end{aligned} \right],\;B_{22} = \left[ \begin{aligned} 1.87 \hfill \\ 1.43 \hfill \\ \end{aligned} \right]\),\(C_{11} = \left[ {\begin{array}{*{20}c} { - 0.01} & {0.25} \\ \end{array} } \right],\;C_{12} = \left[ {\begin{array}{*{20}c} { - 0.39} & {0.01} \\ \end{array} } \right],\;C_{21} = \left[ {\begin{array}{*{20}c} {0.21} & {0.13} \\ \end{array} } \right],\;C_{22} = \left[ {\begin{array}{*{20}c} { - 0.01} & {0.14} \\ \end{array} } \right]\).

Then the corresponding fuzzy membership functions are as follows: \(\mu_{11} (\hat{x}_{1} ) = 1 - 1/(1 + e^{{ - 3.07\hat{x}_{1} }} ),\;\mu_{12} (\hat{x}_{1} ) = 1 - 1/(1 + e^{{ - 3.07\hat{x}_{1} }} ),\) \(\mu_{21} (\hat{x}_{1} ) = 1 - 1/(1 + e^{{ - 3.07\hat{x}_{1} }} ),\;\mu_{22} (\hat{x}_{1} ) = 1 - 1/(1 + e^{{ - 3.07\hat{x}_{1} }} ).\)

The design parameters are chosen as

$$\alpha = 1.13,\;\beta = 1,\;\delta = 2.95,\;\gamma_{12} = 2.2,\; \gamma_{21} = 2.$$

Let

$$\varOmega_{1} = \{ \hat{x} \in R^{2} |\hat{x}^{\rm T} (P_{2} - P_{1} )\hat{x} \ge 0,\hat{x} \ne 0\},$$
$$\varOmega_{2} = \{ \hat{x} \in R^{2} |\hat{x}^{\rm T} (P_{2} - P_{1} )\hat{x} < 0,\hat{x} \ne 0\}.$$

Then \(\tilde{\varOmega }_{1} \cup \tilde{\varOmega }_{2} = R^{2} \backslash \{ 0\}\), the switching law is constructed as

$$\sigma (\hat{x}) = \left\{ \begin{aligned} 1,\quad\hat{x} \in \tilde{\varOmega }_{1} \hfill \\ 2,\quad\hat{x} \in \tilde{\varOmega }_{2} \hfill \\ \end{aligned} \right.$$

Design the output feedback control law as

$$u_{r} = \sum\limits_{r = 1}^{l} {\sum\limits_{i = 1}^{{N_{r} }} {\nu_{r} (\hat{x})\mu_{ri} (\hat{z})} K_{ri} \hat{x}}$$

By solving (39), (41), and (42), we can obtain the positive definite matrices \(Q_{r}\) and \(P_{r}\), the control gains \(K_{rs}\) and the observer gains \(L_{rj}\) as follows, \(Q_{1} = \left[ {\begin{array}{*{20}c} {0.2022} & {0.0941} \\ {0.0941} & {0.2289} \\ \end{array} } \right],\;Q_{2} = \left[ {\begin{array}{*{20}c} {1.5271} & {0.0595} \\ {0.0595} & {0.0638} \\ \end{array} } \right],\;P_{1} = \left[ {\begin{array}{*{20}c} {7.3211} & { - 3.6157} \\ { - 3.6157} & {12.2310} \\ \end{array} } \right]\),

$$P_{2} = \left[ {\begin{array}{*{20}c} {0.9988} & {0.7584} \\ {0.7584} & {2.9803} \\ \end{array} } \right],\;K_{11} = \left[ {\begin{array}{*{20}c} {7.6671} & { - 4.3056} \\ \end{array} } \right],\;K_{12} = \left[ {\begin{array}{*{20}c} {2.5059} & { - 6.3410} \\ \end{array} } \right]$$

\(K_{21} = [\begin{array}{*{20}c} { - 0.7170} & { - 1.3986} \\ \end{array} ],\;K_{22} = \left[ {\begin{array}{*{20}c} { - 0.5202} & { - 0.7937} \\ \end{array} } \right],\;L_{11} = \left[ {\begin{array}{*{20}c} {2.039} \\ {3.1558} \\ \end{array} } \right]\), \(L_{12} = \left[ {\begin{array}{*{20}c} { - 7.5155} \\ {1.9520} \\ \end{array} } \right],\;L_{21} = \left[ {\begin{array}{*{20}c} {8.922} \\ { - 16.5491} \\ \end{array} } \right],\;L_{22} = \left[ {\begin{array}{*{20}c} { - 8.9935} \\ {19.1108} \\ \end{array} } \right]\).

In the simulation, the initial condition is chosen as \(\left[ {\begin{array}{*{20}c} {0.70} & {0.82} & {0.13} & {1.11} \\ \end{array} } \right]^{\rm T}\). Then, the simulation results are shown in Figs. 1, 2, 3, and 4, where Fig. 1 and Fig. 2 show the trajectories of \(x_{i} (i = 1,2)\) and their estimates \(\hat{x}_{i} (i = 1,2)\), respectively; Fig. 3 expresses the trajectories of control input \(u_{r} (r = 1,2)\); Fig. 4 shows the trajectory of switching signal \(\sigma\). From the simulation results, it is clear that the proposed output feedback control method can guarantee the stability of the closed-loop switched fuzzy system.

Fig. 1
figure 1

The trajectories of \(x_{1}\) (solid line) and \(\hat{x}_{1}\) (dotted line)

Full size image
Fig. 2
figure 2

The trajectories of \(x_{2}\) (solid line) and \(\hat{x}_{2}\) (dotted line)

Full size image
Fig. 3
figure 3

The trajectories of control input \(u_{1}\) (solid line) and \(u_{2}\) (dotted line)

Full size image
Fig. 4
figure 4

The trajectory of switching signal

Full size image

Example 2

Consider the mass-spring-damping system [41] shown in Fig. 5 and according to Newton’s law, it follows as

$$\ell \ddot{x} + F_{\text{f}} + F_{\text{s}} = u$$

where \(\ell\) stands for the mass of the spring, \(F_{\text{f}}\) and \(F_{\text{s}}\) are the friction force and the restoring force of the spring, where the variables are the nonlinear or uncertain terms. \(u\) denotes the external control input. Assume that the friction force \(F_{\text{f}} = t_{1} \dot{x}^{3}\) with \(t_{1} > 0\) and the hardening spring force \(F_{\text{s}} = t_{2} x + t_{3} x^{3}\) with constants \(t_{2}\) and \(t_{3}\).

Fig. 5
figure 5

Mass–Spring–Damping system

Full size image

Then, the dynamic equation can be written as

$$\ddot{x} = - (t_{1} /\ell )\dot{x}^{3} - (t_{2} /\ell )x - (t_{3} /\ell )x^{3} + (1/\ell )u$$

where \(x\) stands for the displacement from a reference point. Define \(x(t) = \left[ \begin{aligned} x_{1} (t) \hfill \\ x_{2} (t) \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} x \hfill \\ {\dot{x}} \hfill \\ \end{aligned} \right]\), then

$$\dot{x}(t) = \left[ \begin{aligned} \dot{x}_{1} (t) \hfill \\ \dot{x}_{2} (t) \hfill \\ \end{aligned} \right] = \left[ \begin{array}{c} \dot{x} \hfill \\ - (t_{1} /\ell )\dot{x}^{3} - (t_{2} /\ell )x - (t_{3} /\ell )x^{3} + (1/\ell )u \hfill \\ \end{array} \right]$$

The nonlinear terms are \(- (t_{1} /\ell )\dot{x}^{3}\) and \(- (t_{3} /\ell )x^{3}\). The nonlinear terms satisfies the following conditions for \(x \in [ - 1.7,1.7]\), \(\dot{x} \in [ - 1.7,1.7]\), then we can obtain\(\left\{ \begin{aligned} \begin{array}{*{20}c} { - \frac{{2.89 \cdot t_{3} }}{\ell }x \le - \frac{{t_{3} }}{\ell }x^{3} \le 0 \cdot x} & {x \ge 0} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {0 \cdot x < - \frac{{t_{3} }}{\ell }x^{3} \le - \frac{{2.89 \cdot t_{3} }}{\ell }x} & {x < 0} \\ \end{array} \hfill \\ \end{aligned} \right.,\;\left\{ \begin{aligned} \begin{array}{*{20}c} { - \frac{{2.89 \cdot t_{1} }}{\ell }\dot{x} \le - \frac{{t_{1} }}{\ell }\dot{x}^{3} \le 0 \cdot \dot{x}} & {\dot{x} \ge 0} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {0 \cdot \dot{x} < - \frac{{t_{1} }}{\ell }\dot{x}^{3} \le - \frac{{2.89 \cdot t_{1} }}{\ell }\dot{x}} & {\dot{x} < 0} \\ \end{array} \hfill \\ \end{aligned} \right.\)

Note that the nonlinear terms can be represented by the upper bound and the lower bound.

$$- (t_{3} /\ell )x^{3} = H_{11} \cdot 0 \cdot x - (1 - H_{11} ) \cdot (2.89 \cdot t_{3} /\ell ) \cdot x$$
$$- (t_{1} /\ell )\dot{x}^{3} = H_{21} \cdot 0 \cdot \dot{x} - (1 - H_{21} ) \cdot (2.89 \cdot t_{1} /\ell ) \cdot \dot{x}$$

By solving the above equations, \(H_{11}\) and \(H_{21}\) are obtained as follows:

$$\begin{aligned} H_{11} (x) = 1 - x^{2} /2.89,\;H_{12} (x) = x^{2} /2.89, \hfill \\ H_{21} (\dot{x}) = 1 - \dot{x}^{2} /2.89,\;H_{22} (\dot{x}) = \dot{x}^{2} /2.89. \hfill \\ \end{aligned}$$

When the nonlinear terms reach the upper bound or lower bound, the system will be switched, and the corresponding fuzzy membership functions are represented by \(H_{11}\), \(H_{12}\), \(H_{21}\) and \(H_{22}\), then, the switched fuzzy system with unknown premise variables is constructed by the following four-rule fuzzy model:

$$\begin{aligned} R_{1}^{1} \;:{\text{ If}}\;x\; {\text{is}}\;H_{11} ,\;\dot{x}\; {\text{is}}\;H_{21} ,\;{\text{then}} \hfill \\ \dot{x} = A_{11} x + B_{11} u_{1} ,\;y = C_{11} x. \hfill \\ \end{aligned}$$
$$\begin{aligned} R_{1}^{2} \;:{\text{ If}}\;x\;{\text{is}}\;H_{11} ,\;\dot{x}\;is\;H_{22} ,\;{\text{then}} \hfill \\ \dot{x} = A_{12} x + B_{12} u_{1} ,\;y(t) = C_{12} x. \hfill \\ \end{aligned}$$
$$\begin{aligned} R_{2}^{1} :{\text{ If}}\;x\;{\text{is}}\;H_{12} ,\;\dot{x}\;{\text{is}}\;H_{21} ,{\text{ then}} \hfill \\ \dot{x} = A_{21} x + B_{21} u_{2} ,\;y = C_{21} x. \hfill \\ \end{aligned}$$
$$\begin{aligned} R_{2}^{2} :{\text{ If}}\;x\;{\text{is}}\;H_{12} ,\;\dot{x}\; {\text{is}}\;H_{22} ,{\text{ then}}\; \hfill \\ \dot{x} = A_{22} x + B_{22} u_{2} ,\;y = C_{22} x. \hfill \\ \end{aligned}$$

where \(\ell = 2\), \(t_{1} = 0.1\), \(t_{2} = 0.2\), \(t_{3} = 0.05\).

Then, we obtain

$$A_{11} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - 0.1} & 0 \\ \end{array} } \right],\;A_{12} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - 0.1} & { - 0.1445} \\ \end{array} } \right],\;A_{21} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - 0.2445} & 0 \\ \end{array} } \right],$$
$$A_{22} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - 0.2445} & { - 0.1445} \\ \end{array} } \right],\;B_{11} = \left[ \begin{aligned} 0 \hfill \\ 0.5 \hfill \\ \end{aligned} \right],\;B_{12} = \left[ \begin{aligned} 0 \hfill \\ 0.5 \hfill \\ \end{aligned} \right],\;B_{21} = \left[ \begin{aligned} 0 \hfill \\ 0.5 \hfill \\ \end{aligned} \right],\;B_{22} = \left[ \begin{aligned} 0 \hfill \\ 0.5 \hfill \\ \end{aligned} \right],$$
$$C_{11} = \left[ {\begin{array}{*{20}c} { - 2.01} & {0.15} \\ \end{array} } \right],\;C_{12} = \left[ {\begin{array}{*{20}c} { - 0.34} & {0.34} \\ \end{array} } \right],\;C_{21} = \left[ {\begin{array}{*{20}c} {0.31} & {0.23} \\ \end{array} } \right],\;C_{22} = \left[ {\begin{array}{*{20}c} { - 1.35} & {0.14} \\ \end{array} } \right].$$

Then the corresponding fuzzy membership functions are

$$\mu_{11} (x_{1} ) = 1 - 1/(1 + e^{{ - 5.4x_{1} }} ) \, ,\;\mu_{12} (x_{1} ) = 1 - 1/(1 + e^{{ - 5.4x_{1} }} ),$$
$$\mu_{21} (x_{1} ) = 1 - 1/(1 + e^{{ - 5.4x_{1} }} ),\;\mu_{22} (x_{1} ) = 1 - 1/(1 + e^{{ - 5.4x_{1} }} ).$$

The design parameters are chosen as\(\alpha = 1,\;\beta = 1,\;\delta = 3.2,\;\gamma_{12} = 1.2,\;\gamma_{21} = 1.2.\)

Let

$$\varOmega_{1} = \{ x \in R^{2} |x^{\rm T} (P_{2} - P_{1} )x \ge 0,x \ne 0\},$$
$$\varOmega_{2} = \{ x \in R^{2} |x^{\rm T} (P_{2} - P_{1} )x < 0,x \ne 0\}.$$

Then \(\tilde{\varOmega }_{1} \cup \tilde{\varOmega }_{2} = R^{2} \backslash \{ 0\},\) the switching law is constructed as

$$\sigma (\hat{x}) = \left\{ \begin{aligned} 1, \quad \hat{x} \in \tilde{\varOmega }_{1} \hfill \\ 2, \quad \hat{x} \in \tilde{\varOmega }_{2} \hfill \\ \end{aligned} \right.$$

Design the output feedback controller as

$$u_{r} = \sum\limits_{r = 1}^{l} {\sum\limits_{i = 1}^{{N_{r} }} {\nu_{r} (\hat{x})\mu_{ri} (\hat{z})} K_{ri} \hat{x}}$$

By solving (39), (41) and (42), we can obtain the positive definite matrices \(Q_{r}\) and \(P_{r}\), the control gains \(K_{rs}\) and the observer gain \(L_{rj}\) as follows:\(Q_{1} = \left[ {\begin{array}{*{20}c} {0.6568} & {0.0636} \\ {0.0636} & {0.4710} \\ \end{array} } \right],\;Q_{2} = \left[ {\begin{array}{*{20}c} {0.8923} & {0.1358} \\ {0.1358} & {0.4745} \\ \end{array} } \right],\;P_{1} = \left[ {\begin{array}{*{20}c} {2.3811} & {2.7511} \\ {2.7511} & {9.1005} \\ \end{array} } \right]\), \(P_{2} = \left[ {\begin{array}{*{20}c} {0.8038} & {1.1819} \\ {1.1819} & {8.7461} \\ \end{array} } \right],\;K_{11} = \left[ {\begin{array}{*{20}c} { - 13.0053} & { - 31.5743} \\ \end{array} } \right],\;K_{12} = \left[ {\begin{array}{*{20}c} { - 12.5231} & { - 31.0993} \\ \end{array} } \right]\), \(K_{21} = [\begin{array}{*{20}c} { - 4.2717} & { - 26.6101} \\ \end{array} ],\;K_{22} = \left[ {\begin{array}{*{20}c} { - 5.4128} & { - 29.6035} \\ \end{array} } \right],\;L_{11} = \left[ {\begin{array}{*{20}c} { - 1.0780} \\ { - 0.0661} \\ \end{array} } \right]\),\(L_{12} = \left[ {\begin{array}{*{20}c} { - 0.0185} \\ {0.3067} \\ \end{array} } \right],L_{21} = \left[ {\begin{array}{*{20}c} {1.3036} \\ { - 0.2177} \\ \end{array} } \right],L_{22} = \left[ {\begin{array}{*{20}c} { - 1.6668} \\ {0.3529} \\ \end{array} } \right]\).

The initial condition is chosen as \(\left[ {\begin{array}{*{20}c} {2.08} & {1.62} & {1.67} & {1.71} \\ \end{array} } \right]^{\rm T}\). Then, the simulation results are shown in Figs. 6, 7, and 8, where Figs. 6 and 7 show the trajectories of \(x_{i} (i = 1,2)\) and their estimates \(\hat{x}_{i} (i = 1,2)\), respectively; Fig. 8 shows the trajectory of switching signal. From the simulation results, it is clear that even though the state variables are immeasurable, the fuzzy output feedback controller and the switching law guarantee the stability of mass–spring–damping system.

Fig. 6
figure 6

The trajectories of \(x_{1}\) (solid line) and \(\hat{x}_{1}\) (dotted line)

Full size image
Fig. 7
figure 7

The trajectories of \(x_{2}\) (solid line) and \(\hat{x}_{2}\) (dotted line)

Full size image
Fig. 8
figure 8

The trajectory of switching signal

Full size image

5 Conclusions

In this paper, the output feedback robust stabilization problem has been investigated for a class of switched fuzzy systems, which contain the immeasurable premise variables and the state variables. By using the parallel distributed compensation (PDC) design method, a switched state observer has been designed and estimations of the immeasurable states can be obtained. Based on the designed state observer and the multiple Lyapunov function approach, an output feedback controller and the switching laws have been developed. It has been proved that the proposed output feedback control scheme can guarantee the control system to be asymptotical stable. Compared with the existing results, the main contributions of this paper are as follows. One is that the proposed control method has first solved non-measurable premise variable problem for the switched fuzzy systems. The other is that a novel decoupled method has been proposed to obtain the feasible solutions of the control and observer gain matrixes, instead of the two-step method adopted in the previous literatures.