1 Introduction

The rolling usually has a negative impact on the cargo and crew on board. It is dampened when a vessel uses the roll stabilization systems. The rolling caused by the sea waves affect the comfort of passengers. It is uncomfortable for the crew when a rolling motion happens with large amplitude. In [1], a ship roll prediction scheme was proposed using an adaptive sliding data window, which is designed to represent time-varying nonlinear dynamics of ship roll motion. In order to reduce the rolling effect, the fin stabilizer system was designed in the literature [2,3,4,5,6,7,8]. It can be found that the fin stabilizer is an effective device that can be used to reduce the rolling motion for the ships. One of the fin stabilizer systems is a device comprising fins placed on both sides of the ship’s hull. The fin stabilizer system can create a held-up moment that can resist the sea wave disturbance and reduce the ship’s rolling motion. Recently, some intelligent control techniques have been applied to design the fin stabilizer system [2, 4, 5, 8]. In [2, 4], the fuzzy control and predictive control were employed to design the fin stabilizer system, respectively. Besides, a neural network-based PID control approach was applied in [5]. Moreover, the fin stabilizer design problem based on model-based fuzzy control technique was solved in [8]. In [8], the Takagi–Sugeno (T–S) fuzzy model was employed to represent the nonlinear fin stabilizer system. According to the T–S fuzzy model, the parallel distributed compensation (PDC) [9] method was used to develop sufficient conditions that guarantee the stability of the nonlinear fin stabilizer system.

Over the past few decades, the T–S fuzzy model and its corresponding control techniques have been developed rapidly for the complex nonlinear control systems [10,11,12,13,14,15,16,17,18,19,20,21]. Applying the T–S fuzzy modeling method, one can obtain that the system dynamics can be captured by the sets of linear local dynamic models, and the overall nonlinear complex systems can be approximated smoothly by “blending” of these local models through membership functions. According to the T–S fuzzy model, the PDC technique [9,10,11] was employed to design the fuzzy controllers for the nonlinear systems. Corresponding to the PDC-based fuzzy controller design method, some researches related to relaxed stability condition issues have been investigated in [12, 13]. In [14, 15], an adaptive fuzzy control method was developed for the uncertain nonlinear systems with input constraint. Besides, the H∞ control and neuro-network control were combined with fuzzy control to deal with the control problem for the T–S fuzzy systems in [16, 17], respectively. In [18,19,20,21], the sliding mode control method was applied to design fuzzy controllers for achieving multiple performance requirements. The dissipativity-based fuzzy integral sliding mode control of continuous-time T–S fuzzy systems was developed in [20]. The sliding mode control of fuzzy singularly perturbed systems with application to the electric circuit was studied in [21]. In general, the T–S fuzzy model-based control methods were widely applied in many practical industrial systems [22,23,24,25,26,27,28,29]. For the TCP network systems, the T–S fuzzy model-based control technique was applied to design routers [22]. Also, the similar control method was also applied to the nonlinear ship drum-boiler systems in [23]. In [24, 25], a T–S fuzzy control approach was investigated for the ship steering systems. In [26], a global asymptotic model-free trajectory-independent tracking control methodology for an uncertain marine vehicle was developed. The main technique investigated in [26] was implemented by combining tracking control and adaptive fuzzy control [27]. Moreover, the T–S fuzzy control for the generator systems has been studied in [28, 29]. In many branches of engineering applications and practical systems, the stochastic behaviors are inevitable and need to be considered for the controller design process [19, 24, 28]. Therefore, the stochastic behaviors will also be considered in this paper to study the robust fuzzy control problem for ship fin stabilizing systems.

Generally, the uncertainty is usually considered in the controller design for the robust control problem of T–S fuzzy systems [9, 11, 22, 30,31,32,33]. It is known that the robust control theory is effectively applied to solve the control problem for the systems with perturbations and uncertainties. Robust control was also considered and widely employed for the industrial systems to improve system performance. In order to deal with the uncertainty problem of T–S fuzzy systems, some benefit approaches have been investigated in [9, 11, 22, 30,31,32,33]. Stability analysis is the most important part for the controller design of the uncertain T–S fuzzy systems. Thus, the quadratic stability conditions based on the well-known Lyapunov theory are considered and presented in [9]. For obtaining better performance, pole placement constraint and state variance constraint are considered in the proposed fuzzy control design methodology. Considering the above constraints, some researchers developed approaches to deal with the performance-constrained control problem [18, 19, 24, 32, 34,35,36,37]. In [18, 19, 24, 32,33,34,35,36,37], the state and output variance constraints were considered in the fuzzy controller design process. Besides, the pole placement constraint was considered in the control problem for T–S fuzzy systems [19, 36]. It is known that the pole placement technique can improve the transient performance for the controlled systems. However, to the best of the authors’ knowledge, so far the problem of robust fuzzy control with all of the above performance constraints has not been discussed in the literature. Extending the results of [18, 19, 24, 32, 34,35,36,37], this paper investigates a robust fuzzy control methodology for the ship fin stabilizing systems by considering robust constraint, pole placement constraint and state variance constraint, simultaneously.

In [37], the variance-constrained fuzzy control problem has been studied for the ship fin stabilizing systems. However, the approach developed in [37] just considered the steady-state performance requirement. The transient performance requirement and the uncertainty were not considered in [37]. Therefore, the purpose of this paper is to extend the study of [37] to design a robust fuzzy controller for the nonlinear uncertain ship fin stabilizing systems. The motivation of this paper is to deal with the control problem for the ship fin stabilizing systems subject to transient and steady-state performance requirements. The transient performance requirement considered in this paper is the pole placement constraint. The steady-state performance requirement considered in this paper is the state variance constraint. Up to now, the robust fuzzy control problem with the above performance requirements has not yet been investigated for nonlinear uncertain stochastic systems. Based on the Lyapunov stability theory, some sufficient conditions are derived in this paper to achieve the above transient and steady-state performance requirements. The advantage of the proposed robust fuzzy control approach is that one can use the linear matrix inequality (LMI) technique to solve these sufficient conditions such that the pole placement constraint and state variance constraint can be satisfied for the ship fin stabilizing systems, simultaneously. In order to demonstrate the effectiveness of the proposed robust fuzzy control method, some numerical simulations for the control of a nonlinear uncertain ship lift-feedback-fin stabilizing system are provided in this paper.

This paper is organized as follows: In Sect. 2, a T–S fuzzy model with external disturbances and perturbations is used to represent the nonlinear uncertain ship lift-feedback-fin stabilizing systems. The performance constraints and the proposed control problem are also defined in this section. In Sect. 3, the individual state variance constraint and pole placement constraint are considered in the fuzzy controller design process. Some sufficient conditions are derived subject to the above performance constraints. In Sect. 4, some numerical simulations are provided to demonstrate the applicability and effectiveness of the proposed robust fuzzy control method. The LMI technique is employed to solve the sufficient conditions derived in this paper. At last, some conclusions are provided in Sect. 5.

2 System Description and Problem Statements

A lift-feedback-fin stabilizer control system of a ship consists of a controller, sensor, servo system, fin, etc. [2]. The lift feedback fin encapsulates the nonlinear and uncertain relationship between lift and fin angle, and all the other parts are linear blocks. Thus, all parts except ship can be simplified and united to a controller block when a system is designed.

Sea waves mainly cause rolling of a ship. Sea waves have a statistical rule although they are irregular and stochastic. In this paper, the main energy of sea waves centralizes in the low-frequency range of 0.3–1.25 rad/s by sea wave spectrum theory. Considering the nonlinearities of rolling resilient moment and rolling damp moment, we can describe the nonlinear model of rolling of a ship as follows [2]:

$$\left( {I_{x} + \Delta I_{x} } \right)\ddot{\alpha } + B_{1} \dot{\alpha } + B_{2} \left| {\dot{\alpha }} \right|\dot{\alpha } + C_{1} \alpha + C_{3} \alpha^{3} + C_{5} \alpha^{5} = M_{\text{d}} - M_{\text{s}}$$
(1)

where α denotes the rolling angle of a ship, Ix and ΔIx denote the mass inertia moment and affixing mass inertia moment relative to the vertical axes of the ship, \(M_{\text{d}}\) denotes the disturbance moment of sea waves, \(M_{\text{s}}\) denotes the stable moment of lift feedback fins. Besides, C1, C3, C5, B1, B2 are constants and C1 = Dh, where D denotes the tonnage of a ship and h denotes the height of the steady center of rolling of a ship.

The parameters of a certain ship are D = 1457.26t, h = 1.15 m, Ix + ΔIx = 3.4383 × 106, C3 = 2.097 × 106, C5 = 4.814 × 106, B1 = 0.636 × 106, B2 = 0.79 × 106. Let Mt = Md + Ms, the nonlinear model of this rolling of a ship can be described as follows:

$$\ddot{\alpha } + 0.185\dot{\alpha } + 0.23\left| {\dot{\alpha }} \right|\dot{\alpha } + 0.4874\alpha + 0.61\alpha^{3} + 1.4\alpha^{5} = 2.9084 \times 10^{ - 7} M_{t}$$
(2)

In this paper, we choose the system states as x1 = α, \(x_{2} = \dot{\alpha }\) and the control input as u = Mt. Then, the dynamic equation of the nonlinear lift-feedback-fin system can be given as follows:

$$\dot{x}_{1} = x_{2}$$
(3a)
$$\dot{x}_{2} = - 0.4874x_{1} - 0.61x_{1}^{3} - 1.4x_{1}^{5} - \left( {0.185 + 0.23\left| {x_{2} } \right|} \right)x_{2} + 2.9084 \times 10^{ - 7} u + 0.05\omega$$
(3b)

where x1(t) is the rolling angle of the ship, x2(t) is the rolling angular velocity of the ship, u(t) is the control input that denotes the stable moment of lift feedback fin, ω(t) is the external disturbance input, which expressed in x1, x2, u and ω for simplicity. Applying the T–S fuzzy modeling technique [9], one can obtain the perturbed T–S fuzzy model for the lift-feedback-fin system (3a, b) as follows:

Plant Rules

IF x1(t) is \(\varvec{R}_{ 1}^{i}\) and x2(t) is \(\varvec{R}_{2}^{\ell }\), then

$$\dot{x}\left( t \right) = \left( {{\mathbf{A}}_{i\ell } + {\mathbf{\Delta A}}_{i\ell } } \right)x\left( t \right) + \left( {{\mathbf{B}}_{i\ell } + {\mathbf{\Delta B}}_{i\ell } } \right)u\left( t \right) + {\mathbf{N}}_{i\ell } w\left( t \right)$$
(4a)
$$y\left( t \right) = {\mathbf{C}}_{i\ell } x\left( t \right)\quad i,\ell = 1\sim3$$
(4b)

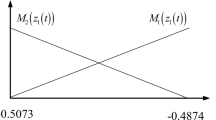
The membership functions of x1(t) and x2(t) are presented in Figs. 1 and 2. The system matrices for the T–S fuzzy model (4a, b) are given as follows:

$$\begin{aligned} {\mathbf{A}}_{11} & = \left[ {\begin{array}{cc} 0 & 1 \\ { - 0.4874} & { - 0.185} \\ \end{array} } \right],\quad {\mathbf{A}}_{21} = \left[ {\begin{array}{cc} 0 & 1 \\ { - 0.5073} & { - 0.185} \\ \end{array} } \right],\quad {\mathbf{A}}_{31} = \left[ {\begin{array}{cc} 0 & 1 \\ { - 0.5272} & { - 0.185} \\ \end{array} } \right], \\ {\mathbf{A}}_{12} & = \left[ {\begin{array}{cc} 0 & 1 \\ { - 0.4874} & { - 0.225} \\ \end{array} } \right],\quad {\mathbf{A}}_{22} = \left[ {\begin{array}{cc} 0 & 1 \\ { - 0.5073} & { - 0.225} \\ \end{array} } \right],\quad {\mathbf{A}}_{32} = \left[ {\begin{array}{cc} 0 & 1 \\ { - 0.5272} & { - 0.225} \\ \end{array} } \right], \\ {\mathbf{A}}_{13} & = \left[ {\begin{array}{cc} 0 & 1 \\ { - 0.4874} & { - 0.265} \\ \end{array} } \right],\quad {\mathbf{A}}_{23} = \left[ {\begin{array}{cc} 0 & 1 \\ { - 0.5073} & { - 0.265} \\ \end{array} } \right],\quad {\mathbf{A}}_{33} = \left[ {\begin{array}{cc} 0 & 1 \\ { - 0.5272} & { - 0.265} \\ \end{array} } \right] \\ {\mathbf{B}}_{11} & = {\mathbf{B}}_{21} = {\mathbf{B}}_{31} = {\mathbf{B}}_{12} = {\mathbf{B}}_{22} = {\mathbf{B}}_{32} = {\mathbf{B}}_{13} = {\mathbf{B}}_{23} = {\mathbf{B}}_{33} = \left[ {\begin{array}{cc} 0 \\ {2.9084 \times 10^{ - 7} } \\ \end{array} } \right], \\ {\mathbf{N}}_{11} & = {\mathbf{N}}_{21} = {\mathbf{N}}_{31} = {\mathbf{N}}_{12} = {\mathbf{N}}_{22} = {\mathbf{N}}_{32} = {\mathbf{N}}_{13} = {\mathbf{N}}_{23} = {\mathbf{N}}_{33} = \left[ {\begin{array}{*{20}c} 0 \\ {0.05} \\ \end{array} } \right], \\ \end{aligned}$$

and \({\mathbf{C}}_{11} = {\mathbf{C}}_{21} = {\mathbf{C}}_{31} = {\mathbf{C}}_{12} = {\mathbf{C}}_{22} = {\mathbf{C}}_{32} = {\mathbf{C}}_{13} = {\mathbf{C}}_{23} = {\mathbf{C}}_{33} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ \end{array} } \right]\).

Besides, the uncertainties of the T–S fuzzy model (4) are selected as follows:

$$\left[ {\begin{array}{cc} {{\mathbf{\Delta A}}_{i\ell } } & {{\mathbf{\Delta B}}_{i\ell } } \\ \end{array} } \right] = {\mathbf{H}}_{i\ell } {\varvec{\Delta}}\left( t \right)\left[ {\begin{array}{cc} {{\mathbf{R}}_{{{\text{a}}i\ell }} } & {{\mathbf{R}}_{{{\text{b}}i\ell }} } \\ \end{array} } \right],\quad i,\ell = 1\sim3$$
(5)

where \({\varvec{\Delta}}\left( t \right) = \sin \left( t \right)\) and

$$\begin{aligned} {\mathbf{H}}_{11} & = {\mathbf{H}}_{21} = {\mathbf{H}}_{31} = {\mathbf{H}}_{12} = {\mathbf{H}}_{22} = {\mathbf{H}}_{32} = {\mathbf{H}}_{13} = {\mathbf{H}}_{23} = {\mathbf{H}}_{33} = \left[ {\begin{array}{cc} {0.1} & 0 \\ 0 & {0.1} \\ \end{array} } \right], \\ {\mathbf{R}}_{{{\text{a}}11}} & = {\mathbf{R}}_{{{\text{a}}21}} = {\mathbf{R}}_{{{\text{a}}31}} = {\mathbf{R}}_{{{\text{a}}12}} = {\mathbf{R}}_{{{\text{a}}22}} = {\mathbf{R}}_{{{\text{a}}32}} = {\mathbf{R}}_{{{\text{a}}13}} = {\mathbf{R}}_{{{\text{a}}23}} = {\mathbf{R}}_{{{\text{a}}33}} = \left[ {\begin{array}{cc} 0 & {0.1} \\ 0 & 0 \\ \end{array} } \right], \\ \end{aligned}$$

and \({\mathbf{R}}_{{{\text{b}}11}} = {\mathbf{R}}_{{{\text{b}}21}} = {\mathbf{R}}_{{{\text{b}}31}} = {\mathbf{R}}_{{{\text{b}}12}} = {\mathbf{R}}_{{{\text{b}}22}} = {\mathbf{R}}_{{{\text{b}}32}} = {\mathbf{R}}_{{{\text{b}}13}} = {\mathbf{R}}_{{{\text{b}}23}} = {\mathbf{R}}_{{{\text{b}}33}} = \left[ {\begin{array}{*{20}c} 0 \\ {2 \times 10^{ - 8} } \\ \end{array} } \right]\).

Fig. 1
figure 1

Membership function of the state x1(t)

Full size image
Fig. 2
figure 2

Membership function of the state x2(t)

Full size image

Then, one can obtain

$${\mathbf{\Delta A}}_{11} = {\mathbf{\Delta A}}_{21} = {\mathbf{\Delta A}}_{31} = {\mathbf{\Delta A}}_{12} = {\mathbf{\Delta A}}_{22} = {\mathbf{\Delta A}}_{32} = {\mathbf{\Delta A}}_{13} = {\mathbf{\Delta A}}_{23} = {\mathbf{\Delta A}}_{33} = \left[ {\begin{array}{*{20}c} 0 & {0.01} \\ 0 & 0 \\ \end{array} } \right]\sin \left( t \right),$$

and \({\mathbf{\Delta B}}_{11} = {\mathbf{\Delta B}}_{21} = {\mathbf{\Delta B}}_{31} = {\mathbf{\Delta B}}_{12} = {\mathbf{\Delta B}}_{22} = {\mathbf{\Delta B}}_{32} = {\mathbf{\Delta B}}_{13} = {\mathbf{\Delta B}}_{23} = {\mathbf{\Delta B}}_{33} = \left[ {\begin{array}{*{20}c} 0 \\ {2 \times 10^{ - 9} } \\ \end{array} } \right]\sin \left( t \right)\).

In order to design a robust fuzzy controller for the perturbed T–S fuzzy model (4a, b) of the nonlinear lift-feedback-fin system (3a, b), a general form of the perturbed T–S fuzzy model is considered in this paper as follows:

Plant Rule i

IF zi1(t) is \({\text{M}}_{i1}\) and … and ziℓ(t) is \({\text{M}}_{i\ell }\), then

$$\dot{x}\left( t \right) = \left( {{\mathbf{A}}_{i} + {\mathbf{\Delta A}}_{i} } \right)x\left( t \right) + \left( {{\mathbf{B}}_{i} + {\mathbf{\Delta B}}_{i} } \right)u\left( t \right) + {\mathbf{N}}_{i} w\left( t \right)$$
(6a)
$$y\left( t \right) = {\mathbf{C}}_{i} x\left( t \right)$$
(6b)

where i = 1, 2, …, r and r is the rules number, Miℓ are fuzzy sets, ℓ is the premised variable number, \(x\left( t \right) \in \Re^{n}\) is the state vector, \(u\left( t \right) \in \Re^{m}\) is control input vector, \(y\left( t \right) \in \Re^{q}\) is output vector, and external disturbance input vector \(w\left( t \right) \in \Re^{j}\) is assumed as a zero-mean Gaussian white noise with intensity \({\mathbf{W}}\), which satisfied the condition \(({\mathbf{W}}{ > 0)}\), ‖w(t)‖ < ɛ and ɛ is a positive scalar. \({\mathbf{A}}_{i} \in \Re^{n \times n}\), \({\mathbf{B}}_{i} \in \Re^{n \times m}\), \({\mathbf{N}}_{i} \in \Re^{n \times j}\), \({\mathbf{C}}_{i} \in \Re^{q \times n}\) are constant matrices, and the uncertainties of the system state (6a, b) are described as the form \(\left[ {\begin{array}{*{20}c} {{\mathbf{\Delta A}}_{i} } & {{\mathbf{\Delta B}}_{i} } \\ \end{array} } \right] = {\mathbf{H}}_{i} {\varvec{\Delta}}_{i} \left( t \right)\left[ {\begin{array}{*{20}c} {{\mathbf{R}}_{ai} } & {{\mathbf{R}}_{bi} } \\ \end{array} } \right]\), \({\varvec{\Delta}}_{i} \left( t \right)\) is the uncertain matrix and \(\left( {{\mathbf{H}}_{i} ,{\mathbf{R}}_{ai} ,{\mathbf{R}}_{bi} } \right)\) are the known matrices.

Let us consider the T–S fuzzy model (6a, b) with the state vector x(t) and the input vector u(t); then, the overall T–S fuzzy model can be rewritten as follows:

$$\dot{x}\left( t \right) = \mathop \sum \limits_{i = 1}^{r} h_{i} \left( {z\left( t \right)} \right)\left\{ {\left( {{\mathbf{A}}_{i} + {\mathbf{\Delta A}}_{i} } \right)x\left( t \right) + \left( {{\mathbf{B}}_{i} + \;{\mathbf{\Delta B}}_{i} } \right)u\left( t \right) + {\mathbf{N}}_{i} w\left( t \right)} \right\}$$
(7a)
$$y\left( t \right) = \mathop \sum \limits_{i = 1}^{r} h_{i} \left( {z\left( t \right)} \right){\mathbf{C}}_{i} x\left( t \right)$$
(7b)

where \({{h_{i} \left( {z\left( t \right)} \right) = \prod\nolimits_{j = 1}^{k} {{\text{M}}_{ij} \left( {z_{j} \left( t \right)} \right)} } \mathord{\left/ {\vphantom {{h_{i} \left( {z\left( t \right)} \right) = \prod\nolimits_{j = 1}^{k} {{\text{M}}_{ij} \left( {z_{j} \left( t \right)} \right)} } {\sum\nolimits_{i = 1}^{r} {\prod\nolimits_{j = 1}^{k} {{\text{M}}_{ij} } \left( {z_{j} \left( t \right)} \right)} }}} \right. \kern-0pt} {\sum\nolimits_{i = 1}^{r} {\prod\nolimits_{j = 1}^{k} {{\text{M}}_{ij} } \left( {z_{j} \left( t \right)} \right)} }}\), hi(z(t)) ≥ 0, ∑ r i=1 hi(z(t)) = 1 and \({\text{M}}_{ij} \left( {z_{j} \left( t \right)} \right)\) is the grade of the membership of zj(t).

In this paper, the PDC method [9,10,11] is applied to design the robust fuzzy controller for the perturbed T–S fuzzy model (7a, b). The important concept of this method is to design the linear controller for each rule in the T–S fuzzy model, and then, one can “blend” the linear controllers of each rule so that the overall fuzzy controller can be obtained. The fuzzy controller for the T–S fuzzy model (7a, b) is constructed as follows:

Controller Rule i

IF zi1(t) is \({\text{M}}_{i1}\) and … and zik(t) is \({\text{M}}_{ik}\), then

$$u\left( t \right) = {\mathbf{F}}_{i} x\left( t \right)$$
(8)

Then, the overall fuzzy controller can be represented by:

$$u\left( t \right) = \sum\limits_{j = 1}^{r} {h_{j} \left( {z\left( t \right)} \right){\mathbf{F}}_{j} x\left( t \right)}$$
(9)

Thus, one can obtain the following closed-loop system form by (7a, b) and (9).

$$\begin{aligned} \dot{x}\left( t \right) & = \sum\limits_{i = 1}^{r} {\sum\limits_{j = 1}^{r} {h_{i} \left( {z\left( t \right)} \right)h_{j} \left( {z\left( t \right)} \right)\left\{ {\left( {\left( {{\mathbf{A}}_{i} + \Delta {\mathbf{A}}_{i} } \right) + \left( {{\mathbf{B}}_{i} + \Delta {\mathbf{B}}_{i} } \right){\mathbf{F}}_{j} } \right)x\left( t \right) + {\mathbf{\rm N}}_{i} w\left( t \right)} \right\}} } \\ & = \sum\limits_{i = 1}^{r} {h_{i}^{2} \left( {z\left( t \right)} \right) \, } {\varvec{\Gamma}}_{ii} x\left( t \right) + 2\sum\limits_{i < j}^{r} {\text{h}_{i} \left( {z\left( t \right)} \right)\text{h}_{j} \left( {z\left( t \right)} \right)} \left( {\frac{{{\varvec{\Gamma}}_{ij} + {\varvec{\Gamma}}_{ji} }}{2}} \right)\text{x} \left( t \right) + \sum\limits_{i = 1}^{r} {\text{h}_{i} \left( {z\left( t \right)} \right)} {\mathbf{\rm N}}_{i} w\left( t \right) \\ \end{aligned}$$
(10)

where \({\varvec{\Gamma}}_{ij} {\mathbf{ = G}}_{ij} {\mathbf{ + H}}_{i} {\varvec{\Delta}}_{i} \left( t \right){\mathbf{R}}_{ij}\), \({\mathbf{G}}_{ij} {\mathbf{ = A}}_{i} {\mathbf{ + B}}_{i} {\mathbf{F}}_{j}\) and \({\mathbf{R}}_{ij} = {\mathbf{R}}_{ai} + {\mathbf{R}}_{bi} {\mathbf{F}}_{j}\).

Considering the stability analysis of the above stochastic uncertain T–S fuzzy model (10), one can obtain the Lyapunov stability conditions introduced in Lemma 1.

Lemma 1

[9] The closed-loop T–S fuzzy model (10) is stable if there exists a common positive definite matrix\({\mathbf{Q}}\)such that the following conditions are satisfied.

$${\varvec{\Gamma}}_{ii}^{\text{T}} {\mathbf{Q}} + {\mathbf{Q\varGamma }}_{ii} < 0,\quad {\text{for}}\quad i = 1,2, \ldots ,r$$
(11)

and

$$\left( {\frac{{{\varvec{\Gamma}}_{ij} + {\varvec{\Gamma}}_{ji} }}{2}} \right)^{\text{T}} {\mathbf{Q}} + {\mathbf{Q}}\left( {\frac{{{\varvec{\Gamma}}_{ij} + {\varvec{\Gamma}}_{ji} }}{2}} \right) < 0,\quad {\text{for}}\quad i < j$$
(12)

The stability of the closed-loop T–S fuzzy model (10) can be ensured by achieving conditions (11) and (12). In addition to the stability performance, this paper also considers performance requirements in the fuzzy controller design. First, a steady-state performance constraint so-called individual state variance constraint is introduced as follows:

Definition 1

For the closed-loop system (10), it is assumed that \({\tilde{\mathbf{X}}}_{i}\) is the steady-state covariance matrix of system state x(t) for each rule, i.e., \({\tilde{\mathbf{X}}}_{i} = \lim_{t \to \infty } E\left( {x\left( t \right)x^{\rm T} \left( t \right)} \right)\), which satisfies \({\tilde{\mathbf{X}}}_{i} = \;{\tilde{\mathbf{X}}}_{i}^{\rm T} > 0\). Considering the uncertainties consist of the T–S fuzzy system (10), the individual state variance matrix and its constraint considered in this paper are introduced as follows:

$$\left[ {{\tilde{\mathbf{X}}}_{i} } \right]_{pp} < \sigma_{p}^{2}$$
(13)

where [·]pp means the pth diagonal element of the matrix [·] and σp, p = 1, 2, …, n are the root-mean-squared individual state variance constraints.

Next, in order to obtain a better transient performance of the system responses, the D-stable pole placement constraint is considered for the T–S fuzzy model (10). The description of the D-stable pole placement constraint can be found as follows:

Definition 2

[38] The D-stable pole placement constraint considered in this paper is defined as that all the poles of each linear subsystem of the closed-loop system (10) can be located at the following specified circle region D.

$$D = \left\{ {x + jy \in C\text{:}\left( {x + q} \right)^{2} + y^{2} < r^{2} } \right\}$$
(14)

where the center of the circle is at the point (− q, 0), the radius is r > 0, and it has the consequent − q + r < 0.

From [38], it can be known that the D-stable conditions for a dynamic system \(\dot{x} = {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}x\) can be referred to as follows: If there is a symmetric matrix \({\mathbf{\rm K}}\) satisfying the following conditions, then the dynamic matrix \({\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}\) of the dynamic system \(\dot{x} = {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}x\) is called D-stable.

$$\left[ {\begin{array}{*{20}c} { - r{\mathbf{\rm K}}} & {q{\mathbf{\rm K}} + {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} {\rm K}}}} \\ {q{\mathbf{\rm K}} + {\mathbf{{\rm K}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{A} }}^{\text{T}} } & { - r{\mathbf{\rm K}}} \\ \end{array} } \right] < 0$$
(15)

where \({\mathbf{\rm K}} > 0\). Furthermore, the corresponding D-stable conditions for the uncertain T–S fuzzy system (10) can be obtained by extending the conditions of (15). The conditions for the D-stability of T–S fuzzy system (10) with uncertainties can be expressed in the following lemma.

Lemma 3

[39] If there exists a common positive definite matrix\({\mathbf{\rm K}}\)such that the following conditions are satisfied, it can be said that each subsystem of the T–S fuzzy system (10) is D-stable.

$$\left[ {\begin{array}{*{20}c} { - r{\mathbf{\rm K}}} & {q{\mathbf{\rm K}} + {\mathbf{\rm K}}\left( {{\varvec{\Gamma}}_{ij} } \right)^{\text{T}} } \\ {q{\mathbf{\rm K}} + \left( {{\varvec{\Gamma}}_{ij} } \right){\mathbf{\rm K}}} & { - r{\mathbf{\rm K}}} \\ \end{array} } \right] < 0$$
(16)

Via the conditions of (16), the closed-loop poles of each dynamic matrix \({\varvec{\Omega}}_{ij}\) can be located in a circle region expressed in Definition 2. The circle region can put a lower bound on both the exponential decay rate and damping ratio of the closed-loop responses. Usually, the D-stable pole placement constraint is widely used to promote the performance for controlling practical systems.

Besides, the following effective lemma was developed in [40] to deal with the uncertainties of the control systems. It will be used to derive the sufficient conditions for the perturbed T–S fuzzy model (10) that satisfying the individual state variance constraints and D-stability constraint, simultaneously.

Lemma 2

[40] Given real compatible dimension matricesA, HandRfor any matrix\({\mathbf{X}} > 0\), ξ > 0 with\({\varvec{\Delta}}^{\text{T}} (t ){\varvec{\Delta}} (t )\le {\mathbf{I}}\)and\({\mathbf{X}} - \xi {\varvec{\Delta}} (t ){\varvec{\Delta}}^{\text{T}} (t )\ge 0\), one can find two results as follows:

$${\mathbf{H\Delta }}\left( t \right){\mathbf{R}}{ + }{\mathbf{R}}^{\text{T}} {\varvec{\Delta}}^{\text{T}} (t ){\mathbf{H}}^{\text{T}} \le \xi {\mathbf{HH}}^{\text{T}} { + }\xi^{ - 1} {\mathbf{R}}^{\text{T}} {\mathbf{R}}$$
(17)

and

$$\left( {{\mathbf{A}}{ + }{\mathbf{H\Delta }} (t ){\mathbf{R}}} \right)^{\text{T}} {\mathbf{X}}^{ - 1} \left( {{\mathbf{A}}{ + }{\mathbf{H\Delta }} (t ){\mathbf{R}}} \right) \le {\mathbf{A}}^{\text{T}} \left( {{\mathbf{X}}{ - }\xi {\mathbf{HH}}^{\text{T}} } \right)^{ - 1} {\mathbf{A}}{ + }\xi^{ - 1} {\mathbf{R}}^{\text{T}} {\mathbf{R}}$$
(18)

The performance constraints considered in this paper have been introduced as the above statements. According to the above transient and steady-state performance constraints, the purpose of this paper is to develop an approach to design a robust fuzzy controller for the perturbed T–S fuzzy system (10). In the following section, the stability conditions subject to the individual state variance constraint and pole placement constraint are derived based on the above lemmas.

3 Robust Fuzzy Controller Design with State Variance Constraint and Pole Placement Constraint

In the previous section, the definitions of the state variance constraint and pole placement constraint have been introduced. The purpose of this section is to combine state variance constraint and pole placement constraint into the stability conditions for the perturbed T–S fuzzy model (10). The sufficient stability conditions, which satisfy the state variance constraint (13) and D-stability constraint (14), for the closed-loop T–S fuzzy model (10) are given as follows.

Theorem 1

If there exists a positive definite matrix\(\overline{{\mathbf{X}}}\), and matrices\({\mathbf{T}}_{i}\)such that the following sufficient conditions are satisfied, then the closed-loop T–S fuzzy system (10) is stable, and the individual state variance constraint (13) and D-stability constraint (14) are all achieved.

$$\left[ {\begin{array}{cc} {{\varvec{\Phi}}_{ii} + {\varvec{\Phi}}_{ii}^{\text{T}} + \xi {\mathbf{H}}_{i} {\mathbf{H}}_{i}^{\text{T}} + {\mathbf{N}}_{i} {\mathbf{WN}}_{i}^{\text{T}} } & * \\ {{\mathbf{R}}_{ii} \overline{{\mathbf{X}}} } & { - \xi {\mathbf{I}}} \\ \end{array} } \right] < 0,\quad {\text{for}}\quad i = 1,2, \ldots ,r$$
(19)
$$\left[ {\begin{array}{cc} {\frac{{\left( {{\varvec{\Phi}}_{ij} + {\varvec{\Phi}}_{ij}^{\text{T}} } \right) + \left( {{\varvec{\Phi}}_{ji} + {\varvec{\Phi}}_{ji}^{\text{T}} } \right)}}{2} + \xi {\mathbf{H}}_{i} {\mathbf{H}}_{i}^{T} } & * \\ {\left( {\frac{{{\mathbf{R}}_{ij} + {\mathbf{R}}_{ji} }}{2}} \right)\overline{{\mathbf{X}}} } & { - \xi {\mathbf{I}}} \\ \end{array} } \right] < 0,\quad {\text{for}}\quad i < j$$
(20)
$$\left[ {\begin{array}{*{20}c} { - {\text{r}}^{2} \overline{{\mathbf{X}}} } & * & * \\ {{\text{q}}\overline{{\mathbf{X}}} + {\mathbf{A}}_{i} \overline{{\mathbf{X}}} + {\mathbf{B}}_{i} {\mathbf{T}}_{i} } & { - \left( {\overline{{\mathbf{X}}} - \xi {\mathbf{HH}}^{\text{T}} } \right)} & * \\ {{\mathbf{R}}_{ai} \overline{{\mathbf{X}}} + {\mathbf{R}}_{bi} {\mathbf{T}}_{i} } & 0 & { - \xi {\mathbf{I}}} \\ \end{array} } \right] < 0$$
(21)
$$\overline{{\mathbf{X}}} - {\text{diag}}\left( {\sigma_{1}^{2} , \ldots ,\sigma_{{n_{x} }}^{2} } \right) < 0$$
(22)

where\({\varvec{\Phi}}_{ij} = {\mathbf{A}}_{i} \overline{{\mathbf{X}}} {\mathbf{ + B}}_{i} {\mathbf{T}}_{j}\), \({\mathbf{T}}_{i} = {\mathbf{F}}_{i} \overline{{\mathbf{X}}}\), \({\mathbf{R}}_{ij} = {\mathbf{R}}_{ai} + {\mathbf{R}}_{bi} {\mathbf{F}}_{j}\), \(\overline{{\mathbf{X}}}\)is the upper bound of the state covariance matrix, the * is the transport element, and the circle region D is defined in Definition 2.

Proof

Because \({\mathbf{T}}_{i} = {\mathbf{F}}_{i} \overline{{\mathbf{X}}}\), the following inequality can be obtained from condition (19) by taking the Schur complement [41].

$${\mathbf{G}}_{ii} \overline{{\mathbf{X}}} + \overline{{\mathbf{X}}} {\mathbf{G}}_{ii}^{T} + \xi {\mathbf{H}}_{i} {\mathbf{H}}_{i}^{T} + \xi^{ - 1} \left( {{\mathbf{R}}_{ii} \overline{{\mathbf{X}}} } \right)^{T} \left( {{\mathbf{R}}_{ii} \overline{{\mathbf{X}}} } \right) + {\mathbf{N}}_{i} {\mathbf{WN}}_{i}^{\text{T}} < 0$$
(23)

Based on inequality (17) of Lemma 3, the following inequality can be obtained from (23) by considering the uncertainties.

$${\mathbf{G}}_{ii} \overline{{\mathbf{X}}} + \overline{{\mathbf{X}}} {\mathbf{G}}_{ii}^{T} + \left( {{\mathbf{H}}_{i} {\varvec{\Delta}}_{i} {\mathbf{R}}_{ii} \overline{{\mathbf{X}}} + \overline{{\mathbf{X}}} {\mathbf{R}}_{ii}^{T} {\varvec{\Delta}}_{i}^{T} {\mathbf{H}}_{i}^{\text{T} } } \right){ + }{\mathbf{N}}_{i} {\mathbf{WN}}_{i}^{\text{T}} < 0$$
(24)

i.e.,

$${\varvec{\Gamma}}_{ii} \overline{{\mathbf{X}}} + \overline{{\mathbf{X}}} {\varvec{\Gamma}}_{ii}^{T} + {\mathbf{N}}_{i} {\mathbf{WN}}_{i}^{\text{T}} < 0$$
(25)

Multiplying the above inequality on the left and right by \(\overline{{\mathbf{X}}}^{ - 1}\), then one can obtain

$$\overline{{\mathbf{X}}}^{ - 1} {\varvec{\Gamma}}_{ii} + {\varvec{\Gamma}}_{ii}^{T} \overline{{\mathbf{X}}}^{ - 1} + \overline{{\mathbf{X}}}^{ - 1} {\mathbf{N}}_{i} {\mathbf{WN}}_{i}^{\text{T}} \overline{{\mathbf{X}}}^{ - 1} < 0$$
(26)

Let \({\mathbf{Q}} = \overline{{\mathbf{X}}}^{ - 1}\), then condition (11) can be satisfied because \(\overline{{\mathbf{X}}}^{ - 1} {\mathbf{N}}_{i} {\mathbf{WN}}_{i}^{\text{T}} \overline{{\mathbf{X}}}^{ - 1} \ge 0\) and inequality (26) is satisfied. Thus, if condition (19) is satisfied, one can obtain that condition (11) is also satisfied. In the same way, one can also conclude that if condition (20) is satisfied, then condition (12) is also satisfied. In summary, if conditions (19) and (20) are satisfied, then the T–S fuzzy model (10) is stable because conditions (11) and (12) of Lemma 1 are satisfied.

Applying the Schur complement [41] to (21), one can obtain the following inequality due to \({\mathbf{T}}_{i} = {\mathbf{F}}_{i} \overline{{\mathbf{X}}}\).

$$- {\text{r}}\overline{{\mathbf{X}}} + \xi^{ - 1} ({\mathbf{R}}_{ii} \overline{{\mathbf{X}}} )^{\text{T}} ({\mathbf{R}}_{ii} \overline{{\mathbf{X}}} ) + \left\{ {\left( {{\text{q}} + {\mathbf{G}}_{ii} } \right)\overline{{\mathbf{X}}} } \right\}^{\text{T}} \left( {\overline{{\mathbf{X}}} - \xi {\mathbf{HH}}^{\text{T}} } \right)^{ - 1} \left\{ {\left( {{\text{q}} + {\mathbf{G}}_{ii} } \right)\overline{{\mathbf{X}}} } \right\} < 0$$
(27)

Based on inequality (18) of Lemma 3, the following condition can be obtained from (27).

$$- {\text{r}}^{2} \overline{{\mathbf{X}}} + \left\{ {\left( {{\text{q}} + {\mathbf{G}}_{ii} } \right)\overline{{\mathbf{X}}} + {\mathbf{H}}_{i} {\varvec{\Delta}}_{i} {\mathbf{R}}_{ii} \overline{{\mathbf{X}}} } \right\}^{\text{T}} \overline{{\mathbf{X}}}^{ - 1} \left\{ {\left( {{\text{q}} + {\mathbf{G}}_{ii} } \right)\overline{{\mathbf{X}}} + {\mathbf{H}}_{i} {\varvec{\Delta}}_{i} {\mathbf{R}}_{ii} \overline{{\mathbf{X}}} } \right\} < 0$$
(28)

Moreover, (28) can be rewritten as the following form.

$$- {\text{r}}^{2} \overline{{\mathbf{X}}} + \left( {q\overline{{\mathbf{X}}} + {\varvec{\Gamma}}_{ij} \overline{{\mathbf{X}}} } \right)^{T} \overline{{\mathbf{X}}}^{ - 1} \left( {q\overline{{\mathbf{X}}} + {\varvec{\Gamma}}_{ij} \overline{{\mathbf{X}}} } \right) < 0$$
(29)

Taking the Schur complement [41] to the above inequality (29) and choosing the positive define matrix \({\mathbf{\rm K}} = \overline{{\mathbf{X}}}\), then the D-stable condition (16) of Lemma 2 can be obtained. That is, the D-stability of the T–S fuzzy model (10) can be ensured if condition (21) is satisfied.

Also, the matrix \(\overline{{\mathbf{X}}}\) described in conditions (19)–(22) can be used to achieve the individual state variance constraint (13). From [42], it can be found that the steady-state covariance matrix \({\tilde{\mathbf{X}}}_{i}\) of system state x(t) for each rule satisfies the following Lyapunov equation.

$${\varvec{\Gamma}}_{ii} {\tilde{\mathbf{X}}}_{i} + {\tilde{\mathbf{X}}}_{i} {\varvec{\Gamma}}_{ii}^{\text{T}} + {\mathbf{N}}_{i} {\mathbf{WN}}_{i}^{\text{T} } = 0$$
(30)

Subtracting (30) from (25), one has

$${\varvec{\Gamma}}_{ii} \left( {\overline{{\mathbf{X}}} - {\tilde{\mathbf{X}}}_{i} } \right) + \left( {\overline{{\mathbf{X}}} - {\tilde{\mathbf{X}}}_{i} } \right){\varvec{\Gamma}}_{ii}^{\text{T}} < 0$$
(31)

From the previous statements, it is known that if conditions (19) and (20) are satisfied, then the T–S fuzzy model (10) is stable. In this case, one can obtain that the matrix \({\varvec{\Gamma}}_{ii}\) is stable. Because the matrix \({\varvec{\Gamma}}_{ii}\) is stable, the fact of \(\overline{{\mathbf{X}}} - {\tilde{\mathbf{X}}}_{i} > 0\) can be obtained from (31). For the fact \(\overline{{\mathbf{X}}} - {\tilde{\mathbf{X}}}_{i} > 0\), then the individual state variance constraint (13) can be achieved if condition (22) is satisfied. That is,

$$\left[ {{\tilde{\mathbf{X}}}} \right]_{pp} < \left[ {\overline{{\mathbf{X}}} } \right]_{pp} \le \sigma_{p}^{2}$$
(32)

Thus, if conditions (19)–(20) are satisfied, then one can find that the closed-loop T–S fuzzy model (10) is stable via Lemma 1. Furthermore, if conditions (21) and (22) are satisfied, then the T–S fuzzy model (10) also achieves the D-stability constraint (14) and individual state variance constraint (13), respectively.

It is obvious that (19) and (20) provide the conditions for the stability synthesis for the T–S fuzzy model (10) with perturbations. The characteristic of the D-stable pole placement constraint is to let all the poles of the control system be placed in the circle LMI region D defined in (14). In Theorem 4 of [43], it can be noticed that the pole placement is fundamentally related to the cases i = j and not necessary for i < j, and it suffices to locate the poles of only dominant term in the prescribed LMI region D. Applying the upper bound state covariance matrix for condition (22), the individual state variance constraint (13) of T–S fuzzy control system (10) under the stochastic behaviors with external disturbance effects can be guaranteed.

Remark 1

The advantage of the proposed design method is that the pole placement and state variance-constrained control problem for the perturbed T–S fuzzy stochastic models can be solved by solving the conditions of Theorem 1 with the LMI technique [41]. However, if the number of sub-models of the T–S fuzzy model (7) is large, it might be difficult to find a common matrix \(\overline{{\mathbf{X}}}\) for the LMI conditions of Theorem 1. Moreover, this constraint is often conservative, and it is well known that a common positive definite matrix does not exist, whereas the system is stable. To overcome this limitation, the designers can employ the relaxed stability condition approaches investigated in [12, 13, 44, 45] to extend the results of Theorem 1.

By solving the sufficient conditions provided in Theorem 1, a PDC-based fuzzy controller (9) can be designed for the T–S fuzzy system (10) to satisfy D-stability constraint (14) and individual state variance constraint (13). For expressing the applicability and effectiveness of the proposed fuzzy controller design approach, a multiple performance-constrained control problem for a nonlinear lift-feedback-fin system is introduced in the next section.

4 Applications to a Nonlinear Lift-Feedback-Fin System

In this section, two numerical examples are provided to show the practicability of the proposed fuzzy control approach. For considering the nonlinear lift-feedback-fin system, its dynamic equation is given in (3a). Its corresponding perturbed T–S fuzzy model is introduced in (4a). According to the perturbed T–S fuzzy model (4a) of the nonlinear lift-feedback-fin system, one can design the robust fuzzy controller by solving the sufficient conditions of Theorem 1. Then, the fuzzy controller can be obtained to guarantee the achievement of individual state variance constraint (13) and D-stability constraint (14), simultaneously.

For the T–S fuzzy model (4a) for the lift-feedback-fin system, two examples are presented in this section for verifying the effectiveness and applicability of the proposed fuzzy controller design method. In the first example, the circle LMI region of the D-stable pole placement constraint is adjusted to discuss transient behaviors of the closed-loop system. In the second example, the fuzzy controller obtained in the first example is compared with the controller developed in [37] to verify the advantage of the proposed fuzzy controller design method. For the beginning of the simulations, the intensity of the external disturbance is defined as \({\mathbf{W}} = 1\), and the individual state variance constraints are given for each state as follows:

$$\sigma_{1}^{2} = 0.1,\quad \sigma_{2}^{2} = 0.2$$
(33)

Example 1

The purpose of this example is to discuss the effect of the pole location for the transient behaviors of the closed-loop T–S fuzzy system. That is, the circle LMI region D(q, r) of the D-stable pole placement constraint in the proposed controller design method is adjusted to investigate the transient behaviors of the closed-loop system. First, the simulation results of the adjustment of the center for the circle region are presented. For the different center q, the control gains of the fuzzy controller (9) can be solved from Theorem 1. By setting r = 3, the control gains for q = − 4, q = − 6 and q = − 8 are shown in Table 1. Therefore, the PDC-based fuzzy controller can be obtained from Table 1 as follows:

$$u\left( t \right) = \sum\limits_{i,\ell = 1}^{3} {h_{i} \left( {x\left( t \right)} \right)h_{\ell } \left( {x\left( t \right)} \right){\mathbf{F}}_{i\ell } } x\left( t \right)$$
(34)
Table 1 Control gains for the different center q of the circle region D in (14)
Full size table

From Table 1, it can be found that the control gain is bigger when the center is adjusted to the more negative location. According to the different center q, all the poles of each subsystem can be found in Table 2, where \({\text{eig}}\left( {{\varvec{\Gamma}}_{ij} } \right)\) denotes the poles of the closed-loop state matrix \({\varvec{\Gamma}}_{ij}\) with setting \({\varvec{\Delta}}_{i} \left( t \right) = 1\). From Table 2, it can be found that the poles are pulled to the more negative location if the center is chosen more negative. Furthermore, it can also be found that the poles have an imaginary part in the case of (q, r) = (− 8, 3), and it may increase the oscillation of the response. The location of the poles in the circle region from the different centers is presented in Fig. 3. Based on the above results, the comparisons of system responses for the different centers are presented in Figs. 4 and 5. In these figures, it can be found that the transient behaviors obtained from the regions (q, r) = (−6, 3) and (q, r) = (− 8, 3) are better than that of the region (q, r) = (− 4, 3). Moreover, the responses of the region (q, r) = (− 6, 3) can obtain the most proper transient behaviors with considering the settling time and the maximum overshoot.

Table 2 Pole locations for the different center q of the circle region D in (14)
Full size table
Fig. 3
figure 3

Location comparison of the poles for the different centers

Full size image
Fig. 4
figure 4

Response of the state x1(t) for the different centers

Full size image
Fig. 5
figure 5

Response of the state x2(t) for the different centers

Full size image

Secondly, the simulation results of the adjustment of the radius for the circle region are presented. By setting the same center q, the control gains of the fuzzy controller (9) for the different radii can be solved from Theorem 1. By setting q = − 6, the control gains for r = 1, r = 3 and r = 5 are shown in Table 3. From Table 3, it can be found that the control gains are bigger when the radius is adjusted to a smaller region. According to the different radius r, all the poles of each subsystem can be found in Table 4. From Table 4, it can be found that the poles are pulled to the more negative location if the designer chooses a smaller radius. However, it can also be found that the poles have an imaginary part in the case of (q, r) = (− 6, 1), and it may increase the oscillation of the response. The location of the poles in the circle region from the different radii is presented in Fig. 6. Based on the above results, the comparisons of system responses between the different radii are presented in Figs. 7 and 8. In Figs. 7 and 8, it can be found that the transient behaviors obtained from the regions (q, r) = (− 6, 1) and (q, r) = (− 6, 3) are better than that of the region (q, r) = (− 6, 5). Moreover, the responses of the region (q, r) = (− 6, 3) provide better transient behaviors than the results of the region (q, r) = (− 6, 1).

Table 3 Control gains for the different radius r of the circle region D in (14)
Full size table
Table 4 Pole locations for the different radius r of the circle region D in (14)
Full size table
Fig. 6
figure 6

Location comparison of the poles for the different radiuses

Full size image
Fig. 7
figure 7

Response of the state x1(t) for the different radiuses

Full size image
Fig. 8
figure 8

Response of the state x2(t) for the different radiuses

Full size image

From the above two simulation results of the adjustment for the circle region, it can be concluded that the controller obtained by choosing the region (q, r) = (− 6, 3) is the best choice for the proposed design method. Thus, the fuzzy controller by setting the region (q, r) = (− 6, 3) is applied in Example 2 to compare with the controller design method developed in [37].

Example 2

In this example, the proposed fuzzy controller design method is compared with the fuzzy control approach developed in [37]. From Example 1, we choose the circle region (q, r) = (− 6, 3) for the D-stable pole placement constraint. Then, the positive definite matrix \(\overline{{\mathbf{X}}}\) and feedback gains \({\mathbf{F}}_{ij}\) can be obtained by solving the sufficient conditions (19)–(24) via MATLAB LMI-Toolbox as follows:

$$\overline{{\mathbf{X}}} = \left[ {\begin{array}{*{20}c} {0.0092} & { - 0.0374} \\ { - 0.0374} & {0.1829} \\ \end{array} } \right]$$
(35)
$${\mathbf{F}}_{ 1 1} = 10^{7} \times \left[ {\begin{array}{*{20}c} { - 9. 4 9 9 9} & { - 3.6 0 8 6} \\ \end{array} } \right]$$
(36a)
$${\mathbf{F}}_{21} = 10^{7} \times \left[ {\begin{array}{*{20}c} { - 9. 4 7 9 3} & { - 3.6 0 3 4} \\ \end{array} } \right]$$
(36b)
$${\mathbf{F}}_{31} = 10^{7} \times \left[ {\begin{array}{*{20}c} { - 9. 4 7 0 4} & { - 3.6 0 2 6} \\ \end{array} } \right]$$
(36c)
$${\mathbf{F}}_{12} = 10^{7} \times \left[ {\begin{array}{*{20}c} { - 9. 4 8 6 1} & { - 3. 5 8 9 6} \\ \end{array} } \right]$$
(36d)
$${\mathbf{F}}_{22} = 10^{7} \times \left[ {\begin{array}{*{20}c} { - 9. 4 7 9 2} & { - 3. 5 8 9 6} \\ \end{array} } \right]$$
(36e)
$${\mathbf{F}}_{32} = 10^{7} \times \left[ {\begin{array}{*{20}c} { - 9. 4 7 2 4} & { - 3. 5 8 9 6} \\ \end{array} } \right]$$
(36f)
$${\mathbf{F}}_{13} = 10^{7} \times \left[ {\begin{array}{*{20}c} { - 9. 4 8 6 1} & { - 3. 5 7 5 9} \\ \end{array} } \right]$$
(36g)
$${\mathbf{F}}_{23} = 10^{7} \times \left[ {\begin{array}{*{20}c} { - 9. 4 7 9 2} & { - 3. 5 7 5 9} \\ \end{array} } \right]$$
(36h)
$${\mathbf{F}}_{33} = 10^{7} \times \left[ {\begin{array}{*{20}c} { - 9. 4 7 2 4} & { - 3. 5 7 5 9} \\ \end{array} } \right]$$
(36i)

In order to verify the advantage of the proposed fuzzy control method, it is compared with the fuzzy control approach developed in [37]. Considering the T–S fuzzy model (4a, b) for the lift-feedback-fin system (3a, b), the fuzzy control gains solved by the methodology of [37] can be shown as follows:

$${\mathbf{F}}_{11} = \left[ {\begin{array}{*{20}c} {147.0585} & {69.0424} \\ \end{array} } \right]$$
(37a)
$${\mathbf{F}}_{21} = \left[ {\begin{array}{*{20}c} {146.1067} & {69.0424} \\ \end{array} } \right]$$
(37b)
$${\mathbf{F}}_{31} = \left[ {\begin{array}{*{20}c} {145.1549} & {69.0424} \\ \end{array} } \right]$$
(37c)
$${\mathbf{F}}_{12} = \left[ {\begin{array}{*{20}c} {147.0585} & {67.1293} \\ \end{array} } \right]$$
(37d)
$${\mathbf{F}}_{22} = \left[ {\begin{array}{*{20}c} {146.1067} & {67.1293} \\ \end{array} } \right]$$
(37e)
$${\mathbf{F}}_{32} = \left[ {\begin{array}{*{20}c} {145.1549} & {67.1293} \\ \end{array} } \right]$$
(37f)
$${\mathbf{F}}_{13} = \left[ {\begin{array}{*{20}c} {147.0585} & {65.2162} \\ \end{array} } \right]$$
(37g)
$${\mathbf{F}}_{23} = \left[ {\begin{array}{*{20}c} {146.1067} & {65.2162} \\ \end{array} } \right]$$
(37h)
$${\mathbf{F}}_{33} = \left[ {\begin{array}{*{20}c} {145.1549} & {65.2162} \\ \end{array} } \right]$$
(37i)

For applying the fuzzy control gains (36a–i) and (37a–i), the corresponding PDC-based fuzzy controllers can be obtained from (34).

In the simulations, the initial condition is selected as \(x\left( 0 \right) = \left[ {\begin{array}{*{20}c} {\frac{\pi }{18}} & 0 \\ \end{array} } \right]\) and the simulation time is set as 60 s. Applying the fuzzy controller (34) with control gains (36a–i) and (37a–i), the simulation responses of the system states are shown in Figs. 9 and 10. It can be found that the proposed robust fuzzy controller provides a better robust performance under the effect of the external disturbance. Moreover, it can also be found that the proposed robust fuzzy controller provides a better transient behavior because the pole placement constraint is considered in the proposed fuzzy control method.

Fig. 9
figure 9

Comparison of the responses of state x1(t) for Example 2

Full size image
Fig. 10
figure 10

Comparison of the responses of state x2(t) for Example 2

Full size image

For checking the state variance constraints, the variance values of system states obtained by the simulation results of the proposed fuzzy control method are given as follows:

$${\text{var}}\left( {x_{1} } \right) = 0.0824,\quad {\text{var}}\left( {x_{2} } \right) = 0.1820$$
(38)

Besides, the following state variance values can be obtained from the simulation results of the method developed in [37].

$${\text{var}}\left( {x_{1} } \right) = 8.2712,\quad {\text{var}}\left( {x_{2} } \right) = 4.1134$$
(39)

The state variance values of (38) are both suppressed under the given constraints σ 21  = 0.1 and σ 22  = 0.2. However, the state variance values of (39) cannot satisfy the specified variance constraints. Therefore, the proposed fuzzy controller design approach provides a better choice for the nonlinear lift-feedback-fin system to control the rolling motion of the ship and to achieve stability, individual state variance constraint and pole placement constraint, simultaneously.

5 Conclusions

In this paper, a robust fuzzy controller design methodology has been investigated for achieving multiple performance constraints for the nonlinear lift-feedback-fin systems modeled by the perturbed T–S fuzzy model. The performance constraints considered in this paper include the stability constraint, individual state variance constraint, and the pole placement constraint. Some sufficient conditions were derived to achieve the above multiple performance constraints. By using the LMI technique to solve these sufficient conditions, a robust fuzzy controller can be designed subject to multiple performance constraints for the perturbed T–S fuzzy models. Finally, the proposed robust fuzzy control method was employed to control a nonlinear lift-feedback-fin system to verify the practicability and applicability. In the future, the proposed design method can be extended to the discrete-time nonlinear stochastic systems. Moreover, the sufficient conditions developed in this paper can be relaxed, and the other performance requirement can be affiliated in the future.